CC1 2021 2022
Télécharger le CC1 2021 2022 en pdf
Page 1 : CorrectionCC1Panorama sur la Physique21 Octobre 2021 — PréIng1Durée : 45 minutes 1h en cas de tiers tempsConsignes :• les documents sont interdits ;• tous les objets électroniques calculatrice, téléphone, tablette, ordinateur de même que les montres con-nectées sont interdits ;• les déplacements et les échanges sont interdits.Instructions pour répondre :• vérifier que le sujet est composé de 8 pages ;• Veillez à ne pas dégrafer les feuilles ;• chaque question ne comporte qu’une seule réponse vraie ;• il n’y a pas de point négatif pour une mauvaise réponse ;• remplir en noir la case correspondant à la bonne réponse ;• utiliser un crayon à papier pour colorier les cases et faire les schémas ;• une case simplement cochée ne sera pas comptabilisée.IdentificationVeuillez coder votre numéro d’étudiant à gauche, et compléter la case à droite. Ce numéro se trouve après votredate de naissance sur votre carte étudiante. La première colonne code le premier chiffre, . . .01234567890123456789012345678901234567890123456789012345678901234567890123456789Nom et prénom :. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .Groupe :. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
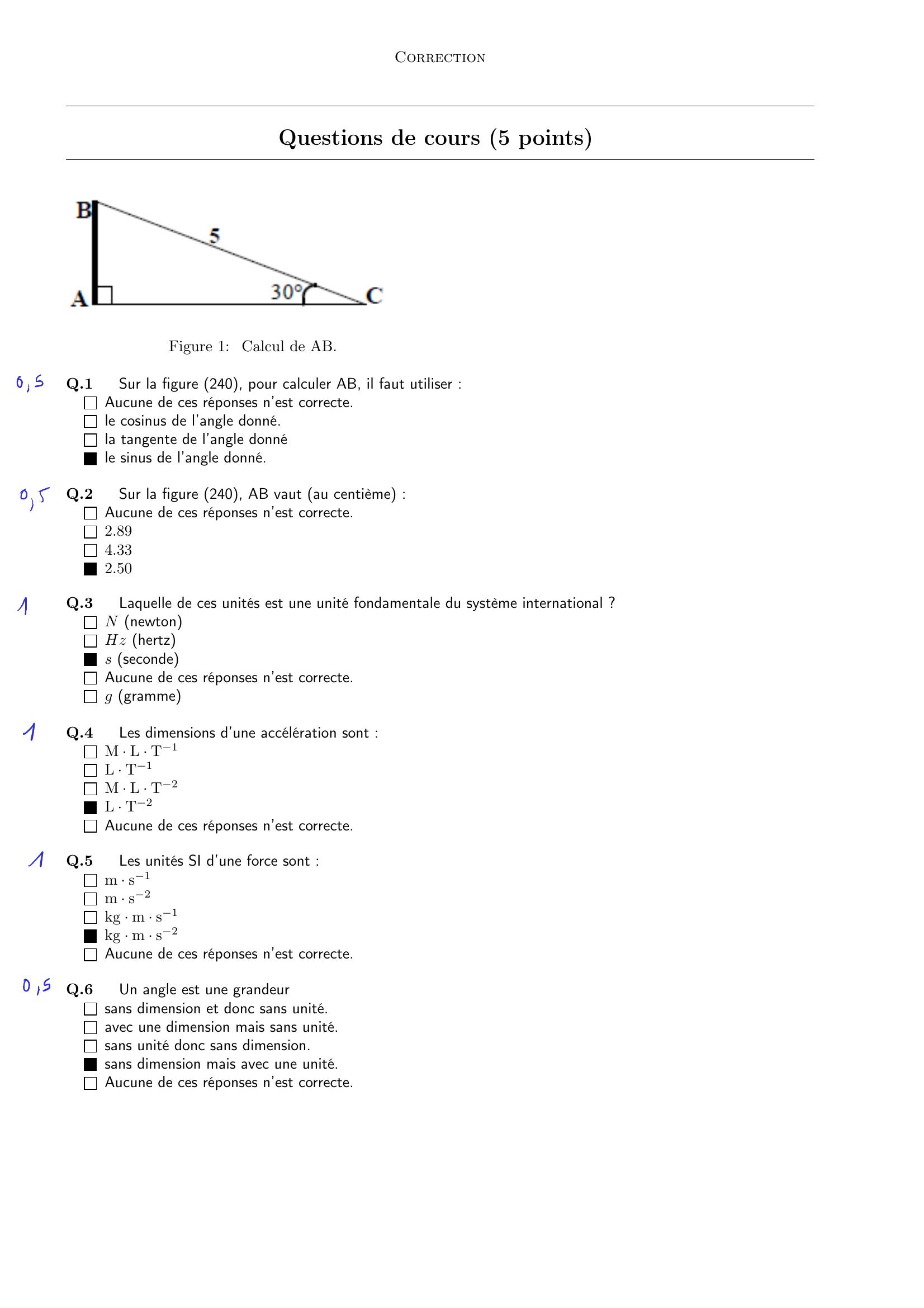
Page 2 : CorrectionQuestions de cours 5 pointsFigure 1: Calcul de AB.Q.1Sur la figure 240, pour calculer AB, il faut utiliser :Aucune de ces réponses n’est correcte.le cosinus de l’angle donné.la tangente de l’angle donnéle sinus de l’angle donné.Q.2Sur la figure 240, AB vaut au centième :Aucune de ces réponses n’est correcte.2.894.332.50Q.3Laquelle de ces unités est une unité fondamentale du système international ?N newtonHz hertzs secondeAucune de ces réponses n’est correcte.g grammeQ.4Les dimensions d’une accélération sont :M ¨ L ¨ T1L ¨ T1M ¨ L ¨ T2L ¨ T2Aucune de ces réponses n’est correcte.Q.5Les unités SI d’une force sont :m ¨ s1m ¨ s2kg ¨ m ¨ s1kg ¨ m ¨ s2Aucune de ces réponses n’est correcte.Q.6Un angle est une grandeursans dimension et donc sans unité.avec une dimension mais sans unité.sans unité donc sans dimension.sans dimension mais avec une unité.Aucune de ces réponses n’est correcte.
Page 3 : CorrectionQ.7Laquelle de ces unités est une unité fondamentale du système international ?Aucune de ces réponses n’est correcte.Pa pascalg grammeJ joulekg kilogramme
Page 4 : CorrectionExercice 1 - Poussée d’Archimède 7 pointsQ.82 pointsLa poussée d’Archimède PA est une force qui est fonction du volume du corps immergé V , de la masse volumique ρdu fluide et de l’accélération de pesanteur g.On exprimera cette force PA sous la forme d’une formule d’équation : PA “ CV αρβgγ, avec C une constante sansdimension.À l’aide d’une analyse dimensionnelle, trouver que les coefficients valent :α “ 3, β “ 1, γ “ 1α “ 1, β “ 0, γ “ 1α “ 53, β “ 1, γ “ 1α “ 1, β “ 1, γ “ 1Aucune de ces réponses n’est correcte.Q.91 pointLa dimension de ρ est en effet donnée par :M ¨ LM ¨ L3M ¨ L3M ¨ L2Aucune de ces réponses n’est correcte.Q.101 pointLa dimension de g est en effet donnée par :M ¨ L ¨ T1L ¨ T1Aucune de ces réponses n’est correcte.L ¨ T2M ¨ L ¨ T2
Page 5 : CorrectionQ.113 pointsDétailler ci-dessous le calcul qui vous a permis d’obtenir les coefficients α, β et γ.-0.5-1-23Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 6 : CorrectionExercice 2 - Période de rotation d’une galaxie 8 pointsQ.122 pointsUne galaxie tourne sur elle-même avec une période T. On suppose que cette période dépend de la constante degravitation G et de la masse volumique moyenne de la galaxie ρ.On cherche l’expression de T en posant que T “ kGαρβ avec k une constante sans dimension.À l’aide d’une analyse dimensionnelle, trouver que les coefficients valent :α “ 12 et β “ 1α “ 12 et β “ 12α “ 12 et β “ 12Aucune de ces réponses n’est correcte.α “ 1 et β “ 1Q.132 pointsLa dimension de G est en effet donnée par :M1 ¨ L3 ¨ T2M1 ¨ L2 ¨ T2Aucune de ces réponses n’est correcte.M1 ¨ L3 ¨ T1M ¨ L3 ¨ T2
Page 7 : CorrectionQ.144 pointsDétailler ci-dessous le calcul qui vous a permis d’obtenir les coefficients α et β.-0.5-1-2-34Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 8 : Correction