CC2 2021 2022
Télécharger le CC2 2021 2022 en pdf
Page 1 : CorrectionCC2Électromagnétisme02 Décembre 2021 — PréIng2Durée : 1h30 2h en cas de tiers tempsConsignes :• les documents sont interdits ;• tous les objets électroniques calculatrice, téléphone, tablette, ordinateur... de même les montres connec-tées sont interdits ;• les déplacements et les échanges sont interdits.Instructions pour répondre :• vérifier que le sujet est composé de 8 pages ;• veillez à ne pas dégrafer les feuilles ;• chaque question ne comporte qu’une seule réponse vraie ;• remplir complétement en noir la case correspondant à la bonne réponse ;• utiliser un crayon à papier pour colorier les cases et faire les schémas ;• une case simplement cochée ne sera pas comptabilisée.IdentificationVeuillez coder votre numéro d’étudiant à gauche, et compléter la case à droite. Ce numéro se trouve après votredate de naissance sur votre carte étudiante. La première colonne code le premier chiffre, . . .01234567890123456789012345678901234567890123456789012345678901234567890123456789Nom et prénom :. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Groupe :. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 2 : CorrectionQuestions de cours 3 pointsQ.1La circulation C du champ électrostatique ÝÑE est donnée par :C “ijSÝÑE . ÝÑdSC “¡VÝÑE . ÝÑdVC “ż BAÝÑE . ÝÑdlAucune de ces réponses n’est correcte.Q.2Puisque le champ électrostatique ÝÑE est à circulation conservative, on définit la fonction potentiel électro-statique par :ÝÑE “ ÝÝÑgradVÝÑE “ ÝÝÑgradVÝÑV “ ÝÝÑgradEAucune de ces réponses n’est correcte.Q.3Le théorème de Gauss énonce que le flux Φ du champ ÝÑE , à travers une surface fermée S est relié à la chargeintérieure qint, contenue dans le volume V délimité par la surface S par :Φ “ijSÝÑE ¨ ÝÑdS “ qintΦ “¡VÝÑE ¨ ÝÑdV “ qint0Φ “ijSÝÑE ¨ ÝÑdS “ qint0Aucune de ces réponses n’est correcte.Q.4La variation dV d’un champ scalaire V pMq est donnée par dV pMq “ ÝÝÑgradV ¨ dÝÝÑOM, où ÝÝÑgradV est legradient du champ scalaire V. Le vecteur gradient ÝÝÑgradV est donc :tangent à la surface équipotentielle passant par M de la fonction scalaire V pMq.un vecteur directeur de la surface équipotentielle passant par M de la fonction scalaire V pMq.normal à la surface équipotentielle passant par M de la fonction scalaire V pMq.Aucune de ces réponses n’est correcte.Q.5Dans le cas d’une distribution volumique de charges, le potentiel électrique est :défini sur la surface chargée et il n’est pas continu à la traversée de la surface.n’est pas défini sur les points où se trouvent les charges.défini et continu en tout point de l’espace.Aucune de ces réponses n’est correcte.Q.6L’énergie potentielle d’interaction entre une charge q et un champ électrostatique ÝÑE créant le potentiel Vest :Ep “ qV KEp “ qE KEp “ qV KAucune de ces réponses n’est correcte.
Page 3 : CorrectionExercice 1 - Cylindre chargé en volume 9 pointsOn considère une distribution volumique uniforme de charges, répartie dans le volume d’un cylindre plein de rayon Ret de longueur infinie. La densité volumique de charges ρ est constante et positive.Q.71 point Dans la base de coordonnées cylindriques, le vecteur champ électrostatique ÝÑE créé par cettedistribution est :dirigé selon pOzq.de direction quelconque.radiale.appartient aux plans d’antisymétrie.Aucune de ces réponses n’est correcte.Q.81 point Déterminer l’expression du champ électrostatique ÝÑE prq, à la distance r de l’axe du cylindre, parapplication du théorème de Gauss, dans le cas où le point M est à l’extérieur du cylindre :Eprq “ ρR220rEprq “ ρr20Eprq “ ρR240rEprq “ ρR230rAucune de ces réponses n’est correcte.Q.91 point Déterminer l’expression du champ électrostatique ÝÑE prq, à la distance r de l’axe du cylindre, parapplication du théorème de Gauss, dans le cas où le point M est à l’intérieur du cylindre :Eprq “ ρR220rEprq “ ρr220Eprq “ ρr20Eprq “ ρr0Aucune de ces réponses n’est correcte.Q.101 point Le potentiel électrostatique, en tout point M, à l’intérieur du cylindre a pour expression :V prq “ ρR220 ln r constanteV prq “ ρr240 constanteV prq “ ρr240 constanteV prq “ ρr20 constanteAucune de ces réponses n’est correcte.Q.111 point Le potentiel électrostatique, en tout point M, à l’extérieur du cylindre a pour expression :V prq “ ρR20 ln r constanteV prq “ ρR220 ln r constanteV prq “ ρR20r constanteV prq “ ρr240 constanteAucune de ces réponses n’est correcte.Q.121 point Si on fixe V pr “ Rq “ 0, le potentiel électrostatique, en tout point M, à l’intérieur du cylindreest tel que la constante vaut :constante “ ρR240constante “ ρR20constante “ ρR240constante “ ρR220 ln RAucune de ces réponses n’est correcte.
Page 4 : CorrectionQ.13Retrouver l’expression du champ électrostatique ÝÑE par application du théorème de Gauss, à l’intérieur età l’extérieur du cylindre.-0.5-12Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
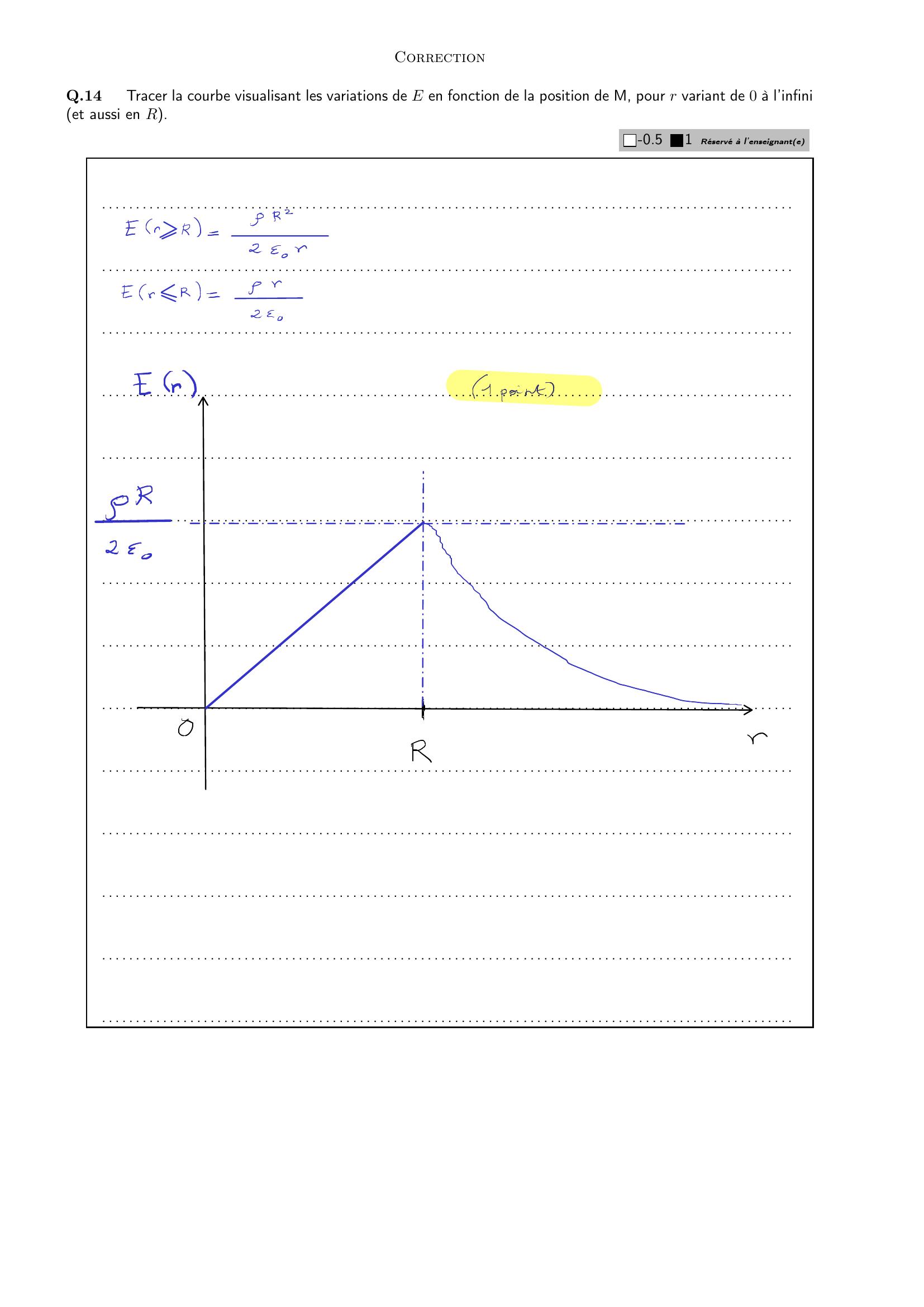
Page 5 : CorrectionQ.14Tracer la courbe visualisant les variations de E en fonction de la position de M, pour r variant de 0 à l’infiniet aussi en R.-0.51Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 6 : CorrectionExercice 2 - Potentiel pour une sphère 8 pointsOn considère une sphère de rayon R et de centre O ayant une distribution volumique de charges de densité ρ uniforme.Q.151 point Le champ électrostatique ÝÑE créé par cette distribution est alors :défini en tout point de l’espace, sauf à la traversée de la surface chargée de la sphère.défini en tout point de l’espace.défini en tout point de l’espace, sauf sur les points de la distribution.Aucune de ces réponses n’est correcte.Q.161 point La direction du champ électrostatique ÝÑE créé par cette distribution est radiale car :tous les plans pM, ÝÑur, ÝÑuθq et pM, ÝÑuθ, ÝÑuφq sont des plans de symétrie.tous les plans pM, ÝÑur, ÝÑuθq et pM, ÝÑuθ, ÝÑuzq sont des plans de symétrie.tous les plans passant par O et par M sont des plans de symétrie.Aucune de ces réponses n’est correcte.Q.171 point En utilisant le théorème de Gauss, on trouve que le champ électrostatique ÝÑE vaut :r ă R : ÝÑE “ ρr30ÝÑurr ă R : ÝÑE “ ρr0ÝÑurr ă R : ÝÑE “ ρr30ÝÑurAucune de ces réponses n’est correcte.Q.181 point En utilisant le théorème de Gauss, on trouve que le champ électrostatique ÝÑE vaut :r ą R : ÝÑE “ ρR330r2 ÝÑurr ą R : ÝÑE “ ρR30r2 ÝÑurr ą R : ÝÑE “ ρR330r2 ÝÑurAucune de ces réponses n’est correcte.Q.191 point Le potentiel électrostatique V créé par cette distributionest défini et continu en tout point de l’espace, sauf à la traversée de la surface chargée de la sphère.est défini et continu en tout point de l’espace.n’est pas défini sur les points où se trouve les charges.Aucune de ces réponses n’est correcte.
Page 7 : CorrectionQ.20À partir de l’expression de ÝÑE , donner l’expression du potentiel électrostatique V avec le potentiel nul àl’infini pour r ă R et r ą R.-0.5-12Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
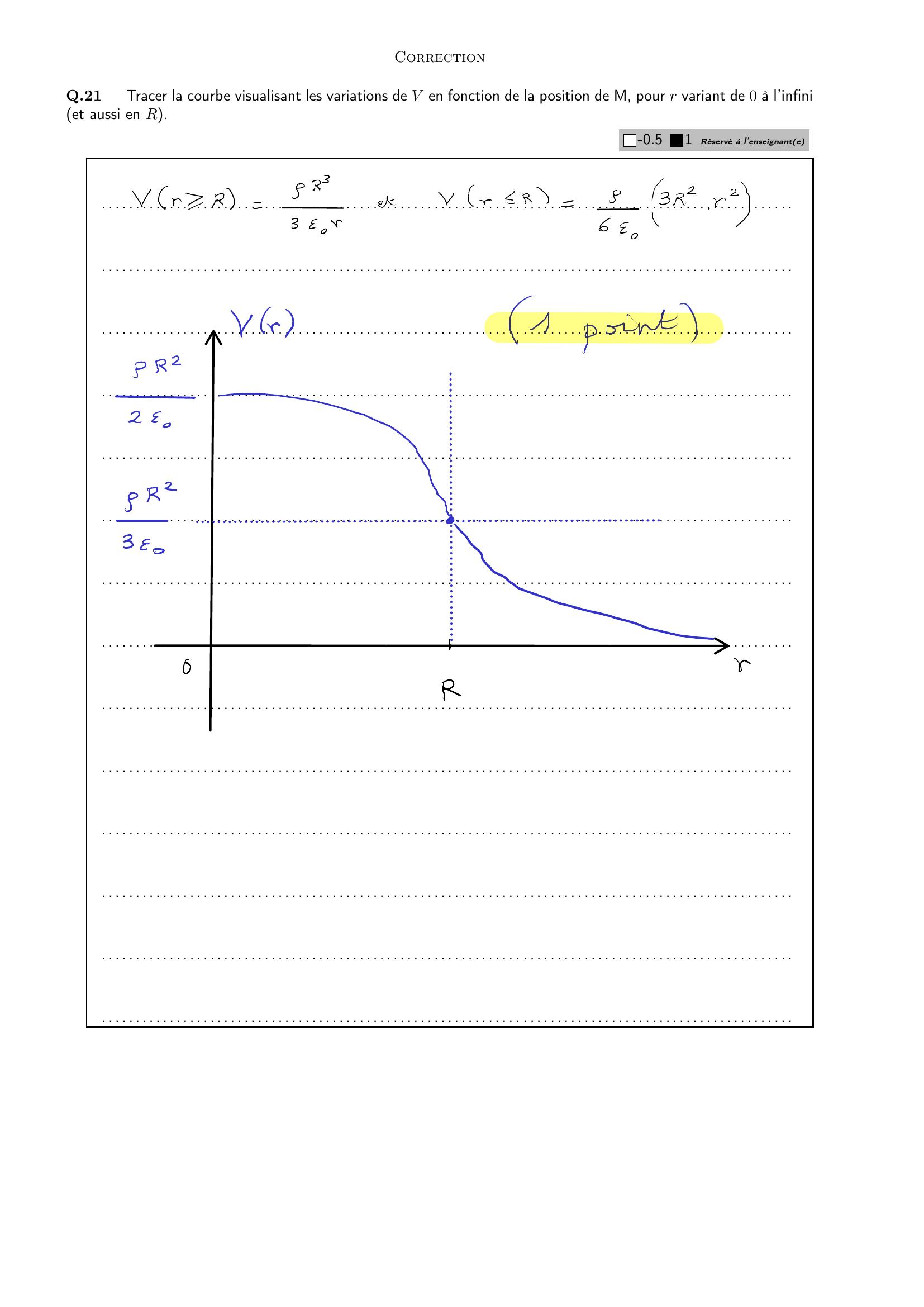
Page 8 : CorrectionQ.21Tracer la courbe visualisant les variations de V en fonction de la position de M, pour r variant de 0 à l’infiniet aussi en R.-0.51Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .