CC3 2022 2023 Correction
Télécharger le CC3 2022 2023 Correction en pdf
Page 1 : CorrectionCC3Électromagnétisme26 Janvier 2023 — PréIng2Durée : 1h30 2h en cas de tiers tempsSont interdits :— les documents ;— tous les objets électroniques calculatrice, téléphone, tablette, ordinateur... de mêmeque les montres connectées ;— les déplacements et les échanges.Consignes :1. Vérifiez que le sujet est composé de 10 pages et 19 questions ;2. Seules les dernières feuilles doivent être rendues ;3. Les questions à rédiger, sur les dernières feuilles, sont indiquées par une icône ♣;4. Remplir complètement au stylo noir la case correspondant à la bonne réponse ;5. Complétez avec vos nom, prénom et groupe cette dernière feuille dès le début officiel del’épreuve ;6. Chaque question ne comporte qu’une seule réponse ;7. Il n’y a pas de point négatif pour une mauvaise réponse ;8. Une case simplement cochée ne sera pas comptabilisée.Le barème est donné à titre indicatif.
Page 2 : CorrectionQuestions de cours 5 pointsQuestion 11 point La loi de Biot et Savart permet de calculer le champ magnétiqueÝÑB en M, pour un fil filiforme parcouru par un courant I. Elle s’énonce :A ÝÑBpMq “¿PP filµ0I4πÝÑdl ^ ÝÝÑPMPM 3B ÝÑBpMq “¿PP filµ0I4πÝÑdl ^ ÝÝÑPMPM 2C ÝÑBpMq “¿PP filµ0I4πÝÑdl ^ ÝÝÑMPMP 2D Aucune de ces réponses n’est correcte.Question 21 point Le théorème d’Ampère relie le champ magnétique ÝÑB et l’intensitédes courants Ii comptés algébriquement qui traversent toute surface ouverte S, s’appuyant surun contour Γ. Il s’énonce :A¿ΓÝÑB ¨ ÝÑdl “ µ0ÿiIiB£ΓÝÑB ¨ ÝÑdl “ µ0ÿiIiC¿ΓÝÑB ^ ÝÑdl “ µ0ÿiIiD£ΓÝÑB ¨ ÝÑdS “ µ0ÿiIiE Aucune de ces réponses n’est correcte.Question 31 point Soient la densité de courant ÝÑj et la densité volumique de charges ρ,l’équation locale de conservation de la charge électrique s’écrit alors :A div ÝÑj BρBt “ 0B div ÝÑj ε0BρBt “ 0C div ÝÑj ε0BρBt “ 0D div ÝÑj BρBt “ 0E Aucune de ces réponses n’est correcte.Question 41 point Les quatre équations de Maxwell pour le champ éléctromagnétiquesont :A div ÝÑE “ ρε0; div ÝÑB “ 0 ; ÝÑrotÝÑE “ BÝÑBBt ; ÝÑrotÝÑB “ µ0ÝÑj µ0ε0BÝÑEBtB div ÝÑE “ ρε0; div ÝÑB “ 0 ; ÝÑrotÝÑE “ BÝÑBBt ; ÝÑrotÝÑB “ µ0ÝÑj µ0ε0BÝÑEBtC div ÝÑE “ ρ ; div ÝÑB “ 0 ; ÝÑrotÝÑE “ BÝÑBBt ; ÝÑrotÝÑB “ µ0ÝÑj µ0ε0BÝÑEBtD Aucune de ces réponses n’est correcte.Question 51 point La loi d’Ohm locale, pour un conducteur de conductivité γ, s’écrit :A ÝÑj “ γ2 ÝÑEB ÝÑj “ γ ÝÑEC ÝÑj “ÝÑEγD Aucune de ces réponses n’est correcte.
Page 3 : CorrectionPavé infini 2 pointsUn pavé d’épaisseur e et de dimensions infinies, est parcouru par un courant uniforme etconstant, de vecteur densité de courant ÝÑj constant, comme détaillé sur la figure ci-dessous.On repère un point M de l’espace dans la base de coordonnées cylindriques : pÝÑu x, ÝÑu y, ÝÑu zq. Leplan Oxy est le plan médian du pavé ; l’axe Oz est perpendiculaire à ses faces.Le courant uniforme circule dans le sens de l’axe pOyq orienté.Soit ÝÑBpMq, le champ magnétique créé par cette distribution de courants en tout point Mpx, y, zqde l’espace.Question 61 point En cherchant les plans de symétrie et d’antisymétrie du champmagnétique, on trouve que :A Le champ magnétique ÝÑBpMq est per-pendiculaire au plan parallèle à pxOzqen M.B Le champ magnétique ÝÑBpMq est per-pendiculaire au plan pyOzq en M.C Le plan parallèle au plan pyOzq en Mest un plan d’antisymétrie.D Le plan parallèle au plan pxOzq en Mest un plan de symétrie.E Aucune de ces réponses n’est correcte.Question 71 point De plus, en regardant les invariances, le vecteur champ magnétiqueÝÑBpMq s’écrit :A ÝÑBpMq “ BpzqÝÑu xB ÝÑBpMq “ BpzqÝÑu yC ÝÑBpMq “ Bpx, yqÝÑu zD ÝÑBpMq “ Bpx, yqÝÑu xE Aucune de ces réponses n’est correcte.
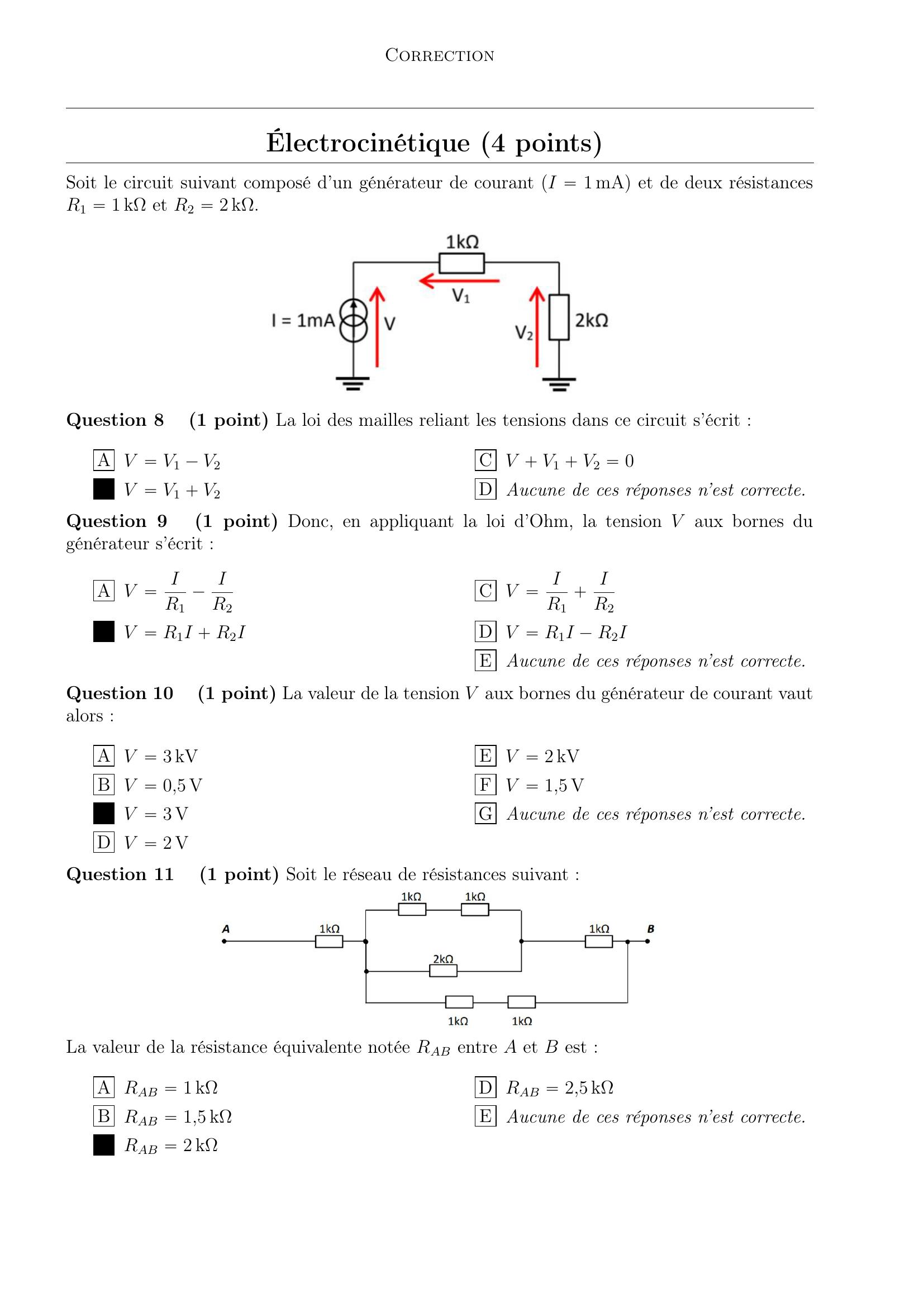
Page 4 : CorrectionÉlectrocinétique 4 pointsSoit le circuit suivant composé d’un générateur de courant I “ 1 mA et de deux résistancesR1 “ 1 kΩet R2 “ 2 kΩ.Question 81 point La loi des mailles reliant les tensions dans ce circuit s’écrit :A V “ V1 V2B V “ V1 V2C V V1 V2 “ 0D Aucune de ces réponses n’est correcte.Question 91 point Donc, en appliquant la loi d’Ohm, la tension V aux bornes dugénérateur s’écrit :A V “ IR1 IR2B V “ R1I R2IC V “ IR1 IR2D V “ R1I R2IE Aucune de ces réponses n’est correcte.Question 101 point La valeur de la tension V aux bornes du générateur de courant vautalors :A V “ 3 kVB V “ 0,5 VC V “ 3 VD V “ 2 VE V “ 2 kVF V “ 1,5 VG Aucune de ces réponses n’est correcte.Question 111 point Soit le réseau de résistances suivant :La valeur de la résistance équivalente notée RAB entre A et B est :A RAB “ 1 kΩB RAB “ 1,5 kΩC RAB “ 2 kΩD RAB “ 2,5 kΩE Aucune de ces réponses n’est correcte.
Page 5 : CorrectionFil infini 5 pointsOn considère un fil de longueur infinie, confondu avec l’axe pOzq. Il est parcouru par un courantI constant orienté vers les z croissants.On repère un point M de l’espace dans la base de coordonnées cylindriques : pÝÑu r, ÝÑu θ, ÝÑu zq.On cherche l’expression du champ magnétique ÝÑBpMq généré par ce fil au point M.Question 121 point En regardant les invariances, le vecteur champ magnétique ÝÑBpMqne dépend que de :A θB zC φD rE Aucune de ces réponses n’est correcte.Question 131 point Du fait des symétries, le vecteur champ magnétique ÝÑBpMq s’écrit :A ÝÑBpMq “ BpθqÝÑu θB ÝÑBpMq “ BprqÝÑu θC ÝÑBpMq “ BpzqÝÑu zD ÝÑBpMq “ BpzqÝÑu rE Aucune de ces réponses n’est correcte.Question 141 point En utilisant le théorème d’Ampère, on peut écrire le vecteur champmagnétique ÝÑBpMq :A ÝÑBpMq “ µ0IπzÝÑu rB ÝÑBpMq “ µ0IπzÝÑu θC ÝÑBpMq “ µ0I2πrÝÑu θD ÝÑBpMq “ 2µ0IπrÝÑu zE Aucune de ces réponses n’est correcte.Question 15 ♣2 points Détailler les calculs permettant d’obtenir l’expression du champmagnétique ÝÑBpMq.
Page 6 : CorrectionSpire 6 pointsUne spire de centre O et de rayon R est parcourue par un courant d’intensité I constante cf.figure ci-dessous.On repère un point M de l’espace dans la base de coordonnées cylindriques : pÝÑu r, ÝÑu θ, ÝÑu zq.On cherche l’expression du champ magnétique ÝÑBpMq créé en un point M de l’axe de révolutionde cette spire.Question 161 point Du fait des invariances, le champ magnétique ÝÑBpMq ne dépend quede :A rB φC θD zE Aucune de ces réponses n’est correcte.Question 171 point Du fait des symétries, le champ magnétique ÝÑBpMq est de la forme :A ÝÑBpMq “ BpθqÝÑu θB ÝÑBpMq “ BprqÝÑu rC ÝÑBpMq “ BprqÝÑu zD ÝÑBpMq “ BpzqÝÑu zE Aucune de ces réponses n’est correcte.Question 182 points Par intégration en utilisant la loi de Biot et Savart, en tout pointde son axe, à une distance z, le champ magnétique ÝÑB s’écrit :A ÝÑBpMq “ µ0IR sin3pαqÝÑu θB ÝÑBpMq “ 2µ0IRsin3pαqÝÑu zC ÝÑBpMq “ µ0I2R sin3pαqÝÑu zD ÝÑBpMq “ µ0IR sin3pαqÝÑu rE Aucune de ces réponses n’est correcte.Question 19 ♣2 points Détailler les calculs permettant d’obtenir l’expression du champmagnétique ÝÑBpMq.
Page 7 : CorrectionNom et prénom :. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Groupe :Les réponses ne doivent être apportées que sur cette feuille.La copie ne sera corrigée que si :— elle comporte vos nom, prénom et groupe ;— les cases sont complètement coloriées avec un stylo noir ;— la feuille réponse ne comporte pas de ratures.Question 1 :ABCDQuestion 2 :ABCDEQuestion 3 :ABCDEQuestion 4 :ABCDQuestion 5 :ABCDQuestion 6 :ABCDEQuestion 7 :ABCDEQuestion 8 :ABCDQuestion 9 :ABCDEQuestion 10 :ABCDEFGQuestion 11 :ABCDEQuestion 12 :ABCDEQuestion 13 :ABCDEQuestion 14 :ABCDEQuestion 16 :ABCDEQuestion 17 :ABCDEQuestion 18 :ABCDE
Page 8 : CorrectionQuestion 15 :Fil infini.5 .51Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 9 : CorrectionQuestion 19 :Spire circulaire.5 .51Réservé à l’enseignante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Page 10 : CorrectionFeuille supplémentaire - indiquer le numéro de la question rédigée