CC3 2023 2024 Correction

Posté le 06/02/2025

Chargé de TD/CM : D. Physique.

9 min de lecture

Télécharger le CC3 2023 2024 Correction en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Page 1 : CorrectionCC3Électromagnétisme18 Janvier 2024 — PréIng2Durée : 1h30 minutes 2h en cas de tiers tempsSont interdits :— les documents ;— tous les objets électroniques calculatrice, téléphone, tablette, ordinateur... de mêmeque les montres connectées ;— les déplacements et les échanges.Consignes :1. Vériﬁez que le sujet est composé de 16 pages et 20 questions ;2. Seules les dernières feuilles doivent être rendues ;3. Complétez la page 9 nom, prénom etc. . . dès le début oﬃciel de l’épreuve ;4. Les détails des calculs demandés doivent être portés sur ces dernières feuilles à l’empla-cement correspondant à la question ;5. Dans les deux grilles, les cases correspondant à la bonne réponse doivent être rempliescomplètement au stylo noir ;6. Chaque question ne comporte qu’une seule réponse possible ;7. Il n’y a de point négatif pour une mauvaise réponse que pour les questions de cours ;8. Une case simplement cochée ne sera pas comptabilisée.Le barème est donné à titre indicatif.

Page 2 : CorrectionDonnéesRotationnel d’un champ vectoriel »U, dans la base de coordonnées cylindriques p»u r, »u θ, »u zq : »rot»U “ˆ1rBUzBθ BUθBz˙»ur ˆBUrBz BUzBr˙»uθ 1rˆBprUθqBr BUrBθ˙»uzQuestions de cours 5 pointsQuestion 10.5 pointEn étudiant les plans de symétrie pour la distribution de courant, on trouve que la directiondu champ magnétique »B en M est :A inclus dans tout plan Π de symétrie, passant par M.B celle de la droite orthogonale à un plan Π de symétrie, passant par M.C celle de la droite intersection d’au moins deux plans de symétrie, passant par M.D Aucune des réponses précédentes n’est correcte.Question 20.5 pointLe théorème d’Ampère relie le champ magnétique »B et l’intensité des courants Ii comptésalgébriquement qui traversent toute surface ouverte S, s’appuyant sur un contour Γ. Il s’énonce :A£Γ»B ¨ »dl “ µ0ÿiIiB¿Γ»B ^ »dl “ µ0ÿiIiC£Γ»B ¨ »dS “ µ0ÿiIiD¿Γ»B ¨ »dl “ µ0ÿiIiE Aucune des réponses précédentes n’estcorrecte.Question 31 pointLa loi de Biot et Savart permet de calculer le champ magnétique »B en M, pour un ﬁlparcouru par un courant I. Elle s’énonce :A»BpMq “¿PP ﬁlµ0I4π»dl ^ »MPMP 2B»BpMq “¿PP ﬁlµ0I4π»dl ^ »PMPM 3C»BpMq “¿PP ﬁlµ0I4π»dl ^ »PMPM 2D Aucune des réponses précédentes n’estcorrecte.

Page 3 : CorrectionQuestion 40.5 pointEn étudiant les plans d’anti-symétrie pour la distribution de courant, on trouve que le vecteurchamp magnétique »B en MA a pour direction celle de la droite orthogonale à un plan Π1 d’anti-symétrie, passant parM.B est inclus dans tout plan Π1 d’anti-symétrie, passant par M.C a pour direction celle de la droite intersection d’un plan de symétrie et d’un plan d’anti-symétrie, passant par M.D Aucune des réponses précédentes n’est correcte.Question 50.5 pointSoit c la vitesse de la lumière dans le vide. Elle s’exprime en fonction des deux constantes ε0et µ0 par :A c2 “1ε0µ0B c “ ε0µ0C c “1ε0µ0D c2 “ ε0µ0E Aucune des réponses précédentes n’estcorrecte.Question 61 pointSoient la densité de courant »j et la densité volumique de charges ρ, l’équation locale de conser-vation de la charge électrique s’écrit alors :A div »j BρBt “ 0B div »j ε0BρBt “ 0C div »j BρBt “ 0D div »j ε0BρBt “ 0E Aucune des réponses précédentes n’estcorrecte.Question 71 pointLes quatre équations de Maxwell pour le champ éléctromagnétique sont :A div »E “ ρε0; div »B “ 0 ; »rot»E “ B»BBt ; »rot»B “ µ0 »j µ0ε0B»EBtB div »E “ ρ ; div »B “ 0 ; »rot»E “ B»BBt ; »rot»B “ µ0 »j µ0ε0B»EBtC div »E “ ρε0; div »B “ 0 ; »rot»E “ B»BBt ; »rot»B “ µ0 »j µ0ε0B»EBtD Aucune des réponses précédentes n’est correcte.

Page 4 : CorrectionCylindre parcouru par un courant 7 pointsOn considère un cylindre plein inﬁniment long, d’axe pOzq et de rayon R. Il est parcouru parun courant I constant et uniforme suivant sa longueur. On repère un point M de l’espace dansla base de coordonnées cylindriques : p»u r, »u θ, »u zq.On cherche l’expression du champ magnétique »BpMq créé en un point M.Question 80.5 pointLa densité de courant surfacique »j s’écrit en fonction de I :A»j “IπR2»u rB»j “Iπr2»u zC»j “IπR2»u zD»j “Iπr2»u zE Aucune des réponses précédentes n’estcorrecteQuestion 90.5 pointEn regardant les invariances, on constate que Bpr, θ, zq ne dépend que de :A ϕB rC zD θE Aucune des réponses précédentes n’est correcteQuestion 101 pointDu fait des plans de symétries, le vecteur champ magnétique »BpMq s’écrit :A»BpMq “ Bpzq»u r et »Bp0q ‰ »0 .B»BpMq “ Bprq»u θ et »Bp0q ‰ »0 .C»BpMq “ Bpzq»u z et »Bp0q ‰ »0 .D»BpMq “ Bpθq»u θ et »Bp0q “ »0 .E»BpMq “ Bprq»u θ et »Bp0q “ »0 .F Aucune des réponses précédentes n’estcorrecteQuestion 111 pointEn utilisant une des équations de Maxwell, on peut écrire le vecteur champ magnétique »BpMqpour r ď R :A»BpMq “ µ0I2πR2r»u θB»BpMq “ µ0I2πr»u θC»BpMq “ µ0I2πr»u zD»BpMq “ µ0I2πR2r»u zE Aucune des réponses précédentes n’est correcte

Page 5 : CorrectionQuestion 121 pointEn utilisant une des équations de Maxwell, on peut écrire le vecteur champ magnétique »BpMqpour r ě R :A»BpMq “ µ0I2πr»u θB»BpMq “ µ0I2πR2r»u zC»BpMq “ µ0I2πR2r»u θD»BpMq “ µ0I2πr»u zE Aucune des réponses précédentes n’est correcteQuestion 133 pointsEn utilisant le théorème d’Ampère, démontrer l’expression du champ magnétique »BpMq pourr ě R, en détaillant les calculs symétries, invariances, contour d’Ampère . . ..Répondez sur la feuille correspondante, à la ﬁn du sujet.

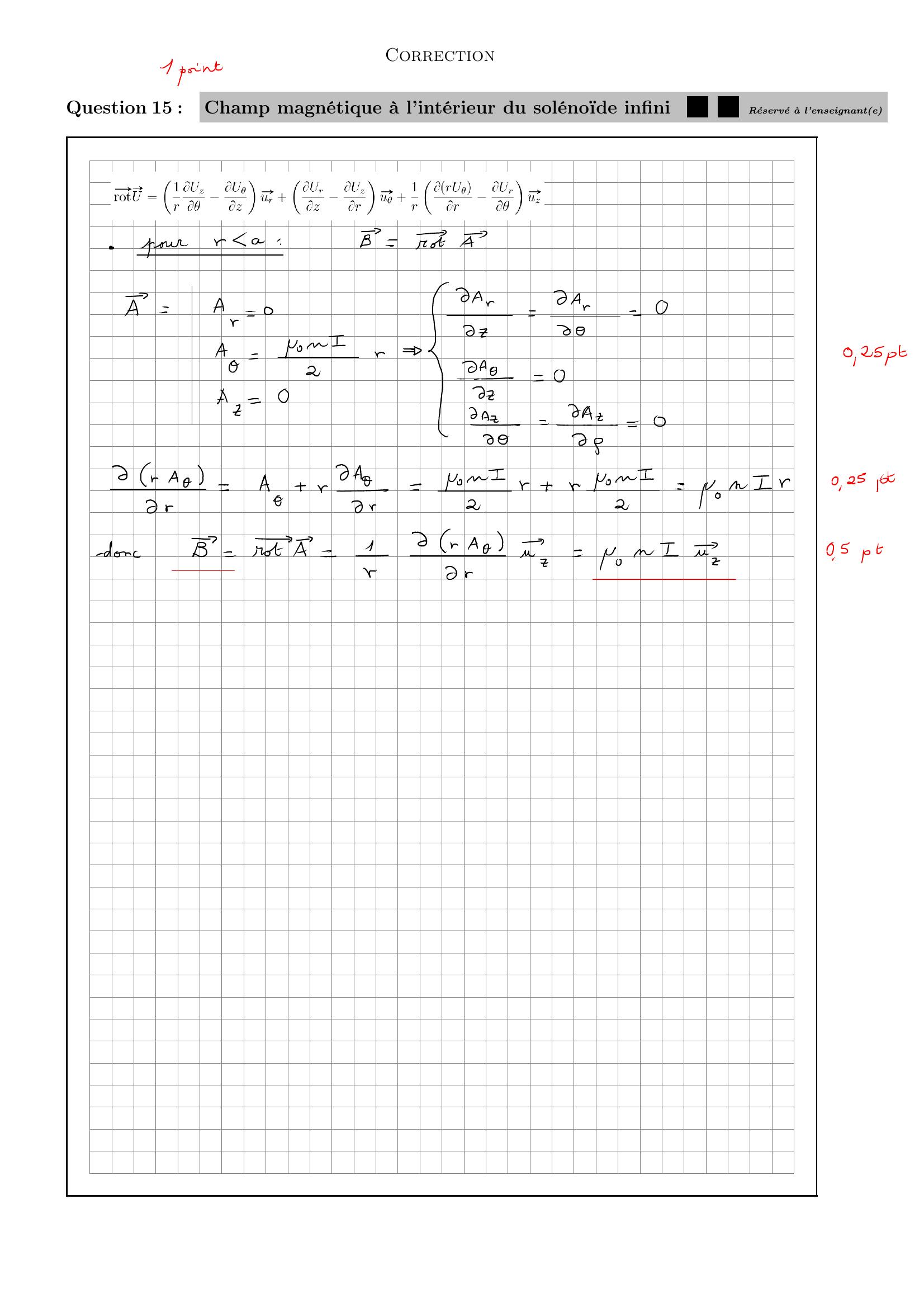
Page 6 : CorrectionSolénoïde inﬁni parcouru par un courant 4 pointsOn considère un solénoïde de rayon a parcouru par un courant d’intensité courant I constantet uniforme, et dont la longueur peut être considérée comme inﬁnie. Son axe Oz coïncide aveccelui du repère cylindrique R “ t0 ; p»ur, »uθ, »uzqu. Il comporte n spires par unité de longueur.On connaît le potentiel vecteur »A en un point quelconque de l’espace déﬁni par sa distance rà l’axe Oz :— si r ă a, »ApMq “ µ0nI2r »uθ— si r ą a, »ApMq “ µ0nI2r a2 »uθOn cherche l’expression du champ magnétostatique »BpMq en tout point de l’espace.Question 141 pointAlors, on peut écrire le vecteur champ magnétique »BpMq pour r ă a :A»BpMq “ »0B»BpMq “ µ0nIruzC»BpMq “ µ0nIr uzD»BpMq “ µ0nI uzE Aucune des réponses précédentes n’est correcteQuestion 151 pointDémontrer l’expression du champ magnétique »BpMq pour r ă a en détaillant les calculs po-tentiel vecteur »A puis calcul de »BpMq . . ..Répondez sur la feuille correspondante, à la ﬁn du sujet.Question 161 pointAlors, on peut écrire le vecteur champ magnétique »BpMq pour r ą a :A»BpMq “ »0B»BpMq “ µ0nI uzC»BpMq “ µ0nIr uzD»BpMq “ µ0nIruzE Aucune des réponses précédentes n’est correcteQuestion 171 pointDémontrer l’expression du champ magnétique »BpMq pour r ą a en détaillant les calculs po-tentiel vecteur »A puis calcul de »BpMq . . ..Répondez sur la feuille correspondante, à la ﬁn du sujet.

Page 7 : CorrectionSpire 6 pointsUne spire de centre O et de rayon R est parcourue par un courant d’intensité I constante etuniforme ﬁg.1. On repère un point M de l’espace dans la base de coordonnées cylindriques :p»u r, »u θ, »u zq.On cherche l’expression du champ magnétique »BpMq créé en un point M de l’axe de révolutionde cette spire.Figure 1 – Spire circulaireQuestion 181 pointDu fait des invariances, le champ magnétique »BpMq ne dépend que de :A θB ϕC rD zE Aucune des réponses précédentes n’est correcte.Question 191 pointDu fait des symétries, le champ magnétique »BpMqA est radial.B est orthoradial.C a une composante radiale et orthora-diale.D est selon pOzq.E Aucune des réponses précédentes n’estcorrecte.Question 204 pointsDémontrer que le champ magnétique »BpMq en un point M de l’axe de révolution de la spires’écrit :»BpMq “ µ0I2R sin3pαq»u zDétailler les calculs : symétries, invariances . . .Répondez sur la feuille correspondante, à la ﬁn du sujet.

Page 8 : Correction

Page 9 : CorrectionÉlectromagnétisme - PréIng2 - CC3 - 2023/2024NOM : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Prénom : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .no Groupe : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Nom du chargé de TD : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .codage du no étudiant horizontalementdans le sens de lecturePremier chiﬀre du no étudiantDernier chiﬀre du no étudiant01234567890123456789012345678901234567890123456789012345678901234567890123456789sens de remplissagedu no étudiant

Page 10 : CorrectionLes réponses au QCM ne doivent être apportées que sur cette feuille.La copie ne sera corrigée que si :— elle comporte vos nom, prénom et groupe ;— les cases sont complètement coloriées avec un stylo noir ;— la feuille-réponse ne comporte pas de ratures.Question 1 :ABCDQuestion 2 :ABCDEQuestion 3 :ABCDQuestion 4 :ABCDQuestion 5 :ABCDEQuestion 6 :ABCDEQuestion 7 :ABCDQuestion 8 :ABCDEQuestion 9 :ABCDEQuestion 10 :ABCDEFQuestion 11 :ABCDEQuestion 12 :ABCDEQuestion 14 :ABCDEQuestion 16 :ABCDEQuestion 18 :ABCDEQuestion 19 :ABCDE