CC3 2023 2024 Correction
Télécharger le CC3 2023 2024 Correction en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Page 1 : CorrectionCC3Panorama sur la Physique18 Janvier 2024 — PréIng1Durée : 1 heure 30 min 2 heures en cas de tiers tempsSont interdits :— les documents ;— tous les objets électroniques calculatrice, téléphone, tablette, ordinateur... de mêmeque les montres connectées ;— les déplacements et les échanges.Consignes :1. Vérifiez que le sujet est composé de 16 pages et 33 questions ;2. Seules les dernières feuilles doivent être rendues ;3. Complétez la page 11 nom, prénom etc. . . dès le début officiel de l’épreuve ;4. Les détails des calculs demandés doivent être portés sur ces dernières feuilles à l’empla-cement correspondant à la question ;5. Dans la grille, la case correspondant à la bonne réponse doit être remplie complètementau stylo noir ;6. Chaque question ne comporte qu’une seule réponse possible ;7. Il n’y a de point négatif pour une mauvaise réponse que pour les questions de cours ;8. Une case simplement cochée ne sera pas comptabilisée.Le barème est donné à titre indicatif.
Page 2 : CorrectionQuestions de cours 6.5 pointsQuestion 11 pointDeux points A et B ont pour coordonnées cartésiennes : A “ p1, 4q et B “ p2, 5q.La droite passant par les deux points A et B a pour équation :A y “ 2x 3B y “ x 3C y “ x ´ 3D Aucune des réponses précédentes n’estcorrecteQuestion 21 pointEn deux dimensions, les coordonnées cartésiennes x et y peuvent s’exprimer en fonction descoordonnées polaires par la formule :A x “ r et y “ r tan θB x “ r sin θ et y “ r cos θC x “ r cos θ et y “ r sin θD Aucune des réponses précédentes n’est correcteQuestion 30.5 pointDeux points C et D ont pour coordonnées cartésiennes : C “ p3, 4q et D “ p´1, 7q alors lanorme du vecteur »CD vaut :A »CD “?50B »CD “?13C »CD “?7D »CD “ 5E Aucune des réponses précédentes n’estcorrecteQuestion 40.5 pointUn point B a pour coordonnées cartésiennes : B “ pb, 0q avec b ă 0.Ses coordonnées polaires sont données par :A rB “?b et θB “ 0B rB “ b2 et θB “ 3π2C rB “ b et θB “ π2D rB “ ´b et θB “ πE Aucune des réponses précédentes n’estcorrecteQuestion 50.5 pointUn point A a pour coordonnées cartésiennes : A “ p0, aq avec a ą 0.Ses coordonnées polaires sont données par :A rA “ a et θA “ π2B rA “ a2 et θA “ 3π2C rA “ ´a et θA “ πD rA “ ?a et θA “ 0E Aucune des réponses précédentes n’estcorrecte
Page 3 : CorrectionQuestion 60.5 pointDans une base orthonormée directe B.O.D, soient deux vecteurs de coordonnées :»v 1 “˜ 340¸et »v 2 “˜ ´170¸.L’angle entre les deux vecteurs vaut :A π2B π3C π6D π4E Aucune des réponses précédentes n’est correcteQuestion 70.5 pointDans une base orthonormée directe B.O.D, soient deux vecteurs de coordonnées :»v 1 “˜ 340¸et »v 2 “˜ ´170¸.Leur norme vaut :A »v 1 “?7 et »v 2 “?13B »v 1 “?50 et »v 2 “ 5C »v 1 “?13 et »v 2 “?7D »v 1 “ 5 et »v 2 “?50E Aucune des réponses précédentes n’estcorrecteQuestion 81 pointDans une B.O.D, soient les deux vecteurs »v 1 “˜ 330¸et »v 2 “˜ 131¸.Le produit vectoriel de ces deux vecteurs a pour valeur :A»v 1 ^ »v 2 “˜ 3´36¸B»v 1 ^ »v 2 “˜ 63´3¸C»v 1 ^ »v 2 “˜ 336¸D Aucune des réponses précédentes n’estcorrecteQuestion 91 pointEn coordonnées cylindriques, le vecteur déplacement élémentaire s’écrit :A d »OM “ dr»u r rdθ»u θ r sin θdφ»u φB d »OM “ dr»u r dθ»u θ dz »u zC d »OM “ dr»u r rdθ»u θ dz »u zD Aucune des réponses précédentes n’est correcte
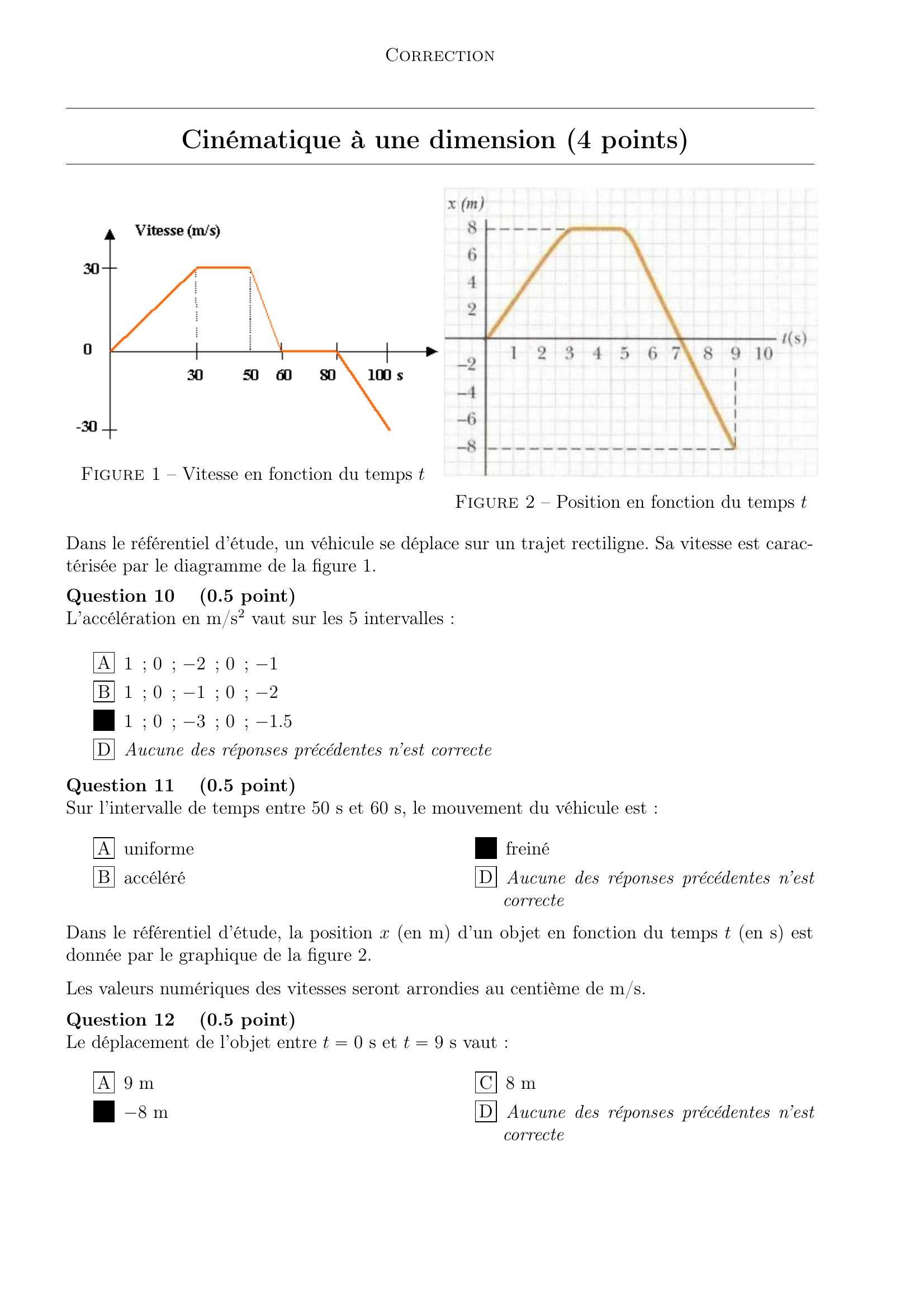
Page 4 : CorrectionCinématique à une dimension 4 pointsFigure 1 – Vitesse en fonction du temps tFigure 2 – Position en fonction du temps tDans le référentiel d’étude, un véhicule se déplace sur un trajet rectiligne. Sa vitesse est carac-térisée par le diagramme de la figure 1.Question 100.5 pointL’accélération en m/s2 vaut sur les 5 intervalles :A 1 ; 0 ; ´2 ; 0 ; ´1B 1 ; 0 ; ´1 ; 0 ; ´2C 1 ; 0 ; ´3 ; 0 ; ´1.5D Aucune des réponses précédentes n’est correcteQuestion 110.5 pointSur l’intervalle de temps entre 50 s et 60 s, le mouvement du véhicule est :A uniformeB accéléréC freinéD Aucune des réponses précédentes n’estcorrecteDans le référentiel d’étude, la position x en m d’un objet en fonction du temps t en s estdonnée par le graphique de la figure 2.Les valeurs numériques des vitesses seront arrondies au centième de m/s.Question 120.5 pointLe déplacement de l’objet entre t “ 0 s et t “ 9 s vaut :A 9 mB ´8 mC 8 mD Aucune des réponses précédentes n’estcorrecte
Page 5 : CorrectionQuestion 130.5 pointLa distance parcourue par l’objet entre t “ 0 s et t “ 9 s est donnée par :A 24 mB 16 mC 8 mD Aucune des réponses précédentes n’estcorrecteQuestion 141 pointLa vitesse moyenne entre t “ 3 s et t “ 9 s a pour valeur :A 2.67 m/sB ´2.67 m/sC 8 m/sD Aucune des réponses précédentes n’estcorrecteQuestion 150.5 pointLa vitesse à t “ 1 s vaut alors :A 2.67 m/sB 8 m/sC ´2.67 m/sD Aucune des réponses précédentes n’estcorrecteQuestion 160.5 pointLa vitesse à t “ 8 s vaut alors :A 4 m/sB ´3.5 m/sC ´4 m/sD Aucune des réponses précédentes n’estcorrecte
Page 6 : CorrectionTir d’adresse 6.5 pointsDans le référentiel terrestre RT approximé galiléen, on considère le jeu d’adresse suivant fig.3,repéré en coordonnées cartésiennes :— à l’instant ti, un objet A de masse mA est lancé depuis O avec une vitesse »v i de normevi faisant un angle α P r0; π2r avec l’horizontale ;— au même instant, un objet B de masse mB est lâché sans vitesse initiale depuis la positionde coordonnées pl; hq.La seule force considérée est la pesanteur associée au champ »g , de norme g.On note pxA; zAq et pxB; zBq les coordonnées de position de A et B respectivement.Nous cherchons comment lancer A pour percuter B avant qu’il ne touche le sol.Figure 3 – Situation à l’instant tiQuestion 171 pointDonner l’expression des accélérations des objets A et B.Puis exprimer les conditions sur la vitesse et la position à l’instant ti pour A puis B.Répondez sur la feuille correspondante, à la fin du sujet.Les équations horaires du mouvement sont telles que voir les 3 questions ci-après :Question 181 pointA xAptq “ vi sinpαqpt ´ tiqB xAptq “ vi sinpαq tC xAptq “ vi cospαq tD xAptq “ vi cospαqpt ´ tiqE Aucune des réponses précédentes n’est correcteQuestion 191 pointA zAptq “ vi cospαqpt ´ tiq ´ g2pt ´ tiq2B zAptq “ vi sinpαq t ´ g2 t2C zAptq “ vi cospαq t ´ g2 t2D zAptq “ vi sinpαqpt ´ tiq ´ g2pt ´ tiq2E Aucune des réponses précédentes n’est correcte
Page 7 : CorrectionQuestion 201 pointA zBptq “ ´g2 t2B zBptq “ ´g2pt ´ tiq2C zBptq “ h ´ g2pt ´ tiq2D zBptq “ h ´ g2 t2E Aucune des réponses précédentes n’est correcteQuestion 212 pointsSans tenir compte du sol :À partir des expressions précédentes, exprimer α en fonction des paramètres du problème afinqu’A et B se percutent.De façon remarquable, de quels paramètres outre mA et mB cette expression ne dépend-ellepas ?Répondez sur la feuille correspondante, à la fin du sujet.Question 220.5 pointLa condition de la question précédente étant vérifiée, la collision entre A et B a lieu strictementau-dessus du sol si :A vi ącg2ph2 l2qhB vi ą ?2ghC vi ącg2l2hD Aucune des réponses précédentes n’est correcte
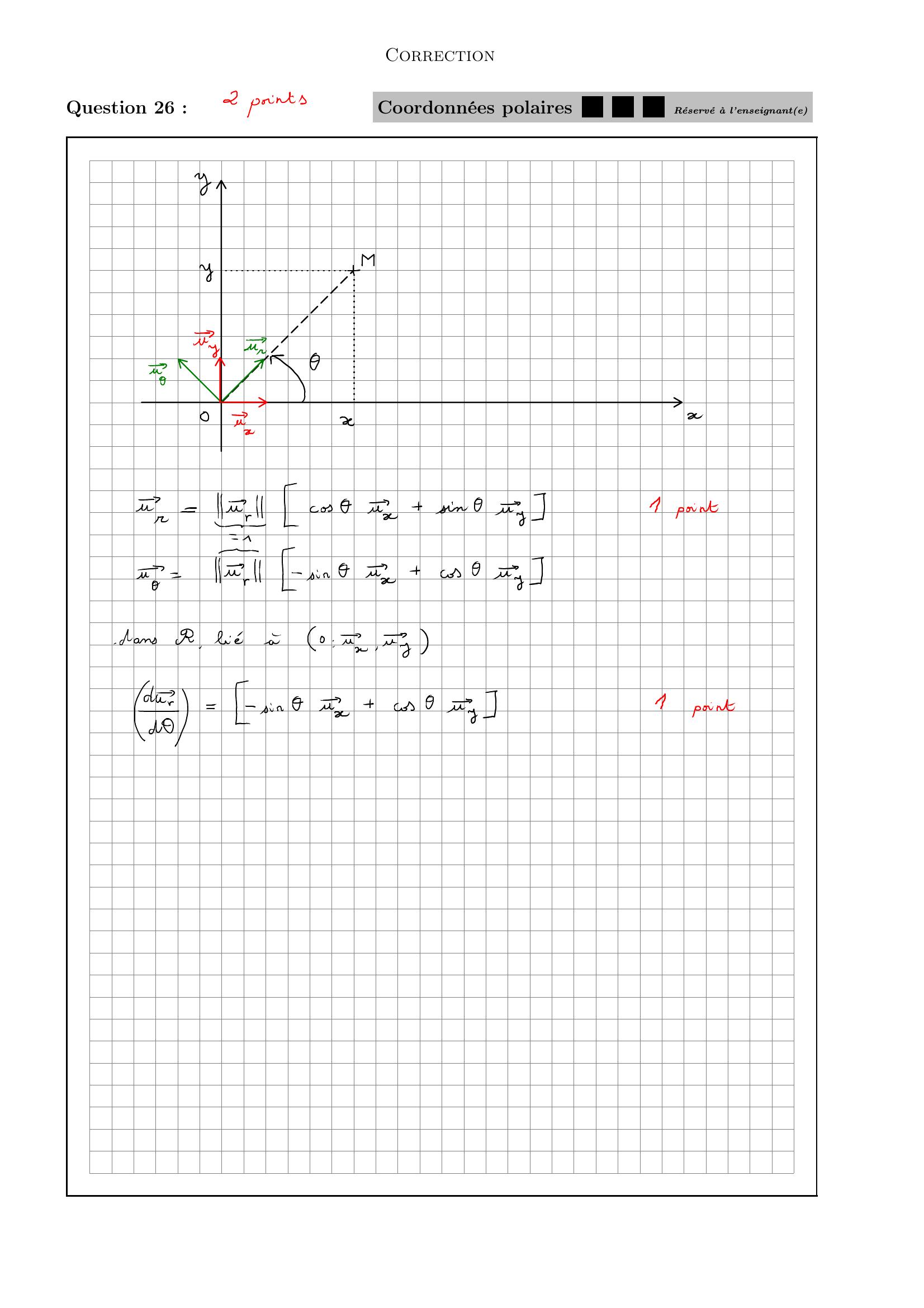
Page 8 : CorrectionCinématique à deux dimensions 7 pointsDans le référentiel R d’étude, on utilise le système de coordonnées cartésiennes px, yq associéeà la base p»u x, »u yq et le système de coordonnées polaires pr, θq associée à la base p»u r, »u θq.Question 230.5 pointLes dérivées des vecteurs de la base polaire sont telles que :Ad»u rdθ “ »u rBd»u rdθ “ ´»u θCd»u rdθ “ »u θD Aucune des réponses précédentes n’est correcteQuestion 240.5 pointOn cherche à exprimer les vecteurs de la base polaire en fonction de ceux de la base cartésienne.Alors :A»u r “ cos θ »u x sin θ »u yB»u r “ sin θ »u x ´ cos θ »u yC»u r “ sin θ »u x cos θ »u yD»u r “ cos θ »u x ´ sin θ »u yE Aucune des réponses précédentes n’est correcteQuestion 250.5 pointLa dérivée du vecteur »u r par rapport à l’angle θ vaut alors :Ad»u rdθ “ ´ cos θ »u x sin θ »u yBd»u rdθ “ cos θ »u x sin θ »u yCd»u rdθ “ ´ sin θ »u x cos θ »u yD d»u rdθ “ sin θ »u x cos θ »u yE Aucune des réponses précédentes n’est correcteQuestion 262 pointsDétailler les calculs précédents permettant d’obtenir l’expression de la dérivée du vecteur »u rpar rapport à l’angle θ, dans la base cartésienne.Répondez sur la feuille correspondante, à la fin du sujet.
Page 9 : CorrectionDans le référentiel R, un point M est animé d’un mouvement circulaire de rayon R. Sa positionest repérée par l’angle θptq des coordonnées polaires.Dans R :Question 270.5 pointLe vecteur vitesse de M est :A»v ptq “ R 9θ»u θB»v ptq “ 9R»u r R 9θ»u θC»v ptq “ 9R»u r ´ R 9θ»u θD»v ptq “ ´R 9θ»u θE Aucune des réponses précédentes n’est correcteQuestion 280.5 pointLe vecteur vitesse de M est de composantes :A purement orthoradialeB radiale et orthoradialeC purement radialeD Aucune des réponses précédentes n’estcorrecteQuestion 290.5 pointLe vecteur accélération de M est :A»a ptq “ ´R 9θ2 »u rB»a ptq “ R´´ 9θ2 »u r :θ»u θ¯C»a ptq “ R:θ»u θD»a ptq “ R´9θ2 »u r ´ :θ»u θ¯E Aucune des réponses précédentes n’est correcteQuestion 300.5 pointLe vecteur accélération de M est de composantes :A radiale centripète et orthoradialeB radiale centrifuge et orthoradialeC purement orthoradialeD purement radialeE Aucune des réponses précédentes n’estcorrecte
Page 10 : CorrectionL’évolution temporelle de θ est donnée par θptq “ ´α2 t2 βt γ avec α, β et γ des constantes.Question 310.5 pointLe vecteur vitesse de M peut alors s’écrire :A»v ptq “ R p´αt βq »u θB»v ptq “ R´ α2 t β˘ »u θC»v ptq “ R´ α2 t ´ β˘ »u θD»v ptq “ R pαt ´ βq »u θE Aucune des réponses précédentes n’est correcteQuestion 320.5 pointLe vecteur accélération de M peut alors s’écrire :A»a ptq “ ´R“pαt βq2 »u r α»u θ‰B»a ptq “ ´R“p´αt βq2 »u r α»u θ‰C»a ptq “ ´Rα»u θD»a ptq “ ´R p´αt βq2 »u rE Aucune des réponses précédentes n’est correcteQuestion 330.5 pointLa vitesse angulaire en rad/s, pour α “ 0 rad/s2, β “ π rad/s et γ “ ´ π2 rad, vaut :A ´π2B πC π2D ´πE Aucune des réponses précédentes n’est correcte
Page 11 : CorrectionPanorama sur la Physique - PréIng1 - CC3 - 2023/2024NOM : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Prénom : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .no Groupe : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Nom du chargé de TD : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .codage du no étudiant horizontalementdans le sens de lecturePremier chiffre du no étudiantDernier chiffre du no étudiant01234567890123456789012345678901234567890123456789012345678901234567890123456789sens de remplissagedu no étudiant
Page 12 : CorrectionLes réponses au QCM ne doivent être apportées que sur cette feuille.La copie ne sera corrigée que si :— elle comporte vos nom, prénom et groupe ;— les cases sont complètement coloriées avec un stylo noir ;— la feuille-réponse ne comporte pas de ratures.Question 1 :ABCDQuestion 2 :ABCDQuestion 3 :ABCDEQuestion 4 :ABCDEQuestion 5 :ABCDEQuestion 6 :ABCDEQuestion 7 :ABCDEQuestion 8 :ABCDQuestion 9 :ABCDQuestion 10 :ABCDQuestion 11 :ABCDQuestion 12 :ABCDQuestion 13 :ABCDQuestion 14 :ABCDQuestion 15 :ABCDQuestion 16 :ABCDQuestion 18 :ABCDEQuestion 19 :ABCDEQuestion 20 :ABCDEQuestion 22 :ABCDQuestion 23 :ABCDQuestion 24 :ABCDEQuestion 25 :ABCDEQuestion 27 :ABCDEQuestion 28 :ABCDQuestion 29 :ABCDEQuestion 30 :ABCDEQuestion 31 :ABCDEQuestion 32 :ABCDEQuestion 33 :ABCDE
Page 13 : CorrectionQuestion 17 :Tir : accélération et conditions initiales .5 .5Réservé à l’enseignante
Page 14 : CorrectionQuestion 21 :Tir : A et B se percutent.25.25 .5 .51Réservé à l’enseignante
Page 15 : CorrectionQuestion 26 :Coordonnées polaires .5 .51Réservé à l’enseignante
Page 16 : CorrectionFeuille supplémentaire - indiquer le numéro de la question rédigée