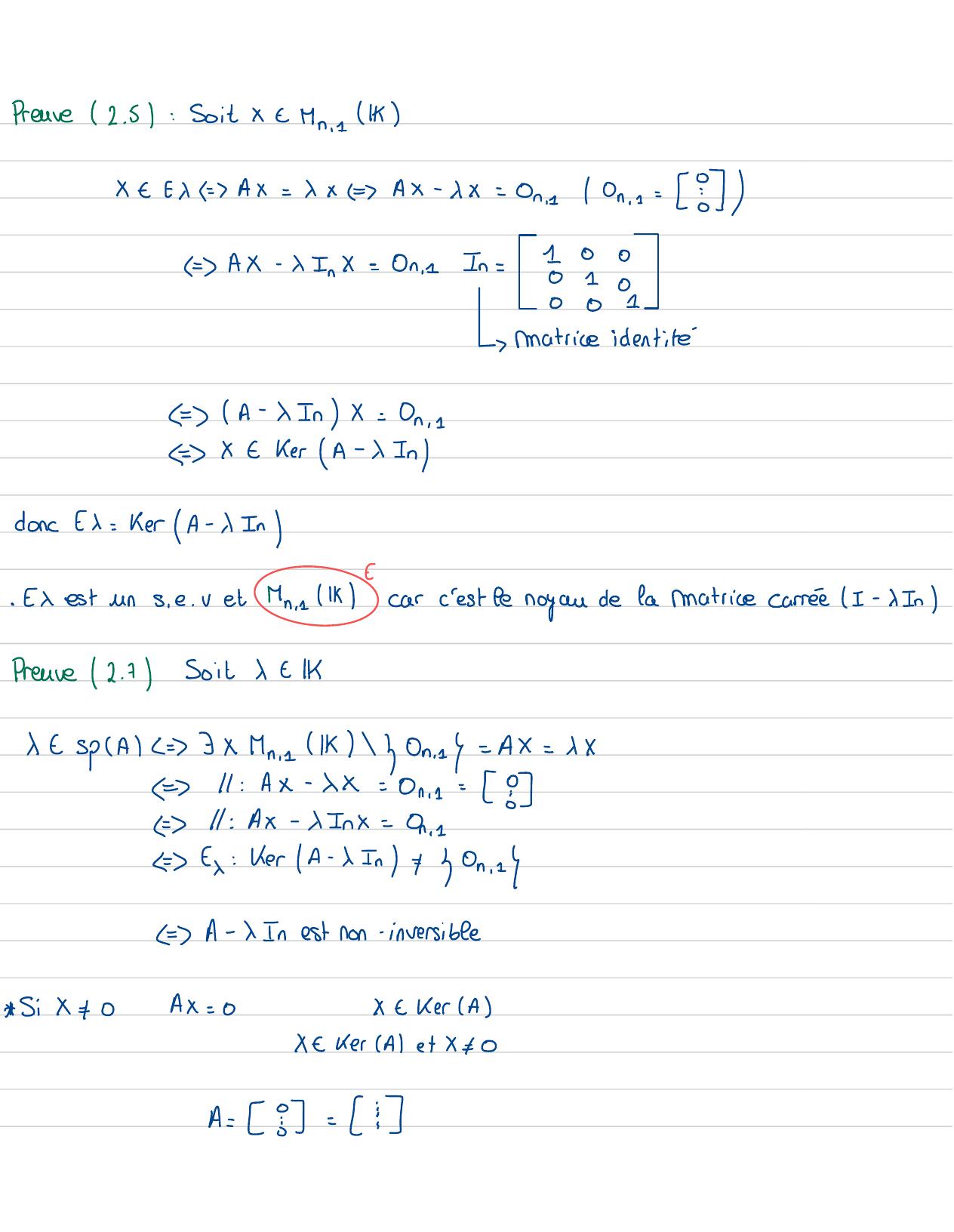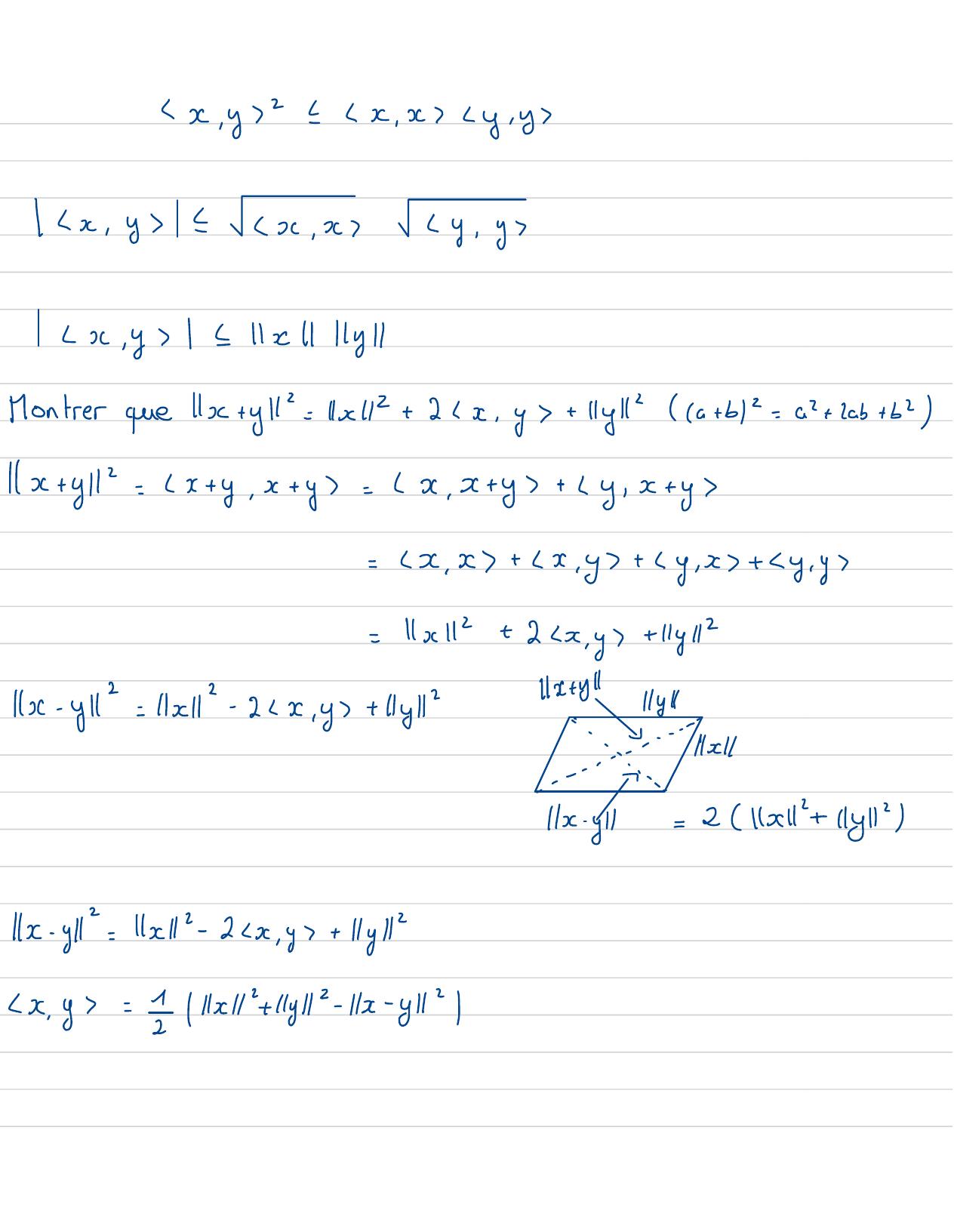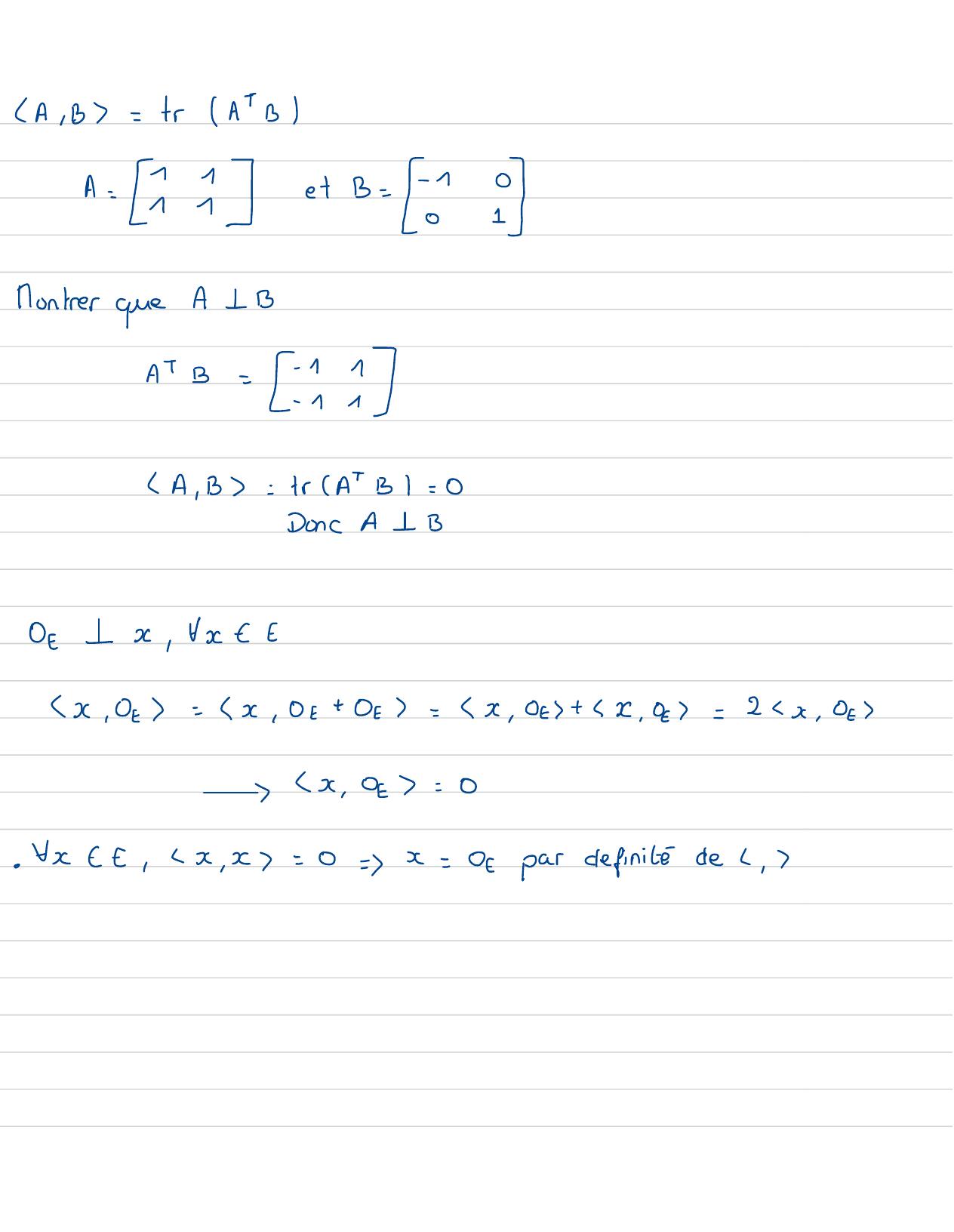CM Annotee

Posté le 08/02/2025

Chargé de TD/CM : M. X.

6 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Page 1 : Algebre bilinéaireCH2022-2023

Page 2 : Réduction des endomorphismes↓t ensemble d'application linéaire dedanslendormorphismesfv= x: image de est colinéaire à Le Vecteur propreestnon nutf02= ,doncon exclut toujours OfExemple 1 :fx ,y=x- 3/2,- x/2+ ya 1 1, 1 f associé &1=1/2f01= f1, 1= 1- 12,- 112+ 1= 112. 1/2= Y21 , 1= 201fV1= 1 V1Vz= 1,- 112= 3/2f02= f1,-= 3121 ,- 2=3/2V2

Page 3 : Exercice: Soit &CCIR2 tyfx ,, xz= xz , x, Trouver tous les élements propres defSolution généraleà faire tout le tempsSoit X ER, Fx: x ,, x2 ER10, 0fx= xxx2, x, = xx ,, x2 x2 , x 1= xx1 , xx2=12- xx,= 021+ x2 x2= xx 1Ix ==Xx 2x,- xx2=01- x/x=0Sx 1- xxx=0as 1 :1- x2= 0== 10u- 1Six=1alorsS=- icI=x= x2 , x , = xz1 , 1=1= 1est revaleur propre de vecteurspropres

Page 4 : x= 1 , 1ser I 1, 112, 213, 3Six=- 1alorsS =I0= 0=- x2 , x, = xz- =, 1x,=- x2=X= 1-1 estune rateur propre de vecteurspropresx= c- 1, 1 aresCEIRCas2:1 -x0danscecas S 0=x= 0 , 0contradictioncar x+0, 0Conclusion:· spf=3- 1, 1· Lesvecteurs propres def sont les élerments de IR de la forme:c- 1, 1pour=- 1avecCEM c1, 1pourX=1

Page 5 : Preuve /proposition 1 . 5 Reas. e.vide: ex1xSoit et-2xfxfx= xx fx- xx=02 fx- Xide x=0tf- xidx= 02↳-Ker f-dide/On a donc Ex= Ker f-xideExest doncunsous espace rectoriel de -car c'estle nogau de l'endomorphismef-dictPreve /1.7:Soit& t 1x espf5xt027: fx= xx 1 : fx- xx= 0t0 11: fx- xic x=0EE11: f -xidex=02= Ex=ker f- xide+ 07= f-xidenon injectif

Page 6 : Remarque:1 Six- spf afors Ex= 022 IVe valeur propre peut-être muffe, danscecason a les équivalents0 = spf Kerf + UtY = fnon injectif3Cependant, un recteur propreest non nul par def une valeur propre peut-êtrenuttePreuve 1. 8 &1 , 22 E IR14101+ 2202=0.=fx 101+ xzVz= 0=x = f01+ x2fVz=0e=21x1V1+ 22x2V2= 02121V1+ 2 1Vz= 0=- 2101= 1221V1- 41XzUz= 0= 1 =- xz21 U1= 0ed'après l'énoncé= o= Or pas de vecteur matte=41= 0je reporte 10+ xzVz= 0=-22= 0

Page 7 : d'and==dz=0=N1, Uz est libreUnri 1imatricecarreendomorphismeA= Mn. kMn, = kX1X= AX=ssolution:VI ,Vz, Vononnuts1 AV1=- V1= V1rect proprede A , associéà la valeur propre &1= 12 AVz=2 V2=V2rectpropre/2=2AV=2 Vz=Vsrect propre/3=12=2Attention: Veet Vsne sont pas lies= sont libreshVz+ BU3=OfL+ 0=0G= 00+ B=0B=0Donc libreA c Mn k

Page 8 : Preuve 2.5:Soit x = Mr. 1 1x = x Ax= xx Ax- xx= On/On == 80E AX-xInX=On , 1In=8o001matrice identiteE A- x InX= On, 1EX=Ker A- x Indonc Ex= Ker A- 1 In· Ex est unsie. VetMn.1 lk" carc'est le noyau de la Matrice carrée I-DInPreave 2. 7Soit& t1Kx t spA= 5 x Mme Ik3On.17= AX=XX=11:Ax -xx= 0 n 1= 8E11 : Ax-xInx=On == Ex: KerA- x In+ On.z=A- x Inest non-inversible S:XOAx= 0X-Ker AX-Ker Alet X + 0A= 8= :

Page 9 : AX=On , 1A- AX=A- 1On , 1x=A- 1On, 1= 8pas inversible =non bijectif, surjectif, injectifMn.1 x1+x2-8D-172n= 2abCD⑧bIcdIo0o0 +38 +IIC1Db01tCD0L⑧⑧ItC00001001f1f2+3-43- Polynome caracteristiqueI espace vectorielsont dedimension finie↳priviligier les matricesBase BB= je ...., en

Page 10 : x=x, e1+ xzez +...+anenX ii1EMr. 1f:= tspf= spAA= Milffx=xxAx= xxproposition3 . 2:POSSIBLE EXAMENSTh. De BasePreave 3. 2 1SoientAct AE MaIK2 matrices sembables7 PC Mr . 1 IK inversible telle queAl=P-ApPAx=det A- DInPx P = In= det P- Ap- x P- 1 In P-det P-1 Ap-p- 1 x In Pl=det P 1 A- x InP=Cet P-1 det A-XIn det1P=cet P-1PA x det /P=PAdetAB= det A cetBdet A 1=1det A

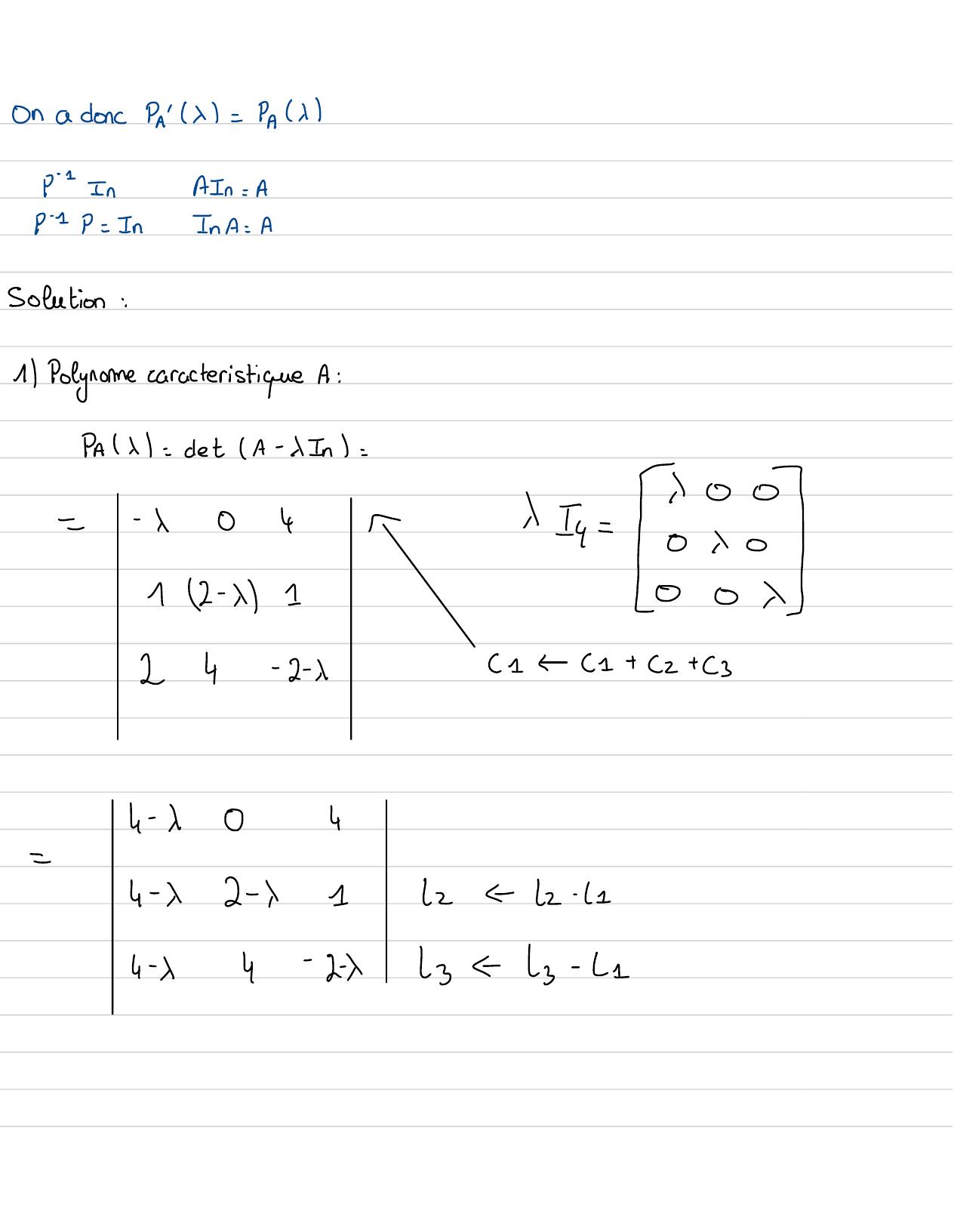
Page 11 : On a donc Pax=PA ip= InAIn= Ap-1P= InIn A= ASolution:1 Polynome caracteristique A:PA11= det A-xIn=-- 104-↓IG= I12- x1O⑧X24- 2- x11+ z+ 234- x04-4- x2 - 112 2- 14- x4- 2xLy Ly- 21

Page 12 : 4- x04-02 - x- 304-6-xyy- 224- x04-02 - x- 302- xx22+ 234- x04-4- x- 4- x- 30- 4- 1- 3I00&0-x=4-x- 4- x- xsp8=spA=G- 4,0. 4

Page 13 : 2Of spAEAnon inversible+-T I non bijectif-I-t-tabc2fhCdef-C hi+ - 1diIui↓est racine PP= x- a....P=X- 1=x-2x+ 1P=x- 1X- 112X- 3orde de multiplicité:nombre de fris qui il est racine17331x- 113x- 3PAX= deEA- x Il= det - 0=det == Ex= x+ 1

Page 14 : SpA=0spA= -:,Solutions :· U1= 1, 1est un vecteur propredef Valeur propre= I3· Uz= 1,1estun vecteur proprece f Valeur propre2= Idir 1R2= 2 car 3U1, 24=2=IVz, Uzest une base de M, formée de recteurs propre de f=fest diagonalisableMisf=-x...nf02fVI0U10=v2

Page 15 : fV= EN1=U1+OV2fUz= zUz=0V1+I:jusAtMnCkA: Mr, eCIcMn , 1XAXPreuve 4. 5 A possèden valeur propre distinctes 2a 2 Xi7!= 1= Vil- 1la famittedes vecteurs propresest libredans Mr. 1 1Mais dirMn .zIK=n=La famillede vecteur propre et avec base deMn , 1 Iket par siteA est diagonalisable

Page 16 : A=22polynome caracteristique1Valeur propre de A:PAd=det A-xIz=3- D1211-C2-2-2- x1-- 2- x- x2 = 22+ 112- x1-=2- X1-x01 - xPAd= 2- x1- xSpAl= 1, 2multiplicité 1= 1multiplicité 2= 1Aest d'urdre2E=A est diagonalisableA admet2 ruleurs propresdistinctes2 sousespace propresf1:Soitx= J - M2, 1 1

Page 17 : Xf 1 AX=x= 21x-2-1y

Page 18 : S. TrigonalisationS. 1Matrice triangulaireA=PDp- 1Siunpeut pas diagonaliseron trigonalise= PTP-A98â B2= 2â 98= 5282Triagonaliser faratrice suivante :A=IOn cherche le spectre :L'ensembledes valeurs propres de A.Spectre AxSpA Pax=012C3PA1=det A- x Iz=- 2- x2- 121- 21+ 2+ 3-11- x- 1- 12-2- x

Page 19 : --1- x2-1=.- -2-1-1- x1- x-1-1- x1- x- 12zz- L1- 1- x2- 2- x-1.12- 2- xzkz- 11=-1- x2-101- x0=1+ x300-1- xPpx=- 1+ x13spA= 3- 1multiplicité- 11=3·sons espacepropreE- 1= kerA+ IgSoitx= 7= M3. 1 1x = G- 1A+ IzX=03, 1

Page 20 : =3- 12... ?= 8- 1+ 2y- 2=0I"+ 2y- z=0=- x+ 2y- z= 0 x=2y- z-x+ 2y- z=0x= 22-+= 2+ = y3+ 2-iSynthese:·PAx=- 1+ x3. SpA= 1 multiplicité- 1=3-1= Vectv= , vzavecV= 2 et v= Edir E-1=2+3= multiplicité+ 11=A est non diagonalisableCependantPrest scindédans IR=A est trigonalisable dans My /IR

Page 21 : Cherchons doncun vecteur vi tel que⑧B= V1 , V2, V3/Soit unebasede M3, 1 R②SAV1,AV2 , AVzsoit triangulaire, iede la formeAU1AV2AV- 10LV1T=0-1 312I 00-1I V3et semblableàAAV1=- V1+OV2+OV3=-V1AV2=0V1-1Vz +OUS =-V2AV=qV1+BU2-1V3 A+ Ivy=2Vx+ 33VzSolution systeme hommogine:Ax=BSX=xh+ XpXh=Solution de AX= 0Xp=Solution deSsoit x- 2-x+ 2y- z=2c- BA+ IgX= dV1+ BV2= E-x+ 2y- z=d-x+ 2y-z= BE0= 2- 2=0=d- B0=2- B- x+ 2y- z= B

Page 22 : Ix= 32-- B=x=2yy2=P== y+ z-i+ , +10 ,0XnXplibre independantdes précédentsOn choisitB= 1= = 1et v=xp= -8On verifie facilement que V1 ,V2, V3est libre-doncunebasede Mr.IRet fa matrice TestT=/0 IEn notantP= v= viv3= ?-!trigonalisable01 I0DOnaA=PTP- 1P+ p 1PDP-1A=PDP- 1 diagonalisableA2=PDP=PDP 1-mIdentité=PDDD= P12p- 1

Page 23 : Normeassociéeaun produit scalaireHall= EstPreuve:MaII . Ilestune normasur t1Xx-2, 11x= 0 5, x=0==0 =car i estdefinie2 FxeE, FyERR,IXcll=xx, xx=xx ; x=xx ;x=x 1x113fx,yt tx+y, x+ yx + x+y , ypor finegatite deminkowski11x+ y= x+ 1yHasparticulet enproduit scalaireInegalite triangulaireest vatable quepour tanorme 2.

Page 24 : ,y2x, xy, yx, y=x, xy, y x, y=x yMontrew que c +yll=11xc12+ 2 x, y+ Hy"a+ b 2=a"+ 2ab+ b2x+ y=x+ y, x+ y=e, x+ y+ y, x+ y=, x+ x,y+ y, x+ xy , y=1x12+ 2x, y+ 1y/211 -y12= x2- 2x, y+ ly2kstyllIly1-.........Ilsl............-k -y1= 2x+ yl"Ik-yll=Ikell2- 2x, yz+ Hy2x, y = Ikell"+ 1y2- 11x- y1" /

Page 25 : A, BT= trA+ BA= 21e+B= 2Runtrer queA 1 BA+B= 2 !A, B= tr AT Bl= 0DoncA- BOf-x, factEx, 02= x, 0+ 07= x , 02+ 1, 0=2xx, 0x , 0z=0· Xx-,7x, x=0=7x= 0par definitédeL ,