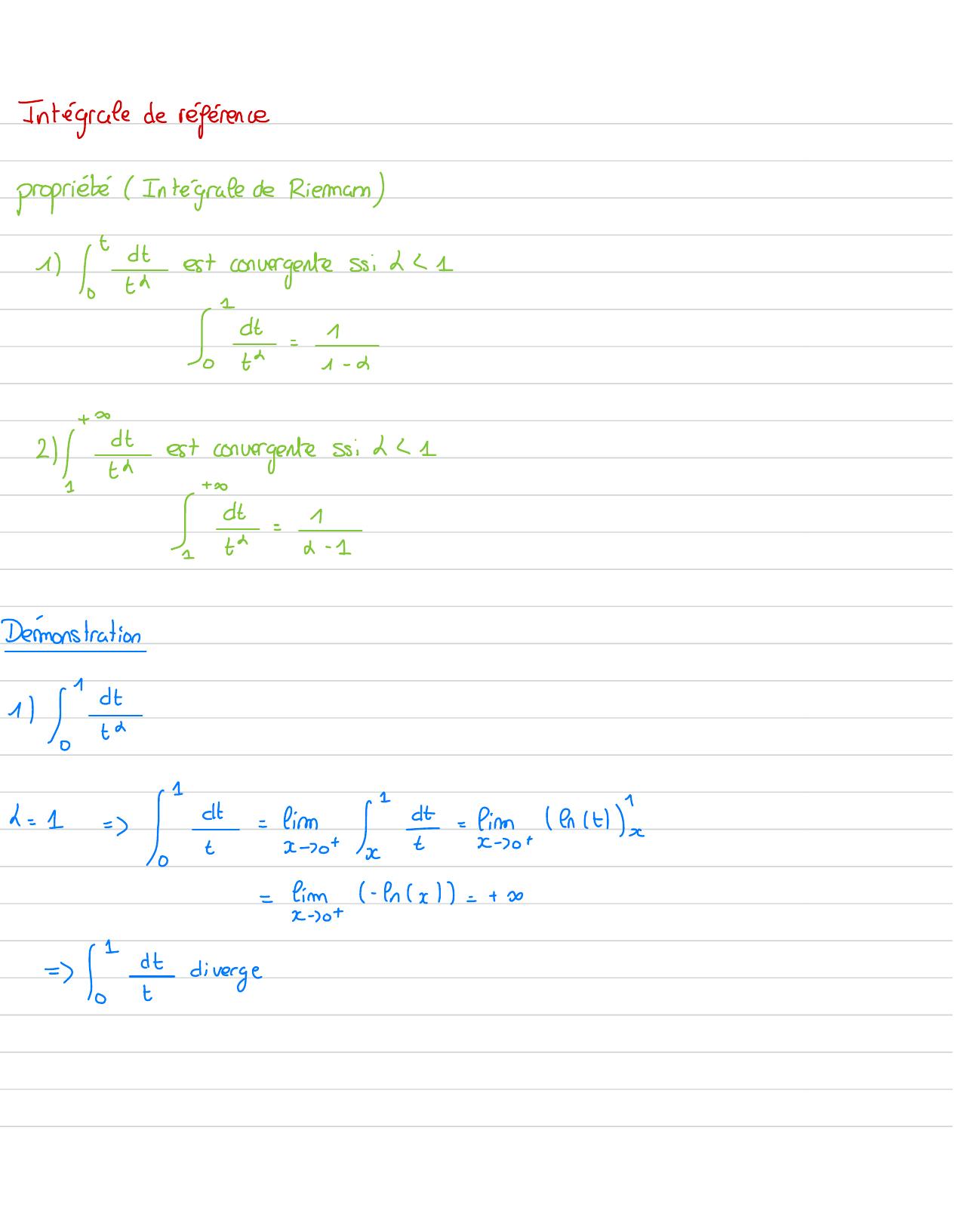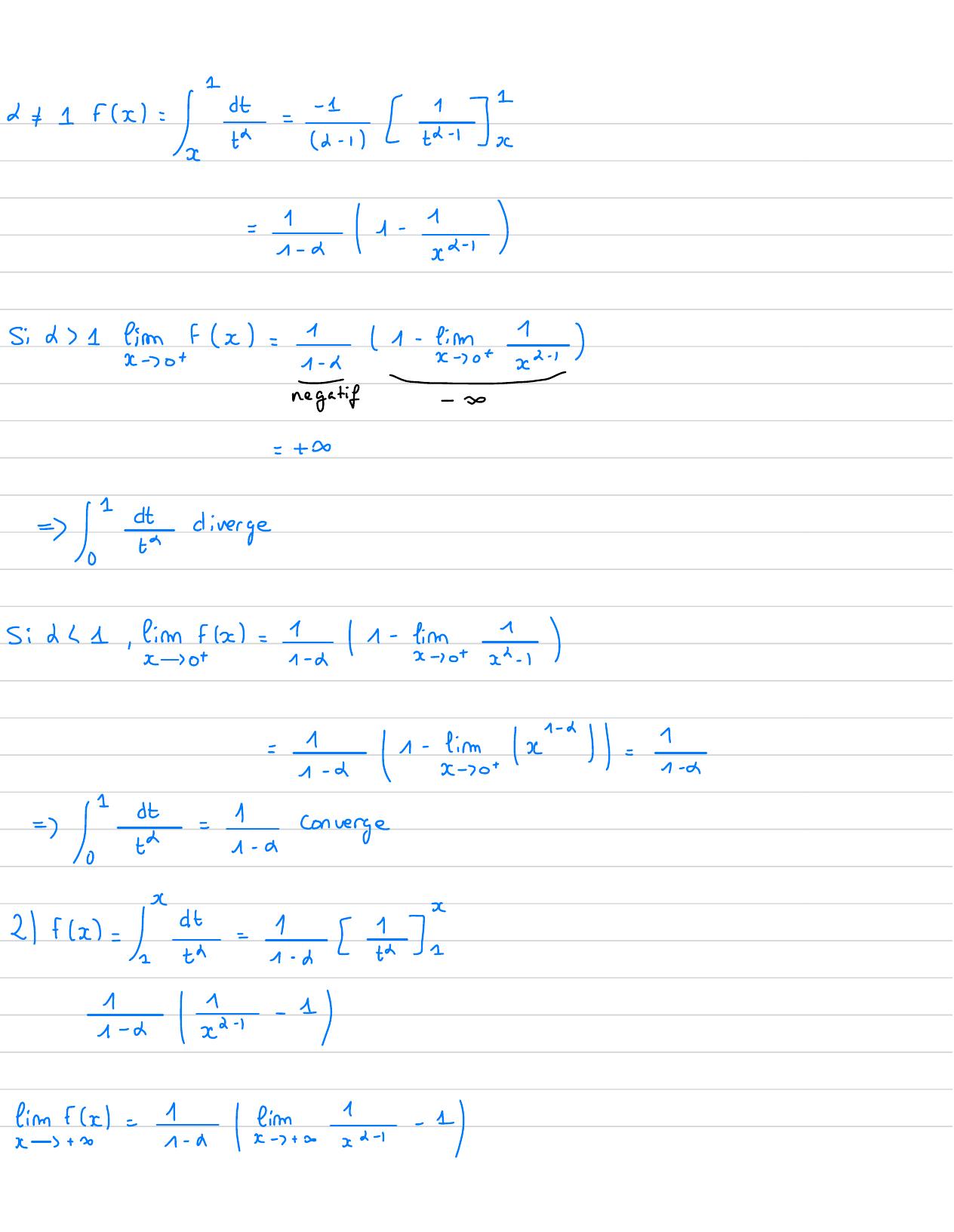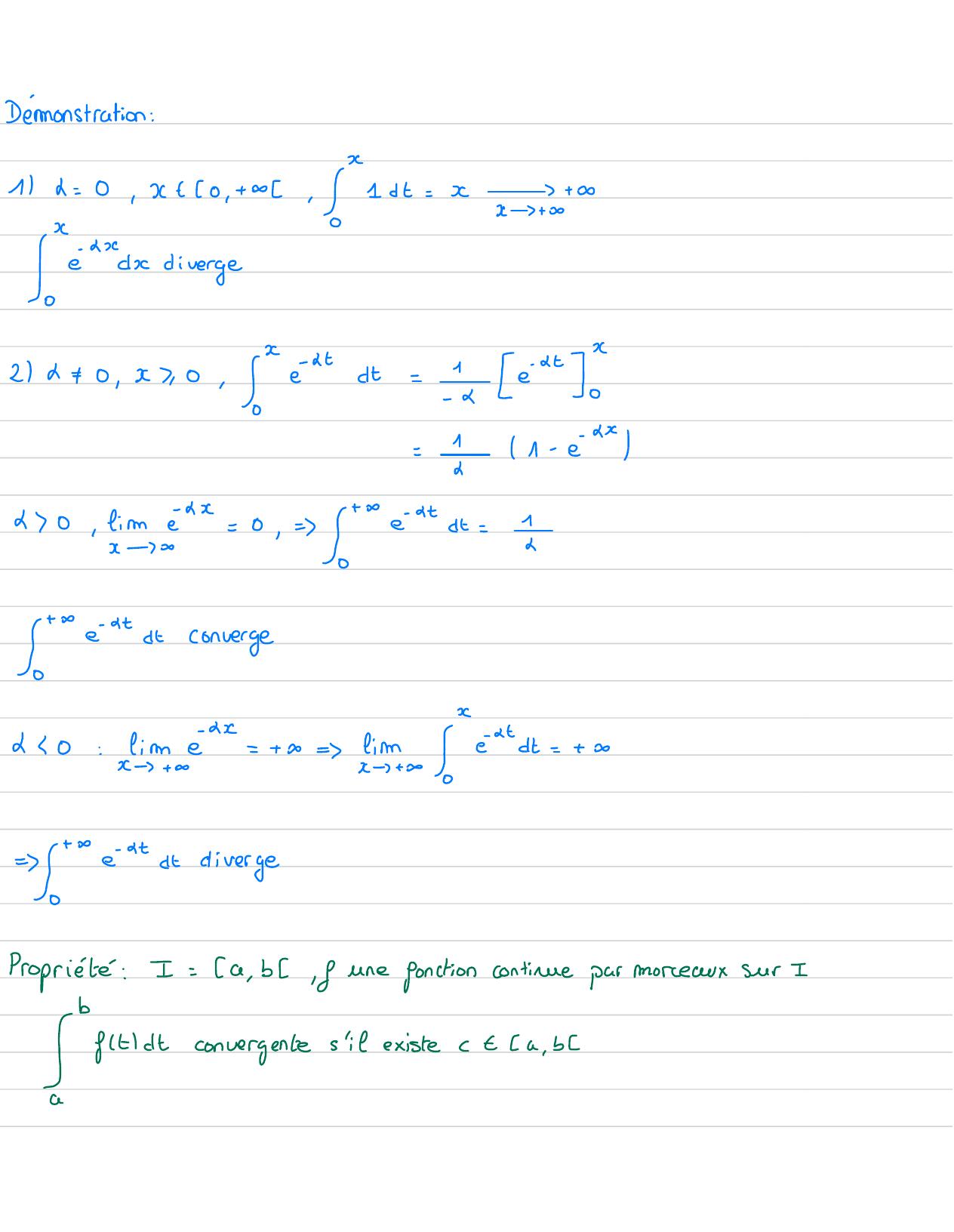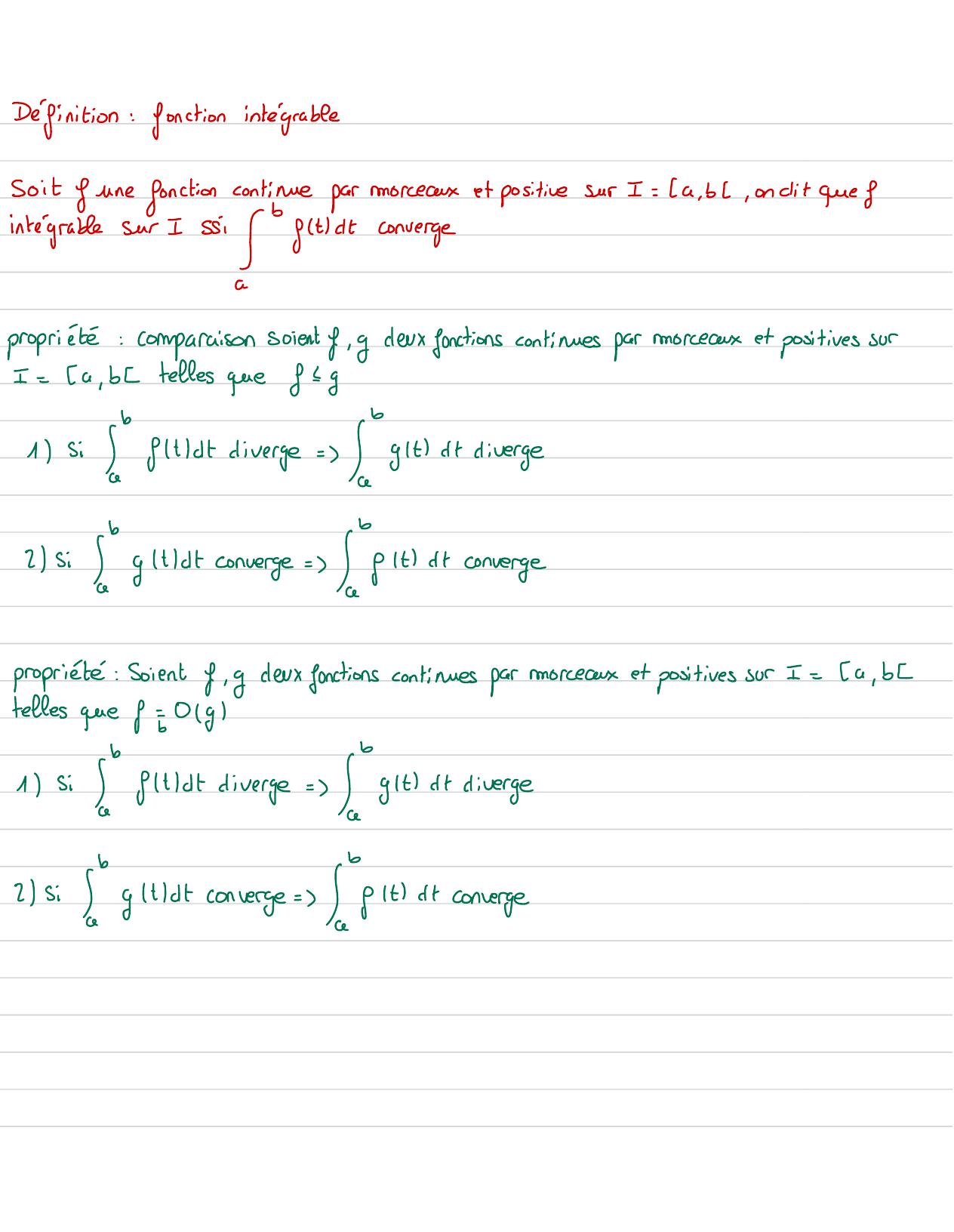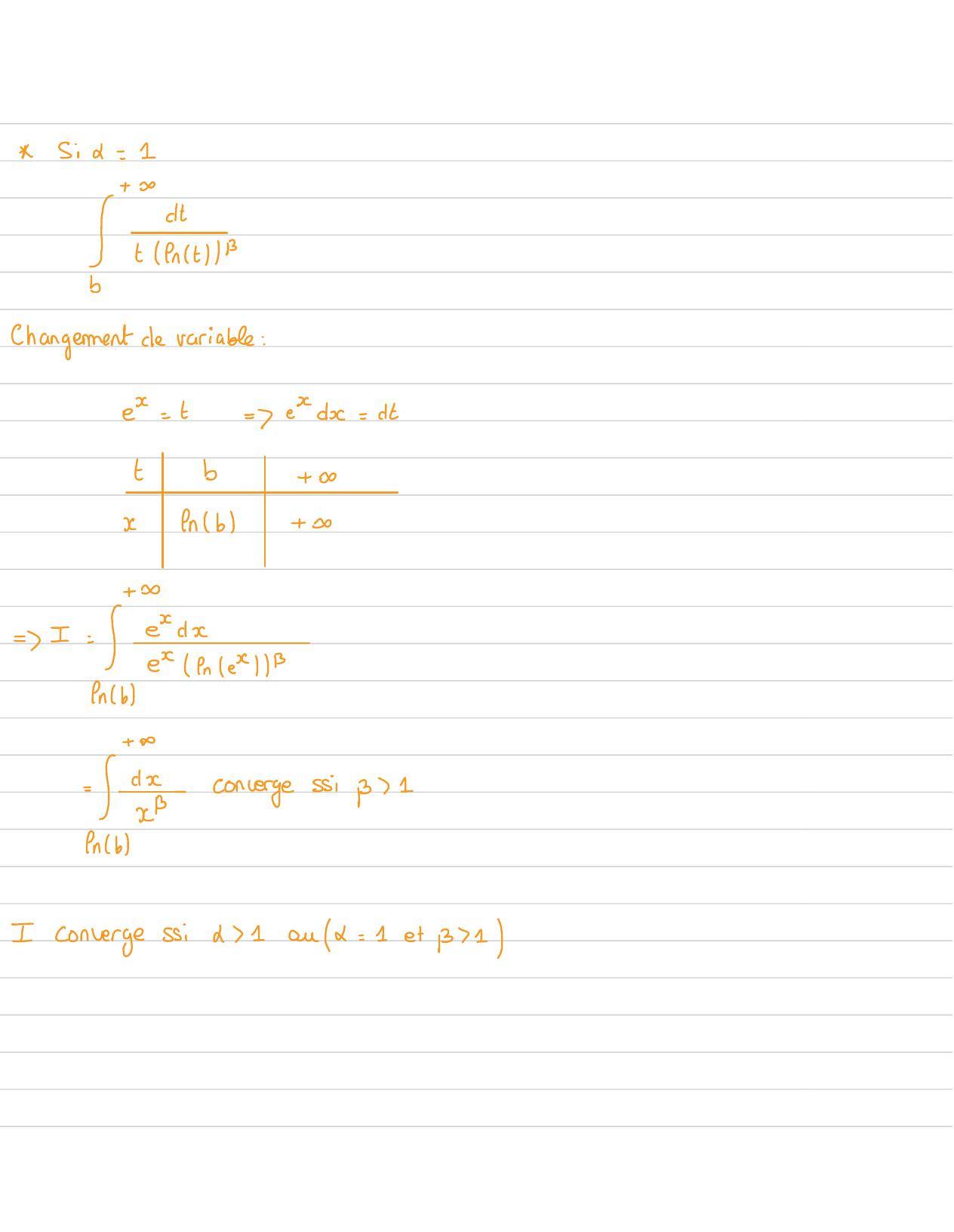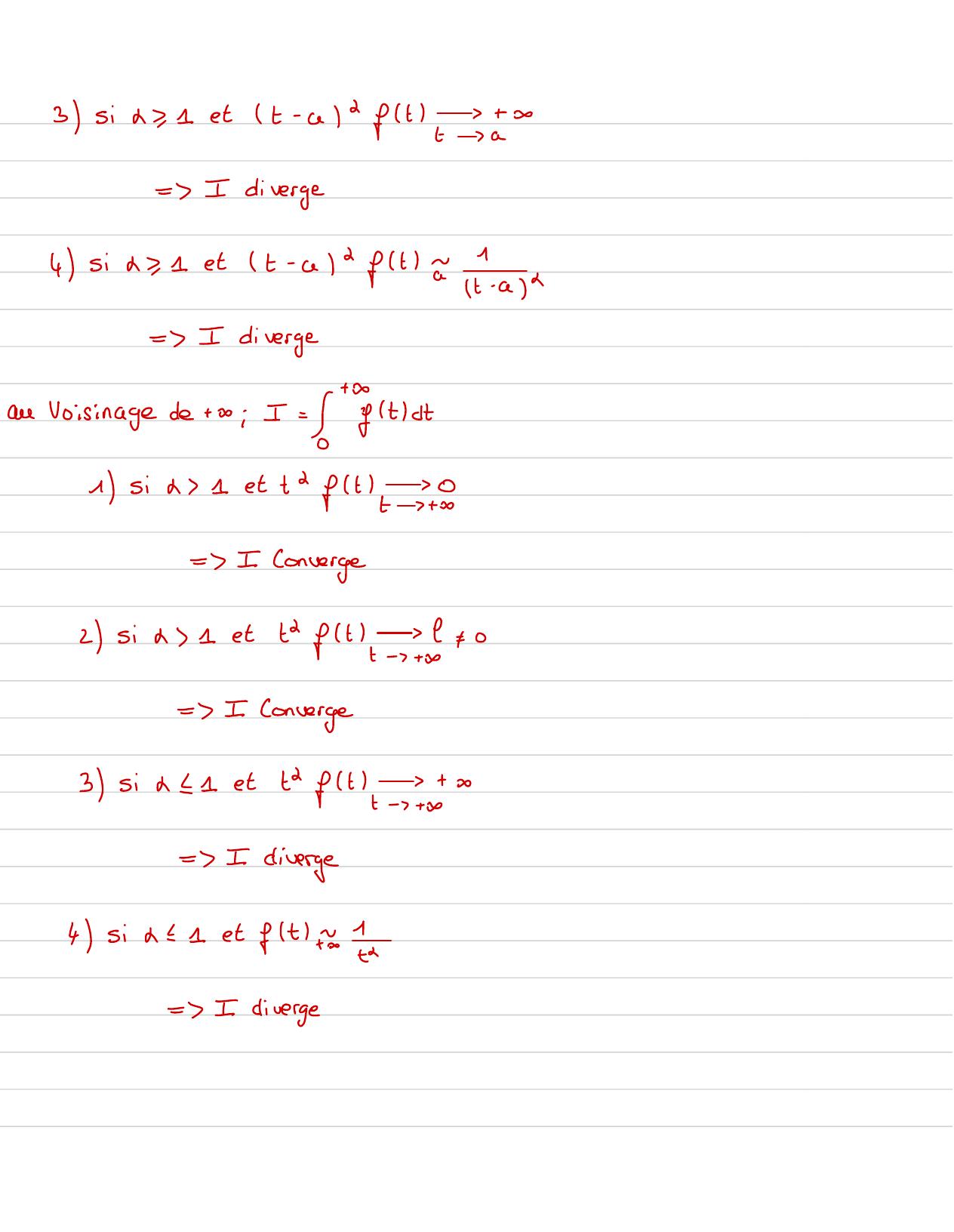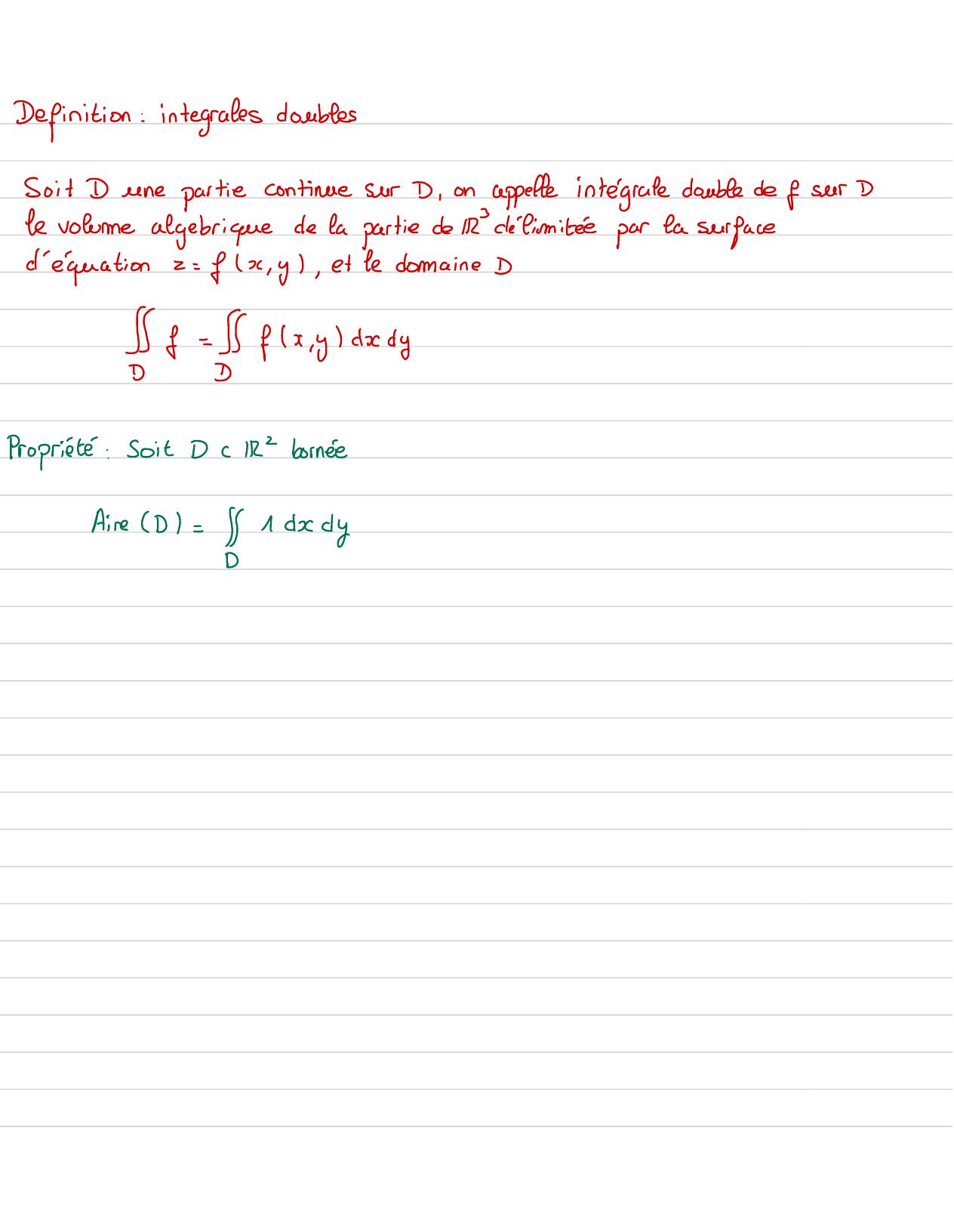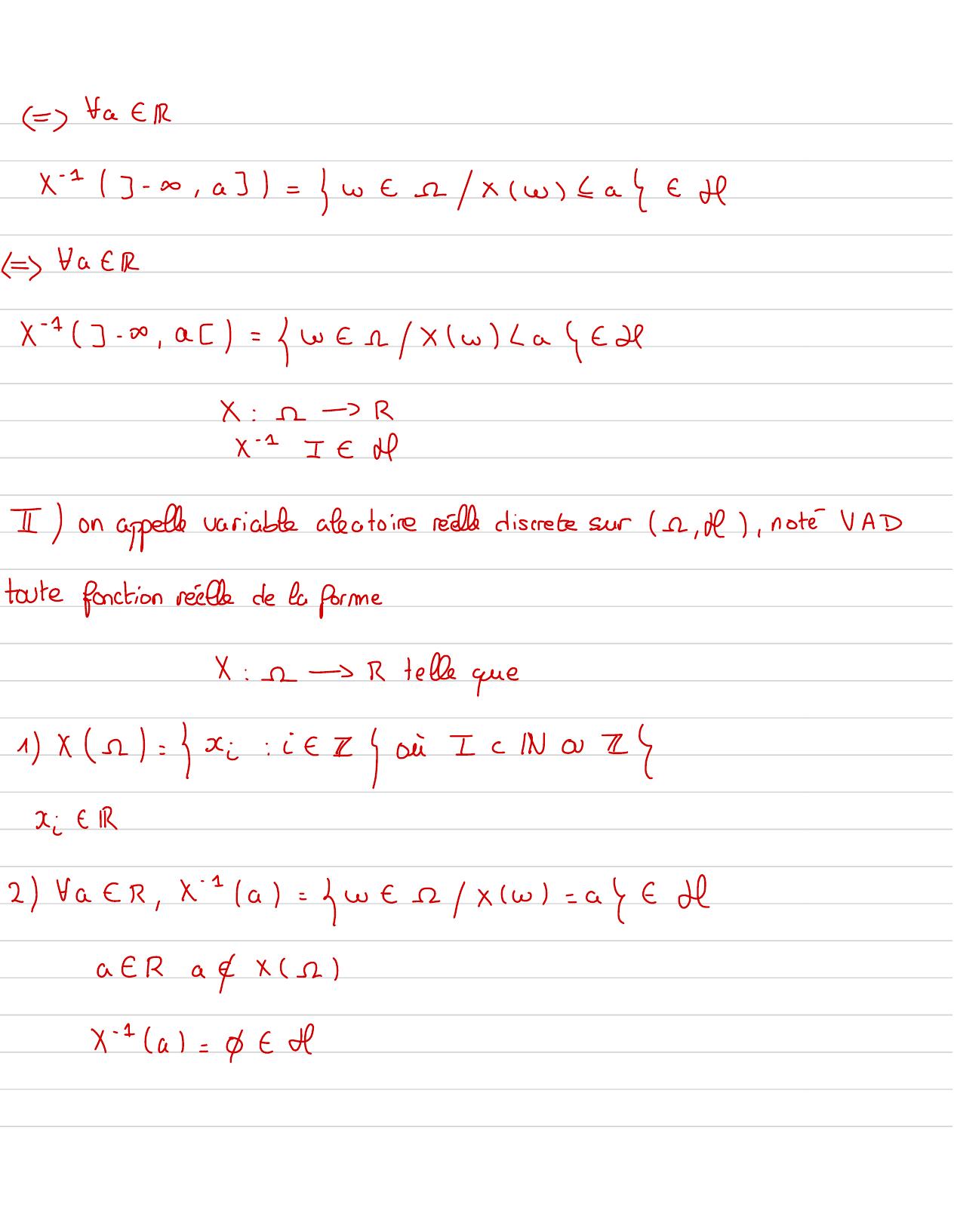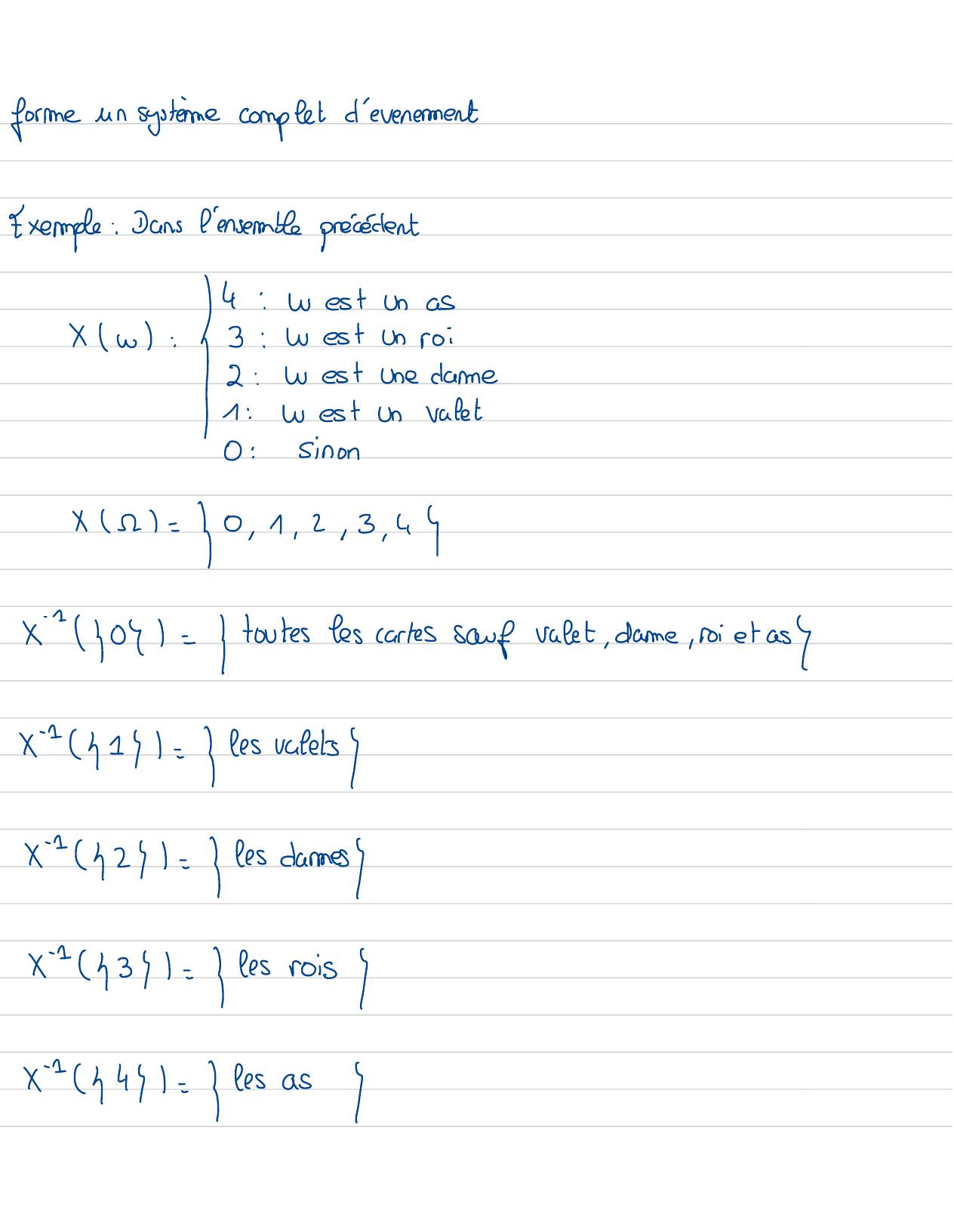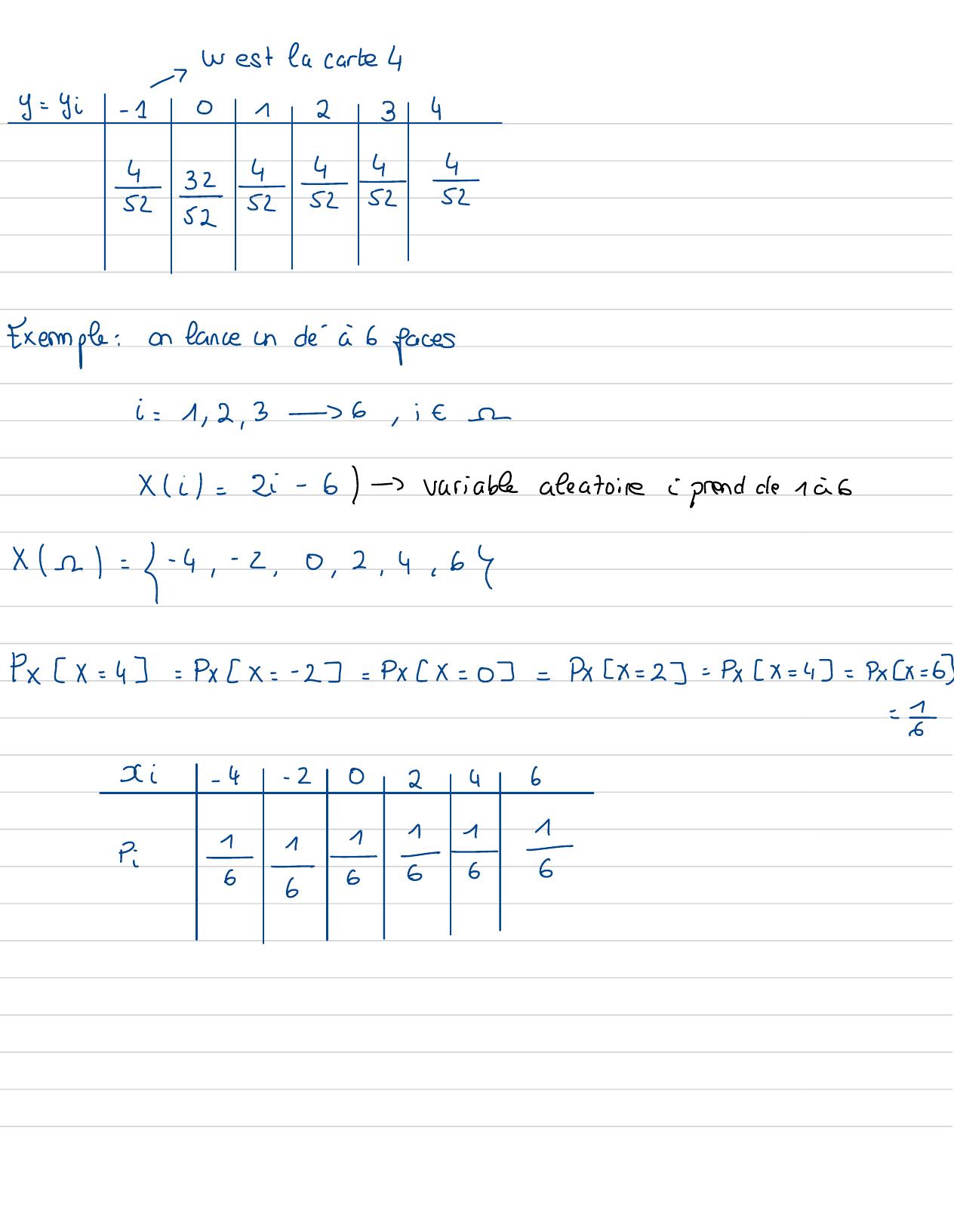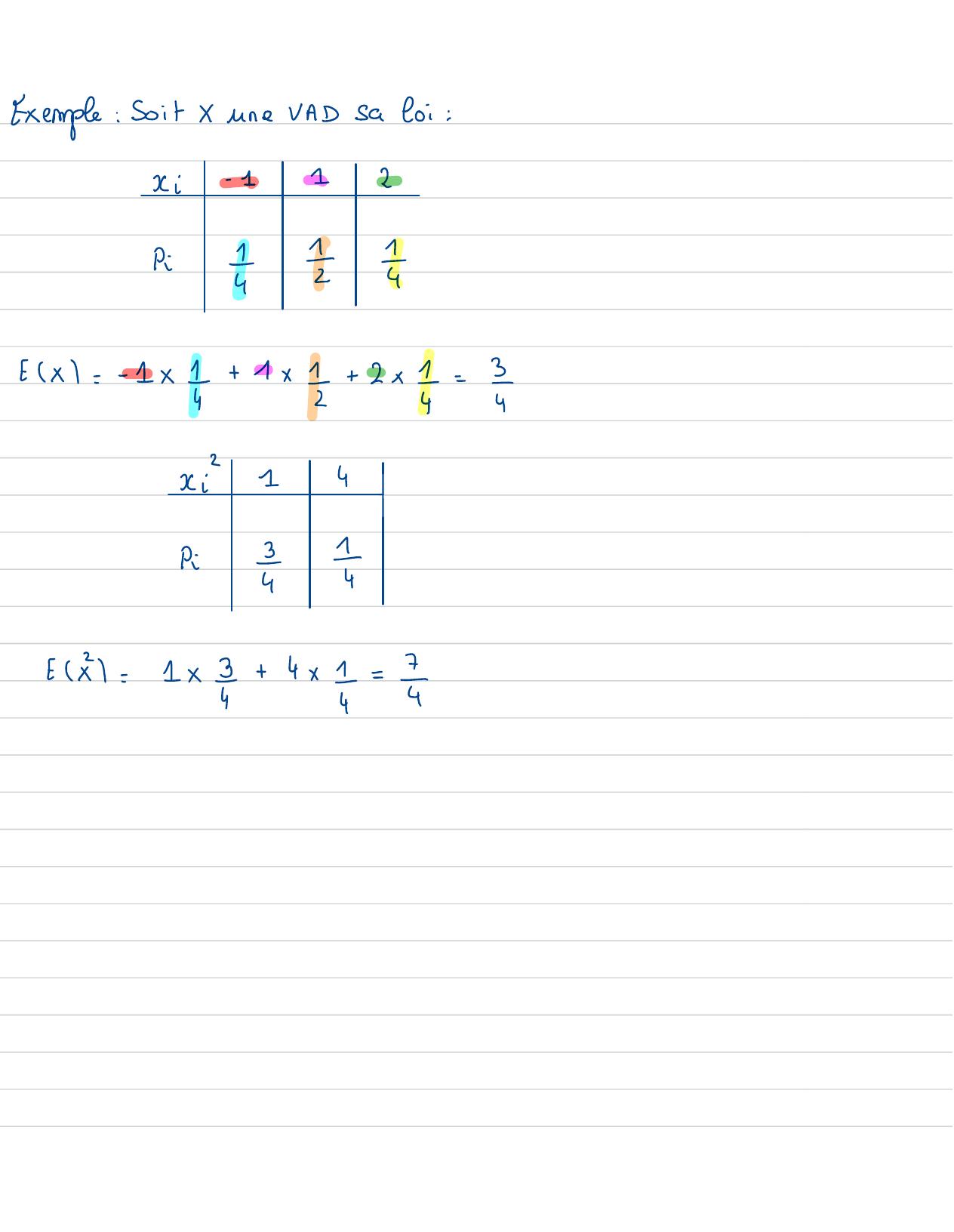CM Annotee

Télécharger le CM Annotee en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

Page 1 : Intégration et probaCM2022- 2023

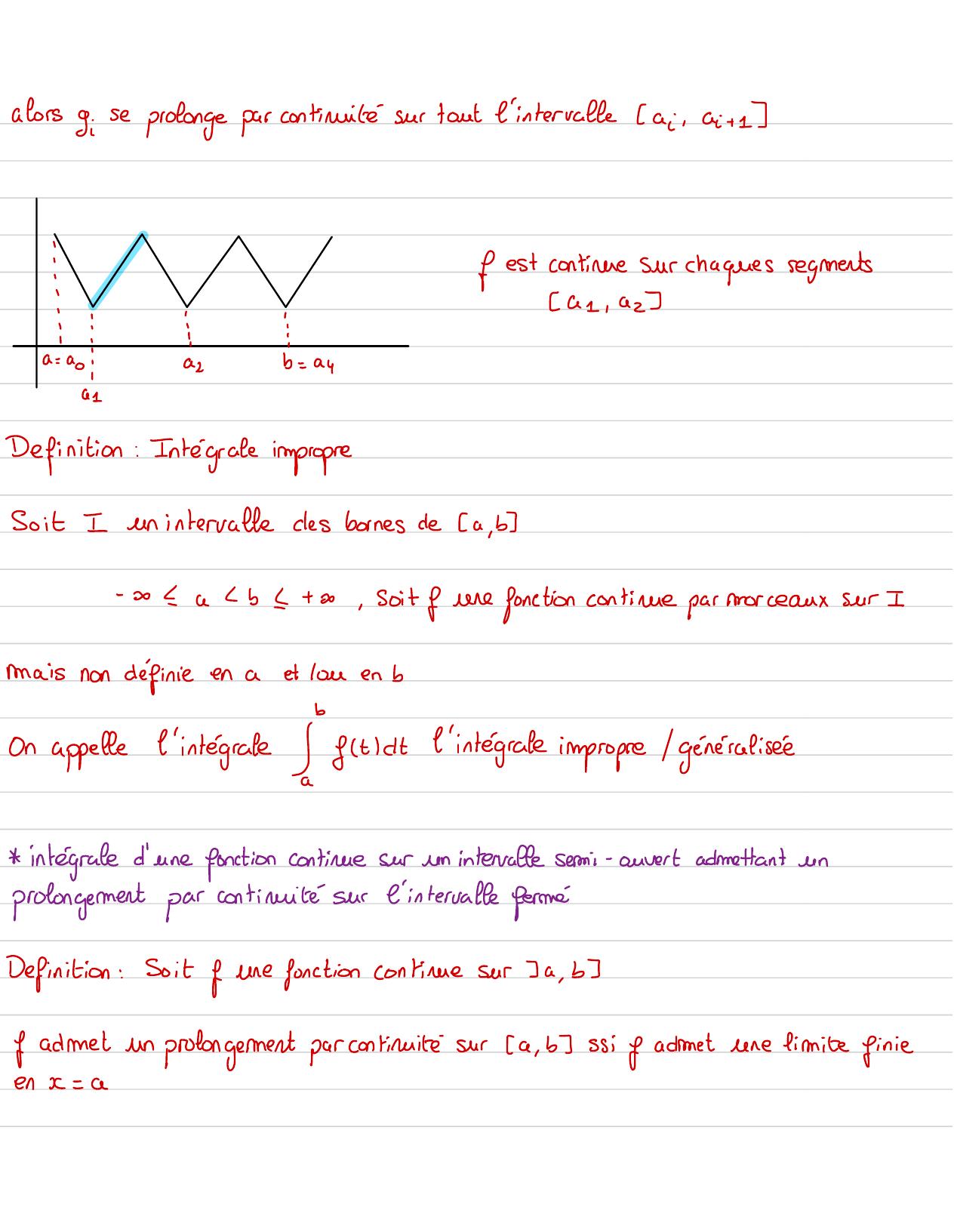
Page 2 : Chapitre 1: Intégrales généraliséesimpropres+ -SElid,flid.flodic,-I fluidiou fn'est pas définie f n'admet pasune limite finieen aCExemple:S1I1:fx=,pas définie epasde limite finieen 02 :fx =I S1Definition:continue par morceauxSoit f:a , b IRune fonctionIest continue par morceaux s'it existeunesubdivisionde l'intervalle a , bde a , b-Go= a a... an= btelle que Fi=0 ,..., n-1 sion pose = f J ai...., ai+1

Page 3 : alors g:se prolonge par continuitésur tout l'intervalle Lai , ai+afest continue sur chaques segments"nzan201 , 02Definition: Intégrale impropreSoit Iun intervaltedes bornes de a, b--ab+ 1, soitune fonction continue par morceauxsur Imaisnon définieenaet louen bon appelle l'intégrate gitctl'intégrate impropregénéralisée intégrale d'une fonction continue sur un intervalle sermi-ouvertadmettant unprolongement parcontinuitésurl'interrafte fermeDefinition:Soit fune function continuesur ba, bf admet un prolongement par continuitésura , b si fadmetune fimmite finieen 1= a

Page 4 : le prolongement par continuité de f sur a, bfx=fx:x--3a , bE eafx :aRemarque:mêmechose pourinterraftea, bThe o rene:Soit I continue sur Ja, b7qui admet un prolongement parcontinuitésura , bnoté I, alors fadmetune intégralebbbfitdt=a fitdt= fittxThéoreme:Soit f continue parmorceaux sur a, b, alors f admet une intégraleSur a, b definie parb-S gltdt-kitstldt-stat casdes intervalles semi-ouverts, on se place sur des intervalles de typeI=a , b, avec be RUG+ bComore chosepour I= ba, b, at 189-0

Page 5 : Definition:Convergence et divergence1=a, b, beRU+ 3Soit f continue parmorceaux sur I If définieen a et pas definieen b. Soitfix - /" gitatOn dit que/ ftdt est convergenteIS"fildexiste ,1convergenteSit admetune limite finiegrandesb ,avec-a , b2Danscecas tai gilat=fins"gitat=elginieDans ecas lä, l est la valeurde cette intégraleDans lecascontraireon dit quel gltdtest divergente

Page 6 : Théorème: 2 1Fat 61,+ 02. !"= Artant=Arctun x- Arctan 1= Arctan 32- /limdt-Arctan-t 2+1=I - ==gitdt =Théorerei1 I estcontinue sur La , b2, a, b EIR telfe que oest prolongeable par continuiteenbIm fleginie ,fltat converge28 estcontinue sur Ca , +3 ,onasigitdtconvergeet fis ft= 1 finiealors=0

Page 7 : Autrement bit:S: li ft existenon nulle,alors+ftd divergeCcontraposédu théorème q2au dessusExemple: Ietft=2t+ 1continue sur 0 ;+ 02t+ 2imgt=2+0=3 gtdt divergenteDefinition:Soit: Ja, bC1continue par morceauxaveca , be1R09+ byon dit que" fitctconverge s'ie existeE7a , btelque fltat etb↳filatconvergeDansce casgitct=1"gltct+gtct

Page 8 : Intégrale de référencepropriété /Intégrale de Riemann1 Iest convergente si11Sdt-10th1- 2+2et est convergente said 1Sdt-1th2- 11Démonstration11a= 1=3= fin- Simonen t=fim-fx=+ 0x -30t= !tdiverge

Page 9 : c+ 1+ xx== i=- 7 -=I-a1- - Sid1firmfx=11- liECx- 01- 4x-70t2- 1- -negatif-=+ 0=divergeSith 1, m= 1 -/1- +--I-a1 - =4-a= !.=11. aConverge21+1xEn eSin, l=- Lien- H

Page 10 : 1 & 1 ,+oc- 1=0=im fx=1D3+ xL-1=+It=1Sta↓- 1converge11- 21 1, him1-+ Ix- x+ xx+ 1= Im+I=lim fx=- 3=!etx- 7+ xtadivergente6= 1, + dt= ms"et= Centt1=eimnx- 0=+ 3=divergenteRemarque :1 ↳astavecasoest convergente si Le+0, a zoestconvergente si =a

Page 11 : Propriété: logarithme néparien-Intdt est convergenteSen1tId=- 1- ↓I It dtest divergenteDemonstration:la primitive de In ten tdtI. P. P /intégration par partiel:av'dt=av-/n'vdtx1dter= entde=dttdV=1dtV=tftdt=tenct- /t-tent -/dt=tfnt- t+ a

Page 12 : fx= /-fntdt= tet- t,-=1- xnx+ xPfx=- 1+ fimx- xnx- 30 , =7= enstdt=- 12yx =ftdtgx= tfnt- t= xx- x+ 1firx -+ygx= enxnx- x+ 1=inx- 1+ 1 == 1en 1tdtest divergentePropriété: exponentielle!+ c !tConverge si 0!+0-!t=2

Page 13 : Démonstration :x3 +11h=0, xt0 ,+ 0. !"+dt=x3 +"da divergeI21a+0, x,0 = 4 xt=e!I11- -G1x20, limé=0,= + =4x0S-- c !converge⑳60: limé=+ b =!" étd= +x -+ 0=-e c !diverge⑳Propriete:I=Ca , b,f une fonctioncontinue par morceauxsur II fitdtconvergentes'it existe t a, ba

Page 14 : tel que itlatetgitlatconvergentCbbdanscecasft1dt= ft1dt+ftdta2cas des intervalles ouvertsI= Ja, b,- x-ab1+ 0Definition:Soit o une fonction continue parmorceaux Sur I= Ja, b,on ditque ! fitdtconverge si:Jctba , btel que fitat ,gitdt convergentS811dt=Sft1dt +SftdExemple: S. IIt 30 , 14un sent pointde singularité ici c'est o1/2StaSes assiseset eStatongltdtdiverge

Page 15 : Cas général:intervalle quelconquePropriété: finéaritéScient f, g deux fonctionscontinuesparmorceauxsur intervalledebornesab, I, FAtsigitatet /gitatconvergentalorsYft+ gt dtconvergeYfz+ xgtdt= ftd+ xgtttExemple: ft=2tr - zEr- e =++S inzdiverge. rdivergeSiten it-Intdt-"-!" i

Page 16 : =ent-1- en t+1=frx-1 -fx + 1-en 1- fnz=en 1! + 913i gites=Simen i ! + en 3=en 3+Ix= gltd=en 13Convergegiter=Propriété:Scient f, g devy fonctionscontinues parmorceauxsur I ouvert desbornesa btelles que /fitldtetSgtctconvergentab1SipositiveSur I= fitat, 02 siggser = gita / git

Page 17 : intégraledes fonctions positivesdes signesconstants Soit& fonction positivesur a , bC, b+ 3mêmechose sig définiesur I a, b ,as- 0Propriete :Soitune fonctioncontinue par morceauxet positive I= a, b 2.5 M 0tel queFace da, bC ./"giEldt -=!gltdtconvergeDemonstration: I positivesur If= xic gitldtet strictementcroissante et majorée par Malle admetune limite finie enb.=fitdtconverge E - admetunefirmite enb, et commune f eststrictementcroissante=f est majoréeSur I= a , bRemarque: sig negativesur I=a, bLit suffitde travailferavec- -70

Page 18 : Définition:fonction integrablesoitune fonctimeclinepar moteauxexpositivesur I= Ca, bL, onclite etintegrablesur I si-propriete: comparaison soient f, gdeux functions continues parmorceauxet positives surI=a, btelles que8 Ig1Sigltdt diverge =git d diverge21s:gitldt converge =gitet convergepropriété Soient f, gdeux fonctions continues parmorceauxet positives sur I=a, btelles que 8 50 91Sigltdt diverge =git d diverge21s:gitldtconverge =gitet converge

Page 19 : propriété: Scient f, gdeux functions continues parmorceauxet positives sur I=a, btelles que 85 019en = o1Sigltdt diverge = glt et diverge21s:gitldtconverge =gitet convergeExemple: Trouver fa naturede I="in E atft= sinEpositiveet continue sur30 , 17An roisinage deolimsin1/t=0t-0↑=sin1t= 0YE!0= !sin 1/t et= fitdtabsolument convergenteRemarque: Soitfrune fonctioncontinueparmorceaux ser I: Ja, b, italtestabsolument convergentesift1dtconvergente

Page 20 : propriete: Soient f, gdeux functions continues parmorceaux et positives I= a, bonsuppose que ghe s'annule pas sur ISig 59 =ftdt et/gitlatsont de même natureExemple: 1ft=EnpositiveetcontinuesurC1, +02en+ 1:hirft-lint2=1t -011t2t -0+2+191tto InmaisetDt2= idt0Fx- 1,+ 0. ?= Ardant=Arctanke- Arctan 1=Arctans- Iima -im Arctancull-I

Page 21 : -Exemple: .yconvergentecar définie et continuesurun intervalleIfermé 0 , 1adt etCoI t v1t2 + 1+ 0+ 2.Tedtconvergentecaret convergentesSt-idt +Et1Propriété: regtede Rierannen asoitune fonctioncontinueparmorceaux et positives I=Ja , bavec alb1 s'ie existe1tel que /t-al ft20t G= ft atconverge2 s'ie existe, 1tel quet -alkfta+ 3t G= ft atdiverge

Page 22 : 3 Siit-aldftfER bconverge sid1=fltdtest E divergesi 2, 1Propriété: Regle de Riemann+ ofestcontinuepar morceaux et positivesur a, +32a701 s'ie existe d1tel quetft0t0= t atconverge2 s'ie existe 61 1tel que+ 2ft3 +t7+ 2= t atdiverge3 Sitg1t - !convergentesi GL 1t altestEdivergenteSiG 1 1

Page 23 : Propriété: function de Bertrand+ 0dtS tft/Bavecb=bestconvergentesidh1a t=1et1Demonstration :ft=1=entBcontinue et positivesur b ,+ o Sid=, 55= 41telquelimgit=hir1=0t + xt + x to2ent B=l'intégrate est convergenteSid1, 75=d+1 122+ 15t2lim I ft=lim=0t + x+ Y/ntB1 - 20-firmt2=+ yparcroissance companiet -+0ent=l'intégrate diverge

Page 24 : Six= 1+!dttfnt/BChangement de variable :e=t=edx= dttb+ ICfnb++ D= I = edfnb&"In le /B+dx:converge si 1nbIconverges: 1ou d= 1et1

Page 25 : Propriete: f fonction continue positivesur I,et fetconvergentealorson a fdt= 0= 1=0Sur I fonctions intégrablescas généraldes fonctionsde signe quelconquesur un intervalle quelconqueDéfinition: Soit June fonctioncontinueparmorceauxsur un intervalle IdesbornesacbOn dit que fest intégrablesur Issi:ftetTconvergente=PftdtDans ce cas , on dit que It etest absolument convergenteaCas particulier: f positive↓fltdtconvergente a "fItatbEabsolument convergente

Page 26 : Theorêne: Règle de Cauchya, b-RxRU+04 albSoit o unefonction définieet continue par morceaux ser da , b,donafit altest convergente si: 370 , 5 ct a, b, Fv2, rzt c, dCavecU1Uz=gittPropriété: inégalité triangulaireSoit o une fonction continue par morceauxet integrable sur I IIfldt0alors/fItdt1gEItIIPropriété:Soit o une fonction continue par morceauxsur un intervalle Ide bomes a bsiest intégrable sur IaforsI.fitatconvergente

Page 27 : Demonstration :aSitatconvergented'après Carchy, FE0 , 5c-da, bdtel que Fr, utc, ddavec esvbgtdt3, /ftdt&eVjg1txtftdt= Yftdt = fittm inégalité triangulairee=ftdt +/gtdt-gtdt +ftdtx+y=x+y=gtdt+ /" ftdt23V= f1txt 23d'après Cauchy IItdtconvergente

Page 28 : Definition: Intégrate sermi-convergenteSoit f une fonction continue par morceaux sur un intervalle Ide bornes a bbon dit que ltdt sermi-convergenteSs: l'intégrate est convergentemais n'estpas absolument convergenteIf n'est pas intégrablePropriété:finéarité et croissanceScient f , Ideux fonctions continues parmorceauxet intégrables sur I1 +x +, xft+ gtdt=xfta+1gtdt2 si f, 0 Sur I, alors ftdt, 03 Sig, gar I, afors fitldt,/ gitdtPropriété: Règle d'AbelR= Rug+ 07Soit a , b ERxRa b, Soient fet gdeux fonctions continues sur da , b telles que

Page 29 : 8 une fonctionpositiveetdécroissante sur La , bteffe que,fin-fx= 0x 6x= /gtdt est bornéeSura , b2a= f. gest intégrable sur a , b1gt at convergenteExemple: I: Isinctetgt= sint ft= 1/t70cmr 1, +0 decroissanteS eint =gt =sin Itdt= ScosCtIS=cos1-cosxbornéesur 1, +37, 1,6x=0s1+ 1= Md'après Abel= sinit'etconvergente

Page 30 : Propriété: Scient fet gdeux fonctions continues parmorceaux ser I telles quef , gsont intégrablessur Ialors fgest intégrable sur ISIIgItat"IgIttgltdtII ft, gt= lig,. lIgIzf, g= 1ftgtdtproduit scalaire1211812: fit'dtCalcul pratique des intégrales généralisées1 utilisation d'une primitivesoit fune fonction continue parmorceaux sur I= La, b2et fune primitive def.ba ftdt= lim fx- faxb- Sif continue sur Ja , bPft dt=firmfx- imfxx b-xat

Page 31 : Exempleto1+ t 3=Edt+I = 13 tdt361++ 3= im+05en11 + 73 !=limn1+ x ==I divergeChangementde variablesoit fune fonction continue parmorceaux ser I, y une bijectionentre Jet I7: 5 c Ideclasse F sur J.sif intégrablealors on a7:JIext=4a181td= S141r11xyalde

Page 32 : Exemple: I= 6+2- tbty= -t0+dy= 2tdty0+ 0+ AI=dye= I 6= Ydy= 1é3=1ime- b- 1= -2y-+ 3Intégration par partie:soit f, gdeux fonctionsde classe csurJa , bba ftgtd= gtft- -g tgItdtprimitive: ft gItdt= gtft- fitgtdEExemple: I= /Arctantere=Arctant, r=1ev=dt,V= t1+ t2I= ↳Arctant-+,atI=tArctant-I+,dt=tArcant - n+ 2+ 1+CCERR

Page 33 : + Arctantdt= Icar definie-lim-I101firm tArctant- 1 fr+ 2+ 1t- x+ 3-+ 03+ Xfirm tArctant- 1en t+ 1t- x+ 3=+ b1- 0=+3=Arctan Aldt diverge↓ArctanstIdt= tArctantIdt!Exemple: Determiner la natureet calculer sa valeurI =Arctant'dtt21ft=Arctant0, continue Sur 1 ; +-

Page 34 : Voisinage de+ 0:t2 ft= Arctant= 3 24= +dtconvergeI= Arctant teArctantv=172+ 10 =1/t2v =-1-2gt=-1Arctant +4dt t2+ 1t1Cit+ 1 + Ett1tat+ b-+Ct2+ 1t 2+ 1t=0=7c= 1tx+y=70=a+ c=7a=- c=- 1t=1=31= Ia+ b+ c1=a+ b+ 2c=a+ c+ b+ c

Page 35 : =1+b+ 1=b=0gt=-Arctant +I-E2+ 1 dt=IArctant + frt- -nt+ 1=- 1Arctant+ Intt2+1SArctanitat= insArctan't at=findArctanes+ence--1xπ+ edi ! Arctanx=0+Hi, s21=en 1=0I= 4- n != =+ en52Propriété: comparaison serie- intégrale Soit f une function continueetdécroissanteet positivesur Cro, +0 Lfin et of statsont de me nature

Page 36 : + 0E1n = 0n2+n+ 11ft= t+ t+ 1positive ,decroissante 0, +0 Let continueSltdtt2x1-12+ t+ 12= gitdtconvergeRésennean Voisinage dea: I = ftdt1six 1ett- adfta=I Converge2 Six 1 ett- adft2 =0=I ConvergeIf Ita-ala &

Page 37 : 3 Six, 1ett- adft ! â-=I diverge14Six, 1ett- adfta i-a=I diverge/an Voisinage de +o ; I= gitdt1six1et + 2 ft+8=I Converge2 six 1et t2ft 2+0t-+y=I Converge3 sin 1et t2ft+ -+0=I diverge4sin=1et ftEn=Idiverge

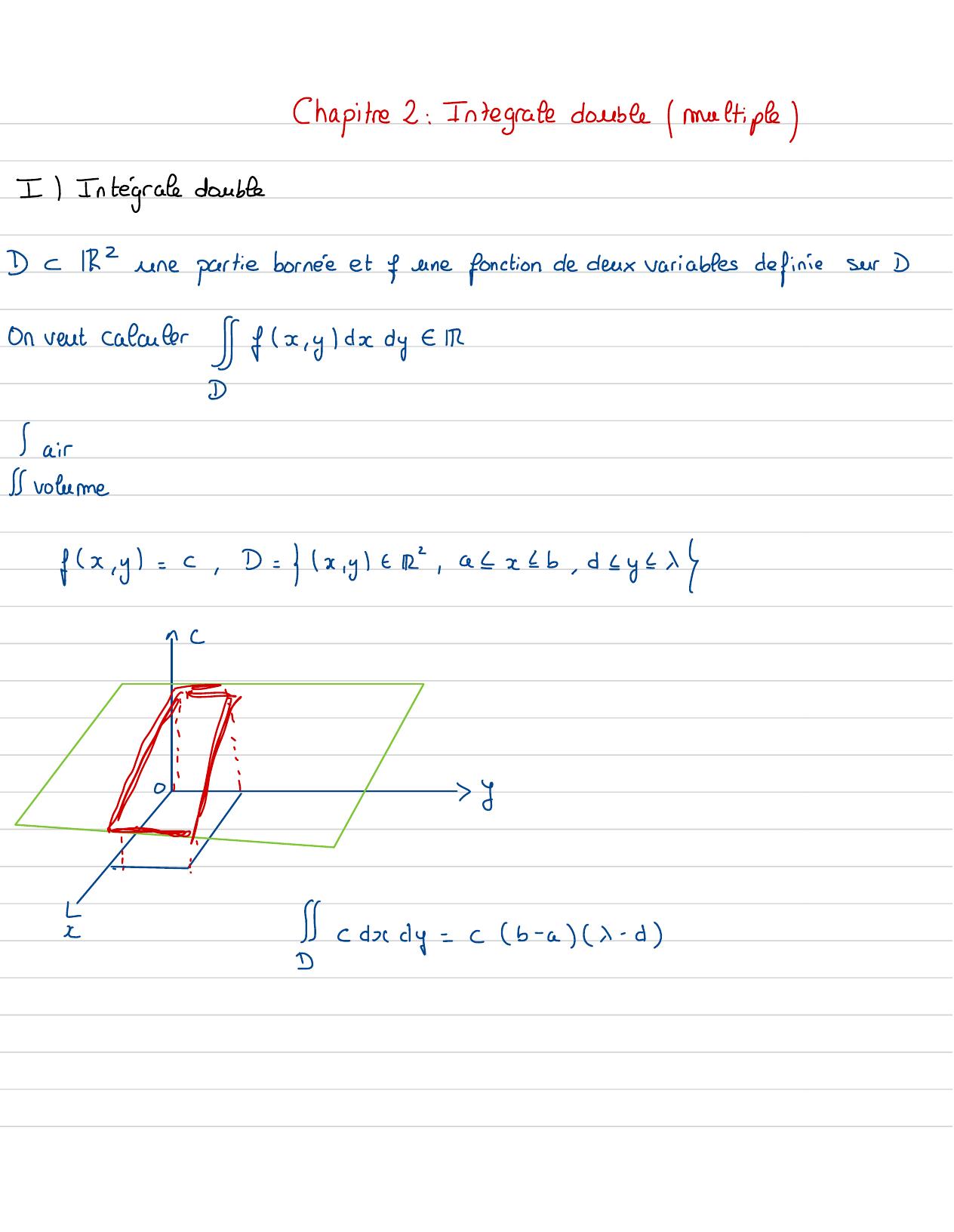
Page 38 : Chapitre 2: Integrate double /multipleI I Intégrale doubleDIR2une partie bornée et f une fonction de deux variables definiesur Don vent calculer fx, ydx by1DSairIS volumefx ,y=c,D= x,yt R, axb, d-y2 xnC⑮ycady=cb- aX- d

Page 39 : Definition: integrales domblessoit b unepartiecontinueset anappelleintegratedoublede feetd'équationz= fx , y,et le domaine CStifx,ydxPropriété:Soit DCIR2bornéeAireD= 1dxdy

Page 40 : par pileici integration par pileavec 01111Exercive:Calculer l'intégrale:411 y=fxfaire petiteeqIpour trouver lesbornesIfx+ ydxdyavecD= x ,y 1ER"- 5,0-7257y= xMy=x2on represente ledomaine:y=x-= 5ut0x= ⑮C= x3=x4=x- x=0= x,- 1=0x= 00= 1=7x=03I x- 1x2+ x+ 1=0-,0=x=0,x= 1tes etae--2xy+ 2yx= ix+ 1x- x"+ 2x"dI:3324 xx=! x++ Ex- -= =+-=2318-10= 284= 30

Page 41 : Exercive:Calculer lintegrate:par trancheIfxcy xdyavec D= x,yex!-xy=x2on represente ledomaine:1-= 5....↓pileon tranche le coraine&8 "reste le même /01y=x, y= ⑮con vert suvoirx=0= y= 0or y varie etx=1=7y= 1pasX01y? 1y= Exc=-x= y2/y= x=x= 0fx ,ytD02y= 1,y= x= VI-+ylddpartranche yest constanty=2 !+ yxxx= y+ yx- y+ y1=By- 3y0- y44=iy- 23- 72i- 2- +=8-25=84x8- 25x1533-158415x84140

Page 42 : Changement de variableThéoreine:SoientU et V cR des ouverts9: r cv ce fermothism Sont deceasseY changementde variableentreWet VSoit DcRune partie bornée , Dc8:YD iune fonction continuefx, ydxdy=8Yx, 01Jye, vdede4D↳le jacobien4: eVu , vYx , v= x , yD4 , xg= f04Isitgu , v=f04u, v=fyu , vfx, ycxy =f9n, v5ye , vdidyYDmultiplication

Page 43 : Exemple:==i!,dxdyorD= x, yERYx, 0 , x + y- = =b= x, 0=- yx+y= 1equation d'un disque"I1 Trouver le domaine2 Jy e , v31fx , vx,y=x, 0, x+ y2= 1=u0, x+- V2= 1 r, 0, x2+ v2= 1=u , vtDYCe , vx,y= a ,- vsye , rs=or10=10-1y- 8-fx, y=x+1u2+1

Page 44 : fk,yldcaly:/ +1=deCommeD= D= I=- I=21=0=I=0Changement polaire, 01: x, y=rcos0,rsin 0r , 0, 0 t 0, 242syr , 0=Y!8-cos0- Usin 0ISin 01rcos 21?=cos 0 +r Sin 0Exemple: I=x y exdyDD= yx, y12/x+ y2= 1cos0- rsin 0x= rcos2, y= rsincaJyr, 0=-↑sinalrcos 0

Page 45 : x , ytD=x+y2 = 1= rcus'0+ r sin 1011 11=7r2= 1 =02r11, Ot0 , 24= r , 01-D= r, 0t + x0 , 25

Page 46 : 1on dit que Ai :.sont indépendantdeuxà deux Si Fi, j ek1, nitjAi et Aj sont indépendants↓On dit queAiYYsont mutuellement indépendants sisous-ensembleIck1,n D,onaP=A : == PAiVariable aléatoires réelles: fonctionsà valeurs riellesX: 1 - RSoit 1, M1un espace probabilisableDefinition:onspelle variable aléatoire réellesur Ter , Je, note VA ,atoute fonction réellede la formeX:1-IRtellequeFI c Rx-111= wee/Xwt= 7- +

Page 47 : = FaEIRx- +j- 0, a3= w- -xw2ae d↳= Fatx- = 3- x, a= we 1/Xwae2X:e- Rx- 1I-Hon appelle variable aleatoire réelle discrete sur , M, notéVADtoute fonction réellede La formeX: e- R telle que1 X - = x:- 0 IcNa 14D: EIR2 FaCR, xa= w= -/xw= abeaatR afXrx- +a= 0&

Page 48 : Remarque:1x-144on te note X= as↓image reciproque quand X= a2x-7- 0, a.onnote x a3 x" 3 a , b,on te note aX= bExemple:on tireau hasardune carte dansun jem de 52 cartes↳l'ensemble des 52 cartesà chaque cartes were, on associe XwI4:WestunasX w:3:Westun roi2:Westune dane1:Westunvalet0:Sinonxr= 30, 1,2, 3, 44Proposition:SoitXune VAD tel queX - = x : /i= 1lesensemble X x : 4i= =

Page 49 : forme un systeme completd'evenementExemple : Dans l'ensembla précédentx w: / .Westunaswestun roiwestune dame1:Westunvalet0:Sinonxr= 30, 1,2, 3, 44x1 3 031=/toutes tescartes saufvalet, dane, roi et asyx- =1= les ratelsx- 421= les daresx- 431= /les roisx- 441= /lesasI

Page 50 : Loi de probabilitédeVADSoit m, H, P/ espace probabiliteSoitXVAD Sur 2, 69xr= xi/i+ IfaER/PxX= a= PX-kay= Pw- -/Xw= aSoitP:= Px x= x : 3Fie Ion appellefoi de probabilité deVADXlou distribution l'ensemble des corples x:, PilDie IExemple:dans l'exemple precedentdujeu de52 cartesX= xi4siPi=Yx= xiI

Page 51 : -W est la carte 4y= yi- 101234-Exemple:on fance undeà 6 facesi=1 , 2, 3-6, iteXi=2i- 6-variablealeatoire: prond de 16xx= - 4,- 2,0.2,4, 63PxX= 4= Pxx =- 2= PxX= 0= Pxx= 2= PxX= 4= Pxx= b=Ixi- 4- 20461-- --Pi-5586s

Page 52 : Remarque: C:, Pil : =ICoi des probabilitésdeUADAssi1 Xi. jeI , i jxi=x;2 2ei= 1, pi0itIfonctionde repartition de variableaféctoireSoit ve, H, P espace probabilise,XVAD sur er,X eh= x: /itIon appellefonction de reparation dex l'application:M - Ix-fx= PxX- x= PX= xixi1xPropriété :1 FxtIRfxt 0 ; 12estune fonction croissantesur IR3tim fx= 0, tim fx= 1x-- xx-3+ 0-estcontinue seulementâ droiteentout pointde1R.

Page 53 : 4Fa , beR, PaX-b= fb- fafoi de probabilitéd'une fancion d'une variable aleatoire discreteSoitXune VAD, y une fonction definiesurX 1g: Xr - Rgoxest l'applicationgoX: r--Rwi gox wI= gxwIgxw= gXw1Proposition: Soit X une VAD telle que X e= x : /itI, soit gunefonction sur X1/ alorsY= gxest Une VADtelle queX 1= yt R/5ieI tel que y= gx : /7 yty2Pyy= y= PX= xiiy= gxiExemple:XVAD definie par la toixi-112P: 144244

Page 54 : Determiner la fo:pour chaque variable alatoire suivante:y= 2x+ 12= x2yi- 13j- Pi2=11· liteprobabi4Ice i-somme de 1+ Imoments d'uneVADSoit 1, H, PIespace probabiliséetXuneVADSur ch, Xe= 0: /itIon posePi= PX= xib/On dit queX adimet une esperance de X forsque la serie. E: Piestabsolument convergente. Dans ce cas l'experancede X2x =:PiSoit gune fonction définiesur Xeà valeurs réellesProposition:Sifinieau laseriegx :/PX= x : 3 /absolument convergentealors faVAD yx admetune espéranceetona Egx= E=g-PX= xi3

Page 55 : Exemple: Soit X Une VAD Sa loi:x :-112Pi1 =4fx=- 1x 11x+ 2x=24"1pi4x=1x+4x=

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55