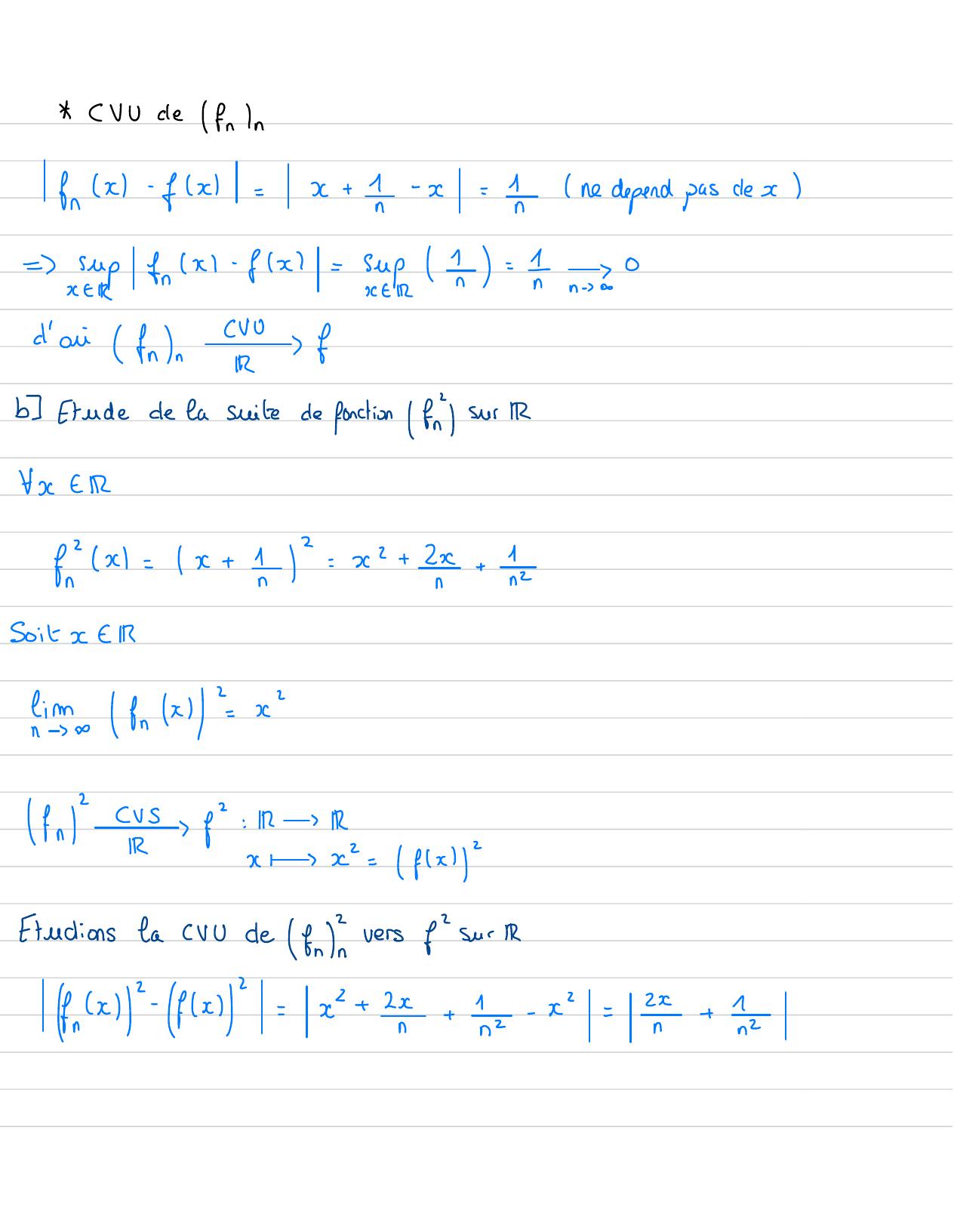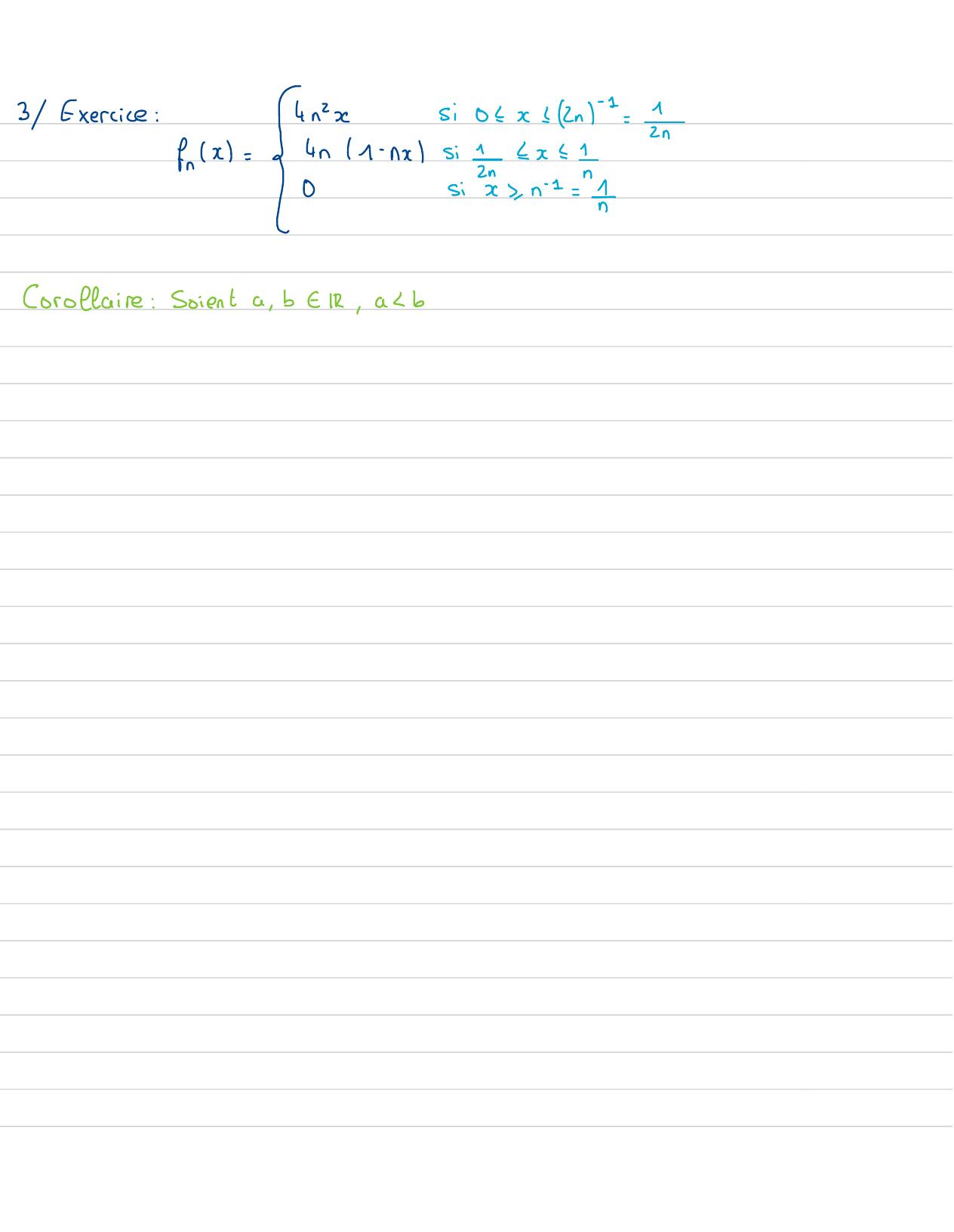CM Annotee
Télécharger le CM Annotee en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
Page 1 : Serie28-2023
Page 2 : Serie à terme quelconqueThéorie:Une SerieE Un est convergentessifa suitedesSommes cartielles est me steite deICauchy, cadFE20 , 5N-CI, Up, N, Xq, N. /Sp-Sp/3Sp= EoUkSq=okCe qui peut s'ecrire:FEz0, ENEN, YpIN, Fq, IN,1uRIEk = p+ 1Corollaire: SoitUnme serie numeriques'itexistedeuxSuitesPrln et Iquln tg:1 FnEI, PrI In2 himPn=92=+ y3 la suite une cu pas versoAlorsUn divergeNEIN
Page 3 : Exemple :Techniquea appliquerdans tousles exosPr=n+ 1Pn=2 neinin= himn= +n- yn+1= 2nIdee trouverunminorantEunestrictement supérieura ohn= ek= gn32Il faut encadrer"Theoree des gendarmes"-2m= Encal- nanl SurR= n + 1k= n+ 1
Page 4 : SeriesAlternéesThéoreime: Regle d'AbellSoientCann et brin deuxSuites Numeriquestq· Cannest me siteà terre positifs,décroissanteet tendvers0.M·La Seite numérique obtest bornéeAlors nanbeconvergeExemple: EtrudierLa convergencede neet de Eirculmettre i terrinespositif· 02// aLaserie VRienanc= 21
Page 5 : Théoremede majoration des seriesàtermes positifs= lcrSirar absoluemment⑭EncrOn aplique ta negled'Abelpour la Seriean= 1n 1br=cosn/nest Wet - 0cosCk?
Page 6 : coSn= ReCecosm=Re Beink= 0=Reein+ 17eni01- e=e-e= eie- ellein-en=2isint=2 :sin = el=12 :Sin -1/2 eil=2sin 1/2donc:Il" /donc bornée
Page 7 : in +1d'or1- 21-eiEincess" sinial↳ECOSR=Re einrenieDonc fa smite n best bornéeOn opliquela Regle d'Abel, on a la convergencederechDef:Une serie Numériques nielle Eir Unestdite alternée,ssi,FnEN, un= -1"UnarFaEN, Men =- -1" /Un
Page 8 : Remarque: IlEiUn est une serie alternéeSSiMn-Mn+1 602 Eir Unest me seriealternéeSiMr=-1" anavecCaninune suiteâ termesconstantExemple:1 EtEn rantDe ret0Sin= 2kSin n= Grisin= 2k+ 1
Page 9 : Theoreine: In specialdesseries alternées"TSCSA"Soit Unme serie alternée telle que MnInneiNsoit une suite réelle positivel decroissanteet tend vers OAlorsMn converge. De plus Fr, no, Rn estdu signe de Mentiet Rn= 1UIanthExercice:On considèreMnInet UnIndeux Suites definiesparUnEIN n+1Un= 1, Un= fcos2n+1Un =, Un=en 1+ sine1Montrer queUn Un2Etudier la convergencedes Seriesun etun3Que peut-on conclure.
Page 10 : en encr oX - 0Xy -0y2 Un== -11. Eade signe constant& un estmeserie alternée·nest une Suitedecroissanted'après te TSCSA I UnCVn I/iun-Unmais les suites ne sont pas de-signesconstanton ne pent pas appliquer e Théoriedes equivalentsdesSeriestermesconstants.
Page 11 : un=en 1+ sin =en 1 +-I+ =n1+ x=X- 2+ ox"=sin - - s osin "Si Mnet Unne gardentpasun signeconstant.Un=oUnavec UnCVSuncV
Page 12 : oUn↳Un cr Rienam -1Un= en 1+ sin =en1+ x=X-1+-+ 0X3X=sinnm =-Sain-olitolet=-5+ Ivo---anbiCRdi
Page 13 : San convergeserie alternée TSCSA↳brdivergeBieram&= 1San converge a revementonconvergeCV absolvementDoncen diverge3On a deux Suites equivalentes MnIn et UnInMaisUn etUn n'ont pas la même nature deconvergencecar ona pas desseriesà termesconstants.Somme de Proce series danetEbn sont absolumeet convergentes,+7alors la seriean: Sa bn-j convergeabsolumentet Zan= San bn = 0n, 0avecCr= bajbn-j
Page 14 : Chapitre:Suites et seriesde fonctionI.Suites de functions1Convergence simpleet convergence uniformeDef: SoitA ? IR etf, f:ARdes fits, FneINiOn ditque la suitede fats f"converge simplementvers f sur Af=": fSi VxAla site numerique fx convergevers fxii On dit queta sitede fonctions fr , converge simplementCVSISur As'it existeune fonction f: A -Rty: Enf simplementQuantification:c f 970, Xx -A, 5x= Mx, Fn, nox ,fx- fx5Exemples:1FnEIN: fn: 20, 1M312 x-x
Page 15 : Etudions la convergence simplede la site de fet frnpour= 1: f, x= f1= 1- 1=00n- 3+ ypourx+ 20 , 12: fx=x"- x3- xn- 3+ 3conclusion:In ces :E0Six= 1- x Six 20 , 12G: 1 +IRx s1+ x· Six= 1y ,x= yn1= 12·xE0, 1·x1: x+ x IRy , x=xn+0Conclusion: fnnne converge pas simplementsur IR+8p 8: 20 . 13 RE0six =0 , 12xy2Si= 1
Page 16 : Rappel:Il fllo= sup fx11f10 - 1 += 1 + UG+ 0lfb- Igle11 f+ yllo 11 f1+ lybeDef:SoitA IRet f. f: Adesfunctions etsoit br: Ilffl= SEErkel -fxiOn ditque la site de fonction frn converge uniformementvers lafonctionf sarA, si linbr=0cad em"fif"= 0n- xNotation :frLiiOndit que frnVU sur As'ie existe une fonction f definiesur Aty: In f
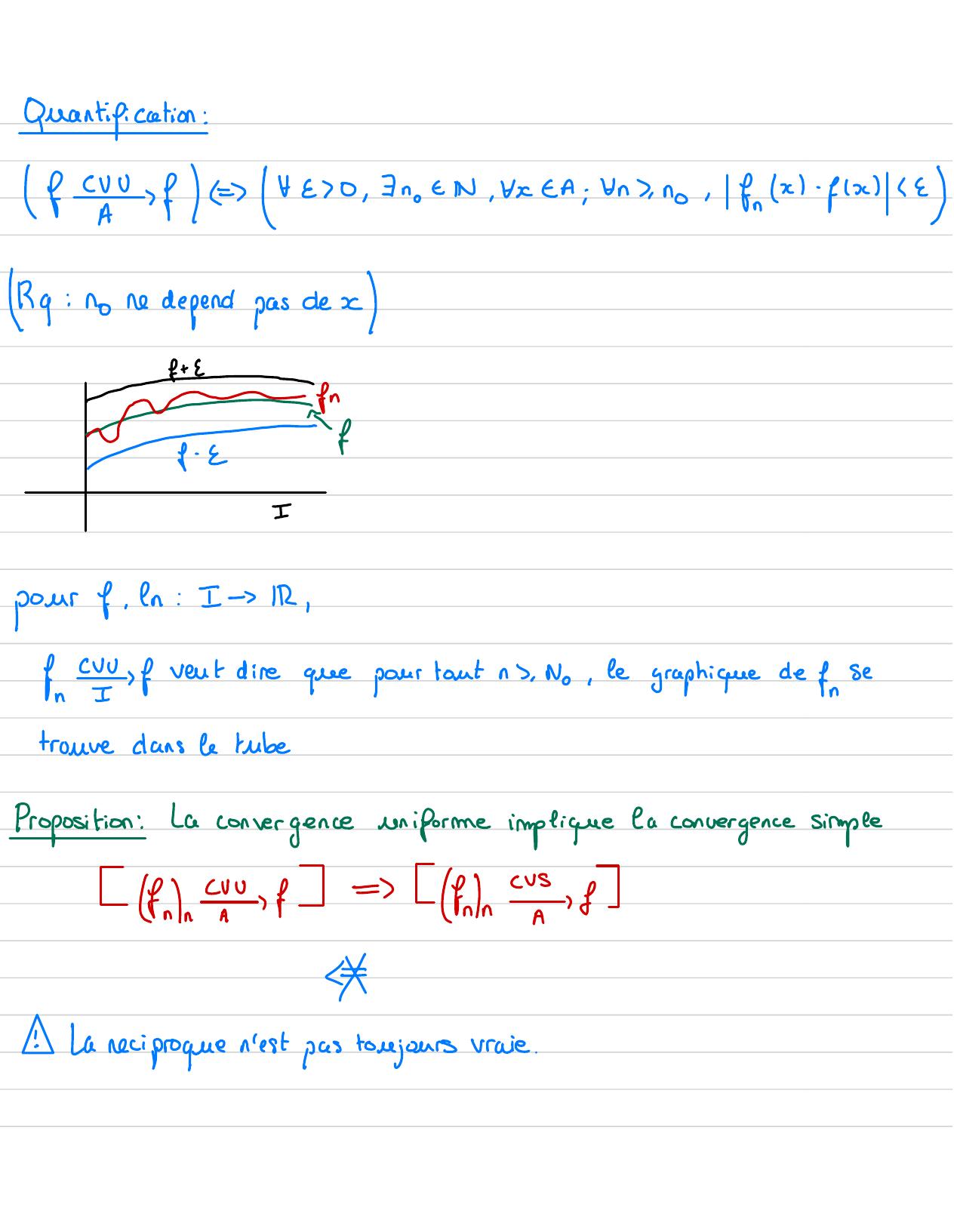
Page 17 : Quantification:f4f 7230, 54 . EN, KEA; And, no,frx -fx2Rg: no ne depend pas decefIpour f. In: It IR,fusfvent direquepour tout nc. No, le graphique def,Setrouvedans le tubeProposition:La convergence uniforme implique la convergence simpleInl8=Faln I:La reciproque n'est pas torejours vraie.
Page 18 : Preuve:on a : Ilfr-f"0, cadefrk- fx-0n - c-=Yx- A,frx- fxn -x +car fxA, 0 fx- fx= supfrx- fxx t AEmesupcest etralierla convergence uniformeRq: silfnhe converge pas simplementalors fulnExemple :f: 0 , 13 Rxxxk1- xc0frn -8 :c1Osic =20. 12E1six= 1Etrudions la convergence Uniforme de frn verssur 20 , 1hnc= crosicCeehnx= six E 20 . 1210Six: 1
Page 19 : Methode 1 :Do=1- 1fn- f0= x= 1- 4=en en /- en +0PuisqueIl fr-fIls fx0- fx0alors hi"fr-flo feksol-flao= etle pbesten 1 Sauf que=Ilfr- 80k014 notre intervallec pour çaon faited'o enP'fMethode 2:Soitic tC0 , 1hnx= fx- fx=xhinx= nic1, 0xO22Ilhally= 1 / 0V. In0d'ai fr if
Page 20 : hn1= 0, donc Sup Ihns=SupInkxt0, 1xt01Montrer que: filn converge runiformementvers f sur 20, a., Fat 0 . 12ona: supfail-fx=Suphux= hnax - 0, ax = 0 , a=a0n- 3+ Dd'or frnafDef :Si En f, Fat 20, 12 respat 0 ,+ xon dit queor converge localement uniformementsur 20,12Irespsur 0 ,+0Theoree:Critèrede Carchy pour la curUne seite frde fals de Adansconverge uniformement Sar A,SiFEC0 , In EN, FEA, En, no, Arm, no:fr -fxNotation :Il fr-fralon 6
Page 21 : Stude de La cvU de frSer I1Etudier ta CVS Sur Iis: fontfalors font f-Si it existe f : I-+g fulne ifPour montrer fanoncuude frn versfLVVonchercheunSiXnEIN, festEtudier la fetKot I choisircontinue surI ethn= fn- fune suite tof n'est pas continueet chercher teIhnkelSPIfrxoL-fxco OSur I alorsen 8Pour montrer laCur de frvers f it faut etudierta fethn =/fr-fet montrer queSe /hnk/ne
Page 22 : Proposition:Soient &nIn IIRS : fr 9nInCUWsur Ialors fn+9nCUW sur IPreuve:Soit fLa limitede la suitede fonction frInSoit g la limitede la sitede fonction 9 n In18n- 9nnf+ gss: /8n+ 9n- 18+ 91ne +Ona: 11 fn+9n-f-g11= 11fn-flIl Sn9llen+ 0n2 +WWd'or le noultat00Exemple: fx=x+ 4,x -IR, nEIN EtudionstaCUUdefuln: paisde8nIn, pais de InilCVSde funfr+ frnSoitER ,frx= x,Inn8:
Page 23 : CVUde fn Infrx- fx=x+ 1- x= 4 nedepend pasdes= Efrx -fx= ERn= -n=d'oi frInCo 8b Etudede La sitede fonction fnY SurFe ERfx=x+ 4= x+ 2+ hSoitCARDim EnsIfn" 82= 181x1"fludions laCVUde frvers f"SurAn"-fx=x+ 2+ 2z- x=2+ 42
Page 24 : pour Co=n,on a:20nsol"- fx0=2+ hun+ 3or IIf"-flo nePar suiten" fa Etudede ta fonction9n= & In cusdeI9nIn surSoitst1, grk= hx+ 4= -+22Pour=0In 10= 0n =0xF 0grk o -donc higx=019nn Y9=0
Page 25 : CUUde /9n/n surgrkl- gx=2+ 4-0=x+ 4nPourc= x,ona:9, x0- g0=1+ 2 1+0n -0d'or Ign-gle0= 84g=0Remarque:gnx= fxx hxavec hnx=4- XxEIR,n=0Ifulnh=0On a: /fuln" 8mais /fuln /Falnf+ 8Ona uniquementtoCVSGI8nst=4xfaInc fahInnY nIhnxfoln Y 8xh
Page 26 : Proposition:Soit I=IR, atI, f: Iccontinueen aSupposonsque /frn 8Alors &est me fonctioncontinueence.Corollaire:une limite uniforme d'ate suitede fonctioncontinueSar Iestuna fonctioncontinuesur IRemarque:Le neomltatest utile pour montrer lanon convergence uniformeCorsqueLa fonction limiten'est pascontinueProposition:Soit fninune suitede fonctioncontinue convergeuniformementSur I vers fI fonctiondefiniesur I. Alors pour tomte suite /ann convergenteverset IOn a :liefnn= fxPreuve :My:mfnn- fx=0fra- fx= fxn- fx+ fx- fxonvartifier l'inégalitétriangulaire
Page 27 : fra- fx= fxn- fx+ fx- fxfx t IIfnx- fx- 11fr-flo-frxn -fx+fx- fx=fan-fake+ 1Ifr-fl0or : xnn++ 3xIet fr une fonctioncontinuesurI Simf , n-fnk=0 =Inn -fx=0Remarque: la CVU de funestuneconditionnecessairedansla propositionExemple: fx= x, xt20 ; 1On a: En38:20 : 13IRx1 41 Sic= 10 Six- 0 : 1 on aaussi fnInfprenonsan=1- 4,n0enne 31
Page 28 : onc f1= 1maism fre=eim1-- 1=2Ona: f1En·EiEn enInterversiondes Limites :d'après l'exemple, lorsque fuln neCVU pasvers fDirLime frx li hi Enx- 1n -0x 1Theoreme:SoitII, atI, f: I IRsupposonsune limitefalnCOverssur Iet que en= himafkalexiste /on aAlors , afal manImportant
Page 29 : Integrates et convergenceuniformeThéonemeValable que pourun intervalborne.1Soita b.Si uneSuite f:20, aIR defonctions integrablesetconvergent uniformementversunefonction f,alors fest integraleseton a:in flick=im fluc eI2 Il existedes Suitesde fonctions integrables If Inqui convergentsimplementvers unefonctionnon integrable, maisDie fic infaldPreuve :1Regardercours Teamsenregistré.2
Page 30 : 3Exercice:↳nxSi0x ! 2n-2=1frx=4n1- nxsi2 nx1ED2nsic, n2= 1Corollaire:Soienta , b EIR, adb
Page 31 : Theoreme:Soit I un intervalleet frnte"I.Seposons que:il I falnCVSSur I vers fii filnCrUSar I versgAlors: feI et f= gc'est-à-direm frs = eimerExemple:frx= n2 /ce aocx1EtudierLa convergence simpleet uniformede fuln Sur 0:12Montrer que f'n converge uniformement sur 20 : 133Montrer que f= limfxestderivablesur 0 : 1 r
Page 32 : Seriede fonction-Continuitéen un pointd'eneSerie f, uniformementconvergente1continuité:Th 11Soit If, meseriede fonction uniformement convergenteSur A.SiXneN Iestcontinueen coCA respectsur AlalorslaSomme= him /Sde Efest continueenco respect sur AlPreuve:voirtoThsur lessuitesde functionsetconsidererSn'neinavecSn= 8+..+faquiestdoncunif convergenteona:no ifn= Eleimg=fakdIntervertir=continuité uniformeet......2limiteenun point: Th2Soit Ef Maseriede fonctions uniformementconvergentesurAet sifx= e existel pourtout no INalorseindixe parnfirmEln convergenteeton aie Ef-of-En- Intégrationtermeà terred'une sériede fonctionsTh:Soit Ef,weseriede fonctions continuesser a, b· Sidfnconvergeuniformement sur du, b alors " Jackeest convergenteet once s gesia :Ef de
Page 33 : Preuve:voir leTh. d'integrationde la limite uniformedes sailesde fonctionsExemple d'application:Soit Ef, wifnk=-1"Convergence simple:On étudie la série numeriqueUnsin Un=fk= 1-1""SUn=E -1"=E- x"serie geometrique quiconvergesi le1c-a- d-1x1I In converge simplement sur J-1 : 1vers Soi S:J-1: 12IRx Sx=11 + xConvergence normale:on etudie laserie numeriqueIlfloIl fallo:seep2nx= sep x"=1= Ef,neconverge pasit-1 , 12it-1 , 12normalementsur 3-1 : 1 LConvergence uniforme: EfConverge reniformementsur AssisupRnx0n3 + 1serie alternée c'est bien pourCV. Unigcar onpent majorer.DEARnx =G =-t ,= c se= x"=Ex-1- x+1+ xxt- 1 : 12SupEn ,EnPach= +=Efnoconverge pas uniformementsur3-1 : 12Soita, b 3-1 : 1
Page 34 : pour - a, b1xn+ 1IKLmax 1ab1+ 1+ x1+ G1+ a= If converge miformementsur tout segment a, bc 7-1 : 12AppliquonsteTh d'integration terreà terre :Choisissonsa, b: 0. tavecoct 1alorson sait que EInde: 8 kid=1=en 31+x=n1+tIlEst-ila= Est-i i-Estn+ 1donon a E-1" En+=en1+ tn+ 1n-= E-1= t=en 1 + 5pour - 30.1nOn pentaussiavoirE - t=en1+tport--1, 1
Page 35 : Derivation termeà terreTh:Soit EfMe seriede fonction declasseEt sur Ilintervallede IRSi a Ial moinsoeItq fn 8convergevers&me constante réellebl faseriede fonctions &In convergeuniformementsur tout intervalle ferme borneCa, bcIvers thefonction G.alors -Ef converge uniformement sur touta, bc Ivers une fonctions: x1 e +/et2- la fonction s =Anest de classeSur Ietona s'cal-Eg'
Page 36 : SerieentièreI DéfinitionMieserieentière peut-être entière respectivement reelleest meseriedefonction Ef,pour laquelle 5meserite complexe respectivement reelle lanheitychaque f est definie In:&erespectivement &: IR 1Rne r anune telleseriesera notée San z"respectivement Eanse" Rayonetdomaine de convergenceSoitnene serieentière complexeau nichte l'ensemble I= GreIR+ty dlantr convergelestun intervalle de112+contenant0.Laborne Superieur de Iest apelie le rayonde convergencede E andDefinition Domainede convergence:Soit dan zuneserieentière complexe respectivement reelle de rayon de convergencer El+,ledomainede convergence de.anzuest Dr=7z- +qzk r·ans" estDr=J- rirExemple:·consideronsanz"onan= n ,on définit doncla serie entièreEn 2Hpourchercher le rayon de convergenceoncherche l'ensemble
Page 37 : ·on regarde la serie numeriqueno etan cherche les valeurs der pourlesquelles In" " convergeEnr estMineSRPserie réelle positive" nir=nr+ 05 : 0n -+ 030Sir=0n-+ 0I= 40y=le rayonde convergencer=0=le domainede convergence Dr= 2Soit Ian z"onan=1n !On etudie Elan r=& 4 ,"c'est eneSRPon spliqueD'Atembertd'ori nitne o 0donc I =0 ;+Le rayon de convergence r=+ xet le domainede convergence·an z" complexe alors Dr= 2e +q2+ 0 y=K· Eanc" récealors Dr= 3-0,+= 1R
Page 38 : uneserie entièresous la forme an zs'écritdanx"ouZanz"Ona definie I= GrtRT ty lanIr" convergey1+ U9 +04La borne supérieur Iest le rayordeconvergenceSansch-forcement IR+=O possible aussi=+0· Pourmeserieentiere niellele domainede convergenceaussipetiintervalleouvert de convergence est 3-R, R · Pourmeserieentiere complexe le domainede convergenceD= yzeD +g/2/CRY=bouleouverte decentre0 et derayonRIllerExemple:1 I anz"onan= 1;ona definiz"Calculonsr -IR+ty Er"convergeErest theseriegeometriquequi convergesi Irl1c-a- d- 1 r 1commenouscherchons - +=r - 0, 12d'où I= C0 , 1
Page 39 : lerayorde convergencedeEz"Vaut R: 1· Si zume senieentiere nichtealorsle durainede convergenceest J-1: 12· Sizume senieentière complexe alorslo domainede convergenceest laboute onvente unité .Lemme d'Abel:Soitdanz"uneserie entière complexe. S'il existe2.-1404ty la suite lan" Ineiestbornée alors Fzt e tq/z/zo laserie↳anz" est absolumentconvergenteet de pluslaserie entière Sanz estnormalementconvergentesur tout disque ferméde centre=et de rayon raver bladRemarque:à toute série complexe anz"est associéeun unique réel d1R+IlIFz& tq1zd, la serieentièrean zu estabsolument1R+09+ b19convergenteFz& +q1zd, la serieentièrean zu est absofumat divergentesionesa↓'la frontiere ,Le réeld est le rayonde convergencedeEanz"ça depend/evom DuSansCUABSdanso etSanz"cVSanz" DVSance" DVABSP- x2anzu V Normale↓estnoté R rayon deconvergencedeEncercle d'incertitude↳ans
Page 40 : Determination pratique de rayon de convergence:utilisationdes règles de Cauchyan de AlembertTh: SoitSanz"une serie entière complexe ty5him"lan= et +au bien Ihimant1= 2-+n -+ yanalorste rayondeconvergencede3 anzuvantR= 1CExemple:Determiner to rayonde convergencede laserie entière Zan:" dans lescas suivant1an= n7r2an=n !22n !110= fI1 "lan=8g=/ + /= 47-1=1- yn=enfn1-= e -4+ 01= ef+ 01exR= 1-n-3 + 0et= e2an+ 1--n + 1 !2n :=n+112n !-n+ 11an24+2Inthl!2"n !22n+ 2 !42n+ 2-2n +1↳↳En. 2n224422= n+=R= 8
Page 41 : utilisation de l'equivalent:Th:SoitZanz"et Ebnz"series entièresde rayonsde convergence respectifsRaetRbsilan /bnafors Ra=Rbn -2+ 0Exemple:rayondeconvergenceSanz"onan= 1+ 1 - ean=1+1- e=emenn+ 1/n-e= et- En+ 07= e in+ 07- e-en+ -e= e1- 2+ 0- e= 2+ 0= anbon chercheto rayon de convergenceEbrz"br+ 1M-1bnn+1n+0=Rb=1=Ra= 1Remarque:SoitLanzuetbrz"2seriesentièresde rayons de convergencesrespectifs Raet Rbsilan/bn/aforsRa, RbPreuve: SwitzetyIzRbalorsEbraest absolument convergenteAcommelanIbn= Ianz"est absolument convergente&121 Rade A et A on déduitque Ra, RbNe
Page 42 : Exemple:Rayon deconvergencede ESincal 2anonclan= IsinnI InSoitR rayonde convergence↳Sin nz"R'rayon deconvergence "On saitR'=1doncRX, 1Siz: 1sin n diverge= R11=R= 1
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42