CM BIS Chapitre1 Champ
Télécharger le CM BIS Chapitre1 Champ en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Page 1 : Physique - 2024-2025ÉlectromagnétismeChapitre 1 – Champ magnétique - Force de LorentzPrésentation rédigée par Émilie Dupont Cergy : emilie.dupont@cyu.fr, CY308
Page 2 : Programme de Magnétostatique
Page 3 : Programme de MagnétostatiqueOn envoie un atome de krypton ionisé 1 fois avec une vitesse de 40 000 m/s dans un spectromètre de masse où il y a un champ magnétique de 0,6 T. L’atome frappe la plaque à une distance de 11,044 cm du point d’entrée de l’atome. Quelle est la masse de l’atome ?4
Page 4 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétique• Antiquité, Grèce : magnétite Magnésia, Turquie, pierre attirant de petits morceaux de fer. Aimants naturels• IXe siècle, Chine : alignement des aimants dans la direction Nord-Sud invention de la boussole.• 1752 : Franklin découvre la nature électrique de la foudre et plusieurs témoignages sur le fait que : ➢ Les orages perturbent les boussoles➢La foudre frappant un navire aimante tous les objets métalliques.Franklin en déduisit « la possibilité d’une communauté de nature entre les phénomènes électriques et magnétiques ». Coulomb 1785 montre la décroissance en 1/r 2 des deux forces.Découverte de la force magnétique :
Page 5 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétique• XIXe siècle : expérience d’Oersted en 1820. ➢L’étude quantitative des interactions entre aimants et courants fut faite par les physiciens Biot et Savart 1820 : force agissant sur un pôle est dirigée perpendiculairement à la direction reliant ce pôle au conducteur et qu’elle varie en raison inverse de la distance.➢Davy en 1821 dans une expérience où il montra qu’un arc électrique était dévié dans l’entrefer d’un gros aimant.• Fin XIXe siècle et XXe siècle : Mise en équations par Maxwell qu’en 1873 et ne trouva d’explication satisfaisante qu’en 1905, dans le cadre de la théorie de la relativité d’Einstein.Découverte de la force magnétique :4 3
Page 6 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce entre les pôles d’un aimants3Il existe deux types de pôles sur un aimant : nord et sud●Les pôles de types contraires s’attirent mutuellement●Les pôles de même type se repoussent mutuellement
Page 7 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueLa Terre est un aimant3 4
Page 8 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiquePas de monopôles magnétiques3 John Mitchell 1750 : 2 pôles de l’aimant toujours exactement la même intensité.Aucun effet sur charges électriques au repos
Page 9 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétique
Page 10 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueChamp magnétique :Lignes de champSi un pôle magnétique subit une force quand il est à un endroit, alors il y a un champ magnétique à cet endroit, noté B.Plus le champ est fort, plus la force sur les pôles est grande1 Le champ est toujours tangent à la ligne de champ, dans la direction de la ligne.2 Plus les lignes de champ s’approchent les unes des autres, plus le champ est fort.3 Les lignes de champ ne peuvent pas apparaître ou disparaître dans le vide.4 Le nombre de lignes de champ qui arrivent ou qui partent d’un pôle est proportionnel à l’intensité du pôle.5 Les lignes de champ ne se croisent pas.
Page 11 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueLignes de champ
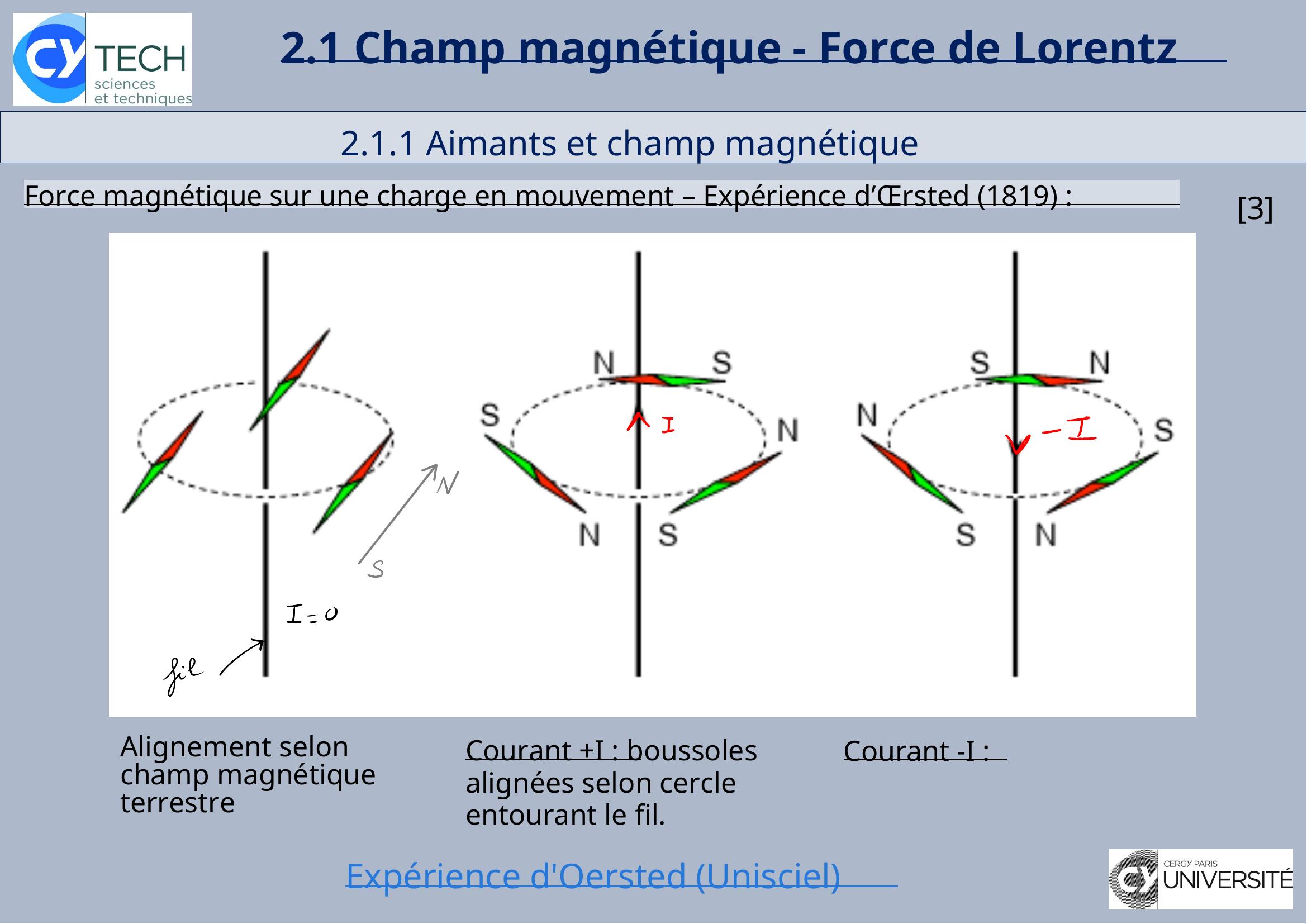
Page 12 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce magnétique sur une charge en mouvement – Expérience d’Œrsted 1819 :3Alignement selon champ magnétique terrestreCourant +I : boussoles alignées selon cercle entourant le fil.Courant -I : Expérience d'Oersted Unisciel
Page 13 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce magnétique sur une charge en mouvement – Expérience d’Œrsted 1819 :3Expérience d'Oersted Unisciel
Page 14 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce magnétique sur une charge en mouvement – Expérience de Rowland 1876 :3Boussole soumise à des forces dont l’intensité diminue avecl’éloignement et dont le sens varie avec :- le sens du mouvement des charges,- le signe des charges
Page 15 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce de Lorentz :Force de Laplace :
Page 16 : 2.1 Champ magnétique - Force de Lorentz 2.1.1 Aimants et champ magnétiqueForce de Laplace :4Définition de l’Ampère :
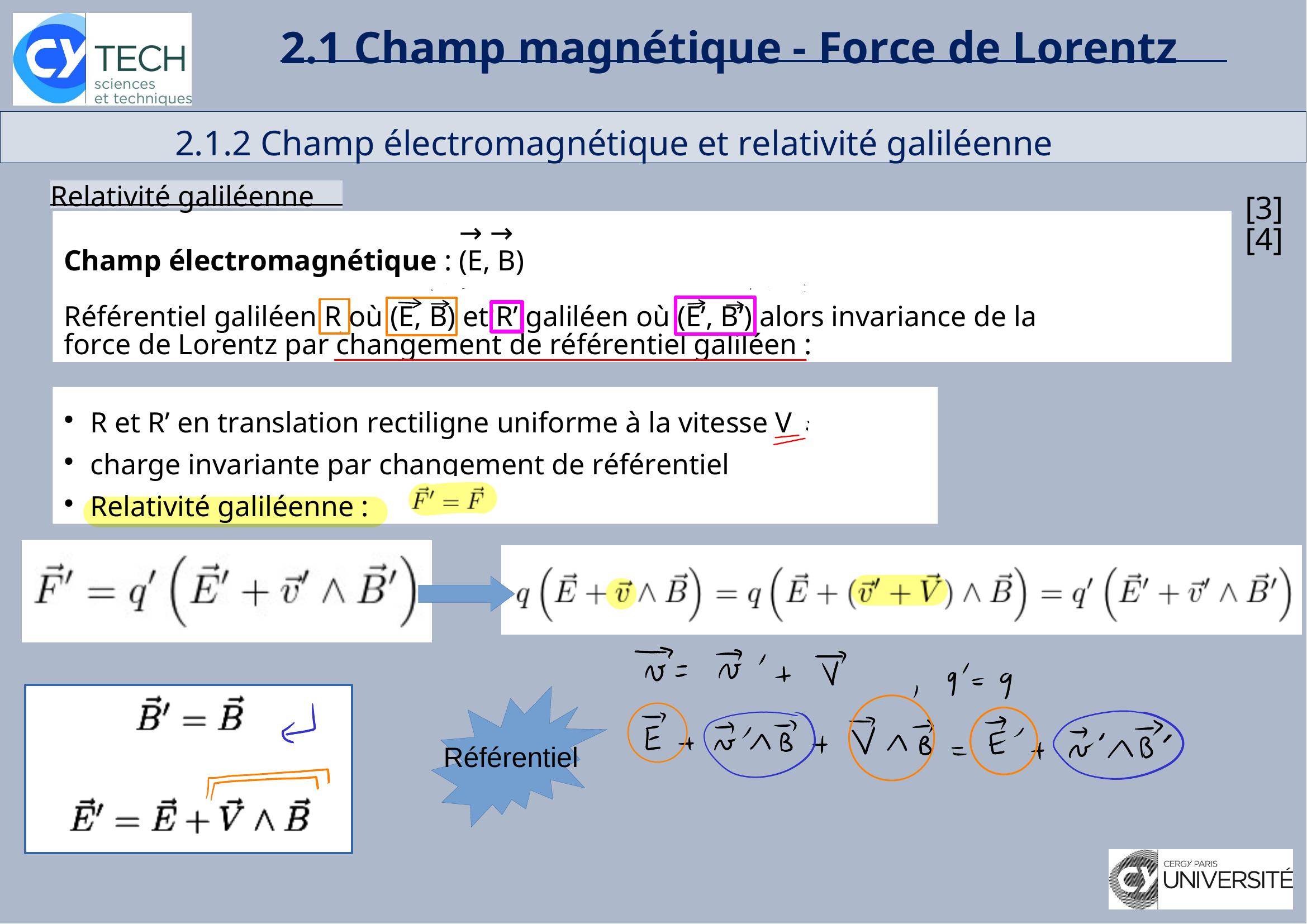
Page 17 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléenne34Relativité galiléenne →→Champ électromagnétique : E, B →→ →→Référentiel galiléen R où E, B et R’ galiléen où E’, B’ alors invariance de la force de Lorentz par changement de référentiel galiléen :●R et R’ en translation rectiligne uniforme à la vitesse V●charge invariante par changement de référentiel●Relativité galiléenne :Référentiel
Page 18 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléenneForce de Lorentz :4 = contribution du champ d’induction magnétique, appelé abusivementchamp magnétique.force magnétique : correction en v/c2 à force de Coulomb
Page 19 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléenneRemarques :Force de Lorentz - Champ magnétique :34• L’expression de B n’est valable que dans le cas où les particules se déplacent à des vitesses très inférieures à c. →magnétostatique• Cette expression dépend du choix du référentiel . → →●B diminue en 1/r2 comme E →●B est défini par un produit vectoriel de deux grandeurs polaires = grandeur axiale ou pseudo-vecteur.●le principe de superposition s’applique au champ magnétique.
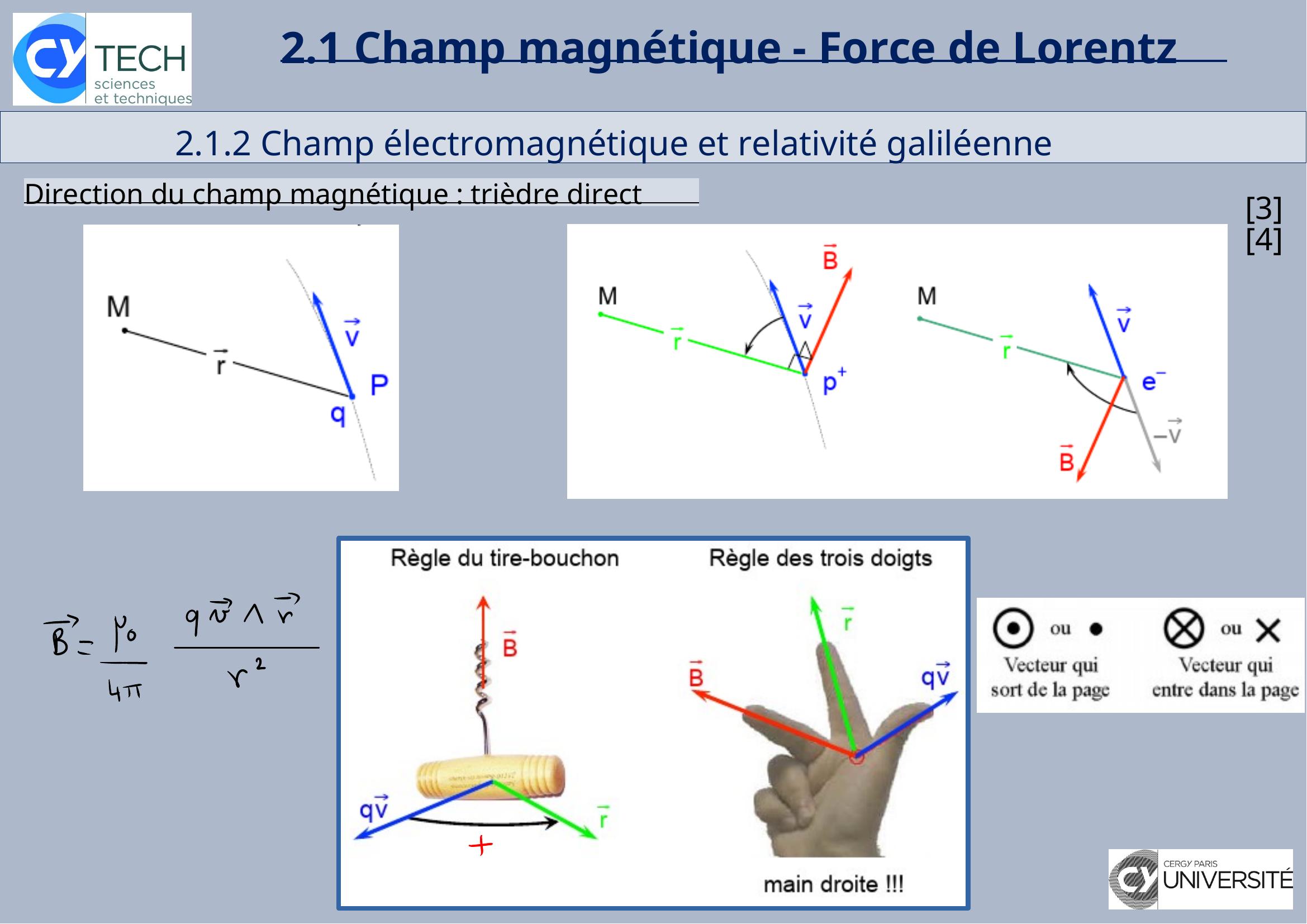
Page 20 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléenneDirection du champ magnétique : trièdre direct34
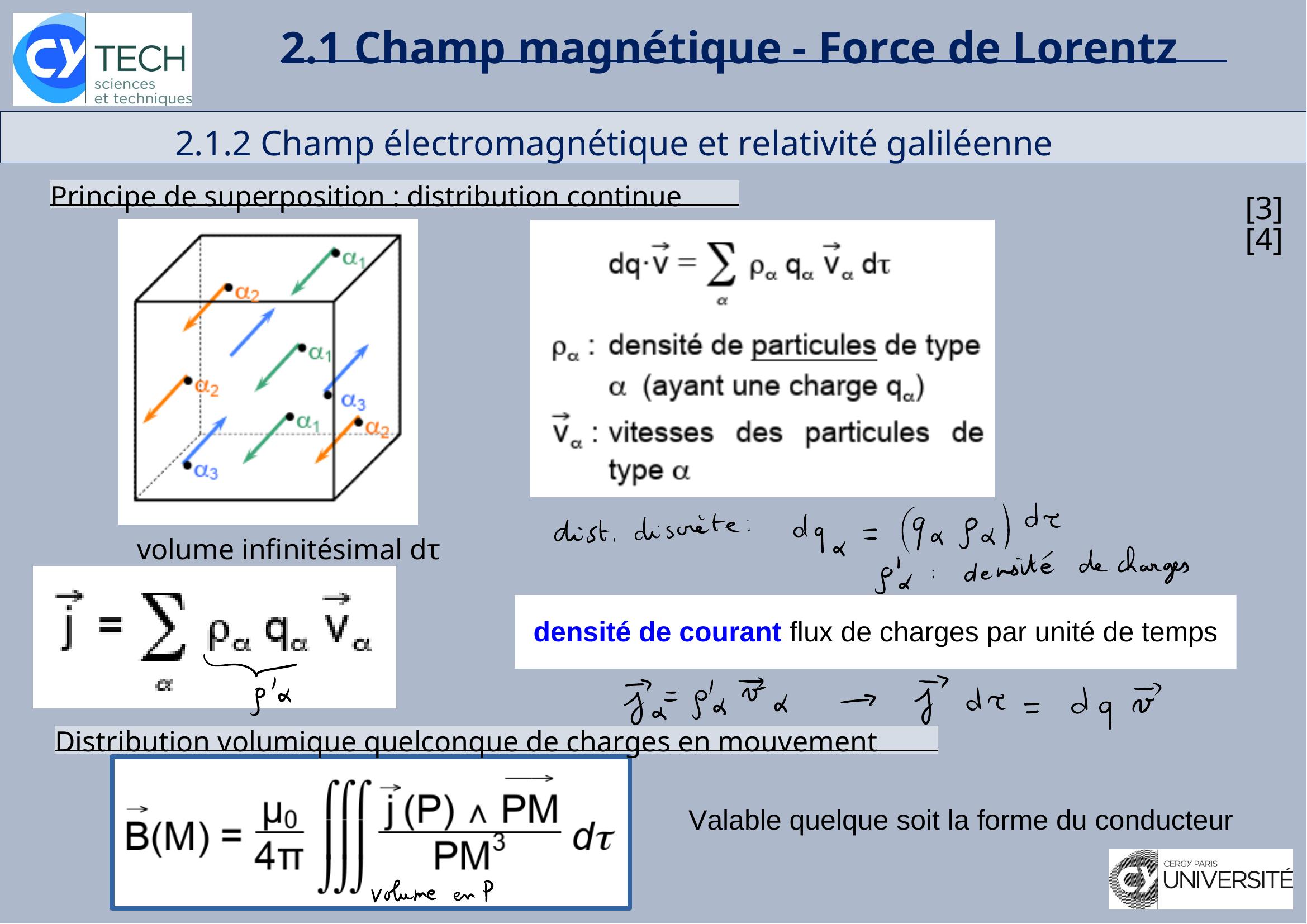
Page 21 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléennePrincipe de superposition : distribution discrète34Principe de superposition : distribution continue
Page 22 : 2.1 Champ magnétique - Force de Lorentz 2.1.2 Champ électromagnétique et relativité galiléenne34Principe de superposition : distribution continue volume infinitésimal dτdensité de courant flux de charges par unité de tempsDistribution volumique quelconque de charges en mouvementValable quelque soit la forme du conducteur
Page 23 : Bibliographie 1 Polycopié de cours2 CUPGE - CY : Introduction à l’électromagnétisme3 Cours LP 203 - Champs électrique et magnétique de Nicolas MENGUY4 Cours de Luc Tremblay, collège Mérici - « Électricité et magnétisme ».5 David Sénéchal - « Histoire des sciences » PHQ399 Université de Sherbrooke, QC6 pour la suite : Khan Academy , Unisciel etc.
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23