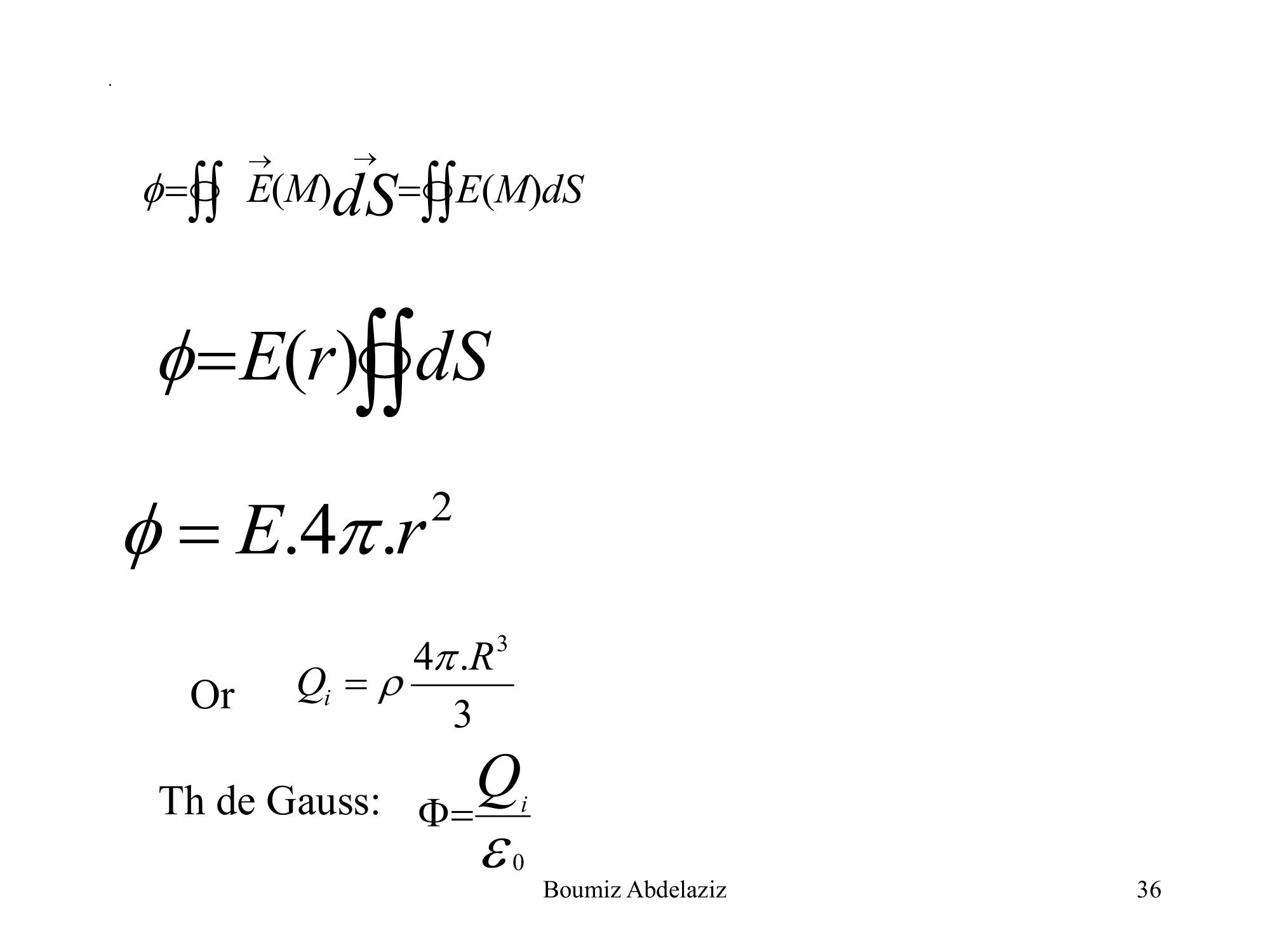CM BIS Chapitre1

Posté le 08/02/2025

Chargé de TD/CM : A. Boumiz.

4 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Page 1 : Chapitre 1Le champ d électrostatique1Boumiz Abdelaziz

Page 2 : .I. Force électrostatique1. Loi de Coulomb.q10q20rAB2Boumiz Abdelaziz

Page 3 : . La Force d’interaction électrostatique entre deux charges ponctuelles q1 et q2est définie par la relation:avec K = 9.109 S.I dans l’air ou le videuest le vecteur unitaire de la droite ABurqqKF2212/13Boumiz Abdelaziz

Page 4 : ..F1/2rqqKF221urqqKF2212/1F2/1==041KOn pose ε0 s’appelle la permittivité de l’air ou du vide4Boumiz Abdelaziz

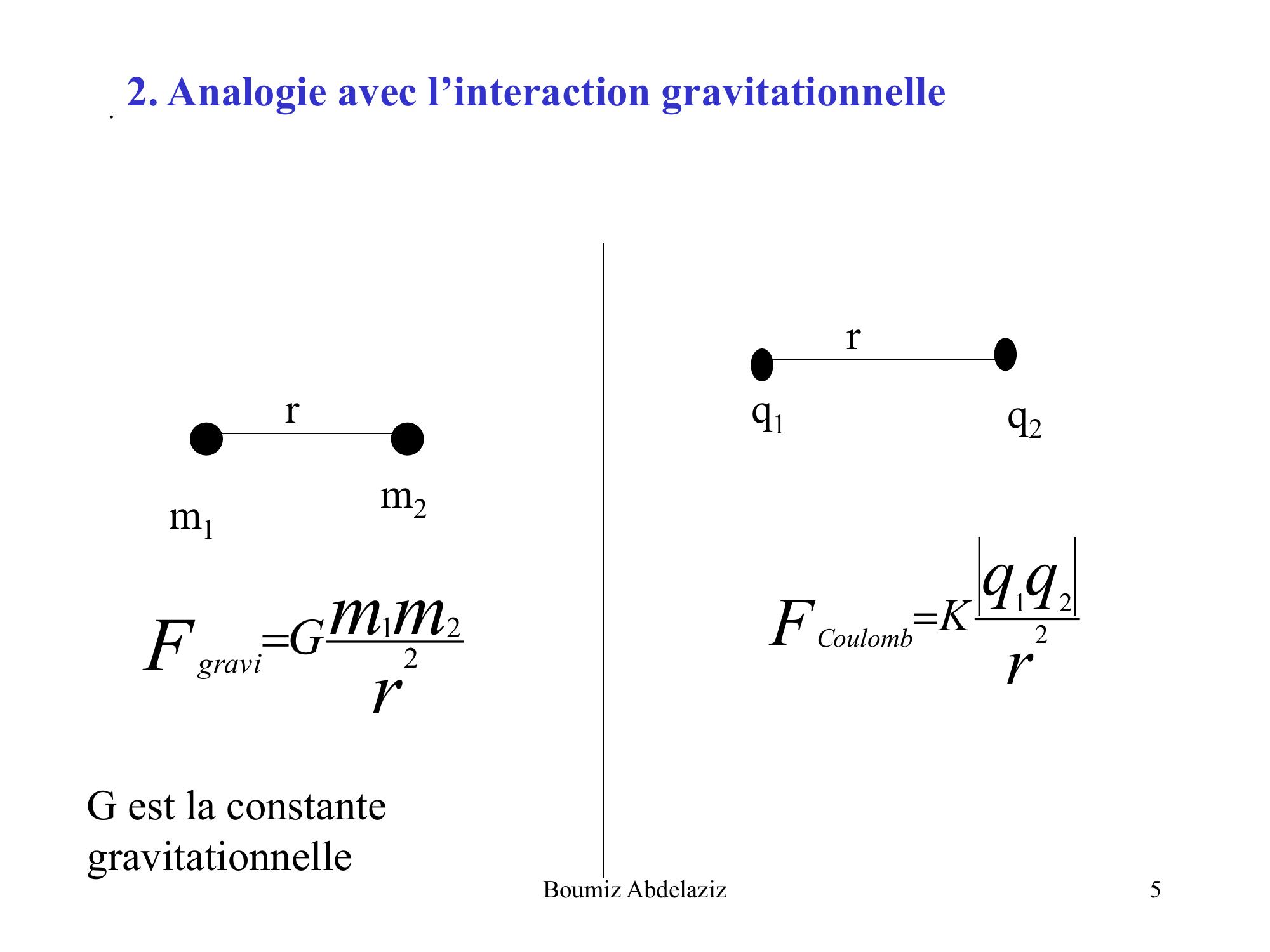
Page 5 : .q2q1m1m2rrrqqFKCoulomb221rmmFGgravi2212. Analogie avec l’interaction gravitationnelleG est la constante gravitationnelle5Boumiz Abdelaziz

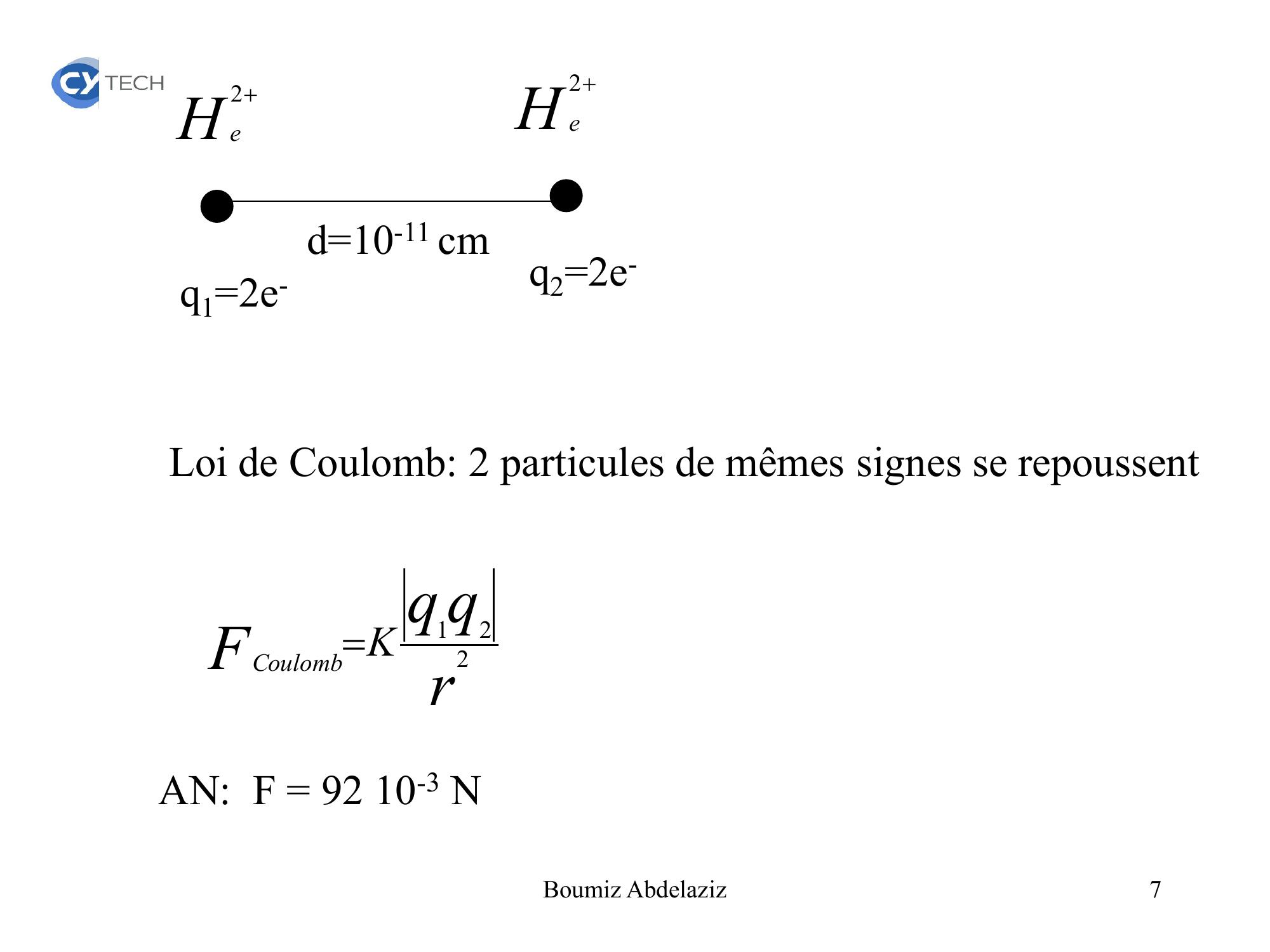
Page 6 : 3. Exemples.Exemple1.Calculer La force de répulsion électrique qui existe entre deux particules noyau d’atome d’hélium contenant deux protons et deux neutrons distantes de 10-11 cm.Charge de l’électron e- = 1,6.10-19 C6Boumiz Abdelaziz

Page 7 : .q1=2e-q2=2e-H e2H e2d=10-11 cmLoi de Coulomb: 2 particules de mêmes signes se repoussent rqqFKCoulomb221AN: F = 92 10-3 N7Boumiz Abdelaziz

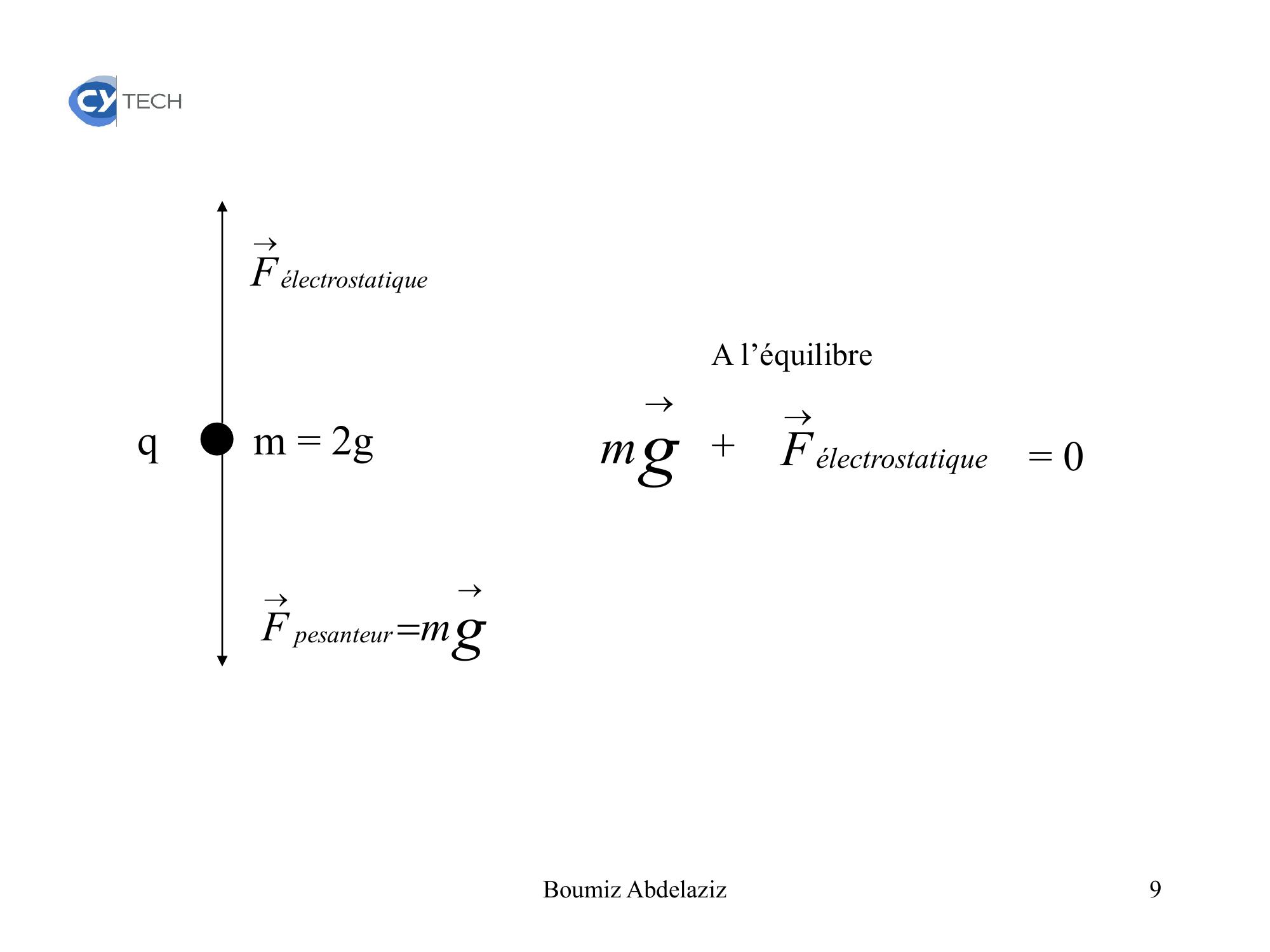
Page 8 : Exemple 2.Quelle charge doit porter une particule de masse 2g, pour demeurer à l’équilibre dans le laboratoire s’il existe un champ électrostatique dirigé vers le bas de 500 v/m ?g = 9.8 ms-2.8Boumiz Abdelaziz

Page 9 : .m = 2gqtiqueélectrostaFgmF pesanteurA l’équilibretiqueélectrostaF+= 0gm9Boumiz Abdelaziz

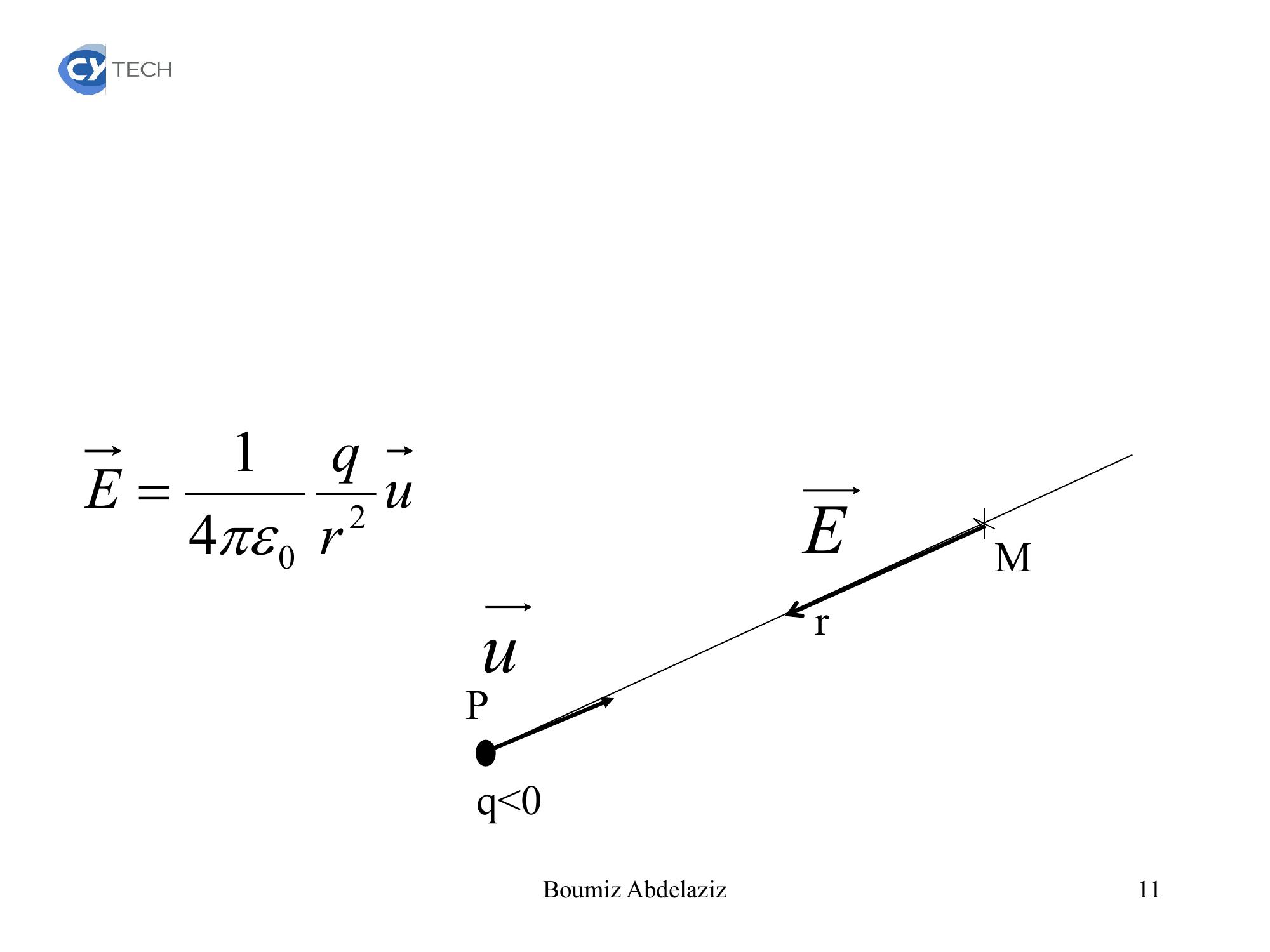
Page 10 : II Le champ électrostatique1. champ électrostatique créé par une charge ponctuellerq0MPuEurqE204110Boumiz Abdelaziz

Page 11 : rq0MPuEurqE204111Boumiz Abdelaziz

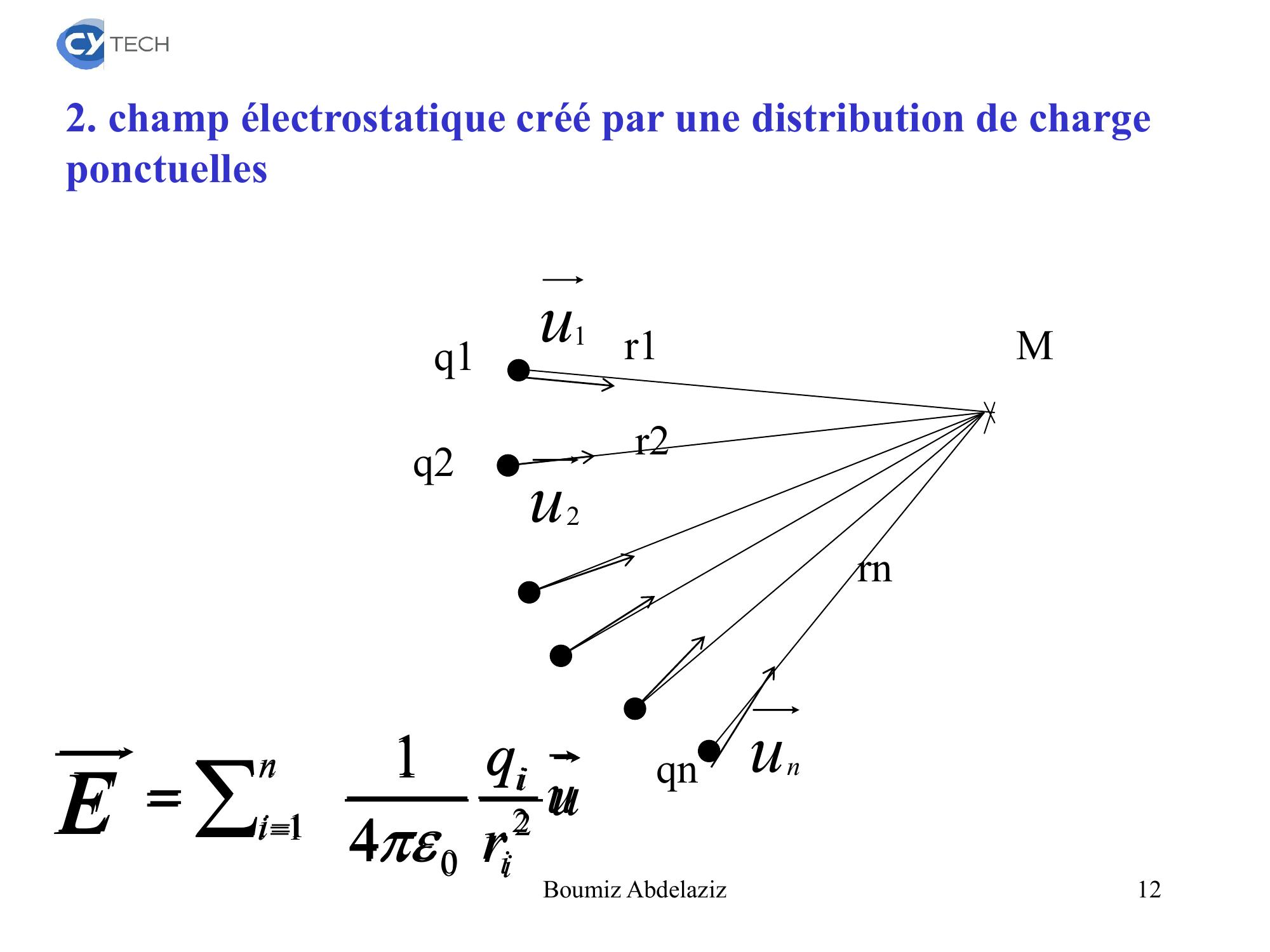
Page 12 : 2. champ électrostatique créé par une distribution de charge ponctuellesMr1r2rnq1q2qnurqiiniE201 41u1u2unurqiiniE201 4112Boumiz Abdelaziz

Page 13 : 3. champ électrostatique créé par une distribution de charge continue3.1. Distributions linéairedq= λdluEMFil chargéPrurdlE204113Boumiz Abdelaziz

Page 14 : -dl est en élément de longueur-dl porte la charge élémentaire dq-Par définition dq= λdl Où λ est la densité linéique de chargedq créé en M le champ élémentaire dE14Boumiz Abdelaziz

Page 15 : 3.2 . Distributions surfaciques3.3. Distributions volumiques15Boumiz Abdelaziz

Page 16 : III Symétries de distributions de charges1. Distribution de symétrie cylindriqueρr,θ,z = ρr Invariance de la distribution de charges par rotation d’angle θ et par translation le long de oz2. Distribution de symétrie sphériqueρr,θ,φ = ρrInvariance de la distribution de charges par rotation d’angle θ et φ16Boumiz Abdelaziz

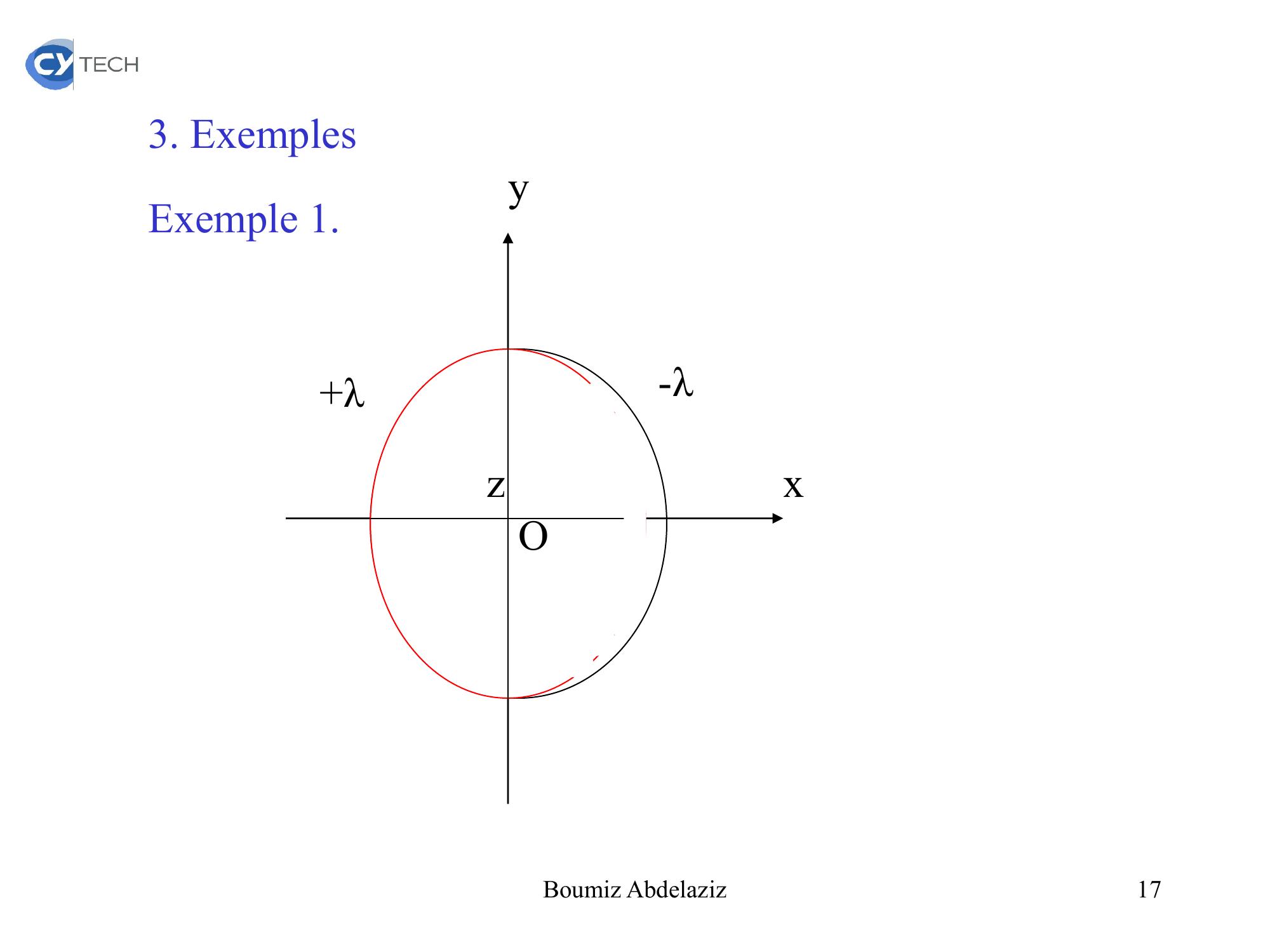
Page 17 : .3. Exemples Exemple 1. xyoz+λ-λOz17Boumiz Abdelaziz

Page 18 : IV Propriétés de symétrie du champ électrostatique1. Symétrie planeVoir FigurePropriété 1Le champ électrostatique appartient au plan de symétrie de charge en chacun de ses points18Boumiz Abdelaziz

Page 19 : .2 Antisymétrie planeVoir FigurePropriété 2Le champ électrostatique est perpendiculaire au plan d’ antisymétrie de charge en chacun de ses points.19Boumiz Abdelaziz

Page 20 : .V Lignes de champ-Tubes de champ1. Lignes de champLe vecteur champ électrostatique est en tout point tangent à une courbe appelée ligne de champ.Ces lignes sont orientées par le sens du champ.Ligne de champChamp électrostatique20Boumiz Abdelaziz

Page 21 : . 1. Tube de champFigureL’ensemble des lignes de champ engendreune surface, appelée tube de champ.Ligne de champ21Boumiz Abdelaziz

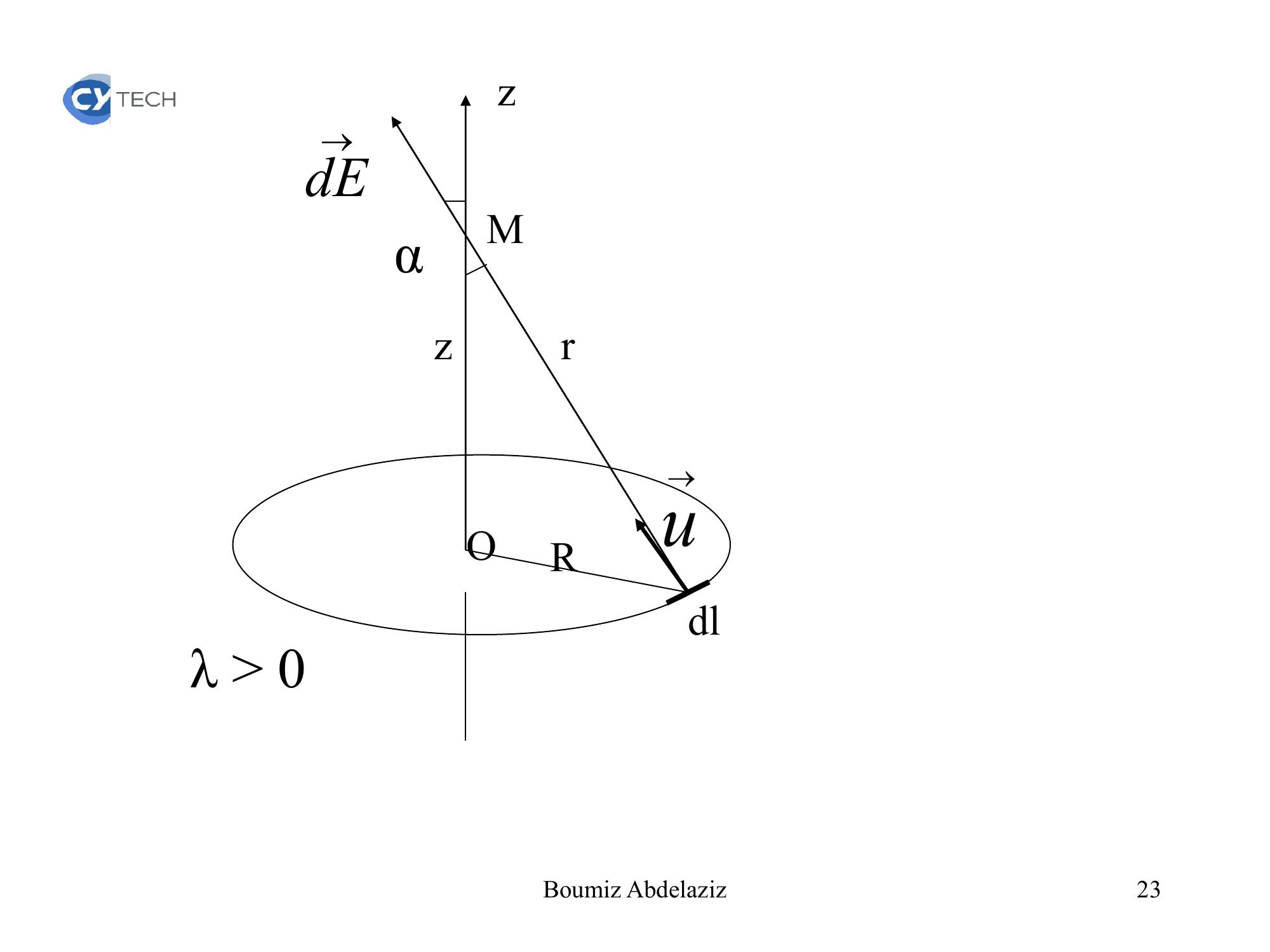
Page 22 : .VI. Exemples de calcul du champ électrostatique1. Champ créé par une spire circulaire en tout point de son axe.Soit une spire circulaire de rayon R, de charge linéique λ 0. Calculer le champ électrostatique en tout point de son axe22Boumiz Abdelaziz

Page 23 : .OMzzRdlαλ 0urdE23Boumiz Abdelaziz

Page 24 : '.MMEdC Soit q une charge placée en un point O.Soit le champ électrostatique créé par q en tout point M de l’espace .Par définition la circulation élémentaire dC le long de 'MMM’ est un point voisin de Mest donnée par la relation:EVII Circulation de E et potentiel électrostatique24Boumiz Abdelaziz

Page 25 : .drrqKdC21rKqddC14021rdqrrC25Boumiz Abdelaziz

Page 26 : ..On constate que la circulation est indépendante du chemin suivi,qu’elle ne dépend que des points de départ et d’arrivée r1 et r2 rqMV04dC= - dV.On pose14210rdrrqC114120rrqC26Boumiz Abdelaziz

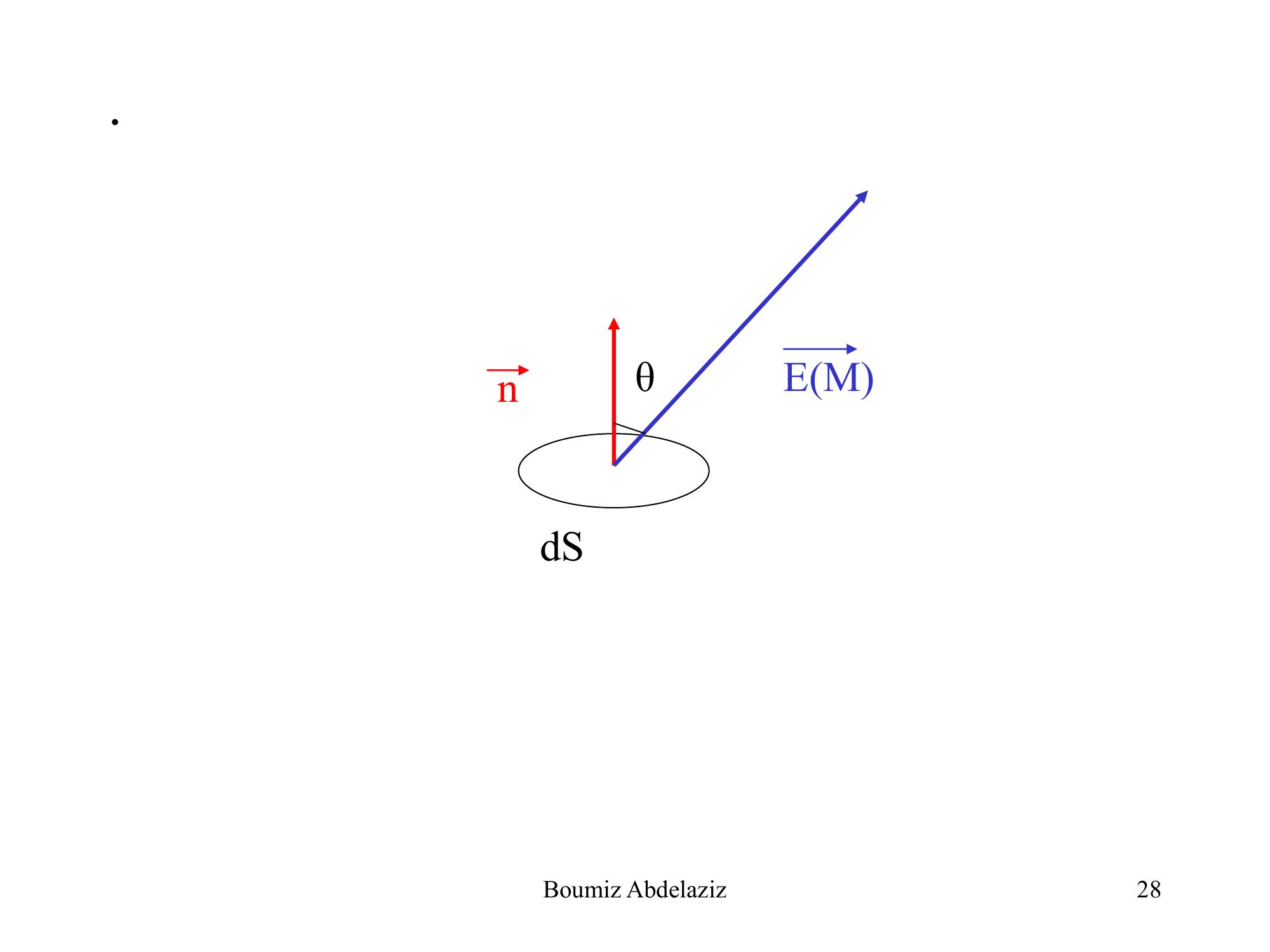
Page 27 : .VIII Le théorème de Gauss1 – Flux du champ électrostatiqueDéfinition :Soit un champ électrostatique défini dans un domaine de l’espace.On appelle flux élémentaire dF du champ à travers la surface dS la quantité :MEMEavecdSMEddSndS 27Boumiz Abdelaziz

Page 28 : .nEMθdS28Boumiz Abdelaziz

Page 29 : . Le vecteur normal n est choisi, parconvention, dirigé vers l’extérieur de la surface fermée.On définit alors le flux sortant à travers la surface fermée, que l’on note :dSME29Boumiz Abdelaziz

Page 30 : .2. Théorème de GaussLe théorème de Gauss permet d’exprimer le flux du champ électrostatique sortant d’une surface fermée, en fonction des charges contenues à l’intérieur de cette surface.30Boumiz Abdelaziz

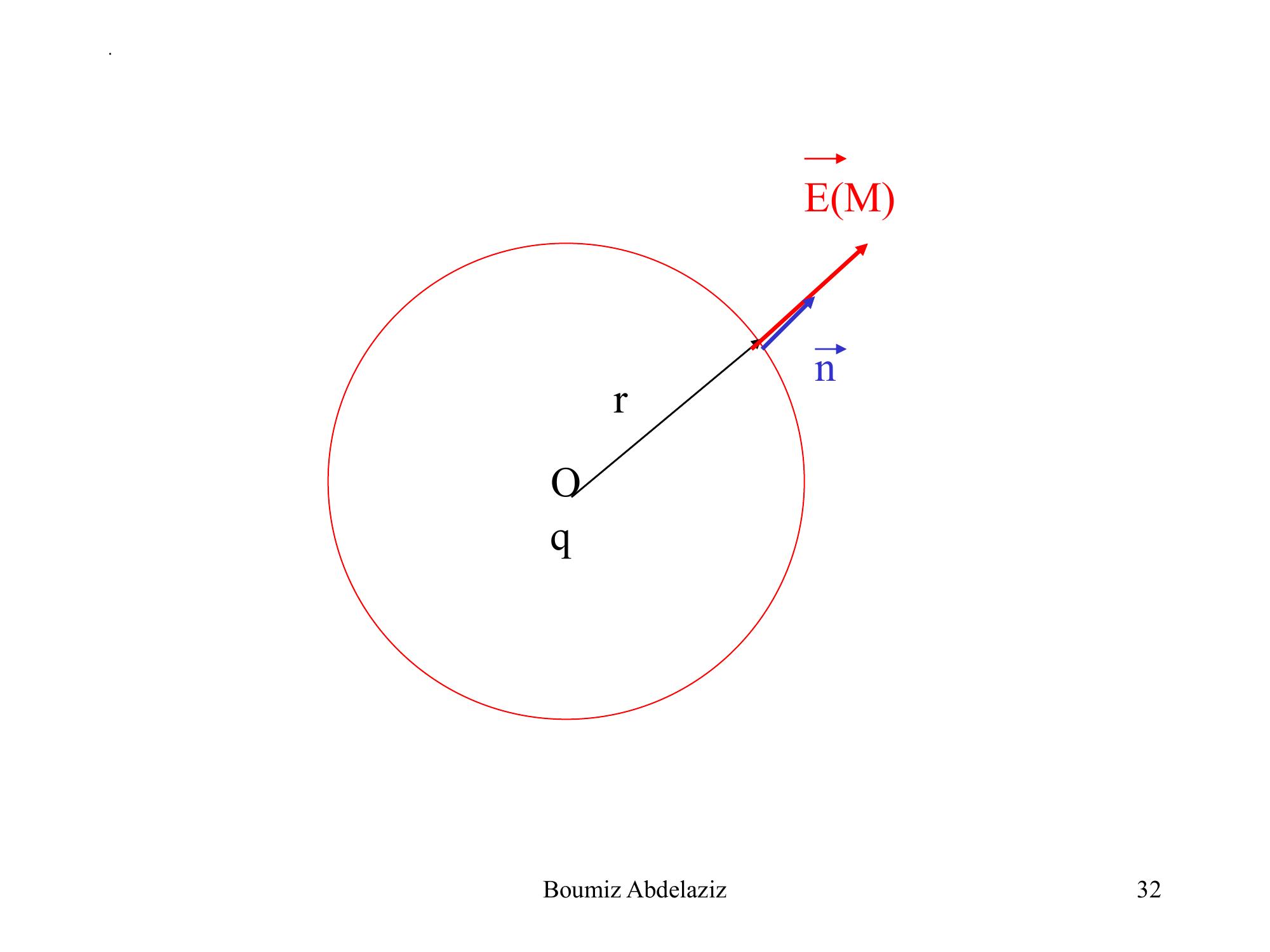
Page 31 : .Soit une charge ponctuelle q placée en O et on choisit comme surface de Gauss la sphère CO,r.31Boumiz Abdelaziz

Page 32 : .OrEMnq32Boumiz Abdelaziz

Page 33 : Enoncée du théorèmeLe flux du champ électrostatique à travers une surface fermée, est égal à la charge interne divisée par ɛ00intQdSME33Boumiz Abdelaziz

Page 34 : .dSrE ordoncsoit24 rE 2041rqE220441rrqF0qF34Boumiz Abdelaziz

Page 35 : .3. ExemplesExemple 1: Champ créé par une sphère pleineSoit une sphère O,R uniformément chargée en volume.Elle porte une charge de densité volumique constante01er cas calcul du champ à l’extérieur rRRrSurface de Gausse35Boumiz Abdelaziz