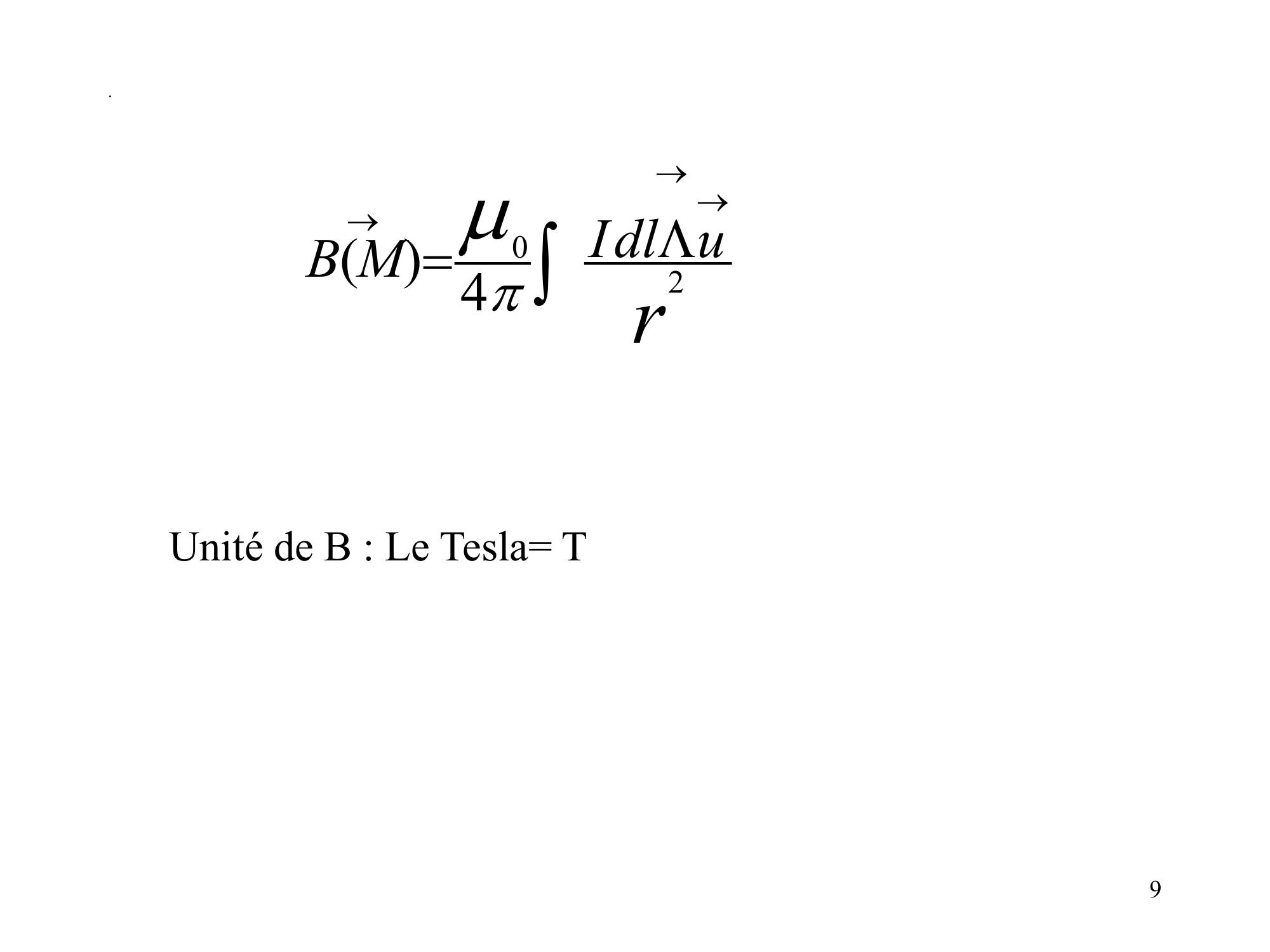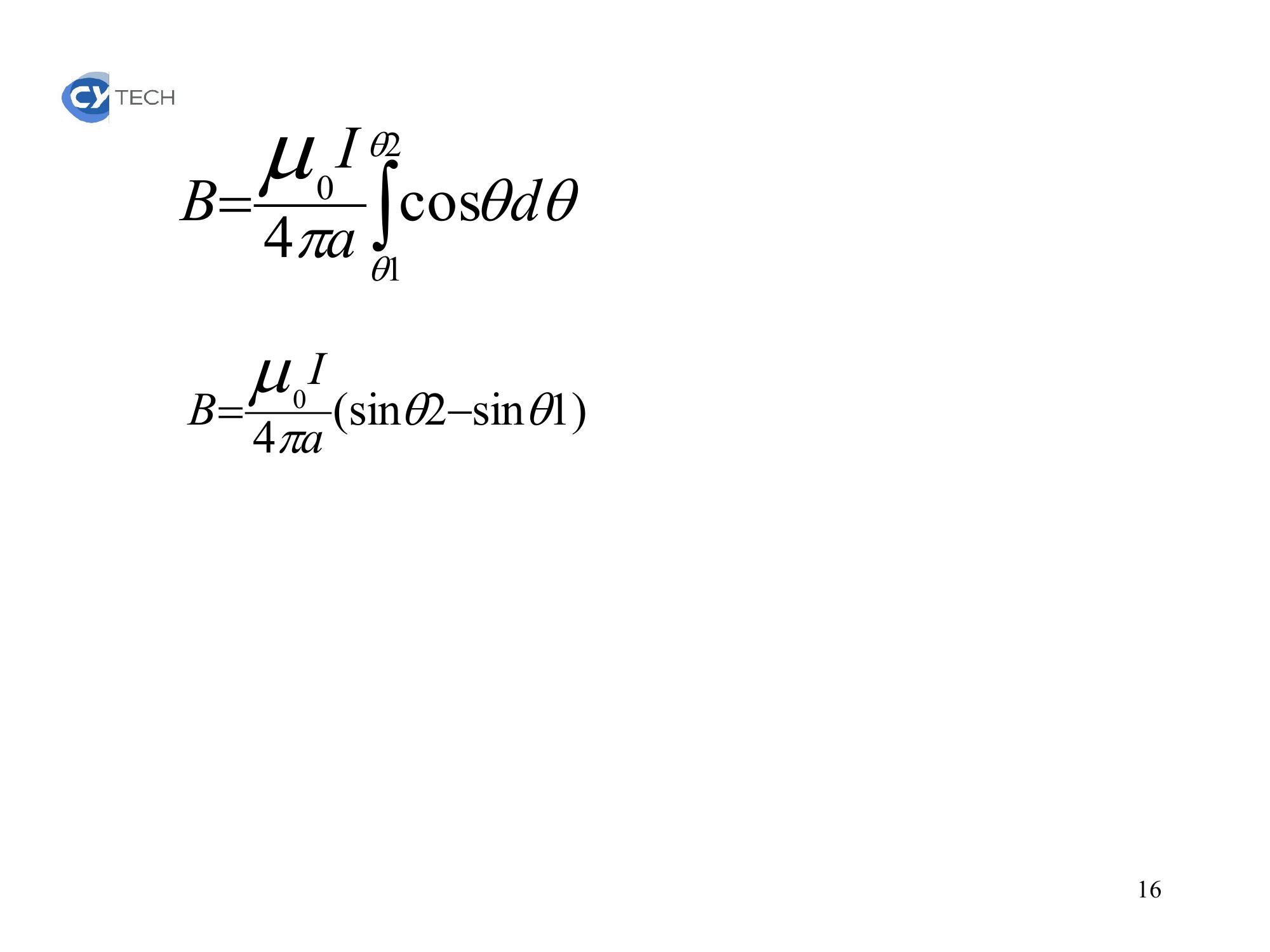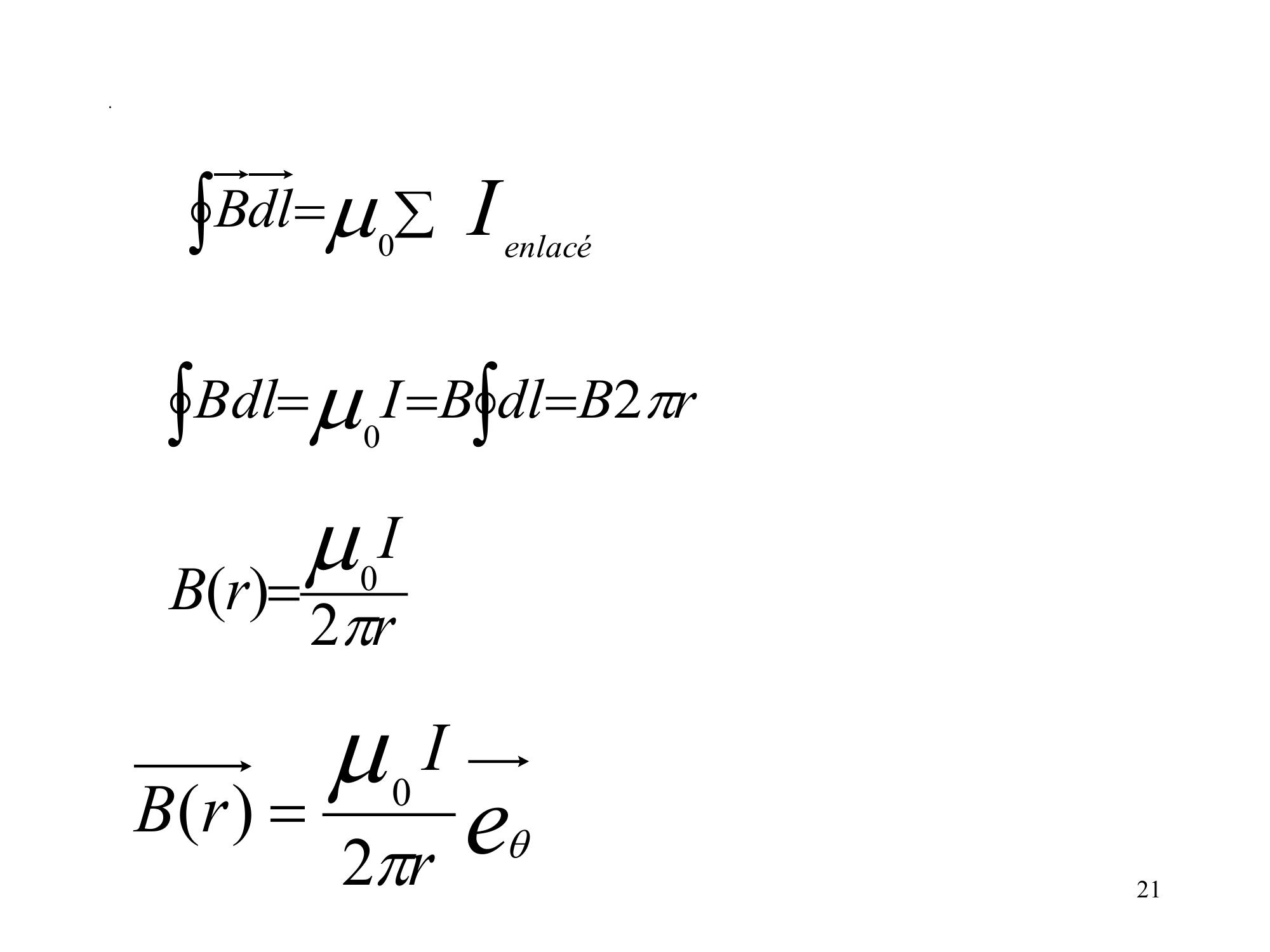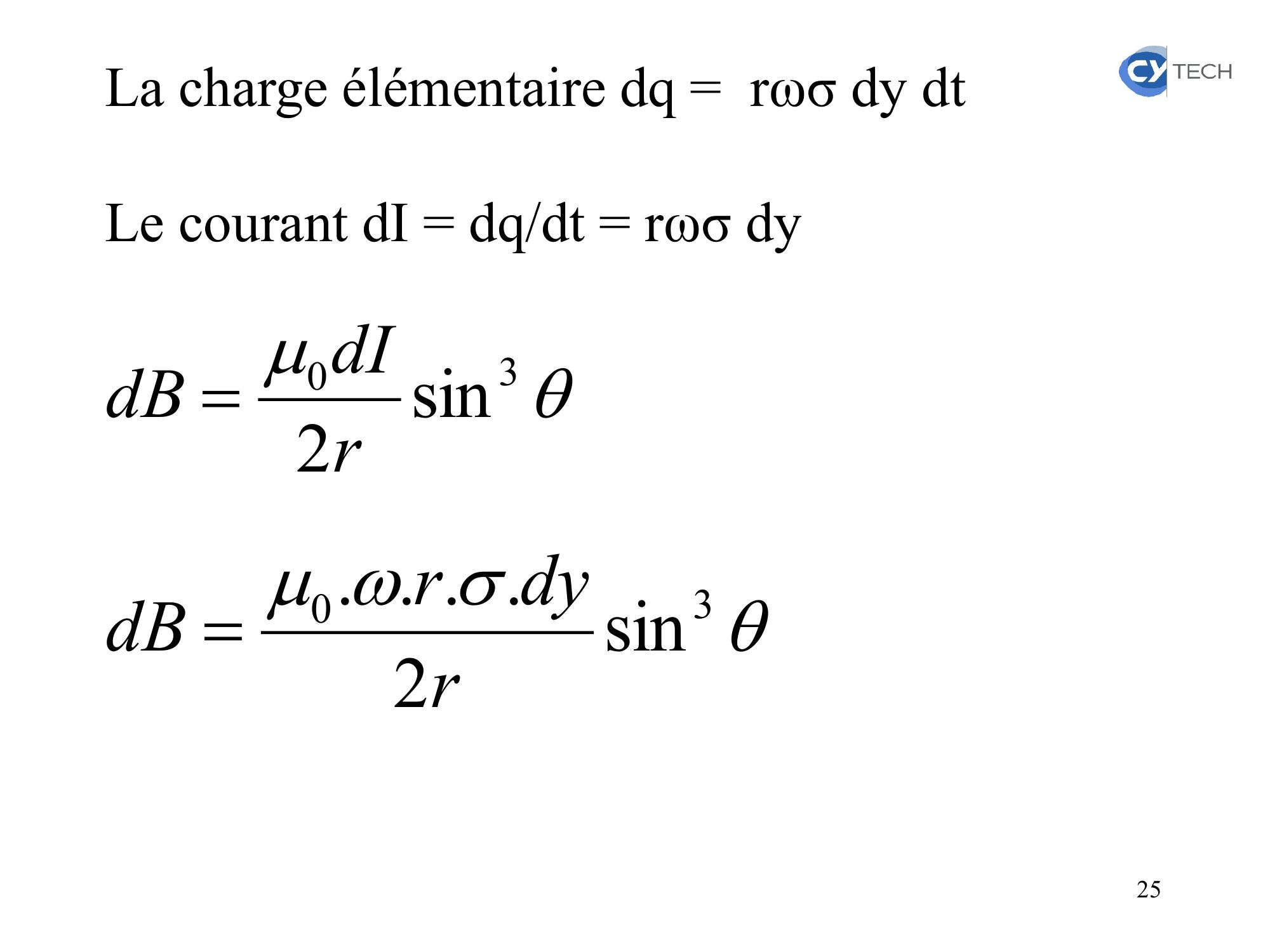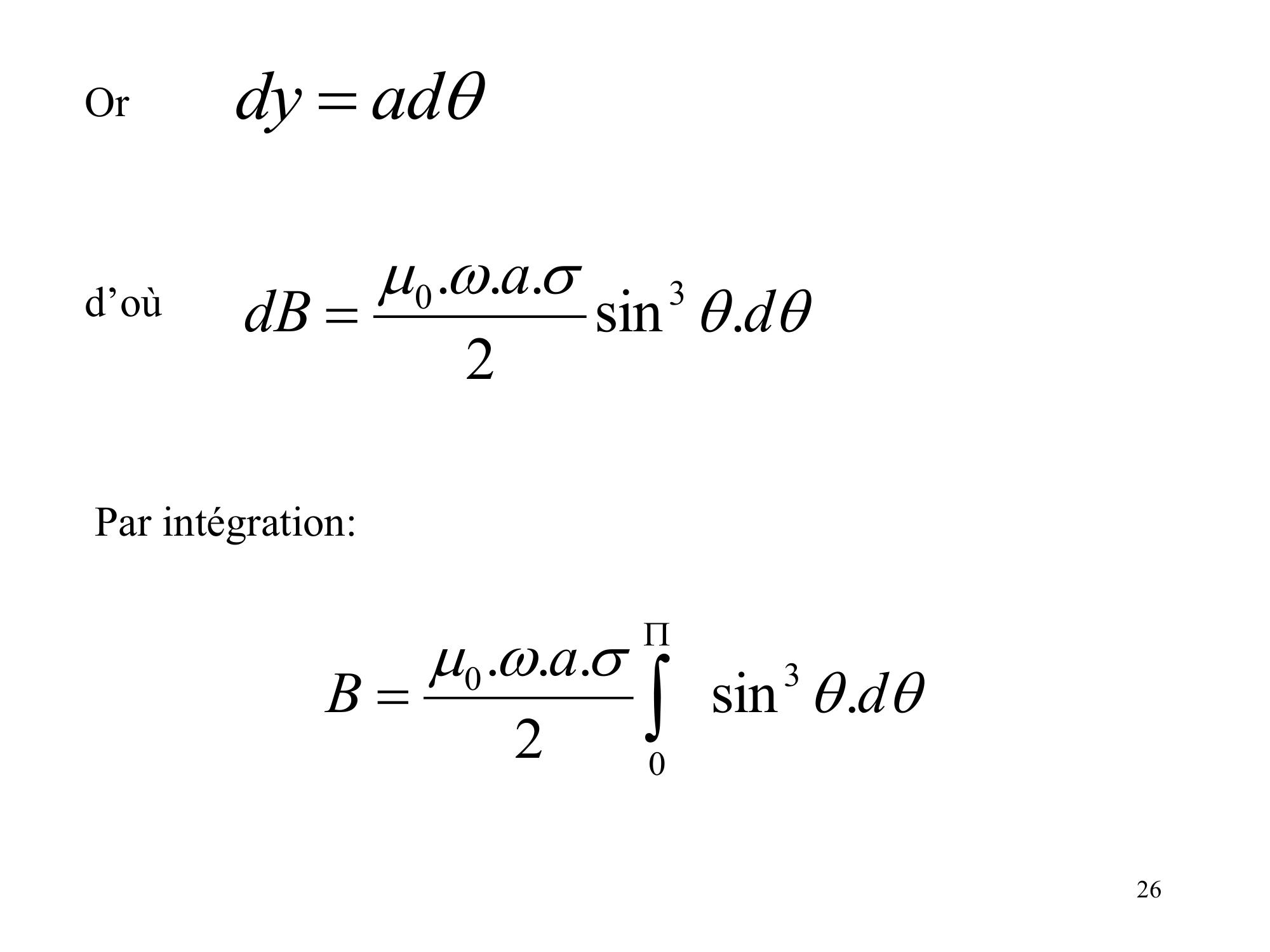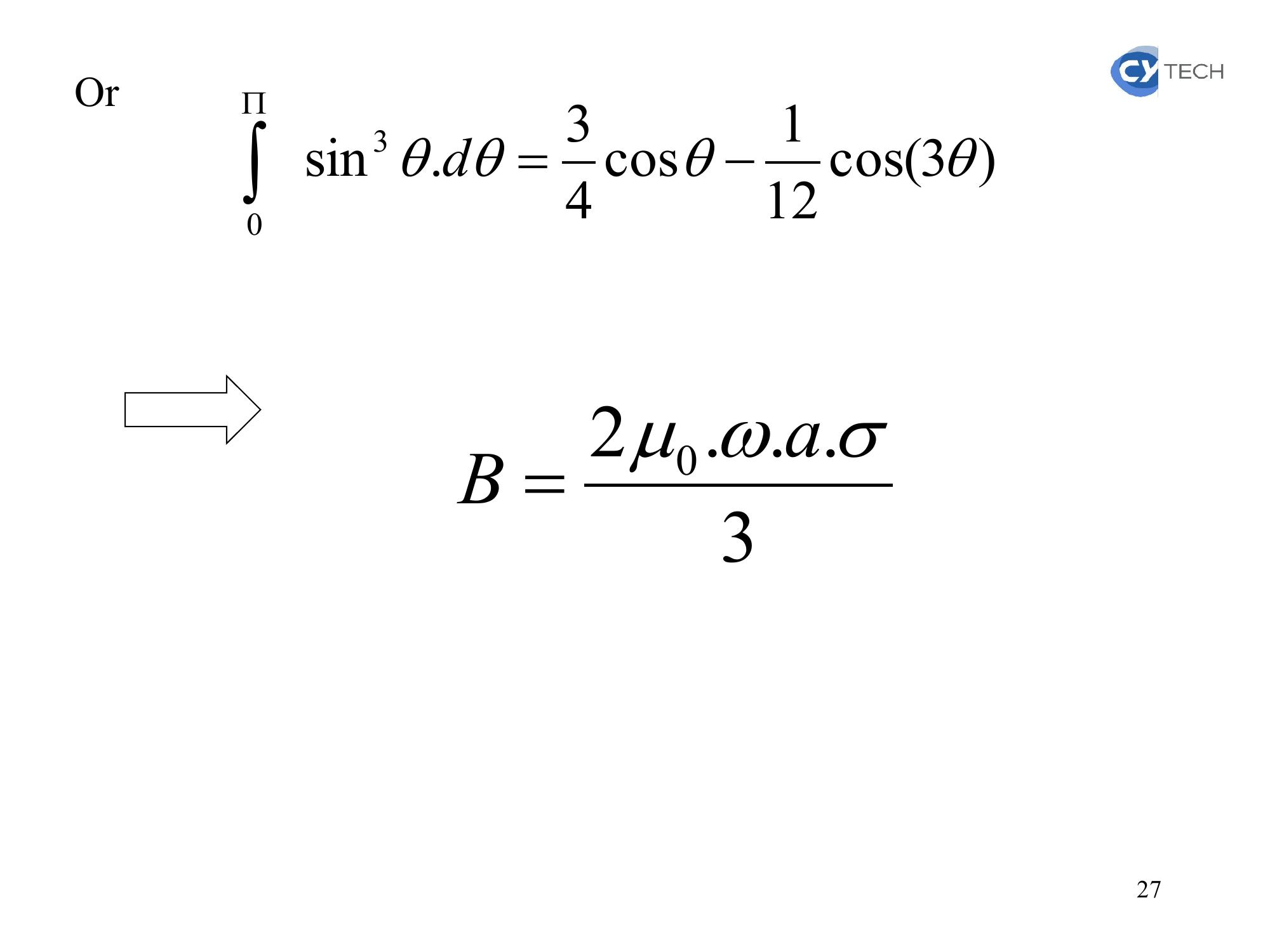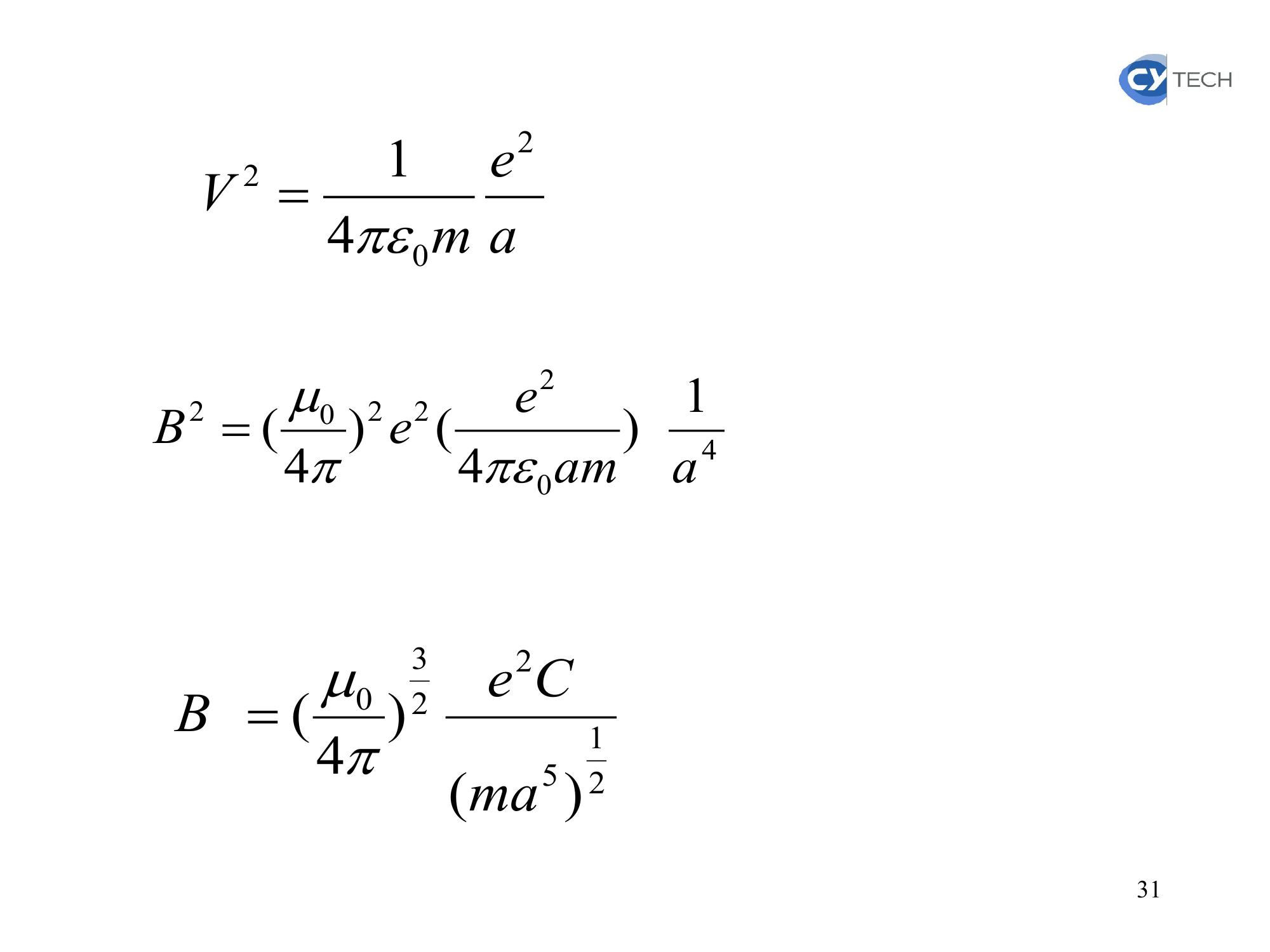CM BIS Chapitre1

Télécharger le CM BIS Chapitre1 en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

Page 1 : .Chapitre 1 bisMagnétostatique1

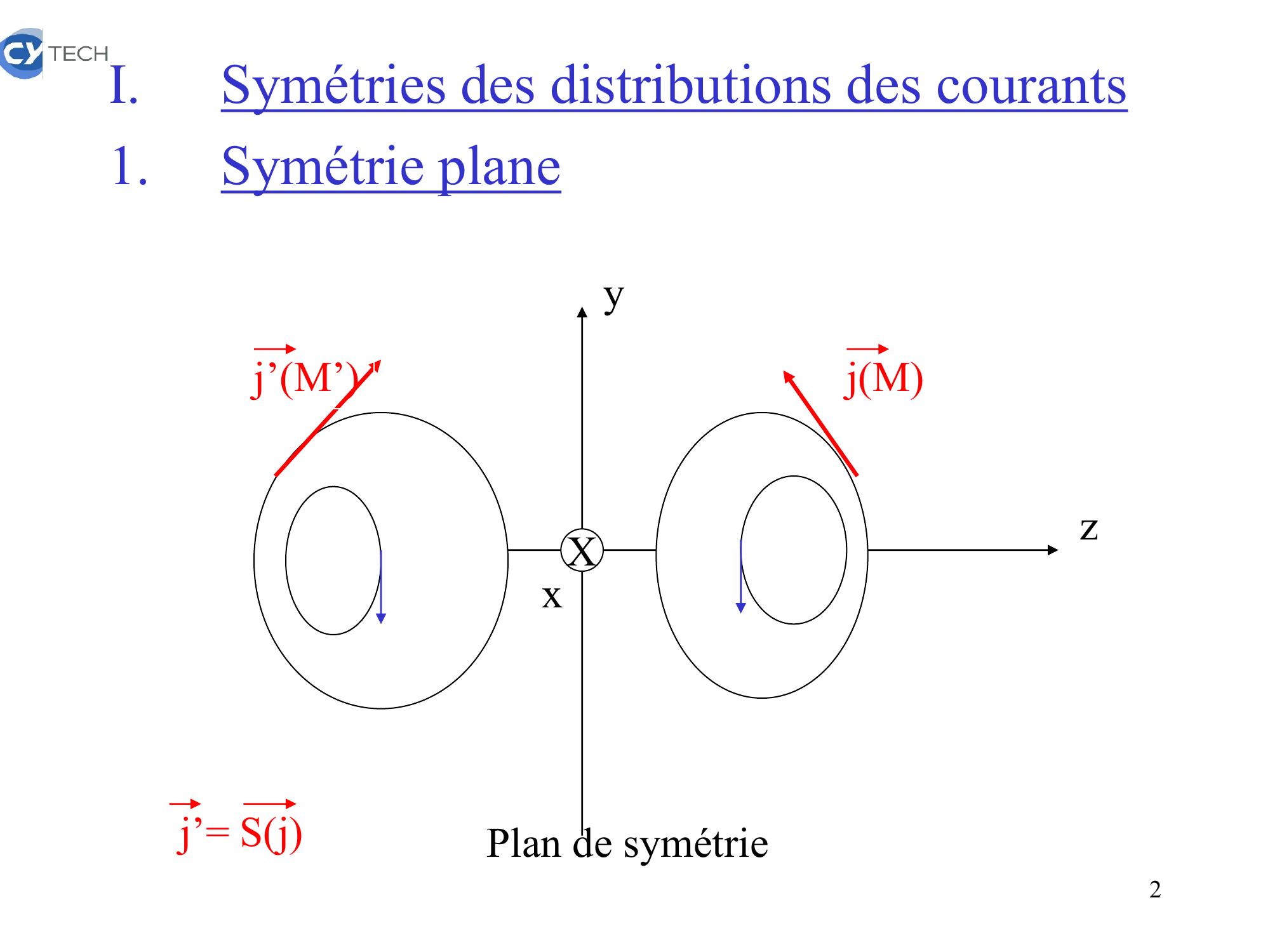
Page 2 : I.Symétries des distributions des courants1.Symétrie planej’M’jMyzxXPlan de symétriej’= Sj2

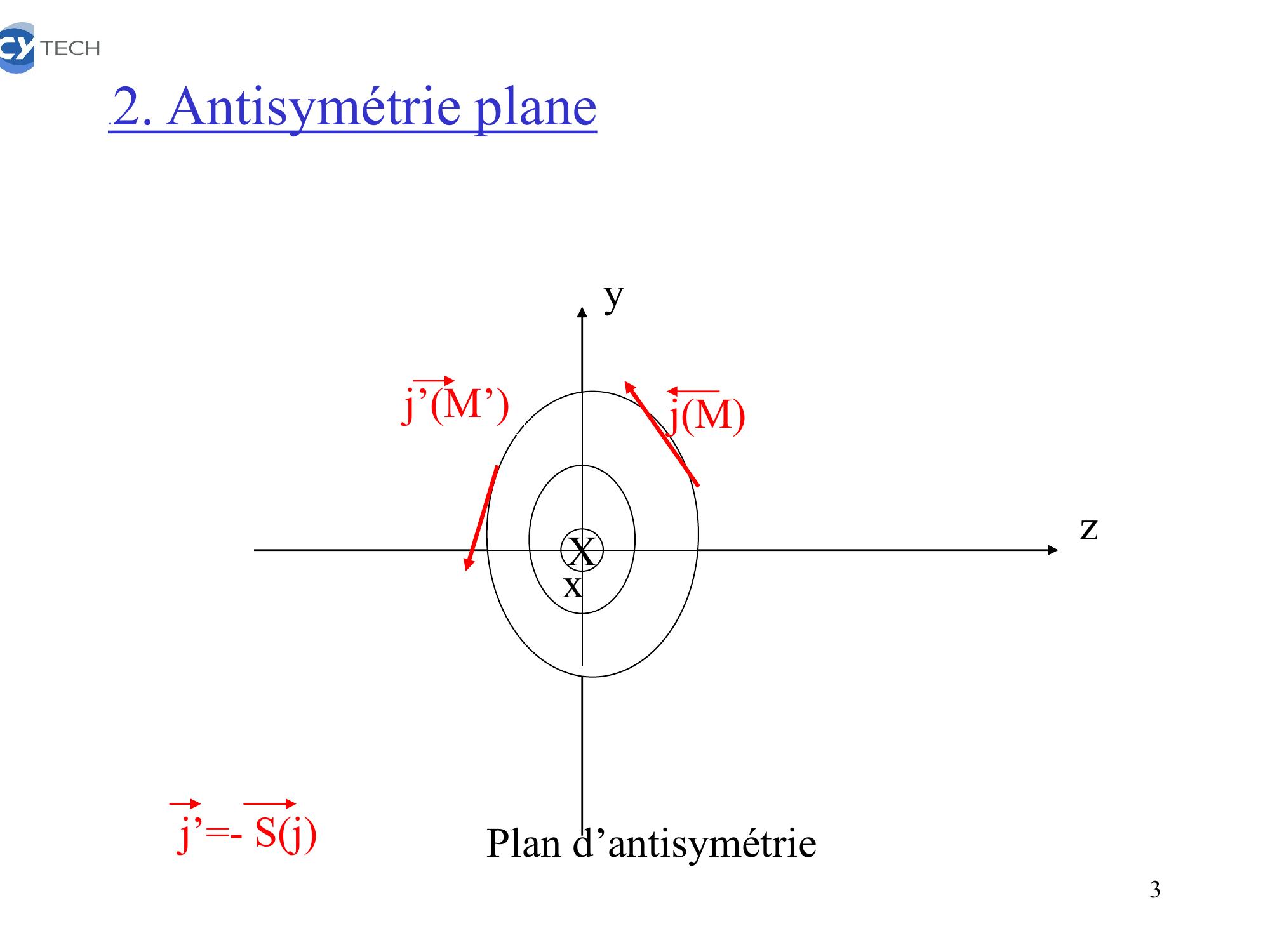
Page 3 : .2. Antisymétrie planej’M’jMyzxXPlan d’antisymétriej’=- Sj3

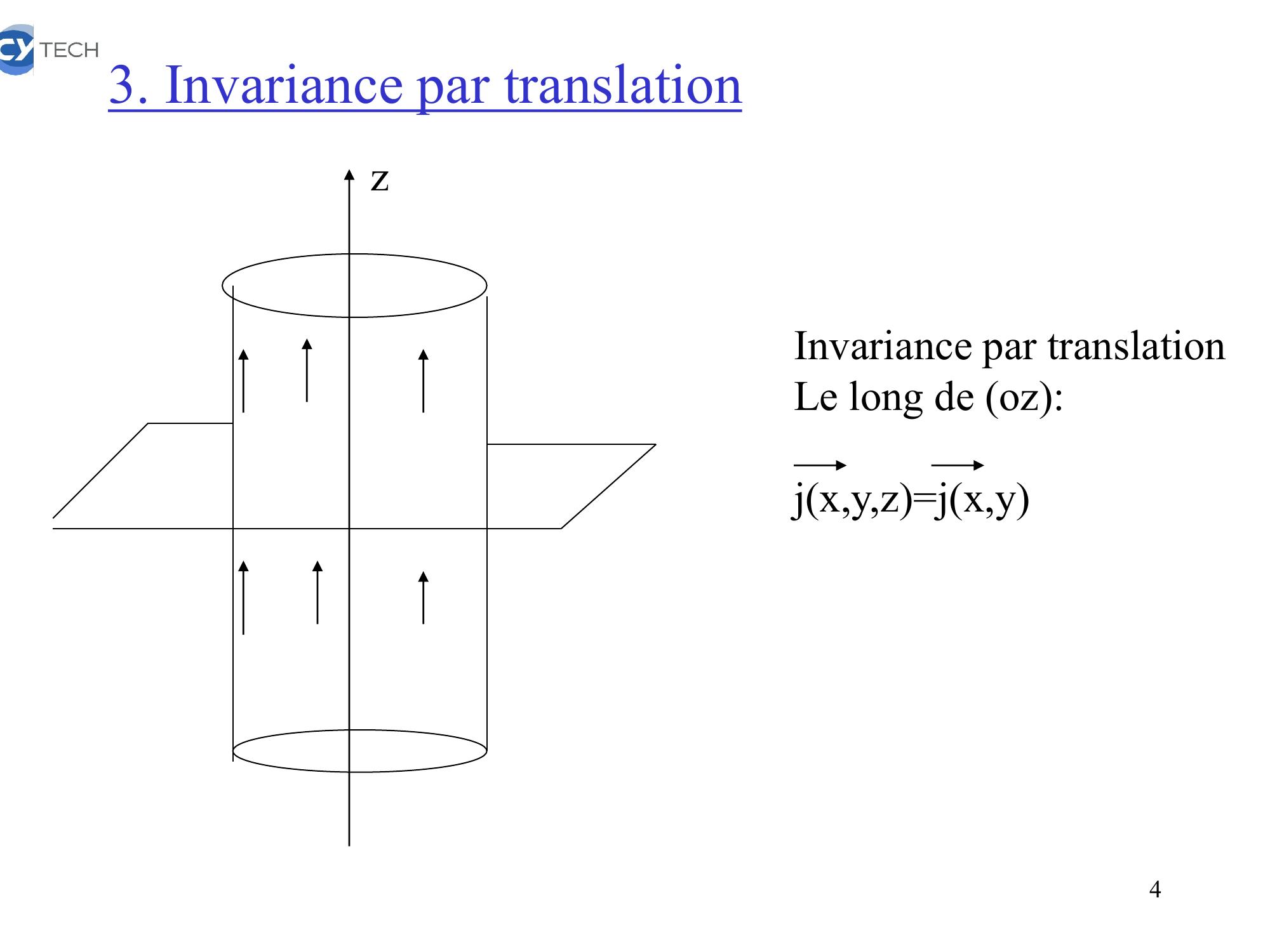
Page 4 : 3. Invariance par translationInvariance par translationLe long de oz:jx,y,z=jx,yz4

Page 5 : . 4. Invariance par rotation autour de ozjr,ɵ,z=jrezzj5

Page 6 : II. Loi de Biot et Savart1. Vecteur élément de courantL’élément de courant pour un circuit filiformedlIdCjdlI6

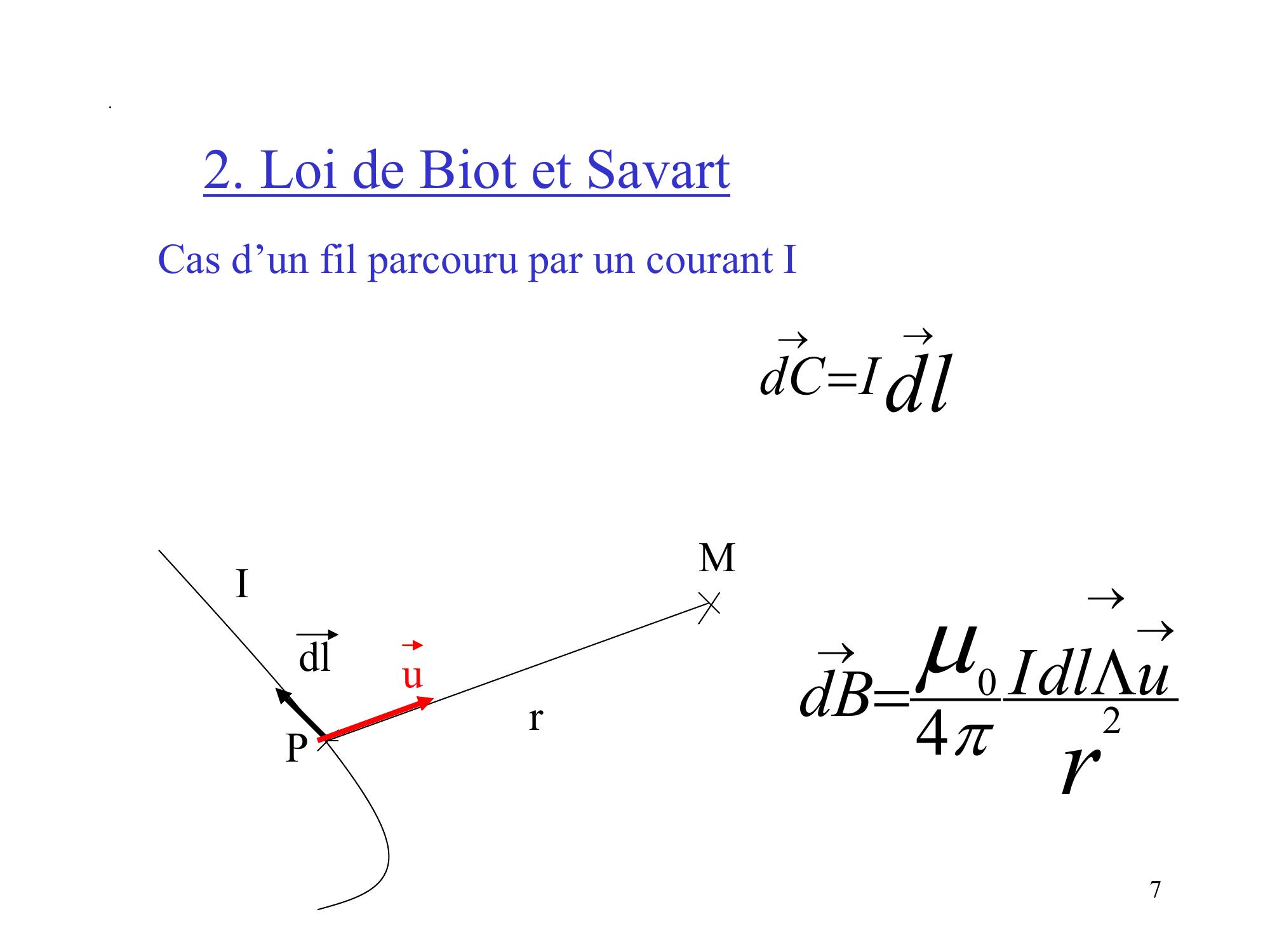
Page 7 : .2. Loi de Biot et SavartCas d’un fil parcouru par un courant IdlIdCdlIPMrudlIdB204ru7

Page 8 : . Cas d’une distribution surfacique de courant 8

Page 9 : .rudlIMB204Unité de B : Le Tesla= T9

Page 10 : .III Propriétés de symétrie du champ magnétostatique1.Symétrie planePropriété Le champ magnétostatique est perpendiculaire au plan de symétrie en chacun de ses points10

Page 11 : .2. Antisymétrie planePropriété 2Le champ magnétostatique est contenu dans le plan d’antisymétrie de courant en chacun de ses points.11

Page 12 : .IV Calcul du champ magnétique1. Champ créé par une spire circulaire en tout point de son axeUne spire circulaire de rayon R, est parcourue par un courant I.1. Établir l’orientation du champ magnétique en tout point de son axe à partir des propriétés de symétrie.2. Exprimer le champ magnétique en tout point de son axeà partir de la loi de Biot et Savard.12

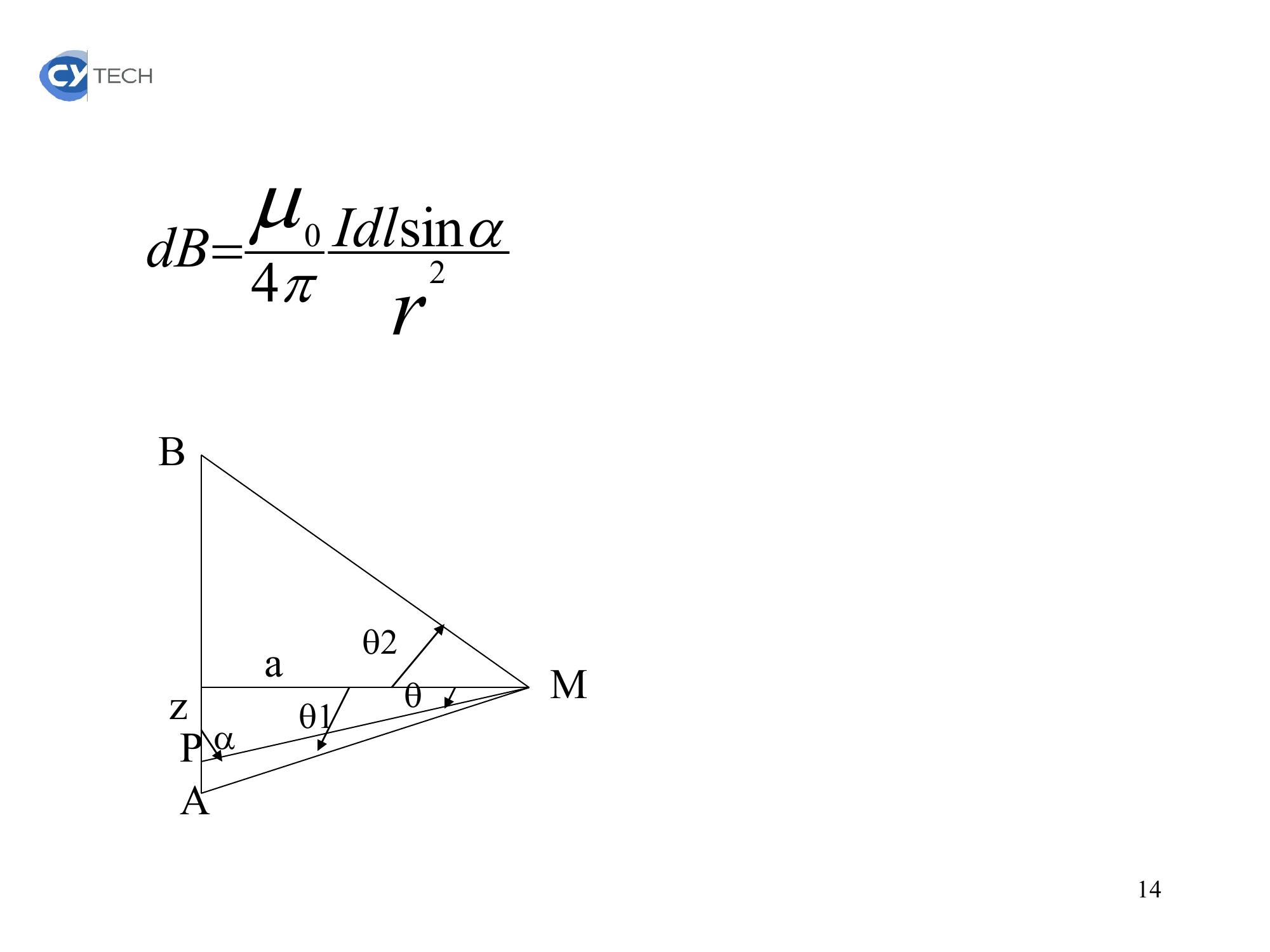
Page 13 : .2. Champ créé par un segmentUn segment AB, de longueur L est parcouru par un courantI, établir l’expression du champ magnétique en tout point M à la distance d du fil.ABPMdBdlIarudlIdB204udl = dzr13

Page 14 : . rIdldB20sin4azABPM1214

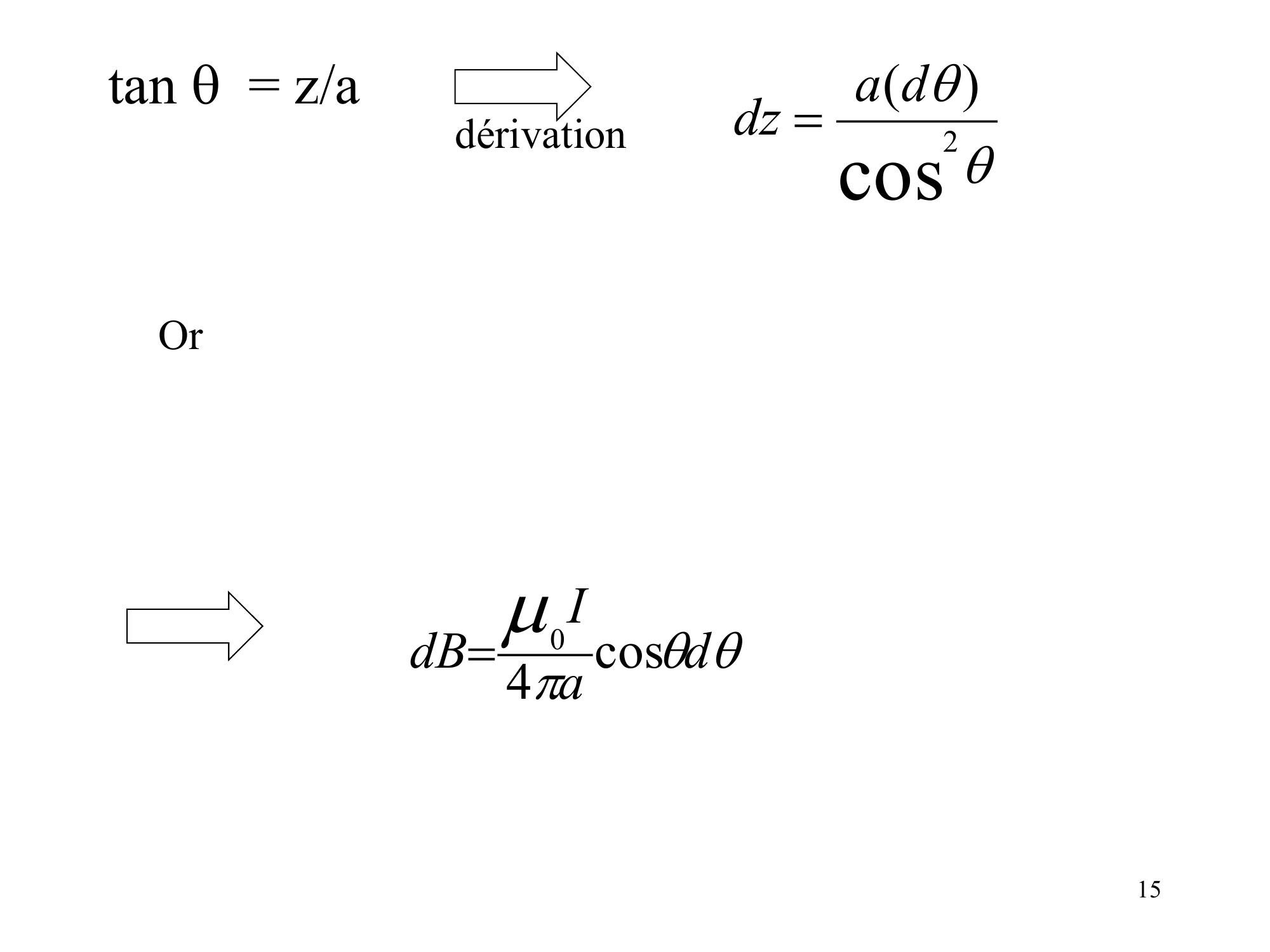
Page 15 : tan = z/a dérivationcos2dadz OrdaIdBcos4015

Page 16 : .daIB210cos41sin2sin40aIB16

Page 17 : 17

Page 18 : .V- Le théorème d’Ampère1. Théorème d’AmpèreLa circulation du champ magnétique le longd’un contour fermé est égale à la somme des courants enlacés multiplié par 0I enlacédlB018

Page 19 : 2. Champ magnétique créé par un fil infiniSoit un fil rectiligne de longueur infinie, parcouru par un courant constant IIzBMBappartient au plan D’antisymétrieBest perpendiculaire Au plan de symétrieContour d’AmpèrerO19

Page 20 : .Tout plan perpendiculaire au fil est un plan d’antisymétrie. Tout plan contenant le fil est un plan desymétrie.B est tangentielerBB20

Page 21 : .I enlacédlB0rBdlBIBdl20rIrB20erIrB2021

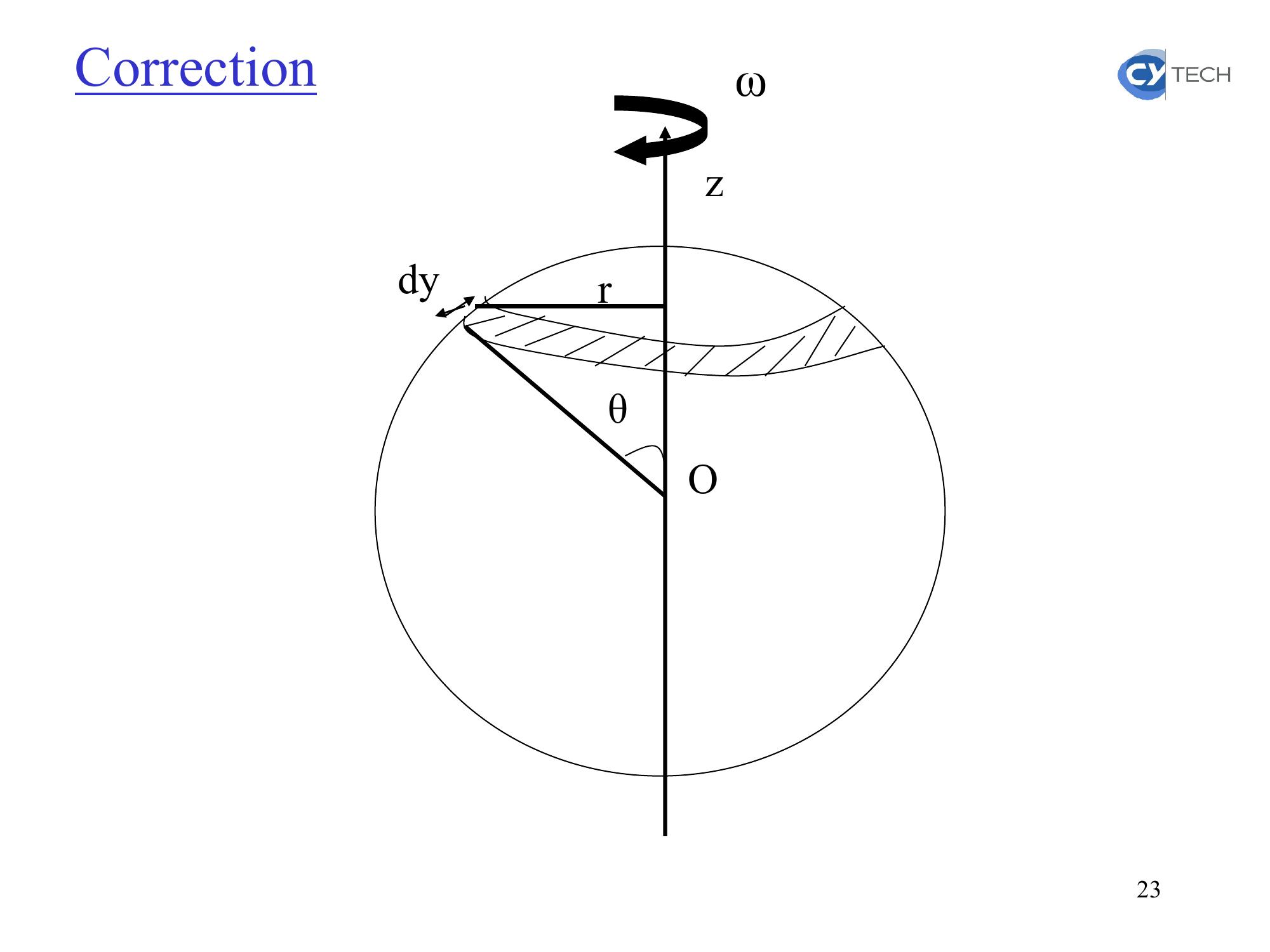
Page 22 : 3 Application 1 : Champ magnétique créé par une sphère en rotationUne sphère creuse de rayon a porte une charge densité de charge σ uniforme, tourne autour de l’un de ses diamètres avec une vitesse angulaire ω.Exprimer le champ magnétique B au centre de la sphère. 22

Page 23 : CorrectionωθrOdyz23

Page 24 : 30 sin2rib le champ magnétique créé par la spire de rayon r en tout point de son axe est donné par l’expression:.Soit une spire de rayon rLa vitesse des charges v = rωLe déplacement de ces charges pendant dt estdl = r.ω.dt24

Page 25 : La charge élémentaire dq = rωσ dy dtLe courant dI = dq/dt = rωσ dy 30sin2rdIdB 30sin2....rdyrdB 25

Page 26 : addy Or dadB.sin2...30d’oùPar intégration:daB.sin2...30026

Page 27 : Or3cos121cos43.sin 30d3...20aB 27

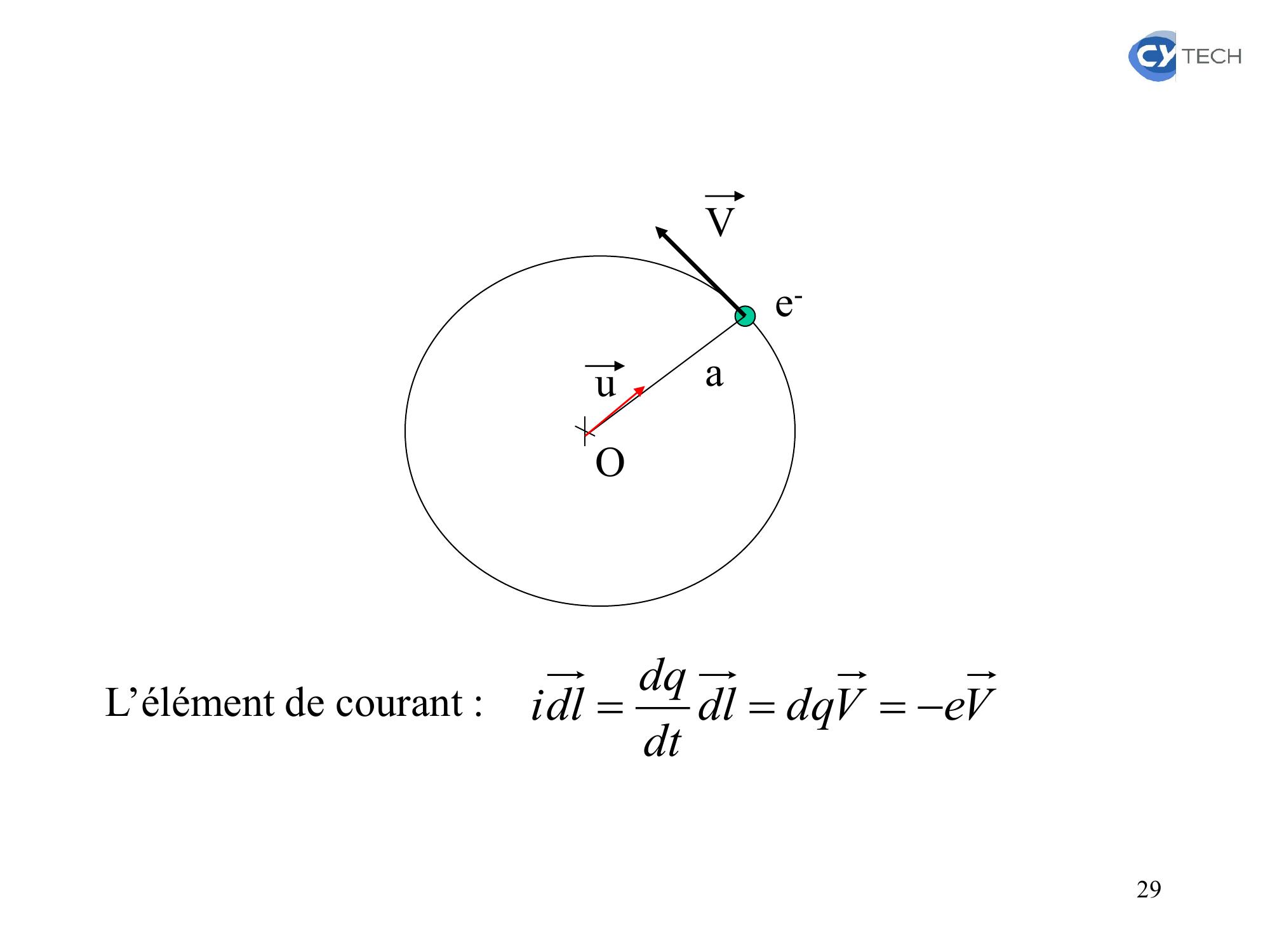
Page 28 : 4 Application2: Champ magnétique créé par un électronExprimer le champ magnétique créé par un électron décrivant un cercle de rayon a autour d’un proton, au point où est placé ce proton. 28

Page 29 : OauVe-L’élément de courant :VeVdqdldtdqdli29

Page 30 : 204ruVeBavec r = aMouvement circulaire, l’accélération:aV 2220241aeamVLa RFD:30

Page 31 : aemV202414022202144aameeB21522304maCeB31

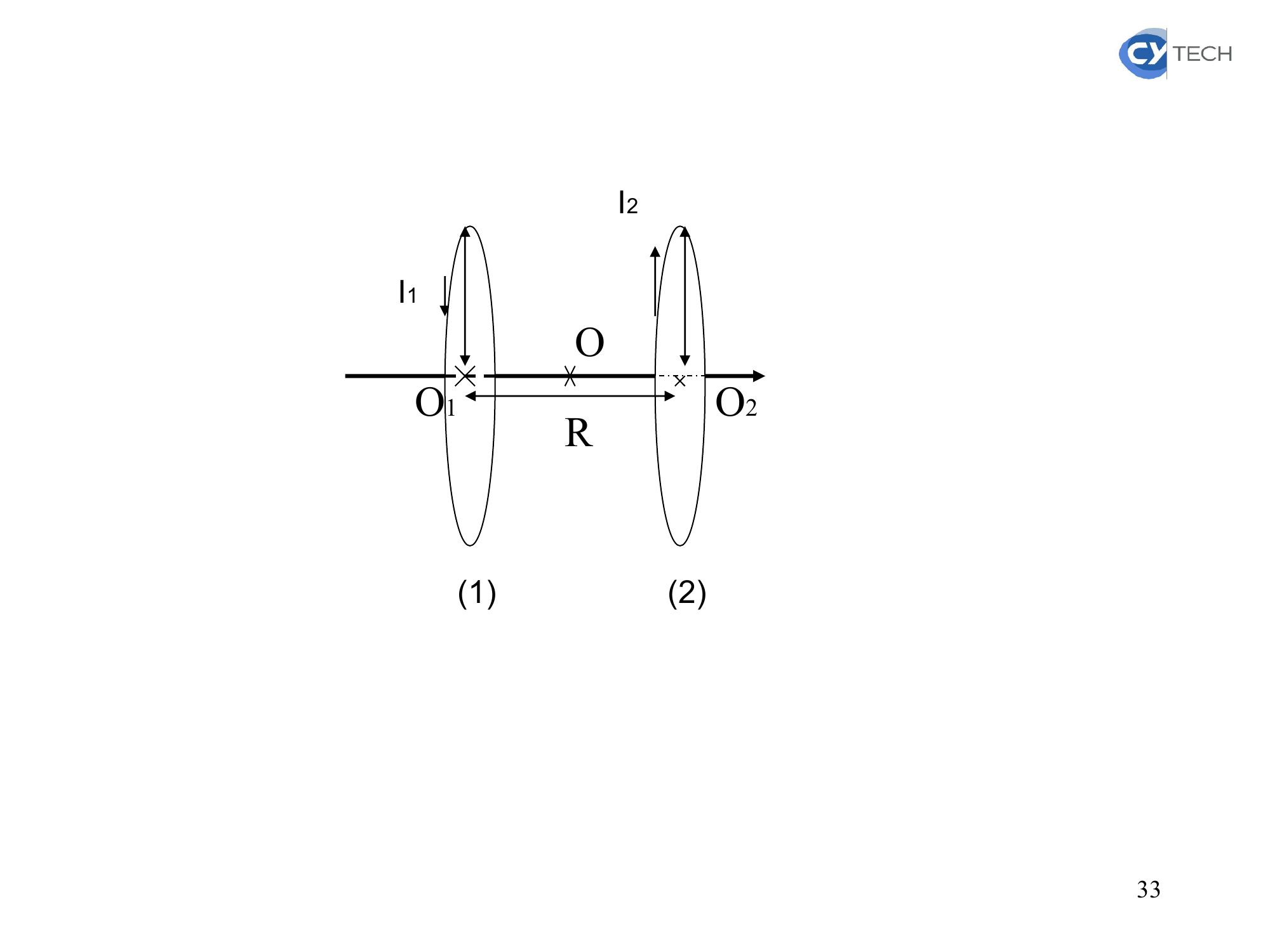
Page 32 : 5 Application 3: Champ magnétique créé par les bobines d’HelmhoDeux bobines plates de N spires, de rayon R,parcourues par un courant d’intensité I,ont leurs centres distants de R. Le sens du courant est tel que les champs créés s’ajoutent dans l’espace situé entre les deux bobines.1. Exprimez le champ magnétique au milieu de leurs centres O.2. . Exprimez le champ magnétique en un point M voisin de O.32

Page 33 : I1I212RO1O2O33

Page 34 : 1. Bobine de très faible largeur les champs crééspar les N spires s’ajoutent.D’autre part, le champ magnétique créé par une spire circulaire en tout point de son axe est donnée par:D’où le champ magnétique total créé par les deux bobines aupoint O: 30 sin2RIb 30sin2..2RINB 34

Page 35 : 35

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35