CM BIS Chapitre2 Biot Savart
Télécharger le CM BIS Chapitre2 Biot Savart en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
Page 1 : Physique - 2022-2023ÉlectromagnétismeChapitre 2 – Loi de Biot et Savart - Théorème de superposition et symétriesPrésentation rédigée par Émilie Dupont Cergy : emilie.dupont@cyu.fr, CY308
Page 2 : Chapitre 1 – Champ magnétique - Force de LorentzChapitre 2 – Loi de Biot et Savart - Théorème de superposition et symétriesChapitre 3 – Induction électromagnétiqueProgramme de Magnétostatique
Page 3 : Programme de Magnétostatiqueen.wikipedia.org/wiki/MagneticdomainBut : Calcul du champ magnétique en régime permanent et dans l'Approximation des Régimes Quasi-Stationnaires A.R.Q.S. régimes lentement variables : magnétostatiqueLe ferromagnétisme et diamagnétisme pas au programme….Ci-dessous: domaine de Weiss etc...
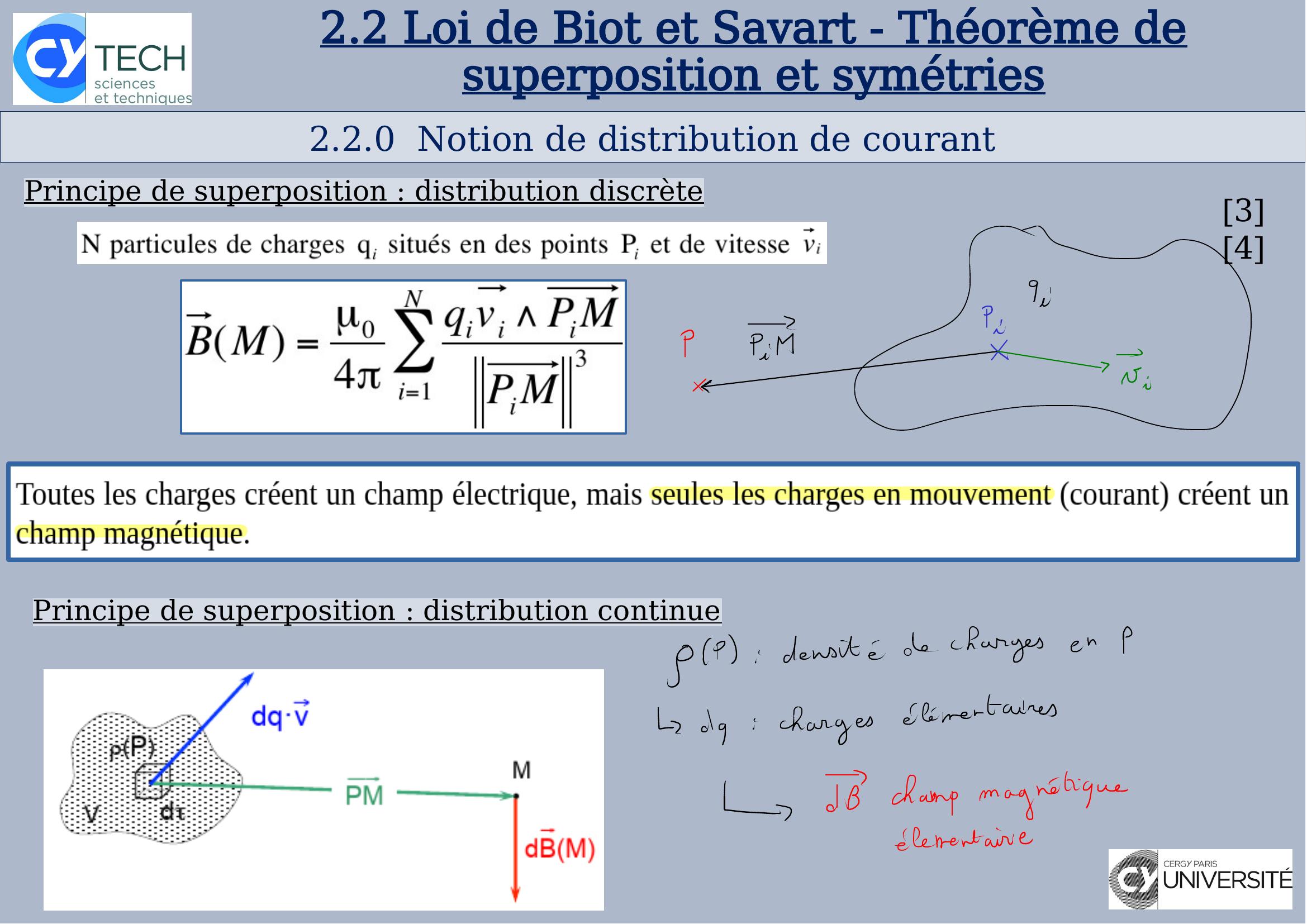
Page 4 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.0 Notion de distribution de courantPrincipe de superposition: distribution discrète34Principe de superposition: distribution continue
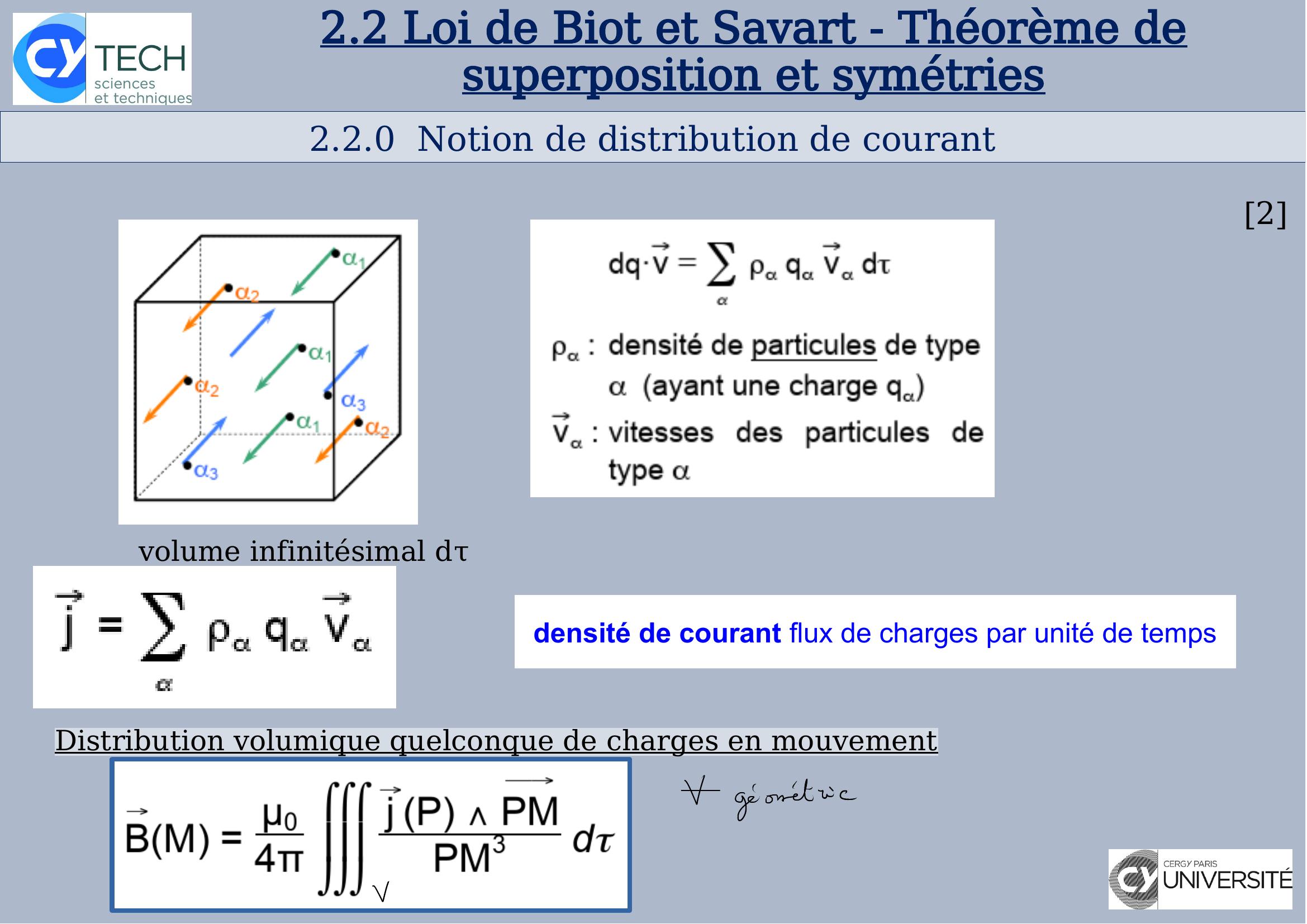
Page 5 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.0 Notion de distribution de courant2 volume infinitésimal dτdensité de courant flux de charges par unité de tempsDistribution volumique quelconque de charges en mouvement
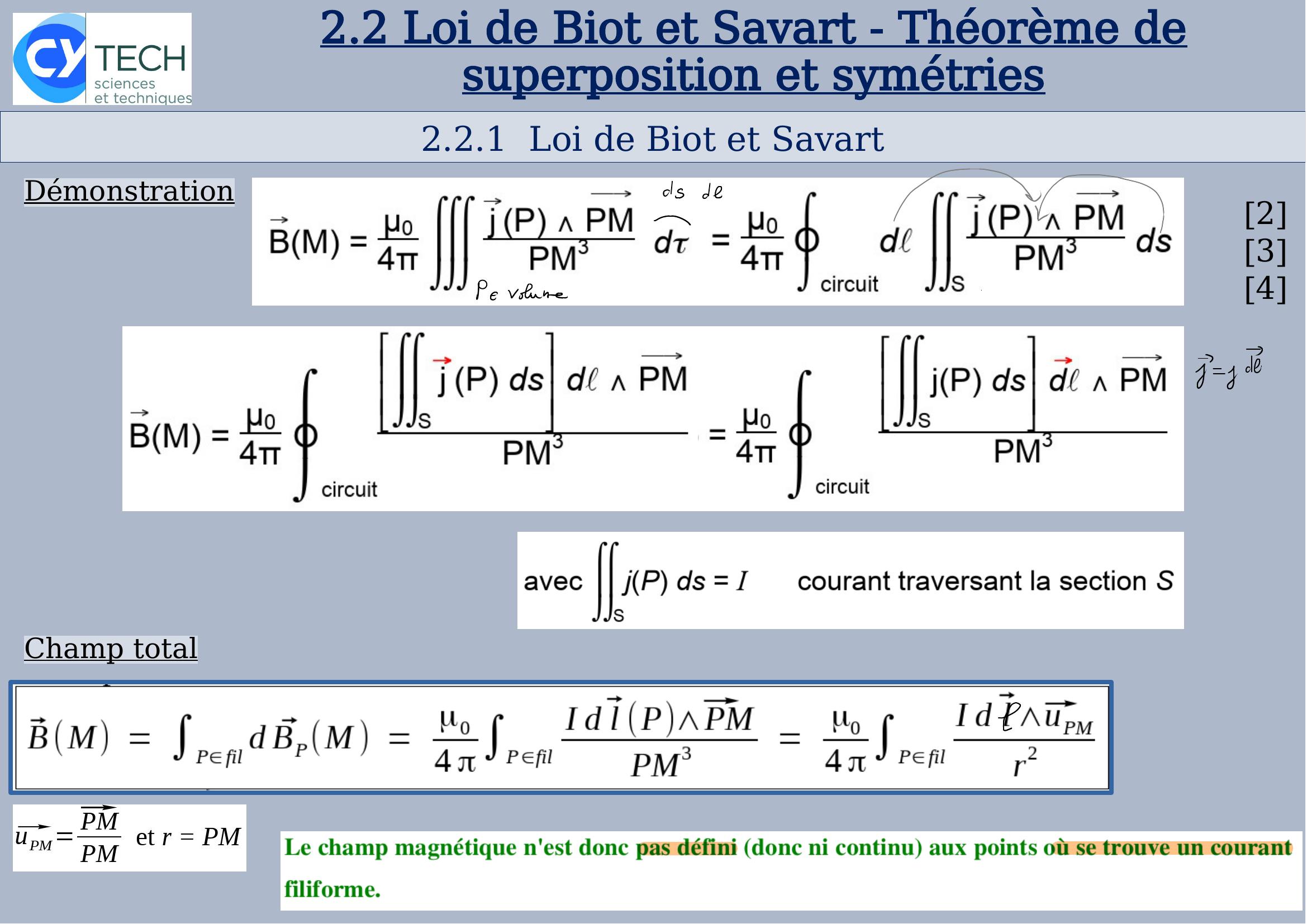
Page 6 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.1 Loi de Biot et Savart234a Énoncé Postulée par Jean-Baptiste Biot et Félix Savart 1820 à partir d'observations expérimentalesFil filiforme parcouru par un courant I: champ mag. en M créé par l'élément de courant Idl ⃗P en P
Page 7 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.1 Loi de Biot et Savart234Champ totalDémonstration
Page 8 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.1 Loi de Biot et Savartb Continuité et discontinuité du champc Transformation des vecteurs axiaux
Page 9 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.2 Invariances d’une distribution de courant2a Densité de couranta.1 Courant volumiqueRégime permanent = I indépendant du temps t.A.R.Q.S. : It varie lentement dans le temps t.Charges mobiles identiques, même vitesse:Plusieurs types de charges mobiles:
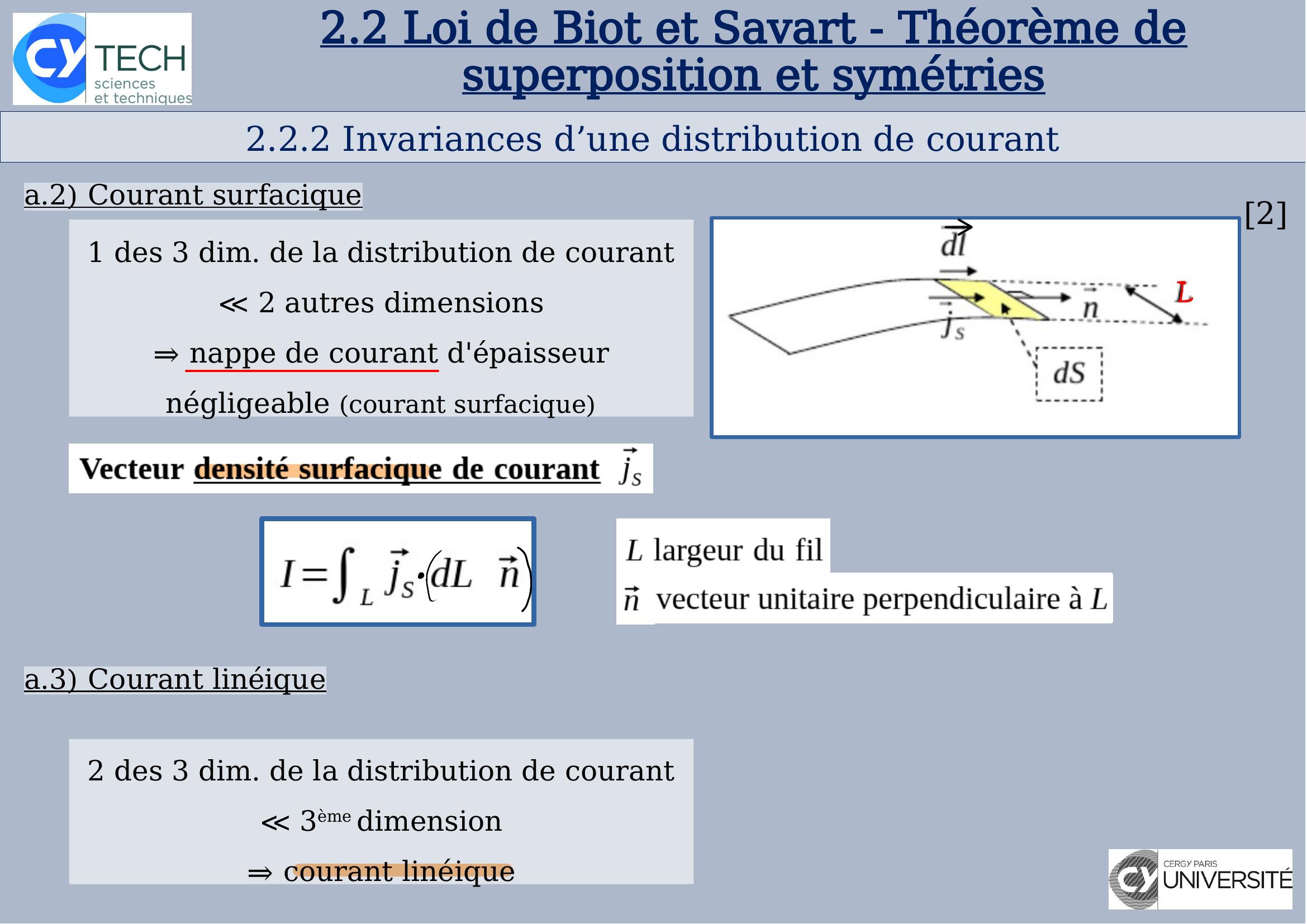
Page 10 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.2 Invariances d’une distribution de courant2a.2 Courant surfaciquea.3 Courant linéique1 des 3 dim. de la distribution de courant 2 autres dimensions⇒ nappe de courant d'épaisseur négligeable courant surfacique2 des 3 dim. de la distribution de courant 3ème dimension⇒ courant linéique
Page 11 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.2 Invariances d’une distribution de courant2b Invariances et symétries d'une distribution de courantUne distribution de courant peut être invariante par translation et/ou par rotation autour d'un axe.Plans de symétrie et anti-symétrie pour la distribution de courant
Page 12 : 2.2Loi de Biot et Savart - Théorème de superposition et symétries2.2.2 Invariances d’une distribution de courant2c Conservation de la charge et loi des nœudsConservation de la chargeQ la charge dans une surface fermée SCourant volumiqueRégime permanent: pour tout surface ferméeCourant constant le long d’un filLoi de nœuds I1=I2+I3
Page 13 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.a Symétries22.2Loi de Biot et Savart - Théorème de superposition et symétries
Page 14 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.b Anti-symétries22.2Loi de Biot et Savart - Théorème de superposition et symétriesc Invariances
Page 15 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.Symétries et anti-symétries22.2Loi de Biot et Savart - Théorème de superposition et symétries
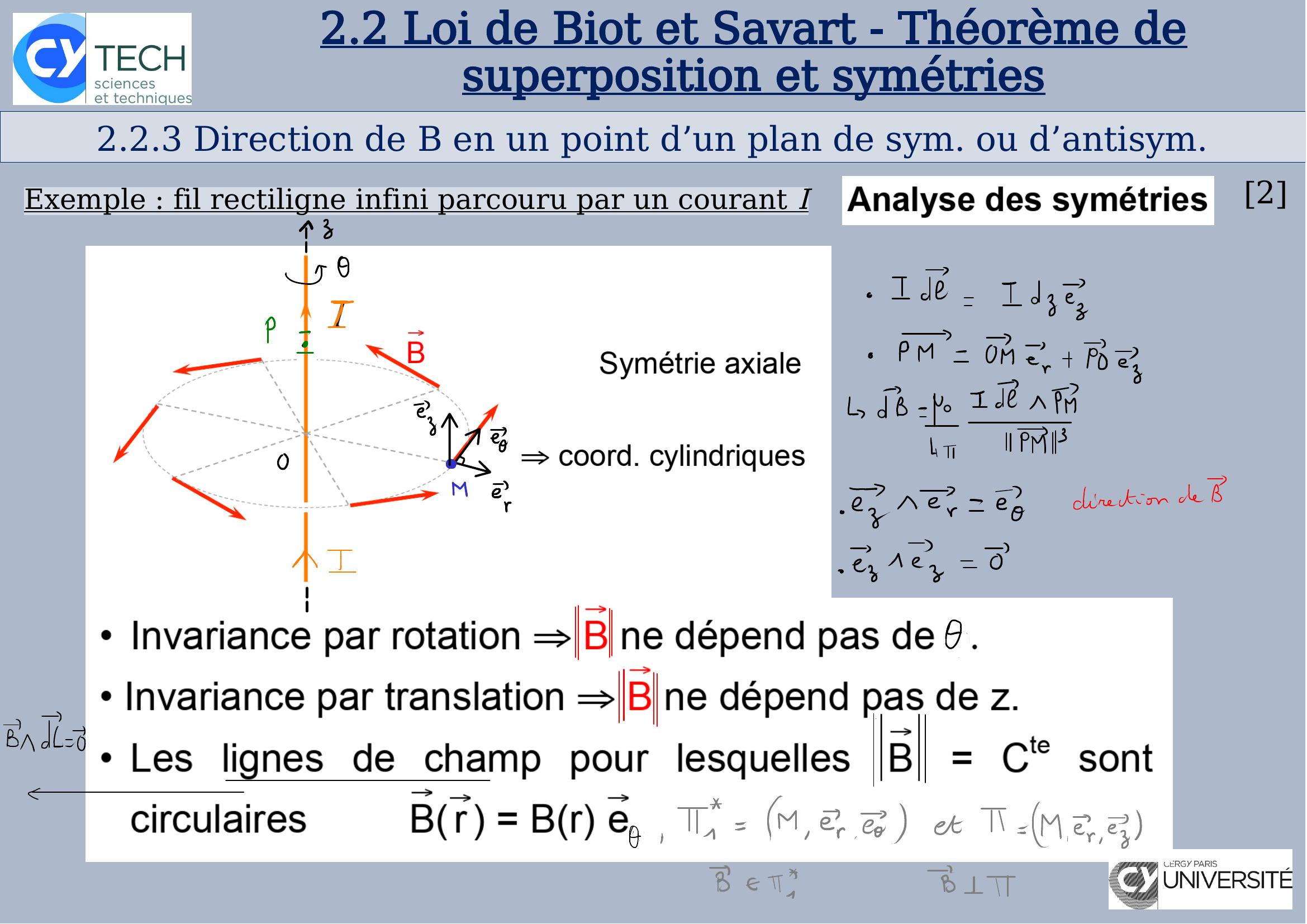
Page 16 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.22.2Loi de Biot et Savart - Théorème de superposition et symétriesExemple: fil rectiligne infini parcouru par un courant I
Page 17 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.122.2Loi de Biot et Savart - Théorème de superposition et symétriesd Lignes et tubes de champ
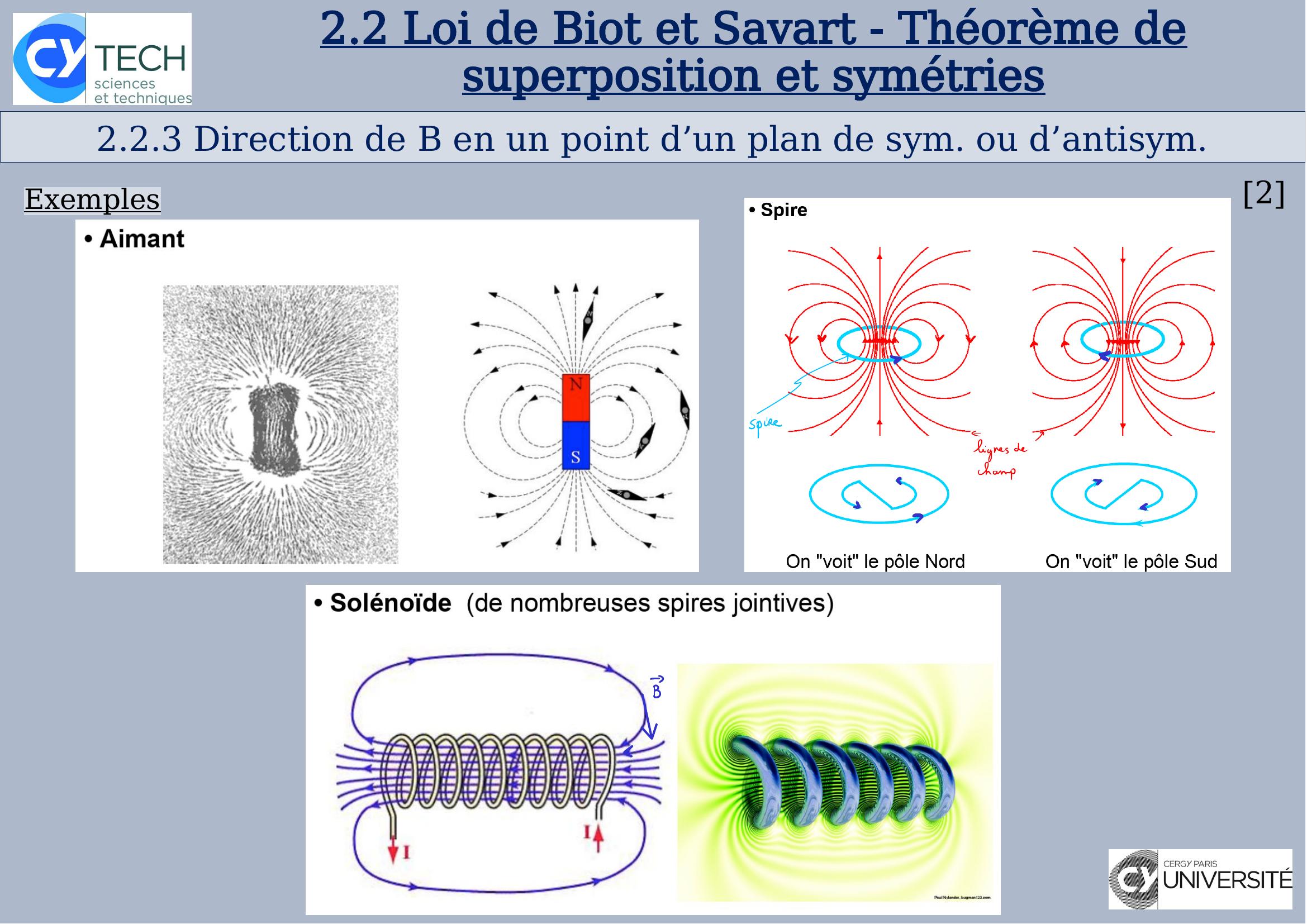
Page 18 : 2.2.3 Direction de B en un point d’un plan de sym. ou d’antisym.22.2Loi de Biot et Savart - Théorème de superposition et symétriesExemples
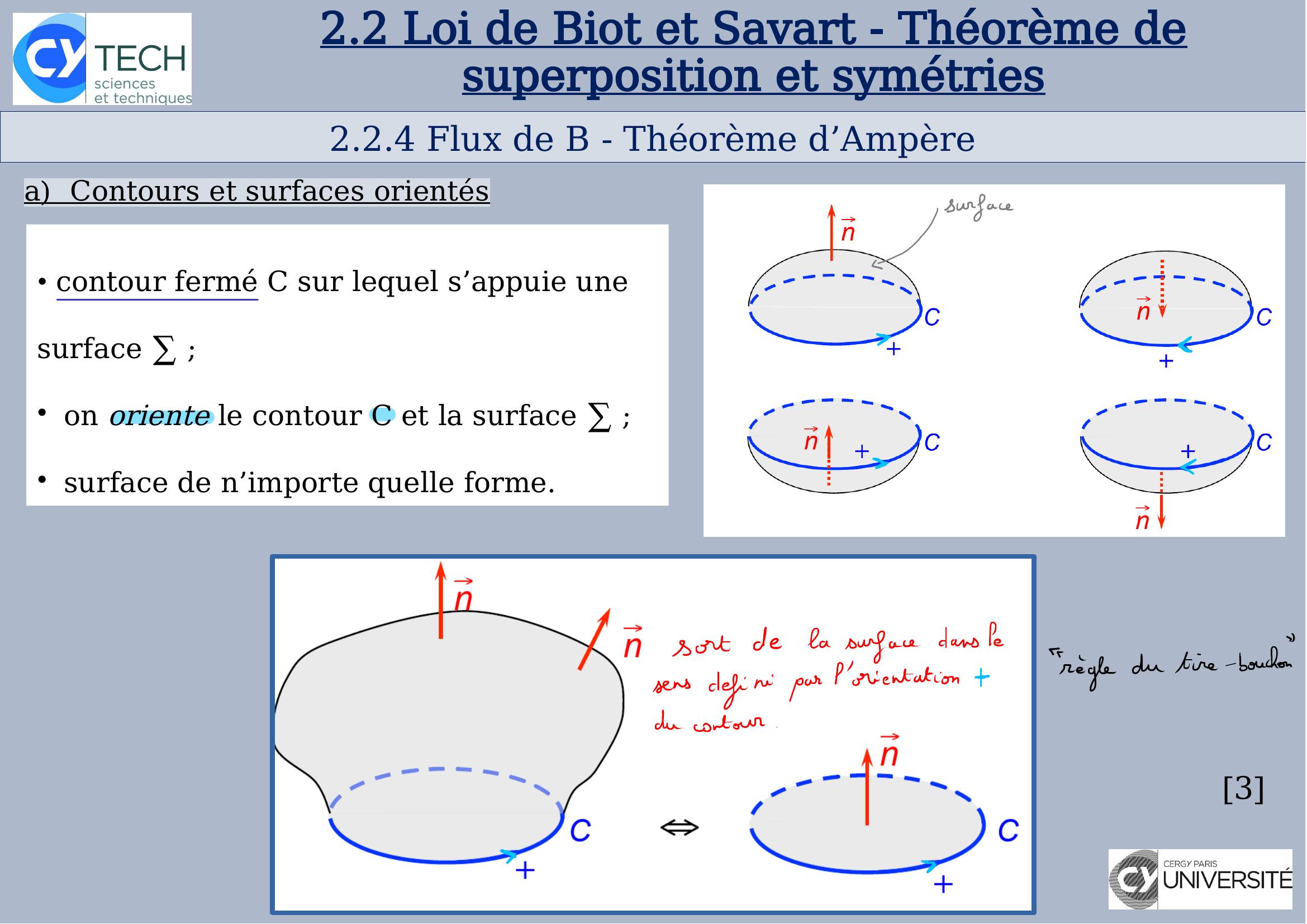
Page 19 : 2.2.4 Flux de B - Théorème d’Ampère32.2Loi de Biot et Savart - Théorème de superposition et symétriesa Contours et surfaces orientés• contour fermé C sur lequel s’appuie une surface ;on oriente le contour C et la surface ;surface de n’importe quelle forme.
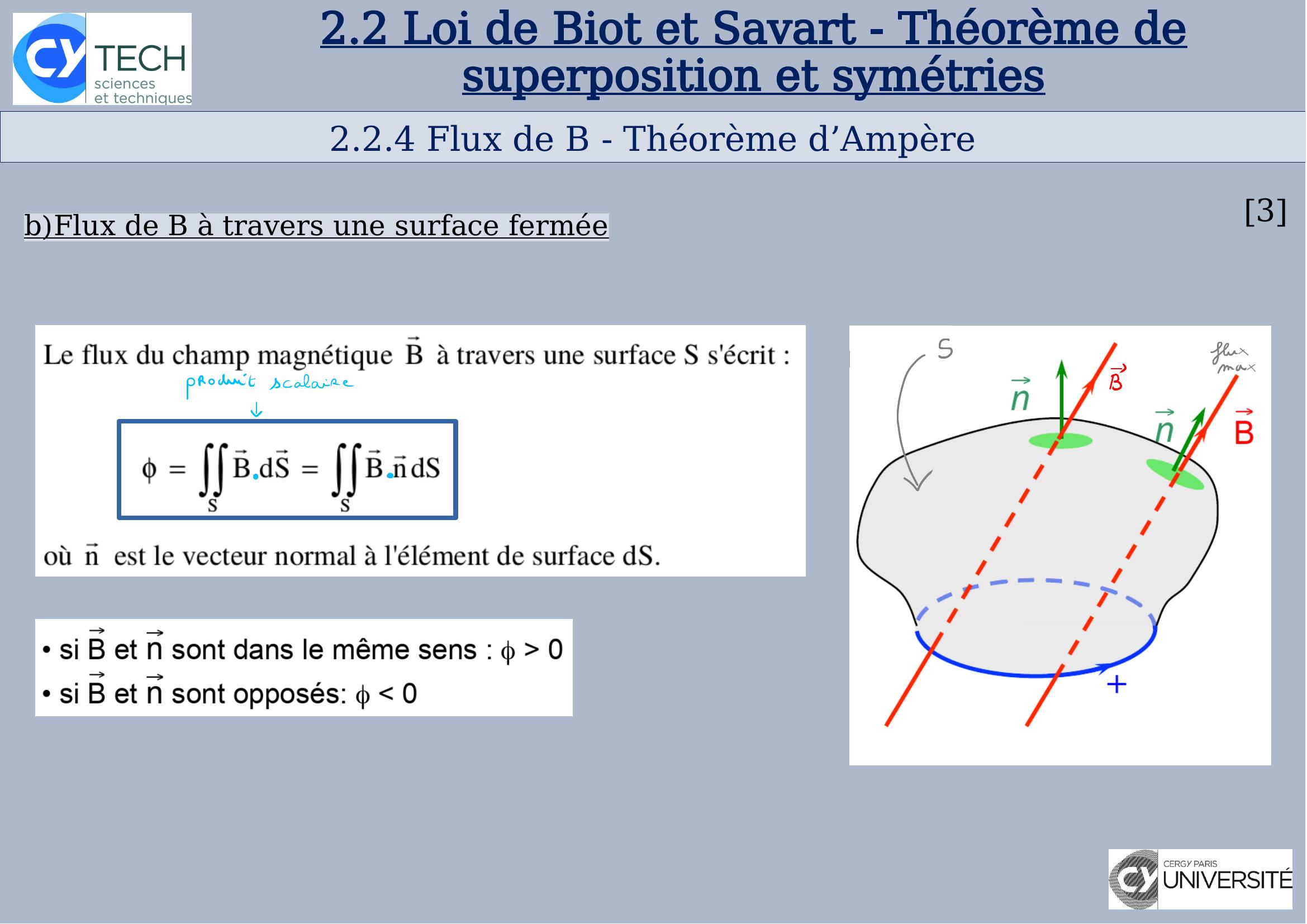
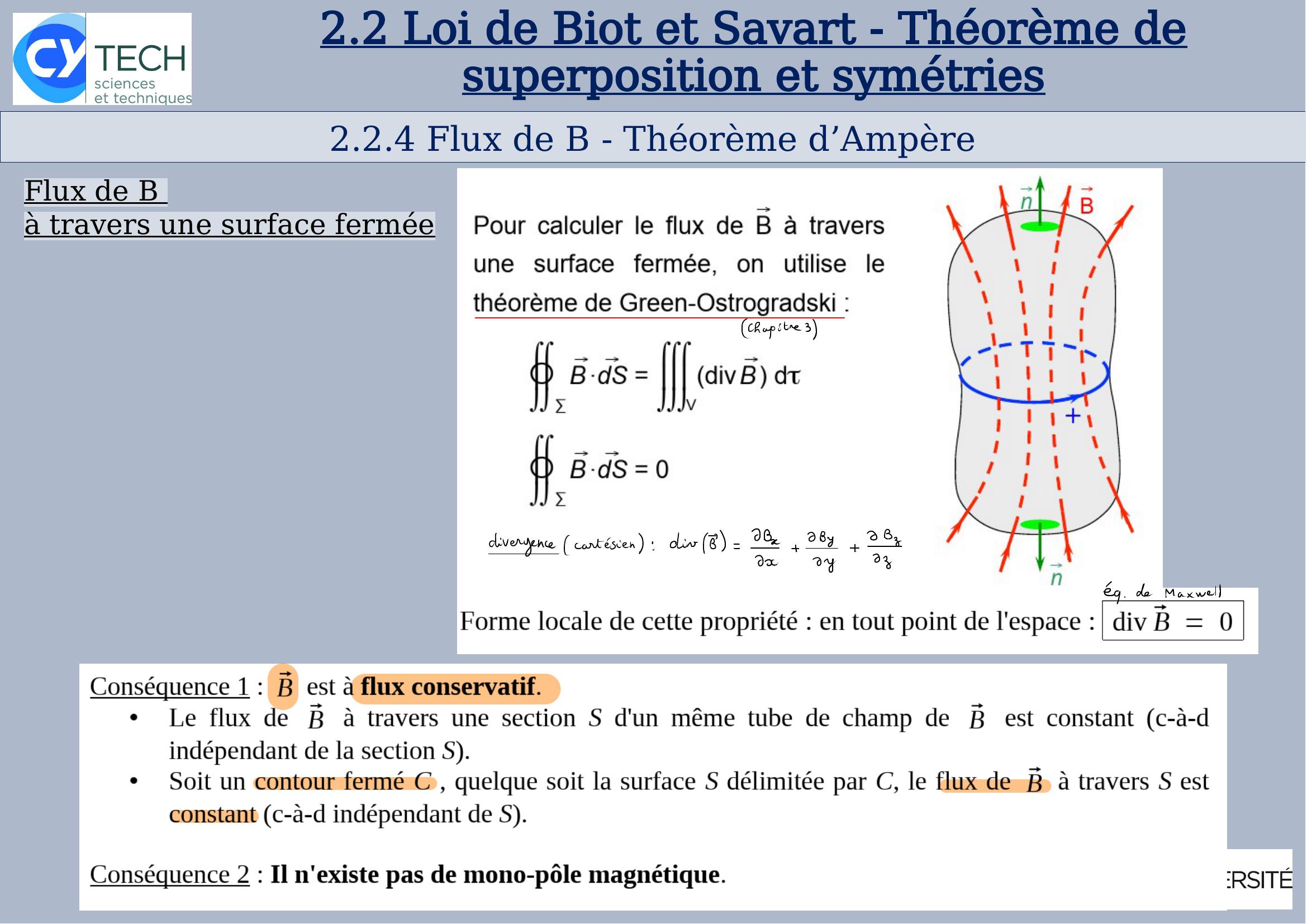
Page 20 : 2.2.4 Flux de B - Théorème d’Ampère32.2Loi de Biot et Savart - Théorème de superposition et symétriesbFlux de B à travers une surface fermée
Page 21 : 2.2.4 Flux de B - Théorème d’Ampère2.2Loi de Biot et Savart - Théorème de superposition et symétriesFlux de B à travers une surface fermée
Page 22 : 2.2.4 Flux de B - Théorème d’Ampère32.2Loi de Biot et Savart - Théorème de superposition et symétriesc Circulation du champ magnétique
Page 23 : 2.2.4 Flux de B - Théorème d’Ampère32.2Loi de Biot et Savart - Théorème de superposition et symétriesd Théorème d’AmpèreC
Page 24 : 2.2.4 Flux de B - Théorème d’Ampère232.2Loi de Biot et Savart - Théorème de superposition et symétries
Page 25 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesMéthode pour utiliser le théorème d'Ampère : pour calculer le champ magnétique
Page 26 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesa Loi d’Ohm locale
Page 27 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesLoi d’Ohm locale ou globale?Loi d’Ohm globale
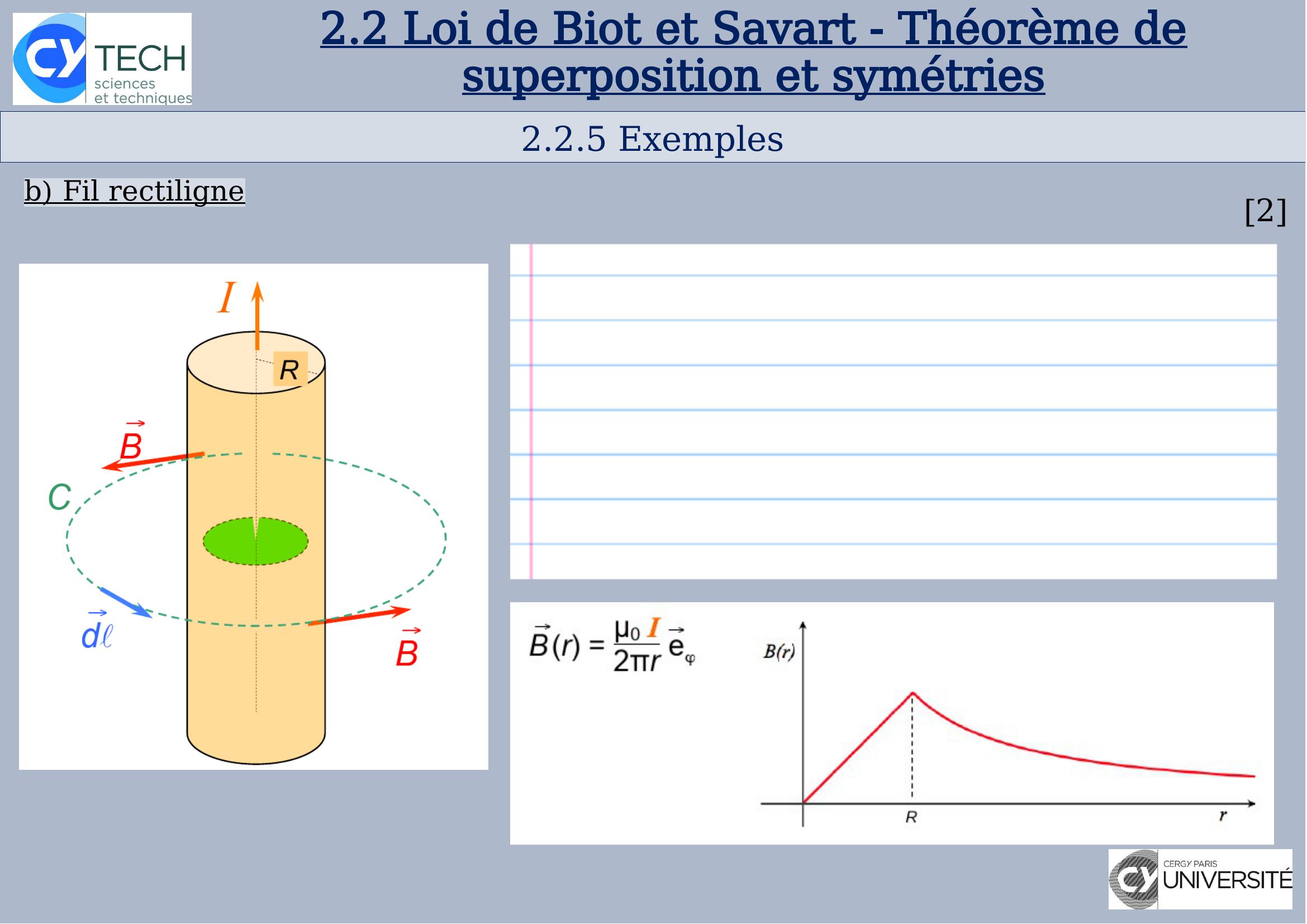
Page 28 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesb Fil rectiligne
Page 29 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesb Fil rectiligne
Page 30 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesb Fil rectiligne
Page 31 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesc Expériences sur le champ magnétique et les courants.
Page 32 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesd SolénoïdeSolénoïde rectiligne infini dont les spires sont traversées par un courant I Solénoïde compte N spires par unité de longueur
Page 33 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesd Solénoïde
Page 34 : 2.2.5 Exemples22.2Loi de Biot et Savart - Théorème de superposition et symétriesd Solénoïde
Page 35 : Bibliographie 1 Polycopié de cours2 CUPGE - CY : Introduction à l’électromagnétisme3 Cours LP 203 - Champs électrique et magnétique de Nicolas MENGUY4 Cours de Luc Tremblay, collège Mérici - « Électricité et magnétisme».5 David Sénéchal - «Histoire des sciences» PHQ399 Université de Sherbrooke, QC6 pour la suite: Khan Academy , Unisciel etc.
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35