CM Chapitre1
Télécharger le CM Chapitre1 en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Page 1 : Chapitre 1 : Oscillateurs harmoniquesOn appelle oscillateur harmonique non amorti, tout système physique décrit par une fonction 𝜓𝑡, qui vérifie l’équation différentielle : 𝑑2𝜓𝑡𝑑𝑡2+ 𝜔02𝜓𝑡= 𝜔02𝜓0𝜓𝑡est une fonction caractéristique du système physique étudié, elle peut être une charge électrique, une tension électrique, une intensité de courant électrique ou une élongation d’un système masse-ressort. 𝜔0 est la pulsation propre de l’oscillateur harmonique : 1
Page 2 : Dans le cas d’une corde vibrante ou d’un système masse-ressort 𝜓𝑡est l’amplitude des vibrations et 𝜓𝑚est sa valeur maximale.𝜙est la phase à l’origine des temps.𝜔0 = 2𝜋𝑓0𝑓0 est la fréquence propre de l’oscillateur.2
Page 3 : La solution de l’équation différentielle précédente est de la forme :𝜓𝑡= 𝜓0 + 𝜓𝑚𝑐𝑜𝑠𝜔0𝑡+ 𝜙Où 𝜓𝑚et 𝜙sont des constantes, que l’on détermine à partir des conditions initiales 𝜓𝑡= 𝜓0 correspond à une position d’équilibre de l’oscillateur harmonique.3
Page 4 : Un exemple simple :L'oscillateur harmonique simple.Sec I.I Soit un bloc de masse M posé sur un plan horizontal, et libre de se déplacer sans frottement, mais attaché à un ressort idéal sans masse lui-même accroché à un mur.C'est un exemple de système a un seul degré de Liberté.4
Page 5 : Rappel:Un ressort idéal et un ressort qui obéit à la loi de Hooke : 𝐸𝑃=12 𝑘𝐿𝐿0 2 =12 𝑘𝑥2avec 𝑥= 𝐿𝐿0Expression dans laquelle 𝑘est la constante de rappel ou de raideur du ressort.𝐿0 est la longueur de a avide du ressort.5
Page 6 : Ԧ𝐹= 𝜕𝐸𝑃𝜕𝑥𝑢𝑥avec 𝐸𝑃=12 𝑘𝑥2d’où Ԧ𝐹=𝜕𝜕𝑥12 𝑘𝑥2 𝑢𝑥= 𝑘𝑥. 𝑢𝑥La deuxième loi de Newton s’écrit :Ԧ𝐹= 𝒎Ԧ𝑎𝒔𝒐𝒊𝒕𝑘𝑥. 𝑢𝑥= 𝒎ሷ𝒙. 𝑢𝑥ሷ𝒙+ 𝜔2𝑥𝑡= 0𝑑2𝑥𝑡𝑑𝑡2+ 𝜔2𝑥𝑡= 0 𝑜𝑢𝑑2𝑑𝑡2 + 𝜔2 𝑥𝑡= 0La solution de cette équation différentielle est :𝑥𝑡= 𝐴𝑐𝑜𝑠𝜔𝑡+ 𝐵𝑠𝑖𝑛𝜔𝑡 où A et B sont des constantes que l’on détermine à partir des conditions initiales :ቊ𝑥0 = 𝐴𝑐𝑜𝑠0 + 𝐵𝑠𝑖𝑛0ሶ𝑥0 = 𝐴𝜔𝑠𝑖𝑛0 + 𝐵𝜔𝑐𝑜𝑠0soit ቊ𝐴= 𝑥0𝐵= ሶ𝑥0 /𝜔6
Page 7 : Exemple : prenons 𝑥0 = 1𝑚𝑒𝑡ሶ𝑥0 = 0𝑚/𝑠⟹ቊ𝑥𝑡= 𝐴𝑐𝑜𝑠𝜔𝑡𝑎𝑣𝑒𝑐𝐴= 1𝑚ሶ𝑥𝑡= 𝐴𝜔𝑠𝑖𝑛𝜔𝑡Remarques :ቊ𝑐𝑜𝑠𝑥= 𝑐𝑜𝑠𝑥+ 2𝜋𝑠𝑖𝑛𝑥= 𝑠𝑖𝑛𝑥+ 2𝜋⟹൞𝑥𝑡+2𝜋𝜔= 𝑥𝑡ሶ𝑥𝑡+2𝜋𝜔= ሶ𝑥𝑡après un temps 𝑇=2𝜋𝜔le système revient à sa position initiale, 𝑇est la période des oscillations et 1𝑇= 𝜈est leur fréquence.7
Page 8 : Le système est dit harmonique simple :Harmonique : les solutions sont des sommes de fonctions trigonométriques.Simple : tous les termes de la solution ont la même fréquence.L’équation différentielle du mouvement de la masse M décrit un grand nombre de systèmes physiques.Qu’est ce que ces systèmes ont en commun ?Pourquoi les systèmes harmoniques sont-ils très répandus ?8
Page 9 : 2propriétésa𝜕𝐸𝜕𝑡= 0avec 𝐸=12 𝑀ሶ𝑥2 +12 𝑘𝑥2bLes équations du mouvement sont linéaires :Si ሷ𝒙𝟏+ 𝜔2𝑥1 = 0𝑒𝑡ሷ𝒙𝟐+ 𝜔2𝑥2 = 0 ⟹ሷ𝑥1 + 𝑥2 + 𝜔2 𝑥1 + 𝑥2 = 0Si un système satisfait les conditions a et b, on pourra le réduire à un ensemble d’oscillateurs harmoniques simples et à l’oscillateur hyperbolique : ሷ𝒙𝜔2𝑥𝑡= 09
Page 10 : Section I-2 : Linéarité et superpositionUne équation est linéaire si pour toutes solutions 𝑓𝑒𝑡𝑔, 𝛼𝑓+ 𝛽𝑔est aussi solution pour toute constantes 𝛼𝑒𝑡𝛽.Une équations aux dérivées ordinaires e. d. o. est de la forme :𝑆𝑡+ 𝛼0𝑓𝑡+ 𝛼1ሶ𝑓𝑡+ 𝛼2ሷ𝑓𝑡 + = 010
Page 11 : est dite homogène si 𝑆𝑡= 0, sinon elle est inhomogène.Etudions le cas homogène : sachant que est linéaire, ses solutions engendrent un espace vectoriel.Cherchons une base, c’est-à-dire un ensemble 𝑓𝑖𝑖=1,2… tel que toute solution de est de la forme :𝑖=1𝑛𝛾𝑖𝑓𝑖𝑎𝑣𝑒𝑐𝜕𝛾𝑖𝜕𝑡= 0On propose comme solution de : 𝑓𝑡= 𝑒𝑘𝑡Or 𝑒𝑘= σ𝑛=0𝑘𝑛𝑛!𝑒𝑡𝑆𝑡= 011
Page 12 : devient : 𝛼0𝑒𝑘𝑡+ 𝛼1𝑘𝑒𝑘𝑡+ 𝛼2𝑘2𝑒𝑘𝑡+ 𝛼3𝑘3𝑒𝑘𝑡+ = 0D’où 𝛼0 + 𝛼1𝑘+ 𝛼2𝑘2 + 𝛼3𝑘3 + = 0polynôme d’ordre n en k.Dans le cas de l’oscillateur harmonique simple :𝛼0 = 𝜔2,𝛼1 = 0 𝑒𝑡𝛼2 = 1 𝑑𝑒𝑔𝑟é 2⟹ሷ𝑓+ 𝜔2𝑓= 0 ⟹𝑟2 + 𝜔2 = 0 ⟹𝑟= ±𝑖𝜔⟹les solutions sont de la forme : 𝑓𝑡= 𝐴𝑒𝑖𝜔𝑡+ 𝐵𝑒𝑖𝜔𝑡12
Page 13 : Rappel -nombres complexes :𝑍= 𝑎+ 𝑖𝑏,ҧ𝑍= 𝑎𝑖𝑏𝑒𝑖𝜃= 𝑐𝑜𝑠𝜃+ 𝑖𝑠𝑖𝑛𝜃𝑓𝑜𝑟𝑚𝑢𝑙𝑒𝑑′𝐸𝑢𝑙𝑒𝑟𝑒𝑖𝜃= 1 + 𝑖𝜃+ 𝑖2𝜃22! + 𝑖3𝜃33! + =1 𝜃22! + 𝜃44! 𝜃66! + + 𝑖𝜃𝜃33! + 𝜃55! …= 𝑐𝑜𝑠𝜃+ 𝑖𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃= 𝑒𝑖𝜃+ 𝑒𝑖𝜃2𝑠𝑖𝑛𝜃= 𝑒𝑖𝜃𝑒𝑖𝜃2𝑖13
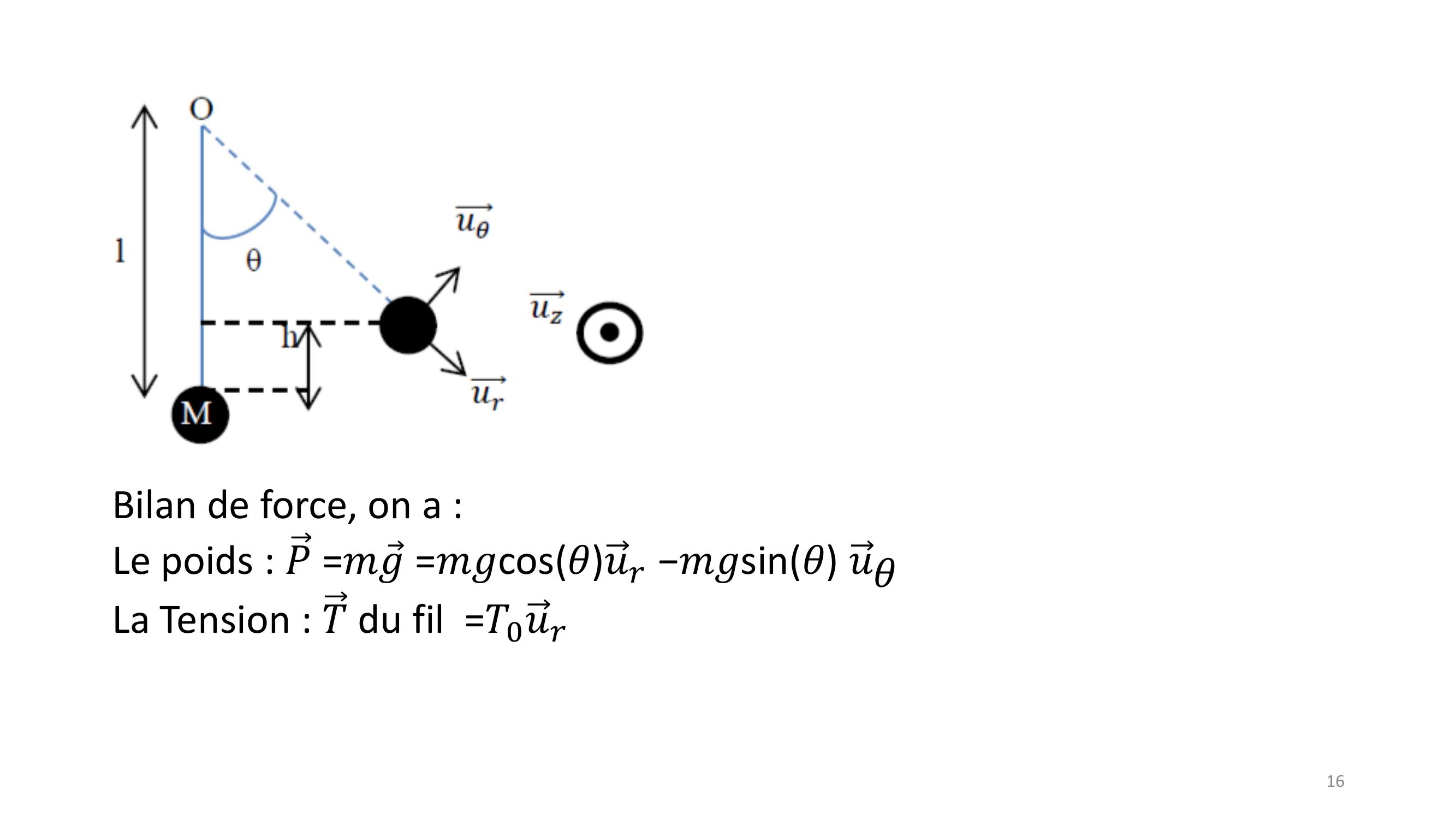
Page 14 : 14Application 1:Un pendule simple constitué d’une masse ponctuelle m suspendue à un fil inextensible de longueur l. On néglige toutes les sources de frottements. On note M le centre de gravité de la masse et O le point de fixation du fil. On repère la position du centre de gravité de la masse par l'angle θ entre la verticale et la direction du fil. On écarte le centre de gravité de la masse d’un angle θ0 et on la lâche sans vitesse. On limite l’étude à des angles θ petits.
Page 15 : 151. Faire un bilan des forces appliqué sur M.2. Décrire le mouvement du centre de gravité de la masse, par application du théorème de l’énergie mécanique,3. Etudiez le mouvement du centre de gravité de la masse, par application du théorème du moment cinétique
Page 16 : 16Bilan de force, on a :Le poids : 𝑃=𝑚Ԧ𝑔=𝑚𝑔cos𝜃𝑢𝑟𝑚𝑔sin𝜃 𝑢𝜃La Tension : 𝑇du fil =𝑇0𝑢𝑟
Page 17 : 17Le théorème de l’énergie mécanique :Δ𝐸𝑀=𝑡𝑟𝑎𝑣𝑎𝑖𝑙𝑑𝑒𝑠𝑓𝑜𝑟𝑐𝑒𝑠𝑛𝑜𝑛𝑐𝑜𝑛𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑣𝑒𝑠Dans cet exemple, il n’y’a pas de frottement, alors pas de forces non conservatives: Δ𝐸𝑀=Δ𝐸𝑐+Δ𝐸𝑝
Page 18 : 18Δ𝐸𝑐=1/2𝑚𝑣2 𝑎𝑣𝑒𝑐𝑣=𝑙ሶ𝜃, ሶ𝜃est 𝑙𝑎𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝑎𝑛𝑔𝑢𝑙𝑎𝑖𝑟𝑒.Δ𝐸𝑝=𝑚𝑔ℎ𝑎𝑣𝑒𝑐ℎ=𝑙1𝑐𝑜𝑠𝜃 dans le cadre de l’approximation des petits angles on a 𝑐𝑜𝑠𝜃1𝜃2/2
Page 19 : 19La solution de l’équation différentielle est:𝜃𝑡=𝐴.𝑐𝑜𝑠𝜔0𝑡+𝐵.𝑠𝑖𝑛𝜔0𝑡𝜃0=𝐴=𝜃0ሶ𝜃𝑡=𝜔0𝐴.𝑠𝑖𝑛𝜔0𝑡+𝜔0𝐵.𝑐𝑜𝑠𝜔0𝑡ሶ𝜃0=𝜔0 soit B=0 Finalement 𝜃𝑡= 𝜃0𝑐𝑜𝑠𝜔0𝑡
Page 20 : 20