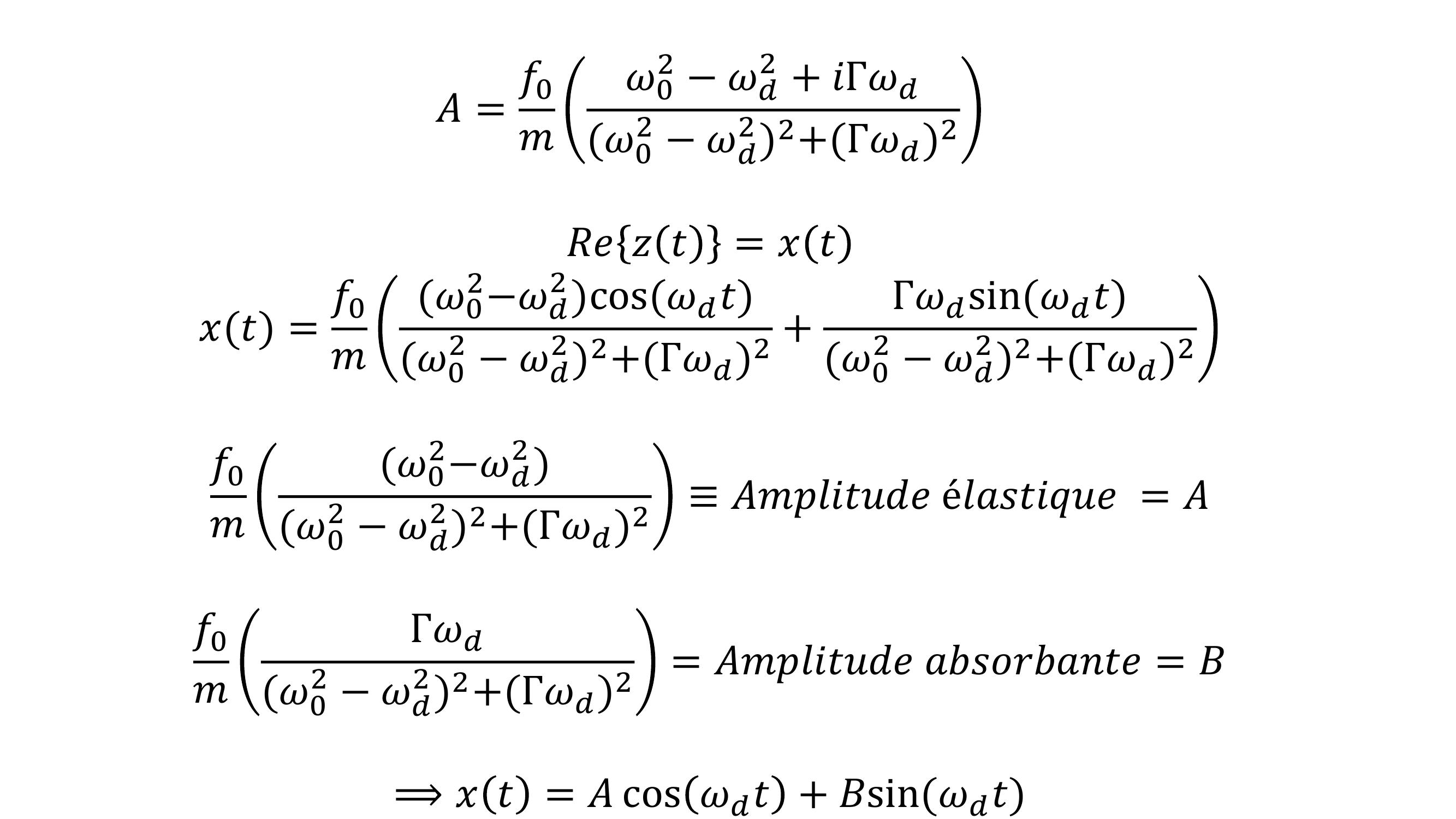CM Chapitre2
Télécharger le CM Chapitre2 en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Page 1 : Chapitre 2Oscillations forcées et résonnance2.1 Oscillateur amorti :On considère le même système masse-ressort horizontal, mais avec un coefficient de viscosité dynamique 𝜇.On établit l’équation différentielle du mouvement :Système : point matériel de masse m se déplaçant le long d’un axe Ox, dont l’origine est fixée au niveau de la position à l’équilibre du point matériel,Référentiel du laboratoire considéré comme galiléen,
Page 2 : Bilan des forces :la force de rappel : 𝑘𝑥𝑢𝑥la force de frottement fluide : 𝑚Γ ሶ𝑥𝑢𝑥le poids est compensé par la réaction de l’axe. Application du principe fondamental de la dynamique, projeté sur l’axe Ox :𝑚ሷ𝑥= 𝑘𝑥𝑚Γ ሶ𝑥⟹ሷ𝑥+ Γ ሶ𝑥+ 𝜔02𝑥= 0𝑎𝑣𝑒𝑐𝜔02 = 𝑘𝑚
Page 3 : l’équation caractéristique associée est :𝑟2 + Γr + 𝜔02 = 0,Δ = Γ2 4𝜔02les racines de celle-ci sont : 𝑟± =Γ± Γ24𝜔022𝑟± = Γ2 ±Γ24 𝜔02Les solutions de l’équation différentielle sont de la forme :𝑥𝑡= 𝐴𝑒𝑟+ 𝑡+ 𝐵𝑒𝑟𝑡
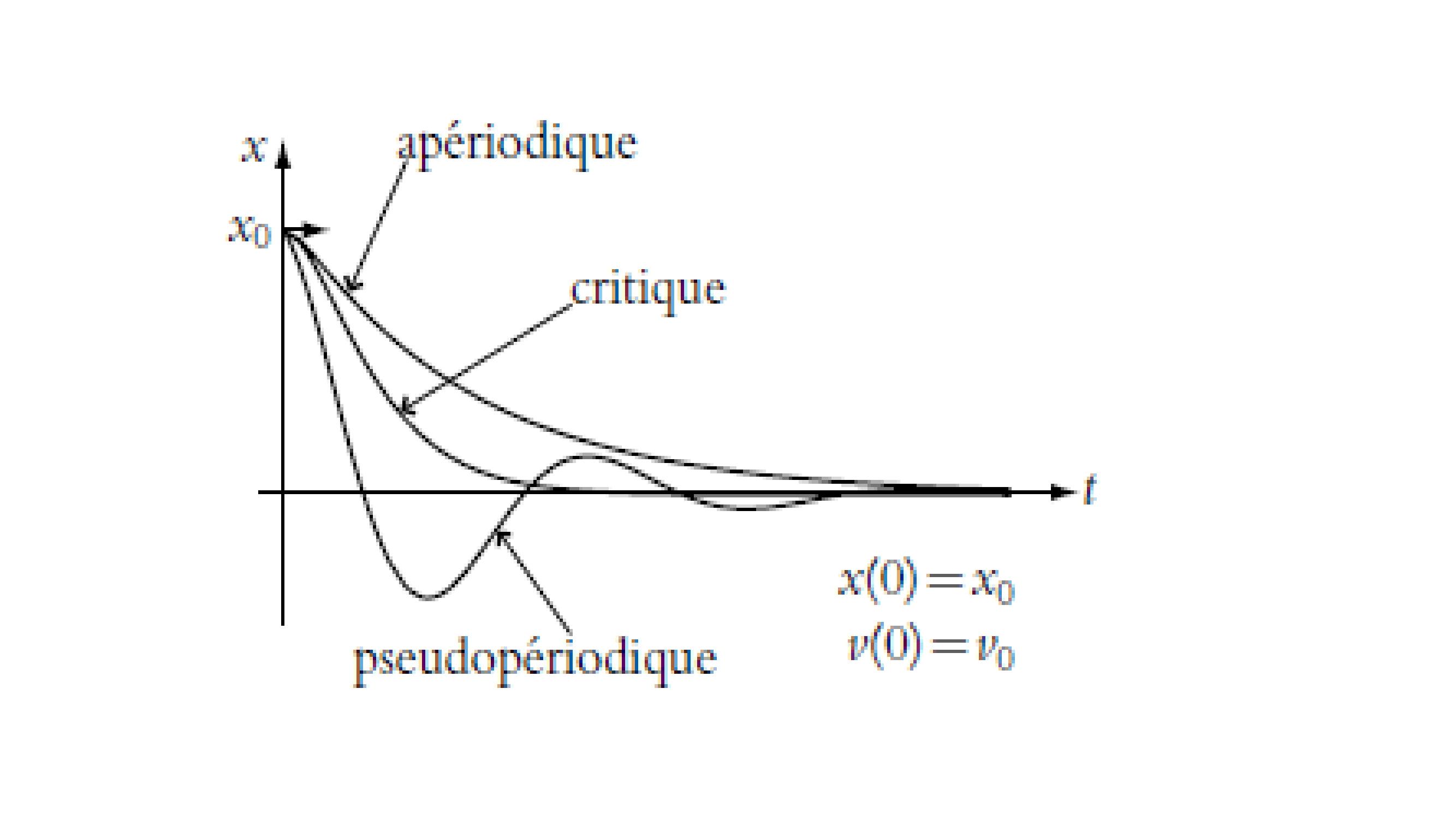
Page 4 : On distingue trois régimes :Cas sur-amorti :Γ2 𝜔0 ⟹𝑟± sont réels𝑟± = Γ2 ±Γ24 𝜔02 0les deux exponentielles 𝑒𝑟+ 𝑡𝑒𝑡𝑒𝑟𝑡 sont des fonctions décroissantes.
Page 5 : Cas sous-amorti:Les racines de l’équation caractéristique sont complexes : 𝑟± = Γ2 ± 𝑖𝜔02 Γ24la solution de l’équation différentielle est donnée par :𝑥𝑡= 𝑒Γ2𝑡𝐴′𝑐𝑜𝑠𝜔𝑡+ 𝐵′𝑠𝑖𝑛𝜔𝑡
Page 6 : le régime est dit pseudopériodique de pseudopériode T égale à la période de la partie périodique: 𝑇= 2𝜋𝜔avec 𝜔2 = 𝜔02 Γ24
Page 7 : Cas critique : Δ = 0 soit Γ2 = 𝜔0 d’où : 𝑟± = Γ2La solution de l’équation différentielle est donnée par:𝑥𝑡= 𝑒Γ2𝑡𝐴+ 𝐵𝑡⟹𝑝𝑎𝑠𝑑′𝑜𝑠𝑐𝑖𝑙𝑙𝑎𝑡𝑖𝑜𝑛𝑠
Page 8 :
Page 9 : 2.2 Oscillateurs entretenusSoit un oscillateur auquel on applique une force externe parallèle à l’axe Ox : Ԧ𝑓𝑡= 𝑓𝑡𝑢𝑥L’équation du mouvement devient :𝑚ሷ𝑥+ 𝑘𝑥+ 𝑚Γ ሶ𝑥= 𝑓𝑡⟹ሷ𝑥+ Γ ሶ𝑥+ 𝜔02𝑥= 𝑓𝑡𝑚Supposons que ft est périodique de la forme : 𝑓𝑡= 𝑓0cos𝜔𝑑𝑡 où 𝜔𝑑est la pulsation d’entraînement.
Page 10 : Remarque :Si x’t est la solution particulière de et yt est la solution de l’équation homogène de ሷ𝑦+ Γ ሶ𝑦+ 𝜔02𝑦= 0 ⟹𝑥′ 𝑡+ 𝑦𝑡 est solution de ⟹la solution générale de est 𝑥′ 𝑡+ 𝑦𝑡
Page 11 : En notation complexeSoit ҧ𝑓𝑡la fonction complexe associée à ft: ҧ𝑓𝑡= 𝑓0𝑒𝑖𝜔𝑑𝑡𝑠𝑖ሷ𝑧𝑡+ Γ ሶ𝑧𝑡+ 𝜔02𝑧𝑡=ҧ𝑓𝑡𝑚⟹𝑅𝑒𝑧𝑡= 𝑥𝑡Posons 𝑧𝑡= 𝐴𝑒𝑖𝜔𝑑𝑡⟹𝜔𝑑2𝑧𝑡𝑖Γ𝜔𝑑𝑧𝑡+ 𝜔02𝑧𝑡=ҧ𝑓𝑡𝑚⟹𝜔𝑑2 𝑖Γ𝜔𝑑+ 𝜔02 𝐴=𝑓0𝑚d’où 𝐴=𝑓0𝑚𝜔𝑑2 𝑖Γ𝜔𝑑+ 𝜔02 = 𝑓0𝑚1𝜔02𝜔𝑑2 𝑖Γ𝜔𝑑𝜔02 𝜔𝑑2 + 𝑖Γ𝜔𝑑𝜔02𝜔𝑑2 + 𝑖Γ𝜔𝑑𝐴= 𝑓0𝑚𝜔02 𝜔𝑑2 + 𝑖Γ𝜔𝑑𝜔02 𝜔𝑑22+Γ𝜔𝑑2
Page 12 : 𝐴= 𝑓0𝑚𝜔02 𝜔𝑑2 + 𝑖Γ𝜔𝑑𝜔02 𝜔𝑑22+Γ𝜔𝑑2𝑅𝑒𝑧𝑡= 𝑥𝑡𝑥𝑡 = 𝑓0𝑚𝜔02𝜔𝑑2cos𝜔𝑑𝑡𝜔02 𝜔𝑑22+Γ𝜔𝑑2 +Γ𝜔𝑑sin𝜔𝑑𝑡𝜔02 𝜔𝑑22+Γ𝜔𝑑2𝑓0𝑚𝜔02𝜔𝑑2𝜔02 𝜔𝑑22+Γ𝜔𝑑2𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒é𝑙𝑎𝑠𝑡𝑖𝑞𝑢𝑒= 𝐴𝑓0𝑚Γ𝜔𝑑𝜔02 𝜔𝑑22+Γ𝜔𝑑2= 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒𝑎𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑡𝑒= 𝐵⟹𝑥𝑡= 𝐴cos 𝜔𝑑𝑡+ 𝐵sin𝜔𝑑𝑡
Page 13 : Résonance :Si 𝜔02 = 𝜔𝑑2, Alors 𝑥𝑡= 𝑓0𝑚𝜔𝑑Γ sin𝜔𝑑𝑡Si Γest petit, l’amplitude de 𝑥𝑡est alors très grand !Ce phénomène est la résonance en amplitude.Le travail de la force 𝑓𝑡 durant l’intervalle de temps 𝑡1, 𝑡2 est:𝑊𝑡1⟶𝑡2 = 𝑡1𝑡2 𝑃𝑡𝑑𝑡où Pt est la puissance.𝑃𝑡= 𝑓𝑡ሶ𝑥𝑡𝑃𝑡= 𝑓0 cos 𝜔𝑑𝑡𝐴𝜔𝑑sin 𝜔𝑑𝑡+ 𝐵𝜔𝑑cos𝜔𝑑𝑡𝑃𝑡= 𝐴𝑓0𝜔𝑑cos 𝜔𝑑𝑡𝑠𝑖𝑛𝜔𝑑𝑡+ 𝐵𝑓0𝜔𝑑𝑐𝑜𝑠2𝜔𝑑𝑡
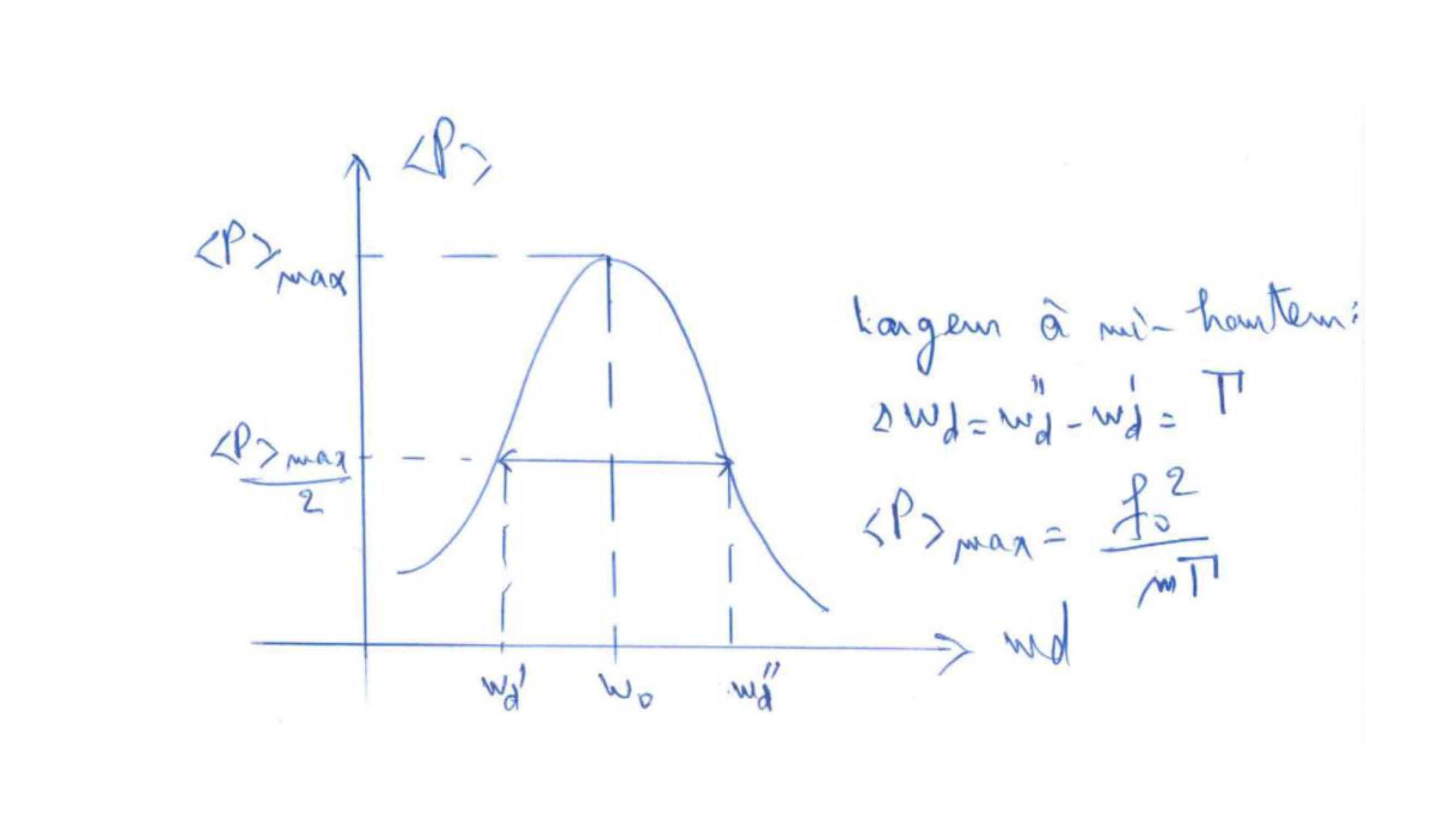
Page 14 : Le terme : cos 𝜔𝑑𝑡𝑠𝑖𝑛𝜔𝑑𝑡=12 𝑠𝑖𝑛2𝜔𝑑𝑡𝑜𝑠𝑐𝑖𝑙𝑙𝑒𝑒𝑛𝑡𝑟𝑒+ 𝑒𝑡Le terme : 𝑐𝑜𝑠2𝜔𝑑𝑡est toujours positif.න𝑡𝑡+𝑇2𝑠𝑖𝑛2𝜔𝑑𝑡𝑑𝑡= 0𝑜ù 𝑇𝑒𝑠𝑡𝑙𝑎𝑝é𝑟𝑖𝑜𝑑𝑒𝑊𝑡⟶𝑡+𝑇= 𝐵𝑓0𝜔𝑑𝑡𝑡+𝑇𝑐𝑜𝑠2𝜔𝑑𝑡𝑑𝑡= 𝐵𝑓0𝜋La puissance moyenne sur une période : 𝑃=𝑊𝑡⟶𝑡+𝑇𝑇= 𝐵𝑓0𝜔𝑑soit 𝑃=𝑓02𝑚Γ𝜔𝑑2𝜔02𝜔𝑑22+Γ𝜔𝑑2maximum pour𝜔𝑑= 𝜔0
Page 15 :
Page 16 : RemarquePour l’oscillateur amortis :𝑥𝑡= 𝑒Γ2𝑡𝐴′𝑐𝑜𝑠𝜔𝑡+ 𝐵′𝑠𝑖𝑛𝜔𝑡La demi-vie de xt : Le temps au bout duquel l’amplitude de xt est divisée par 2. Ce temps est proportionnel à 1Γ ⟶la largeur du pic à la résonance est inversement Proportionnelle au temps de vie de l’oscillateur.
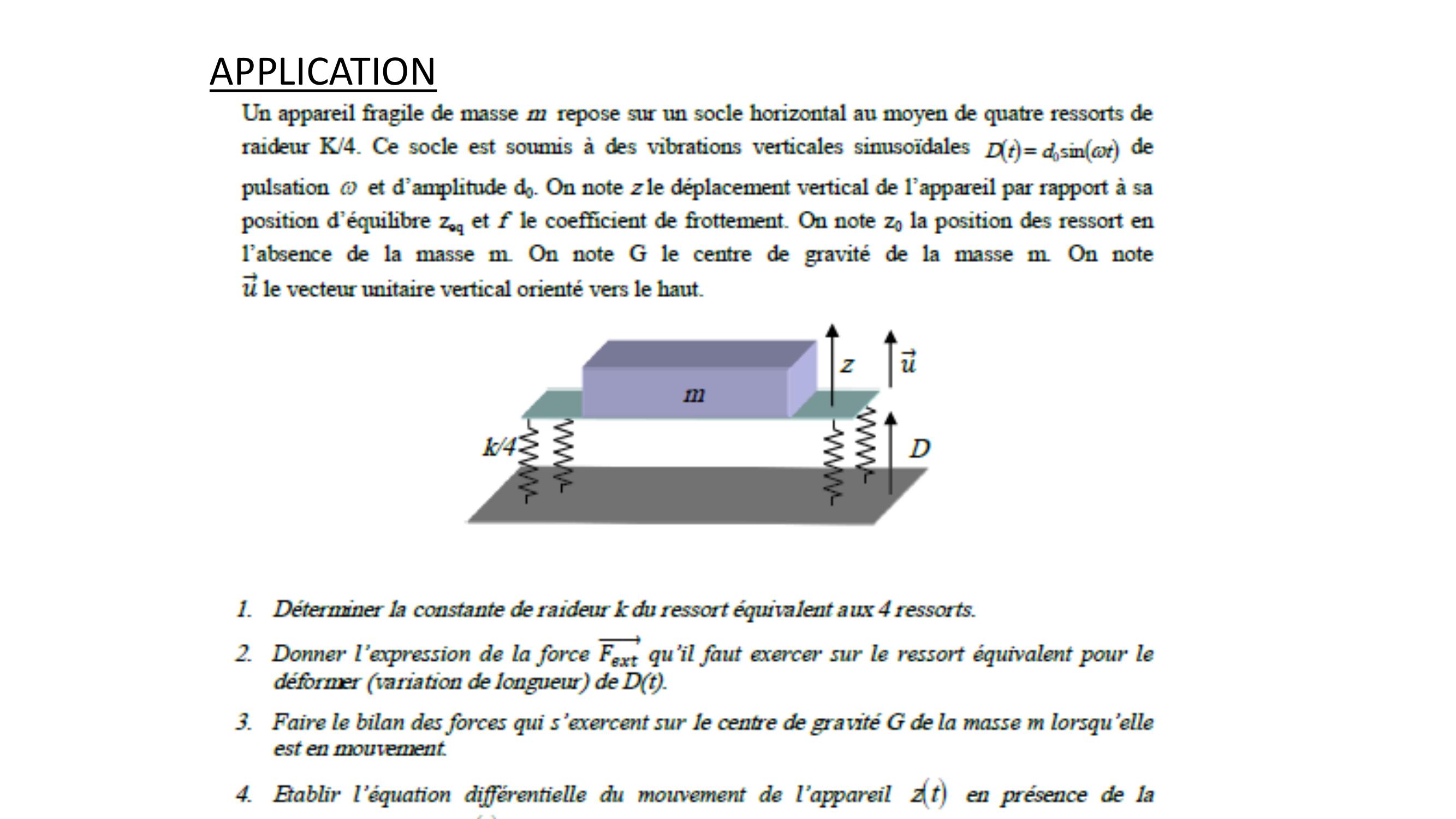
Page 17 : APPLICATION
Page 18 :
Page 19 :
Page 20 : 6
Page 21 : 7
Page 22 :
Page 23 :
Page 24 :
Page 25 :
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25