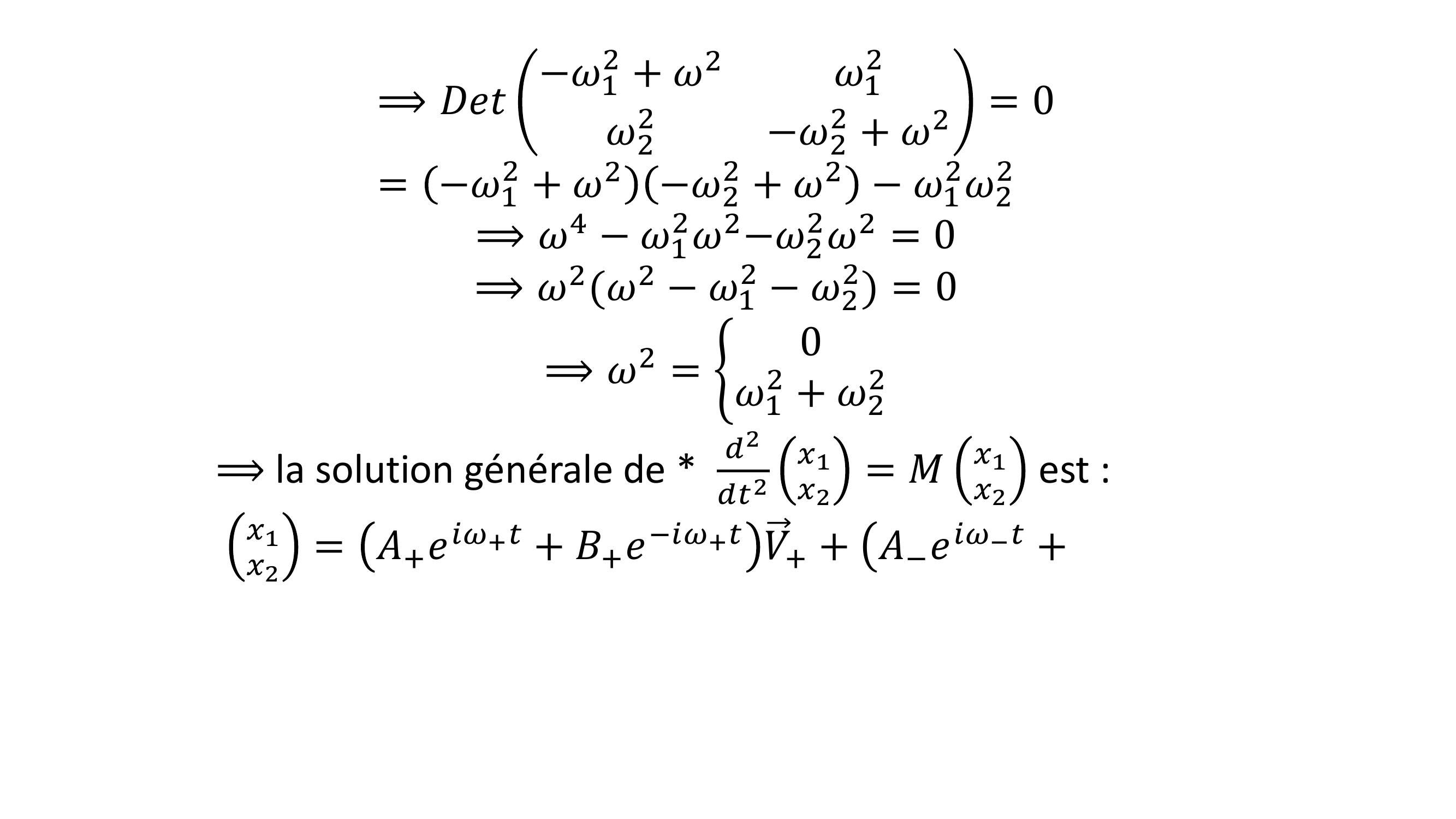CM Chapitre3
Télécharger le CM Chapitre3 en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Page 1 : Chapitre 3 : Oscillations couplés et modes normauxSection I : deux oscillateurs couplésSoient deux blocs de masses 𝑚1 et 𝑚2 posés sur un plan horizontal, ils sont liés par un ressort idéal de constante de raideur k et de longueur au repos 𝐿0.On néglige les forces de frottements.
Page 2 : Force exercée sur 𝑚1: Ԧ𝐹1 = 𝑘𝑥2 𝑥1𝑢𝑥Force exercée sur 𝑚2 : Ԧ𝐹2 = 𝑘𝑥1 𝑥2𝑢𝑥Deuxième loi de Newton : ቊ𝑚1 ሷ𝑥1 = 𝑘𝑥2 𝑥1𝑚2 ሷ𝑥2 = 𝑘𝑥1 𝑥2posons 𝜔12 =𝑘𝑚1 𝑒𝑡𝜔22 =𝑘𝑚2⟹𝑑2𝑑𝑡2𝑥1𝑥2=𝜔12𝜔12𝜔22𝜔22𝑥1𝑥2Pour résoudre ce système d’équations différentielles, on va chercher les modes propres ou modes normaux :
Page 3 : 𝑥1𝑥2= 𝑒𝑖𝜔𝑡𝐴𝐵⟹𝑑2𝑑𝑡2𝑥1𝑥2= 𝜔2𝑥1𝑥2⟹𝜔2𝑥1𝑥2= 𝑀𝑥1𝑥2𝑜ù 𝑀=𝜔12𝜔12𝜔22𝜔22⟹𝑀𝐴𝐵= 𝜔2𝐴𝐵⟹𝐴𝐵est vecteur propre de M de valeur propre 𝜔2⟹𝜔2 est une valeur propre de M⟹𝐷𝑒𝑡𝑀+ 𝜔2𝐼𝑑= 0
Page 4 : ⟹𝐷𝑒𝑡𝜔12 + 𝜔2𝜔12𝜔22𝜔22 + 𝜔2= 0= 𝜔12 + 𝜔2𝜔22 + 𝜔2 𝜔12𝜔22⟹𝜔4 𝜔12𝜔2𝜔22𝜔2 = 0⟹𝜔2𝜔2 𝜔12 𝜔22 = 0⟹𝜔2 = ቊ0𝜔12 + 𝜔22⟹la solution générale de 𝑑2𝑑𝑡2𝑥1𝑥2= 𝑀𝑥1𝑥2 est :𝑥1𝑥2= 𝐴+𝑒𝑖𝜔+𝑡+ 𝐵+𝑒𝑖𝜔+𝑡𝑉+ + ൫𝐴𝑒𝑖𝜔𝑡+
Page 5 : Section II : n oscillateurs couplésPlus généralement, les équations du mouvement de n oscillateurs couplés linéairement est de la forme : 𝑀𝑑2𝑑𝑡2 Ԧ𝑋+ 𝑘Ԧ𝑋= 0 𝑜ù Ԧ𝑋= 𝑥1, 𝑥2, … . . , 𝑥𝑛Couplage linéaire : l’interaction entre les oscillateurs peut être décrit par un potentiel 𝑉 Ԧ𝑋 qui est un polynôme d’ordre 2 en 𝑥1, 𝑥2, … . . : 𝑉Ԧ𝑋= σ𝑖,𝑗𝑘𝑖,𝑗𝑥𝑖𝑥𝑗Puisque 𝑥𝑖𝑥𝑗= 𝑥𝑗𝑥𝑖⟹k est symétrique !M est la matrice de masse : 𝑀=𝑀1000𝑀2000matrice d’ordre N symétrique.
Page 6 : Section II-1 : Méthodes généralesL’équation du mouvement peut s’écrire :ሷԦ𝑋+ 𝑀1𝐾Ԧ𝑋= 0Soit 𝑌𝑖𝑖=1,2…𝑛un ensemble complet de vecteurs propres orthonormés de 𝑀1𝐾, i.e.𝑀1𝐾𝑌𝑖= 𝜆𝑖𝑌𝑖𝑌𝑖𝑣𝑒𝑐. 𝑝𝑟𝑜𝑝𝑟𝑒𝑒𝑡𝑌𝑖𝑇. 𝑌𝑗= 𝛿𝑖𝑗= ቊ0 𝑠𝑖𝑖𝑗1 𝑠𝑖𝑖= 𝑗⟹𝛼𝑖𝑡𝑖=1,2…𝑛𝑡𝑒𝑙𝑠𝑞𝑢𝑒Ԧ𝑋= 𝑗=1𝑛𝛼𝑗𝑌𝑗
Page 7 : ⟹𝑗=1𝑛ሷ𝛼𝑗𝑌𝑗+ 𝑗=1𝑛𝛼𝑗𝑀1𝐾𝑌𝑗= 0𝑎𝑣𝑒𝑐𝑀1𝐾𝑌𝑗= 𝜆𝑗𝑌𝑗⟹𝑗=1𝑛 ሷ𝛼𝑗+ 𝛼𝑗𝜆𝑗𝑌𝑗= 0⟹𝑗ሷ𝛼𝑗+ 𝛼𝑗𝜆𝑗= 0𝑜ù 𝛼𝑗𝑠𝑜𝑛𝑡𝑙𝑒𝑠𝑐𝑜𝑜𝑟𝑑𝑜𝑛𝑛é𝑒𝑠𝑛𝑜𝑟𝑚𝑎𝑙𝑒𝑠⟹les coefficients se comportent comme des oscillateurs harmoniques simples de pulsation 𝜔𝑗=𝜆𝑗Remarque 1 : donc 𝑌𝑖𝑖=1,2…𝑛est une base de 𝑅𝑛Remarque 2 : on ne peut pas être certain que 𝜆𝑗 0 !
Page 8 : Section II-2 : valeurs initialesL’équation à résoudre : ሷԦ𝑋+ 𝑀1𝐾Ԧ𝑋= 0Avec conditions initiales : Ԧ𝑋0 = Ԧ𝑋0 𝑒𝑡ሶԦ𝑋0 = 𝑉0.En termes des 𝛼𝑗on a: Ԧ𝑋= σ𝑗=1𝑛𝛼𝑗𝑌𝑗⟹𝛼𝑗𝑡= 𝑌𝑗𝑇. Ԧ𝑋tAvec conditions initiales ci-dessus:⟹ቐ𝛼𝑗𝑡= 𝑌𝑗𝑇. Ԧ𝑋0ሶ𝛼𝑗𝑡= 𝑌𝑗𝑇. 𝑉0
Page 9 : Section II-3 : frottementsሷԦ𝑋+ Γ ሶԦ𝑋+ 𝑀1𝐾Ԧ𝑋= 0Γ est une matricePosons Ԧ𝑋𝑡= 𝑒𝑖𝜔𝑡Ԧ𝑋0où Ԧ𝑋0 est indépendant du temps.⟹𝜔2𝐼𝑑𝑖𝜔Γ + 𝑀1𝐾Ԧ𝑋0 = 0𝐼𝑑étant la matrice identité⟹Ԧ𝑋0 est un vecteur propre de valeur propre nulle, de la matrice : 𝜔2𝐼𝑑𝑖𝜔Γ + 𝑀1𝐾
Page 10 : Section II-4 : oscillations entretenuesSoit Ԧ𝐹𝑡 une force externe appliquée au système étudié :ሷԦ𝑋+ Γ ሶԦ𝑋+ 𝑀1𝐾Ԧ𝑋= 𝑀1 Ԧ𝐹𝑡On suppose que Ԧ𝐹𝑡= Ԧ𝐹0𝑒𝑖𝜔𝑑𝑡Si la force Ԧ𝐹𝑡n’oscille pas dans la même direction sur toutes les composantes, on utilise le principe de superposition.
Page 11 : Posons Ԧ𝑋𝑡= Ԧ𝐴𝑒𝑖𝜔𝑑𝑡⟹Ԧ𝐴= 𝜔𝑑2𝐼𝑑𝑖𝜔𝑑Γ + 𝑀1𝐾1 Ԧ𝐹0Remarque 1 : si la matrice 𝜔2𝐼𝑑𝑖𝜔Γ + 𝑀1𝐾n’est pas inversible ⟹résonance !Remarque 2 : la solution générale est la somme de la sol générale de l’équation homogène et une solution particulière, par exemple celle proposée: Ԧ𝑋𝑡= Ԧ𝐴𝑒𝑖𝜔𝑑𝑡.Rappel : Equation de l’oscillateur harmonique simple :ሷ𝑋+ 𝜔2𝑋= 0𝜔: 𝑝𝑢𝑙𝑠𝑎𝑡𝑖𝑜𝑛
Page 12 : Solution générale : 𝑋𝑡= 𝐴cos 𝜔𝑡+ 𝐵sin𝜔𝑡Avec friction : ሷ𝑋+ Γ ሶ𝑋+ 𝜔02𝑋= 0Solution générale :𝑥𝑡= 𝑒Γ2𝑡𝐴𝑒𝜔𝑡+ 𝐵𝑒𝜔𝑡𝑎𝑣𝑒𝑐𝜔=Γ24 𝜔02 𝑠𝑢𝑟𝑐𝑟𝑖𝑡𝑖𝑞𝑢𝑒𝑎𝑝é𝑟𝑖𝑜𝑑𝑖𝑞𝑢𝑒𝐴+ 𝐵𝑡𝑐𝑟𝑖𝑡𝑖𝑞𝑢𝑒𝐴𝑐𝑜𝑠𝜔𝑡+ 𝐵𝑠𝑖𝑛𝜔𝑡𝑎𝑣𝑒𝑐𝜔=𝜔02 Γ24𝑠𝑜𝑢𝑠𝑐𝑟𝑖𝑡𝑖𝑞𝑢𝑒𝑝𝑠𝑒𝑢𝑑𝑜𝑝é𝑟𝑖𝑜𝑑𝑖𝑞𝑢𝑒
Page 13 : Entretenuሷ𝑋+ Γ ሶ𝑋+ 𝜔02𝑋= 𝐹𝑡/𝑀Solution générale : 𝑋0 𝑡+ 𝑋𝐹𝑡Où 𝑋0 𝑡est la solution générale de et 𝑋𝐹𝑡est la solution particulière de
Page 14 : Système de n oscillateurs𝑀𝑑2𝑑𝑡2 Ԧ𝑋+ 𝑘Ԧ𝑋= 0 𝑜ù Ԧ𝑋= 𝑥1, 𝑥2, … . . , 𝑥𝑛M est la matrice de masseSolution générale : Ԧ𝑋𝑡= σ𝑗=1𝑛𝐴𝑗𝑒𝑖𝜔𝑗𝑡+ 𝐵𝑗𝑒𝑖𝜔𝑗𝑡𝑉𝑗où 𝑉𝑗est un vecteur propre de 𝑀1𝐾de valeur propre 𝜔𝑗Modes propres : Ԧ𝑋𝑗± = 𝑒±𝑖𝜔𝑗𝑡𝑉𝑗
Page 15 :