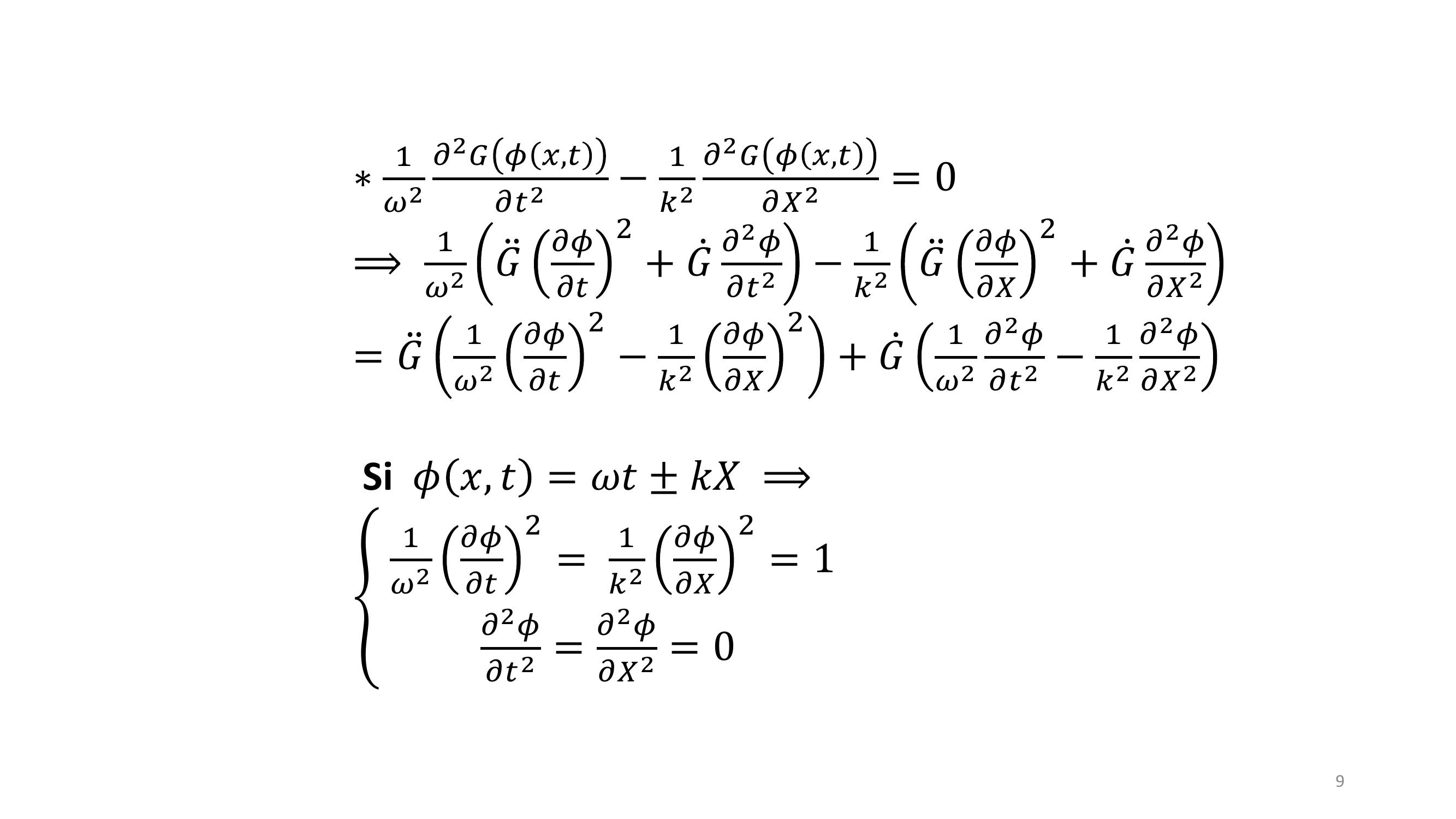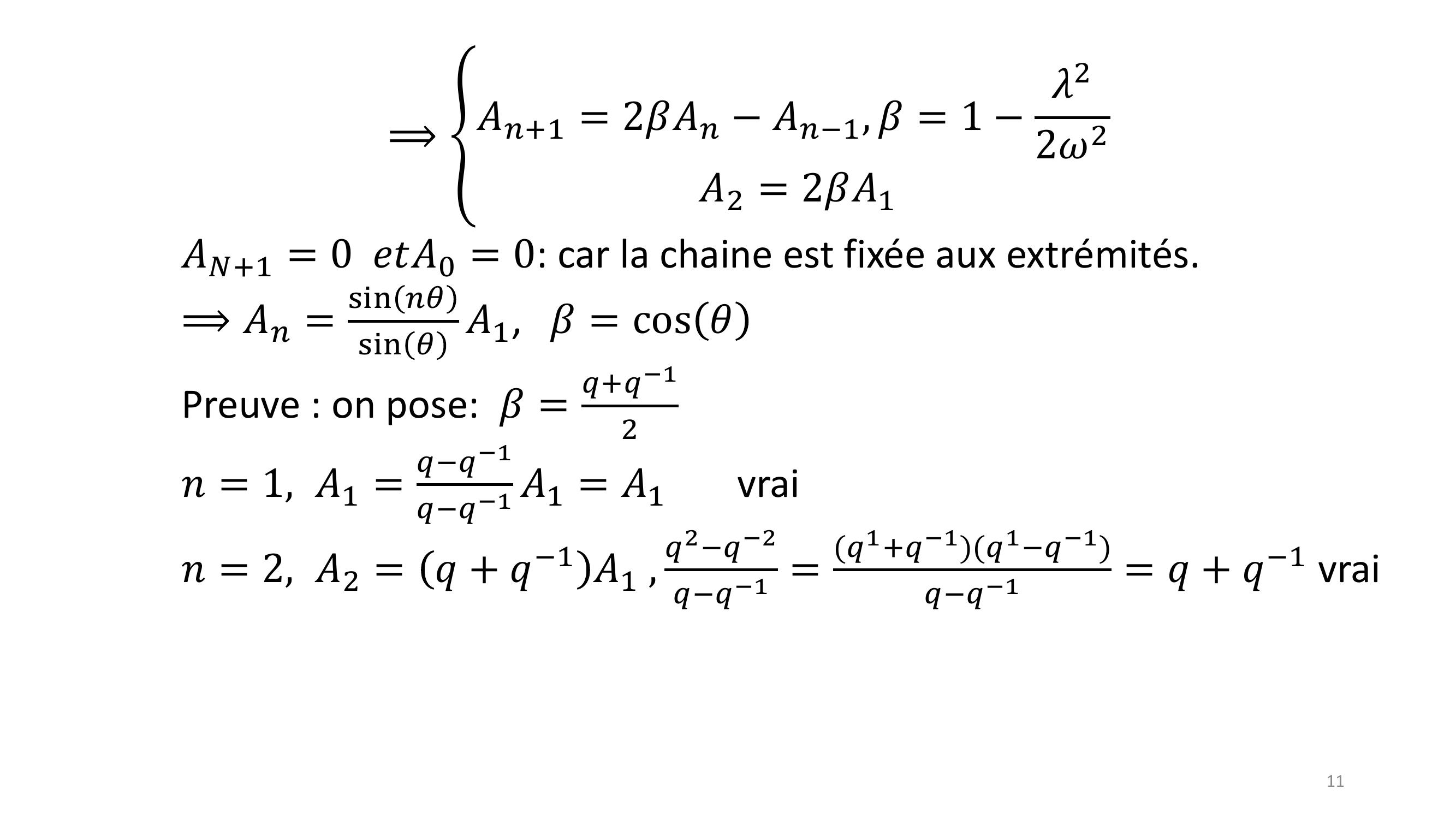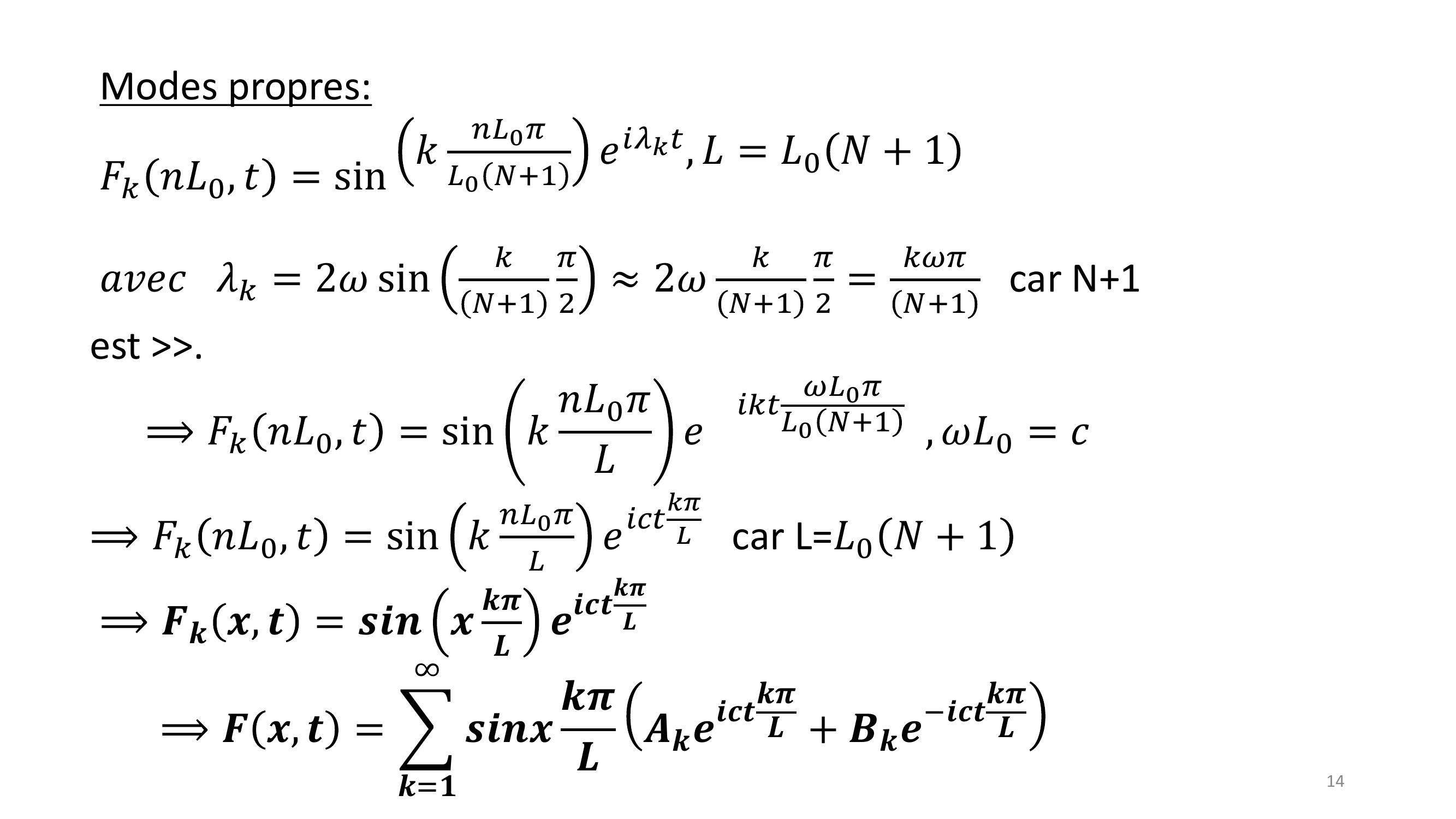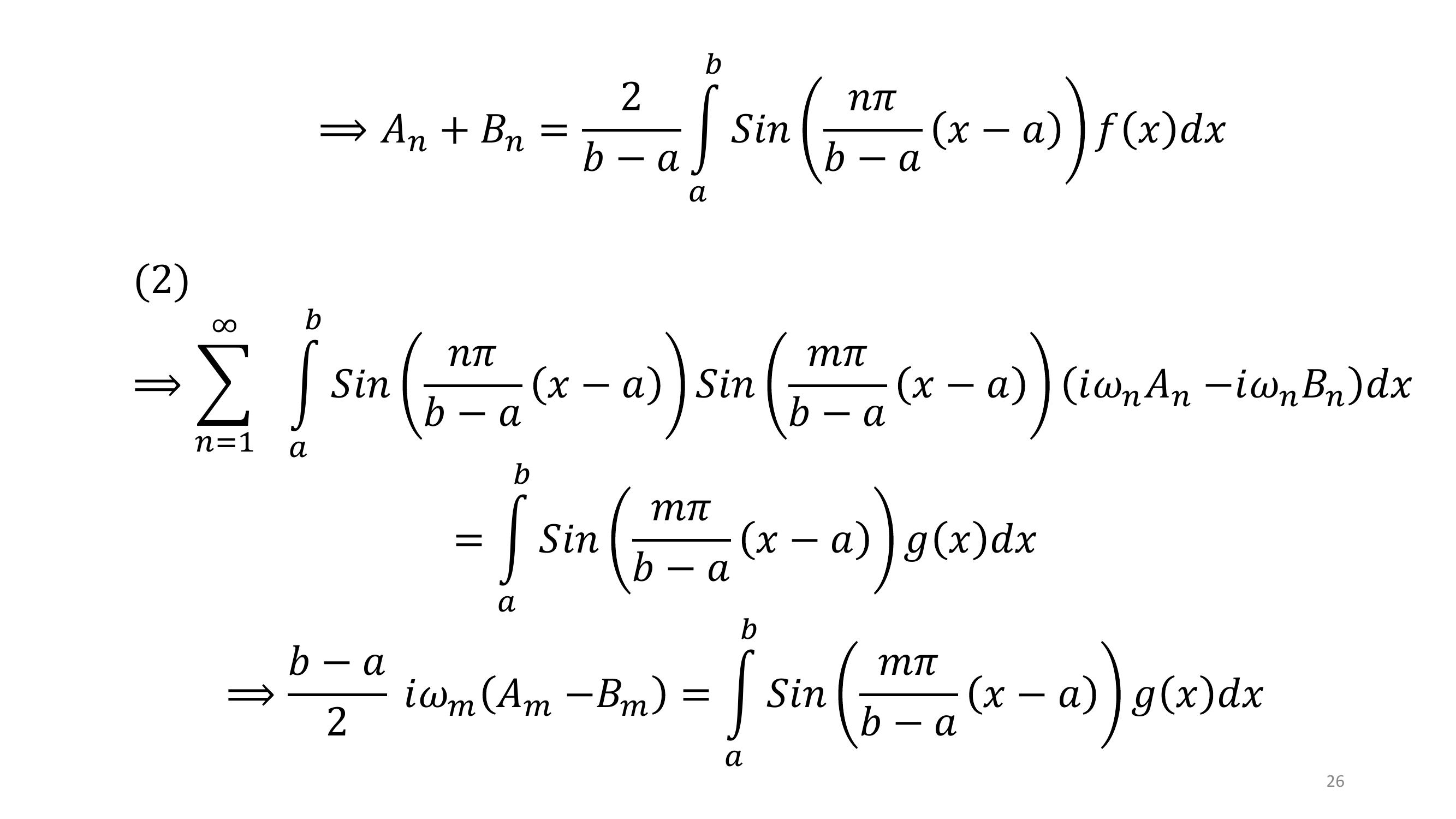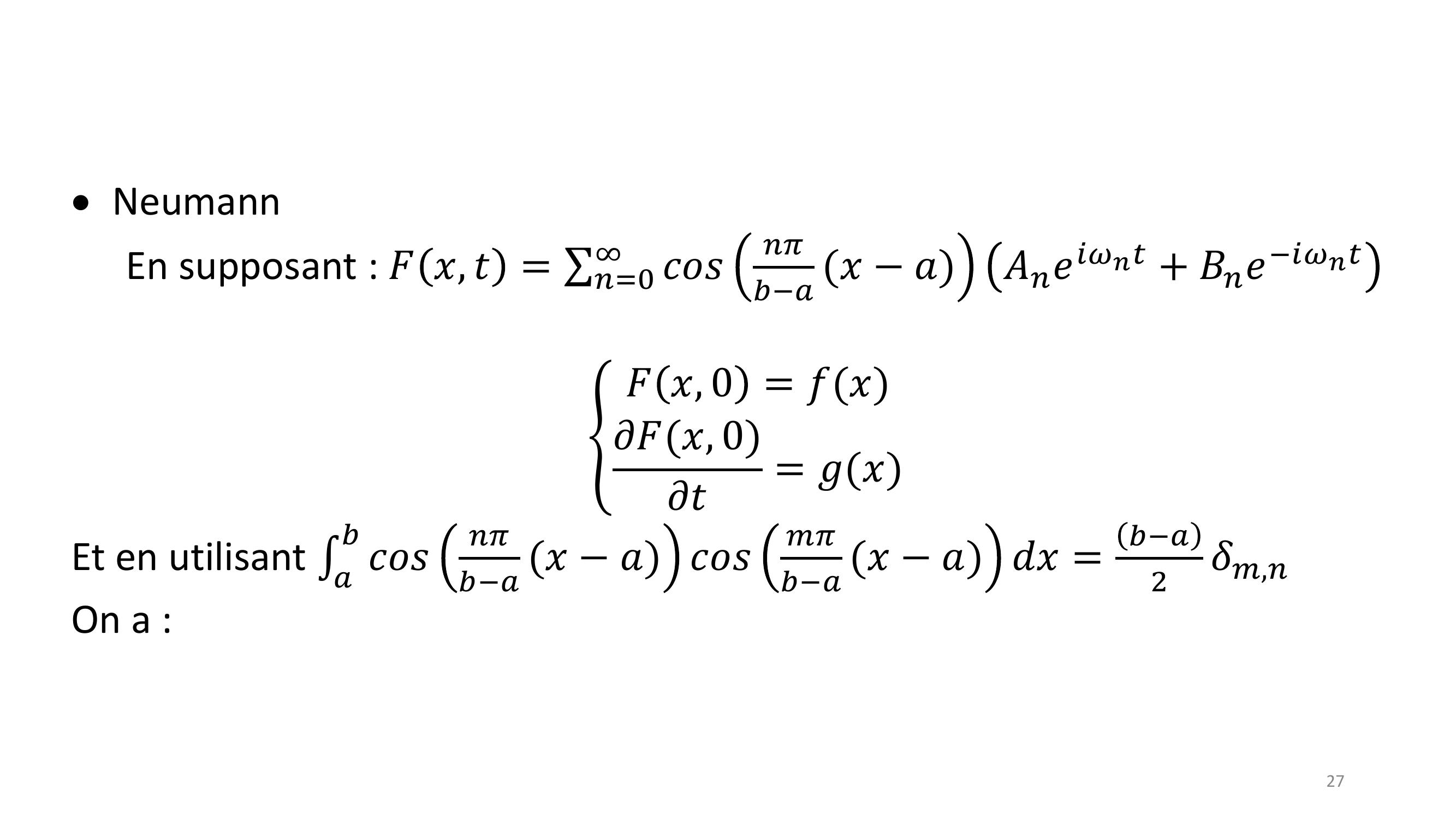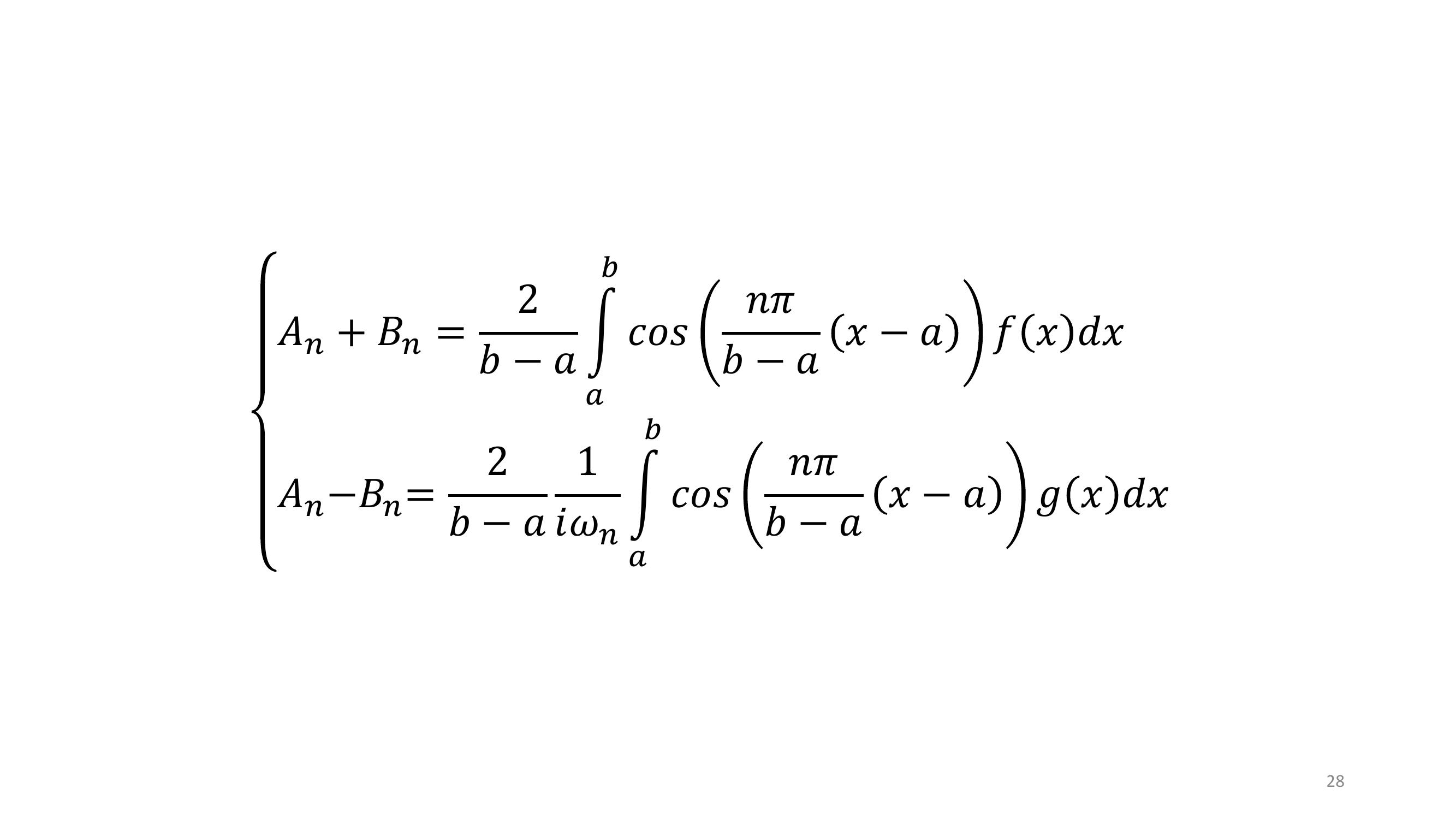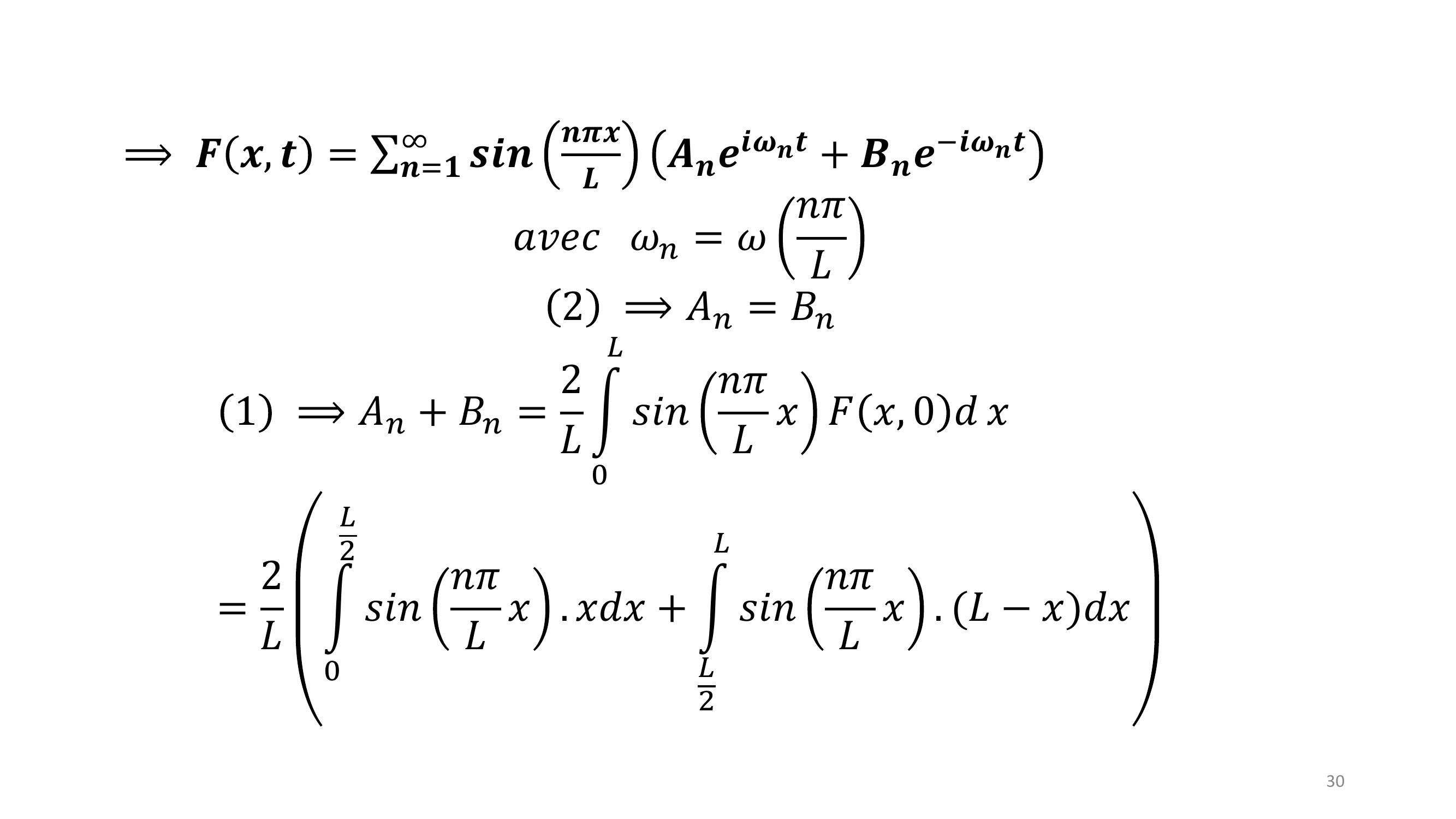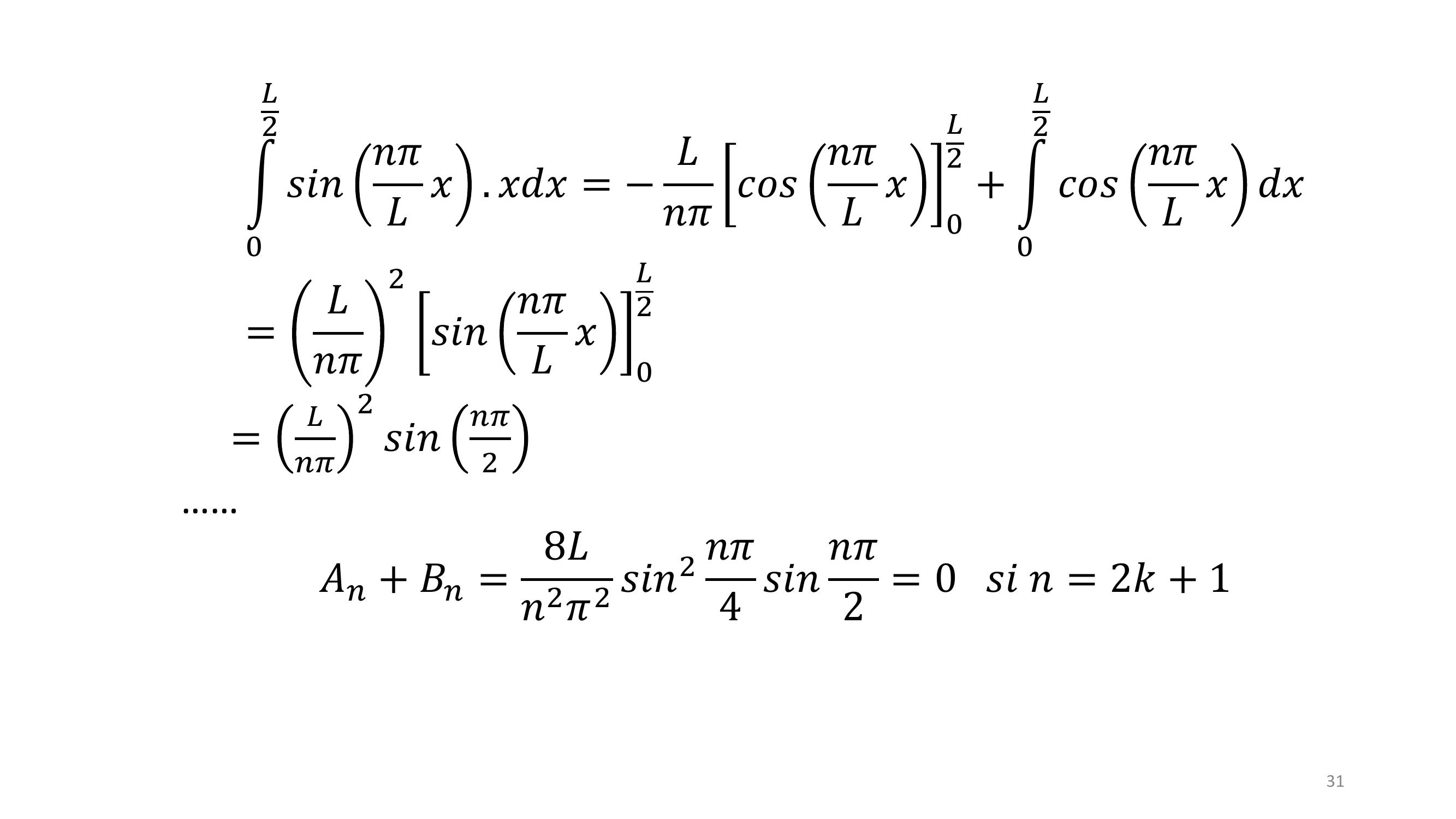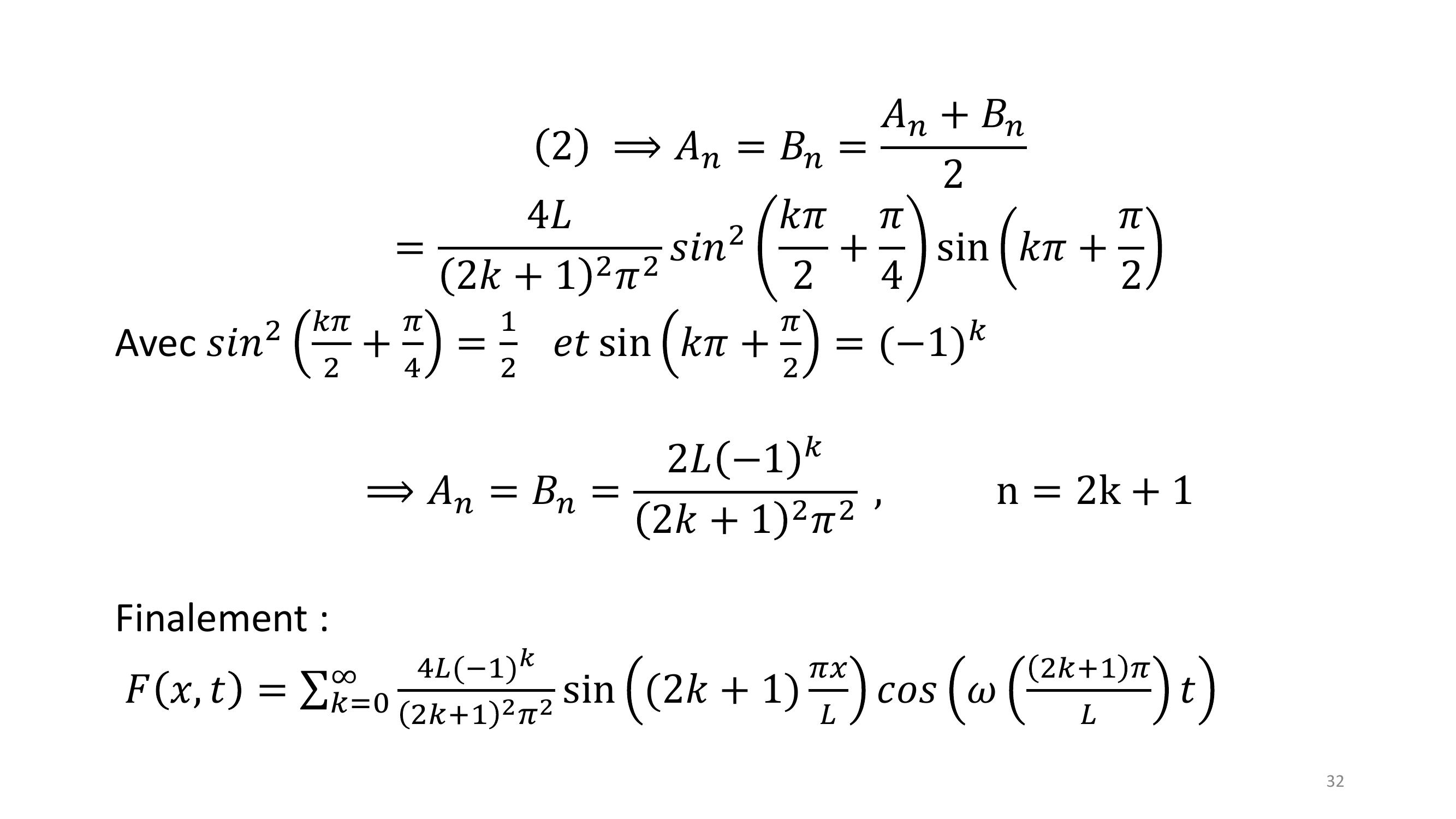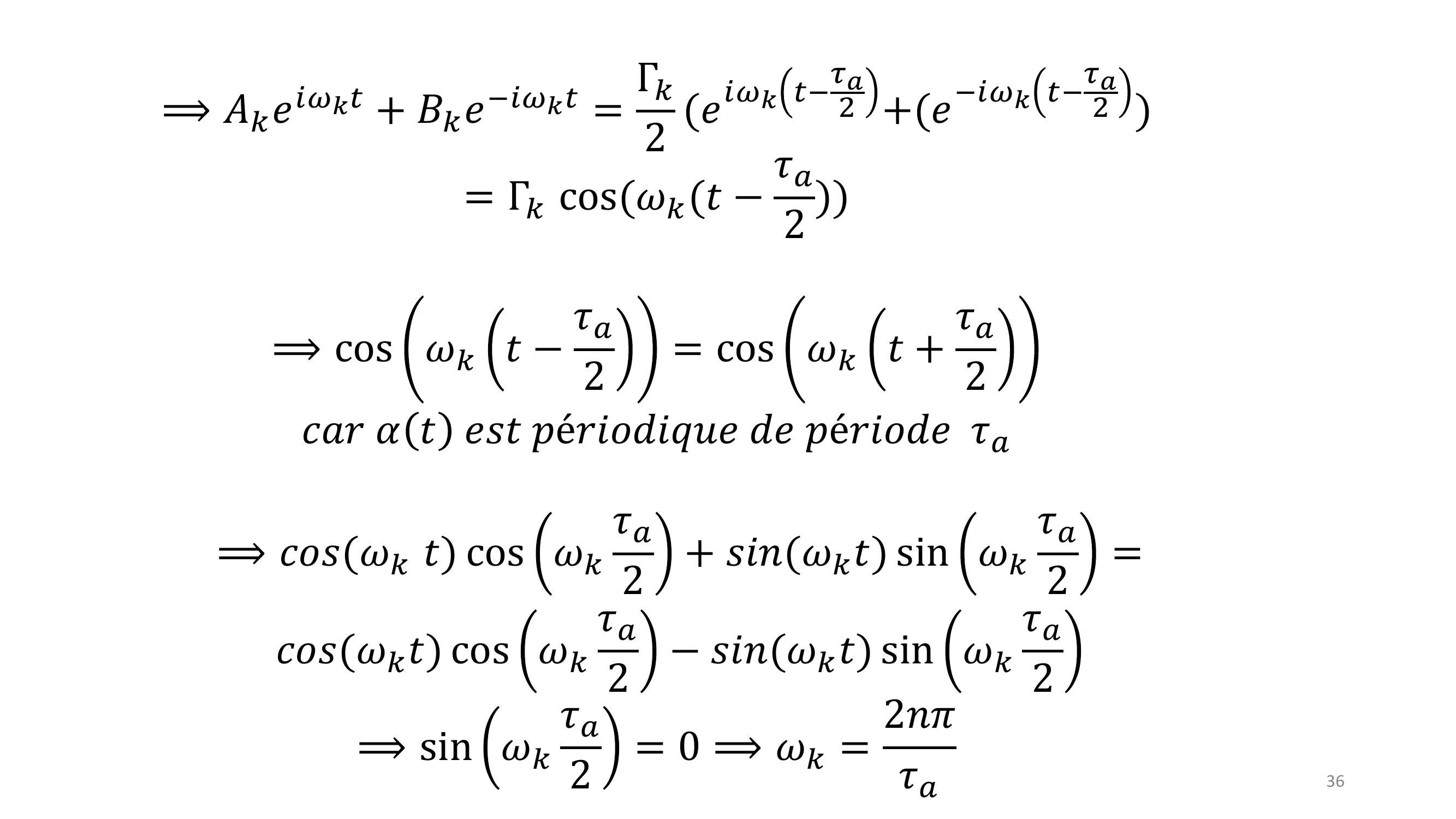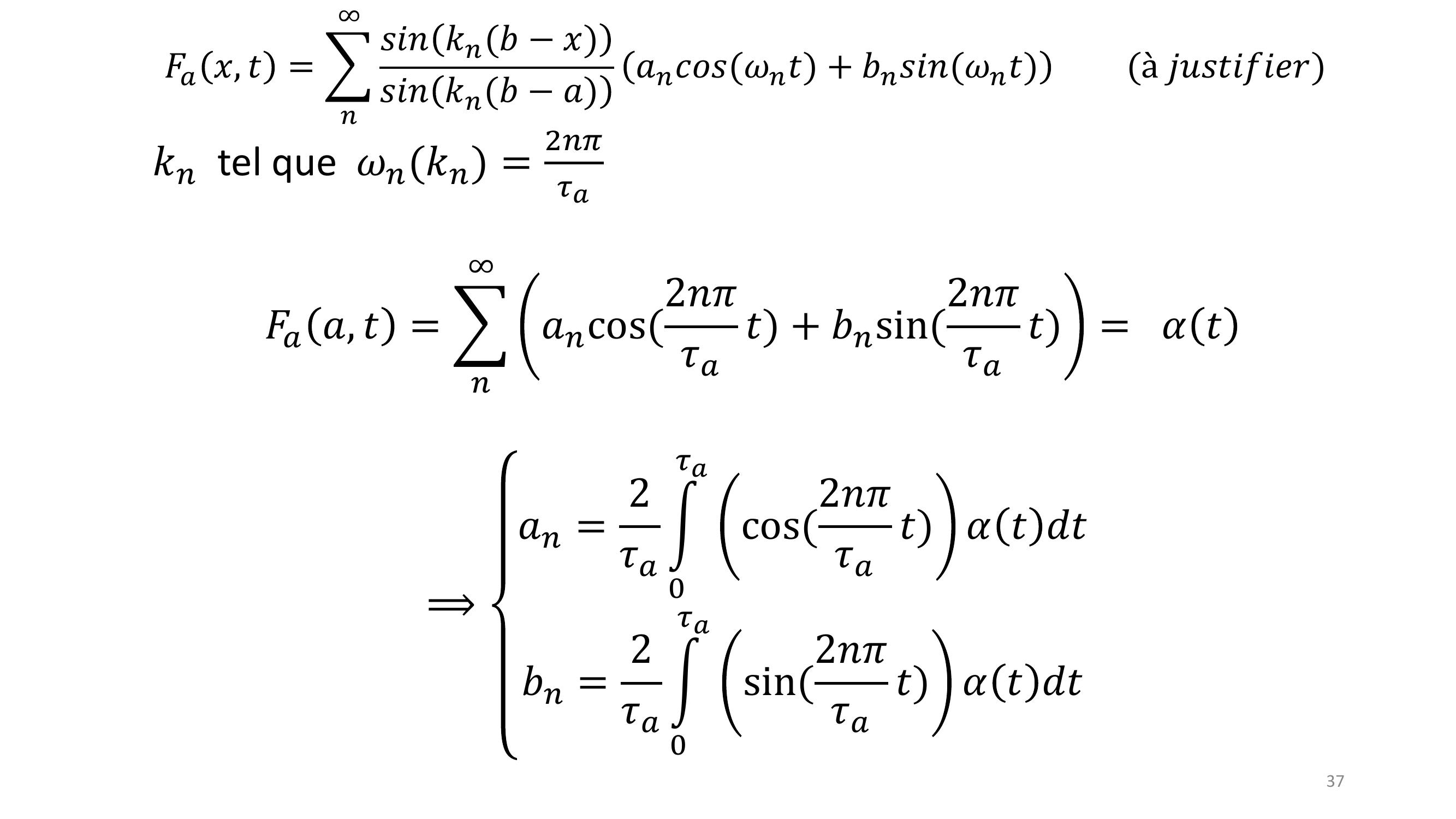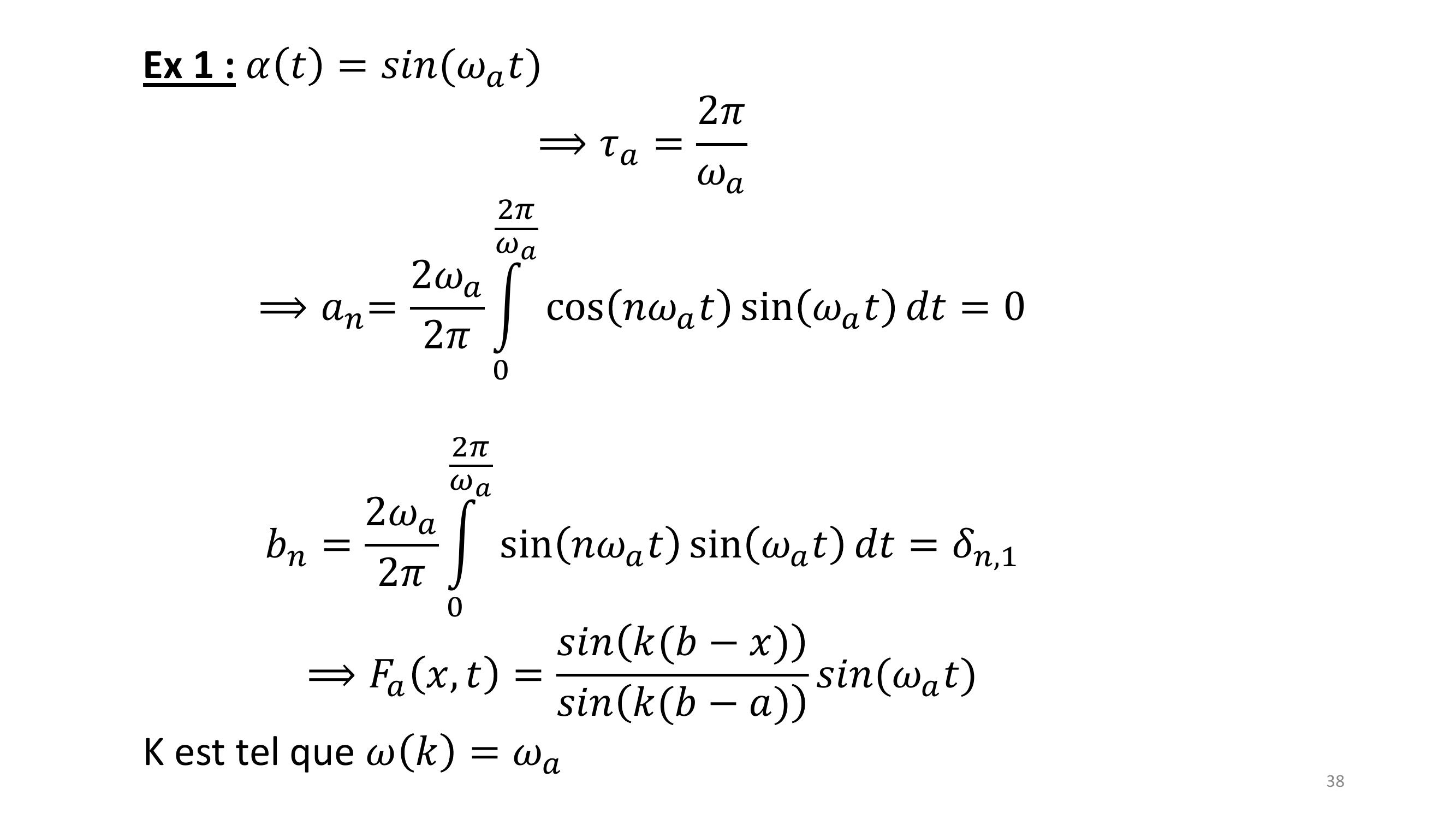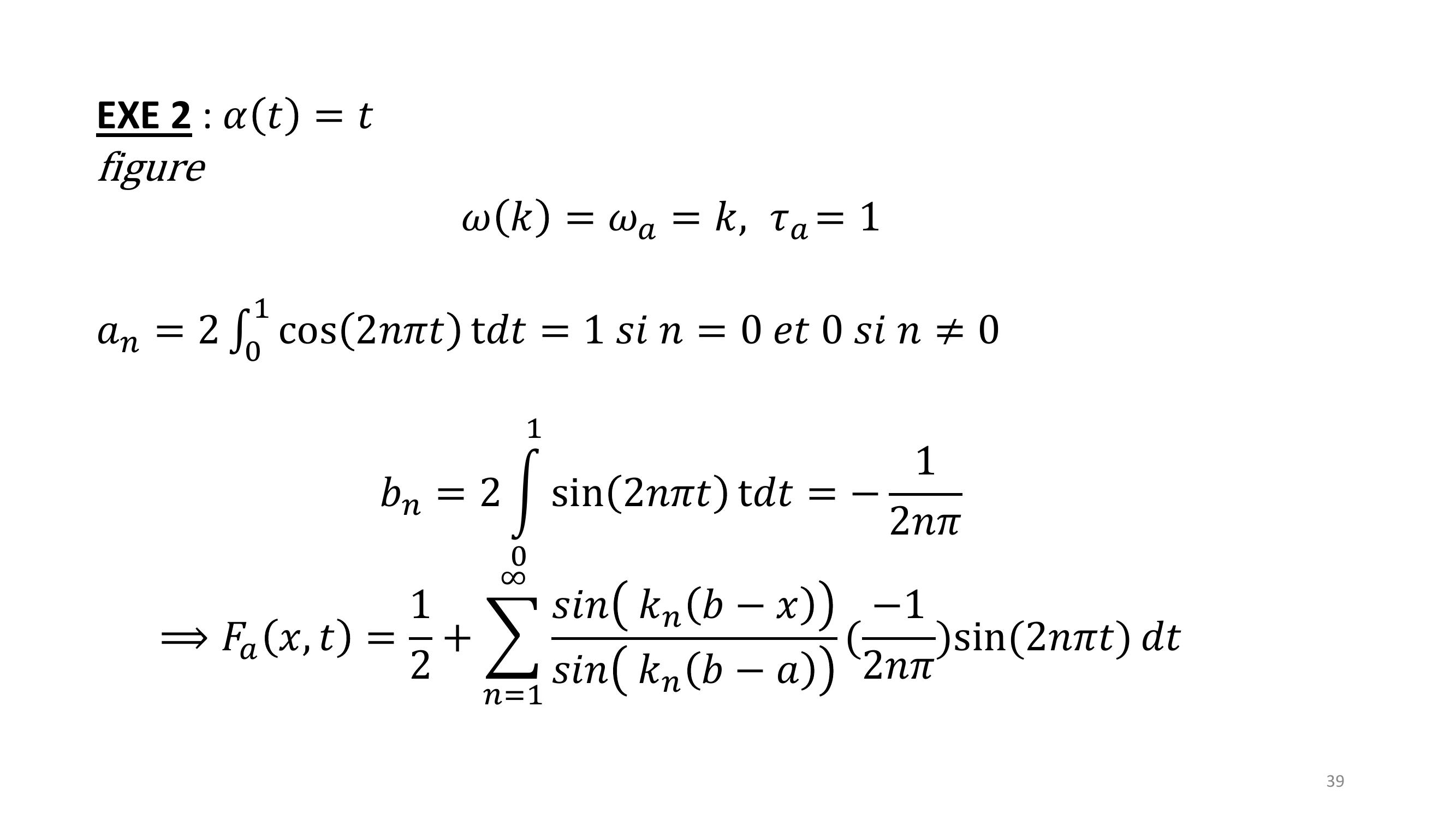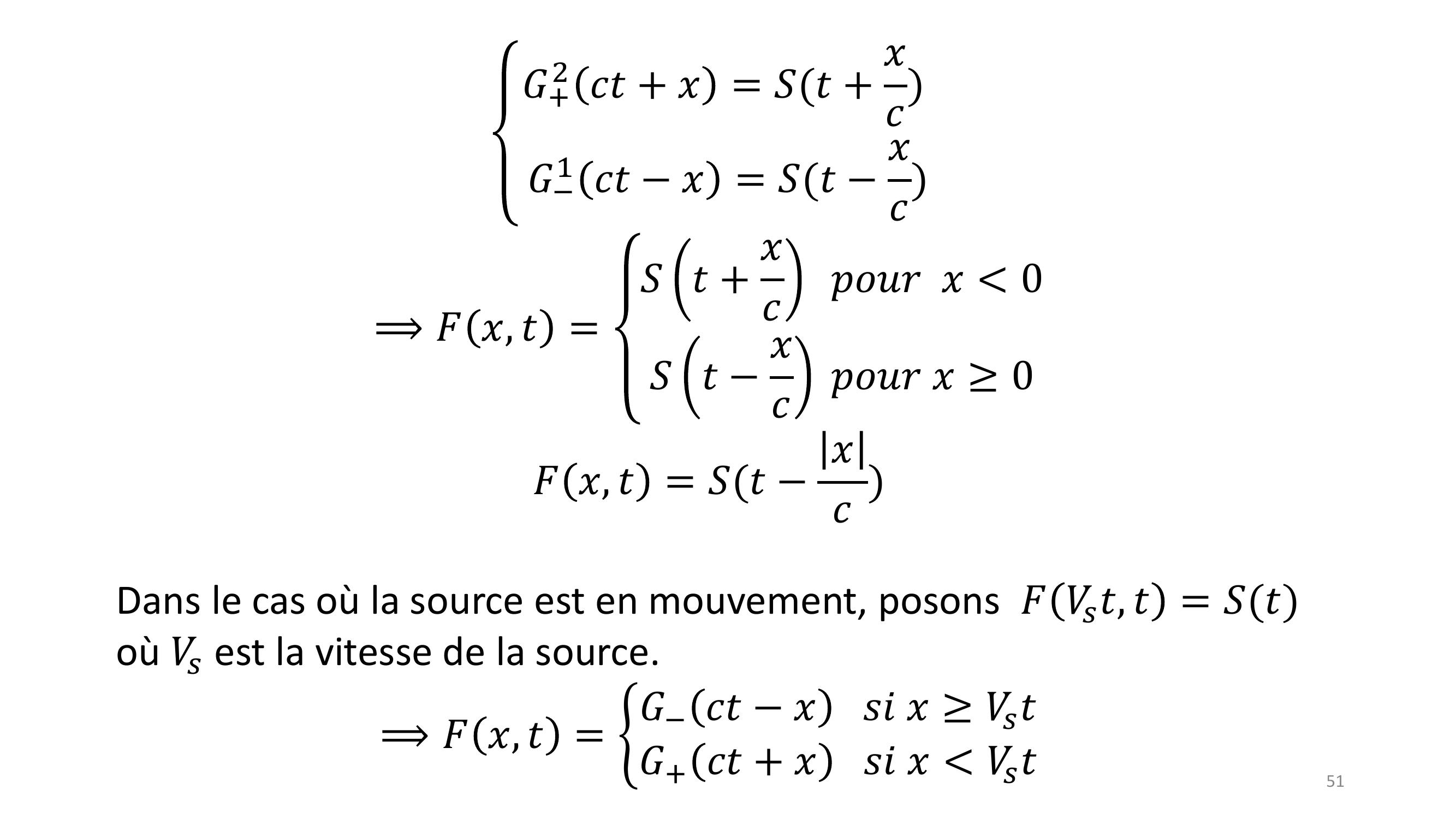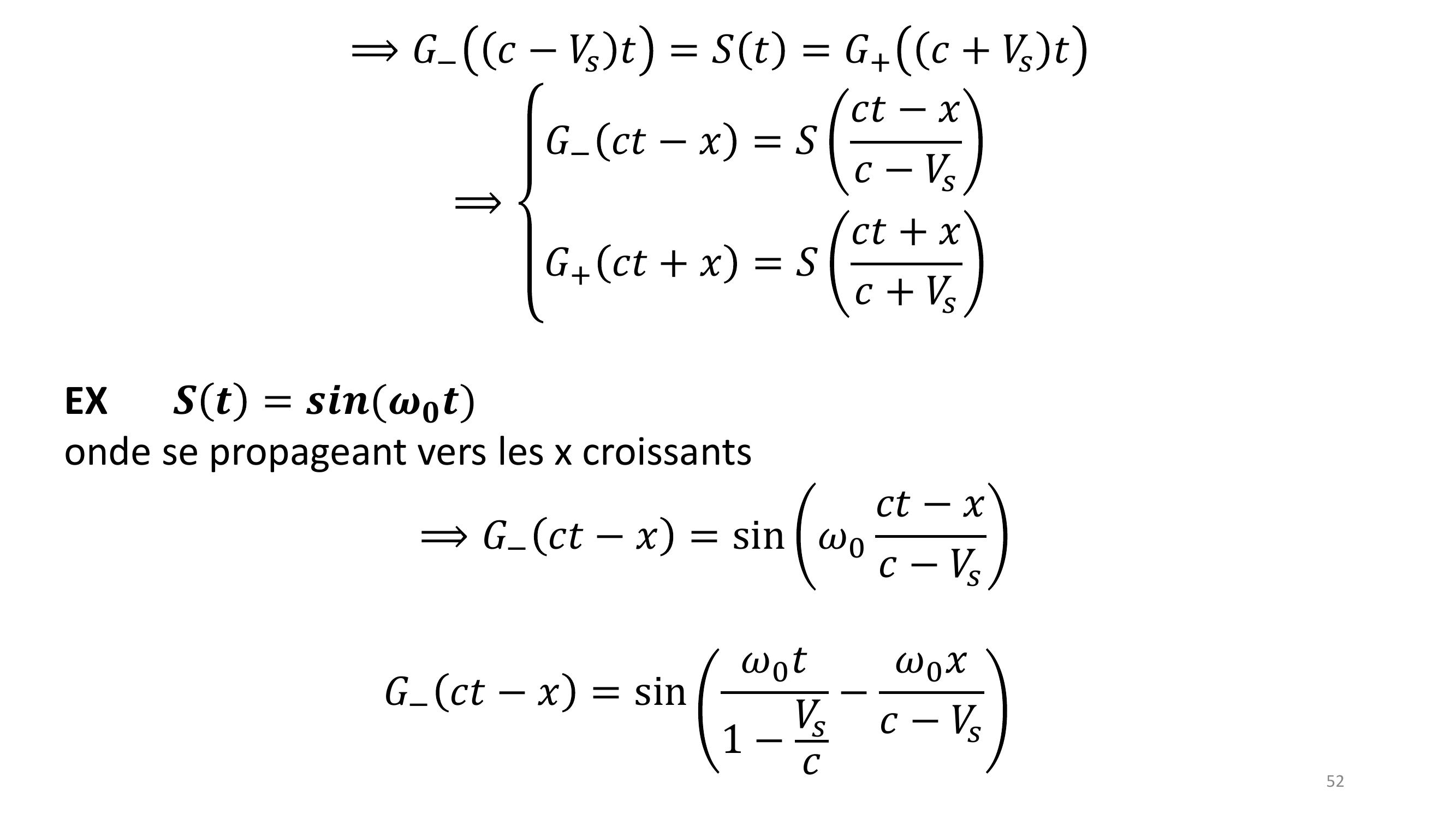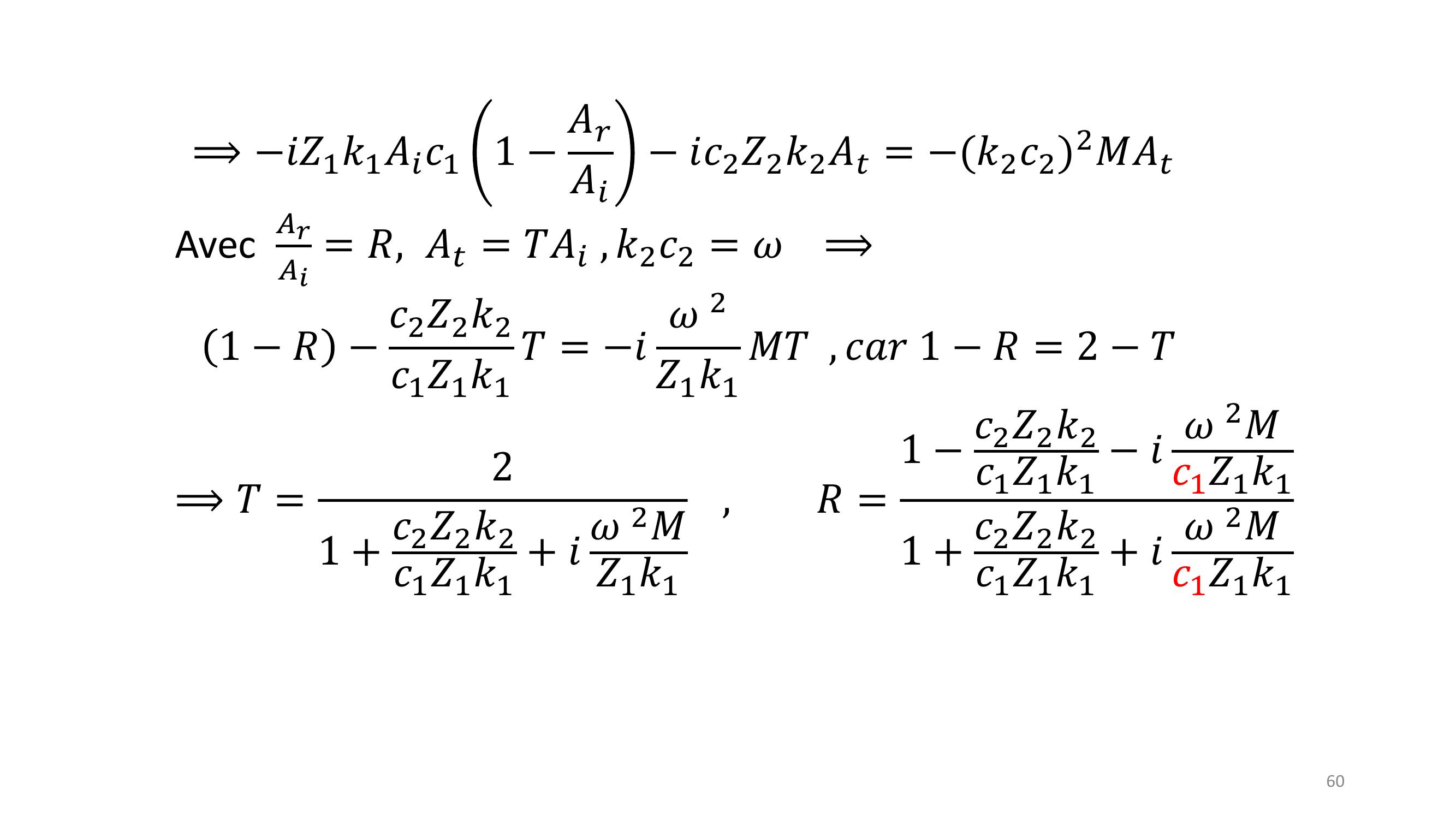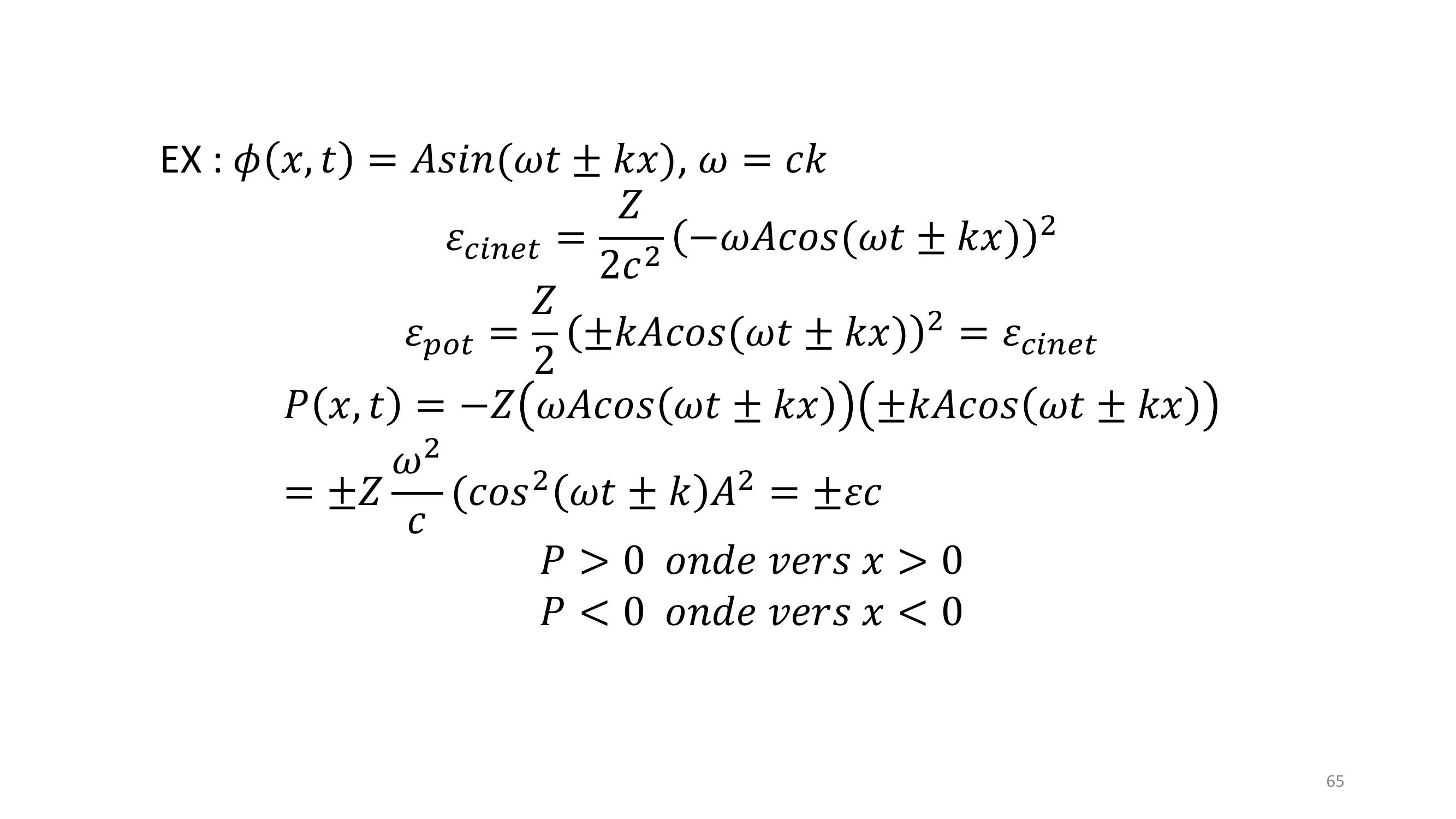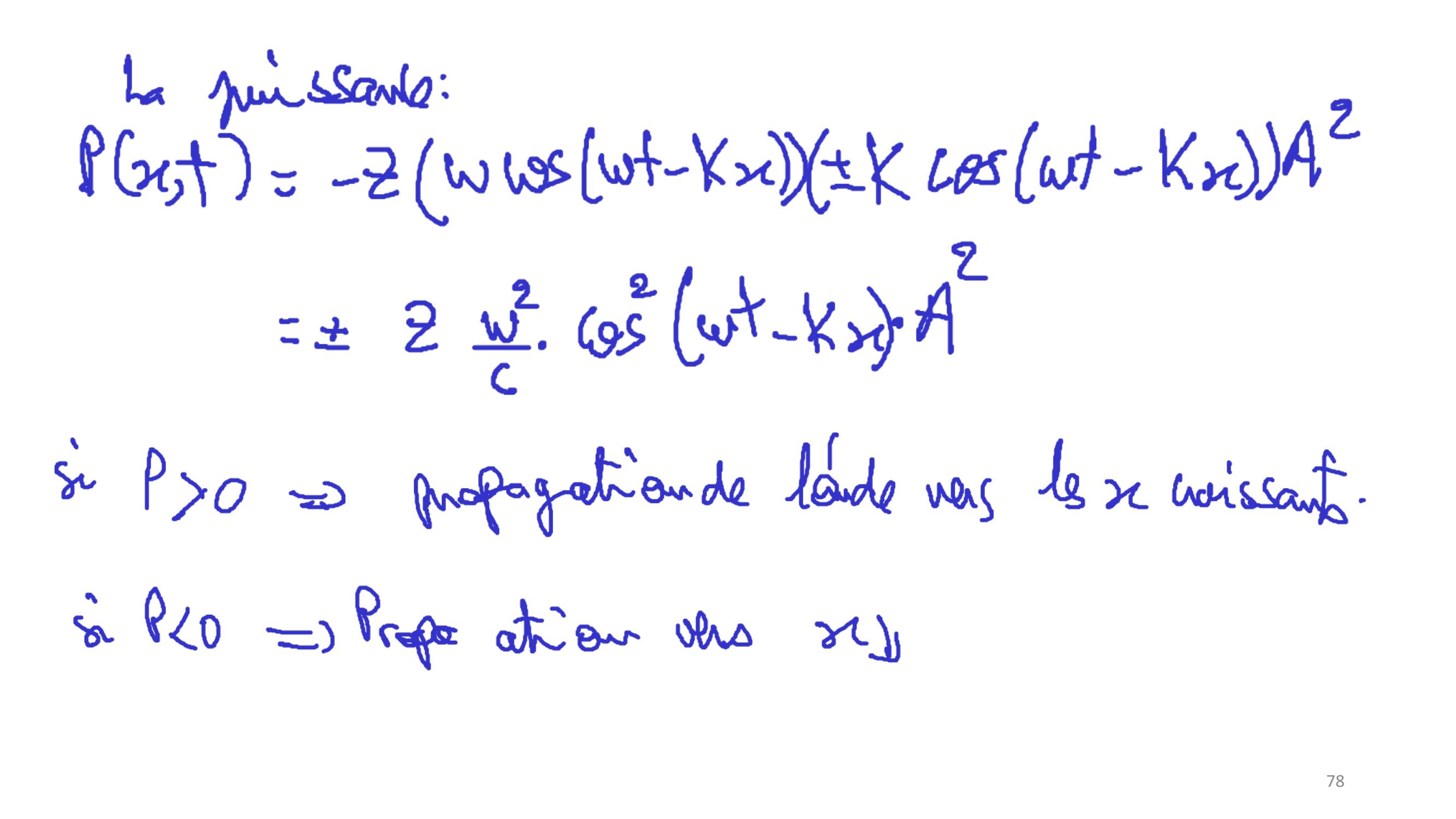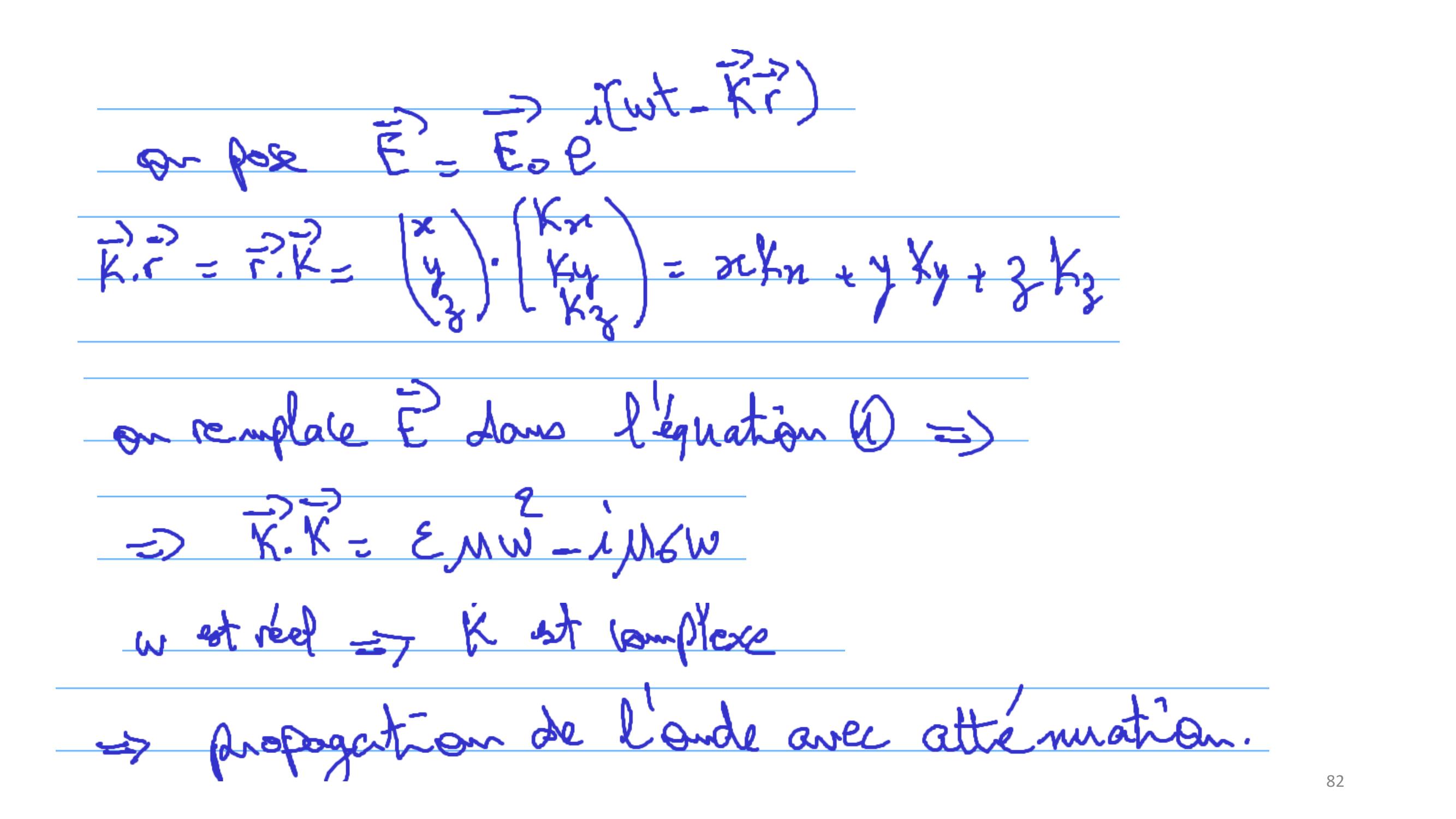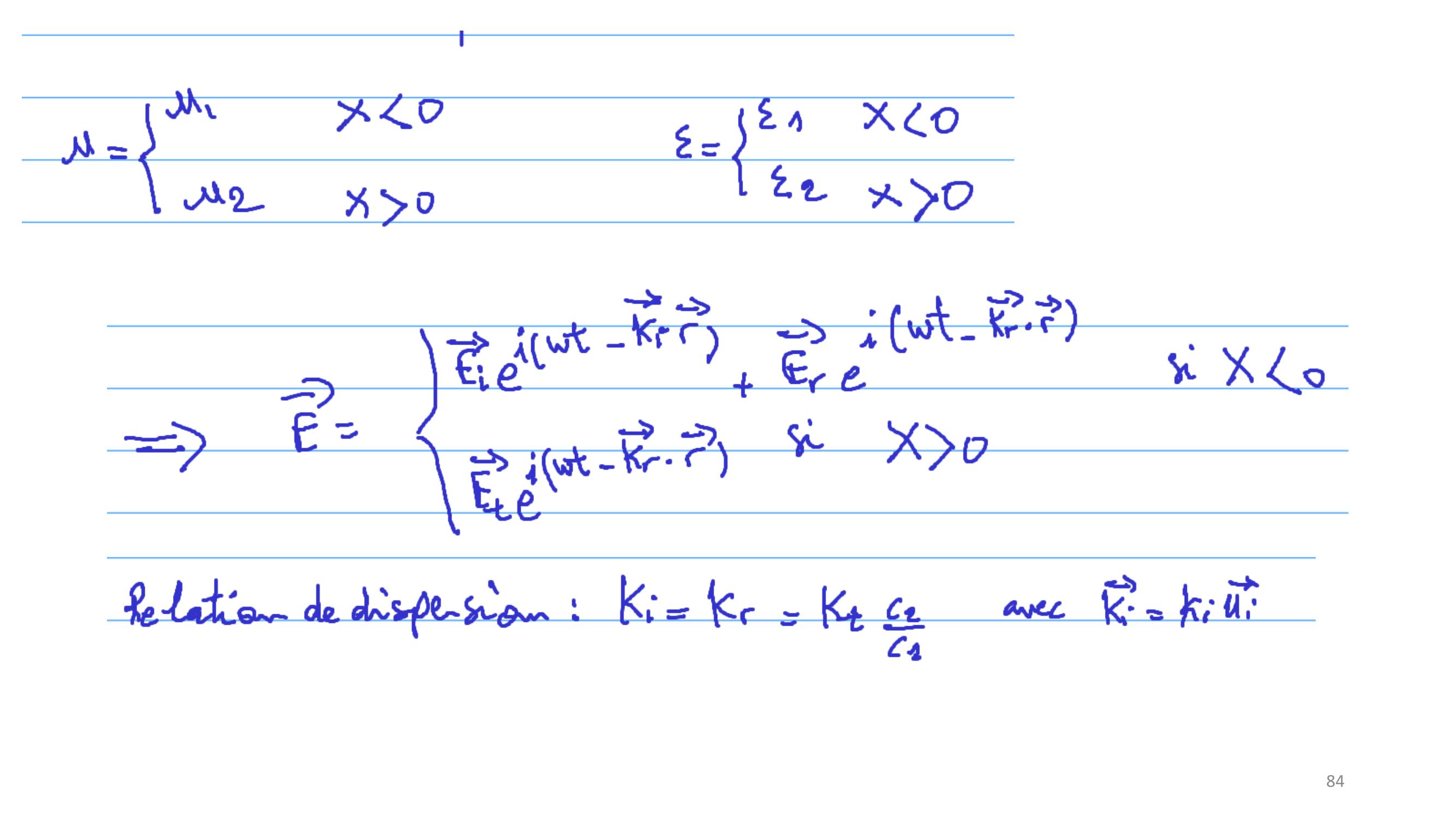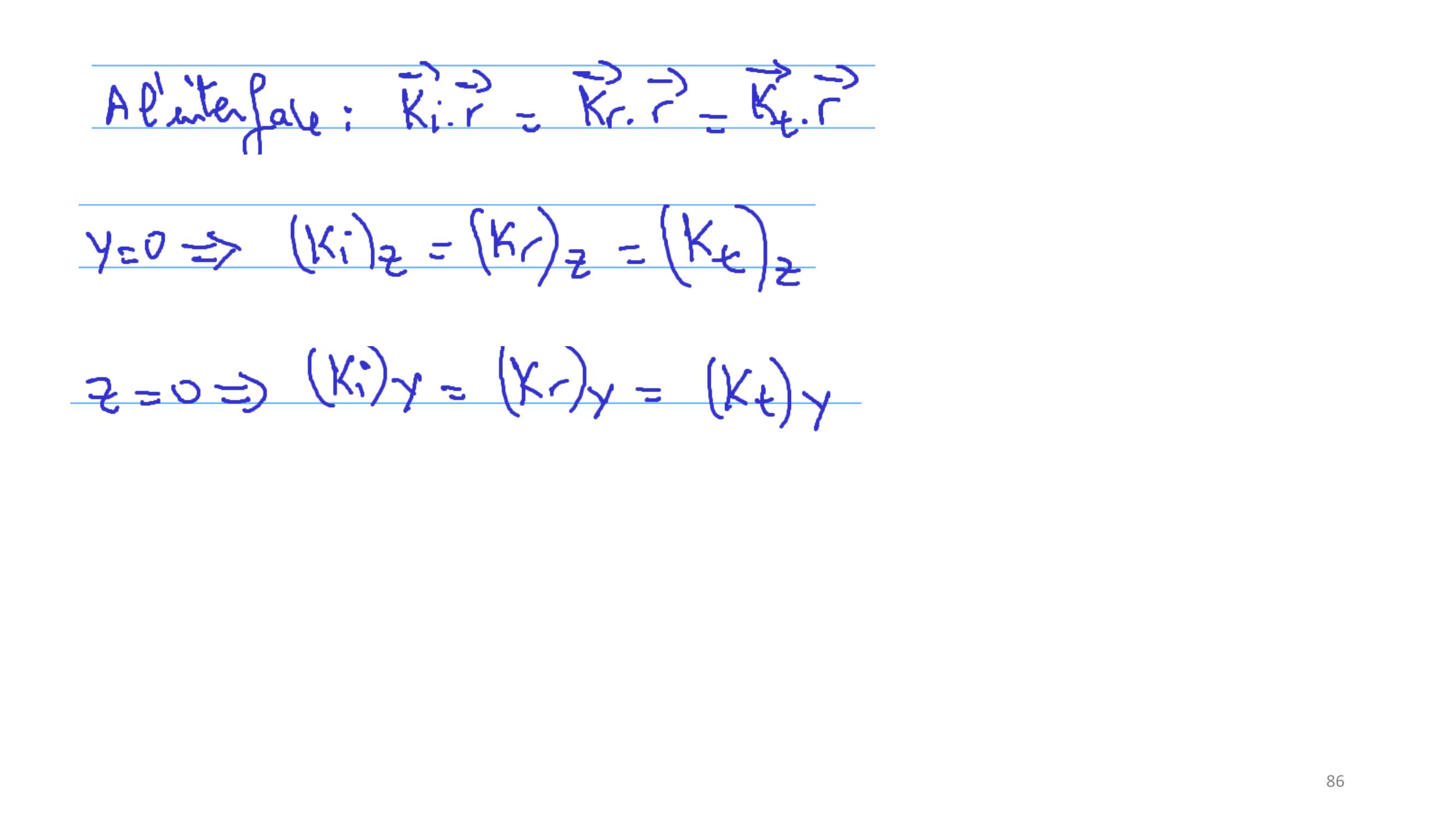CM Chapitre4

Posté le 08/02/2025

Chargé de TD/CM : A. Boumiz.

19 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87

Page 1 : Chapitre 4 : OndesSection 4.1 : chaine de N oscillateurs Une chaine est constituée de N petits blocs identiques, de même masse M, espacés de la même distance 𝐿0 et alignés suivant la droite Ox. Une petite perturbation, modifie l’équilibre initial, elle se déplace de proche en proche le long de la chaine de blocs et provoque un petit déplacement de chaque bloc.1

Page 2 : Admettons que les forces d’interaction de chaque bloc peut être limitée à ses deux voisins immédiats n+1 et n-1 pour le bloc net que ces interactions sont de même type que la tension d’un système masse-ressort de constante de raideur k.Soit 𝑋𝑛la position de la masse n par rapport à sa position d’équilibre 1 𝑛𝑁.21 2 3N-1 N𝐾0 n-1 𝐾0 n 𝐾0 n+1

Page 3 : Déterminons l’équation du mouvement du nième bloc : Bilan des forces de rappel exercées par les blocs n+1 et n-1 sur le bloc n :Projection de la force de rappel exercée par le bloc n+1 :𝒇𝒏+𝟏→𝒏= 𝐾0𝑿𝒏𝑿𝒏+𝟏Projection de la force de rappel exercée par Le bloc n-1 :𝒇𝒏𝟏→𝒏= 𝐾0𝑿𝒏𝑿𝒏𝟏La deuxième loi de Newton s’écrit :𝑴ሷ𝑿𝒏= 𝒇𝒏𝟏→𝒏+ 𝒇𝒏+𝟏→𝒏Soit : 𝒎ሷ𝑿𝒏= 𝐾0𝑿𝒏+𝟏𝑿𝒏 𝐾0𝑿𝒏𝑿𝒏𝟏D’oùሷ𝑿𝒏+𝐾0𝑴𝟐𝑿𝒏𝑿𝒏𝟏𝑿𝒏+𝟏= 𝟎posons𝐾0𝑴= 𝝎𝟐3

Page 4 : 𝜔0 Étant la pulsation propre de chacun des N blocs identiques constituant la chaîne.Nous constatons que les termes 𝑿𝒏s’additionnent et ne s’éliminent pas.La solution 𝑋𝑛dépend de 𝑋𝑛1 et de 𝑋𝑛+1 cela veut dire que le mouvement du bloc n, dépend du mouvement de ses voisins immédiats n+1 et n-1 : la perturbation se déplace de proche en proche, il s’agit d’une onde mécanique, qui se propage le long de la chaîne de blocs. 4

Page 5 : 5ሷ𝑋𝑛+ 2𝜔2𝑋𝑛𝜔2 𝑋𝑛1 + 𝑋𝑛+1 = 0Equation du mouvement du nième blocEquation du mouvement du premier bloc𝑋0 = 0ሷ𝑋1 + 2𝜔2𝑋1 𝜔2 𝑋0 + 𝑋1 = 0Equation du mouvement du dernier bloc ሷ𝑋𝑁+ 2𝜔2𝑋𝑁𝜔2 𝑋𝑁1 + 𝑋𝑛+1 = 0

Page 6 : Limite continueOn s’intéresse à la limite N grand et 𝐿0 petit, soit 𝐹𝑋, 𝑡telle que𝐹𝑛𝐿0, 𝑡= 𝑋𝑛𝑡⟹𝑋𝑛±1 𝑡= 𝐹 𝑛±1𝐿0, 𝑡𝐹𝑛𝐿0, 𝑡±ቤ𝜕𝐹𝜕𝑋𝐿0𝑋=𝑛𝐿0± 12อ𝜕2𝐹𝜕𝑋2 𝐿02𝑋=𝑛𝐿0⟹𝟐𝑿𝒏𝑿𝒏𝟏𝑿𝒏+𝟏= อ𝜕2𝐹𝑋, 𝑡𝜕𝑋2𝐿02𝑋=𝑛𝐿06

Page 7 : 𝜕2𝐹𝑛𝐿0, 𝑡𝜕𝑡2𝜔2𝐿02อ𝜕2𝐹𝑋, 𝑡𝜕𝑋2𝑋=𝑛𝐿0= 0⟹1𝜔2𝜕2𝐹𝑋,𝑡𝜕𝑡21𝑘2𝜕2𝐹𝑋,𝑡𝜕𝑋2= 0avec 𝜔2 =𝐾0𝑀𝑜ù 𝜔𝑒𝑠𝑡𝑙𝑎𝑝𝑢𝑙𝑠𝑎𝑡𝑖𝑜𝑛𝑒𝑡𝑘2 =1𝐿02 , 𝑘est le nombre d’onde en cm -1.𝜕2𝐹𝑋,𝑡𝜕𝑋2𝑘2𝜔2𝜕2𝐹𝑋,𝑡𝜕𝑡2= 0,𝑘2𝜔2 =1𝑐2 où c est la vitesse de phaseD’où l’équation d’onde :𝜕2𝐹𝑋,𝑡𝜕𝑋21𝑐2𝜕2𝐹𝑋,𝑡𝜕𝑡2= 07

Page 8 : Solution de l’équation d’onde :Soit Gz une fonction, qui dépend d’une seule variable z et 𝜙𝑥, 𝑡 une fonction qui dépend des deux variables 𝑥𝑒𝑡𝑡:𝜕𝜕𝑡𝐺𝜙𝑥, 𝑡=ሶ𝐺𝜕𝜙𝜕𝑡𝜕2𝜕𝑡2 𝐺𝜙𝑥, 𝑡=ሷ𝐺𝜕𝜙𝜕𝑡2+ ሶ𝐺𝜕2𝜙𝜕𝑡2𝜕2𝜕𝑋2 𝐺𝜙𝑥, 𝑡=ሷ𝐺𝜕𝜙𝜕𝑋2+ ሶ𝐺𝜕2𝜙𝜕𝑋28

Page 9 : 1𝜔2𝜕2𝐺𝜙𝑥,𝑡𝜕𝑡21𝑘2𝜕2𝐺𝜙𝑥,𝑡𝜕𝑋2= 0⟹1𝜔2ሷ𝐺𝜕𝜙𝜕𝑡2+ ሶ𝐺𝜕2𝜙𝜕𝑡21𝑘2ሷ𝐺𝜕𝜙𝜕𝑋2+ ሶ𝐺𝜕2𝜙𝜕𝑋2=ሷ𝐺1𝜔2𝜕𝜙𝜕𝑡21𝑘2𝜕𝜙𝜕𝑋2+ ሶ𝐺1𝜔2𝜕2𝜙𝜕𝑡2 1𝑘2𝜕2𝜙𝜕𝑋2Si 𝜙𝑥, 𝑡= 𝜔𝑡± 𝑘𝑋⟹൞1𝜔2𝜕𝜙𝜕𝑡2=1𝑘2𝜕𝜙𝜕𝑋2= 1𝜕2𝜙𝜕𝑡2 =𝜕2𝜙𝜕𝑋2 = 09

Page 10 : La solution générale de l’équation d’onde est :𝐹𝑋, 𝑡= 𝐺+ 𝜔𝑡+ 𝑘𝑋+ 𝐺𝜔𝑡𝑘𝑋𝐺+ 𝑒𝑡𝐺sont deux fonctions 𝐶2 arbitraires.Rappel : la solution générale d’une équation différentielle d’ordre n contient n fonctions arbitraires.SolutionOn pose 𝑋𝑛= 𝐴𝑛𝑒𝑖𝜆𝑡ሷ𝑋𝑛+ 𝐾0𝑴2𝑋𝑛𝑋𝑛1 𝑋𝑛+1 = 0 ⟹𝜆2𝐴𝑛+ 2𝜔2𝐴𝑛𝜔2 𝐴𝑛1 + 𝐴𝑛+1 = 010

Page 11 : ⟹൞𝐴𝑛+1 = 2𝛽𝐴𝑛𝐴𝑛1, 𝛽= 1 𝜆22𝜔2𝐴2 = 2𝛽𝐴1𝐴𝑁+1 = 0 𝑒𝑡𝐴0 = 0: car la chaine est fixée aux extrémités.⟹𝐴𝑛=sin 𝑛𝜃sin 𝜃𝐴1, 𝛽= cos 𝜃Preuve : on pose: 𝛽=𝑞+𝑞12𝑛= 1, 𝐴1 =𝑞𝑞1𝑞𝑞1 𝐴1 = 𝐴1vrai𝑛= 2, 𝐴2 = 𝑞+ 𝑞1 𝐴1 ,𝑞2𝑞2𝑞𝑞1 =𝑞1+𝑞1𝑞1𝑞1𝑞𝑞1= 𝑞+ 𝑞1 vrai11

Page 12 : Supposons le résultat vrai pour 𝐴𝑛et 𝐴𝑛1𝐴𝑛+1 =𝑞+ 𝑞1 𝑞𝑛𝑞𝑛𝑞𝑞1 𝑞𝑛1𝑞1𝑛𝑞𝑞1𝐴1⟹𝐴𝑛+1𝐴1= 𝑞𝑛+1𝑞𝑛1𝑞𝑞1= sin 𝑛𝜃sin 𝜃⟹𝑋𝑛= sin 𝑛𝜃sin 𝜃𝐴1𝑒𝑖𝜆𝑡Or 𝑋𝑁+1 = 0 ⟹sin 𝑁+ 1 𝜃 = 0 ⟹𝜃𝑘=𝑘𝜋𝑁+112

Page 13 : 1 𝜆𝑘22𝜔2 = 𝑐𝑜𝑠𝜃𝑘Or 𝑐𝑜𝑠𝜃𝑘= 1 2𝑠𝑖𝑛2 𝜃𝑘2 et 𝜃𝑘=𝑘𝜋𝑁+1𝜆𝑘= 2𝜔sin𝑘𝑁+ 1𝜋2D’où les modes propres sont : 𝑿𝒏𝒌=𝒔𝒊𝒏𝒏𝜽𝒌𝒔𝒊𝒏𝜽𝒌𝒆𝒊𝝀𝒌𝒕, k=1, …, N+1Pulsations propres : 𝜆𝑘= 2𝜔sin𝑘𝑁+ 1𝜋2 ,𝜃𝑘=𝑘𝜋𝑁+ 113

Page 14 : 14Modes propres:𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿0 𝑁+1𝑒𝑖𝜆𝑘𝑡, 𝐿= 𝐿0 𝑁+ 1𝑎𝑣𝑒𝑐𝜆𝑘= 2𝜔sin𝑘𝑁+1𝜋22𝜔𝑘𝑁+1𝜋2 =𝑘𝜔𝜋𝑁+1car N+1 est .⟹𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿𝑒𝑖𝑘𝑡𝜔𝐿0𝜋𝐿0 𝑁+1 , 𝜔𝐿0 = 𝑐⟹𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿𝑒𝑖𝑐𝑡𝑘𝜋𝐿car L=𝐿0 𝑁+ 1⟹𝑭𝒌𝒙, 𝒕= 𝒔𝒊𝒏𝒙𝒌𝝅𝑳𝒆𝒊𝒄𝒕𝒌𝝅𝑳⟹𝑭𝒙, 𝒕= ෍𝒌=𝟏𝒔𝒊𝒏𝒙𝒌𝝅𝑳𝑨𝒌𝒆𝒊𝒄𝒕𝒌𝝅𝑳+ 𝑩𝒌𝒆𝒊𝒄𝒕𝒌𝝅𝑳

Page 15 : 154-2 vitesse de groupe , vitesse de phase et conditions aux limitesEquation d’onde :1𝑐2𝜕2𝐹𝑥,𝑡𝜕𝑡2𝜕2𝐹𝑥,𝑡𝜕𝑥2= 0D’où la relation de dispersion : 𝜔2𝑐2 𝑘2 = 0 ⟹𝜔2 = 𝑘2𝑐2Les modes propres :𝝓𝒋,𝒌± = 𝒆±𝒊𝝎𝒋𝒌𝒕𝒌𝒙𝜙𝑗,𝑘±𝑥, 𝑡= 𝜙𝑗,𝑘±𝑥+ 𝜆, 𝑡= 𝜙𝑗,𝑘±𝑥, 𝑡+ 𝜏Avec 𝜆=2𝜋𝐾: longueur d’onde et 𝜏: période

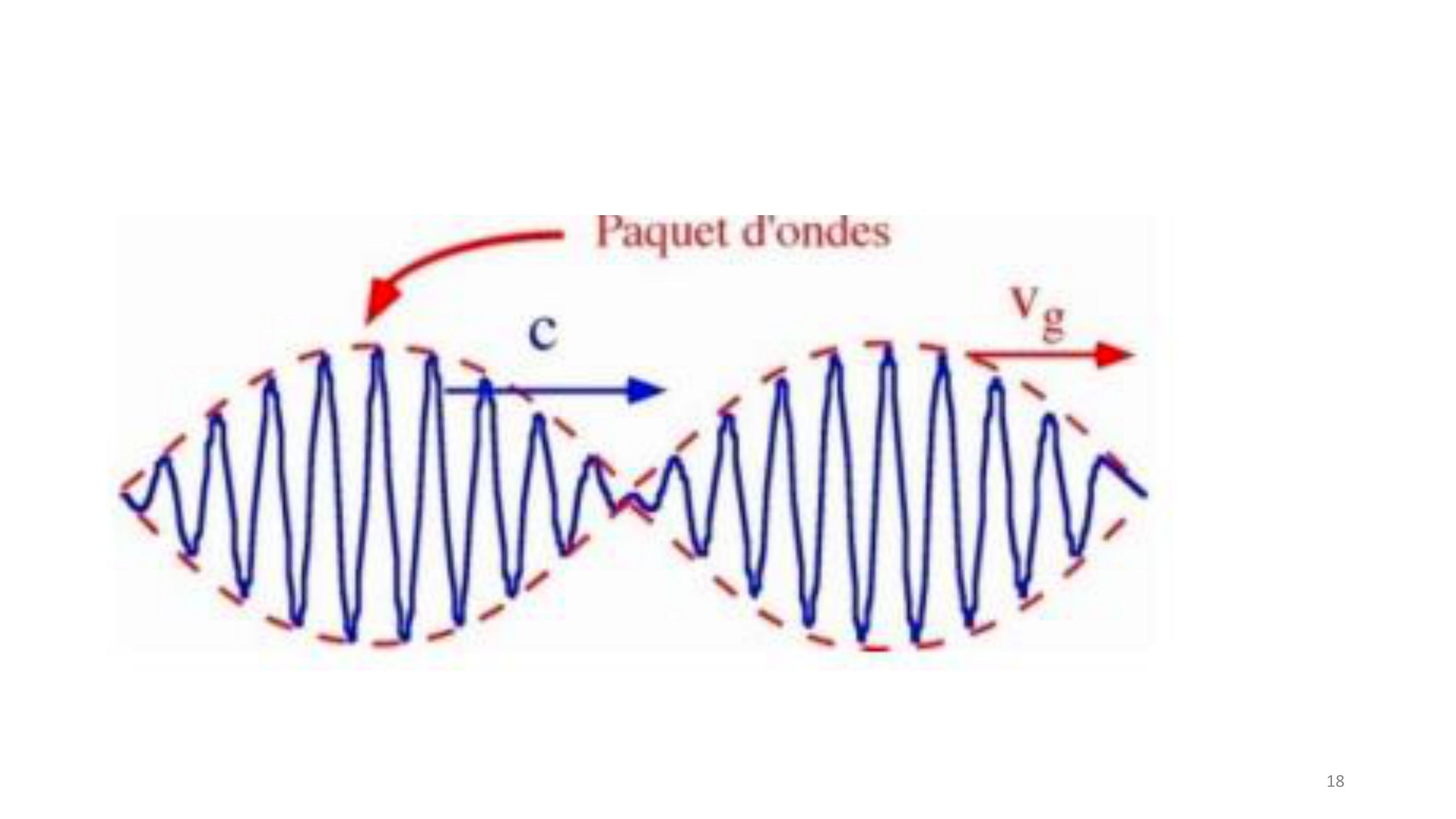
Page 16 : 16D’autre part, 𝜙𝑗,𝑘±𝑥+ Δ𝑥, 𝑡+ Δ𝑡= 𝑒±𝑖𝜔𝑗𝑡𝐾𝑥𝑒±𝑖𝜔𝑗Δ𝑡𝐾Δ𝑥 = 𝜙𝑗,𝑘±𝑥, 𝑡⟺Δ𝑥Δ𝑡=𝜔𝑗𝐾= vitesse de phaseVitesse de groupe :Le rapport 𝜔𝑗𝐾a les unités d’une vitesse et 𝜕𝜔𝑗𝜕𝐾aussi ! c’est la vitesse de groupe, mais que mesure –t-elle ?Pour Δ𝑘petit 𝜙𝑗,𝑘+Δ𝑘±𝑥, 𝑡 = 𝑒±𝑖𝜔𝑗𝑘+Δ𝑘𝑡𝑘+Δ𝑘𝑥 𝑒±𝑖𝜔𝑗𝑘𝑡𝑘𝑥𝑒±𝑖Δ𝑘𝜕𝜔𝑗𝜕𝑘𝑡𝑥⟹le terme 𝑒±𝑖Δ𝑘𝜕𝜔𝑗𝜕𝑘𝑡𝑥 correspond à une onde se déplaçant à la vitesse :𝜕𝜔𝑗𝜕𝑘

Page 17 : 17Vitesse de groupeSoient deux ondes progressives𝜙1 = cos𝜔1𝑡𝑘1𝑥, 𝜔𝑖= 𝜔𝑘𝑖𝜙2 = cos𝜔2𝑡𝑘2𝑥⟹𝜙1 + 𝜙2= 2𝑐𝑜𝑠𝜔1 + 𝜔22𝑡𝑘1 + 𝑘22𝑥. 𝑐𝑜𝑠𝜔1 𝜔22𝑡𝑘1 𝑘22𝑥.𝑜𝑛𝑑𝑒𝑑𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝜔1 + 𝜔2𝑘1 + 𝑘2. 𝑜𝑛𝑑𝑒𝑑𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝜔1 𝜔2𝑘1 𝑘2Ce dernier facteur est l’enveloppe

Page 18 : 18

Page 19 : 19Section 4.2.1 : conditions aux bords/limitesLes ED doivent être accompagnées par des conditions aux bords /limites pour avoir une solution bien définie :Dirichlet : 𝐹𝑎, 𝑡= 𝛼, 𝐹𝑏, 𝑡= 𝛽,𝑥𝑎, 𝑏Neumann :𝜕𝐹𝜕𝑥𝑎, 𝑡= 𝛼,𝜕𝐹𝜕𝑥𝑏, 𝑡= 𝛽Mixte : mélange !Il est évident que si 𝐹1 𝑒𝑡𝐹2 sont les solutions de l’équation différentielle linéaire telle que ቊ𝐹1 𝑎, 𝑡= 𝛼, 𝐹1 𝑏, 𝑡= 𝛽𝐹2 𝑎, 𝑡= 0, 𝐹2 𝑏, 𝑡= 0Alors 𝐹1 +𝐹2 𝑒𝑠𝑡𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑑𝑒𝑙′𝐸𝐷avec les conditions aux bords vérifiées par les premières équations du système ci-dessus.

Page 20 : 20Commençons par l’étude des cas : 𝛼= 𝛽= 0 !On considère 𝜙𝑘𝑥, 𝑡= σ𝑗=1𝑁𝑟𝑛𝑒𝑖𝜔𝑗𝑡𝑘𝑥 + 𝑠𝑛𝑒𝑖𝜔𝑗𝑡𝑘𝑥On veut résoudre pour 𝑟𝑛𝑒𝑡𝑠𝑛!⟹𝜙𝑘𝑎, 𝑡= 𝑒𝑖𝑘𝑎෍𝑗=1𝑁𝑟𝑛𝑒𝑖𝜔𝑗𝑡+ 𝑒𝑖𝑘𝑎෍𝑗=1𝑁𝑠𝑛𝑒𝑖𝜔𝑗𝑡= 0Equation d’onde : 𝜔1 = 𝜔2 = 𝜔𝑘,𝑁= 2⟹𝜙𝑘𝑎, 𝑡= 𝑒𝑖𝜔𝑡𝑟1𝑒𝑖𝑘𝑎+ 𝑠2𝑒𝑖𝑘𝑎+ 𝑒𝑖𝜔𝑡𝑟2𝑒𝑖𝑘𝑎+ 𝑠1𝑒𝑖𝑘𝑎= 0⟺൝𝑟1 = 𝑠2𝑒2𝑖𝑘𝑎𝑟2 = 𝑠1𝑒2𝑖𝑘𝑎Mais 𝜙𝑘𝑏, 𝑡= 0 ⟺൝𝑟1 = 𝑠2𝑒2𝑖𝑘𝑏𝑟2 = 𝑠1𝑒2𝑖𝑘𝑏

Page 21 : 21⟹𝑒2𝑖𝑘𝑏𝑎= 1⟹𝑘𝑛=𝑛𝜋𝑏𝑎,𝑛𝑍⟹𝜙𝑛= 𝑠𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡avec 𝜔= 𝜔𝑛𝜋𝑏𝑎= 𝜔𝑛⟹𝐹𝑥, 𝑡= ෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡𝑠é𝑟𝑖𝑒𝑑𝑒𝐹𝑜𝑢𝑟𝑟𝑖𝑒𝑟𝐹𝑎, 𝑡= 𝐹𝑏, 𝑡= 0Mais il nous manque une solution particulière de l’ED avec :𝐹𝑎, 𝑡= 𝛼𝑡𝑒𝑡𝐹𝑏, 𝑡= 𝛽𝑡

Page 22 : 22Or de telles solutions dépendent trop de l’équation différentielle ED !Par des arguments similaires, les conditions de Neumann homogène donnent :𝐹𝑥, 𝑡= ෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡: 𝑠é𝑟𝑖𝑒𝑑𝑒𝐹𝑜𝑢𝑟𝑟𝑖𝑒𝑟቉𝜕𝐹𝜕𝑥𝑥=𝑎=቉𝜕𝐹𝜕𝑥𝑥=𝑏= 0

Page 23 : 23Section 4.2.2 : conditions initialesEn plus des bords en x, il faut donner les conditions aux bords en t les conditions initiales :ቐ𝐹𝑥, 0 = 𝑓𝑥𝜕𝐹𝑥, 0𝜕𝑡= 𝑔𝑥En supposant la solution:𝐹𝑥, 𝑡= σ𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡On veut alors résoudre :1෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛= 𝑓𝑥2෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑖𝜔𝐴𝑛𝑖𝜔𝐵𝑛= 𝑔𝑥

Page 24 : 24Recherche des 𝑨𝒏𝒆𝒕𝑩𝒏:Multiplions l’équation 1 par 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎:1 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛= 𝑓𝑥𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎Intégrons entre a et b:1⟹σ𝑛=1׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥

Page 25 : 25Proposition : ׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎 𝑑𝑥=𝑏𝑎2𝛿𝑛,𝑚𝛿𝑛,𝑚= ቊ1 𝑠𝑖𝑛= 𝑚0 𝑠𝑖𝑛𝑜𝑛1⟹σ𝑛=1׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥⟹෍𝑛=1𝑏𝑎2𝛿𝑛,𝑚𝐴𝑛+ 𝐵𝑛= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥

Page 26 : 26⟹𝐴𝑛+ 𝐵𝑛=2𝑏𝑎න𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥2⟹෍𝑛=1න𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑖𝜔𝑛𝐴𝑛𝑖𝜔𝑛𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥⟹𝑏𝑎2𝑖𝜔𝑚𝐴𝑚𝐵𝑚= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥

Page 27 : 27Neumann En supposant : 𝐹𝑥, 𝑡= σ𝑛=0𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑛𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑛𝑡ቐ𝐹𝑥, 0 = 𝑓𝑥𝜕𝐹𝑥, 0𝜕𝑡= 𝑔𝑥Et en utilisant ׬𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎 𝑐𝑜𝑠𝑚𝜋𝑏𝑎𝑥𝑎 𝑑𝑥=𝑏𝑎2𝛿𝑚,𝑛On a :

Page 28 : 28𝐴𝑛+ 𝐵𝑛=2𝑏𝑎න𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥𝐴𝑛𝐵𝑛=2𝑏𝑎1𝑖𝜔𝑛න𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥

Page 29 : 29Exemple : corde pincéeOn veut résoudre l’équation d’onde :1𝑐2𝜕2𝐹𝑋, 𝑡𝜕𝑡2𝜕2𝐹𝑋, 𝑡𝜕𝑋2= 0Avec les conditions initiales : 𝐹0, 𝑡= 𝐹𝐿, 𝑡= 01𝐹𝑥, 0 = ቊ𝑥𝑠𝑖𝑥 𝐿/2𝐿𝑥𝑠𝑖𝑥𝐿/2𝐹𝑥, 02𝜕𝐹𝑥, 0𝜕𝑡= 0

Page 30 : 30⟹𝑭𝒙, 𝒕= σ𝒏=𝟏𝒔𝒊𝒏𝒏𝝅𝒙𝑳𝑨𝒏𝒆𝒊𝝎𝒏𝒕+ 𝑩𝒏𝒆𝒊𝝎𝒏𝒕𝑎𝑣𝑒𝑐𝜔𝑛= 𝜔𝑛𝜋𝐿2⟹𝐴𝑛= 𝐵𝑛1⟹𝐴𝑛+ 𝐵𝑛= 2𝐿න0𝐿𝑠𝑖𝑛𝑛𝜋𝐿𝑥𝐹𝑥, 0 𝑑𝑥= 2𝐿න0𝐿2𝑠𝑖𝑛𝑛𝜋𝐿𝑥. 𝑥𝑑𝑥+ න𝐿2𝐿𝑠𝑖𝑛𝑛𝜋𝐿𝑥. 𝐿𝑥𝑑𝑥

Page 31 : 31න0𝐿2𝑠𝑖𝑛𝑛𝜋𝐿𝑥. 𝑥𝑑𝑥= 𝐿𝑛𝜋𝑐𝑜𝑠𝑛𝜋𝐿𝑥0𝐿2 + න0𝐿2𝑐𝑜𝑠𝑛𝜋𝐿𝑥𝑑𝑥=𝐿𝑛𝜋2𝑠𝑖𝑛𝑛𝜋𝐿𝑥0𝐿2E =𝐿𝑛𝜋2𝑠𝑖𝑛𝑛𝜋2……𝐴𝑛+ 𝐵𝑛=8𝐿𝑛2𝜋2 𝑠𝑖𝑛2 𝑛𝜋4 𝑠𝑖𝑛𝑛𝜋2 = 0 𝑠𝑖𝑛= 2𝑘+ 1

Page 32 : 322⟹𝐴𝑛= 𝐵𝑛= 𝐴𝑛+ 𝐵𝑛2=4𝐿2𝑘+ 1 2𝜋2 𝑠𝑖𝑛2 𝑘𝜋2 + 𝜋4 sin 𝑘𝜋+ 𝜋2Avec 𝑠𝑖𝑛2𝑘𝜋2 +𝜋4=12𝑒𝑡sin 𝑘𝜋+𝜋2= 1𝑘⟹𝐴𝑛= 𝐵𝑛=2𝐿1 𝑘2𝑘+ 1 2𝜋2 ,n = 2k + 1Finalement :𝐹𝑥, 𝑡= σ𝑘=04𝐿1𝑘2𝑘+1 2𝜋2 sin 2𝑘+ 1𝜋𝑥𝐿𝑐𝑜𝑠𝜔2𝑘+1 𝜋𝐿𝑡

Page 33 : 33Section 4.2.3 : conditions aux bords inhomogènes périodiquesConsidérons le cas où 𝐹𝑎, 𝑡= 𝛼𝑡,𝐹𝑏, 𝑡= 𝛽𝑡et𝛼𝑡+ 𝜏𝑎= 𝛼𝑡,𝛽𝑡+ 𝜏𝑏= 𝛽𝑡C’àd 𝛼est périodique de période 𝜏𝑎et 𝛽est périodique de période 𝜏𝑏.On applique le principe de superposition, on pose 𝐹= 𝐹𝑎+ 𝐹𝑏où𝐹𝑎𝑎, 𝑡= 𝛼𝑡, 𝐹𝑎𝑏, 𝑡= 0𝐹𝑏𝑎, 𝑡= 0, 𝐹𝑏𝑏, 𝑡= 𝛽𝑡

Page 34 : 34On commence par 𝐹𝑎:On sait que la condition en b 𝐹𝑎𝑏, 𝑡= 0 implique que la solution est de la forme :𝐹𝑎𝑥, 𝑡= ෍𝑘=0𝑆𝑖𝑛𝑘𝑏𝑥𝐴𝑘𝑒𝑖𝜔𝑘𝑡+ 𝐵𝑘𝑒𝑖𝜔𝑘𝑡Avec 𝐹𝑎𝑎, 𝑡= 𝛼𝑡⟹෍𝑘=0𝑆𝑖𝑛𝑘𝑏𝑎𝐴𝑘𝑒𝑖𝜔𝑘𝑡+ 𝐵𝑘𝑒𝑖𝜔𝑘𝑡= 𝛼𝑡Or , 𝛼𝑡+ 𝜏𝑎= 𝛼𝑡à t=0 : 𝛼0 = 𝛼𝜏𝑎⟹෍𝑘=0𝑆𝑖𝑛𝑘𝑏𝑎𝐴𝑘+ 𝐵𝑘= ෍𝑘=0𝑆𝑖𝑛𝑘𝑏𝑎𝐴𝑘𝑒𝑖𝜔𝑘𝜏𝑎+ 𝐵𝑘𝑒𝑖𝜔𝑘𝜏𝑎

Page 35 : 35P𝑎𝑟𝑖𝑑𝑒𝑛𝑡𝑖𝑓𝑖𝑐𝑎𝑡𝑖𝑜, 𝑜𝑛𝑎𝐴𝑘+ 𝐵𝑘= 𝐴𝑘𝑒𝑖𝜔𝑘𝜏𝑎+ 𝐵𝑘𝑒𝑖𝜔𝑘𝜏𝑎⟹𝐴𝑘1 𝑒𝑖𝜔𝑘𝜏𝑎= 𝐵𝑘𝑒𝑖𝜔𝑘𝜏𝑎1 𝑒𝑖𝜔𝑘𝜏𝑎𝑠𝑜𝑖𝑡𝐴𝑘= 𝐵𝑘𝑒𝑖𝜔𝑘𝜏𝑎𝑑′𝑜ù𝐵𝑘= 𝐴𝑘𝑒𝑖𝜔𝑘𝜏𝑎Posons Γ𝑘= 2𝐴𝑘𝑒𝑖𝜔𝑘𝜏𝑎2⟹𝐴𝑘= Γ𝑘2 𝑒𝑖𝜔𝑘𝜏𝑎2𝐵𝑘= Γ𝑘2 𝑒𝑖𝜔𝑘𝜏𝑎2

Page 36 : 36⟹𝐴𝑘𝑒𝑖𝜔𝑘𝑡+ 𝐵𝑘𝑒𝑖𝜔𝑘𝑡= Γ𝑘2 𝑒𝑖𝜔𝑘𝑡𝜏𝑎2 +𝑒𝑖𝜔𝑘𝑡𝜏𝑎2 = Γ𝑘cos𝜔𝑘𝑡𝜏𝑎2 ⟹cos 𝜔𝑘𝑡𝜏𝑎2= cos 𝜔𝑘𝑡+ 𝜏𝑎2𝑐𝑎𝑟𝛼𝑡𝑒𝑠𝑡𝑝é𝑟𝑖𝑜𝑑𝑖𝑞𝑢𝑒𝑑𝑒𝑝é𝑟𝑖𝑜𝑑𝑒𝜏𝑎⟹𝑐𝑜𝑠𝜔𝑘𝑡 cos 𝜔𝑘𝜏𝑎2+ 𝑠𝑖𝑛𝜔𝑘𝑡 sin 𝜔𝑘𝜏𝑎2=𝑐𝑜𝑠𝜔𝑘𝑡 cos 𝜔𝑘𝜏𝑎2𝑠𝑖𝑛𝜔𝑘𝑡 sin 𝜔𝑘𝜏𝑎2⟹sin 𝜔𝑘𝜏𝑎2= 0 ⟹𝜔𝑘= 2𝑛𝜋𝜏𝑎

Page 37 : 37𝐹𝑎𝑥, 𝑡= ෍𝑛𝑠𝑖𝑛𝑘𝑛𝑏𝑥𝑠𝑖𝑛𝑘𝑛𝑏𝑎𝑎𝑛𝑐𝑜𝑠𝜔𝑛𝑡 + 𝑏𝑛𝑠𝑖𝑛𝜔𝑛𝑡à 𝑗𝑢𝑠𝑡𝑖𝑓𝑖𝑒𝑟𝑘𝑛tel que 𝜔𝑛𝑘𝑛 =2𝑛𝜋𝜏𝑎𝐹𝑎𝑎, 𝑡= ෍𝑛𝑎𝑛cos2𝑛𝜋𝜏𝑎𝑡 + 𝑏𝑛sin2𝑛𝜋𝜏𝑎𝑡= 𝛼𝑡⟹𝑎𝑛= 2𝜏𝑎න0𝜏𝑎cos2𝑛𝜋𝜏𝑎𝑡 𝛼𝑡𝑑𝑡𝑏𝑛= 2𝜏𝑎න0𝜏𝑎sin2𝑛𝜋𝜏𝑎𝑡 𝛼𝑡𝑑𝑡

Page 38 : 38Ex 1 : 𝛼𝑡= 𝑠𝑖𝑛𝜔𝑎𝑡⟹𝜏𝑎= 2𝜋𝜔𝑎⟹𝑎𝑛= 2𝜔𝑎2𝜋න02𝜋𝜔𝑎cos 𝑛𝜔𝑎𝑡sin 𝜔𝑎𝑡𝑑𝑡= 0𝑏𝑛= 2𝜔𝑎2𝜋න02𝜋𝜔𝑎sin 𝑛𝜔𝑎𝑡sin 𝜔𝑎𝑡𝑑𝑡= 𝛿𝑛,1⟹𝐹𝑎𝑥, 𝑡= 𝑠𝑖𝑛𝑘𝑏𝑥𝑠𝑖𝑛𝑘𝑏𝑎 𝑠𝑖𝑛𝜔𝑎𝑡K est tel que 𝜔𝑘= 𝜔𝑎

Page 39 : 39EXE 2 : 𝛼𝑡= 𝑡figure𝜔𝑘= 𝜔𝑎= 𝑘, 𝜏𝑎= 1𝑎𝑛= 2 ׬01 cos 2𝑛𝜋𝑡t𝑑𝑡= 1 𝑠𝑖𝑛= 0 𝑒𝑡0 𝑠𝑖𝑛0𝑏𝑛= 2 න01sin 2𝑛𝜋𝑡t𝑑𝑡= 12𝑛𝜋⟹𝐹𝑎𝑥, 𝑡= 12 + ෍𝑛=1𝑠𝑖𝑛𝑘𝑛𝑏𝑥𝑠𝑖𝑛𝑘𝑛𝑏𝑎 12𝑛𝜋sin2𝑛𝜋𝑡 𝑑𝑡

Page 40 : 40Section 4.3 Ondes en milieux semi-infinisFigure + 2 ème loi de newtonOn considère une onde transversale se propageant le long d’une corde, le long de l’axe des x positifs x=0 à l’infini.1𝑐2𝜕2𝐹𝑥,𝑡𝜕𝑡2𝜕2𝐹𝑥,𝑡𝜕𝑥2= 0 𝑥 0, 𝑐2 =𝑇0𝜇où 𝑇0 est la tension de la corde en N et 𝜇sa masse linéique en 𝑘𝑔. 𝑚1.Figure P45La solution générale d’une telle équation différentielle est donnée par :

Page 41 : 41𝐹𝑥, 𝑡= 𝐺+ 𝑐𝑡+ 𝑥+ 𝐺𝑐𝑡𝑥, 𝐺+ 𝑒𝑡𝐺sont des fonctions arbitraires où 𝐺+ est l’onde qui se propage vers les x décroissants vers mois l’infini et 𝐺est celle qui se propage vers plus l’infini.Admettons que 𝐺+ est connue : une onde que nous avons générée et qui se propage vers les x0.Pour les conditions de Dirichlet F0,t = 0 on a : 𝐹0, 𝑡= 𝐺+ 𝑐𝑡+ 𝐺𝑐𝑡= 0 ⟹𝐺+ 𝑐𝑡= 𝐺𝑐𝑡⟹𝐹𝑥, 𝑡= 𝐺+ 𝑐𝑡+ 𝑥𝐺+ 𝑐𝑡𝑥, 𝐺+ 𝑐𝑡+ 𝑥étant l’onde incidente et 𝐺+ 𝑐𝑡𝑥est l’onde réfléchie. 𝐺𝑧= 𝑅𝐺+ 𝑧, R est le facteur de réflexion de l’onde incidente, R=-1 il s’agit d’une réflexion dure extrémité fixe.

Page 42 : 42Pour les conditions de Neumann : ቃ𝜕𝐹0,𝑡𝜕𝑥𝑥=0 = 0 on a :𝐺′+ 𝑐𝑡𝐺′𝑐𝑡= 0 ⟹𝐺′+ 𝑐𝑡= 𝐺′𝑐𝑡⟹𝐺𝑐𝑡𝑥= 𝐺+ 𝑐𝑡+ 𝑥+ ConstanteCette constante est nulle si la corde est au repos.⟹𝑅= 1 0: 𝑟é𝑓𝑙𝑒𝑥𝑖𝑜𝑛𝑑𝑢𝑟𝑒Si on suppose plutôt des conditions hybrides :𝛼𝐹𝑡, 0 + 𝛽቉𝜕𝐹𝑥, 𝑡𝜕𝑥𝑥=0= 0

Page 43 : 43Il est alors plus difficile de répondre. Prenons par exemple𝐺+ 𝑧= 𝐴+𝑒𝑖𝑘𝑧, 𝐺𝑧= 𝐴𝑒𝑖𝑘𝑧𝐺+ 𝑐𝑡+ 𝑥= 𝐴+𝑒𝑖𝑘𝑐𝑡+𝑘𝑥, 𝑎𝑣𝑒𝑐𝑘𝑐= 𝜔⟹𝛼𝐴+ + 𝛽𝑖𝑘𝐴+ + 𝛼𝐴𝛽𝑖𝑘𝐴= 0𝐴= 𝐴+𝛼+ 𝛽𝑖𝑘𝛼+ 𝛽𝑖𝑘⟹𝑅𝑘= 𝛼+ 𝛽𝑖𝑘𝛼+ 𝛽𝑖𝑘= 𝛽2𝑘2 𝛼2𝛽2𝑘2 + 𝛼2 2𝑖𝛼𝛽𝑘𝛽2𝑘2 + 𝛼2

Page 44 : 44EXE : 𝛼= 𝛽= 1⟹𝑅𝑘= 𝑘2 1𝑘2 + 1 2𝑖𝑘𝑘𝑘2 + 1⟹𝑠𝑖𝐺+ 𝑐𝑡+ 𝑥= sin 𝜔𝑡+ 𝑘𝑥= 𝐼𝑚𝑒𝑖𝑘𝑐𝑡+𝑘𝑥𝜔= 𝑘𝑐⟹𝐺𝑧= 𝑘2 1𝑘2 + 1 sin 𝑘𝑧2𝑘𝑘𝑘2 + 1 cos 𝑘𝑧𝐺𝑐𝑡𝑘𝑥= 𝑘2 1𝑘2 + 1 sin 𝜔𝑡𝑘𝑥2𝑘𝑘𝑘2 + 1 cos 𝜔𝑡𝑘𝑥

Page 45 : 45Section 4.3.1 : Interfaces entre milieux semi-infinisOn considère deux milieux semi-infinis se rejoignant à une interface :Le domaine 1 D1 correspond à 𝑥0, dans lequel les ondes se propagent à la vitesse 𝑐1.Le domaine 2 D2 correspond à 𝑥 0, dans lequel les ondes se propagent à la vitesse 𝑐2.Les ondes 𝐹1 𝑒𝑡𝐹2 qui s’y propagent satisfont les équations d’ondes :1𝑐12𝜕2𝐹1 𝑥,𝑡𝜕𝑡2𝜕2𝐹1 𝑥,𝑡𝜕𝑥2= 0et 1𝑐22𝜕2𝐹2 𝑥,𝑡𝜕𝑡2𝜕2𝐹2 𝑥,𝑡𝜕𝑥2= 0Avec 𝐹1 0, 𝑡= 𝐹2 0, 𝑡et ቚ𝜕𝐹1𝑥,𝑡𝜕𝑥𝑥=0 =ቚ𝜕𝐹2𝑥,𝑡𝜕𝑥𝑥=0

Page 46 : 46D’où 𝐹1 𝑥, 𝑡= 𝐺+1 𝑐1𝑡+ 𝑥+ 𝐺1 𝑐1𝑡𝑥Et 𝐹2 𝑥, 𝑡= 𝐺+2 𝑐2𝑡+ 𝑥+ 𝐺2 𝑐2𝑡𝑥On s’intéresse au cas particulier où 𝐺+1 𝑐1𝑡+ 𝑥est connue et 𝐺2 𝑐2𝑡𝑥= 0,c’est-à-dire que l’onde incidente qui provient de + : 𝐺+1 𝑐1𝑡+ 𝑥est connue. Elle donne lieu :A une onde réfléchie en x=0 : 𝐺1 𝑐1𝑡𝑥, qui retourne vers +Et une onde transmise qui se dirige vers : 𝐺+2 𝑐2𝑡+ 𝑥.

Page 47 : 47Exemple : 𝐺+1 𝑧= 𝐴𝑒𝑖𝑘1𝑧, 𝐺1 𝑧= 𝐴𝑅𝑒𝑖𝑘1𝑧et 𝐺+2 𝑧= 𝐴𝑇𝑒𝑖𝑘2𝑧La continuité de l’onde en z=0 impose:𝐺+1 𝑐1𝑡+ 𝐺1 𝑐1𝑡= 𝐴𝑒𝑖𝜔1𝑡+ 𝐴𝑅𝑒𝑖𝜔1𝑡= 𝐴𝑇𝑒𝑖𝜔2𝑡𝜔1 = 𝑐1𝑘1 𝑒𝑡𝜔2 = 𝑐2𝑘2⟹𝐴+ 𝐴𝑅 = 𝐴𝑇𝑒𝑖𝜔2𝜔1𝑡Les trois termes 𝐴𝑅, 𝐴𝑇𝑒𝑡𝐴sont indépendants du temps⟹𝜔2 = 𝜔1 ⟹𝐴+ 𝐴𝑅= 𝐴𝑇

Page 48 : 48ቚ𝜕𝑥𝐺+1 𝑐1𝑡+ 𝑥+ 𝜕𝑥𝐺1 𝑐1𝑡𝑥𝑥=0 = 𝐴𝑖𝑘1𝑒𝑖𝜔1𝑡𝐴𝑅𝑖𝑘1𝑒𝑖𝜔1𝑡=ቚ𝜕𝑥𝐺+2 𝑐2𝑡+ 𝑥𝑥=0 = 𝐴𝑇𝑖𝑘2𝑒𝑖𝜔2𝑡⟹𝑘1𝑘2 =𝐴𝑇𝐴𝐴𝑅a𝜔2 = 𝜔1 ⟹𝑘1𝑐1 = 𝑘2𝑐2 ⟹𝑘1𝑘2 =𝑐1𝑐2 b© 𝐴+ 𝐴𝑅= 𝐴𝑇⟹𝐴𝑇𝐴= 1 +𝐴𝑅𝐴Les trois conditions a, b et c ⟹𝑹= 𝐴𝑅𝐴= 𝑐2 𝑐1𝑐2 + 𝑐1𝑒𝑠𝑡𝑙𝑒𝑐𝑜𝑒𝑓𝑓. 𝑑𝑒𝑟é𝑓𝑙𝑒𝑥𝑖𝑜𝑛𝑻= 𝐴𝑇𝐴=2𝑐2𝑐2 + 𝑐1𝑒𝑠𝑡𝑙𝑒𝑐𝑜𝑒𝑓𝑓. 𝑑𝑒𝑡𝑟𝑎𝑛𝑠𝑚𝑖𝑠𝑠𝑖𝑜𝑛

Page 49 : 49Remarque : Si les milieux sont dispersifs, on peut faire la même chose.Si 𝑐2 𝑐1 , 𝑅 0 ⟹c’est une réflexion molle !Si 𝑐2 𝑐1 , 𝑅 0 ⟹c’est une réflexion dure !

Page 50 : 50Section 4.3.2 : Bord inhomogèneOn considère le cas d’une source immobile à l’origine, c’à d on a la condition aux bords : 𝐹0, 𝑡= 𝑆𝑡L’axe des x est considéré comme deux milieux semi-infinis, se rencontrant en x=0.⟹𝐹𝑥, 𝑡= ൝𝐺+1 𝑐𝑡+ 𝑥+ 𝐺1 𝑐𝑡𝑥𝑥0𝐺+2 𝑐𝑡+ 𝑥+ 𝐺2 𝑐𝑡𝑥𝑥 0On suppose que S est la seule source d’ondes, donc pas d’ondes provenant de l’infini : 𝐺+1= 𝐺2= 0, d’où les conditions au bord : 𝐺+2 𝑐𝑡= 𝑆𝑡= 𝐺1 𝑐𝑡

Page 51 : 51𝐺+2 𝑐𝑡+ 𝑥= 𝑆𝑡+ 𝑥𝑐𝐺1 𝑐𝑡𝑥= 𝑆𝑡𝑥𝑐⟹𝐹𝑥, 𝑡=𝑆𝑡+ 𝑥𝑐𝑝𝑜𝑢𝑟𝑥 0𝑆𝑡𝑥𝑐𝑝𝑜𝑢𝑟𝑥0𝐹𝑥, 𝑡= 𝑆𝑡𝑥𝑐Dans le cas où la source est en mouvement, posons 𝐹𝑉𝑠𝑡, 𝑡= 𝑆𝑡où 𝑉𝑠est la vitesse de la source. ⟹𝐹𝑥, 𝑡= ቊ𝐺𝑐𝑡𝑥𝑠𝑖𝑥𝑉𝑠𝑡𝐺+ 𝑐𝑡+ 𝑥𝑠𝑖𝑥 𝑉𝑠𝑡

Page 52 : 52⟹𝐺𝑐𝑉𝑠𝑡= 𝑆𝑡= 𝐺+𝑐+ 𝑉𝑠𝑡⟹𝐺𝑐𝑡𝑥= 𝑆𝑐𝑡𝑥𝑐𝑉𝑠𝐺+ 𝑐𝑡+ 𝑥= 𝑆𝑐𝑡+ 𝑥𝑐+ 𝑉𝑠EX𝑺𝒕= 𝒔𝒊𝒏𝝎𝟎𝒕onde se propageant vers les x croissants⟹𝐺𝑐𝑡𝑥= sin 𝜔0𝑐𝑡𝑥𝑐𝑉𝑠𝐺𝑐𝑡𝑥= sin𝜔0𝑡1 𝑉𝑠𝑐𝜔0𝑥𝑐𝑉𝑠

Page 53 : 53⟹𝑜𝑛𝑑𝑒𝑑𝑒𝑝𝑢𝑙𝑠𝑎𝑡𝑖𝑜𝑛𝜔=𝜔01𝑉𝑠𝑐et de longueur d’onde 𝜆= 𝜆01 𝑉𝑠𝑐𝐺+ 𝑐𝑡+ 𝑥= sin 𝜔0𝑐𝑡+ 𝑥𝑐+ 𝑉𝑠= sin𝜔0𝑡1 + 𝑉𝑠𝑐+ 𝜔0𝑐𝑥1 + 𝑉𝑠𝑐⟹𝑜𝑛𝑑𝑒𝑑𝑒𝑝𝑢𝑙𝑠𝑎𝑡𝑖𝑜𝑛𝜔=𝜔01+𝑉𝑠𝑐et de longueur d’onde 𝜆= 𝜆01 +𝑉𝑠𝑐C’est l’effet DopplerRemarque : 𝜔0𝜆0 = 2𝜋𝑐= 𝜆𝜔⟹les deux ondes ont la même vitesse de phase, c.

Page 54 : 54Section 4.3.3 : interface massiveOn considère deux cordes semi-infinies, de densité linéique de masse 𝜇1𝑒𝑡𝜇2, s’étendant chacune sur l’axe des x de part et d’autre de l’origine. Au point x=0, elles sont attachées à un anneau de masse m libre de glisser sans frottements le long d’une tige verticale :Fifure 1

Page 55 : 55On considère une onde 𝜙𝑖arrivant de se déplace vers + et on veut connaitre l’onde réfléchie 𝜙𝑟et transmise 𝜙𝑡.On suppose que les oscillations transversales de la corde sont dans le plan de la tige :Figure 2 :On suppose que 𝜙𝑖= 𝐴𝑖𝑒𝑖𝑘1 𝑐1𝑡𝑥, 𝜙𝑟= 𝐴𝑟𝑒𝑖𝑘1 𝑐1𝑡+𝑥,𝜙𝑡= 𝐴𝑡𝑒𝑖𝑘2 𝑐2𝑡𝑥L’onde doit être continue en x=0 : 𝐴𝑖𝑒𝑖𝑘1 𝑐1𝑡+ 𝐴𝑟𝑒𝑖𝑘1 𝑐1𝑡= 𝐴𝑡𝑒𝑖𝑘2 𝑐2𝑡⟹𝑘1𝑐1 = 𝑘2𝑐2,1 + 𝐴𝑟𝐴𝑖= 𝐴𝑡𝐴𝑖

Page 56 : 56Or l’anneau a une masse non nulle, la dérivée par rapport à x n’est pas nécessairement continue !!EX : si 𝑀⟶, l’anneau est immobile ⟹𝜙𝑡𝑜𝑡0, 𝑡= 0 ⟹𝐴𝑡= 0𝐴𝑟= 𝐴𝑖⟹il nous faut l’équation du mouvement de l’anneau !⟹on doit connaitre la force exercée par les ondes sur l’anneau.Approche intuitive :La déformation 𝜙𝑥, 𝑡 est homogène à une distance

Page 57 : 57⟹𝜕𝜙𝑥, 𝑡𝜕𝑡= 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒𝑡𝑒𝑚𝑝𝑠= 𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝜕𝜙𝑥, 𝑡𝜕𝑥= 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒= 𝑒𝑥𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛𝑠𝑎𝑛𝑠𝑢𝑛𝑖𝑡éSi 𝜙est petite, on s’attends à ce que Ԧ𝐹soit proportionnelle à 𝜙Or Ԧ𝐹s’exprime en N soit 𝑀.𝐿𝑇2 =𝑑𝑒𝑛𝑠𝑖𝑡é 𝑙𝑖𝑛é𝑖𝑞𝑢𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒2⟹Ԧ𝐹= 𝛼𝜇𝑐2 𝜕𝜙𝑥, 𝑡𝜕𝑥+ 𝛽𝜇𝑐𝜕𝜙𝑥, 𝑡𝜕𝑡𝑢𝑦

Page 58 : 58Si on considère une onde 𝜙𝑥, 𝑡= 𝐺± 𝑐𝑡± 𝑥⟹Ԧ𝐹± = 𝛽𝜇𝑐2 ± 𝛼𝜇𝑐2 𝐺±′ 𝑢𝑦= 𝛽± 𝛼𝜇𝑐2𝐺±′ 𝑢𝑦𝜇𝑐2 = 𝑇0 : tension de la corde.𝛽± 𝛼= 𝑐𝑜𝑒𝑓. 𝑠𝑎𝑛𝑠𝑢𝑛𝑖𝑡é𝑠.𝑍= 𝜇𝑐=𝑇0𝑐𝑖𝑚𝑝é𝑑𝑎𝑛𝑐𝑒𝑑𝑒𝑙𝑎𝑐𝑜𝑟𝑑𝑒.Considérons le cas : 𝜙𝑥, 𝑡= 𝐴𝑒𝑐𝑡𝑥22figure 3𝜕𝜙𝜕𝑥= 𝑐𝑡𝑥𝐴𝑒𝑐𝑡𝑥22𝜕𝜙𝜕𝑡= 𝑐𝑐𝑡𝑥𝐴𝑒𝑐𝑡𝑥22⟹Ԧ𝐹= 𝑍𝑐𝜕𝜙𝜕𝑥𝑢𝑦fin de de cet exmple

Page 59 : 59Dans le cas de l’anneau, on a :Ԧ𝐹𝑔𝑎𝑢𝑐ℎ𝑒= 𝑍1𝑐1𝜕𝜙𝑖𝜕𝑥+ 𝜕𝜙𝑟𝜕𝑥𝑥=0. 𝑢𝑦= 𝑖𝑐1𝑍1 𝑘1𝐴𝑖+ 𝑘1𝐴𝑟𝑒𝑖𝑘1 𝑐1𝑡𝑢𝑦= 𝑖𝑐1𝑍1𝑘1𝐴𝑖1 𝐴𝑟𝐴𝑖𝑒𝑖𝑘1 𝑐1𝑡𝑢𝑦Ԧ𝐹𝑑𝑟𝑜𝑖𝑡𝑒= 𝑐2𝑍2𝜕𝜙𝑡𝜕𝑥𝑥=0. 𝑢𝑦= 𝑖𝑐2𝑍2𝑘2𝐴𝑡𝑒𝑖𝑘2 𝑐2𝑡𝑢𝑦𝑀Ԧ𝑎= 𝑀𝜕2𝜙𝜕2𝑡𝑢𝑦= 𝑘2𝑐22𝑀𝐴𝑡𝑒𝑖𝑘2 𝑐2𝑡𝑢𝑦⟹Ԧ𝐹𝑔𝑎𝑢𝑐ℎ𝑒Ԧ𝐹𝑑𝑟𝑜𝑖𝑡𝑒= 𝑀Ԧ𝑎

Page 60 : 60⟹𝑖𝑍1𝑘1𝐴𝑖𝑐1 1 𝐴𝑟𝐴𝑖𝑖𝑐2𝑍2𝑘2𝐴𝑡= 𝑘2𝑐22𝑀𝐴𝑡Avec 𝐴𝑟𝐴𝑖= 𝑅, 𝐴𝑡= 𝑇𝐴𝑖, 𝑘2𝑐2 = 𝜔⟹1 𝑅𝑐2𝑍2𝑘2𝑐1𝑍1𝑘1𝑇= 𝑖𝜔2𝑍1𝑘1𝑀𝑇, 𝑐𝑎𝑟1 𝑅= 2 𝑇⟹𝑇=21 + 𝑐2𝑍2𝑘2𝑐1𝑍1𝑘1 + 𝑖𝜔2𝑀𝑍1𝑘1,𝑅=1 𝑐2𝑍2𝑘2𝑐1𝑍1𝑘1 𝑖𝜔2𝑀𝑐1𝑍1𝑘11 + 𝑐2𝑍2𝑘2𝑐1𝑍1𝑘1 + 𝑖𝜔2𝑀𝑐1𝑍1𝑘1

Page 61 : 61Remarque :On peut ajouter un terme 𝛼𝜕𝜙𝜕𝑡 à la force, sans changer les équations du mouvement :Si Ԧ𝐹= 𝛼𝜕𝜙𝜕𝑡𝑍𝜕𝜙𝜕𝑥𝑢𝑦⟹𝑖𝑍1𝑘1𝑐1𝐴𝑖1 𝑅+ 𝑖𝜔𝛼𝐴𝑖+ 𝐴𝑟𝑖𝑐2𝑍2𝑘2𝐴𝑡+ 𝑖𝜔𝐴𝑡=…

Page 62 : 62Section 4.4 : Ondes et énergieOn considère les oscillations transversales d’une corde de densité linéique de masse 𝜇sous une tension 𝑇0.On se propose de déterminer la quantité d’énergie transportée par de telles ondes.L’énergie est homogène à :𝐸𝑚𝑎𝑠𝑠𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒2⟹La densité linéique d’énergie cinétique est donnée par:𝜀𝑐: densité linéique 𝑑𝑒𝑚𝑎𝑠𝑠𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒2

Page 63 : 63Posons la densité d’énergie sous la forme :𝜀= 𝛼𝜇𝑅é𝑒𝑙𝜕𝜙𝜕𝑡2+ 𝛽𝜇𝑐2𝑅𝑒𝜕𝜙𝜕𝑥2+ 𝛾𝜇𝑐𝑅é𝑒𝑙𝜕𝜙𝜕𝑡𝑅é𝑒𝑙𝜕𝜙𝜕𝑥𝜀= 2𝛼𝜀𝑐𝑖𝑛𝑒𝑡+ 2𝛽𝜀𝑝𝑜𝑡+ 𝛾𝜇𝑐? Signification du terme 𝛾𝜇𝑐? On a vu que 𝑍𝜕𝜙𝜕𝑥= force exercée par la corde⟹𝛾𝜇𝑐𝜕𝜙𝜕𝑡𝜕𝜙𝜕𝑥= 𝛾𝜕𝜙𝜕𝑡𝑍𝜕𝜙𝜕𝑥Expression où 𝜕𝜙𝜕𝑡est une vitesse et 𝑍𝜕𝜙𝜕𝑥est une forceOr force x vitesse = puissance

Page 64 : 64⟹𝑃𝑥, 𝑡= 𝑍𝜕𝜙𝜕𝑡𝜕𝜙𝜕𝑥, on ne considère que la partie réelle de 𝜙.𝜀= 𝑍2𝑐𝜕𝜙𝜕𝑡2+ 𝑐𝑍2𝜕𝜙𝜕𝑥2Le premier terme est égal à l’énergie cinétique et le second terme est égal à l’énergie potentielle.

Page 65 : 65EX : 𝜙𝑥, 𝑡= 𝐴𝑠𝑖𝑛𝜔𝑡± 𝑘𝑥, 𝜔= 𝑐𝑘𝜀𝑐𝑖𝑛𝑒𝑡= 𝑍2𝑐2 𝜔𝐴𝑐𝑜𝑠𝜔𝑡± 𝑘𝑥 2𝜀𝑝𝑜𝑡= 𝑍2 ±𝑘𝐴𝑐𝑜𝑠𝜔𝑡± 𝑘𝑥 2 = 𝜀𝑐𝑖𝑛𝑒𝑡𝑃𝑥, 𝑡= 𝑍𝜔𝐴𝑐𝑜𝑠𝜔𝑡± 𝑘𝑥±𝑘𝐴𝑐𝑜𝑠𝜔𝑡± 𝑘𝑥= ±𝑍𝜔2𝑐𝑐𝑜𝑠2 𝜔𝑡± 𝑘𝐴2 = ±𝜀𝑐𝑃 0 𝑜𝑛𝑑𝑒𝑣𝑒𝑟𝑠𝑥 0𝑃 0 𝑜𝑛𝑑𝑒𝑣𝑒𝑟𝑠𝑥 0

Page 66 : 66Section 4.5 : Ondes vectorielles –Les ondes électromagnétiques OELes OE sont des ondes vectorielles 𝐸, 𝐵I-Introduction:L’électromagnétisme est fondée sur les quatre équations de Maxwell et la force de Lorentz.Le champ électromagnétique est solution des quatre équations locales ci-dessous dont la justification, l’interprétation et le contenu physique feront l’objet de ce paragraphe.Les quatre équations de Maxwell : 𝑅𝑜𝑡𝐸= 𝜕𝐵𝜕𝑡,𝑅𝑜𝑡𝐵= 𝜇0Ԧ𝑗+ 𝜀0𝜇0𝜕𝐸𝜕𝑡,𝑑𝑖𝑣𝐸= 𝜌𝜀0𝑒𝑡𝑑𝑖𝑣𝐵= 0

Page 67 : 67Sur le plan historique, chacune de ces quatre équations a été étudiée séparément et a permis de rendre compte d’un phénomène physique donné.Maxwell a eu l’idée de les considérer comme un ensemble indissociable.Constantes et unités𝜇0est la perméabilité magnétique, elle caractérise la faculté d'un matériau à modifier un champ magnétique.𝜀0est la permittivité du vide. 𝒄=𝟏𝜇0𝜀0est la vitesse de la lumière dans le vide

Page 68 : 68Obtention des équations de propagation du champ EM : On calcule le rotationnel de l’équation de Maxwell-Faraday : 𝑅𝑜𝑡𝐸= 𝜕𝐵𝜕𝑡⟹𝑅𝑜𝑡𝑅𝑜𝑡𝐸= 𝑅𝑜𝑡𝜕𝐵𝜕𝑡= 𝜕𝑅𝑜𝑡𝐵𝜕𝑡Or 𝑅𝑜𝑡𝑅𝑜𝑡= 𝑔𝑟𝑎𝑑𝑑𝑖𝑣avec𝑅𝑜𝑡𝐵= 𝜇0Ԧ𝑗+ 𝜀0𝜇0𝜕𝐸𝜕𝑡et 𝑑𝑖𝑣𝐸=𝜌𝜀0⟹𝑔𝑟𝑎𝑑𝜌𝜀0 𝐸=𝜕𝜕𝑡𝜇0Ԧ𝑗+ 𝜀0𝜇0𝜕𝐸𝜕𝑡

Page 69 : 69Pour la propagation du champ magnétique on a:M.A : 𝑅𝑜𝑡𝐵= 𝜇0Ԧ𝑗+ 𝜀0𝜇0𝜕𝐸𝜕𝑡On applique l’opérateur rotationnel à M.A :𝑅𝑜𝑡𝑅𝑜𝑡𝐵= 𝑔𝑟𝑎𝑑𝑑𝑖𝑣𝐵Δ𝐵Or 𝑅𝑜𝑡𝐸= 𝜕𝐵𝜕𝑡d’où l’équation de propagation du champ magnétique :Δ𝐵𝜀0𝜇0𝜕2𝐵𝜕𝑡2 = 𝜇0𝑅𝑜𝑡Ԧ𝑗= 𝜇0 𝑅𝑜𝑡Ԧ𝑗+ 𝜀0𝜇0𝜕𝜕𝑡𝑅𝑜𝑡𝐸

Page 70 : 70Avec 𝑅𝑜𝑡𝐸= 𝜕𝐵𝜕𝑡d’où l’équation de propagation du champ magnétique :Δ𝐵𝜀0𝜇0𝜕2𝐵𝜕𝑡2 = 𝜇0𝑅𝑜𝑡Ԧ𝑗2 cas particulier de la propagation du champ électromagnétique dans le vide sans charges ni courants :𝜌= 0 𝑒𝑡Ԧ𝑗= 0d’où :Δ𝐸𝜀0𝜇0𝜕2𝐸𝜕𝑡2 = 0 etΔ𝐵𝜀0𝜇0𝜕2𝐵𝜕𝑡2 = 0

Page 71 : 71Exemple : cas d’une onde plane- Structure de l’onde plane uniforme𝐸= 𝐸0𝑒𝑥𝑝𝑖ωt 𝑘Ԧ𝑟et 𝐵= 𝐵0𝑒𝑥𝑝𝑖ωt 𝑘Ԧ𝑟L’onde plane progressive sinusoïdale doit également satisfaire le théorème de Gauss.En absence de charges électriques 𝜌= 0On montre pour une onde plane progressive sinusoïdale :𝛻𝐸= 𝑖𝑘𝐸= 0Soit encore 𝑘. 𝐸= 0:ce qui revient à dire que le champ électrique 𝐸est perpendiculaire à la direction de propagation donnée par le vecteur d’onde 𝑘.Le champ électrique est dit transversal.

Page 72 : 72L’onde plane progressive sinusoïdale doit également satisfaire l’équation de Maxwell-Faraday :𝛻𝐸= 𝜕𝐵𝜕𝑡On montre pour une onde progressive sinusoïdale :𝛻= 𝑖𝑘d ’où ik E = = iωBOn en déduit le champ magnétique 𝐵=𝑘𝐸𝜔𝒆𝒕𝝎𝟐= 𝒄𝟐𝒌𝟐

Page 73 : 73Les propriétés du produit vectoriel, nous permettent de déduire que :- Le champ magnétique est perpendiculaire au plan formé par les vecteurs 𝑘, 𝐸 .- Le champ magnétique 𝐵d’une onde plane progressive OPP est transversal, c’est-à-dire perpendiculaire à la direction de propagation.- Le trièdre 𝐸, 𝐵, 𝑘 est un trièdre direct.

Page 74 : 74Section 4-5-1 : PolarisationΔ𝐸𝜀0𝜇0𝜕2𝐸𝜕𝑡2 = 0, Δ𝐵𝜀0𝜇0𝜕2𝐵𝜕𝑡2 = 0et 𝛻𝐸= 𝜕𝐵𝜕𝑡Considérons une OE plane OEP se propageant suivant les z croissants :𝐸= 𝐸0𝑒𝑥𝑝𝑖ωt 𝑘Ԧ𝑟et 𝐵= 𝐵0𝑒𝑥𝑝𝑖ωt 𝑘Ԧ𝑟

Page 75 : 75Une onde polarisée suivant 𝑢𝑥: 𝑢𝑥𝑒𝑥𝑝𝑖ωt 𝑘𝑧etUne onde polarisée suivant 𝑢𝑦: 𝑢𝑦𝑒𝑥𝑝𝑖ωt 𝑘𝑧De façon générale :𝐸𝐶𝐷= 𝑢𝑥+ 𝑖𝑢𝑦 𝑒𝑥𝑝𝑖ωt 𝑘𝑧Circulaire droite𝐸𝐶𝐺= 𝑢𝑥𝑖𝑢𝑦 𝑒𝑥𝑝𝑖ωt 𝑘𝑧Circulaire gaucheApplication : Lunettes 3DLes deux composantes d’une onde lumineuse sont indépendantes⟹On peut projeter une image différente selon chaque polarisation, puis mettre un filtre ne laissant passer qu’une seule image sur chaque œil.

Page 76 : 76Section 4-5-2 : Energie/ Impulsion𝜀𝑒𝑚= densité d’énergie électrique + densité d’énergie magnétiqueConsidérons dans le milieu, un volume limité par une surface S. 𝜀𝑒𝑚= 12 𝜺𝟎𝑹𝒆𝑬𝟐+ 𝑹𝒆𝑩𝟐𝝁𝟎On peut comparer avec l’expression de l’énergie, d’une onde sur une corde𝜀=𝑍2𝑐𝜕𝜙𝜕𝑡2+𝑐𝑍2𝜕𝜙𝜕𝑥2slide 64Le premier terme est égal à l’énergie cinétique et le second terme est égal à l’énergie potentielle.