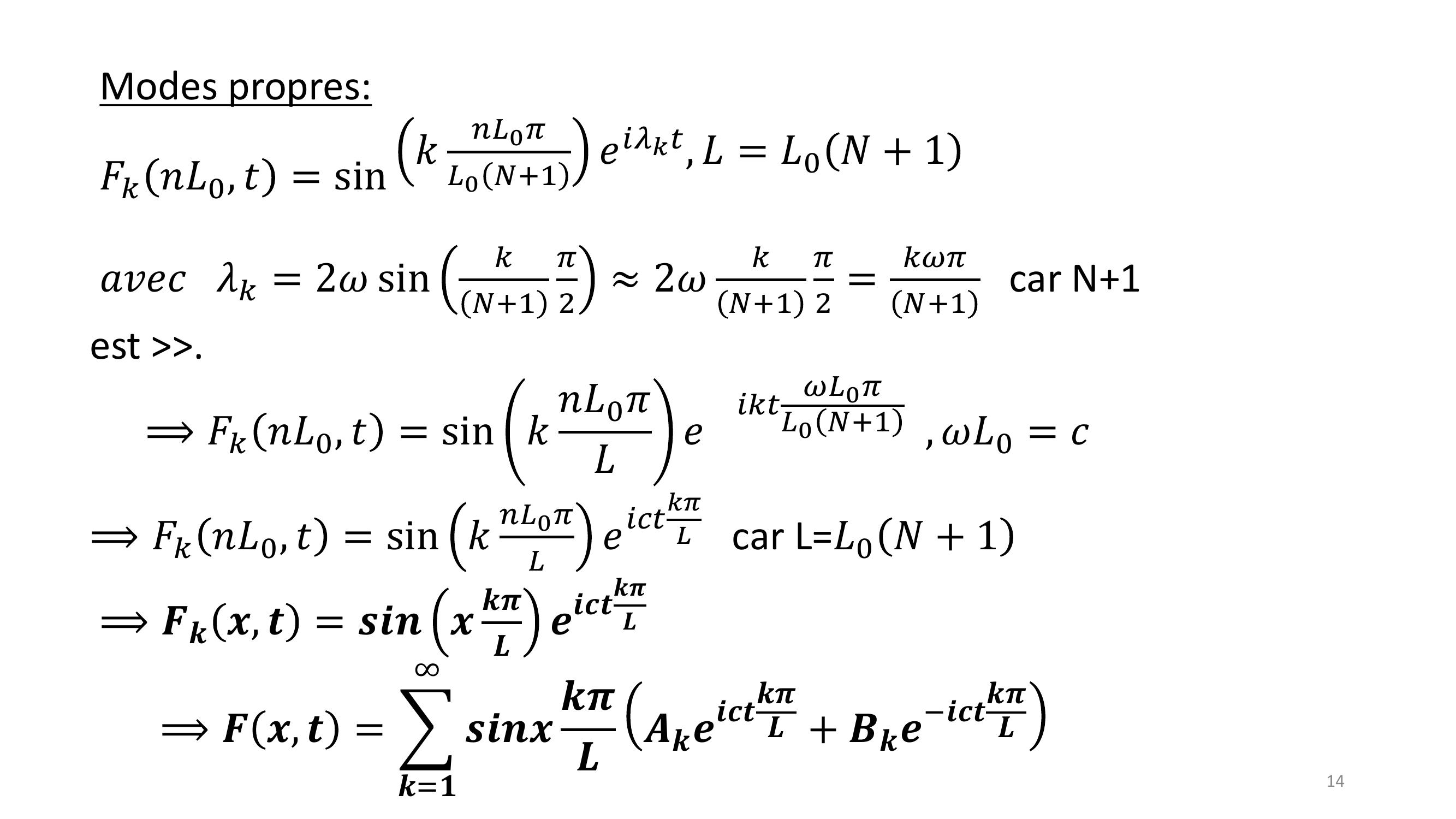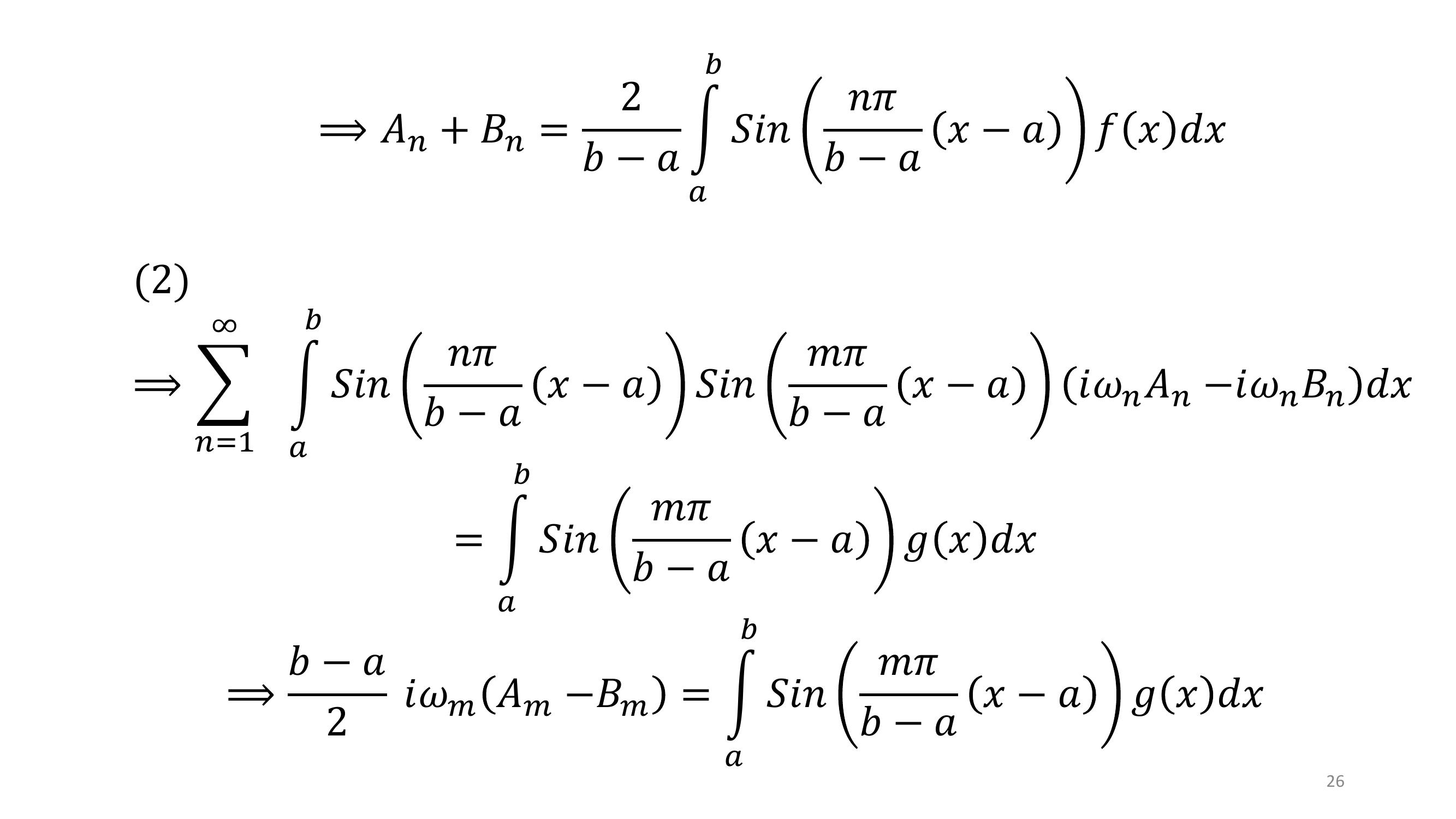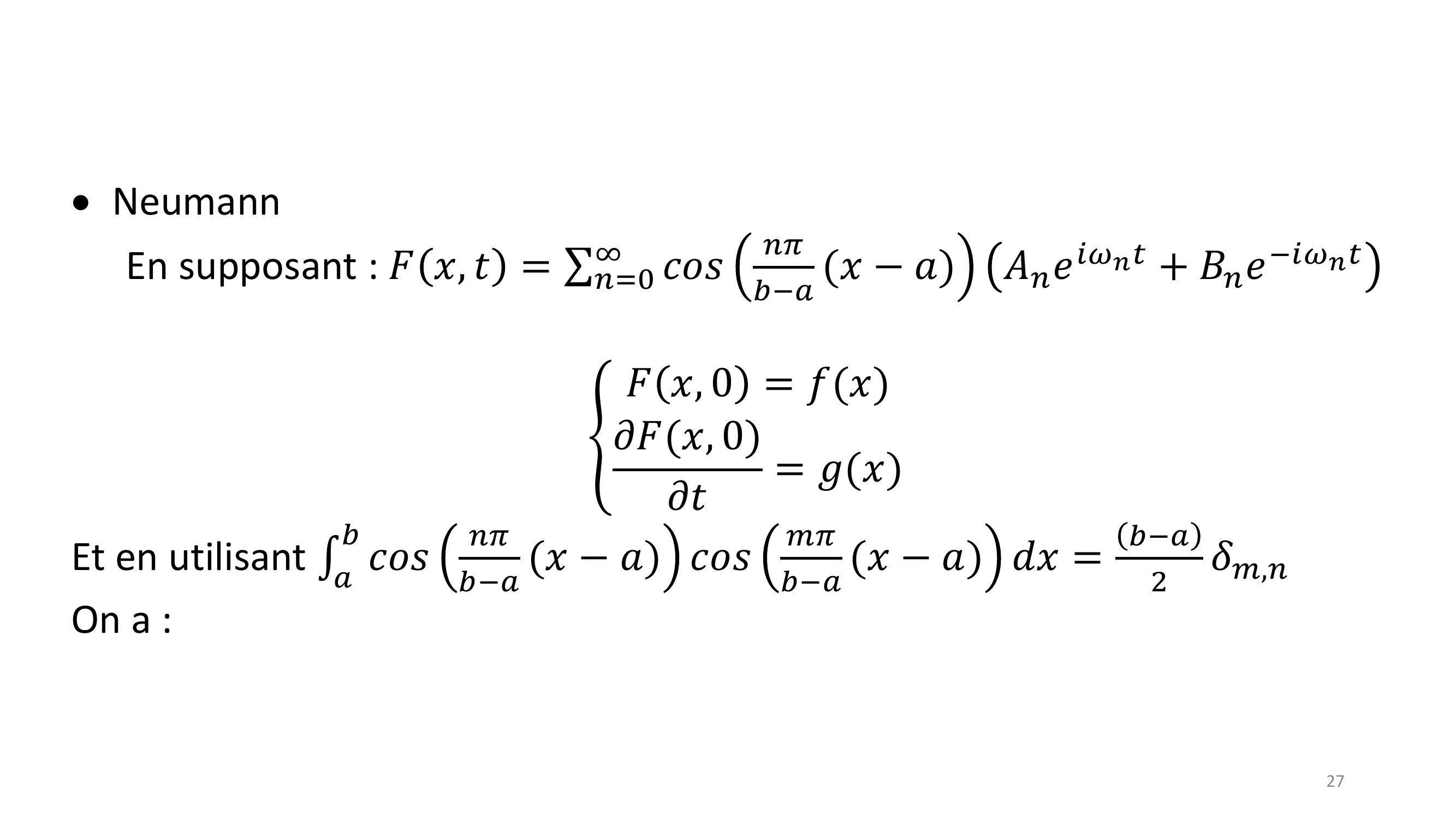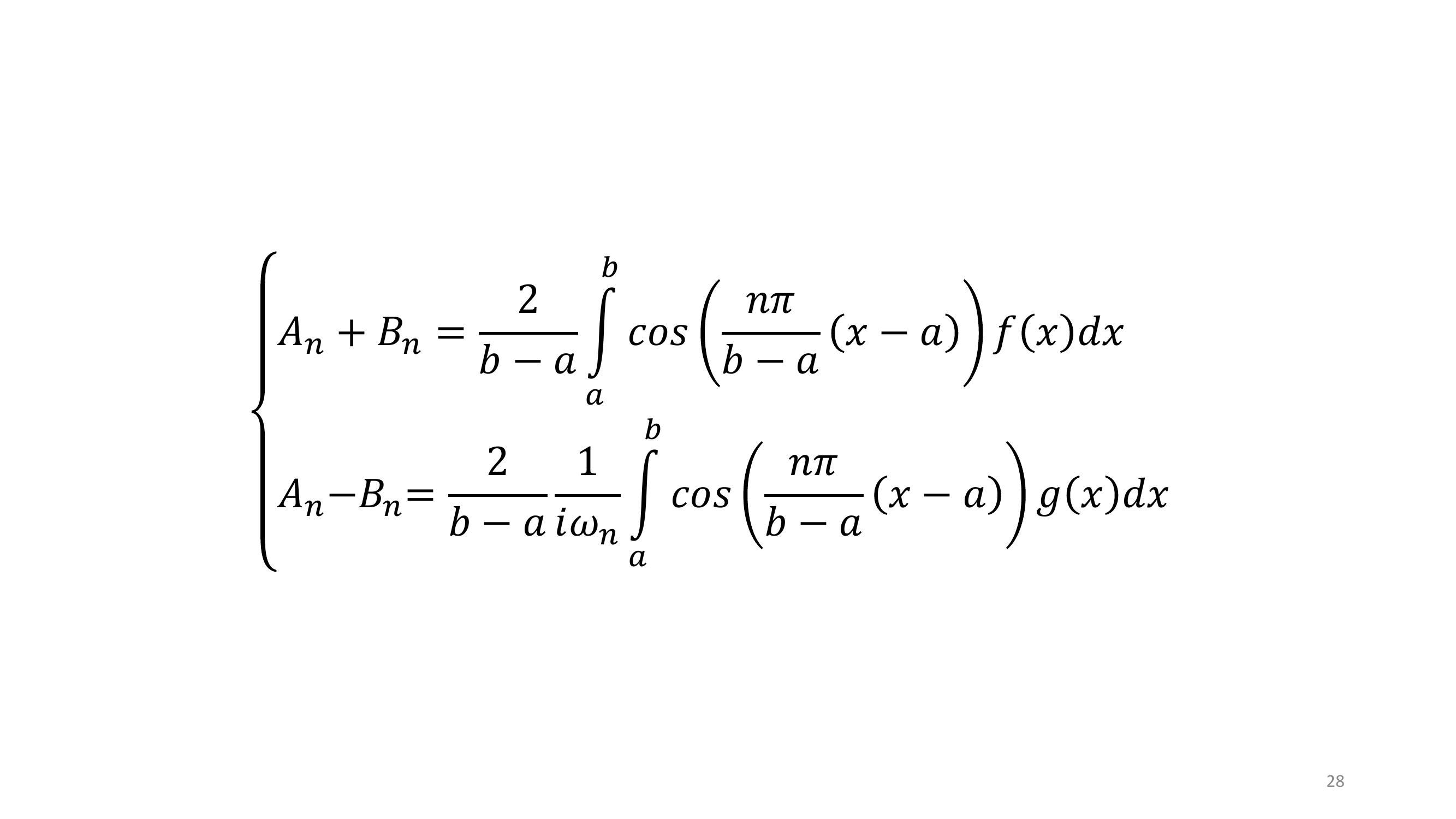CM Chapitre4

Télécharger le CM Chapitre4 en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

Page 1 : Chapitre 4 : OndesSection 4.1 : chaine de N oscillateurs Une chaine est constituée de N petits blocs identiques, de même masse M, espacés de la même distance 𝐿0 et alignés suivant la droite Ox. Une petite perturbation, modifie l’équilibre initial, elle se déplace de proche en proche le long de la chaine de blocs et provoque un petit déplacement de chaque bloc.1

Page 2 : Admettons que les forces d’interaction de chaque bloc peut être limitée à ses deux voisins immédiats n+1 et n-1 pour le bloc net que ces interactions sont de même type que la tension d’un système masse-ressort de constante de raideur k.Soit 𝑋𝑛la position de la masse n par rapport à sa position d’équilibre 1 𝑛𝑁.21 2 3N-1 N𝐾0 n-1 𝐾0 n 𝐾0 n+1

Page 3 : Déterminons l’équation du mouvement du nième bloc : Bilan des forces de rappel exercées par les blocs n+1 et n-1 sur le bloc n :Projection de la force de rappel exercée par le bloc n+1 :𝒇𝒏+𝟏→𝒏= 𝐾0𝑿𝒏𝑿𝒏+𝟏Projection de la force de rappel exercée par Le bloc n-1 :𝒇𝒏𝟏→𝒏= 𝐾0𝑿𝒏𝑿𝒏𝟏La deuxième loi de Newton s’écrit :𝑴ሷ𝑿𝒏= 𝒇𝒏𝟏→𝒏+ 𝒇𝒏+𝟏→𝒏Soit : 𝒎ሷ𝑿𝒏= 𝐾0𝑿𝒏+𝟏𝑿𝒏 𝐾0𝑿𝒏𝑿𝒏𝟏D’oùሷ𝑿𝒏+𝐾0𝑴𝟐𝑿𝒏𝑿𝒏𝟏𝑿𝒏+𝟏= 𝟎posons𝐾0𝑴= 𝝎𝟐3

Page 4 : 𝜔0 Étant la pulsation propre de chacun des N blocs identiques constituant la chaîne.Nous constatons que les termes 𝑿𝒏s’additionnent et ne s’éliminent pas.La solution 𝑋𝑛dépend de 𝑋𝑛1 et de 𝑋𝑛+1 cela veut dire que le mouvement du bloc n, dépend du mouvement de ses voisins immédiats n+1 et n-1 : la perturbation se déplace de proche en proche, il s’agit d’une onde mécanique, qui se propage le long de la chaîne de blocs. 4

Page 5 : 5ሷ𝑋𝑛+ 2𝜔2𝑋𝑛𝜔2 𝑋𝑛1 + 𝑋𝑛+1 = 0Equation du mouvement du nième blocEquation du mouvement du premier bloc𝑋0 = 0ሷ𝑋1 + 2𝜔2𝑋1 𝜔2 𝑋0 + 𝑋1 = 0Equation du mouvement du dernier bloc ሷ𝑋𝑁+ 2𝜔2𝑋𝑁𝜔2 𝑋𝑁1 + 𝑋𝑛+1 = 0

Page 6 : Limite continueOn s’intéresse à la limite N grand et 𝐿0 petit, soit 𝐹𝑋, 𝑡telle que𝐹𝑛𝐿0, 𝑡= 𝑋𝑛𝑡⟹𝑋𝑛±1 𝑡= 𝐹 𝑛±1𝐿0, 𝑡𝐹𝑛𝐿0, 𝑡±ቤ𝜕𝐹𝜕𝑋𝐿0𝑋=𝑛𝐿0± 12อ𝜕2𝐹𝜕𝑋2 𝐿02𝑋=𝑛𝐿0⟹𝟐𝑿𝒏𝑿𝒏𝟏𝑿𝒏+𝟏= อ𝜕2𝐹𝑋, 𝑡𝜕𝑋2𝐿02𝑋=𝑛𝐿06

Page 7 : 𝜕2𝐹𝑛𝐿0, 𝑡𝜕𝑡2𝜔2𝐿02อ𝜕2𝐹𝑋, 𝑡𝜕𝑋2𝑋=𝑛𝐿0= 0⟹1𝜔2𝜕2𝐹𝑋,𝑡𝜕𝑡21𝑘2𝜕2𝐹𝑋,𝑡𝜕𝑋2= 0avec 𝜔2 =𝐾0𝑀𝑜ù 𝜔𝑒𝑠𝑡𝑙𝑎𝑝𝑢𝑙𝑠𝑎𝑡𝑖𝑜𝑛𝑒𝑡𝑘2 =1𝐿02 , 𝑘est le nombre d’onde en cm -1.𝜕2𝐹𝑋,𝑡𝜕𝑋2𝑘2𝜔2𝜕2𝐹𝑋,𝑡𝜕𝑡2= 0,𝑘2𝜔2 =1𝑐2 où c est la vitesse de phaseD’où l’équation d’onde :𝜕2𝐹𝑋,𝑡𝜕𝑋21𝑐2𝜕2𝐹𝑋,𝑡𝜕𝑡2= 07

Page 8 : Solution de l’équation d’onde :Soit Gz une fonction, qui dépend d’une seule variable z et 𝜙𝑥, 𝑡 une fonction qui dépend des deux variables 𝑥𝑒𝑡𝑡:𝜕𝜕𝑡𝐺𝜙𝑥, 𝑡=ሶ𝐺𝜕𝜙𝜕𝑡𝜕2𝜕𝑡2 𝐺𝜙𝑥, 𝑡=ሷ𝐺𝜕𝜙𝜕𝑡2+ ሶ𝐺𝜕2𝜙𝜕𝑡2𝜕2𝜕𝑋2 𝐺𝜙𝑥, 𝑡=ሷ𝐺𝜕𝜙𝜕𝑋2+ ሶ𝐺𝜕2𝜙𝜕𝑋28

Page 9 : 1𝜔2𝜕2𝐺𝜙𝑥,𝑡𝜕𝑡21𝑘2𝜕2𝐺𝜙𝑥,𝑡𝜕𝑋2= 0⟹1𝜔2ሷ𝐺𝜕𝜙𝜕𝑡2+ ሶ𝐺𝜕2𝜙𝜕𝑡21𝑘2ሷ𝐺𝜕𝜙𝜕𝑋2+ ሶ𝐺𝜕2𝜙𝜕𝑋2=ሷ𝐺1𝜔2𝜕𝜙𝜕𝑡21𝑘2𝜕𝜙𝜕𝑋2+ ሶ𝐺1𝜔2𝜕2𝜙𝜕𝑡2 1𝑘2𝜕2𝜙𝜕𝑋2Si 𝜙𝑥, 𝑡= 𝜔𝑡± 𝑘𝑋⟹൞1𝜔2𝜕𝜙𝜕𝑡2=1𝑘2𝜕𝜙𝜕𝑋2= 1𝜕2𝜙𝜕𝑡2 =𝜕2𝜙𝜕𝑋2 = 09

Page 10 : La solution générale de l’équation d’onde est :𝐹𝑋, 𝑡= 𝐺+ 𝜔𝑡+ 𝑘𝑋+ 𝐺𝜔𝑡𝑘𝑋𝐺+ 𝑒𝑡𝐺sont deux fonctions 𝐶2 arbitraires.Rappel : la solution générale d’une équation différentielle d’ordre n contient n fonctions arbitraires.SolutionOn pose 𝑋𝑛= 𝐴𝑛𝑒𝑖𝜆𝑡ሷ𝑋𝑛+ 𝐾0𝑴2𝑋𝑛𝑋𝑛1 𝑋𝑛+1 = 0 ⟹𝜆2𝐴𝑛+ 2𝜔2𝐴𝑛𝜔2 𝐴𝑛1 + 𝐴𝑛+1 = 010

Page 11 : ⟹൞𝐴𝑛+1 = 2𝛽𝐴𝑛𝐴𝑛1, 𝛽= 1 𝜆22𝜔2𝐴2 = 2𝛽𝐴1𝐴𝑁+1 = 0 𝑒𝑡𝐴0 = 0: car la chaine est fixée aux extrémités.⟹𝐴𝑛=sin 𝑛𝜃sin 𝜃𝐴1, 𝛽= cos 𝜃Preuve : on pose: 𝛽=𝑞+𝑞12𝑛= 1, 𝐴1 =𝑞𝑞1𝑞𝑞1 𝐴1 = 𝐴1vrai𝑛= 2, 𝐴2 = 𝑞+ 𝑞1 𝐴1 ,𝑞2𝑞2𝑞𝑞1 =𝑞1+𝑞1𝑞1𝑞1𝑞𝑞1= 𝑞+ 𝑞1 vrai11

Page 12 : Supposons le résultat vrai pour 𝐴𝑛et 𝐴𝑛1𝐴𝑛+1 =𝑞+ 𝑞1 𝑞𝑛𝑞𝑛𝑞𝑞1 𝑞𝑛1𝑞1𝑛𝑞𝑞1𝐴1⟹𝐴𝑛+1𝐴1= 𝑞𝑛+1𝑞𝑛1𝑞𝑞1= sin 𝑛𝜃sin 𝜃⟹𝑋𝑛= sin 𝑛𝜃sin 𝜃𝐴1𝑒𝑖𝜆𝑡Or 𝑋𝑁+1 = 0 ⟹sin 𝑁+ 1 𝜃 = 0 ⟹𝜃𝑘=𝑘𝜋𝑁+112

Page 13 : 1 𝜆𝑘22𝜔2 = 𝑐𝑜𝑠𝜃𝑘Or 𝑐𝑜𝑠𝜃𝑘= 1 2𝑠𝑖𝑛2 𝜃𝑘2 et 𝜃𝑘=𝑘𝜋𝑁+1𝜆𝑘= 2𝜔sin𝑘𝑁+ 1𝜋2D’où les modes propres sont : 𝑿𝒏𝒌=𝒔𝒊𝒏𝒏𝜽𝒌𝒔𝒊𝒏𝜽𝒌𝒆𝒊𝝀𝒌𝒕, k=1, …, N+1Pulsations propres : 𝜆𝑘= 2𝜔sin𝑘𝑁+ 1𝜋2 ,𝜃𝑘=𝑘𝜋𝑁+ 113

Page 14 : 14Modes propres:𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿0 𝑁+1𝑒𝑖𝜆𝑘𝑡, 𝐿= 𝐿0 𝑁+ 1𝑎𝑣𝑒𝑐𝜆𝑘= 2𝜔sin𝑘𝑁+1𝜋22𝜔𝑘𝑁+1𝜋2 =𝑘𝜔𝜋𝑁+1car N+1 est .⟹𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿𝑒𝑖𝑘𝑡𝜔𝐿0𝜋𝐿0 𝑁+1 , 𝜔𝐿0 = 𝑐⟹𝐹𝑘𝑛𝐿0, 𝑡= sin 𝑘𝑛𝐿0𝜋𝐿𝑒𝑖𝑐𝑡𝑘𝜋𝐿car L=𝐿0 𝑁+ 1⟹𝑭𝒌𝒙, 𝒕= 𝒔𝒊𝒏𝒙𝒌𝝅𝑳𝒆𝒊𝒄𝒕𝒌𝝅𝑳⟹𝑭𝒙, 𝒕= ෍𝒌=𝟏𝒔𝒊𝒏𝒙𝒌𝝅𝑳𝑨𝒌𝒆𝒊𝒄𝒕𝒌𝝅𝑳+ 𝑩𝒌𝒆𝒊𝒄𝒕𝒌𝝅𝑳

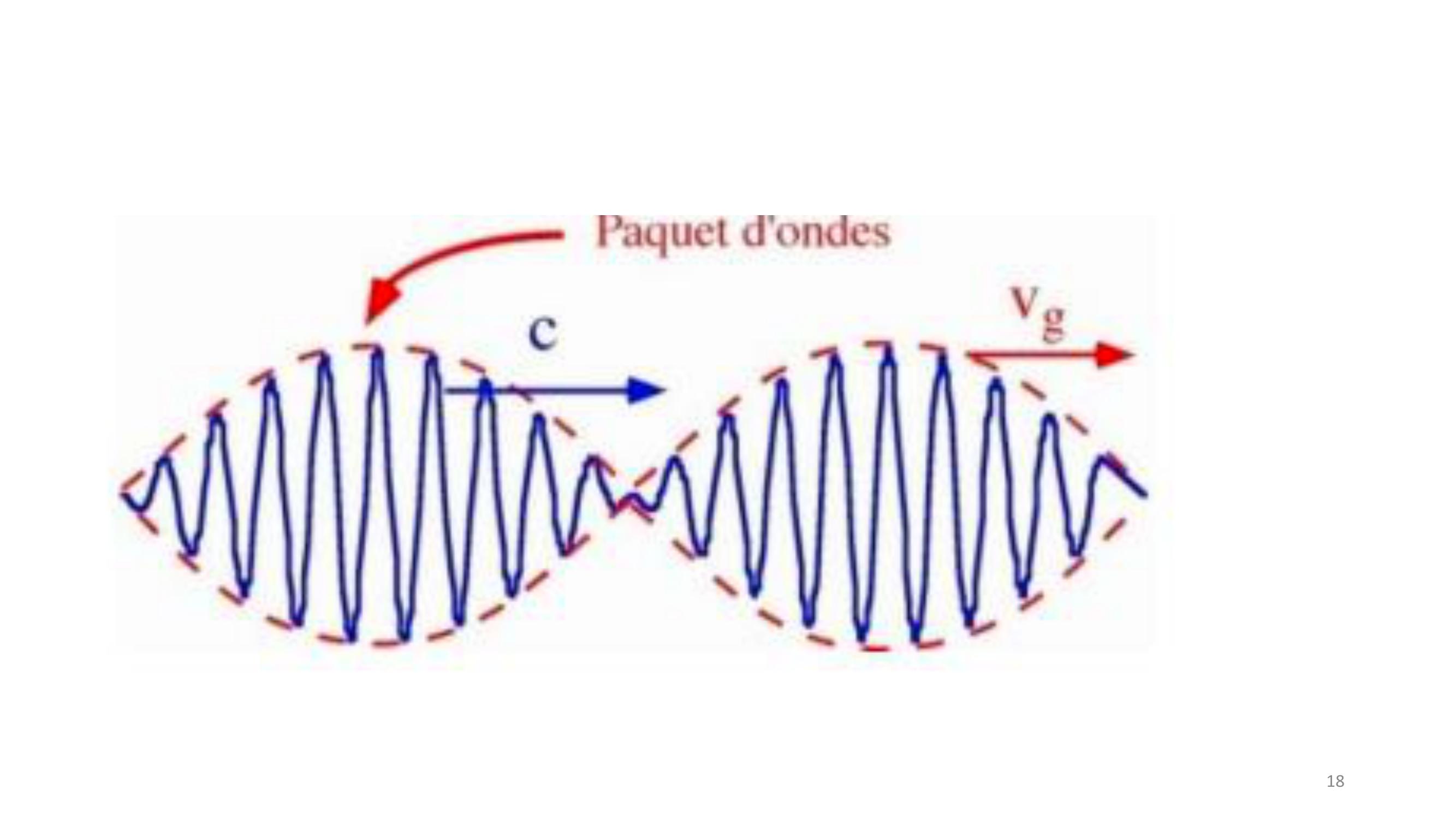
Page 15 : 154-2 vitesse de groupe , vitesse de phase et conditions aux limitesEquation d’onde :1𝑐2𝜕2𝐹𝑥,𝑡𝜕𝑡2𝜕2𝐹𝑥,𝑡𝜕𝑥2= 0D’où la relation de dispersion : 𝜔2𝑐2 𝑘2 = 0 ⟹𝜔2 = 𝑘2𝑐2Les modes propres :𝝓𝒋,𝒌± = 𝒆±𝒊𝝎𝒋𝒌𝒕𝒌𝒙𝜙𝑗,𝑘±𝑥, 𝑡= 𝜙𝑗,𝑘±𝑥+ 𝜆, 𝑡= 𝜙𝑗,𝑘±𝑥, 𝑡+ 𝜏Avec 𝜆=2𝜋𝐾: longueur d’onde et 𝜏: période

Page 16 : 16D’autre part, 𝜙𝑗,𝑘±𝑥+ Δ𝑥, 𝑡+ Δ𝑡= 𝑒±𝑖𝜔𝑗𝑡𝐾𝑥𝑒±𝑖𝜔𝑗Δ𝑡𝐾Δ𝑥 = 𝜙𝑗,𝑘±𝑥, 𝑡⟺Δ𝑥Δ𝑡=𝜔𝑗𝐾= vitesse de phaseVitesse de groupe :Le rapport 𝜔𝑗𝐾a les unités d’une vitesse et 𝜕𝜔𝑗𝜕𝐾aussi ! c’est la vitesse de groupe, mais que mesure –t-elle ?Pour Δ𝑘petit 𝜙𝑗,𝑘+Δ𝑘±𝑥, 𝑡 = 𝑒±𝑖𝜔𝑗𝑘+Δ𝑘𝑡𝑘+Δ𝑘𝑥 𝑒±𝑖𝜔𝑗𝑘𝑡𝑘𝑥𝑒±𝑖Δ𝑘𝜕𝜔𝑗𝜕𝑘𝑡𝑥⟹le terme 𝑒±𝑖Δ𝑘𝜕𝜔𝑗𝜕𝑘𝑡𝑥 correspond à une onde se déplaçant à la vitesse :𝜕𝜔𝑗𝜕𝑘

Page 17 : 17Vitesse de groupeSoient deux ondes progressives𝜙1 = cos𝜔1𝑡𝑘1𝑥, 𝜔𝑖= 𝜔𝑘𝑖𝜙2 = cos𝜔2𝑡𝑘2𝑥⟹𝜙1 + 𝜙2= 2𝑐𝑜𝑠𝜔1 + 𝜔22𝑡𝑘1 + 𝑘22𝑥. 𝑐𝑜𝑠𝜔1 𝜔22𝑡𝑘1 𝑘22𝑥.𝑜𝑛𝑑𝑒𝑑𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝜔1 + 𝜔2𝑘1 + 𝑘2. 𝑜𝑛𝑑𝑒𝑑𝑒𝑣𝑖𝑡𝑒𝑠𝑠𝑒𝜔1 𝜔2𝑘1 𝑘2Ce dernier facteur est l’enveloppe

Page 18 : 18

Page 19 : 19Section 4.2.1 : conditions aux bords/limitesLes ED doivent être accompagnées par des conditions aux bords /limites pour avoir une solution bien définie :Dirichlet : 𝐹𝑎, 𝑡= 𝛼, 𝐹𝑏, 𝑡= 𝛽,𝑥𝑎, 𝑏Neumann :𝜕𝐹𝜕𝑥𝑎, 𝑡= 𝛼,𝜕𝐹𝜕𝑥𝑏, 𝑡= 𝛽Mixte : mélange !Il est évident que si 𝐹1 𝑒𝑡𝐹2 sont les solutions de l’équation différentielle linéaire telle que ቊ𝐹1 𝑎, 𝑡= 𝛼, 𝐹1 𝑏, 𝑡= 𝛽𝐹2 𝑎, 𝑡= 0, 𝐹2 𝑏, 𝑡= 0Alors 𝐹1 +𝐹2 𝑒𝑠𝑡𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑑𝑒𝑙′𝐸𝐷avec les conditions aux bords vérifiées par les premières équations du système ci-dessus.

Page 20 : 20Commençons par l’étude des cas : 𝛼= 𝛽= 0 !On considère 𝜙𝑘𝑥, 𝑡= σ𝑗=1𝑁𝑟𝑛𝑒𝑖𝜔𝑗𝑡𝑘𝑥 + 𝑠𝑛𝑒𝑖𝜔𝑗𝑡𝑘𝑥On veut résoudre pour 𝑟𝑛𝑒𝑡𝑠𝑛!⟹𝜙𝑘𝑎, 𝑡= 𝑒𝑖𝑘𝑎෍𝑗=1𝑁𝑟𝑛𝑒𝑖𝜔𝑗𝑡+ 𝑒𝑖𝑘𝑎෍𝑗=1𝑁𝑠𝑛𝑒𝑖𝜔𝑗𝑡= 0Equation d’onde : 𝜔1 = 𝜔2 = 𝜔𝑘,𝑁= 2⟹𝜙𝑘𝑎, 𝑡= 𝑒𝑖𝜔𝑡𝑟1𝑒𝑖𝑘𝑎+ 𝑠2𝑒𝑖𝑘𝑎+ 𝑒𝑖𝜔𝑡𝑟2𝑒𝑖𝑘𝑎+ 𝑠1𝑒𝑖𝑘𝑎= 0⟺൝𝑟1 = 𝑠2𝑒2𝑖𝑘𝑎𝑟2 = 𝑠1𝑒2𝑖𝑘𝑎Mais 𝜙𝑘𝑏, 𝑡= 0 ⟺൝𝑟1 = 𝑠2𝑒2𝑖𝑘𝑏𝑟2 = 𝑠1𝑒2𝑖𝑘𝑏

Page 21 : 21⟹𝑒2𝑖𝑘𝑏𝑎= 1⟹𝑘𝑛=𝑛𝜋𝑏𝑎,𝑛𝑍⟹𝜙𝑛= 𝑠𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡avec 𝜔= 𝜔𝑛𝜋𝑏𝑎= 𝜔𝑛⟹𝐹𝑥, 𝑡= ෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡𝑠é𝑟𝑖𝑒𝑑𝑒𝐹𝑜𝑢𝑟𝑟𝑖𝑒𝑟𝐹𝑎, 𝑡= 𝐹𝑏, 𝑡= 0Mais il nous manque une solution particulière de l’ED avec :𝐹𝑎, 𝑡= 𝛼𝑡𝑒𝑡𝐹𝑏, 𝑡= 𝛽𝑡

Page 22 : 22Or de telles solutions dépendent trop de l’équation différentielle ED !Par des arguments similaires, les conditions de Neumann homogène donnent :𝐹𝑥, 𝑡= ෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡: 𝑠é𝑟𝑖𝑒𝑑𝑒𝐹𝑜𝑢𝑟𝑟𝑖𝑒𝑟቉𝜕𝐹𝜕𝑥𝑥=𝑎=቉𝜕𝐹𝜕𝑥𝑥=𝑏= 0

Page 23 : 23Section 4.2.2 : conditions initialesEn plus des bords en x, il faut donner les conditions aux bords en t les conditions initiales :ቐ𝐹𝑥, 0 = 𝑓𝑥𝜕𝐹𝑥, 0𝜕𝑡= 𝑔𝑥En supposant la solution:𝐹𝑥, 𝑡= σ𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑡On veut alors résoudre :1෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛= 𝑓𝑥2෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑖𝜔𝐴𝑛𝑖𝜔𝐵𝑛= 𝑔𝑥

Page 24 : 24Recherche des 𝑨𝒏𝒆𝒕𝑩𝒏:Multiplions l’équation 1 par 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎:1 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎෍𝑛=1𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛= 𝑓𝑥𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎Intégrons entre a et b:1⟹σ𝑛=1׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥

Page 25 : 25Proposition : ׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎 𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎 𝑑𝑥=𝑏𝑎2𝛿𝑛,𝑚𝛿𝑛,𝑚= ቊ1 𝑠𝑖𝑛= 𝑚0 𝑠𝑖𝑛𝑜𝑛1⟹σ𝑛=1׬𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝐴𝑛+ 𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥⟹෍𝑛=1𝑏𝑎2𝛿𝑛,𝑚𝐴𝑛+ 𝐵𝑛= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥

Page 26 : 26⟹𝐴𝑛+ 𝐵𝑛=2𝑏𝑎න𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥2⟹෍𝑛=1න𝑎𝑏𝑆𝑖𝑛𝑛𝜋𝑏𝑎𝑥𝑎𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑖𝜔𝑛𝐴𝑛𝑖𝜔𝑛𝐵𝑛𝑑𝑥= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥⟹𝑏𝑎2𝑖𝜔𝑚𝐴𝑚𝐵𝑚= න𝑎𝑏𝑆𝑖𝑛𝑚𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥

Page 27 : 27Neumann En supposant : 𝐹𝑥, 𝑡= σ𝑛=0𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝐴𝑛𝑒𝑖𝜔𝑛𝑡+ 𝐵𝑛𝑒𝑖𝜔𝑛𝑡ቐ𝐹𝑥, 0 = 𝑓𝑥𝜕𝐹𝑥, 0𝜕𝑡= 𝑔𝑥Et en utilisant ׬𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎 𝑐𝑜𝑠𝑚𝜋𝑏𝑎𝑥𝑎 𝑑𝑥=𝑏𝑎2𝛿𝑚,𝑛On a :

Page 28 : 28𝐴𝑛+ 𝐵𝑛=2𝑏𝑎න𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝑓𝑥𝑑𝑥𝐴𝑛𝐵𝑛=2𝑏𝑎1𝑖𝜔𝑛න𝑎𝑏𝑐𝑜𝑠𝑛𝜋𝑏𝑎𝑥𝑎𝑔𝑥𝑑𝑥

Page 29 : 29Exemple : corde pincéeOn veut résoudre l’équation d’onde :1𝑐2𝜕2𝐹𝑋, 𝑡𝜕𝑡2𝜕2𝐹𝑋, 𝑡𝜕𝑋2= 0Avec les conditions initiales : 𝐹0, 𝑡= 𝐹𝐿, 𝑡= 01𝐹𝑥, 0 = ቊ𝑥𝑠𝑖𝑥 𝐿/2𝐿𝑥𝑠𝑖𝑥𝐿/2𝐹𝑥, 02𝜕𝐹𝑥, 0𝜕𝑡= 0

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29