CM Chapitre5 Mecanique
Télécharger le CM Chapitre5 Mecanique en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Page 1 : Panorama sur la PhysiqueChapitre 5 – Mécanique5.1 Les 3 principes fondamentaux de la dynamique5.2 F=ma: équation différentiellePrésentation rédigée par Émilie Dupont Cergy : emilie.dupont@cyu.fr, CY308I Physique - 2023-2024
Page 2 : I Physique - 2021-2022Programme de Panorama sur la Physique●Chapitre 1 - Introduction●Chapitre 2- Introduction à la pensée scientifique●Chapitre 3- Optique: l’étude de la lumière●Chapitre 4 – Cinématique: la description du mouvement●Chapitre 5 - Mécanique
Page 3 : Programme de Panorama sur la Physique●Chapitre 1 - Introduction●Chapitre 2- Introduction à la pensée scientifique●Chapitre 3- Optique: l’étude de la lumière●Chapitre 4 – Cinématique: la description du mouvement●Chapitre 5 - Mécanique
Page 4 : Référentiels en mouvement relatif: composition des vitesses5.1.1 Des référentiels pas comme les autres : le 1er principehttps://www.youtube.com/watch?v=ZzF73XtFiTo
Page 5 : Référentiels en mouvement relatif: composition des vitesses5.1.1 Des référentiels pas comme les autres : le 1er principe1. Le comportement physique d’un objet dans unréférentiel donné ne permet pas de dire si ceréférentiel est fixe ou en translation avec vitesse constante.C’est un principe de la physique. 2. Un même mouvement vu depuis deux référentiels enmouvement relatif n’est pas le même.Comment déduire l’un de l’autre ?Changements de référentiel.
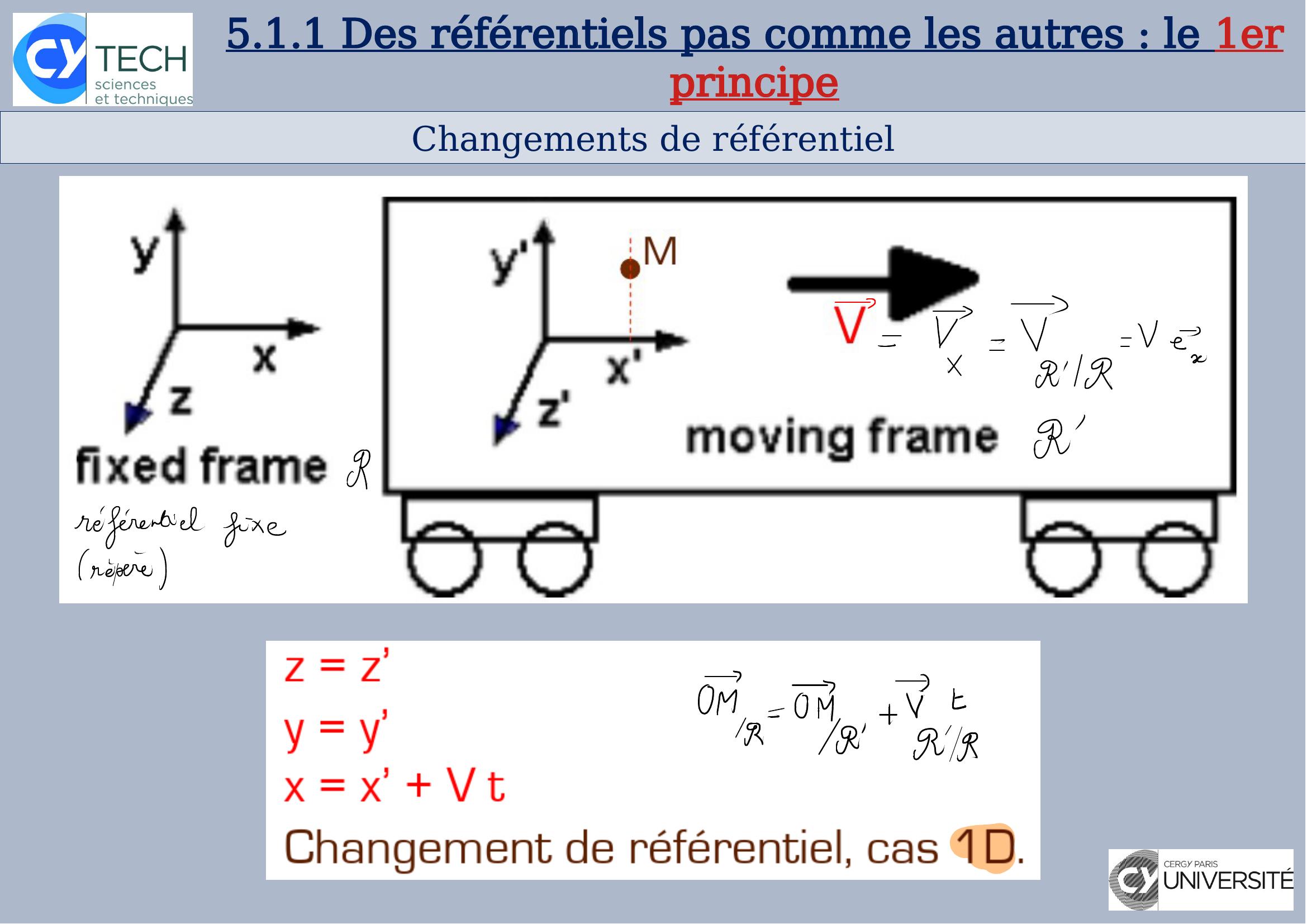
Page 6 : Changements de référentiel5.1.1 Des référentiels pas comme les autres : le 1er principe
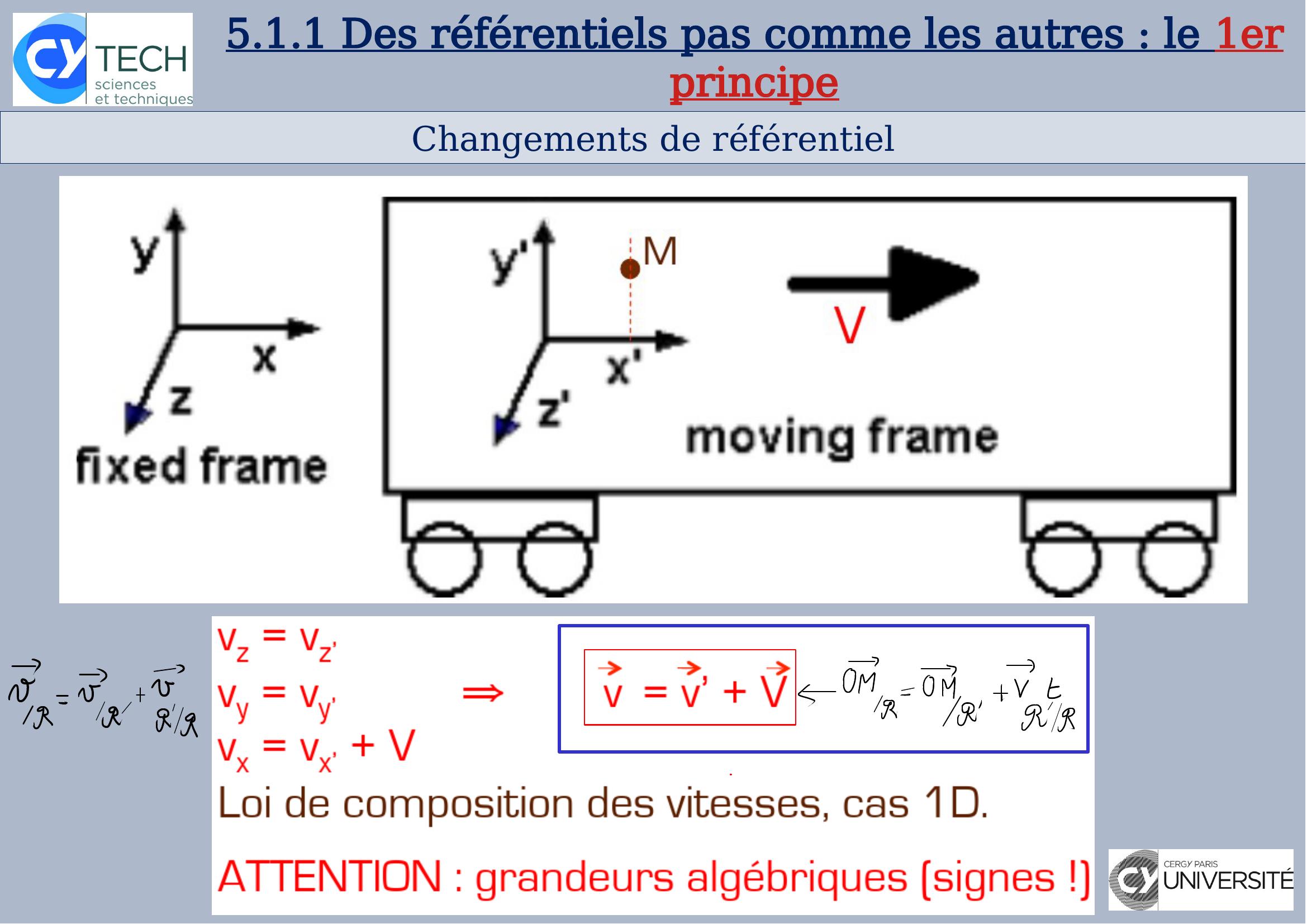
Page 7 : Changements de référentiel5.1.1 Des référentiels pas comme les autres : le 1er principe
Page 8 : Questions5.1.1 Des référentiels pas comme les autres : le 1er principeUn oiseau et un avion volent dans la même direction.Par rapport au sol, la vitesse de l’oiseau est V, celle de l’avion v.Quelle est la vitesse de l’avion vue par l’oiseau!?Quelle est la vitesse de l’avion vue par l’oiseau!?
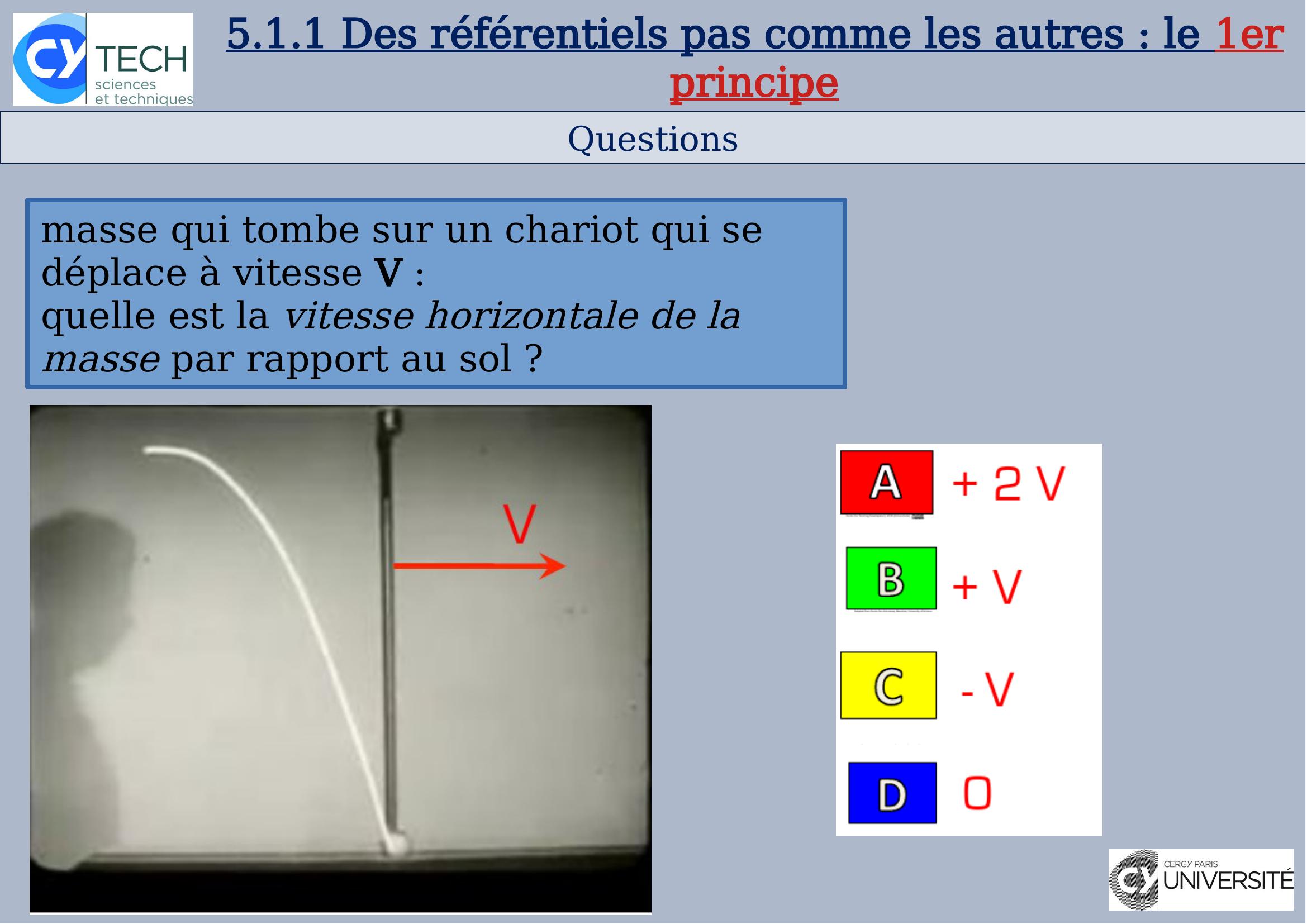
Page 9 : I Physique - 2020-2021Questions5.1.1 Des référentiels pas comme les autres : le 1er principemasse qui tombe sur un chariot qui se déplace à vitesse V :quelle est la vitesse horizontale de la masse par rapport au sol ?
Page 10 : Principe de relativité de Galilée5.1.1 Des référentiels pas comme les autres : le 1er principePrincipe de relativité de Galilée : Les lois de la mécanique sontidentiques dans tous les référentiels inertiels.Mais c’est quoi un référentiel inertiel ?1er principe ou PRINCIPE D’INERTIE : Il existe une classe de référentiels en translation uniforme les uns par rapport aux autres, appelés galiléens ou inertiels, dans lesquels tout point matériel isolé c’est à dire sur lequel s’exerce une résultante des forces nulle est soit au repos soit en translation rectiligne uniforme.c’est quoi, cette force qui doit être nulle!? c’est quoi un système isolé!?
Page 11 : 2nd principe ou PRINCIPE FONDAMENTAL DE LA DYNAMIQUE5.1.2 Le 2nd principe comme définition dynamique de la forceINTERACTION :deux systèmes physiques objets peuvent interagir = influencer chacun l’état de l’autre et notamment son état de mouvementsystème isolé : suffisamment éloigné de tout pour ne pas interagir2nd principe:Dans un référentiel inertiel un corps de masse m constante subit une accélération proportionnelle à la résultante des forces extérieures qui s’exercent sur lui et inversement proportionnelle à sa masse m :ou
Page 12 : FILM : un test en apesanteurhttp://www.nasa.gov/audience/foreducators/diypodcast/nl-video-index.html
Page 13 : Lois de la dynamique: questions ouvertes5.1.3 Le 3ème principeéquilibre des forces,action et réaction 3ème principe
Page 14 : Forces: Pesanteur5.1.3 Le 3ème principeExpériences :• chute de 2 masses différentes• tube de Newton
Page 15 : Forces: Pesanteur5.1.3 Le 3ème principe
Page 16 : Forces: Pesanteur5.1.3 Le 3ème principeMais: G = 6,67 10-11 S.I.!r12 = rterre + h rterre si h rterre = 6400 km
Page 17 : I Physique - 2020-2021Équilibre5.1.3 Le 3ème principeEQUILIBRE = objet au repos :
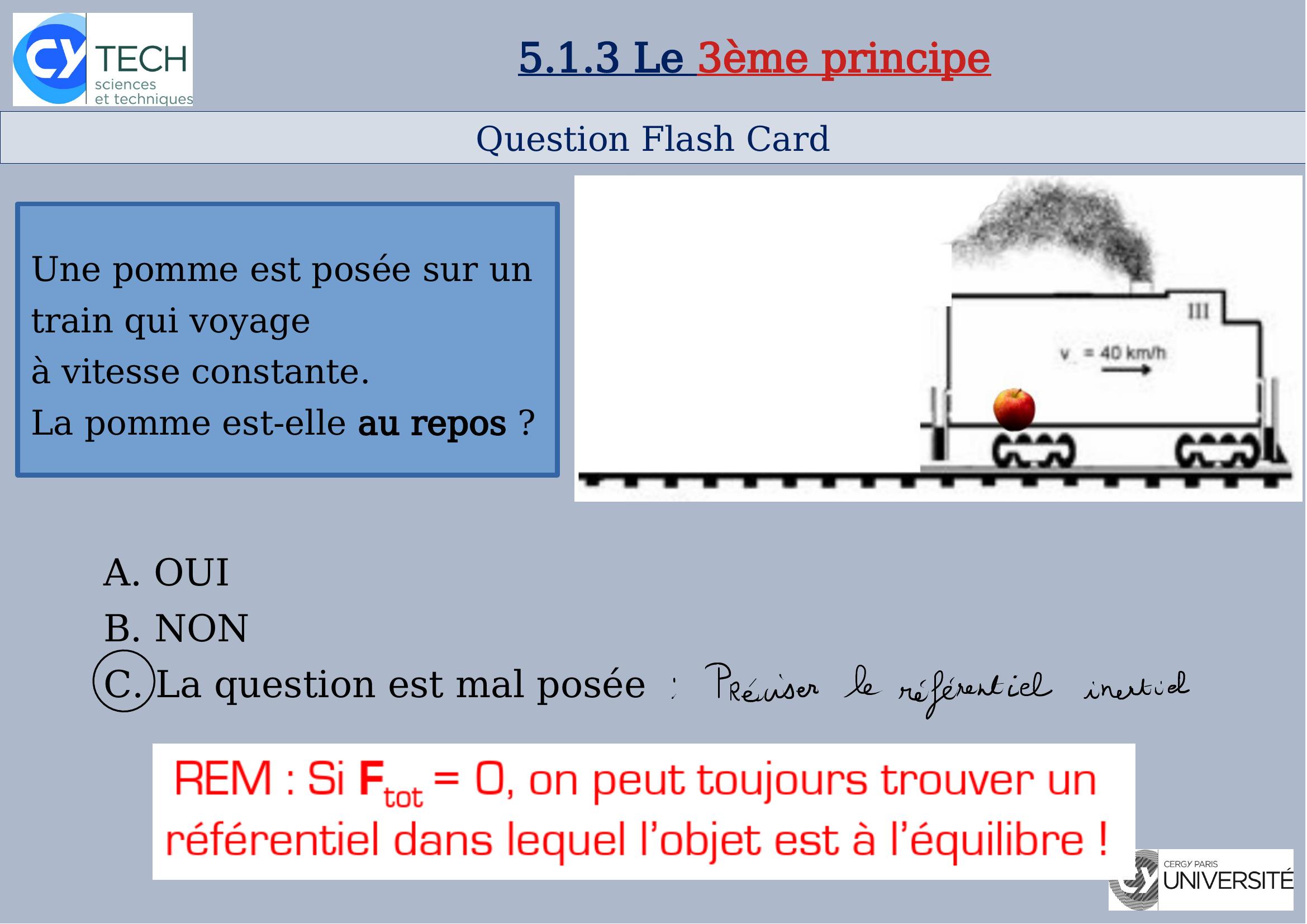
Page 18 : Question Flash Card5.1.3 Le 3ème principeUne pomme est posée sur un train qui voyageà vitesse constante. La pomme est-elle au repos ?A. OUIB. NONC. La question est mal posée
Page 19 : Équilibre5.1.3 Le 3ème principeDiagramme Objet Interaction DOI➢faire l'inventaire de tous les objets concernés➢faire l'inventaire de toutes les interactionsentre objets :• interactions directes dites de contact :trait plein• interactions indirectes dites à distance :trait pointillé➢entourer sur le diagramme le système étudié.
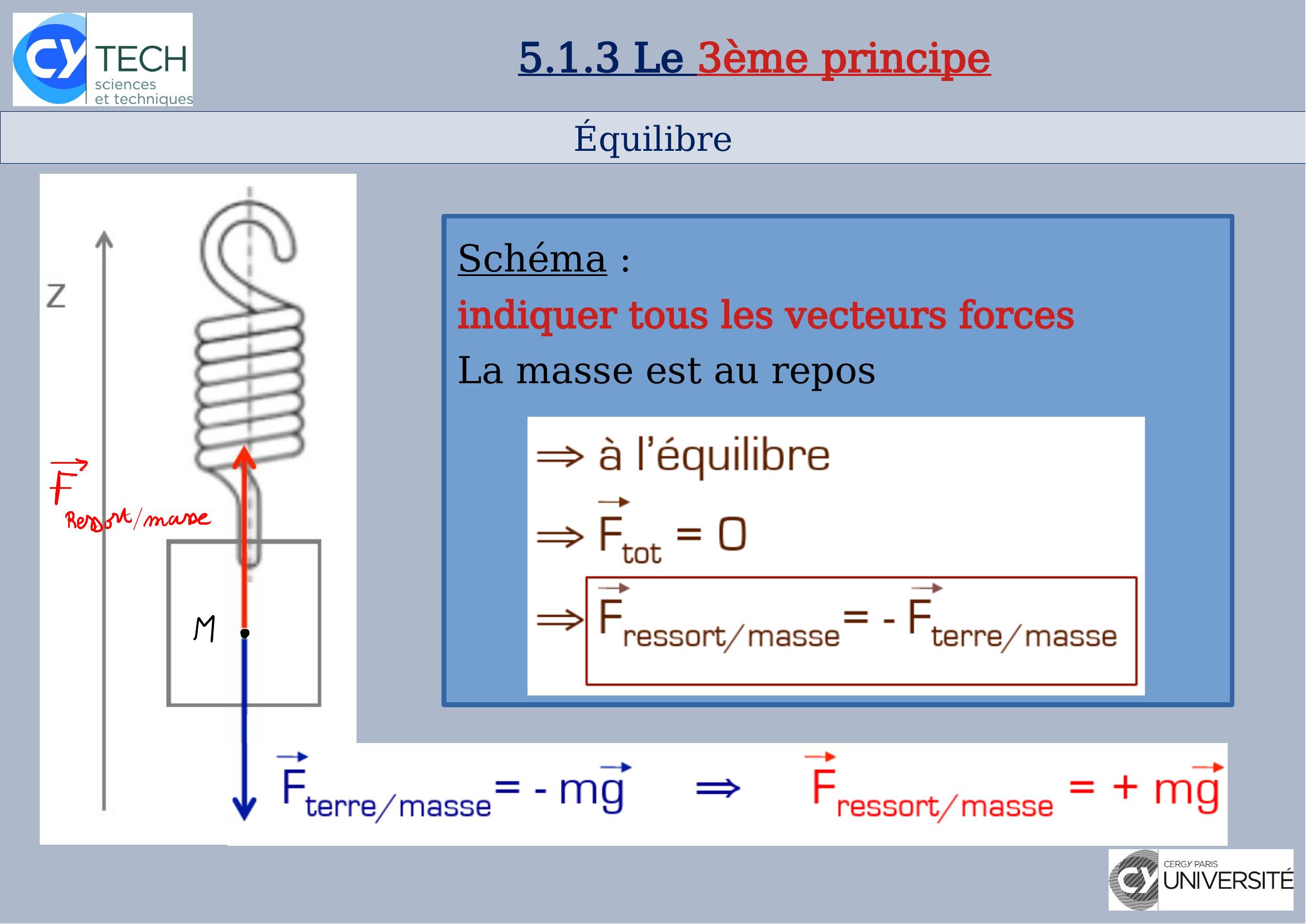
Page 20 : Équilibre5.1.3 Le 3ème principeSchéma :indiquer tous les vecteurs forcesLa masse est au repos
Page 21 : Énoncé5.1.3 Le 3ème principeREM : On ne parle pas d’équilibre, cette relation est toujours réalisée, même s’il y a une dynamique !
Page 22 : Action et réaction: Exemple : patineurs5.1.3 Le 3ème principehttps://www.youtube.com/watch?feature=playerdetailpage&v=WvExCwmThELe patineur de gauche pèse 72 kg, tandis que le patineur de droite pèse 95 kg. Puisqu'il y a action-réaction, la force appliquée aux deux patineurs est équivalente. Donc, il est normal que le patineur de 95 kg parcourra une distance moindre.
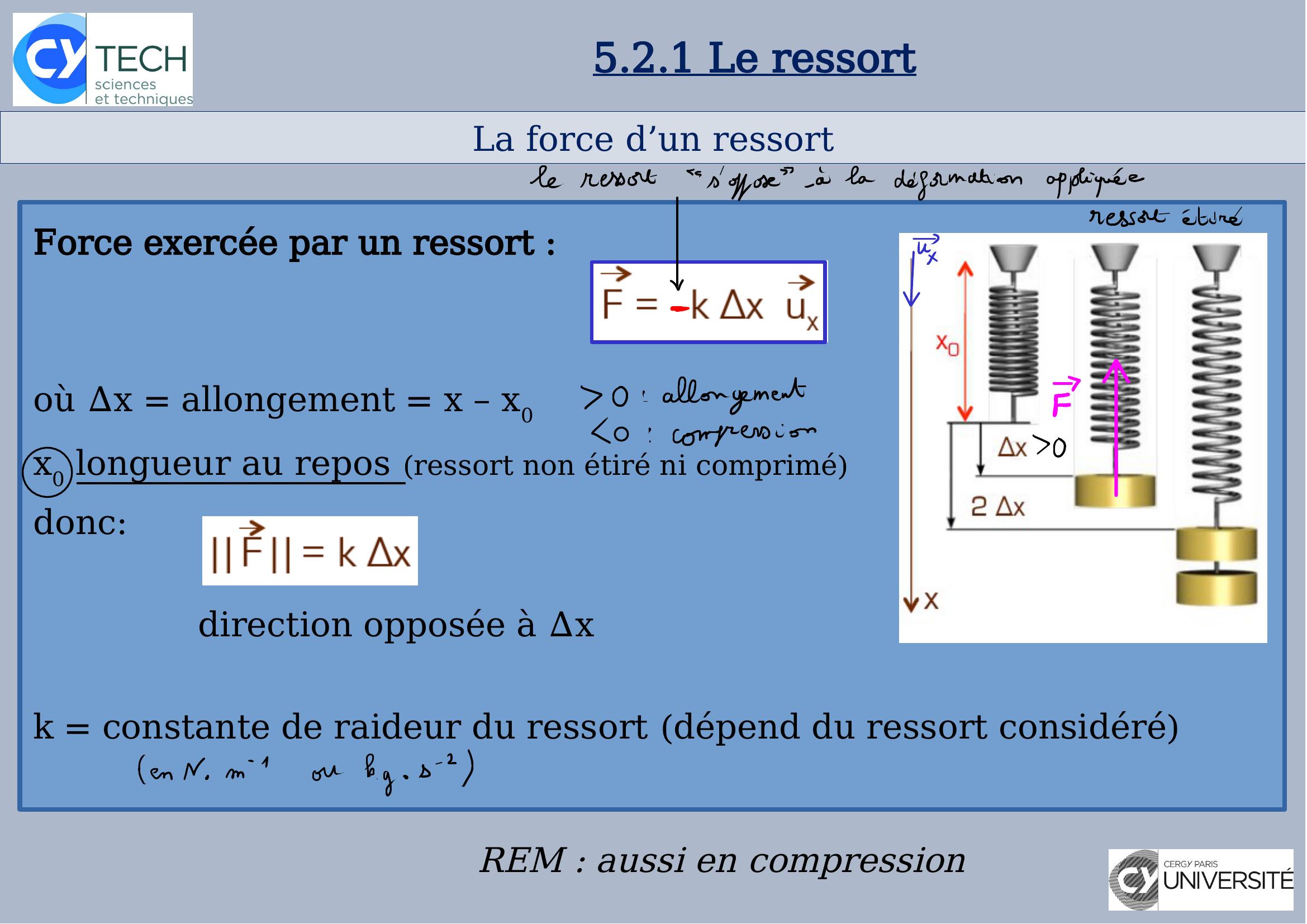
Page 23 : La force d’un ressort5.2.1 Le ressortForce exercée par un ressort :où Δx = allongement = x – x0x0 longueur au repos ressort non étiré ni comprimédonc:direction opposée à Δxk = constante de raideur du ressort dépend du ressort considéréREM : aussi en compression
Page 24 : La force d’un ressort5.2.1 Le ressortdynamomètre : un ressort étalonnépour mesurer des forcesForce :Dimensions :F = ma = ?Unité : Newton N1 N = ?k = ?
Page 25 : La force d’un ressort5.2.1 Le ressortForce :Dimensions :F = ma = M L T-2Unité : Newton N1 N = 1kg x 1m x 1s-2k = M T-2dynamomètre
Page 26 : Résumé5.2.2 F=ma: équation différentielle
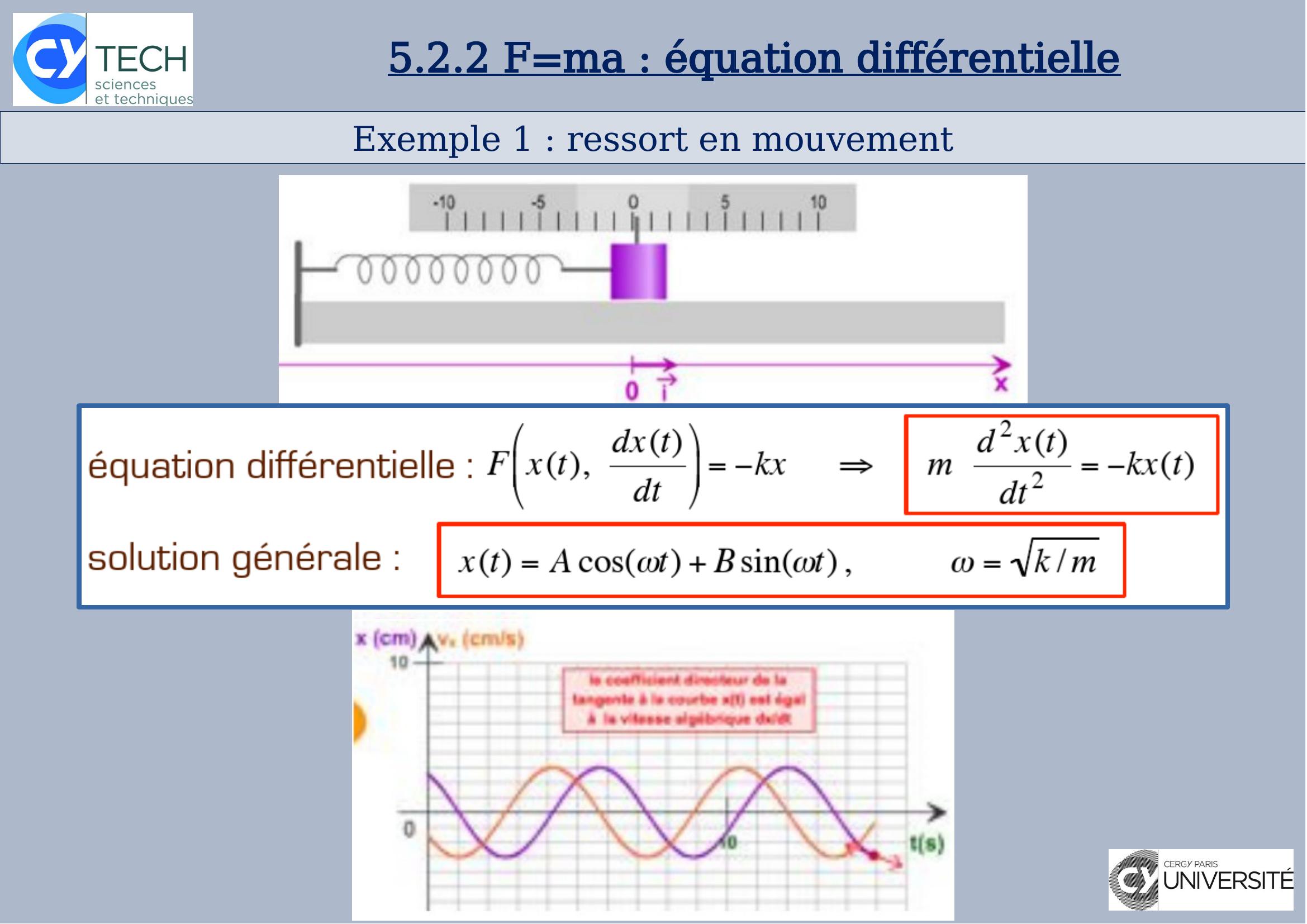
Page 27 : Question centrale de la dynamique5.2.2 F=ma: équation différentielledéterminer la dynamique d’un objet = déterminer son mouvement,prédire l’évolution de sa position : xtéquation différentielle du second ordre à résoudrepour obtenir la fonction xt
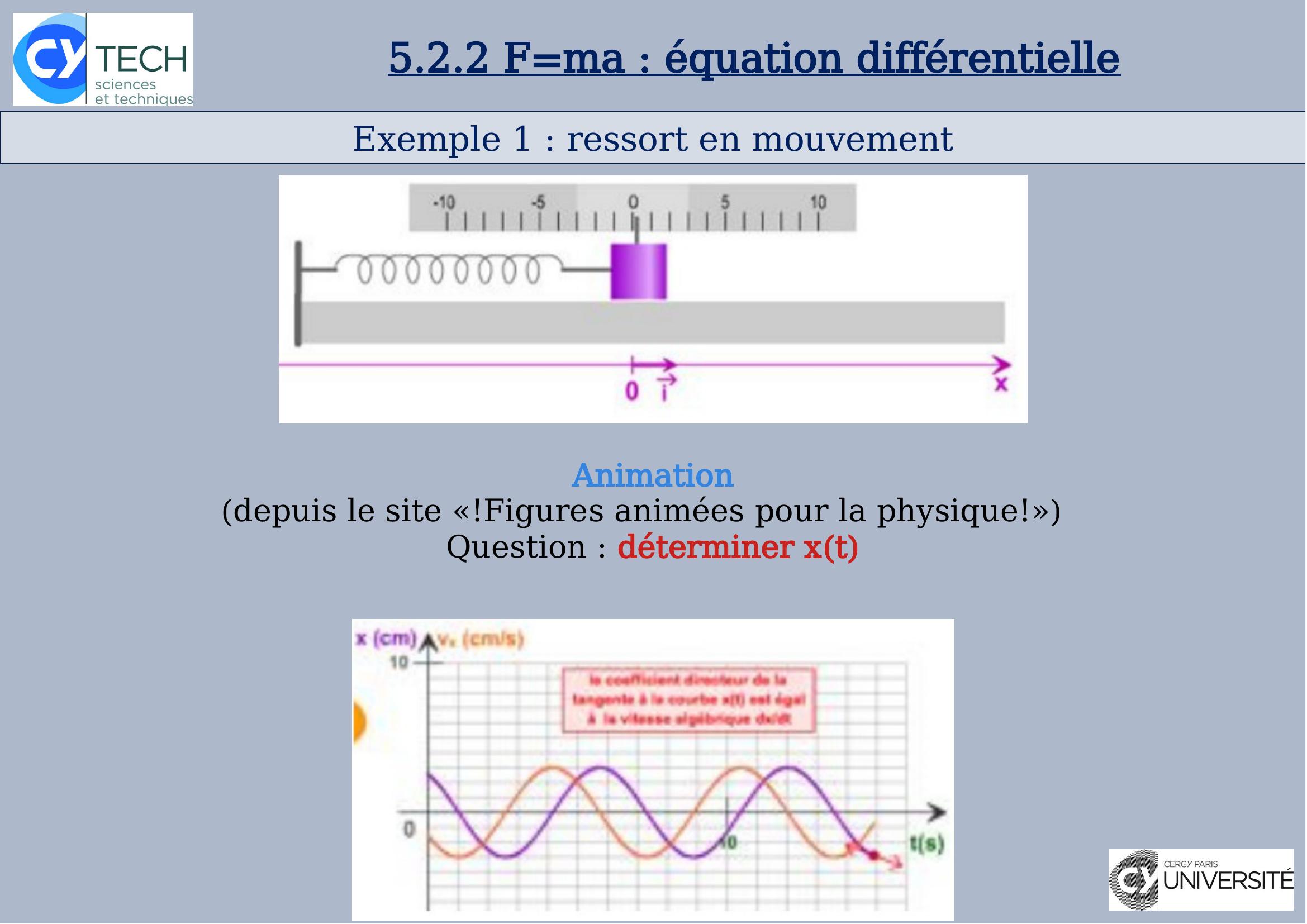
Page 28 : Exemple 1: ressort en mouvement5.2.2 F=ma: équation différentielleAnimationdepuis le site «!Figures animées pour la physique!»Question: déterminer xt
Page 29 : Exemple 1: ressort en mouvement5.2.2 F=ma: équation différentielle
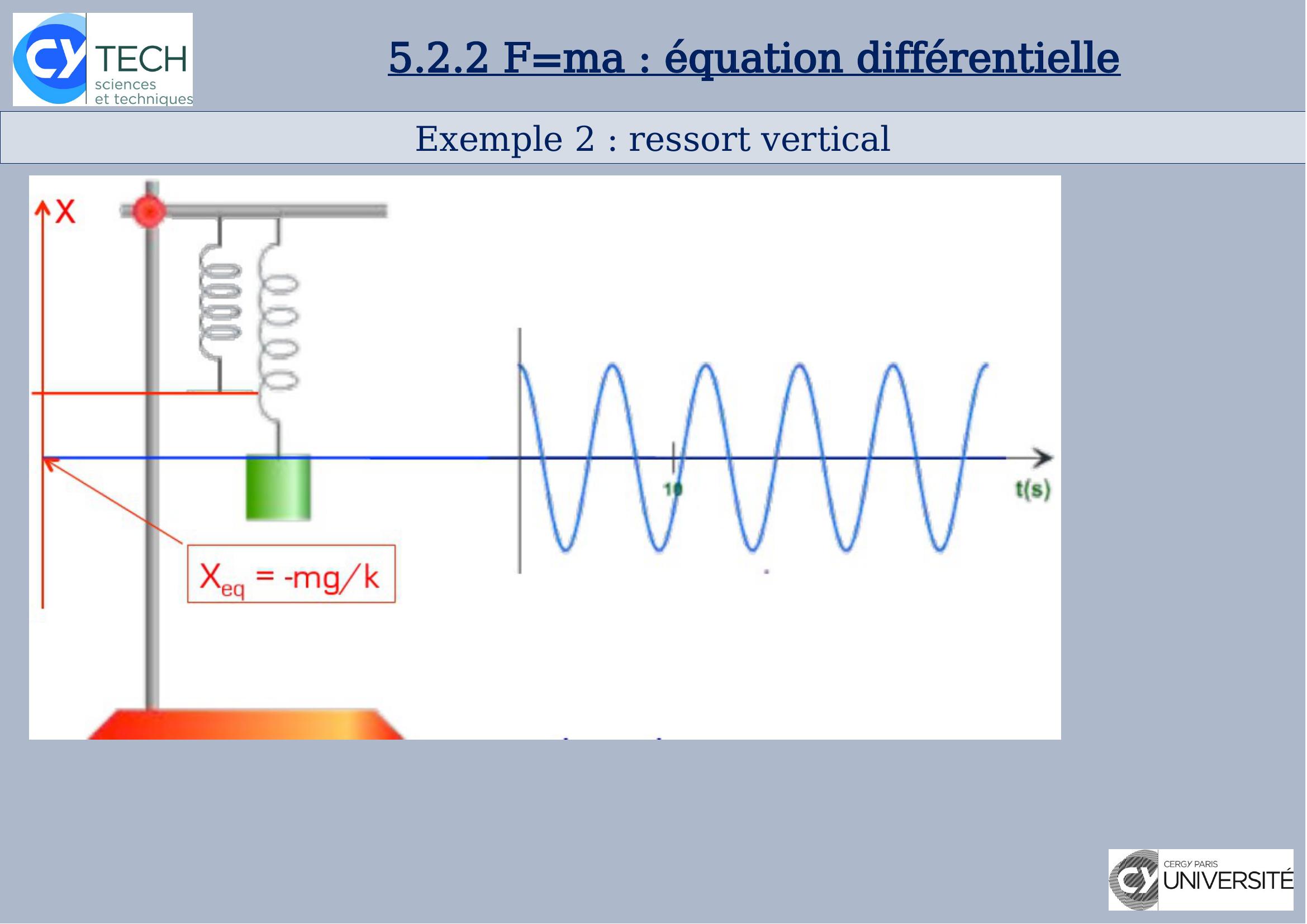
Page 30 : Exemple 2: ressort vertical5.2.2 F=ma: équation différentielleAnimationdepuis le site «!Figures animées pour la physique!»Question: déterminer xt
Page 31 : Exemple 2: ressort vertical5.2.2 F=ma: équation différentielle
Page 32 : Bibliographie 1Polycopié de cours2 Maria Barbi - 1P001 Concepts et Methodes de la Physique - groupes MIPI3 David Sénéchal - Mécanique I - D. Senechal -PHQ1144 Claude Pasquier - Mécanique5 pour la suite: Khan Academy , Unisciel etc...
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32