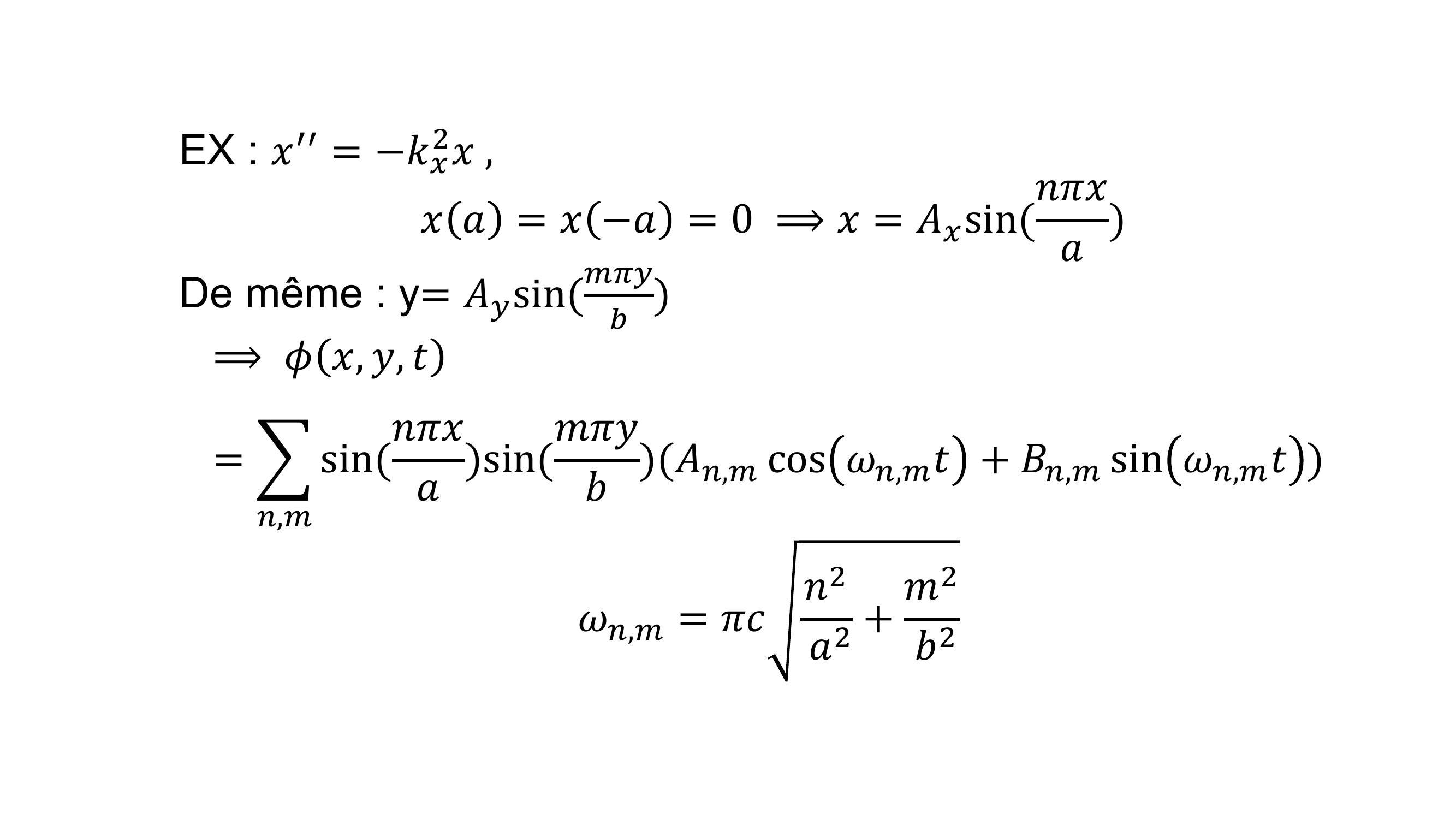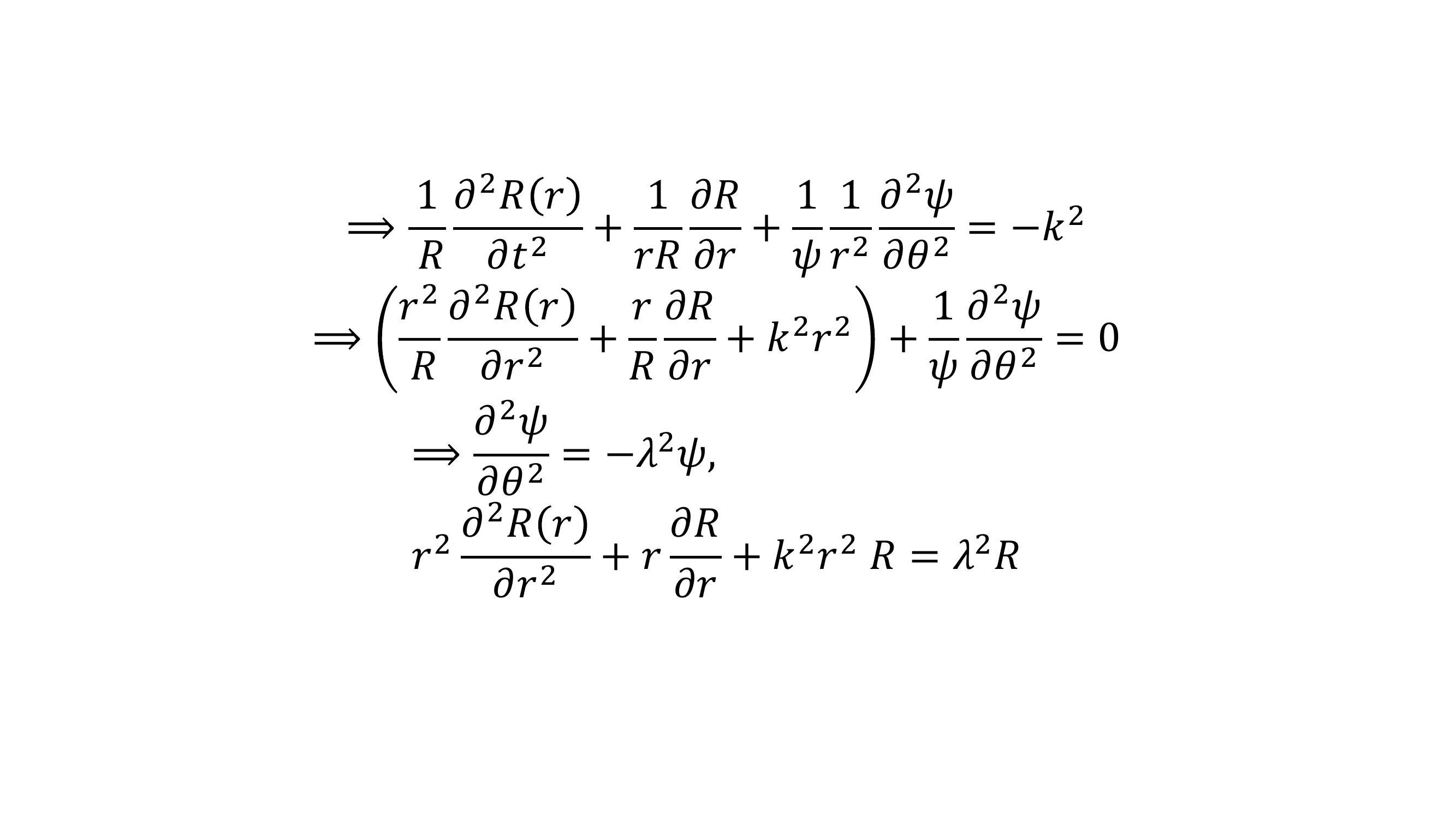CM Chapitre5
Télécharger le CM Chapitre5 en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13
Page 1 : Chapitre 5Ondes en dimension 2 et 3Section 5.1 : ondes scalairesSection 5.1.1 : Dimension 2EX : les vibrations d’une peau de tambour sont décrites par l’équation :1𝑐2𝜕2𝐹𝑥, 𝑦, 𝑡𝜕𝑡2𝜕2𝐹𝑥, 𝑦, 𝑡𝜕𝑥2𝜕2𝐹𝑥, 𝑦, 𝑡𝜕𝑦2= 0Avec 𝑐2 =𝑁𝜌ℎoù 𝜌est la densité de masse de la membrane, h est son épaisseur et N est la tension dans la membrane.
Page 2 : Pour toute fonction Fz différentielle deux fois :𝜕𝜕𝑡𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝑐𝐹′ , 𝜕2𝜕𝑡2 𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝑐2𝐹′′𝜕𝜕𝑥𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝛼𝐹′ , 𝜕2𝜕𝑥2 𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝛼2𝐹′′𝜕𝜕𝑦𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝛽𝐹′ , 𝜕2𝜕𝑦2 𝐹𝑐𝑡𝛼𝑥𝛽𝑦= 𝛽2𝐹′′⟹1𝑐2𝜕2𝐹𝑐𝑡𝛼𝑥𝛽𝑦𝜕𝑡2𝜕2𝐹𝑐𝑡𝛼𝑥𝛽𝑦𝜕𝑥2𝜕2𝐹𝑐𝑡𝛼𝑥𝛽𝑦𝜕𝑦2= 0⟹1 𝛼2 𝛽2 𝐹′′ = 0
Page 3 : ⟹Pour tout vecteur 𝑘= 𝑘𝑥, 𝑘𝑦 de norme 1, et toute fonction dérivable deux fois𝐹𝑐𝑡𝑘. Ԧ𝑟,Ԧ𝑟= 𝑥, 𝑦 est solution de l’équation d’onde en deux D.𝑘: direction de propagation de l’onde.Autre méthode : séparation des variablesAnsatz : 𝜙𝑥, 𝑦, 𝑡= 𝑋𝑥𝑌𝑦𝑇𝑡⟹𝑋𝑌𝑇′′𝑐2 𝑌𝑇𝑋′′ 𝑋𝑇𝑌′′ = 0On divise par XYT :𝑇′′𝑇𝑐2 = 𝑋′′𝑋+ 𝑌′′𝑌
Page 4 : Posons𝑇′′𝑇𝑐2 = 𝜔2𝑐2 ⟹𝑋′′𝑋+𝑌′′𝑌= 𝜔2𝑐2 ⟹𝑘𝑥, 𝑘𝑦, 𝜔Tels que 𝑘𝑥2 + 𝑘𝑦2 =𝜔2𝑐2Et ൞𝑇" = 𝜔2𝑇𝑋" = 𝑘𝑥2𝑋𝑌" = 𝑘𝑦2𝑌Trois oscillateurs harmoniques !⟹𝜙𝑥, 𝑦, 𝑡= 𝑘𝑥,𝑘𝑦𝐴𝑘𝑥,𝑘𝑦𝑒𝑖𝜔𝑡𝑘. Ԧ𝑟+ 𝐵𝑘𝑥,𝑘𝑦𝑒𝑖𝜔𝑡+𝑘. Ԧ𝑟+𝐶𝑘𝑥,𝑘𝑦𝑒𝑖𝜔𝑡𝑘. Ԧ𝑟 + 𝐷𝑘𝑥,𝑘𝑦𝑒𝑖𝜔𝑡+𝑘. Ԧ𝑟Relation de dispersion : 𝜔2 = 𝑐2𝑘𝑥2 + 𝑘𝑦2
Page 5 : Conditions aux bords :FigEn 1 D, on devait spécifier :൞𝜙𝑎, 𝑡, 𝜙𝑏, 𝑡𝑡𝜙𝑥, 0𝑥𝑎, 𝑏𝜕𝑡𝜙𝑥, 0𝑥𝑎, 𝑏
Page 6 : En second, le domaine est bordé par des surfaces S1 et on doit donner 𝜙𝑥, 𝑦, 𝑡pour toute paire 𝑥, 𝑦appartenant à S1EX : figure𝑆1 =𝑥, 𝑦𝑡𝑒𝑙𝑞𝑢𝑒𝑥= 𝑎, 𝑦𝑏𝑜𝑢𝑦= 𝑏, 𝑥𝑎𝑉1 =𝑥, 𝑦, 𝑡𝑡𝑒𝑙𝑞𝑢𝑒𝑥𝑎,𝑦𝑏𝜙𝑥, 𝑦, 0𝑒𝑡𝜕𝑡𝜙𝑥, 𝑦, 0 doivent être donnés sur l’intersection de 𝑉1 avec un plan 𝑥, 𝑦, 𝑡0 , 𝑡0 constant les conditions initiales.
Page 7 : EX : 𝑥′′ = 𝑘𝑥2𝑥,𝑥𝑎= 𝑥𝑎= 0 ⟹𝑥= 𝐴𝑥sin𝑛𝜋𝑥𝑎De même : y= 𝐴𝑦sin𝑚𝜋𝑦𝑏⟹𝜙𝑥, 𝑦, 𝑡= 𝑛,𝑚sin𝑛𝜋𝑥𝑎sin𝑚𝜋𝑦𝑏𝐴𝑛,𝑚cos 𝜔𝑛,𝑚𝑡+ 𝐵𝑛,𝑚sin 𝜔𝑛,𝑚𝑡𝜔𝑛,𝑚= 𝜋𝑐𝑛2𝑎2 + 𝑚2𝑏2
Page 8 : Section V.1.2 Coordonnées polairesDifférents choix de coordonnées peuvent produire des conditions aux bords simples ou complexes, selon la forme de la surface délimitant le domaine de l’onde.Par exemple en coordonnées polaires :𝑟=𝑥2 + 𝑦2 , 𝑥= 𝑟𝑐𝑜𝑠𝜃,𝑦= 𝑟𝑐𝑜𝑠𝜃,𝜃= arccos𝑥𝑟Il est aisé de décrire les conditions sur un bord circulaire !
Page 9 : Que devient alors l’équation d’onde ?Soit𝜕𝜕𝑥= 𝜕𝑟𝜕𝑥𝜕𝜕𝑟+ 𝜕𝜃𝜕𝑥𝜕𝜕𝜃= 𝑐𝑜𝑠𝜃𝜕𝜕𝑟𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃𝜕𝜕𝑦= 𝜕𝑟𝜕𝑦𝜕𝜕𝑟+ 𝜕𝜃𝜕𝑦𝜕𝜕𝜃= 𝑠𝑖𝑛𝜃𝜕𝜕𝑟+ 𝑐𝑜𝑠𝜃𝑟𝜕𝜕𝜃⟹𝜕2𝜕𝑥2 =𝑐𝑜𝑠𝜃𝜕𝜕𝑟𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃2= 𝑐𝑜𝑠2𝜃𝜕2𝜕𝑟2 + 𝑐𝑜𝑠𝜃𝜕𝜕𝑟𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃𝑐𝑜𝑠𝜃𝜕𝜕𝑟+ 𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃= 𝑐𝑜𝑠2𝜃𝜕2𝜕𝑟2 + 𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃𝑟2𝜕𝜕𝜃𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝑟𝜕𝜕𝜃𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃𝑟𝜕𝜕𝜃𝜕𝜕𝑟+ 𝑠𝑖𝑛2𝜃𝑟𝜕𝜕𝜃𝜕𝜕𝑟+ 𝑠𝑖𝑛2𝜃𝑟2𝜕2𝜕𝜃2 + 𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃𝑟2𝜕2𝜕𝜃2= 𝑐𝑜𝑠2𝜃𝜕2𝜕𝑟2 + 2𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃𝑟2𝜕𝜕𝜃+𝑠𝑖𝑛2𝜃𝑟𝜕𝜕𝜃𝜕𝜕𝑟+𝑠𝑖𝑛2𝜃𝑟2𝜕2𝜕𝜃2
Page 10 : ⟹𝜕2𝜕𝑥2 + 𝜕2𝜕𝑦2 = 𝜕2𝜕𝑟2 + 1𝑟𝜕𝜕𝑟+ 1𝑟2𝜕2𝜕𝜃2D’où l’équation d’onde en coordonnées polaires :1𝑐2𝜕2𝜙𝜕𝑡2 𝜕2𝜙𝜕𝑟2 + 1𝑟𝜕𝜙𝜕𝑟+ 1𝑟2𝜕2𝜙𝜕𝜃2= 0Séparation des variables :𝜙𝑟, 𝜃, 𝑡= 𝐹𝑟, 𝜃𝐺𝑡 ⟹
Page 11 : ⟹1𝐺𝑡1𝑐2𝜕2𝐺𝑡𝜕𝑡21𝐹𝜕2𝜕𝑟2 + 1𝑟𝜕𝜕𝑟+ 1𝑟2𝜕2𝜕𝜃2 𝐹= 0Où 𝜕2𝜕𝑟2 +1𝑟𝜕𝜕𝑟+1𝑟2𝜕2𝜕𝜃2= = 𝑙𝑎𝑝𝑙𝑎𝑐𝑖𝑒𝑛⟹𝜕2𝐺𝑡𝜕𝑡2= 𝑘2𝑐2𝐺𝑡𝐹𝑟, 𝜃= 𝑘2𝐹𝑟, 𝜃On sépare les variables : 𝐹𝑟, 𝜃= 𝑅𝑟𝜓𝜃
Page 12 : ⟹1𝑅𝜕2𝑅𝑟𝜕𝑡2+ 1𝑟𝑅𝜕𝑅𝜕𝑟+ 1𝜓1𝑟2𝜕2𝜓𝜕𝜃2 = 𝑘2⟹𝑟2𝑅𝜕2𝑅𝑟𝜕𝑟2+ 𝑟𝑅𝜕𝑅𝜕𝑟+ 𝑘2𝑟2+ 1𝜓𝜕2𝜓𝜕𝜃2 = 0⟹𝜕2𝜓𝜕𝜃2 = 𝜆2𝜓,𝑟2 𝜕2𝑅𝑟𝜕𝑟2+ 𝑟𝜕𝑅𝜕𝑟+ 𝑘2𝑟2 𝑅= 𝜆2𝑅
Page 13 : Partie angulaire𝜕2𝜓𝜕𝜃2 = 𝜆2𝜓⟹𝜓𝜃= 𝐵𝑐𝑜𝑠𝜆𝜃+ 𝐶𝑠𝑖𝑛𝜆𝜃Or on doit d’avoir 𝜓𝜃= 𝜓𝜃+ 2𝜋⟹𝜓0 = 𝐵= 𝜓2𝜋= 𝐵𝑐𝑜𝑠2𝜋𝜆+ 𝐶𝑠𝑖𝑛2𝜋𝜆⟹𝜆est un entierPartie radiale𝑟2𝐹′′ + 𝑟𝐹′ + 𝑘2𝑟2 𝐹= 𝜆2𝐹