CM Comparaison locale
Télécharger le CM Comparaison locale en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
Page 1 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceComparaison locale de fonctions réelles9 septembre 2024Comparaison locale de fonctions réelles
Page 2 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalence1 Négligeabilité2 Domination3 EquivalenceEquivalences et exponentielleEquivalences et logarithme4 Lien entre négligeabilité, domination et équivalenceComparaison locale de fonctions réelles
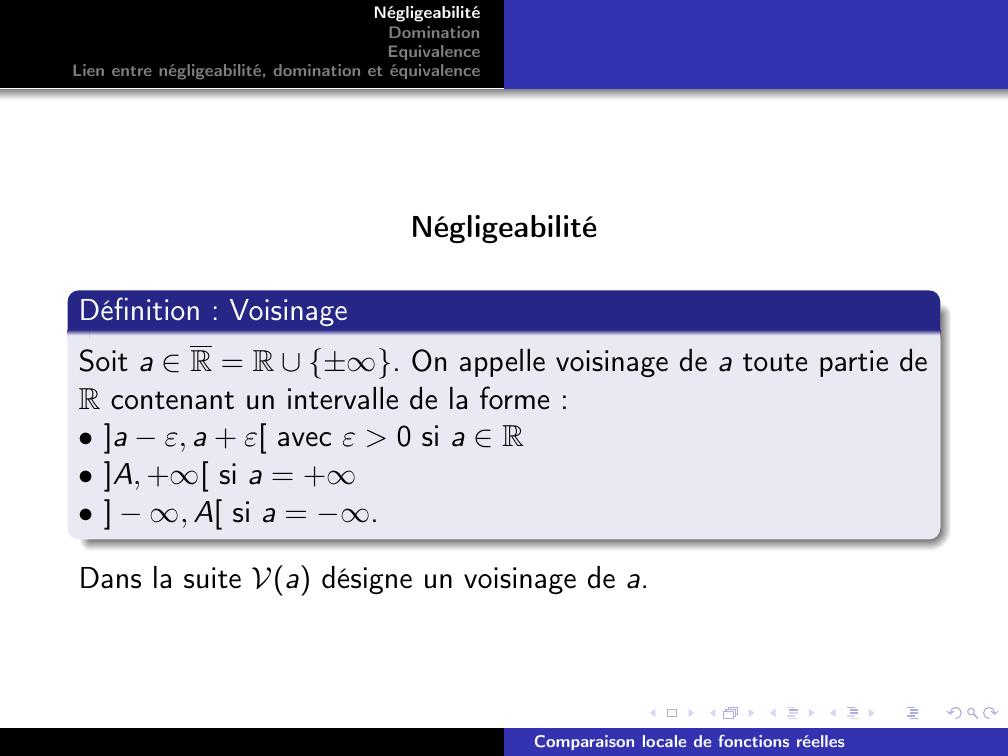
Page 3 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceNégligeabilitéDéfinition : VoisinageSoit a R = R ±. On appelle voisinage de a toute partie deR contenant un intervalle de la forme :• a ε, a + ε avec ε 0 si a R• A, + si a = +• , A si a = .Dans la suite Va désigne un voisinage de a.Comparaison locale de fonctions réelles
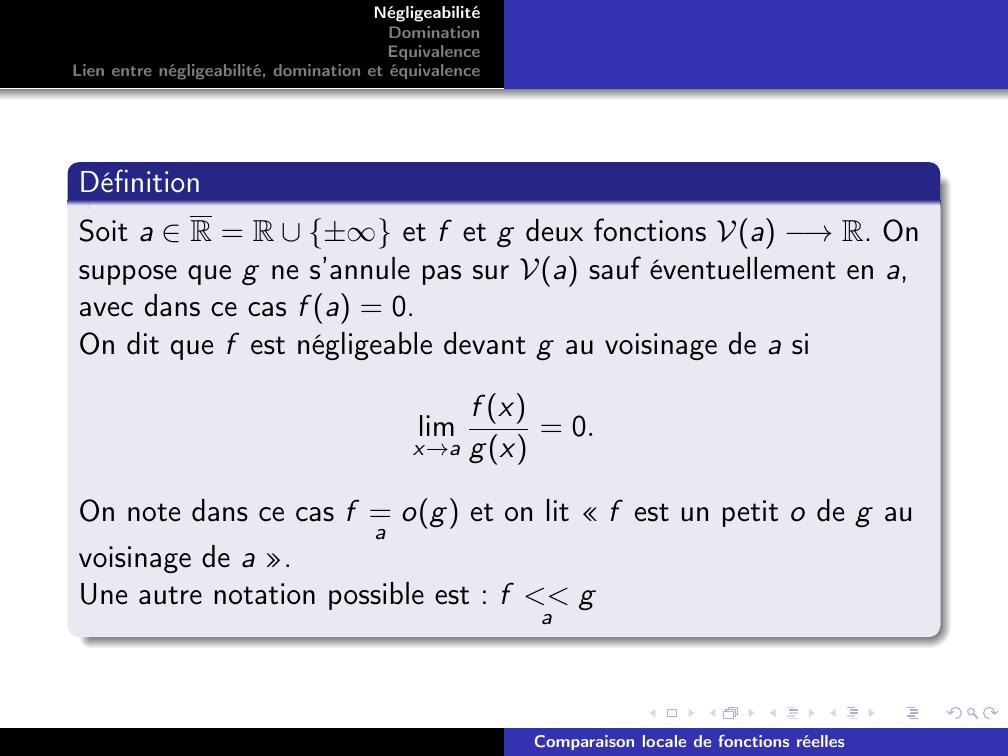
Page 4 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceDéfinitionSoit a R = R ± et f et g deux fonctions Va →R. Onsuppose que g ne s’annule pas sur Va sauf éventuellement en a,avec dans ce cas f a = 0.On dit que f est négligeable devant g au voisinage de a silimx→af xgx = 0.On note dans ce cas f =a og et on lit « f est un petit o de g auvoisinage de a ».Une autre notation possible est : f agComparaison locale de fonctions réelles
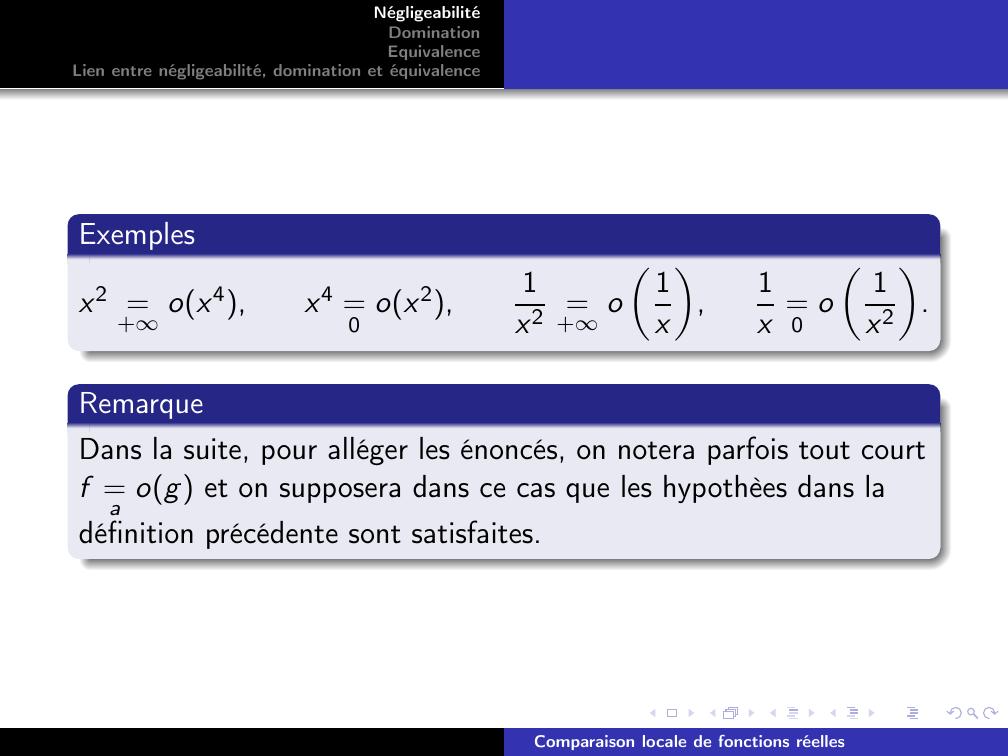
Page 5 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceExemplesx2 =+ox4,x4 =0 ox2,1x2 =+o1x,1x =0 o 1x2.RemarqueDans la suite, pour alléger les énoncés, on notera parfois tout courtf =a og et on supposera dans ce cas que les hypothèes dans ladéfinition précédente sont satisfaites.Comparaison locale de fonctions réelles
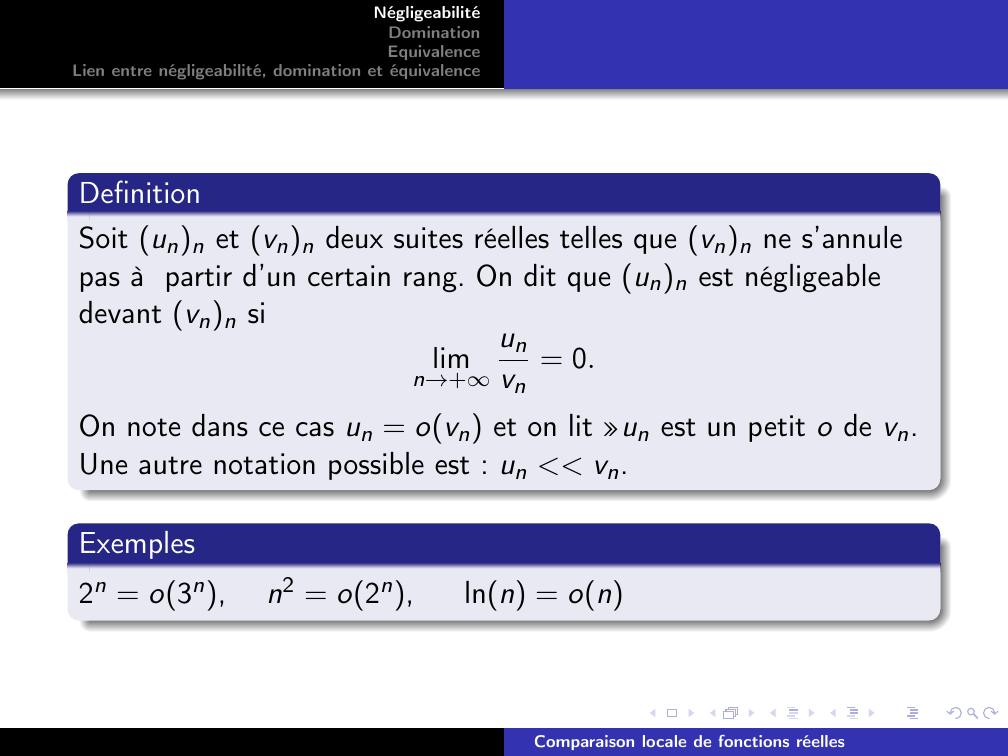
Page 6 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceDefinitionSoit unn et vnn deux suites réelles telles que vnn ne s’annulepas à partir d’un certain rang. On dit que unn est négligeabledevant vnn silimn→+unvn= 0.On note dans ce cas un = ovn et on lit »un est un petit o de vn.Une autre notation possible est : un vn.Exemples2n = o3n,n2 = o2n,lnn = onComparaison locale de fonctions réelles
Page 7 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalencePropositionSoit f : Va →R et ℓR. On a :limx→a f x = ℓ⇔f =a ℓ+ o1.En particulier, limx→a f x = 0 ⇔f =a o1. Ainsi, o1 est unefonction de limite nulle en a.Comparaison locale de fonctions réelles
Page 8 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceProposition : Opérations sur les petits o1 Transitivité :Si g = og et g = oh, alors f = oh.2 Multiplication par un réel non nul :Si f = og, alors pour tout λ R, f = oλg et λf = og.3 Somme de petits o d’une même fonction :Si f1 = og et f2 = og, alors f1 + f2 = og.4 Produit :Si f1 = og1 et f2 = og2, alors f1f2 = og1g2.Si f = og, alors fh = ogh.5 Composition à droite :Si f =a og et limx→b hx = a, alors f ◦h =b og ◦h.Comparaison locale de fonctions réelles
Page 9 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceRemarqueLa composition à droite s’interprètre comme un changement devariables. Voici deux exemples :• Pour comparerln x et ln x au voisinage de +, on poseu = hx = ln x :on alimx→+hx = +et x =+ox, alorsln x =+oln x.• Pour comparer e1x et 1x au voisinage de 0+, on poseu = hx = 1x :on a limx→0+ hx = +et x =+oex, alors 1x =0+ oe1x .Comparaison locale de fonctions réelles
Page 10 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceOpérations interdites !1 Il est interdit d’additionner des relations de négligeabilitémembre à membre. Les égalités f1 = og1 et f2 = og2n’entrainent pas que f1 + f2 = og1 + g2.Par exemple, x 1 =+ox2 et 1 =+o1 x2, maisx ̸=+o1.2 Il est interdit de composer une relation de négligeabilité par lagauche. Si f = og, on n’a pas forcément f ◦f = oh ◦g.Par exemple, ln x =+ox, mais1ln x ̸=+o1x. Ainsi, onne peut pas composer par x 7→1x par la gauche.Comparaison locale de fonctions réelles
Page 11 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceThéorème :Croissances comparées usuellesSoit a, b R2.Au voisinage de +:1 Si a b, alors xa =+oxb.2 Si 0 a b, alors ax =+obx.3 Si a 0, alors ln xb =+oxa.4 Si a 0, alors xb =+oeax.Au voisinage de 0 :1 Si a b, alors xb =0 oxa.2 Si a 0, alors xa =0 oln xb.Comparaison locale de fonctions réelles
Page 12 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceDominationDefinitionSoit a R = R ± et f et g deux fonctions Va →R. Onsuppose que g ne s’annule pas sur Va sauf éventuellement en a,avec dans ce cas f a = 0.On dit que f est dominée par g au voisinage de a si la fonction f /gest bornée au voisinage de a.On note dans ce cas f =a Og et on lit « f est un grand O de gau voisinage de a ».Exemplessin1x=0 O1,x2 =0 Ox,2x2 =+Ox2,x2 =0 Ox.Comparaison locale de fonctions réelles
Page 13 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceRemarquef =a O1 ⇔f est bornée au voisinage de a.Proposition : Opérations sur les grand OToutes les opérations énoncées pour les petits o restent valablespour les grands O.Opérations interdites !Les opérations interdites pour les petits o additionner membreà membre et composition par la gauche restent interdites pour lesgrands O.Comparaison locale de fonctions réelles
Page 14 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeEquivalenceDefinitionSoit a R = R ± et f et g deux fonctions Va →R. Onsuppose que g ne s’annule pas sur Va sauf éventuellement en a,avec dans ce cas f a = 0.On dit que f est équivalente à g au voisinage de a silimx→af xgx = 1.On note dans ce cas f a g.Remarque importanteNe jamais écrire f 0 car la fonction nulle ne vérifie pas lesconditions de la définition.Comparaison locale de fonctions réelles
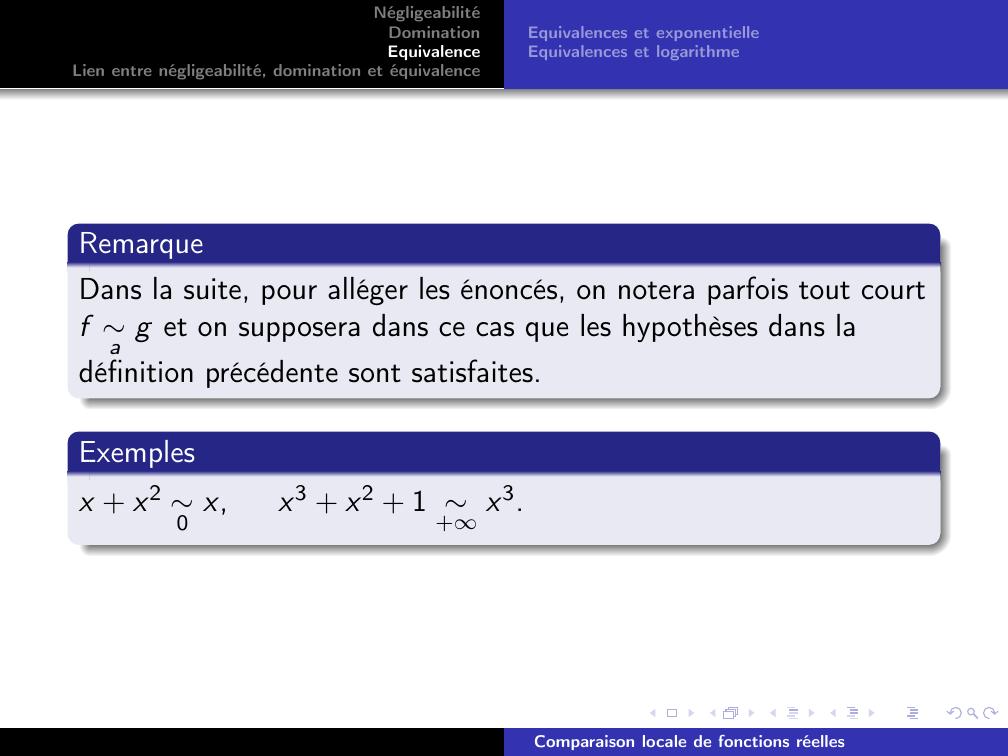
Page 15 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeRemarqueDans la suite, pour alléger les énoncés, on notera parfois tout courtf a g et on supposera dans ce cas que les hypothèses dans ladéfinition précédente sont satisfaites.Exemplesx + x2 0 x,x3 + x2 + 1 +x3.Comparaison locale de fonctions réelles
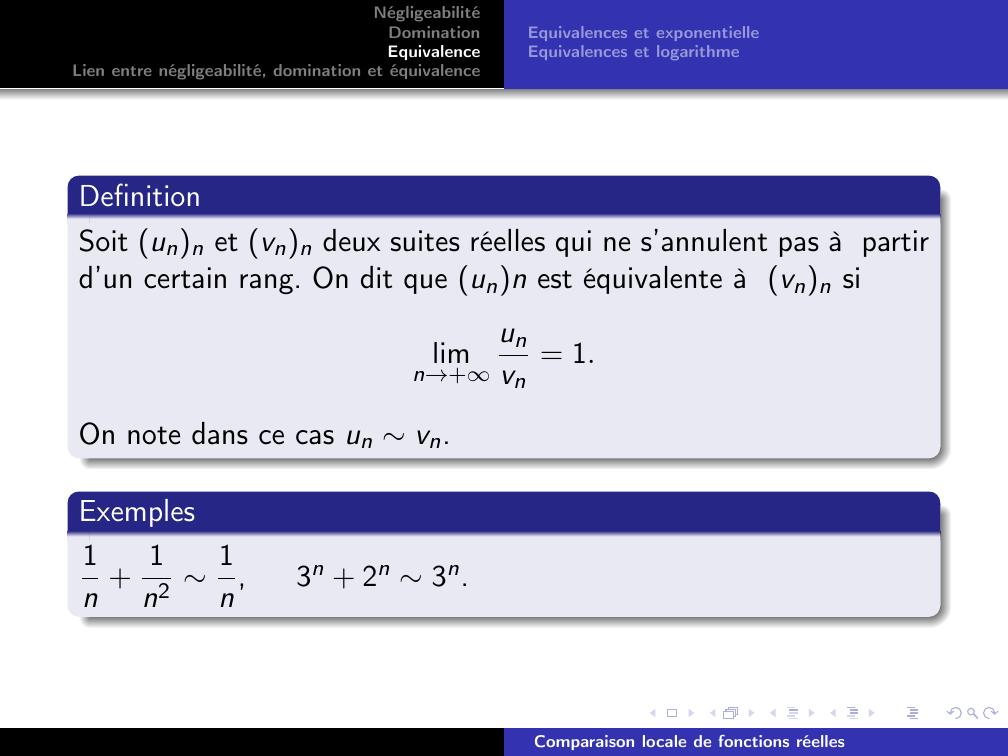
Page 16 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeDefinitionSoit unn et vnn deux suites réelles qui ne s’annulent pas à partird’un certain rang. On dit que unn est équivalente à vnn silimn→+unvn= 1.On note dans ce cas un vn.Exemples1n + 1n2 1n,3n + 2n 3n.Comparaison locale de fonctions réelles
Page 17 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeProposition : Equivalents usuels• Tout polynôme est équivalent à son terme de plus haut degré auvoisinage de ±.• Tout polynôme est équivalent à son terme de plus petit degré auvoisinage de 0.• Si f admet un développement limité au voisinage de 0, alors f estéquivalente au terme non nul de plus faible ordre au voisinage de 0.1/ ex 1 0 x2/ ln1 + x 0 x3/ 1 + xα 1 0 αx4/ sin x 0 x5/1 cos x 0x226/ tan x 0 x7/ arcsin x 0 x8/ arctan x 0 x9/ sh x 0 x10/ ch x 1 0x2211/ th x 0 xComparaison locale de fonctions réelles
Page 18 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmePropositionLa relation "est équivalente à " est une relation d’équivalence :pour toutes fonctions f , g et h, on a• Réflexivité : f a f• Symétrie : si f a g, alors g a f• Transitivité : si f a g et g a h, alors f a h.Il s’agit d’une vérification directe.Comparaison locale de fonctions réelles
Page 19 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeProposition1 Lien limites/équivalence :• Pour tout ℓR, limx→a = ℓ⇔f a ℓ.• Si f a g, alors soit f et g ont toutes les deux une limite ena, en l’occurence la màªme, soit aucune de ces deux fonctionsne possà¨de de limite en a.2 Lien négligeabilité/équicalence :• f a g ⇔f =a g + og.• f =a og ⇔f + g a g.3 Signe et équivalence :• Si f a g, alors f et g sont de màªme signe au voisinage dea.• Si f ne s’annule pas au voisinage de a et f a g, alors g nes’annule pas au voisinage de a.Comparaison locale de fonctions réelles
Page 20 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeProposition : Opérations sur les équivalences1 Produit :Si f a f1 et g a g1, alors fg a f1g1.2 Inverse :Si f a g et f ne s’annule pas au voisinage de a, alors 1f a1g .3 Puissance :Si f a g et f est strictement posistive au voisinage de a, alorspour tout réel α, f α a gα.Attention : α ne dépend pas de la variable x.4 Composition à droite :Si f a g et limx→b hx = a, alors f ◦h b g ◦g.Comparaison locale de fonctions réelles
Page 21 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeOpérations interdites !1 Il est interdit d’additionner des équivalents : si f a f1 etg a g1, on n’a pas nécessairement f + g a f1 + g1.Par exemple, x + 1 +x et x + 3 +x + 1, mais on n’aclairement pas 4 +1.2 Il est interdit de composer un équivalent par la gauche : sif a g, on n’a pas forcément h ◦f a h ◦g.Par exemple, x +x + ln x, mais on n’a pas ex +xex encomposant par x 7→ex par la gauche.Comparaison locale de fonctions réelles
Page 22 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeExercice : Calculer les limites suivantes en utilisant leséquivalences :1limx→051 + 6x 31 + x3 sinx ln1 + x2 a, b 0limx→+ a1x + b1x2!xComparaison locale de fonctions réelles
Page 23 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeEquivalence et exponentielleRemarque importanteOn ne peut pas composer un équivalent à gauche parl’exponentielle : si f a g, on n’a pas forcément ef a eg.Par exemple, x +x + 1 mais on n’a pas ex +ex+1 carlimx→+ex + 1ex= e ̸= 1.Toutefois, sous certaines hypothèses, on peut composer à gauchepar l’exponentielle :PropositionOn a :ef a eg ⇔limx→af g = 0.Comparaison locale de fonctions réelles
Page 24 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeEn effet, si ef a eg, alors limx→aef xegx = 1, d’ou limx→a ef xgx = 1.En utilisant la continuité de la fonction x 7→ln x en 1, on a :limx→af xgx = limx→aln ef xgx= lnlimx→a ef xgx= ln 1 = 0Réciproquement, si limx→af x gx = 0, en utilisant la continuitéde la fonction x 7→ex en 0, on a :limx→aef xegx = limx→a ef xgx = elimf xgx = e0 = 1.Comparaison locale de fonctions réelles
Page 25 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmeEquivalences et logarithmeRemarque importanteOn ne peut pas composer un équivalent à gauche par lelogarithme : si f a g et f est strictement positive au voisinage dea, an n’a pas forcément ln f a ln g.Par exemple, 1 + x 0 1 + 2x mais on n’a pasln1 + x 0 ln1 + 2x car limx→0ln1 + 2xln1 + x = 2 ̸= 1.Toutefois, sous certaines conditions, on peut composer à gauchepar le logarithme :Comparaison locale de fonctions réelles
Page 26 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceEquivalences et exponentielleEquivalences et logarithmePropositionSi f a g, avec f strictement positive au voisinage de a, et si lafonction x 7→1ln gx est bornée au voisinage de a en particulier,si limx→a gx ̸= 1, alors ln f a ln g.Comparaison locale de fonctions réelles
Page 27 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceLien entre négligeabilité, domination et équivalenceProposition• La négligeabilité entraine la domination :f =a og ⇒f =a Og.• L’équivalence entraine la domination :f a g ⇒f =a Og.En effet, il est clair que si la limite en a d’une fonction ici f /gvaut 0 ou 1, alors cette fonction est bornée au voisinage de a.Comparaison locale de fonctions réelles
Page 28 : NégligeabilitéDominationEquivalenceLien entre négligeabilité, domination et équivalenceExemple :ex =0 1 + x + x22 + x36 + ox3, alors ex =0 1 + x + x22 + Ox3cosx =0 1 x22 + ox2, alors cosx =0 1 + Ox2Exercice :Montrer quenXk=11k =+lnn + O1 ou encorenXk=11k +lnnIndication :1-Rappelons que x 1, ln1 + x x2-Posons les deux suites suivantes :un =nXk=11k lnn + 1 et vn =nXk=11k lnn,montrer que les deux suites un et vn sont adjacentes.Comparaison locale de fonctions réelles
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28