CM Comportement Asymptotique

Télécharger le CM Comportement Asymptotique en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87

Page 1 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLComportements Asymptotiques1Relations de comparaisons de suitesDomination, négligeabilitéEquivalence2Relations de comparaisons de fonctionsDomination, négligeabilitéEquivalence3Développements limitésGénéralitésFormule de Taylor-YoungOpérations sur les D.L.4Application des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesD. CransacAnalyse

Page 2 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDénitionSoit un et vn deux suites.On dit que :un est dominée par vn si la suiteunvnest bornée.On note alors un = O vn.la suite un est négligeable devant vn ou que vn estprépondérante devant la suite unsi la suiteunvnconverge vers 0.On note alors un = o vn.Exemples.On a : cosn + 4n2= O 1n2car cosn + 4 est bornée.On a : n3 sinn = on5En eet :limn→+n3 sinnn5= sinnn2→n→+0 théorème d'encadrementD. CransacAnalyse

Page 3 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceRemarques.un est bornée si et seulement si un = O1.un converge vers 0 si et seulement si un = o1.un = o vn =⇒un = O vn .PropositionSoient un , vn et wn trois suites.Si un = O vn et vn = O wn,alors un = O wn transitivité de la relation O .Si un = o vn et vn = o wn, alors un = o wn transitivité de larelation o .Démonstration.On démontre le deuxième point, le premier point est analogue.Soit un une suite telle que un = o wn et wn = o tn .Alors, pour tout n n0, on a : unwn= unvn· vnwn→n→+0 · 0 = 0.Ainsi, un = o tn .D. CransacAnalyse

Page 4 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient un , vn , wn et tn quatre suites telles que wn et tn nes'annulent pas à partir d'un certain rang. Soit λ, µ K2.Si un = O wn et vn = O wn, alors λun + µvn = O wn .Si un = o wn et vn = o wn, alors λun + µvn = o wn .Si un = O wn et vn = O tn, alors unvn = O wntnSi un = O wn et vn = o tn, alors unvn = o wntn .Exemplesn2=n→+on4.2n=n→+o 3n.1n2=n→+o1n.D. CransacAnalyse

Page 5 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceRappelDénition Exponentielle d'exposant réel quelconqueSoit a R+et b R,ab = eb ln aDémonstration.On aln ab = b ln aen appliquant la fonction exponentielle on obtient le résultat.D. CransacAnalyse

Page 6 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionlimn→+ln nn= 0Démonstration.On étudie φx = ln x x.φ′x = 1 xx, donc sur 1; + φ est décroissante . Comme φ1 = 1,φ 0, donc0 ⩽ln x ⩽x sur 1; +Si on remplace x par x, on obtient 0 ⩽ln x ⩽x =⇒0 ⩽12 ln x ⩽x0 ⩽ln xx⩽2xEn passant à la limite en +, d'après le théorème des gendarmes on alimx→+ln xx= 0D. CransacAnalyse

Page 7 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionlimn→+1 + 1nn= eDémonstration.1 + 1nn= en ln1+ 1n Orln1 + XX= ln1 + X ln1 + 0X 0→X→0 1etlimn→+1n = 0 donc, par composition,limn→+ln1 + 1n1n= 1 =limn→+n ln1 + 1nOn en déduit, par composition, quelimn→+1 + 1nn= eD. CransacAnalyse

Page 8 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceProposition croissances comparéesSoit α, β R avec α, β 0, et q 1. Alors :lnβ n = o nαnα = o qnqn = o n!n! = o nnDémonstration.On étudie le rapport nαqn = eα ln nn ln q = enα ln nn ln qOn a αln nnln q →ln qn→+donc nαln nnln q→n→+carq 1Or eX→X→0donc par composition enα ln nn ln q→n→+0On a bien nαqn→n→+0D. CransacAnalyse

Page 9 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.On étudie le rapport lnβ nnα= eβ lnln nα ln n = eln nβ lnln nln n αOr ln XX→0X→+et ln n →+n→+donc par compositionlnln nln n→0n→+donc β lnln nln nα→n→+αdonc ln nβ lnln nln nα→n→+.Or eX→X→0donc par composition eln nβ lnln nln n α→n→0On a bien lnβ nnα→n→0D. CransacAnalyse

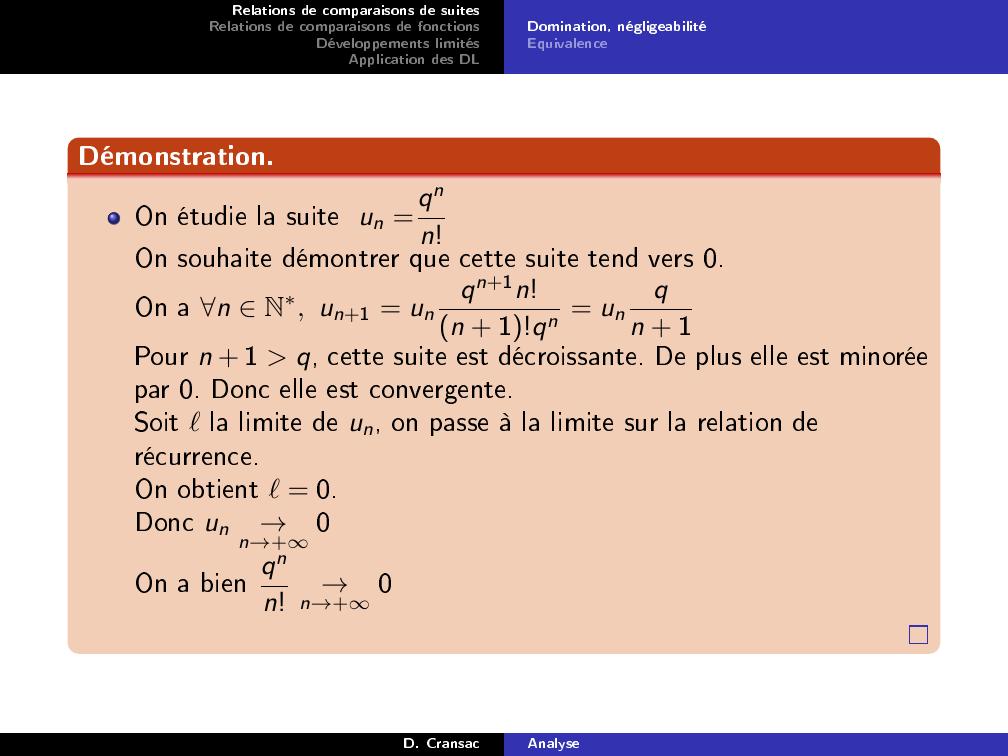
Page 10 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.On étudie la suite un =qnn!On souhaite démontrer que cette suite tend vers 0.On a n N, un+1 = unqn+1n!n + 1!qn = unqn + 1Pour n + 1 q, cette suite est décroissante. De plus elle est minoréepar 0. Donc elle est convergente.Soit ℓla limite de un, on passe à la limite sur la relation derécurrence.On obtient ℓ= 0.Donc un→n→+0On a bien qnn!→n→+0D. CransacAnalyse

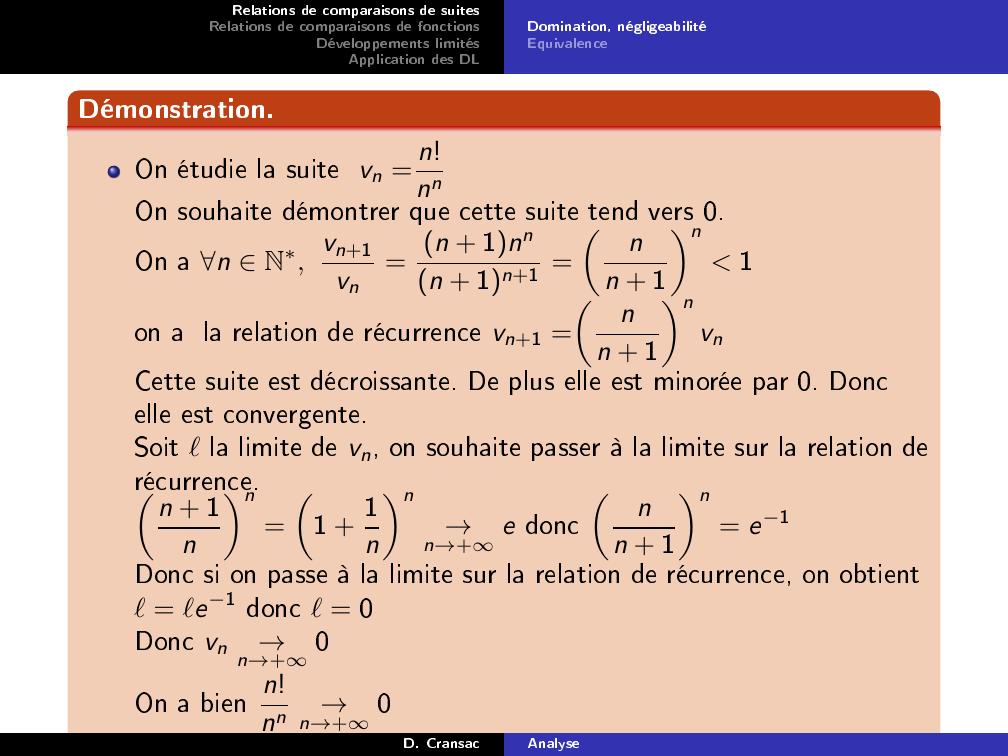
Page 11 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.On étudie la suite vn = n!nnOn souhaite démontrer que cette suite tend vers 0.On a n N, vn+1vn= n + 1nnn + 1n+1 =nn + 1n 1on a la relation de récurrence vn+1 =nn + 1nvnCette suite est décroissante. De plus elle est minorée par 0. Doncelle est convergente.Soit ℓla limite de vn, on souhaite passer à la limite sur la relation derécurrence.n + 1nn=1 + 1nn→n→+e doncnn + 1n= e1Donc si on passe à la limite sur la relation de récurrence, on obtientℓ= ℓe1 donc ℓ= 0Donc vn→n→+0On a bien n!nn→n→+0D. CransacAnalyse

Page 12 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceOn en déduit directement la proposition suivante :Proposition1nα = o 1lnβ1qn = o 1nα1n! = o 1qn1nn = o 1n!D. CransacAnalyse

Page 13 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceRemarque.En notant un vn au lieu de un = o vn, on a donc lorsque n tend vers+:1nn 1n! 1qn 1nα 1lnβ nlnβ n nα qn n! nn.D. CransacAnalyse

Page 14 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceEquivalenceDénitionSoit un et vn deux suites.On dit que unnN est équivalente à vnnN,si la suiteunvnconverge vers 1.On note alorsun vnExemple. On a n n + 1. En eet,n + 1n=r1 + 1n. Or,limn→+1 + 1n= 1 et par composition par la fonction racine, continueen 1, on a bienlimn→+n + 1n=1 = 1.D. CransacAnalyse

Page 15 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionLa relation est une relation d'équivalence sur l'ensemble des suitesne s'annulant pas, c'est à dire :est réexive : un un ;est symétrique : un vn ⇒vn un ;est transitive : si un vn et vn wn, alors un wn.D. CransacAnalyse

Page 16 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient un , vn.un vn ⇐⇒un vn = o vn .un vn=⇒un = O vn et vn = O un.Démonstration.un vn ⇔limn→+unvn = 1 ⇔limn→+unvn 1= 0⇔limn→+un vnvn= 0 ⇔un vn = o vn .Si un vn alorsunvnnn0converge vers 1 donc bornée. De plus, commeunvnnn0converge vers 1 alors unvn donc un est non nulle à partir d'uncertain rang et vnunnn0converge vers 1 donc vnunnn0est bornée.D. CransacAnalyse

Page 17 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient un , vn , wn et tn quatre suites telles que un wn etvn tn. Alors on a :unvn wntnunvnwntnp N, upn w pnDémonstration.On a, pour n N, unwnvnzn = unvn × wnzn→n→+1 par produit de limitesPour n N, on aunvnwnzn= unznvnwn = unvn ×wnzn1→n→+1comme quotient de limites.Enn, pour n et p N, on a upnv pn =unvnp→n→+1p = 1 par opérationssur les limites.D. CransacAnalyse

Page 18 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceExemple.Montrons que n6n6720.En eet, pour tout j N xé, on a n j n ;par conséquent : n6= 16!5Yj=0n j 16!5Yj=0n = n6720D. CransacAnalyse

Page 19 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceATTENTION ! ! ! !On ne peut ni ajouter, ni soustraire, les équivalents :n + 1 n + 2 et n n mais on n'a pas 1 2On ne compose pas les équivalents :si f est une fonction même continue sur R et si un vn, on n'apas forcément f un f vn :si un = n2 + n, vn = n2 et f = exp, on a un vn, mais :f unf vn = en2+nn2 = en→n→++, donc f un ̸f vn .Lors d'une mise en puissance d'un équivalent, l'exposant doit êtreconstant :on a 1 + 1n 1 mais1 + 1nn̸1nen eet1 + 1nn→e, donc1 + 1nne.En règle générale, on ne sépare pas les limitesD. CransacAnalyse

Page 20 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoit un une suite et ℓR.limn→+un = ℓ⇐⇒un ℓDémonstration.En eet, silimn→+un = ℓ̸= 0 alors un ne s'annule pas à partir d'uncertain rang et on a : unℓ→n→+ℓℓ= 1. Donc un ℓ.Réciproquement, si un ℓ, alors puisque ℓ̸= 0, unℓ→n→+1 doncun = unℓℓ→n→+ℓD. CransacAnalyse

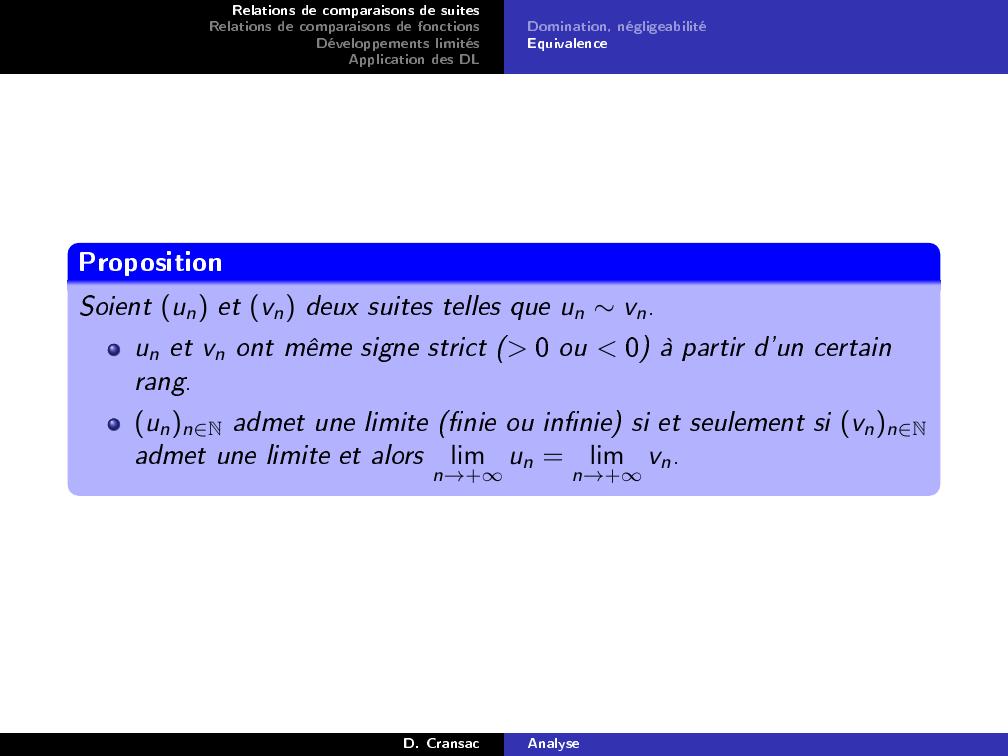
Page 21 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient un et vn deux suites telles que un vn.un et vn ont même signe strict 0 ou 0 à partir d'un certainrang.unnN admet une limite nie ou innie si et seulement si vnnNadmet une limite et alorslimn→+un =limn→+vn.D. CransacAnalyse

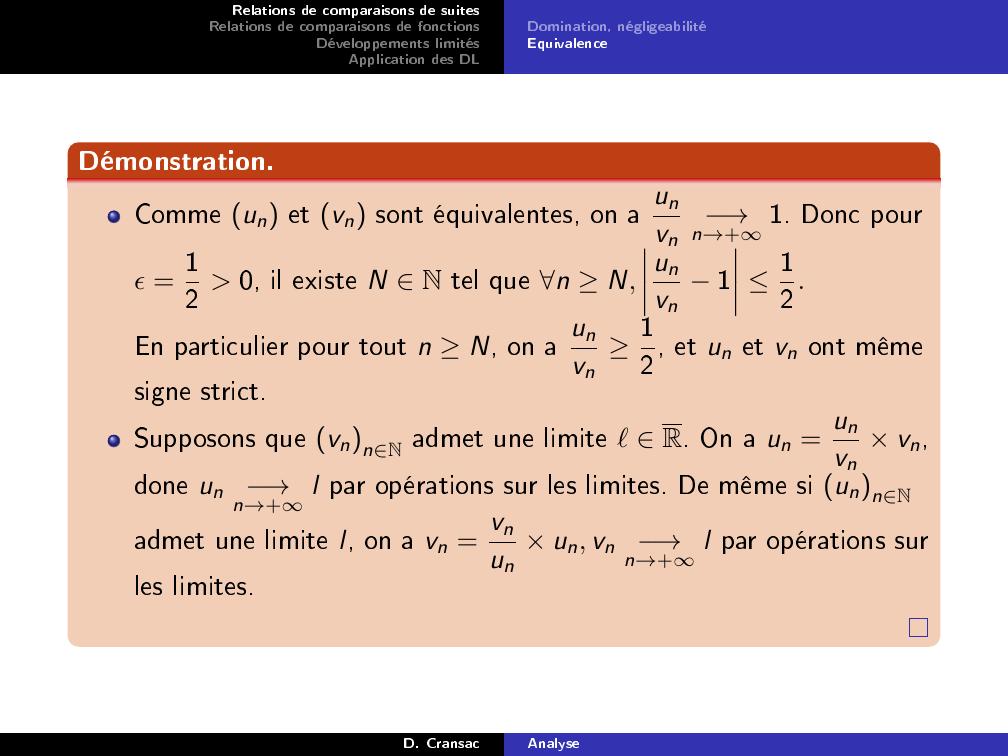
Page 22 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.Comme un et vn sont équivalentes, on a unvn→n→+1. Donc pourϵ = 12 0, il existe N N tel que n N,unvn1 12.En particulier pour tout n N, on a unvn12, et un et vn ont mêmesigne strict.Supposons que vnnN admet une limite ℓR. On a un = unvn× vn,done un→n→+l par opérations sur les limites. De même si unnNadmet une limite l, on a vn = vnun× un, vn→n→+l par opérations surles limites.D. CransacAnalyse

Page 23 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceRelations de comparaisons de fonctionsI désignera un intervalle réel non vide et non réduit à un point, a unpoint de I ou une extrémité de I éventuellement ±D désignera I ou I\a ;toutes les fonctions considérées seront dénies sur D à valeurs dansK = R ou C, et supposées non nulles sur I\a de sorte que lequotient de deux fonctions est toujours bien déni sur I\a ;si les fonctions sont dénies en a, on supposera de plus qu'elles sontcontinues en a.D. CransacAnalyse

Page 24 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDénitionSoient f et g : D →K. On dit que :f est dominée par g au voisinage de a si fg est bornée au voisinagede a.On note alors f x = Ogx ou f = Og.f est négligeable devant g au voisinage de a si limx→af xgx = 0.On note alors f x = ogx ou f = og.Exemples.x2 sinx3= Ox2:En eet pour I = R, x 7→x2 et x 7→x2 sinx3sont dénies sur R\0 etpour tout x R, on a :x2 sinx3x2 =sinx3 ⩽1.Si p q, xp =+o xq et xq =0 o xp :En eet pour I = R, x 7→xp et x 7→xq ne s'annulent pas sur I\0 etlimx→+xpxq = 0 = limx→0xqxpD. CransacAnalyse

Page 25 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceRemarque.Pour f : D →R, on a :f est bornée au voisinage de a si et seulement si f = O1.f converge vers 0 au voisinage de a si et seulement si f = o1.f x = ogx =⇒f x = Ogx.D. CransacAnalyse

Page 26 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoit α, β R+2ln xβ =+o xαxβ =+o eαxlnβ x =0 o 1xαeαx =o 1xβD. CransacAnalyse

Page 27 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceEquivalenceDénitionSoient f et g : D →K.On dit que f est équivalente à g au voisinage de a si limx→af xgx = 1.On note alors f x a gx ou f a g.Exemple.sin x 0 x :en eet pour I = R, x 7→x ne s'annule pas su r I \ 0 etlimx→0sin xx= 1Remarque :Si f est continue en a, on a : f x f a si f a ̸= 0.aSi f est dérivable en a, on a : f x f a f ′ax a si f ′a ̸= 0.Si Px = apxp + ap1xp1 + . . . aqxqp q est une fonction polynomiale,alors :Px +apxpetPx 0 aqxq.D. CransacAnalyse

Page 28 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient f et g dénies sur D.f x a gx ⇐⇒f x gx = ogx.f x a gx=⇒f x = Ogx et gx = Of x.PropositionLa relation a est une relation d'équivalence, c'est à dire :a est réexive : f a f ;a est symétrique : f a g ⇒g a f ;a est transitive : f a g et g a h impliquent f a h.D. CransacAnalyse

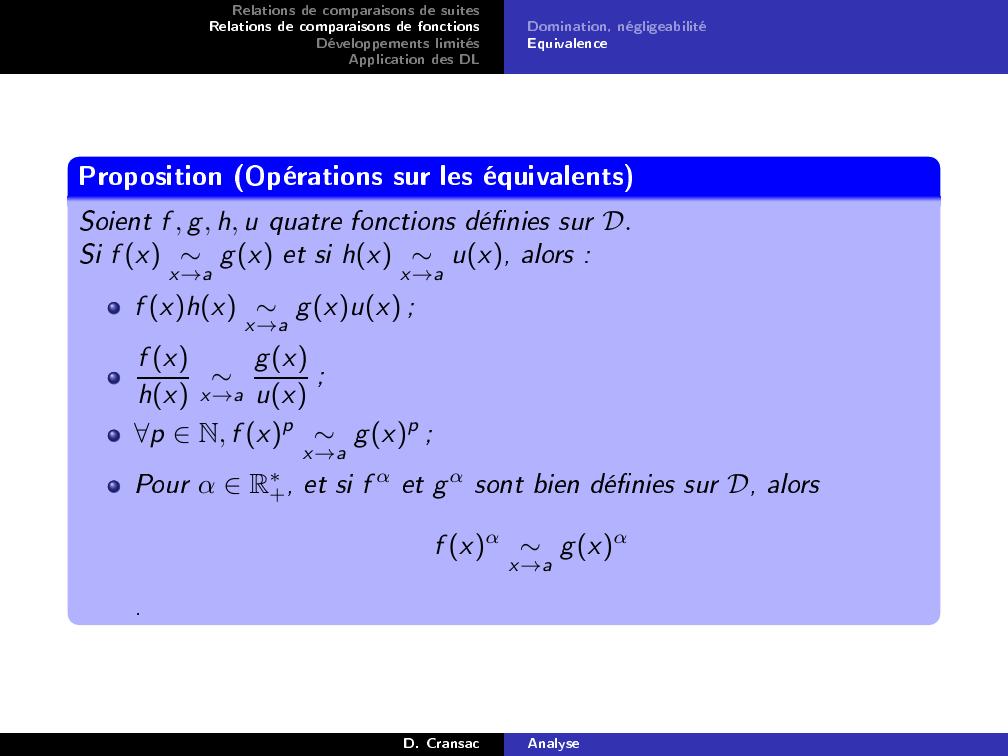
Page 29 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceProposition Opérations sur les équivalentsSoient f , g, h, u quatre fonctions dénies sur D.Si f x x→a gx et si hx x→a ux, alors :f xhx x→a gxux ;f xhx x→agxux ;p N, f xp x→a gxp ;Pour α R+, et si f α et g α sont bien dénies sur D, alorsf xα x→a gxα.D. CransacAnalyse

Page 30 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.On a, pour x D, f xhxgxux = f xgx × hxux →x→a 1 par produit delimites.Pour x D, on af xhxgxux= f xuxgxhx = f xgx ×hxux1→x→a 1comme quotient de limites.Pour x D et p N, on a f xpgxp = f xgxp→x→a 1p = 1 paropérations sur les limites.Pour tout x D, f αxg αx = f xgxα= eα lnf xgx. Commef xgx →x→a 1 donc eα lnf xgx →x→a 1.D. CransacAnalyse

Page 31 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceProposition Équivalents classiques au voisinage de 0 ex 1 0 xln1 + x 0 xsin x 0 xtan x 0 xarcsin x 0 xarctan x 0 xsh x 0 xth x 0 x1 + xα 1 0 αxavec α R1 cosx 0x221 chx 0 x22D. CransacAnalyse

Page 32 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceDémonstration.On a :1 cos x = 1 cos2x1 + cosx =sin2x1 + cosx x22car sinx 0 x et 1 + cosx 0 2.De même, :1 chx = 1 ch2x1 + chx = sh2x1 + chx 0 x22Dans tous les autres cas, on utilise la propriété ci-dessous.PropositionSi f est dérivable en a, si f ′a ̸= 0,f x f a f ′ax aD. CransacAnalyse

Page 33 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceProposition Composition à droite dans un équivalentSoient f et g deux fonctions dénies sur D.On suppose que g ne s'annule pas au voisinage de a et que f x a gx.Soit φ une fonction à valeurs dans D telle que limt→b φt = a avecb R ±.On a :f ◦φt b g ◦φtDémonstration.En utilisant le théorème de composition pour les limites, on peut écrire :limt→bfg φt = limx→afg x = 1D'où le résultat.D. CransacAnalyse

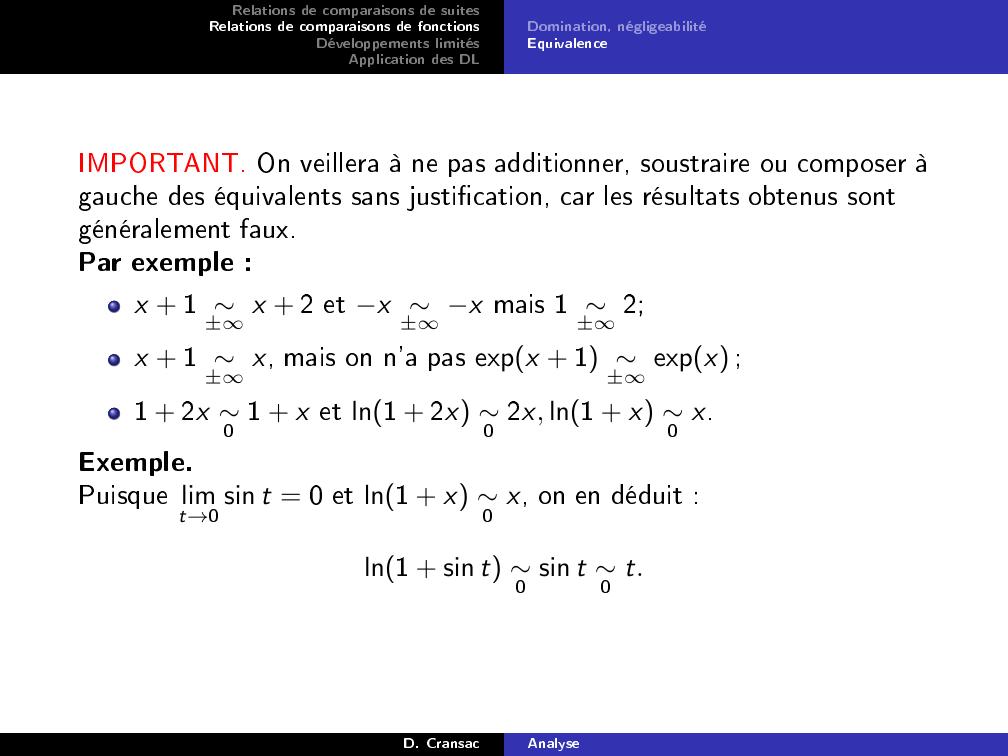
Page 34 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceIMPORTANT. On veillera à ne pas additionner, soustraire ou composer àgauche des équivalents sans justication, car les résultats obtenus sontgénéralement faux.Par exemple :x + 1 ±x + 2 et x ±x mais 1 ±2;x + 1 ±x, mais on n'a pas expx + 1 ±expx ;1 + 2x 0 1 + x et ln1 + 2x 0 2x, ln1 + x 0 x.Exemple.Puisque limt→0 sin t = 0 et ln1 + x 0 x, on en déduit :ln1 + sin t 0 sin t 0 t.D. CransacAnalyse

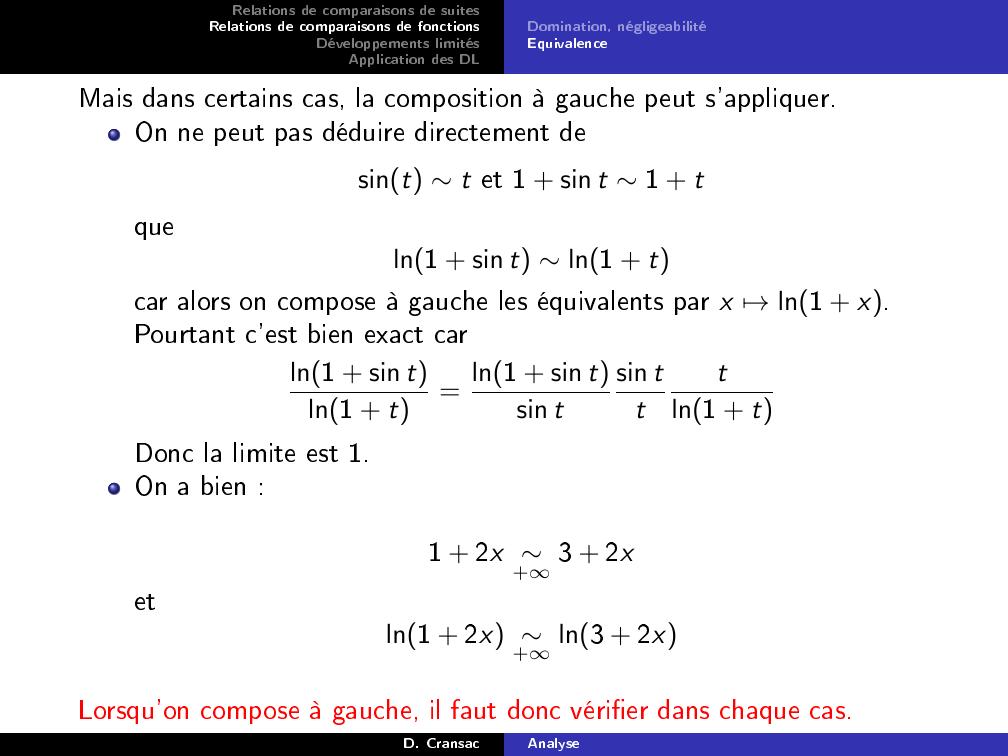
Page 35 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalenceMais dans certains cas, la composition à gauche peut s'appliquer.On ne peut pas déduire directement desint t et 1 + sin t 1 + tqueln1 + sin t ln1 + tcar alors on compose à gauche les équivalents par x 7→ln1 + x.Pourtant c'est bien exact carln1 + sin tln1 + t= ln1 + sin tsin tsin tttln1 + tDonc la limite est 1.On a bien :1 + 2x +3 + 2xetln1 + 2x +ln3 + 2xLorsqu'on compose à gauche, il faut donc vérier dans chaque cas.D. CransacAnalyse

Page 36 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLDomination, négligeabilitéEquivalencePropositionSoient f , g : D →R deux fonctions telle que f x a gx.Si g est de signe constant 0 ou 0 au voisinage de a, alors fest de même signe strict que g au voisinage de a.Si g admet une limite nie ou innie en a alors f admet une limiteen a et limx→a f x = limx→a gx.Démonstration.On a f xgx →x→a 1, donc par dénition de la limite, en posant ϵ = 12 0, ilexiste r 0 tel que x a r, a + r D,f xgx 1 12 et pourx a r, a + r D, f xf x 12, donc f x et gx ont même signe strict.Supposons que gx →x→a l. Pour tout x D, on a f x = f xgx × gx,donc gx →x→a l par opérations sur les limites.D. CransacAnalyse

Page 37 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Développements limitésDans toute cette section :I désignera un intervalle réel non vide et non réduit à un pointa désignera un réel appartenant à ¯I= Iextrémité de I D désignera I ou I\aToutes les fonctions considérées seront dénies sur D à valeurs dansK = R ou C.D. CransacAnalyse

Page 38 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.DénitionOn dit que f : D →K admet un développement limité en a à l'ordren N en abrégé DLna s'il existe a0, . . . , an Kn+1 tel quef x = a0 + a1x a + · · · + anx an + o x an .Remarque On distingue dans ce développement limité :Sa partie régulière, qui est la fonction polynomiale :Pnx = a0 + a1x a + . . . + anx an =nXk=0pkx akle reste o x an, fonction négligeable devant x an lorsquex →a, qui s'écrit aussix anεnx aoù εn : D →K est telle que limx→0 εx = 0.D. CransacAnalyse

Page 39 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExemplesLa fonctionf : 1, +→Rx7→x x2 + x3 ln1 + xadmet un développement limité à l'ordre 3 en 0.En eet, comme ln1 + x →x→0 0, on a x3 ln1 + x = ox3, ce quipermet d'écrire :f x = x x2 + ox3D. CransacAnalyse

Page 40 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.On sait que n ⩾11 xn+11 x= 1 + x + x2 + . . . + xnDonc11 x = 1 + x + x2 + . . . + xn + xn+11 xIl vient11 x 1 + x + x2 + . . . + xn = xnx1 xOn en conclut que11 x=x→0 1 + x + x2 + . . . + xn + oxnD. CransacAnalyse

Page 41 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.PropositionUne fonction f admet, au voisinage de a R, un développement limité àl'ordre nsi et seulement sila fonction g : h 7→f a + h admet au voisinage de 0 un développementlimité à l'ordre n.On a de plusf x =x→anXk=0akx ak +o x an ⇐⇒f a+h =h→0nXk=0akhk +ohkD. CransacAnalyse

Page 42 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExempleCalculons le DL23 de f x = 1x . On pose h = x 3. On a alors :f x = f 3 + h =13 + h = 1311 + h3On utilise alors le DL en 0 de la fonction x →11 x calculéprécédemment pour obtenir nalement :f 3 + h = 131 h3 + h29 + oh2et donc :f x = 13 x 39+ x 3227+ ox 32D. CransacAnalyse

Page 43 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Proposition Unicité d'un DLSi f admet un développement limité à l'ordre n en a, celui-ci est unique.Démonstration.Par l'absurde, supposons quef x =nXk=0akx ak + o x an =nXk=0bkx ak + o x anavec a0, . . . , an ̸= b0, . . . , bn .Soit p le plus petit entier tel que bp ̸= ap.Alors, pour tout 0 k p, on a ak bk = 0. On af x nXk=0akx ak = o x an etf x nXk=0bkx ak = o x an.D. CransacAnalyse

Page 44 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Ainsi, pour tout x ̸= a :0 = f x f x =nXk=0ak bk x ak + o x anEn divisant par x ap :0 = ap bp + x anXk=p+1ak bk x akp1 + ox anpDonc0 →x→a ap bpD'où ap = bp, ce qui constitue une contradiction.D. CransacAnalyse

Page 45 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Proposition Troncature d'un DLSupposons que f admette un développement limité à l'ordre n en a,f x =x→a a0 + a1x a + · · · + anx an + o x anAlors pour tout p J0, nK, f admet un développement limité à l'ordre pen a obtenu en tronquant le développement limité à l'ordre p :f x =x→a a0 + a1x a + · · · + apx ap + o x apD. CransacAnalyse

Page 46 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Si f admet un développement limité à l'ordre n en a dont la partierégulière est x 7→nXk=0akx ak, alors, pour tout p n, on a :f x =nXk=0akx ak + o x an=pXk=0akx ak +nXk=p+1akx ak + o x an=pXk=0akx ak + x apnXk=p+1akx akp + o x an=pXk=0akx ak + x apnXk=p+1akx akp + o x anzoxapD. CransacAnalyse

Page 47 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.PropositionSi f est paire resp. impaire et admet un développement limité à l'ordren en 0, ce développement limité ne contient que des termes pairs resp.impairs.Démonstration.Supposons par exemple f paire, et notonsf x = a0 + a1x + · · · + anxn + o xnson développement limité en 0 .On a alorsf x = f x = a0 + a1x + · · · + anxn + o xncar une fonction négligeable devant xn l'est aussi devant xn. Parunicité du DL, ak = 1kak pour tout k J0, nK.On a donc pour tout k impair, ak = ak donc ak = 0.D. CransacAnalyse

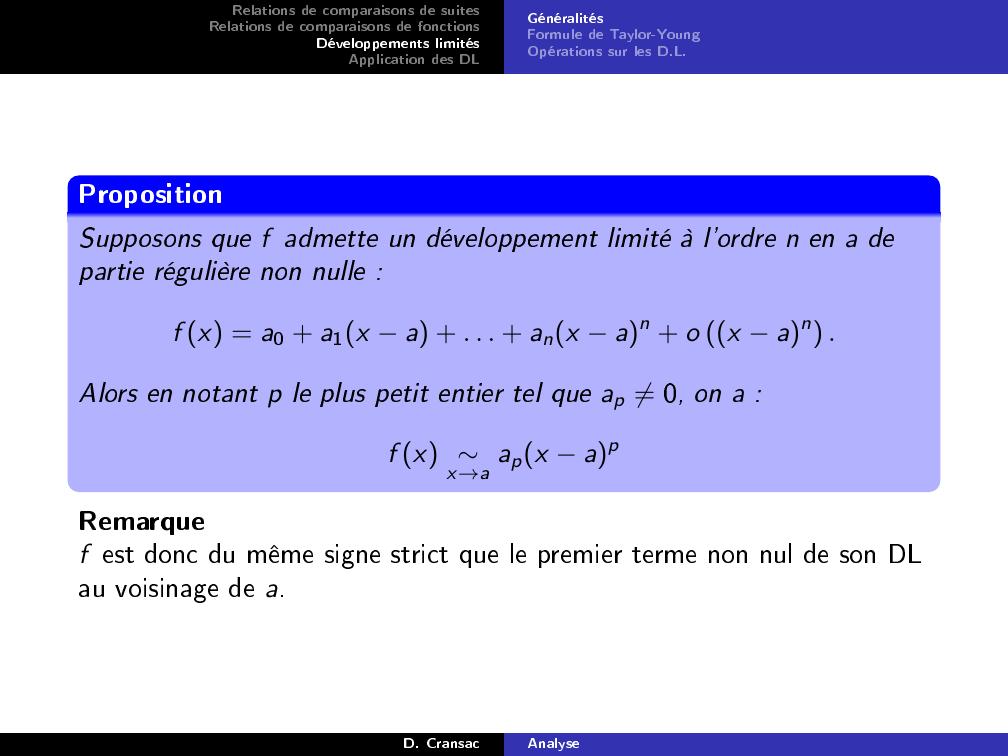
Page 48 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.PropositionSupposons que f admette un développement limité à l'ordre n en a departie régulière non nulle :f x = a0 + a1x a + . . . + anx an + o x an .Alors en notant p le plus petit entier tel que ap ̸= 0, on a :f x x→a apx apRemarquef est donc du même signe strict que le premier terme non nul de son DLau voisinage de a.D. CransacAnalyse

Page 49 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Comme pour k J0, p 1K, ak = 0, on af x = apx ap + · · · + anx an + oax an, puisf xapx ap = 1+ ap+1apx a+· · ·+ anapx anp+ox anp→x→a 1.D. CransacAnalyse

Page 50 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Formule de Taylor-YoungThéorème Lemme de primitivation des développements limitésSoient I un intervalle, g DI, R, a I et n N.Sig ′x =x→a o x an alors gx =x→a ga + ox an+1.Démonstration.Pour tout x I\a, g est continue sur a, x ou x, a et dérivable sur a, xou x, a , donc d'après le théorème des accroissementsnis :gx gax a= g ′ cxpour un certain cx a, x ou x, a.Ce procédé nous fournit une fonction c : I\a →R telle que pour toutx I\a : cx a x a.Par encadrement : limx→a cx = a, donc :gx gax an+1 =g ′ cxx an =g ′ cxcx anz→0x→0×cx ax anz⩽1→x→a 0D. CransacAnalyse

Page 51 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Théorème Primitivation des développements limitésSoient I un intervalle, f DI, R et a I.Si f ′ possède un développement limité à l'ordre n au voisinage de a :f ′x =nXx→0akx ak + o x anavec a0, . . . , an R,alors f possède un développement limité à l'ordre n + 1 au voisinage dea :f x = f a +nXx=0akx ak+1k + 1+ ox an+1.RemarqueOn peut donc toujours primitiver terme à terme le développement limitéd'une dérivée !D. CransacAnalyse

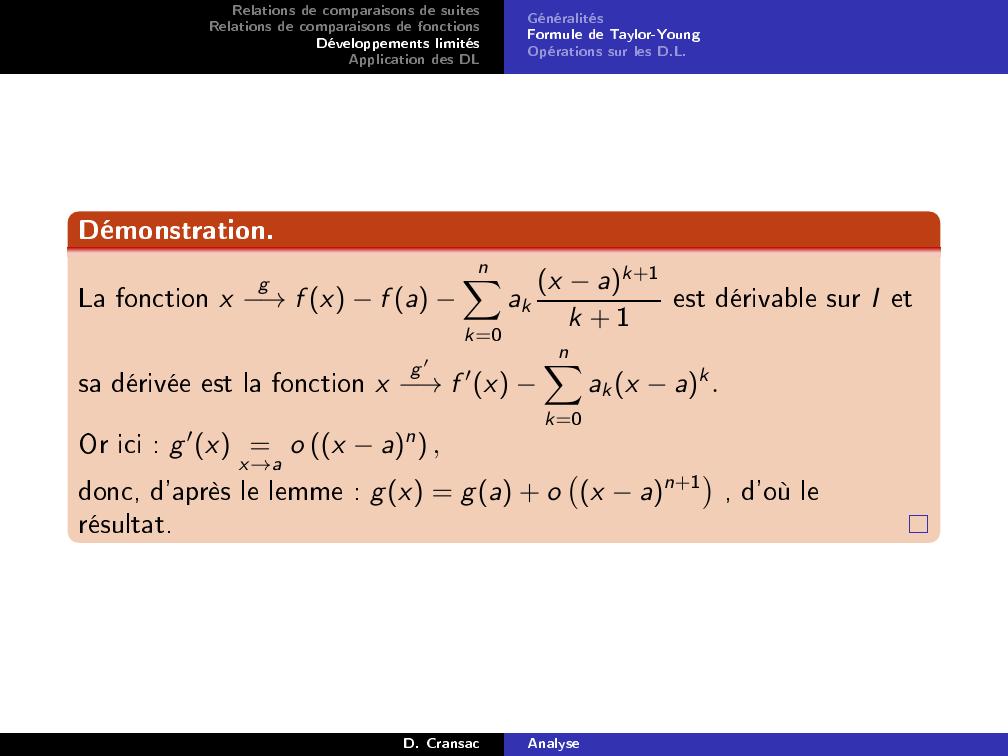
Page 52 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.La fonction xg→f x f a nXk=0akx ak+1k + 1est dérivable sur I etsa dérivée est la fonction xg ′→f ′x nXk=0akx ak.Or ici : g ′x =x→a o x an ,donc, d'après le lemme : gx = ga + ox an+1, d'où lerésultat.D. CransacAnalyse

Page 53 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Exemplen N: ln1 + x =nXk=11k1 xkk + o xnn N: ln1 + x = x x22 + x33 x44 + . . . + 1n1 xnn + o xn .Démonstration.Puisque :11 x =n1Xk=0xk + oxn1, alors :11 + x =n1Xk=01kxk + oxn1en remplaçant x par x.Primitivons : ln1 + x =nXk=11k1 xkk + o xn sachant que :ln 1 = 0et que pour tout k N, 1k+1 = 1k1D. CransacAnalyse

Page 54 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Théorème Formule de Taylor YoungSoit I un intervalle, n N, f C nI, R, et a I.Alors f possède un développement limité à l'ordre n au voisinage de a etf x =nXk=0f kak!x ak + ox anRemarqueCe résultat est un théorème d'existence de développement limités.On a les résultats suivants :Continuité ⇔existence d'un développement limité à l'ordre 0.Dérivabilité ⇔existence d'un développement limité à l'ordre 1.f de classe C n⇒existence d'un développement limité à l'ordre nATTENTION La dernière proposition n'est qu'une implication.D. CransacAnalyse

Page 55 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Initialisation : Nous savons déjà que pour toute fonction f : I →R continue :f x = f a + o1.Hérédité : Soit n N.On suppose la proposition vraie au rang n.Soit f C n+1I, R. La fonction f ′ est de classe C n sur I, donc par hypothèsede récurrence :f ′x =nXk=0f ′k ak!x ak + o x an=nXk=0f k+1ak!x ak + o x anLe théorème de primitivation des développements limités montre aussitôt lerésultat souhaité :f x = f a +nXk=0f k+1ak!x ak+1k + 1+ ox an+1D. CransacAnalyse

Page 56 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.f x = f a +nXk=0f k+1ak!x ak+1k + 1+ ox an+1= f a +nXk=0f k+1ak + 1! x ak+1 + ox an+1= f a +n+1Xk=1f kak!x ak + ox an+1=n+1Xk=0f kak!x ak + ox an+1.D. CransacAnalyse

Page 57 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExemplePour tout n N :ex =nXk=0xkk! + o xnex = 1 + x + x22 + x36 + x424 + . . . + xnn! + o xn.Pour tout n N :cos x =nXk=01kx2k2k!+ ox2ncos x = 1 x22 + x424 + . . . + 1nx2n2n!+ ox2n.D. CransacAnalyse

Page 58 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Remarque.On l'a dit, la formule de Taylor-Young est dicile à appliquer en pratiquepour obtenir un DL, car elle impose de calculer les dérivées successives dela fonction.On présente dans cette section des résultats permettant d'obtenir des DLà partir de DL connus :par intégration de DL.par opérations combinaison linéaire, produits,... sur les DL.D. CransacAnalyse

Page 59 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Combinaison linéaire, produitPropositionSupposons que f et g admettent des développements limités à l'ordre nen 0 :f x = Pnx + o xn et x = Qnx + o xn .λ, µ K2, λf + µg a un développement limité à l'ordre n en 0 :etλf + µgx= λPn + µQn x + o xn .fg a un développement limité à l'ordre n en 0 etfgx=TnPQx + o xnoù TnPQ désigne la troncature à l'ordre n du polynôme PQ.D. CransacAnalyse

Page 60 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.On a :λf + µgx =x→0 λPn + µQn x + o xnC'est le DLn0 de λf + µg car λPn + µQn est une fonctionpolynomiale de degré n.On a par produit des développements limités :f xgx =x→0 Pnx + o xn Qnx + o xn = PnxQnx+o xncar Pnxo xn + Qnxo xn + o xn o xn est négligeable devantxn en 0 . On sait que PnxQnx = Tn PnQn x + xn+1Rnx oùRn est une fonction polynomiale. On en déduit quePnxQnx = Tn PnQn x + o xn et donc :f xgx =x→0 Tn PnQn x + o xnqui est le DLn0 de fg car Tn PnQn est une fonction polynomialede degré n.D. CransacAnalyse

Page 61 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExempleCalculons le DL30 de x 7→cos x sin x :cos x sin x =1 x22 + ox3 x x36 + ox3= x x36 x32 + ox3= x 23x3 + ox3Calculons le DL30 de la fonction f : x 7→ex1 x .11 x = 1 + x + x2 + x3 + ox3etex = 1 + x + x22 + x36 + ox3D'où par produit :f x =1 + x + x2 + x3 + ox3 1 + x + x22 + x36 + ox3ce qui donne, en développant et en simpliant :f x = 1 + x + x +x22 + x2 + x2+x36 + x32 + 2x3+ ox3= 1 + 2x + 52x2 + 83x3 + ox3D. CransacAnalyse

Page 62 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.CompositionPropositionSi f : I →J et g : J →K ont des développements limités en 0 à l'ordren :f x = Pnx + o xn;gx = Qnx + o xn ,si limx→0 f x = 0, alors la composée g ◦f a un développement limitég ◦f x = Tn Qn ◦Pn x + o xn .Démonstration.Puisque limx→0 f x = 0, on peut factoriser dans le DL de f en 0 :f x = Pnx + o xn = xPn1x + oxn1.g ◦f x =nXk=0qk Pnx + o xnk + xn Pn1x + oxn1n εgf x.D. CransacAnalyse

Page 63 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.On regarde à présent chaque terme de cette expression :Pnx + o xnk : en développant par la formule du binôme, on aun terme en Pnxk et tous les autres termes contiennent o xn etsont négligeables devant xn. Ainsi, on a :Pnx + o xnk = Pnxk + o xn .xn Pn1x + oxn1n εgf x : on alimx→0Pn1x + oxn1n εgf x = 0, donc :xn Pn1x + oxn1n εgf x = o xn .D. CransacAnalyse

Page 64 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Finalement, on obtient que :g ◦f x =nXk=0qk Pnxk + o xn = Qn ◦Pnx + o xn .Et comme Qnx ◦Pnx = Tn Qn ◦Pn x + xn+1Rnx où Rn est unefonction polynomiale, on en déduit queQnx ◦Pnx = Tn Qn ◦Pn x + o xnC'est bien le DLn0 de g ◦f car Tn Qn ◦Pn est une fonctionpolynomiale de degré n.D. CransacAnalyse

Page 65 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExempleDéterminons le DL40 de x 7→f x = 1 + xx. Pour toutx I, f x = ex ln1+x avec limx→0 x ln1 + x = 0.On utilise la composition des DL. Le développement limité à l'ordre 4 dex 7→x ln1 + x s'écrit :x ln1 + x = xx x22 + x33 + ox3= x2 x32 + x43 + ox4z=ux.On a ux2 = x4 + ox4, ux3 = ox4. Il sut donc de faire leDL20 de l'exponentielle :eu = 1 + u + u22 + ou2On obtient en substituant composition à droite :1+xx = 1+x2 x32 + x43+12x4+ox4= 1+x2x32 +56x4+ox4D. CransacAnalyse

Page 66 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Quotient de DLPropositionSoient f , g : D →K.Si f et g ont des développements limités à l'ordre n en 0 et si g admetune limite nie non nulle en 0,alors fg admet un développement limité à l'ordre n en 0.D. CransacAnalyse

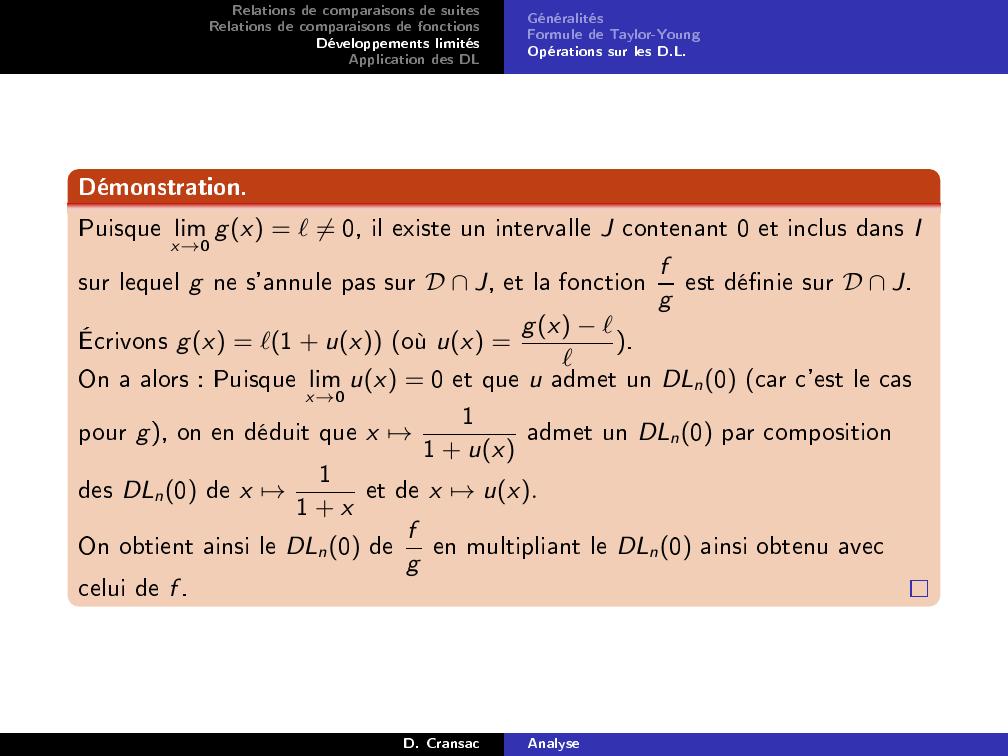
Page 67 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Démonstration.Puisque limx→0 gx = ℓ̸= 0, il existe un intervalle J contenant 0 et inclus dans Isur lequel g ne s'annule pas sur D J, et la fonction fg est dénie sur D J.Écrivons gx = ℓ1 + ux où ux = gx ℓℓ.On a alors : Puisque limx→0 ux = 0 et que u admet un DLn0 car c'est le caspour g, on en déduit que x 7→11 + ux admet un DLn0 par compositiondes DLn0 de x 7→11 + x et de x 7→ux.On obtient ainsi le DLn0 de fg en multipliant le DLn0 ainsi obtenu aveccelui de f .D. CransacAnalyse

Page 68 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.RemarquePour faire le DL en 0 d'un quotient x 7→1gx avec lim0 g ̸= 0, on seramènera toujours comme dans la preuve précédente à undéveloppement limité d'une fonction de la forme :x 7→11 + uxavecux →x→0 0.D. CransacAnalyse

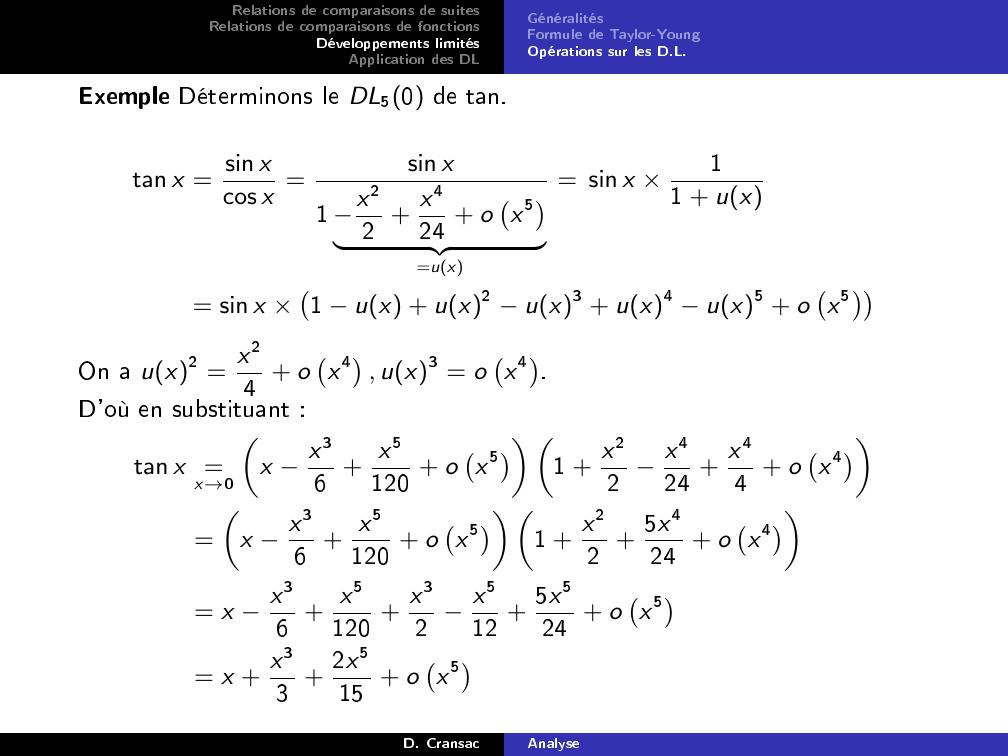
Page 69 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Exemple Déterminons le DL50 de tan.tan x = sin xcos x =sin x1 x22 + x424 + ox5z=ux= sin x ×11 + ux= sin x ×1 ux + ux2 ux3 + ux4 ux5 + ox5On a ux2 = x24 + ox4, ux3 = ox4.D'où en substituant :tan x =x→0x x36 + x5120 + ox5 1 + x22 x424 + x44 + ox4=x x36 + x5120 + ox5 1 + x22 + 5x424 + ox4= x x36 + x5120 + x32 x512 + 5x524 + ox5= x + x33 + 2x515 + ox5D. CransacAnalyse

Page 70 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.RemarqueSi g tend vers 0, il est encore possible que la fonction fg possède undéveloppement limité : si f et g admettent des DLn0 de formes normalisées :f x = xp1 ap1 + ap1+1x + . . . + an1xn1p1 + oxn1p1gx = xp2 bp2 + bp2+1x + . . . + bn2xn2p2 + oxn2p2avec ap1, bp2 ̸= 0, alors le quotient s'écrit :f xgx = xp1p2 ap1 + ap1+1x + . . . + an1xn1p1 + oxn1p1bp2 + bp2+1x + . . . + bn2xn2p2 + o xn2p2!z=hxComme bp2 ̸= 0, la proposition précédente, assure que la fonction h possède undéveloppement limité.De plus, le terme constant du développement limité de la fonction h vaut ap1bp2donc est non nul.Par suite fg admet un développement limité si et seulement si p1 p2 N,c'est à dire p2 p1, et son ordre est min n1 p1, n2 p2.D. CransacAnalyse

Page 71 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.ExempleDéterminer, s'il existe, le DL30 de la fonction x 7→ex 1 xln1 + x .Prédiction de l'ordre des DL à choisir au brouillon :f x = ex 1 xln1 + x =x22 + x36 + x424 + . . .x + x22 + x33 + . . . =x2 12 + x6 + x224 + . . .x1 + x2 + x23 + . . .= x ×"12 + x6 + x224 + . . .1 + x2 + x23 + . . .z=hxPour obtenir le DL30 de f , il faut donc le DL20 de h ce quinécessite un DL20 du numérateur et du dénominateur de h. Celanécessite donc un DL40 de x 7→ex 1 x on a factorisé par x2 et un DL30 de x 7→ln1 + x on a factorisé par x .D. CransacAnalyse

Page 72 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Rédaction :ex 1x = x22 + x36 + x424 +ox4etln1+x = xx22 + x33 +ox3ou sous forme normalisée :ex1x = x212 + x6 + x224 + ox2et ln1+x = x1 x2 + x23 + ox2On obtient l'écriture suivante :f x = x ×12 + x6 + x224 + ox2×11 x2 + x23 + ox2z=uxComme on a :ux2 = x24 + ox2on obtient :11 x2 + x23 + o x2=11 ux = 1 + x2 x212 + ox2D. CransacAnalyse

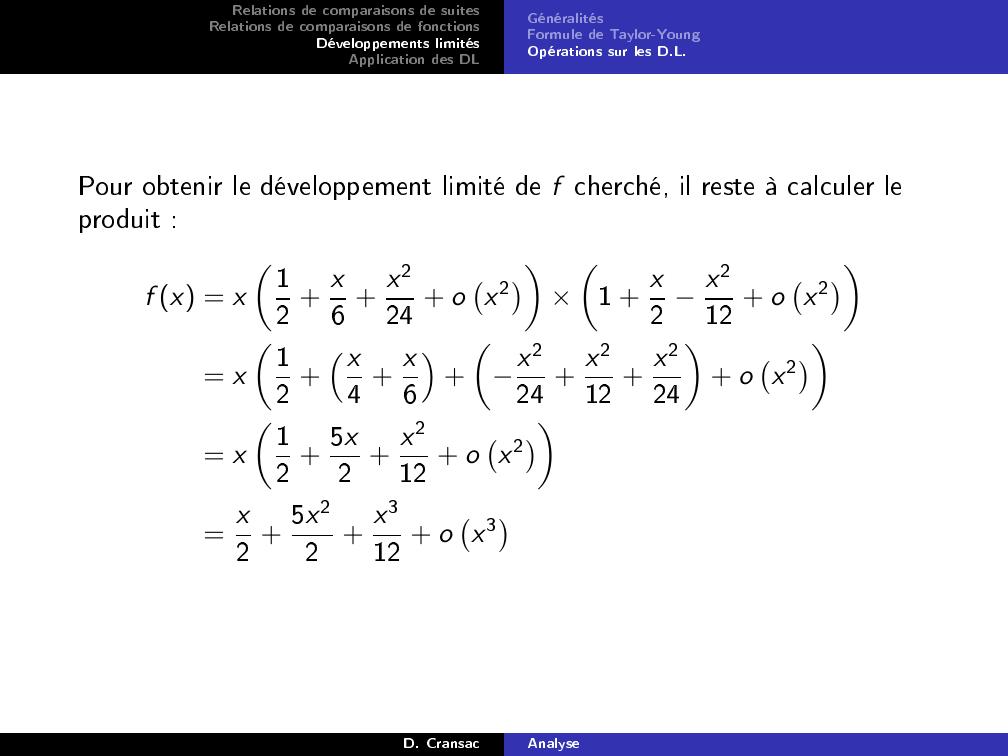
Page 73 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLGénéralitésFormule de Taylor-YoungOpérations sur les D.L.Pour obtenir le développement limité de f cherché, il reste à calculer leproduit :f x = x12 + x6 + x224 + ox2×1 + x2 x212 + ox2= x12 +x4 + x6+x224 + x212 + x224+ ox2= x12 + 5x2 + x212 + ox2= x2 + 5x22+ x312 + ox3D. CransacAnalyse

Page 74 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesApplication des Développements LimitésD. CransacAnalyse

Page 75 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesRappelSupposons que f admette un développement limité à l'ordre n en a departie régulière non nulle. On écrit sa forme normalisée :f x = xap ap + ap+1x a + . . . + anpx anp + ox anp.Alors on a : f x x→a apx apExempleDéterminons un équivalent au voisinage de 0 desin2x sh2x2x sin x tan x2 .Cherchons un équivalent du numérateur :sin2x = 2x 43x3 + ox3etsh2x = 2x + 43x3 + ox3ce qui donne : sin2x sh2x 83x3.Cherchons un équivalent du dénominateur.2x sin x tan x = 2x x 16x3 + ox3x + 13x3 + ox3= 16x3 + ox316x3D. CransacAnalyse

Page 76 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesOn en déduit par produit et quotient d'équivalents :sin2x sh2x2x sin x tan x2 83x316x32 96x3D. CransacAnalyse

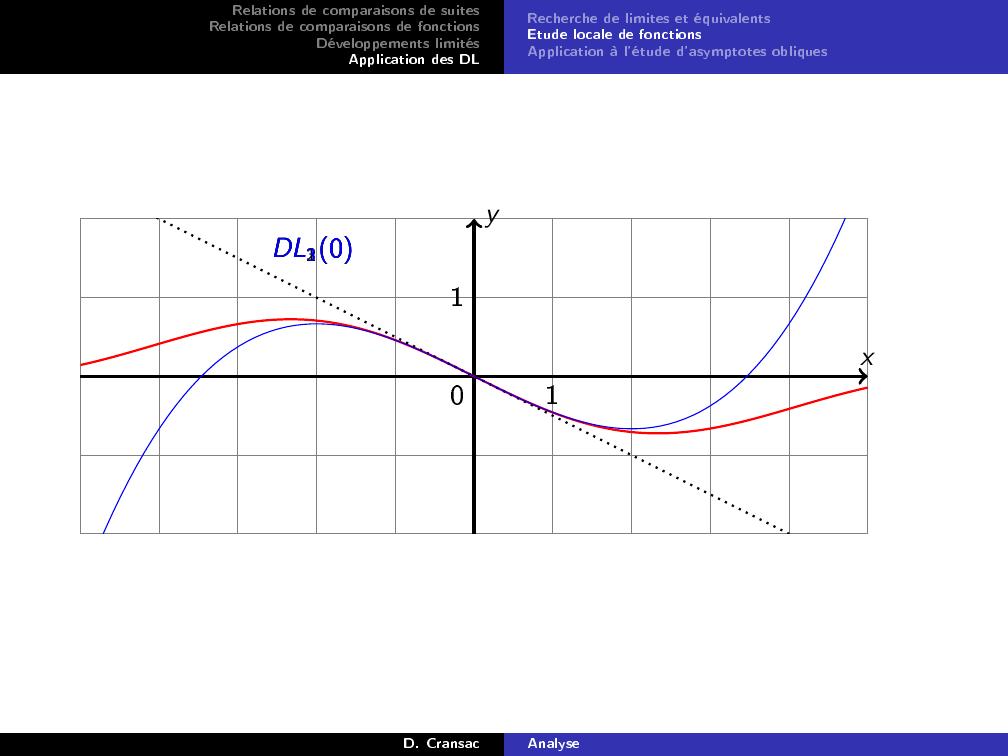
Page 77 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesRappel Si f admet un DL1a, f est dérivable en a et la courbereprésentative de f admet une tangente en a.Pour déterminer la position relative de la courbe représentative d'unefonction f par rapport à sa tangente, on cherche un equivalent dex 7→f x f a x af ′a en a en eectuant un DL de f :f xf af ′ax a apx apavecap Ret p N\0, 1Alors x 7→f x f a f ′ax a est du signe de apx ap auvoisinage de a :si p est pair, f x f a f ′ax a est de signe constant auvoisinage de a. La courbe est au-dessus ou en-dessous de satangente en a suivant le signe de ap .si p est impair, f x f a f ′ax a change de signe en a.La courbe traverse sa tangente en a. On parle de point d'inexion.D. CransacAnalyse

Page 78 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesxy110DL10DL20DL30D. CransacAnalyse

Page 79 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesRemarque.Dans le cas d'un point critique a, c'est à dire si f ′a = 0, cette étudenous dit si on a un extremum local si n pair ou non si n est impair.ExempleSoit f : x 7→cos x 1x.f admet le DL30 suivant :f x = 12x + 124x3 + ox3Ainsi f est dérivable en 0, et f ′0 = 12. Comme f x + 12x x→0124x3,qui change de signe en 0, la courbe représentative de f traverse satangente en 0 . Ainsi f admet un point d'inexion en 0 .D. CransacAnalyse

Page 80 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesDénitionSoit f : I →R dénie au voisinage de ±. On dit que f possède unDLn± si la fonction g : u →f1upossède un DLn0.Exemple Calculons le DL2 de f : x 7→xx 1. On pose u = 1x . Alorsgu =11 u=u→0 1 + u + u2 + ou2et on en déduit le DL2 de f :f x=x→+1 + 1x + 1x2 + o 1x2D. CransacAnalyse

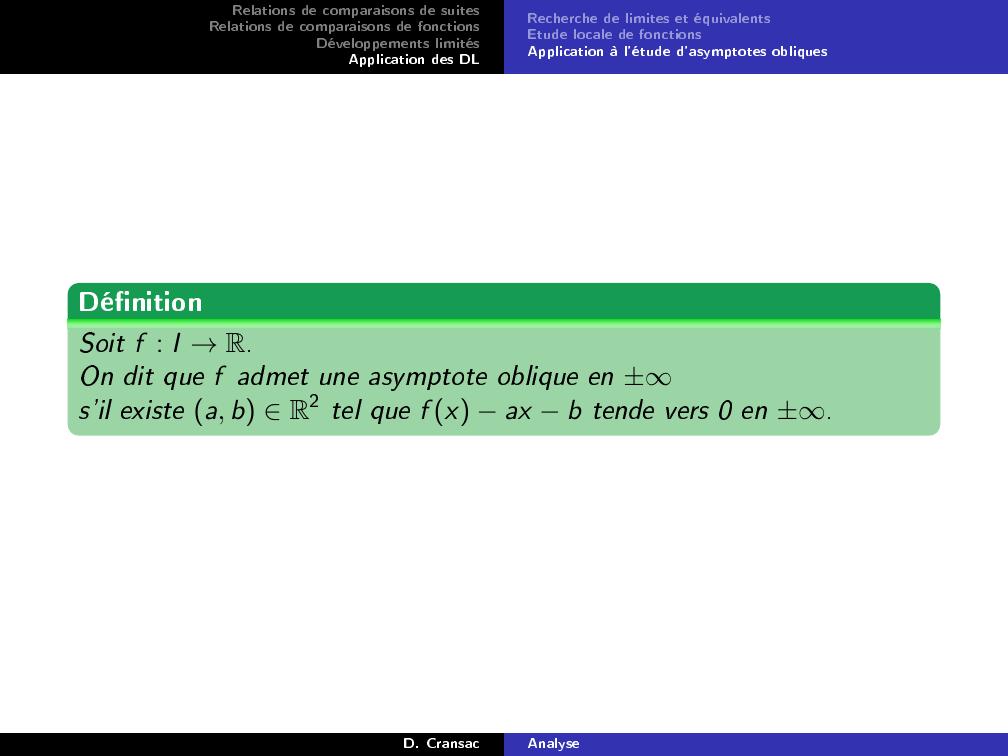
Page 81 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesDénitionSoit f : I →R.On dit que f admet une asymptote oblique en ±s'il existe a, b R2 tel que f x ax b tende vers 0 en ±.D. CransacAnalyse

Page 82 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesSoit f : I →R telle que f x →x→+±.On souhaite préciser son comportement en +, en étudiant l'existenceéventuelle d'une asymptote oblique et sa position relative par rapport àCf . Pour cela, on procèdera comme suit :On eectue un DL2+ de f xx:f xx=x→+a0 + a1x + a2x2 + o1/x2.En multipliant par x, il vient f x=x→+a0x + a1 + a2x + o1/x. Lacourbe admet alors la droite y = a0x + a1 pour asymptote obliqueen +.La position de la courbe de f par rapport à l'asymptote oblique estdonnée par le signe de a2x si a2 = 0, on augmente l'ordre du DLjusqu'à trouver un coecient non nul.D. CransacAnalyse

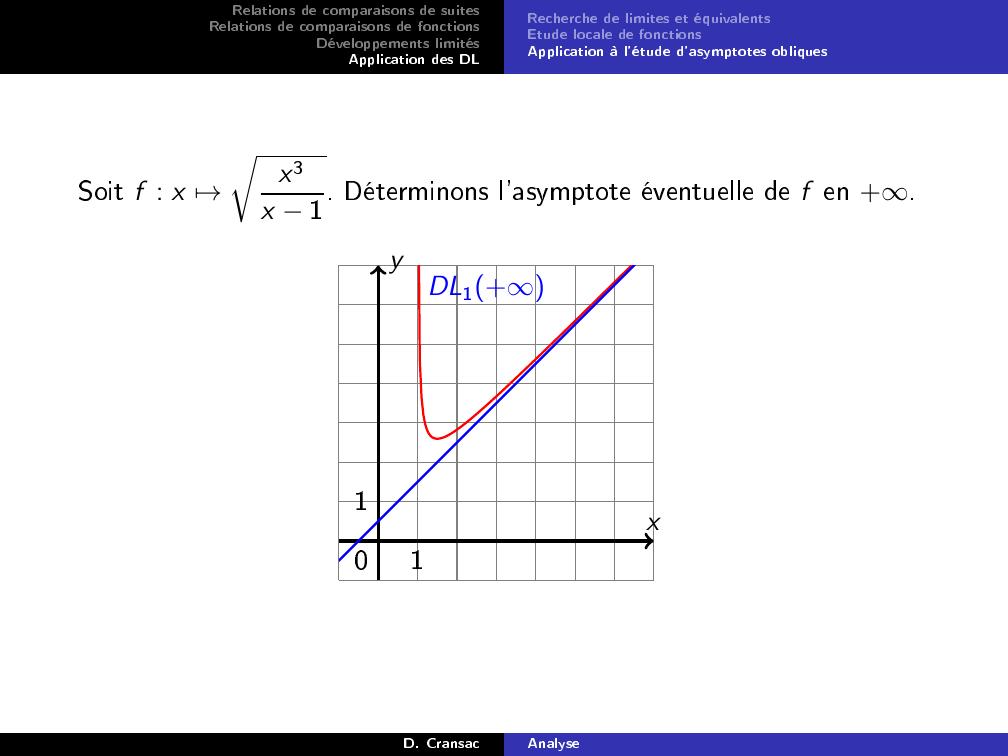
Page 83 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesSoit f : x 7→rx3x 1. Déterminons l'asymptote éventuelle de f en +.xy110DL1+D. CransacAnalyse

Page 84 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesExemple. Soit f : x 7→rx3x 1. Déterminons l'asymptote éventuelle def en +.On pose u = 1x et on étudie f xx= ufu1=11 u on recherchel'asymptote en +, donc 0 u 1 .On eectue le DL0 de u 7→11 u :11 u = 1 + u2 + 3u28+ ou→0u2Donc on obtient f x = x + 12 + 38x +ox→+x1.La droite y = x + 12 est asymptote à la courbe et le graphe de f estau-dessus de l'asymptote au voisinage de + carf x x 12 38x 0.D. CransacAnalyse

Page 85 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquesDÉVELOPPEMENTS LIMITÉS USUELSLes formules du tableau qui suit doivent être connues PAR COEUR sansdélai et sans la moindre hésitation.Pour les fonctions paires, les développements limités sont donnés àl'ordre 2n pour tout n N, mais par exemple, puisque vous connaissez undéveloppement limité de la fonction cosinus au voisinage de 0 aux ordres0, 2, 4, 6 . . ., bien sûr que vous en connaissez un à l'ordre 3 , il sut detronquer au bon endroit :cos x = 1 x22 + ox3.Notez bien que ce développement est PLUS FIN que le développement àl'ordre 2 :cos x =x→0 1 x22 + ox2. Sur le développement à l'ordre 3,on ne voit pas de terme d'ordre 3 mais ce n'est qu'une impression, IL Y AUN TERME D'ORDRE 3 , avec un coecient 0 .À l'ordre 2, c'est diérent, on ne voit pas de terme d'ordre 3 parce qu'untel terme est réellement invisble à ce niveau de précision.D. CransacAnalyse

Page 86 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliques11 x =nXx→0xk + o xn =x→0= 1 + x + x2 + . . . + xn + o xnln1 + x =x→0nXk=11k1 xkk + o xnln1 + x =x→0 x x22 + x33 x44 + . . . + 1n1 xnn + o xnex =x→0nXk=0xkk! + o xn =x→0 1 + x + x22 + x36 + x424 + . . . + xnn! + o xn1 + xα =x→0 1 + αx + αα 12x2 + αα 1α 26x3 + . . .+αα 1α 2 . . . α n + 1n!xn + o xnD. CransacAnalyse

Page 87 : Relations de comparaisons de suitesRelations de comparaisons de fonctionsDéveloppements limitésApplication des DLRecherche de limites et équivalentsEtude locale de fonctionsApplication à l'étude d'asymptotes obliquessin x =x→0nXk=01kx2k+12k + 1! + ox2n+1sin x =x→0 x x36 + x5120 + . . . + 1nx2n+12n + 1! + ox2n+1cos x =x→0nXk=01k x2k2k! + ox2ncos x = 1 x22 + x424 + . . . + 1n x2n2n! + ox2nArctan x =nXx→01k x2k+12k + 1 + ox2n+1Arctan x = x x33 + x55 x77 + . . . + 1n x2n+12n + 1 + ox2n+1tan x =x→0 x + x33 + ox3D. CransacAnalyse

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87