CM Rappels

Posté le 06/02/2025

Chargé de TD/CM : D. Physique.

2 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

Page 1 : .Chapitre 0 – Repérage spatial Sources: polycopiéhttps://www.equipes.lps.u-psud.fr/PASQUIER/enseignement/mecaS2/Mecaniquechap1coordonnees.pdf

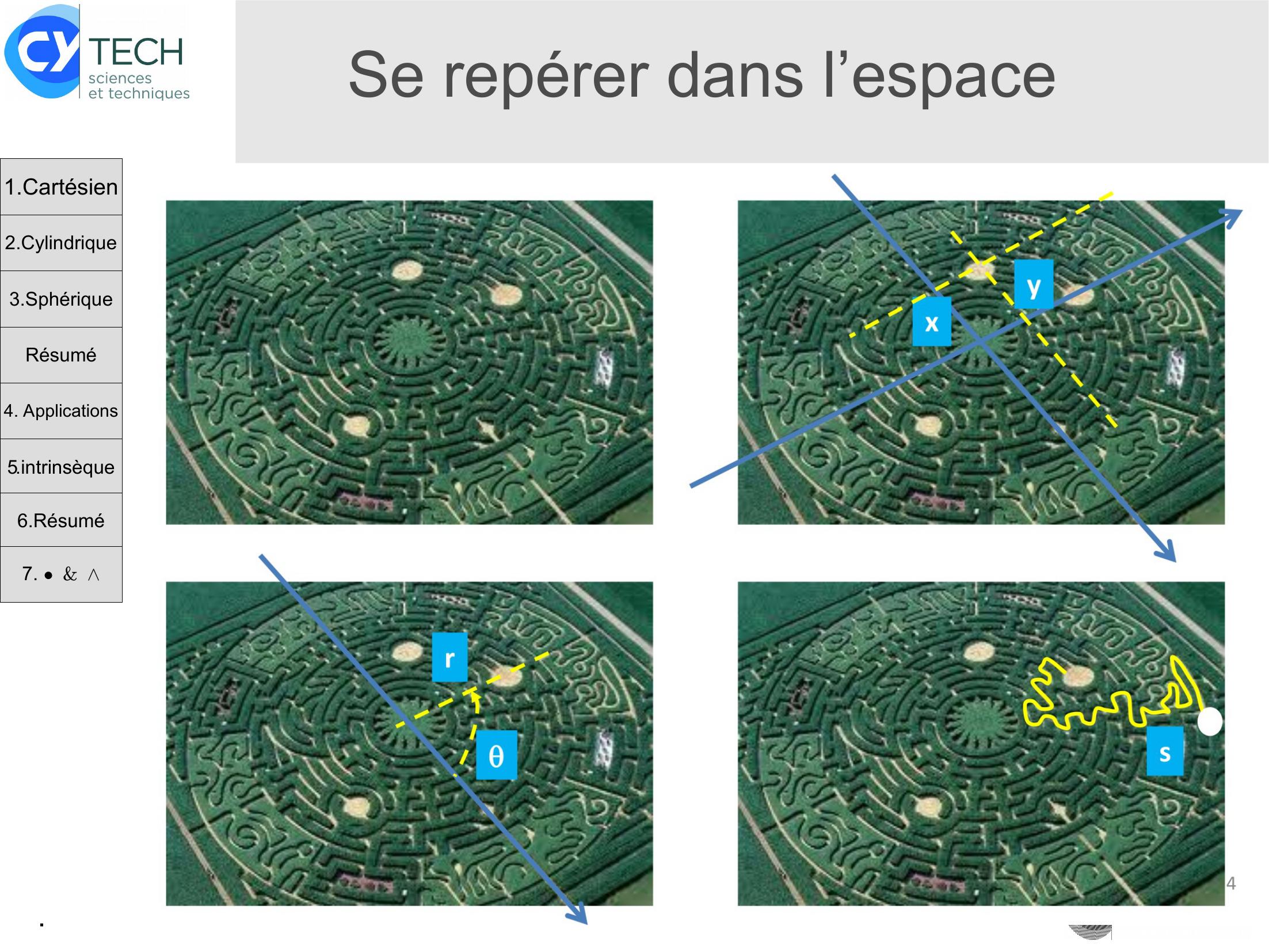
Page 2 : .Se repérer dans l’espace1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 3 : .1. Coordonnées cartésiennes1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel de positionici, car vecteurs de la base constants5.intrinsèque6.Résumé7. &

Page 4 : .1. Coordonnées cartésiennes1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel d’aireÉlément différentiel de volume5.intrinsèque6.Résumé7. &

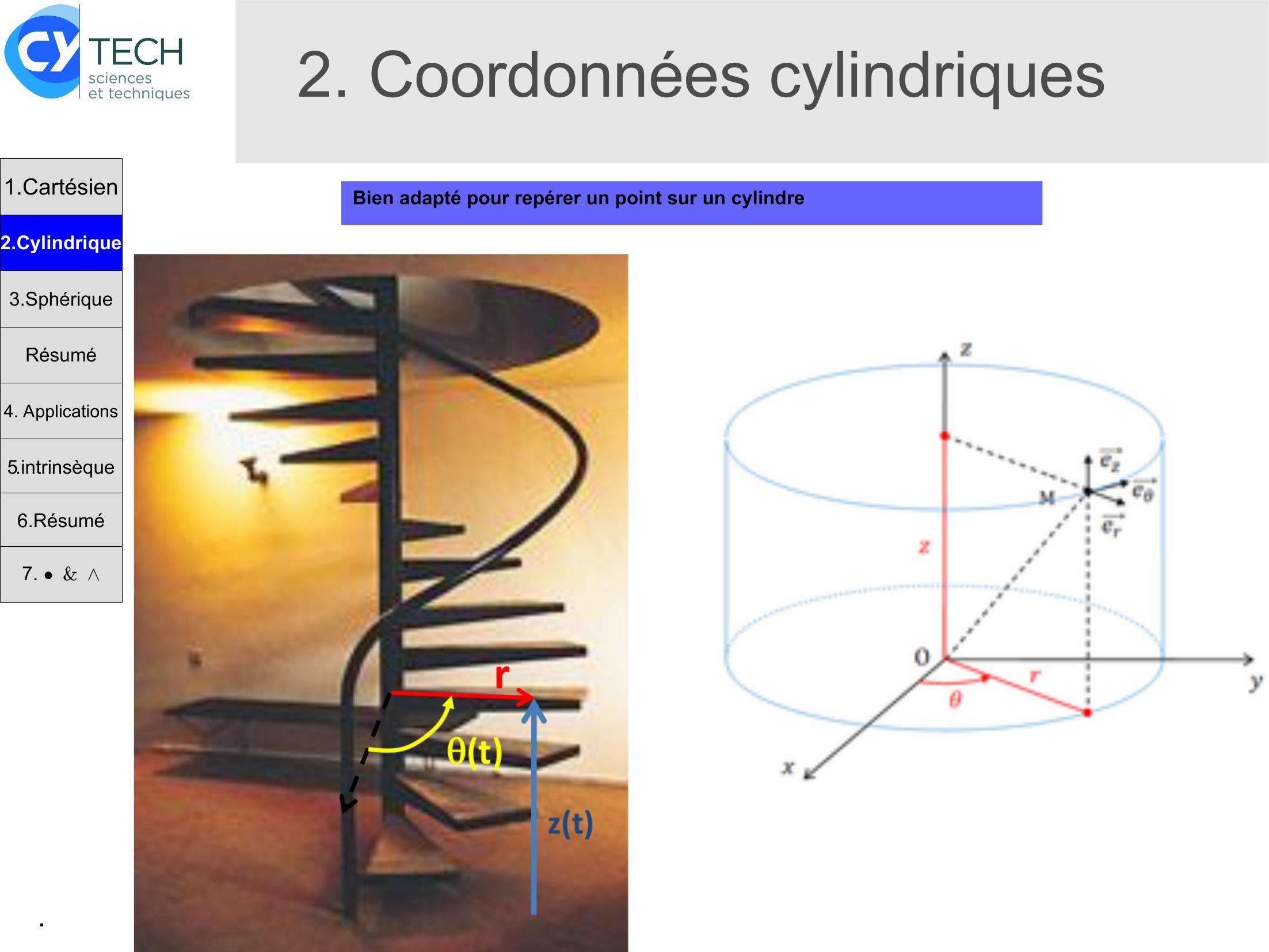
Page 5 : .2. Coordonnées cylindriquesBien adapté pour repérer un point sur un cylindre1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 6 : .2. Coordonnées cylindriques1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel de position5.intrinsèque6.Résumé7. &

Page 7 : .2. Coordonnées cylindriques1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel de volumeÉlément différentiel d’aire5.intrinsèque6.Résumé7. &

Page 8 : .3. Coordonnées sphériquesBien adapté pour repérer un point sur une sphère1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 9 : .3. Coordonnées sphériques1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel de positionFigure: Élément d’aire en coordonnées sphériques Électromagnétisme 1 – 1ère année , H. Gié et J.P. Sarmant, Tec&Doc5.intrinsèque6.Résumé7. &

Page 10 : .3. Coordonnées sphériques1.Cartésien2.Cylindrique3.SphériqueRésumé4. ApplicationsÉlément différentiel de volumeÉlément différentiel d’aire5.intrinsèque6.Résumé7. &

Page 11 : .4. Applications1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications1 Volume d’une sphère pleine de centre 0 et de rayon R :2 Surface d’une sphère pleine de centre 0 et de rayon R :5.intrinsèque6.Résumé7. &

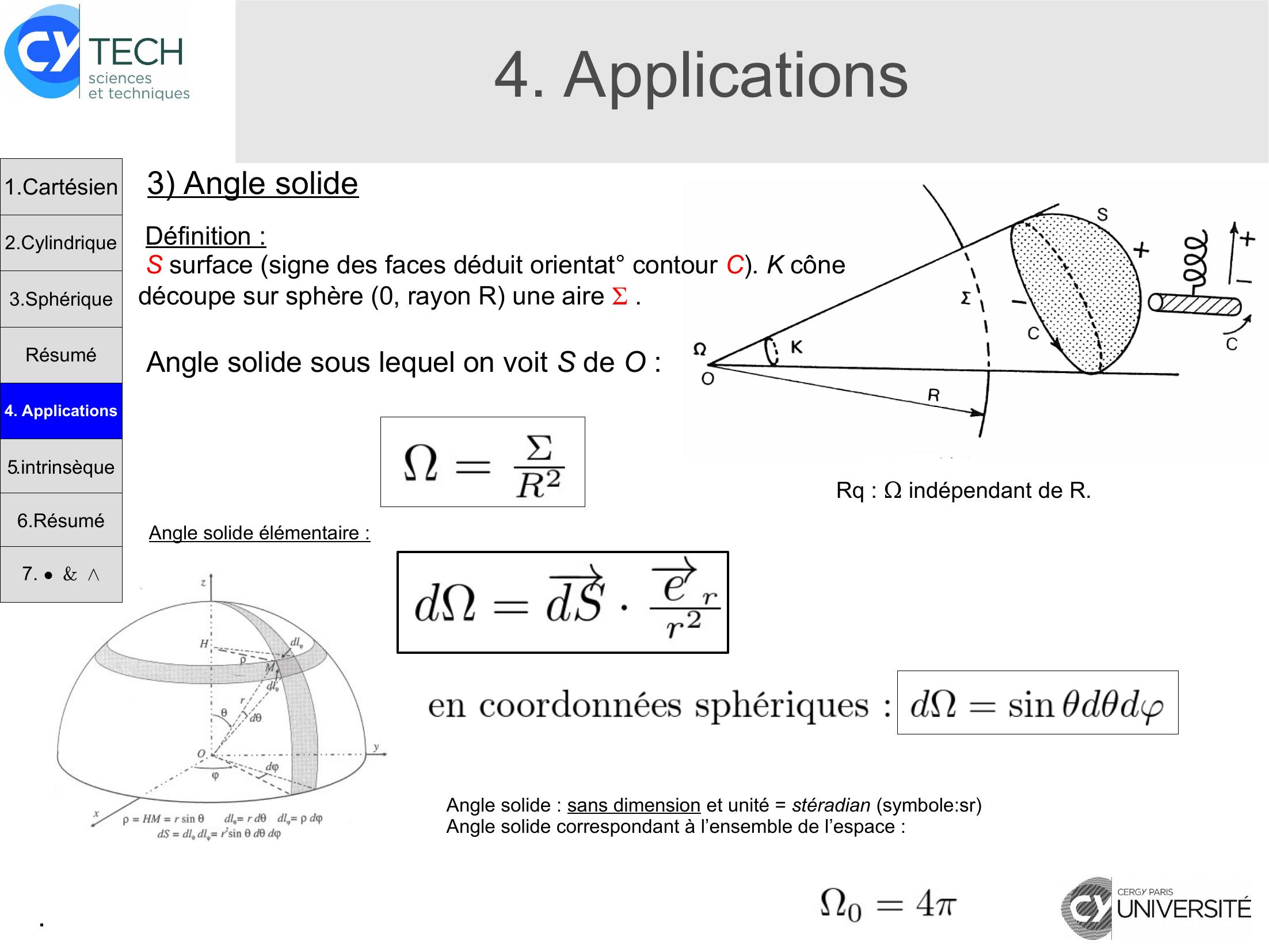
Page 12 : .4. Applications1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications3 Angle solide Définition : S surface signe des faces déduit orientat° contour C. K cône découpe sur sphère 0, rayon R une aire Σ . Angle solide sous lequel on voit S de O :Angle solide élémentaire :Rq : Ω indépendant de R.Angle solide : sans dimension et unité = stéradian symbole:srAngle solide correspondant à l’ensemble de l’espace :5.intrinsèque6.Résumé7. &

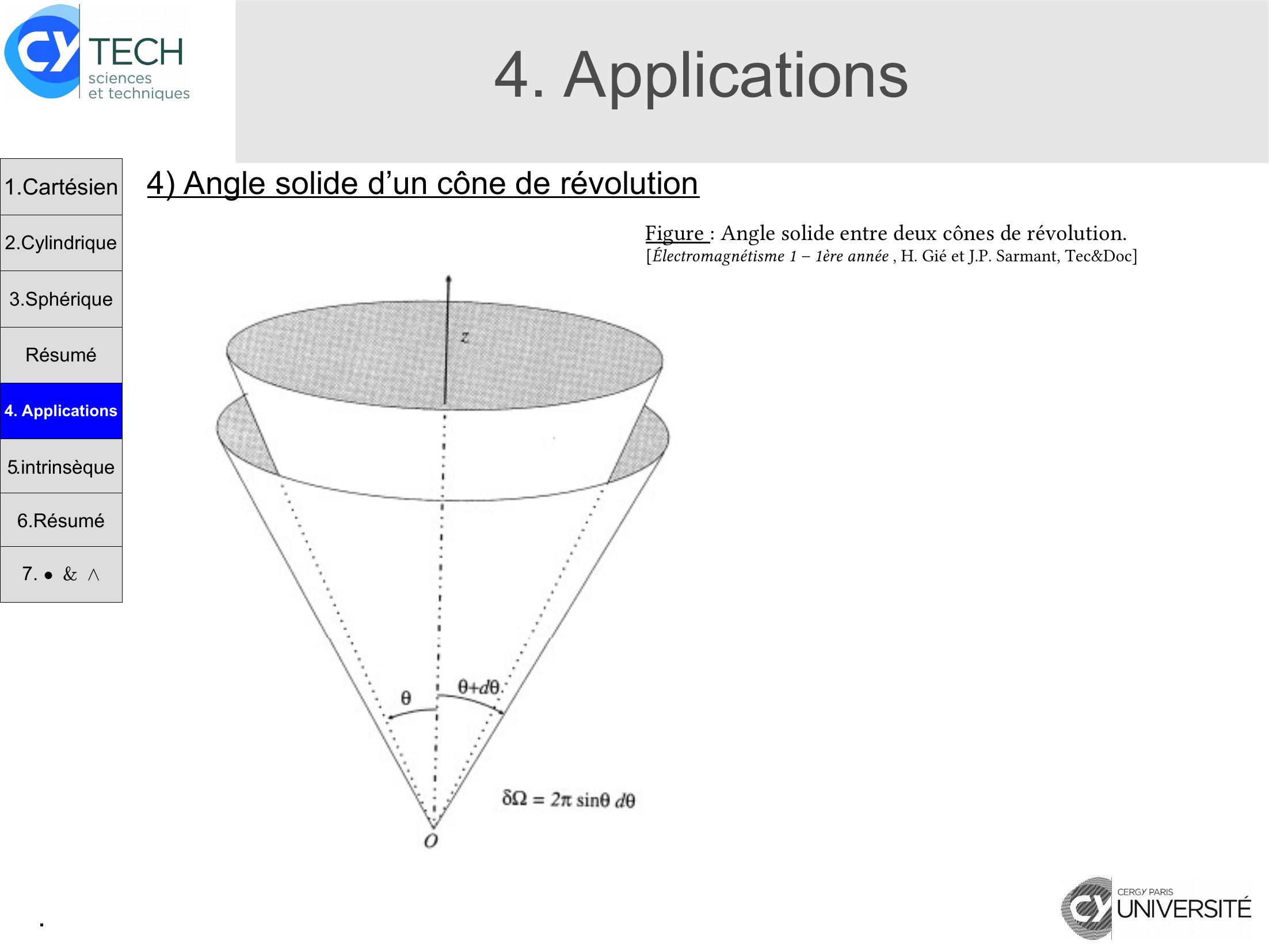
Page 13 : .4. Applications1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications4 Angle solide d’un cône de révolutionFigure: Angle solide entre deux cônes de révolution. Électromagnétisme 1 – 1ère année , H. Gié et J.P. Sarmant, Tec&Doc5.intrinsèque6.Résumé7. &

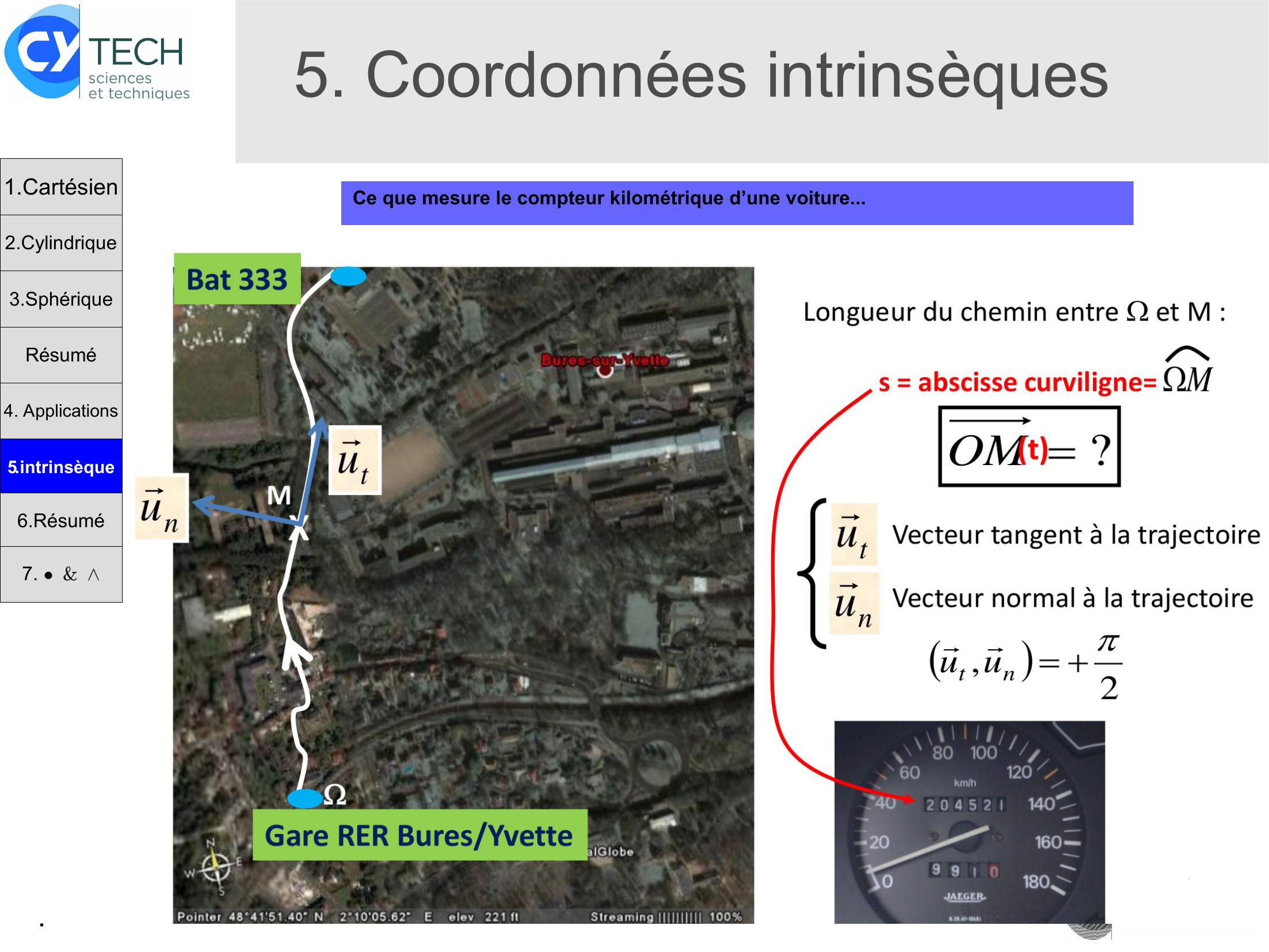
Page 14 : .Ce que mesure le compteur kilométrique d’une voiture...5. Coordonnées intrinsèques1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 15 : .6. Résumé1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 16 : .7. Produit scalaire & Produit vectorielEn Mécanique 1 et 2, on modélise les mouvements et leurs causes, les forces, par des vecteurs.Afin de résoudre les problèmes de Mécanique, d’Électromagnétisme etc… , on a besoin de projeter les vecteurs sur des directions particulières en utilisant les produits scalaires.En présence de rotations, on utilise également le produit vectoriel, ce qui sera un cas rencontré souvent en Électromagnétisme 1 et 2 lors qu’on s’intéressera au champ magnétique.1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

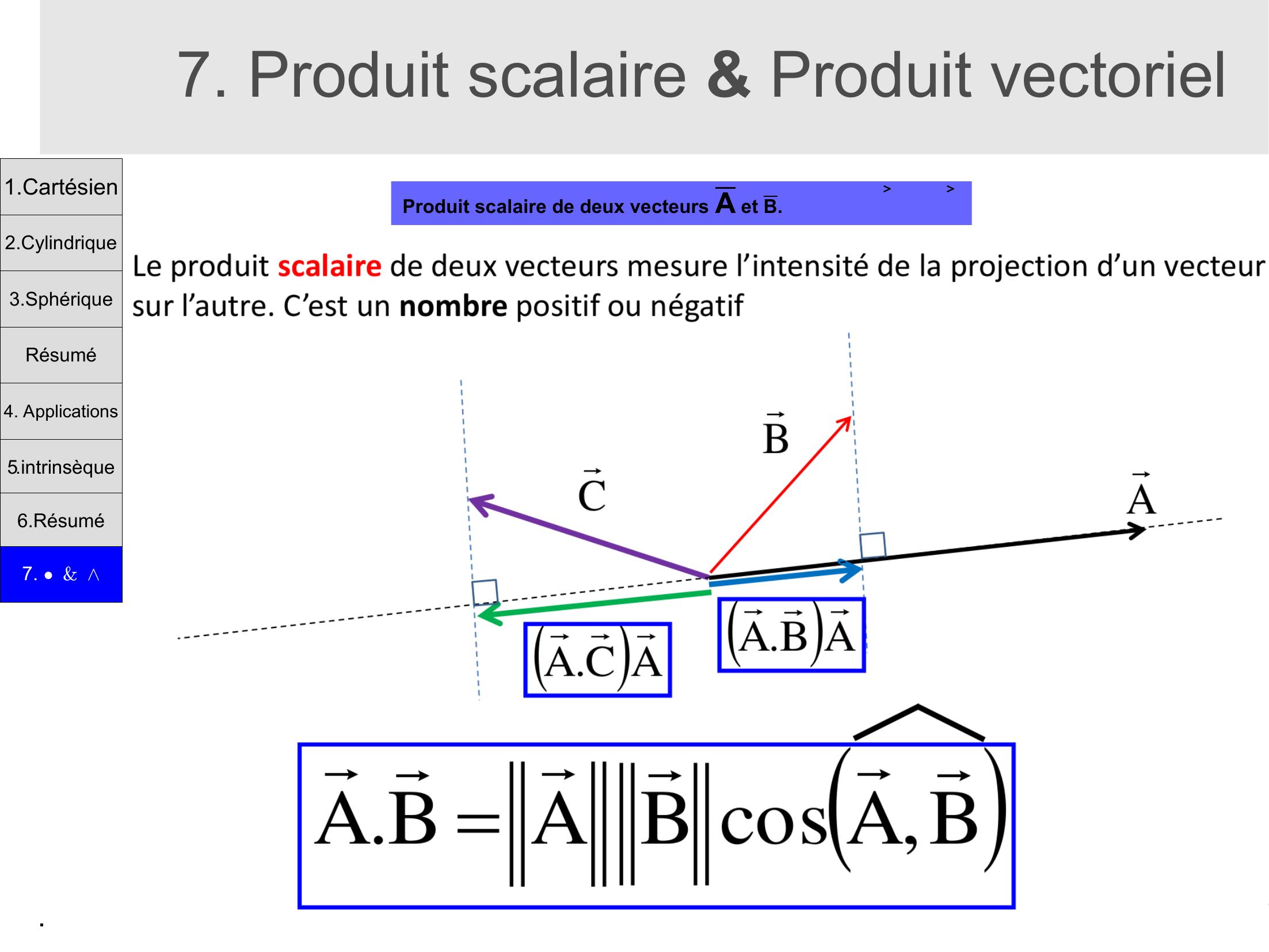
Page 17 : .7. Produit scalaire & Produit vectorielProduit scalaire de deux vecteurs A et B.1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

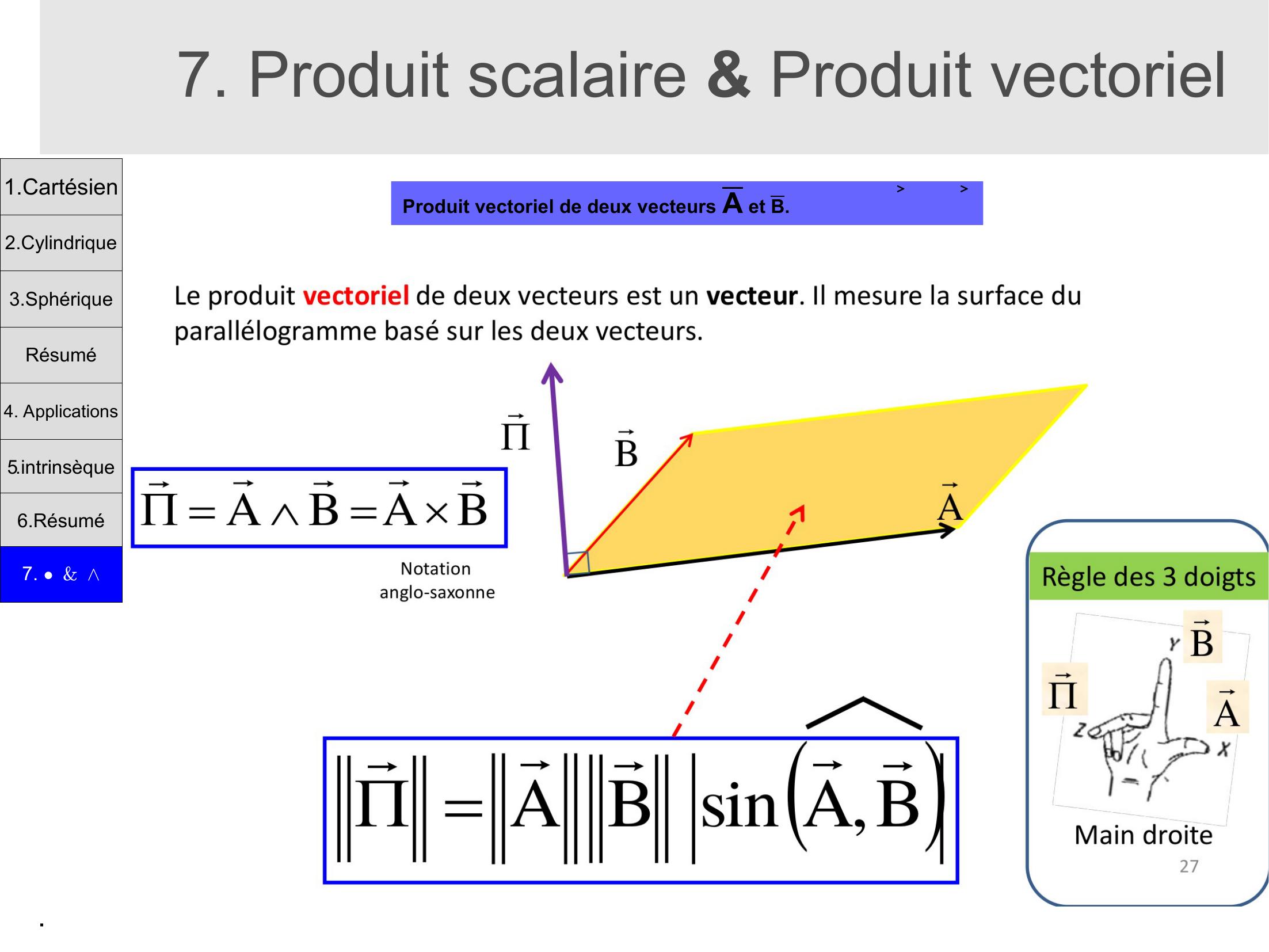
Page 18 : .7. Produit scalaire & Produit vectorielProduit vectoriel de deux vecteurs A et B.1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

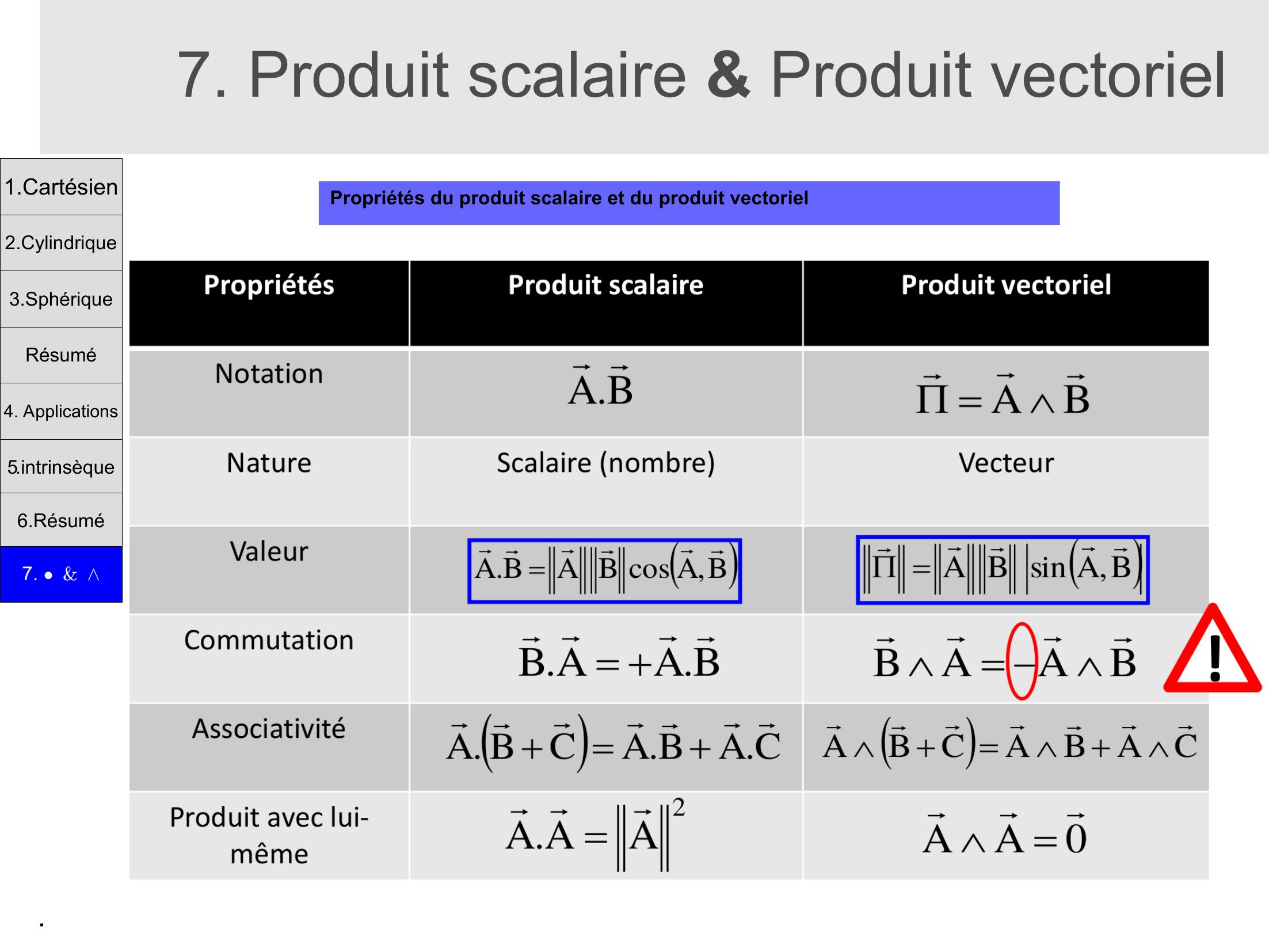
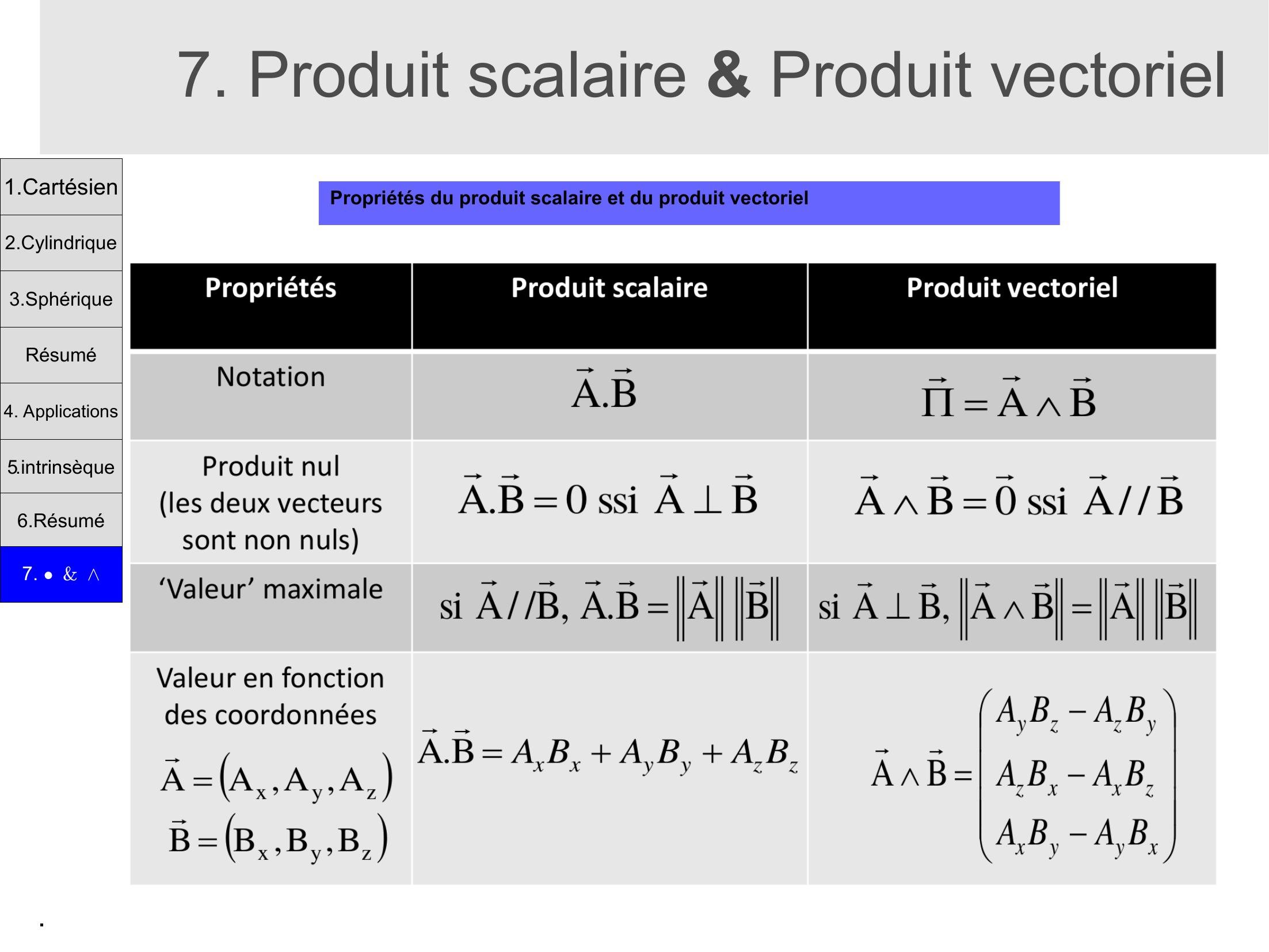
Page 19 : .7. Produit scalaire & Produit vectorielPropriétés du produit scalaire et du produit vectoriel1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

Page 20 : .7. Produit scalaire & Produit vectorielPropriétés du produit scalaire et du produit vectoriel1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

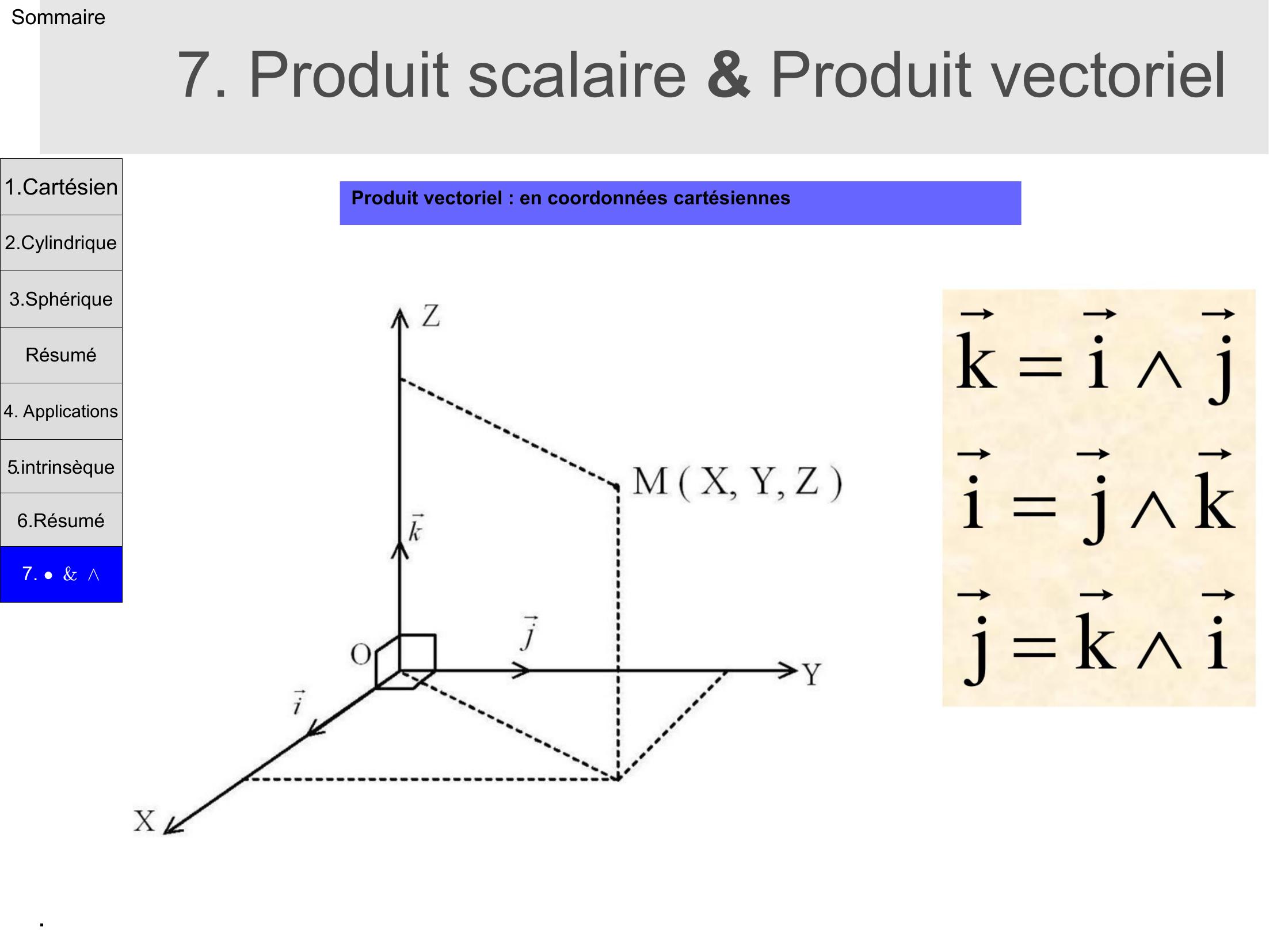
Page 21 : .Sommaire7. Produit scalaire & Produit vectorielProduit vectoriel : en coordonnées cartésiennes1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &

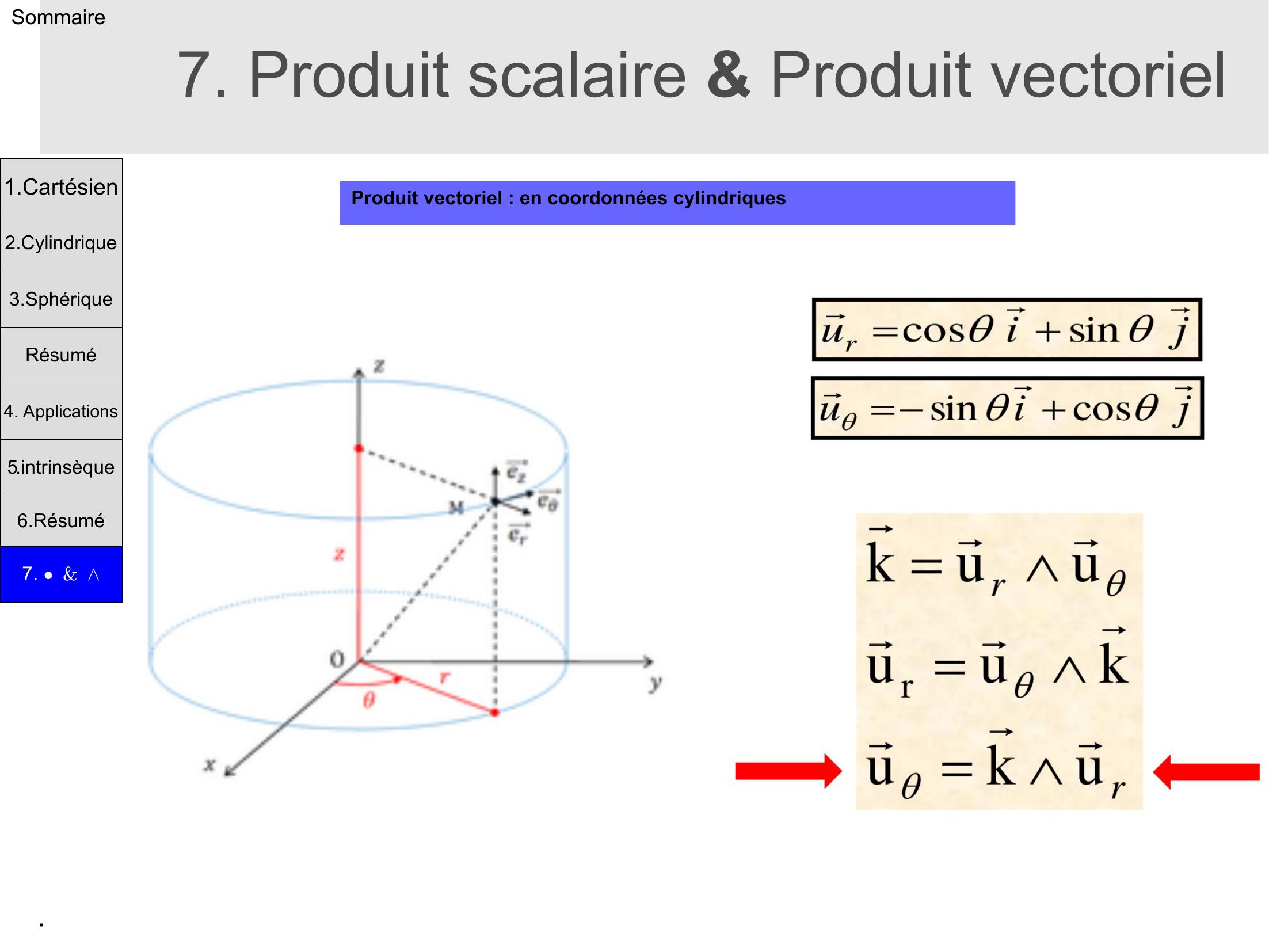
Page 22 : .Sommaire7. Produit scalaire & Produit vectorielProduit vectoriel : en coordonnées cylindriques1.Cartésien2.Cylindrique3.SphériqueRésumé4. Applications5.intrinsèque6.Résumé7. &