CM0 Continuite
Télécharger le CM0 Continuite en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Page 1 : Théorème des valeurs intermédiairesImage d'un intervalleAnalyse - Deuxième Semestre 2022Responsable CM :Didier Cransac groupes 1 - 2 - 3 - 4 - GEMSUPMECA - MISE - SIC - ENSA-VBureau : CY 201e-mail : dcc@cy-tech.fr - didier.cransac@cyu.frResponsable TD :Didier Cransac groupe 1Mohamed Bathiti groupe 2Jihan Joder groupe 3, MISE, SICThi Hien groupe 4Zahra GEM, Ensa-V, SupMeca, GCÉvaluation : DS : 11 Mars, 7 Avril, 2 Mai INTERROGATIONS, QCM et DMD. CransacAnalyse
Page 2 : Théorème des valeurs intermédiairesImage d'un intervalleComment travaillerApprendre le cours avant de venir en TD.Préparer les exercices des TD.Refaire les exercices des TD régulièrement pas juste avant les DS.Travailler les corrigés de tous les TD même ceux qui n'ont pas étérésolus en classe.Ne pas hésiter à consulter les documents fournis par d'autresprofesseurs dans les autres TD ou sur internet.D. CransacAnalyse
Page 3 : Théorème des valeurs intermédiairesImage d'un intervallePlanChapitre 0 : Les grands théorèmes de la ContinuitéChapitre 1 : Dérivation.Chapitre 2 : Comportement asymptotiqueChapitre 3 : IntégrationChapitre 4 : Equations diérentiellesD. CransacAnalyse
Page 4 : Théorème des valeurs intermédiairesImage d'un intervalleCONTINUITE RAPPEL1Théorème des valeurs intermédiairesEnoncéDémonstrationAntécédents2Image d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsD. CransacAnalyse
Page 5 : Théorème des valeurs intermédiairesImage d'un intervalleEnoncéDémonstrationAntécédentsLes grands théorèmes de la ContinuitéThéorème Théorème des valeurs intermédiaires TVISoit f: I →R une fonction continue et a b I, tels quef af b 0.Alors il existe c dans a; b tel quef c = 0.D. CransacAnalyse
Page 6 : Théorème des valeurs intermédiairesImage d'un intervalleEnoncéDémonstrationAntécédentsLes grands théorèmes de la ContinuitéDémonstration.Supposons que a b. On construit par récurrence deux suitesadjacentesannNetbnnNd'éléments de a, b dont la limite commune c vérie f c = 0.Construisons annN et bnnN. On pose a0 = a et b0 = b.Pour n N, nous allons dénir an et bn de façon d'avoirbn an = b a2netf anf bn 0.Pour cela, posons mn = an + bn2. Ainsisi f anf mn 0, on pose an+1 = an et bn+1 = mn.si f anf mn 0, on pose an+1 = mn et bn+1 = bn.Dans chacun de ces deux cas, on obtientf an+1f bn+1 0etbn+1 an+1 = bn an2= b a2n+1D. CransacAnalyse
Page 7 : Théorème des valeurs intermédiairesImage d'un intervalleEnoncéDémonstrationAntécédentsLes grands théorèmes de la ContinuitéDémonstration.Montrons que les suites annN et bnnN sont adjacentes. ParconstructionannN est croissante, etbnnN est décroissante.De plus, par construction, pour tout n N, nous avonsbn+1 an+1 = b a2n+1=⇒limn→+bn an = 0.Les suites annN et bnnN sont donc adjacentes et convergent vers lamême limite c a, b.Comme f est continue, en passant à la limite dans l'inégalité f anf bn 0,on obtientf c2 = flimn→+anflimn→+bn=limn→+f anf bn 0.Ainsi, f 2c 0. Donc f c = 0 et le théorème est démontré.D. CransacAnalyse
Page 8 : Théorème des valeurs intermédiairesImage d'un intervalleEnoncéDémonstrationAntécédentsLes grands théorèmes de la ContinuitéThéorème Théorème des valeurs intermédiaires, version existence d'un antécédent Soit a, b R avec a b et f : a, b →R une fonction continue sura, b. Alors pour tout y entre f a et f b, il existe c a, b tel quef c = y.Démonstration.Soit y entre f a et f b et posons gx = f x y. AlorsLa fonction g est continue, etga et gb sont de signes contraires, c'est-à-dire ga · gb 0.Par le théorème des valeurs intermédiaires, il existe donc c a, b, telquef c = y.D. CransacAnalyse
Page 9 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsLes grands théorèmes de la continuitéComme corollaire du résultat précédent nous avons le théorème suivant.Théorème Théorème des valeurs intermédiaires, version imaged'un intervalle Si I est un intervalle et si f est continue sur I, alors f I est un intervalle.Démonstration.Supposons que f I n'est pas un intervalle. Alors il existe y R, a I etb I réels tels que f a y f b. Si on applique le théorème desvaleurs intermédiaires, on montre qu'il existe c a; b tel que y = f cce qui est contradictoire.D. CransacAnalyse
Page 10 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsRemarque : Si I est un intervalle et f : I →R une fonction continue,cette version du TVI arme que f I est également un intervalle, maisne signie pas que I et f I sont de même nature. Il se peut que I soitouvert et f I un segment intervalle fermé, ou bien que I soitsemi-ouvert et f I ouvert, etc.Exemples :f x = sinxetf π, π = 1, 1;gx = x2etg 1, 1 = 0, 1.D. CransacAnalyse
Page 11 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsLes grands théorèmes de la ContinuitéThéorème Théorème des bornes atteintesToute fonction continue sur un segment intervalle fermé y estbornée et atteint ses bornes.Autrement dit, si f : a, b →R est continue sur a, b, alors ilexiste c a, b et d a, b tels que pour tout x a, b, nous avonsf c f x f d.L'image d'un segment par une fonction continue est un segment.Remarque :Nous avons vu que la continuité ne préserve pas la forme desintervalles en général, mais un segment est toujours transformé enun segment.Sur un intervalle borné qui n'est pas un segment, une fonctioncontinue n'est pas nécessaireement bornée.Par exemple, la fonction tangente suriπ2 , π2h.D. CransacAnalyse
Page 12 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsLes grands théorèmes de la ContinuitéThéorème Réciproque d'une fonction continueSoit I un intervalle et soit f : I →R une fonction continue.Alors f est injective sur I si et seulement si f est strictement monotone.Démonstration.Si f est strictement monotone alorsx, y R2, si x ̸= y alors x y et f x f y ou x y etf x f y. Dans tous les cas, f x ̸= f y donc la fonction f estinjective.D. CransacAnalyse
Page 13 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsDémonstration.Réciproquement, supposons que f est injective et continue.Soient a b deux réels tels de I = a; b.On peut toujours supposer que f a f b sinon on considère f Soit c, d a; b2 avec c dSi f c ⩽f a alors f a admet un antécédent sur c; b donc f n'est pasinjective.Si f c ⩾f b alors f b admet un antécédent sur a; c donc f n'est pasinjective.Donc f c f a; f bOn eectue le même raisonnement pour d et l'intervalle c; b, on obtientque f c f d donc la fonction f est strictement croissante sur I.D. CransacAnalyse
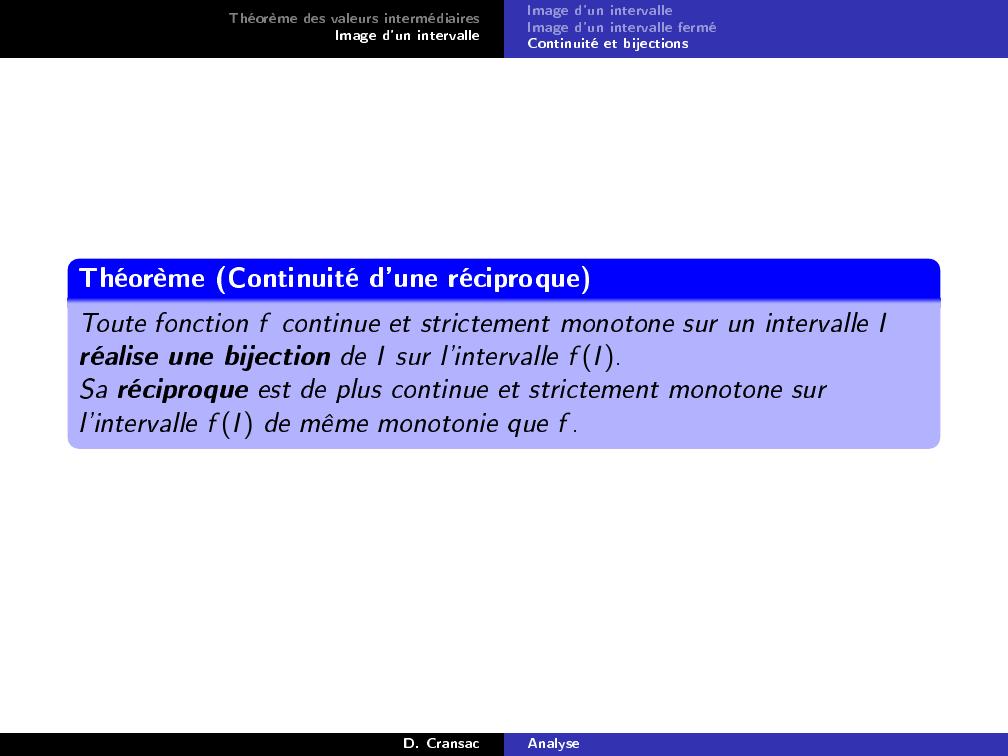
Page 14 : Théorème des valeurs intermédiairesImage d'un intervalleImage d'un intervalleImage d'un intervalle ferméContinuité et bijectionsThéorème Continuité d'une réciproqueToute fonction f continue et strictement monotone sur un intervalle Iréalise une bijection de I sur l'intervalle f I.Sa réciproque est de plus continue et strictement monotone surl'intervalle f I de même monotonie que f .D. CransacAnalyse