CM05 Recursivite
Télécharger le CM05 Recursivite en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
Page 1 : INFORMATIQUE 1I V. L A R É C U R S I V I T É
Page 2 : Rappel: un exemple de fonction●L’opérateur factoriel se note “!”. Par définition :𝑁! = 1 2 3 … 𝑁1 𝑁
Page 3 : Rappel: un exemple de fonction●L’opérateur factoriel se note “!”. Par définition :𝑁! = 1 2 3 … 𝑁1 𝑁●La fonction suivante permet de calculer la factorielle d’un nombre passé en paramètre : // Fonction qui calcule la factorielle d’un nombre// Conditions d’appel : nb un entier positif ou nulFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 1 à nb+1 FAIRE //pourquoi cet encadrement? Peut-on faire mieux ?res ← resiFIN POURRETOURNER res // on retourne le résultatFIN
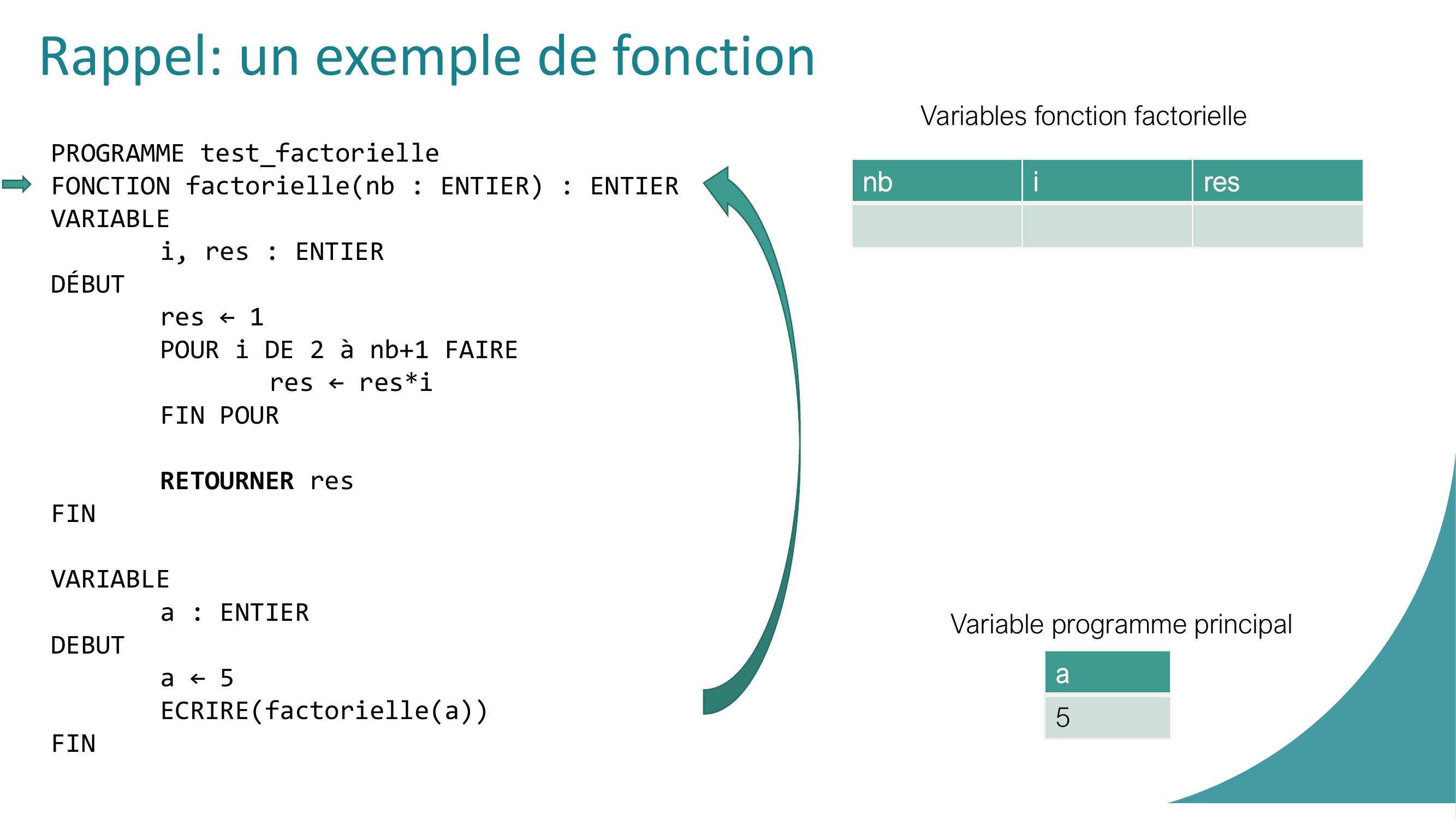
Page 4 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFIN
Page 5 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINaVariable programme principal
Page 6 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variable programme principal
Page 7 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbiresVariable programme principal
Page 8 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires5Variable programme principal
Page 9 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires51Variable programme principal
Page 10 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaa5Variables fonction factoriellenbires521Variable programme principal
Page 11 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires522Variable programme principal
Page 12 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires532Variable programme principal
Page 13 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires532Variable programme principal
Page 14 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires536Variable programme principal
Page 15 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires546Variable programme principal
Page 16 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires546Variable programme principal
Page 17 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires5424Variable programme principal
Page 18 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires5524Variable programme principal
Page 19 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires5524Variable programme principal
Page 20 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires55120Variable programme principal
Page 21 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires56120Variable programme principal
Page 22 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires56120Variable programme principal
Page 23 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variables fonction factoriellenbires56120Variable programme principal
Page 24 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variable programme principal
Page 25 : Rappel: un exemple de fonctionPROGRAMME testfactorielleFONCTION factoriellenb : ENTIER : ENTIERVARIABLEi, res : ENTIERDÉBUTres ← 1 POUR i DE 2 à nb+1 FAIREres ← resiFIN POURRETOURNER resFINVARIABLEa : ENTIER DEBUT a ← 5ECRIREfactorielleaFINa5Variable programme principal120
Page 26 : Des boucles partout !●La fonction factorielle, comme de très nombreux algorithmes, exploite une boucle expliciteTANT QUE, POUR
Page 27 : Une autre écriture.●La fonction factorielle, comme de très nombreux algorithmes, exploite une boucle expliciteTANT QUE, POUR●On a par definition 𝑁! = 1 2 3 … 𝑁1 𝑁. Cette formule peut-être récrite de la manière suivante : 𝑁! = 𝑁𝑁1 !𝑎𝑣𝑒𝑐1! = 1
Page 28 : Une autre écriture●La fonction factorielle, comme de très nombreux algorithmes, exploite une boucle expliciteTANT QUE, POUR●On a par definition 𝑁! = 1 2 3 … 𝑁1 𝑁. Cette formule peut-être récrite de la manière suivante : 𝑁! = 𝑁𝑁1 !𝑎𝑣𝑒𝑐1! = 1Cette relation entre N! et N-1! est dites de recurrence.
Page 29 : Les fonctions récursives : définition●Une fonction est recursive recursive lorsqu’elle s’apelle elle-même. ●Elle se base sur des relations de recurrence.●Puisqu’elle s’apelle elle-même, certaines instructions seront répétées plusieures fois. Une fonction récursive va donc faire office de boucle implicite.●Une fonction qui utilise une boucle explicite POUR, TANT QUE est dite itérative
Page 30 : Les fonctions récursives : définition●Une fonction est recursive recursive lorsqu’elle s’apelle elle-même. ●Elle se base sur des relations de recurrence.●Puisqu’elle s’apelle elle-même, certaines instructions seront répétées plusieures fois. Une fonction récursive va donc faire office de boucle implicite.●Une fonction qui utilise une boucle explicite POUR, TANT QUE est dite itérative●Un même algorithme peut avoir une definition recursive ou iterative !𝑁! = 𝑁𝑁1 𝑁2 2 1𝑁! = ቊ1 𝑠𝑖𝑁= 1𝑁𝑁1 ! 𝑠𝑖𝑛𝑜𝑛Definition iterative Définition récursive
Page 31 : Un exemple complet// Fonction qui calcule la factorielle d’un nombre// Conditions d’appel : nb un entier positifFONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER // on déclare une variable résultatDÉBUTSI nb = 1 ALORS// cas trivialres ←1SINONres ←nb factoriellenb - 1 // récursivitéFIN SIRETOURNER res // on retourne le résultatFIN𝑁! = ቊ1 𝑠𝑖𝑁= 1𝑁𝑁1 ! 𝑠𝑖𝑛𝑜𝑛
Page 32 : Arbre de récursivité.●Un arbre de récursivité illustre les appels et le retours successif d’une fonction recursive.●Il permet, entre autre, de comprendre la manière dont fonctionne l’algorithme récursif. ●Exemple : que se passe-t-il lorsque l’on appelle factorielle5?
Page 33 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FIN
Page 34 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle5 ←5factorielle4
Page 35 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle5 ←5factorielle4 la fonction a donc besoindu résultat de factorielle4pour renvoyer un résultat!
Page 36 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FIN
Page 37 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FIN
Page 38 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FIN
Page 39 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FIN
Page 40 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle2 ←
Page 41 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle2 ← 2factorielle1
Page 42 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle2 ← 2factorielle1 factorielle1 ←
Page 43 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle 5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 FONCTION factoriellenb : ENTIER : ENTIERVARIABLEres : ENTIER DÉBUTSI nb = 1 ALORSres ← 1SINONres ← nb factoriellenb - 1 FIN SIRETOURNER res FINfactorielle2 ← 2factorielle1 factorielle1 ← 1
Page 44 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle 5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 factorielle2 ← 2factorielle1 factorielle1 ← 1On fait remonter les retours succéssifs !
Page 45 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle 5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 factorielle2 ← 2factorielle1 =2factorielle1 ← 1On fait remonter les retours succéssifs !
Page 46 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 factorielle3 ←3factorielle2 = 6factorielle2 ← 2factorielle1 = 2factorielle1 ← 1On fait remonter les retours succéssifs !
Page 47 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 factorielle4 ←4factorielle3 = 24factorielle3 ←3factorielle2 = 6factorielle2 ← 2factorielle1 = 2factorielle1 ← 1On fait remonter les retours succéssifs !
Page 48 : Arbre de récursivité.●Exemple : que se passe-t-il lorsque l’on appelle factorielle5? factorielle5 ←5factorielle4 = 120factorielle4 ←4factorielle3 = 24factorielle3 ←3factorielle2 = 6factorielle2 ← 2factorielle1 = 2factorielle1 ← 1On fait remonter les retours succéssifs !
Page 49 : Arbre de récursivité.●Arbre de récursivité de factorielle 5:factorielle5 ←5factorielle4 = 120 4factorielle3 = 24 3factorielle2 = 6 2factorielle1 = 2 1
Page 50 : Composantes d’une fonction récursivefx = si cx alorsgxsinon hfsx, x●cx est dite condition d’arrêt ;●gx est le cas trivial, il peut retourner une valeur constante ;●sx est la fonction “successeur” de x ;●hfsx,x est l’appel récursif, fonction de x et du successeur de x. Si h est la fonction identité, la récursivité est dite terminale; non terminale sinon.
Page 51 : Types de récursivité●Une fonction récursive peut être simple ou multiple cf fibonacci ;●Une fonction récursive peut être terminale ou non terminale ;●Une fonction récursive peut être croisée ;●Dans tous les cas, une fonction récursive doit se terminer !! Il faut définir une bonne condition d’arret.
Page 52 : Récursivité non terminaleFONCTION factoriellenb : ENTIER : ENTIERDÉBUTSI nb = 0 ALORS// condition d’arretRETOURNER 1 // cas trivialSINONRETOURNER nb factoriellenb - 1// récursivitéFIN SIFINUne fonction recursive est non terminale lorsqu’il y’ a une opération sur la valeur retounée et pas uniquementun appel à la fonction.
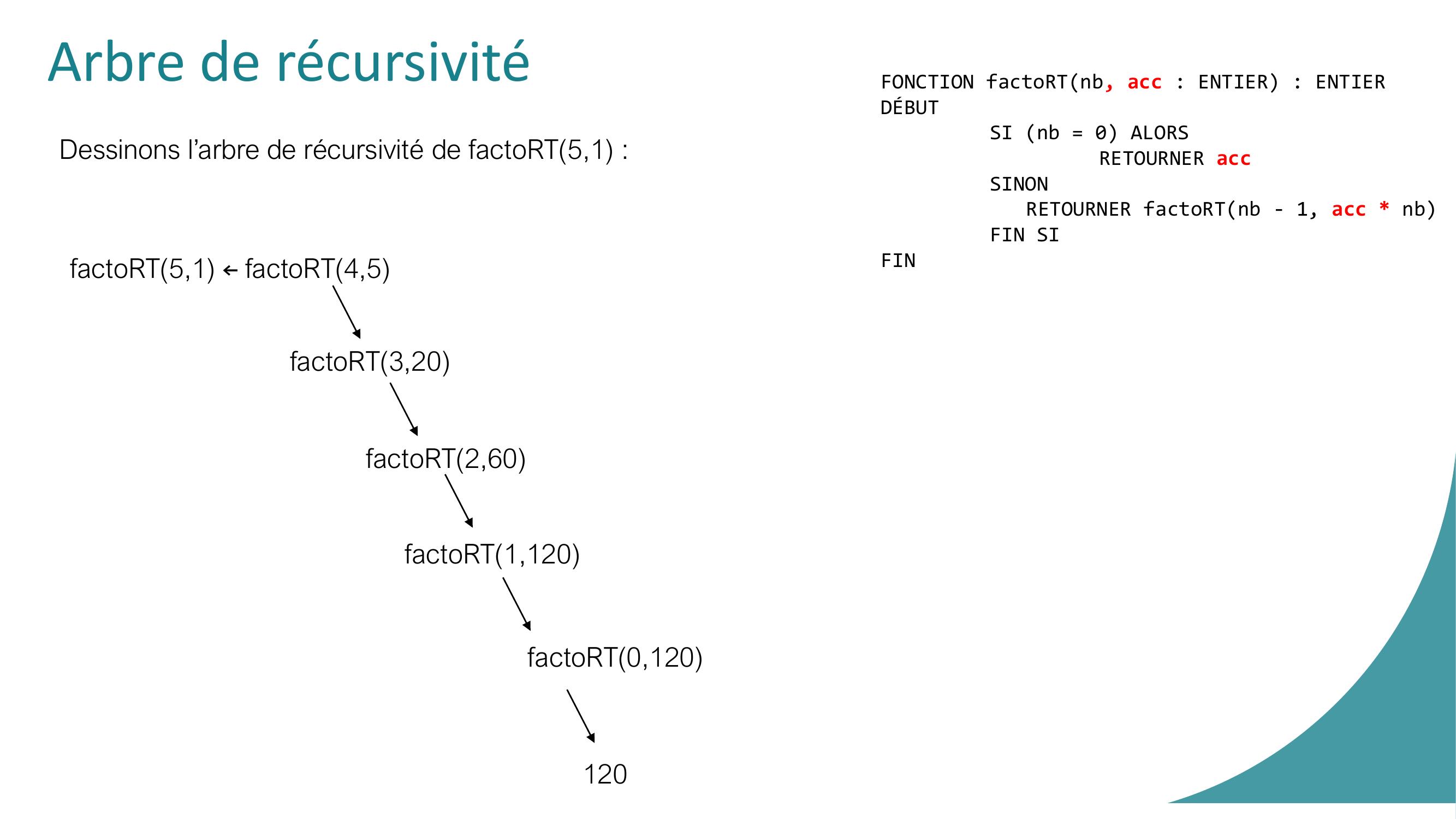
Page 53 : Récursivité terminale// Conditions : nb un entier positif, acc = 1FONCTION factoRTnb, acc : ENTIER : ENTIERDÉBUTSI nb = 0 ALORS// cas trivialRETOURNER accSINONRETOURNER factoRTnb - 1, acc nb // récursivitéFIN SI FINVARIABLEnb: ENTIER DEBUTnb ← 5factoRTnb, 1 // le second paramètres est fixé à 1FINUne fonction recursive est terminale lorsque la valeur retournée est directement la valeur obtenue par un appel récursif.
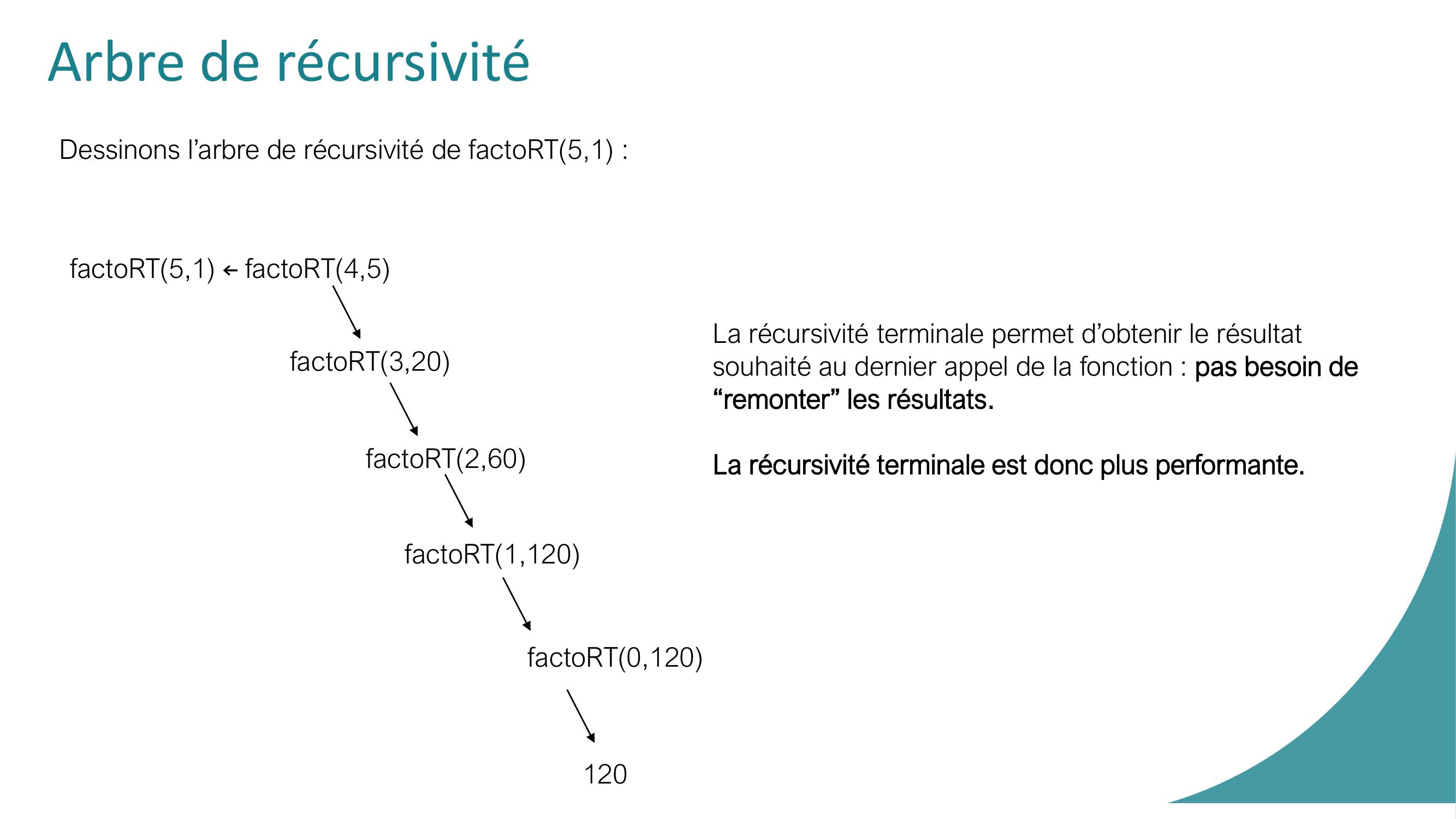
Page 54 : Arbre de récursivitéDessinons l’arbre de récursivité de factoRT5,1 : FONCTION factoRTnb, acc : ENTIER : ENTIERDÉBUTSI nb = 0 ALORSRETOURNER accSINONRETOURNER factoRTnb - 1, acc nb FIN SI FINfactoRT5,1 ←factoRT4,5 factoRT3,20factoRT2,60factoRT1,120factoRT0,120120
Page 55 : Arbre de récursivitéDessinons l’arbre de récursivité de factoRT5,1 : factoRT5,1 ←factoRT4,5 factoRT3,20factoRT2,60factoRT1,120factoRT0,120120La récursivité terminale permet d’obtenir le résultatsouhaité au dernier appel de la fonction : pas besoin de “remonter” les résultats.La récursivité terminale est donc plus performante.
Page 56 : Récursivité multiple• La récursivité d’une fonction est multiple lorsqu’elle comporte plusieurs invocations récursives. • Exemple: la suite de Fibonaccila suite de Fibonacci est une suite dans laquelle chaque terme est la somme des deux termes qui le précèdent.𝐹𝑛= ቐ0 𝑠𝑖𝑛= 01 𝑠𝑖𝑛= 1𝐹𝑛1 + 𝐹𝑛2 𝑠𝑖𝑛𝑜𝑛
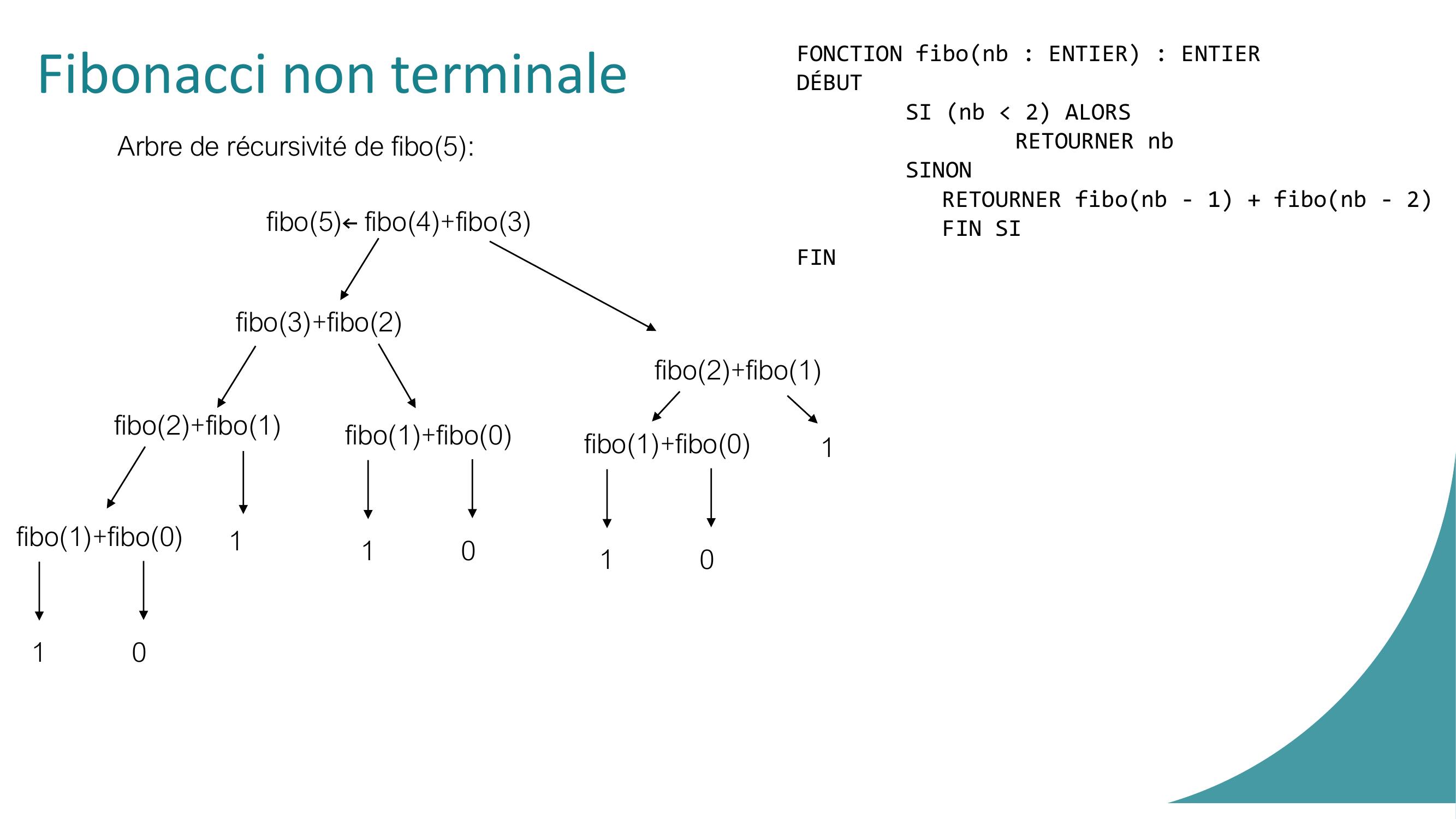
Page 57 : Fibonacci non terminale// ATTENTION ! Les versions non terminales des récursions peuvent poser des problèmes de performanceFONCTION fibonb : ENTIER : ENTIERDÉBUTSI nb 2 ALORS// cas trivialRETOURNER nbSINONRETOURNER fibonb - 1 + fibonb - 2// récursivitéFIN SIFIN
Page 58 : Fibonacci non terminaleFONCTION fibonb : ENTIER : ENTIERDÉBUTSI nb 2 ALORSRETOURNER nbSINONRETOURNER fibonb - 1 + fibonb - 2 FIN SIFINArbre de récursivité de fibo5:fibo5←fibo4+fibo3 fibo3+fibo2 fibo2+fibo1 fibo1+fibo0 110fibo2+fibo1 fibo1+fibo0 101fibo1+fibo0 10
Page 59 : Fibonacci terminaleFONCTION fiboRTnb, fnm2, fnm1 : ENTIER : ENTIERDÉBUTSI nb = 0 ALORS// cas trivialRETOURNER fnm2SINONRETOURNER fiboRTnb - 1, fnm1, fnm1 + fnm2 //récursivitéFIN SIFINFONCTION fibonb : ENTIER : ENTIERDÉBUTRETOURNER fiboRTnb, 0, 1FIN
Page 60 : Fibonacci terminaleFONCTION fiboRTnb, fnm2, fnm1 : ENTIER : ENTIERDÉBUTSI nb = 0 ALORSRETOURNER fnm2SINONRETOURNER fiboRTnb - 1, fnm1, fnm1 + fnm2 FIN SIFINFONCTION fibonb : ENTIER : ENTIERDÉBUTRETOURNER fiboRTnb, 0, 1FINArbre de récursivité de fibo5:fibo5←fiboRT5,0,1fiboRT4,1,1fiboRT3,1,2fiboRT2,2,3fiboRT1,3,5fiboRT0,5,85
Page 61 : // Cet algorithme se termine-t-il ?FONCTION exemple1n : ENTIER : ENTIERDÉBUTSI n = 0 ALORSRETOURNER 1SINONRETOURNER n exemple1n‐2FIN SIFINProblème de terminaisonSi n est impair, la fonction ne finis jamais!
Page 62 : // Cet algorithme se termine-t-il ? FONCTION exemple2n : REEL : REELDÉBUTSI n = 0 ALORSRETOURNER 1SINONRETOURNER exemple2n/2FIN SIFINProblème de terminaisonn va tendre vers 0 mais ne l’atteind pas !
Page 63 : Récursivité croisée// ATTENTION ! Ici encore aux problèmes de terminaisonFONCTION estPairnb : ENTIER : BOOLEENDÉBUTSI nb = 0 ALORS// cas trivialRETOURNER VRAIFIN SISI nb = 1 ALORS// cas trivialRETOURNER FAUXFIN SIRETOURNER estImpairnb - 1 // récursivitéFIN SIFINFONCTION estImpairnb : ENTIER : BOOLEENDÉBUTSI nb = 1 ALORS// cas trivialRETOURNER VRAIFIN SI SI nb = 0 ALORS// cas trivialRETOURNER FAUX FIN SIRETOURNER estPairnb - 1 // récursivitéFIN SIFIN
Page 64 : Récursivité croiséeArbre de récursivité de estPair5:FONCTION estPairnb : ENTIER : BOOLEENDÉBUTSI nb = 0 ALORSRETOURNER VRAIFIN SISI nb = 1 ALORSRETOURNER FAUXFIN SIRETOURNER estImpairnb - 1 FINFONCTION estImpairnb : ENTIER : BOOLEENDÉBUTSI nb = 1 ALORSRETOURNER VRAIFIN SI SI nb = 0 ALORSRETOURNER FAUX FIN SIRETOURNER estPairnb - 1 FINestPaire5←estImpair4estPair3estImpair2estPair1FAUX
Page 65 : Boucle explicite ou récursivité ? •Les boucles explicites c’est pratique mais …oIl existe des énoncés qui sont par essence récursif : cf les tours de Hanoï, le démineur, ... ;oIl existe des objets mathématiques récursifs : les suites, les fractales, les chaînes de Markov... ;oIl existe des objets informatiques récursifs : les listes chaînées, piles, files ;oOn peut exprimer naturellement des problèmes sous forme récursive : n! = n n-1!
Page 66 : Boucle explicite ou récursivité ? •Les boucles explicites c’est pratique mais …oIl existe des énoncés qui sont par essence récursif.oIl existe de nombreux cas où la récursivité est plus efficace plus rapide que la version itérative : parcours d’arbre, recursivité multiple … Mais ce n’est pas toujours le cas ! Les fonctions recursives non-terminales sont généralement similaires en terme de rapidité à leur equivalent iterative.
Page 67 : Avantages et inconvénients●Intuitive et économique pour le programmeur○compacte et élégante, facile à analyser○proche des mathématiques cela devrait être un avantage pour vous !○adapté aux structures de données récursives cf listes chaînées au 2nd semestre●Peut-être coûteuse pour la machine○Sauvegarde des résultats intermédiaires, peut être dépassée stack overflow○utilisation de la récursivité terminale pas toujours possible●Tout algorithme récursif peut être exprimé sous forme itérative pas toujours simplement…
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67