CM06 Complexite
Télécharger le CM06 Complexite en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
Page 1 : Algorithmique procédurale Complexité
Page 2 : QuestionDeux algorithmes qui pour les mêmes données d’entréedonnent le même résultat sont-ils équivalents?
Page 3 : Notion de complexité•La complexité algorithmique permet de mesurer lesperformances d’un algorithme et de le comparer avec d’autres algorithmes réalisant les mêmes fonctionnalités.•Un bon algorithme :•répond correctement au problème posé•est rapide complexité temporelle•utilise peu de mémoire complexité spatiale•On s'intéresse surtout à la complexité temporelle ce quin'était pas forcément le cas quand les mémoires coutaientcher.
Page 4 : Complexité temporelle vs. spatialeRègle de l'espace-temps informatique :Pour gagner du temps de calcul, on doit dépenser de l’espace mémoire.Exemple 1: stockage de calcul intermédiairex, y: REEL;x - 3.7;y - sinxsinx;Cette méthode n‘a pas de variable supplémentaire et calcule sinx deux fois.x, y, z: REEL;x - 3.7;z - sinx; y - zz;Cette méthode investit une variable pour stocker sinusx.
Page 5 : Complexité temporelle vs. spatialeRègle de l'espace-temps informatique :Pour gagner du temps de calcul, on doit dépenser de l’espace mémoire.Exemple 2: échange de deux variables entièresx, y: ENTIER;X -0 y-1x - y-xx - y-xx - y+xCette méthode n‘a pas de variable supplémentaire mais réalise 3 opérations arithmétiques.x, y, z: ENTIER;x -0 y -1z - xx - yx - zCette méthode investit une variable z et réalise uniquement 3 affectations.
Page 6 : Opérations élémentaires•Toute opération élémentaire s’exécute en temps constant ou presque:•opérations arithmétiques•affectations•comparaisons•La performance d’un algorithme dépend typiquement dela taille des données en entrée.•Plus la taille de l’entrée est grande, plus il faudra dutemps pour trouver la solution.
Page 7 : Exemple 1Comment ouvrir un cadenas de N chiffresdont on ne connait pas la combinaison?
Page 8 : Exemple 1Comment ouvrir un cadenas de N chiffresdont on ne connait pas la combinaison?a Tester toutes les combinaisonsb Trouver chaque molette independementc Le casser
Page 9 : Exemple 1Comment ouvrir un cadenas de N chiffresdont on ne connait pas la combinaison?a Tester toutes les combinaisonsMeilleur des cas : 1 essaisPire cas : 10𝑁essaisEsperance : 5 10𝑁1 essais- lien exponentiel entre le nombre de chiffres du cadenas et ne nombre d’essais
Page 10 : Exemple 1Comment ouvrir un cadenas de N chiffresdont on ne connait pas la combinaison?b Trouver chaque molette independamentMeilleur des cas : 1 essaisPire cas : 10 𝑁essaisEsperance : 5 𝑁essais- lien linéaire entre le nombre de chiffresdu cadenas et ne nombre d’essais
Page 11 : Exemple 1Comment ouvrir un cadenas de N chiffresdont on ne connait pas la combinaison?cCasser le cadenasNombre d’essais : 1Pas de lien entre N et le nombre d’essais ! Mais le cadenas est cassé …
Page 12 : Exemple 2Quel est le temps estimatif pour trouver un mot dans un dictionnaire d’un million de mots, en supposant qu’une comparaison prend une milliseconde ?
Page 13 : Exemple 2Quel est le temps estimatif pour trouver un mot dans un dictionnaire d’un million de mots, en supposant qu’une comparaison prend une milliseconde ?a Recherche séquentielle:On regarde tous les mots un par un dans l’ordre.b Recherche dichotomique:On regarde « au milieu » du dictionnaire, en fonction de la lettre au recommence sur la bonne moitié du dictionnaire.
Page 14 : Exemple 2Quel est le temps estimatif pour trouver un mot dans un dictionnaire d’un million de mots, en supposant qu’une comparaison prend une milliseconde ?a Recherche séquentielle:Meilleur cas: 1 𝑚𝑠Pire cas :103 106 = 103𝑠 16 𝑚𝑖𝑛Esperance : 500 𝑠 8 𝑚𝑖𝑛Lien linéaire entre nombre de mots et temps de recherche.
Page 15 : Exemple 2Quel est le temps estimatif pour trouver un mot dans un dictionnaire d'un million de mots, en supposant qu'une comparaison prend 1 milliseconde ?b Recherche dichotomique• Le nombre de mots à vérifier est divisé par deux à chaque tour : 106/2𝑘k nombre de tours de recherche• Meilleur cas : 1 tour• Dans le pire cas, on ne trouve le mot que lorsque l'on a terminé de diviserl'ensemble des mots restants par 2 et qu'il ne reste plus qu'un seul mot à comparer:1 1062𝑘𝑘log2 106 20 ms
Page 16 : Exemple 2Quel est le temps estimatif pour trouver unmot dans un dictionnaire d’un million de mots,en supposant qu’une comparaison prendune milliseconde ?a Recherche séquentielle : 16 minb Recherche dichotomique: 20 ms
Page 17 : Configurations caractéristiques•Soit d une donnée de taille n et Ci un nombred'opérations élémentaires pour exécuter l'algorithme sur i.•On distingue•Le pire des cas:•Le cas moyen :Max Cii donnéede tailleni donnée de taille n•Le meilleur des cas : Min Cii donnée de taille noù pi est la probabilité d’avoir en entrée la donnée iRmq: Le calcul du meilleur cas n’est pas très utile dans la pratique. Le cas moyen est souvent difficile à calculer.On s’intéresse surtout au pire cas car onsouhaite borner le temps d'exécution.piCi
Page 18 : Calcul des opérations élémentairesPour déterminer la complexité d’unalgorithme, on recense toutes les opérationsélémentaires:•opérations arithmétiques•affectations•comparaisonsOn distingue deux types d’algorithme:•algorithme itératif•algorithme récursif
Page 19 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFIN
Page 20 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFIN1 affectation
Page 21 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFIN1 affectation
Page 22 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFIN1 affectation1 addition
Page 23 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFIN1 affectation n1 addition n
Page 24 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFINaddiction : n+1 affectation : 1 stockage de n+1
Page 25 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFINaddiction : 1: n+1n : incrementation iaffectation : 1 stockage de n+1n+1 affectation de i
Page 26 : Exemple: Algorithme itératifFONCTION sommen : ENTIER : ENTIERVARIABLES i, s : ENTIERDEBUTs ← 0POUR i DE 1 A n+1 F A I R E12345s ←s + iFIN POURRETOURNER sFINcomparaison : n+1 in+1
Page 27 : •Nombre d'affectations•1•1•n + 1•n•1ligne 1ligne 2 : stockage de ndans une variable ligne 2 : gestion de compteurligne 3 : boucle exécutée n foisligne 5•Nombre de comparaisons•n + 1ligne 2 : gestion de compteur•Nombre d'additions•n•n•1ligne 2 : gestion de compteurligne 3 : boucle exécutée n foisLigne 2: n+1Exemple: Algorithme itératif
Page 28 : ExerciceCombien d’opérations élémentaires•opérations arithmétiques•affectations•comparaisonssont effectuées dans ces calculs x2n ?VARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN
Page 29 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucle
Page 30 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucleOp. arithm. +,1Affectations11Comparaisons
Page 31 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucleOp. arithm. +,2N1+NAffectations1+2N1+NComparaisons
Page 32 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucleOp. arithm. +,2N+21+N+1Affectations1+2N+11+N+1Comparaisons
Page 33 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucleOp. arithm. +,2N+2+2N1+N+1+NAffectations1+2N+1 +2N+11+N+1+N+1Comparaisons2N+1N+1
Page 34 : ExerciceVARIABLES i, X2, X : ENTIERDEBUTX2 ← 1POUR I DE 1 A 2N+1 FAIREX2 ←X2XFIN POURFINVARIABLES i, X2, X : ENTIERDEBUTX2 ←XX;POUR i DE 1 A N +1 FAIREX2 ← X2X2FIN POURFIN2N tours de boucleN tours de boucleOp. arithm. +,2+2N+2N = 4N+22+N+N = 2N+2Affectations1+1+2N+1+2N = 4N+32+N+1+N = 2N+3Comparaisons2N+1N+1
Page 35 : Exercice1Quelle est la complexité de cet algorithme en nombre d'additions et de divisions ?resultat ← 0POUR i DE 1 à n+1 FAIREPOUR j DE i A i + 3 FAIRE resultat ← resultat +i/i+jFIN POURFIN POUR234
Page 36 : ExerciceQuelle est la complexité de cet algorithme en nombre d'additions et de divisions ?resultat ← 0POUR i DE 1 à n+1 FAIREPOUR j DE i A i + 3 FAIRE resultat ← resultat +i/i+jFIN POURFIN POUR12342 additions 1 division : 3 opérations
Page 37 : ExerciceQuelle est la complexité de cet algorithme en nombre d'additions et de divisions ?resultat ← 0POUR i DE 1 à n+1 FAIREPOUR j DE i A i + 3 FAIRE resultat ← resultat +i/i+jFIN POURFIN POUR12342 additions 1 division : 3 operation Boucle 2 est exécutée 3 fois i à i+2 inclus:33 operations3 additions j+1 + 1 additions i+3= 13
Page 38 : ExerciceQuelle est la complexité de cet algorithme en nombre d'additions et de divisions ?resultat ← 0POUR i DE 1 à n+1 FAIREPOUR j DE i A i + 3 FAIRE resultat ← resultat +i/i+jFIN POURFIN POUR12342 additions 1 division : 3 operation Boucle 2 est exécutée 3 fois i à i+2 inclus:12 opérationBoucle 1 exécutée n fois13 n operation+ n addition i+1 + 1 addition n+1- 13n+n+1=14n+1 operations arithmétiques !
Page 39 : Déterminer une équation de récurrence en fonction du nombred'opérations élémentaires et résoudre cette équation.FONCTION factn : ENTIER :ENTIERDEBUTSI n = 1 ALORSRETOURNER 1SINONRETURNER n factn-1FIN SIFINExemple: Algorithme récursif
Page 40 : Déterminer une équation de récurrence en fonction du nombred'opérations élémentaires et résoudre cette équation.FONCTION factn : ENTIER :ENTIERDEBUTSI n = 1 ALORSRETOURNER 1SINONRETURNER n factn-1FIN SIFINExemple: Algorithme récursif⚫Nombre d'affectations A
Page 41 : Déterminer une équation de récurrence en fonction du nombred'opérations élémentaires et résoudre cette équation.FONCTION factn : ENTIER :ENTIERDEBUTSI n = 1 ALORSRETOURNER 1SINONRETURNER n factn-1FIN SIFINExemple: Algorithme récursif⚫Nombre de comparaisons C
Page 42 : Déterminer une équation de récurrence en fonction du nombred'opérations élémentaires et résoudre cette équation.FONCTION factn : ENTIER :ENTIERDEBUTSI n = 1 ALORSRETOURNER 1SINONRETURNER n factn-1FIN SIFINExemple: Algorithme récursif⚫Nombre d’opérations arithmétiques OP
Page 43 : ⚫Nombre d'affectations A• 𝑛= 1 𝐴1 = 1• 𝑛 1 𝐴𝑛= 1 + 𝐴𝑛1 = 1 + 1 +𝐴𝑛2 = = 𝑛⚫Nombre de comparaisons C• 𝑛= 1 𝐶1 = 1• 𝑛 1 𝐶𝑛= 1 + 𝐶𝑛1 = 1 + 1 +𝐶𝑛2 = = 𝑛⚫Nombre d’opérations arithmétiques OP• 𝑛= 1 𝑂𝑃1 = 0• 𝑛 1 𝑂𝑃𝑛= 2 + 𝑂𝑃𝑛1 = 2 + 2 +𝐶𝑛2 = = 2 𝑛1Exemple: Algorithme récursif
Page 44 : Ordres de complexité• Danslapratique,iln’estsouventpasnécessaire de comptabiliser chaque opérationélémentaire d’un algorithme pour avoir uneidée de sa complexité.• Il suffira de trouver un ordre de complexité quiclassifie la performance de l’algorithme enfonction de la taille des données d’entrée.
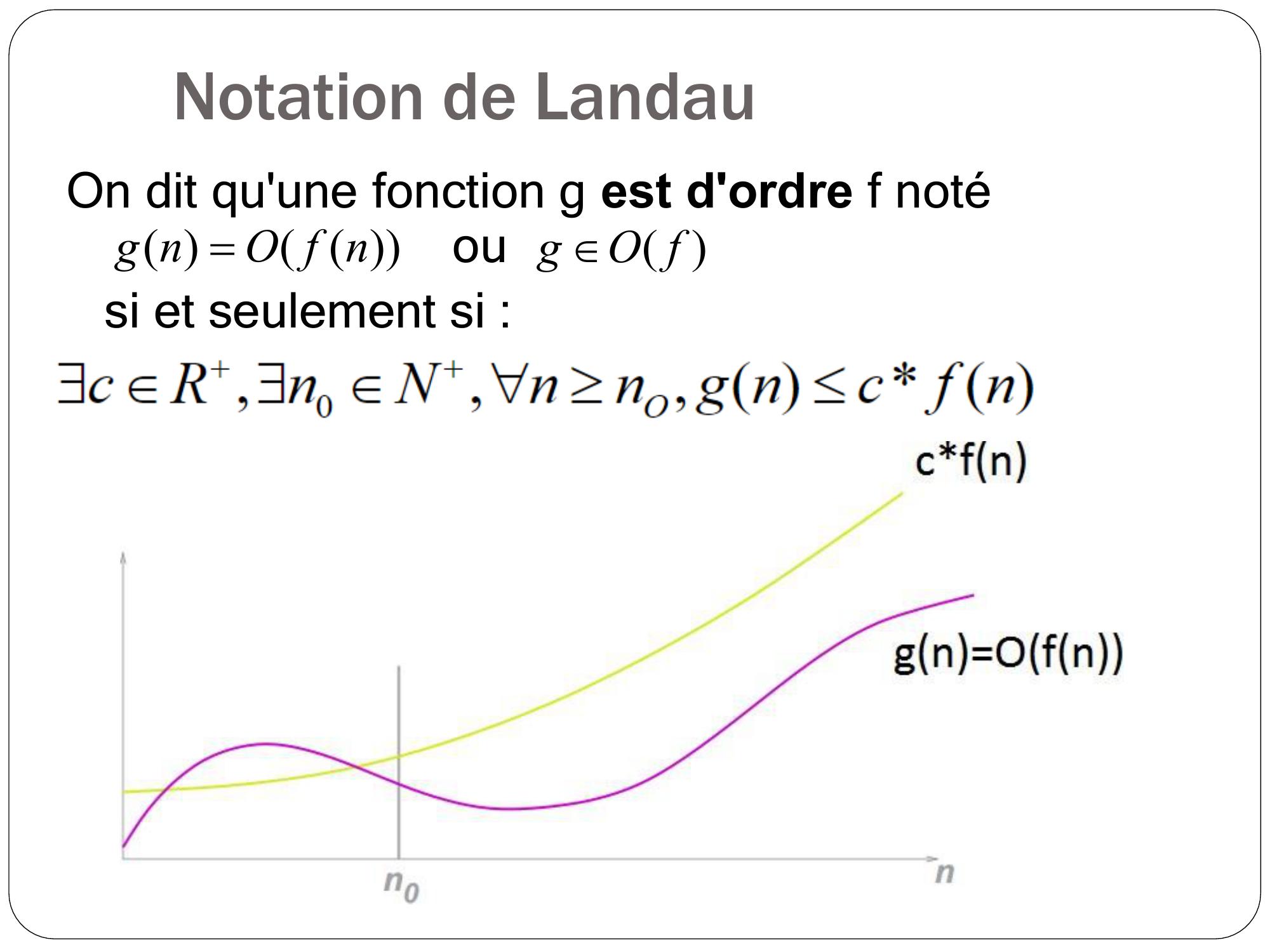
Page 45 : Notation de LandauOn dit qu'une fonction g est d'ordre f notégn O f nou g O f si et seulement si :
Page 46 : Exemplesf n n3gn n2 12n hn 5n3Prouvez quef Oh,hO f g O f , g On2f Og
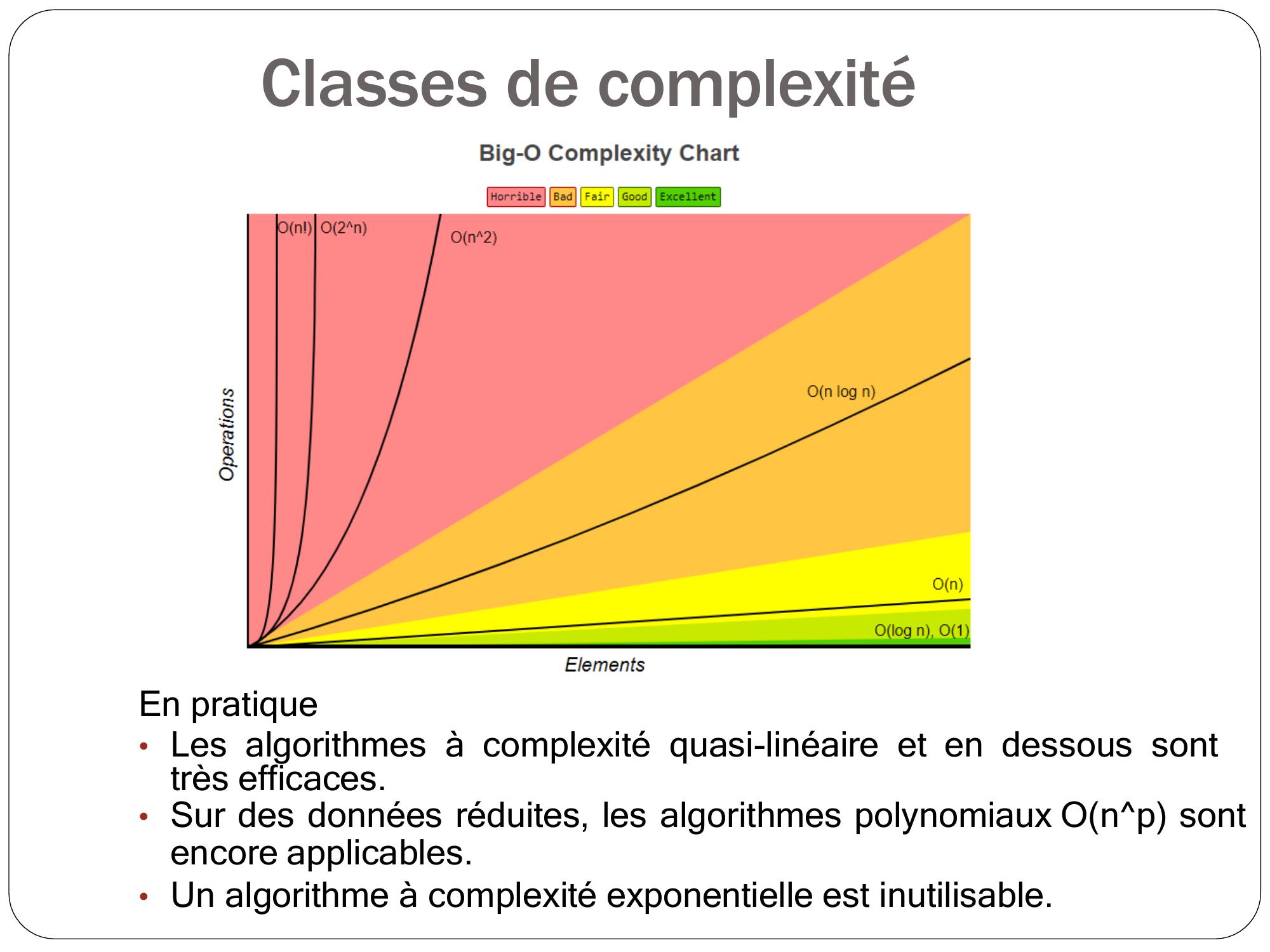
Page 47 : Classes de complexité• O1 : temps constant• Olog n : logarithmique• On : linéaire• On log n : quasi-linéaire• Ona : polynomial• O2n : exponentiel• …
Page 48 : Classes de complexitéEn pratique• Les algorithmes à complexité quasi-linéaire et en dessous sonttrès efficaces.• Sur des données réduites, les algorithmes polynomiaux On^p sontencore applicables.• Un algorithme à complexité exponentielle est inutilisable.
Page 49 : Classes de complexité: exemple•Tester toutes les combinaisons:10𝑁essais : complexité exponentielle O10^n•Trouver chaque molette independement10N essais : complexité linéaire On•Le casser:1 essais : complexité à temps constant O1
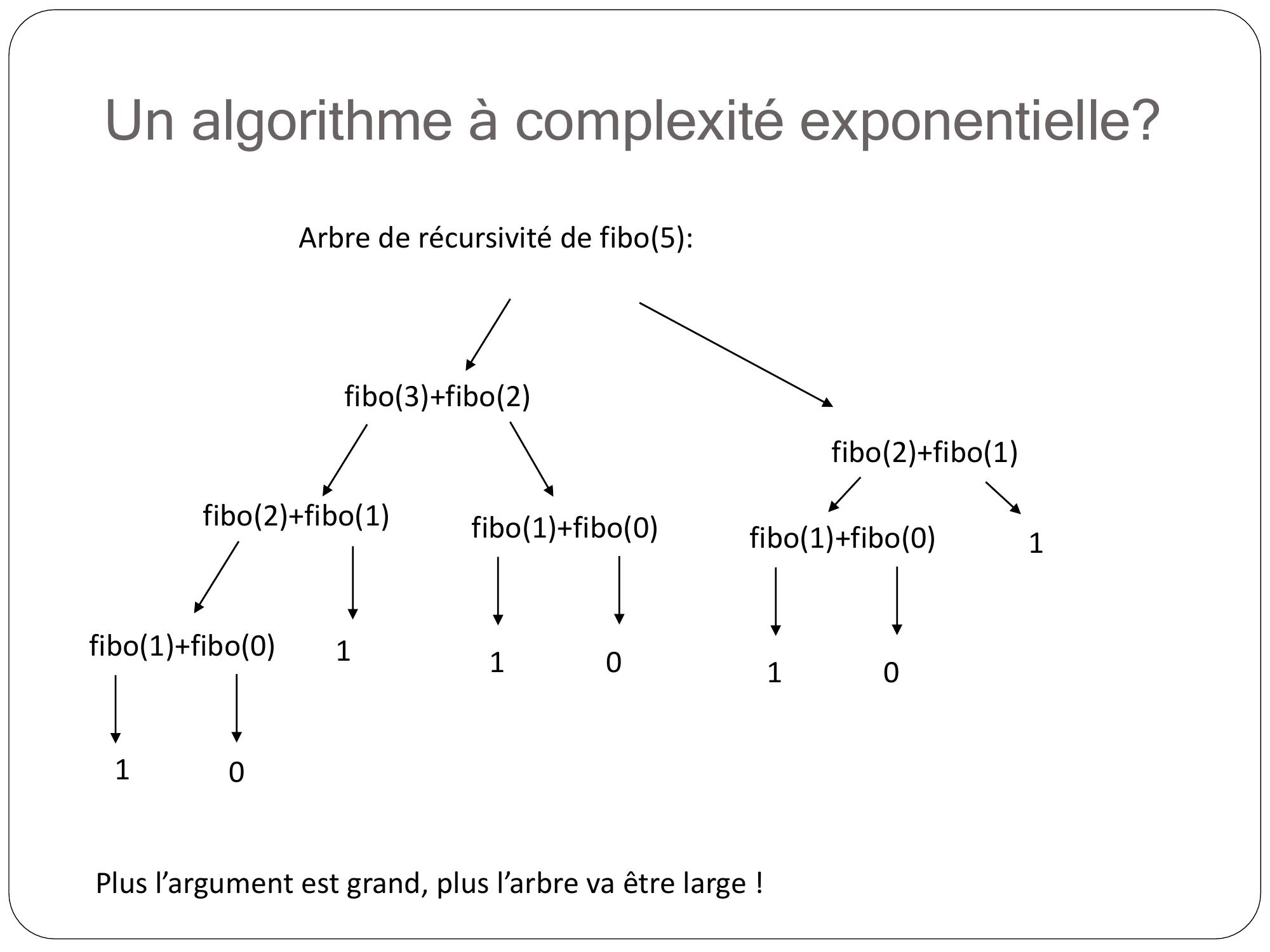
Page 50 : Un algorithme à complexité exponentielle?FONCTION fibon: ENTIER :ENTIERDEBUTSI n2 ALORS RETOURNER nSINON RETOURNER fibo n-1 + fibo n-2FIN SI FIN 𝐹𝑖𝑏𝑜𝑛= ቐ0 𝑠𝑖𝑛= 01 𝑠𝑖𝑛= 1𝐹𝑖𝑏𝑜𝑛1 + 𝐹𝑖𝑏𝑜𝑛2 𝑠𝑖𝑛𝑜𝑛
Page 51 : Un algorithme à complexité exponentielle?Arbre de récursivité de fibo5:fibo3+fibo2 fibo2+fibo1 fibo1+fibo0 110fibo2+fibo1 fibo1+fibo0 10fibo1+fibo0 10Plus l’argument est grand, plus l’arbre va être large !1
Page 52 : Choisissons l’affectation comme opération élémentaire. On note An le nombre d’affectations au rang nA0 = 0A1 = 0An = 1 + An-1 + An-2= 1 + 2An-1= 1 + 21 + 2An-2 = 2n-1On peut montrerUn algorithme à complexité exponentielle?Estimation simplifiée
Page 53 : Complexité : conclusion•La notion de complexité permet de classer des algorithmes enfonction de leur perfomance.•La complexité temporelle indique le nombre d’operations à effectueren fonction de la donnée d’entrée•On s’interesse à l’ordre des complexités exponentielle, linéaire ect.•Objectifs :•Banir la complexité exponentielle ! •Choisir l’algorithme avec la meilleure complexité.
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53