CM08 tris rapides
Télécharger le CM08 tris rapides en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
Page 1 : Informatique IITris rapides
Page 2 : Rappel ⚫Les tris vus au cours précédents étaient d’ordre de complexité 𝑂𝑛2 .https://fr.wikipedia.org/wiki/Algorithmedetri
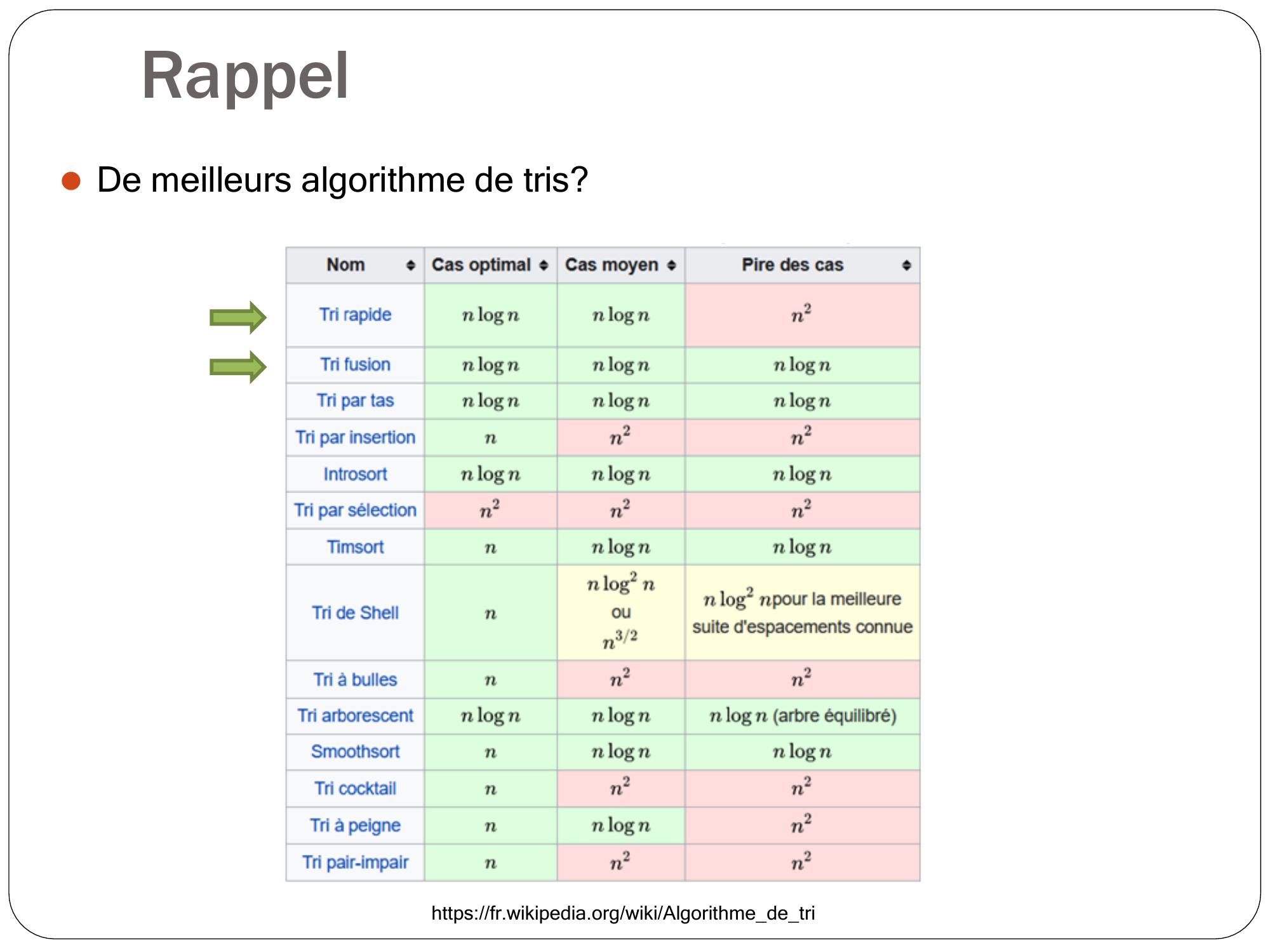
Page 3 : Rappel ⚫De meilleurs algorithme de tris? https://fr.wikipedia.org/wiki/Algorithmedetri
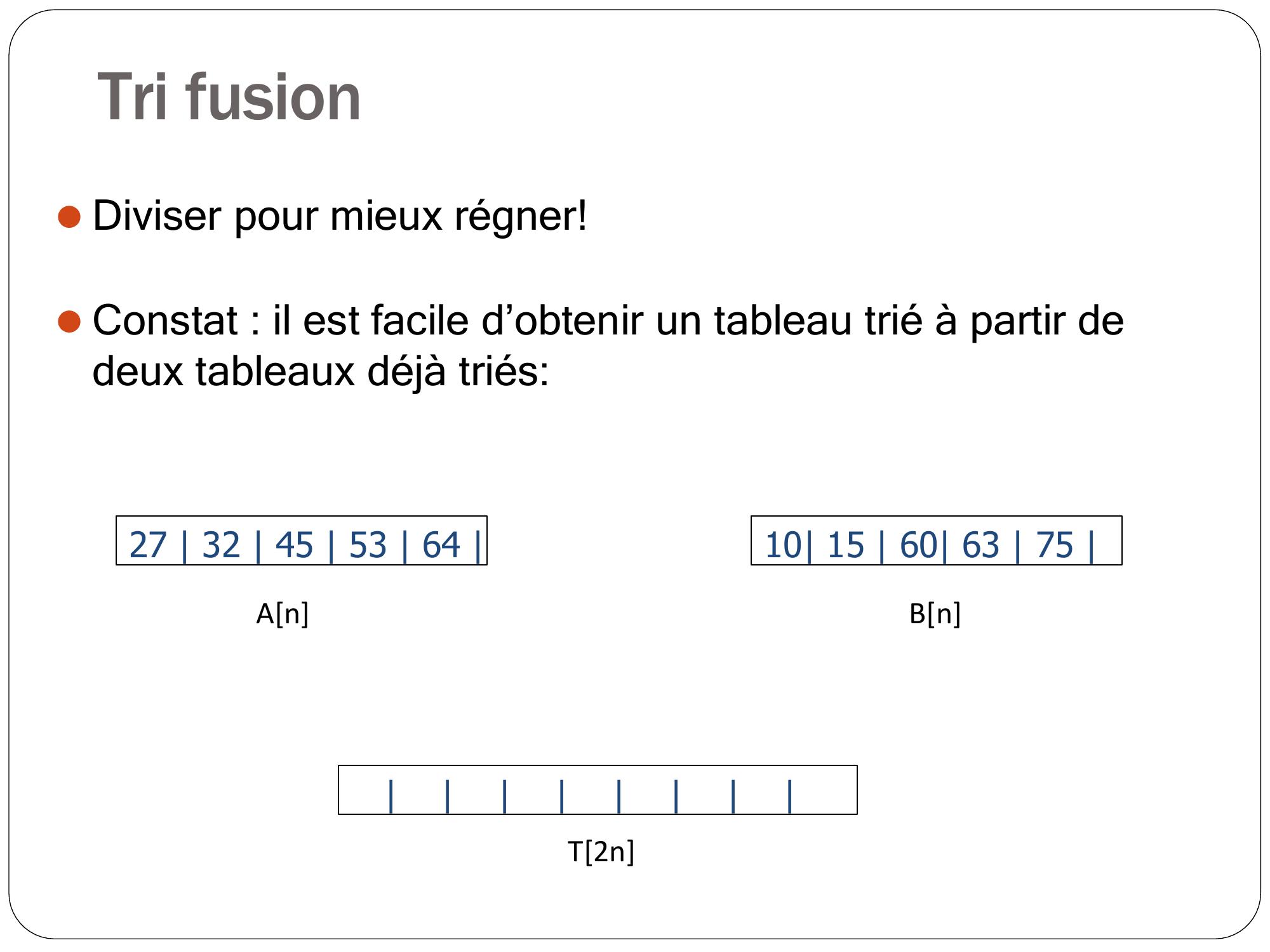
Page 4 : Tri fusion 27 32 45 53 64 ⚫Diviser pour mieux régner!⚫Constat : il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 AnBnT2n
Page 5 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 Le plus petit élément est forcement iciCase à remplir
Page 6 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 Le plus petit élément est forcement iciCase à remplir
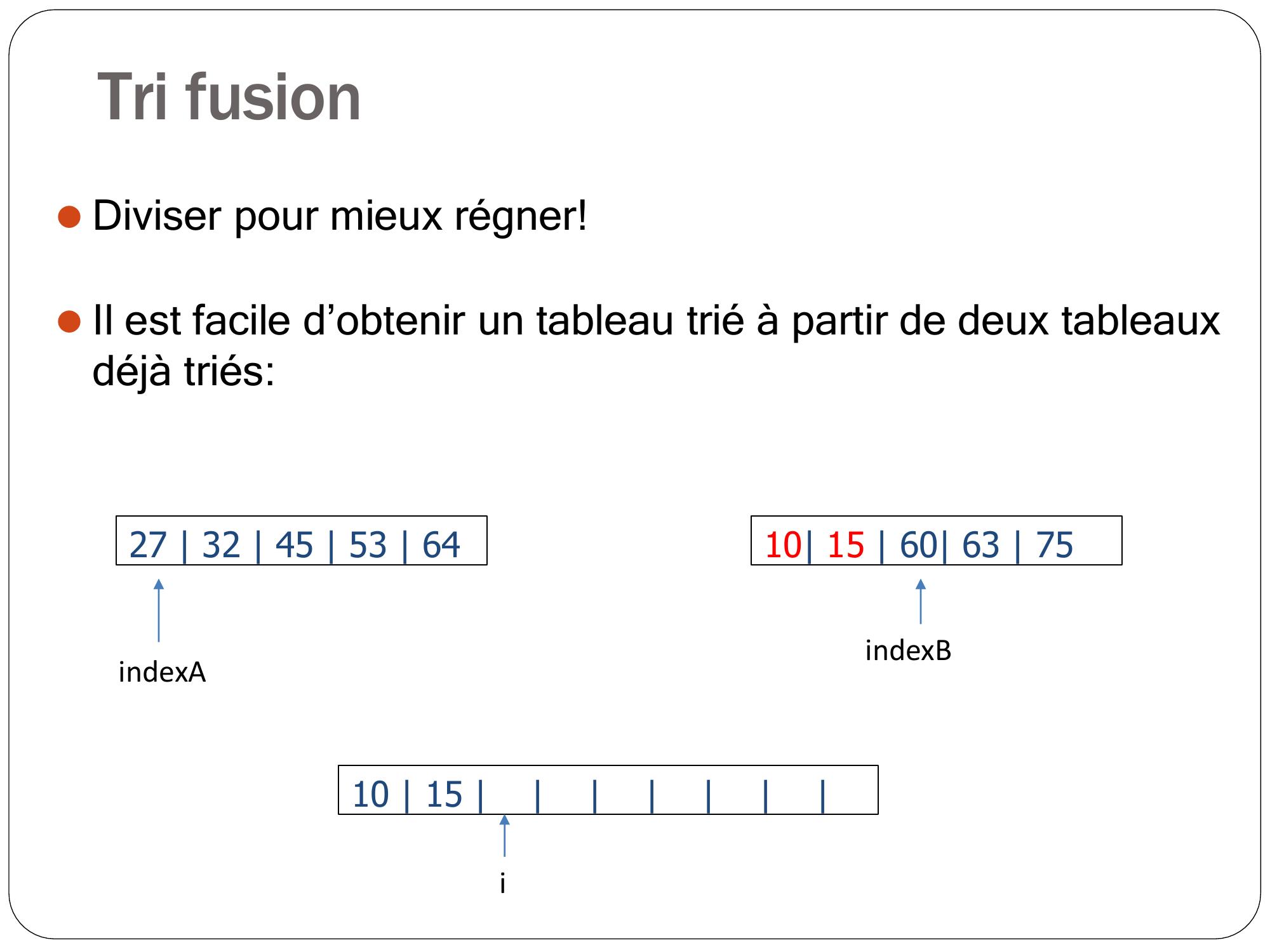
Page 7 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 iindexAindexB
Page 8 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 iindexAindexB
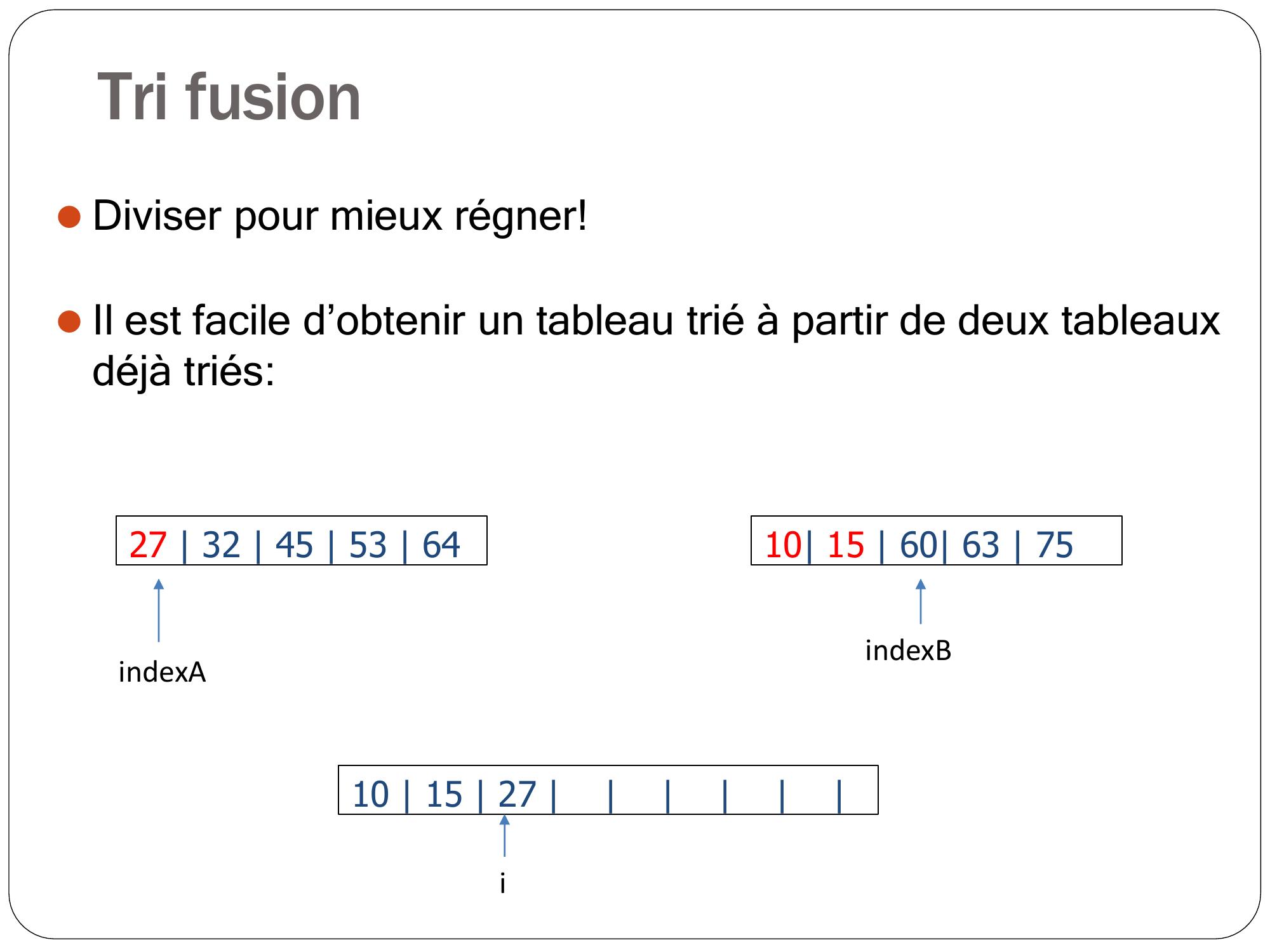
Page 9 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 iindexAindexB
Page 10 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 iindexAindexB
Page 11 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 45 iindexAindexB
Page 12 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 45 53 iindexAindexB
Page 13 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 45 53 iindexAindexB
Page 14 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 45 53 60 iindexAindexB
Page 15 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 75 10 15 27 32 45 53 60 63 64 iindexAindexB
Page 16 : Tri fusion 27 32 45 53 64⚫Diviser pour mieux régner!⚫Il est facile d’obtenir un tableau trié à partir de deux tableaux déjà triés:10 15 60 63 7510 15 27 32 45 53 60 63 64 75 iindexAindexB
Page 17 : Tri fusion ⚫Algorithme de fusion de deux tableaux triés: PROCEDURE fusion2tabAn, Bn, C2n :Tableau de TVariableindexA, indexB, i : ENTIERDEBUTindexA ← 0indexB ← 0POUR i de 0 à 2n FAIRESIAindexABindexB ALORSCi ← AindexAindexA ← indexA +1SINONCi ← BindexBindexB ← indexB+1FIN SIFIN POURFIN
Page 18 : Tri fusion ⚫Algorithme de fusion de deux tableaux triés: Parcours et remplissage du tableau finalPROCEDURE fusion2tabAn, Bn, C2n :Tableau de TVariableindexA, indexB, i : ENTIERDEBUTindexA ← 0indexB ← 0POUR i de 0 à 2n FAIRESIAindexABindexB ALORSCi ← AindexAindexA ← indexA +1SINONCi ← BindexBindexB ← indexB+1FIN SIFIN POURFIN
Page 19 : Tri fusion ⚫Algorithme de fusion de deux tableaux triés: Parcours des tableauxPROCEDURE fusion2tabAn, Bn, C2n :Tableau de TVariableindexA, indexB, i : ENTIERDEBUTindexA ← 0indexB ← 0POUR i de 0 à 2n FAIRESIAindexABindexB ALORSCi ← AindexAindexA ← indexA +1SINONCi ← BindexBindexB ← indexB+1FIN SIFIN POURFIN
Page 20 : Tri fusion ⚫Algorithme de fusion de deux tableaux triés: Exercice : rajouter les conditions sur les indices !PROCEDURE fusion2tabAn, Bn, C2n :Tableau de TVariableindexA, indexB, i : ENTIERDEBUTindexA ← 0indexB ← 0POUR i de 0 à 2n FAIRESIAindexABindexB ALORSCi ← AindexAindexA ← indexA +1SINONCi ← BindexBindexB ← indexB+1FIN SIFIN POURFIN
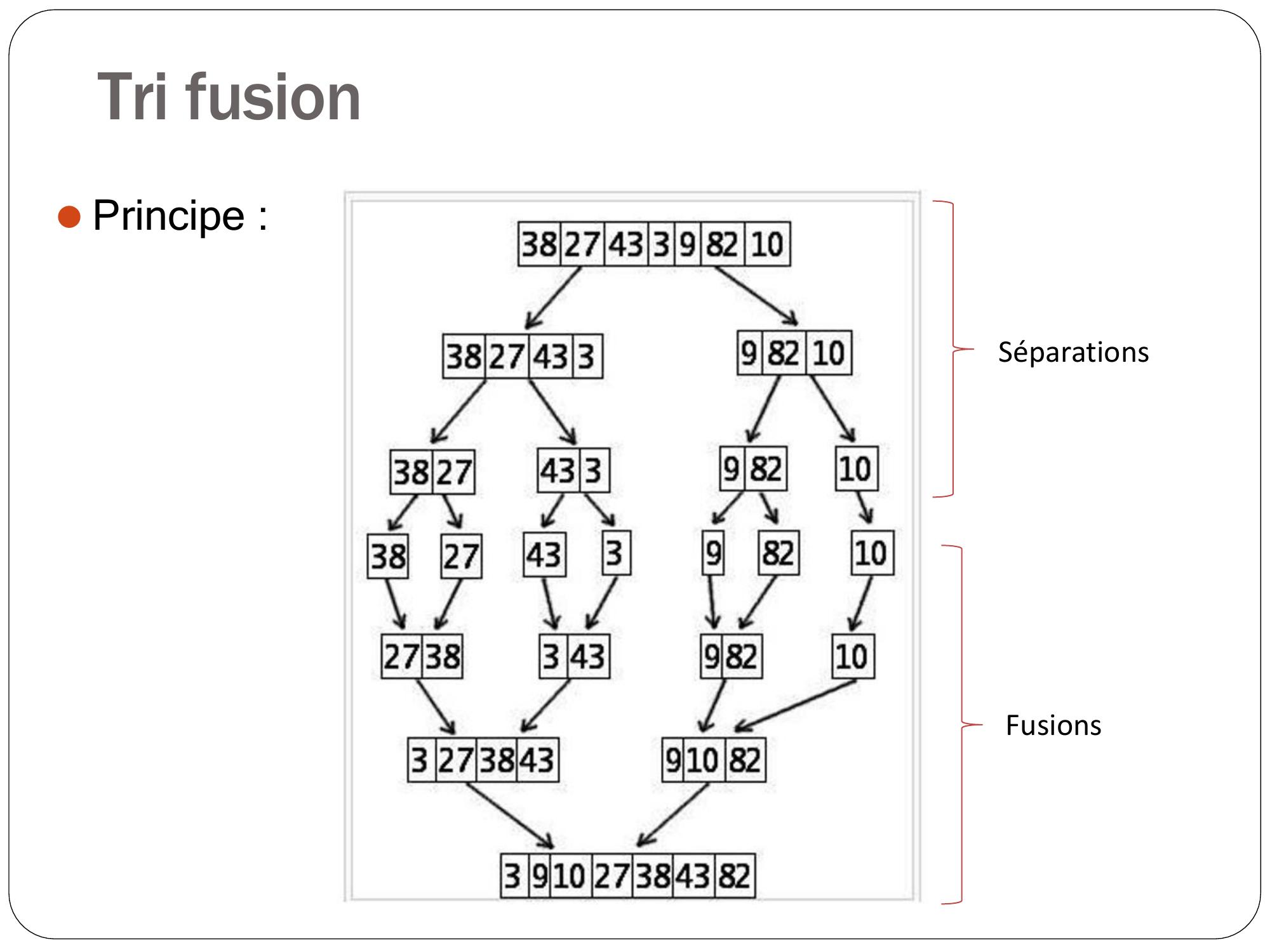
Page 21 : Tri fusion ⚫Principe :⚫Séparer les tableaux en deux⚫Recommencer sur chaque partie jusqu’à avoir des tableau de 1 cases.⚫Fusionner les tableaux
Page 22 : Tri fusion ⚫Principe :SéparationsFusions
Page 23 : Tri fusion ⚫Principe :⚫Séparer les tableaux en deux⚫Recommencer sur chaque partie jusqu’à avoir des tableau de 1 cases.⚫Fusionner les tableaux⚫La separation et la fusion se font par recursivité⚫En pratique, pas besoin de plusieurs tableaux différents : on travaille sur les sous-tableaux.
Page 24 : Tri fusion PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFIN
Page 25 : Tri fusion Initialise les paramètres de triFusionRecPROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFIN
Page 26 : Tri fusion PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFINIndice du milieu du tableau
Page 27 : PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFINTri fusion Recursivité sur les deux moitié du tableaux
Page 28 : PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFINTri fusion Division du tableau par la gauche
Page 29 : PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFINTri fusion Division du tableau par la droite
Page 30 : PROCEDURE triFusionAn : Tableau de TDébuttriFusionRecA, 0, n-1FinPROCEDURE triFusionRecAn :Tableau de T; debut, fin : EntierVARIABLEmilieu : ENTIERDEBUTSI debut fin ALORSmilieu ← deb+fin DIV 2triFusionRecA, debut, milieutriFusionRecA, milieu+1, finfusionnerA, debut, milieu, finFIN SIFINTri fusion Fusion des sous tableau
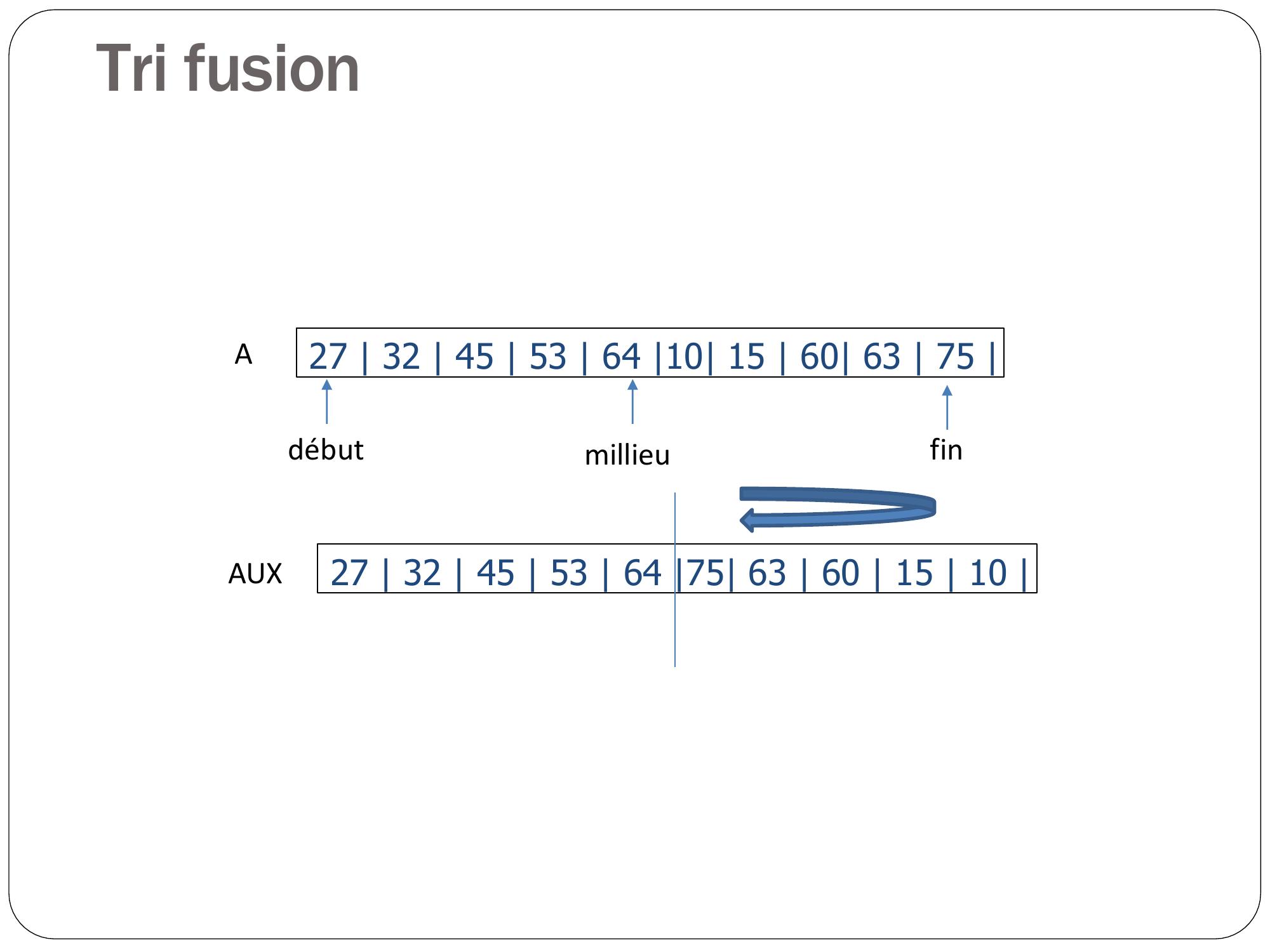
Page 31 : Tri fusion 27 32 45 53 64 10 15 60 63 75 Adébutfinmillieu
Page 32 : Tri fusion 27 32 45 53 64 10 15 60 63 75 Adébutfinmillieu27 32 45 53 64 75 63 60 15 10 AUX
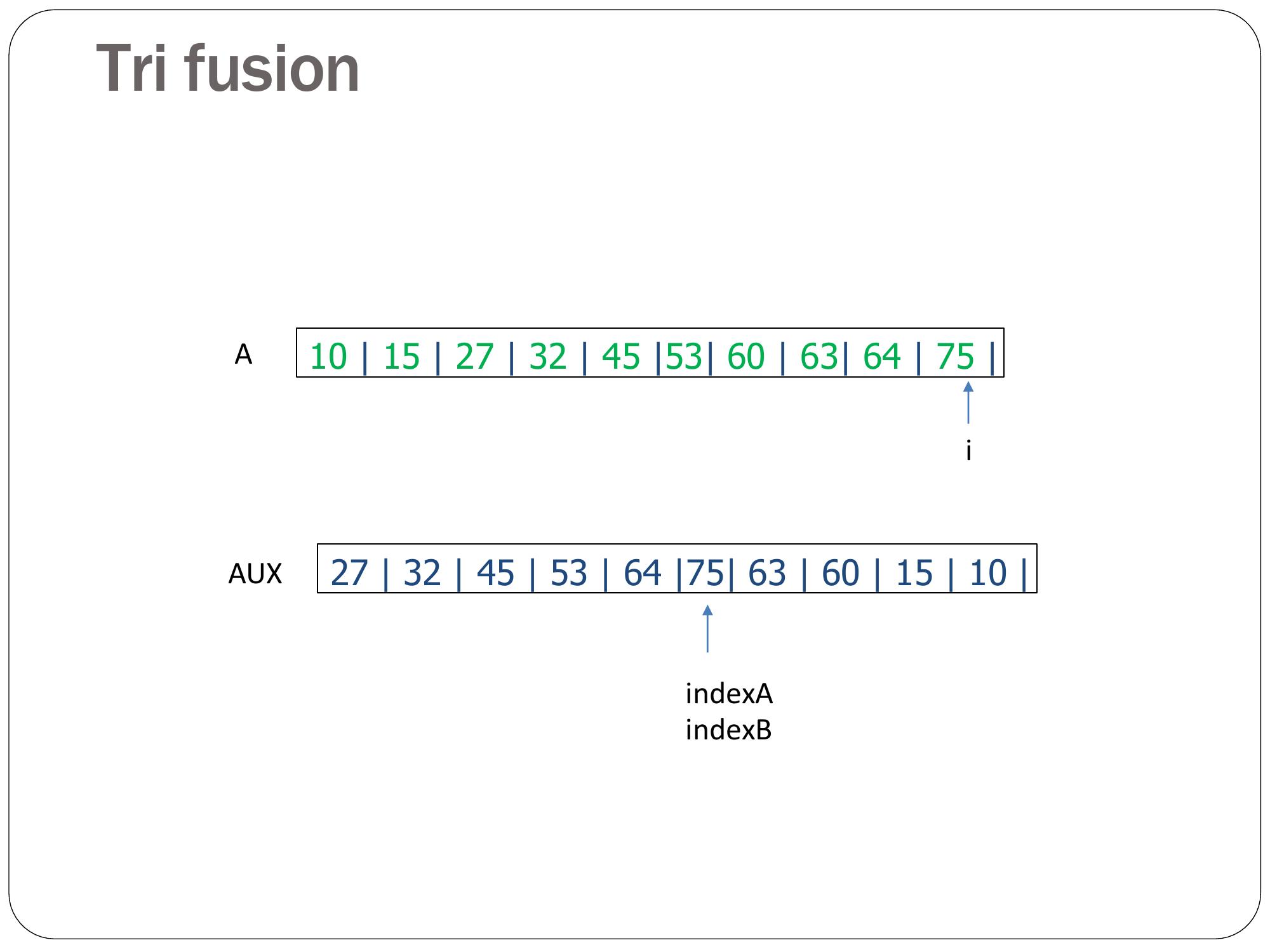
Page 33 : Tri fusion 27 32 45 53 64 10 15 60 63 75 Ai27 32 45 53 64 75 63 60 15 10 AUXindexAindexB
Page 34 : Tri fusion 10 32 45 53 64 10 15 60 63 75 Ai27 32 45 53 64 75 63 60 15 10 AUXindexAindexB
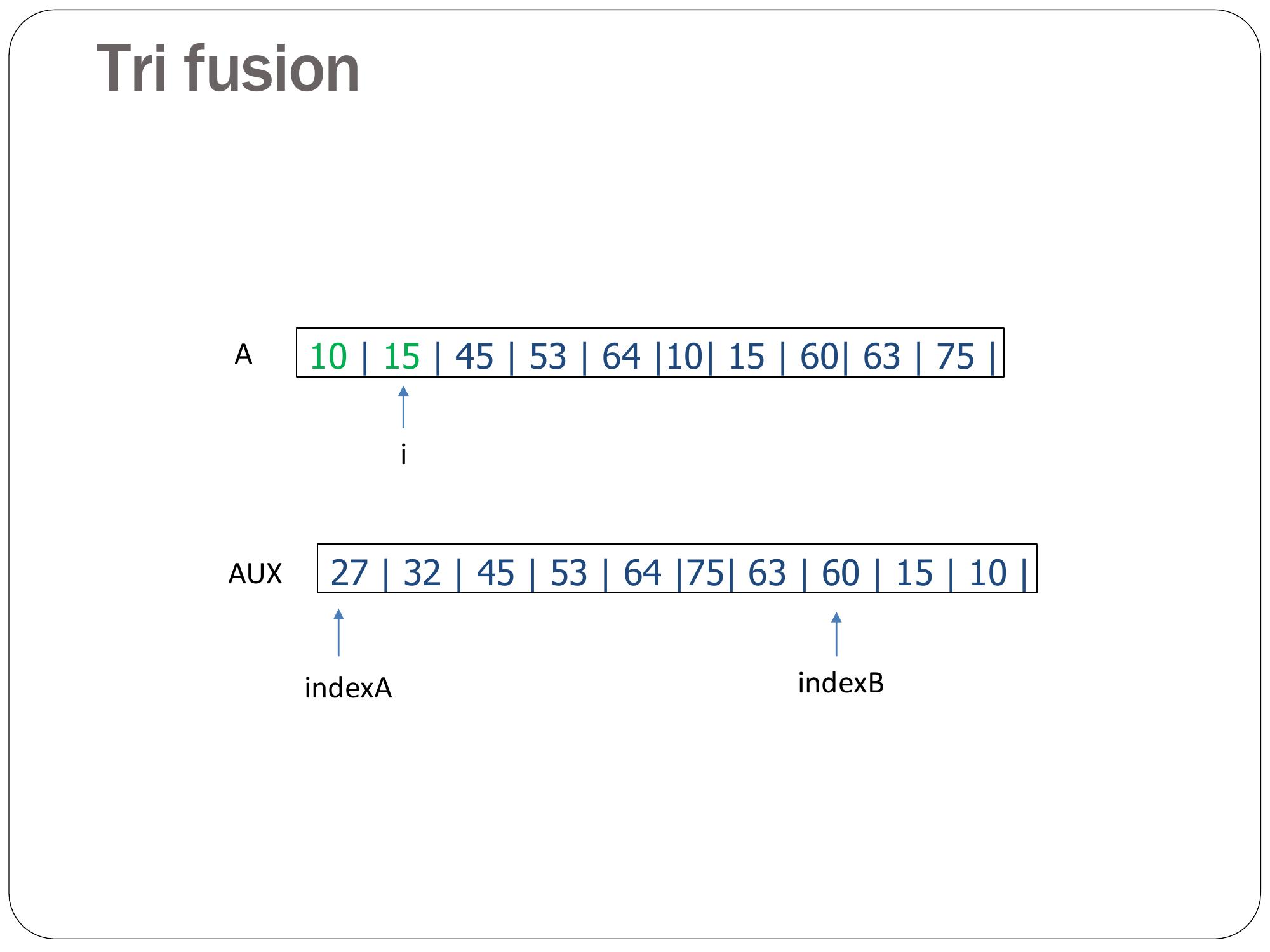
Page 35 : Tri fusion 10 15 45 53 64 10 15 60 63 75 Ai27 32 45 53 64 75 63 60 15 10 AUXindexAindexB
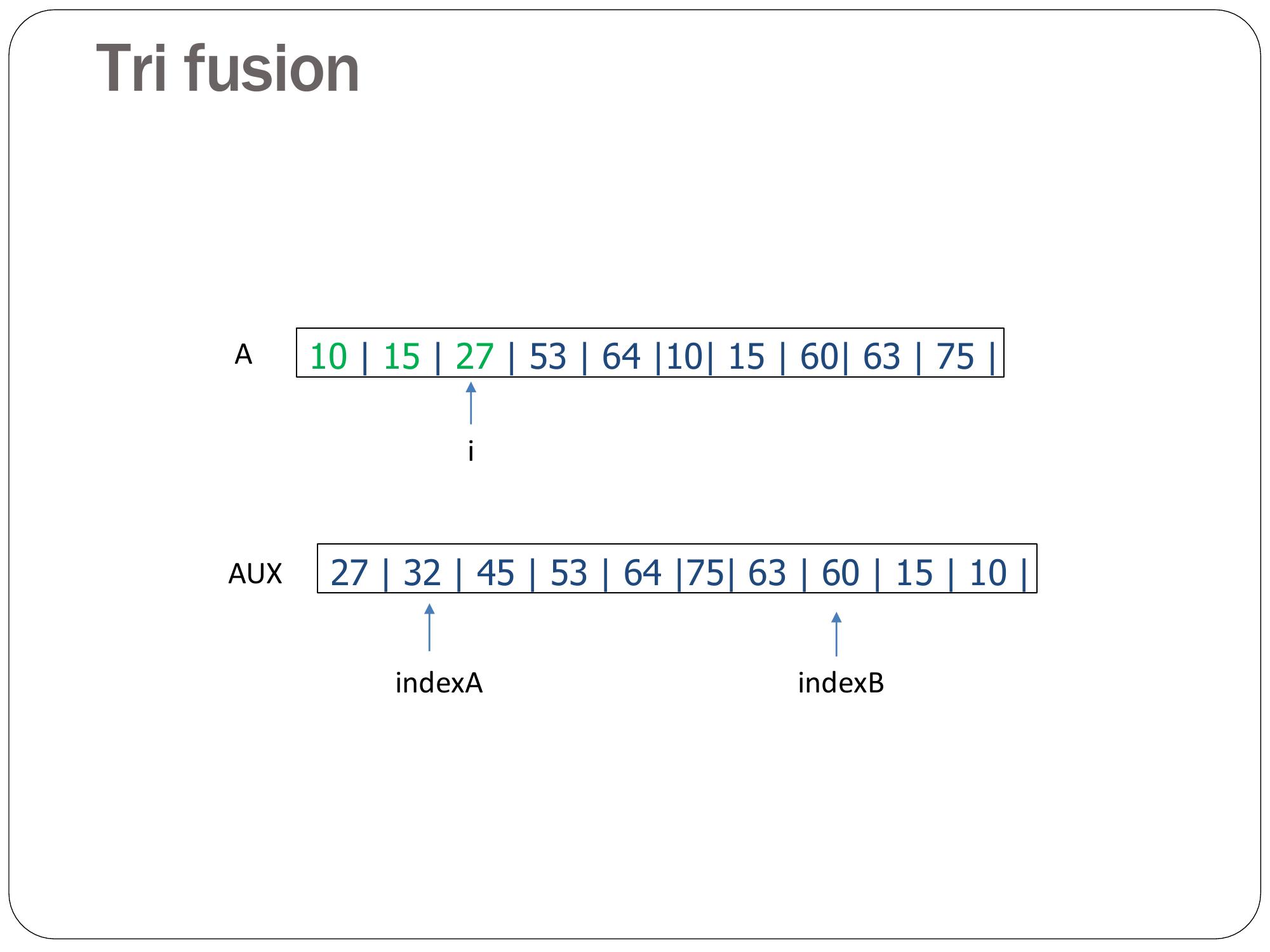
Page 36 : Tri fusion 10 15 27 53 64 10 15 60 63 75 Ai27 32 45 53 64 75 63 60 15 10 AUXindexAindexB
Page 37 : Tri fusion 10 15 27 32 45 53 60 63 64 75 Ai27 32 45 53 64 75 63 60 15 10 AUXindexBindexA
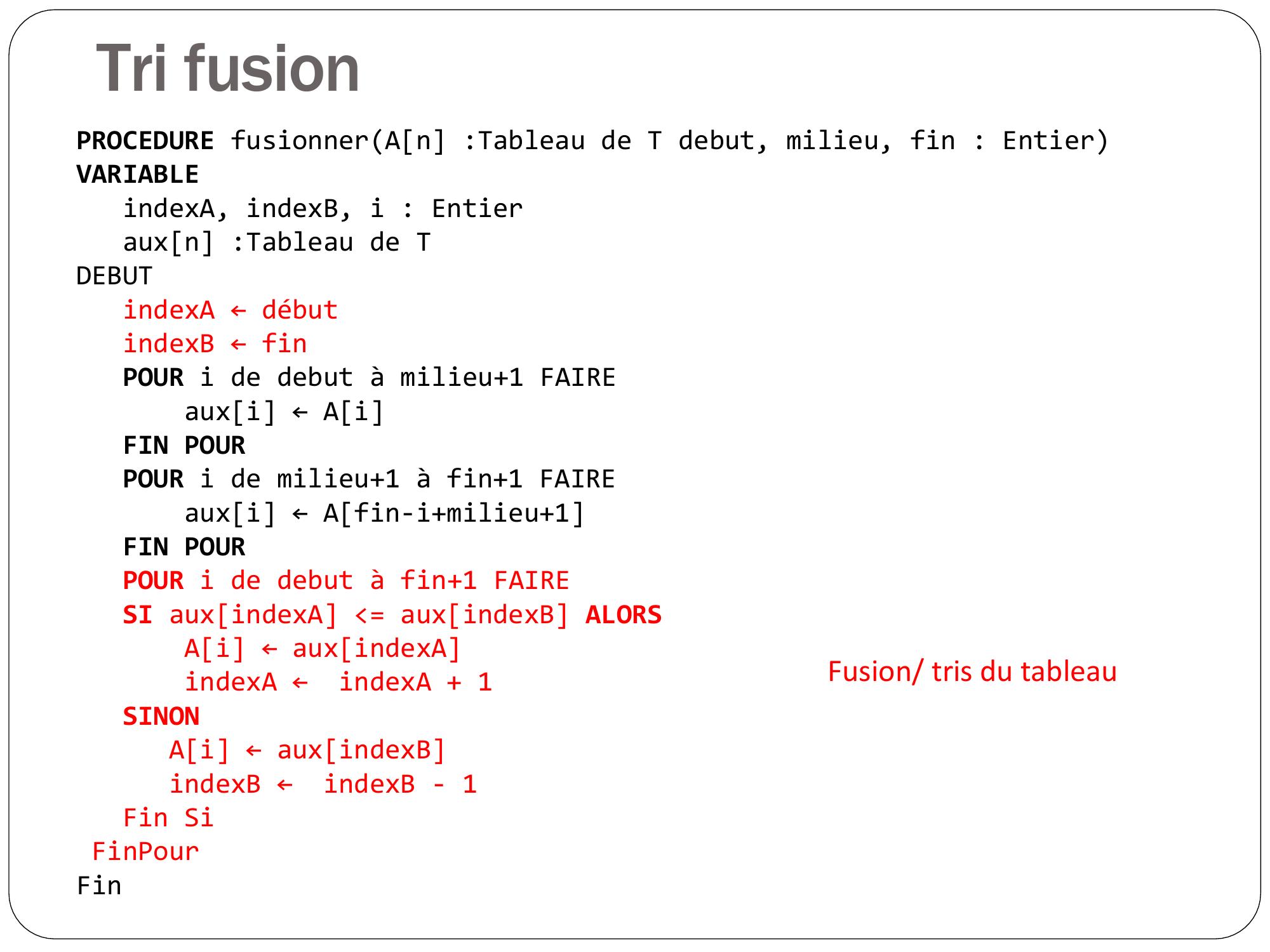
Page 38 : Tri fusion PROCEDURE fusionnerAn :Tableau de T debut, milieu, fin : EntierVARIABLEindexA, indexB, i : Entier auxn :Tableau de TDEBUTindexA ← débutindexB ← finPOUR i de debut à milieu+1 FAIRE auxi ← Ai FIN POURPOUR i de milieu+1 à fin+1 FAIRE auxi ← Afin-i+milieu+1 FIN POURPOUR i de debut à fin+1 FAIRESI auxindexA = auxindexB ALORSAi ← auxindexAindexA ←indexA + 1SINONAi ← auxindexBindexB ←indexB - 1Fin SiFinPourFin
Page 39 : Tri fusion Recopie du tableau. La seconde partie estrecopiée “ à lenvers”PROCEDURE fusionnerAn :Tableau de T debut, milieu, fin : EntierVARIABLEindexA, indexB, i : Entier auxn :Tableau de TDEBUTindexA ← débutindexB ← finPOUR i de debut à milieu+1 FAIRE auxi ← Ai FIN POURPOUR i de milieu+1 à fin+1 FAIRE auxi ← Afin-i+milieu+1 FIN POURPOUR i de debut à fin+1 FAIRESI auxindexA = auxindexB ALORSAi ← auxindexAindexA ←indexA + 1SINONAi ← auxindexBindexB ←indexB - 1Fin SiFinPourFin
Page 40 : Tri fusion PROCEDURE fusionnerAn :Tableau de T debut, milieu, fin : EntierVARIABLEindexA, indexB, i : Entier auxn :Tableau de TDEBUTindexA ← débutindexB ← finPOUR i de debut à milieu+1 FAIRE auxi ← Ai FIN POURPOUR i de milieu+1 à fin+1 FAIRE auxi ← Afin-i+milieu+1 FIN POURPOUR i de debut à fin+1 FAIRESI auxindexA = auxindexB ALORSAi ← auxindexAindexA ←indexA + 1SINONAi ← auxindexBindexB ←indexB - 1Fin SiFinPourFinFusion/ tris du tableau
Page 41 : Tri fusion : complexité ⚫Le nombre d’operation ne dépend pas de l’état du tableau pas de meilleur ou de pire cas.⚫Complexité de la fusion: On ⚫Comparaison de TriFusionRec:Complexité en 𝑂𝑛log𝑛𝐶0 = 1𝐶𝑛= 𝑛+ 𝐶𝑛/2
Page 42 : Tri rapide quicksort•La méthode de tri la plus utilisée voir algorithme•Principe:•Partitionner le tableau en deux parties séparées par un pivot :•Les éléments à la gauche du pivot doivent lui êtreinférieurs•Les éléments à sa droite doivent lui être supérieurs.•Appliquer récursivement l’algorithme sur les deux sous parties.
Page 43 : •Principe:•Partitionner le tableau en deux parties séparées par un pivot :•Les éléments à la gauche du pivot doivent lui êtreinférieurs•Les éléments à sa droite doivent lui être supérieurs.Tri rapide quicksortExemple :4 23 3 42 2 14 45 18 38 164 14 3 2 16 23 45 18 38 42
Page 44 : Tri rapide quicksort•Principe:•Partitionner le tableau en deux parties séparées par un pivot :•Les éléments à la gauche du pivot doivent lui êtreinférieurs•Les éléments à sa droite doivent lui être supérieurs.•Appliquer récursivement l’algorithme sur les deux sous parties.
Page 45 : Tri rapide : partitionnement ⚫1. Parcourir de gauche à droite jusqu’à trouver un élément supérieur au pivot.=On isole le pivot en début du tableau=
Page 46 : Tri rapide : partitionnement 1. Parcourir de gauche à droite jusqu’à trouver un élément supérieur au pivot.=2. Parcourir de droite à gauche jusqu’à trouver un élément inférieur au pivot==
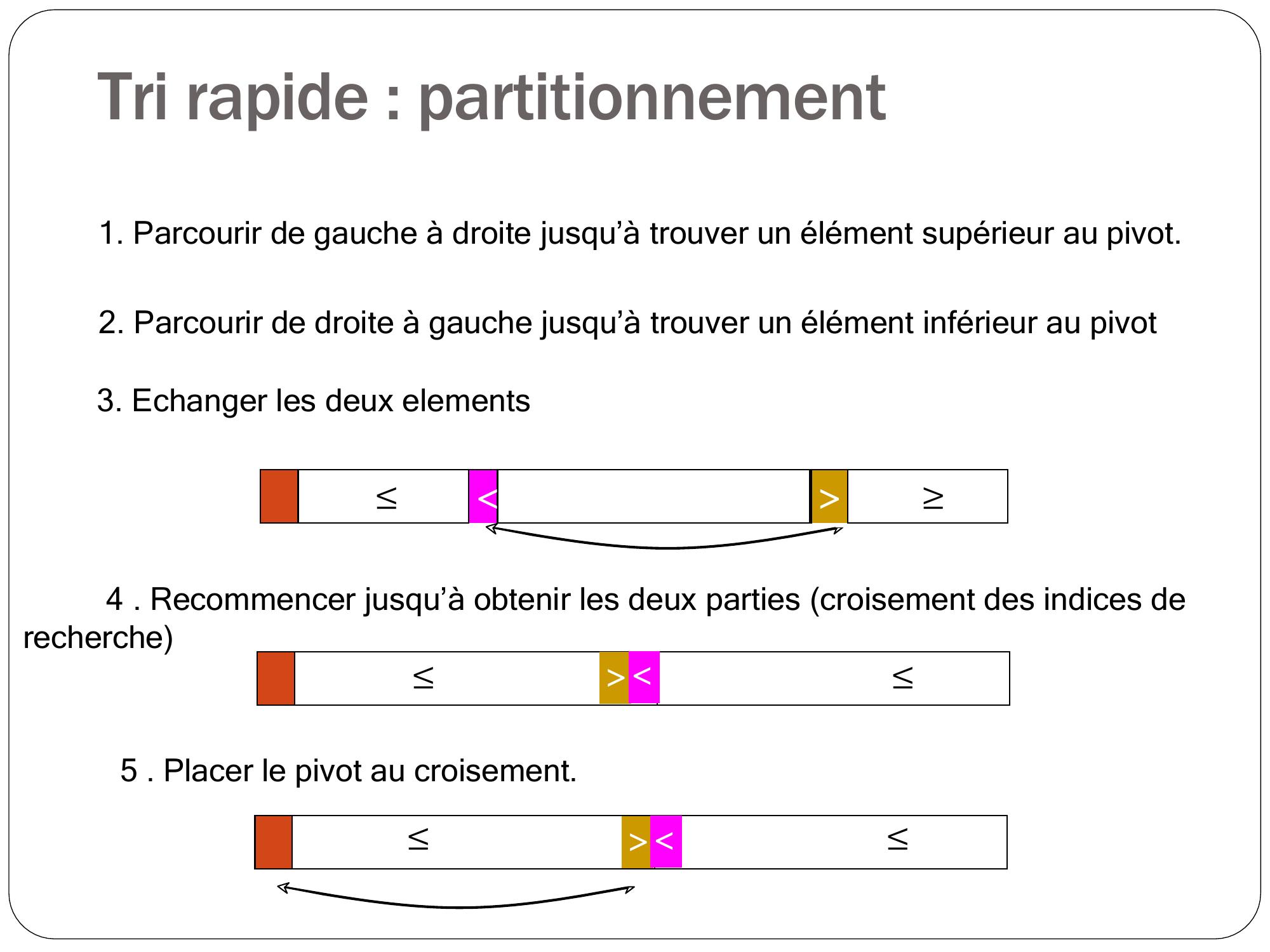
Page 47 : Tri rapide : partitionnement 1. Parcourir de gauche à droite jusqu’à trouver un élément supérieur au pivot.=2. Parcourir de droite à gauche jusqu’à trouver un élément inférieur au pivot==3. Echanger les deux elements==4 . Recommencer jusqu’à obtenir les deux parties croisement des indices de recherche
Page 48 : Tri rapide : partitionnement 1. Parcourir de gauche à droite jusqu’à trouver un élément supérieur au pivot.2. Parcourir de droite à gauche jusqu’à trouver un élément inférieur au pivot3. Echanger les deux elements==4 . Recommencer jusqu’à obtenir les deux parties croisement des indices de recherche ==5 . Placer le pivot au croisement. ==
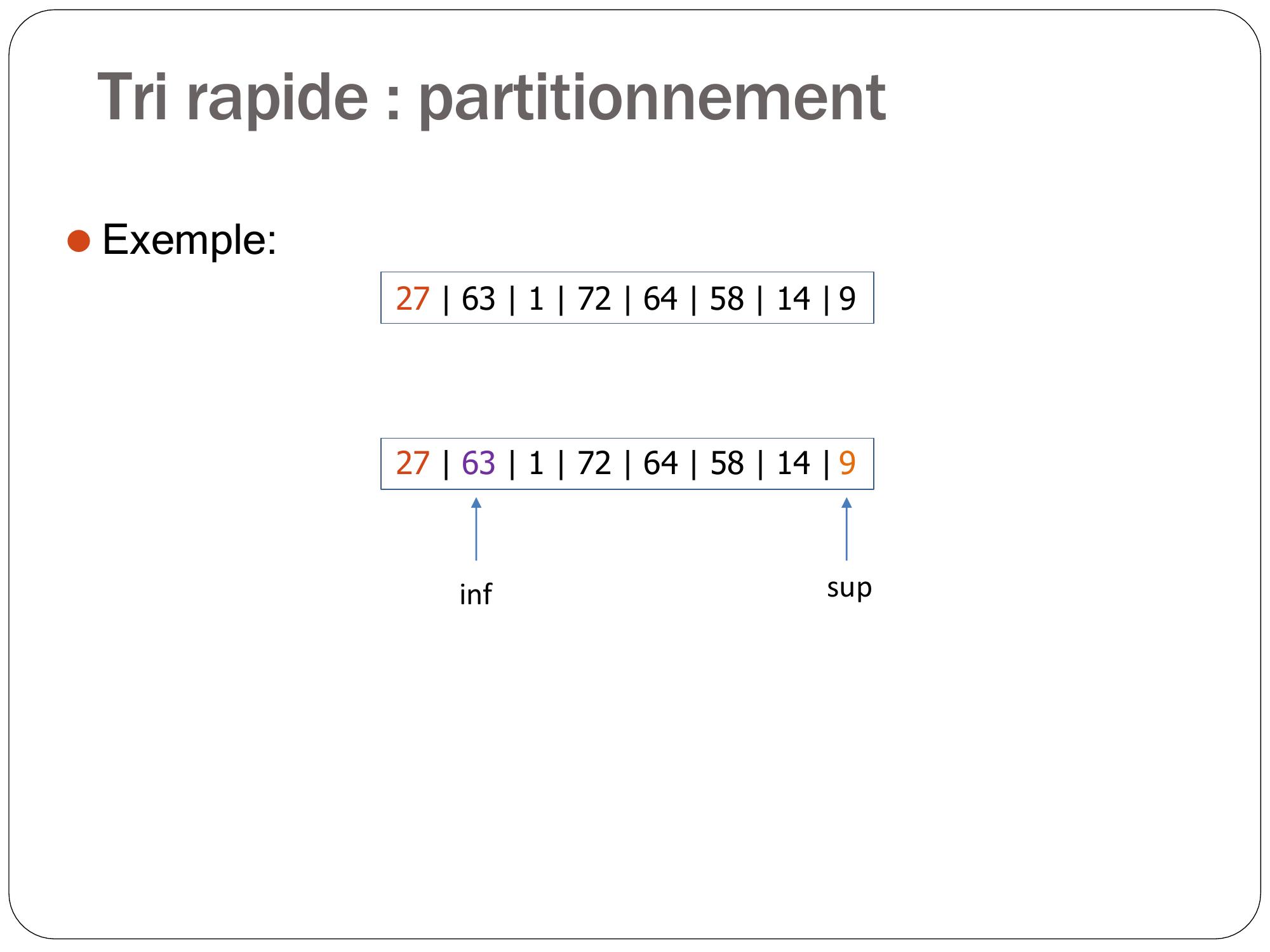
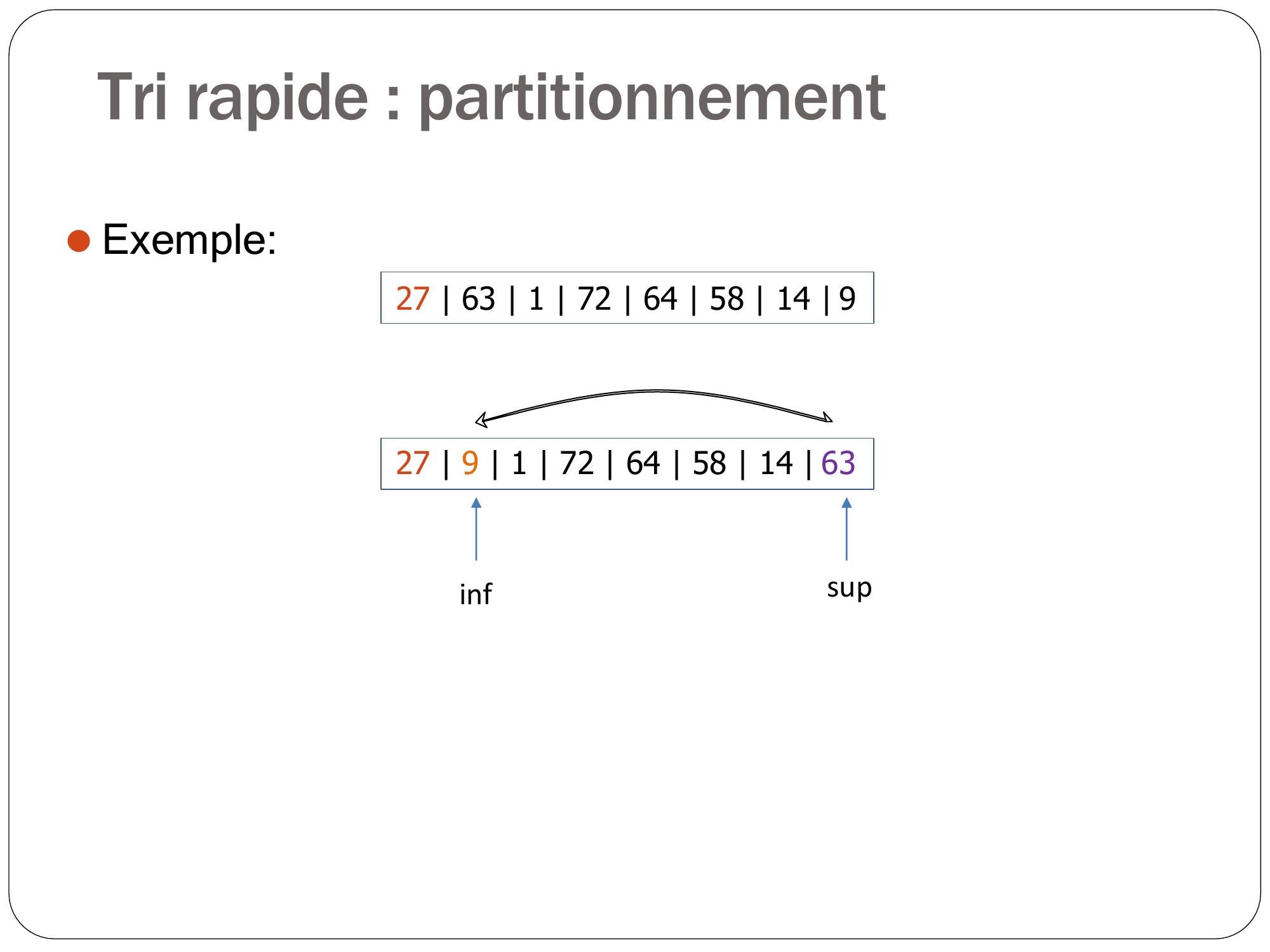
Page 49 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 9
Page 50 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 63 1 72 64 58 14 9infsup
Page 51 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 72 64 58 14 63infsup
Page 52 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 72 64 58 14 63infsup
Page 53 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 72 64 58 14 63infsup
Page 54 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 72 64 58 14 63infsup
Page 55 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 14 64 58 72 63infsup
Page 56 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 14 64 58 72 63infsup
Page 57 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 14 64 58 72 63inf sup
Page 58 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 927 9 1 14 64 58 72 63infsup
Page 59 : Tri rapide : partitionnement ⚫Exemple:27 63 1 72 64 58 14 914 9 1 27 64 58 72 63
Page 60 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebutsup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFIN
Page 61 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebut sup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFINIci le pivot est la première case du tableau
Page 62 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebut sup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFINGestion des indices inf et sup
Page 63 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebut sup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFINEchange des éléments
Page 64 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebut sup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFINPlacement du pivot
Page 65 : Tri rapideFONCTION partitionAn Tableau de T; debut, fin : Entier : ENTIERVARIABLEinf, sup, tmp : ENTIERDEBUTinf ←debut+1sup ←finTANT QUE inf=sup FAIRETANT QUEAsup Adebut sup ←sup-1FIN TANT QUETANT QUE Ainf Adebutinf ←inf+1FIN TANT QUESI infsup ALORStmp ←Asup;Asup ←Ainf;Ainf ←tmpFIN SIFIN TANT QUEtmp ←Adebut; Adebut ←Asup; Asup ←tmpRETOURNER supFINOn retourne l’emplacement du pivot
Page 66 : Tri rapidePROCEDURE triRapideTableau de TDébuttriRapideRecA, 0, n-1FinPROCEDURE triRapideRecTableau de T; debut, fin : ENTIERVARIABLEpivot : ENTIERDEBUTSI debut fin ALORSpivot ← partitionA, debut, fintriRapideRecA, debut, pivot-1triRapideRecA, pivot+1, finFIN SIFIN
Page 67 : •Meilleur cas tableau déjà trié:•Nombre de comparaisons : n•Nombre d’échanges : 0Complexité : OnTri rapide : complexité •Pire cas le pivot choisit est la plus grande valeur•Nombre de comparaisons : n-1+n-2+…+1 = nn-1/2Complexité : On²
Page 68 : •Pire cas le pivot choisit est la plus grande valeur•Nombre de comparaisons : n-1+n-2+…+1 = nn-1/2Complexité : On²Tri rapide : complexité •Cas moyen Complexité : Onlogn•Meilleur cas tableau déjà trié:•Nombre de comparaisons : n•Nombre d’échanges : 0Complexité : On
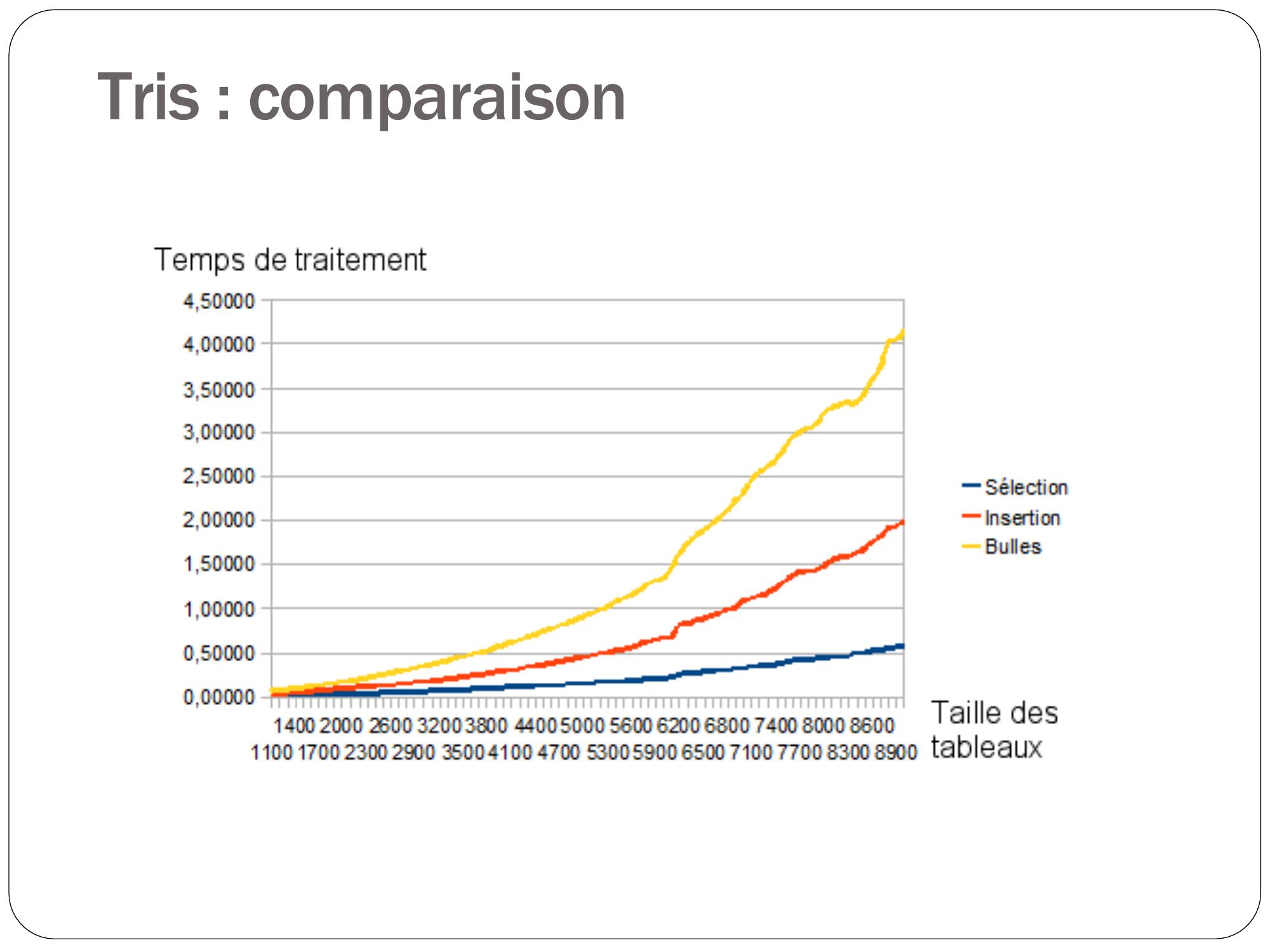
Page 69 : Tris : comparaison
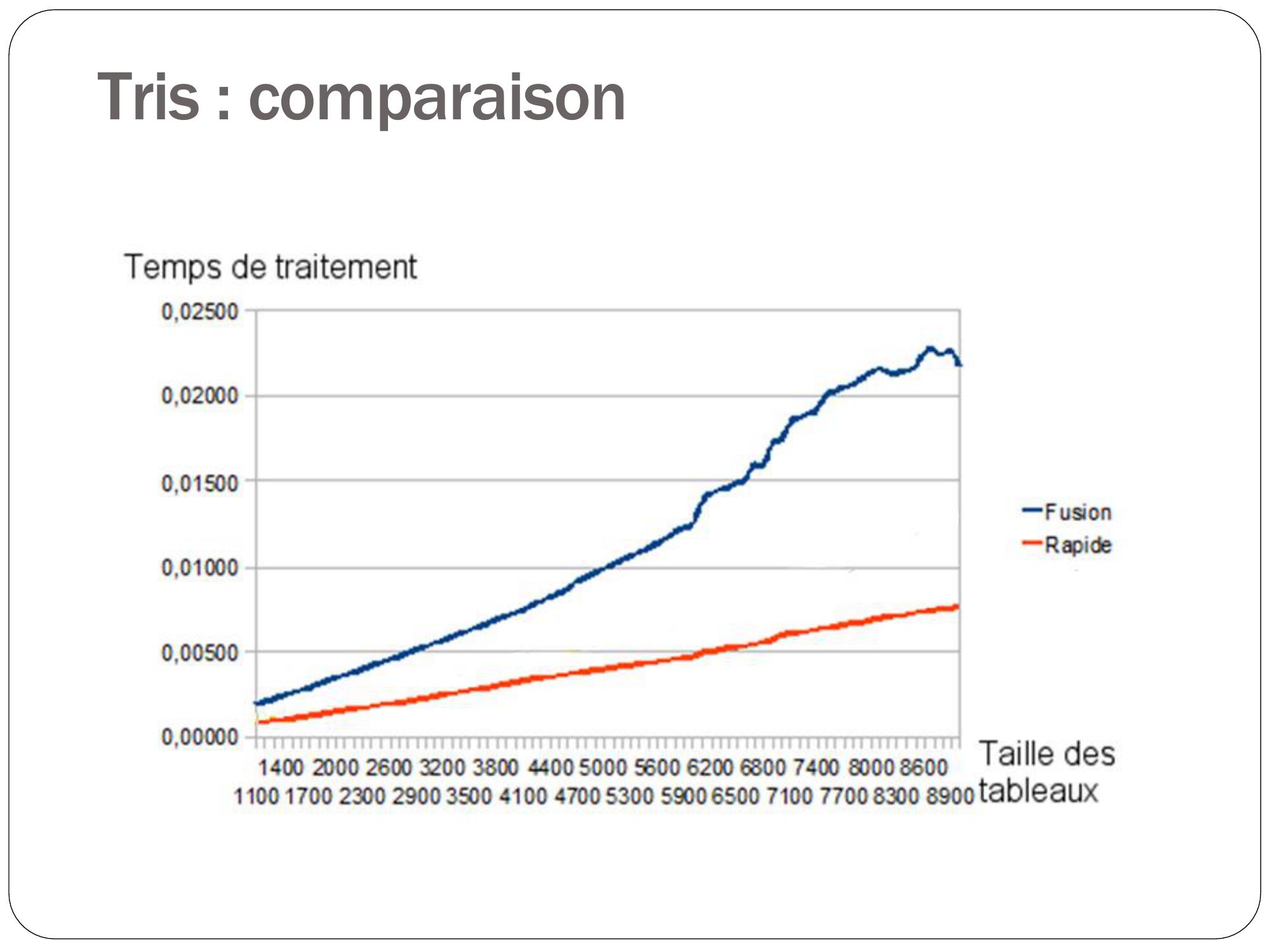
Page 70 : Tris : comparaison
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70