CM1 Analyse Univariee
Télécharger le CM1 Analyse Univariee en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Page 1 : CM 1 : Arbres de décision et forêts aléatoires30h TD/TPÉvaluation 1ère et 2nde session : Examen 2h sur machine / Etude préalable d’un ou plusieurs jeux de donnéesSupports pédagogiques : Support de présentation et énoncé de TD/TP à chaque séanceTutoriel sur l’ensemble du programmeL’objectif de ce module est d’introduire les méthodes permettant d’extraire de l’information pertinente de corpus de données. A l’issue de cette formation, vous serez capables de :•faire apparaitre des comportements particuliers des objets observés détecter les individus ayant un comportement atypique, trouver des ensemble d’individus ayant un comportement similaire,•trouver des liens entre les variables étudiées ex: est-ce que le PIB d’un pays est lié à l’investissement en R&D, est-ce qu’un médicament a un impact sur le taux de guérison?,•utiliser le langage dédié aux statistiques R pas programmer mais utiliser.Seules les méthodes descriptives seront abordées dans ce module. Il se complète avec les modules de 2ème année : IA modèles de prévision/machine learning et statistiques gestion de l’incertitudeData exploration
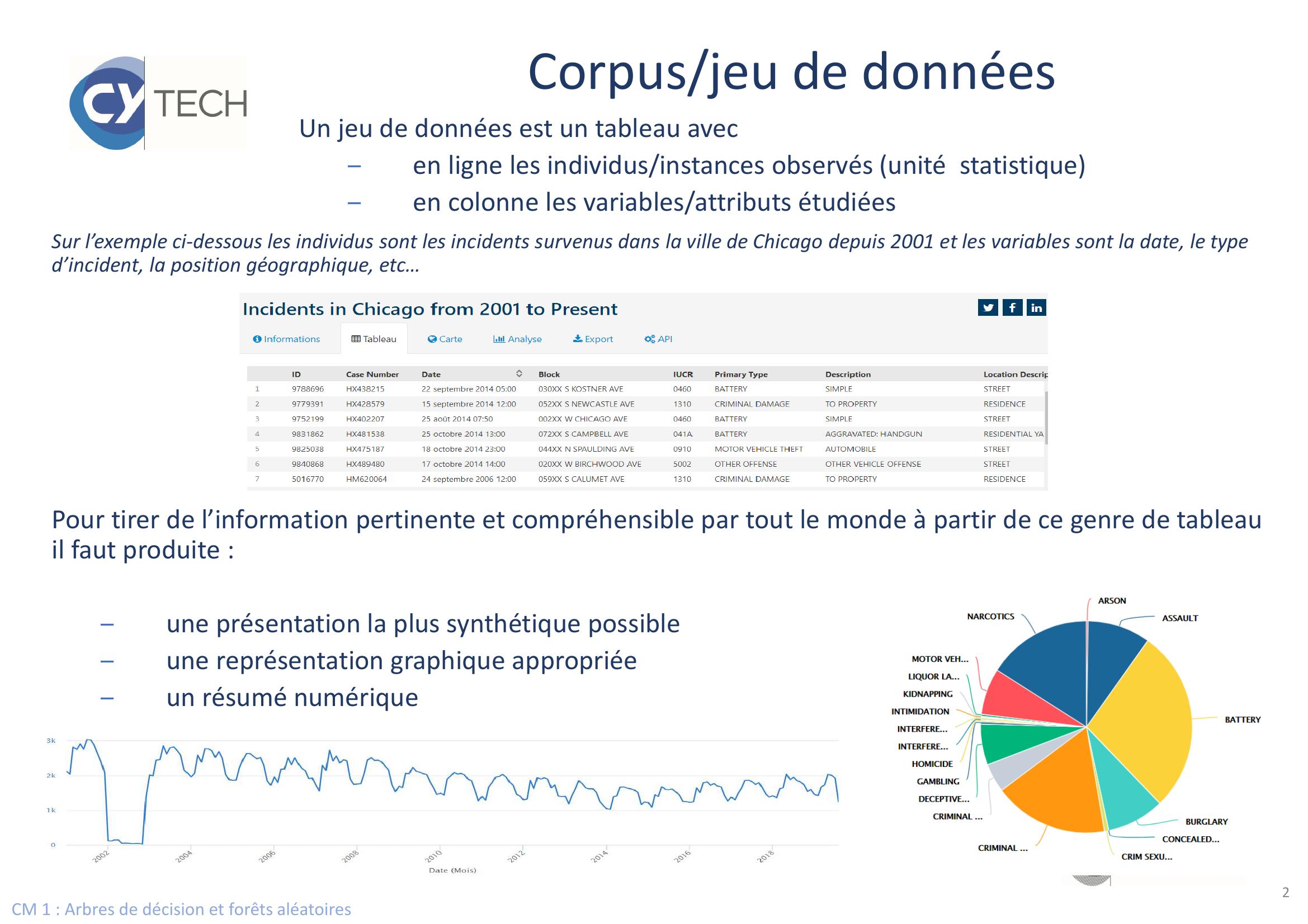
Page 2 : CM 1 : Arbres de décision et forêts aléatoiresCorpus/jeu de donnéesSur l’exemple ci-dessous les individus sont les incidents survenus dans la ville de Chicago depuis 2001 et les variables sont la date, le type d’incident, la position géographique, etc…Pour tirer de l’information pertinente et compréhensible par tout le monde à partir de ce genre de tableau il faut produite :–une présentation la plus synthétique possible–une représentation graphique appropriée–un résumé numériqueUn jeu de données est un tableau avec–en ligne les individus/instances observés unité statistique–en colonne les variables/attributs étudiées2
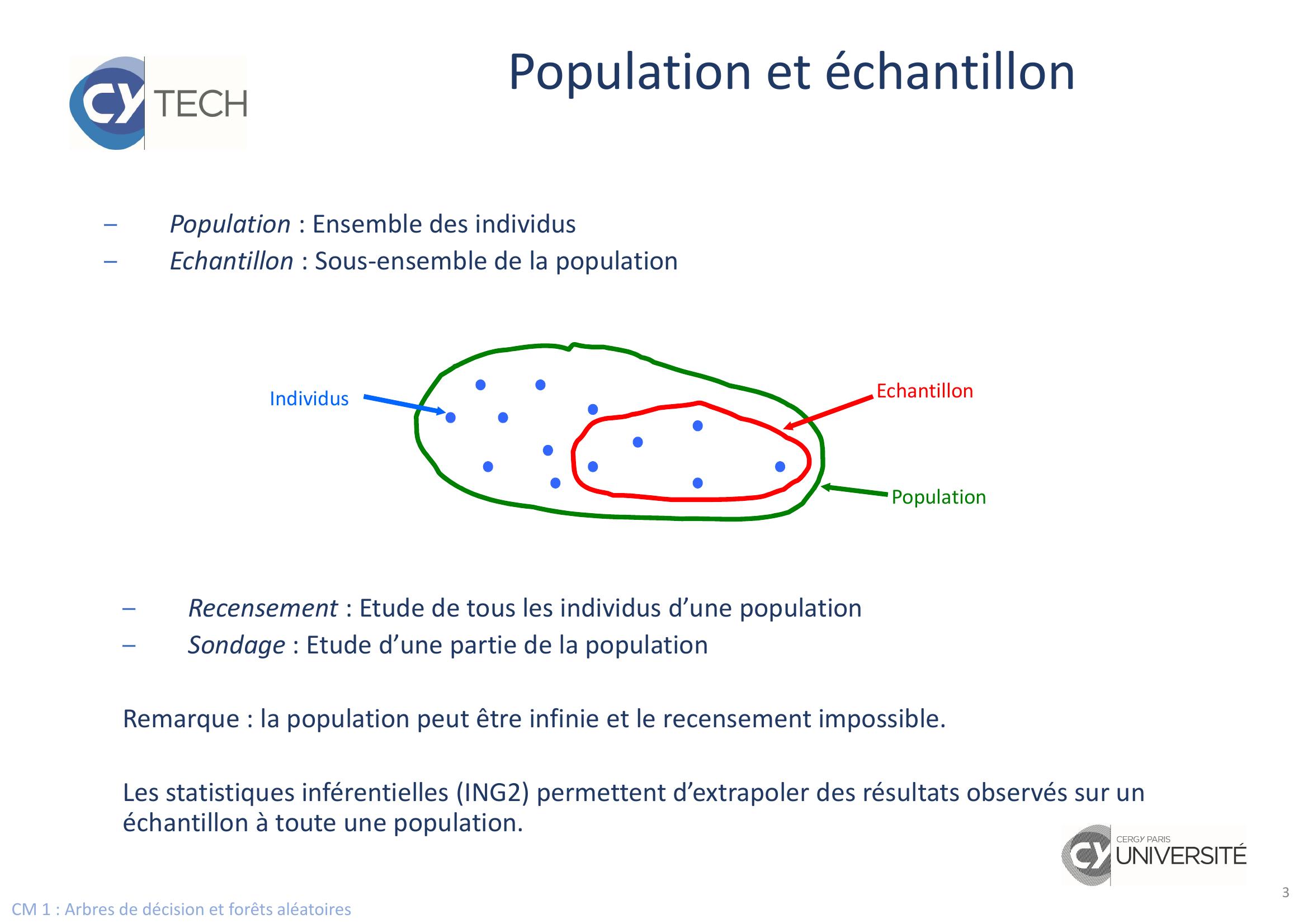
Page 3 : CM 1 : Arbres de décision et forêts aléatoiresPopulation et échantillon–Population : Ensemble des individus–Echantillon : Sous-ensemble de la populationIndividusEchantillonPopulation–Recensement : Etude de tous les individus d’une population –Sondage : Etude d’une partie de la populationRemarque : la population peut être infinie et le recensement impossible.Les statistiques inférentielles ING2 permettent d’extrapoler des résultats observés sur un échantillon à toute une population.3
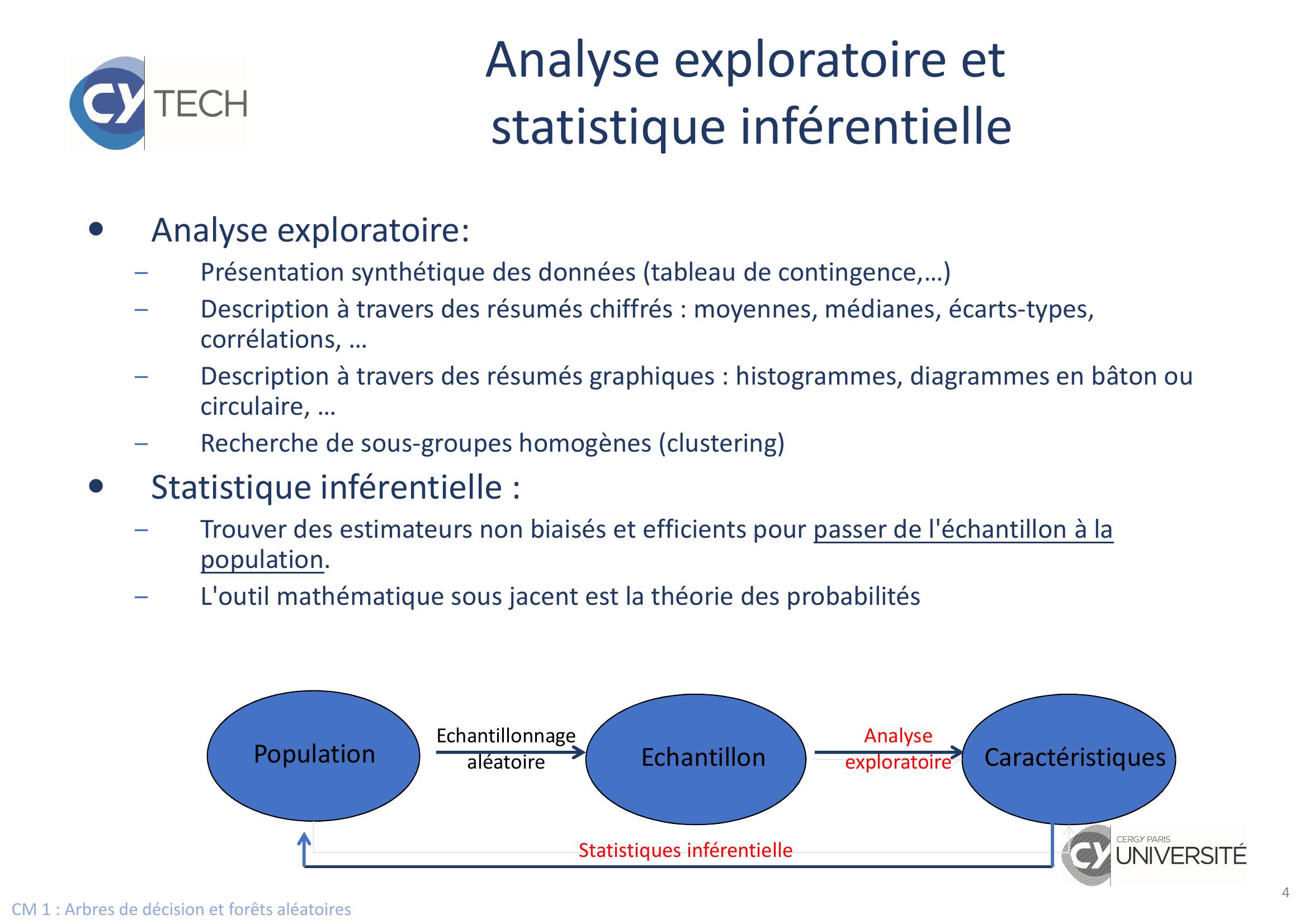
Page 4 : CM 1 : Arbres de décision et forêts aléatoiresAnalyse exploratoire: –Présentation synthétique des données tableau de contingence,…–Description à travers des résumés chiffrés : moyennes, médianes, écarts-types, corrélations, …–Description à travers des résumés graphiques : histogrammes, diagrammes en bâton ou circulaire, …–Recherche de sous-groupes homogènes clusteringStatistique inférentielle : –Trouver des estimateurs non biaisés et efficients pour passer de l'échantillon à la population.–L'outil mathématique sous jacent est la théorie des probabilitésPopulationEchantillonCaractéristiquesEchantillonnagealéatoireAnalyse exploratoireStatistiques inférentielleAnalyse exploratoire etstatistique inférentielle4
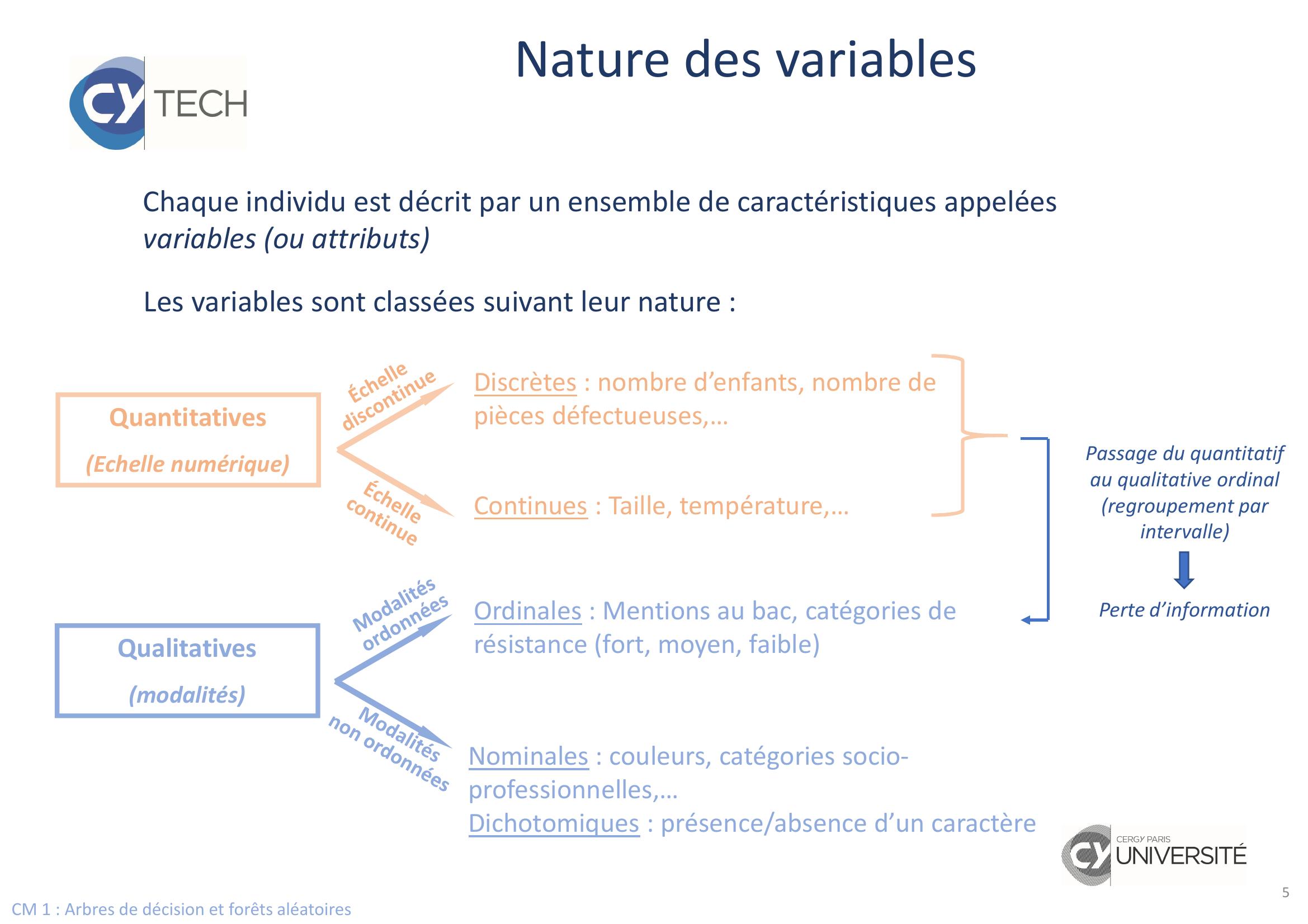
Page 5 : CM 1 : Arbres de décision et forêts aléatoires5Chaque individu est décrit par un ensemble de caractéristiques appelées variables ou attributsLes variables sont classées suivant leur nature :QuantitativesEchelle numériqueQualitativesmodalitésDiscrètes : nombre d’enfants, nombre de pièces défectueuses,…Continues : Taille, température,…Nominales : couleurs, catégories socio-professionnelles,…Dichotomiques : présence/absence d’un caractèreOrdinales : Mentions au bac, catégories de résistance fort, moyen, faibleNature des variablesPassage du quantitatif au qualitative ordinal regroupement par intervallePerte d’information
Page 6 : CM 1 : Arbres de décision et forêts aléatoires6Les statistiques univariées : On ne s'intéresse qu'à une seule variable. Ex : Les salaires en Europe, nombre d'enfants par ménage, Temps de visite sur un site, Etude de l'âge des habitants d'un pays par classe d'âge.Les statistiques bivariées : On s'intéresse à l'étude simultanée de deux variables pour mesurer leur dépendance. Ex : le vote est-il différent d'une CSP à l'autre ?Les statistiques multivariées : On s'intéresse à l'étude simultanée de p variables. Même problématique que pour le bidimensionnel mais avec p assez grand.Ex : Etude du bien-être par département à travers de critères géo-socio-économiques ensoleillement, nombre de théâtres, taux de suicides, infrastructure routière, …A chaque type de variable qualitatif nominal, quantitatif continu,… correspond un traitement spécifique.Différents types d’analyseVu au lycée
Page 7 : CM 1 : Arbres de décision et forêts aléatoires7Etape 1 : Définir précisément le problème étudié :1 Quels sont les objectifs de l'étude ?recensement des différentes questions poséesdéduction des différentes études statistiques à opérerdéfinition des variables étudiées avec leur type2 Quelle est la population étudiée ?définition précise de l'unité statistiquedéfinition du périmètre spatio-temporel 3 Comment récupérer et stocker l'information?Enquête ou données existantes ou un mixteChoix de la technique d'échantillonnageRécupération des données et validation des données récupéréesEtape 2 : Exécution des études statistiques avec les logiciels appropriésEtape 3 : Rédaction du document de synthèse1Rappel du contexte : objectifs de l'étude, périmètre de l'étude, définitions des études statistiques2Insertion par étude des résumés chiffrés et graphiques3Interprétation des résultats en cohérence avec le périmètre et les résumés Méthodologie d'étude statistique
Page 8 : CM 1 : Arbres de décision et forêts aléatoires8Analyse univariéeRappels et compléments
Page 9 : CM 1 : Arbres de décision et forêts aléatoires9Effectif : Pour chaque variable, il s’agit de compter le nombre d’individus ayant la même valeur/modalité xi. On utilisera le terme effectif de la valeur/modalité i. On notera cet effectif ni.Fréquence : Quand on aura besoin de ramener les effectifs en pourcentage. On parlera alors de fréquences. On notera cette fréquence fi,fi = ni / n où n est l'effectif total.La fréquence permet de comparer des échantillons de tailles différentesTaux de chômage4,4;9,699,6;14,8714,8;19,9119,9;25,12Total20Une présentation synthétique des données commence par un tableau de contingence. Zone Euro avant 2010Pas Euro35Zone Euro65Total100Zone Euro avant 2010Pas Euro7Zone Euro13Total20PaysTaux de chômagePIBZone Euro avant 2010Allemagne5,537430,1Zone EuroAutriche4,440064,8Zone EuroBelgique7,637727,8Zone EuroDanemark7,540189,9Pas Euro…………N.B. Le tableau de contingence des variables continues nécessite une regroupement des valeurs cf. histogrammeReprésentation synthétique
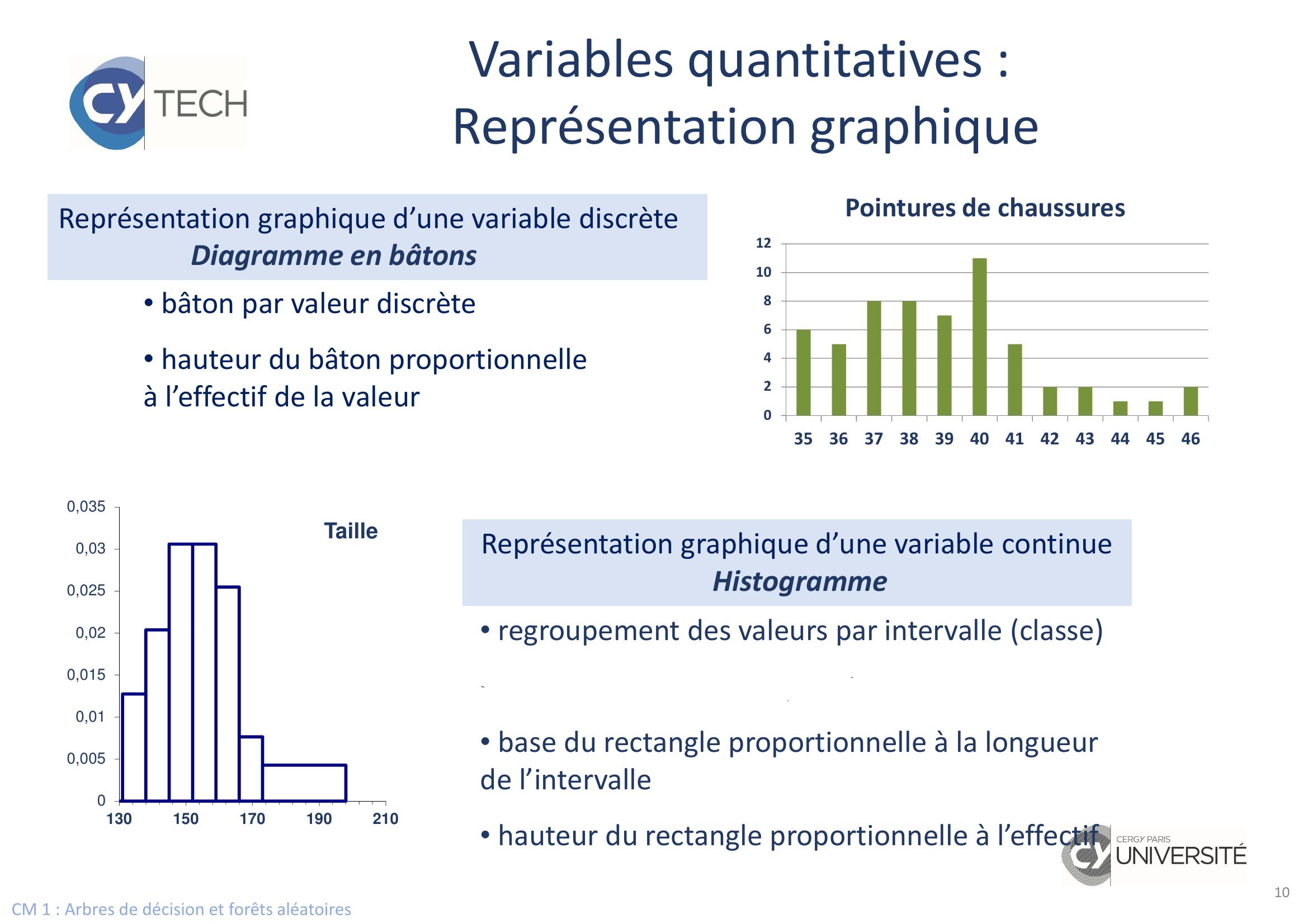
Page 10 : CM 1 : Arbres de décision et forêts aléatoires10Variables quantitatives : Représentation graphiqueReprésentation graphique d’une variable discrète Diagramme en bâtonsReprésentation graphique d’une variable continueHistogramme• bâton par valeur discrète• hauteur du bâton proportionnelle à l’effectif de la valeur024681012353637383940414243444546Pointures de chaussures00,0050,010,0150,020,0250,030,035130150170190210Taille• regroupement des valeurs par intervalle classe• nombre de classes E1+10×log10n/3• base du rectangle proportionnelle à la longueur de l’intervalle• hauteur du rectangle proportionnelle à l’effectif
Page 11 : CM 1 : Arbres de décision et forêts aléatoires11Variables quantitatives : Résumés numériquesOn distingue deux types de résumés numériques : • Les indicateurs de position moyenne, mode, médiane, quartiles. Ils positionnent la série des valeurs observées autour d’une tendance centrale.• Les indicateurs de dispersion variance, écart-type, étendue inter-quartile. Ils indiquent la fluctuation des valeurs de la série autour d’une tendance centrale en général.
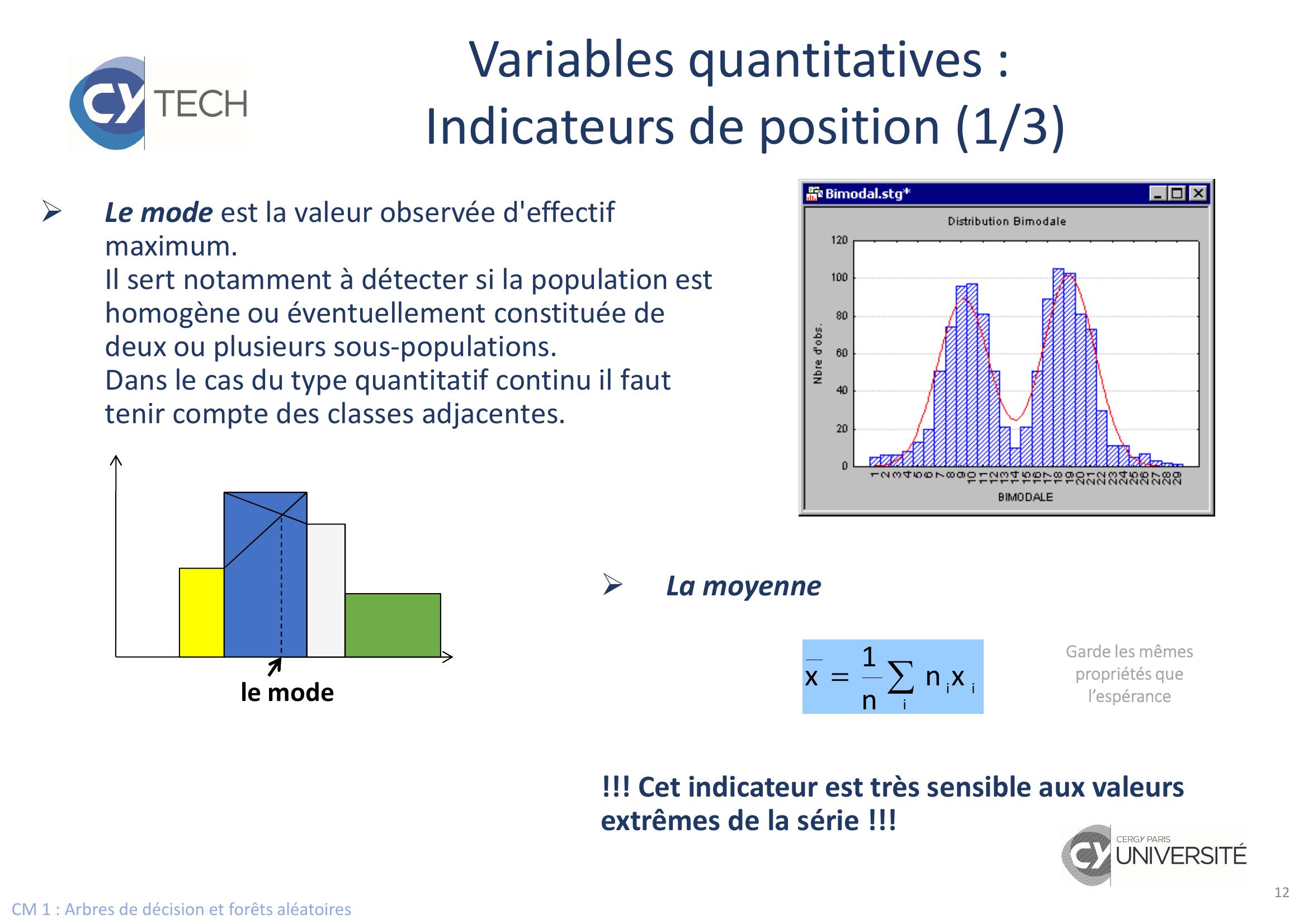
Page 12 : CM 1 : Arbres de décision et forêts aléatoires12Variables quantitatives : Indicateurs de position 1/3Le mode est la valeur observée d'effectif maximum. Il sert notamment à détecter si la population est homogène ou éventuellement constituée de deux ou plusieurs sous-populations.Dans le cas du type quantitatif continu il faut tenir compte des classes adjacentes. le modeLa moyenne!!! Cet indicateur est très sensible aux valeursextrêmes de la série !!!=iiixnn1xGarde les mêmes propriétés que l’espérance
Page 13 : CM 1 : Arbres de décision et forêts aléatoires13Variables quantitatives : Indicateurs de position 2/3Les quartiles :- La médiane est la valeur qui sépare la population en deux groupes d’effectifs égaux. Elle n’a de sens que sur une série rangée par ordre croissant. - Le 1er quartile Q1 est la valeur qui sépare la série en ¼ inférieur et ¾ supérieur.- Le 3ème quartile Q3 est la valeur qui sépare la série en ¾ inférieur et ¼ supérieur.La représentation graphique des ces indicateurs est la boite de Tukey. Elle permet d’avoir une aperçu graphique rapide de la distribution des valeurs de la série et permet beaucoup d’interprétation. Les valeurs extrêmes de cette représentation sont les « moustaches » définies en général parm=Q1-1,5×Q3-Q1 et M=Q3+1,5×Q3-Q1 Toutes valeurs de la série en dehors des moustaches est considérée comme atypique
Page 14 : CM 1 : Arbres de décision et forêts aléatoires14Variables quantitatives : Indicateurs de position 3/3Note1234567Elève L9108710911Elève P1421656516Elève L7899101011Elève P2556141616Série ordonnéeMoyenneMédianeQ1Q3mMElève L9,19810513Elève P9,16514027,5Différence de fluctuation des notes indicateurs de dispersionElève PElève L
Page 15 : CM 1 : Arbres de décision et forêts aléatoires15Variables quantitatives : Indicateurs de dispersionLa variance mesure l’écart au carré entre les valeurs de la série et leur moyenneAfin de garder la même unité que la variable, on utilise l’écart-typeTout comme la moyenne ces deux indicateurs sont sensibles aux valeurs extrêmes de la série.L’écart-médian mesure l’écart entre les valeurs de la série et leur médiane=i2ii2xxnn1s2ss ==iiimedxnn1emOn peut aussi utiliser l’étendue de la série ou l’écart inter-quartiles iixminxmax13QQVarianceEcart-typeemQ3-Q1Elève L1,811,3418Elève P35,485,964,855Garde les mêmes propriétés que la variance théorique
Page 16 : CM 1 : Arbres de décision et forêts aléatoires16Variables quantitatives : Variables centrées-réduitesOn définit la série centrée-réduite de la façon suivante :=xiisxxxLa série est dite :•centrée car de moyenne nulle•réduite car de variance égale à 1PaysTaux de chômagePIBAllemagne5,537430,1Autriche4,440064,8Belgique7,637727,8Danemark7,540189,9Espagne25,131903,8Estonie10,120393,3………Moyenne10,634851,6Ecart-type5,7714203,93PaysTaux de chômagePIBAllemagne-0,880,18Autriche-1,080,37Belgique-0,520,20Danemark-0,540,38Espagne2,51-0,21Estonie-0,09-1,02………Moyenne00Ecart-type11normalisationxxs1xxn1s1xxn1s1sxxn1xn1xxn1kkxn1kkxn1kxkn1kk=========1ss1xxn1s1sxxn1xn1xxn1s2x2xn1k2k2x2n1kxkn1k2n1k2k2x==========Démonstration
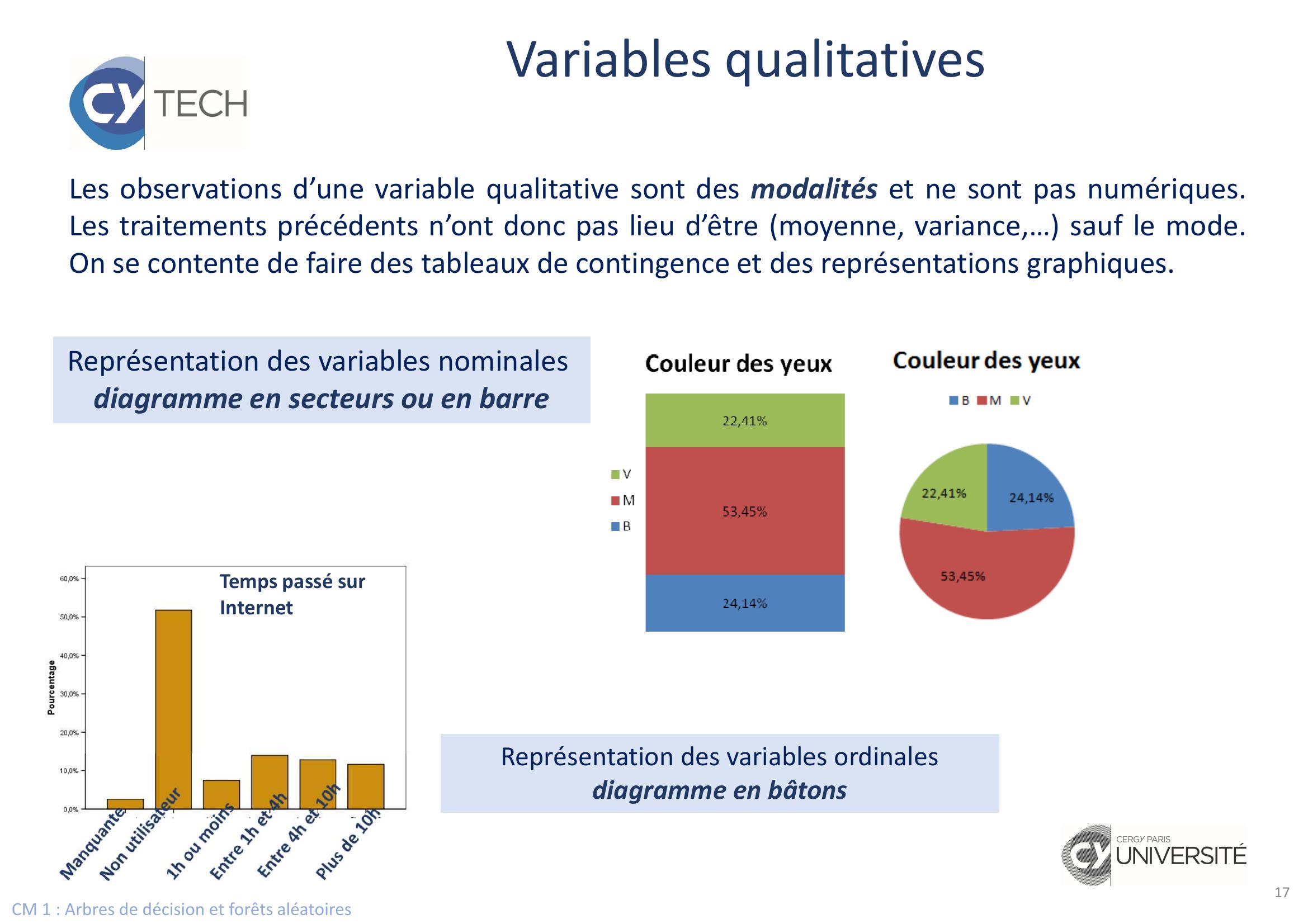
Page 17 : CM 1 : Arbres de décision et forêts aléatoires17Variables qualitativesLes observations d’une variable qualitative sont des modalités et ne sont pas numériques.Les traitements précédents n’ont donc pas lieu d’être moyenne, variance,… sauf le mode.On se contente de faire des tableaux de contingence et des représentations graphiques.Temps passé sur InternetReprésentation des variables nominalesdiagramme en secteurs ou en barre Représentation des variables ordinales diagramme en bâtons
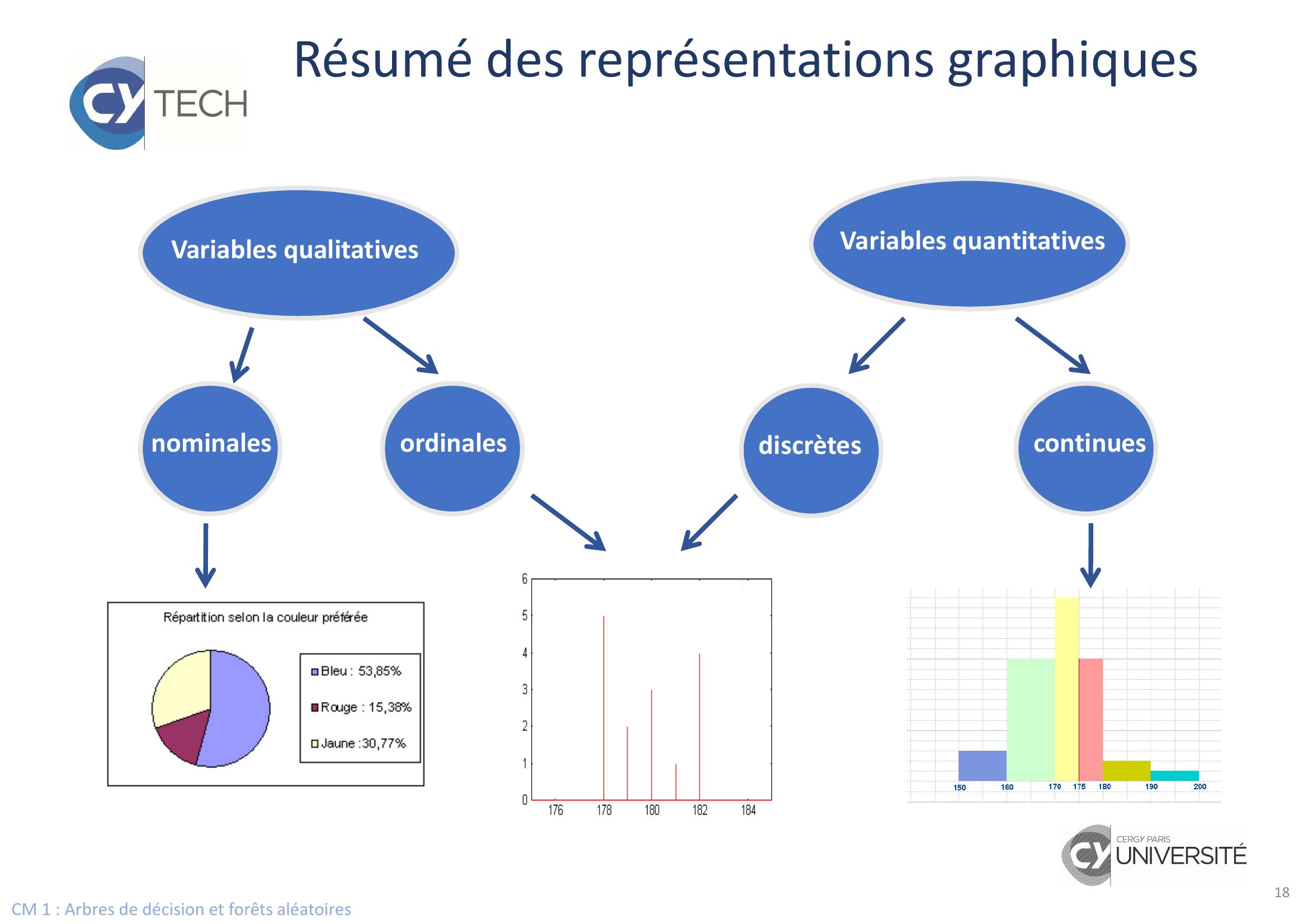
Page 18 : CM 1 : Arbres de décision et forêts aléatoires18Résumé des représentations graphiquesEISTI : Département Mathématique : Introduction à la statistique descriptive1818Variables qualitativesVariables quantitativesnominalesordinalesdiscrètescontinues