CM1 Listes Chaines
Télécharger le CM1 Listes Chaines en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87
Page 1 : INFORMATIQUE 3I . L E S L I S T E S C H A I N É E SEva ANSERMIN & Renaud VERIN & Romuald GRIGNONv1.00
Page 2 : Un point sur l’informatique 3• I. Algorithmie : listes chaînées, piles/files, arbres… • 7 CM• 8 semaines de TD • 3 DS• II . Script shell • 2 CM• 4 semaines de TD• 1 DS• III. Projet : 4 séancesRègles d’évaluation :• N-1 sur les notes de DS• 0.7 notes de DS + 0.3 note de projet2E.ANSERMIN R.VERIN R.GRIGNON
Page 3 : I. Rappels 3E.ANSERMIN R.VERIN R.GRIGNON
Page 4 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 11541155…5340…10 02810 029……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;4E.ANSERMIN R.VERIN R.GRIGNON
Page 5 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 11541155…5340…10 02810 029……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;5E.ANSERMIN R.VERIN R.GRIGNON
Page 6 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 1154???1155…5340…10 02810 029……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;a6E.ANSERMIN R.VERIN R.GRIGNON
Page 7 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 1154???1155…5340…10 02810 0290 NULL……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap17E.ANSERMIN R.VERIN R.GRIGNON
Page 8 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 115451155…5340…10 02810 0290 NULL……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap18E.ANSERMIN R.VERIN R.GRIGNON
Page 9 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 115451155…5340…10 02810 0291154……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap19E.ANSERMIN R.VERIN R.GRIGNON
Page 10 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 115451155…5340…10 02810 0291154……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap1a=510E.ANSERMIN R.VERIN R.GRIGNON
Page 11 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 115451155…5340…10 02810 0291154……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap1a=5p1=511E.ANSERMIN R.VERIN R.GRIGNON
Page 12 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 1154101155…5340…10 02810 0291154……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap1a=5p1=512E.ANSERMIN R.VERIN R.GRIGNON
Page 13 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !Adresse Valeur 1154101155…5340…10 02810 0291154……22 222inta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;ap1a=5p1=5a=1013E.ANSERMIN R.VERIN R.GRIGNONEva ANSERMIN & Romuald GRIGNON
Page 14 : Pointeur et pseudo-code •Un pointeur est :•Une variable dont la valeur est une adresse mémoire…•L’adresse mémoire d’une autre variable !int maininta;int p1 = NULL;a= 5;p1 = &a;printf" a =d \n",a;printf"p1=p \n",p1;p1 = 10;printf" a =d \n",a;return 0;VARIABLE a: entierp1 : pointeur sur entier DEBUTa ← 5p1 ←adresse de aECRIRE«a=»+aECRIRE«p1 =»+p1p1 ← 10ECRIRE« a =»+aFIN14E.ANSERMIN R.VERIN R.GRIGNON
Page 15 : Les tableaux•Les valeurs d’un tableau sont à la suite dans la mémoire.•Lorsqu’un tableau est déclaré :•Un espace mémoire de la bonne taille est réservé.•Un pointeur constant portant le nom du tableau est créé. Il pointe sur la première case du tableau. VARIABLE tab5: tableau d’entiersDEBUTtab - 1,3FINAdresse Valeur 115413000…………22 2221154tab0tab1tab2tab3tab4tab15E.ANSERMIN R.VERIN R.GRIGNON
Page 16 : Les tableaux : contraintes•Il est obligatoire de connaître la taille d’un tableau lors de sa déclaration.•Même lors d’une allocation dynamique, la taille de l’espace mémoire à allouer doit être donnée. •Solutions possibles:•Déclarer une taille de tableau suffisament grande :Il faut être certain qu’on ne dépassera pasRisque de mémoire « gachée »•Imposer une limite de taille à l’utilisateur Application limitée•Utiliser une liste chaînée.16E.ANSERMIN R.VERIN R.GRIGNON
Page 17 : II. Listes chaînées : principe17E.ANSERMIN R.VERIN R.GRIGNON
Page 18 : Les listes chaînées•Une liste chaînée est un objet informatique permettant de stocker des éléments dans un ordre précis comme un tableau.•Contrairement à un tableau, les éléments d’une liste chaînée ne sont pas à la suite dans la mémoire. •Même lors d’une allocation dynamique, la taille de l’espace mémoire à allouer doit être donnée. •Un élément stocké dans une liste chaînée est toujours accompagné d’un pointeur indiquant où se trouve l’élément suivant de la liste dans la mémoire.Les éléments de la liste ne sont pas à la suite dans la mémoire mais on sait toujours où se trouve l’élément suivant grâce à un pointeur !18E.ANSERMIN R.VERIN R.GRIGNON
Page 19 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, une structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc… •Un pointeur vers l’occurrence suivante 19E.ANSERMIN R.VERIN R.GRIGNON
Page 20 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, un structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc...•Un pointeur vers l’occurrence suivante Structure Chainon :elmt : Elementsuivant : pointeur sur structure Chainon20E.ANSERMIN R.VERIN R.GRIGNON
Page 21 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, un structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc...•Un pointeur vers l’occurrence suivante •Exemple : Structure Chainon :elmt : Elementsuivant : pointeur sur structure ChainonStructure Chainon :elmt : entier suivant : pointeur sur structure Chainon21E.ANSERMIN R.VERIN R.GRIGNON
Page 22 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, un structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc...•Un pointeur vers l’occurrence suivante •Exemple : Structure Chainon :elmt : Elementsuivant : pointeur sur structure ChainonStructure Chainon :elmt : réel suivant : pointeur sur structure Chainon22E.ANSERMIN R.VERIN R.GRIGNON
Page 23 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, un structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc...•Un pointeur vers l’occurrence suivante •Exemple : Structure Chainon :elmt : Elementsuivant : pointeur sur structure ChainonStructure Chainon :elmt : Etudiant suivant : pointeur sur structure Chainon23E.ANSERMIN R.VERIN R.GRIGNON
Page 24 : Constitution d’une liste chaînée•Une liste chaînée est constituée de chaînons, un structure qui contient :•L’ élément à stocker entier, flottant, tableau de caractères etc...•Un pointeur vers l’occurrence suivante •Exemple en C : Structure Chainon :elmt : Elementsuivant : pointeur sur structure Chainontypedef struct chainonint nombre;struct chainon suivant; Chainon;struct chainonint nombre;struct chainon suivant;;typedef struct chainon Chainon;OU24E.ANSERMIN R.VERIN R.GRIGNON
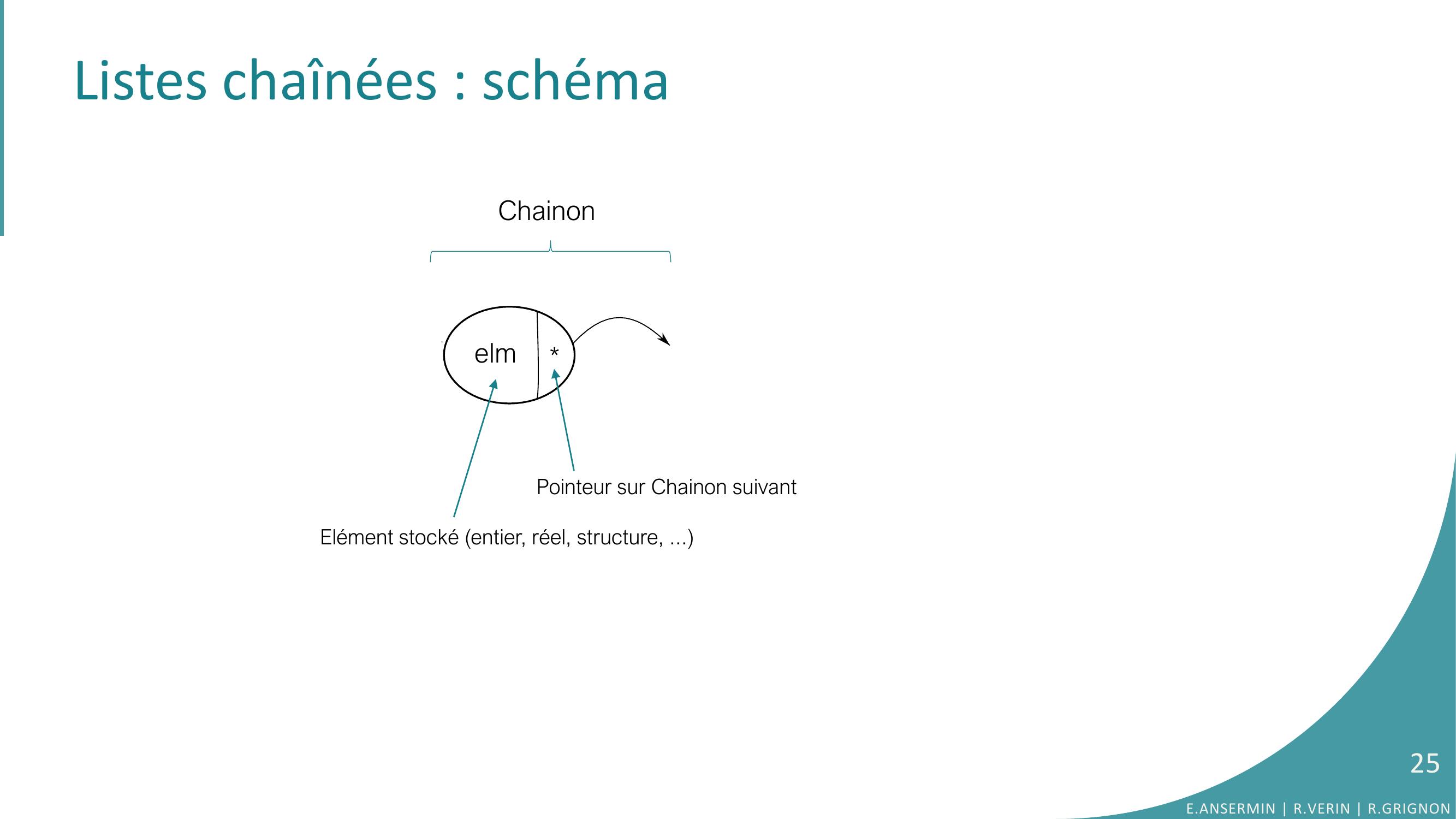
Page 25 : Listes chaînées : schéma elmChainonElément stocké entier, réel, structure, ...Pointeur sur Chainon suivant25E.ANSERMIN R.VERIN R.GRIGNON
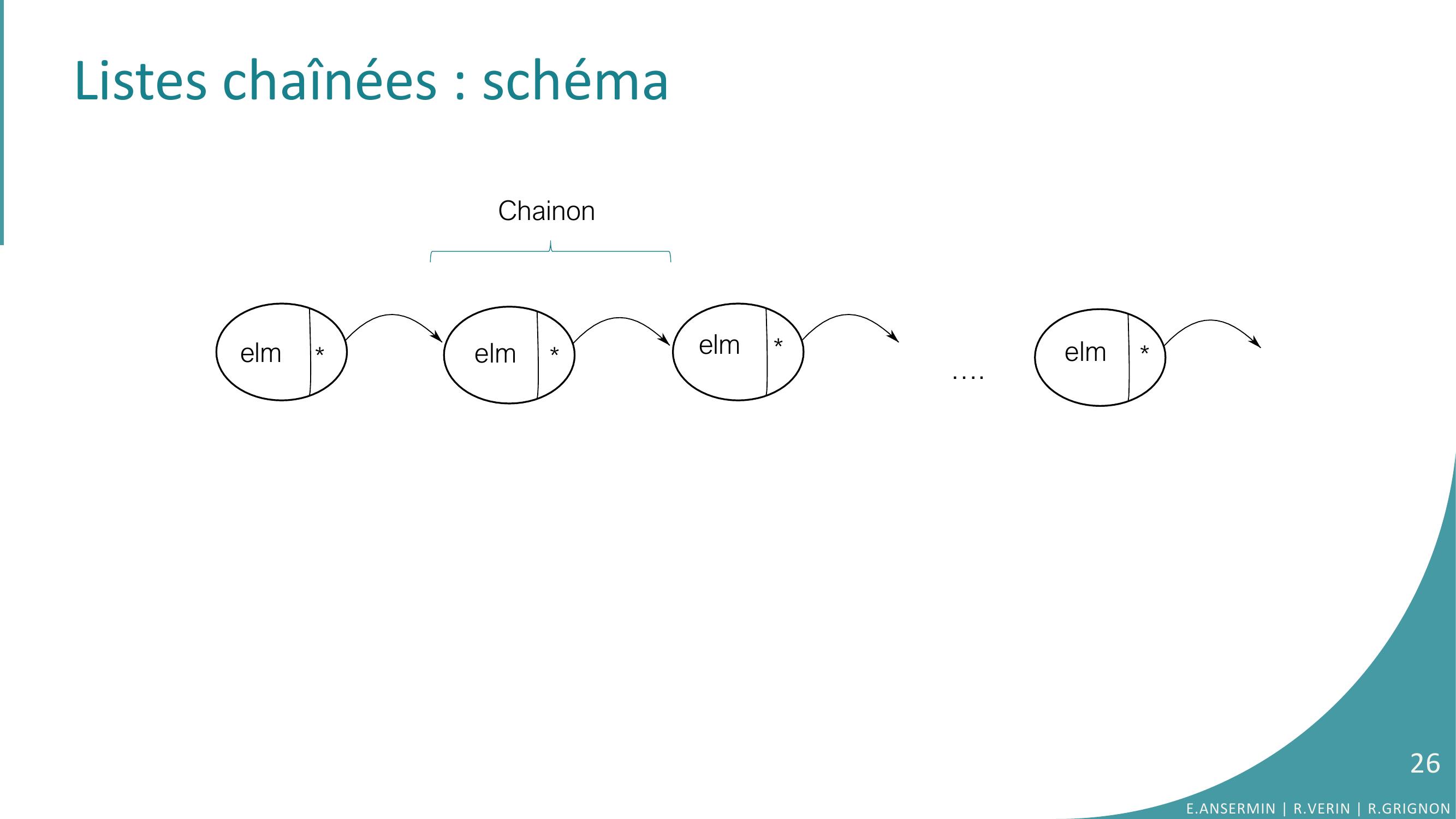
Page 26 : Listes chaînées : schéma Chainonelmelmelmelm….26E.ANSERMIN R.VERIN R.GRIGNON
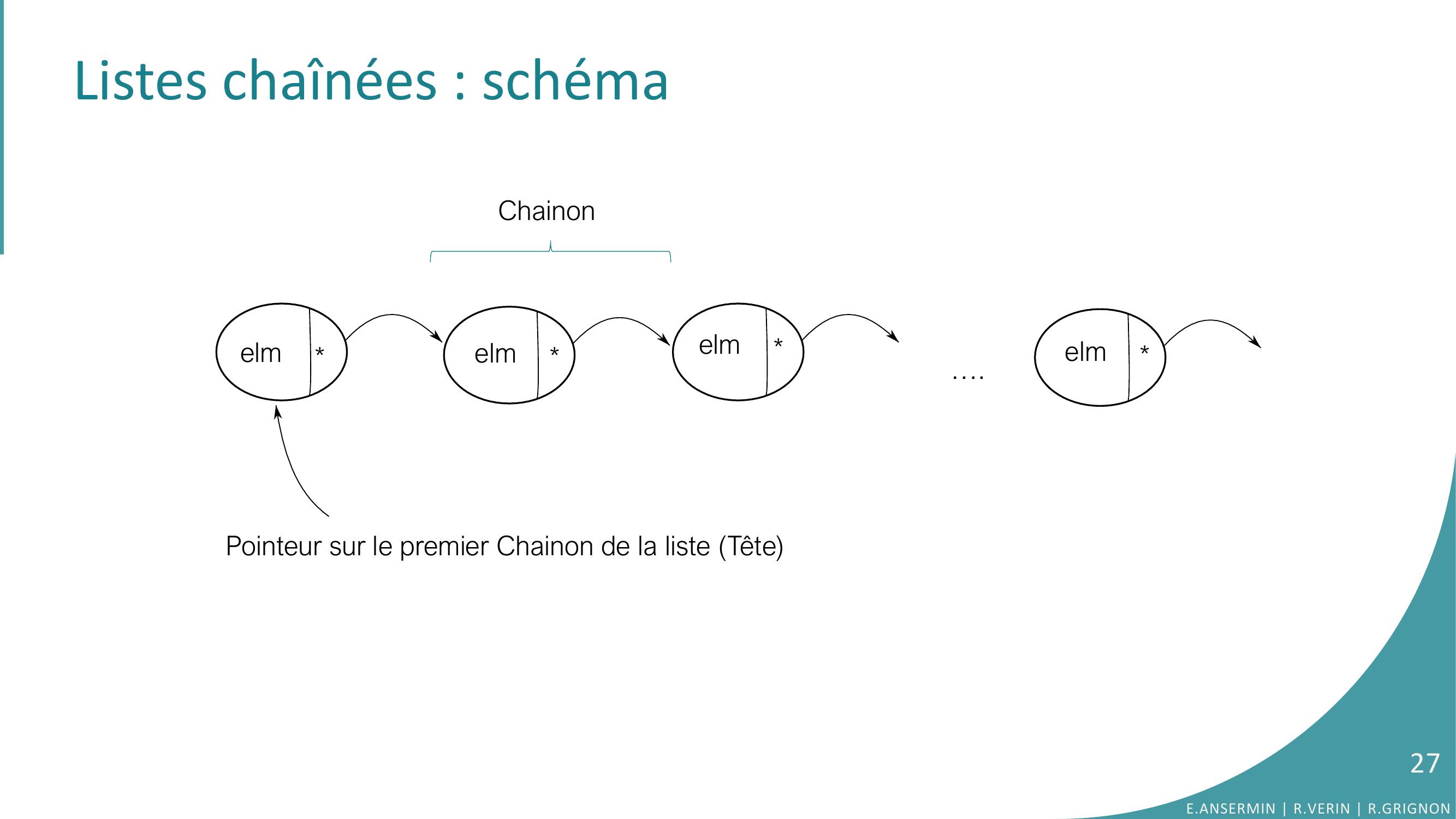
Page 27 : Listes chaînées : schéma Chainonelmelmelmelm….Pointeur sur le premier Chainon de la liste Tête27E.ANSERMIN R.VERIN R.GRIGNON
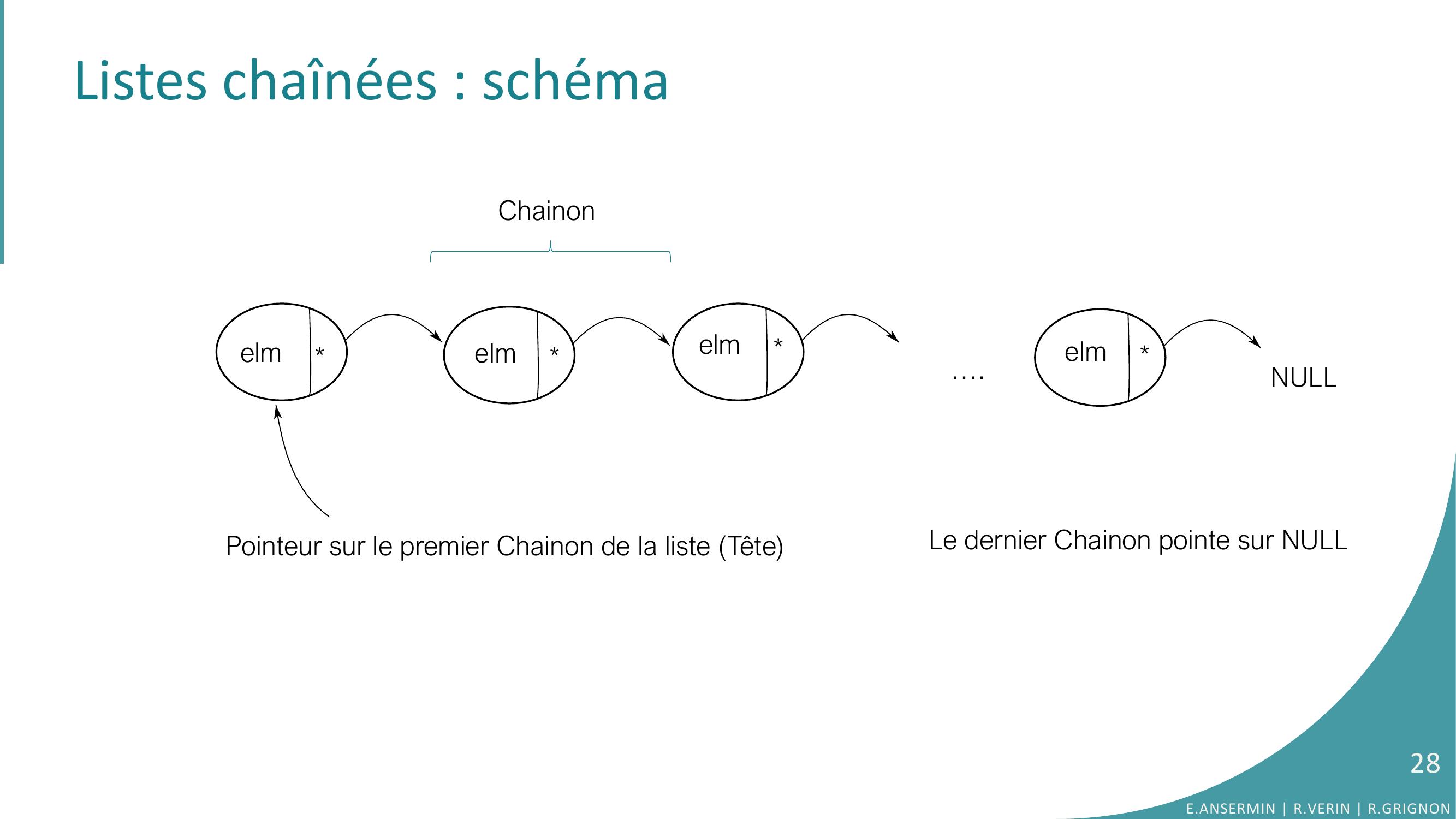
Page 28 : Listes chaînées : schéma Chainonelmelmelmelm….Pointeur sur le premier Chainon de la liste TêteNULLLe dernier Chainon pointe sur NULL28E.ANSERMIN R.VERIN R.GRIGNON
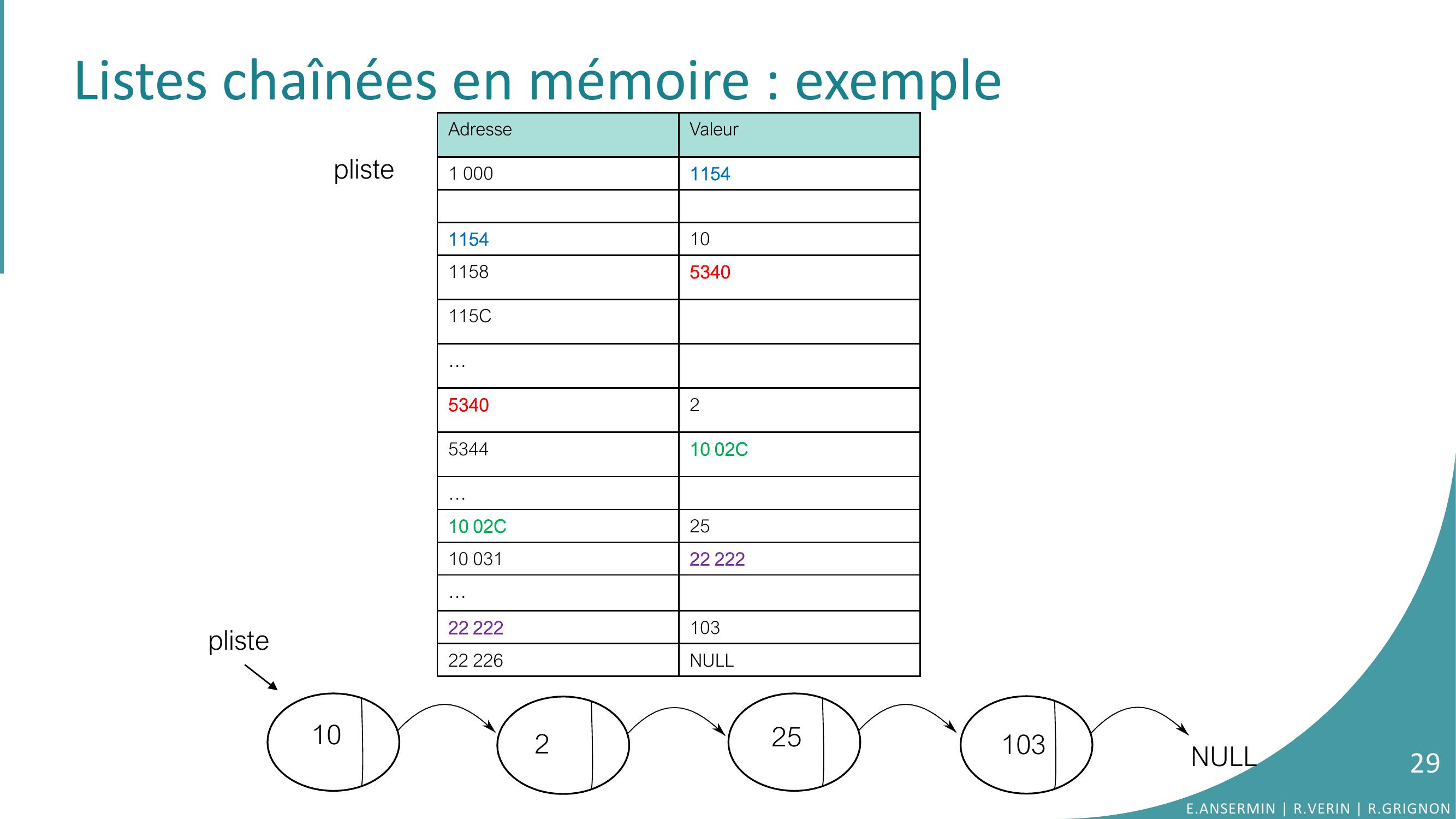
Page 29 : Listes chaînées en mémoire : exempleAdresseValeur1 000115411541011585340115C…53402534410 02C…10 02C2510 03122 222…22 22210322 226NULLpliste10225103NULLpliste29E.ANSERMIN R.VERIN R.GRIGNON
Page 30 : II. Listes chaînées : opérations30E.ANSERMIN R.VERIN R.GRIGNON
Page 31 : Listes chaînées : construction1. Initialisation de la chaîne : initialisation pointeur sur Chainon NULL plisteNULL31E.ANSERMIN R.VERIN R.GRIGNON
Page 32 : Listes chaînées : construction1. Initialisation de la chaîne : initialisation pointeur sur Chainon NULL2. Création d’un Chainon plisteNULLNULL1032E.ANSERMIN R.VERIN R.GRIGNON
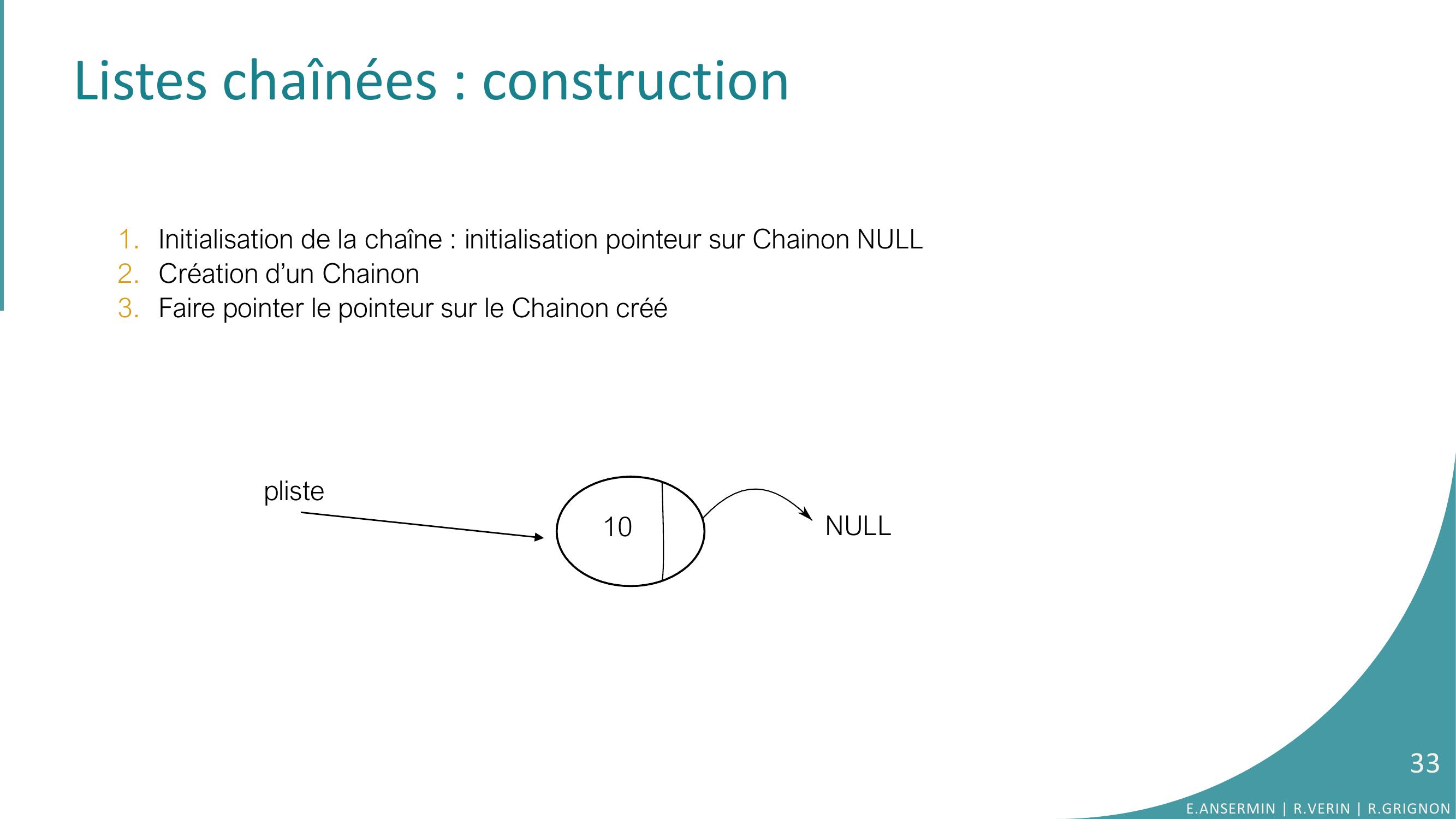
Page 33 : Listes chaînées : construction1. Initialisation de la chaîne : initialisation pointeur sur Chainon NULL2. Création d’un Chainon3. Faire pointer le pointeur sur le Chainon créé plisteNULL1033E.ANSERMIN R.VERIN R.GRIGNON
Page 34 : Liste chaînée : construction1. Initialisation de la chaîne : initialisation pointeur sur Chainon NULL2. Création d’un Chainon Chainon creationChainon//déclaration du ChainonChainon c = mallocsizeofChainon;ifc==NULLexit1;printf"Entrer la valeur : ";if scanf"d", &c-elmt != 1 exit2;c-suivant=NULL;return c;Remarque : nous verrons plus tard l’intérêt d’utiliser le malloc34E.ANSERMIN R.VERIN R.GRIGNON
Page 35 : Listes chaînées : construction1. Initialisation de la chaîne : initialisation pointeur sur Chainon NULL2. Création d’un Chainon3. Pointer le pointeur sur le Chainon créé Chainon creationChainon//déclaration du ChainonChainon c = mallocsizeofChainon;ifc==NULLexit1;printf"Entrer la valeur : ";if scanf"d", &c-elmt != 1 exit2;c-suivant=NULL;return c;int mainChainon pliste = NULL; //initialisationpListe = creationChainon;…return 0;35E.ANSERMIN R.VERIN R.GRIGNON
Page 36 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.pliste10225103NULLp1 ←plistep1 = pliste;36E.ANSERMIN R.VERIN R.GRIGNON
Page 37 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.10225103NULLplistep1 ←plistep1 = pliste;37E.ANSERMIN R.VERIN R.GRIGNON
Page 38 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.•On passe au Chainon suivant et on traite son élément10225103NULLplistep1 ←suivantp1p1 = p1 - suivant; 38E.ANSERMIN R.VERIN R.GRIGNON
Page 39 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.•On passe au Chainon suivant et on traite son élément.10225103NULLplistep1 ←suivantp1p1 = p1 - suivant; 39E.ANSERMIN R.VERIN R.GRIGNON
Page 40 : Liste chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.•On passe au Chainon suivant et on traite son élément.•…10225103NULLplistep1 ←suivantp1p1 = p1 - suivant; 40E.ANSERMIN R.VERIN R.GRIGNON
Page 41 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.•On passe au Chainon suivant et on traite son élément.•…•Jusqu’à arriver au pointeur NULL10225103NULLplistep1 ←suivantp1p1 = p1 - suivant; 41E.ANSERMIN R.VERIN R.GRIGNON
Page 42 : Listes chaînées : parcours•Pour parcourir une liste chaînée :•On déclare un pointeur = pliste. Il pointe donc sur le premier élément.•On traite le premier élément.•On passe au Chainon suivant et on traite son élément.•…•Jusqu’à arriver au pointeur NULL10225103NULLplisteOn doit parcourir les éléments 1 par 1 ! On ne peut pas utiliser d’indice comme pour les tableaux.p1 ←suivantp1p1 = p1 - suivant; 42E.ANSERMIN R.VERIN R.GRIGNON
Page 43 : Listes chaînées : parcours10225103NULLplisteprocédure traiterListepliste : pointeur sur ChainonVARIABLE p1 : pointeur sur ChainonDEBUTp1 ←pliste;TANT QUE p1 NULL FAIREtraiter elementp1p1 ← suivantp1FIN TANT QUEp1 ←suivantp143E.ANSERMIN R.VERIN R.GRIGNON
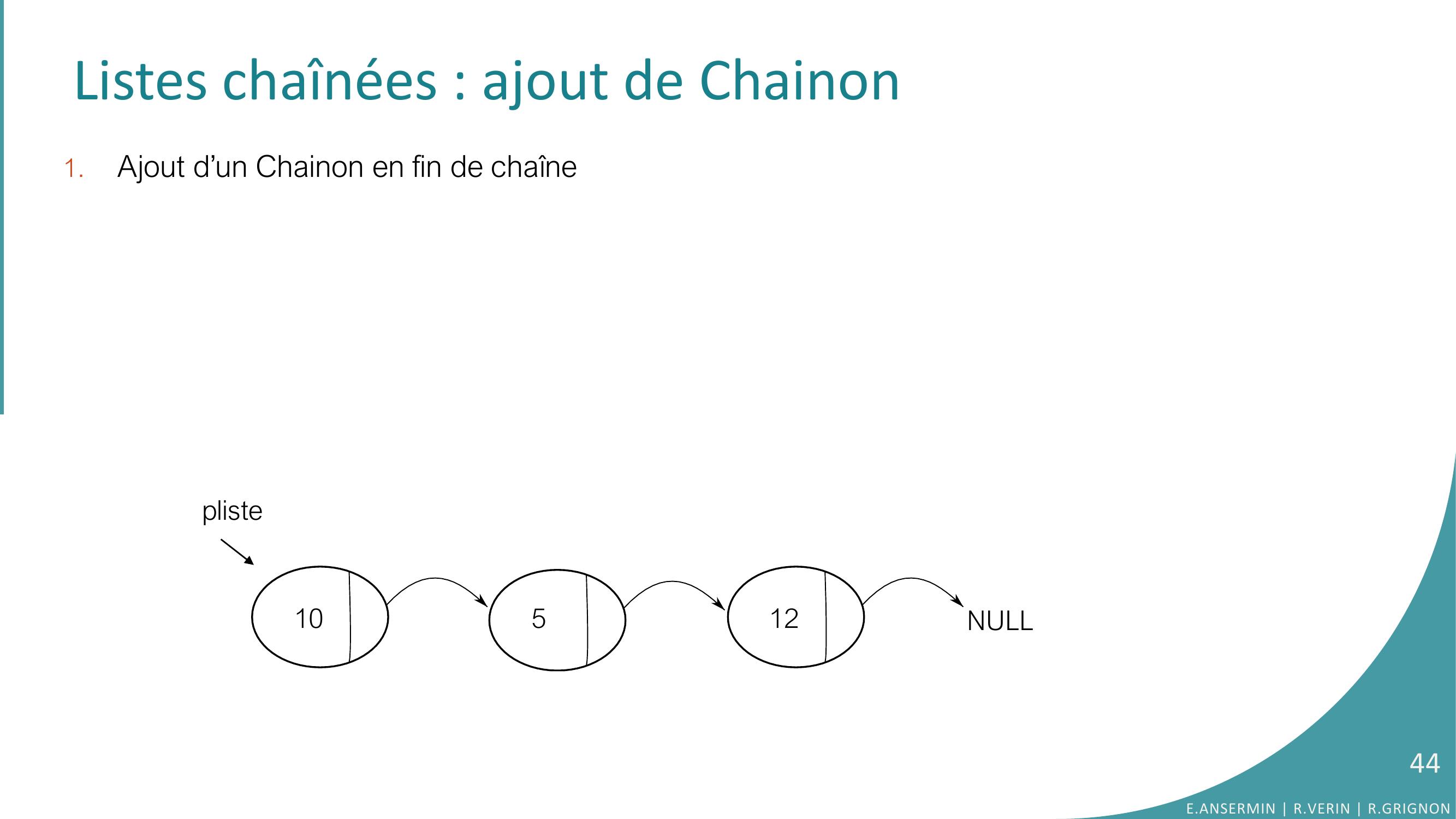
Page 44 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînepliste10512NULL44E.ANSERMIN R.VERIN R.GRIGNON
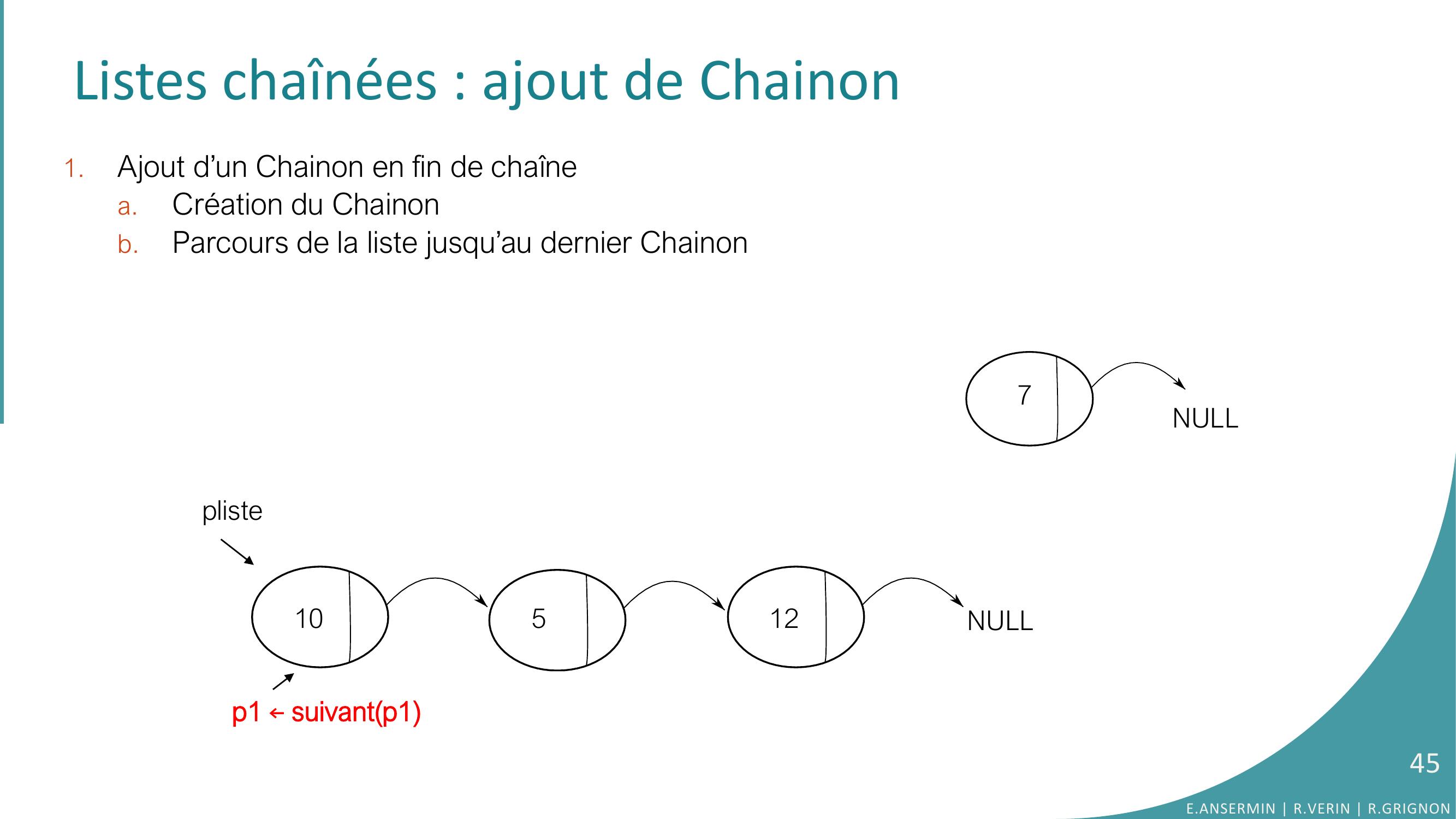
Page 45 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînea.Création du Chainonb.Parcours de la liste jusqu’au dernier Chainonpliste10512NULL7NULLp1 ←suivantp145E.ANSERMIN R.VERIN R.GRIGNON
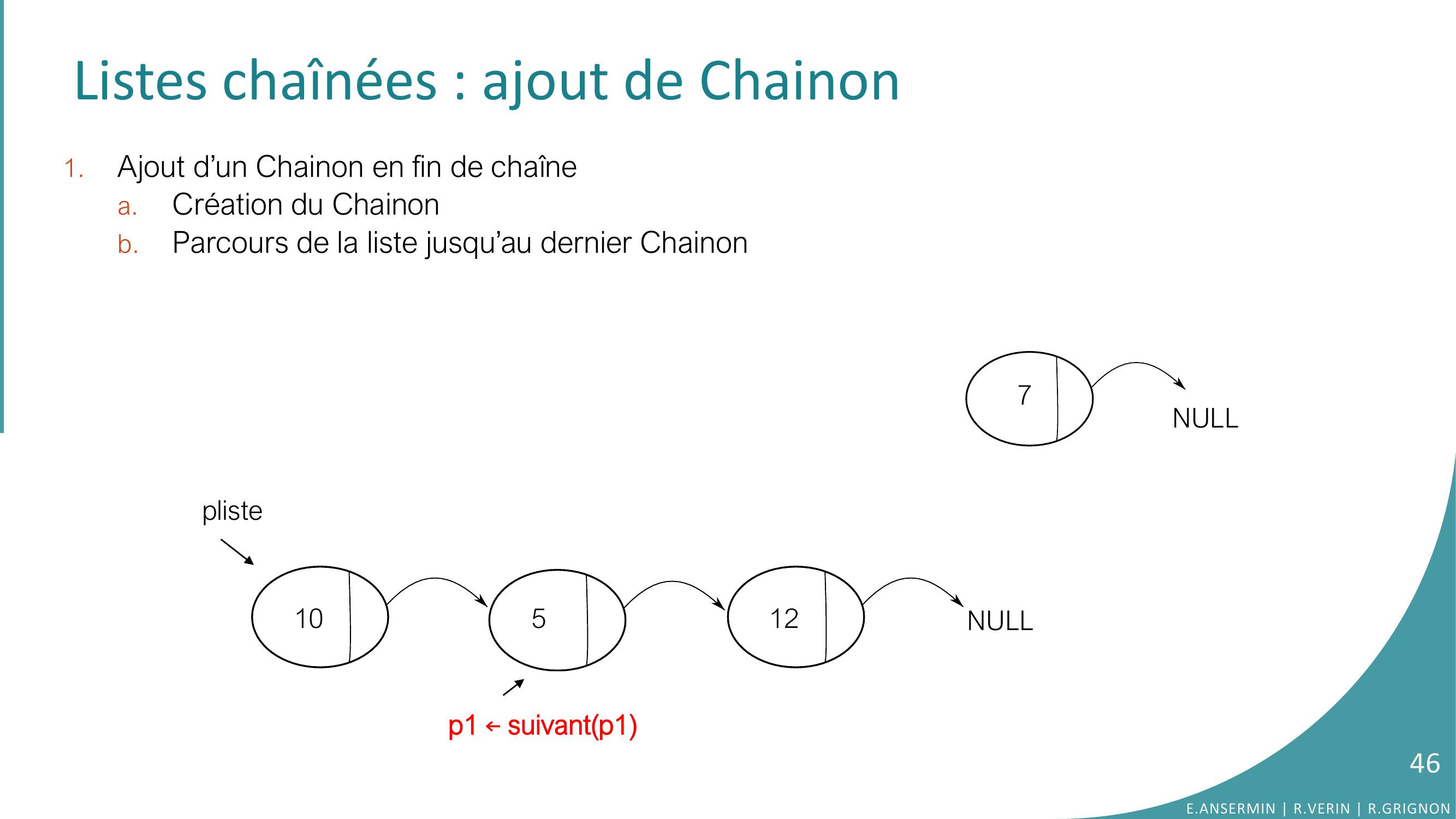
Page 46 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînea.Création du Chainonb.Parcours de la liste jusqu’au dernier Chainonpliste10512NULL7NULLp1 ←suivantp146E.ANSERMIN R.VERIN R.GRIGNON
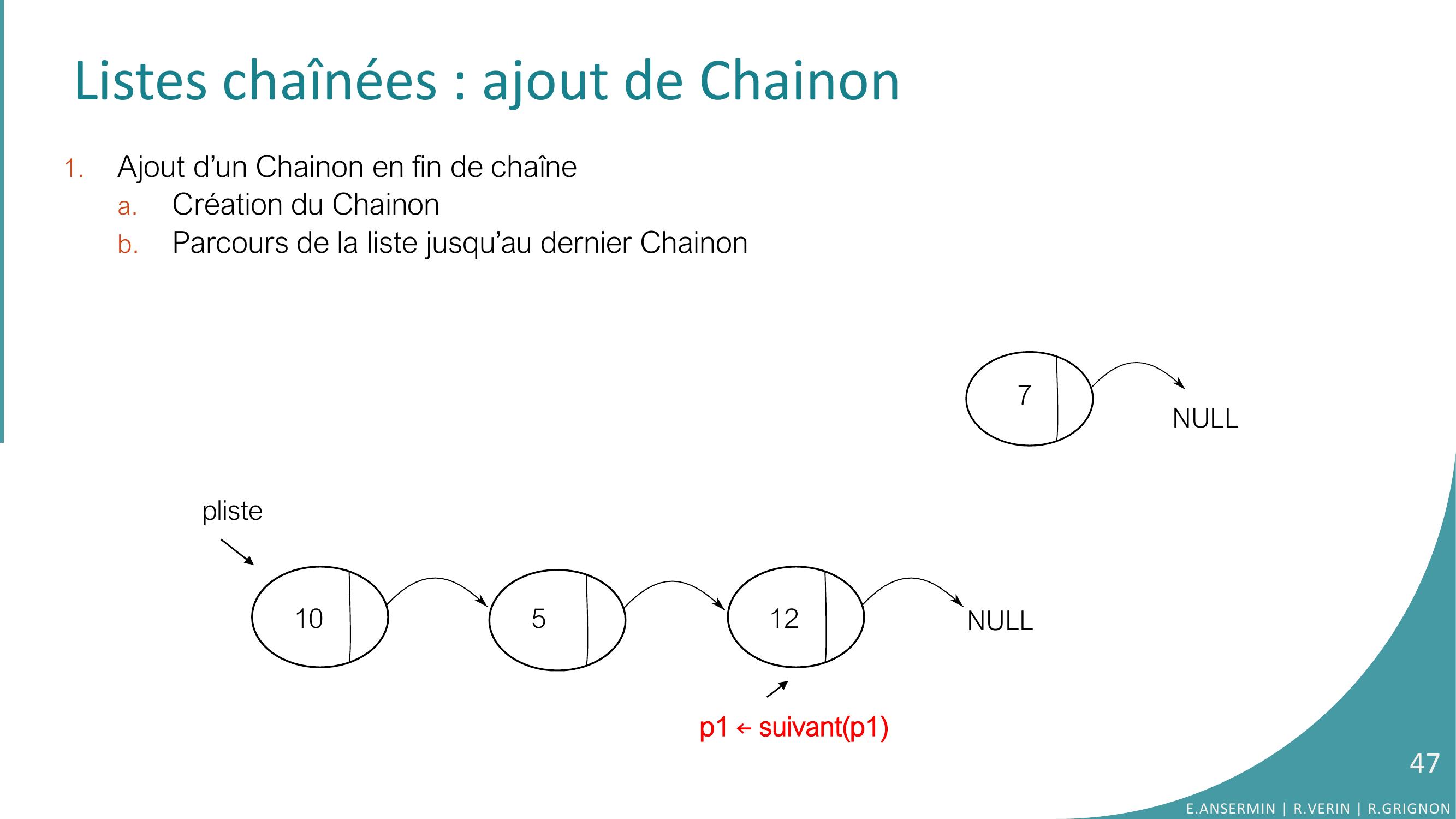
Page 47 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînea.Création du Chainonb.Parcours de la liste jusqu’au dernier Chainonpliste10512NULL7NULLp1 ←suivantp147E.ANSERMIN R.VERIN R.GRIGNON
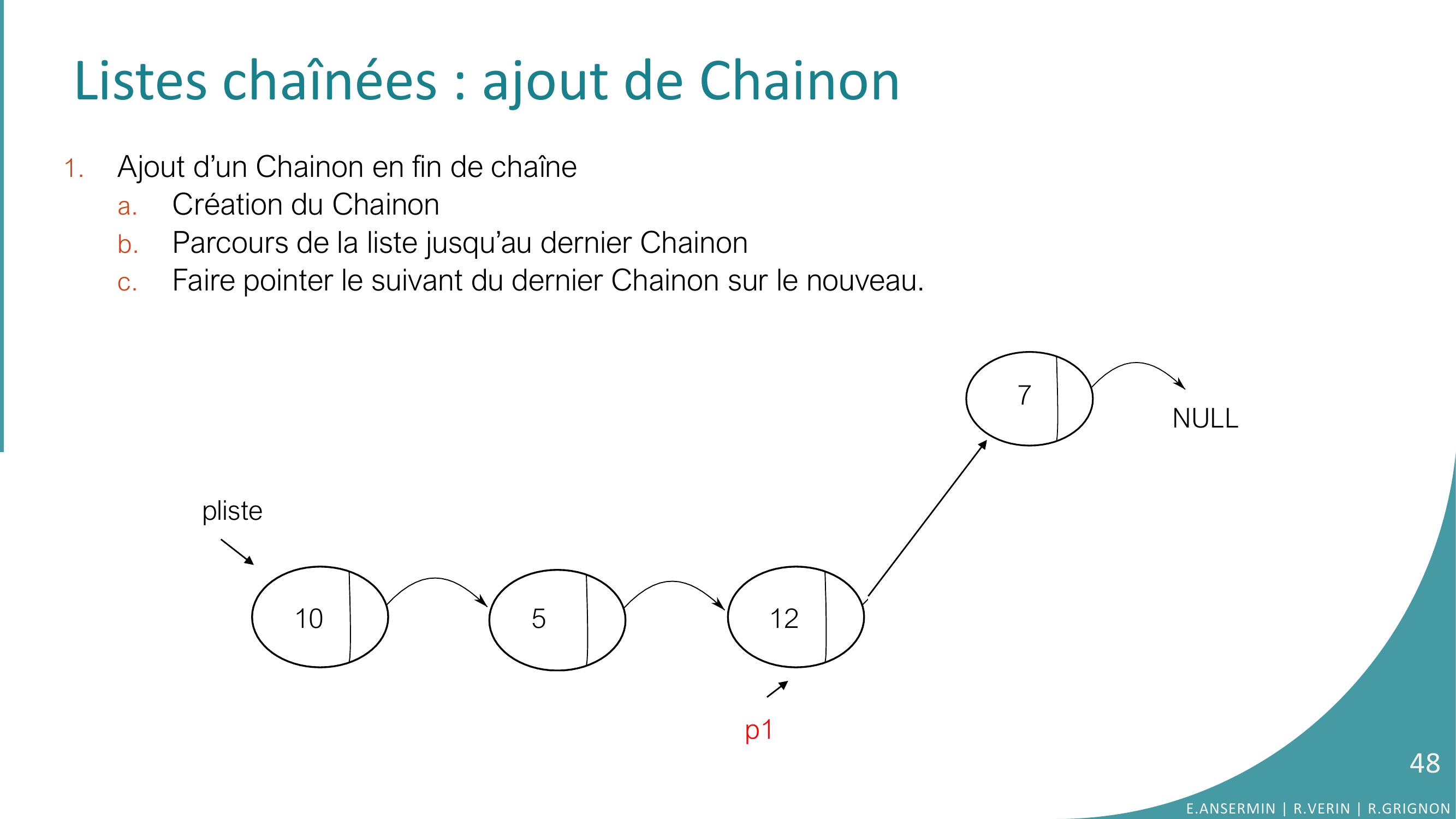
Page 48 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînea.Création du Chainonb.Parcours de la liste jusqu’au dernier Chainonc.Faire pointer le suivant du dernier Chainon sur le nouveau. pliste105127NULLp148E.ANSERMIN R.VERIN R.GRIGNON
Page 49 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaînea.Création du Chainonb.Parcours de la liste jusqu’au dernier Chainonc.Faire pointer le suivant du dernier Chainon sur le nouveau. fonction insertFinpliste : pointeur sur Chainon : pointeur sur ChainonVARIABLE nouveau, p1 : pointeur sur ChainonDEBUTnouveau ←creationChainon // etape ap1 ←plisteTANT QUEsuivantp1 NULL FAIRE// étape bp1 ← suivantp1FIN TANT QUEsuivantp1 ← nouveau// étape c // par convention on retourne le début de liste// même si il n’a pas été modifiéRETOURNER plisteFINComplexitétemporelleON49E.ANSERMIN R.VERIN R.GRIGNON
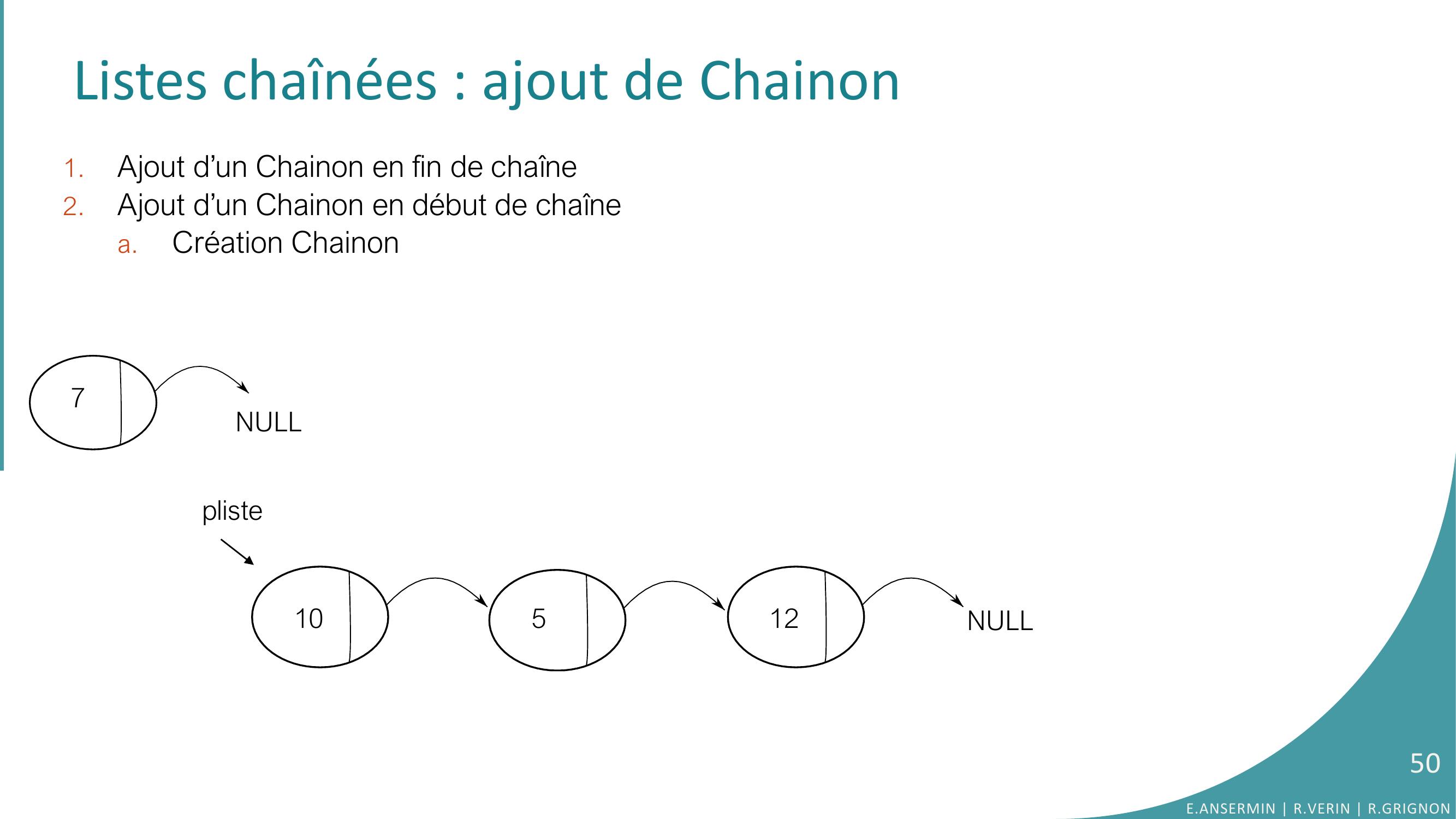
Page 50 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaînea.Création Chainonpliste10512NULLNULL750E.ANSERMIN R.VERIN R.GRIGNON
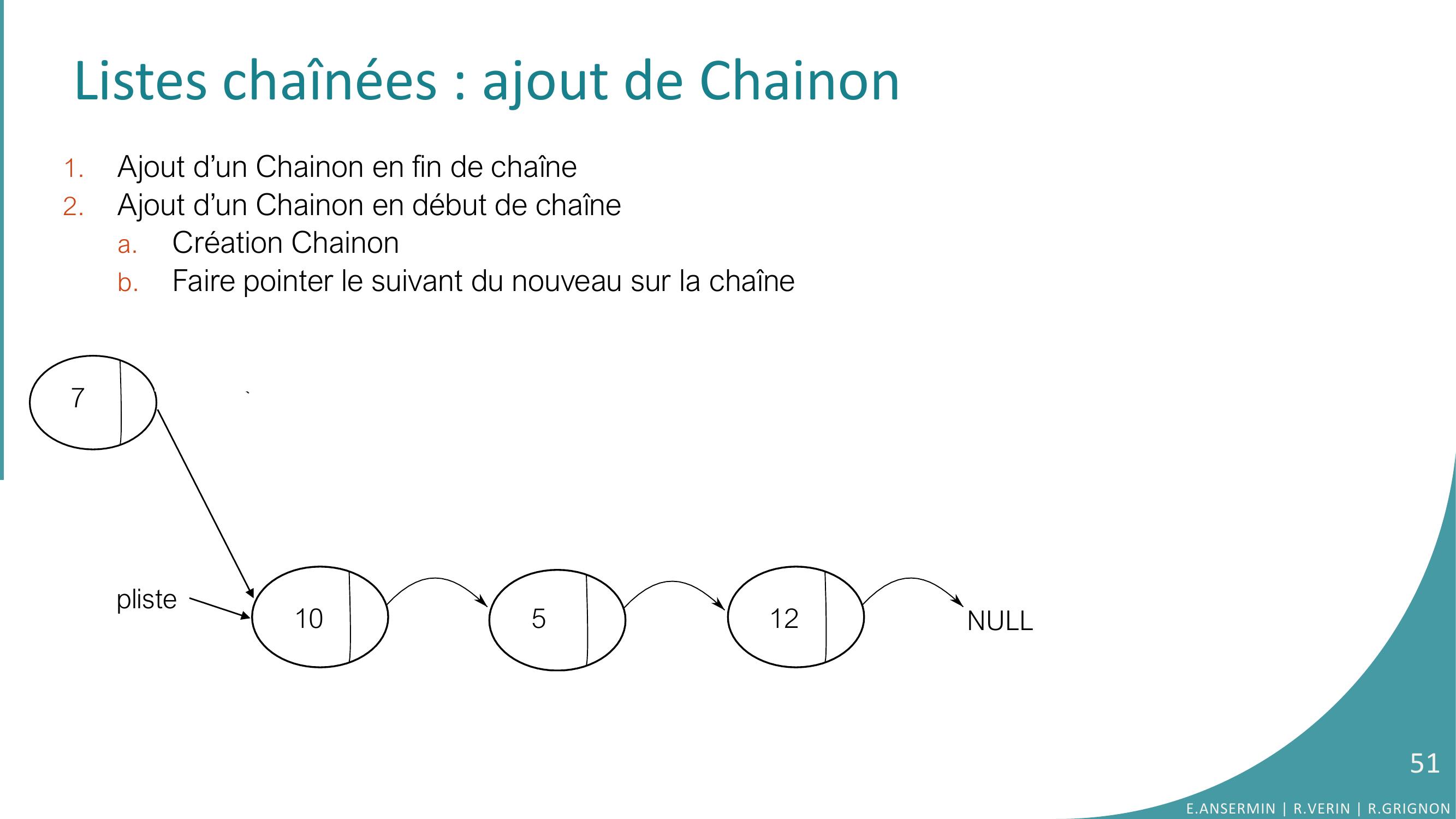
Page 51 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaînea.Création Chainonb.Faire pointer le suivant du nouveau sur la chaîne pliste10512NULL751E.ANSERMIN R.VERIN R.GRIGNON
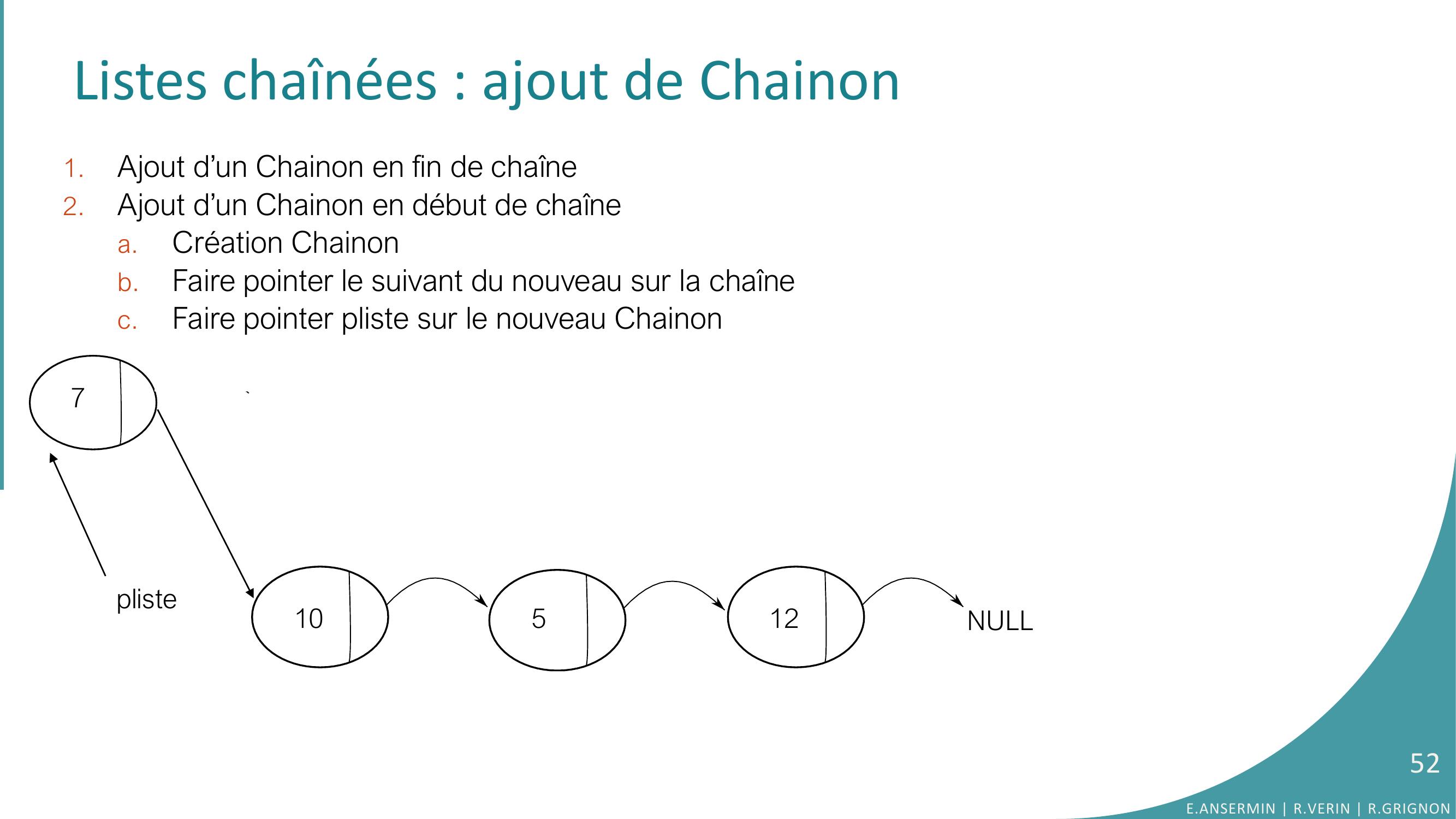
Page 52 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaînea.Création Chainonb.Faire pointer le suivant du nouveau sur la chaînec.Faire pointer pliste sur le nouveau Chainon 10512NULL7pliste52E.ANSERMIN R.VERIN R.GRIGNON
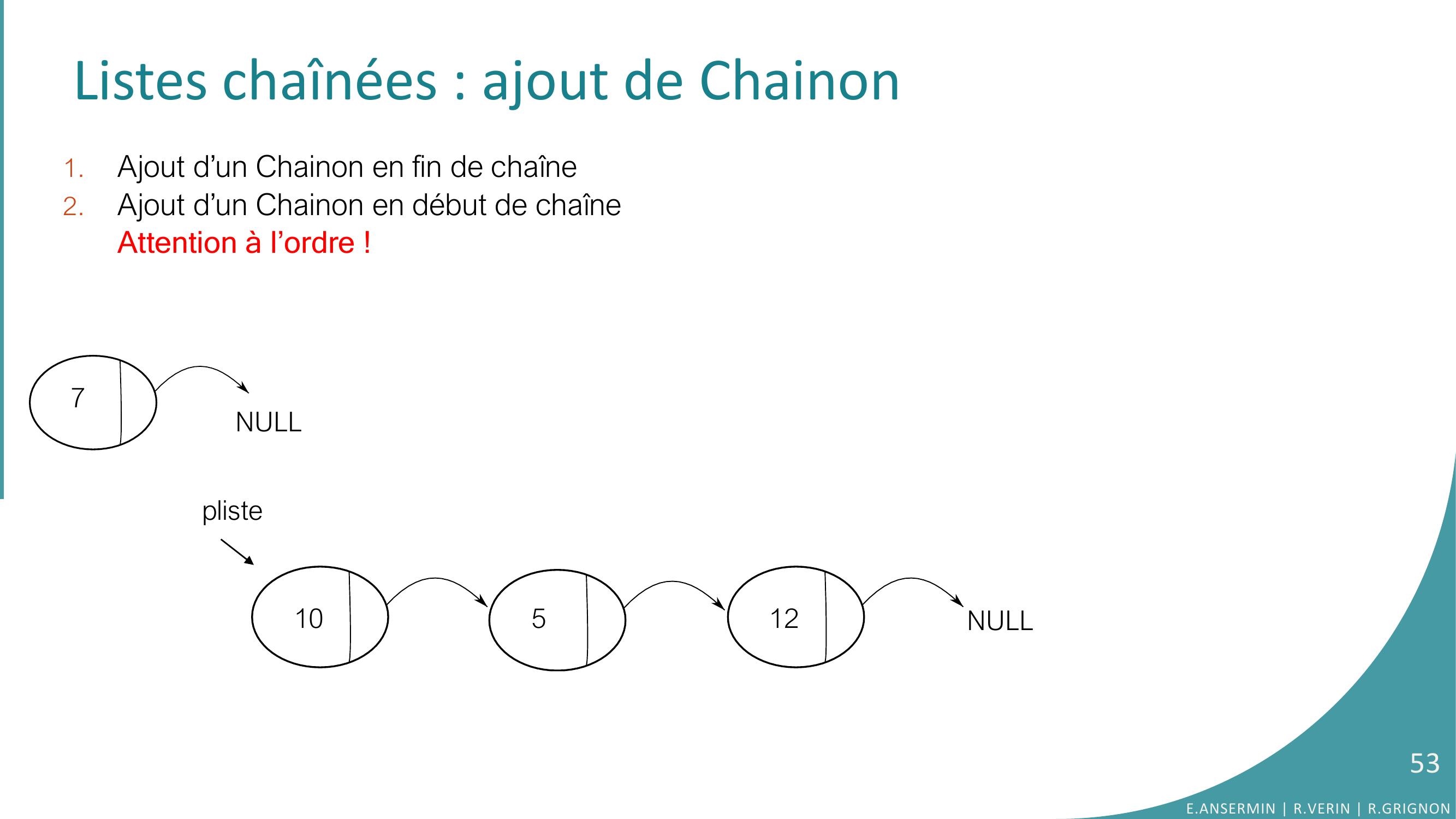
Page 53 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîneAttention à l’ordre !pliste10512NULLNULL753E.ANSERMIN R.VERIN R.GRIGNON
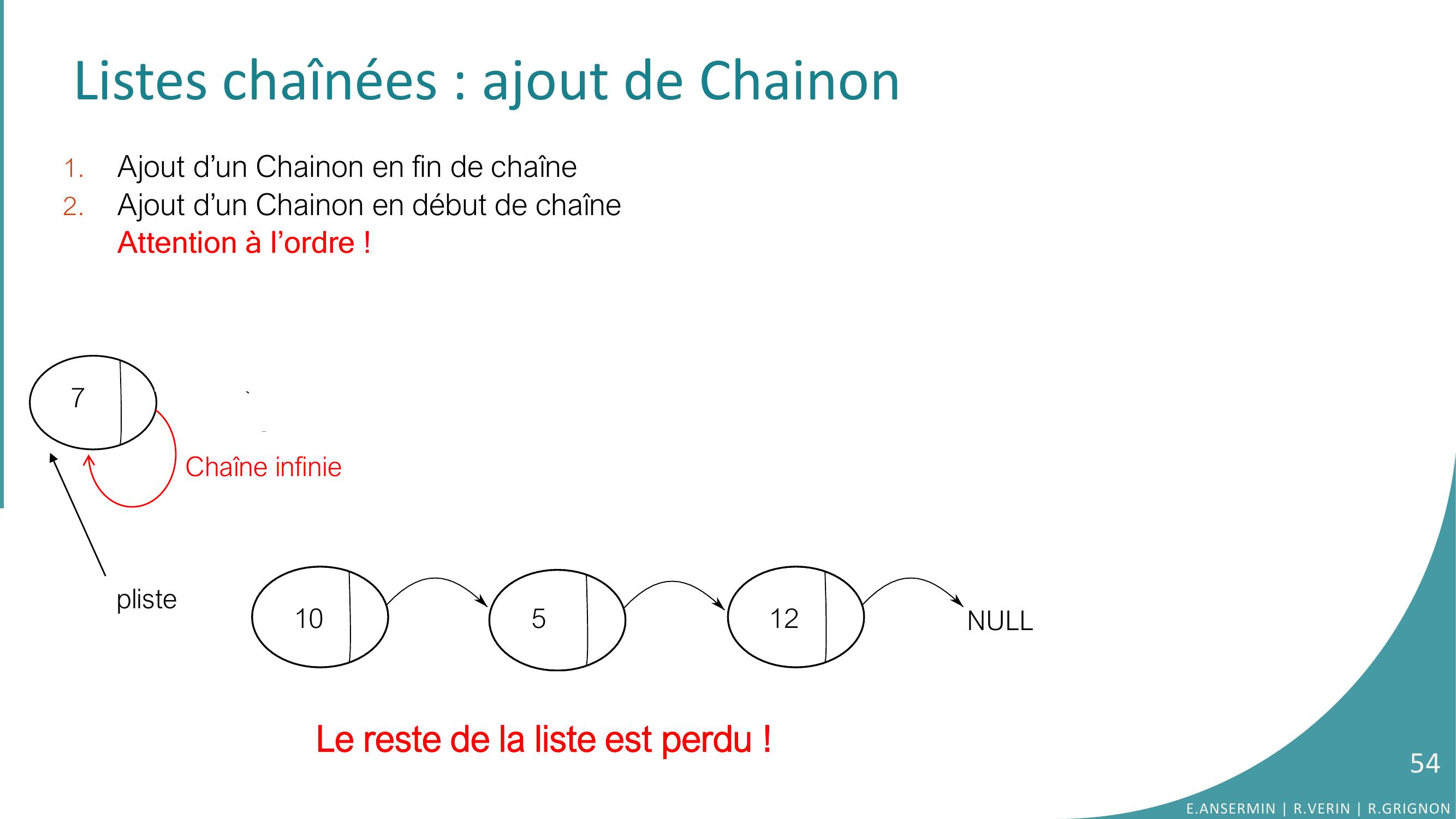
Page 54 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîneAttention à l’ordre !10512NULLNULL7Le reste de la liste est perdu !plisteChaîne infinie54E.ANSERMIN R.VERIN R.GRIGNON
Page 55 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaînea.Création Chainonb.Faire pointer le suivant du nouveau sur la chaînec.Faire pointer pliste sur le nouveau Chainon Fonction insertDebut pliste : pointeur sur Chainon : pointeur sur ChainonVARIABLEnouveau : pointeur sur ChainonDEBUTnouveau ←creationChainon // étape asuivantnouveau ← pliste// étape bpliste ← nouveau // étape c RETOURNER plisteFINLe pointeur sur le début de la liste ayant été modifié, il faut le retourner !!ComplexitétemporelleO155E.ANSERMIN R.VERIN R.GRIGNON
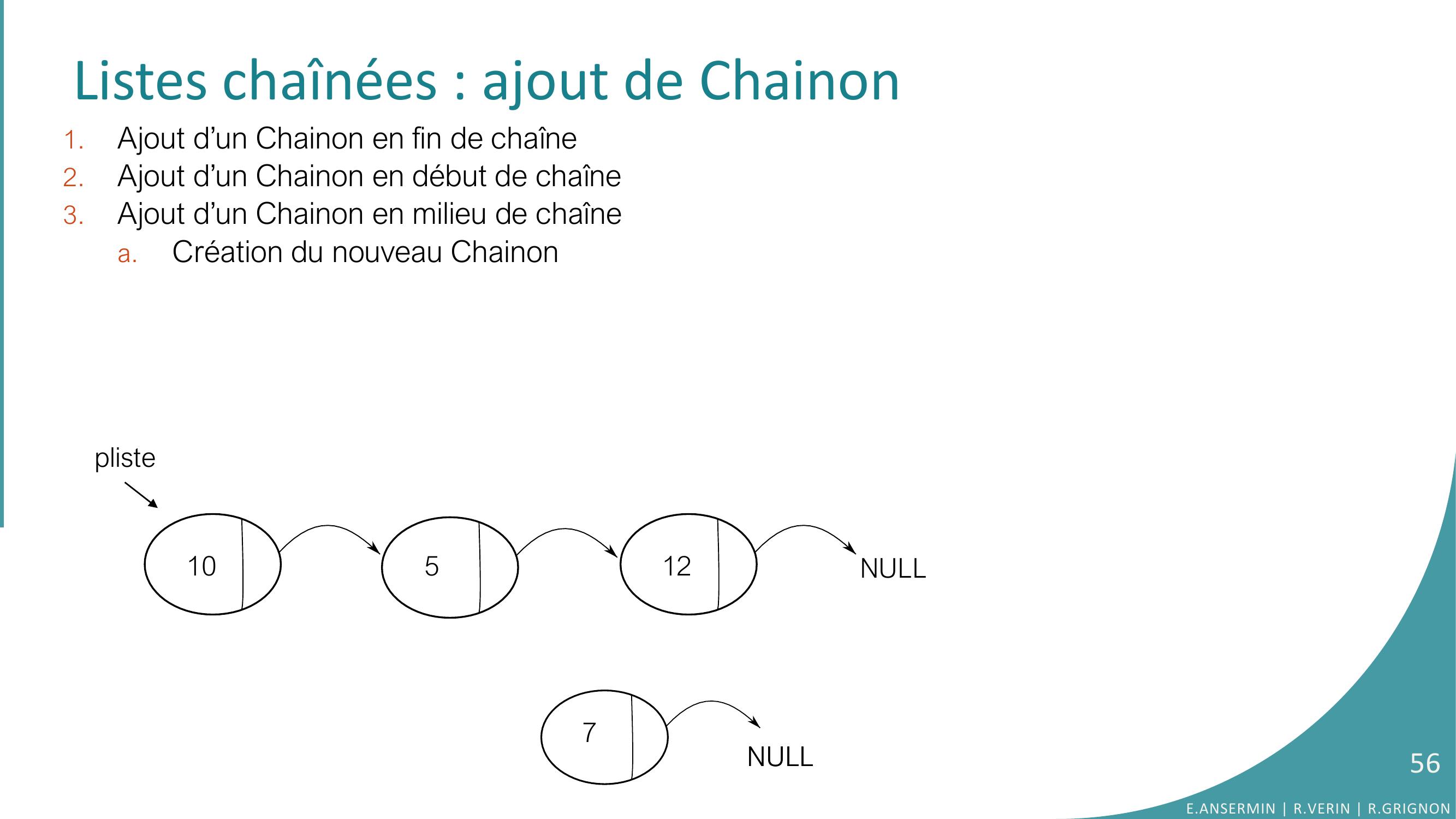
Page 56 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaînea.Création du nouveau Chainon10512NULLplisteNULLNULL756E.ANSERMIN R.VERIN R.GRIGNON
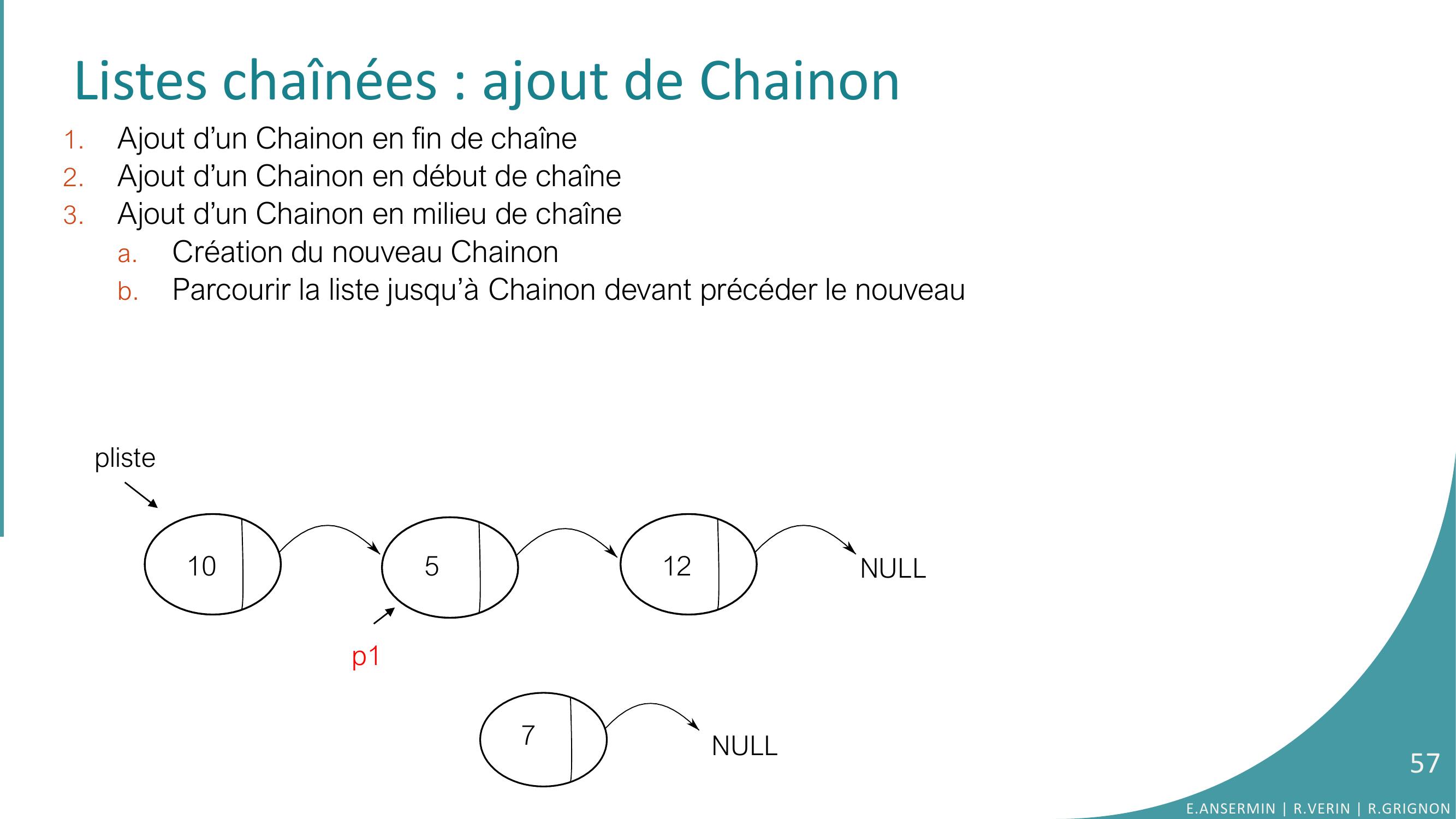
Page 57 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaînea.Création du nouveau Chainonb.Parcourir la liste jusqu’à Chainon devant précéder le nouveau10512NULLpliste7p1NULL57E.ANSERMIN R.VERIN R.GRIGNON
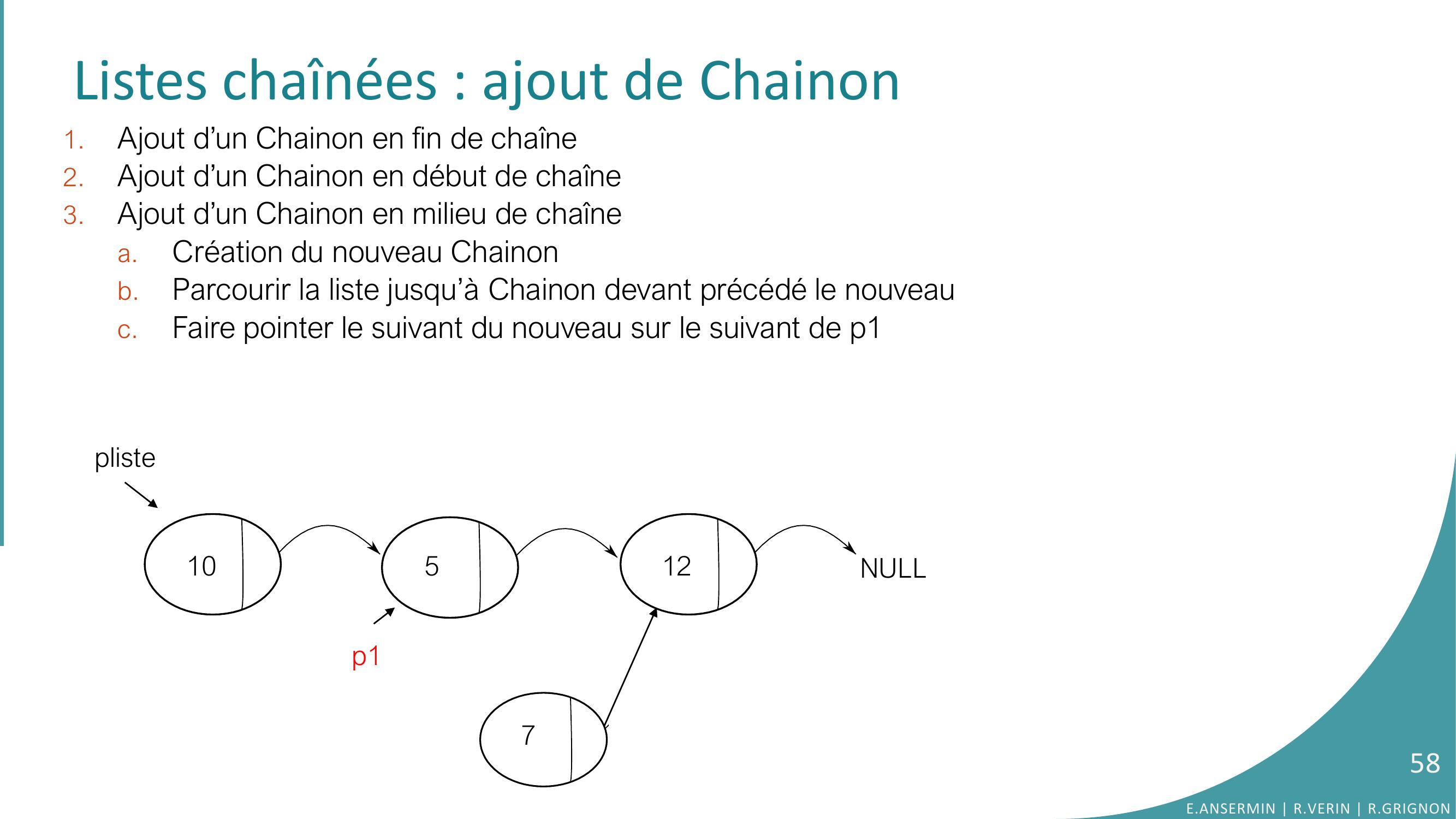
Page 58 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaînea.Création du nouveau Chainonb.Parcourir la liste jusqu’à Chainon devant précédé le nouveauc.Faire pointer le suivant du nouveau sur le suivant de p110512NULLpliste7p158E.ANSERMIN R.VERIN R.GRIGNON
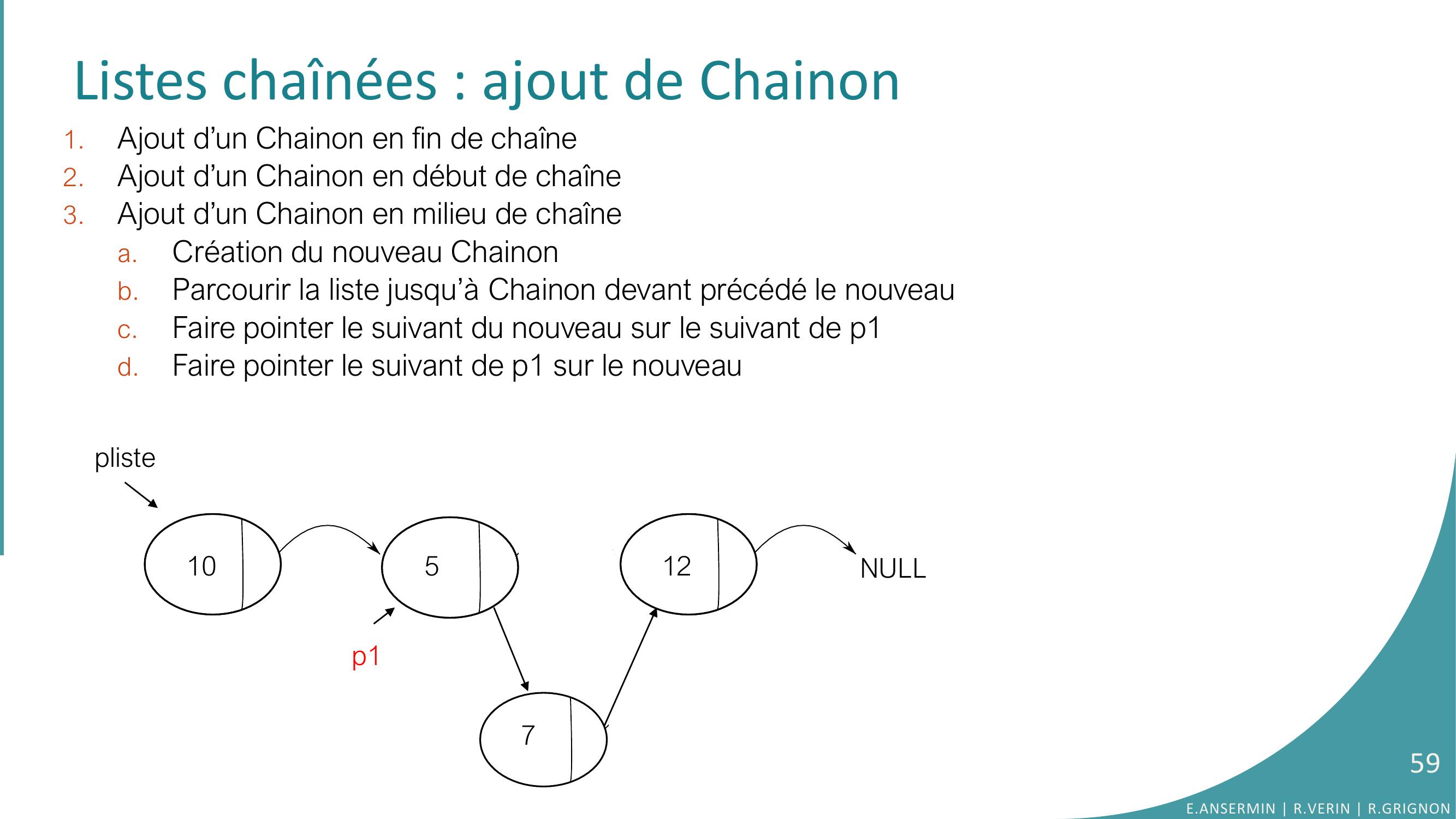
Page 59 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaînea.Création du nouveau Chainonb.Parcourir la liste jusqu’à Chainon devant précédé le nouveauc.Faire pointer le suivant du nouveau sur le suivant de p1d.Faire pointer le suivant de p1 sur le nouveau 10512NULLpliste7p159E.ANSERMIN R.VERIN R.GRIGNON
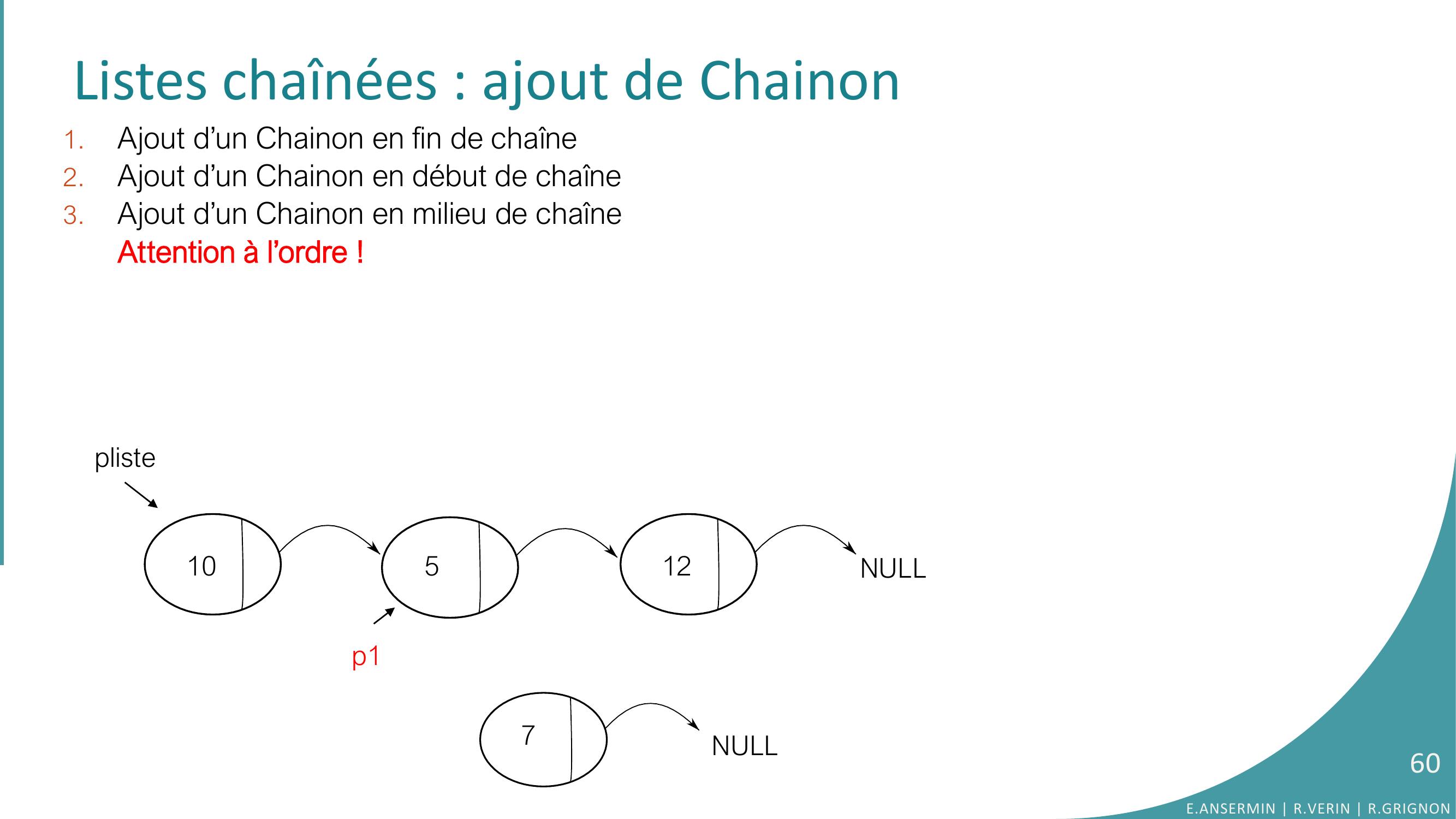
Page 60 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaîneAttention à l’ordre !10512NULLpliste7p1NULL60E.ANSERMIN R.VERIN R.GRIGNON
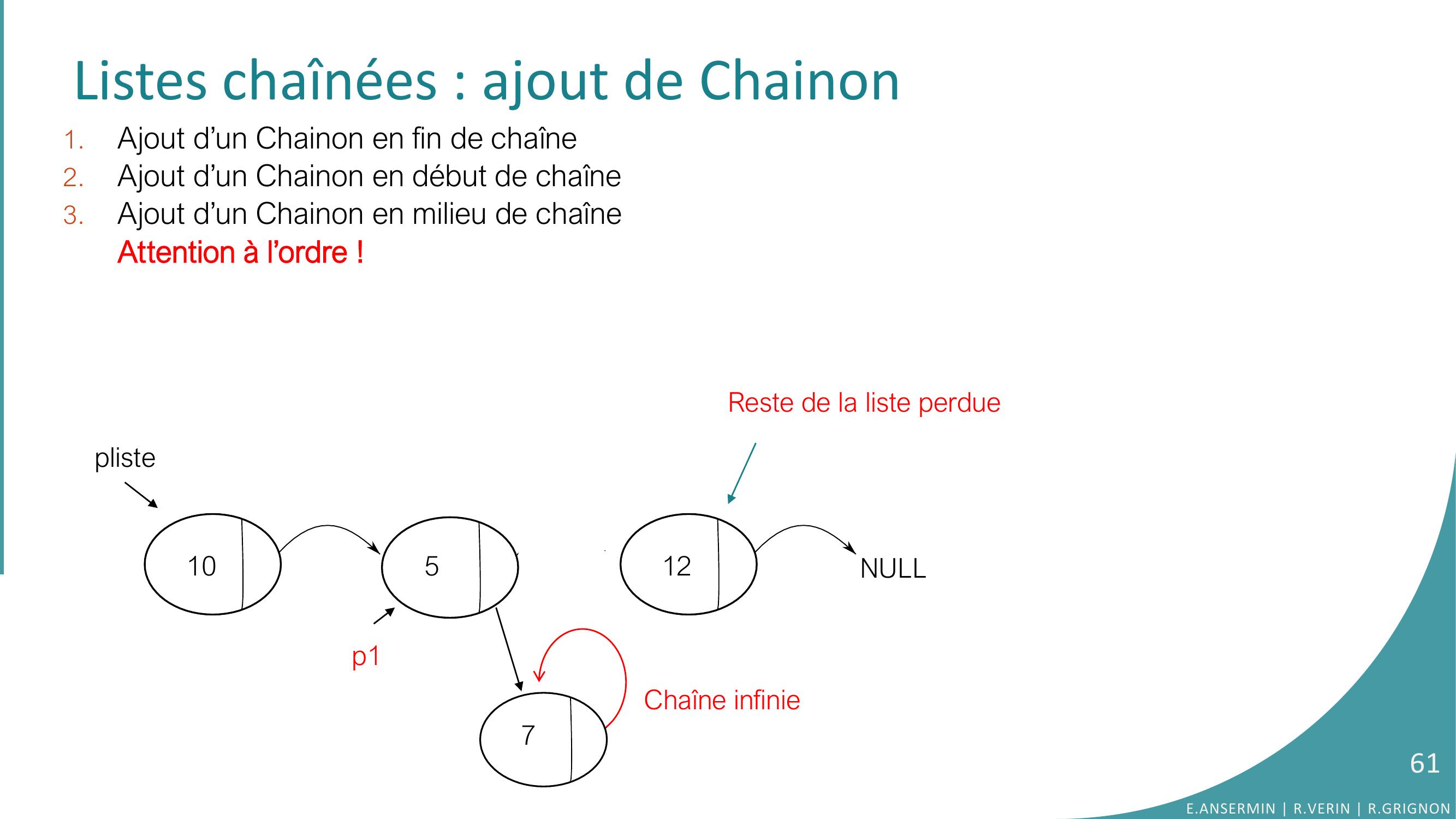
Page 61 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaîneAttention à l’ordre !10512NULLpliste7p1NULLReste de la liste perdueChaîne infinie61E.ANSERMIN R.VERIN R.GRIGNON
Page 62 : Listes chaînées : ajout de Chainon 1.Ajout d’un Chainon en fin de chaîne2.Ajout d’un Chainon en début de chaîne3.Ajout d’un Chainon en milieu de chaînea.Parcourir la liste jusqu’à Chainon devant précéder le nouveaub.Création du nouveau Chainonc.Faire pointer le suivant du nouveau sur le suivant de p1d.Faire pointer le suivant de p1 sur le nouveau 62E.ANSERMIN R.VERIN R.GRIGNON
Page 63 : Listes chaînées : ajout de Chainon a.Parcourir la liste jusqu’à Chainon devant précéder le nouveaub.Création du nouveau Chainonc.Faire pointer le suivant du nouveau sur le suivant de p1d.Faire pointer le suivant de p1 sur le nouveau fonction insertPos pliste : pointeur sur Chainon, pos: entier pointeur sur ChainonVARIABLEnouveau, p1 : pointeurs sur Chainoni: entier DEBUTSI pos EST EGAL A 0 OU pliste EST EGAL A NULL ALORS // insertion à l’indice 0pliste ←insertDebutplisteSINONp1 ← plistePOUR i DE 0 à pos FAIRE// étape aSI p1 EST EGAL A NULL ALORSERREUR// pos nombre de chainonsSINONp1 ←suivantp1FIN SI FIN POURnouveau ← creationChainon // étape bsuivantnouveau ← suivantp1// étape csuivantp1 ← nouveau // étape dFIN SIRETOURNER plisteFIN63E.ANSERMIN R.VERIN R.GRIGNON
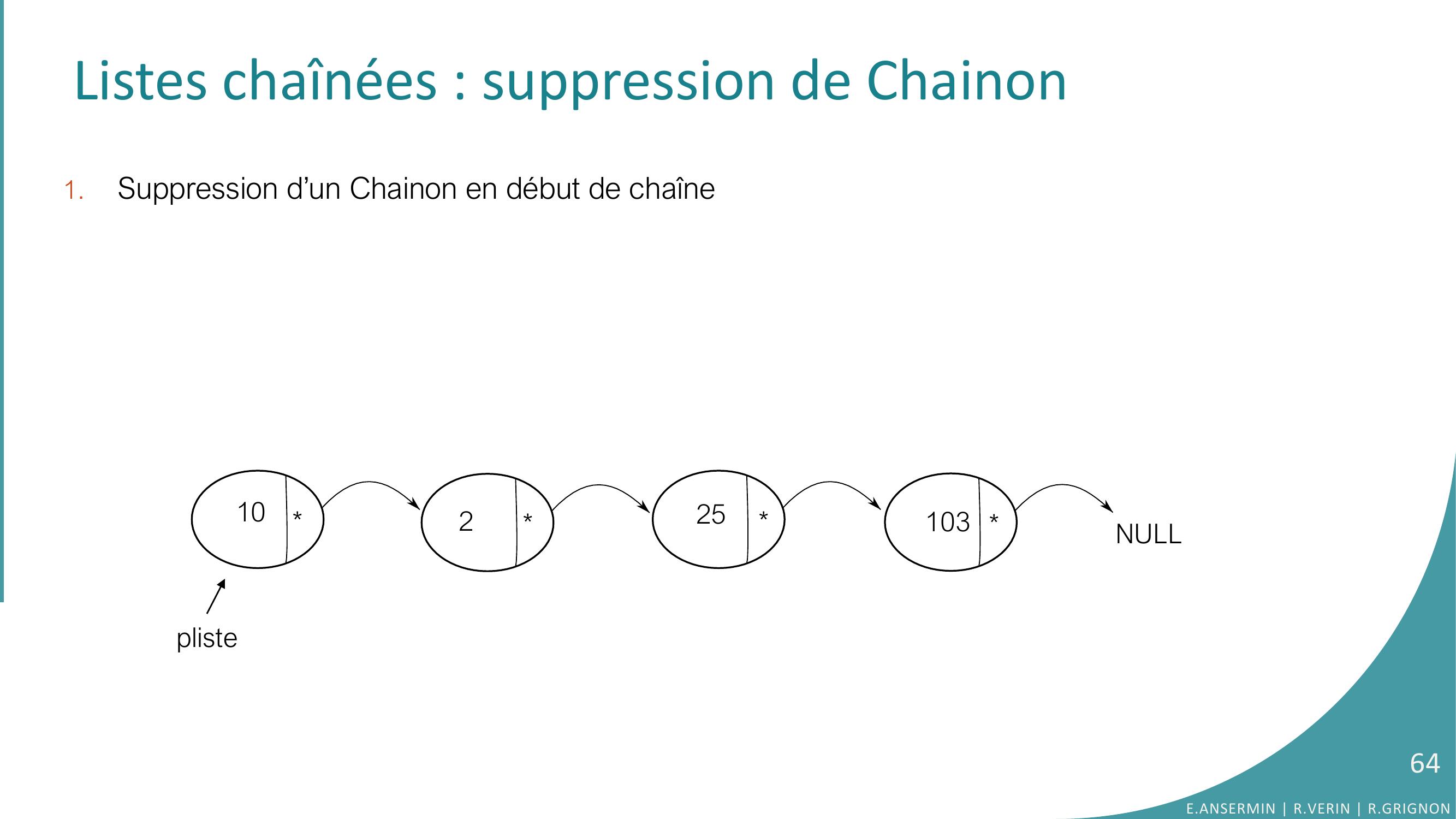
Page 64 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaîne10225103NULLpliste64E.ANSERMIN R.VERIN R.GRIGNON
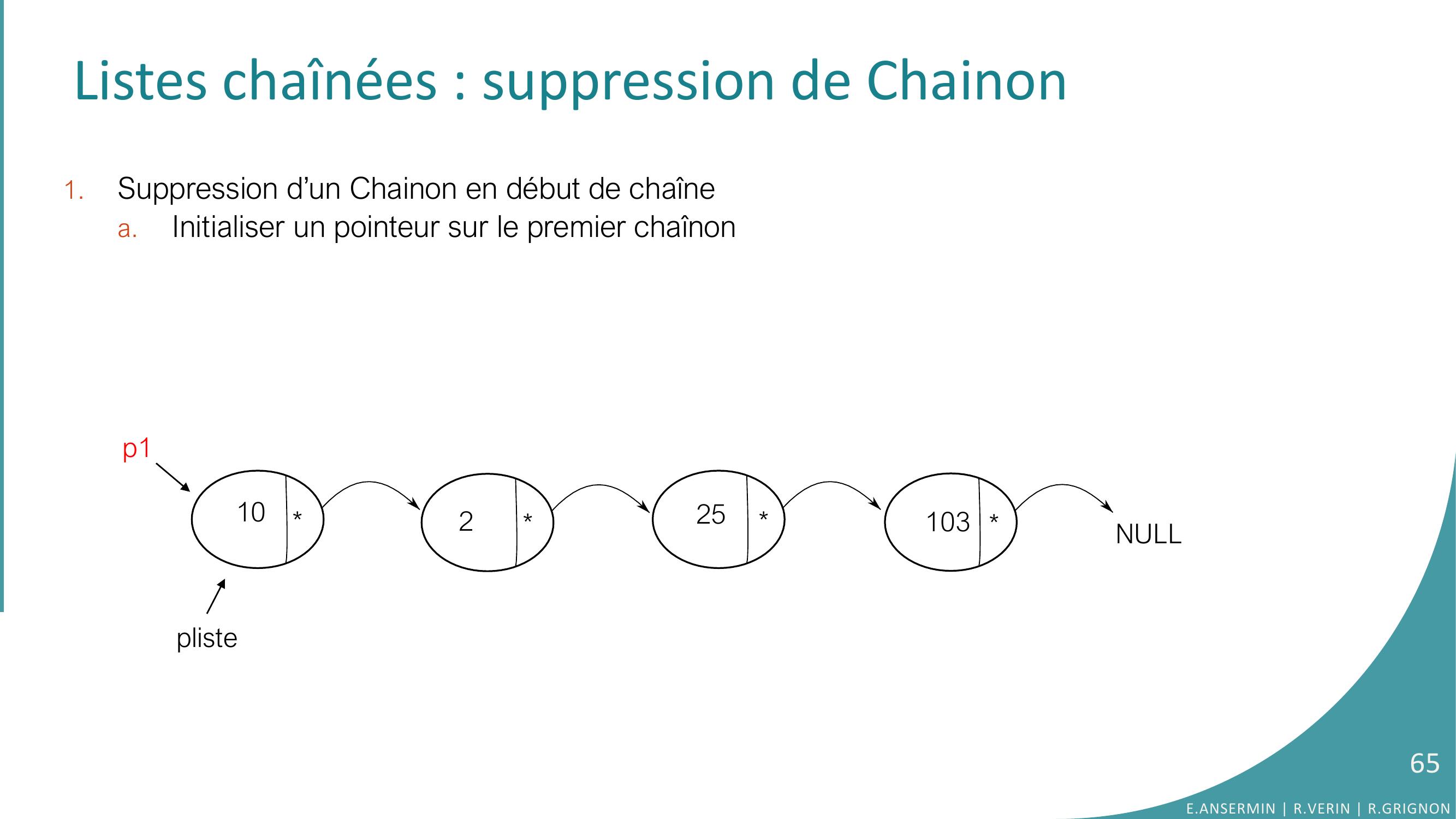
Page 65 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaînea.Initialiser un pointeur sur le premier chaînon10225103NULLplistep165E.ANSERMIN R.VERIN R.GRIGNON
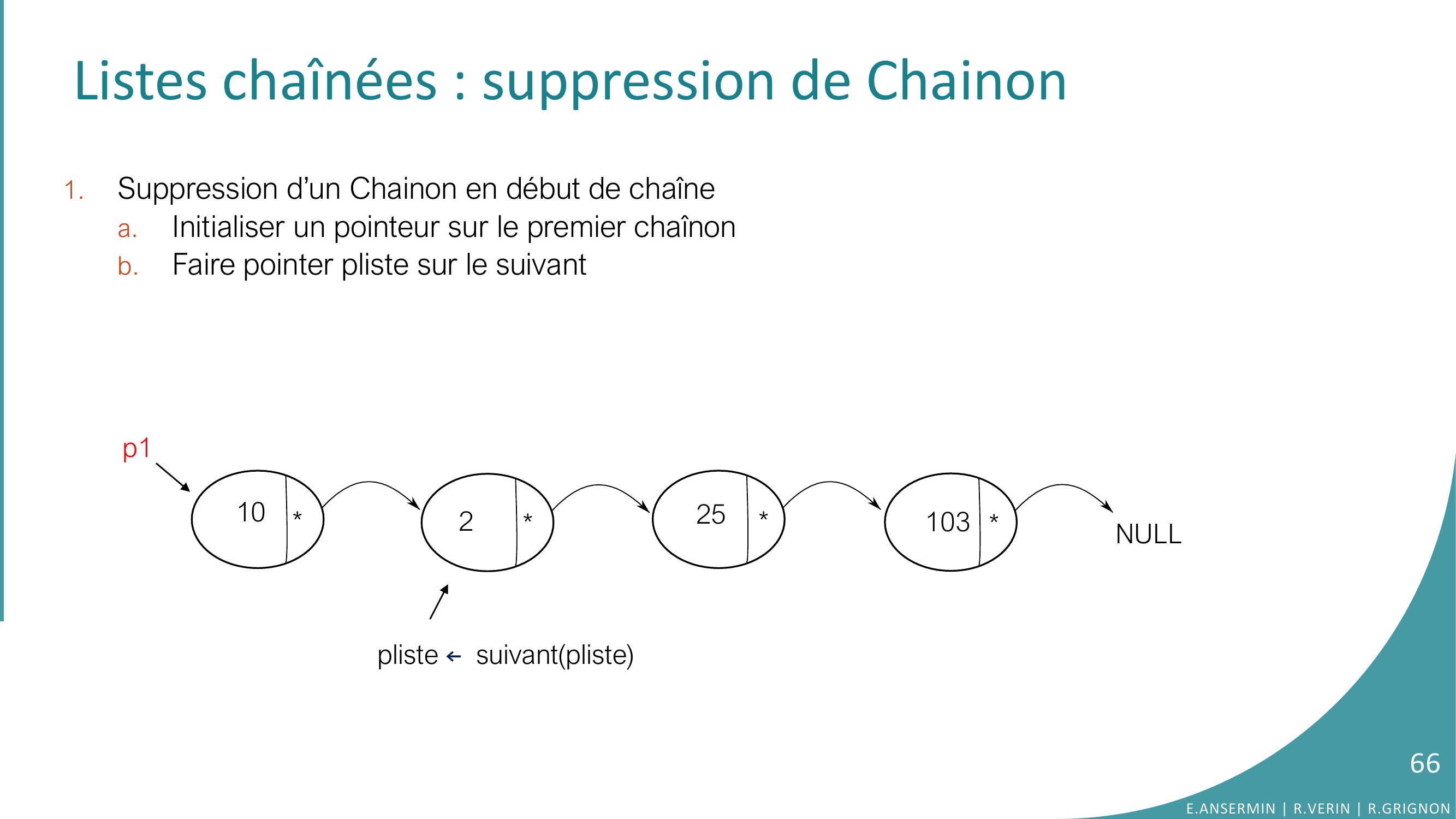
Page 66 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaînea.Initialiser un pointeur sur le premier chaînonb.Faire pointer pliste sur le suivant10225103NULLpliste ← suivantplistep166E.ANSERMIN R.VERIN R.GRIGNON
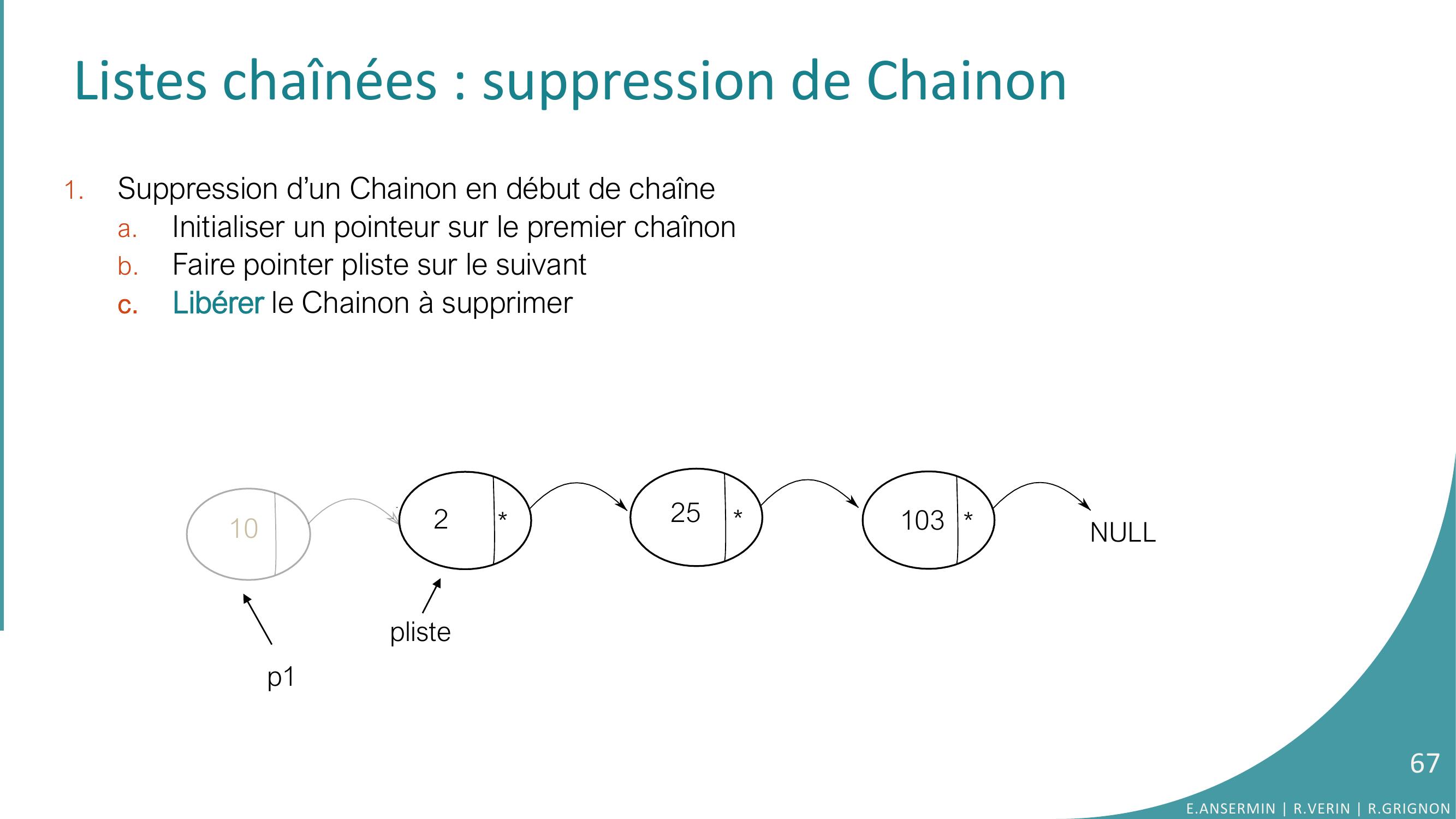
Page 67 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaînea.Initialiser un pointeur sur le premier chaînonb.Faire pointer pliste sur le suivantc.Libérer le Chainon à supprimer 10225103NULLplistep110p167E.ANSERMIN R.VERIN R.GRIGNON
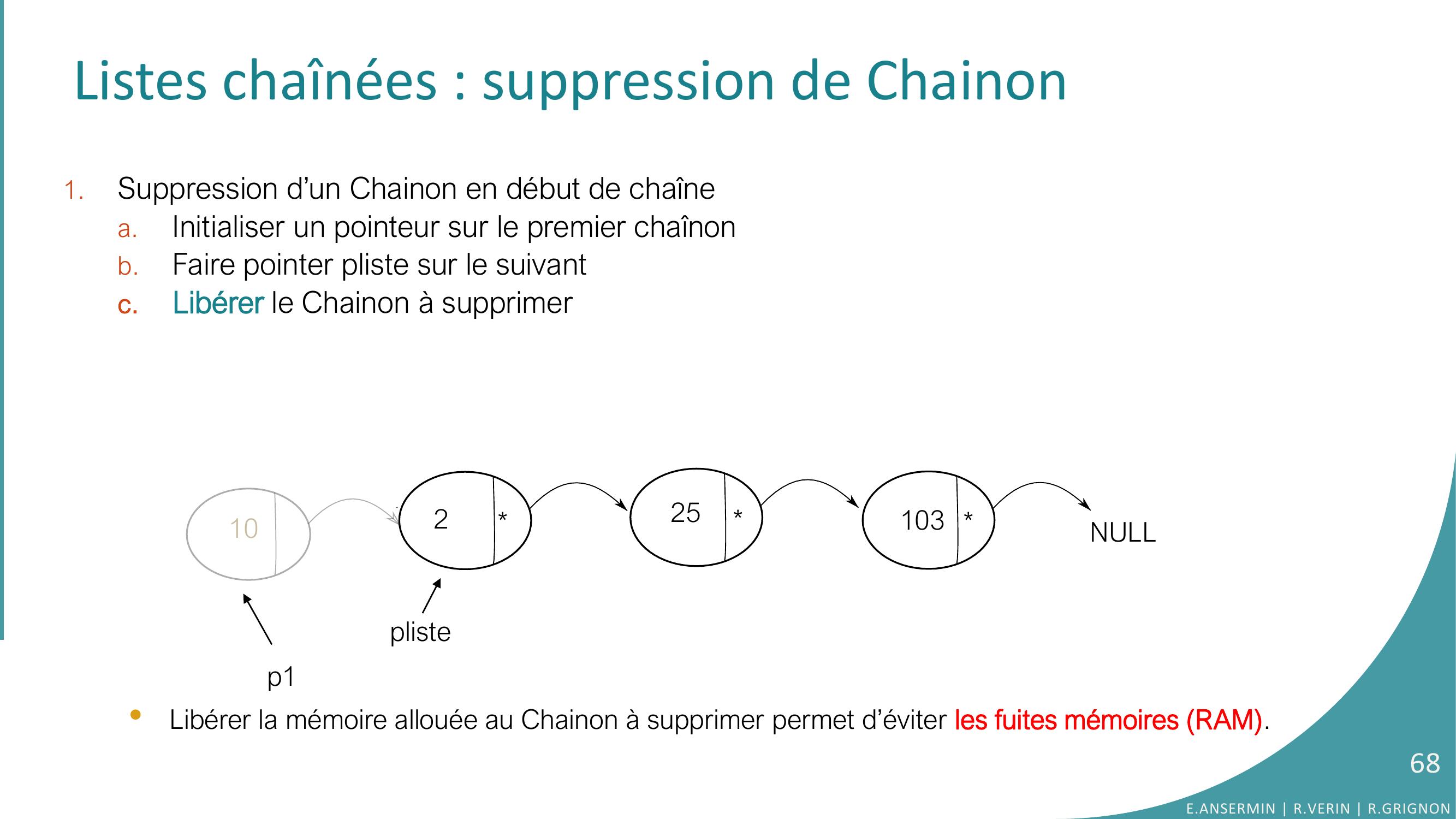
Page 68 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaînea.Initialiser un pointeur sur le premier chaînonb.Faire pointer pliste sur le suivantc.Libérer le Chainon à supprimer 10225103NULLplistep110p1•Libérer la mémoire allouée au Chainon à supprimer permet d’éviter les fuites mémoires RAM. 68E.ANSERMIN R.VERIN R.GRIGNON
Page 69 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaînea.Initialiser un pointeur sur le premier chaînonb.Faire pointer pliste sur le suivantc.Libérer le Chainon à supprimer Chainon suppDebutChainon plisteChainon p1;// on vérifie si la liste contient au moins un Chainonifpliste==NULLexit1;p1=pliste; // étape apliste=p1-suivant; // étape bfreep1; // étape c : ‘libérerp1’ en pseudo-codereturn pliste;69E.ANSERMIN R.VERIN R.GRIGNON
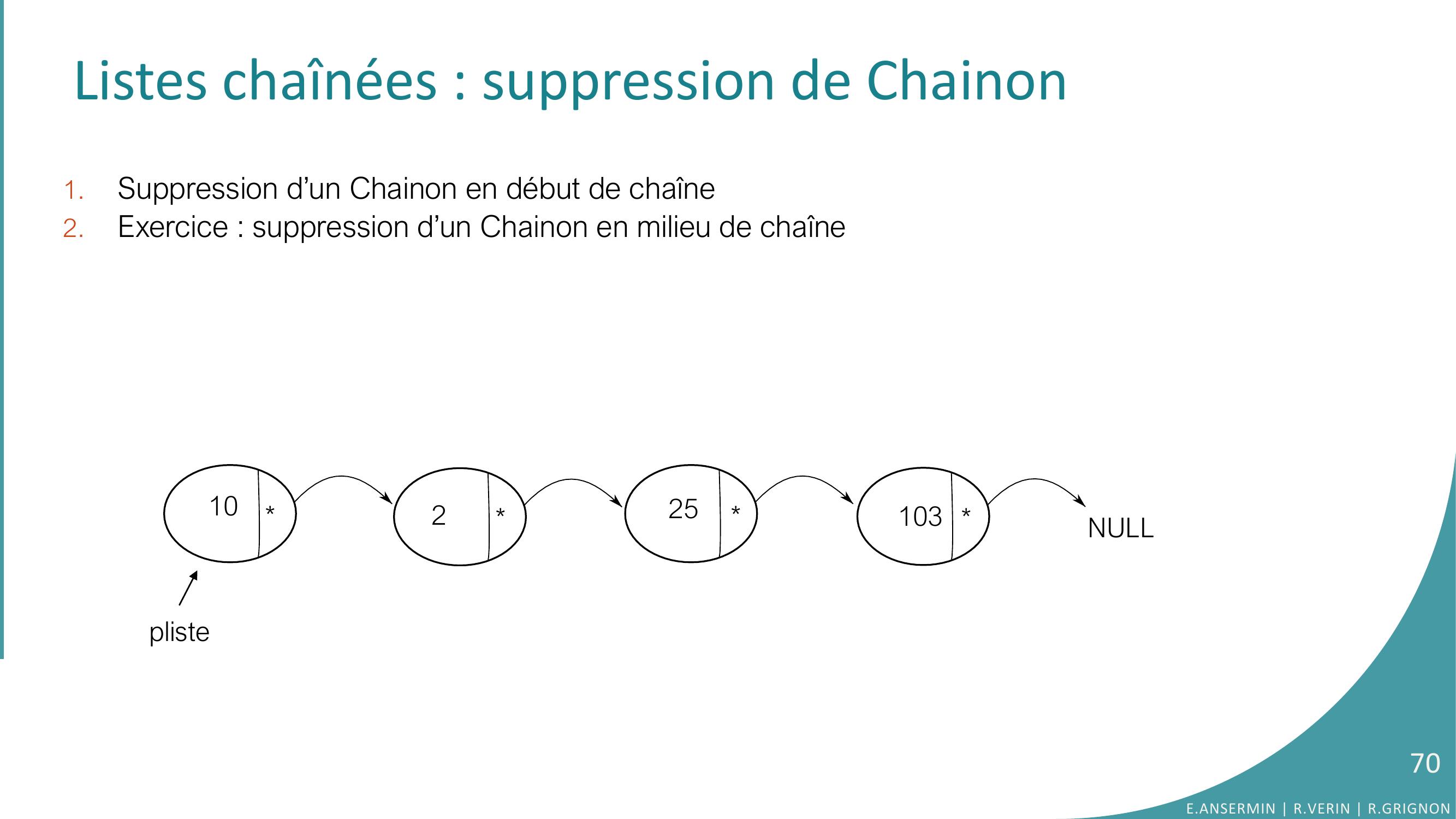
Page 70 : Listes chaînées : suppression de Chainon1.Suppression d’un Chainon en début de chaîne2.Exercice : suppression d’un Chainon en milieu de chaîne10225103NULLpliste70E.ANSERMIN R.VERIN R.GRIGNON
Page 71 : III. Listes doublement chaînées71E.ANSERMIN R.VERIN R.GRIGNON
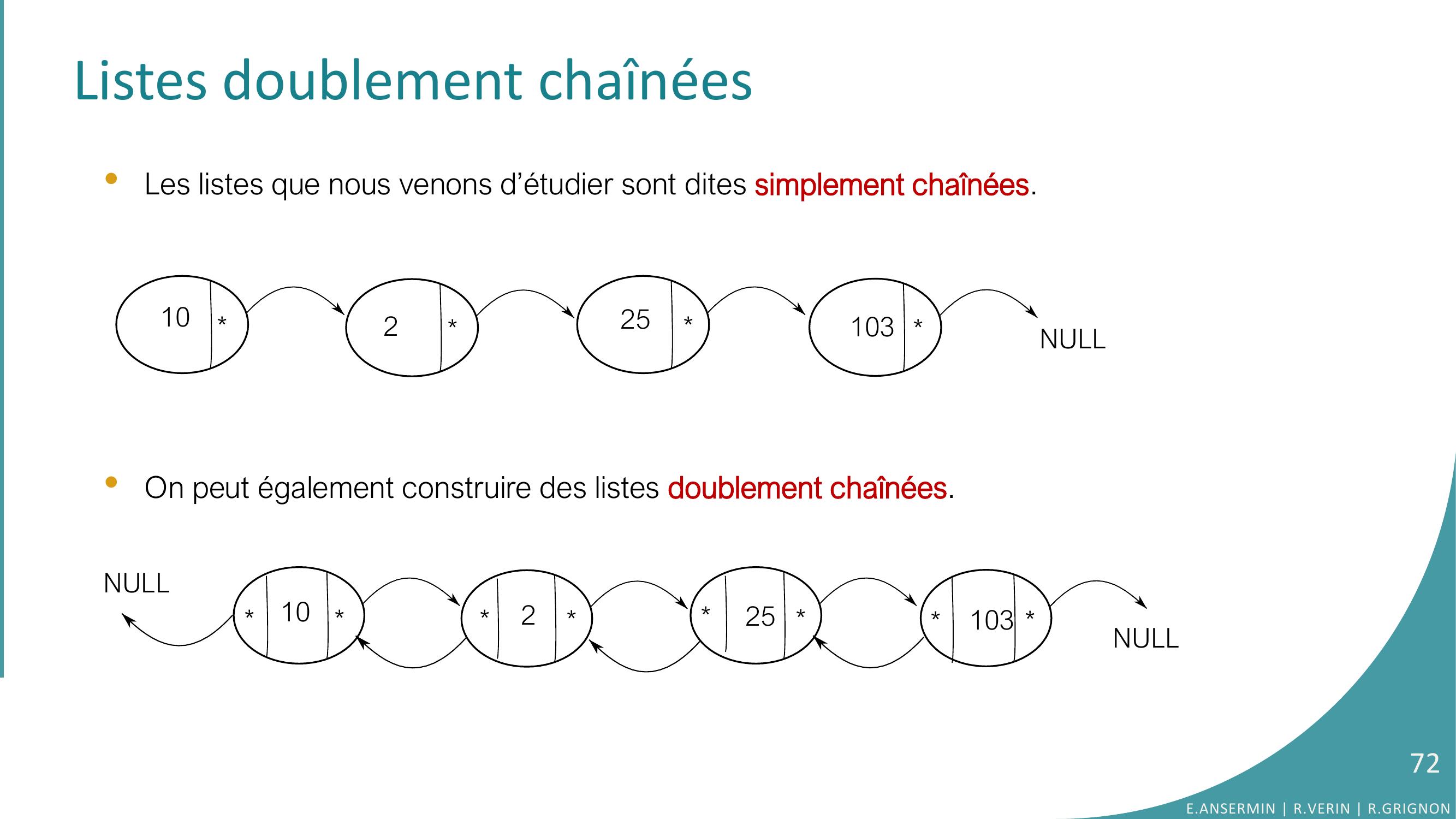
Page 72 : Listes doublement chaînées•Les listes que nous venons d’étudier sont dites simplement chaînées.•On peut également construire des listes doublement chaînées.10225103NULL10225103NULLNULL72E.ANSERMIN R.VERIN R.GRIGNON
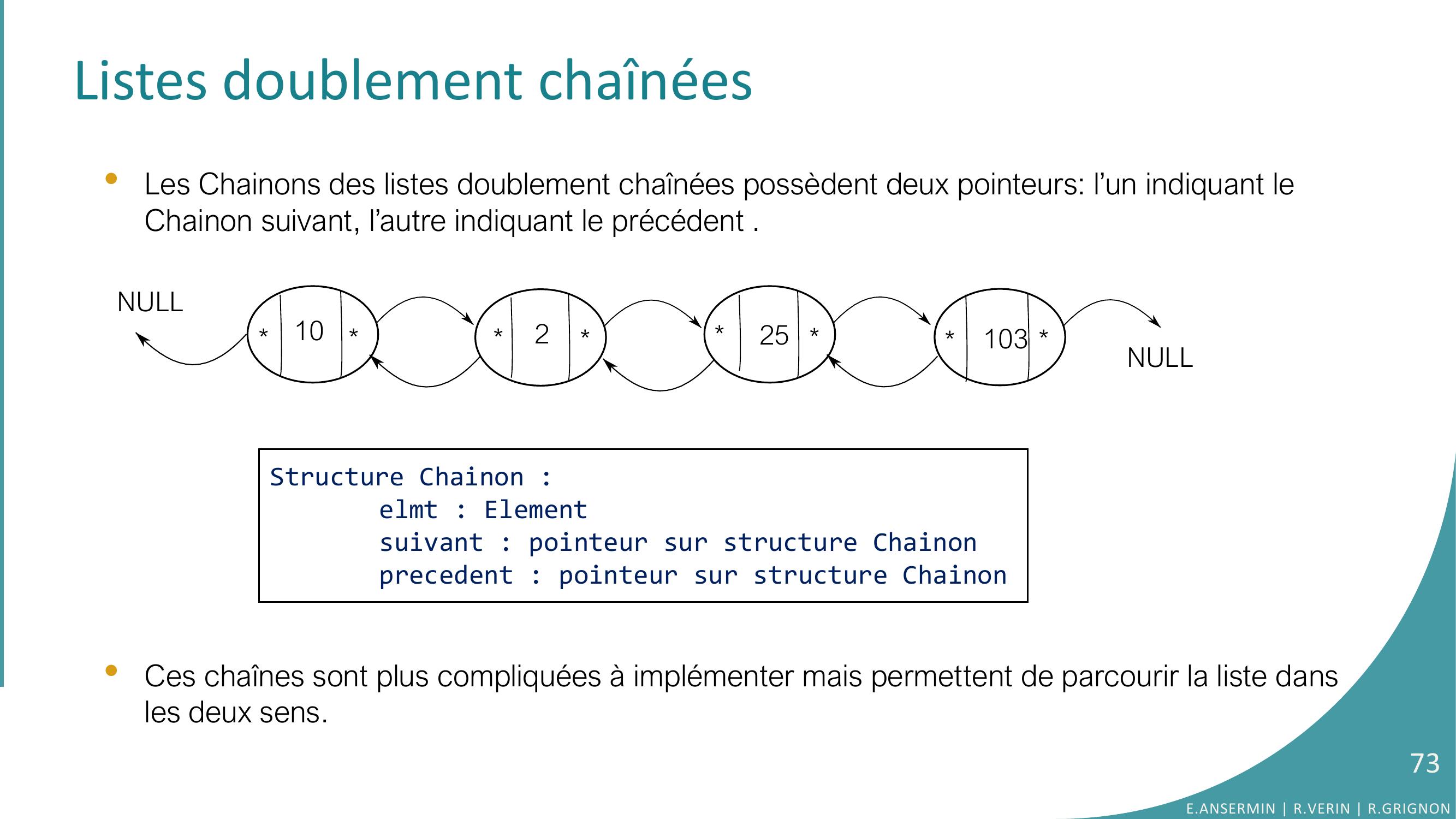
Page 73 : Listes doublement chaînées•Les Chainons des listes doublement chaînées possèdent deux pointeurs: l’un indiquant le Chainon suivant, l’autre indiquant le précédent .•Ces chaînes sont plus compliquées à implémenter mais permettent de parcourir la liste dans les deux sens. 10225103NULLNULLStructure Chainon :elmt : Elementsuivant : pointeur sur structure Chainonprecedent : pointeur sur structure Chainon73E.ANSERMIN R.VERIN R.GRIGNON
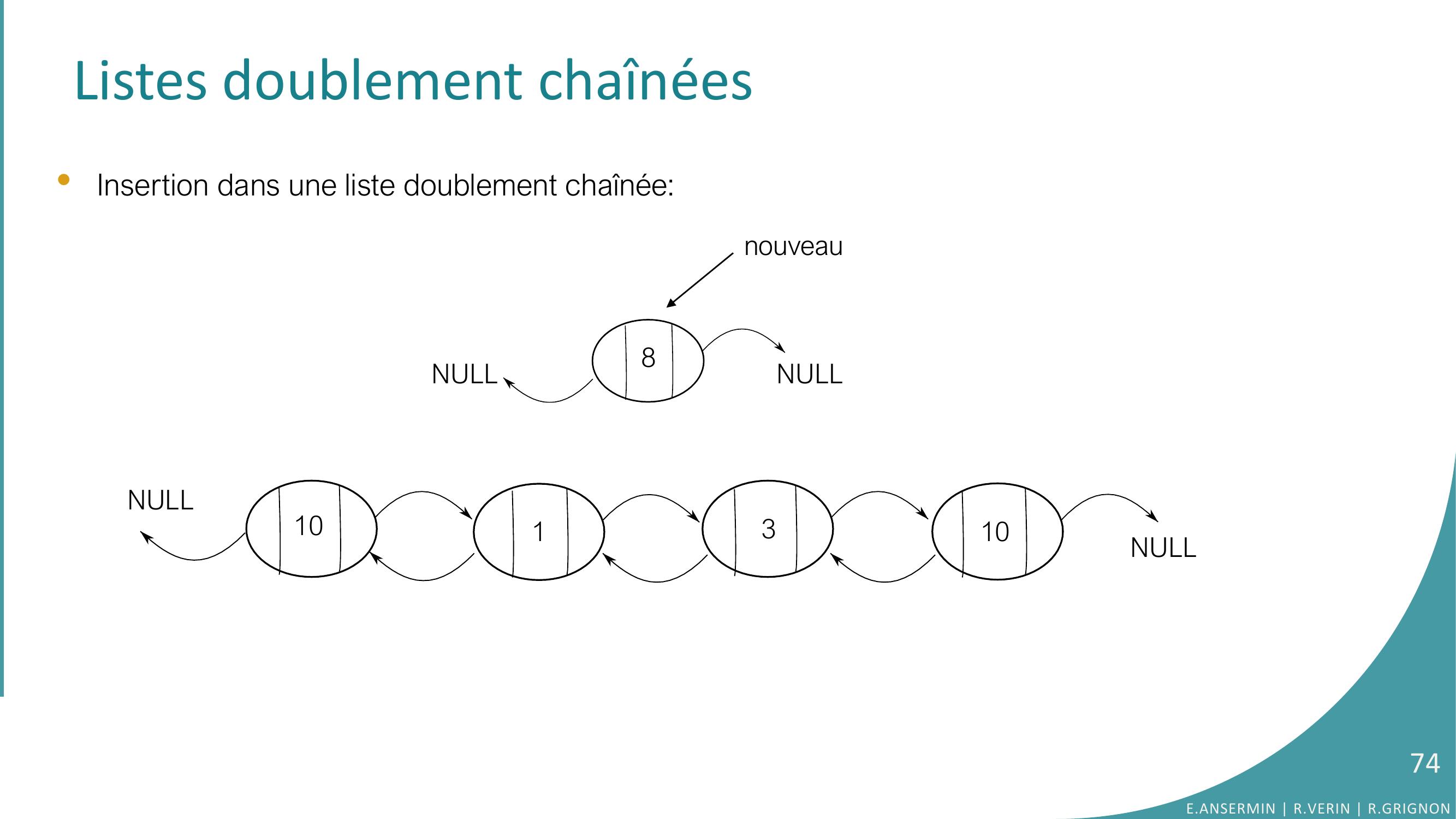
Page 74 : Listes doublement chaînées•Insertion dans une liste doublement chaînée: NULLNULL1010138NULLNULLnouveau74E.ANSERMIN R.VERIN R.GRIGNON
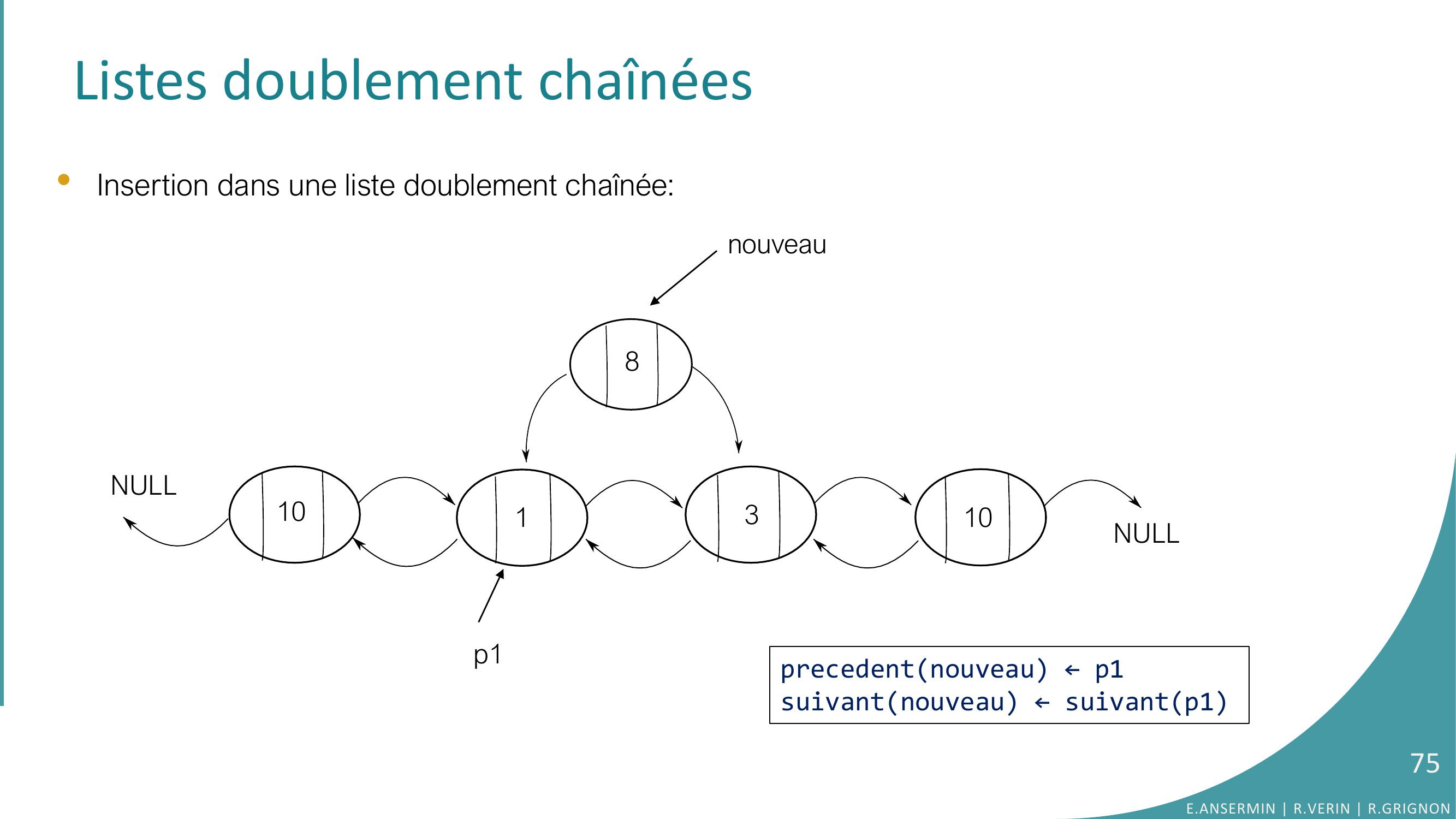
Page 75 : Listes doublement chaînées•Insertion dans une liste doublement chaînée: NULLNULL1010138p1precedentnouveau ←p1suivantnouveau ←suivantp1nouveau75E.ANSERMIN R.VERIN R.GRIGNON
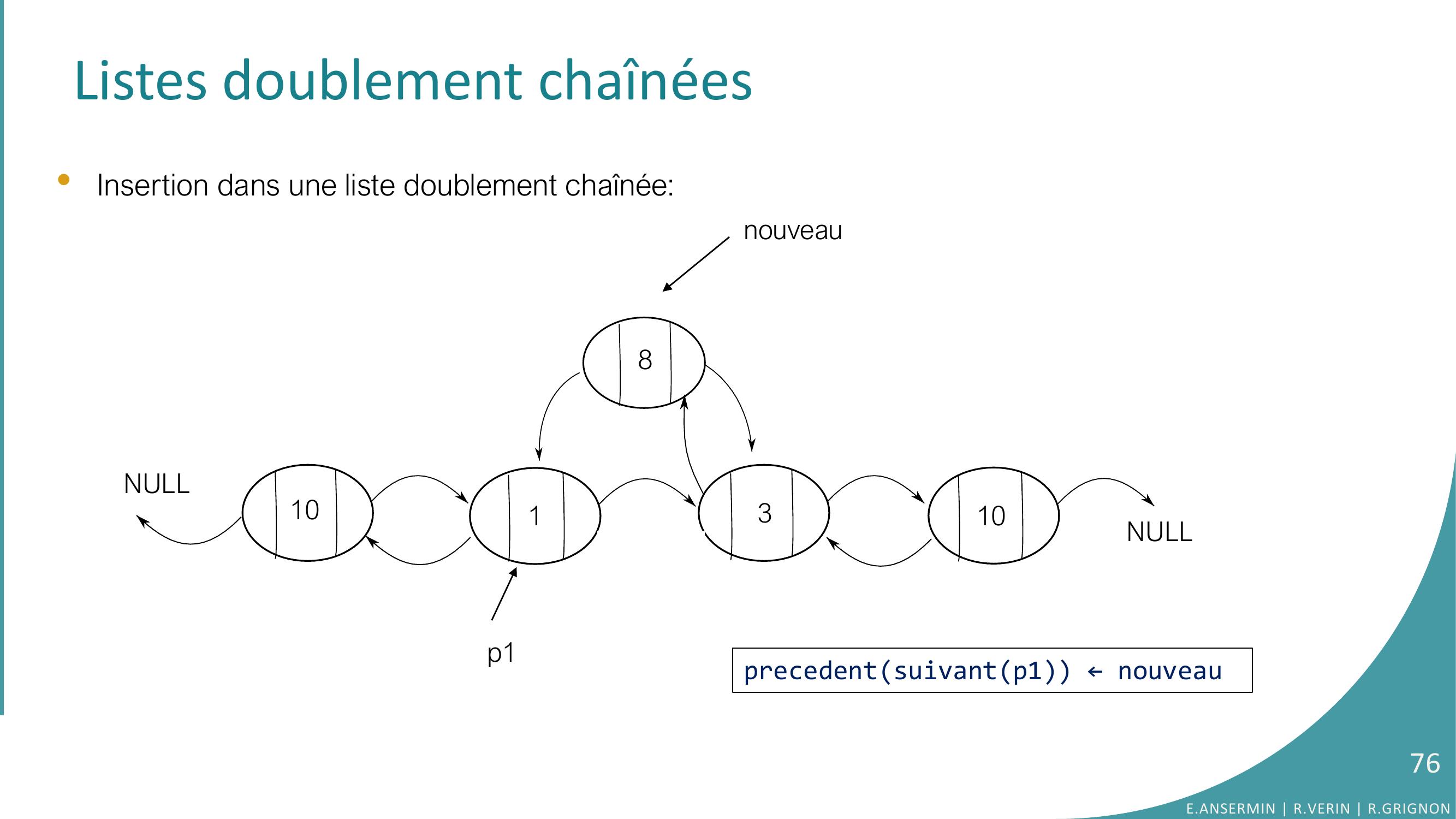
Page 76 : Listes doublement chaînées•Insertion dans une liste doublement chaînée: NULLNULL1010138p1nouveauprecedentsuivantp1 ← nouveau76E.ANSERMIN R.VERIN R.GRIGNON
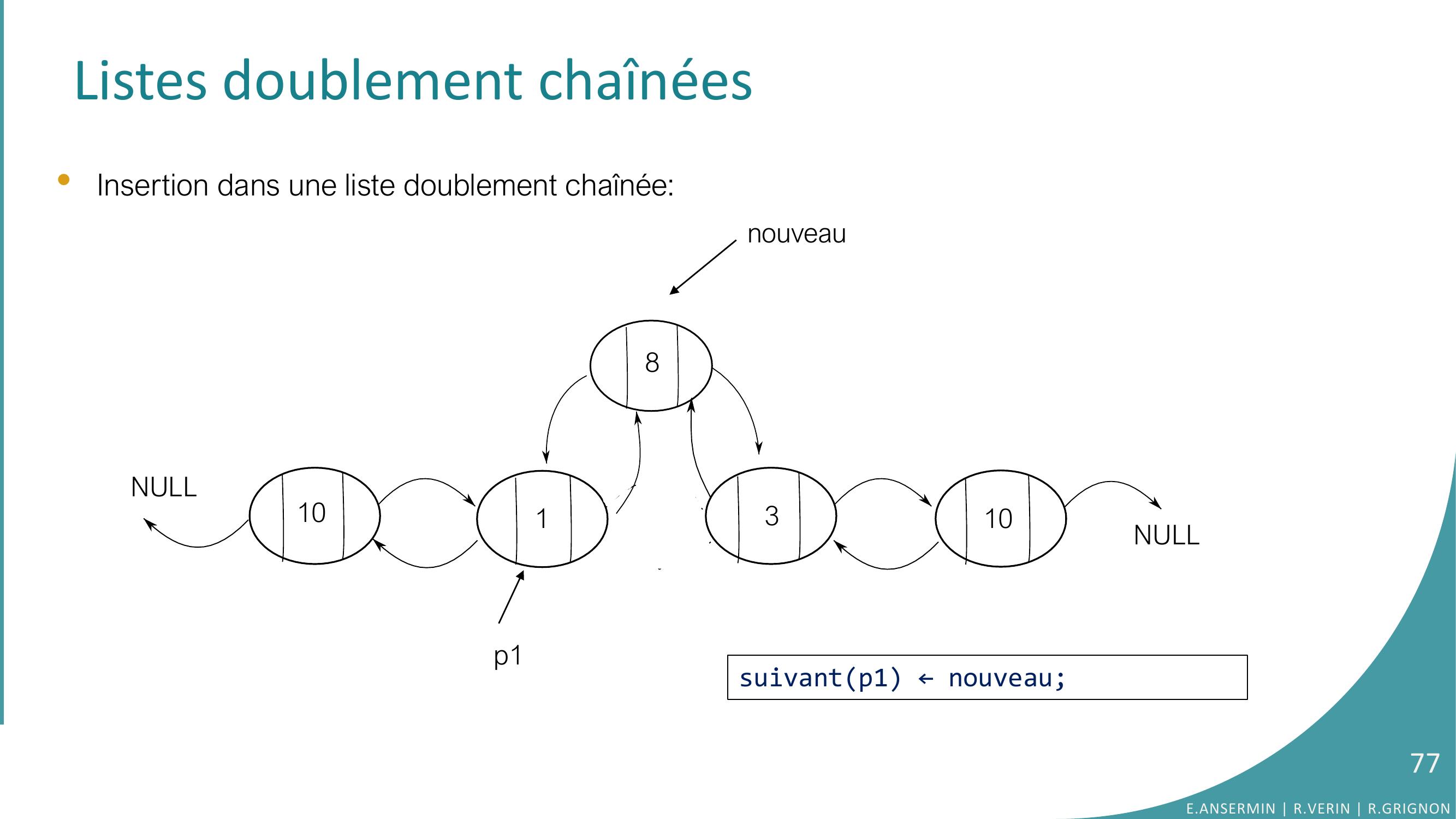
Page 77 : Listes doublement chaînées•Insertion dans une liste doublement chaînée: NULLNULL1010138p1nouveausuivantp1 ← nouveau;77E.ANSERMIN R.VERIN R.GRIGNON
Page 78 : IV. Listes chaînées ou tableaux ? 78E.ANSERMIN R.VERIN R.GRIGNON
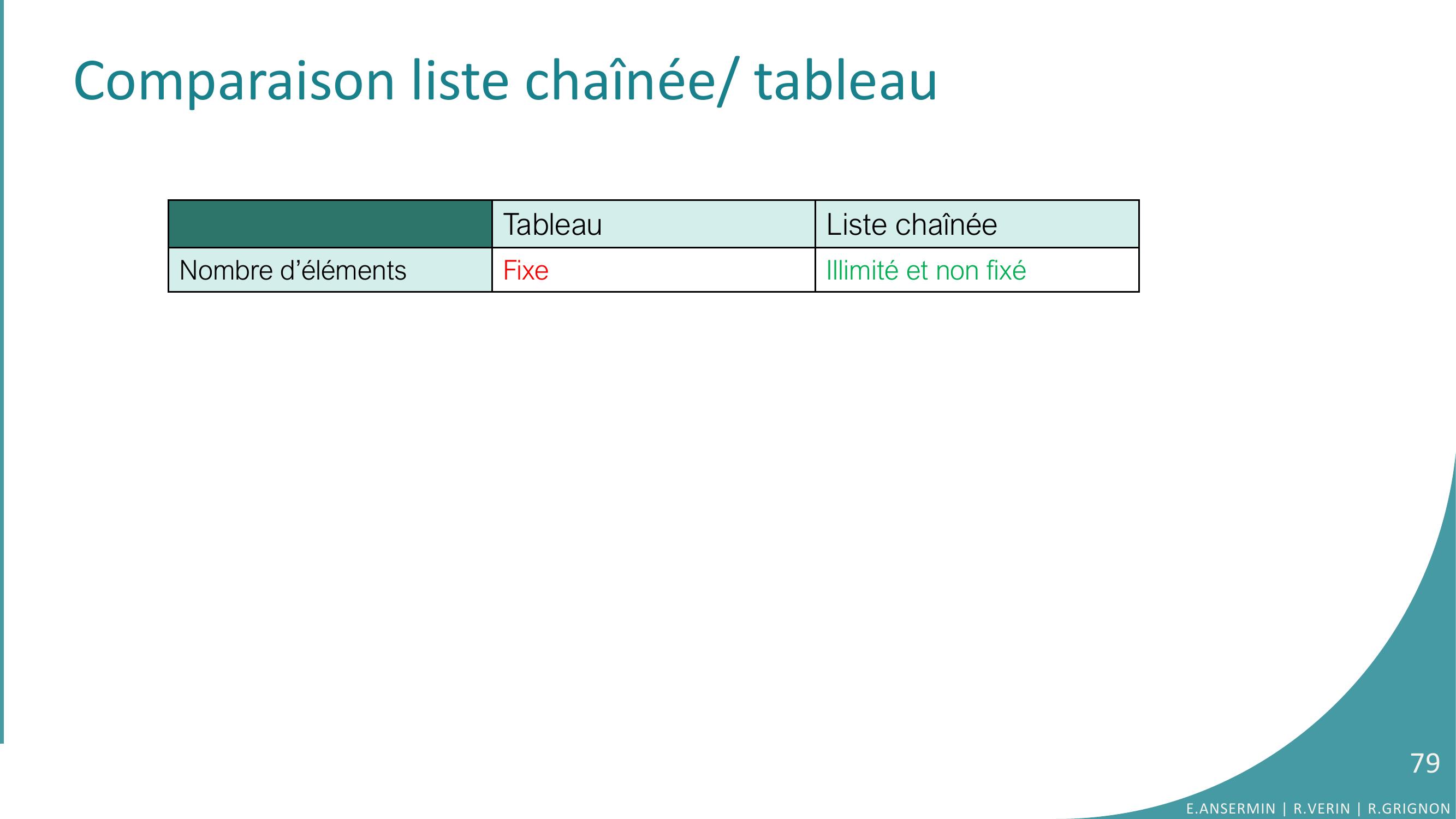
Page 79 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’éléments Fixe Illimité et non fixé79E.ANSERMIN R.VERIN R.GRIGNON
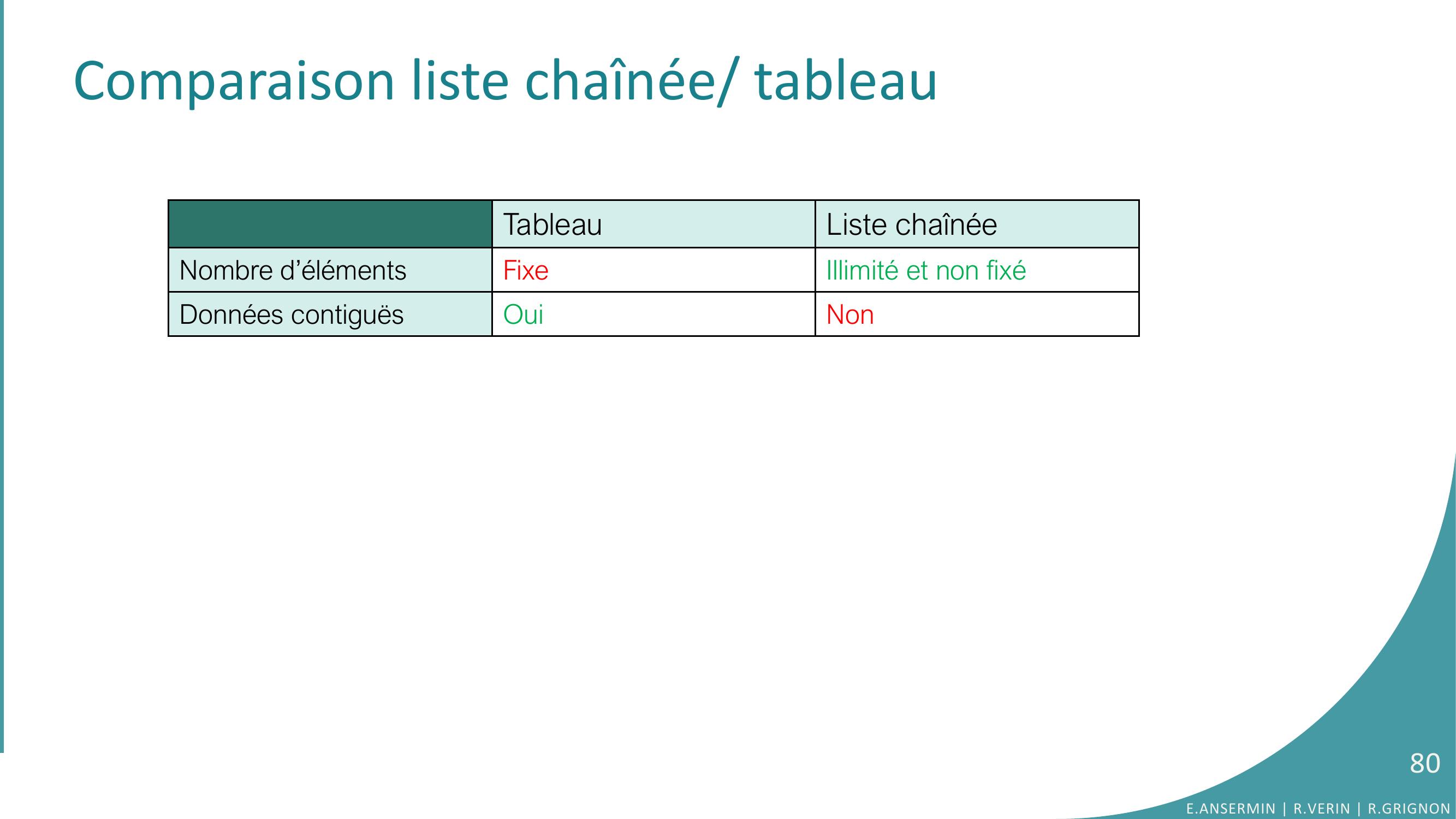
Page 80 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’éléments Fixe Illimité et non fixéDonnées contiguësOuiNon80E.ANSERMIN R.VERIN R.GRIGNON
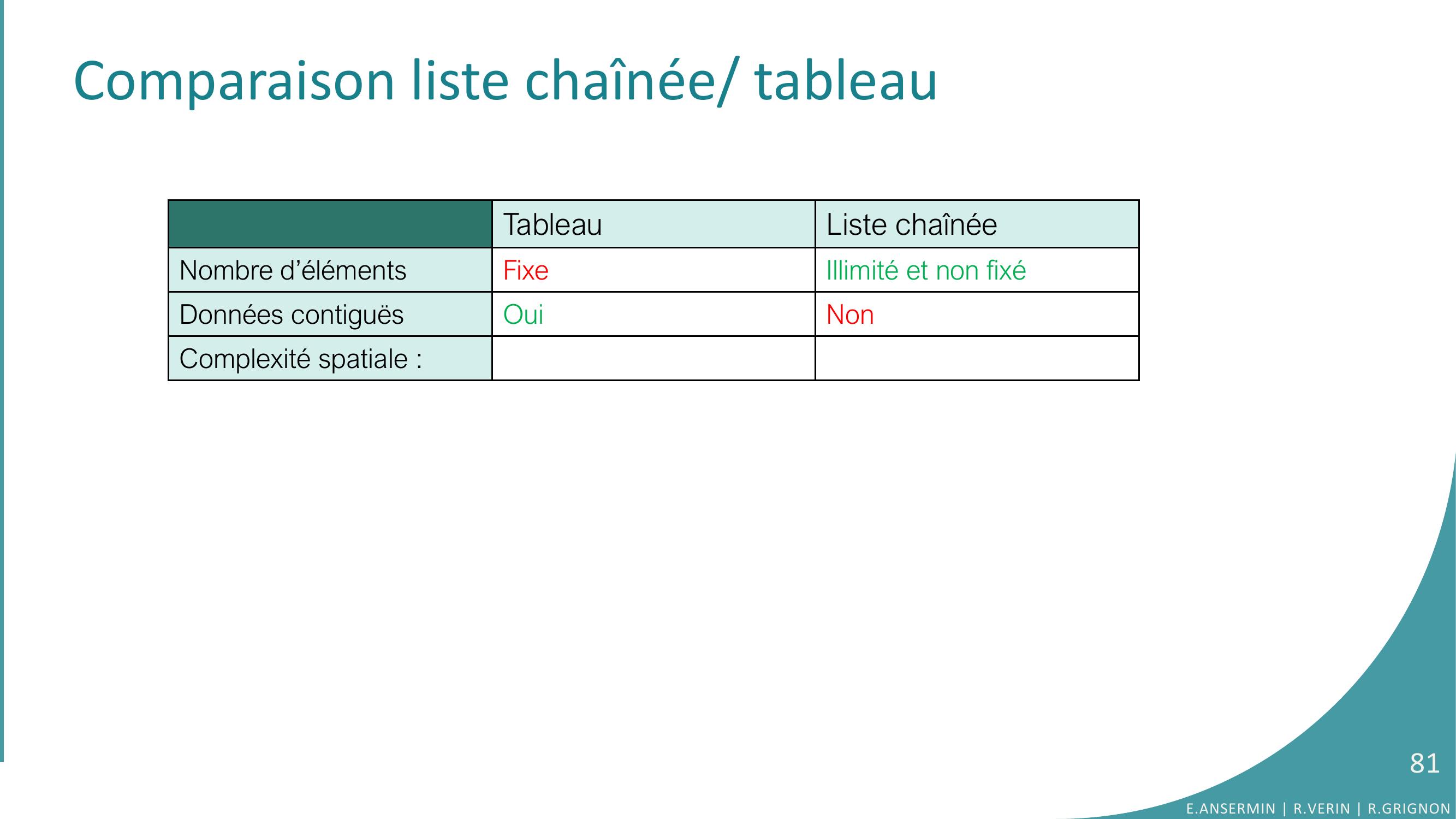
Page 81 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élémentsFixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :81E.ANSERMIN R.VERIN R.GRIGNON
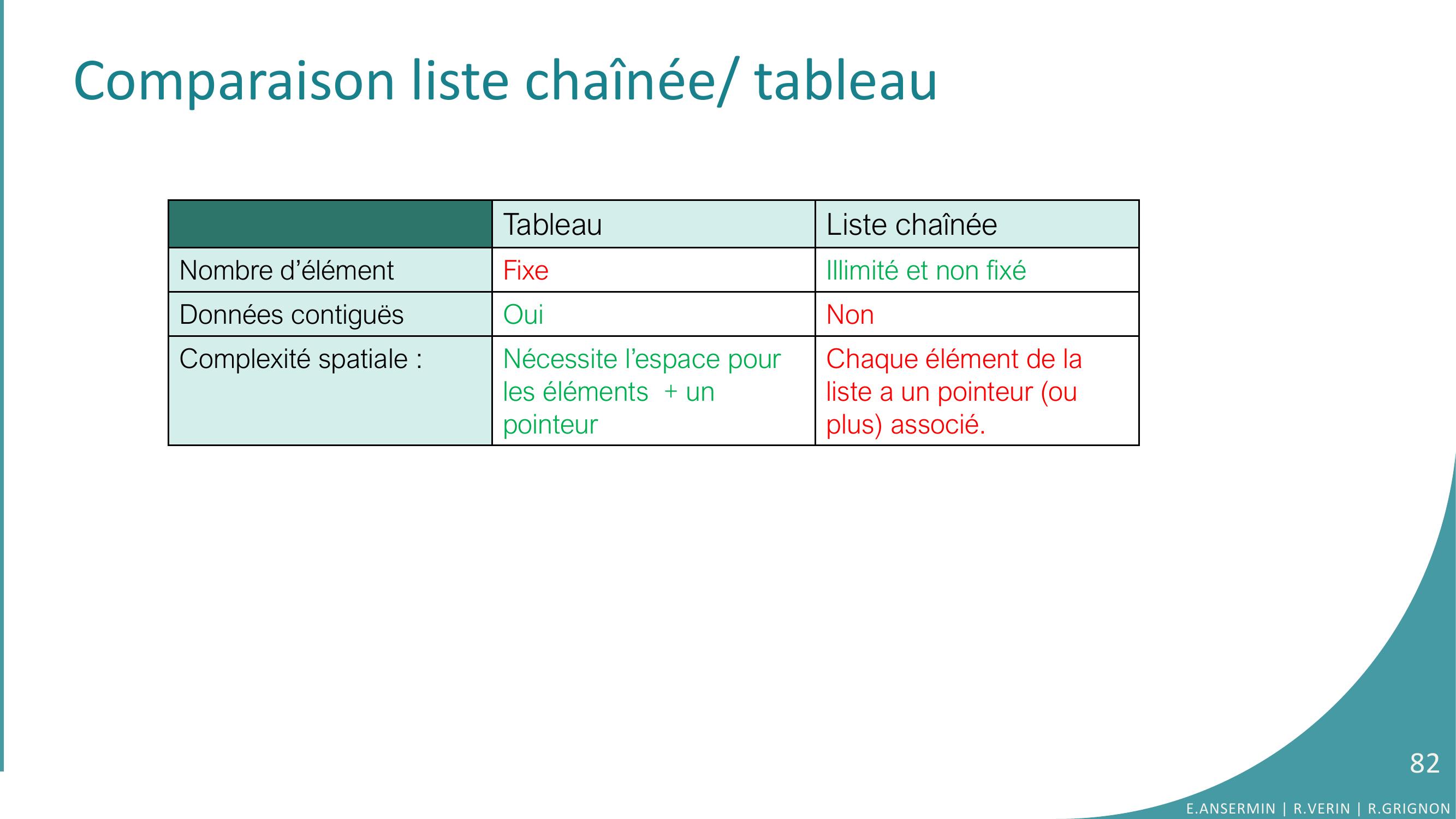
Page 82 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élément Fixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :Nécessite l’espace pour les éléments + un pointeurChaque élément de la liste a un pointeur ou plus associé.82E.ANSERMIN R.VERIN R.GRIGNON
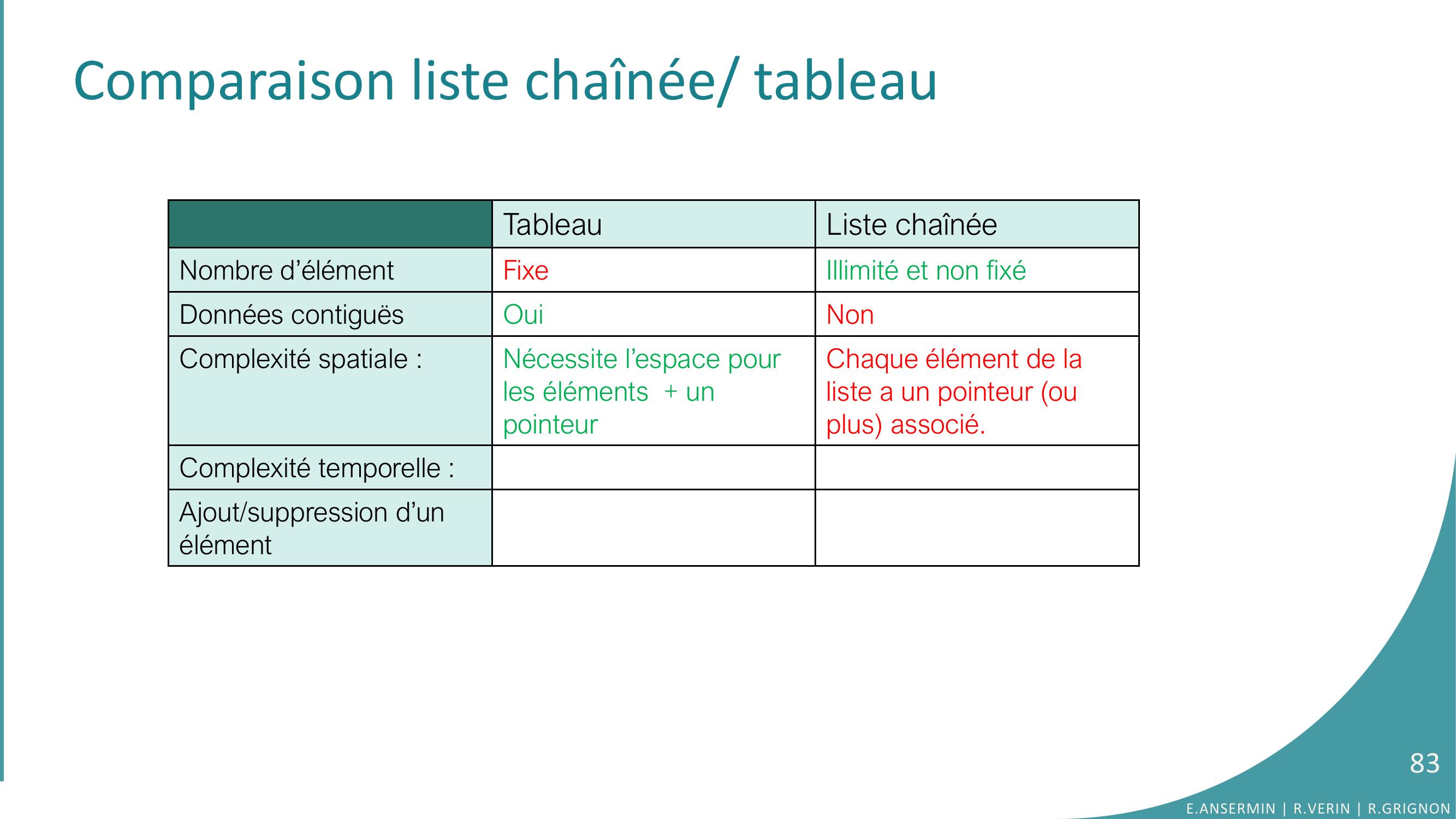
Page 83 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élément Fixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :Nécessite l’espace pour les éléments + un pointeurChaque élément de la liste a un pointeur ou plus associé.Complexité temporelle : Ajout/suppression d’un élément83E.ANSERMIN R.VERIN R.GRIGNON
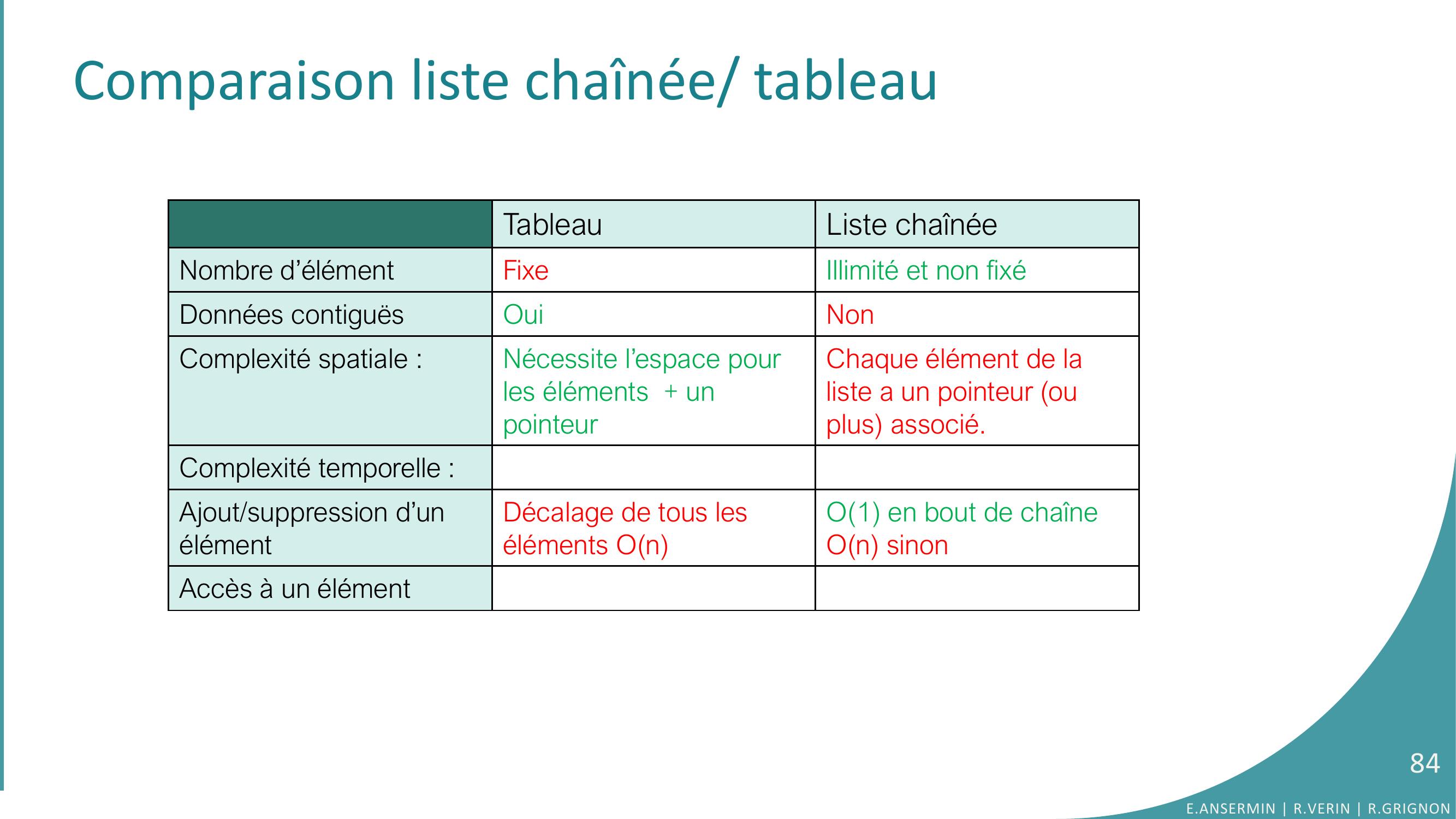
Page 84 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élément Fixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :Nécessite l’espace pour les éléments + un pointeurChaque élément de la liste a un pointeur ou plus associé.Complexité temporelle : Ajout/suppression d’un élémentDécalage de tous les éléments OnO1 en bout de chaîneOn sinonAccès à un élément84E.ANSERMIN R.VERIN R.GRIGNON
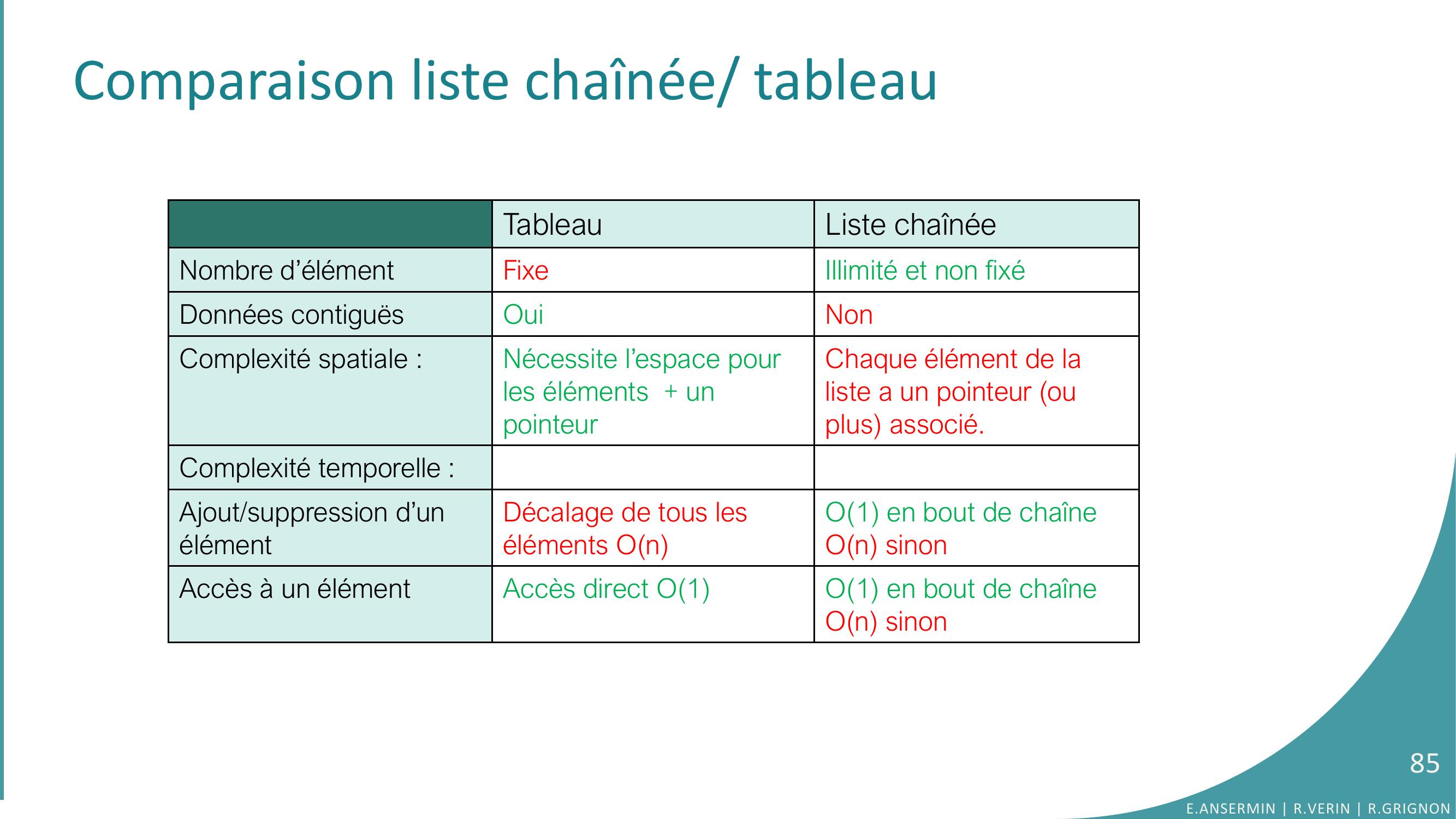
Page 85 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élément Fixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :Nécessite l’espace pour les éléments + un pointeurChaque élément de la liste a un pointeur ou plus associé.Complexité temporelle : Ajout/suppression d’un élémentDécalage de tous les éléments OnO1 en bout de chaîneOn sinonAccès à un élémentAccès direct O1O1 en bout de chaîneOn sinon85E.ANSERMIN R.VERIN R.GRIGNON
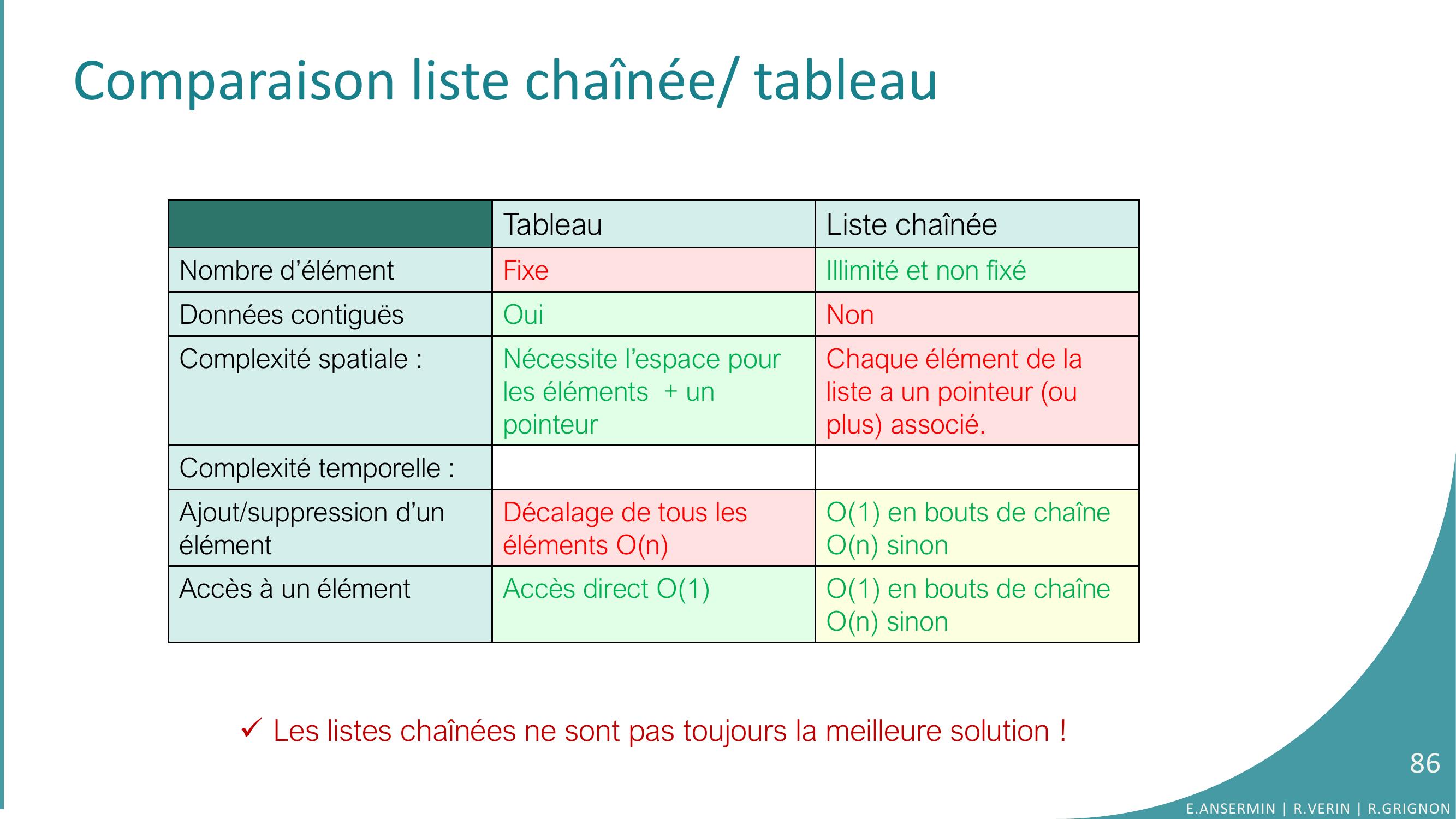
Page 86 : Comparaison liste chaînée/ tableauTableauListe chaînéeNombre d’élément Fixe Illimité et non fixéDonnées contiguësOuiNonComplexité spatiale :Nécessite l’espace pour les éléments + un pointeurChaque élément de la liste a un pointeur ou plus associé.Complexité temporelle : Ajout/suppression d’un élémentDécalage de tous les éléments OnO1 en bouts de chaîneOn sinonAccès à un élémentAccès direct O1O1 en bouts de chaîneOn sinonLes listes chaînées ne sont pas toujours la meilleure solution !86E.ANSERMIN R.VERIN R.GRIGNON
Page 87 : Pour résumer•Une liste chaînée est constituée d’éléments et de pointeurs associés indiquant l’emplacement mémoire de l’élément suivant et/ou précédent.•Il faut donc bien gérer les pointeurs !!•Ce principe permet à la liste chaînée de ne pas avoir un nombre fixé d’éléments, contrairement au tableau.•La liste chaînée simplifie également certaines opérations par rapport au tableau. Elle n’est cependant pas toujours la meilleure solution.•Le principe des listes chaînées est à la base de nombreux autres objets informatiques … et à la base de votre programme d’algorithmie de deuxième année !87E.ANSERMIN R.VERIN R.GRIGNON
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87