CM1 Systeme
Télécharger le CM1 Systeme en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
Page 1 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSystèmes d'Equations LinéairesD. CransacAnalyse
Page 2 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesConventionDans les énoncés, K représentera l'ensemble C ou l'ensemble R.Dénition Équation linéaireSoit p N.On appelle équation linéaire à p inconnues x1, . . . , xp, une équation dela formea1x1 + · · · + apxp = b avec a1, . . . , ap, b Kp+1Une solution d'une telle équation est notée sous fome d'un n-upletqu'on appelera vecteur dans la suite du cours :s1, . . . , sp KpOn appelle équation homogène associée à l'équation linéaire,l'équation obtenue en remplaçant b par 0.D. CransacAnalyse
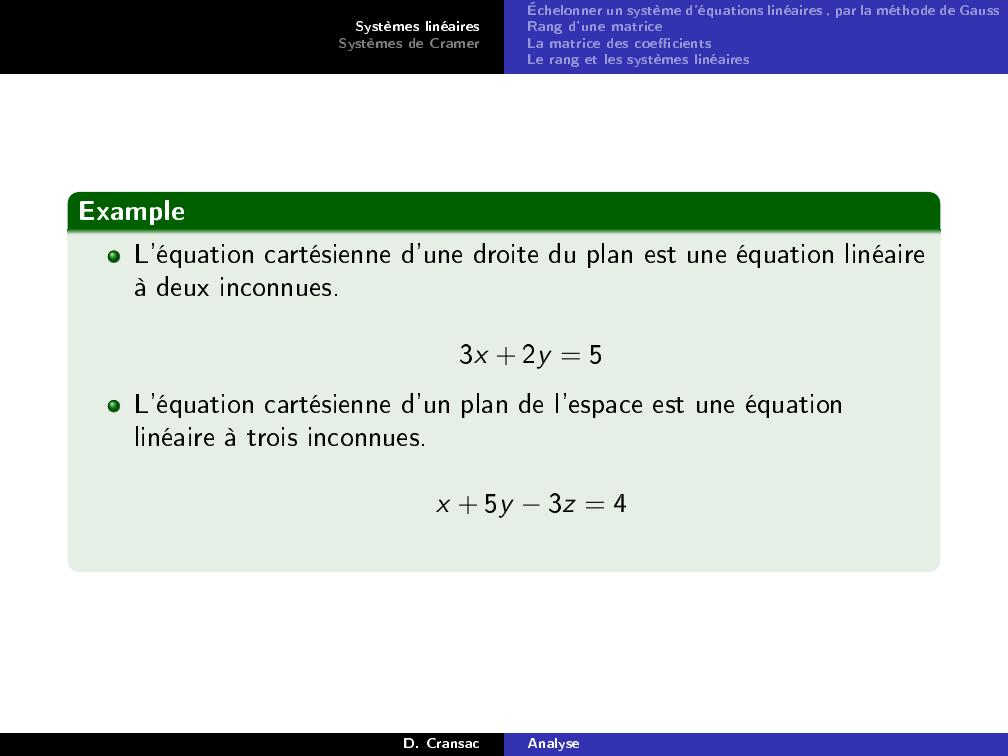
Page 3 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesExampleL'équation cartésienne d'une droite du plan est une équation linéaireà deux inconnues.3x + 2y = 5L'équation cartésienne d'un plan de l'espace est une équationlinéaire à trois inconnues.x + 5y 3z = 4D. CransacAnalyse
Page 4 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesRemarqueLe n-uplet 0, . . . , 0 est toujours solution d'une équation homogène.En eeta10 + · · · + ap0 = 0Si s1, . . . , sp est solution d'une équation homogène alors pour toutλ K, λs1, . . . , λsp est aussi solution.En eet si a1s1 + · · · + apsp = 0 alorsa1λs1 + · · · + apλsp = λa1λs1 + · · · + apλsp = λ0 = 0Si s1, . . . , sp ets′1, . . . , s′psont solutions d'une équationhomogène alorss1 + s′1, . . . , sp + s′pest aussi solution.En eet si a1s1 + · · · + apsp = 0 et a1s′1 + · · · + aps′p = 0 alorsa1s1 + s′1 + · · · + apsp + s′p= a1s1 + · · · + apsp + a1s′1 + · · · + aps′p= 0 + 0=0Les deux dernières propriétés caractérisent une équation linéaire.D. CransacAnalyse
Page 5 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDénition Système linéaireSoit n et p appartenant à N.On appelle système linéaire de n équations à p inconnues x1, . . . , xpun système de la forme :a1.1x1 + · · · + a1.pxp =b1......an.1x1 + · · · + an.pxp =bnoù les ai.j et bi1 ⩽i ⩽n, 1 ⩽j ⩽p sont des éléments de K.Un vecteur s1, . . . , sp Kp est solution du système si et seulement si ilest solution de toutes les équations linéaires composant le système.On appelle système d'équations homogènes le système obtenu enremplaçant tous les bi par 0 .D. CransacAnalyse
Page 6 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesUn premier exempleRésoudre le système :Sx+2y+zt=4y3z+3t=52z+t=24t=16SolutionS ⇔x+2y+zt=4y3z+3t=52z+4=2t=4⇔x+2y+zt=4y3z+3t=52z=6t=4D. CransacAnalyse
Page 7 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesS ⇔x+2y+zt=4y9+12=5z=3t=4⇔x+2y+zt=4y=5 3z=3t=4⇔x+2y+zt=4y=5 3z=3t=4⇔x+4+34=4y=2z=3t=4⇔x=1y=2z=3t=4D. CransacAnalyse
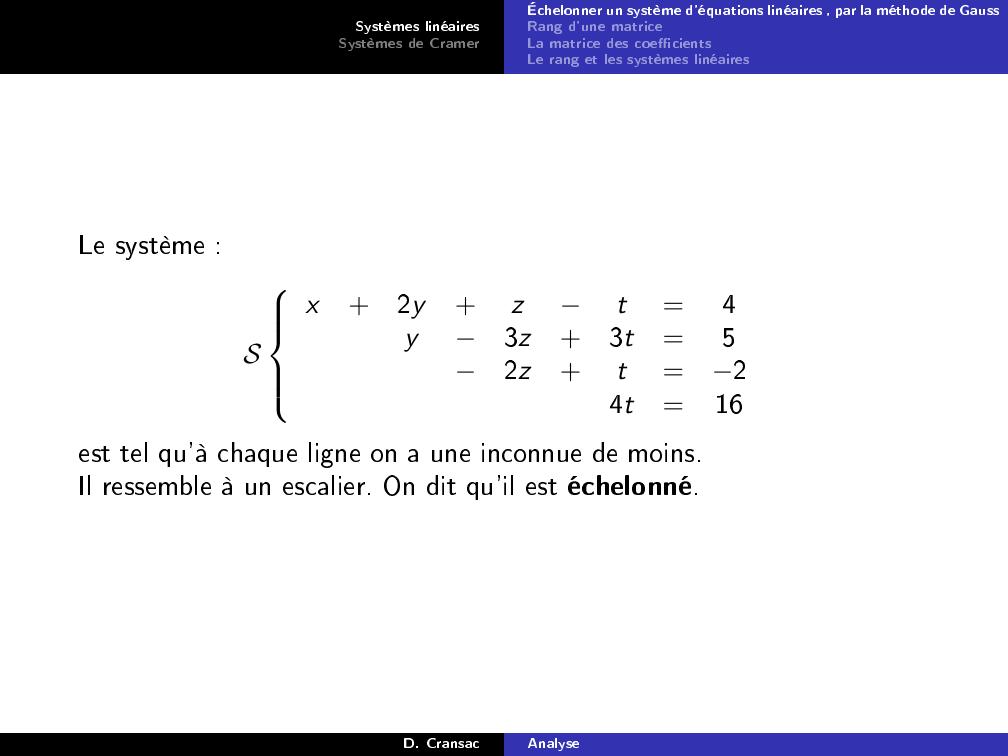
Page 8 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesLe système :Sx+2y+zt=4y3z+3t=52z+t=24t=16est tel qu'à chaque ligne on a une inconnue de moins.Il ressemble à un escalier. On dit qu'il est échelonné.D. CransacAnalyse
Page 9 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDénition Système échelonnéeUn système est dit échelonnée en lignes s'il vérie les deux propriétéssuivantes :1Si une ligne est entièrement nulle 0 = 0, toutes les lignes suivantesle sont aussi.2A partir de la deuxième ligne, dans chaque ligne non entièrementnulle 0 = 0, le premier coecient non nul à partir de la gauche estsitué à droite strictement du premier coecient non nul de la ligneprécédente.S′′x+2y+zt=4y3z+3t=52z+t=24t=16D. CransacAnalyse
Page 10 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesImportantLes systèmes échelonnés sont très faciles à résoudre : on commence parla dernière équation et on "remonte" pour exprimer l'inconnuesupplémentaire qui apparaît en fonction de celles obtenues dans leséquations en-dessous.S′′x+2y+zt=4y3z+3t=52z+t=24t=16D. CransacAnalyse
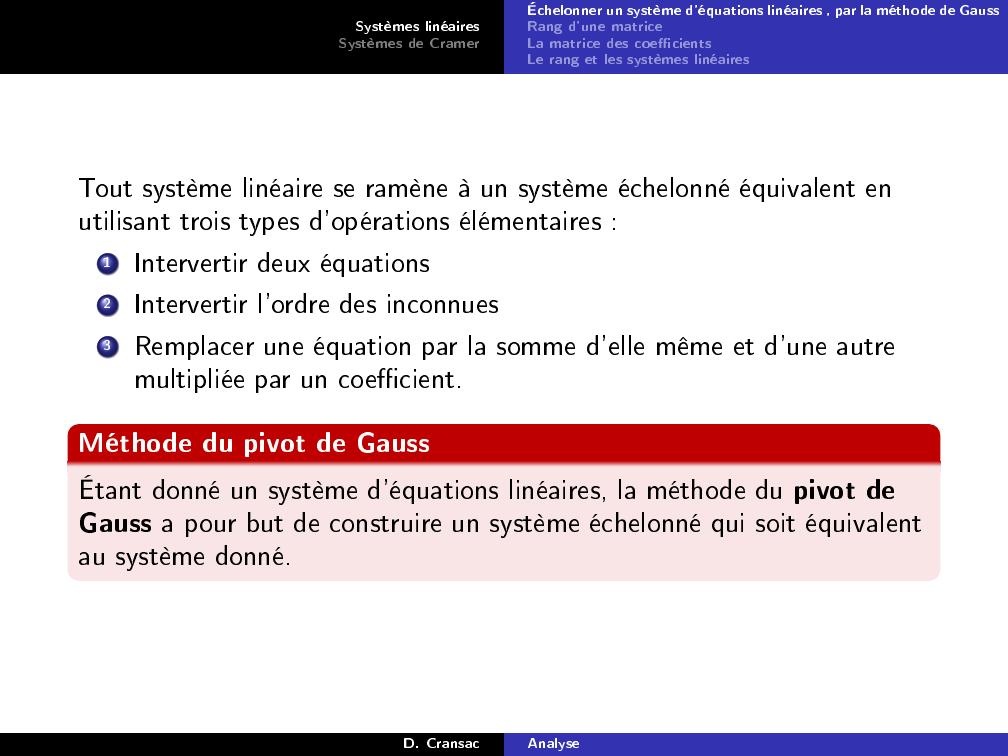
Page 11 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesTout système linéaire se ramène à un système échelonné équivalent enutilisant trois types d'opérations élémentaires :1Intervertir deux équations2Intervertir l'ordre des inconnues3Remplacer une équation par la somme d'elle même et d'une autremultipliée par un coecient.Méthode du pivot de GaussÉtant donné un système d'équations linéaires, la méthode du pivot deGauss a pour but de construire un système échelonné qui soit équivalentau système donné.D. CransacAnalyse
Page 12 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDeuxième exempleOn va commencer par présenter la méthode du pivot de Gauss sur unexemple.Considérons le système dont les inconnues sont x, y, z, t et où a, bsont des paramètres xés.Sx+2y+zt=aE12x+4yz5t=5aE2x2y+z+3t=bE3Choisissons une équation avec un coecient non nul pour la premièreinconnue x.Ici la première équation convient avec le coecient 1, pour x, qu'onappelle le premier pivot.On va utiliser ce pivot pour faire disparaître l'inconnue x des autreséquations.D. CransacAnalyse
Page 13 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSx+2y+zt=aE12x+4yz5t=5aE2x2y+z+3t=bE3Pour cela on ajoute à ces équations la première multiplié par uncoecient convenable.On obtient un système linéaire équivalent :S′x+2y+zt=aE ′1 = E13z3t=3aE ′2 = E2 2E1+2z+2t=b + aE ′3 = E3 + E1Examinons maintenant le système obtenu en supprimant la premièreéquation.On remarque que la variable x n'y apparaît pas. La variable suivante ynon plus. On est ramené à un système de deux équations avec ici deuxvariables en moins.D. CransacAnalyse
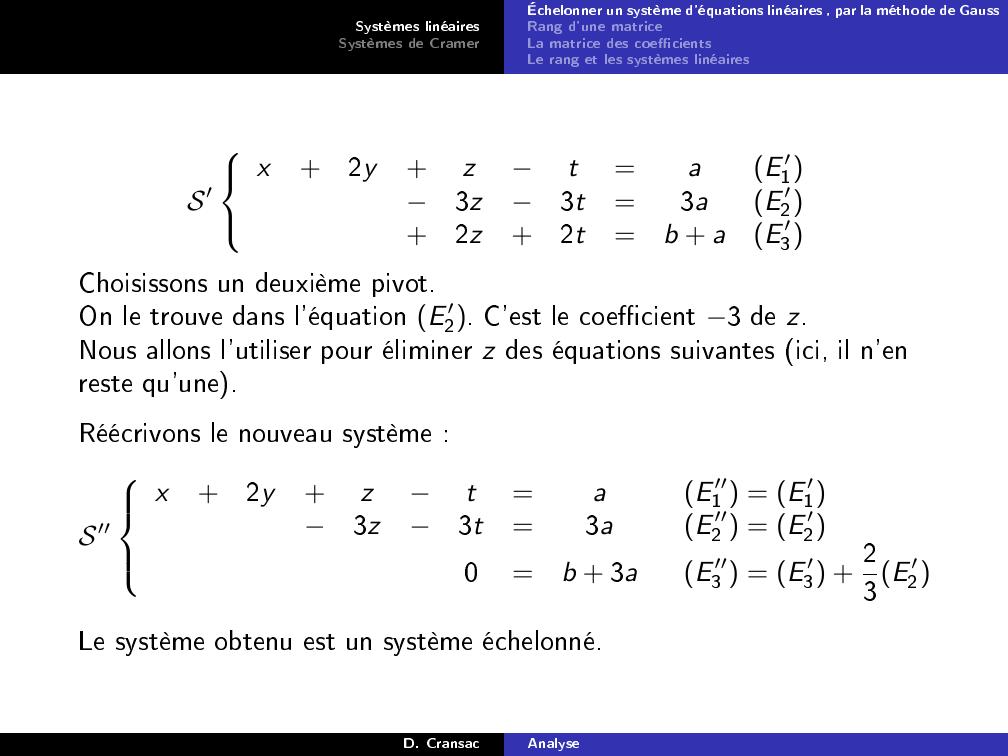
Page 14 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesS′x+2y+zt=aE ′13z3t=3aE ′2+2z+2t=b + aE ′3Choisissons un deuxième pivot.On le trouve dans l'équation E ′2. C'est le coecient 3 de z.Nous allons l'utiliser pour éliminer z des équations suivantes ici, il n'enreste qu'une.Réécrivons le nouveau système :S′′x+2y+zt=aE ′′1 = E ′13z3t=3aE ′′2 = E ′20=b + 3aE ′′3 = E ′3 + 23E ′2Le système obtenu est un système échelonné.D. CransacAnalyse
Page 15 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDescription de l'algorithme du pivot de GaussRappelons que le but est d'obtenir un système équivalent au systèmedonné et qui soit échelonné c'est-à-dire de la forme :xn1+a1,n1+1xn1+1+.........+a1,nxnxn2+a2,n2+1xn2+1 + ...+a2,nxn...xnp + ap,np+1xnp+1 + ...+ap,nxn00avec 1 ⩽p ⩽m et 1 ⩽n1 n2 ... np ⩽n.D. CransacAnalyse
Page 16 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesAvec l'exemple précédent on peut comprendre facilement lefonctionnement de l'algorithme pour un système quelconque d'équations.1On cherche un pivot, premier coecient non nul d'une certainevariable x dans une des équations. Par permutation, cette équationdevient la première équation.2On utilise ce pivot et cette équation pour éliminer x des équationssuivantes. Pour cela on ajoute cette équation multipliée par uncoecient convenable aux équations suivantes3S'il y a des équations dont le premier membre est nul 0 = . . . on lesplace en dernier.4On recommence à l'étape 1 avec le système privé de la premièreéquation.L'algorithme s'arrête lorsqu'il ne reste plus que des équations 0 = . . ..D. CransacAnalyse
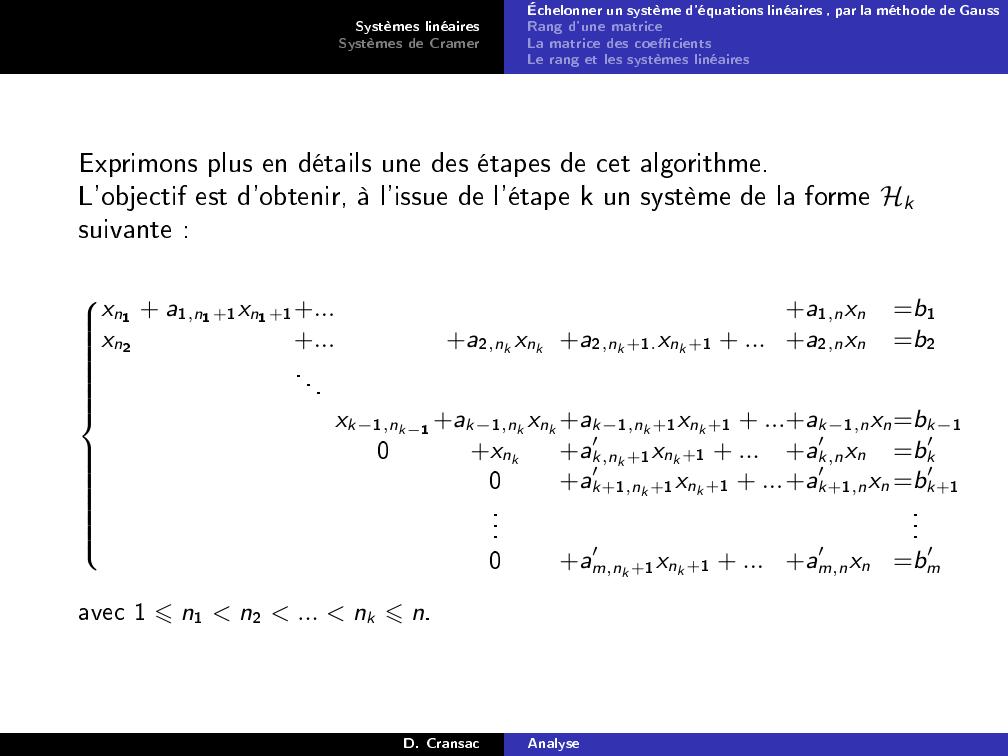
Page 17 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesExprimons plus en détails une des étapes de cet algorithme.L'objectif est d'obtenir, à l'issue de l'étape k un système de la forme Hksuivante :xn1 + a1,n1+1xn1+1+...+a1,nxn=b1xn2+...+a2,nk xnk +a2,nk +1.xnk +1 + ... +a2,nxn=b2...xk1,nk1+ak1,nk xnk +ak1,nk +1xnk +1 + ...+ak1,nxn=bk10+xnk+a′k,nk +1xnk +1 + ...+a′k,nxn=b′k0+a′k+1,nk +1xnk +1 + ...+a′k+1,nxn =b′k+1......0+a′m,nk +1xnk +1 + ...+a′m,nxn=b′mavec 1 ⩽n1 n2 ... nk ⩽n.D. CransacAnalyse
Page 18 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSystème à l'état k 1xn1+a1,n1+1xn1+1+...+ a1,nxn = b1xn2+...+a2,nk xnk+a2,nk +1.xnk +1 + ... + a2,nxn = b2...xk1,nk1+ak1,nk xnk +ak1,nk +1xnk +1 + ...+ak1,nxn=bk10+ak,nk xnk+ak,nk +1xnk +1 + ... + ak,nxn = bk0+ak+1,nk xnk +ak+1,nk +1xnk +1 + ...+ak+1,nxn=bk+1......0+am,nk xnk+am,nk +1xnk +1 + ... + am,nxn = bmavec 1 ⩽n1 n2 ... nk ⩽n.D. CransacAnalyse
Page 19 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSystème après normalisation du pivot :xn1+a1,n1+1xn1+1+...+ a1,nxn = b1xn2+...+a2,nk xnk+a2,nk +1.xnk +1 + ... + a2,nxn = b2...xk1,nk1+ak1,nk xnk +ak1,nk +1xnk +1 + ...+ak1,nxn=bk10+xnk+a′k,nk +1xnk +1 + ... + a′k,nxn = b′k0+ak+1,nk xnk +ak+1,nk +1xnk +1 + ...+ak+1,nxn=bk+1......0+am,nk xnk+am,nk +1xnk +1 + ... + am,nxn = bmavec 1 ⩽n1 n2 ... nk ⩽n.D. CransacAnalyse
Page 20 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSystème à l'étape kxn1 + a1,n1+1xn1+1+...+a1,nxn=b1xn2+...+a2,nk xnk +a2,nk +1.xnk +1 + ...+a2,nxn=b2...xk1,nk1+ak1,nk xnk +ak1,nk +1xnk +1 + ... +ak1,nxn =bk10+xnk+a′k,nk +1xnk +1 + ...+a′k,nxn=b′k0+a”k+1,nk +1xnk +1 + ...+a”k+1,nxn=b”k+1......0+a”m,nk +1xnk +1 + ... +a”m,nxn=b”mavec 1 ⩽n1 n2 ... nk ⩽n.D. CransacAnalyse
Page 21 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDécrivons à présent l'étape k de la méthode du Pivot de Gauss : étantdonné un système de la forme Hk1, nous allons le transformer de façonà obtenir un système de la forme Hk.Nous noterons Ej la j eme équation du système.On ne modie pas les k 1 premières équations du système linéaire.Si tous les coecients al,m avec l ⩾k et m nk1 sont nuls,alors, pour tout l ⩾k, l'équation El s'écrit : 0 = bl. Le système adonc la forme voulue. L'algorithme s'arrête.Sinon, on pose nk := minm : l ⩾k : al,m ̸= 0. Alors, quitte àéchanger la ligne k avec une ligne p ⩾k telle que ap,nk ̸= 0, on seramène au cas où ak,nk est non nul ce sera notre pivot pour l'étapek.On remplace alors l'équation Ek par1ak,nkEk pour se ramener à :ak,nk = 1.Puis, pour tout p k, on remplace Ep par Ep ap,nkEk and'éliminer les termes en xnk des équations k + 1, ..., m.Le système d'équations linéaires ainsi obtenu est alors de la formeHk, l'étape k est nie.D. CransacAnalyse
Page 22 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesRésolution du premier exempleOn avait obtenu :S′′x+2y+zt=aE ′′1 3z3t=3aE ′′2 0=b + 3aE ′′3 Si b + 3a = 0, on peut déterminer x, y, z, t solutions du système.Si b + 3a ̸= 0, le système n'admet aucune solution. En eet pour toutx, y, z, t, la dernière équation ne sera pas vériée.La dernière équation est appellée équation de compatiblité.Par ailleurs, si t et y sont xées, on ne peut obtenir qu'une seule valeurde z et de x.On dit que x et z qui correspondent au pivot sont des inconnuesprincipales.D. CransacAnalyse
Page 23 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesProposition1Les inconnues des lignes non nulles s'appellent les inconnuesprincipales, ou pivots2Un système échelonné possède des solutions si et seulement si leséquations de compatibilité sont satisfaites portant sur lesdonnées.3Si ces conditions sont satisfaites alors toute donnée des inconnuesnon principales détermine une unique solution du système. Celaéquivaut à dire que les solutions du système sont paramétrées par lesinconnues non principales.D. CransacAnalyse
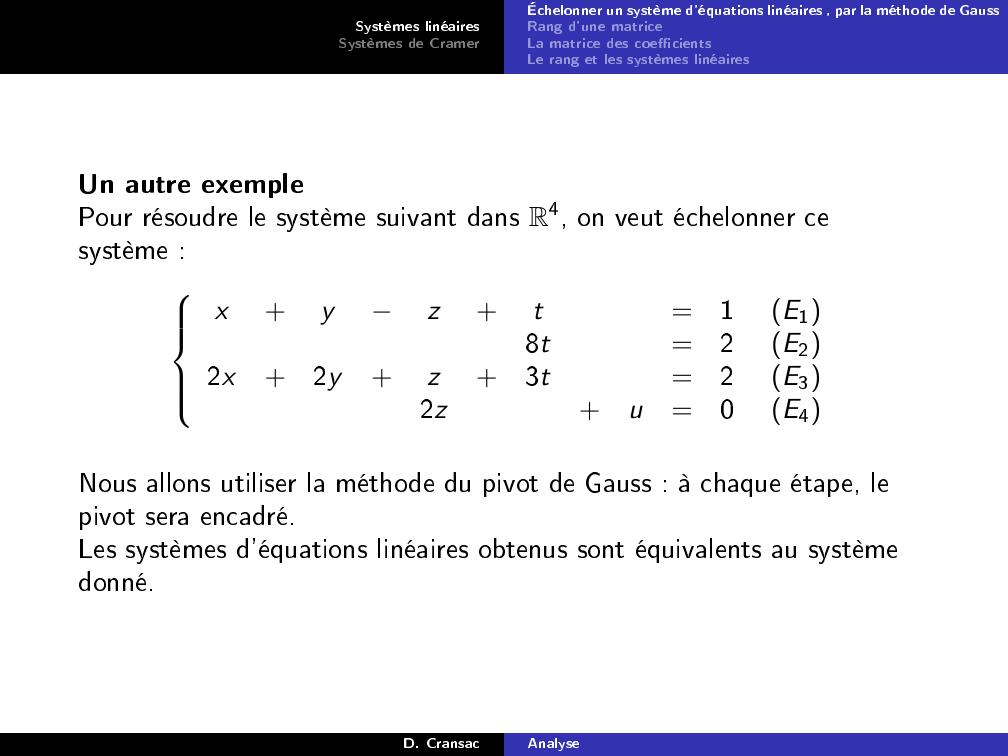
Page 24 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesUn autre exemplePour résoudre le système suivant dans R4, on veut échelonner cesystème :x+yz+t=1E18t=2E22x+2y+z+3t=2E32z+u=0E4Nous allons utiliser la méthode du pivot de Gauss : à chaque étape, lepivot sera encadré.Les systèmes d'équations linéaires obtenus sont équivalents au systèmedonné.D. CransacAnalyse
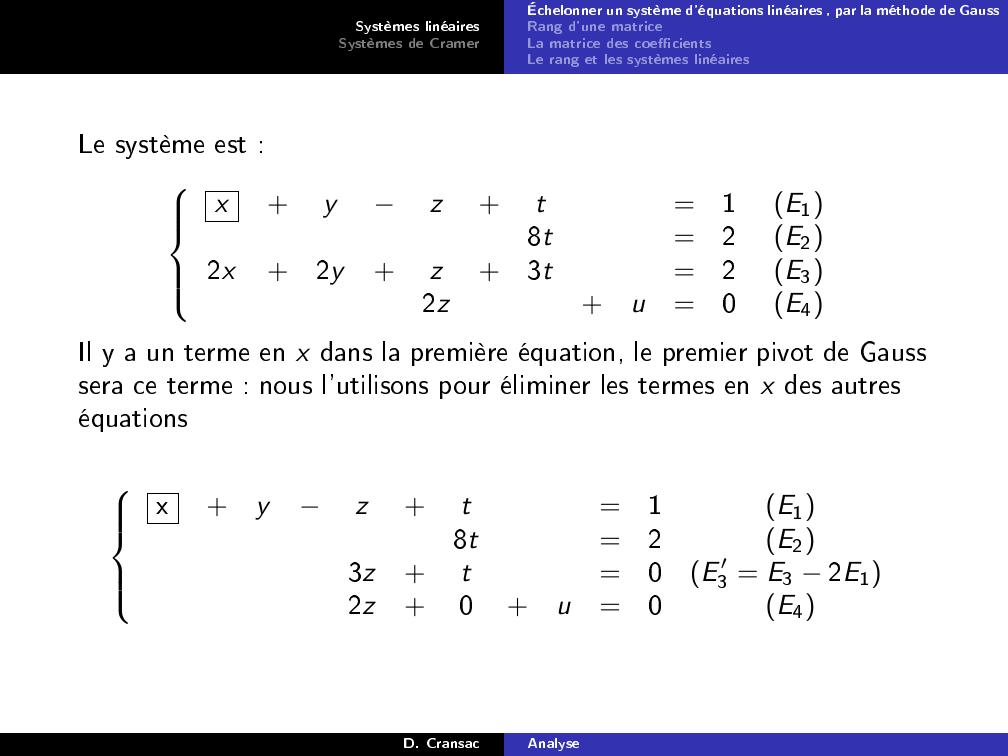
Page 25 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesLe système est :x+yz+t=1E18t=2E22x+2y+z+3t=2E32z+u=0E4Il y a un terme en x dans la première équation, le premier pivot de Gausssera ce terme : nous l'utilisons pour éliminer les termes en x des autreséquationsx+yz+t=1E18t=2E23z+t=0E ′3 = E3 2E12z+0+u=0E4D. CransacAnalyse
Page 26 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesNous oublions à présent la première ligne.Il n'y a pas de terme en y dansles équations E2, E ′3 et E4.Il y a un terme en z dans E ′3 mais pas dansE2 ; nous permutons donc les équations E2 et E ′3x+yz+t=1E13z+t=0E ′2 = E ′38t=2E ′′3 = E22z+0+u=0E4Nous divisons la deuxième équation par 3 de sorte à avoir z au lieu de 3zdans la deuxième équationx+yz+t=1E1z+13t=0E ′′2 = 13E ′28t=2E ′′3 2z+0+u=0E4D. CransacAnalyse
Page 27 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesLe terme en z de la deuxième équation est le nouveau pivot de Gauss ;nous l'utilisons pour éliminer les termes en z des équations situés endessousx+yz+t=1E1z+13t=0E ′′2 8t=2E ′′3 23t+u=0E ′4 = E4 2E ′′2 Nous oublions à présent la deuxième équation ; il y a un terme en t dansla troisième équation, nous divisons la troisième équation par 8 de sorte àavoir t à la place de 8t dans cette équationx+yz+t=1E1z+13t=0E ′′2 t=14E ′′′3 = 18E ′′3 23t+u=0E ′4D. CransacAnalyse
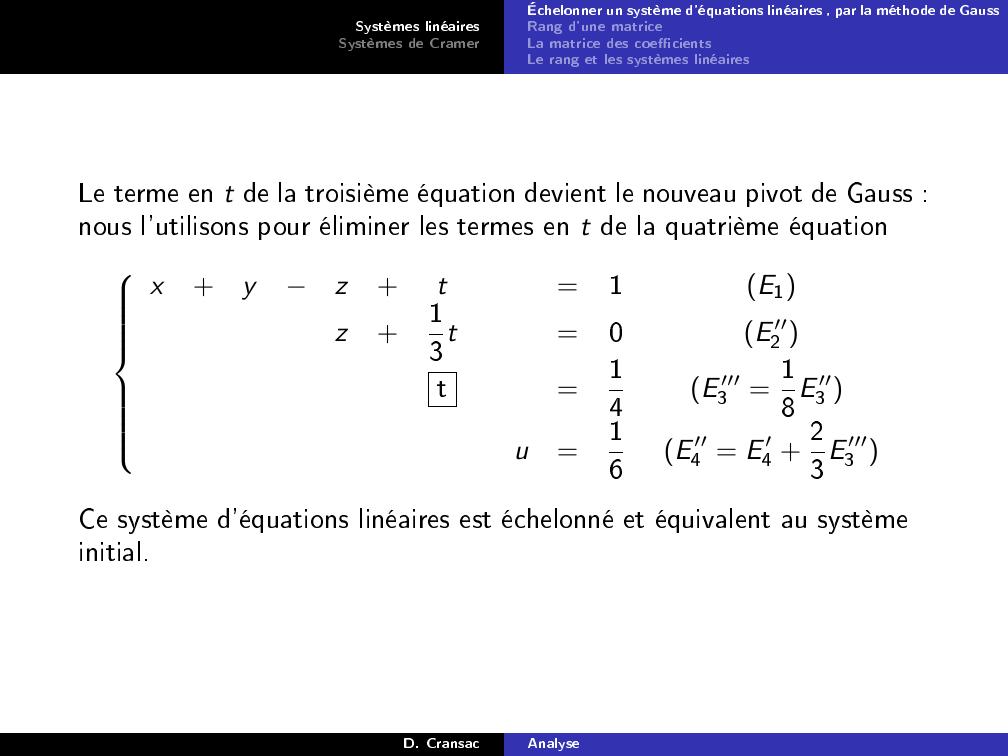
Page 28 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesLe terme en t de la troisième équation devient le nouveau pivot de Gauss :nous l'utilisons pour éliminer les termes en t de la quatrième équationx+yz+t=1E1z+13t=0E ′′2 t=14E ′′′3 = 18E ′′3 u=16E ′′4 = E ′4 + 23E ′′′3 Ce système d'équations linéaires est échelonné et équivalent au systèmeinitial.D. CransacAnalyse
Page 29 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesRang d'une matriceD. CransacAnalyse
Page 30 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDénition Dénition temporaire d'une matriceSoient n et m deux entiers naturels non nul.Une matrice de dimension n × m est un tableau d'éléments de K avec nlignes et m colonnes.On note une telle matrice :aij =a11a12. . .a1ma21a22. . .a2m. . .. . .. . .. . .an1an2. . .anmD. CransacAnalyse
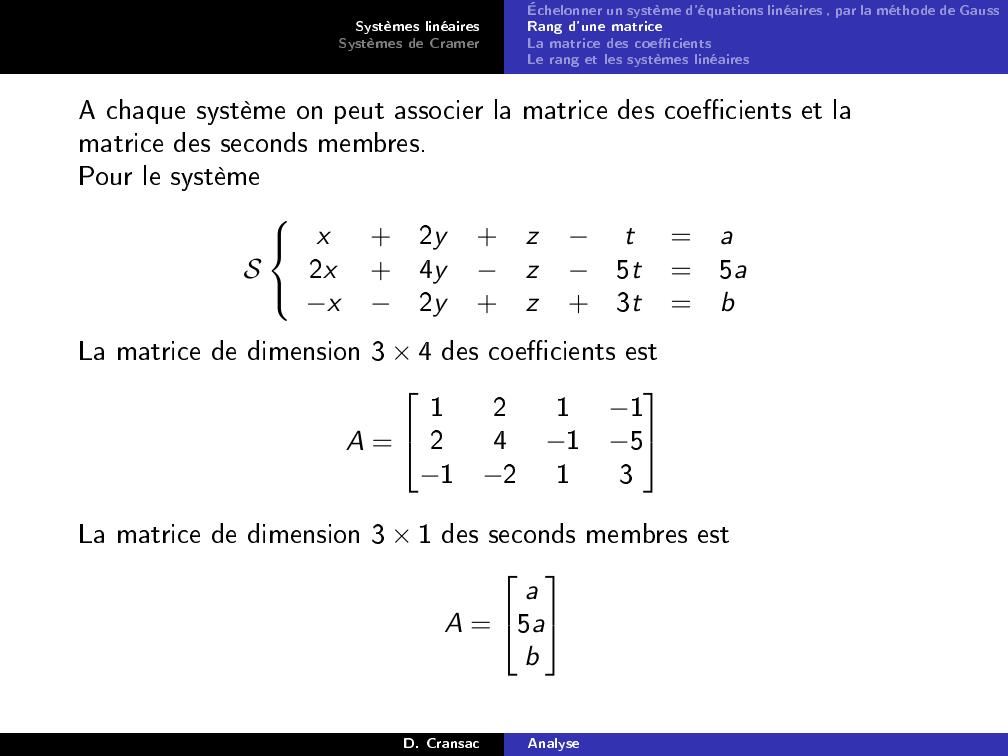
Page 31 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesA chaque système on peut associer la matrice des coecients et lamatrice des seconds membres.Pour le systèmeSx+2y+zt=a2x+4yz5t=5ax2y+z+3t=bLa matrice de dimension 3 × 4 des coecients estA =121124151213La matrice de dimension 3 × 1 des seconds membres estA =a5abD. CransacAnalyse
Page 32 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDenitionUne matrice B est dite échelonnée en lignes si1chaque ligne non nulle de B commence avec strictement plus de 0que la ligne précédente, et2les lignes nulles ne contenant que des 0 de B viennent en bas aprèsles lignes non nulles.Toute matrice A peut se réduire à une matrice échelonnée en lignes B parune suite d'opérations élémentaires sur les lignes.On appelle B la forme échelonnée en lignes de A.D. CransacAnalyse
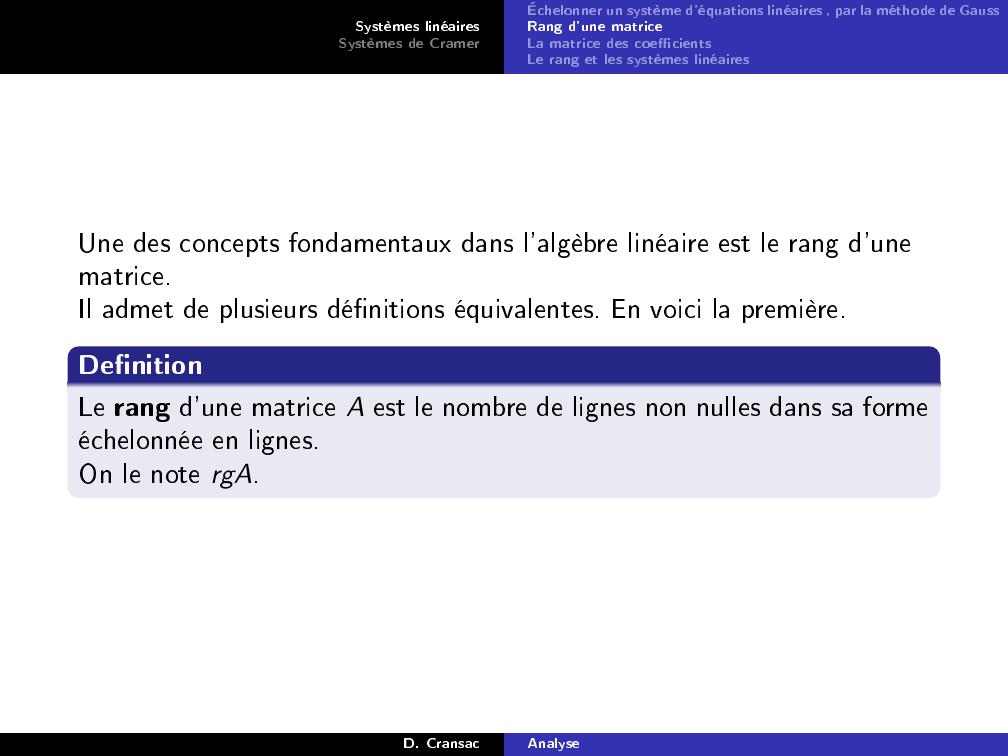
Page 33 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesUne des concepts fondamentaux dans l'algèbre linéaire est le rang d'unematrice.Il admet de plusieurs dénitions équivalentes. En voici la première.DenitionLe rang d'une matrice A est le nombre de lignes non nulles dans sa formeéchelonnée en lignes.On le note rgA.D. CransacAnalyse
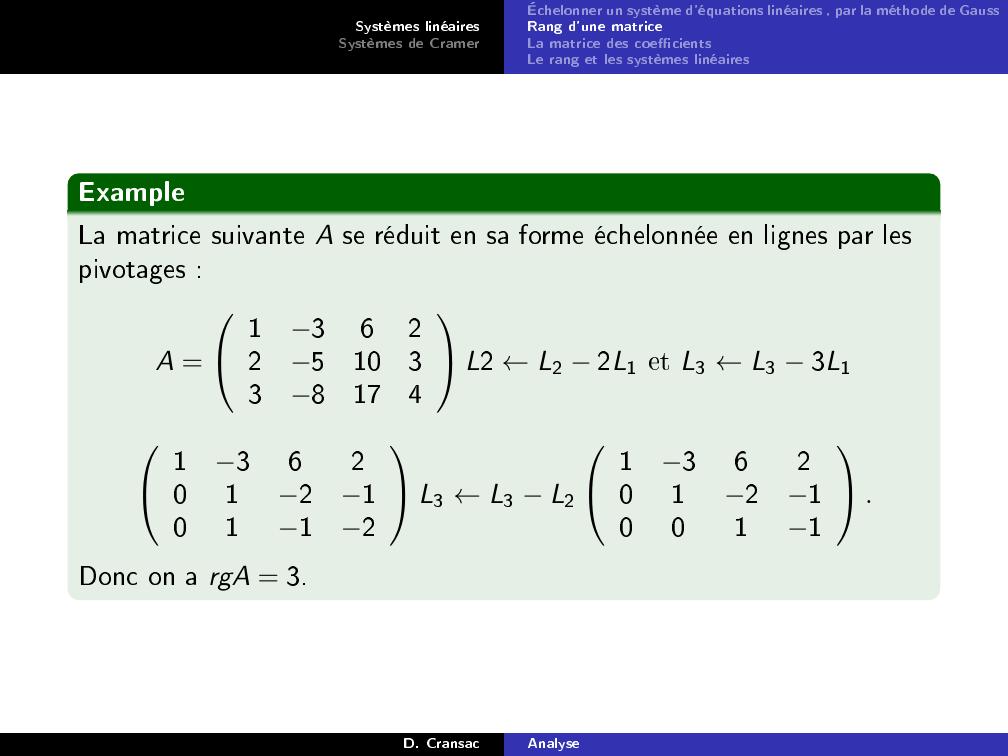
Page 34 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesExampleLa matrice suivante A se réduit en sa forme échelonnée en lignes par lespivotages :A =13622510338174L2 ←L2 2L1 et L3 ←L3 3L1136201210112L3 ←L3 L2136201210011.Donc on a rgA = 3.D. CransacAnalyse
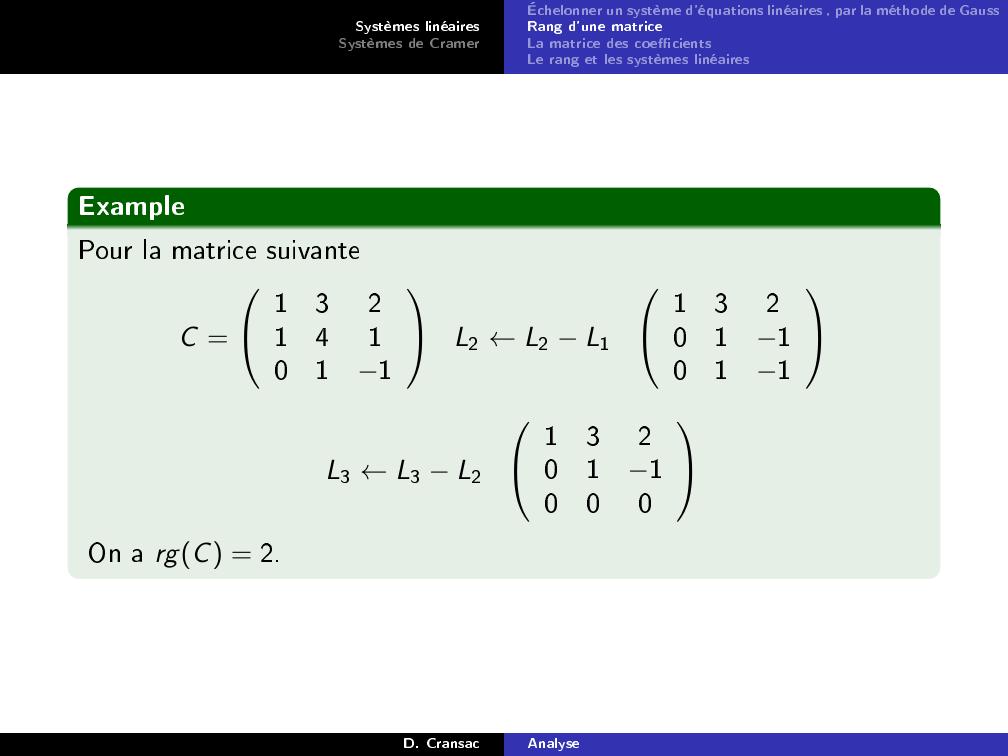
Page 35 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesExamplePour la matrice suivanteC =132141011L2 ←L2 L1132011011L3 ←L3 L2132011000On a rgC = 2.D. CransacAnalyse
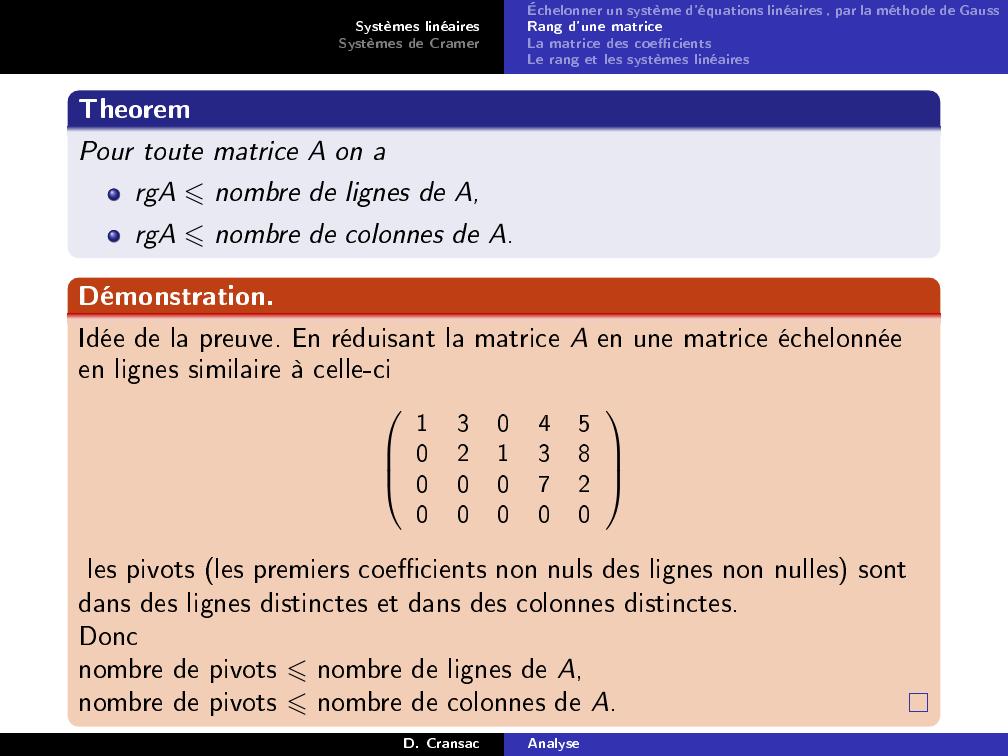
Page 36 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesTheoremPour toute matrice A on argA ⩽nombre de lignes de A,rgA ⩽nombre de colonnes de A.Démonstration.Idée de la preuve. En réduisant la matrice A en une matrice échelonnéeen lignes similaire à celle-ci13045021380007200000les pivots les premiers coecients non nuls des lignes non nulles sontdans des lignes distinctes et dans des colonnes distinctes.Doncnombre de pivots ⩽nombre de lignes de A,nombre de pivots ⩽nombre de colonnes de A.D. CransacAnalyse
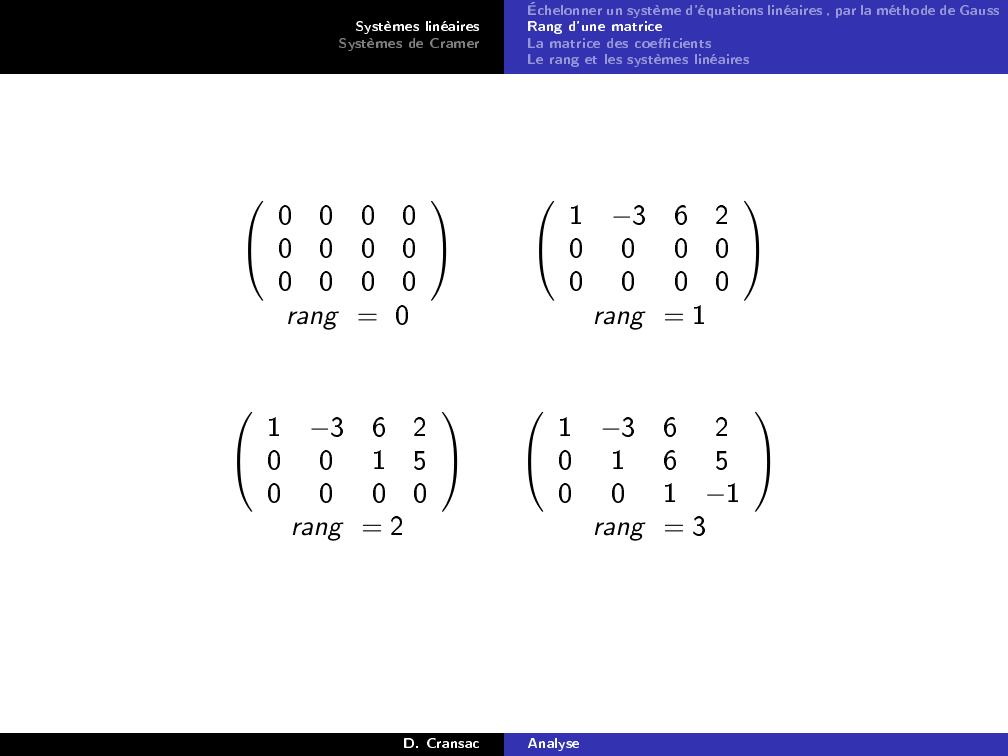
Page 37 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéaires000000000000136200000000rang = 0rang = 1136200150000136201650011rang = 2rang = 3D. CransacAnalyse
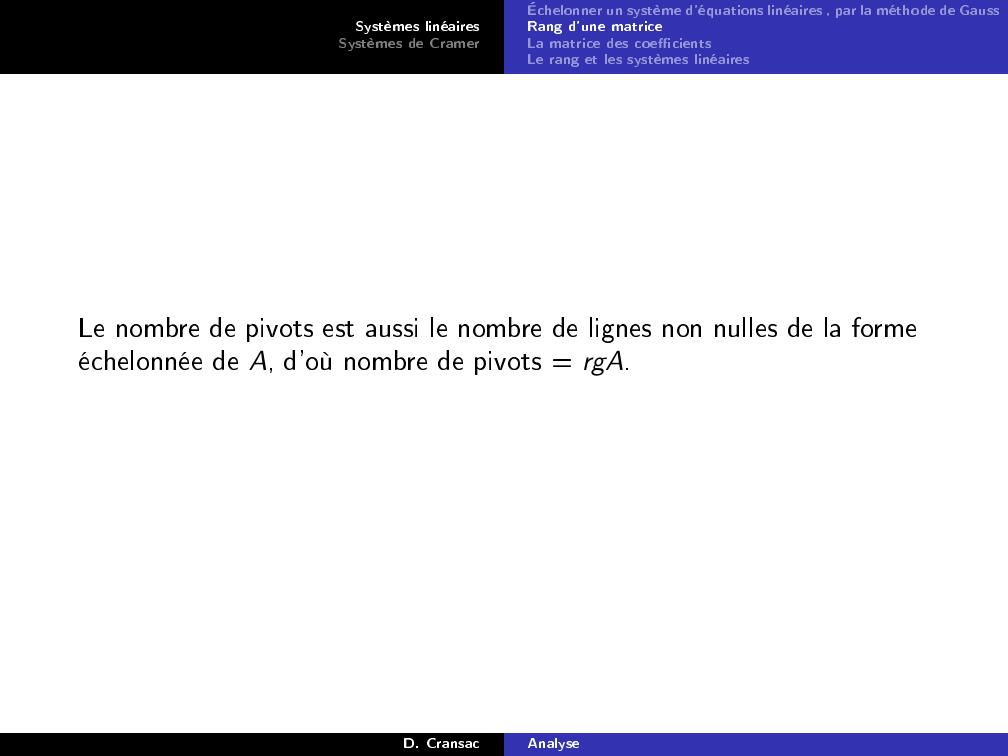
Page 38 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesLe nombre de pivots est aussi le nombre de lignes non nulles de la formeéchelonnée de A, d'où nombre de pivots = rgA.D. CransacAnalyse
Page 39 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesOn a vu qu'on peut associer une matrice à chaque membre d'un systèmelinéaire. Pour le systèmex 3y + 6z + 2w=1,2x 5y + 10z + 3w=0,3x 8y + 17z + 4w=1,on a les matricesA =13622510338174b =101avec A la matrice des coecients regroupant les coecients des variablesdu membre de gauche du système, et le vecteur colonne b contient lemembre de droite.Quand on met les deux ensemble, on a la matrice dite augmentée.B =13621251030381741D. CransacAnalyse
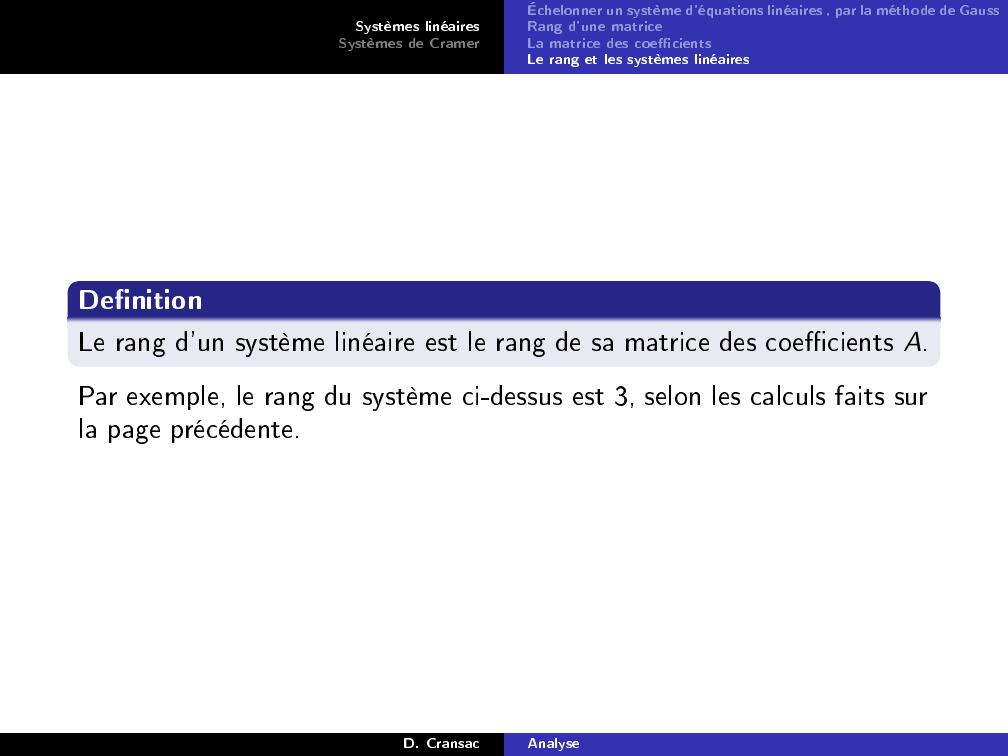
Page 40 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesDenitionLe rang d'un système linéaire est le rang de sa matrice des coecients A.Par exemple, le rang du système ci-dessus est 3, selon les calculs faits surla page précédente.D. CransacAnalyse
Page 41 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesRésolution avec une matrice augmentée.PropositionLorsque l'ont a appliqué la méthode de Gauss à une matriceaugmentée, on a deux cas de gures :On considère la ligne la plus basse qui ne contient pas que des 0Si elle contient uniquement une valeur non nulle sur la dernièrecolonne second membre alors le système n'admet aucune solution.Sinon le système admet au moins une solution.Le nombre d'inconnues principales est égal au nombre de pivots, ilest égal au rang de la matrice.D. CransacAnalyse
Page 42 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesx+yz=2E1xy=0E2x+4y+z=2E3⇔xy=0E ′1 = E2x+yz=2E ′2 = E1x+4y+z=2E ′3⇔xy=0E1”2yz=2E2” = E ′2 E ′15y+z=2E3” = E ′3 E ′1⇔xy=0E12yz=2E272z=7E3 = E3” 5/2E2”⇔xy=02yz=1z=2⇔x=0y=0z=1D. CransacAnalyse
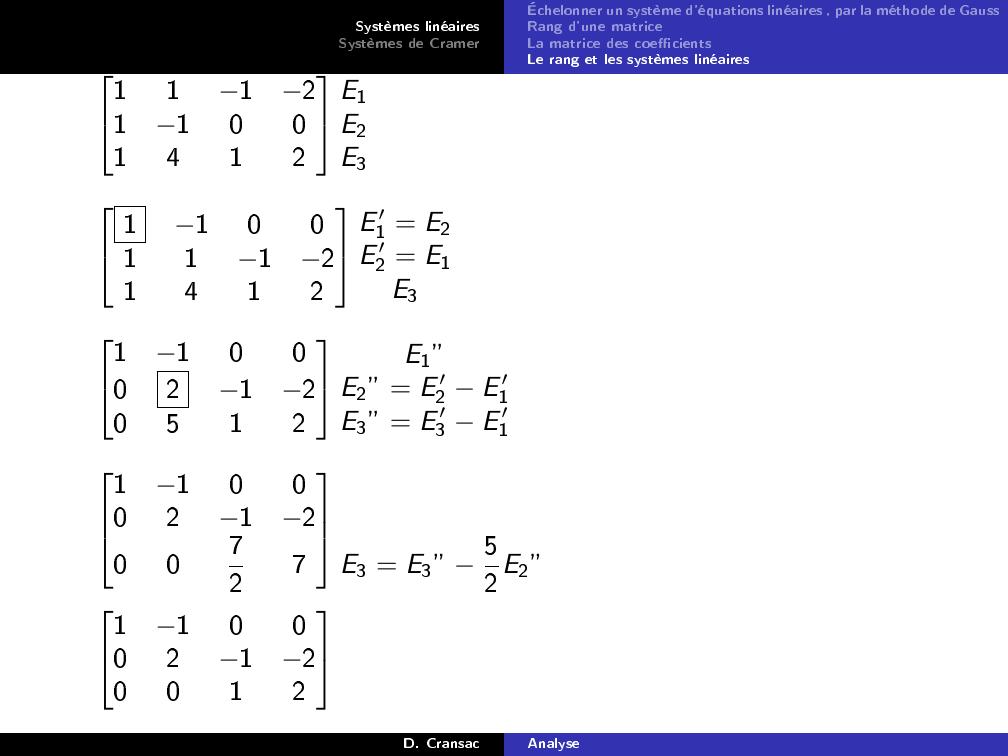
Page 43 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéaires111211001412E1E2E3110011121412E ′1 = E2E ′2 = E1E3110002120512E1”E2” = E ′2 E ′1E3” = E ′3 E ′11100021200727E3 = E3” 52E2”110002120012D. CransacAnalyse
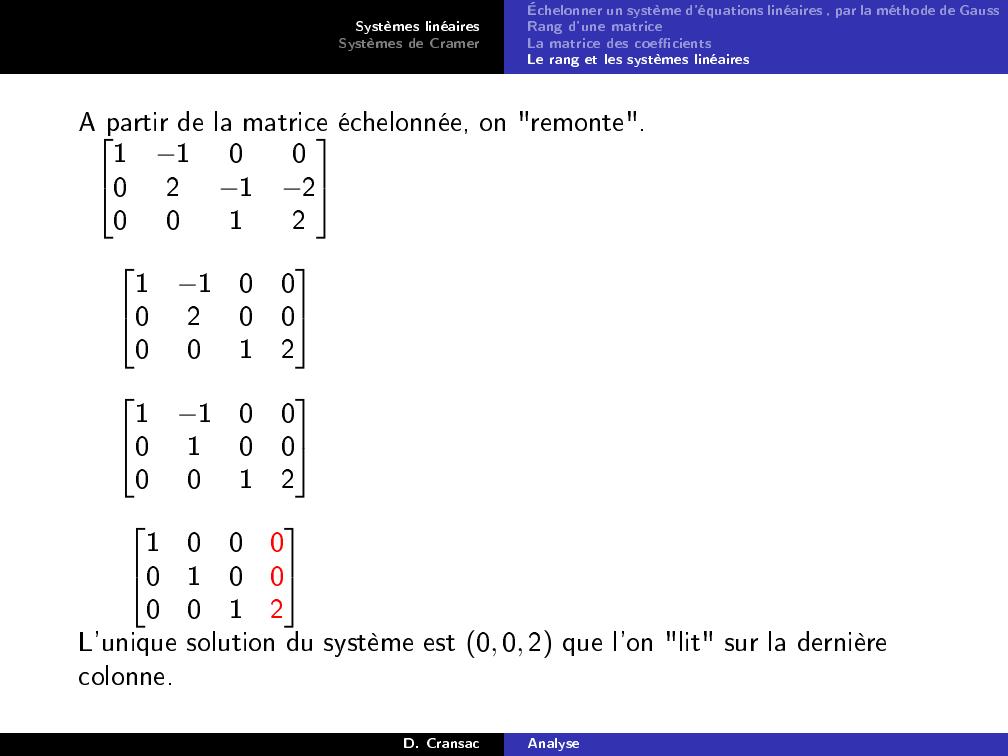
Page 44 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesA partir de la matrice échelonnée, on "remonte".110002120012110002000012110001000012100001000012L'unique solution du système est 0, 0, 2 que l'on "lit" sur la dernièrecolonne.D. CransacAnalyse
Page 45 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSi l'on obtient la matrice augmentée :124800020000Il n'y a pas de solution car sur la dernière ligne où il n'y a pas quedes 0, seul le second membre n'est pas nul.Si l'on obtient la matrice augmentée :124800110000Il n'y a que deux pivots principaux donc il y a une innité desolutions. Pour les décrire, on revient au systèmex+2y+4z=8z=1 ⇔x+2y+4z=8z=1 ⇔Les inconnues principales sont x etz et s'expriment en fonction des autres inconnues y qui peuvent êtreconsidérées comme des paramètres :E ⇔x=2y 4z + 8z=1⇔x=2y + 4z=1L'ensemble des solutions est donc S = 2y + 4; y; 1, y RD. CransacAnalyse
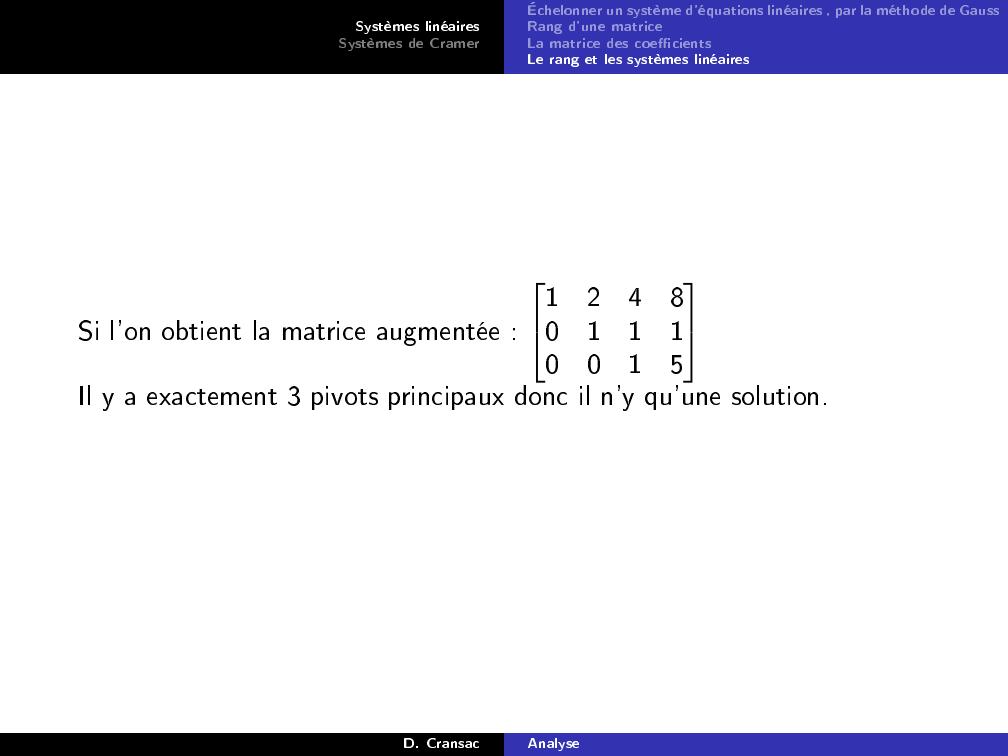
Page 46 : Systèmes linéairesSystèmes de CramerÉchelonner un système d'équations linéaires , par la méthode de GaussRang d'une matriceLa matrice des coecientsLe rang et les systèmes linéairesSi l'on obtient la matrice augmentée :124801110015Il y a exactement 3 pivots principaux donc il n'y qu'une solution.D. CransacAnalyse
Page 47 : Systèmes linéairesSystèmes de CramerOn peut donner des critères selon lesquels un système aura une solutionunique.TheoremUn système est de Cramer si et seulement si son système admet une seulesolution.TheoremUn système de n équations à n inconnues est un système de Cramer si laméthode du pivot de Gauss fait apparaître successivement n pivots nonnuls ce qui est équivalent au fait que le rang de la matrice du systèmeest n.D. CransacAnalyse
Page 48 : Systèmes linéairesSystèmes de CramerExercicePour quelles valeurs du paramètre ℓle système suivant est-il de Cramer ?2x + 3y + z = 4x + y + 2z = 57x + 3y + ℓ5z = 7SolutionOn construit la matrice augmentée et on en détermine une formeéchelonnée :2314112573ℓ571125231473ℓ57112505514010ℓ+ 94211250551400ℓ114Si ℓ= 1, le système n'admet pas de solution.Si ℓ̸= 1 le système admet une unique solution : il est de rang 3.C'est un système de Cramer.D. CransacAnalyse
Page 49 : Systèmes linéairesSystèmes de CramerMéthodologie pour résoudre un système d'équations linéairesAvant tout calcul, observer le système, les inconnues, les coecients, lessignes.Réorganiser le système et simplier les multiples s'il y a diviser leséquations par une constante.Regrouper les équations similaires.Quelques cas classiques :1Eectuer les somme, demi-somme, diérence, demi-diérence.2Utiliser la substitution si les coecents sont simples 1 ou -1.3Penser à essayer la somme de toutes les équations.RésolutionAttention aux équations de compatibilité.S'il a une innité de solutions, dénir les inconnues principales etcelles qui joueront le rôle de paramètre.Prendre soin de bien décrire les solutions.D. CransacAnalyse
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49