CM1 Tribu et application mesurable

Télécharger le CM1 Tribu et application mesurable en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Page 1 : Ingénieurs 1ère année : Mathématiques appliquéesMesure et intégrationCM1 – Tribu et application mesurableNisrine FORTIN CAMDAVANT

Page 2 : 1Introduction au module2Algèbre de Boole et tribu3Tribu engendrée, tribu borélienneTribu engendréeTribu borélienne4Application mesurable

Page 3 : Introduction au module et organisation

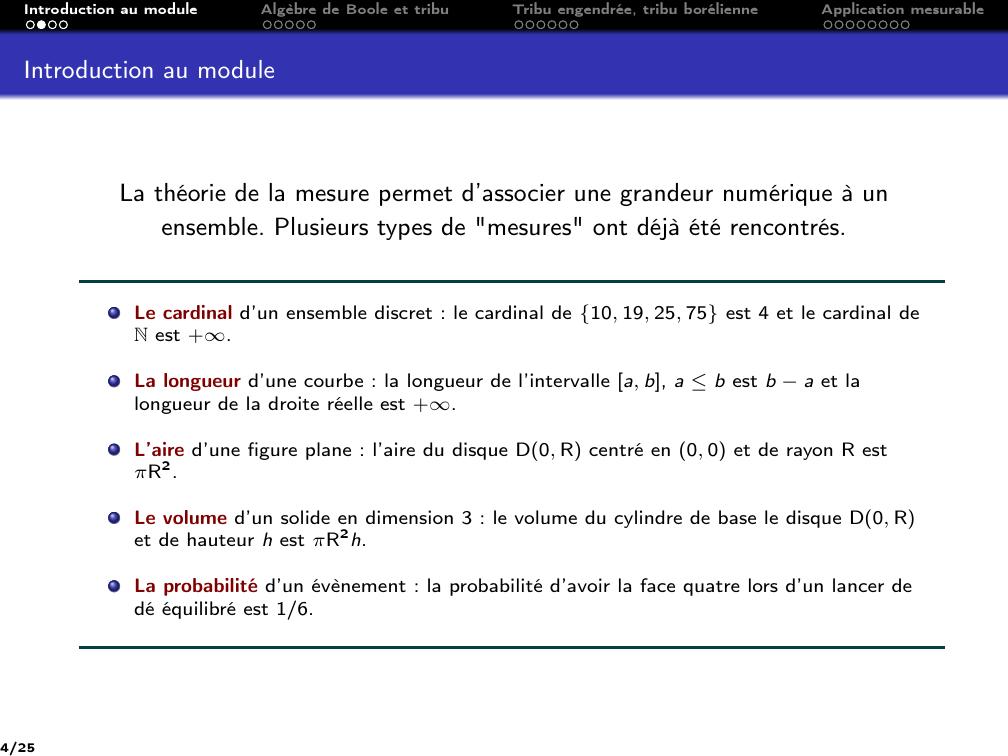
Page 4 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableIntroduction au moduleLa théorie de la mesure permet d’associer une grandeur numérique à unensemble. Plusieurs types de "mesures" ont déjà été rencontrés.Le cardinal d’un ensemble discret : le cardinal de 10, 19, 25, 75 est 4 et le cardinal deN est +.La longueur d’une courbe : la longueur de l’intervalle a, b, a b est b a et lalongueur de la droite réelle est +.L’aire d’une figure plane : l’aire du disque D0, R centré en 0, 0 et de rayon R estπR2.Le volume d’un solide en dimension 3 : le volume du cylindre de base le disque D0, Ret de hauteur h est πR2h.La probabilité d’un évènement : la probabilité d’avoir la face quatre lors d’un lancer dedé équilibré est 1/6.4/25

Page 5 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableAperçu sur l’organisation du moduleCes exemples forment des cas particuliers d’une notion plus générale demesures Chapitre 2, outil de base pour une nouvelle théorie del’intégration, dite intégrale de Lebesgue Chapitre 3.L’intégrale au sens de Lebesgue généralise la notion de l’intégrale deRiemann. Cette nouvelle théorie s’applique à une classe de fonctionsbeaucoup plus grande les fonctions mesurables, cette dernière étend lanotion de continuité de fonctions Chapitre 1.Une mesure est associée à une famille d’ensembles à mesurer, appeléetribu de parties Chapitre 1. Ainsi, une tribu va englober des ensemblesmesurables par une mesure donnée.On définira les fonctions qui préservent la propriété de mesurabilité del’image réciproque d’un ensemble mesurable.Cette théorie s’appliquera à des théorèmes de convergence beaucoup pluspuissants : théorème de convergence monotone, théorème de convergencedominée Chapitre 4.5/25

Page 6 : Algèbre de Boole et tribu

Page 7 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableIntuitivement, si on se place dans un ensemble non vide Ω, une tribu définie surΩcontiendra des sous-ensembles de Ω. Ces ensembles qu’on mesure seront"rassemblés" de la façon suivante ::::::::::::::::::::::::::::::::::::::::::::::::::::::La mesure choisie doit nous permettre de mesurer ΩdoncΩdoit appartenir à la tribu ;Si A appartient à la tribu, on peut donc la mesurer et on souhaite que lecomplémentaire de A dans Ωsoit aussi mesurable donc on impose dans ladéfinitionla condition de stabilité par passage au complémentaire ;Si on sait mesurer deux parties A et B appartiennent donc à la tribu, onsouhaite que leur union soit aussi mesurable donc on impose dans ladéfinitionla condition de stabilité par union dénombrable.:::::::::::::::::::::::::::::::::::::::::::::::::::::7/25

Page 8 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableAlgèbre de Boole et tribuAlgèbre de BooleSoit A PΩ. On dit que A est une algèbre de Boole de parties de Ω si ellevérifie les propriétés suivantes :1ΩA,2A A =⇒Ω\A A,3A A, B A =⇒A B A.TribuSoit T PΩ, on dit que T est une tribu de parties ou σ-algèbre si ellevérifie :1ΩT ,2la stabilité par passage au complémentaire : A T =⇒Ω\A T ,3la stabilité par réunion dénombrable : Si An T pout tout n N alorsSnNAn T .8/25

Page 9 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableAlgèbre de Boole et tribu::::::::::Conséquence::Une tribu est une algèbre de Boole stable par réunion dénombrable.TSi An T pour tout n N alors TnNAn T .Démonstration TD 1♢La plus petite tribu de Ωest T = , Ω , elle est appelée tribugrossière.♢La plus grande tribu de Ωest T = P Ω , elle est appelée tribudiscrète.Exemples.9/25

Page 10 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableLa tribu traceSoient T une tribu de parties sur Ωet U Ω.TU = A U, A T est une tribu sur U. Cette tribu est appelée la tribu trace sur U.Tribu traceDémonstration TD 1.10/25

Page 11 : Tribu engendrée, tribu borélienne

Page 12 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu engendrée, tribu borélienneEn général, une tribu contient énormément d’éléments d’où le nom de tribu.⇝Souvent, on ne peut pas décrire tous les éléments d’une tribu mais celan’a pas d’importance.⇝En effet, ce qu’il faut retenir, sont certaines parties de Ωde la tribu et ondoit rester dans la tribu lorsqu’on itère sur les éléments de la tribu lesopérationsde complémentarité,de réunion dénombrable.12/25

Page 13 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu engendréeSoit Ωun ensemble et H PΩ.DéfinitionOn dit que T est la tribu engendrée par H si T est la plus petite tribu au sensde l’inclusion de parties de Ωcontenant H.On note dans ce cas, T = σH.PropositionσH existe toujours, c’est l’intersection de toutes les tribus sur Ωcontenant H.13/25

Page 14 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu engendrée - ExemplesSi H = ou bien si H = Ω, alorsσH = , Ω.Si H = A ou bien si H = Ac où A ̸= et A ̸= Ω, alorsσH = , Ω, A, Ac.Soient Ω= a, b, c, H = a; b ; on peut décrire la tribu engendréepar H :σH =ΩzΩtribu;; a; bzles éléments de H;b, c z ac;a, c z bc; a, b z ab;czabc.14/25

Page 15 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu engendréeSoient H1 PΩ et H2 PΩ.1H1 σH1.⇝Par définition de σH1.2Si T est une tribu contenant H alors σH T .⇝Par définition de σH.3Si H1 H2 alors σH1 σH2.⇝H1 H2 σ H2 .⇝σ H2 est une tribu.⇝Donc σ H2 est une tribu qui contient H1 et comme σ H1est la plus petite tribu contenantH1 alorsσ H1 σ H2 .Propriétés.15/25

Page 16 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu borélienneSi l’ensemble Ωpossède une structure topologique, la notion de tribuengendrée permet de définir la plus petite tribu adaptée à cette structure.Définition : Soit Ω, d un espace métrique. On appelle tribu boréliennede Ω, la tribu engendrée par les ouverts de Ω, d. On la note BΩ et seséléments sont appelés les boréliens de Ω.Définition : La tribu borélienne sur R respectivement R est la tribuengendrée par les intervalles ouverts de R.T définit une topologie sur Ωsi ΩT , T , la stabilité par union finie ou infinie etpar intersection finie est vérifiée.Ω, d est un espace métrique lorsque Ωest muni d’une distance d : Ω→R+ vérifiantles propriétés suivantes 1. dx, y = 0 ⇔x = y, 2. dx, y = dy, x et 3.dx, z dx, y + dy, z.16/25

Page 17 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableTribu borélienne1; 2 BR, en effet, 1; 2 = 1; 2 1 et♢1; 2 BR,♢1 =+Tn=11 1n ; 1 + 1nzAnBR.Exemple.17/25

Page 18 : Application mesurableLa notion de fonctions mesurables étend la notion de fonctions continues. Elleprend son sens sur des ensembles munis d’une tribu et joueront un rôleimportant dans l’intégration au sens de Lebesgue.On appelle espace mesurable tout couple Ω, T formé par un ensemble Ωetune tribu T sur Ω.Les ensembles mesurables sont les parties de Ωqui appartiennent à T : A estmesurable si A T .

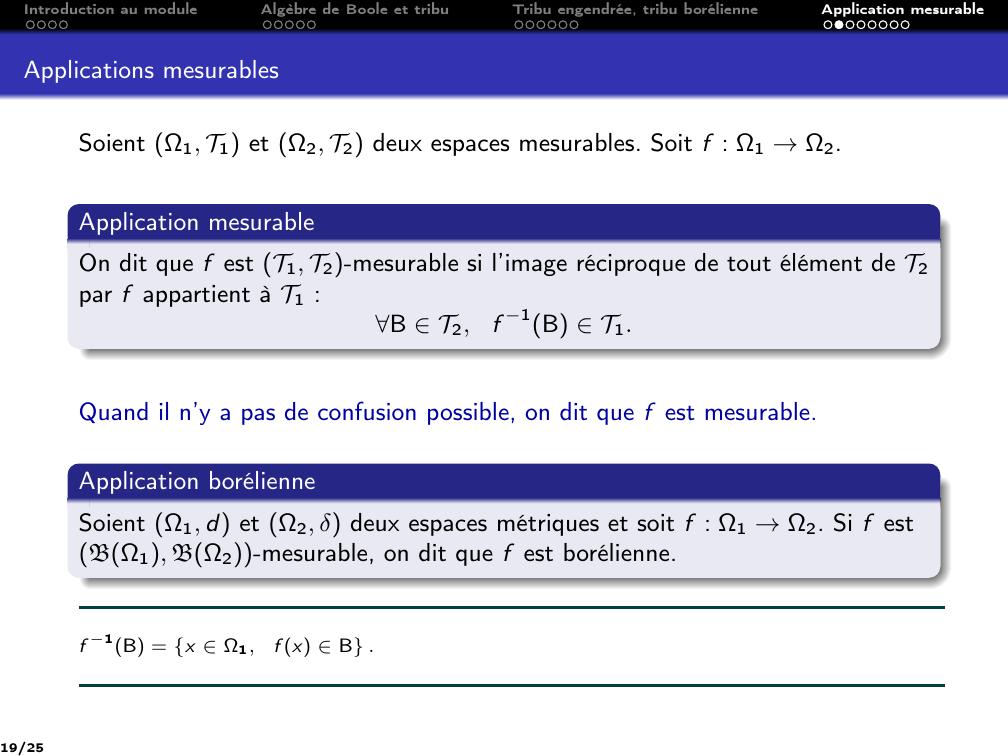
Page 19 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableApplications mesurablesSoient Ω1, T1 et Ω2, T2 deux espaces mesurables. Soit f : Ω1 →Ω2.Application mesurableOn dit que f est T1, T2-mesurable si l’image réciproque de tout élément de T2par f appartient à T1 :B T2,f 1B T1.Quand il n’y a pas de confusion possible, on dit que f est mesurable.Application borélienneSoient Ω1, d et Ω2, δ deux espaces métriques et soit f : Ω1 →Ω2. Si f estBΩ1, BΩ2-mesurable, on dit que f est borélienne.f 1B = x Ω1,f x B .19/25

Page 20 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableSi f est une fonction constante alors f est mesurable, en effet :x Ω1, f x = y0,où y0 Ω2.Soit B TY alors f 1B = x Ω1, y0 B =si y0 /BΩ1si y0 BPuisque T1 est une tribu sur Ω1 alors Ω1 T1 et T1, ainsif 1B T1.La fonction constante est donc mesurable.Exemple.20/25

Page 21 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurable1Soit f : Ω1, T1 →Ω2, T2. Si T2 = σ C2 alors f est mesurable siet seulement siB C2,f 1 B T1.Démonstration – Voir Notes de cours.2Soient Ω, T un espace mesurable et A une partie de Ω.La fonction indicatrice 1A est mesurable si et seulement si A T .Démonstration – Voir TD 1.3Soient Ω1, T1, Ω2, T2 et Ω3, T3 des espaces mesurables. Soientf : Ω1 →Ω2 une fonction T1, T2-mesurableg: Ω2 →Ω3 une fonction T2, T3-mesurablealors g ◦f est T1, T3-mesurable.⇝Démonstration – Voir TD 1.Propriétés.21/25

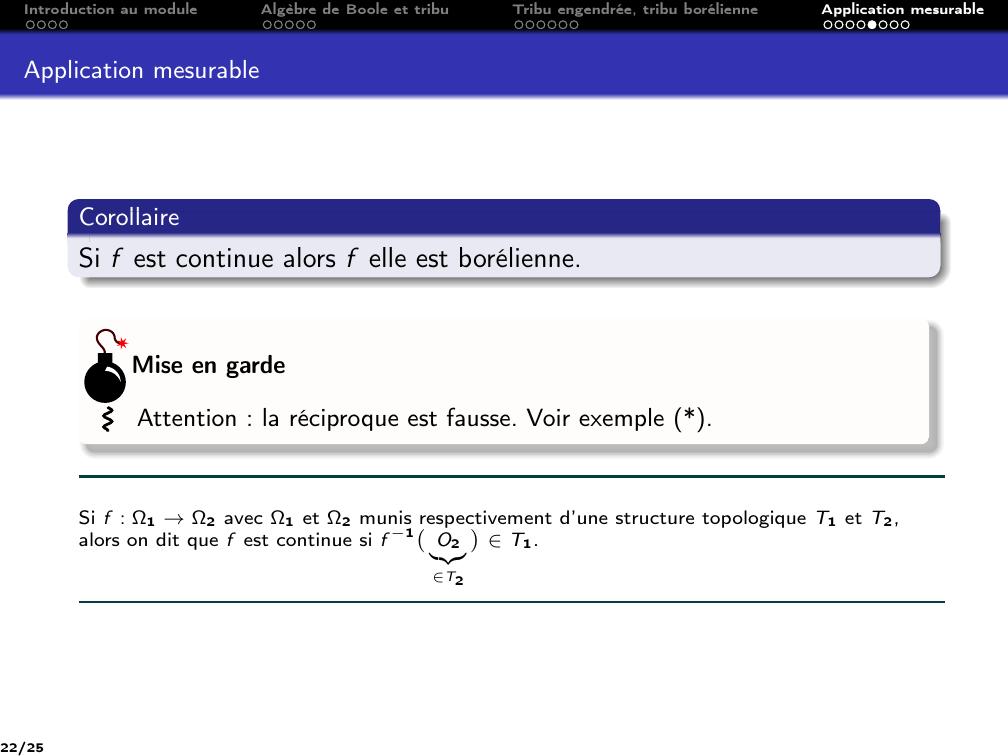
Page 22 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableApplication mesurableCorollaireSi f est continue alors f elle est borélienne.Attention : la réciproque est fausse. Voir exemple .Mise en gardeSi f : Ω1 →Ω2 avec Ω1 et Ω2 munis respectivement d’une structure topologique T1 et T2,alors on dit que f est continue si f 1O2zT2T1.22/25

Page 23 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableSoit Ω, T un espace mesurable, f , g : Ω, T →R, BR des fonc-tions mesurables et λ R, alorsf + g,fg,λf ,minf , g,maxf , g.sont mesurables.Opérations sur les fonctions mesurables numériquesDémonstrations – Voir Notes de cours.Soient fn : Ω→R des fonctions mesurables, alorsinfn fn,supn fn,lim infnfnetlim supnfnsont mesurables à valeurs dans R.Soit f : Ω→R une fonction mesurable, alors f est une fonctionmesurable.ConséquencesDémonstrations – TD 1.23/25

Page 24 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurablePropositionSoit Unn une suite finie ou infinie d’éléments disjoints deux à deux dans T1telle que Ω1 = SnNUn. Soit f : Ω1 →Ω2, alors f est T1, T2-mesurable si etseulement si fUn restriction de f à Un est TUn, T2-mesurable pour tout n.24/25

Page 25 : Introduction au moduleAlgèbre de Boole et tribuTribu engendrée, tribu borélienneApplication mesurableΩ1 = Ω2 = R, T1 = T2 = BR.f :Ω1 →Ω2x 7→f x =1xsi x ̸= 01si x = 0On note U0 = ; 0, U1 = 0 et U2 =0; +. ; 0 est ouvert ⇒U0 BR.0 est fermé ⇒U1 BR.0; + est ouvert ⇒U2 BR.U0 U1 U2 = R.fU0 est continue ⇒f est TU0, BR-mesurable.fU1 est constante ⇒f est T0, BR-mesurable.fU2 est continue ⇒f est TU2, BR-mesurable.f est donc BR, BR-mesurable.Exemple.25/25

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25