CM1 VARC

Posté le 31/12/2025

Chargé de TD/CM :

25 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

Page 1 : Variables aléatoires réelles continuesKhalid El Amine I.Department of MathematicsDans tout ce chapitre : Ωest un univers. Ω, A est un espace probabilisable. Ω, A, P est un espace probabilisé. R sera toujours muni de la tribu de Borel, BR. Toutes les variables aléatoires sont dénies sur un espace probabilisé Ω, A, P et à valeurs dansl'espace probabilisable R, BR. On considère les variables aléatoires réelles X telles que XΩ est non discret.1Variable aléatoire réelleDénition 1.1 Variable aléatoire réelleOn appelle variable aléatoire réelle v.a.r. en abrégé sur Ω, A toute fonctionX : Ω, A →R, BRvériant :X1B A,B BR• XΩ est appelé univers image de Ωpar X.Proposition 1.2 Soit X : Ω, A →R, BR une fonction. AlorsX est une v.a.r. sur Ω, A, si et seulement si, X1 , x A,x RPreuve.1.1Loi d'une variable aléatoire réelleDénition 1.3 Loi d'une v.a.r.Soit X : Ω, A →R, BR une v.a.r.. Soit P une probabilité sur Ω, A. La fonctionPX : BR→RB7→PXB = PX1Best appelée probabilité image de P par X, ou loi de X sous P.Remarque. PX est parfois notée LX et simplement appelée loi de X.1

Page 2 : 2K. El AmineProposition 1.4 Soit X : Ω, A →R, BR une v.a.r.. Soit P une probabilité sur Ω, A. AlorsPX est une probabilité sur R, BRi.eR, BR, PX est un espace probabilisé.Proof.Remarque. Dans la suite, on notera simplement X : Ω→R au lieu de X : Ω, A →R, BR.1.2Fonction de répartition d'une variable aléatoire réelleDénition 1.5 Fonction de répartition d'une v.a.r.Soit X une v.a.r.. La fonctionFX : R→Rx7→FXx = PX , xest appelée fonction de répartition de X, abrégée en f.r..Remarque.• x R, FXx 0, 1.• FXx représente la probabilité de toutes les réalisations inférieures ou égales au réel x.• La f.r. FX est aussi appelée fonction de distribution cumulative de X, abrégée en f.d.c..Proposition 1.6 Soit X une v.a.r. et FX sa f.r.. Alors :1 FX est croissante sur R2limx→FXx = 0 etlimx→+FXx = 13 FX est continue à droite sur RPreuve.Remarque. Comme FX est monotone et bornée, elle admet une limite nie à gauche en tout pointde R.On rappelle le théorème suivantThéorème 1.7 Si une fonction est monotone sur un intervalle de R, alors l'ensemble des points oùelle n'est pas continue est ni ou dénombrable.Remarque. Toute f.r. est donc continue sur R, sauf éventuellement sur une partie discrète.Proposition 1.8 Soit F : R →R une fonction.Si1 F est croissante sur R2limx→Fx = 0 etlimx→+Fx = 13 F est continue à droite sur RAlors, F est la f.r. d'une certaine v.a.r..Proof.

Page 3 : v.a.r. continues3Notations. Pour alléger les notations, on écrira : X B pour l'ensemble X1B où B BR, i.e. :X B = X1B = ω Ω: Xw BDe même : X = x = X1x = ω Ω: Xw = x, où x R. X x = X1 , x = ω Ω: Xω x X x = X1 , x = ω Ω: Xω x a X b = X1a, b = ω Ω: a Xω b etc. a RFXa = limx→aFXx and FXa+ = limx→a+ FXxProposition 1.9 Soit X une v.a.r. et FX sa f.r.. Soit a, b R avec a b. Alors :1 PX a = FXa2 PX a = 1 FXa3 Pa X b = FXb FXa4 PX = a = FXa+ FXaPreuve.Proposition 1.10 Soit X et Y deux v.a.r. sur le même Ω, A, P. AlorsFX = FY , si et seulement si, PX = PYPreuve.Remarque. La fonction de répartition FX d'une v.a.r. caractérise complètement sa loi PX.1.3Indépendance de variables aléatoires réelles1.3.1Indépendance de deux variables aléatoires réellesDénition 1.11 Indépendance de deux v.a.rsSot X et Y deux v.a.rs sur le même Ω, A, P. X et Y sont dites indépendantes, si et seulement si,B, B′ BR les événement X1B et Y 1B′ sont indépendantsNotation. Notons I, l'ensemble des intervalles de R.Proposition 1.12 Soit X et Y deux v.a.rs sur le même Ω, A, P.Les assertions suivantes sont équivalentes1 X et Y sont indépendantes.2 B, B′ BR2 ,PX B Y B′ = PX BPY B′3 I, I′ I2 ,PX I Y I′ = PX IPY I′4 x, y R2 ,PX x Y y = PX xPY yPreuve.

Page 4 : 4K. El AmineRappel. Si A est un événement, alors sa fonction indicatrice IA est une v.a.r..Proposition 1.13 Deux événements A et A′ sont indépendant, si et seulement si, leurs fonctionsindicatrices IA et IA′ sont indépendantes.Proof.1.3.2Indépendance d'une suite de variables aléatoires réellesDénition 1.14 Indépendance d'une suite nie de v.a.rsSoit n N avec n 1. Soit X1, . . . , Xn une suite nie de n v.a.rs sur le même Ω, A, P.La suite X1, . . . , Xn est dite indépendante, si et seulement si,B1, . . . , Bn BRn, la suite d'événements X11 B1, . . . , X1n Bn est indépendanteProposition 1.15 Soit n N avec n 1. Soit X1, . . . , Xn une suite nie de n v.a.rs sur Ω, A, P.Les assertions suivantes sont équivalentes1 X1, . . . , Xn est une suite indépendante2 B1, . . . , Bn BRn , PX1 B1. . .Xn Bn = PX1 B1 · · · PXn Bn3 I1, . . . , In In , PX1 I1 . . . Xn In = PX1 I1 · · · PIn Bn4 x1, . . . , xn Rn , PX1 x1 . . . Xn xn = PX1 x1 . . . PXn xnProof.Proposition 1.16 Soit n N avec n 1. Soit X1, . . . , Xn une suite nie de n v.a.rs sur Ω, A, P.Pour chaque i 1, n, soit fi : R →R une fonction quelconque. AlorsX1, . . . , Xn est indépendante =⇒f1X1, . . . , fnXn est indépendantePreuve.Dénition 1.17 Indépendance d'une suite innie de v.a.rsSoit XnnNune suite de v.a.rs sur Ω, A, P.La suite XnnNest dite indépendante, si etseulement si, pour toute partie nie I de N, avec I 1, la suite nie XiiI est indépendante.

Page 5 : v.a.r. continues52Variable aléatoire réelle continueDénition 2.1 v.a.r. continueUne v.a.r. X est dite continue, si et seulement si, sa f.r. FX est continue sur R.Proposition 2.2 Soit X une v.a.r.. AlorsX est continue, si et seulement si, PX = x = 0, x RPreuve.Remarque. Soit a R. PX = a = 0 n'implique pas que l'événement X = a est impossible. Sic'était le cas, alors pour tout x R, l'événement X = x serait impossible et X ne pourrait prendreaucune valeur.Proposition 2.3 Soit X une v.a.r. continue. Alors, B BR,B est discret =⇒PX B = 0Preuve.Exercice. Supposons que X soit une v.a.r. continue.1 Que vaut PX Q ?2 Que vaut PX 0, 1 Q?Solution.Proposition 2.4 Soit X une v.a.r. continue de f.r. FX. Pour tout a, b R avec a b :• PX a = PX a = FXa• PX a = PX a = 1 FXa• Pa X b = Pa X b = Pa X b = Pa X b = FXb FXaPreuve. Par application de de l'égalité PX = x = 0, x R et de la dénition d'une f.r. d'unev.a.r..3Variable aléatoire réelle absolument continue3.1Fonction de densité de probabilitéDénition 3.1 Fonction de densité de probabilitéSoit f : R →R une fonction.On dit que f est une fonction de densité de probabilité f.d.p. en abrégé sur R, si et seulement si,1 fx 0, x R2 f est continue sur R sauf sur une partie nie.3Z +fxdx = 1

Page 6 : 6K. El AmineExemple. Soit f : R →R la fonction dénie parfx = xI1,1Vérier que f est une fonction de densité de probabilité.Solution.Remarque. Soit f une fonction de densité de probabilité. f peut ne pas être bornée. f 0 sur R etZRfxdx = 1 ⇏f 1 sur R ; contrairement à la fonction de masse deprobabilité. fx ne correspond pas à une valeur de probabilité.Exemple. Soit f : R →R dénit parfx =14xsi 0 x 10sinonMontrer que f est fonction de densité de probabilité.Solution.3.2Variable aléatoire réelle absolument continueDénition 3.2 v.a.r. absolument continueUne v.a.r. X est dite absolument continue ou de loi absolument continue, si et seulement si,il existe une f.d.p. noté fX, telle que :B BRPX B =ZBfXxdxDans ce cas• fX est alors appelée fonction de densité de probabilité de X.• SX = x R : fXx ̸= 0 est appelé support de la loi de X.Rappel. La loi de probabilité d'une v.a.r. X, noté PX, est une probabilité sur R, BR. Elle estdénit parB BRPXB = PX BRemarque. Il n'y a pas d'unicité de la f.d.p. pour une v.a.r. X.Si fX est une f.d.p. de X, alors n'importe quelle f.d.p.f égale à fX sauf par exemple sur unensemble ni de points est aussi une f.d.p. de X. Par exemplef1x = I0,1 ;f2x = I0,1 ;f3x = I0,1 ;f4x = I0,1sont des f.d.p. de la même v.a.r..Exemple. Si X est une v.a.r. absolument continue de f.d.p. fX, alors :PX 1, 3 =Z1,3fXxdx =Z 31fXxdxOn rappelle que X 1, 3 se note 1 X 3.Proposition 3.3 Soit X une v.a.r..Si X est absolument continue, alors X est continuePreuve. a RPX = a = PX a =ZafXxdx =Z aafXadx = fXaZ aa1dx = fXa × 0 = 0

Page 7 : v.a.r. continues73.3Fonction de répartition d'une variable aléatoire réelle absolument con-tinueThéorème 3.4 Soit X une v.a.r. absolument continue, de f.d.p. fX. La f.r. de X, notée FX estdonnée par :FXx =Z xfXtdtx RPreuve. Vient de la formule de la loi d'une v.a.r. absolument continue.FXx = PX x = PX , x =Z xfXtdtGraphe de FX:Exemple. Soit f : R →R la fonction dénie par fx = c1 xI0,1x, où c R.1 Déterminer la constante c pour que f soit une f.d.p.. Tracer la courbe de f.2 Supposons que X soit une v.a.r. absolument continue ayant f pour f.d.p..Déterminer FX, la f.r. de X et dessiner sa courbe.Solution.Proposition 3.5 Soit X une v.a.r. absolument continue de f.d.p. fX et de f.r. FX.Pour tout a, b R avec a b :• PX a = PX a = FXa =Z afXtdt• PX a = PX a = 1 FXa =Z +afXtdt• Pa X b = FXb FXa =Z bafXtdt• Pa X b = Pa X b = Pa X b = Pa X bPreuve. Par application de de l'égalité PX = x = 0, x R ; de la dénition d'une f.r. d'unev.a.r. et de la dénition de la loi d'une v.a.r. absolument continue.Représentations graphique de PX a, PX a et Pa X b :

Page 8 : 8K. El AmineProposition 3.6 Soit X une v.a.r. et FX sa f.r..Si X est absolument continue de f.d.p. fX, alors1 FX est continue sur R.2 FX est de classe C1 sur R, sauf sur une partie nie.3 Si fX est continue en x0 R, alors FX est dérivable en ce point et on a :F′Xx0 = fXx0Preuve.La réciproque du résultat ci-dessus est donnée par leThéorème 3.7 Soit X une v.a.r. de f.r. FX.Si FX vérie :1 FX est continue sur R.2 FX est de classe C1 sur R, sauf en un nombre ni de points.Alors1 X est une v.a.r. absolument continue.2 Toute fonction f : R →R telle quef 0sur Rfx = F′Xxen tout point x où FX est dérivableest une f.d.p. de X.Preuve.Remarque Importante. Si X est une v.a.r. absolument continue de f.r. FX, alors FX est dérivablepresque partout théorème de diérentiation de Lebesgue. Ceci permet d'associer à X une f.d.p.fX de façon canonique. Dans la pratique on prendrafXx =F ′Xxen tout point x où FX est dérivable0ailleursExemple. Soit X une v.a.r. dont la f.r. FX est dénit parFXx =0if x 0xif 0 x 11if 1 xMontrer que X est absolument continue et proposer une f.d.p. de X.Solution.

Page 9 : v.a.r. continues9Figure 1: Fonction de CantorDiscussion.Existence de v.a.r. continue mais non absolument continue.Dans tous les cas raisonnables, une v.a.r. continue aura une f.d.p. ; c'est-à-dire qu'elle sera absolumentcontinue. Toutefois, il est possible d'établir l'existence de v.a.rs qui sont continues mais pas absolumentcontinues. Un exemple remarquable est la loi de Cantor. La f.r. F de la loi de Cantor est continuesur R et dérivable de dérivée nulle presque partout, mais elle n'est pas absolument continue.La loi de Cantor est une loi de probabilité singulière dont le support est l'ensemble de Cantor. Saf.r. est représentée par l'escalier de Cantor, aussi appelé escalier du diable voir gure 1.La loi de Cantor a les propriétés suivantes : Elle n'est pas absolument continue par rapport à la mesure de Lebesgue, car elle n'admet pasde fonction de densité de probabilité. Elle n'est pas discrète, car elle n'admet pas de fonction de masse de probabilité. Elle n'est pas non plus une loi mixte des deux lois citées ci-dessus. Son support est non discret et de mesure de Lebesgue nulle.4Moments d'une variable aléatoire réelle absolument continueOn abrégera souvent variable aléatoire réelle absolument continue en v.a.r.a.c..4.1EspéranceDénition 4.1 EspéranceSoit X une v.a.r.a.c. de f.d.p. fX. On dit que X admet une espérance, si est seulement si,Z +xfXxdx +Dans ce cas, l'espérance de X est notée EX et elle est dénie par :EX =Z +xfXxdx

Page 10 : 10K. El AmineRemarque.Z +xfXxdx existe toujours, c'est un élément de 0, +.La nitude de cette intégrale garantie que l'espérance EX est bien dénie.Exemple. Loi de Cauchy standardSoit X une v.a.r.a.c. de f.d.p.fXx = 1π11 + x2x RMontrer que X n'admet pas d'espérance.Solution.4.2Propriétés de l'espéranceThéorème 4.2 Théorème de transfertSoit X : Ω→R une v.a.r.a.c. de f.d.p. fX.Soit g : R →R une fonction continue par morceaux g mesurable sut. Alors• La v.a.r. gX est absolument continue.• SiZ +gxfXxdx , alors, gX admet une espérance. Elle est donnée parEgX =Z +gxfXxdxPreuve.Exemple. Soit X une v.a.r.a.c. de f.d.p.fXx = 3x2I0,1xQue vaut a EX ? b EX2 ? c EX + X2 ?Solution.Corollaire 4.3 Soit X une v.a.r.a.c. admettant une espérance. Soit a, b R. Alors la v.a.r. aX + best absolument continue et admet un espérance donnée parEaX + b = aEX + bPreuve.Remarque. En paticulierEaX = aEX;Ea = aProposition 4.4 Croissance de l'espéranceSoit X et Y deux v.a.r.a.cs. sur le même Ω, A, P, chacune admettant une espérance. AlorsY X=⇒EY EXEn particulier :0 X=⇒0 EXet pour a, b R :a X b=⇒a EX bPreuve.

Page 11 : v.a.r. continues11Théorème 4.5 Linéarité de l'espéranceSoit X et Y deux v.a.r.a.cs. sur le même Ω, A, P, chacune admettant une espérance. Soit a, b R.Alors, la v.a.r. aX + bY admet une espérance et :EaX + bY = aEX + bEY En particulierEX + Y = EX + EY Preuve.Note.Même si X et Y sont absolument continues, rien ne garantie que la v.a.r.aX + bY soitabsolument continue.4.3Variance & Ecart-typeDénition 4.6 Variance & Ecart-typeSoit X une v.a.r.a.c. de f.d.p. fX et admettant une espérance EX. La variance de X est dénit par :V X = EX EX2 =Z +x EX2fXxdxsous réserve de convergence de l'intégrale. L'écart-type de X est dénit par :σX =pV Xsous réserve d'existence de V X.Remarque.• V X est l'écart quadratique moyen de la variable aléatoire X par rapport à sa valeur moyenne.• V X est donc un indicateur mesurant la dispersion des valeurs x de X autour de leurs moyennepondérée EX. Plus précisément, c'est σX =pV X qui mesure l'étendue de cette dispersion.Une petite variance signie que X est fortement concentré et une grande variance signie que X estdispersée.Dénition 4.7 v.a.r. centrée resp. centrée réduiteSoit X une v.a.r.a.c.. On dit que : X est centrée, si elle admet une espérance nulle, i.e. EX = 0. X est centrée réduite, si elle admet une espérance nulle et une variance égale à 1,i.e. EX = 0 et V X = 1.Théorème 4.8 Soit X une v.a.r.a.c.. Si X admet une espérance, alors X EX est centrée. Si X admet une variance non nulle, alors X= X EXσXest centrée réduite.Preuve.

Page 12 : 12K. El Amine4.4Moments d'ordre supérieurDénition 4.9 MomentsSoit X une v.a.r.a.c. de f.d.p. fX. Soit m N. Sous réserve de convergence absolue de l'intégrale : Le moment d'ordre m de X est déni parEXm =Z +xmfXxdx Le moment centré d'ordre m de X est déni parEX EXm =Z +x EXmfXxdxProposition 4.10 Soit X une v.a.r.. Si X admet un moment d'ordre m Nalors X admet desmoments de tout ordre j J1, mK.Preuve.Théorème 4.11 Formule de Köenig-HuyghensSoit X une v.a.r.. Si EX2 existe, alors V X existe et elle est donné par :V X = EX2 E2XPreuve.Proposition 4.12 Soit X une v.a.r. admettant une variance. Alors : V X 0 V aX + b = a2V X,a, b RPreuve.Exemple. Soit X une v.a.r.a.c. telle queEX = 34 et EX2 = 351 Calculer V X.2 Soit Y une nouvelle v.a.r. dénie par Y = 3X 2. Calculer a EY et b V Y .Solution.4.5Cas de deux v.a.r.a.cs indépendantesProposition 4.13 Soit X et Y deux v.a.rs admettant chacune un moment d'ordre 2.Si X et Y sont indépendantes, alors :EXY = EXEY andV X + Y = V X + V Y Preuve.

Page 13 : v.a.r. continues135Lois continues usuelles Toutes les v.a.rs absolument continues ci-après sont dénies sur un espace probabilisé Ω, A, P. v.a.r. absolument continue sera abrégée en v.a.r.a.c..5.1Loi continue uniformeDénition 5.1 Soit a et b deux réels, avec a b. On dit qu'une v.a.r.a.c. X suit une loi continueuniforme sur a, b, si et seulement si, elle admet pour f.d.p.fXx =1b aIa,bxOn note alorsX Ua, bModélisation. La distribution uniforme Ua, b est utiliser pour modéliser une v.a.r. pouvant seproduire équitablement entre a et b.Interprétation. X Ua, b signie : u, v a, b et u′, v′ a, bv u = v′ u′=⇒PX u, v = PX u′, v′i.e. si u, v et u′, v′ sont deux segments de même longueur, alors les événements X u, v etX u′, v′ sont équiprobable.Exemple.Un nombre représenté par X est choisie au hasard entre a et b.X est supposé êtreuniformément distribuée veut dire que la probabilité que X tombe dans un intervalle de longueur l nedépend que de l, pas de la position de l'intervalle dans a, b.Exercice. Soit X Ua, b. Vérier que fX est une f.d.p..Solution.Proposition 5.2 Si X Ua, b, alors :EX = a + b2etV X = b a212Preuve.Proposition 5.3 Si X Ua, b, alors sa f.r. est donnée par :FXx =0si x ax ab asi a x b1si b xPreuve.

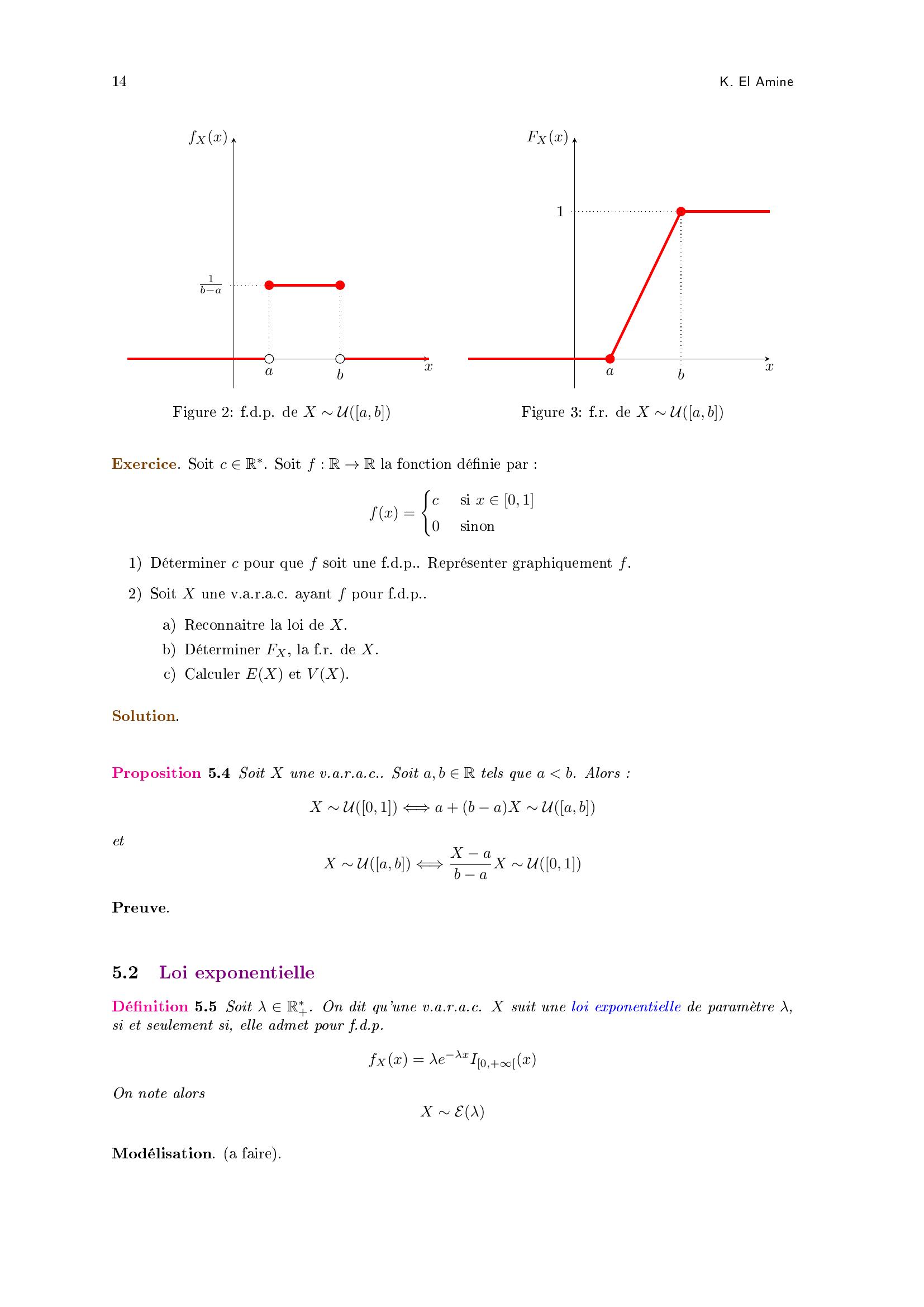
Page 14 : 14K. El Amine1baabxfXxFigure 2: f.d.p. de X Ua, b1abxFXxFigure 3: f.r. de X Ua, bExercice. Soit c R. Soit f : R →R la fonction dénie par :fx =csi x 0, 10sinon1 Déterminer c pour que f soit une f.d.p.. Représenter graphiquement f.2 Soit X une v.a.r.a.c. ayant f pour f.d.p..a Reconnaitre la loi de X.b Déterminer FX, la f.r. de X.c Calculer EX et V X.Solution.Proposition 5.4 Soit X une v.a.r.a.c.. Soit a, b R tels que a b. Alors :X U0, 1 ⇐⇒a + b aX Ua, betX Ua, b ⇐⇒X ab a X U0, 1Preuve.5.2Loi exponentielleDénition 5.5 Soit λ R+. On dit qu'une v.a.r.a.c. X suit une loi exponentielle de paramètre λ,si et seulement si, elle admet pour f.d.p.fXx = λeλxI0,+xOn note alorsX EλModélisation. a faire.

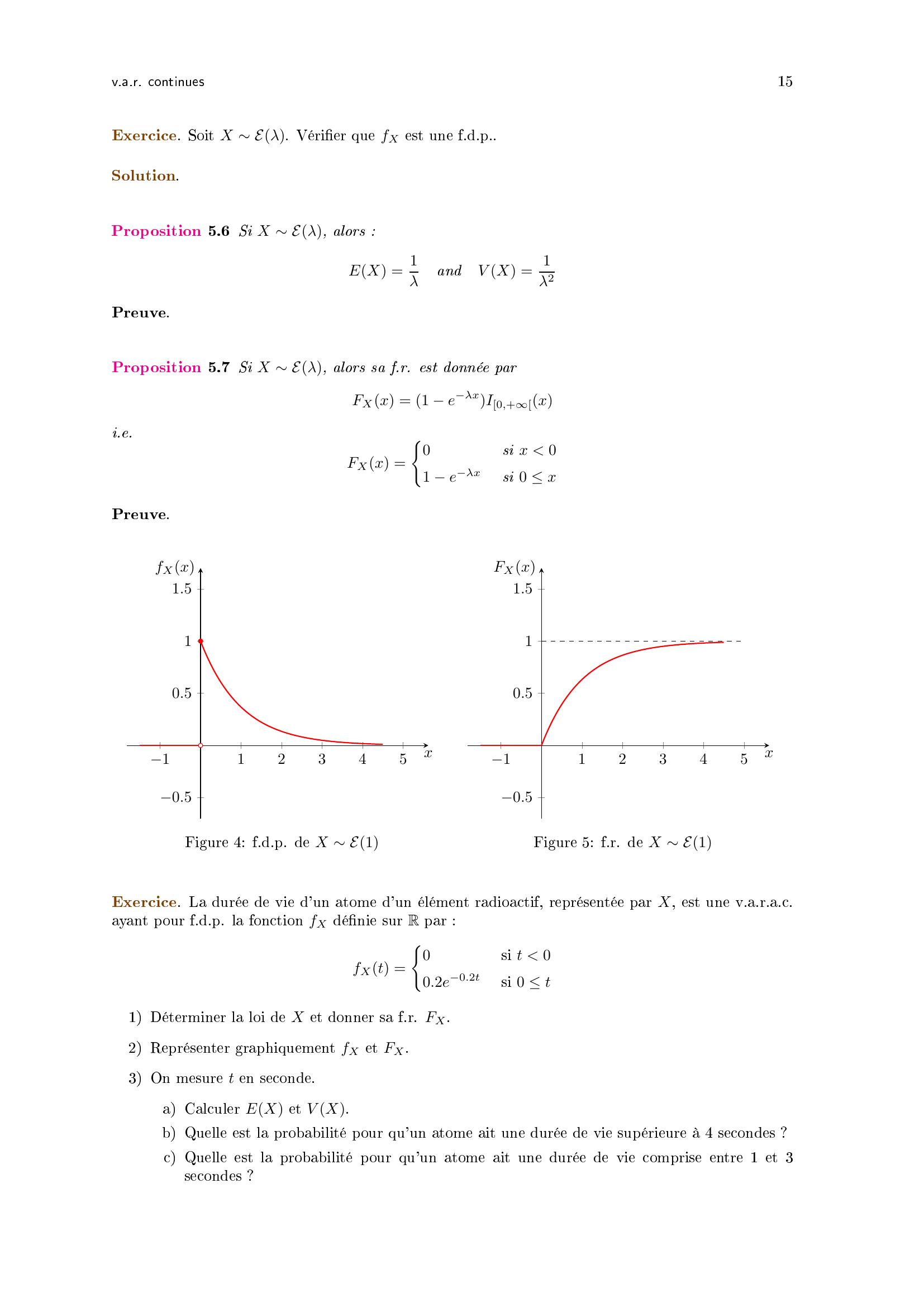
Page 15 : v.a.r. continues15Exercice. Soit X Eλ. Vérier que fX est une f.d.p..Solution.Proposition 5.6 Si X Eλ, alors :EX = 1λandV X = 1λ2Preuve.Proposition 5.7 Si X Eλ, alors sa f.r. est donnée parFXx = 1 eλxI0,+xi.e.FXx =0si x 01 eλxsi 0 xPreuve.1123450.50.511.5xfXxFigure 4: f.d.p. de X E11123450.50.511.5xFXxFigure 5: f.r. de X E1Exercice. La durée de vie d'un atome d'un élément radioactif, représentée par X, est une v.a.r.a.c.ayant pour f.d.p. la fonction fX dénie sur R par :fXt =0si t 00.2e0.2tsi 0 t1 Déterminer la loi de X et donner sa f.r. FX.2 Représenter graphiquement fX et FX.3 On mesure t en seconde.a Calculer EX et V X.b Quelle est la probabilité pour qu'un atome ait une durée de vie supérieure à 4 secondes ?c Quelle est la probabilité pour qu'un atome ait une durée de vie comprise entre 1 et 3secondes ?

Page 16 : 16K. El AmineSolution.Proposition 5.8 Soit X une v.a.r.a.c.. Soit λ R+. alors :X E1 ⇐⇒1λX EλetX Eλ ⇐⇒λX E1Preuve.5.3Loi normale ou loi de GaussLa distribution normale joue un rôle central dans la théorie des probabilités et les statistiques. Unede ses premières applications était due à C.F. Gauss, qui l'utilisa en 1809 pour modéliser les erreursd'observation en astronomie.5.3.1Loi NormaleDénition 5.9 Soit µ R et σ R+. On dit qu'une v.a.r.a.c. X suit une loi normale ou loi deGauss de paramètres µ, σ2, si et seulement si, elle admet pour f.d.p.fXx =1σ2π e12 xµσ 2On note alorsX Nµ, σ2Remarque. Il n'existe pas d'expression analytique simple d'une primitive de la fonction x 7→ex2.On admettra queZ +e12 x2dx =2πExercice. Soit X Nµ, σ2. Vérier que fX est une f.d.p.. Représenter graphiquement fX.Solution.Propriété 5.10 Si X Nµ, σ2, alors sa f.d.p. vérie les propriétés suivantes :1 fX est symétrique par rapport au point µ : fXµ x = fXµ + x,x R.2 fX est maximale au point µ : fXx fXµ,x R.3limx→fXx =limx→+fXx = 0.Preuve.Proposition 5.11 Si X Nµ, σ2, sa f.r. est donnée parFXx =Z x1σ2π e12 tµσ 2dtx RPreuve. C'est simplement la dénition d'une f.r..

Page 17 : v.a.r. continues17Remarque. Soit X Nµ, σ2.Puisque fX est de classe Csur R, FX est aussi de classe Csur R etF ′Xx = fXx x RProposition 5.12 Si X Nµ, σ2, alorsEX = µetV X = σ2Preuve. Voir la sous-section sur la loi normale standard.Proposition 5.13 Transformation aneSoit a, b R avec a ̸= 0. AlorsX Nµ, σ2 =⇒Y = aX + b Naµ + b, aσ2Preuve.Corollaire 5.14 Soit X une v.a.r.a.c.. soit µ R et σ R+. Alors :X Nµ, σ2 ⇐⇒X= X µσN0, 1etX N0, 1 ⇐⇒σX + µ Nµ, σ2Preuve.Remarque. L'intérêt de ce résultat est de ramener tous les calculs sur les lois normales à des calculssur la loi normale standard voir ci-après.5.3.2Loi normale StandardDénition 5.15 La loi normale Nµ, σ2 où µ = 0 et σ = 1 est appelée loi normale standard, et estnotée donc N0, 1.• La f.d.p. de la loi normale standard est souvent noté par la lettre grecque ϕ, i.e.ϕx =12π e12 x2x R• La f.r. de la loi normale standard est souvent noté par la lettre grecque Φ, i.e.Φx =Z xϕtdtx RProposition 5.16 Si X N0, 1, alors :EX = 0etV X = 1Preuve.Corollaire 5.17 Si X Nµ, σ2, alorsEX = µetV X = σ2Preuve.

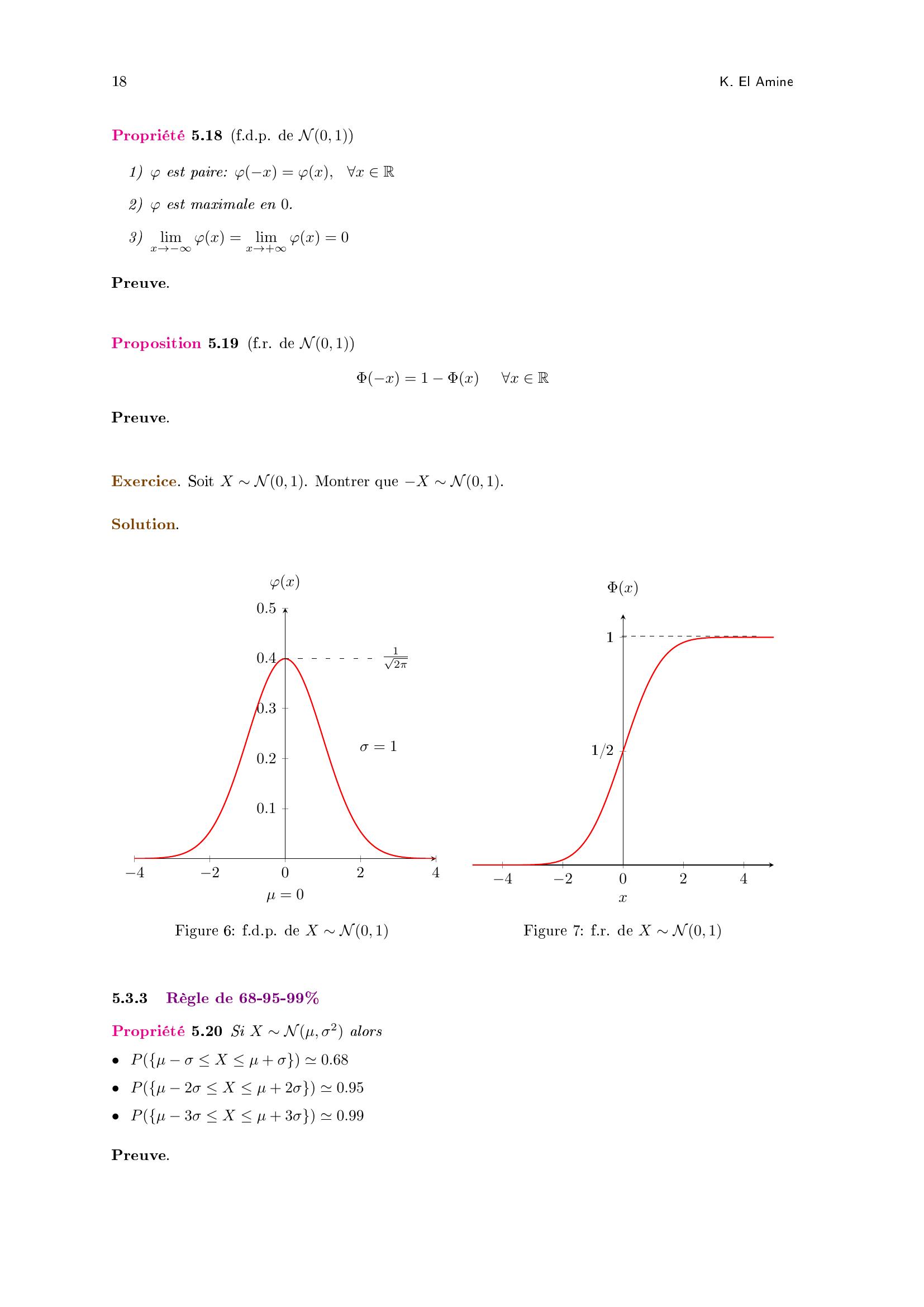
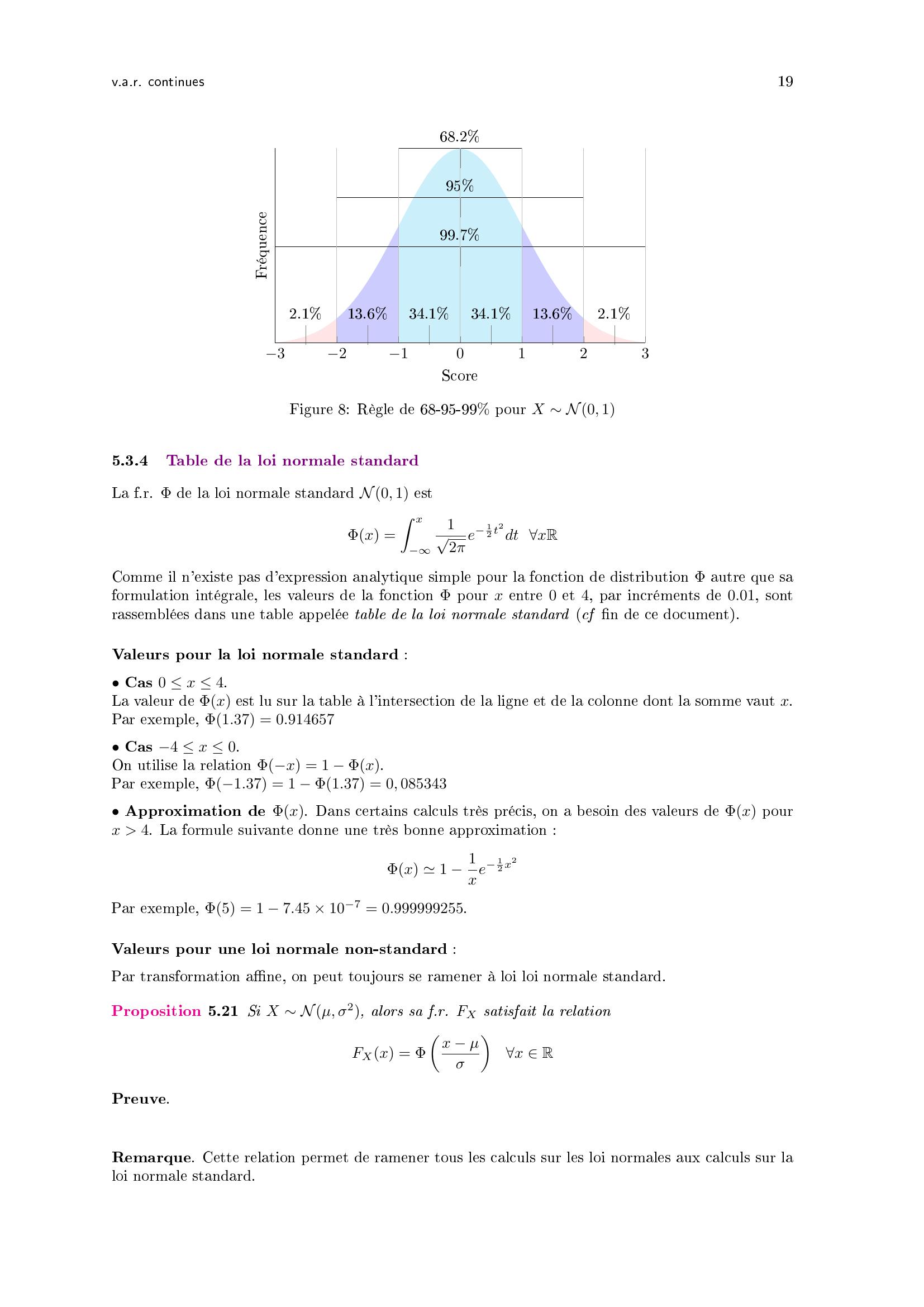
Page 18 : 18K. El AminePropriété 5.18 f.d.p. de N0, 11 ϕ est paire: ϕx = ϕx,x R2 ϕ est maximale en 0.3limx→ϕx =limx→+ϕx = 0Preuve.Proposition 5.19 f.r. de N0, 1Φx = 1 Φxx RPreuve.Exercice. Soit X N0, 1. Montrer que X N0, 1.Solution.420240.10.20.30.40.5µ = 0ϕx12πσ = 1Figure 6: f.d.p. de X N0, 1420241/21xΦxFigure 7: f.r. de X N0, 15.3.3Règle de 68-95-99Propriété 5.20 Si X Nµ, σ2 alors• Pµ σ X µ + σ 0.68• Pµ 2σ X µ + 2σ 0.95• Pµ 3σ X µ + 3σ 0.99Preuve.

Page 19 : v.a.r. continues1968.29599.734.134.113.613.62.12.13210123ScoreFréquenceFigure 8: Règle de 68-95-99 pour X N0, 15.3.4Table de la loi normale standardLa f.r. Φ de la loi normale standard N0, 1 estΦx =Z x12π e12 t2dt xRComme il n'existe pas d'expression analytique simple pour la fonction de distribution Φ autre que saformulation intégrale, les valeurs de la fonction Φ pour x entre 0 et 4, par incréments de 0.01, sontrassemblées dans une table appelée table de la loi normale standard cf n de ce document.Valeurs pour la loi normale standard :• Cas 0 x 4.La valeur de Φx est lu sur la table à l'intersection de la ligne et de la colonne dont la somme vaut x.Par exemple, Φ1.37 = 0.914657• Cas 4 x 0.On utilise la relation Φx = 1 Φx.Par exemple, Φ1.37 = 1 Φ1.37 = 0, 085343• Approximation de Φx. Dans certains calculs très précis, on a besoin des valeurs de Φx pourx 4. La formule suivante donne une très bonne approximation :Φx 1 1xe12 x2Par exemple, Φ5 = 1 7.45 × 107 = 0.999999255.Valeurs pour une loi normale non-standard :Par transformation ane, on peut toujours se ramener à loi loi normale standard.Proposition 5.21 Si X Nµ, σ2, alors sa f.r. FX satisfait la relationFXx = Φx µσx RPreuve.Remarque. Cette relation permet de ramener tous les calculs sur les loi normales aux calculs sur laloi normale standard.

Page 20 : 20K. El AmineExemple. Soit X Nµ, σ2 = N6, 22. Calculer FX3.Solution. On aFX3 = Φ3 µσ= Φ3 62= Φ1.5 = 1 Φ1.5 1 0.9331930, 066807

Page 21 : z0.000.010.020.030.040.050.060.070.080.090.000.500000 0.503989 0.507978 0.511966 0.515953 0.519939 0.523922 0.527903 0.531881 0.5358560.100.539828 0.543795 0.547758 0.551717 0.555670 0.559618 0.563559 0.567495 0.571424 0.5753450.200.579260 0.583166 0.587064 0.590954 0.594835 0.598706 0.602568 0.606420 0.610261 0.6140920.300.617911 0.621720 0.625516 0.629300 0.633072 0.636831 0.640576 0.644309 0.648027 0.6517320.400.655422 0.659097 0.662757 0.666402 0.670031 0.673645 0.677242 0.680822 0.684386 0.6879330.500.691462 0.694974 0.698468 0.701944 0.705401 0.708840 0.712260 0.715661 0.719043 0.7224050.600.725747 0.729069 0.732371 0.735653 0.738914 0.742154 0.745373 0.748571 0.751748 0.7549030.700.758036 0.761148 0.764238 0.767305 0.770350 0.773373 0.776373 0.779350 0.782305 0.7852360.800.788145 0.791030 0.793892 0.796731 0.799546 0.802337 0.805105 0.807850 0.810570 0.8132670.900.815940 0.818589 0.821214 0.823814 0.826391 0.828944 0.831472 0.833977 0.836457 0.8389131.000.841345 0.843752 0.846136 0.848495 0.850830 0.853141 0.855428 0.857690 0.859929 0.8621431.100.864334 0.866500 0.868643 0.870762 0.872857 0.874928 0.876976 0.879000 0.881000 0.8829771.200.884930 0.886861 0.888768 0.890651 0.892512 0.894350 0.896165 0.897958 0.899727 0.9014751.300.903200 0.904902 0.906582 0.908241 0.909877 0.911492 0.913085 0.914657 0.916207 0.9177361.400.919243 0.920730 0.922196 0.923641 0.925066 0.926471 0.927855 0.929219 0.930563 0.9318881.500.933193 0.934478 0.935745 0.936992 0.938220 0.939429 0.940620 0.941792 0.942947 0.9440831.600.945201 0.946301 0.947384 0.948449 0.949497 0.950529 0.951543 0.952540 0.953521 0.9544861.700.955435 0.956367 0.957284 0.958185 0.959070 0.959941 0.960796 0.961636 0.962462 0.9632731.800.964070 0.964852 0.965620 0.966375 0.967116 0.967843 0.968557 0.969258 0.969946 0.9706211.900.971283 0.971933 0.972571 0.973197 0.973810 0.974412 0.975002 0.975581 0.976148 0.9767052.000.977250 0.977784 0.978308 0.978822 0.979325 0.979818 0.980301 0.980774 0.981237 0.9816912.100.982136 0.982571 0.982997 0.983414 0.983823 0.984222 0.984614 0.984997 0.985371 0.9857382.200.986097 0.986447 0.986791 0.987126 0.987455 0.987776 0.988089 0.988396 0.988696 0.9889892.300.989276 0.989556 0.989830 0.990097 0.990358 0.990613 0.990863 0.991106 0.991344 0.9915762.400.991802 0.992024 0.992240 0.992451 0.992656 0.992857 0.993053 0.993244 0.993431 0.9936132.500.993790 0.993963 0.994132 0.994297 0.994457 0.994614 0.994766 0.994915 0.995060 0.9952012.600.995339 0.995473 0.995604 0.995731 0.995855 0.995975 0.996093 0.996207 0.996319 0.9964272.700.996533 0.996636 0.996736 0.996833 0.996928 0.997020 0.997110 0.997197 0.997282 0.9973652.800.997445 0.997523 0.997599 0.997673 0.997744 0.997814 0.997882 0.997948 0.998012 0.9980742.900.998134 0.998193 0.998250 0.998305 0.998359 0.998411 0.998462 0.998511 0.998559 0.9986053.000.998650 0.998694 0.998736 0.998777 0.998817 0.998856 0.998893 0.998930 0.998965 0.9989993.100.999032 0.999065 0.999096 0.999126 0.999155 0.999184 0.999211 0.999238 0.999264 0.9992893.200.999313 0.999336 0.999359 0.999381 0.999402 0.999423 0.999443 0.999462 0.999481 0.9994993.300.999517 0.999534 0.999550 0.999566 0.999581 0.999596 0.999610 0.999624 0.999638 0.9996513.400.999663 0.999675 0.999687 0.999698 0.999709 0.999720 0.999730 0.999740 0.999749 0.9997583.500.999767 0.999776 0.999784 0.999792 0.999800 0.999807 0.999815 0.999822 0.999828 0.9998353.600.999841 0.999847 0.999853 0.999858 0.999864 0.999869 0.999874 0.999879 0.999883 0.9998883.700.999892 0.999896 0.999900 0.999904 0.999908 0.999912 0.999915 0.999918 0.999922 0.9999253.800.999928 0.999931 0.999933 0.999936 0.999938 0.999941 0.999943 0.999946 0.999948 0.9999503.900.999952 0.999954 0.999956 0.999958 0.999959 0.999961 0.999963 0.999964 0.999966 0.9999674.000.999968 0.999970 0.999971 0.999972 0.999973 0.999974 0.999975 0.999976 0.999977 0.999978α0.250.10.050.0250.010.0050.0010.0005zα 0.674490 1.281552 1.644854 1.959964 2.326348 2.575829 3.090232 3.290527zα/2 1.150349 1.644854 1.959964 2.241403 2.575829 2.807034 3.290527 3.480756Fonction de repartition de Z ⇠N0, 1: Φz =1p2⇡zR1et22 dtQuantile z↵deﬁni par PZ z↵ = ↵avec Z ⇠N0, 1