CM1 logique et raisonnement

Télécharger le CM1 logique et raisonnement en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463

Page 1 : Algebre-Premier semestre 2021CY TechAlgebre - Premier semestre 2021Responsable CM :Didier Cransac groups 5-6-7Bureau :CY 201e-mail :didier.cransac@cyu.frResponsable TD :Didier Cransac groupe 5Didier Cransac groupe 6Jihan Khoder groupe 7Evaluation :• DS 1 : 28/10/21• DS 2 : 09/12/21• DS 3 : 20/01/22• Divers : a definir.N. Arancibia - relu par D. CransacAlgebre

Page 2 : Algebre-Premier semestre 2021Acces aux documentsComptes Teams :Preing 1 globaln33vzumGroupe Alebre I CM DCbr01qzwGroupe 54n9f431Groupe 6grwo6rfGroupe 7wp2pahrEn cas de difficulte : didier.cransac@cyu.frN. Arancibia - relu par D. CransacAlgebre

Page 3 : Algebre-Premier semestre 2021En attendant....Les documents seront deposes surmath.cransac.free.frIdentifiant :nom 7 lettres maximum + initiale du prenomExemple :Nom Prenoma pour identifiantJean FontainefontainjDidier CransaccransacdMot de passe :cytechEn cas de difficulte : didier.cransac@cyu.frN. Arancibia - relu par D. CransacAlgebre

Page 4 : Algebre-Premier semestre 2021ThemesN. Arancibia - relu par D. CransacAlgebre

Page 5 : Algebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre

Page 6 : Logique et raisonnementCe chapitre regroupe les differents points de vocabulaire, notations etraisonnement necessaires pour la conception et la redaction efficace d’unedemonstration mathematique.Nous allons donc apprendre a bien ecrire et a bien argumenter enmathematiques.N. Arancibia - relu par D. CransacAlgebre

Page 7 : Logique et raisonnementCe chapitre regroupe les differents points de vocabulaire, notations etraisonnement necessaires pour la conception et la redaction efficace d’unedemonstration mathematique.Nous allons donc apprendre a bien ecrire et a bien argumenter enmathematiques.Themes detaillesN. Arancibia - relu par D. CransacAlgebre

Page 8 : Logique et raisonnementCe chapitre regroupe les differents points de vocabulaire, notations etraisonnement necessaires pour la conception et la redaction efficace d’unedemonstration mathematique.Nous allons donc apprendre a bien ecrire et a bien argumenter enmathematiques.Themes detaillesRudiments de LogiquePropositions.Quantificateurs.Implication, contraposition, equivalence.N. Arancibia - relu par D. CransacAlgebre

Page 9 : Logique et raisonnementCe chapitre regroupe les differents points de vocabulaire, notations etraisonnement necessaires pour la conception et la redaction efficace d’unedemonstration mathematique.Nous allons donc apprendre a bien ecrire et a bien argumenter enmathematiques.Themes detaillesRudiments de LogiquePropositions.Quantificateurs.Implication, contraposition, equivalence.Modes de RaisonnementContrapositionPar l’absurdePar analyse-syntheseRecurrenceN. Arancibia - relu par D. CransacAlgebre

Page 10 : Rudiments de LogiqueEn Mathematiques on travaille avec des objets et des situations quidoivent ˆetre clairement decrits.Pour cela on utilise des Definitions.Une definition decrit donc une situation ou un objet et donne un nom.Une definition n’est pas vraie ou fausse, elle ne peut pas se discuter.L’enjeu d’une definition est de creer des objets qui auront descaracteristiques mathematiques interessantes.N. Arancibia - relu par D. CransacAlgebre

Page 11 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.N. Arancibia - relu par D. CransacAlgebre

Page 12 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :N. Arancibia - relu par D. CransacAlgebre

Page 13 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? N. Arancibia - relu par D. CransacAlgebre

Page 14 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 N. Arancibia - relu par D. CransacAlgebre

Page 15 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 16 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair N. Arancibia - relu par D. CransacAlgebre

Page 17 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 N. Arancibia - relu par D. CransacAlgebre

Page 18 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 est une proposition fausse.N. Arancibia - relu par D. CransacAlgebre

Page 19 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 est une proposition fausse.l’entier 49 est un carre N. Arancibia - relu par D. CransacAlgebre

Page 20 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 est une proposition fausse.l’entier 49 est un carre est une proposition vraie 72 = 49.N. Arancibia - relu par D. CransacAlgebre

Page 21 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 est une proposition fausse.l’entier 49 est un carre est une proposition vraie 72 = 49.30 = 5 N. Arancibia - relu par D. CransacAlgebre

Page 22 : Rudiments de LogiqueDefinition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle onpeut poser la question :P est-elle vraie ? Exemples :3 × 3 = 9 est une proposition vraie.7 est pair est une proposition fausse.8 = 2 est une proposition fausse.l’entier 49 est un carre est une proposition vraie 72 = 49.30 = 5 n’est pas un proposition l’ecriture 30 ne represente rienN. Arancibia - relu par D. CransacAlgebre

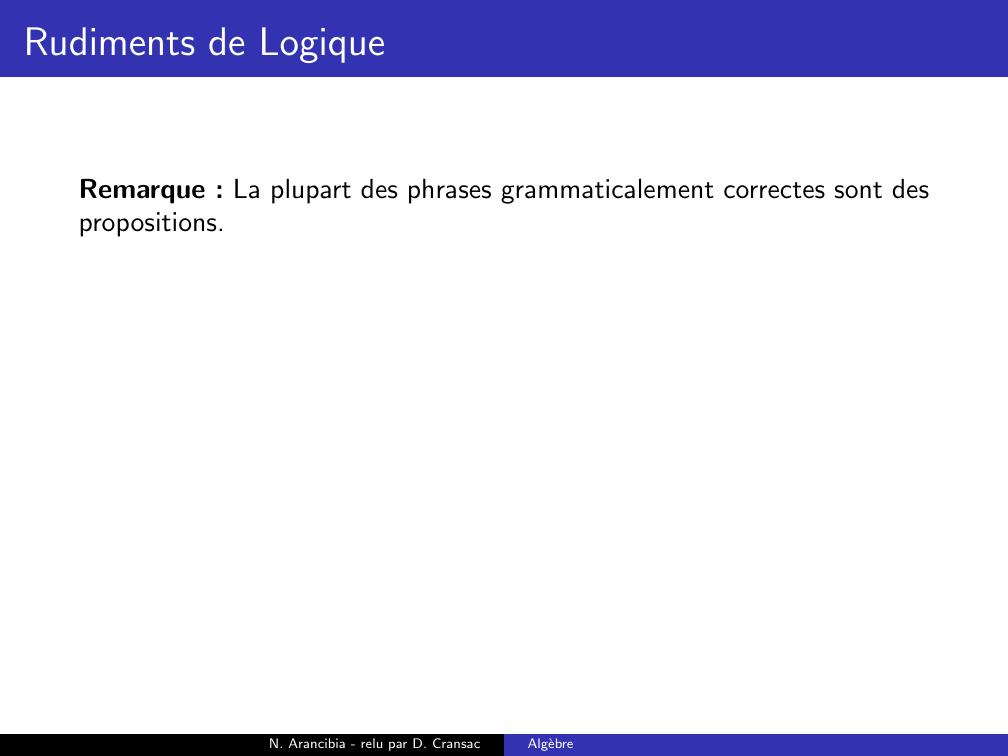
Page 23 : Rudiments de LogiqueRemarque : La plupart des phrases grammaticalement correctes sont despropositions.N. Arancibia - relu par D. CransacAlgebre

Page 24 : Rudiments de LogiqueRemarque : La plupart des phrases grammaticalement correctes sont despropositions.Mais par exemple :Dis-le-moi ! ,Bonjour Quelle heure est-il ? , ouComment vas-tu ? N. Arancibia - relu par D. CransacAlgebre

Page 25 : Rudiments de LogiqueRemarque : La plupart des phrases grammaticalement correctes sont despropositions.Mais par exemple :Dis-le-moi ! ,Bonjour Quelle heure est-il ? , ouComment vas-tu ? ne sont pas des propositions.N. Arancibia - relu par D. CransacAlgebre

Page 26 : Rudiments de LogiqueRemarque : La plupart des phrases grammaticalement correctes sont despropositions.Mais par exemple :Dis-le-moi ! ,Bonjour Quelle heure est-il ? , ouComment vas-tu ? ne sont pas des propositions.La question :Est-il vrai que bonjour ? , n’a aucun sens.N. Arancibia - relu par D. CransacAlgebre

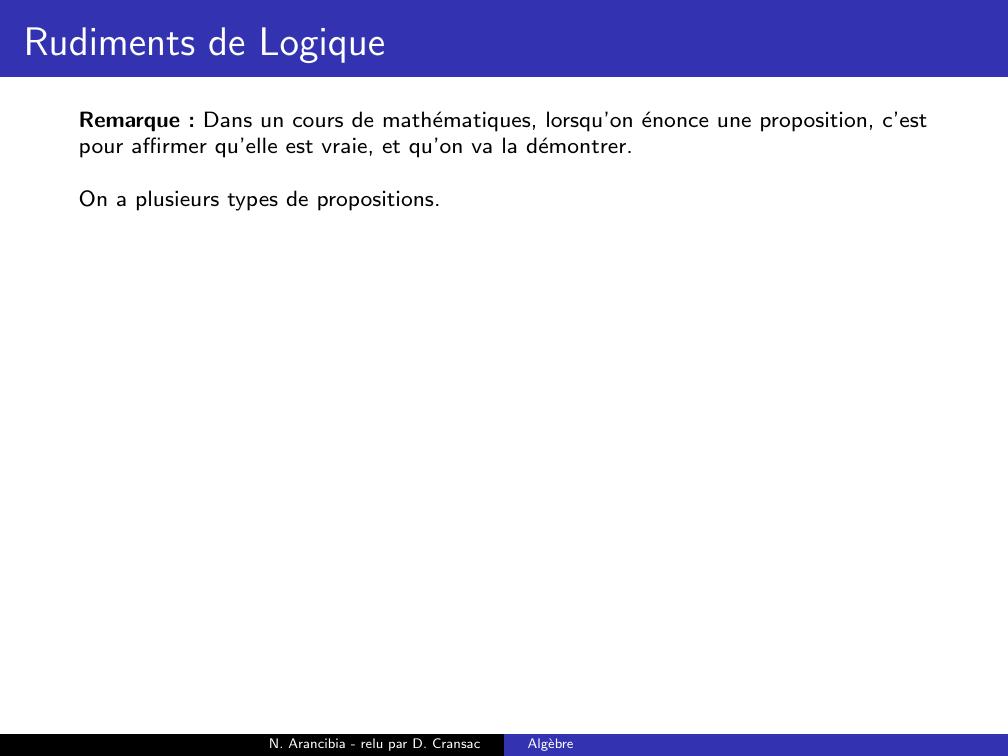
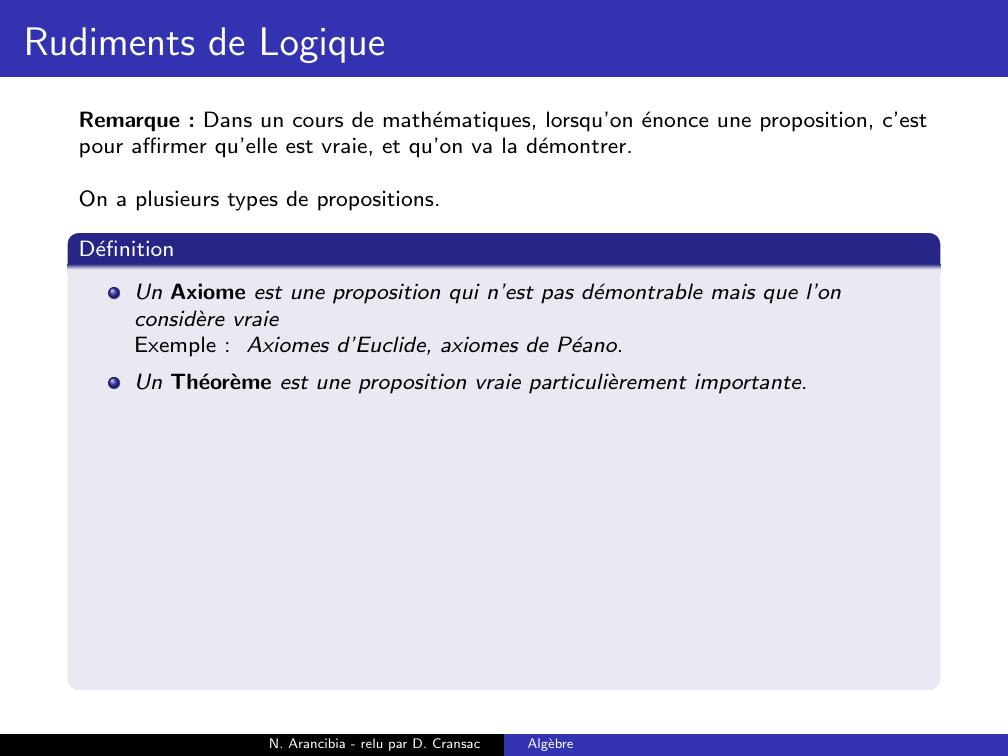
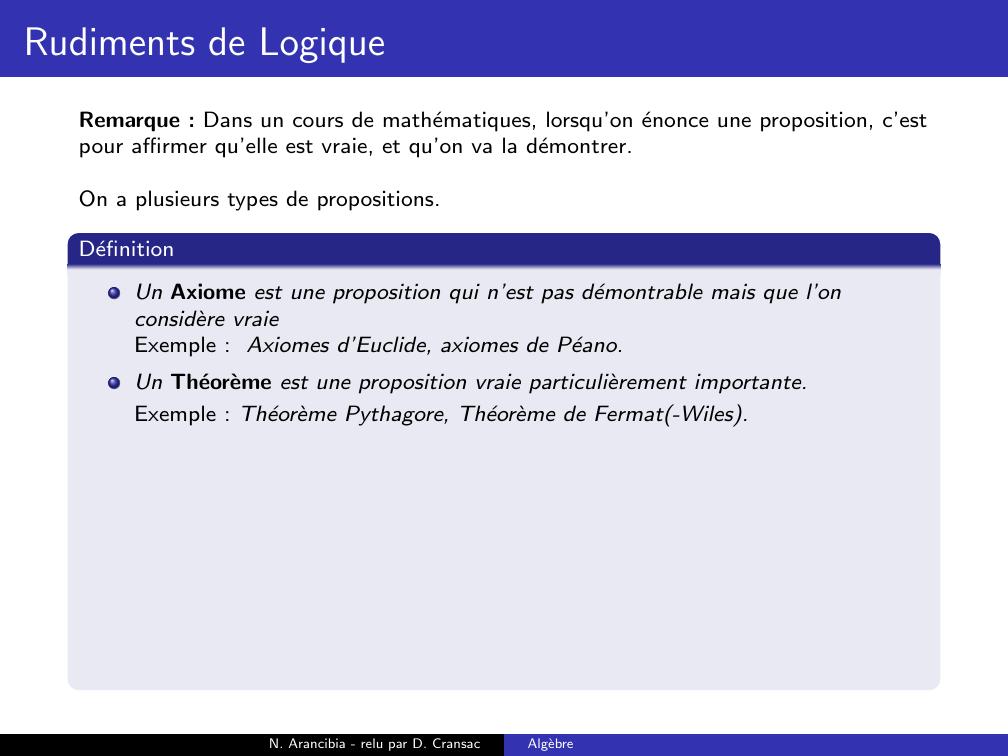
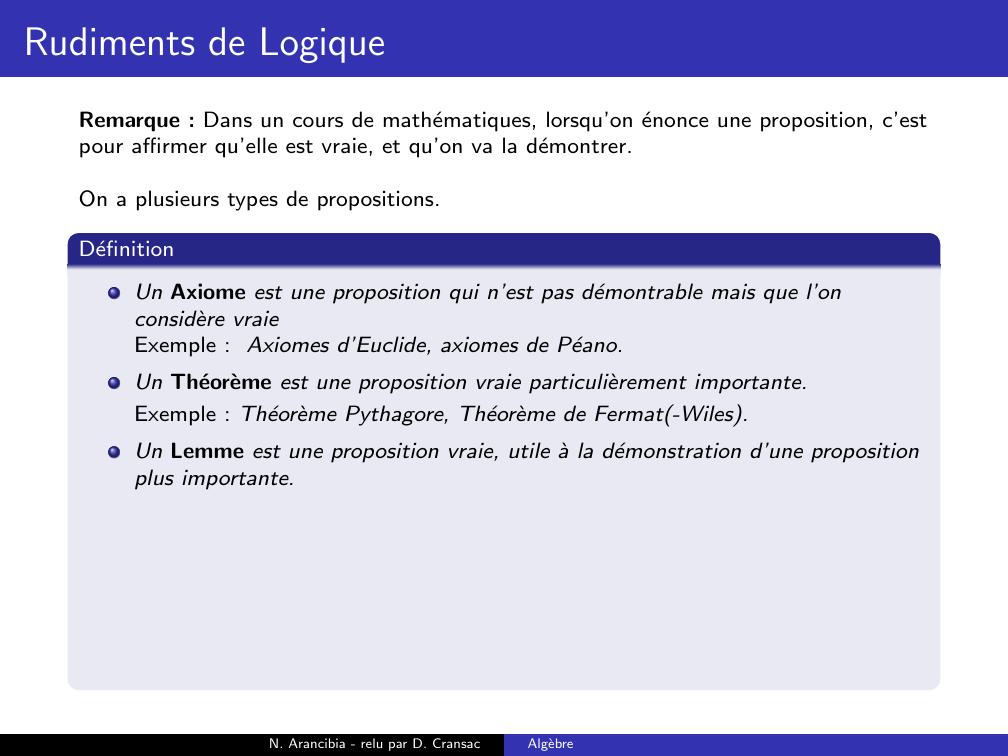
Page 27 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.N. Arancibia - relu par D. CransacAlgebre

Page 28 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.N. Arancibia - relu par D. CransacAlgebre

Page 29 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.N. Arancibia - relu par D. CransacAlgebre

Page 30 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus importante.N. Arancibia - relu par D. CransacAlgebre

Page 31 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus importante.Exemple : Lemme de Zorn.N. Arancibia - relu par D. CransacAlgebre

Page 32 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus importante.Exemple : Lemme de Zorn.Un Corollaire est une proposition vraie, consequence immediate d’une autreproposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 33 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus importante.Exemple : Lemme de Zorn.Un Corollaire est une proposition vraie, consequence immediate d’une autreproposition vraie.Une Conjecture est une proposition qu’on pense generalement vraie, sans enavoir la preuve.N. Arancibia - relu par D. CransacAlgebre

Page 34 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une proposition, c’estpour affirmer qu’elle est vraie, et qu’on va la demontrer.On a plusieurs types de propositions.DefinitionUn Axiome est une proposition qui n’est pas demontrable mais que l’onconsidere vraieExemple : Axiomes d’Euclide, axiomes de Peano.Un Theoreme est une proposition vraie particulierement importante.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus importante.Exemple : Lemme de Zorn.Un Corollaire est une proposition vraie, consequence immediate d’une autreproposition vraie.Une Conjecture est une proposition qu’on pense generalement vraie, sans enavoir la preuve.Exemple : Conjecture de Goldbach.N. Arancibia - relu par D. CransacAlgebre

Page 35 : Rudiments de LogiqueTheoreme de Fermat-Wiles :Il n’existe pas de nombres entiers strictement positifs x, y et z tels que :xn + y n = zn pour n N, n 2Lemme de Zorn :si un ensemble ordonne est tel que toute chaˆıne sous-ensembletotalement ordonne possede un majorant, alors il possede un elementmaximal.Conjecture de Goldbach :Tout nombre entier pair superieur a 3 peut s’ecrire comme la somme dedeux nombres premiers.N. Arancibia - relu par D. CransacAlgebre

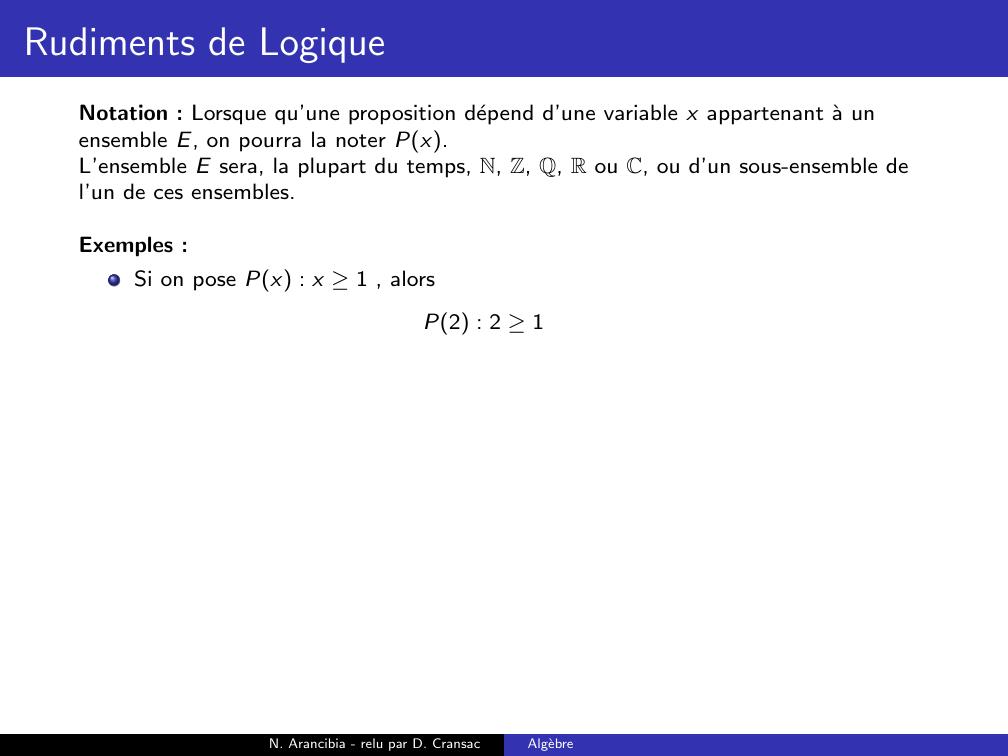
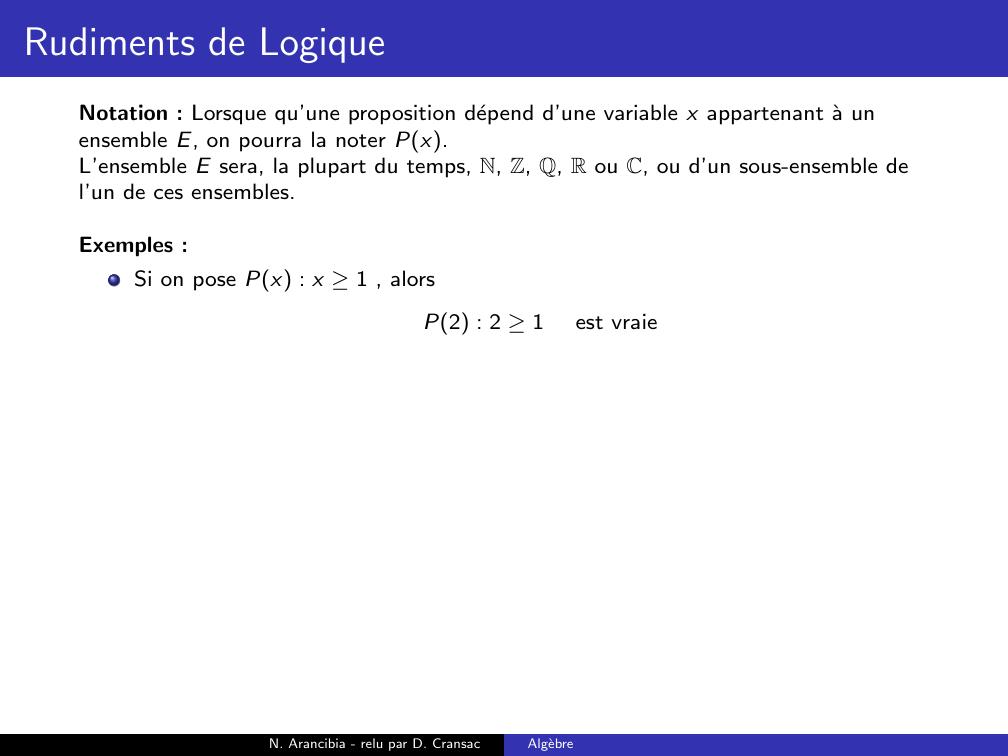
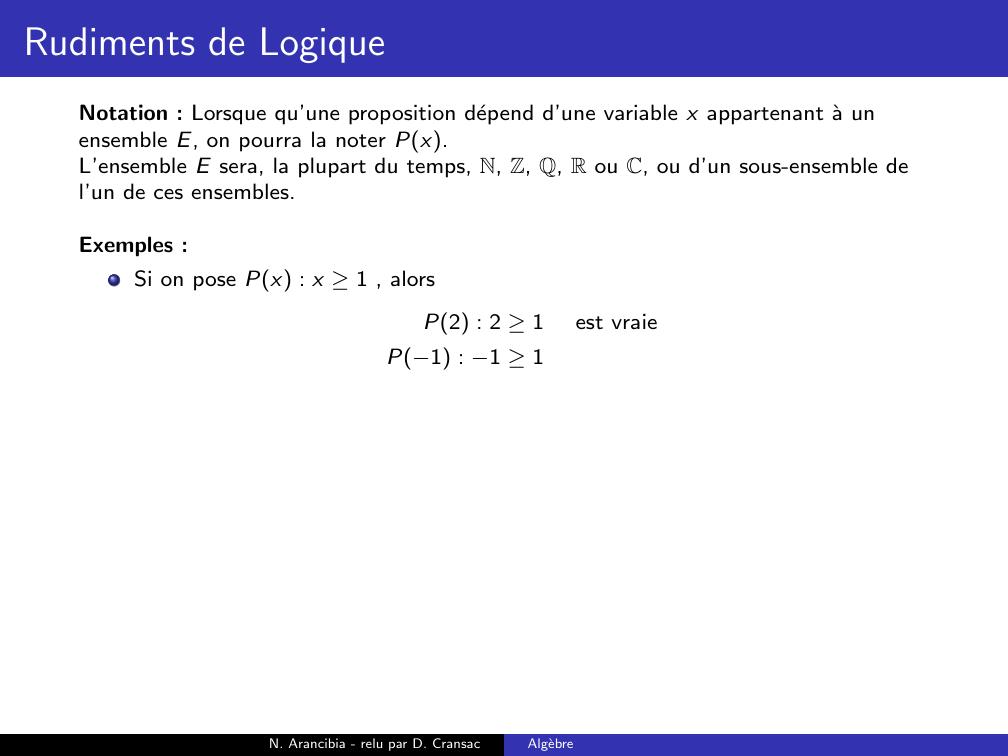
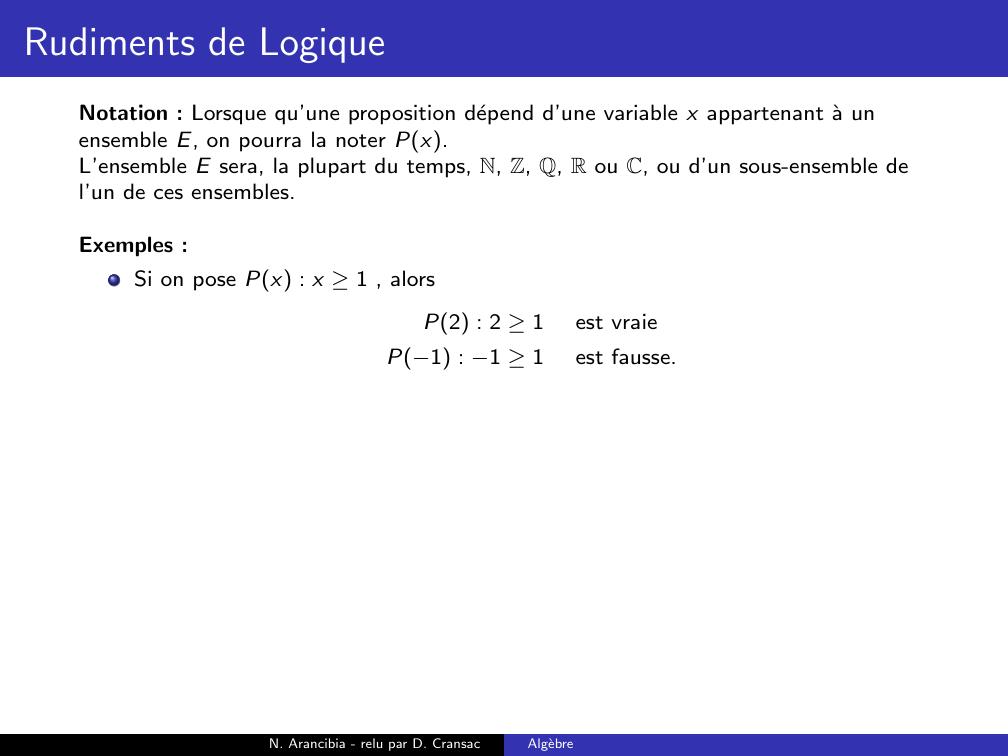
Page 36 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.N. Arancibia - relu par D. CransacAlgebre

Page 37 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1N. Arancibia - relu par D. CransacAlgebre

Page 38 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1N. Arancibia - relu par D. CransacAlgebre

Page 39 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieN. Arancibia - relu par D. CransacAlgebre

Page 40 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1N. Arancibia - relu par D. CransacAlgebre

Page 41 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.N. Arancibia - relu par D. CransacAlgebre

Page 42 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.N. Arancibia - relu par D. CransacAlgebre

Page 43 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier N. Arancibia - relu par D. CransacAlgebre

Page 44 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7.N. Arancibia - relu par D. CransacAlgebre

Page 45 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 46 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraieP8.N. Arancibia - relu par D. CransacAlgebre

Page 47 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraieP8est fausse.N. Arancibia - relu par D. CransacAlgebre

Page 48 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraieP8est fausseP6700417.N. Arancibia - relu par D. CransacAlgebre

Page 49 : Rudiments de LogiqueNotation : Lorsque qu’une proposition depend d’une variable x appartenant a unensemble E, on pourra la noter Px.L’ensemble E sera, la plupart du temps, N, Z, Q, R ou C, ou d’un sous-ensemble del’un de ces ensembles.Exemples :Si on pose Px : x 1 , alorsP2 : 2 1est vraieP1 : 1 1est fausse.On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisibleque par 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraieP8est fausseP6700417est vraieProuve par L. Euler 1732 .N. Arancibia - relu par D. CransacAlgebre

Page 50 : Rudiments de LogiqueNous disposons de deux types d’outils pour construire de nouvellespropositions :les operations sur les propositions :les quantificateurs :N. Arancibia - relu par D. CransacAlgebre

Page 51 : Rudiments de LogiqueNous disposons de deux types d’outils pour construire de nouvellespropositions :les operations sur les propositions :Negation nonConjonction etDisjonction ouImplication ⇒Equivalence ⇔les quantificateurs :N. Arancibia - relu par D. CransacAlgebre

Page 52 : Rudiments de LogiqueNous disposons de deux types d’outils pour construire de nouvellespropositions :les operations sur les propositions :Negation nonConjonction etDisjonction ouImplication ⇒Equivalence ⇔les quantificateurs :Pour tout Il existe N. Arancibia - relu par D. CransacAlgebre

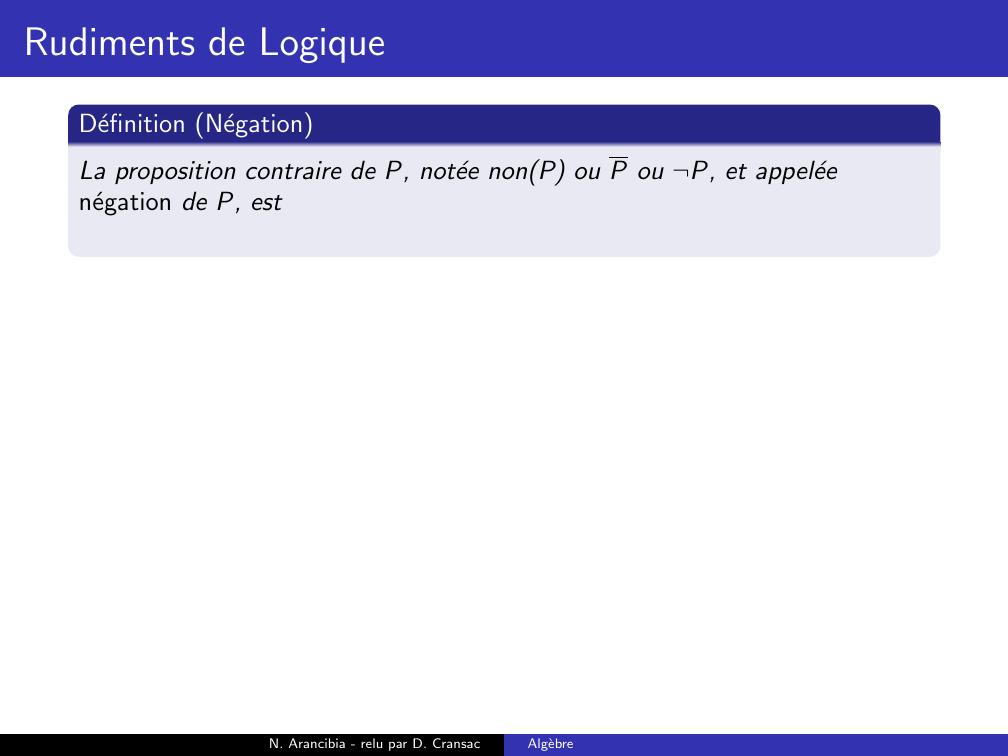
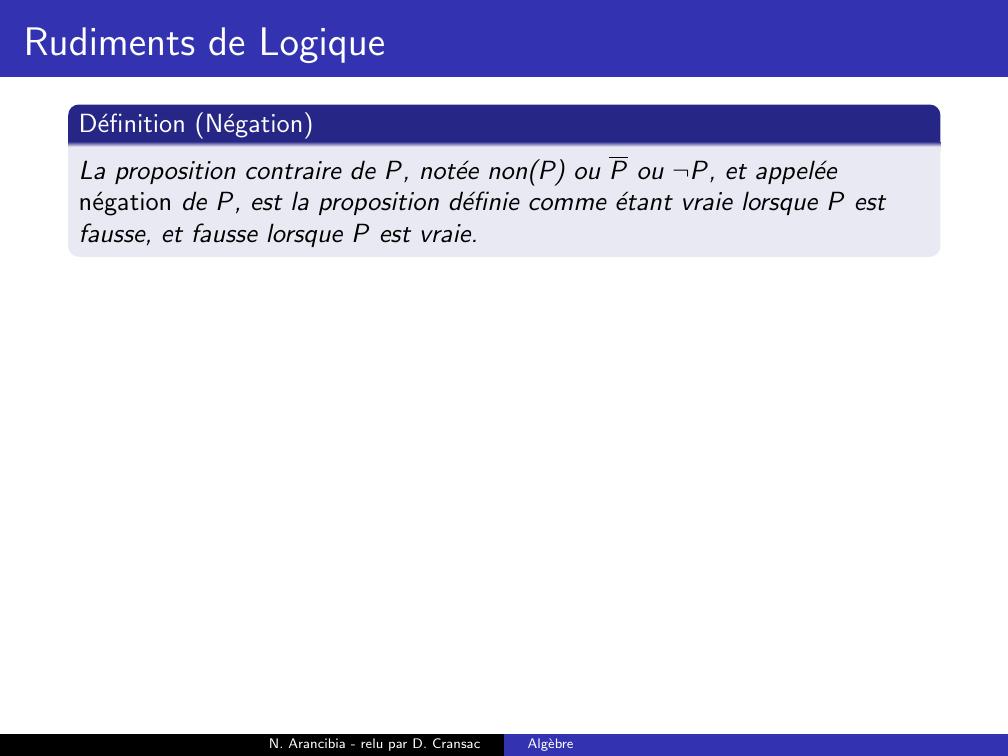
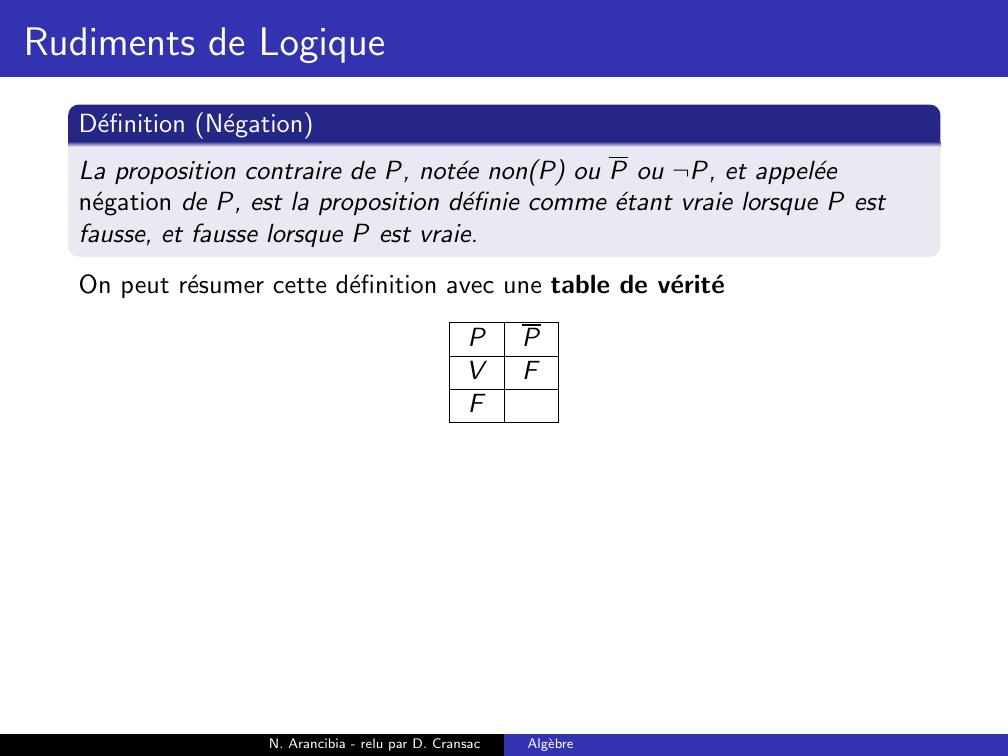
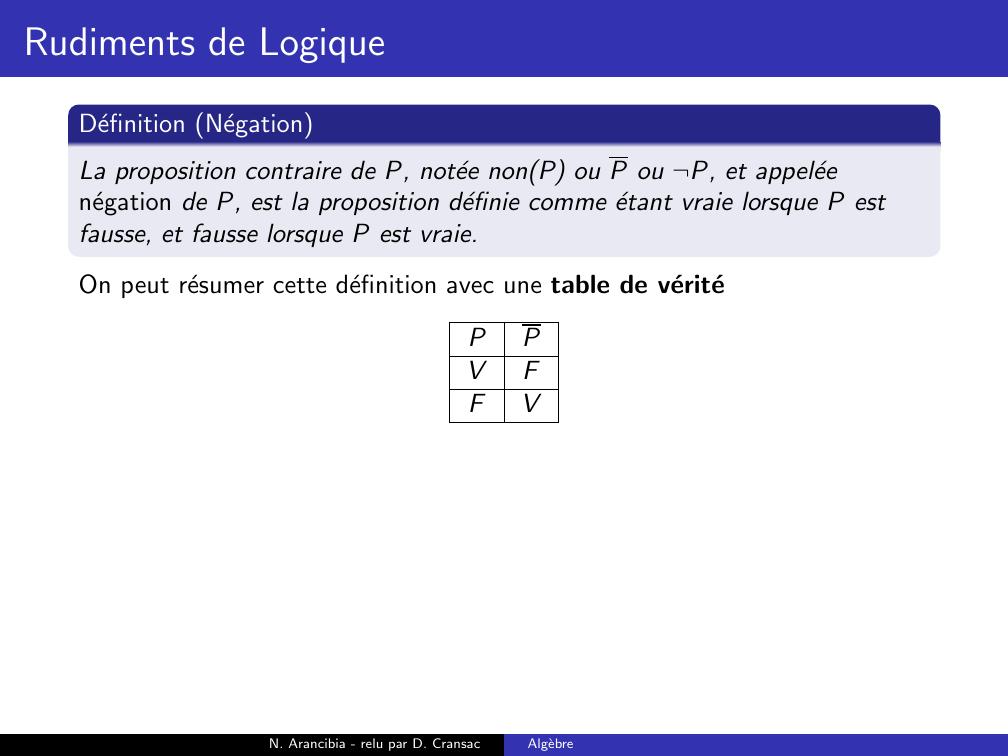
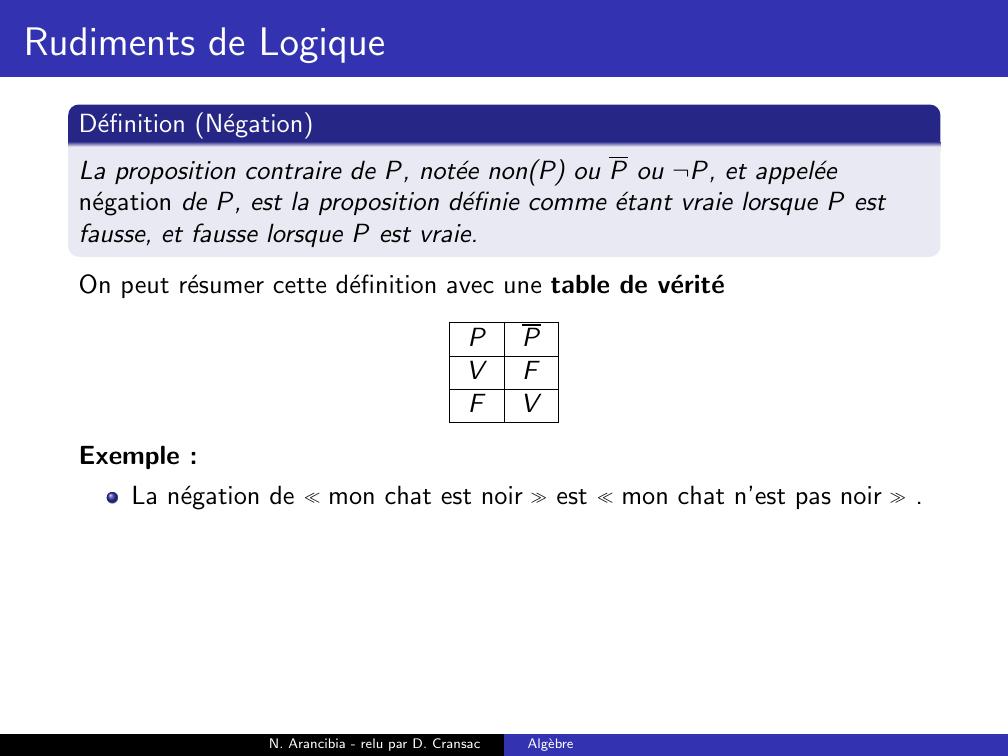
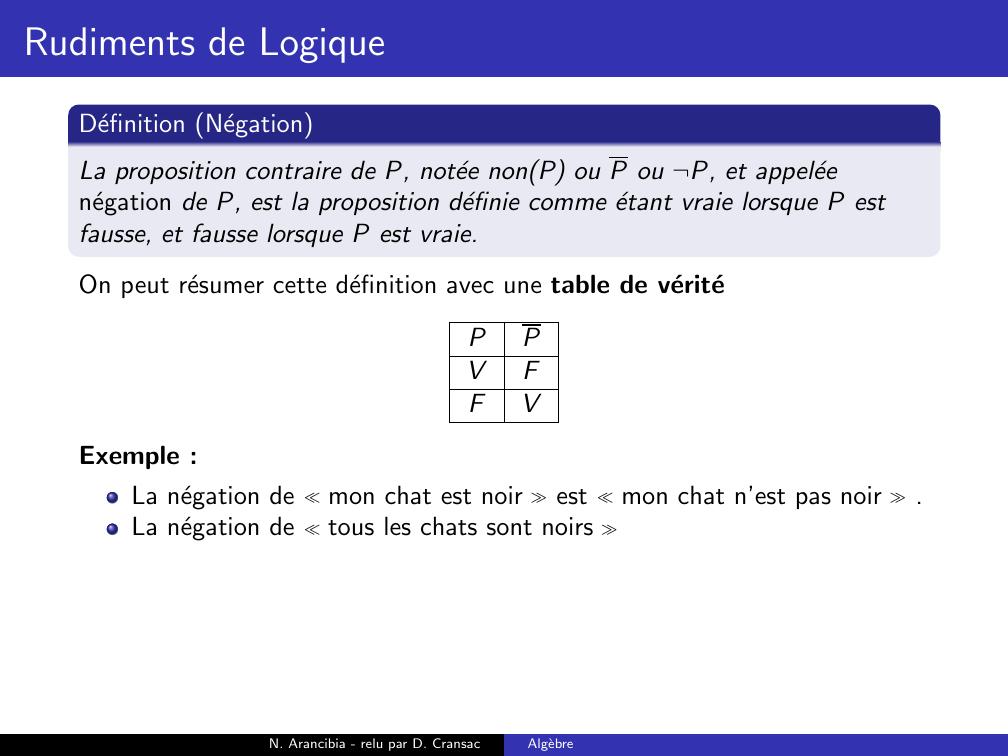
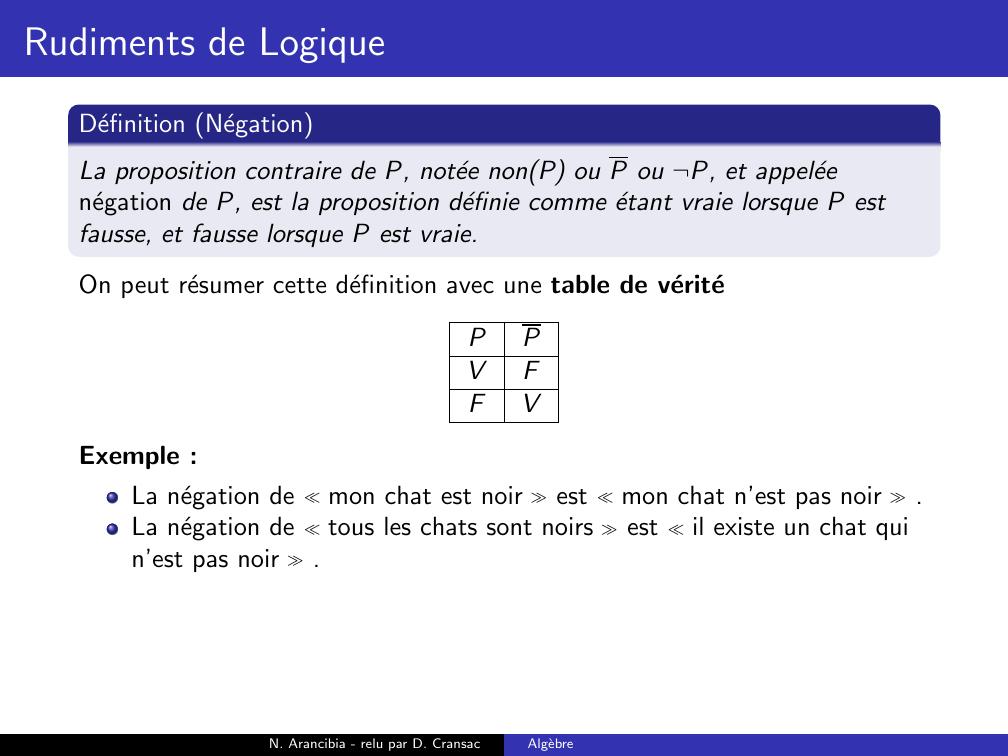
Page 53 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, estN. Arancibia - relu par D. CransacAlgebre

Page 54 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.N. Arancibia - relu par D. CransacAlgebre

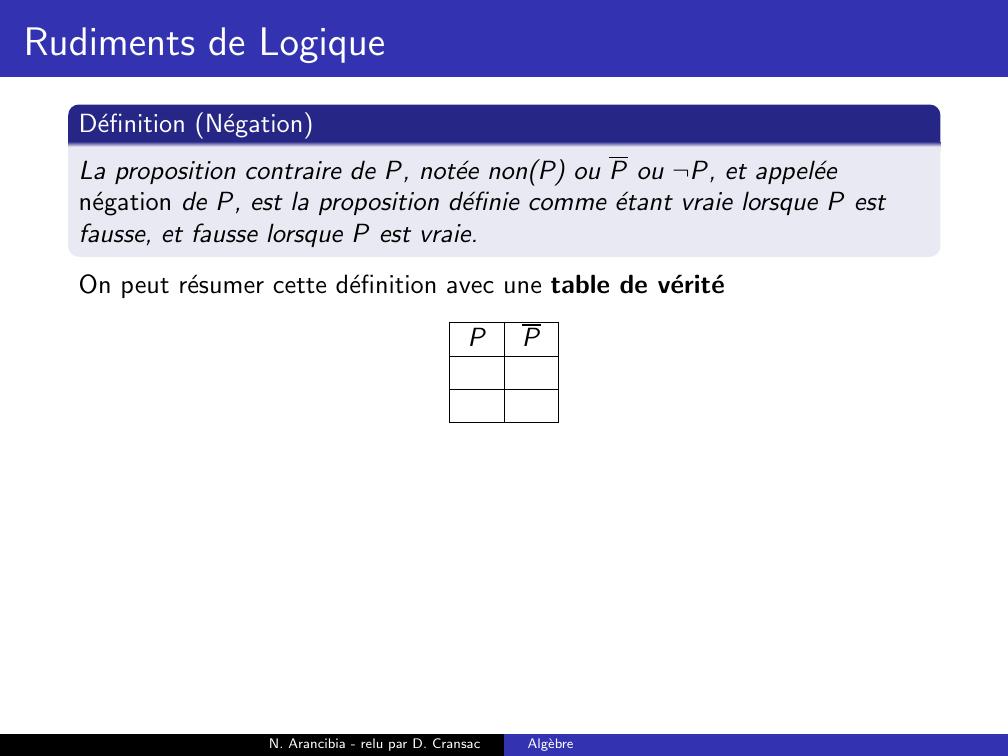
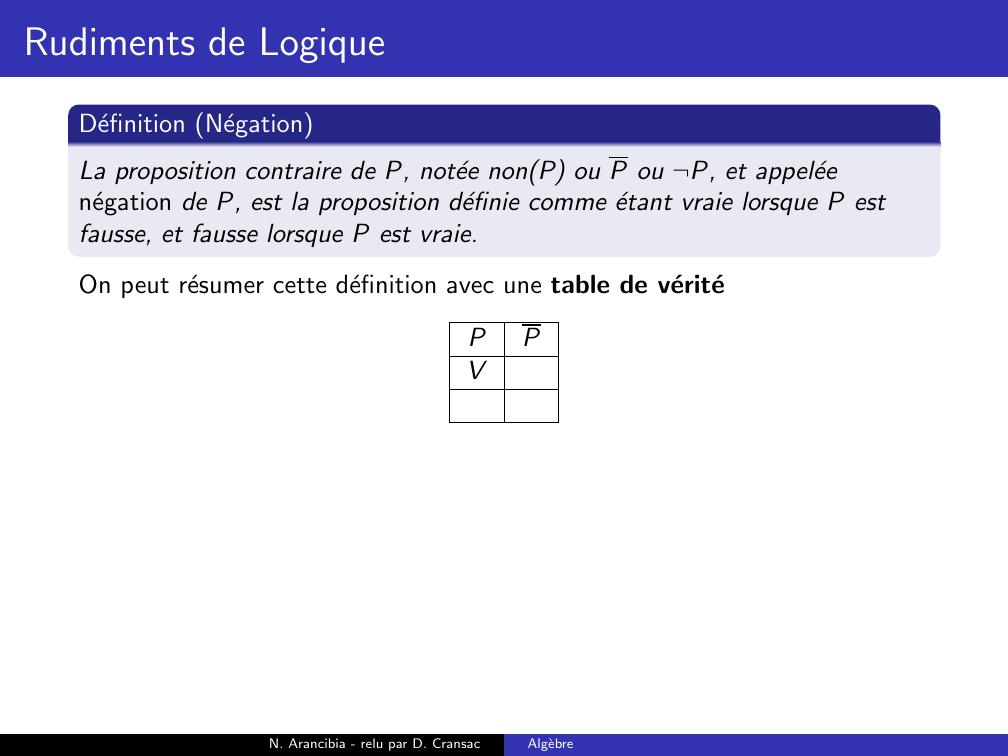
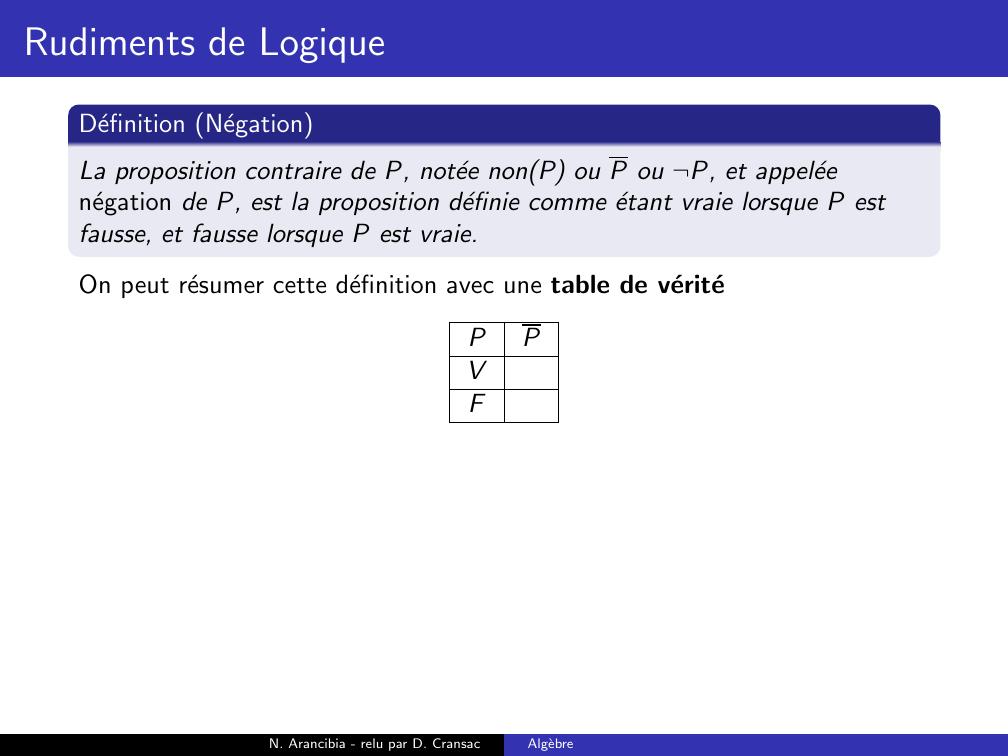
Page 55 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veriteN. Arancibia - relu par D. CransacAlgebre

Page 56 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPN. Arancibia - relu par D. CransacAlgebre

Page 57 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVN. Arancibia - relu par D. CransacAlgebre

Page 58 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFN. Arancibia - relu par D. CransacAlgebre

Page 59 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFN. Arancibia - relu par D. CransacAlgebre

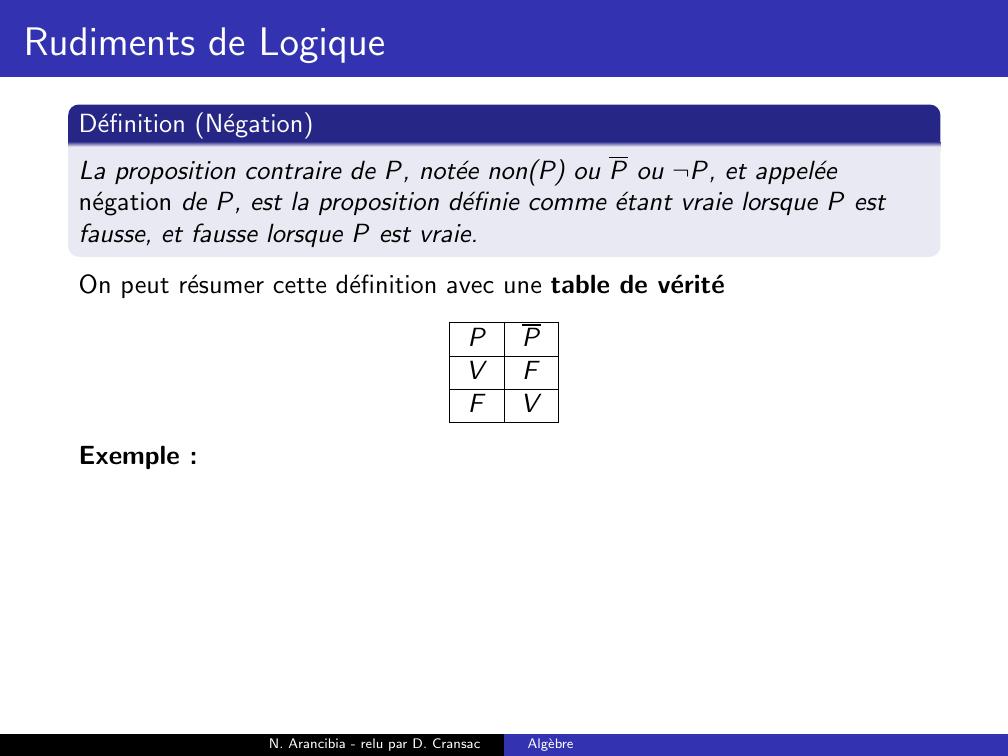
Page 60 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVN. Arancibia - relu par D. CransacAlgebre

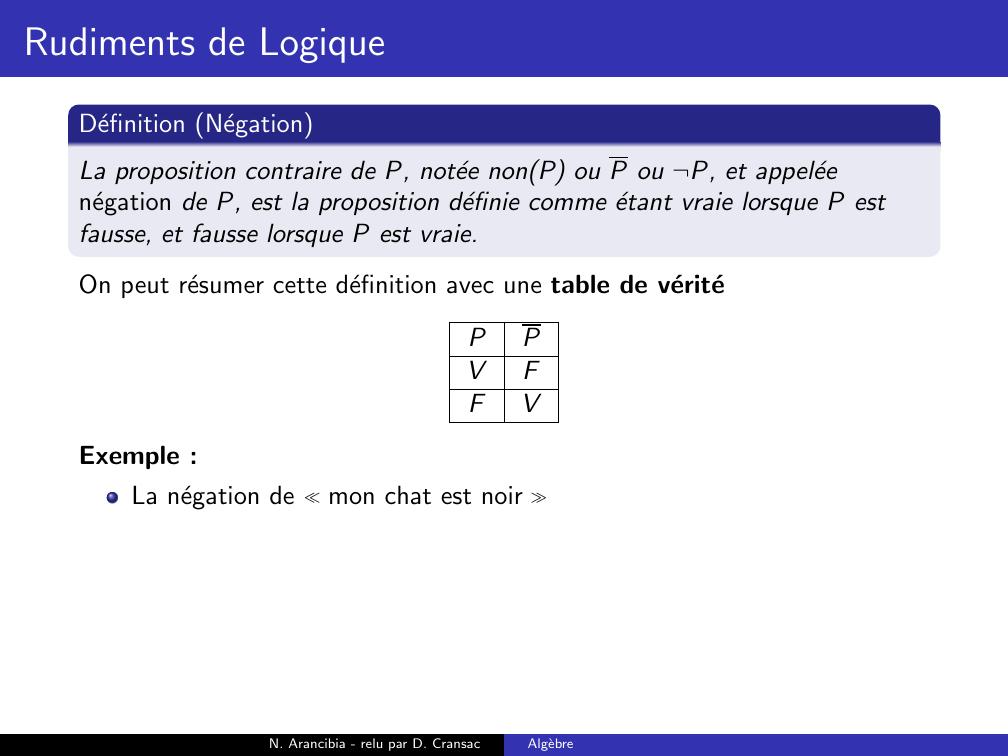
Page 61 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :N. Arancibia - relu par D. CransacAlgebre

Page 62 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir N. Arancibia - relu par D. CransacAlgebre

Page 63 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .N. Arancibia - relu par D. CransacAlgebre

Page 64 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs N. Arancibia - relu par D. CransacAlgebre

Page 65 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .N. Arancibia - relu par D. CransacAlgebre

Page 66 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .La negation de x 0N. Arancibia - relu par D. CransacAlgebre

Page 67 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .La negation de x 0est x 0N. Arancibia - relu par D. CransacAlgebre

Page 68 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .La negation de x 0est x 0et non pas x 0.N. Arancibia - relu par D. CransacAlgebre

Page 69 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .La negation de x 0est x 0et non pas x 0.La negation de f est la fonction nulle N. Arancibia - relu par D. CransacAlgebre

Page 70 : Rudiments de LogiqueDefinition NegationLa proposition contraire de P, notee nonP ou P ou ¬P, et appeleenegation de P, est la proposition definie comme etant vraie lorsque P estfausse, et fausse lorsque P est vraie.On peut resumer cette definition avec une table de veritePPVFFVExemple :La negation de mon chat est noir est mon chat n’est pas noir .La negation de tous les chats sont noirs est il existe un chat quin’est pas noir .La negation de x 0est x 0et non pas x 0.La negation de f est la fonction nulle est f n’est pas la fonctionnulle ou encoref ne s’annule pas en au moins un point N. Arancibia - relu par D. CransacAlgebre

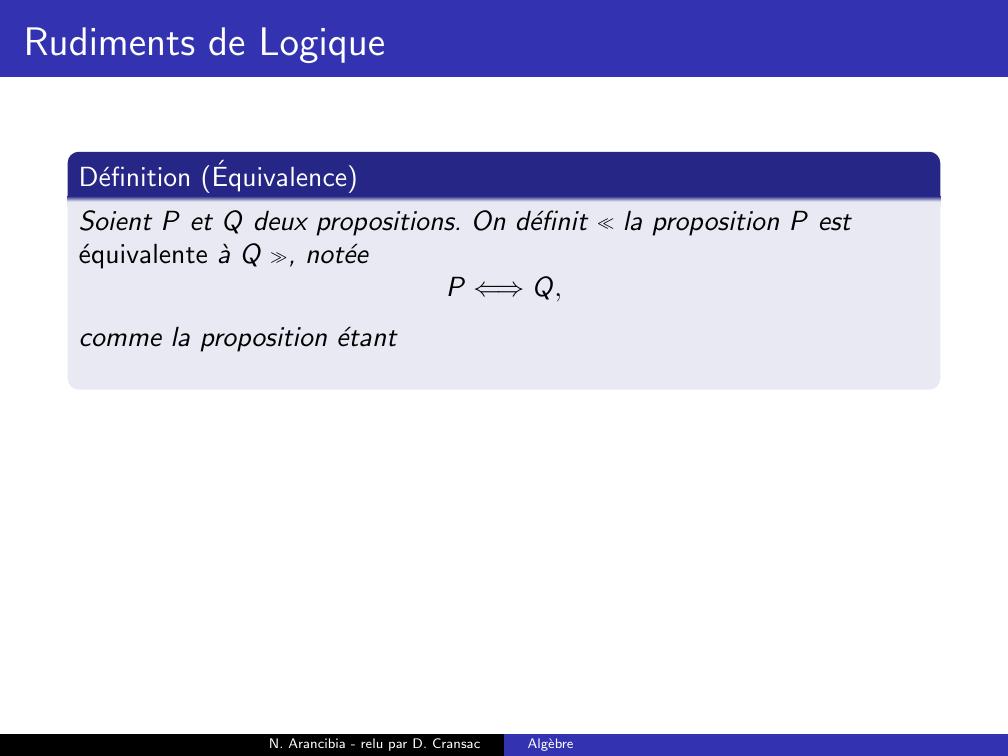
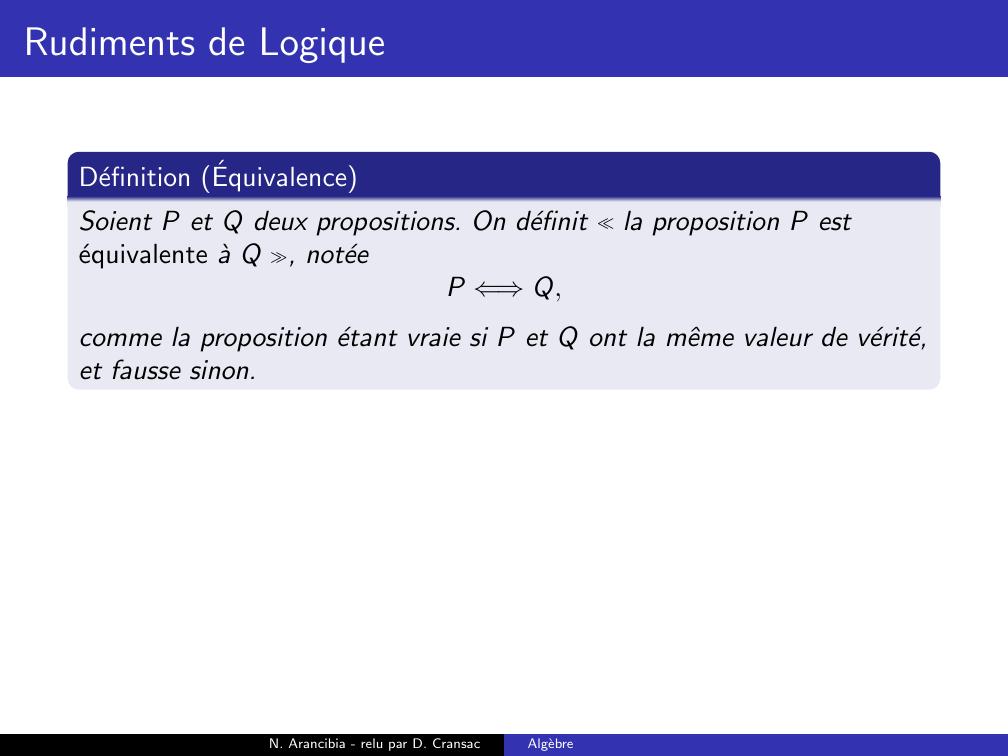
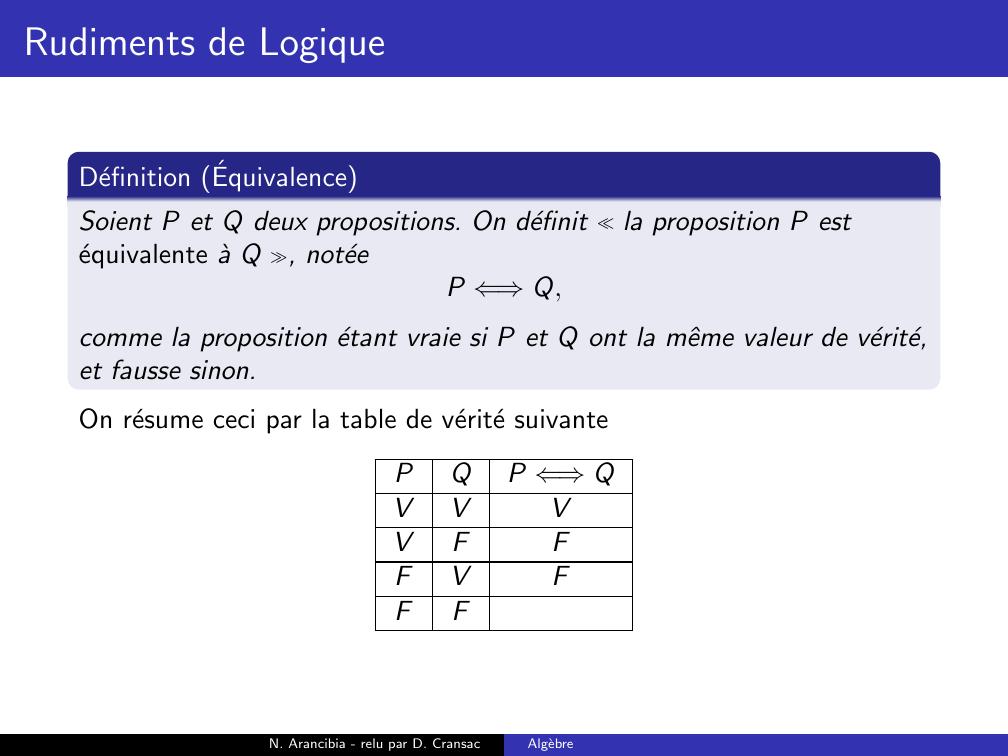
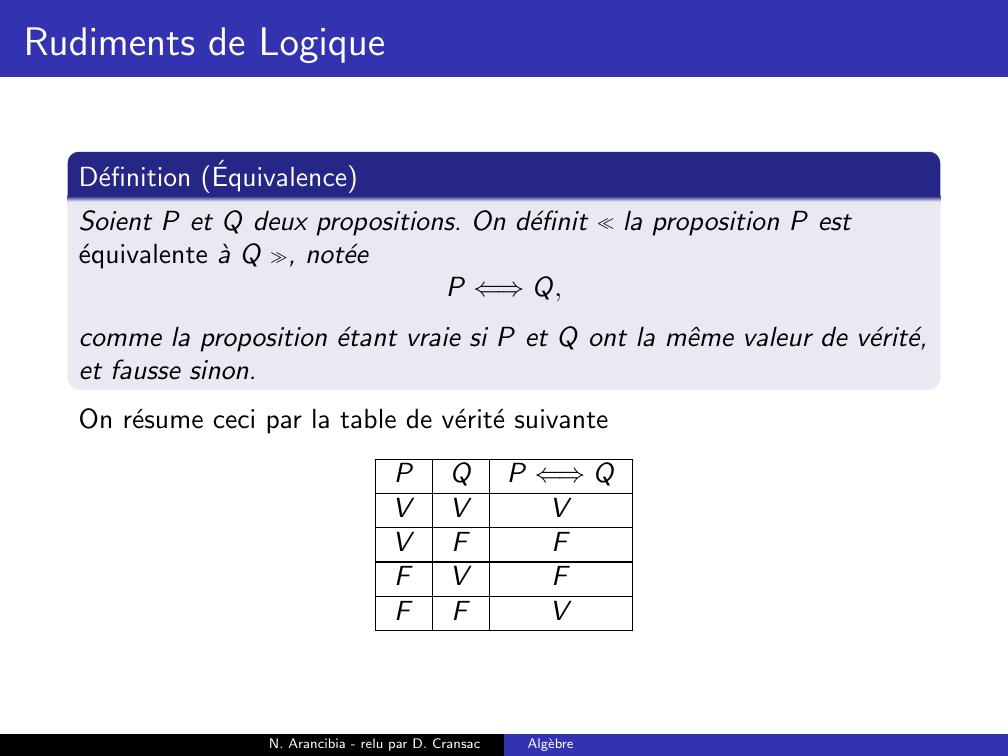
Page 71 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etantN. Arancibia - relu par D. CransacAlgebre

Page 72 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.N. Arancibia - relu par D. CransacAlgebre

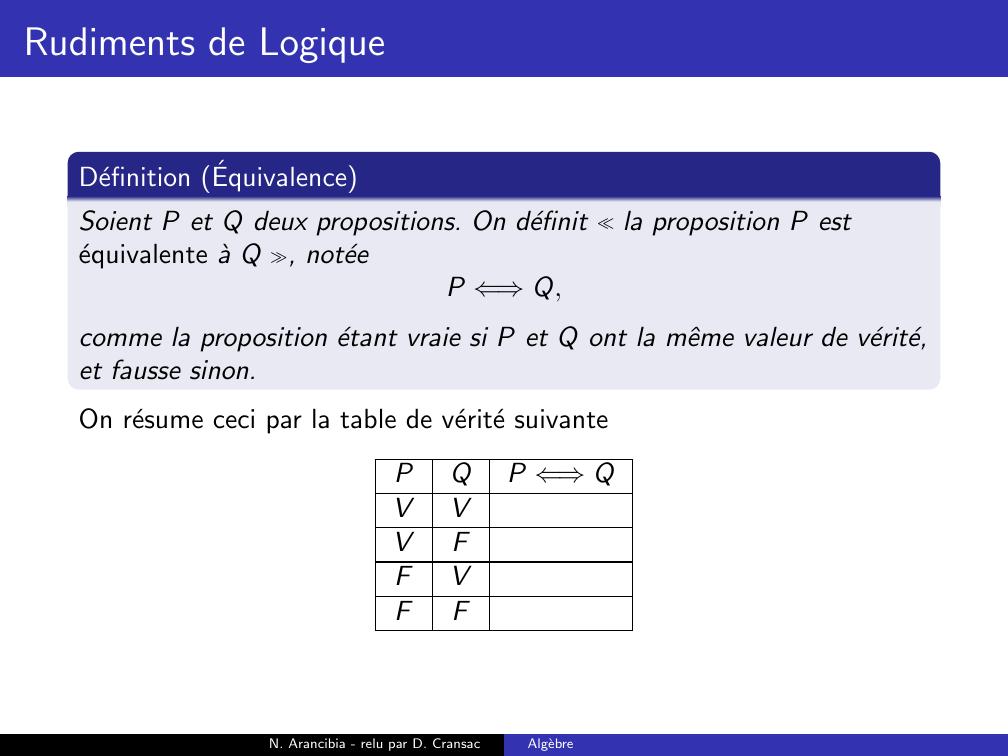
Page 73 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.On resume ceci par la table de verite suivantePQP ⇐⇒QVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

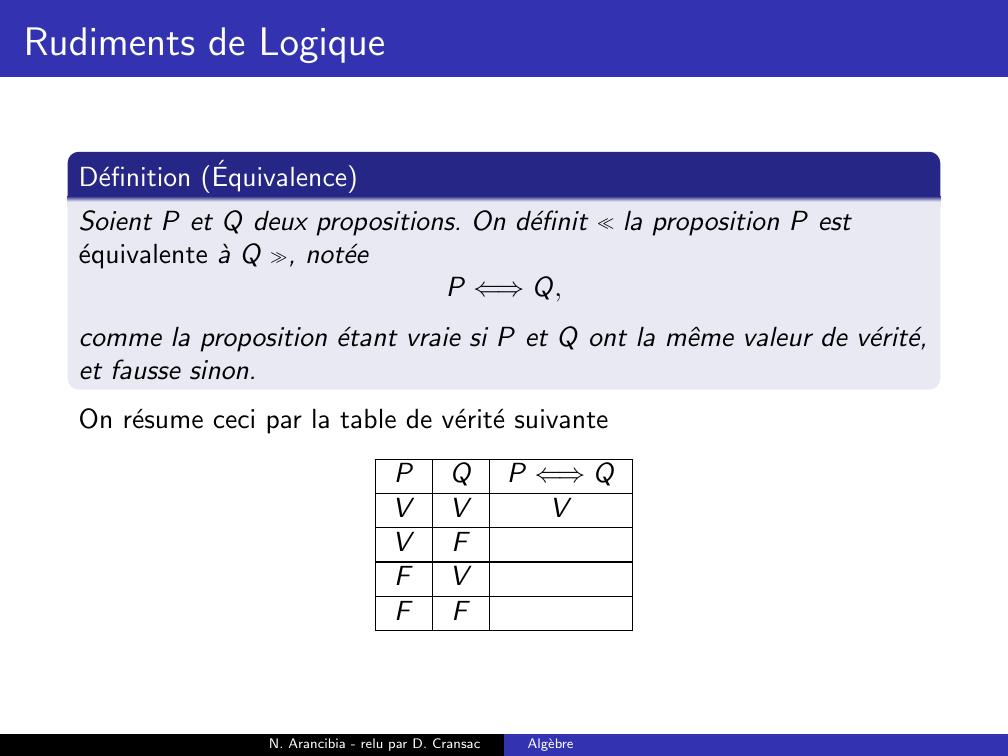
Page 74 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.On resume ceci par la table de verite suivantePQP ⇐⇒QVVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

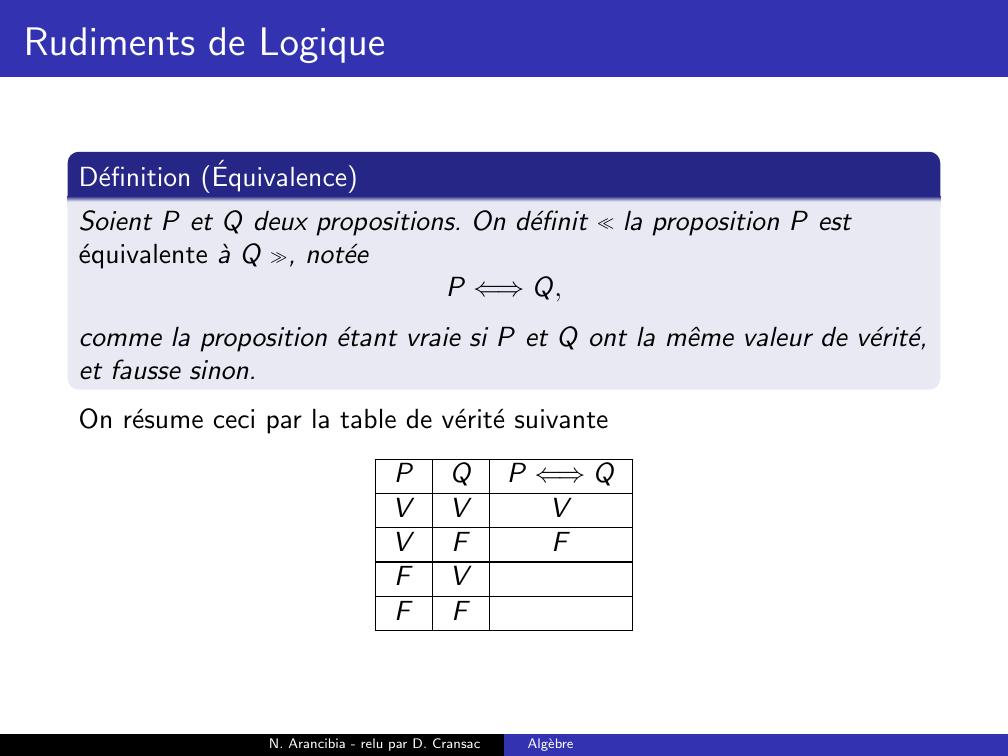
Page 75 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.On resume ceci par la table de verite suivantePQP ⇐⇒QVVVVFFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 76 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.On resume ceci par la table de verite suivantePQP ⇐⇒QVVVVFFFVFFFN. Arancibia - relu par D. CransacAlgebre

Page 77 : Rudiments de LogiqueDefinition EquivalenceSoient P et Q deux propositions. On definit la proposition P estequivalente a Q , noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite,et fausse sinon.On resume ceci par la table de verite suivantePQP ⇐⇒QVVVVFFFVFFFVN. Arancibia - relu par D. CransacAlgebre

Page 78 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estN. Arancibia - relu par D. CransacAlgebre

Page 79 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;N. Arancibia - relu par D. CransacAlgebre

Page 80 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.N. Arancibia - relu par D. CransacAlgebre

Page 81 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivante :PQP et QVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 82 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivante :PQP et QVVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 83 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivante :PQP et QVVVVFFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 84 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivante :PQP et QVVVVFFFVFFFN. Arancibia - relu par D. CransacAlgebre

Page 85 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la conjonction.DefinitionA deux propositions P et Q, on peut associer la conjonction de P et Q noteeP et Q ou P Qqui estvraie si les deux propositions P et Q sont vraies ;fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivante :PQP et QVVVVFFFVFFFFN. Arancibia - relu par D. CransacAlgebre

Page 86 : Rudiments de LogiqueExemples :Soit ABCD un rectangle. La propositionL’angleABC est droit et les diagonalesAC et BD se coupent en leur milieu est vraie ou fausse ?ABCDN. Arancibia - relu par D. CransacAlgebre

Page 87 : Rudiments de LogiqueExemples :Soit ABCD un rectangle. La propositionL’angleABC est droit et les diagonalesAC et BD se coupent en leur milieu est vraie ou fausse ?ABCDElle est vraie.En effetL’angleABC est droit N. Arancibia - relu par D. CransacAlgebre

Page 88 : Rudiments de LogiqueExemples :Soit ABCD un rectangle. La propositionL’angleABC est droit et les diagonalesAC et BD se coupent en leur milieu est vraie ou fausse ?ABCDElle est vraie.En effetL’angleABC est droit est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 89 : Rudiments de LogiqueExemples :Soit ABCD un rectangle. La propositionL’angleABC est droit et les diagonalesAC et BD se coupent en leur milieu est vraie ou fausse ?ABCDElle est vraie.En effetL’angleABC est droit est une proposition vraie.Les diagonales AC et BD se coupent en leur milieu N. Arancibia - relu par D. CransacAlgebre

Page 90 : Rudiments de LogiqueExemples :Soit ABCD un rectangle. La propositionL’angleABC est droit et les diagonalesAC et BD se coupent en leur milieu est vraie ou fausse ?ABCDElle est vraie.En effetL’angleABC est droit est une proposition vraie.Les diagonales AC et BD se coupent en leur milieu est uneproposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 91 : Rudiments de LogiqueExemples :Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est-elle vraie ou fausse ?ABCN. Arancibia - relu par D. CransacAlgebre

Page 92 : Rudiments de LogiqueExemples :Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est-elle vraie ou fausse ?ABCElle est fausse.En effetAB AC + CB N. Arancibia - relu par D. CransacAlgebre

Page 93 : Rudiments de LogiqueExemples :Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est-elle vraie ou fausse ?ABCElle est fausse.En effetAB AC + CB est une proposition fausse.N. Arancibia - relu par D. CransacAlgebre

Page 94 : Rudiments de LogiqueExemples :Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est-elle vraie ou fausse ?ABCElle est fausse.En effetAB AC + CB est une proposition fausse.ABC+CAB+ dBCA = π N. Arancibia - relu par D. CransacAlgebre

Page 95 : Rudiments de LogiqueExemples :Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est-elle vraie ou fausse ?ABCElle est fausse.En effetAB AC + CB est une proposition fausse.ABC+CAB+ dBCA = π est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

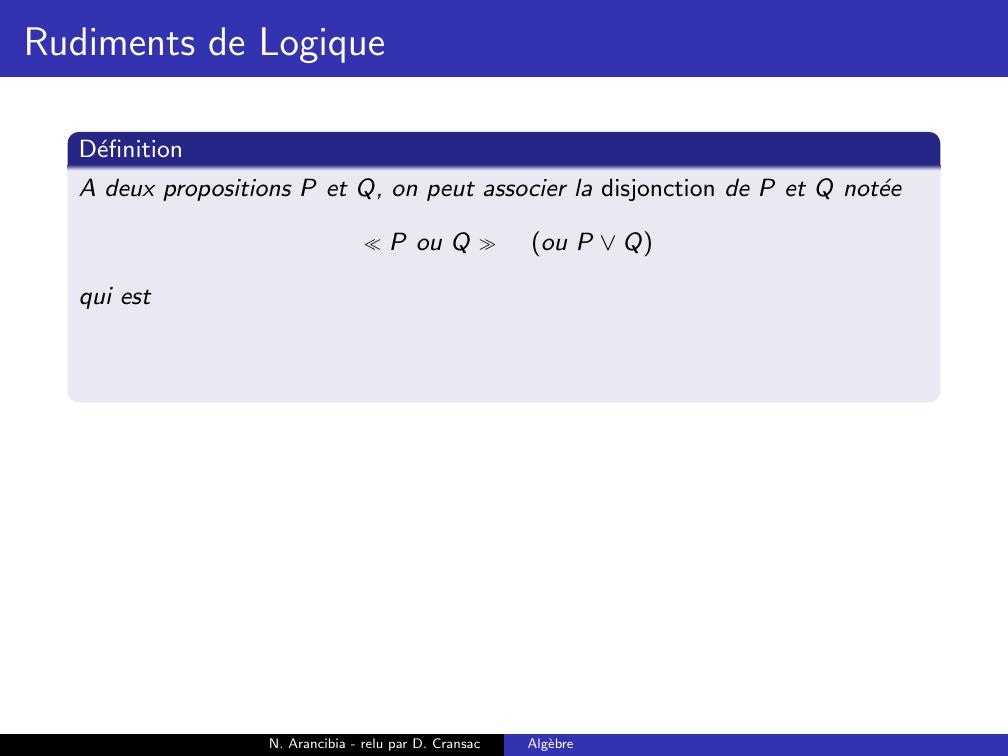
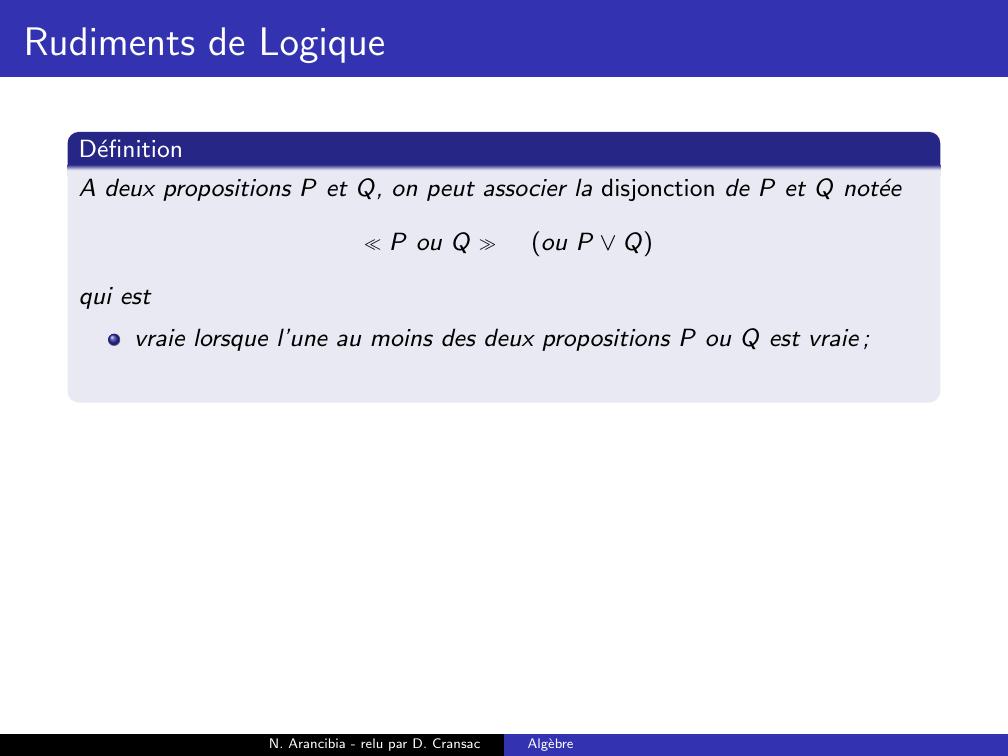
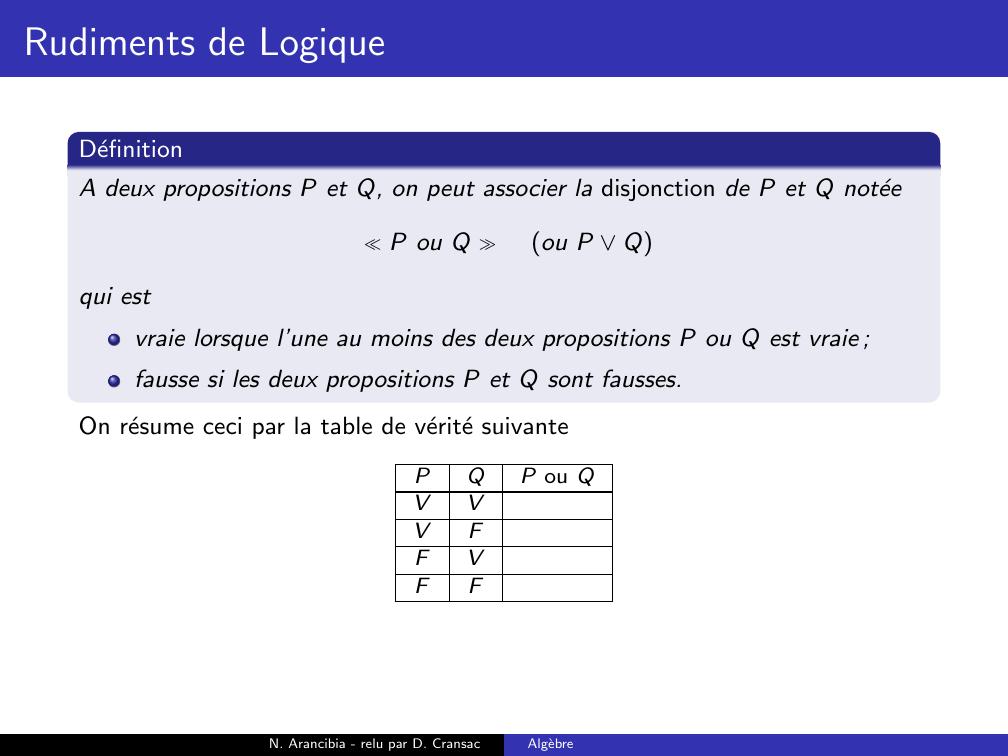
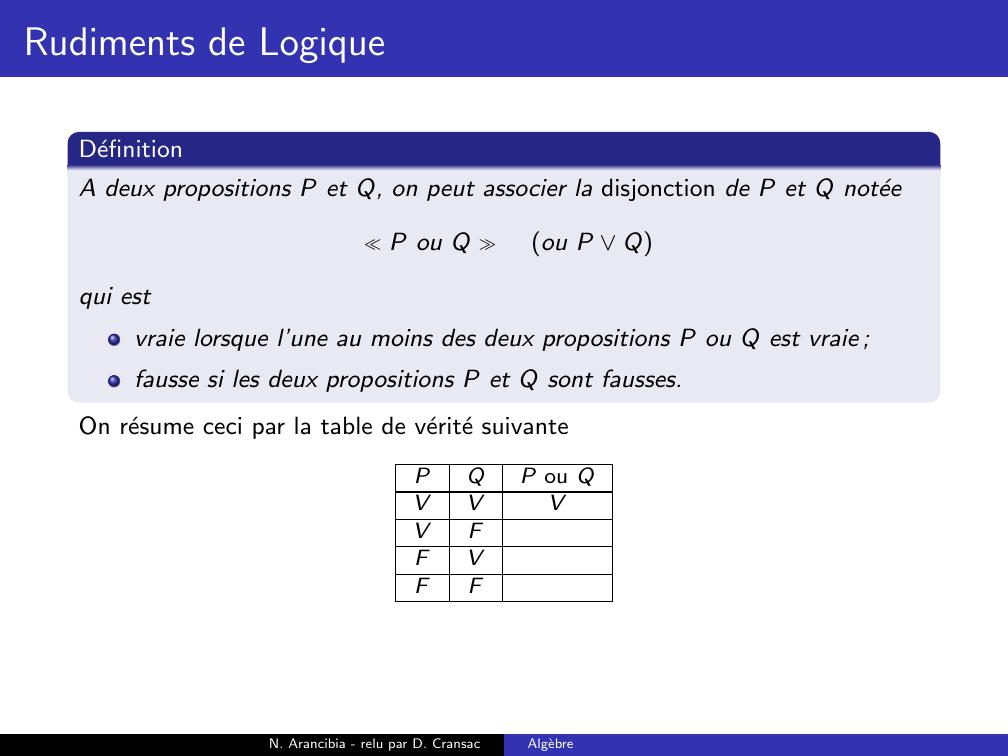
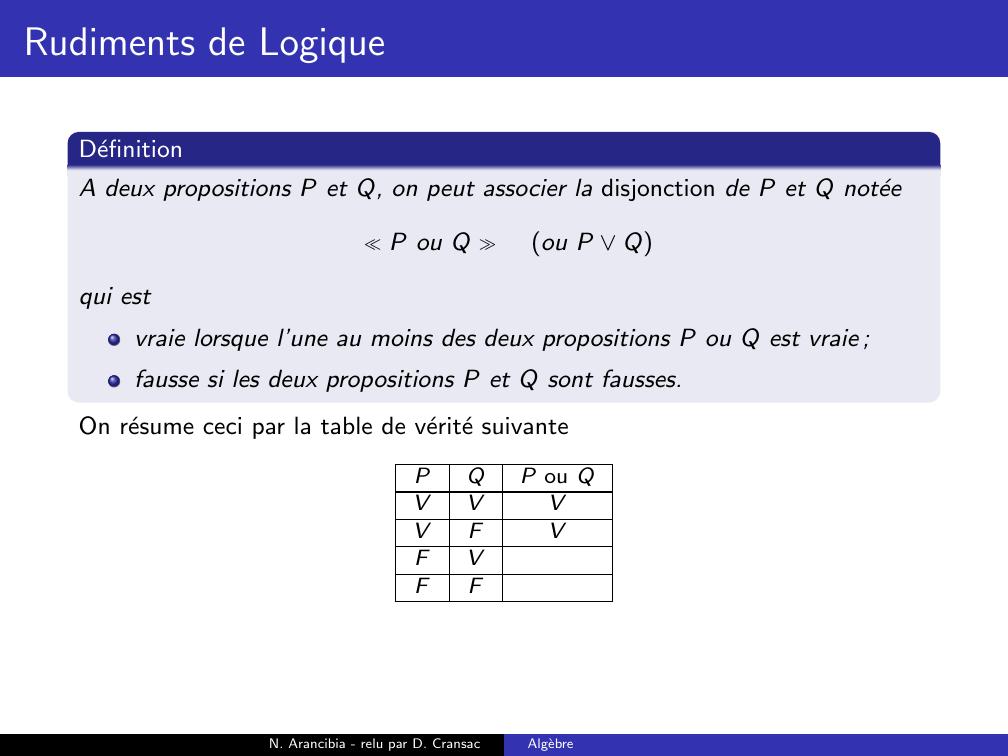
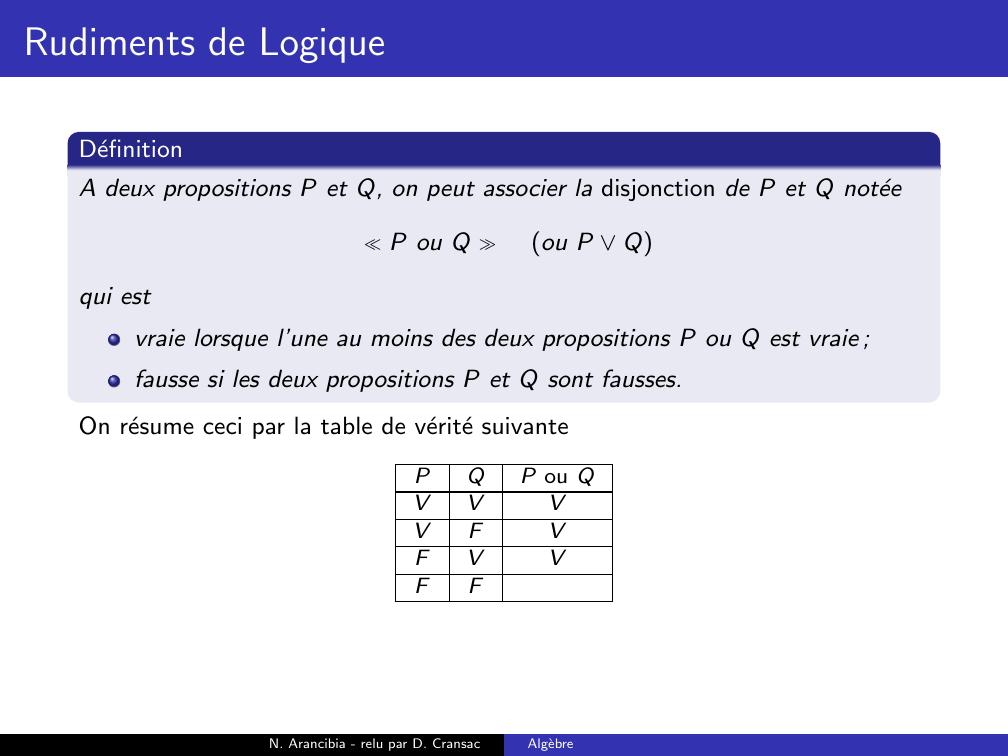
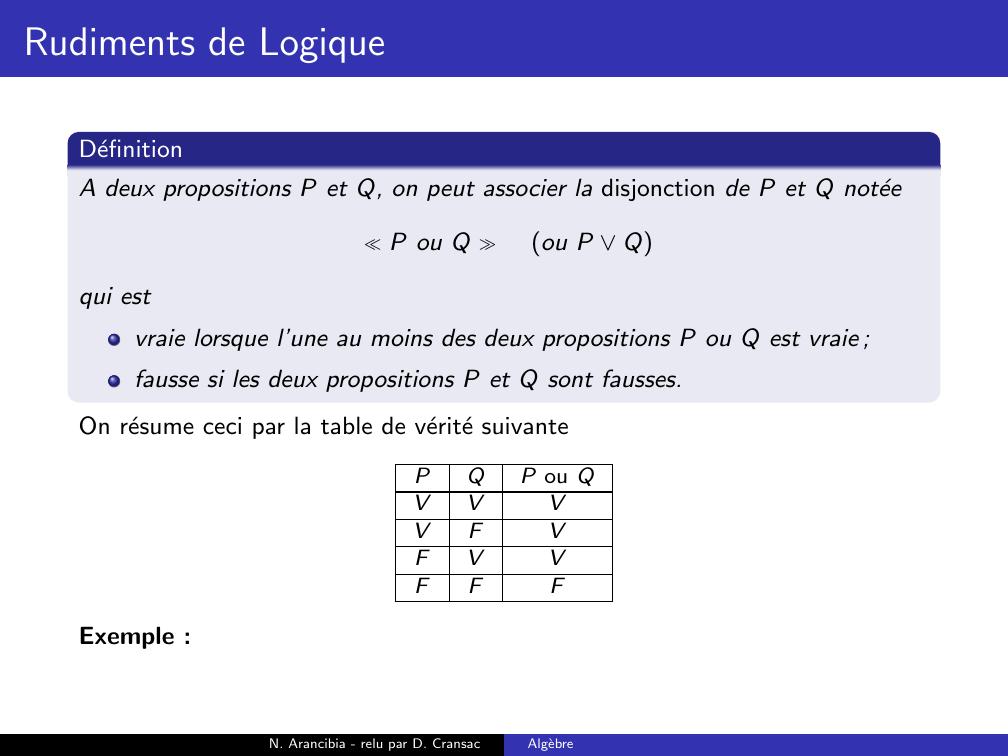
Page 96 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estN. Arancibia - relu par D. CransacAlgebre

Page 97 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;N. Arancibia - relu par D. CransacAlgebre

Page 98 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.N. Arancibia - relu par D. CransacAlgebre

Page 99 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 100 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 101 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVFFN. Arancibia - relu par D. CransacAlgebre

Page 102 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVVFFN. Arancibia - relu par D. CransacAlgebre

Page 103 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVVFFFN. Arancibia - relu par D. CransacAlgebre

Page 104 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVVFFFExemple :N. Arancibia - relu par D. CransacAlgebre

Page 105 : Rudiments de LogiqueDefinitionA deux propositions P et Q, on peut associer la disjonction de P et Q noteeP ou Q ou P Qqui estvraie lorsque l’une au moins des deux propositions P ou Q est vraie ;fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVVFFFExemple : Propriete vraie :Pour tout triangle ABC, AB AC + CBouABC+CAB+ dBCA = π N. Arancibia - relu par D. CransacAlgebre

Page 106 : Rudiments de LogiqueRemarque : On prendra garde au fait que le ou logique est un ouinclusif , contrairement au ou du langage courant qui lui est tressouvent un ou exclusif N. Arancibia - relu par D. CransacAlgebre

Page 107 : Rudiments de LogiqueRemarque : On prendra garde au fait que le ou logique est un ouinclusif , contrairement au ou du langage courant qui lui est tressouvent un ou exclusif Distinguer :1le ou exclusif de la langue fran¸caise : Fromage ou DessertOn ne peut pas avoir les deux.N. Arancibia - relu par D. CransacAlgebre

Page 108 : Rudiments de LogiqueRemarque : On prendra garde au fait que le ou logique est un ouinclusif , contrairement au ou du langage courant qui lui est tressouvent un ou exclusif Distinguer :1le ou exclusif de la langue fran¸caise : Fromage ou DessertOn ne peut pas avoir les deux.2le ou logique ou inclusif : On recrute un informaticien quisait coder en C++ ou en PythonOn peut avoir les deux.N. Arancibia - relu par D. CransacAlgebre

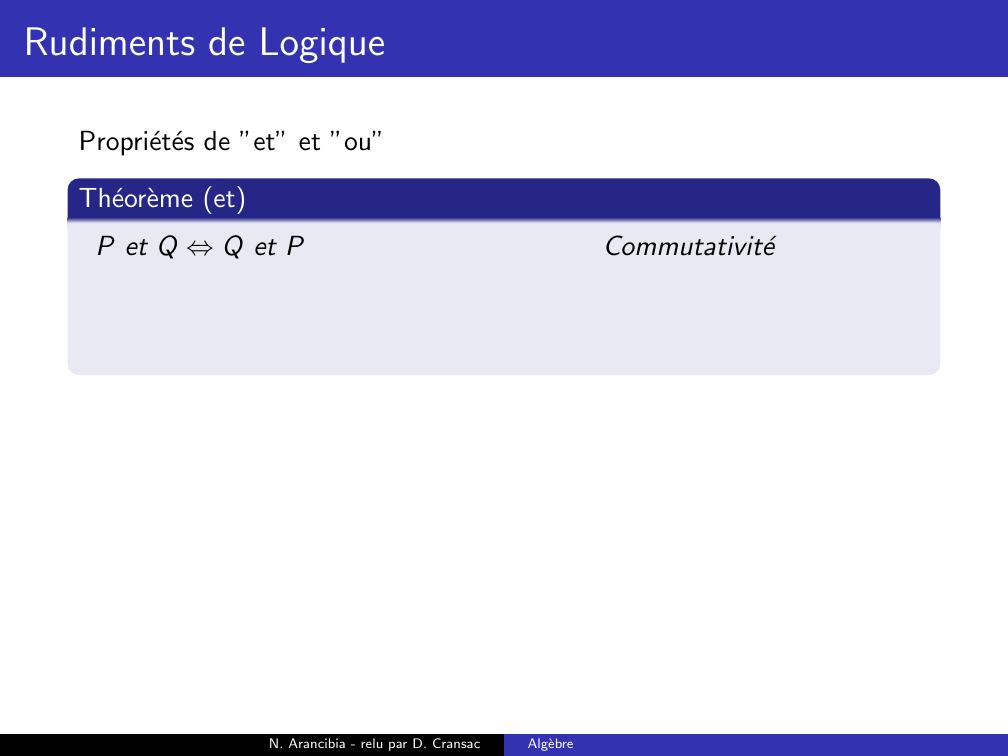
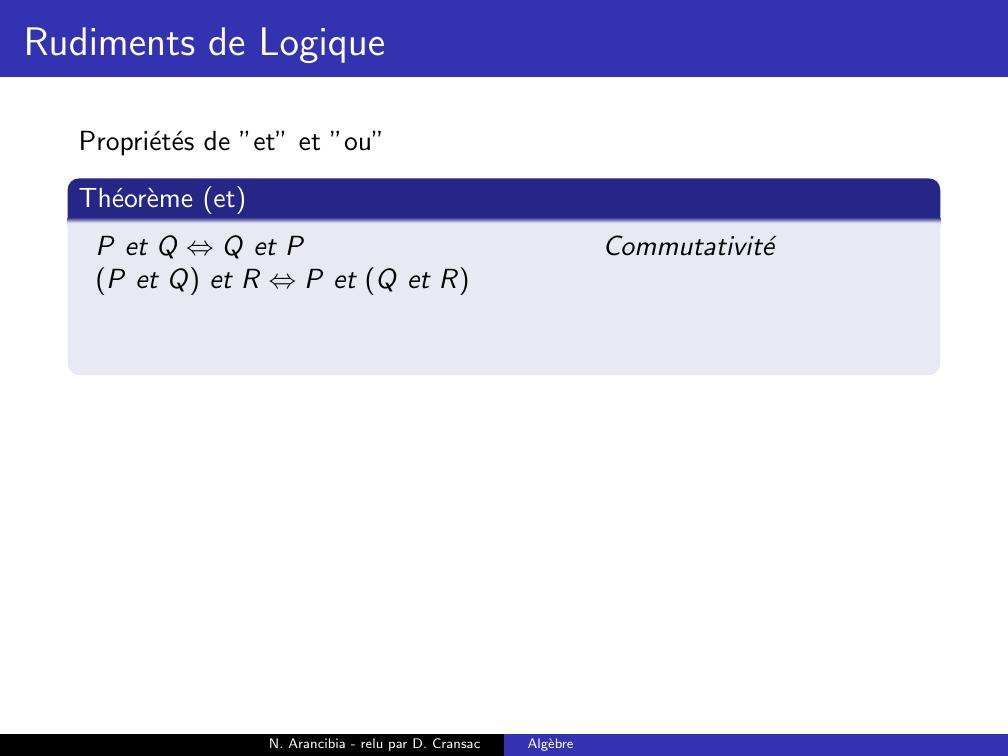
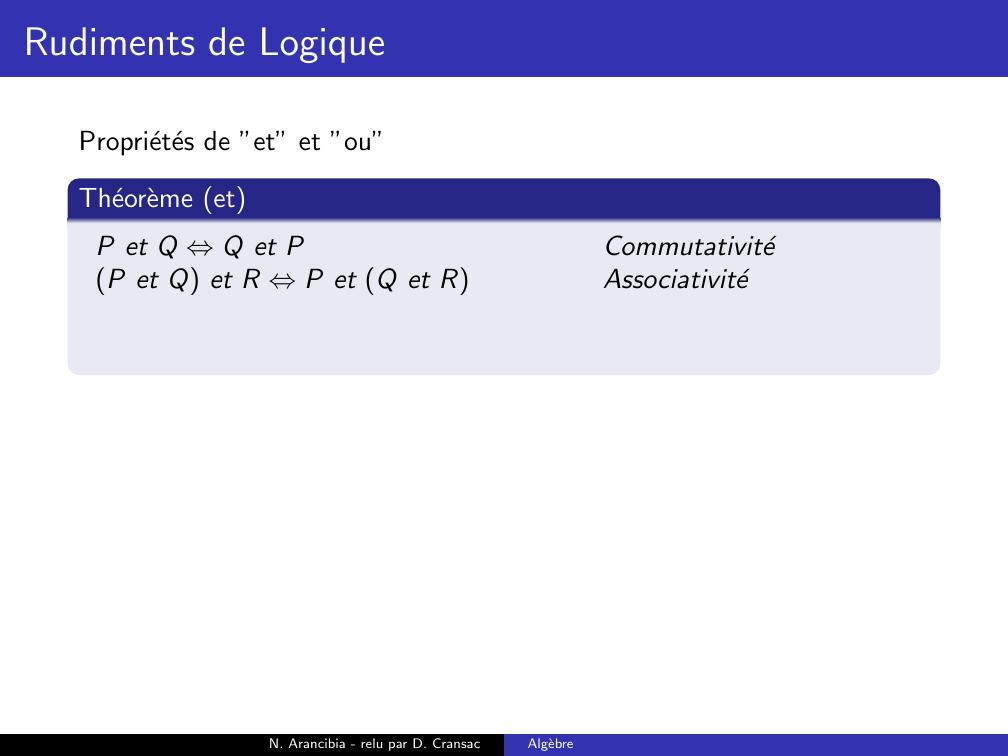
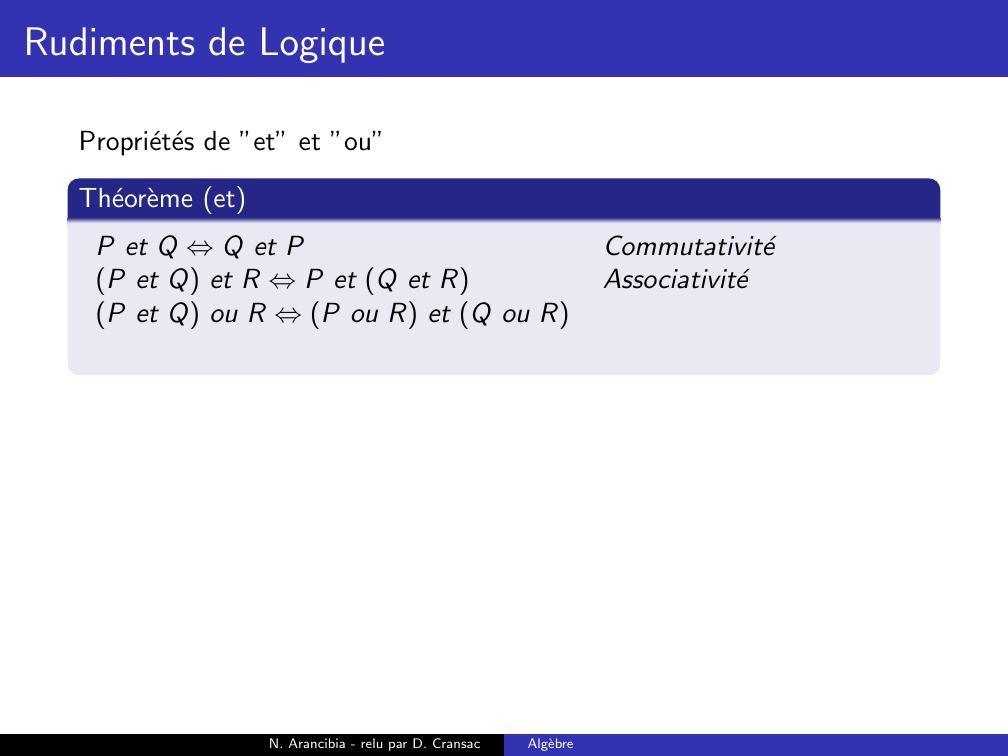
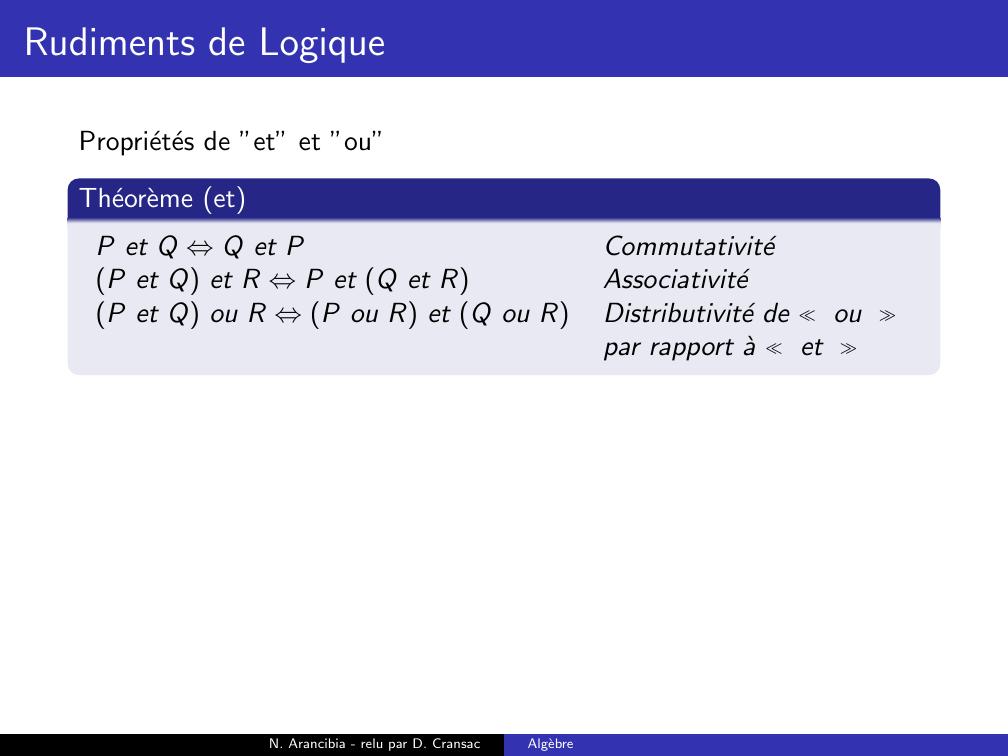
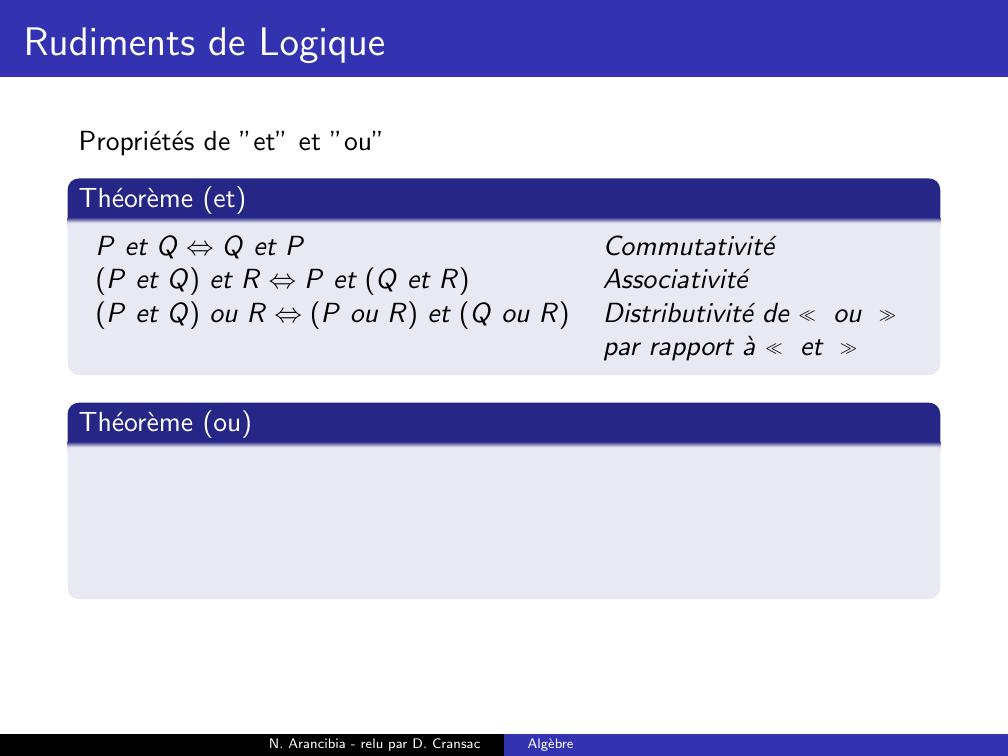
Page 109 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PN. Arancibia - relu par D. CransacAlgebre

Page 110 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteN. Arancibia - relu par D. CransacAlgebre

Page 111 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RN. Arancibia - relu par D. CransacAlgebre

Page 112 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RAssociativiteN. Arancibia - relu par D. CransacAlgebre

Page 113 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RAssociativiteP et Q ou R ⇔P ou R et Q ou RN. Arancibia - relu par D. CransacAlgebre

Page 114 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RAssociativiteP et Q ou R ⇔P ou R et Q ou RDistributivite de oupar rapport a etN. Arancibia - relu par D. CransacAlgebre

Page 115 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RAssociativiteP et Q ou R ⇔P ou R et Q ou RDistributivite de oupar rapport a etTheoreme ouN. Arancibia - relu par D. CransacAlgebre

Page 116 : Rudiments de LogiqueProprietes de ”et” et ”ou”Theoreme etP et Q ⇔Q et PCommutativiteP et Q et R ⇔P et Q et RAssociativiteP et Q ou R ⇔P ou R et Q ou RDistributivite de oupar rapport a etTheoreme ouP ou Q ⇔Q ou PCommutativiteP ou Q ou R ⇔P ou Q ou RAssociativiteP ou Q et R ⇔P et R ou Q et RDistributivite de etpar rapport a ouRemarque : Les proprietes sont symetriques pour les deux operateurs”et” et ”ou”.N. Arancibia - relu par D. CransacAlgebre

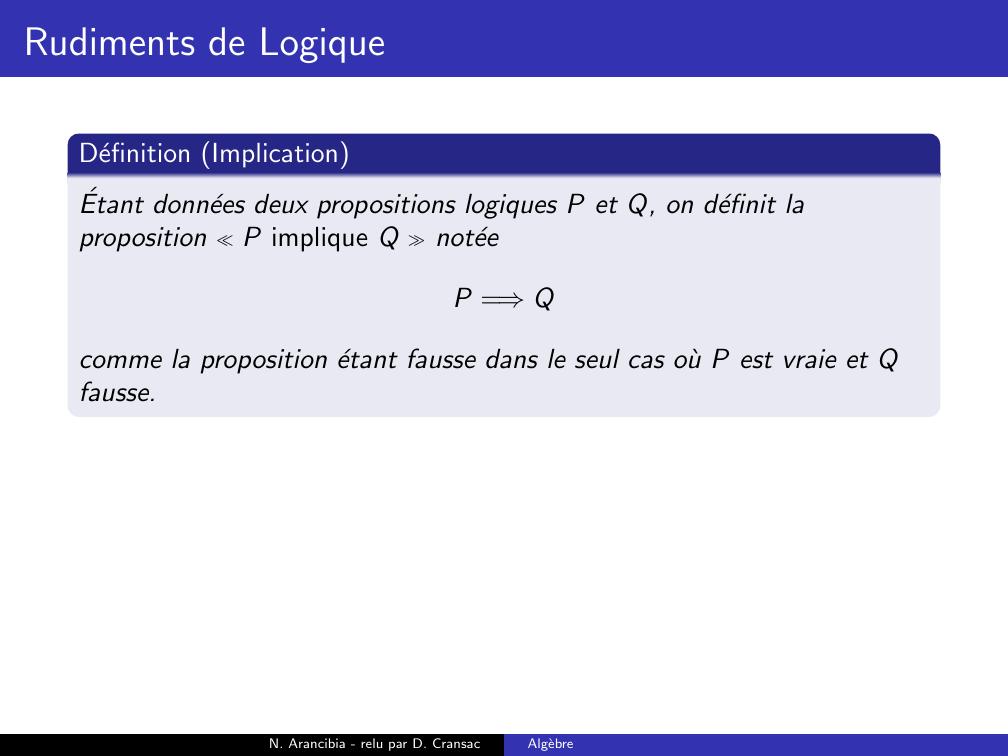
Page 117 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse.N. Arancibia - relu par D. CransacAlgebre

Page 118 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.N. Arancibia - relu par D. CransacAlgebre

Page 119 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 120 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVVFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 121 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVVFFFVFFN. Arancibia - relu par D. CransacAlgebre

Page 122 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVVFFFVVFFN. Arancibia - relu par D. CransacAlgebre

Page 123 : Rudiments de LogiqueDefinition ImplicationEtant donnees deux propositions logiques P et Q, on definit laproposition P implique Q noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Qfausse. On appelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVVFFFVVFFVN. Arancibia - relu par D. CransacAlgebre

Page 124 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.N. Arancibia - relu par D. CransacAlgebre

Page 125 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.N. Arancibia - relu par D. CransacAlgebre

Page 126 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.N. Arancibia - relu par D. CransacAlgebre

Page 127 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.Ce choix est en fait raisonnable.N. Arancibia - relu par D. CransacAlgebre

Page 128 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.Ce choix est en fait raisonnable.Imaginons par exemple l’assertion suivante :N. Arancibia - relu par D. CransacAlgebre

Page 129 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.Ce choix est en fait raisonnable.Imaginons par exemple l’assertion suivante :P =⇒Q : J’ai eu une discussion avec mon chienimplique mon chien parle.N. Arancibia - relu par D. CransacAlgebre

Page 130 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.Ce choix est en fait raisonnable.Imaginons par exemple l’assertion suivante :P =⇒Q : J’ai eu une discussion avec mon chienimplique mon chien parle.Bien entendu, cette implication est vraieN. Arancibia - relu par D. CransacAlgebre

Page 131 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive.En effet, si P est fausse, alors l’implication est necessairement vraie.En particulier, faux implique faux est consideree comme vraie enmathematique.Ce choix est en fait raisonnable.Imaginons par exemple l’assertion suivante :P =⇒Q : J’ai eu une discussion avec mon chienimplique mon chien parle.Bien entendu, cette implication est vraie , mais niP : J’ai eu une discussion avec un chienniQ : mon chien parlene le sont.N. Arancibia - relu par D. CransacAlgebre

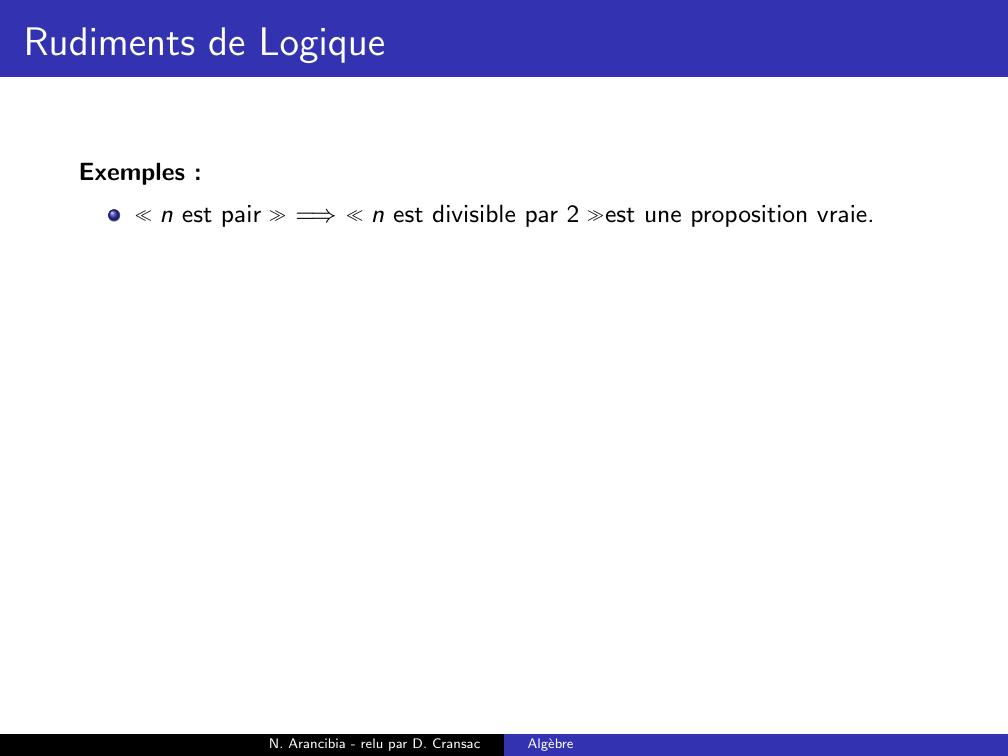
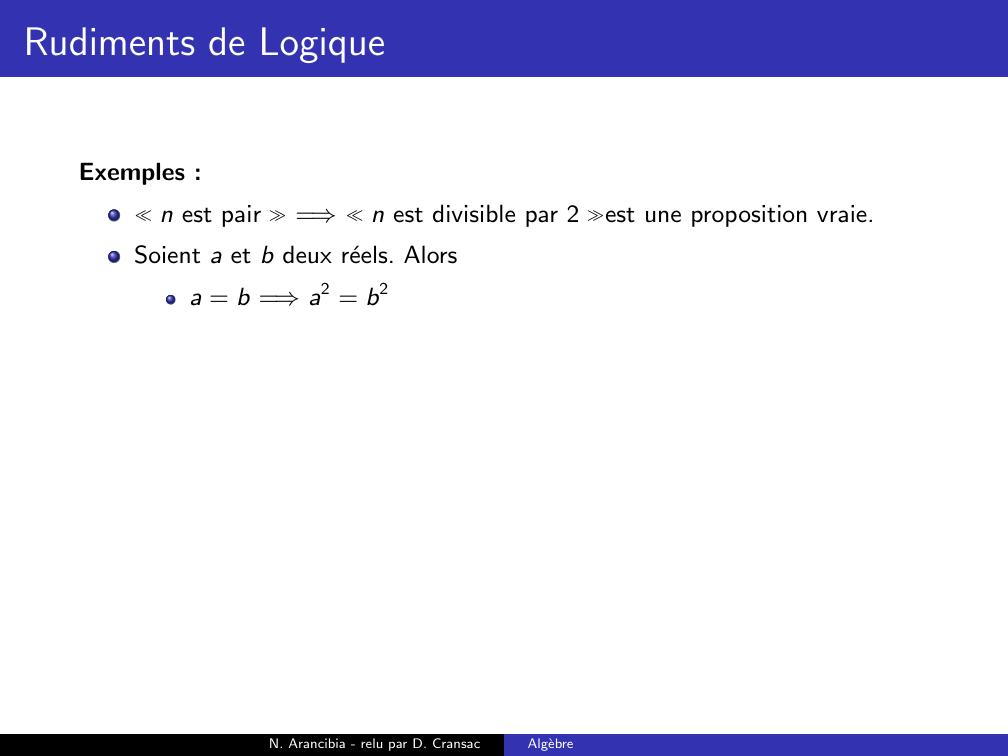
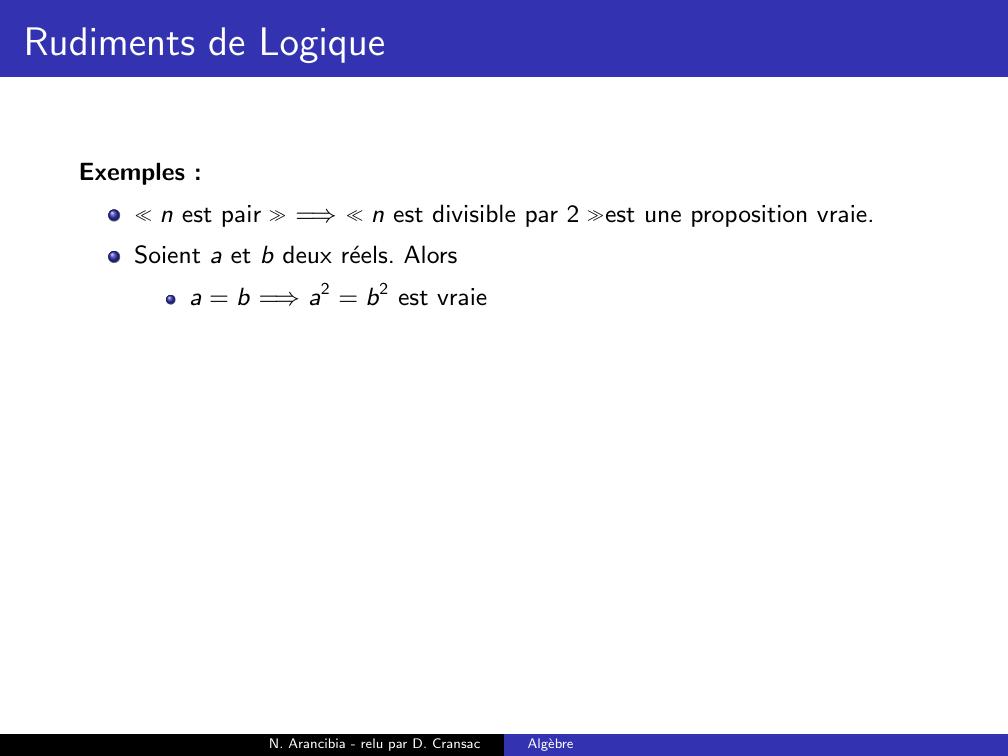
Page 132 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 133 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2N. Arancibia - relu par D. CransacAlgebre

Page 134 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2 est vraieN. Arancibia - relu par D. CransacAlgebre

Page 135 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2 est vraie , maisa2 = b2 =⇒a = b est fausse on peut trouver un cas ou c’est faux.N. Arancibia - relu par D. CransacAlgebre

Page 136 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2 est vraie , maisa2 = b2 =⇒a = b est fausse on peut trouver un cas ou c’est faux.Vocabulaire : Nous utiliserons souvent le vocabulaire suivant, si P =⇒Q estvraie , nous dirons :si P alors Q.N. Arancibia - relu par D. CransacAlgebre

Page 137 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2 est vraie , maisa2 = b2 =⇒a = b est fausse on peut trouver un cas ou c’est faux.Vocabulaire : Nous utiliserons souvent le vocabulaire suivant, si P =⇒Q estvraie , nous dirons :si P alors Q.L’assertion P est alors appelee une condition suffisante de Q :Pour que Q soit vraie, il suffit que P soit vraie.N. Arancibia - relu par D. CransacAlgebre

Page 138 : Rudiments de LogiqueExemples :n est pair =⇒n est divisible par 2 est une proposition vraie.Soient a et b deux reels. Alorsa = b =⇒a2 = b2 est vraie , maisa2 = b2 =⇒a = b est fausse on peut trouver un cas ou c’est faux.Vocabulaire : Nous utiliserons souvent le vocabulaire suivant, si P =⇒Q estvraie , nous dirons :si P alors Q.L’assertion P est alors appelee une condition suffisante de Q :Pour que Q soit vraie, il suffit que P soit vraie.L’assertion Q est alors appelee une condition necessaire de P :Pour que P soit vraie, il faut que Q soit vraie.N. Arancibia - relu par D. CransacAlgebre

Page 139 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Il suffit que je prenne le Metro et que je marche.N. Arancibia - relu par D. CransacAlgebre

Page 140 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.N. Arancibia - relu par D. CransacAlgebre

Page 141 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.VraiN. Arancibia - relu par D. CransacAlgebre

Page 142 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.Vrai2Pour montrer que 231 n’est pas premierIl suffit que je le decompose en produit de nombres premiers.N. Arancibia - relu par D. CransacAlgebre

Page 143 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.Vrai2Pour montrer que 231 n’est pas premierIl suffit que je le decompose en produit de nombres premiers.Il faut que je le decompose en produit de nombres premiers.N. Arancibia - relu par D. CransacAlgebre

Page 144 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.Vrai2Pour montrer que 231 n’est pas premierIl suffit que je le decompose en produit de nombres premiers.Vrai :231 = 3 × 7 × 11 suffit pour montrer que 231 n’est pas premier.Il faut que je le decompose en produit de nombres premiers.N. Arancibia - relu par D. CransacAlgebre

Page 145 : Rudiments de Logiqueil faut et il suffit Distinguer :1Pour aller visiter la Tour Eiffel,Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.Il suffit que je prenne le Metro et que je marche.Vrai2Pour montrer que 231 n’est pas premierIl suffit que je le decompose en produit de nombres premiers.Vrai :231 = 3 × 7 × 11 suffit pour montrer que 231 n’est pas premier.Il faut que je le decompose en produit de nombres premiers.Faux : je peux aussi ecrire 231 = 3 × 77.N. Arancibia - relu par D. CransacAlgebre

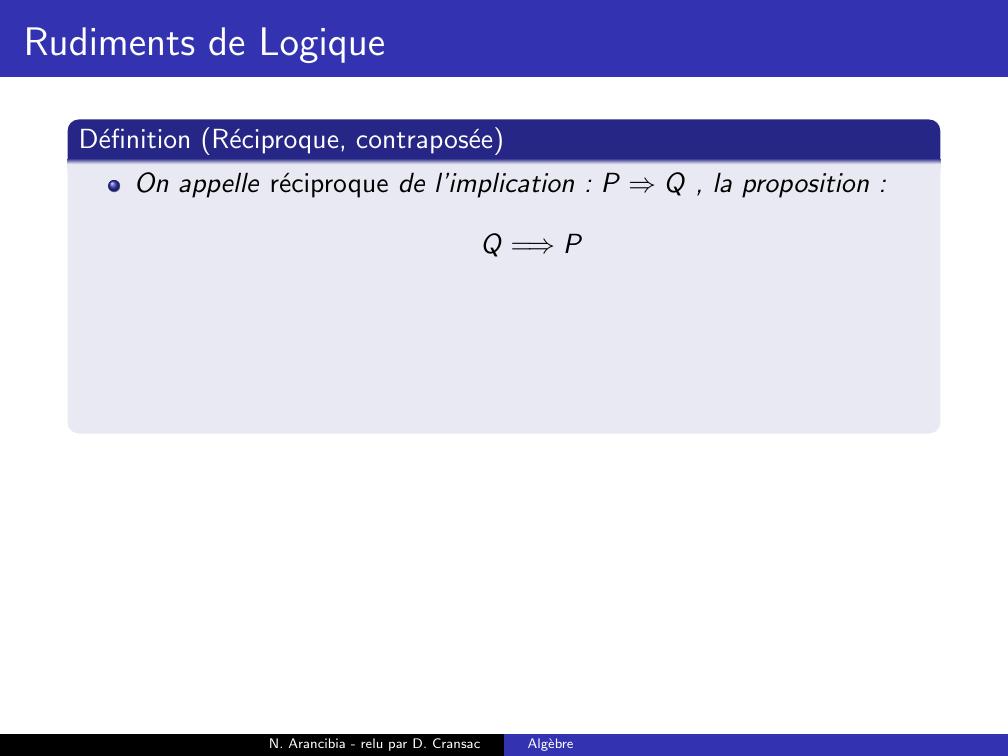
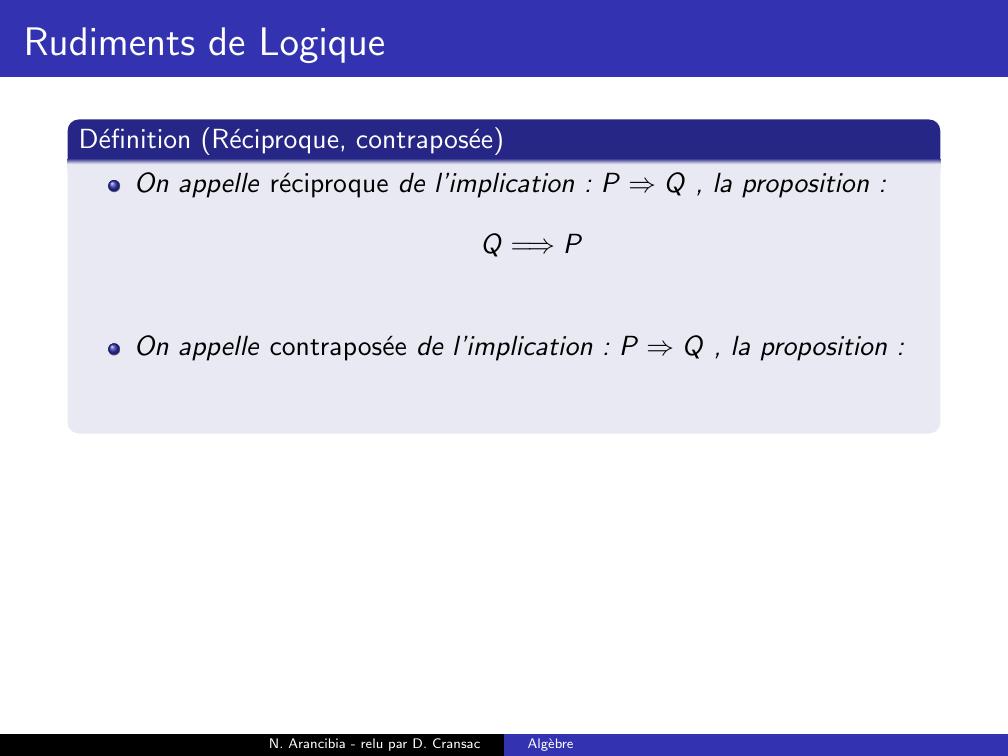
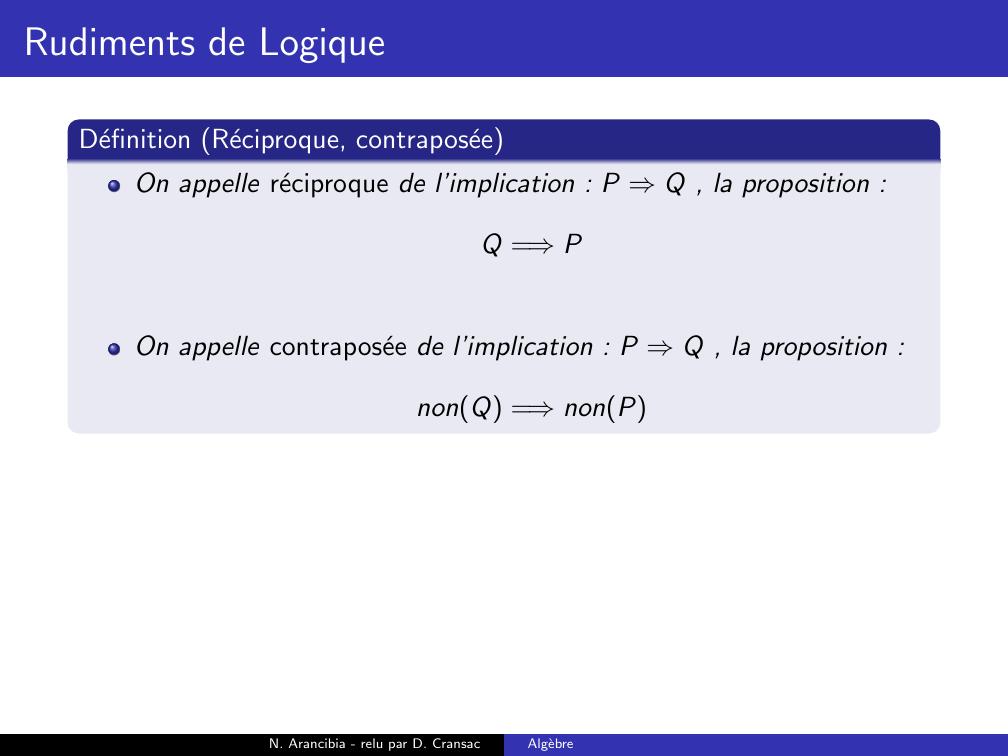
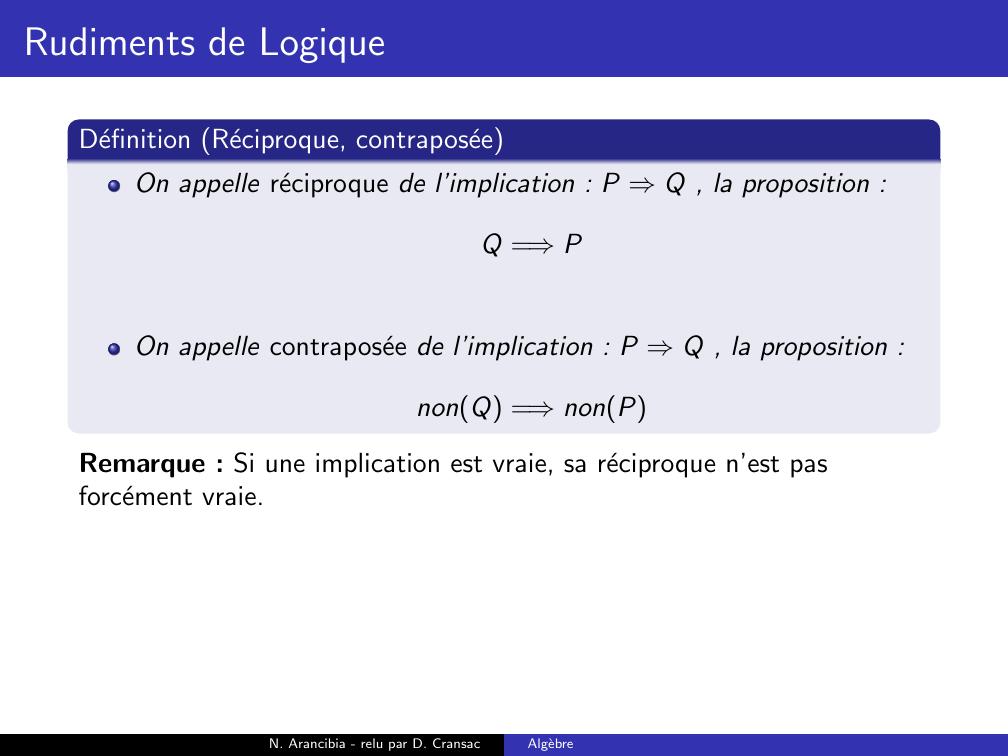
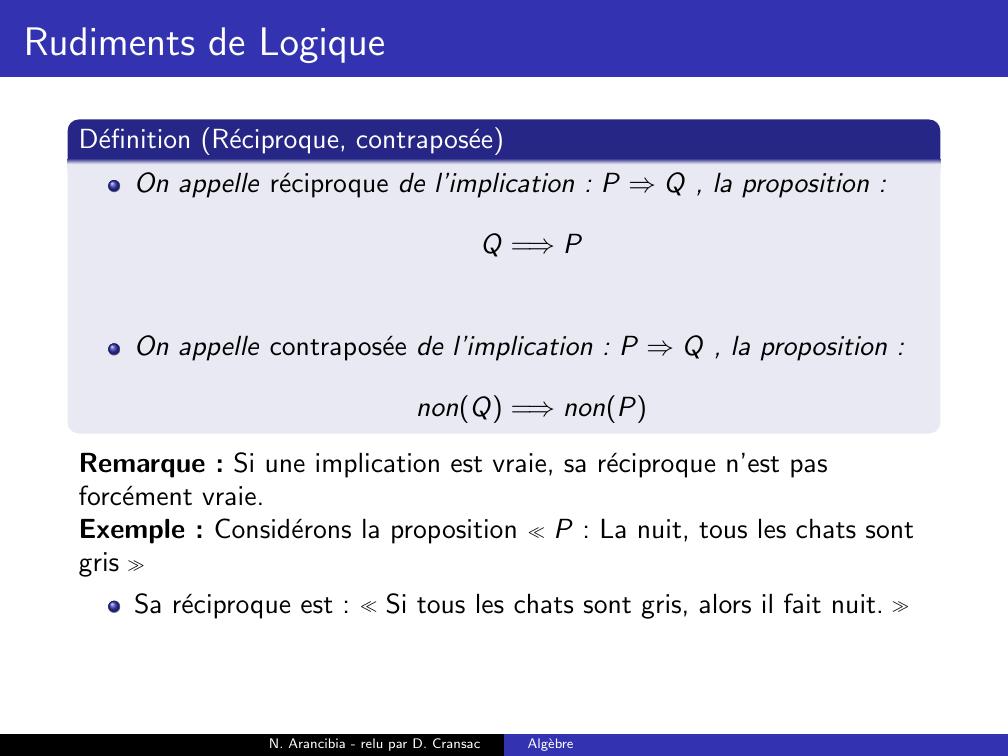
Page 146 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒PN. Arancibia - relu par D. CransacAlgebre

Page 147 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :N. Arancibia - relu par D. CransacAlgebre

Page 148 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPN. Arancibia - relu par D. CransacAlgebre

Page 149 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPRemarque : Si une implication est vraie, sa reciproque n’est pasforcement vraie.N. Arancibia - relu par D. CransacAlgebre

Page 150 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPRemarque : Si une implication est vraie, sa reciproque n’est pasforcement vraie.Exemple : Considerons la proposition P : La nuit, tous les chats sontgris Sa reciproque est :N. Arancibia - relu par D. CransacAlgebre

Page 151 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPRemarque : Si une implication est vraie, sa reciproque n’est pasforcement vraie.Exemple : Considerons la proposition P : La nuit, tous les chats sontgris Sa reciproque est : Si tous les chats sont gris, alors il fait nuit. N. Arancibia - relu par D. CransacAlgebre

Page 152 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPRemarque : Si une implication est vraie, sa reciproque n’est pasforcement vraie.Exemple : Considerons la proposition P : La nuit, tous les chats sontgris Sa reciproque est : Si tous les chats sont gris, alors il fait nuit. Sa contraposee est :N. Arancibia - relu par D. CransacAlgebre

Page 153 : Rudiments de LogiqueDefinition Reciproque, contraposeeOn appelle reciproque de l’implication : P ⇒Q , la proposition :Q =⇒POn appelle contraposee de l’implication : P ⇒Q , la proposition :nonQ =⇒nonPRemarque : Si une implication est vraie, sa reciproque n’est pasforcement vraie.Exemple : Considerons la proposition P : La nuit, tous les chats sontgris Sa reciproque est : Si tous les chats sont gris, alors il fait nuit. Sa contraposee est : Si au moins un chat n’est pas gris, alors ilfait jour. N. Arancibia - relu par D. CransacAlgebre

Page 154 : Rudiments de LogiqueVocabulaire :Lorsque P et Q sont equivalentes , on dit queP est vraie si et seulement si Q est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 155 : Rudiments de LogiqueVocabulaire :Lorsque P et Q sont equivalentes , on dit queP est vraie si et seulement si Q est vraie.P est une condition necessaire et suffisante CNS de Q.N. Arancibia - relu par D. CransacAlgebre

Page 156 : Rudiments de LogiqueVocabulaire :Lorsque P et Q sont equivalentes , on dit queP est vraie si et seulement si Q est vraie.P est une condition necessaire et suffisante CNS de Q.Pour que Q soit vraie il faut et il suffit que P soit vraie.N. Arancibia - relu par D. CransacAlgebre

Page 157 : Rudiments de LogiqueVocabulaire :Lorsque P et Q sont equivalentes , on dit queP est vraie si et seulement si Q est vraie.P est une condition necessaire et suffisante CNS de Q.Pour que Q soit vraie il faut et il suffit que P soit vraie.ou, tout simplement,P est equivalente a QN. Arancibia - relu par D. CransacAlgebre

Page 158 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.N. Arancibia - relu par D. CransacAlgebre

Page 159 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee.N. Arancibia - relu par D. CransacAlgebre

Page 160 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.N. Arancibia - relu par D. CransacAlgebre

Page 161 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.N. Arancibia - relu par D. CransacAlgebre

Page 162 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 163 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 164 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 165 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 166 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVVFFVFFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 167 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVVFFVFFFVVFVVFVFVVOn retrouve la mˆeme table de verite que la proposition P ⇒Q.N. Arancibia - relu par D. CransacAlgebre

Page 168 : Rudiments de LogiqueRemarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. Utilisons cette remarque pour etudier certaines regles decalcul sur l’implication et l’equivalence.TheoremeToute implication est equivalente a sa contraposee. Autrement dit :P =⇒Q ⇐⇒nonQ =⇒nonP.Demonstration.On ecrit la table de verite de la proposition Q =⇒P.PPQQQ =⇒PP =⇒QVFVFVVVFFVFFFVVFVVFVFVVVOn retrouve la mˆeme table de verite que la proposition P ⇒Q. La propositionP ⇒Q et la proposition Q ⇒P sont donc equivalentes.N. Arancibia - relu par D. CransacAlgebre

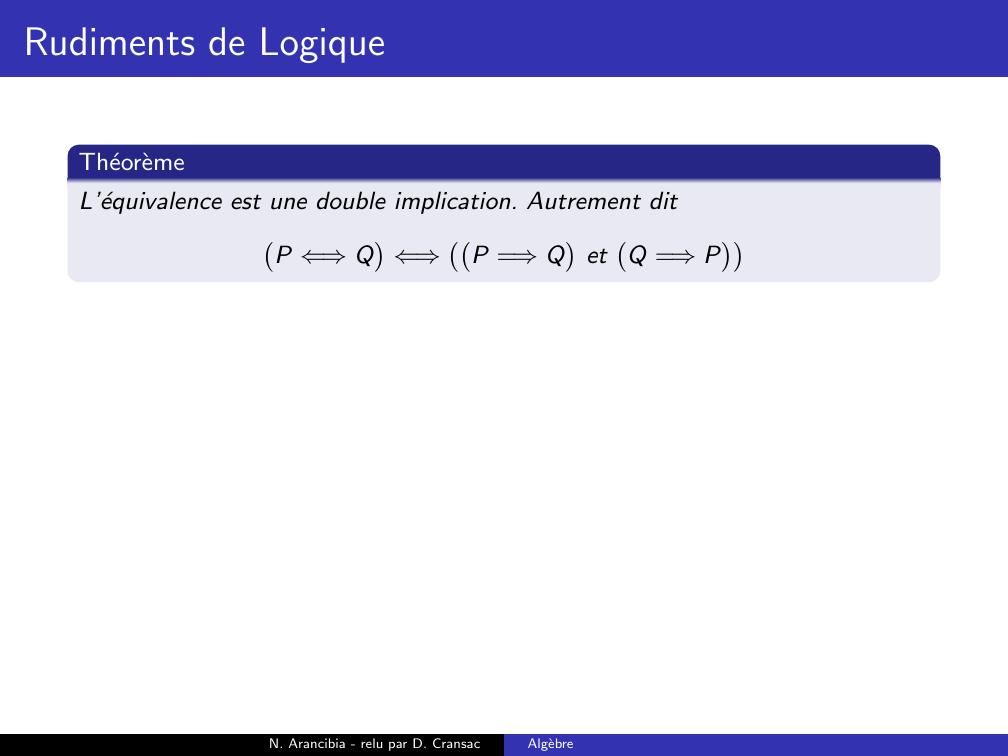
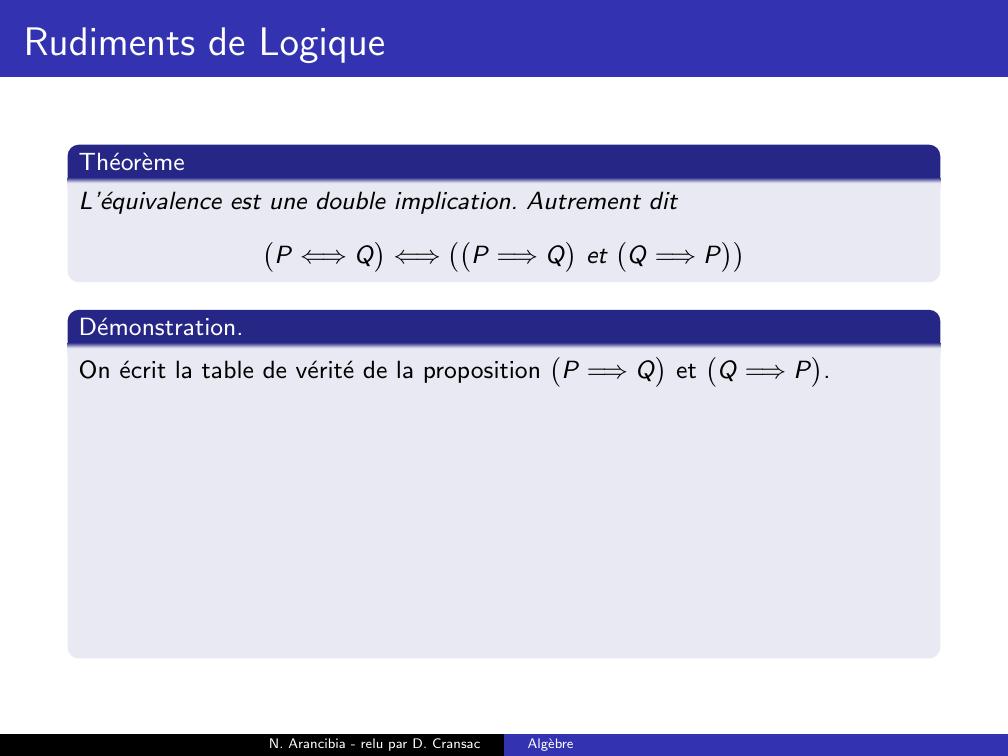
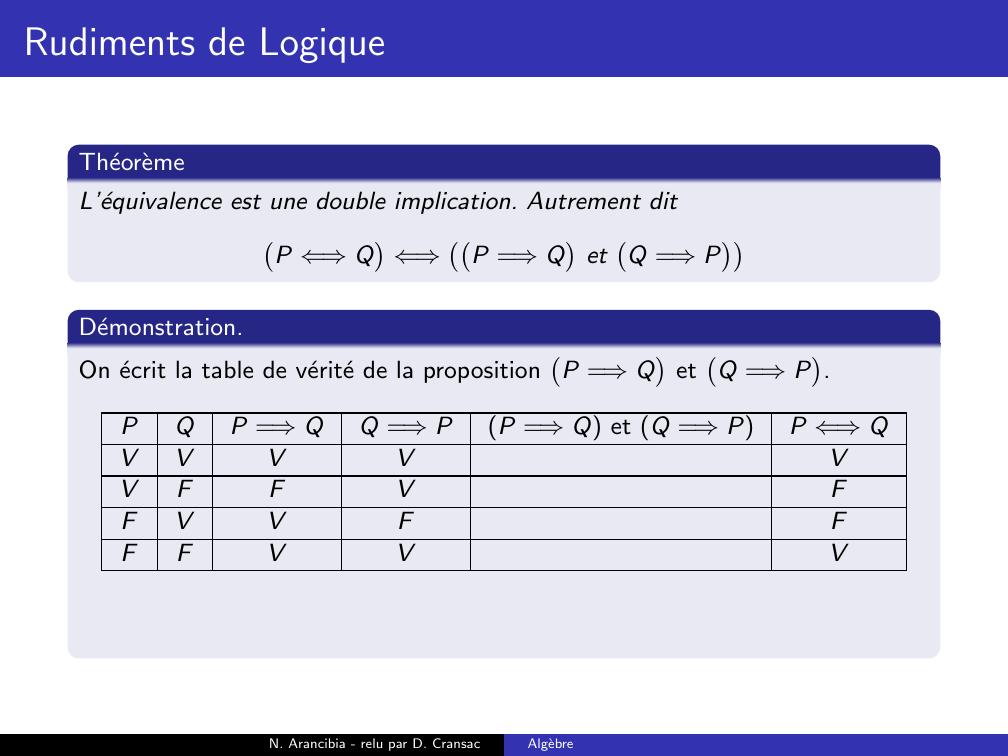
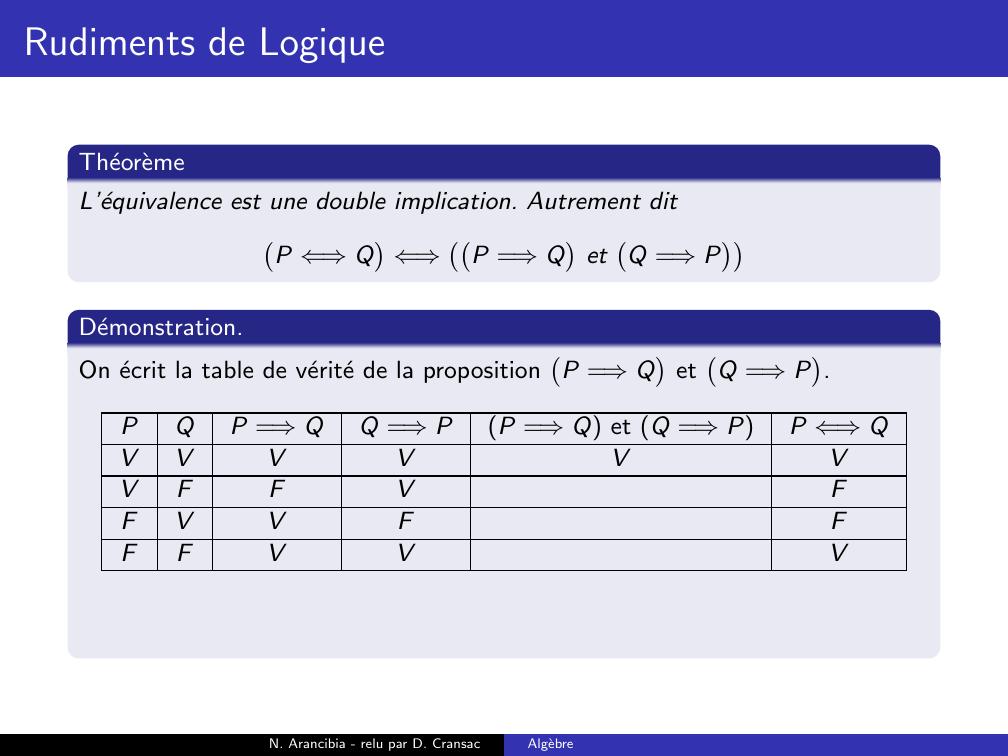
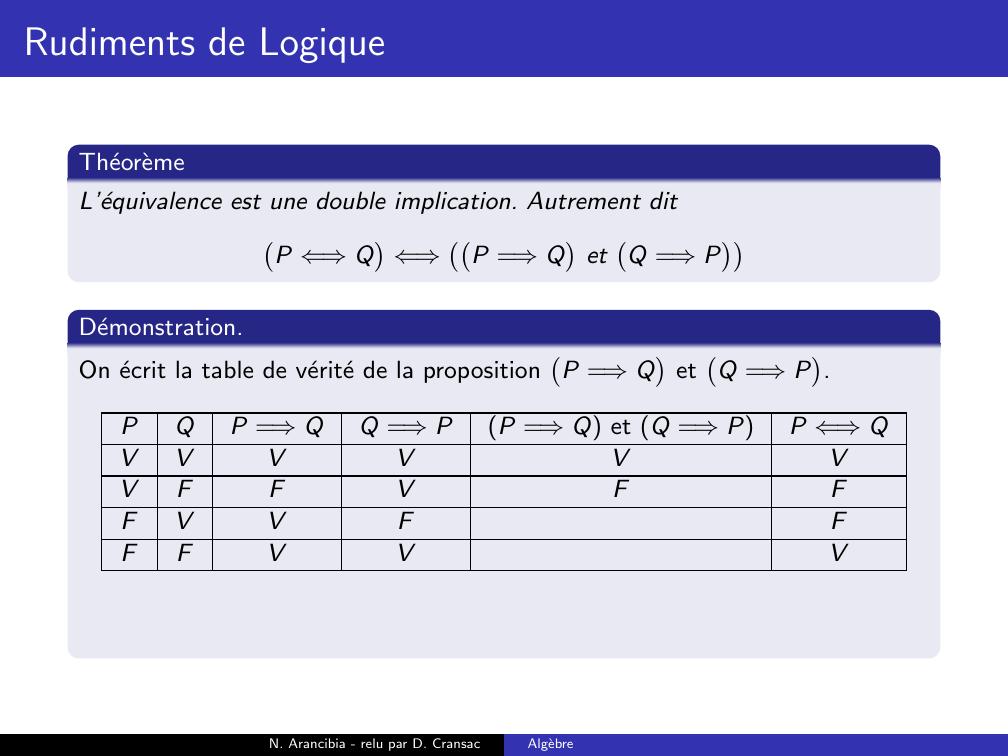
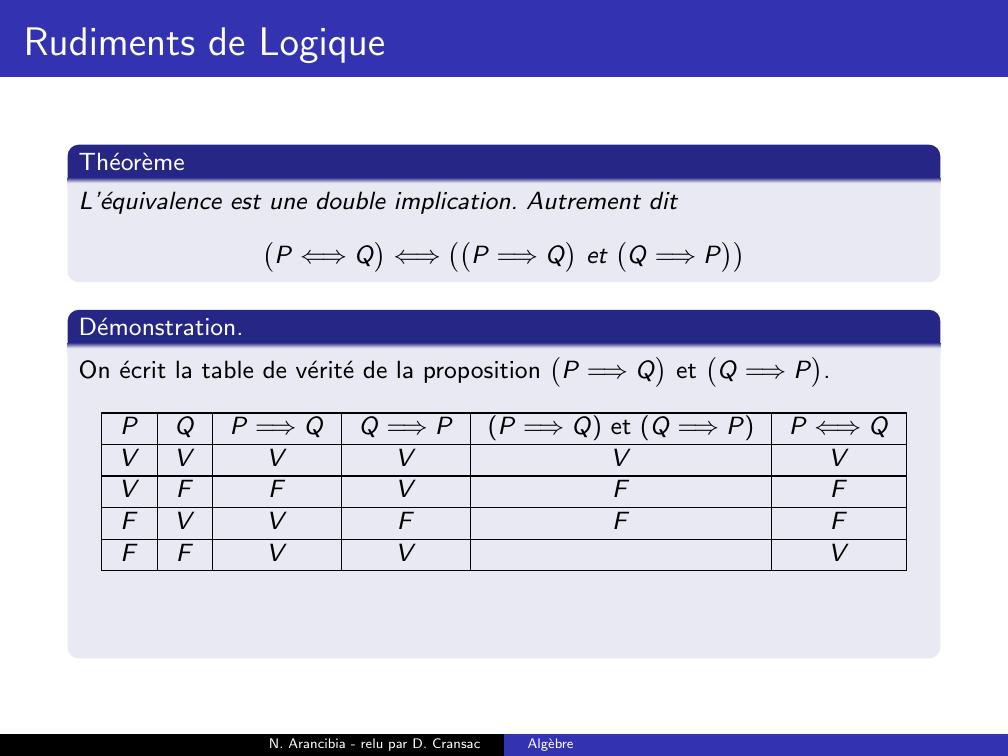
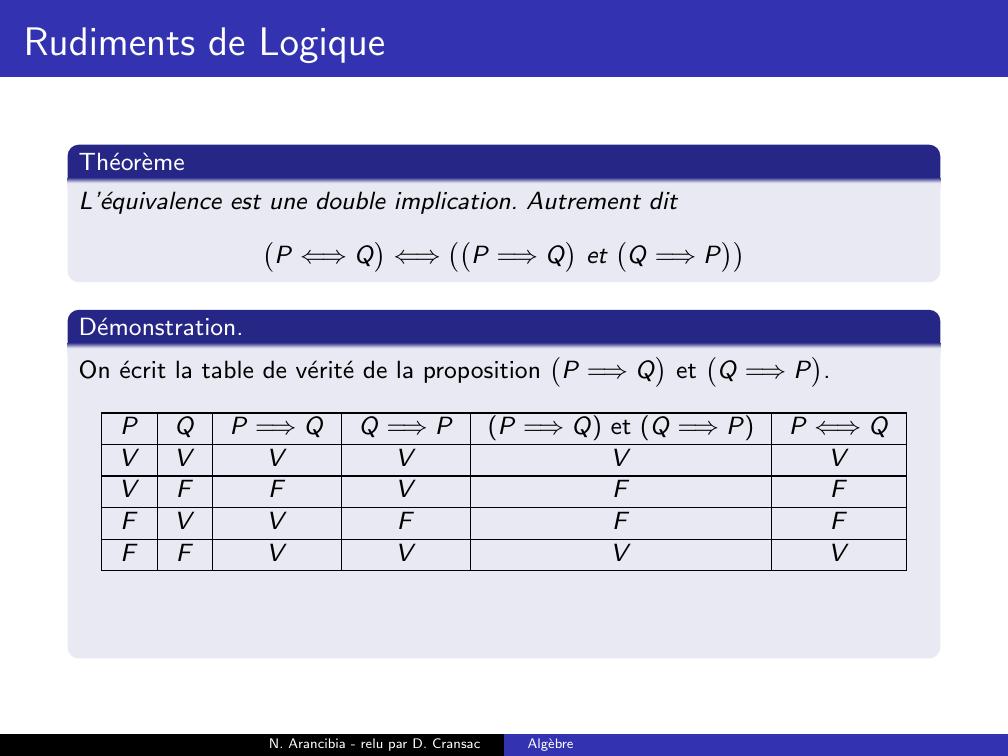
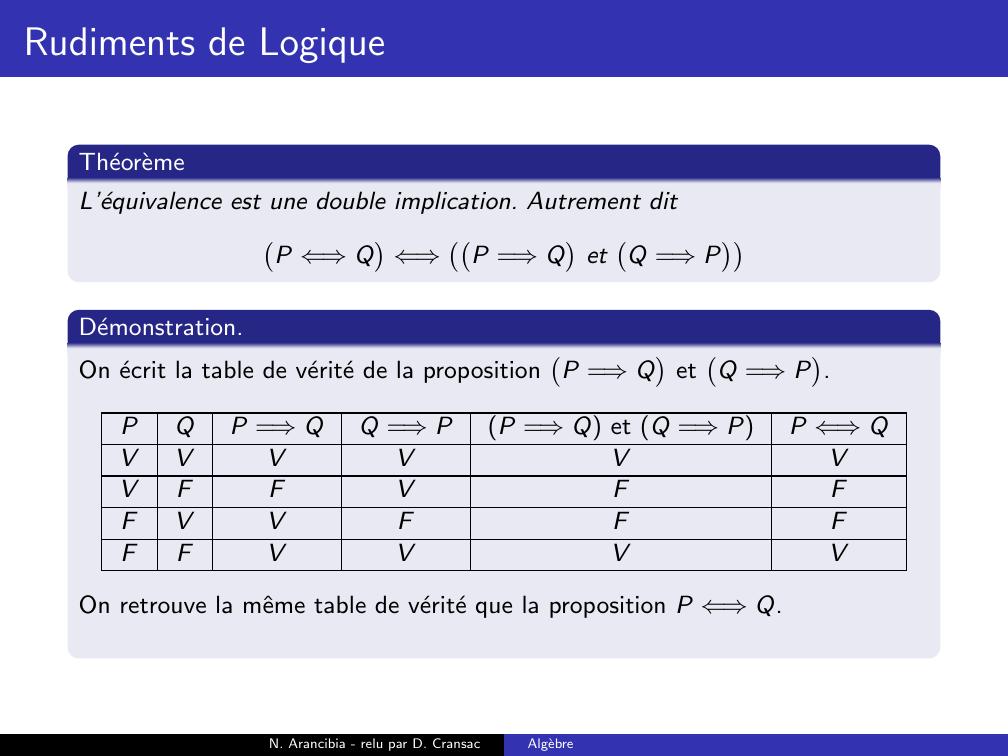
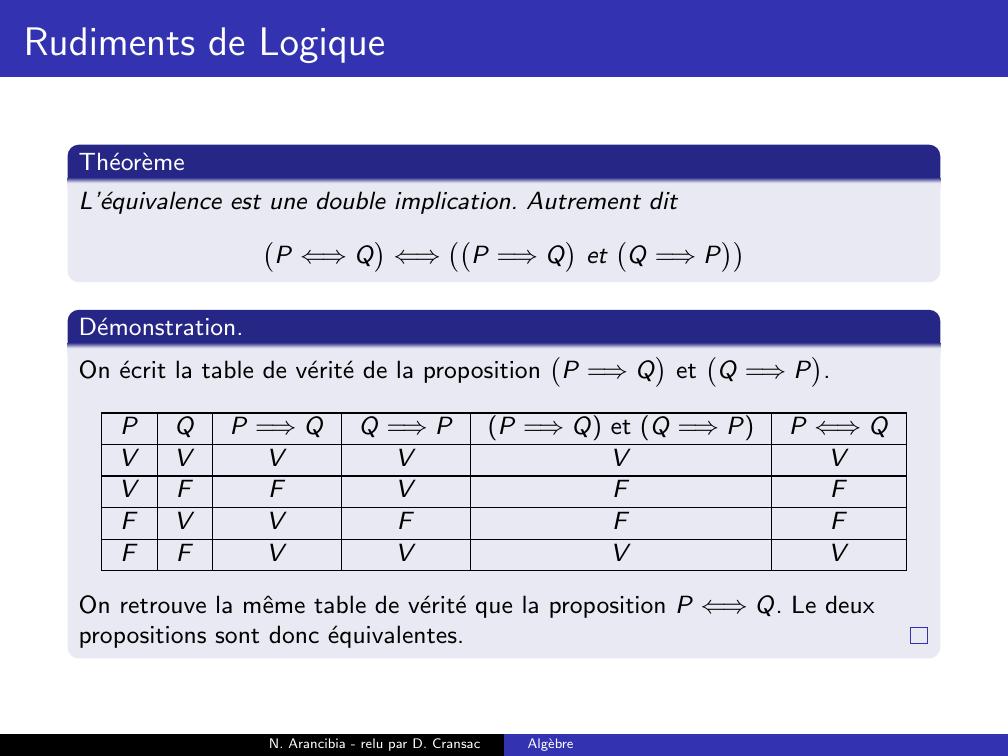
Page 169 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PN. Arancibia - relu par D. CransacAlgebre

Page 170 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.N. Arancibia - relu par D. CransacAlgebre

Page 171 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVFFVFFVVFFFFVVVN. Arancibia - relu par D. CransacAlgebre

Page 172 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFVVFFFFVVVN. Arancibia - relu par D. CransacAlgebre

Page 173 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFVVVN. Arancibia - relu par D. CransacAlgebre

Page 174 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFFVVVN. Arancibia - relu par D. CransacAlgebre

Page 175 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFFVVVVN. Arancibia - relu par D. CransacAlgebre

Page 176 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFFVVVVOn retrouve la mˆeme table de verite que la proposition P ⇐⇒Q.N. Arancibia - relu par D. CransacAlgebre

Page 177 : Rudiments de LogiqueTheoremeL’equivalence est une double implication. Autrement ditP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFFVVVVOn retrouve la mˆeme table de verite que la proposition P ⇐⇒Q. Le deuxpropositions sont donc equivalentes.N. Arancibia - relu par D. CransacAlgebre

Page 178 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganN. Arancibia - relu par D. CransacAlgebre

Page 179 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.N. Arancibia - relu par D. CransacAlgebre

Page 180 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.N. Arancibia - relu par D. CransacAlgebre

Page 181 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.N. Arancibia - relu par D. CransacAlgebre

Page 182 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite :N. Arancibia - relu par D. CransacAlgebre

Page 183 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite : Double negation :Pnon Pnon non PVFVFFVFVN. Arancibia - relu par D. CransacAlgebre

Page 184 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite : Double negation :Pnon Pnon non PVFVVFFVFVN. Arancibia - relu par D. CransacAlgebre

Page 185 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite : Double negation :Pnon Pnon non PVFVVFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 186 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite : Double negation :Pnon Pnon non PVFVVFVFVFFVN. Arancibia - relu par D. CransacAlgebre

Page 187 : Rudiments de LogiqueEtudions comme la negation modifie et nous permet de creer des nouvellespropositions.Theoreme Lois de MorganDouble negation : P ⇐⇒nonnonP.Conjonction : nonP et Q ⇐⇒nonP ou nonQ.Disjonction : nonP ou Q ⇐⇒nonP et nonQ.Demonstration.On ecrit les tables de verite : Double negation :Pnon Pnon non PVFVVFVFVFFVFN. Arancibia - relu par D. CransacAlgebre

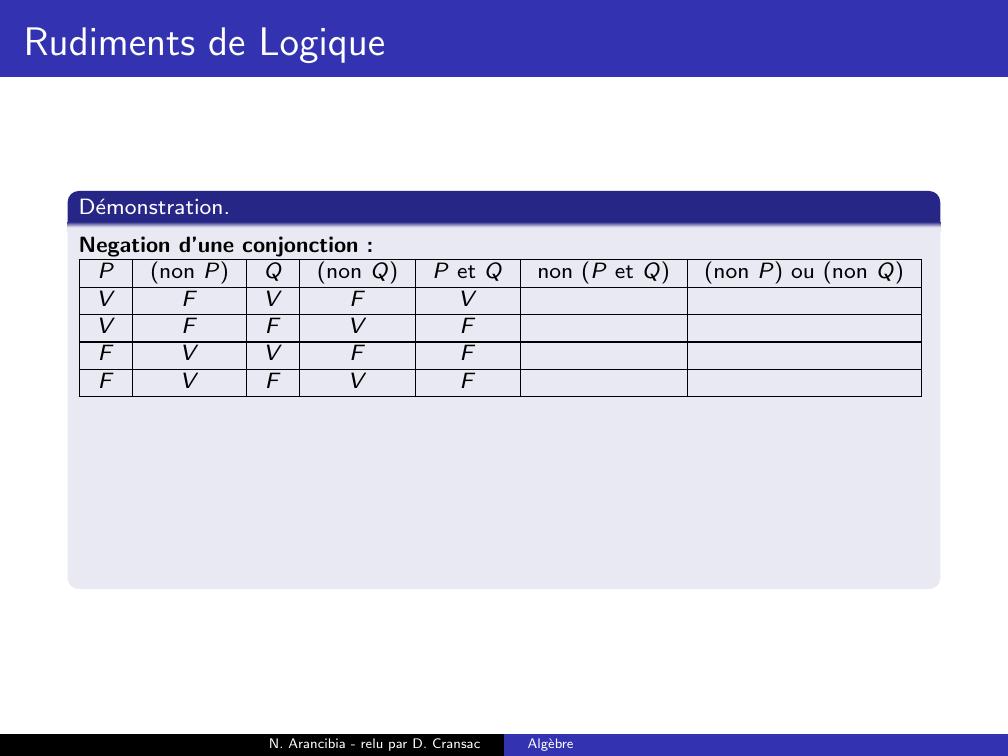
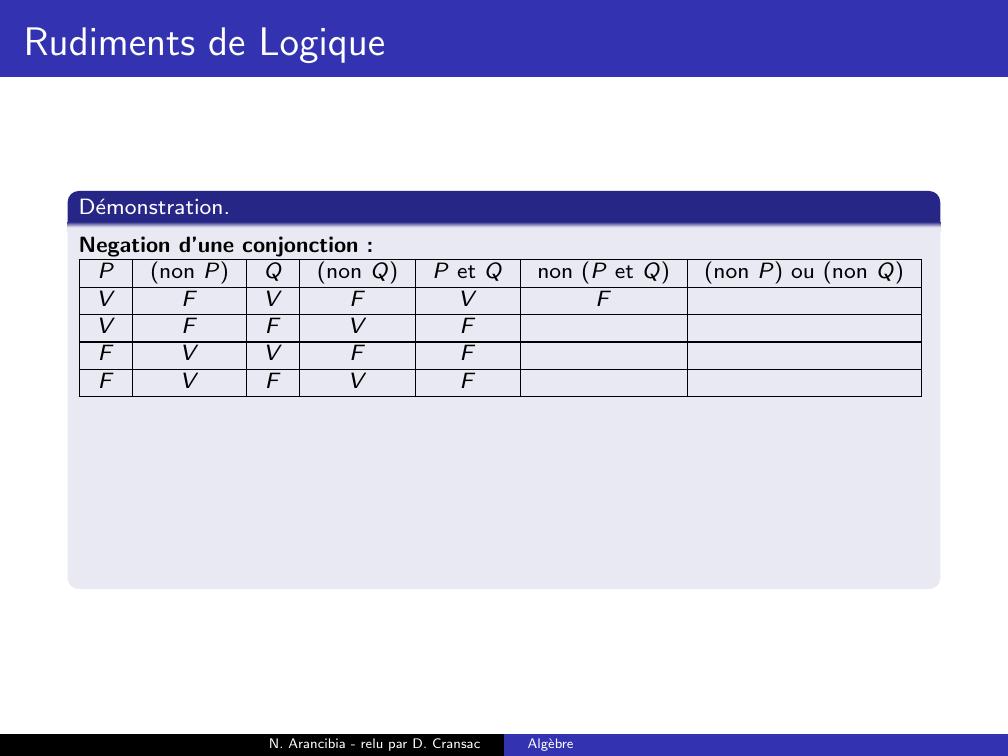
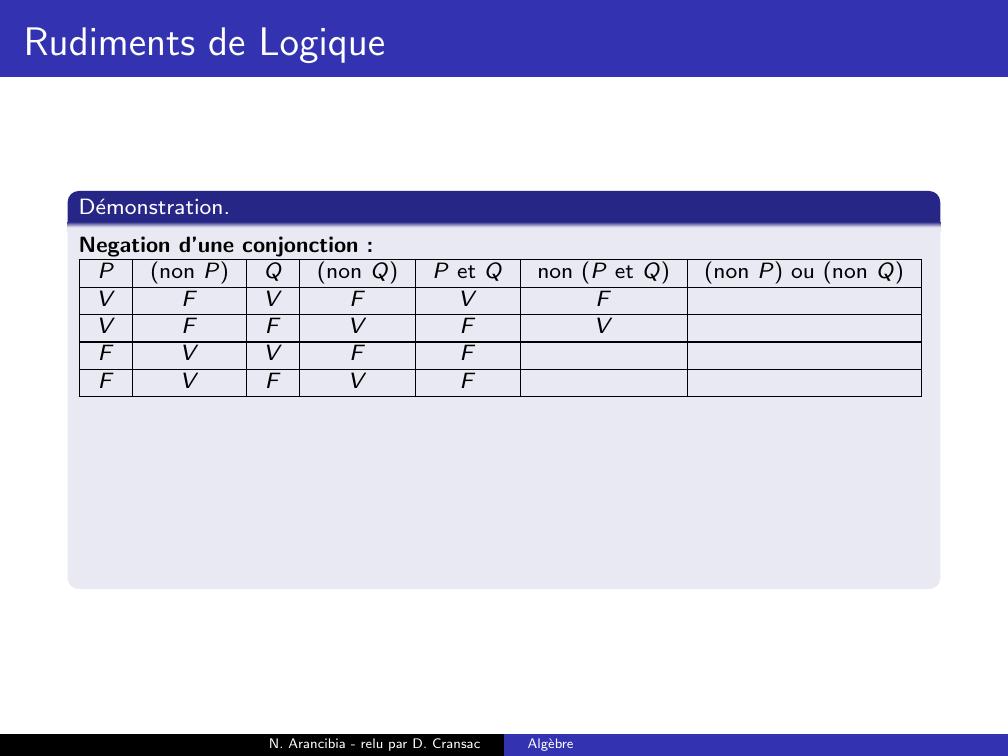
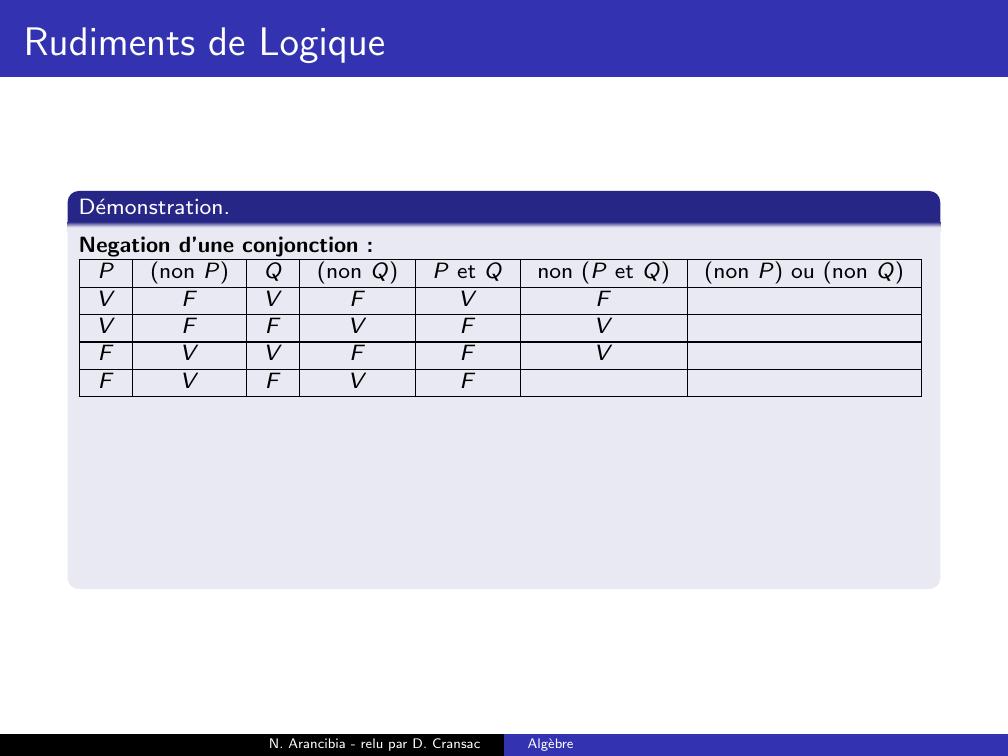
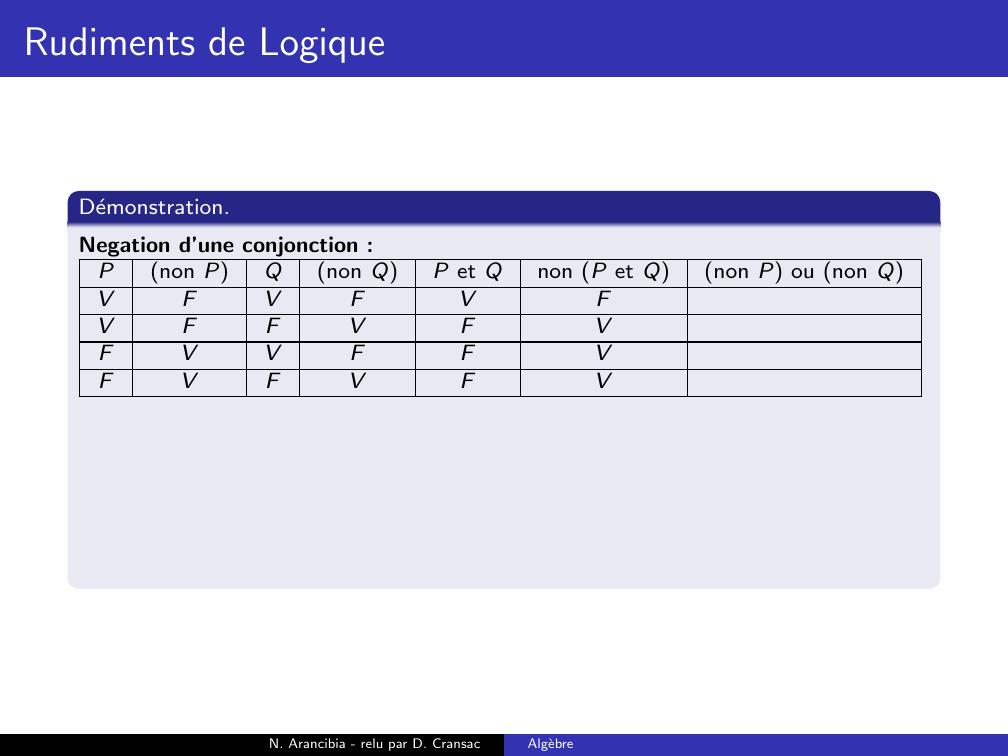
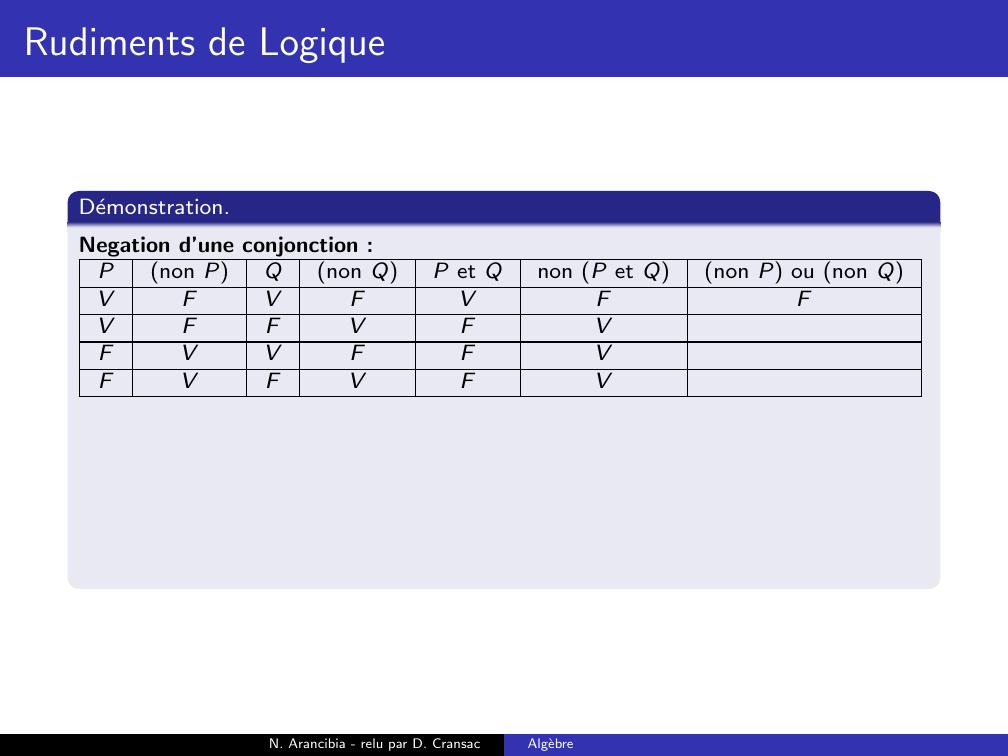
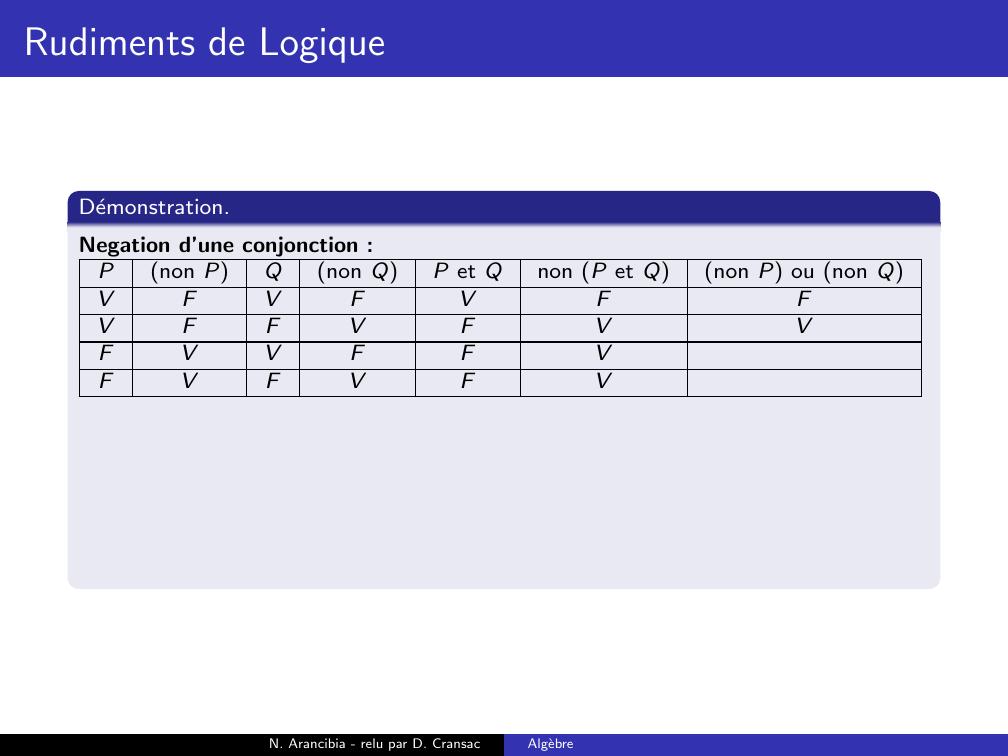
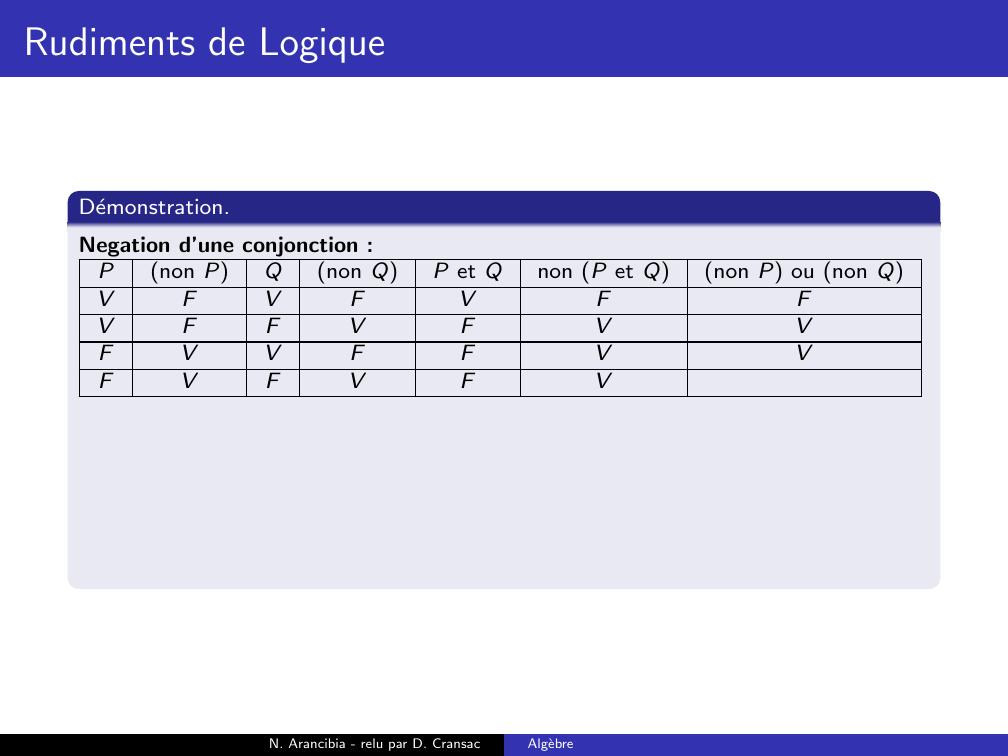
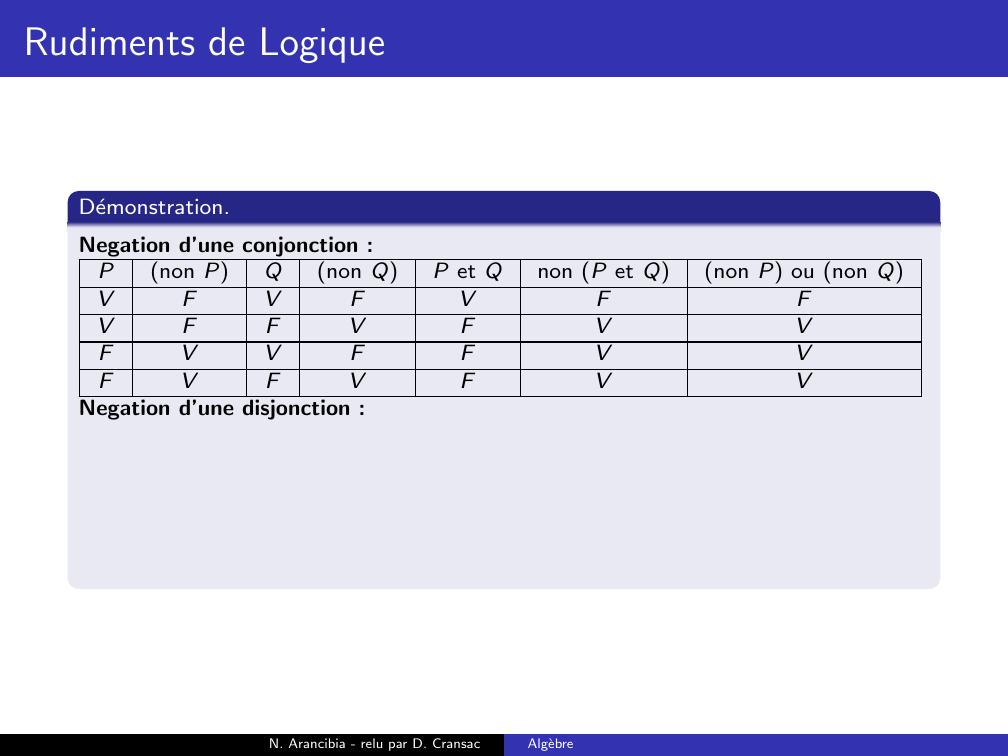
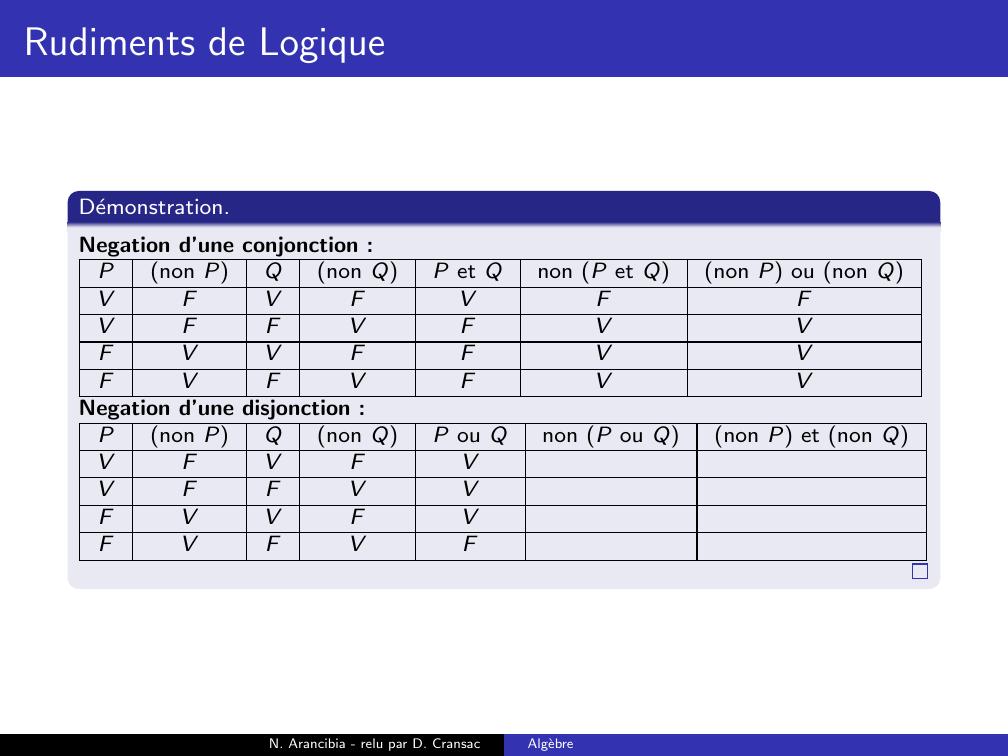
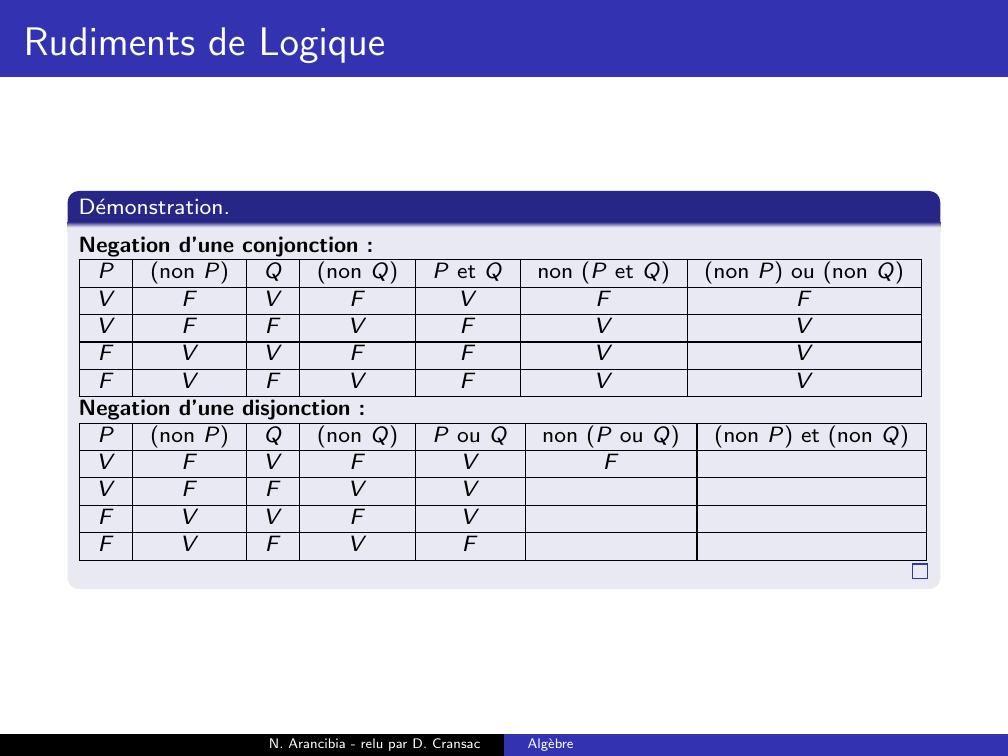
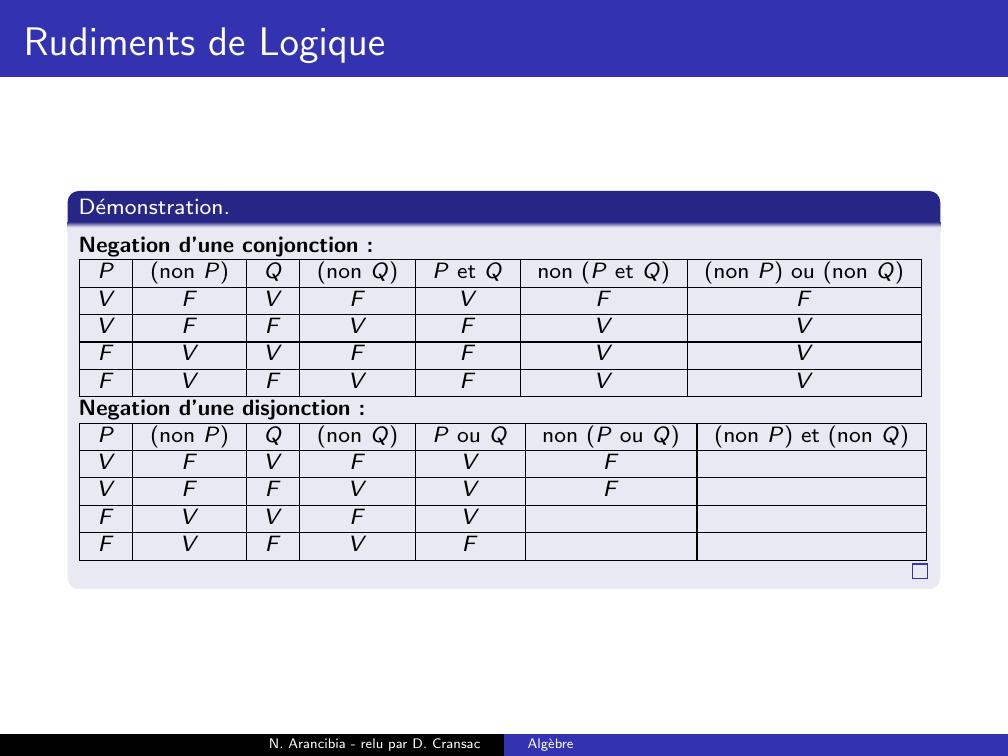
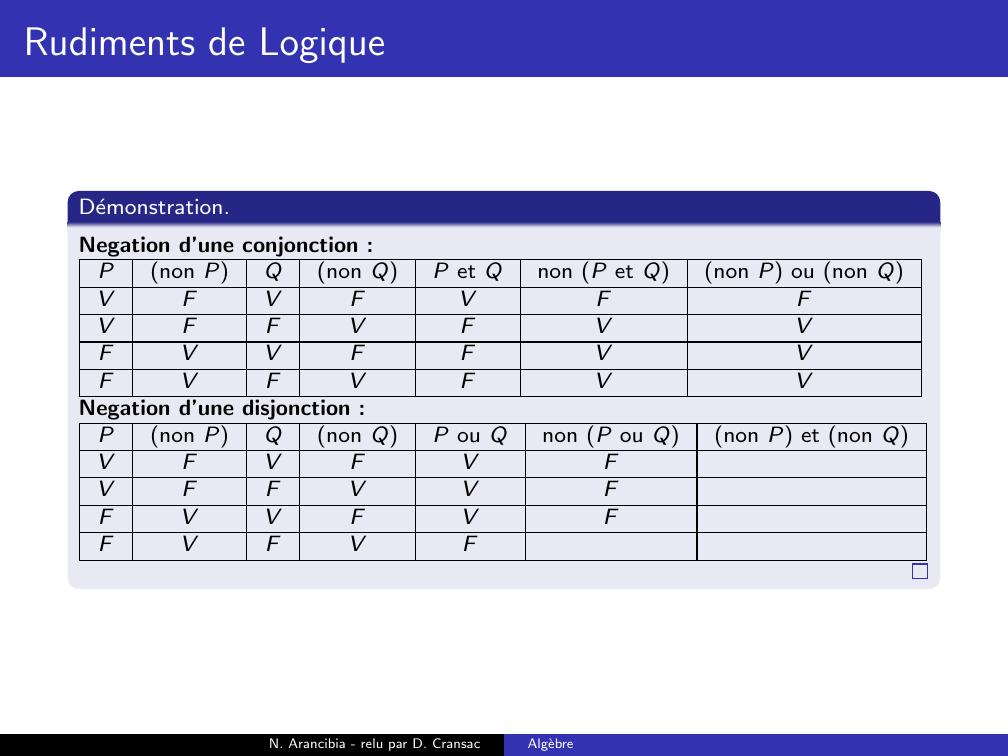
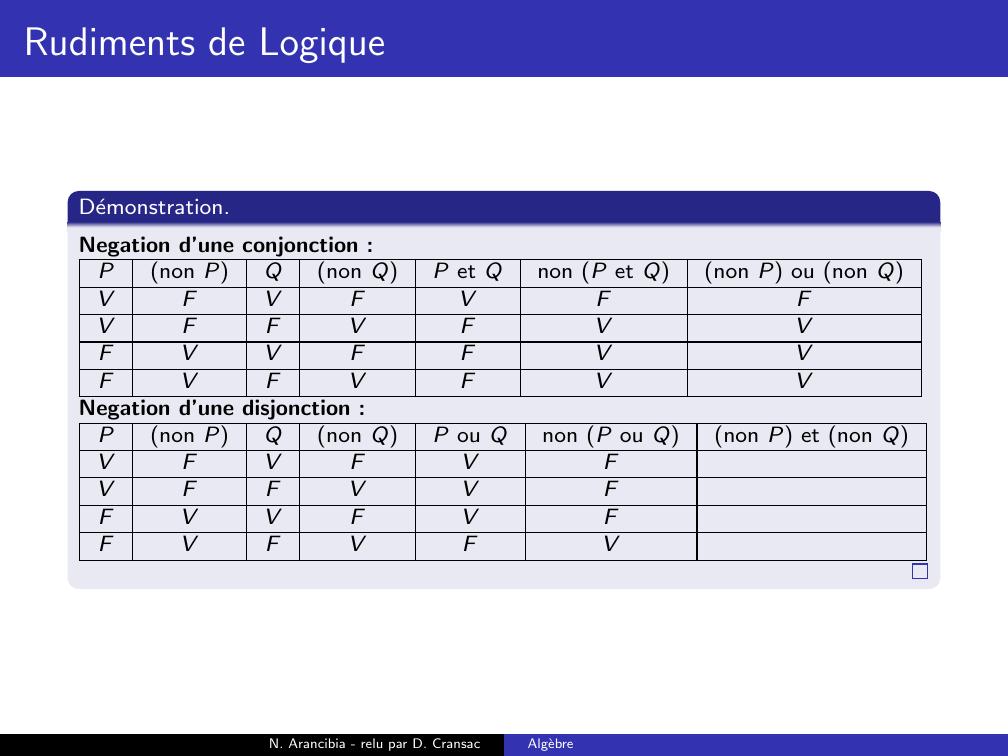
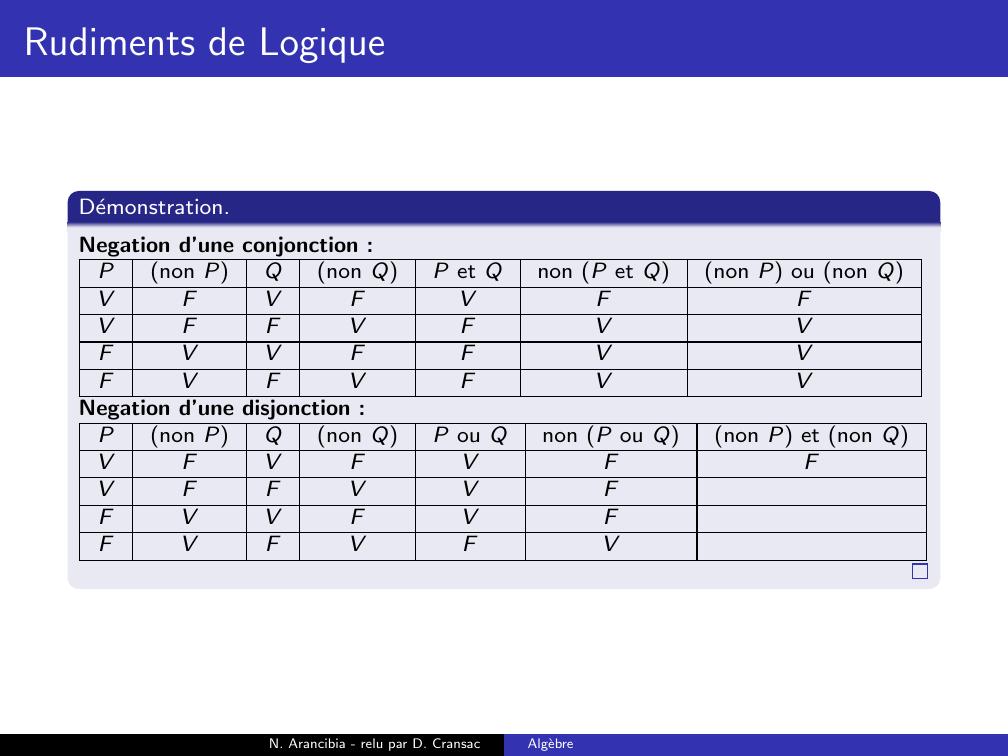
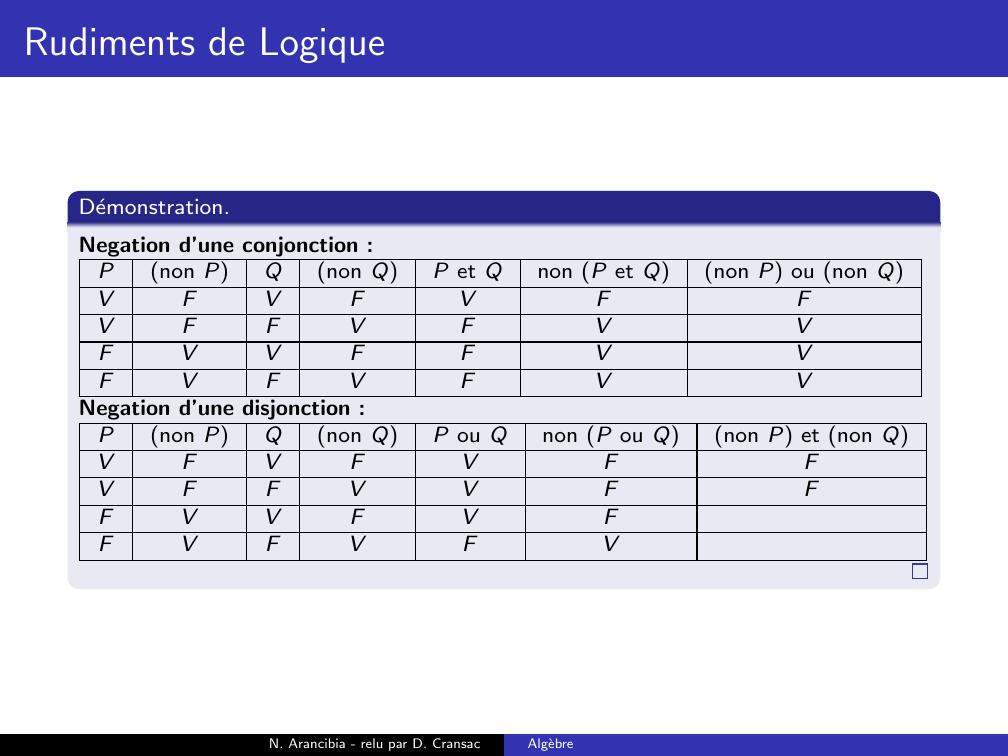
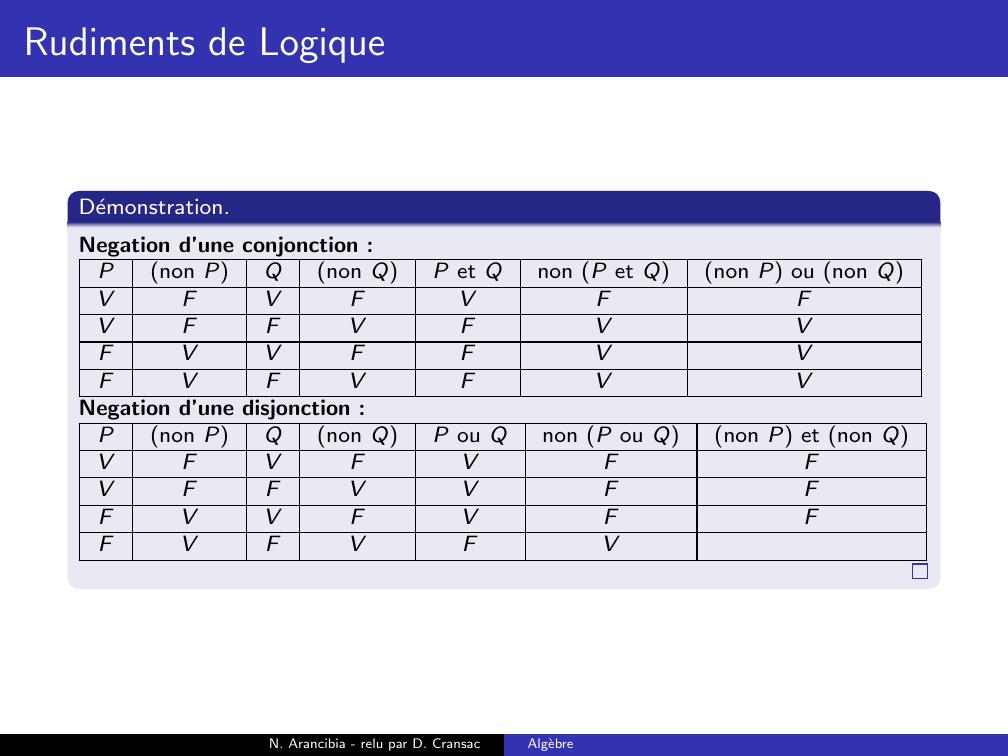
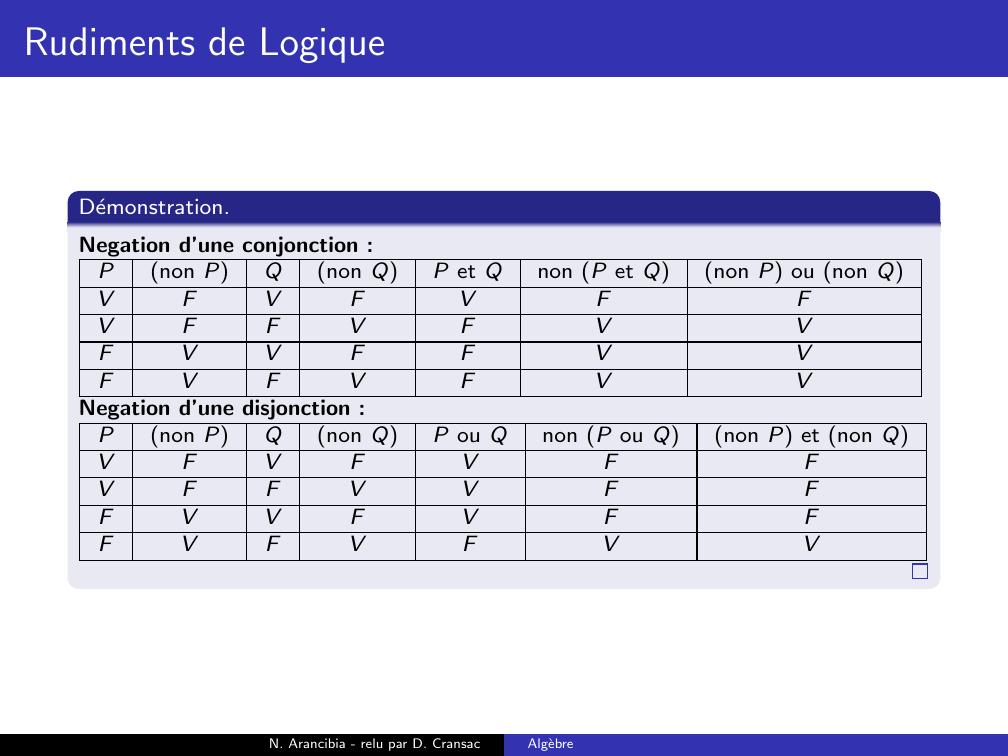
Page 188 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVVFFVFFVVFFFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 189 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFVFFVFFVVFFFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 190 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFVFFVFVFVVFFFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 191 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFVFFVFVFVVFFVFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 192 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFVFFVFVFVVFFVFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 193 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVFVVFFVFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 194 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 195 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 196 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :N. Arancibia - relu par D. CransacAlgebre

Page 197 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVVFFVVFVVFVFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 198 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFVFFVVFVVFVFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 199 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFVFFVVFFVVFVFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 200 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFVFFVVFFVVFVFFVFVFN. Arancibia - relu par D. CransacAlgebre

Page 201 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFVFFVVFFVVFVFFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 202 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFFVFFVVFFVVFVFFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 203 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFFVFFVVFFFVVFVFFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 204 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFFVFFVVFFFVVFVFFFVFVFVN. Arancibia - relu par D. CransacAlgebre

Page 205 : Rudiments de LogiqueDemonstration.Negation d’une conjonction :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVNegation d’une disjonction :Pnon PQnon QP ou Qnon P ou Qnon P et non QVFVFVFFVFFVVFFFVVFVFFFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 206 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou QN. Arancibia - relu par D. CransacAlgebre

Page 207 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.N. Arancibia - relu par D. CransacAlgebre

Page 208 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite :N. Arancibia - relu par D. CransacAlgebre

Page 209 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 210 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVVFFVFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 211 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVVFFVFFFVVFVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 212 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVVFFVFFFVVFVVFVFVVN. Arancibia - relu par D. CransacAlgebre

Page 213 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVVFFVFFFVVFVVFVFVVVN. Arancibia - relu par D. CransacAlgebre

Page 214 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFVFFVFFFVVFVVFVFVVVN. Arancibia - relu par D. CransacAlgebre

Page 215 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFVFFVFFVFVVFVVFVFVVVN. Arancibia - relu par D. CransacAlgebre

Page 216 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFVFFVFFVFVVFVVFFVFVVVN. Arancibia - relu par D. CransacAlgebre

Page 217 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFVFFVFFVFVVFVVFFVFVVVFN. Arancibia - relu par D. CransacAlgebre

Page 218 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFFVFFVFFVFVVFVVFFVFVVVFN. Arancibia - relu par D. CransacAlgebre

Page 219 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFFVFFVFFVVFVVFVVFFVFVVVFN. Arancibia - relu par D. CransacAlgebre

Page 220 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFFVFFVFFVVFVVFVVFFFVFVVVFN. Arancibia - relu par D. CransacAlgebre

Page 221 : Rudiments de LogiqueFinalement, etudions comme la negation modifie l’implication.PropositionNous avonsP =⇒Q⇐⇒nonP ou Q,et par negation :nonP ⇒Q ⇐⇒P et nonQ.Demonstration.On ecrit les tables de verite : Negation d’une implication :PPQQP ⇒QP ou QP ⇒QP et QVFVFVVFFVFFVFFVVFVVFVVFFFVFVVVFFN. Arancibia - relu par D. CransacAlgebre

Page 222 : QuantificateursQue signifie ?sin x = xN. Arancibia - relu par D. CransacAlgebre

Page 223 : QuantificateursQue signifie ?sin x = x1Resoudre dans x R, sin x = xN. Arancibia - relu par D. CransacAlgebre

Page 224 : QuantificateursQue signifie ?sin x = x1Resoudre dans x R, sin x = x2Pour tout reel x, sin x = xN. Arancibia - relu par D. CransacAlgebre

Page 225 : QuantificateursQue signifie ?sin x = x1Resoudre dans x R, sin x = x2Pour tout reel x, sin x = x3Il existe un reel x tel que sin x = xN. Arancibia - relu par D. CransacAlgebre

Page 226 : QuantificateursQue signifie ?sin x = x1Resoudre dans x R, sin x = x2Pour tout reel x, sin x = x3Il existe un reel x tel que sin x = x4x un point du plan : sin x = x n’est pas une proposition valide.N. Arancibia - relu par D. CransacAlgebre

Page 227 : QuantificateursLes deux proprietesz est pair et z est paire sont ambig¨ues : on ne sait pas ce que represente z.N. Arancibia - relu par D. CransacAlgebre

Page 228 : QuantificateursLes deux proprietesz est pair et z est paire sont ambig¨ues : on ne sait pas ce que represente z.On evite donc d’ecrire des proprietes sans preciser ce que represente z.N. Arancibia - relu par D. CransacAlgebre

Page 229 : QuantificateursLes deux proprietesz est pair et z est paire sont ambig¨ues : on ne sait pas ce que represente z.On evite donc d’ecrire des proprietes sans preciser ce que represente z.On ecrira doncTout entier z est pair et Il existe une fonction z qui est paire N. Arancibia - relu par D. CransacAlgebre

Page 230 : QuantificateursLes deux proprietesz est pair et z est paire sont ambig¨ues : on ne sait pas ce que represente z.On evite donc d’ecrire des proprietes sans preciser ce que represente z.On ecrira doncTout entier z est pair et Il existe une fonction z qui est paire Il faut donc preciser ce qu’est z et, tres souvent, a quel ensemble ilappartient ce qui revient la plupart du temps a definir ses proprietes.Pour cela on utilise les quantificateurs : Pour tout et Il existe N. Arancibia - relu par D. CransacAlgebre

Page 231 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifieN. Arancibia - relu par D. CransacAlgebre

Page 232 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. N. Arancibia - relu par D. CransacAlgebre

Page 233 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncN. Arancibia - relu par D. CransacAlgebre

Page 234 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etN. Arancibia - relu par D. CransacAlgebre

Page 235 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etfausse sinon : si au moins un objet dans E n’a pas la propriete P.N. Arancibia - relu par D. CransacAlgebre

Page 236 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etfausse sinon : si au moins un objet dans E n’a pas la propriete P.Exemple :x R, x2 ̸= 1 est une propositionN. Arancibia - relu par D. CransacAlgebre

Page 237 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etfausse sinon : si au moins un objet dans E n’a pas la propriete P.Exemple :x R, x2 ̸= 1 est une proposition vraie, car le carre d’un reel esttoujours positif.N. Arancibia - relu par D. CransacAlgebre

Page 238 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etfausse sinon : si au moins un objet dans E n’a pas la propriete P.Exemple :x R, x2 ̸= 1 est une proposition vraie, car le carre d’un reel esttoujours positif.x R, sin x 1N. Arancibia - relu par D. CransacAlgebre

Page 239 : QuantificateursUn autre outil pour definir de nouvelles propositions est la notion dequantificateur.Definition Quantificateur universel Le symbole place devant une variable x signifie pour tout x , quelque soit x .Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E, Px. RemarqueLa proposition : x E, Px est doncvraie si tout objet dans E a la propriete P, etfausse sinon : si au moins un objet dans E n’a pas la propriete P.Exemple :x R, x2 ̸= 1 est une proposition vraie, car le carre d’un reel esttoujours positif.x R, sin x 1 est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 240 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieN. Arancibia - relu par D. CransacAlgebre

Page 241 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx .N. Arancibia - relu par D. CransacAlgebre

Page 242 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx . La propositionx E, Pxse lit doncN. Arancibia - relu par D. CransacAlgebre

Page 243 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx . La propositionx E, Pxse lit doncIl existe un element x de E tel que Px. N. Arancibia - relu par D. CransacAlgebre

Page 244 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx . La propositionx E, Pxse lit doncIl existe un element x de E tel que Px. Le symbole ! place devant une variable x signifieN. Arancibia - relu par D. CransacAlgebre

Page 245 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx . La propositionx E, Pxse lit doncIl existe un element x de E tel que Px. Le symbole ! place devant une variable x signifieil existe un unique x.N. Arancibia - relu par D. CransacAlgebre

Page 246 : QuantificateursDefinition Quantificateur existentiel Le symbole place devant une variable x signifieil existe au moins unx . La propositionx E, Pxse lit doncIl existe un element x de E tel que Px. Le symbole ! place devant une variable x signifieil existe un unique x.RemarqueLa proposition : x E, Px est doncvraie si au moins un objet dans E a la propriete P, etfausse sinon : si aucun objet dans E n’a pas la propriete P.N. Arancibia - relu par D. CransacAlgebre

Page 247 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionN. Arancibia - relu par D. CransacAlgebre

Page 248 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.N. Arancibia - relu par D. CransacAlgebre

Page 249 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une propositionN. Arancibia - relu par D. CransacAlgebre

Page 250 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.N. Arancibia - relu par D. CransacAlgebre

Page 251 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une propositionN. Arancibia - relu par D. CransacAlgebre

Page 252 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.N. Arancibia - relu par D. CransacAlgebre

Page 253 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une propositionN. Arancibia - relu par D. CransacAlgebre

Page 254 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.N. Arancibia - relu par D. CransacAlgebre

Page 255 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.N. Arancibia - relu par D. CransacAlgebre

Page 256 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.On peut le constater en comparant par exemple les propositions :N. Arancibia - relu par D. CransacAlgebre

Page 257 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.On peut le constater en comparant par exemple les propositions :x R, y R+, x2 = yN. Arancibia - relu par D. CransacAlgebre

Page 258 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.On peut le constater en comparant par exemple les propositions :x R, y R+, x2 = y , est une proposition vraie.N. Arancibia - relu par D. CransacAlgebre

Page 259 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.On peut le constater en comparant par exemple les propositions :x R, y R+, x2 = y , est une proposition vraie.y R+, x R, x2 = yN. Arancibia - relu par D. CransacAlgebre

Page 260 : QuantificateursExemples :n 2, 3, 4, · · · , n ̸= 23, 23/n N est une propositionfausse.z C, z2 = 1 est une proposition vraie car par examplei2 = 1.!n N, 1 2n 3 est une proposition vraie. En effet 1 est leseul entier satisfaisant la proposition.r Q, p N, pr Z est une proposition vraie definition.Remarque. L’ordre des quantificateurs est important.On peut le constater en comparant par exemple les propositions :x R, y R+, x2 = y , est une proposition vraie.y R+, x R, x2 = y , est une proposition fausse.N. Arancibia - relu par D. CransacAlgebre

Page 261 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.N. Arancibia - relu par D. CransacAlgebre

Page 262 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estN. Arancibia - relu par D. CransacAlgebre

Page 263 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estx E, non Px.N. Arancibia - relu par D. CransacAlgebre

Page 264 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estx E, non Px.Remarque : C’est-a dire, pour nier une proposition contenant desquantificateurs, on change les en et reciproquementN. Arancibia - relu par D. CransacAlgebre

Page 265 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estx E, non Px.Remarque : C’est-a dire, pour nier une proposition contenant desquantificateurs, on change les en et reciproquement , puis on nie laconclusion.N. Arancibia - relu par D. CransacAlgebre

Page 266 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estx E, non Px.Remarque : C’est-a dire, pour nier une proposition contenant desquantificateurs, on change les en et reciproquement , puis on nie laconclusion. La negation dex, y, Px, y.N. Arancibia - relu par D. CransacAlgebre

Page 267 : QuantificateursTheoreme Negation des quantificateursLa negation de : x E, Px estx E, non Px.La negation de : x E, Px estx E, non Px.Remarque : C’est-a dire, pour nier une proposition contenant desquantificateurs, on change les en et reciproquement , puis on nie laconclusion. La negation dex, y, Px, y.estx, y, nonPx, y.N. Arancibia - relu par D. CransacAlgebre

Page 268 : QuantificateursExemples : Ecrire la negation de chacune des propositions suivantes :x R, sin x2 + cos x2 = 1x R, sin x2 + cos x2 ̸= 1x R, x2 + x 2 = 0M R+, x R, f x MN. Arancibia - relu par D. CransacAlgebre

Page 269 : QuantificateursExemples : Ecrire la negation de chacune des propositions suivantes :x R, sin x2 + cos x2 = 1x R, sin x2 + cos x2 ̸= 1x R, x2 + x 2 = 0x R, x2 + x 2 ̸= 0M R+, x R, f x MN. Arancibia - relu par D. CransacAlgebre

Page 270 : QuantificateursExemples : Ecrire la negation de chacune des propositions suivantes :x R, sin x2 + cos x2 = 1x R, sin x2 + cos x2 ̸= 1x R, x2 + x 2 = 0x R, x2 + x 2 ̸= 0M R+, x R, f x MM R, x R, f x MN. Arancibia - relu par D. CransacAlgebre

Page 271 : EcritureMentionnons que l’usage des symboles et est restreint auxpropositions. Ces symboles sont des quantificateurs, ils n’ont leur placequ’a l’interieur d’une proposition ecrite sous forme symbolique.N. Arancibia - relu par D. CransacAlgebre

Page 272 : EcritureMentionnons que l’usage des symboles et est restreint auxpropositions. Ces symboles sont des quantificateurs, ils n’ont leur placequ’a l’interieur d’une proposition ecrite sous forme symbolique.Dans une phrase en fran¸cais, nous utilisons pour tout et il existe.N. Arancibia - relu par D. CransacAlgebre

Page 273 : EcritureMentionnons que l’usage des symboles et est restreint auxpropositions. Ces symboles sont des quantificateurs, ils n’ont leur placequ’a l’interieur d’une proposition ecrite sous forme symbolique.Dans une phrase en fran¸cais, nous utilisons pour tout et il existe.De mˆeme, nous n’utiliserons pas ⇒mais les termes alors ou donc.N. Arancibia - relu par D. CransacAlgebre

Page 274 : Modes de RaisonnementNous avons introduit la notion de proposition et donne une liste d’outilspour construire des propositions plus complexes a partir de propositionssimples.N. Arancibia - relu par D. CransacAlgebre

Page 275 : Modes de RaisonnementNous avons introduit la notion de proposition et donne une liste d’outilspour construire des propositions plus complexes a partir de propositionssimples.Mais il demeure une question importante, comment fait-on pour verifierla veracite d’une proposition ?N. Arancibia - relu par D. CransacAlgebre

Page 276 : Modes de RaisonnementNous avons introduit la notion de proposition et donne une liste d’outilspour construire des propositions plus complexes a partir de propositionssimples.Mais il demeure une question importante, comment fait-on pour verifierla veracite d’une proposition ?Pour cela nous allons a present introduire differents modes deraisonnement qui vont nous permettre de montrer ou, au moins, derendre plus facile la preuve d’une assertion.N. Arancibia - relu par D. CransacAlgebre

Page 277 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct :N. Arancibia - relu par D. CransacAlgebre

Page 278 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 279 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.N. Arancibia - relu par D. CransacAlgebre

Page 280 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 281 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair.N. Arancibia - relu par D. CransacAlgebre

Page 282 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair.N. Arancibia - relu par D. CransacAlgebre

Page 283 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair. Comme n est un entier pair, il existe k N tel que n = 2k.N. Arancibia - relu par D. CransacAlgebre

Page 284 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair. Comme n est un entier pair, il existe k N tel que n = 2k.Doncn2 = 4k2N. Arancibia - relu par D. CransacAlgebre

Page 285 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair. Comme n est un entier pair, il existe k N tel que n = 2k.Doncn2 = 4k2 = 22k2.N. Arancibia - relu par D. CransacAlgebre

Page 286 : Modes de RaisonnementPour montrer une implication : P =⇒Q, plusieurs types de raisonnementpeuvent ˆetre mis en oeuvre.1Raisonnement direct : On montre que, si la proposition P est vraie, alorsla proposition Q est vraie. Quand on procede ainsi pour montrer queP =⇒Q, on ecrit sans reflechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Exemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair. Comme n est un entier pair, il existe k N tel que n = 2k.Doncn2 = 4k2 = 22k2.C’est-a-dire n2 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 287 : Modes de raisonnement2Raisonnement par contraposition : nonQ ⇒nonPRappelons que si la propositionnonQ =⇒nonPest vraie,N. Arancibia - relu par D. CransacAlgebre

Page 288 : Modes de raisonnement2Raisonnement par contraposition : nonQ ⇒nonPRappelons que si la propositionnonQ =⇒nonPest vraie,alors la propositionP =⇒Qest vraie.N. Arancibia - relu par D. CransacAlgebre

Page 289 : Modes de raisonnement2Raisonnement par contraposition : nonQ ⇒nonPRappelons que si la propositionnonQ =⇒nonPest vraie,alors la propositionP =⇒Qest vraie.C’est-a-dire, pour montrer P ⇒QN. Arancibia - relu par D. CransacAlgebre

Page 290 : Modes de raisonnement2Raisonnement par contraposition : nonQ ⇒nonPRappelons que si la propositionnonQ =⇒nonPest vraie,alors la propositionP =⇒Qest vraie.C’est-a-dire, pour montrer P ⇒Q il suffit de montrernonQ ⇒nonP.N. Arancibia - relu par D. CransacAlgebre

Page 291 : Modes de raisonnement2Raisonnement par contraposition : nonQ ⇒nonPRappelons que si la propositionnonQ =⇒nonPest vraie,alors la propositionP =⇒Qest vraie.C’est-a-dire, pour montrer P ⇒Q il suffit de montrernonQ ⇒nonP.Pour cela on ecrit sans reflechir :Supposons nonQ vraie. Montrons que nonP est vraie....Preuve de nonP.N. Arancibia - relu par D. CransacAlgebre

Page 292 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.N. Arancibia - relu par D. CransacAlgebre

Page 293 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.N. Arancibia - relu par D. CransacAlgebre

Page 294 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impairN. Arancibia - relu par D. CransacAlgebre

Page 295 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.N. Arancibia - relu par D. CransacAlgebre

Page 296 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12N. Arancibia - relu par D. CransacAlgebre

Page 297 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12N. Arancibia - relu par D. CransacAlgebre

Page 298 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12 = 4k2 + 4k + 1N. Arancibia - relu par D. CransacAlgebre

Page 299 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12 = 4k2 + 4k + 1 = 22k2 + 2k + 1.N. Arancibia - relu par D. CransacAlgebre

Page 300 : Modes de raisonnementExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair , il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12 = 4k2 + 4k + 1 = 22k2 + 2k + 1.C’est-a-dire n2 est impair.N. Arancibia - relu par D. CransacAlgebre

Page 301 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQN. Arancibia - relu par D. CransacAlgebre

Page 302 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQLe principe du raisonnement par l’absurde s’enonce alors ainsi :N. Arancibia - relu par D. CransacAlgebre

Page 303 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQLe principe du raisonnement par l’absurde s’enonce alors ainsi :Si d’une proposition on arrive a tirer une contradiction, c’est qu’elle estfausse.N. Arancibia - relu par D. CransacAlgebre

Page 304 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQLe principe du raisonnement par l’absurde s’enonce alors ainsi :Si d’une proposition on arrive a tirer une contradiction, c’est qu’elle estfausse.Donc, quand on veut montrer qu’une proposition P est vraie, on peut raisonnerpar l’absurde de la maniere suivante :N. Arancibia - relu par D. CransacAlgebre

Page 305 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQLe principe du raisonnement par l’absurde s’enonce alors ainsi :Si d’une proposition on arrive a tirer une contradiction, c’est qu’elle estfausse.Donc, quand on veut montrer qu’une proposition P est vraie, on peut raisonnerpar l’absurde de la maniere suivante :Faisons l’hypothese que P est fausse ou que nonP est vraie....Obtention d’une contradiction.N. Arancibia - relu par D. CransacAlgebre

Page 306 : Modes de raisonnementUn type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et nonQLe principe du raisonnement par l’absurde s’enonce alors ainsi :Si d’une proposition on arrive a tirer une contradiction, c’est qu’elle estfausse.Donc, quand on veut montrer qu’une proposition P est vraie, on peut raisonnerpar l’absurde de la maniere suivante :Faisons l’hypothese que P est fausse ou que nonP est vraie....Obtention d’une contradiction.Contradiction ! C’est donc l’hypothese de depart qui est fausse. Par consequentP est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 307 : Modes de raisonnementExemple : On sait que π est irrationnel.Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel.N. Arancibia - relu par D. CransacAlgebre

Page 308 : Modes de raisonnementExemple : On sait que π est irrationnel.Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel.Soient p Z et q Nπ3 = pqN. Arancibia - relu par D. CransacAlgebre

Page 309 : Modes de raisonnementExemple : On sait que π est irrationnel.Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel.Soient p Z et q Nπ3 = pqIl vientπ = 3pqN. Arancibia - relu par D. CransacAlgebre

Page 310 : Modes de raisonnementExemple : On sait que π est irrationnel.Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel.Soient p Z et q Nπ3 = pqIl vientπ = 3pqdonc π est rationnel.N. Arancibia - relu par D. CransacAlgebre

Page 311 : Modes de raisonnementExemple : On sait que π est irrationnel.Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel.Soient p Z et q Nπ3 = pqIl vientπ = 3pqdonc π est rationnel.C’est absurde on peut donc conclure que π3 est irrationnel .N. Arancibia - relu par D. CransacAlgebre

Page 312 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqN. Arancibia - relu par D. CransacAlgebre

Page 313 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.N. Arancibia - relu par D. CransacAlgebre

Page 314 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pairN. Arancibia - relu par D. CransacAlgebre

Page 315 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.N. Arancibia - relu par D. CransacAlgebre

Page 316 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.N. Arancibia - relu par D. CransacAlgebre

Page 317 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22N. Arancibia - relu par D. CransacAlgebre

Page 318 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22N. Arancibia - relu par D. CransacAlgebre

Page 319 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22=2p′22N. Arancibia - relu par D. CransacAlgebre

Page 320 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22=2p′22= 4p′22N. Arancibia - relu par D. CransacAlgebre

Page 321 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22=2p′22= 4p′22= 2p′2.Ceci montre que q2 est pair et donc que q est pair.N. Arancibia - relu par D. CransacAlgebre

Page 322 : Modes de raisonnementExemple : Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que 2 est rationnel et ecrivons-le donc sousforme irreductible :2 = pqavec p, q Net p et q premiers entre eux n’ont pas de diviseur commun.L’egalite :p2 = 2q2 = 2q2montre que p2 est pair , et donc que p est pair d’apres l’exemple precedent.Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22=2p′22= 4p′22= 2p′2.Ceci montre que q2 est pair et donc que q est pair. Disonsq = 2q′, pour un certain q′ Z.N. Arancibia - relu par D. CransacAlgebre

Page 323 : Modes de raisonnementNous avions suppose la fraction pq irreductible , mais finalement nousl’avons reduitepq = 2p′2q′ = p′q′ .N. Arancibia - relu par D. CransacAlgebre

Page 324 : Modes de raisonnementNous avions suppose la fraction pq irreductible , mais finalement nousl’avons reduitepq = 2p′2q′ = p′q′ .Contradiction !N. Arancibia - relu par D. CransacAlgebre

Page 325 : Modes de raisonnementNous avions suppose la fraction pq irreductible , mais finalement nousl’avons reduitepq = 2p′2q′ = p′q′ .Contradiction ! Comme voulu,2 est irrationnel.N. Arancibia - relu par D. CransacAlgebre

Page 326 : Modes de raisonnementRemarque : Le raisonnement par l’absurde nous donne une autre fa¸conde montrer l’implicationP =⇒Q.En effet, comme P ⇒Q est equivalent a la propositionnonP ou Q,N. Arancibia - relu par D. CransacAlgebre

Page 327 : Modes de raisonnementRemarque : Le raisonnement par l’absurde nous donne une autre fa¸conde montrer l’implicationP =⇒Q.En effet, comme P ⇒Q est equivalent a la propositionnonP ou Q,on en deduit que si la propositionP et nonQ = nonnonP ou Qconduit a une contradictionN. Arancibia - relu par D. CransacAlgebre

Page 328 : Modes de raisonnementRemarque : Le raisonnement par l’absurde nous donne une autre fa¸conde montrer l’implicationP =⇒Q.En effet, comme P ⇒Q est equivalent a la propositionnonP ou Q,on en deduit que si la propositionP et nonQ = nonnonP ou Qconduit a une contradiction , alors P =⇒Q est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 329 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.N. Arancibia - relu par D. CransacAlgebre

Page 330 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a.N. Arancibia - relu par D. CransacAlgebre

Page 331 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.N. Arancibia - relu par D. CransacAlgebre

Page 332 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2N. Arancibia - relu par D. CransacAlgebre

Page 333 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.N. Arancibia - relu par D. CransacAlgebre

Page 334 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.Or n 0 et a 0 donc a + n 0.N. Arancibia - relu par D. CransacAlgebre

Page 335 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.Or n 0 et a 0 donc a + n 0.a + n est un diviseur de 1 donc a + n = 1 et par consequent a n = 1.N. Arancibia - relu par D. CransacAlgebre

Page 336 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.Or n 0 et a 0 donc a + n 0.a + n est un diviseur de 1 donc a + n = 1 et par consequent a n = 1.On effectue la difference des deux egalites pour obtenir 2n = 0 doncn = 0.N. Arancibia - relu par D. CransacAlgebre

Page 337 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.Or n 0 et a 0 donc a + n 0.a + n est un diviseur de 1 donc a + n = 1 et par consequent a n = 1.On effectue la difference des deux egalites pour obtenir 2n = 0 doncn = 0.Puisque n est strictement positif, cela est une contradiction.N. Arancibia - relu par D. CransacAlgebre

Page 338 : Modes de raisonnementExemple : Demontrons, en raisonnant par l’absurde, que si n N, alorsn2 + 1 n’est pas le carre d’un entier naturel.Preuve : Supposons que n est un entier positif et que n2 + 1 est le carred’un entier naturel a. C’est-a-direa2 = n2 + 1.Donc1 = a2 n2 = a na + n.Or n 0 et a 0 donc a + n 0.a + n est un diviseur de 1 donc a + n = 1 et par consequent a n = 1.On effectue la difference des deux egalites pour obtenir 2n = 0 doncn = 0.Puisque n est strictement positif, cela est une contradiction.D’ou on conclut que n2 + 1 n’est pas le carre d’un entier naturel.N. Arancibia - relu par D. CransacAlgebre

Page 339 : Modes de raisonnementPour montrer une equivalence :P ⇐⇒Q,on a deux possibilites :Soit on raisonne par double implicationN. Arancibia - relu par D. CransacAlgebre

Page 340 : Modes de raisonnementPour montrer une equivalence :P ⇐⇒Q,on a deux possibilites :Soit on raisonne par double implication et on montre separement lespropositionsP =⇒QetQ =⇒P.N. Arancibia - relu par D. CransacAlgebre

Page 341 : Modes de raisonnementPour montrer une equivalence :P ⇐⇒Q,on a deux possibilites :Soit on raisonne par double implication et on montre separement lespropositionsP =⇒QetQ =⇒P.C’est-a-dire on ecritN. Arancibia - relu par D. CransacAlgebre

Page 342 : Modes de raisonnementPour montrer une equivalence :P ⇐⇒Q,on a deux possibilites :Soit on raisonne par double implication et on montre separement lespropositionsP =⇒QetQ =⇒P.C’est-a-dire on ecritSupposons P vraie. Montrons que Q est vraie....Preuve de Q.N. Arancibia - relu par D. CransacAlgebre

Page 343 : Modes de raisonnementPour montrer une equivalence :P ⇐⇒Q,on a deux possibilites :Soit on raisonne par double implication et on montre separement lespropositionsP =⇒QetQ =⇒P.C’est-a-dire on ecritSupposons P vraie. Montrons que Q est vraie....Preuve de Q.ReciproquementSupposons Q vraie. Montrons que P est vraie....Preuve de P.N. Arancibia - relu par D. CransacAlgebre

Page 344 : Modes de raisonnementExemple : On a vu que :Si n est un entier pair, alors n2 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 345 : Modes de raisonnementExemple : On a vu que :Si n est un entier pair, alors n2 est pair.Si n2 est pair, alors n est pair.N. Arancibia - relu par D. CransacAlgebre

Page 346 : Modes de raisonnementExemple : On a vu que :Si n est un entier pair, alors n2 est pair.Si n2 est pair, alors n est pair.Donc n est pair si et seulement si n2 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 347 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve :N. Arancibia - relu par D. CransacAlgebre

Page 348 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R.N. Arancibia - relu par D. CransacAlgebre

Page 349 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est trivialeN. Arancibia - relu par D. CransacAlgebre

Page 350 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est triviale , car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.N. Arancibia - relu par D. CransacAlgebre

Page 351 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est triviale , car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.Pour la implication reciproque,x2 + y 2 = 0 =⇒x = y = 0;N. Arancibia - relu par D. CransacAlgebre

Page 352 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est triviale , car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.Pour la implication reciproque,x2 + y 2 = 0 =⇒x = y = 0;si : x2 + y 2 = 0, alors :x20 = y 20,N. Arancibia - relu par D. CransacAlgebre

Page 353 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est triviale , car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.Pour la implication reciproque,x2 + y 2 = 0 =⇒x = y = 0;si : x2 + y 2 = 0, alors :x20 = y 20,doncx2 = y 2 = 0N. Arancibia - relu par D. CransacAlgebre

Page 354 : Modes de raisonnementExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐x = y = 0est triviale , car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.Pour la implication reciproque,x2 + y 2 = 0 =⇒x = y = 0;si : x2 + y 2 = 0, alors :x20 = y 20,doncx2 = y 2 = 0et enfin : x = y = 0.N. Arancibia - relu par D. CransacAlgebre

Page 355 : Modes de raisonnementSoit on raisonne directement par equivalence en changeant peu apeu P en Q :P ⇐⇒· · · ⇐⇒· · · ⇐⇒Q.Remarque :Dans la plupart des cas c’est mieux de montrer des implicationsplutˆot que des equivalences.N. Arancibia - relu par D. CransacAlgebre

Page 356 : Modes de raisonnementSoit on raisonne directement par equivalence en changeant peu apeu P en Q :P ⇐⇒· · · ⇐⇒· · · ⇐⇒Q.Remarque :Dans la plupart des cas c’est mieux de montrer des implicationsplutˆot que des equivalences. Le raisonnement par equivalence estsouvent inutile et generateur d’erreurs logiques.N. Arancibia - relu par D. CransacAlgebre

Page 357 : Modes de raisonnementSoit on raisonne directement par equivalence en changeant peu apeu P en Q :P ⇐⇒· · · ⇐⇒· · · ⇐⇒Q.Remarque :Dans la plupart des cas c’est mieux de montrer des implicationsplutˆot que des equivalences. Le raisonnement par equivalence estsouvent inutile et generateur d’erreurs logiques.Le raisonnement par equivalence permet de montrer qu’uneproposition est vraie en montrant qu’elle est equivalente a uneproposition dont on sait deja qu’elle est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 358 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve :N. Arancibia - relu par D. CransacAlgebre

Page 359 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2 ⇐⇒2xy x2 + y 2N. Arancibia - relu par D. CransacAlgebre

Page 360 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2 ⇐⇒2xy x2 + y 2⇐⇒0 x2 2xy + y 2N. Arancibia - relu par D. CransacAlgebre

Page 361 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2 ⇐⇒2xy x2 + y 2⇐⇒0 x2 2xy + y 2⇐⇒0 x y2.N. Arancibia - relu par D. CransacAlgebre

Page 362 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2 ⇐⇒2xy x2 + y 2⇐⇒0 x2 2xy + y 2⇐⇒0 x y2.La derniere proposition etant vraie, la premiere l’est egalement.N. Arancibia - relu par D. CransacAlgebre

Page 363 : Modes de raisonnementExemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2 ⇐⇒2xy x2 + y 2⇐⇒0 x2 2xy + y 2⇐⇒0 x y2.La derniere proposition etant vraie, la premiere l’est egalement.Remarque Dans de tels cas, on peut aussi raisonner de fa¸con plusdirecte :12x2 + y 2 xy = x2 y 2 2xy2= x y22Or x y2 0 donc 12x2 + y 2 xy 0 donc la propriete est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 364 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.N. Arancibia - relu par D. CransacAlgebre

Page 365 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit :N. Arancibia - relu par D. CransacAlgebre

Page 366 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.N. Arancibia - relu par D. CransacAlgebre

Page 367 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve :N. Arancibia - relu par D. CransacAlgebre

Page 368 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12.N. Arancibia - relu par D. CransacAlgebre

Page 369 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12. On a0 x 12 = x2 2x + 1.N. Arancibia - relu par D. CransacAlgebre

Page 370 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12. On a0 x 12 = x2 2x + 1.Donc2x x2 + 1N. Arancibia - relu par D. CransacAlgebre

Page 371 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12. On a0 x 12 = x2 2x + 1.Donc2x x2 + 1N. Arancibia - relu par D. CransacAlgebre

Page 372 : Modes de raisonnementPour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les differentes situations selon les valeurs de x.On procede toujours comme suit : on ecrit sans reflechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12. On a0 x 12 = x2 2x + 1.Donc2x x2 + 1=⇒2xx2 + 1 1=⇒xx2 + 1 12.N. Arancibia - relu par D. CransacAlgebre

Page 373 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete PN. Arancibia - relu par D. CransacAlgebre

Page 374 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px.N. Arancibia - relu par D. CransacAlgebre

Page 375 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px....Verifications que x satisfait Px.N. Arancibia - relu par D. CransacAlgebre

Page 376 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px....Verifications que x satisfait Px.Exemple : Montrer que x R, y R, z R, z x + y.Preuve :N. Arancibia - relu par D. CransacAlgebre

Page 377 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px....Verifications que x satisfait Px.Exemple : Montrer que x R, y R, z R, z x + y.Preuve : Soient x R, y R.N. Arancibia - relu par D. CransacAlgebre

Page 378 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px....Verifications que x satisfait Px.Exemple : Montrer que x R, y R, z R, z x + y.Preuve : Soient x R, y R. Apres reflexion, posons :z = x + y + 1.N. Arancibia - relu par D. CransacAlgebre

Page 379 : Modes de raisonnementQuand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P , on ecritsans reflechir :Posons x = · · ·l’exemple qu’on a en tˆete.Verifions que Px....Verifications que x satisfait Px.Exemple : Montrer que x R, y R, z R, z x + y.Preuve : Soient x R, y R. Apres reflexion, posons :z = x + y + 1.Alors comme voulu : z x + y.N. Arancibia - relu par D. CransacAlgebre

Page 380 : Modes de raisonnementLa difficulte, bien sˆur, ne consiste souvent pas a verifier que x a lapropriete P , mais a avoir l’idee d’un exemple de tel objet x.N. Arancibia - relu par D. CransacAlgebre

Page 381 : Modes de raisonnementLa difficulte, bien sˆur, ne consiste souvent pas a verifier que x a lapropriete P , mais a avoir l’idee d’un exemple de tel objet x.Il n’existe helas pas de regle generale pour avoir des idees.N. Arancibia - relu par D. CransacAlgebre

Page 382 : Modes de raisonnementLa difficulte, bien sˆur, ne consiste souvent pas a verifier que x a lapropriete P , mais a avoir l’idee d’un exemple de tel objet x.Il n’existe helas pas de regle generale pour avoir des idees.Donnons tout de mˆeme une methode qui peut s’averer utile pour trouverx.N. Arancibia - relu par D. CransacAlgebre

Page 383 : Modes de raisonnementLa difficulte, bien sˆur, ne consiste souvent pas a verifier que x a lapropriete P , mais a avoir l’idee d’un exemple de tel objet x.Il n’existe helas pas de regle generale pour avoir des idees.Donnons tout de mˆeme une methode qui peut s’averer utile pour trouverx.Pour determiner les solutions d’un probleme, ou plus precisementl’ensemble des elements d’un ensemble E qui satisfont une propriete P,on raisonne souvent par analyse-synthese.N. Arancibia - relu par D. CransacAlgebre

Page 384 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.N. Arancibia - relu par D. CransacAlgebre

Page 385 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 386 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quelles sontles valeurs possibles de x ?N. Arancibia - relu par D. CransacAlgebre

Page 387 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quelles sontles valeurs possibles de x ?SyntheseN. Arancibia - relu par D. CransacAlgebre

Page 388 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quelles sontles valeurs possibles de x ?Synthese : On montre que ces conditions obtenues sont suffisantes, et onresout le probleme.N. Arancibia - relu par D. CransacAlgebre

Page 389 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quelles sontles valeurs possibles de x ?Synthese : On montre que ces conditions obtenues sont suffisantes, et onresout le probleme. Pour cela, posonsx = · · ·Ici, les possibles valeurs de x trouvees dans l’analyse.N. Arancibia - relu par D. CransacAlgebre

Page 390 : Modes de raisonnementAnalyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire.Pour cela on ecrit : Soit x E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quelles sontles valeurs possibles de x ?Synthese : On montre que ces conditions obtenues sont suffisantes, et onresout le probleme. Pour cela, posonsx = · · ·Ici, les possibles valeurs de x trouvees dans l’analyse.Verifions que x E et que Px est vraie....Verification que x appartient a E et satisfait la propriete P.N. Arancibia - relu par D. CransacAlgebre

Page 391 : Modes de raisonnementEn Resume :Dans l’analyse, on restreint le nombre des solutions possibles.N. Arancibia - relu par D. CransacAlgebre

Page 392 : Modes de raisonnementEn Resume :Dans l’analyse, on restreint le nombre des solutions possibles.Dans la synthese, on verifie que les possibilites obtenues dansl’analyse sont en fait des solutions.N. Arancibia - relu par D. CransacAlgebre

Page 393 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation.N. Arancibia - relu par D. CransacAlgebre

Page 394 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = xN. Arancibia - relu par D. CransacAlgebre

Page 395 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = xN. Arancibia - relu par D. CransacAlgebre

Page 396 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2N. Arancibia - relu par D. CransacAlgebre

Page 397 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.N. Arancibia - relu par D. CransacAlgebre

Page 398 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alorsnecessairement x = 3 ou x = 2.N. Arancibia - relu par D. CransacAlgebre

Page 399 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alorsnecessairement x = 3 ou x = 2.Synthese : On teste a present les valeurs obtenuesN. Arancibia - relu par D. CransacAlgebre

Page 400 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alorsnecessairement x = 3 ou x = 2.Synthese : On teste a present les valeurs obtenues : 2 ne convient paspuisque2 + 6 = 2 ̸= 2,N. Arancibia - relu par D. CransacAlgebre

Page 401 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alorsnecessairement x = 3 ou x = 2.Synthese : On teste a present les valeurs obtenues : 2 ne convient paspuisque2 + 6 = 2 ̸= 2,mais 3 convient car on a bien3 + 6 = 3.N. Arancibia - relu par D. CransacAlgebre

Page 402 : Modes de raisonnementExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alorsnecessairement x = 3 ou x = 2.Synthese : On teste a present les valeurs obtenues : 2 ne convient paspuisque2 + 6 = 2 ̸= 2,mais 3 convient car on a bien3 + 6 = 3.Nous avons ainsi montre que l’equation x + 6 = x admet une unique solutionx = 3.N. Arancibia - relu par D. CransacAlgebre

Page 403 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .N. Arancibia - relu par D. CransacAlgebre

Page 404 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble NN. Arancibia - relu par D. CransacAlgebre

Page 405 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble N :toute partie non vide A de l’ensemble N a un plus petit element m.N. Arancibia - relu par D. CransacAlgebre

Page 406 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble N :toute partie non vide A de l’ensemble N a un plus petit element m. Cecisignifie :N. Arancibia - relu par D. CransacAlgebre

Page 407 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble N :toute partie non vide A de l’ensemble N a un plus petit element m. Cecisignifie :d’une part que m est un element de A N,N. Arancibia - relu par D. CransacAlgebre

Page 408 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble N :toute partie non vide A de l’ensemble N a un plus petit element m. Cecisignifie :d’une part que m est un element de A N,d’autre part que m est inferieur ou egal a tout element de A, c’est a direx A,m x.N. Arancibia - relu par D. CransacAlgebre

Page 409 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une propriete essentielle de l’ensemble N :toute partie non vide A de l’ensemble N a un plus petit element m. Cecisignifie :d’une part que m est un element de A N,d’autre part que m est inferieur ou egal a tout element de A, c’est a direx A,m x.Cette propriete est la base du Raisonnement par Recurrence.N. Arancibia - relu par D. CransacAlgebre

Page 410 : Raisonnement par recurrenceProposition Recurrence SimpleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :Initialisation : P0 est vraie, eHeredite : pour tout n N, si Pn est vraie, alors Pn + 1 est vraie.Alors la propriete Pn est vraie pour tout n N.N. Arancibia - relu par D. CransacAlgebre

Page 411 : Raisonnement par recurrenceProposition Recurrence SimpleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :Initialisation : P0 est vraie, eHeredite : pour tout n N, si Pn est vraie, alors Pn + 1 est vraie.Alors la propriete Pn est vraie pour tout n N.Remarque. L’initialisation peut commencer a un entier k0 N arbitraire pasnecessairement 0 et dans ce cas la propriete n’est demontree vraie qu’a partirdu rang k0 : SiPk0 est vraie,Pour tout entier n superieur ou egal a k0, Pn est vraie, alors Pn + 1est vraie.Alors la propriete Pn est vraie pour tout entier superieur ou egal a k0.N. Arancibia - relu par D. CransacAlgebre

Page 412 : Raisonnement par recurrenceDemonstration.SoitA = n N : Pn est vraie.Pour montrer que A = N, on raisonne par l’absurde. Dans ce cas, lecomplementaire de la partie A dans N est non vide. Elle admet donc un pluspetit element que l’on note p. Puisque 0 A, on ap 1.De plus par definition de pp 1 0ne peut appartenir au complementaire de A. On a donc p 1 A. AinsiPp 1 est vraie, ce qui implique que Pp est vraie, et donc que p appartienta A. Finalement,p Aetp N \ A.Contradiction ! ! !N. Arancibia - relu par D. CransacAlgebre

Page 413 : Raisonnement par recurrenceQuand on veut montrer par recurrence quen N, Pnon redige ainsi :Initialisation : Verification que P0 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 414 : Raisonnement par recurrenceQuand on veut montrer par recurrence quen N, Pnon redige ainsi :Initialisation : Verification que P0 est vraie.Heredite : On veut montrer n N, Pn vraie =⇒Pn + 1N. Arancibia - relu par D. CransacAlgebre

Page 415 : Raisonnement par recurrenceQuand on veut montrer par recurrence quen N, Pnon redige ainsi :Initialisation : Verification que P0 est vraie.Heredite : Soit n N. Supposons Pn vraie.N. Arancibia - relu par D. CransacAlgebre

Page 416 : Raisonnement par recurrenceQuand on veut montrer par recurrence quen N, Pnon redige ainsi :Initialisation : Verification que P0 est vraie.Heredite : Soit n N. Supposons Pn vraie. Montrons quePn + 1 est vraie....Preuve que Pn + 1 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 417 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0N. Arancibia - relu par D. CransacAlgebre

Page 418 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 419 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite :N. Arancibia - relu par D. CransacAlgebre

Page 420 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraieN. Arancibia - relu par D. CransacAlgebre

Page 421 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.N. Arancibia - relu par D. CransacAlgebre

Page 422 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 423 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.N. Arancibia - relu par D. CransacAlgebre

Page 424 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduitN. Arancibia - relu par D. CransacAlgebre

Page 425 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.N. Arancibia - relu par D. CransacAlgebre

Page 426 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on aN. Arancibia - relu par D. CransacAlgebre

Page 427 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on a2n 1.N. Arancibia - relu par D. CransacAlgebre

Page 428 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on a2n 1.Par consequent2n+1 n + 2n n + 1.N. Arancibia - relu par D. CransacAlgebre

Page 429 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on a2n 1.Par consequent2n+1 n + 2n n + 1.C’est-a-dire 2n+1 n + 1.N. Arancibia - relu par D. CransacAlgebre

Page 430 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0 , donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on a2n 1.Par consequent2n+1 n + 2n n + 1.C’est-a-dire 2n+1 n + 1. Fin de la recurrence. Par consequent pour tout entiernaturel n, 2n n.N. Arancibia - relu par D. CransacAlgebre

Page 431 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation :N. Arancibia - relu par D. CransacAlgebre

Page 432 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 433 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite :N. Arancibia - relu par D. CransacAlgebre

Page 434 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N.N. Arancibia - relu par D. CransacAlgebre

Page 435 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraieN. Arancibia - relu par D. CransacAlgebre

Page 436 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pairN. Arancibia - relu par D. CransacAlgebre

Page 437 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pairN. Arancibia - relu par D. CransacAlgebre

Page 438 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 439 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1N. Arancibia - relu par D. CransacAlgebre

Page 440 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1N. Arancibia - relu par D. CransacAlgebre

Page 441 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1 = 32k + 1 1N. Arancibia - relu par D. CransacAlgebre

Page 442 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1 = 32k + 1 1 = 6k + 3 1N. Arancibia - relu par D. CransacAlgebre

Page 443 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1 = 32k + 1 1 = 6k + 3 1 = 23k + 1.C’est-a-dire 3n+1 1 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 444 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie , c’est-a-dire3n 1 est pair⇐⇒3n 1 = 2k,k Z.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1 = 32k + 1 1 = 6k + 3 1 = 23k + 1.C’est-a-dire 3n+1 1 est pair.Fin de la recurrence. Par consequent, pour tout entier naturel n, 3n 1 est pair.N. Arancibia - relu par D. CransacAlgebre

Page 445 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn , maisseulementPn + 2dePn et Pn + 1.N. Arancibia - relu par D. CransacAlgebre

Page 446 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn , maisseulementPn + 2dePn et Pn + 1.Le principe du raisonnement par recurrence prend dans ce cas la forme suivante.N. Arancibia - relu par D. CransacAlgebre

Page 447 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn , maisseulementPn + 2dePn et Pn + 1.Le principe du raisonnement par recurrence prend dans ce cas la forme suivante.Proposition Recurrence DoubleN. Arancibia - relu par D. CransacAlgebre

Page 448 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn , maisseulementPn + 2dePn et Pn + 1.Le principe du raisonnement par recurrence prend dans ce cas la forme suivante.Proposition Recurrence DoubleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :P0 et P1 sont vraies,pour tout n N, si Pn et Pn + 1 sont vraies, alors Pn + 2 estvraie.Alors la propriete Pn est vraie pour tout n N.N. Arancibia - relu par D. CransacAlgebre

Page 449 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn , maisseulementPn + 2dePn et Pn + 1.Le principe du raisonnement par recurrence prend dans ce cas la forme suivante.Proposition Recurrence DoubleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :P0 et P1 sont vraies,pour tout n N, si Pn et Pn + 1 sont vraies, alors Pn + 2 estvraie.Alors la propriete Pn est vraie pour tout n N.Remarque : Les recurrences classiques sont dites simples et il existe bienentendu des recurrences triples, etc.N. Arancibia - relu par D. CransacAlgebre

Page 450 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pnon redige ainsi :Initialisation :N. Arancibia - relu par D. CransacAlgebre

Page 451 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pnon redige ainsi :Initialisation : Verification que P0 et P1 sont vraies.N. Arancibia - relu par D. CransacAlgebre

Page 452 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pnon redige ainsi :Initialisation : Verification que P0 et P1 sont vraies.Heredite :N. Arancibia - relu par D. CransacAlgebre

Page 453 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pnon redige ainsi :Initialisation : Verification que P0 et P1 sont vraies.Heredite : Soit n N. Supposons Pn et Pn + 1 sont vraies.Montrons que Pn + 2 est vraie....Preuve que Pn + 2 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 454 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pnon redige ainsi :Initialisation : Verification que P0 et P1 sont vraies.Heredite : Soit n N. Supposons Pn et Pn + 1 sont vraies.Montrons que Pn + 2 est vraie....Preuve que Pn + 2 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 455 : Modes de raisonnementTheoreme Recurrence forteOn considere une propriete Pn dependant de l’entier n N, et onsuppose que :P0 est vraie,pour tout n N, si Pk est vraie pour k n, alors Pn + 1 estvraie.Alors la propriete Pn est vraie pour tout n N.N. Arancibia - relu par D. CransacAlgebre

Page 456 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite :N. Arancibia - relu par D. CransacAlgebre

Page 457 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite :N. Arancibia - relu par D. CransacAlgebre

Page 458 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.N. Arancibia - relu par D. CransacAlgebre

Page 459 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.Soit n + 1 est premier,N. Arancibia - relu par D. CransacAlgebre

Page 460 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.Soit n + 1 est premier, Soit il se decompose produit de deux entiers p etq avec p 1 et q 1 donc p n + 1 et q n + 1.N. Arancibia - relu par D. CransacAlgebre

Page 461 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.Soit n + 1 est premier, Soit il se decompose produit de deux entiers p etq avec p 1 et q 1 donc p n + 1 et q n + 1.D’apres l’hypothese de recurrence, ces deux entiers se decomposent enproduit de nombres premiers donc leur produit n + 1 est un produit denombres premiers.N. Arancibia - relu par D. CransacAlgebre

Page 462 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.Soit n + 1 est premier, Soit il se decompose produit de deux entiers p etq avec p 1 et q 1 donc p n + 1 et q n + 1.D’apres l’hypothese de recurrence, ces deux entiers se decomposent enproduit de nombres premiers donc leur produit n + 1 est un produit denombres premiers.Dans tous les cas n + 1 est premier ou se decompose en produit denombres premiers. Or d’apres l’hypothese de recurrence c’est vrai pourtout entier k n + 1 donc Pn + 1 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 463 : Modes de raisonnementExemple : Montrer que tout entier n 2 se decompose en produit denombres premiers.Preuve : On veut montrer la propriete : n N, n 2Pn : k N, k n, k est premier ou se decompose en produit denombres premiersInitialisation : 2 est premier donc P2 est vraie.Heredite : Soit n N, n 2 supposons Pn.Soit n + 1 est premier, Soit il se decompose produit de deux entiers p etq avec p 1 et q 1 donc p n + 1 et q n + 1.D’apres l’hypothese de recurrence, ces deux entiers se decomposent enproduit de nombres premiers donc leur produit n + 1 est un produit denombres premiers.Dans tous les cas n + 1 est premier ou se decompose en produit denombres premiers. Or d’apres l’hypothese de recurrence c’est vrai pourtout entier k n + 1 donc Pn + 1 est vraie.Conclusion : Donc n N, n 2, n est premier ou se decompose enproduit de nombres premiers.N. Arancibia - relu par D. CransacAlgebre

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463