CM2 Groupes

Télécharger le CM2 Groupes en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

Page 1 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDans tout ce chapitre, E est un ensemble.DénitionOn appelle loi de composition interne sur E lci toute application deE × E dans E.Exemplep :R2→Rx, y7→x + yDénitionOn appelle magma tout couple constitué d'un ensemble et d'une lci.ExampleR, + est un magma.Z, est un magma.N, n'est pas un magma : en eet 3 4 /N1/45D. CransacAnalyse

Page 2 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDans toute la suite, est une lci sur E.DénitionSoit E, un magma.On dit que E est associatif si pour tout x, y, z E, on a :x y z = x y zL'élément x y z = x y z est alors noté x y z.On dit que E est commutatif si pour tout x, y E, on a :x y = y xSoit une seconde lci sur E.On dit que dans E est distributive par rapport à si pour toutx, y, z E, on a :x y z = x y x zy z x = y x z x.2/45D. CransacAnalyse

Page 3 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueOn dit que dans E, est distributive à gauche par rapport à si pourtout x, y, z E, on a :x y z = x y x zDe même, on a la notion de distributivité à droite.3/45D. CransacAnalyse

Page 4 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExample1C, R, Q, Z, N avec + ou × sont associatifs, mais pas Z, car1 2 3 ̸= 1 2 3.2C, R, Q, Z, N avec + ou × sont commutatifs, mais pas Z, , niFR, R, ◦.3Sur C, R, Q, Z, N la loi de composition interne × est distributive parrapport à +.4PE, et sont distributives l'une par rapport à l'autre.4/45D. CransacAnalyse

Page 5 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénition Elément neutreSoit e E.On dit que e est un élément neutre à gauche resp. à droite pour sipour tout x E on ae x = xOn dit que e est un élément neutre à droite resp. à droite pour sipour tout x E on ax e = xOn dit que e est un élément neutre pour si c'est un élément neutre àgauche et à droite, i.e.x E, e x = x e = x5/45D. CransacAnalyse

Page 6 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénition Elément inversibleSoit e un neutre pour et soit x E.On dit que x est inversible à gauche s'il existe un élément y Etel quey x = eUn tel élément y s'appelle UN inverse à gauche x.On dit que x est inversible à droite s'il existe un élément y E telquex y = eUn tel élément y s'appelle UN inverse à droite x.On dit que x est inversible s'il est inversible à gauche et à droite,i.e. il existe y E tel quey x = x y = eDans ce cas y est UN inverse de x.6/45D. CransacAnalyse

Page 7 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExample0 est un élément neutre pour + dans R, C, Q, Z, N.1 est un élément neutre pour × dans R, C, Q.IdE est un élément neutre pour ◦composition dans FE, E et lesbijections sont tous les éléments inversibles de cet ensemble.Remarque1Être inversible seulement à gauche ou à droite ne sut pas pour êtreinversible tout court.Soit f :N→Nn7→2n et g :N→Nn7→n2Si n pair0Si n impairOn a g ◦f = Id pour tout h FN, N, f ◦h ̸= Id car 3 parexemple n'a pas d'antécédent par f ◦h donc f ◦h n'est pas l'identité.2Un neutre est toujours inversible et est son propre inverse.En eet, par dénition du neutre, e e = e e = e7/45D. CransacAnalyse

Page 8 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesPropositionSi admet un neutre, alors ce neutre est unique.Démonstration.Soient e et e′ deux neutres.Alors e e′ = e car e′ est une neutreet e e′ = e′ car e est un neutre.donc e = e′.8/45D. CransacAnalyse

Page 9 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesPropositionOn suppose la loi associative, et admettant un neutre e.Si un élément est inversible, alors il a un seul inverse.Démonstration.Soient y et y ′ deux inverses de x E.Alors y x = e et x y ′ = e.Donc y x y ′ = y e = y et y x y ′ = e y ′ = y ′, d'oùy = y ′.9/45D. CransacAnalyse

Page 10 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueOn utilise souvent les notations additives et multiplicatives.1En notation additive, est notée +x + x + · · · + x nfois se note nx.Si x est inversible, son inverse se note x. On l'appelle alorsl'opposé de x.On notera le neutre d'une telle structure 0 ou 0E.2En notation multiplicative, est en général notée par × et cesymbole est même souvent omisx × x × · · · × x nfois se note xnSi x est inversible, son inverse se note x1. On l'appelle alorsl'inverse de x.On notera le neutre d'une telle structure 1 ou 1E.10/45D. CransacAnalyse

Page 11 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesPour éviter toute erreur, on essaiera au maximum de n'utiliser la notationadditive que pour des lois qui ont les mêmes propriétés que la loi + surR.La notation + est en général réservée à des lci commutatives et pourlesquelles les éléments sont tous inversibles.Par exemple, noter + une lci non commutative peut-être déroutant, ainsique pour une lci pour laquelle tous les éléments ne sont pas inversibles.11/45D. CransacAnalyse

Page 12 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesLa notation multiplicative est la plus couramment utilisée pour des loisassociativesPar exemple il est fréquent d'utiliser × même pour une lci noncommutative et pour laquelle les éléments ne sont pas tous inversibles.AttentionEn général on aura xy ̸= yx, et x1 n'existera pas forcément !Dans toute la suite, on adoptera la notation multiplicative, et on supposeque E a un neutre noté 1.12/45D. CransacAnalyse

Page 13 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesPropositionOn suppose la loi associative. Soient x, y, z E.1Simplication par un inversible : si x est inversible, alorsx y = x z ⇔y = z2Inverse d'un produit : si x et y sont inversibles alors x y l'est aussietx y1 = y 1 x13Puissances négatives : si x est inversible, on pose pour n N,xn =x1n. Alors xn = xn1.4Inverse d'un inverse : si x est inversible, x1 l'est aussi etx11 = x.Attention : l'inverse de x y n'a aucune raison d'être x1 y 1.13/45D. CransacAnalyse

Page 14 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration.On a xy = xz ⇔x1xy = x1xz ⇔ey = ez ⇔y = zxyy 1x1 = xyy 1x1 = xex1 = xx1 = e et de mêmey 1x1xy = y 1x1xy = y 1ey = y 1xx1 = e Doncy 1x1 est bien l'inverse à gauche et à droite de xy..Par récurrence.Initialisation : Vrai si n = 0.Hérédité : Soit n N, si on suppose vraie pour vrai pour n, alorsxn+1 xn1 = xn x x1 xn = xn e xn = xn xn = e.Vrai par unicité de l'inverse.14/45D. CransacAnalyse

Page 15 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionSoit E, un magma et F une partie de E.On dit que F est une partie stable de E par si pour tousx, y F, x y F.Example1, 1 est une partie stable de R, ×, mais pas 2, 2.15/45D. CransacAnalyse

Page 16 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionOn appelle groupe tout magma associatif, ayant un neutre, et dont toutélément est inversible.Si un groupe est commutatif ce qui signie en fait que sa loi estcommutative, il est dit abélien.Par défaut on utilise la notation multiplicative pour un groupe, sauf pourles groupes abéliens pour lesquels on utilise la notation additive.16/45D. CransacAnalyse

Page 17 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExample1C, R, Q, Z sont des groupes avec la loi +, mais pas avec la loi ×.2Pour n N, pour E = Cn, E = Rn, E = Qn ou E = Zn.On dénit l'addition + parx1, x2, . . . , xn + y1, y2, . . . , yn = x1 + y1, x2 + y2, . . . , xn + ynalors E, + sont des groupes avec la loi +.3C, R, Q, sont des groupes avec la loi ×.4N, + n'est pas un groupe..En eet 3 n'admet pas d'opposé dans N5N, × n'est pas un groupe.En eet 3 n'admet pas d'inverse dans N17/45D. CransacAnalyse

Page 18 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionSoit X un ensemble non vide.On appelle groupe des permutations de X l'ensemble des bijections deX dans X muni de la loi de composition ◦.On le note SX.18/45D. CransacAnalyse

Page 19 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDans toute la suite, G, est un groupe de neutre e. On adopte lanotation multiplicative.DénitionOn appelle sous-groupe de G, tout ensemble H vériant lespropriétés suivantes :1H G ;2e H ;3Stabilité par produit : x, y H, x y H ;4Stabilité par passage à l'inverse : x H, on a x1 H.ExampleSont des sous-groupes :1e et G dans G, .2U ensemble des complexes de module 1 dans C, ×.3nZ dans Z, +.4H = f SR f 0 = 0 dans SR, ◦.19/45D. CransacAnalyse

Page 20 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesPropositionUn ensemble H est un sous groupe de G, si et seulement si H est unsous-ensemble non vide de G et pour tout x, y H2, on ax1 y HDémonstration.Montrons l'implication et sa réciproque :1"⇒" Supposons que H est un sous-groupe de G.Alors H contient eet n'est donc pas vide.De plus, soit x, y H.H étant stable par passage à l'inverse,on a alors x1 H et par stabilité par produit, on a doncx1 y H.20/45D. CransacAnalyse

Page 21 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration.2"⇐" Réciproquement, supposons que H est non vide et que pourtout x, y H2, on a x1 y H.Montrons que H possède les trois propriétés énumérées dans sadénition :1H étant non vide, il possède au moins un élément x0. On a alorse = x10x0 H.2Soit x H. On a alors x, e H2, donc x1 e = x1 H.3Soit x, y H. D'après ce qui précède, on a alors x1 H, doncx1, y H2, donc x y =x11 y H.RemarqueOn a aussi la propriété équivalente en remplaçant ci-dessus la conditionx1 y H par x y 1 H.21/45D. CransacAnalyse

Page 22 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionSoit G, un groupe et H, un sous-groupe de G, .On peut dénir sur H une loi appellée loi induite △telle quex, y H, x△y = x yRemarquePar la suite, par soucis de simplication on notera la loi sur H : △avec lemême symbole que la lci sur G : TheoremUn sous-groupe muni de la loi induite du groupe est lui-même ungroupe.22/45D. CransacAnalyse

Page 23 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration.Soit G, un groupe de neutre e et H un sous-groupe de G.1Montrons qu'on peut restreindre : G × G →G au départ à H × Het à l'arrivée à H.On a H × H G × G, donc la restriction au départ est légitime,pour eectuer la restriction à l'arrivée, il sut de montrer que pourtout x, y H2, on a x y H, c'est-à-dire que H est stable par .Or H est un sous-groupe de G : la dénition d'un sous-groupeassure cette stabilité.23/45D. CransacAnalyse

Page 24 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration.2H muni de la loi induite par est un magma associatif.En eet G, est un magma associatif, on a doncx, y, z G 3x y z = x y zOr H G doncx, y, z H3x y z = x y zDonc la restriction de à H est associative, d'où le résultat.3e est neutre pour la loi induite par sur H. En eet, e est le neutrede , doncx Ge x = x e = xD'où le résultat.24/45D. CransacAnalyse

Page 25 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration.4Tout élément de H admet un inverse pour la loi induite par .En eet tout élément x de H admet un inverse x1 dans G pour laloi et par stabilité de l'inverse sur le sous-groupe H, on a x1 H.Donc tout élément de H admet un inverse dans H pour la loi induitepar .5On déduit des points précédents que H muni de la loi induite par est un groupe.25/45D. CransacAnalyse

Page 26 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueLa réciproque de ce théorème est également vraie bien que moinsutilisée : si H est un sous-ensemble de G tel que, muni de la loi induitepar celle de G, H soit un groupe, alors H est un sous-groupe de G.ExampleSi n N, Un est un sous-groupe de U, ×, donc Un, × est un groupe.26/45D. CransacAnalyse

Page 27 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueIl est plus facile de montrer qu'un ensemble est un sous-groupe que demontrer que c'est un groupe pas besoin de redémontrer l'associativité,etc..Par exemple U, × est un groupe, vu comme sous-groupe de C, ×.À chaque fois que l'on essaiera de montrer qu'un ensemble est munid'une structure de groupe, on tentera de le voir comme un sous-grouped'un groupe bien connu.27/45D. CransacAnalyse

Page 28 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesMorphismes de groupes28/45D. CransacAnalyse

Page 29 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionSoient G, et G ′, deux groupes et φ : G →G ′.1On dit que φ est un morphisme du groupe G, dans le groupeG ′, , six, y G,φx y = φx φy.2Tout morphisme d'un groupe dans lui-même est appeléendomorphisme.3Tout morphisme de G dans G ′ qui est une bijection est appeléisomorphisme de G sur G ′.Dans ce cas on dit que G et G ′ sont isomorphes.Un morphisme qui est à la fois un isomorphisme et unendomorphisme est appelé automorphisme.29/45D. CransacAnalyse

Page 30 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExample1Z, +→Z, +x7→2xest un morphisme, mais pas un isomorphisme.2C, ×→R, ×z7→zest un morphisme, mais pas unisomorphisme.3R, +→C, ×x7→eixest un morphisme, mais pas un isomorphisme.4R, +→R+, ×x7→exest un isomorphisme de réciproque ln, quiest aussi un isomorphisme.30/45D. CransacAnalyse

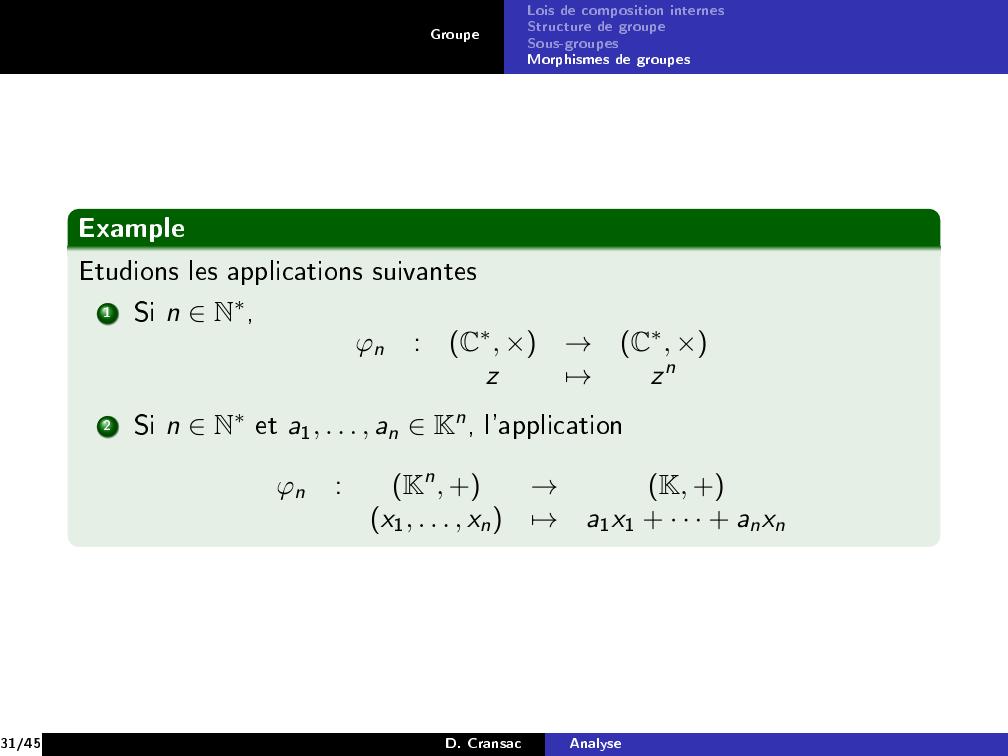
Page 31 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExampleEtudions les applications suivantes1Si n N,φn:C, ×→C, ×z7→zn2Si n Net a1, . . . , an Kn, l'applicationφn:Kn, +→K, +x1, . . . , xn7→a1x1 + · · · + anxn31/45D. CransacAnalyse

Page 32 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDans toute la suite, G, et G ′, sont deux groupes de neutres e et e′,on adopte une notation multiplicative, et φ : G →G ′ est un morphisme.TheoremSoit φ un morphisme de G sur G ′, on a, e et e′ désignant les neutres deG et G ′ :1φe = e′2x G, φx1 = φx1.Démonstration.1On a φe φe = φe e = φe = φe e′, donc en simpliantpar φe, on en déduit φe = e′.2Soit x G. Alors φx1 φx = φx1 x = φe = e.32/45D. CransacAnalyse

Page 33 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesCorollarySous les mêmes hypothèses, on ax Gk Zφxk = φxk.Démonstration.On démontre par récurrence :Soit x G.Initialisation : D'après le théorème précédent, on aφx0 = φe = e′ = φx0.Hérédité : Soit n N, on suppose φxn = φxn.On a alors φxn+1 = φxnx = φxnφx = φxnφx = φxn+1D'après le théorème précédent, pour tout n N,φxn = φxn1d'où φxn = φxn. On en déduit le résultat.33/45D. CransacAnalyse

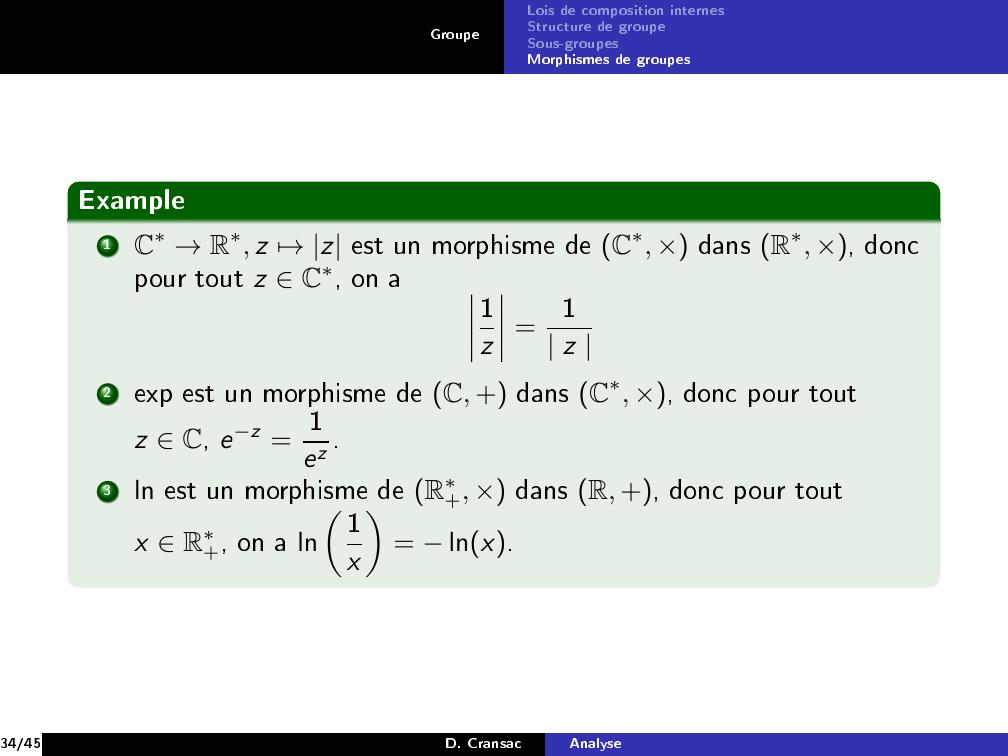
Page 34 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesExample1C→R, z 7→z est un morphisme de C, × dans R, ×, doncpour tout z C, on a1z =1 z 2exp est un morphisme de C, + dans C, ×, donc pour toutz C, ez = 1ez .3ln est un morphisme de R+, × dans R, +, donc pour toutx R+, on a ln1x= lnx.34/45D. CransacAnalyse

Page 35 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheorem1La composée de deux morphismes de groupes est un morphisme degroupe.Plus précisément, soit G1, 1, G2, 2 et G3, 3 trois groupes, φun morphisme de G1 dans G2 et φ un morphisme de G2 dans G3.Alors ψ ◦φ est un morphisme de G1 dans G3.2La fonction réciproque d'un isomorphisme en tant qu'applicationbijective est un isomorphisme.Plus précisément, soit G1, 1 et G2, 2 deux groupes et φ unisomorphisme de G1 sur G2. Alors φ1 est un isomorphisme de G2sur G1.Démonstration.Pour tout x, y G 21 , ψ ◦φxy = ψφxy = ψφxφy =ψφxψφy = ψ ◦φxψ ◦φyPour tout x, y G 22 ,φφ1xφ1y = φφ1xφφ1y = xy = φφ1xy.On a donc en appliquant φ1, φ1xφ1y = φ1xy35/45D. CransacAnalyse

Page 36 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheoremL'image d'un sous-groupe par un morphisme de groupes est unsous-groupe.Démonstration.Soient G, et G ′, deux groupes de neutres respectifs e et e′, etφ : G →G ′ un morphisme de groupes. Soit H un sous-groupe de G.Montrons que φH est un sous-groupe de G ′.1On a évidemment φH G ′ et de plus e H et e′ = φe φH.2Soit x′, y ′ φH. Alors x′ possède un antécédent x H et y ′ unantécédent y H par φ. On a alors successivementx′ y ′1=φx φy1par dénition dex et y=φx φy 1car φ est un morphisme=φx y 1car φ est un morphismeDonc x′ y ′1 φH et nalement φH est donc un sous-groupede G ′.36/45D. CransacAnalyse

Page 37 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheoremL'image réciproque d'un sous-groupe par un morphisme est unsous-groupe.Démonstration.Gardons les même notations que dans le premier point, et notons H′ unsous-groupe de G ′.1On a évidemment φ1H′ G et de plus e′ H′ ete′ = φe H′ donc e φ1H′.2Soit x, y φ1H′.Alors φx, φy H′donc φx y 1 = φx φy1 H′donc x y 1 φ1H′.φ1H est donc un sous-groupe de G.37/45D. CransacAnalyse

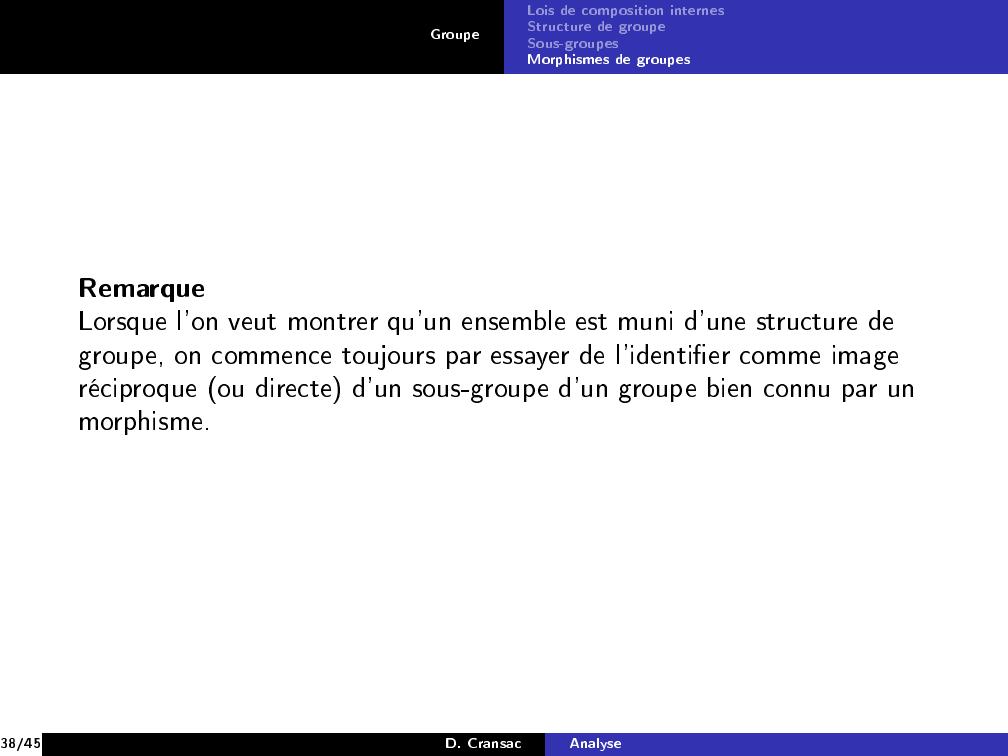
Page 38 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueLorsque l'on veut montrer qu'un ensemble est muni d'une structure degroupe, on commence toujours par essayer de l'identier comme imageréciproque ou directe d'un sous-groupe d'un groupe bien connu par unmorphisme.38/45D. CransacAnalyse

Page 39 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDénitionSoit φ : G →G ′ un morphisme de groupe.1On appelle noyau de φ, noté Ker φ, l'image réciproque de e′ parφ, autrement dit l'ensemble des antécédents de e′ par φKer φ = x G φx = e′.2On appelle image de φ notée Imφ, l'image directe de G par φ.Autrement ditImφ = φx x G.39/45D. CransacAnalyse

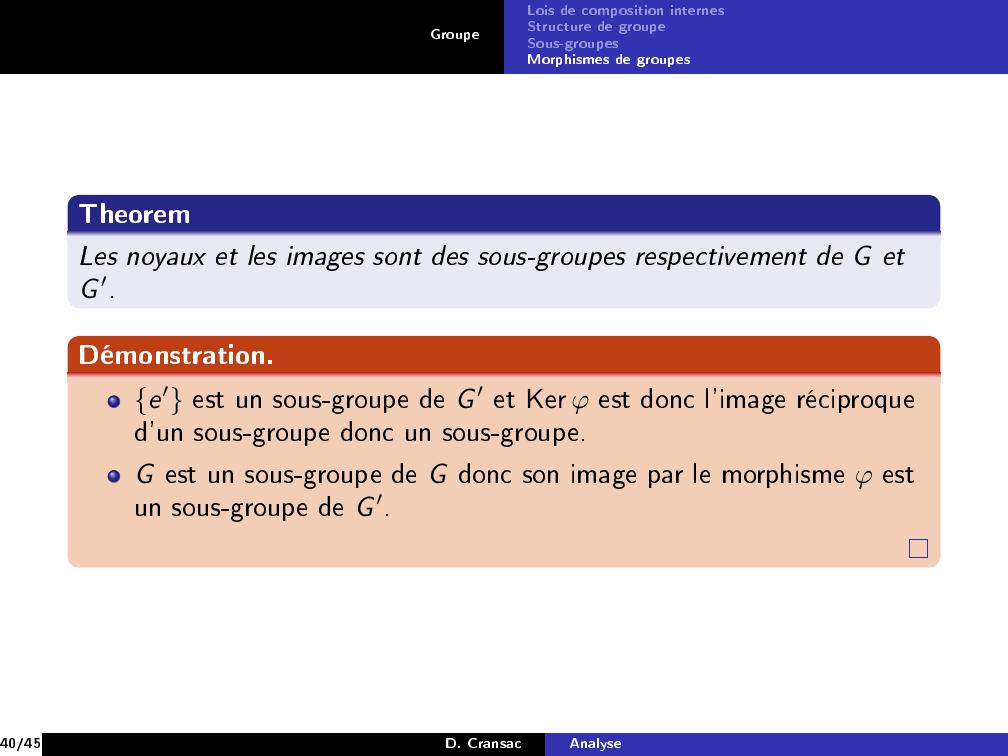
Page 40 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheoremLes noyaux et les images sont des sous-groupes respectivement de G etG ′.Démonstration.e′ est un sous-groupe de G ′ et Ker φ est donc l'image réciproqued'un sous-groupe donc un sous-groupe.G est un sous-groupe de G donc son image par le morphisme φ estun sous-groupe de G ′.40/45D. CransacAnalyse

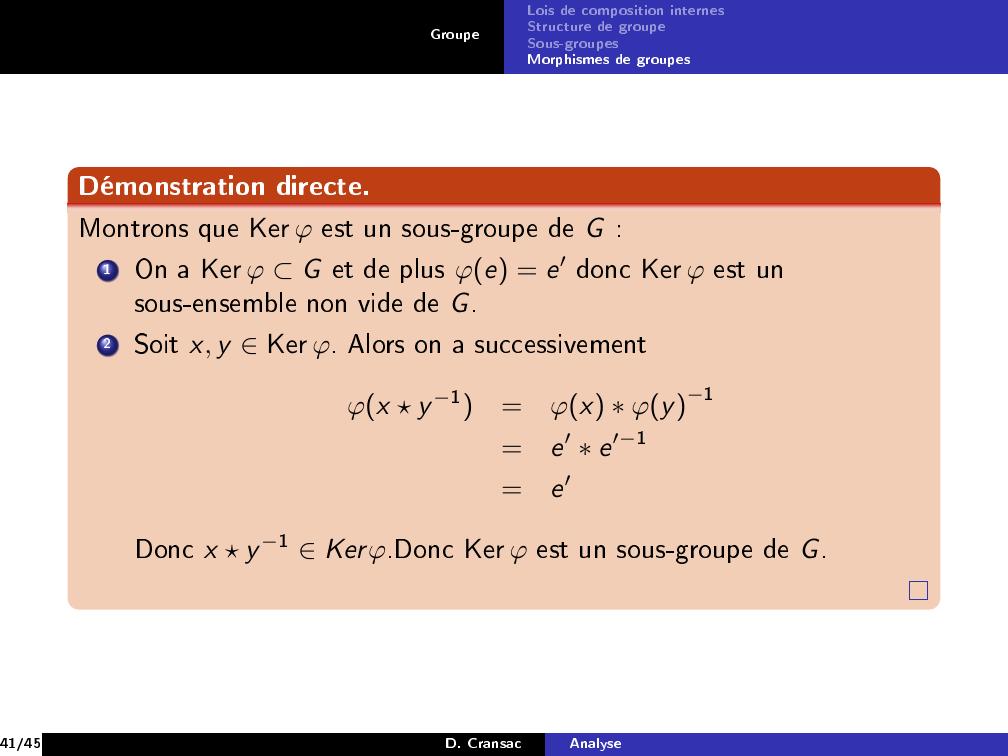
Page 41 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesDémonstration directe.Montrons que Ker φ est un sous-groupe de G :1On a Ker φ G et de plus φe = e′ donc Ker φ est unsous-ensemble non vide de G.2Soit x, y Ker φ. Alors on a successivementφx y 1=φx φy1=e′ e′1=e′Donc x y 1 Kerφ.Donc Ker φ est un sous-groupe de G.41/45D. CransacAnalyse

Page 42 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarqueLorsque l'on veut montrer qu'un ensemble est muni d'une structure degroupe, on commence toujours par essayer de l'identier comme noyauou image d'un morphisme.ExampleU est le noyau du morphisme module , de C, × dans R, ×.42/45D. CransacAnalyse

Page 43 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheoremφ surjectif si et seulement si Imφ = G ′.Démonstration.Dénition !43/45D. CransacAnalyse

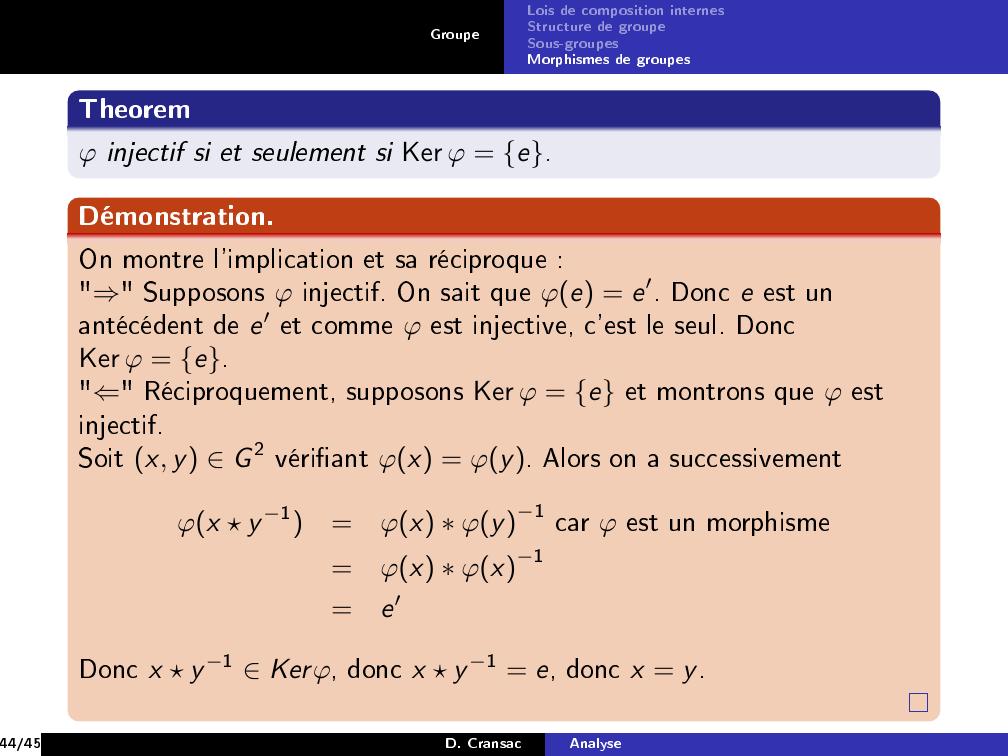
Page 44 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesTheoremφ injectif si et seulement si Ker φ = e.Démonstration.On montre l'implication et sa réciproque :"⇒" Supposons φ injectif. On sait que φe = e′. Donc e est unantécédent de e′ et comme φ est injective, c'est le seul. DoncKer φ = e."⇐" Réciproquement, supposons Ker φ = e et montrons que φ estinjectif.Soit x, y G 2 vériant φx = φy. Alors on a successivementφx y 1=φx φy1 car φ est un morphisme=φx φx1=e′Donc x y 1 Kerφ, donc x y 1 = e, donc x = y.44/45D. CransacAnalyse

Page 45 : GroupeLois de composition internesStructure de groupeSous-groupesMorphismes de groupesRemarquePour montrer qu'un morphisme est injectif, on utilisera TOUJOURS lenoyau et JAMAIS ou presque la méthode classique pour des fonctionsquelconques : c'est beaucoup plus rapide !45/45D. CransacAnalyse

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45