CM2 Introduction a la mesure

Télécharger le CM2 Introduction a la mesure en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Page 1 : Ingénieurs 1ère année : Mathématiques appliquéesMesure et intégrationCM2 – Introduction à la mesureNisrine FORTIN CAMDAVANT

Page 2 : 1Fonction d’ensembles et mesures2Exemples3Conséquences de la σ-additivité4Ensembles négligeables5Espaces mesurés complets

Page 3 : Fonction d’ensembles et mesures

Page 4 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsFonction d’ensemblesSoit Ωun ensemble non vide et T PΩ. Une fonctionm : T →0, +est appelée une fonction d’ensembles positive.Une "mesure abstraite" est une fonction d’ensemble vérifiant certainespropriétés. Une propriété que l’on exigera d’une telle fonction sera l’additivitéau sens suivant :La σ-additivitéUne fonction m : T →0, + est σ-additive si et seulement si pour toutesuite AnnN dans T vérifiant SnNAn T et An Ap = pour n ̸= p,m nNAn!=XnNm An .4/26

Page 5 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsOn appelle mesure positive une fonction d’ensemble positive, σ-additive, définiesur une tribu T et vérifiant m = 0.si T est une tribu de parties de Ωet si m : T →0, +, m est unemesure positive sur T si et seulement si les conditions suivantes sontvérifiées :1m = 02AnnN T N avec An Ap = pour n ̸= p alorsm nNAn=XnNmAn.Autrement dit,5/26

Page 6 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsExemplesSoit x0 Ω. On pose :mA =1si x0 A0si x0 /ASi Ωest muni d’une tribu T , m est une mesure appelée mesure de Diracde masse 1 et concentrée au point x0 et elle est notée δx0.Mesure de DiracSoit m : PΩ →0, + définie parmA =card Asi A est fini+si A est infinim est une mesure.m aura beaucoup d’intérêt pour Ω= N.Mesure de comptage6/26

Page 7 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsExemplesSoit Ωl’ensemble des unions finies d’intervalles semi-ouverts. SiA = a1, b1a2, b2· · · an, bnavec a1 b1 a2 b2 · · · an bn. On posemA =nXi=1bi ai .En prolongeant m à la plus petite tribu contenant Ω, on obtient la mesurede Lebesgue sur R, notée λ.Mesure de Lebesgue sur Rλx= 0, x R.λai, bi= λai, bi= λai, bi= bi ai.7/26

Page 8 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsPropriétés : conséquences de la σ-additivitéSoit Ωun ensemble, T est une tribu de parties de Ωet m unemesure positive sur T . On a alors les propriétés suivantes :8/26

Page 9 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés complets1A, BT 2. A B =⇒mA mB.⇝Démonstration – Voir TD 2.2An T pour tout n N, alors m SnNAnXnNmAn.⇝Démonstration – Voir TD 2.3An T pour tout n N, avec An An+1 n alorsm nNAn=limn→+mAn.⇝Démonstration – Voir Notes de cours.4An T pour tout n N, avec An+1 An n et mA0 +alorsm \nNAn=limn→+mAn.⇝Démonstration – Voir Notes de cours.Propriétés.9/26

Page 10 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsRemarques⇝Dans la propriété 4. de la proposition précédente, on peut remplacerl’hypothèse”mA0 +”par "il existe k N tel que mAk +".⇝Si on ne met pas l’hypothèse mA0 +ou il existe k N tel quemAk +, la propriété 4. n’est plus valable.::::::::Exemple : Prenons Ω= N, T = PN, m la mesure de comptage surN.Soit An = n, n + 1, . . ., TnNAn = , donc m TnNAn= 0. D’autrepart mAn = +n N, donc m TnNAn̸= limn mAn.Mise en garde.10/26

Page 11 : Ensembles négligeablesLes ensembles négligeables jouent un rôle très important dans la théoriede la mesure et de l’intégration.Les ensembles négligeables vont permettre d’exprimer le fait que certainespropriétés ponctuelles continuité, convergence simple, majoration,...n’ont pas lieu en tout point mais seulement "presque partout", c’est àdire sur le complémentaire d’un ensemble négligeable.Il s’avère techniquement nécessaire de ne pas restreindre la notiond’ensemble négligeable aux seuls sous-ensembles mesurables.

Page 12 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEnsembles négligeablesDans tout ce chapitre, Ωdésigne un ensemble quelconque non vide, T unetribu de parties de Ωet m une mesure positive sur T . Le triplet Ω, T , m estappelé un espace mesuré.Définition1On dit qu’un ensemble N T est m-négligeable si mN = 0.2On dit qu’une partie N de Ωest m-négligeable s’il existe A T tel queN A et mA = 0.12/26

Page 13 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEnsembles négligeables – ExemplesOn considère l’espace mesuré Ω, T , m où Ω= a; b; c, a, b et c des réels et= Ω, , a, b, c .Cas où m = δc est la mesure de Dirac concentrée en c.⇝Les parties mesurables de mesure nulle : δc = 0, δc a, b = 0 carc /a, b.⇝Les parties non mesurables négligeables :♢a a, b et δc a, b = 0 donc a est δc-négligeable.♢b a, b et δc a, b = 0 donc b est δc-négligeable.Les ensembles δc-négligeables sont donc , a, b, a et b.13/26

Page 14 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEnsembles négligeables – ExemplesCas où m = µd est la mesure de comptage.⇝Les parties mesurables de mesure nulle : µd = 0.⇝Les parties non mesurables négligeables : La seule partie mesurable demesure nulle est l’ensemble vide et ce dernier ne contient aucune partie deΩ.L’unique ensemble µd-négligeable est donc .14/26

Page 15 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEnsembles négligeables – ExemplesCas où m = λ est la mesure de Lebesgue.⇝Les parties mesurables de mesure nulle : λ = 0,λ Ω = λ a, b, c = 0 car a, b, c est dénombrable.a, b Ω, c Ωet λ Ω = 0 donc λ a, b = λ c = 0.⇝Les parties non mesurables négligeables : Toutes les parties de Ωsont pardéfinition inclues dans Ω, λ Ω = 0 donc toutes les parties de Ωsontλ-négligeables.Les ensembles λ-négligeables sont donc toutes les parties de Ω.15/26

Page 16 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEnsembles négligeables – Propriétés1est m-négligeable.2Si N est un ensemble m-négligeable, N′ T avec N′ N, alors N′ estm-négligeable.3La réunion d’une famille dénombrable d’ensembles m-négligeables estm-négligeable.::::::::::::Démonstration. Voir Notes de cours.16/26

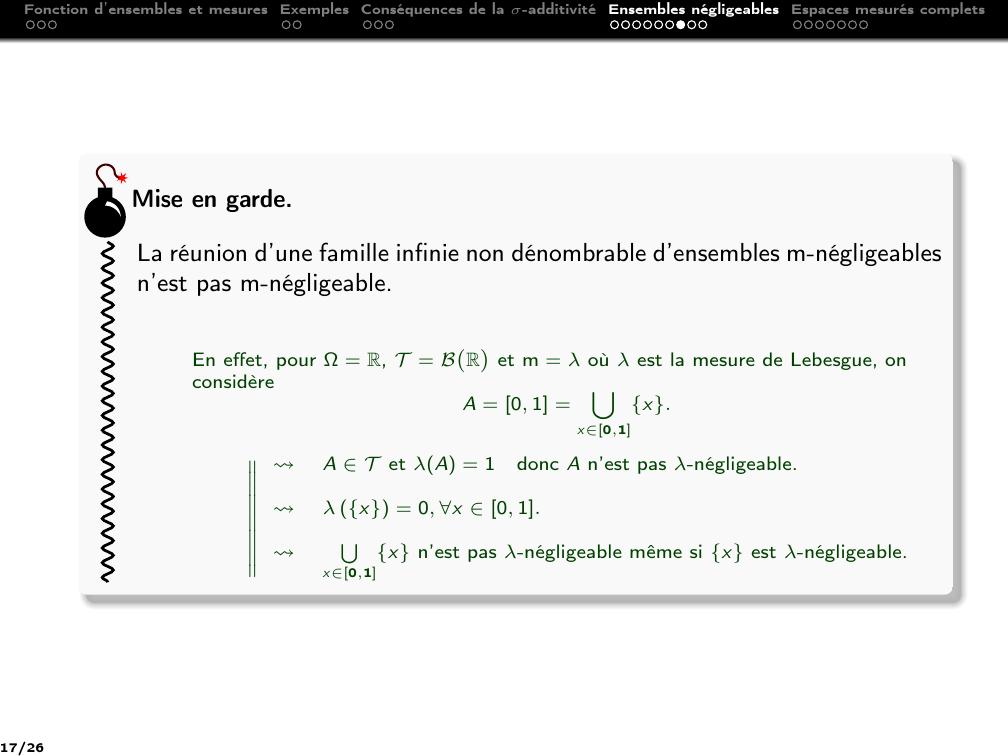
Page 17 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsLa réunion d’une famille infinie non dénombrable d’ensembles m-négligeablesn’est pas m-négligeable.En effet, pour Ω= R, T = BRet m = λ où λ est la mesure de Lebesgue, onconsidèreA = 0, 1 =x0,1x.⇝A T et λA = 1donc A n’est pas λ-négligeable.⇝λ x = 0, x 0, 1.⇝Sx0,1x n’est pas λ-négligeable même si x est λ-négligeable.Mise en garde.17/26

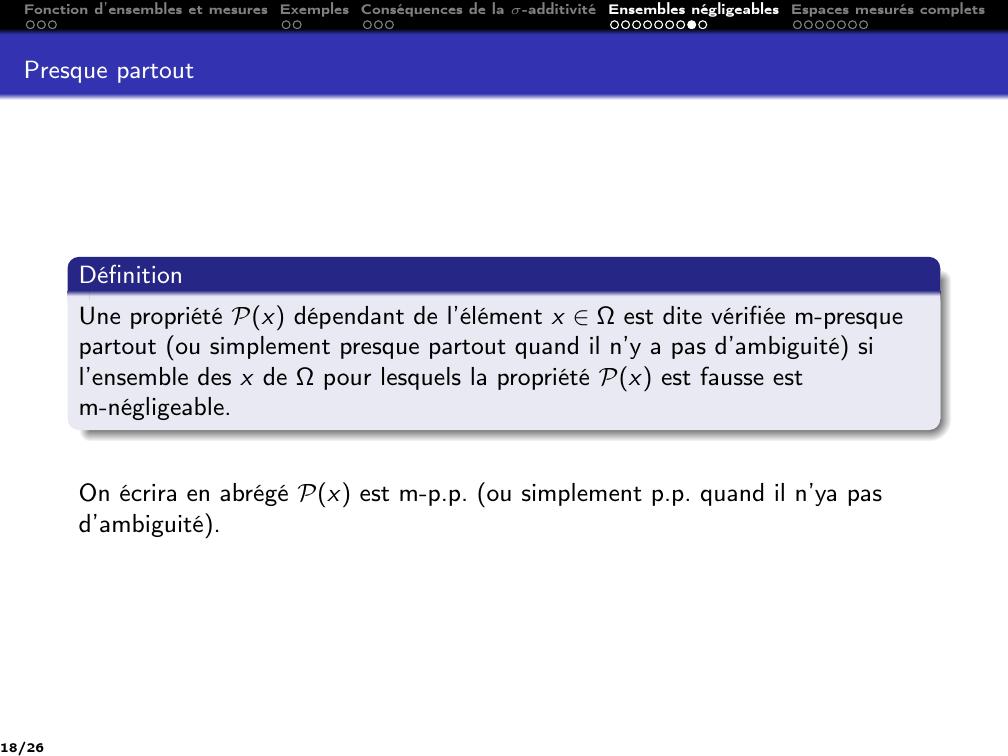
Page 18 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsPresque partoutDéfinitionUne propriété Px dépendant de l’élément x Ωest dite vérifiée m-presquepartout ou simplement presque partout quand il n’y a pas d’ambiguité sil’ensemble des x de Ωpour lesquels la propriété Px est fausse estm-négligeable.On écrira en abrégé Px est m-p.p. ou simplement p.p. quand il n’ya pasd’ambiguité.18/26

Page 19 : Espaces mesurés complets

Page 20 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEspaces mesurés completsOn a vu qu’une partie N de Ωm-négligeable n’est pas nécessairement unélément de la tribu T .⇝Pourtant pour respecter le principe de monotonie croissante de la mesurem, il est naturel d’attribuer à N la mesure 0.⇝On est alors en train d’élargir la tribu T .D’où la définition suivante :DéfinitionSi toutes les parties de Ωm-négligeables sont mesurables, on dit que l’espaceΩ, T , m est complet.20/26

Page 21 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsEspaces mesurés complets – ExempleOn considère l’espace mesuré Ω, T , m où Ω= a; b; c, a, b et c des réels etT = Ω, , a, b, c.:::Cas ::où::::::m = δc:::est::la::::::mesure:::de ::::Dirac:::::::::concentrée:::en ::c. L’ensemble desparties δc-négligeables estN = , a, b , a , ba est δc-négligeable mais non mesurable donc Ω, T , δc n’est pas unespace mesuré complet.:::Cas ::où:::::::m = µd :::est ::la ::::::mesure ::de:::::::::comptage. L’ensemble des partiesµd-négligeables estN = .est µd-négligeable et mesurable donc Ω, T , µd est un espace mesurécomplet.:::Cas ::où::::::m = λ:::est ::la ::::::mesure ::de::::::::Lebesgue. L’ensemble des partiesλ-négligeables estN = P Ω .a est λ-négligeable mais non mesurable donc Ω, T , λ n’est pas unespace mesuré complet.21/26

Page 22 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsComplétion d’un espace mesurableLorsqu’un espace mesuré Ω, T , m n’est pas complet, on peut le complétercanoniquement de la façon suivante :PropriétéSoit Ω, T , m un espace mesuré et soit N l’ensemble des partiesm-négligeables. On considèreeT = A N; A T et N N.Pour tout A T et pour tout N N, on pose emA N = mA. Alors1eT est une tribu sur Ωcontenant T ;2em définit une mesure positive sur eT qui coïncide avec m sur T ;3Si on note eN la famille des sous-ensembles de Ωem-négligeables alorseN = N ;4Ω, eT , em est un espace mesuré complet.::::::::::::Démonstration. Voir TD 2.22/26

Page 23 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsComplétion d’un espace mesurableDéfinitionOn dit que Ω, eT , em est le complété de l’espace mesuré Ω, T , m.RemarquesUn espace mesuré complet est égal à son complété.La tribu eT dépend et de la tribu T et de la mesure m par rapport àlaquelle on effectue la complétion.Si Px est une propriété dépendant de x Ωalors, Px est vraie m-p.p.si et seulement si Px est vraie em-p.p.23/26

Page 24 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsComplétion d’un espace mesurable – ExempleOn considère l’espace mesuré Ω, T , m où Ω= a; b; c, a, b et c des réels etT = Ω, , a, b, c.:::Cas ::où::::::m = δc:::est::la::::::mesure:::de ::::Dirac:::::::::concentrée:::en ::c. L’ensemble desparties δc-négligeables estN = , a, b , a , bΩ, T , δc n’est pas un espace mesuré complet et son complété est obtenupar union des ensembles mesurables et les ensembles négligeables :N NA TΩa, bcΩa, bca, bΩa, ba, bΩaΩaa, ba, cbΩba, bb, cLa tribu complétée dans ce cas est donc˜T = Ω, , a, b, c, a, b, a, c, b, c .24/26

Page 25 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsComplétion d’un espace mesurable – ExempleOn considère l’espace mesuré Ω, T , m où Ω= a; b; c, a, b et c des réels etT = Ω, , a, b, c.:::Cas ::où:::::::m = µd :::est ::la ::::::mesure ::de:::::::::comptage. Ω, T , µd est un espacemesuré complet donc˜T = T .:::Cas ::où::::::m = λ:::est ::la ::::::mesure ::de::::::::Lebesgue. L’ensemble des partiesλ-négligeables estN = P Ω .Ω, T , λ n’est pas un espace mesuré complet et dans ce cas˜T = P Ω.25/26

Page 26 : Fonction d’ensembles et mesuresExemplesConséquences de la σ-additivitéEnsembles négligeablesEspaces mesurés completsSi Ω, T , m = R, BR, λ. L’espace R, BR, λ n’est pas complet.AlorsLa tribu eT est la tribu de Lebesgue sur R et on la note LR ;La mesure eλ s’appelle aussi la mesure de Lebesgue et sera aussinotée λ au lieu de eλ ;Les éléments de LR sont appelés parties mesurables au sens deLebesgue ou parties Lebesgue-mesurables.Exemple : La tribu de Lebesgue LR26/26

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26