CM2 Quanti Quanti
Télécharger le CM2 Quanti Quanti en pdf
Page 1 : CM 2 : Analyse bivariée quantitatif-quantitatifData explorationStatistiques descriptives bivariéesObserver simultanément des individus d'une population sur deux caractèresMesurer un lien éventuel entre deux caractères en utilisant un résumé chiffré qui traduit l'importance de ce lienQualifier ce lien : –en cherchant une relation numérique approchée entre deux caractères quantitatifs–en cherchant des correspondances entre les modalités de deux caractères qualitatifs• qualitatif ×qualitatif2 types de variables 3 types de croisements : • qualitatif ×quantitatif• quantitatif ×quantitatif
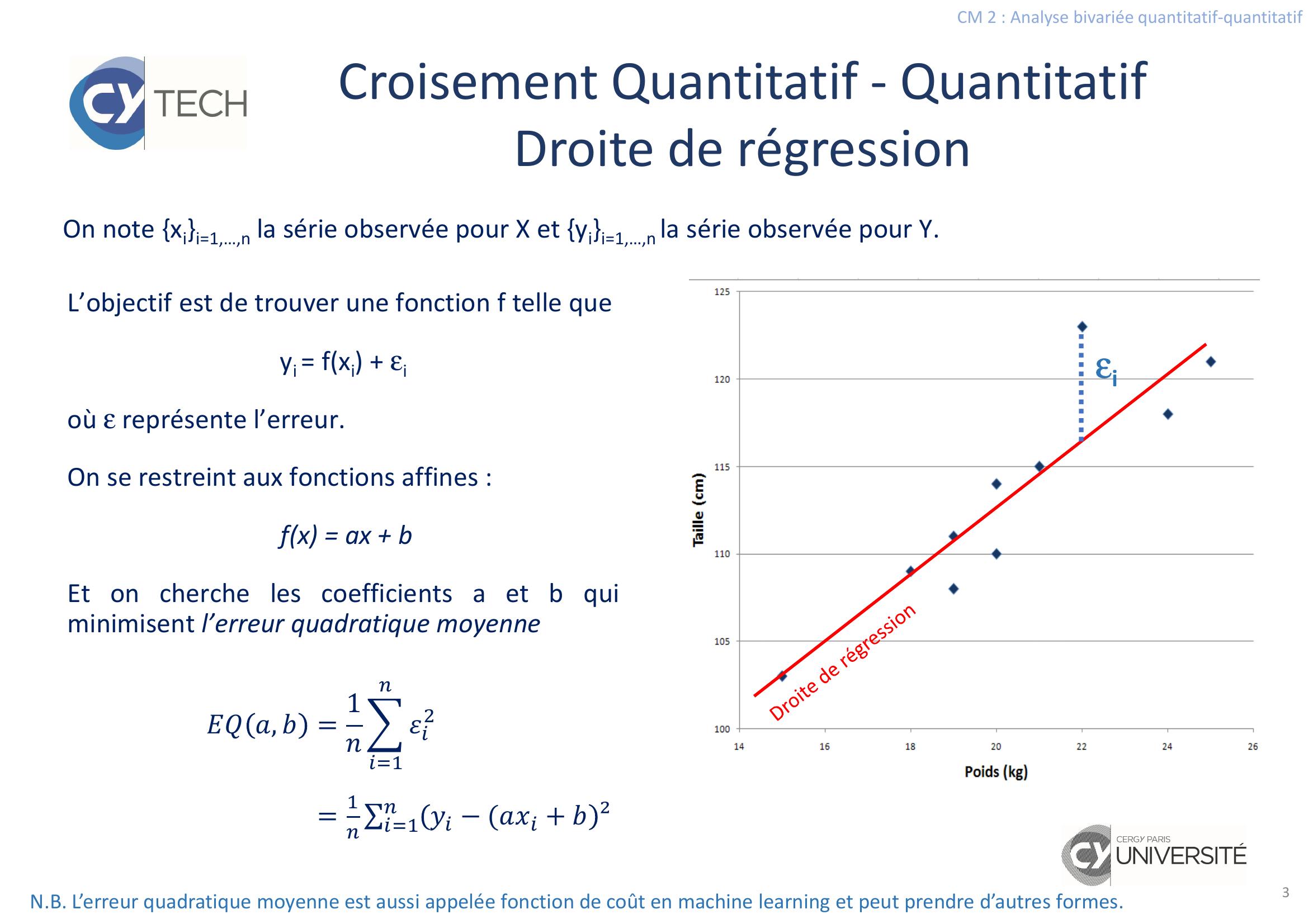
Page 2 : CM 2 : Analyse bivariée quantitatif-quantitatif2Croisement Quantitatif - QuantitatifNuage de pointsOn considère X et Y deux variables quantitatives sur un échantillon de taille n. Les objectifs sont :•Déterminer s’il y a un lien corrélation entre les deux variables.•Construire un modèle permettant d’expliquer Y par X ou vice-versa s’il y a un lien.Le modèle pourra alors servir à faire de la prévision, c-a-d prévoir des valeurs de Y pour denouvelles valeurs de X.La première étape consiste à constater visuellementsicelienexiste.Lareprésentationgraphiqueappropriée est le nuage de points.On cherche à repérer une forme particulière dans lenuage qui traduirai le lien entre X et Y. En particulier,une forme allongée traduit une relation de droiteentre les deux variables.Enfant12345678910Taille121123108118111109114103110115Poids25221924191820152021Etude du lien entre la taille X et le poids Y chez les enfants de 6 ans
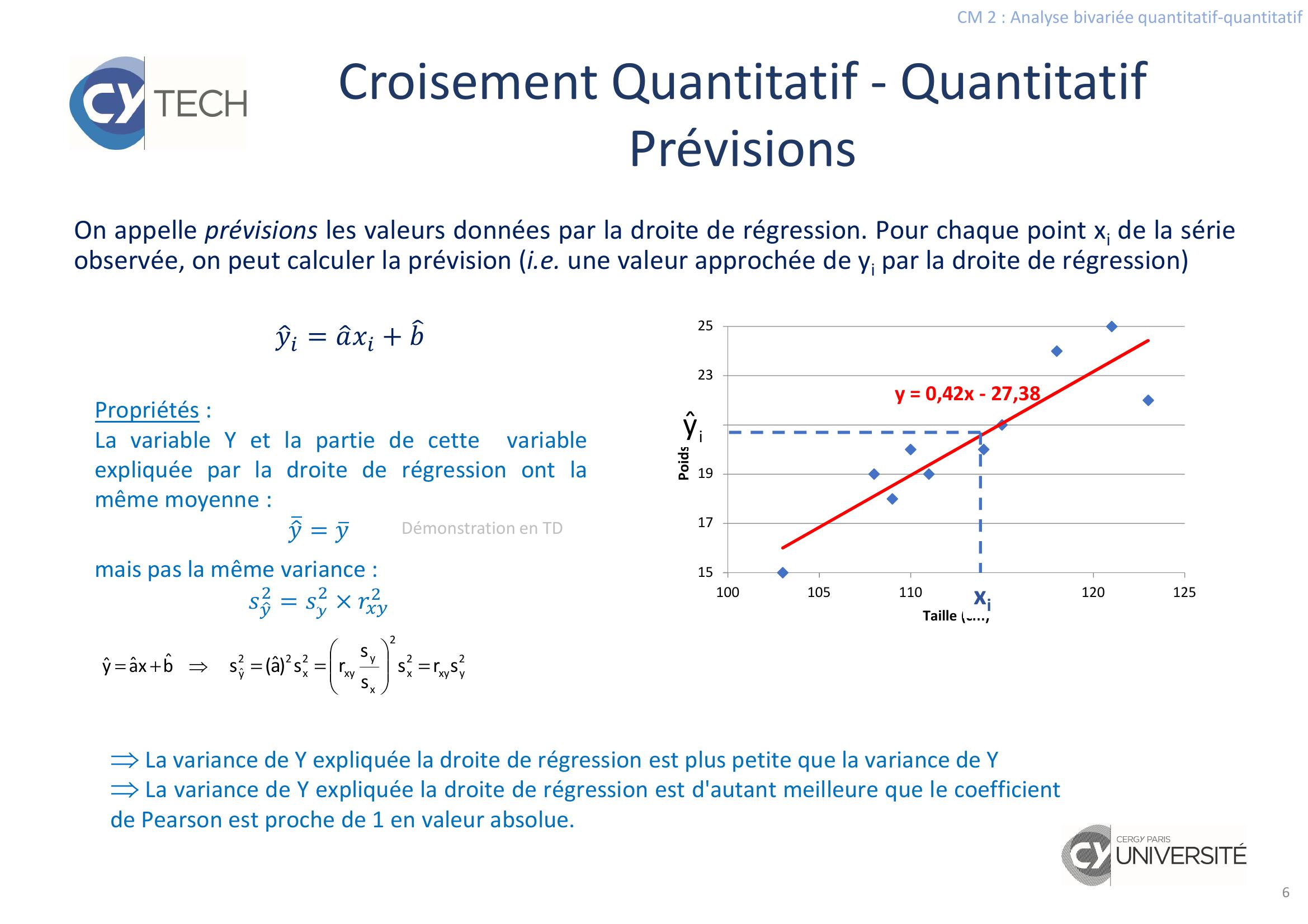
Page 3 : CM 2 : Analyse bivariée quantitatif-quantitatifCroisement Quantitatif - QuantitatifDroite de régression3On note xii=1,…,n la série observée pour X et yii=1,…,nla série observée pour Y.L’objectif est de trouver une fonction f telle queyi = fxi + εioù ε représente l’erreur.On se restreint aux fonctions affines : fx = ax + bEt on cherche les coefficients a et b quiminimisent l’erreur quadratique moyenne , = 1 = + ²εiN.B. L’erreur quadratique moyenne est aussi appelée fonction de coût en machine learning et peut prendre d’autres formes.
Page 4 : CM 2 : Analyse bivariée quantitatif-quantitatif4Par minimisation de l’erreur quadratique moyenne, on obtient les coefficients : =et = ̅où !" = ̅ est la covariance entre X et Y. = + est appelée droite de régression de Y en X. Elle traduit les variations de Y qui peuventêtre expliquées par X. Attention la droite de régression de X en Y n'est nécessairement la mêmeque celle de Y en XExemple : Etude du lien entre l'âge et le poids chez les enfants de 6 ans̅!" !"113,2020,3038,628,4616,27L’équation de la droite de Y en X : y=0,42 x – 27,38 L’équation de la droite de X en Y : y=1,92 x – 74,15Le « chapeau » au dessus de a et b signifie que la valeur obtenue est une estimation sur un échantillonCroisement Quantitatif - QuantitatifCoefficients de la droite de régressionOn résout le système :EQa,b=0 et &EQa,b=0 La covariance empirique garde les mêmes propriétés que la covariance théorique
Page 5 : CM 2 : Analyse bivariée quantitatif-quantitatif5Croisement Quantitatif - QuantitatifCovariance et coefficient de corrélation•r est proche de 1 alors X et Y sont très liés entre eux par une droite affine.•r 0 : globalement X et Y varient en sens inverse .•r 0 : globalement X et Y varient dans le même sens .•r 0 : on ne peut rien dire sur un lien éventuel entre X et Y.La covariance est un indicateur numérique du lien entre X et Y : plus il est éloigné de 0, plus lesvariables sont liées.L’inconvénient est qu’il n’est par normé. Pour pallier ce problème, on définit le coefficient decorrélation linéaire coefficient de Pearson à valeurs dans -1,1'!" = .On a alors = = '!" .Le coefficient de corrélation correspond à la covariance des séries centrées et réduites Exemple : Etude du lien entre l'âge et le poids chez les enfants de 6 ansOn trouverxy=0,90•rxy 1 L’équation de droite est donc pleinement justifiée •rxy 0 plus la taille est grande et plus le poids est important et vice-versaLe coefficient directeur de la droite est proportionnel à la covariance!!! Cela ne signifie pas qu’il n’y a pas de lien entre X et Y
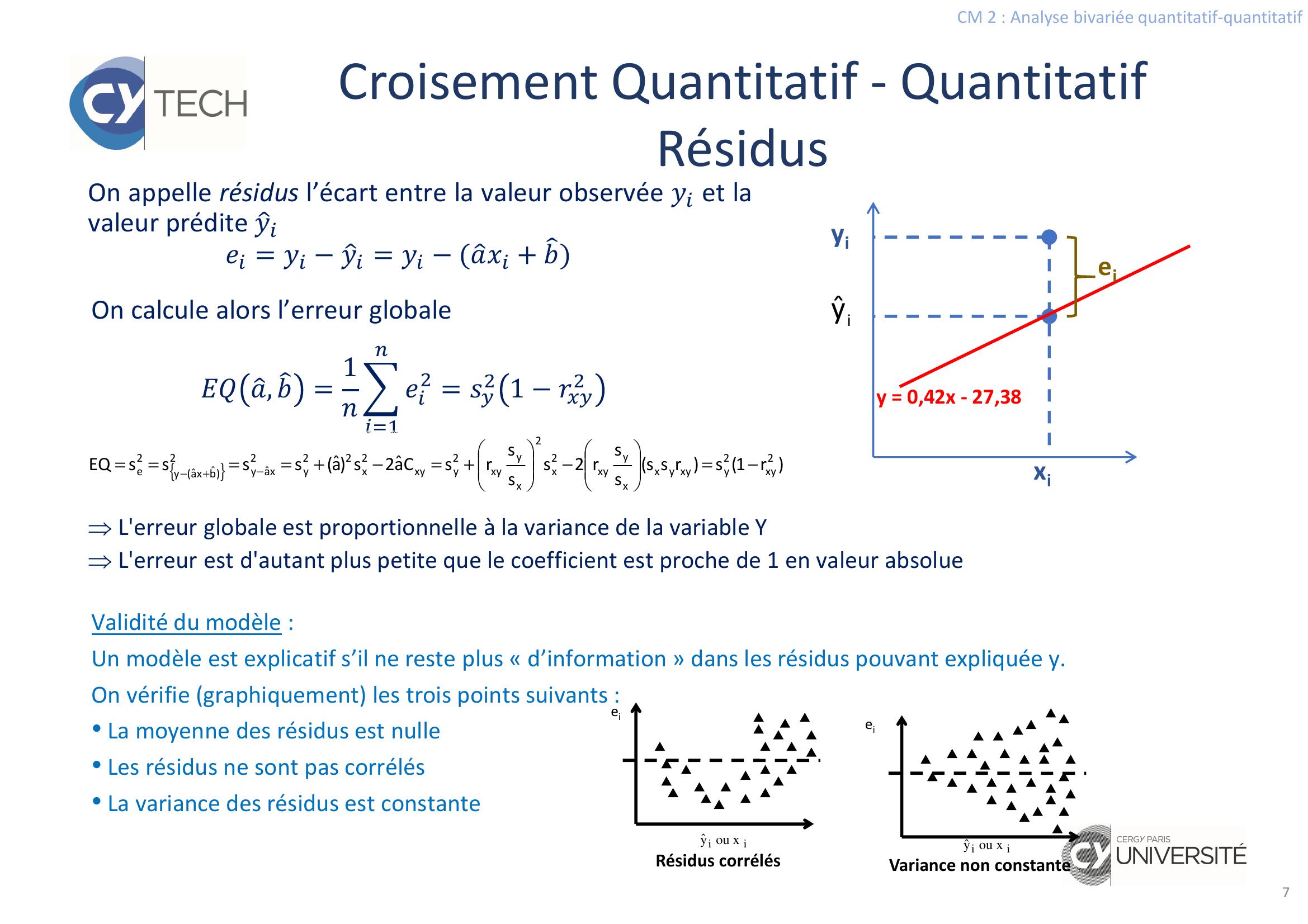
Page 6 : CM 2 : Analyse bivariée quantitatif-quantitatif6On appelle prévisions les valeurs données par la droite de régression. Pour chaque point xi de la sérieobservée, on peut calculer la prévision i.e. une valeur approchée de yi par la droite de régression = + Propriétés :La variable Y et la partie de cettevariableexpliquée par la droite de régression ont lamême moyenne : = mais pas la même variance :" = " × '!"La variance de Y expliquée la droite de régression est plus petite que la variance de YLa variance de Y expliquée la droite de régression est d'autant meilleure que le coefficientde Pearson est proche de 1 en valeur absolue.+=bˆxaˆyˆ2yxy2x2xyxy2x22yˆsrsssrsaˆs===y = 0,42x - 27,38151719212325100105110115120125Poids kgTaille cmxiiyˆDémonstration en TDCroisement Quantitatif - QuantitatifPrévisions
Page 7 : CM 2 : Analyse bivariée quantitatif-quantitatif7Croisement Quantitatif - QuantitatifRésidusL'erreur globale est proportionnelle à la variance de la variable YL'erreur est d'autant plus petite que le coefficient est proche de 1 en valeur absolueOn calcule alors l’erreur globale , = 1 = " 1 '!"On appelle résidus l’écart entre la valeur observée et lavaleur prédite = = + Validité du modèle :Un modèle est explicatif s’il ne reste plus « d’information » dans les résidus pouvant expliquée y.On vérifie graphiquement les trois points suivants :• La moyenne des résidus est nulle• Les résidus ne sont pas corrélés• La variance des résidus est constantexiiyˆyieiy = 0,42x - 27,38ii ou x yˆeiVariance non constanteii ou x yˆRésidus corréléseir1srssssr2sssrsCaˆ2saˆssssEQ2xy2yxyyxxyxy2x2xyxy2yxy2x22y2xaˆy2bˆxaˆy2e=+=+====+
Page 8 : CM 2 : Analyse bivariée quantitatif-quantitatif8Croisement Quantitatif - QuantitatifDécomposition de la variancerésiduelle varianceexpliquéevariancetotalevariance2e2yˆ2ysss+=Nous avons vu que la variance de la variable Y n’est pas égale à la variance des valeurs prédites.Cependant elle peut se décomposer comme suit :En divisant cette égalité par la variance totale, on obtient le pourcentage de variance de yexpliquée par le modèle, ce qu’on appelle encore le coefficient de détermination,+ ="" = '!" 0,1Dans l’exemple précédent, on a la décomposition de la variance suivante :VariancesRégression6,17Résidus1,44Total7,61D’où R²=6,17/7,61=0,81. Cela signifieque 81 de la variation des poidsobservés est expliquée par la droite derégression : poids = 0,42×taile - 27,38Démonstration en TD
Page 9 : CM 2 : Analyse bivariée quantitatif-quantitatif9Croisement Quantitatif - QuantitatifOutliers9Un modèle peut s’avérer très précis pour ajuster les valeurs observées mais très mauvais en ce qui concerne la prévision de nouvelles valeurs.Détection des observations influentes atypiques/outliers• On retire la ième observation de l’ensemble des données• On ajuste un nouveau modèle sans la ième donnée• On calcule y-i la prévision de yi avec le nouveau modèle• On calcule le résidus , e-i=yi-y-iOn a oùObservation est influente si une faible variation entraine une modification importante des caractéristiques du modèle.iii-ih-1ee=====n1iii2in1i2ih-1en1en1PRESS2Le PRESS predicted residual sum of squares donne une indication sur les qualités prédictives du modèleSous l’hypothèse de normalité des résidus, les résidus standardisés,doivent être compris IDC entre ±2iiiih1eσ=δˆ2x2iiisxx1n1n1h+=Un résidus important signale une observation influenteUn levier1/nhii1proche de 1 indique une observation influente
Page 10 : CM 2 : Analyse bivariée quantitatif-quantitatif10Croisement Quantitatif - Quantitatiftransformation•Les droites de régression n'explique que les liaisons linéaires.•Si X et Y sont liées par une relation de la forme Y=aX² alors rXY=0Le coefficient de corrélation linéaire de Pearson ne peut pas détecter cette liaison.•Il n'existe pas de mesure universelle pour détecter des relations quelconques •On essaie par des transformations de se ramener à une droite affineFamilleFonctionsTransformationForme affineexponentielle puissance inverselogistiquebxeay.=log'yy =xbay.log'+=baxy =log' log'xxyy=='.log'xbay+=xbay+=xx1'='.'xbay+=.11bxaey++==yyy1log'bxay+= .'