CM2 Relations Binaires
Télécharger le CM2 Relations Binaires en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Page 1 : IntroductionLogique et RaisonnementEnsembleRelations BinairesAlgebre-Premier semestre 20211Introduction2Logique et Raisonnement3Ensemble4Relations BinairesN. Arancibia - relu par D. CransacAlgebre
Page 2 : IntroductionLogique et RaisonnementEnsembleRelations BinairesAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre
Page 3 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesDefinitionSoient E et F deux ensembles. On appelle relation R de E sur F la donneed’une partieR E × F.La partie R est appele le graphe de la relation R.On dit qu’un element x E est en relation avec un element y F six, y R.On exprime cette situation en ecrivant xRy. C’est-a-direxRy ⇐⇒x, y R.Finalement, si E = F la relation R est appelee relation binaire.N. Arancibia - relu par D. CransacAlgebre
Page 4 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesExemple :La relation d’inclusion dans l’ensemble des parties de EARB ⇐⇒A B.Ici doncR = A, B PE × PE : A B.Sur tout ensemble E, on peut definir la relation egalitexRy ⇐⇒x = y.Ici doncR = a, b E × E : a = b.Les relations et sur R, sont aussi des relations binaires.N. Arancibia - relu par D. CransacAlgebre
Page 5 : IntroductionLogique et RaisonnementEnsembleRelations BinairesLa relation de divisibilite sur les entiers relatifsmRn ⇐⇒mnm divise n.Ici doncR = m, n Z × Z : mn Z.Cas particulier : si A = 1; 2; 3; 4 et m, n A × A : mn Z.mn12341RRRR2RR3R4RRemarque : Parce que le couple x, y n’est pas egal au couple y, x, larelation xRy peut ˆetre vraie sans que la relation yRx le soit.N. Arancibia - relu par D. CransacAlgebre
Page 6 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesN. Arancibia - relu par D. CransacAlgebre
Page 7 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesEtudions certaines proprietes eventuelles des relations binaires.DefinitionSoit R une relation binaire sur E.On dit que R est reflexive si :x E,xRxOn dit que R est transitive si :x E, y E, z E,xRyetyRz =⇒xRzExamples :sur R est reflexive mais sur R n’est pas reflexive.̸= sur R n’est pas reflexive, n’est pas transitive.N. Arancibia - relu par D. CransacAlgebre
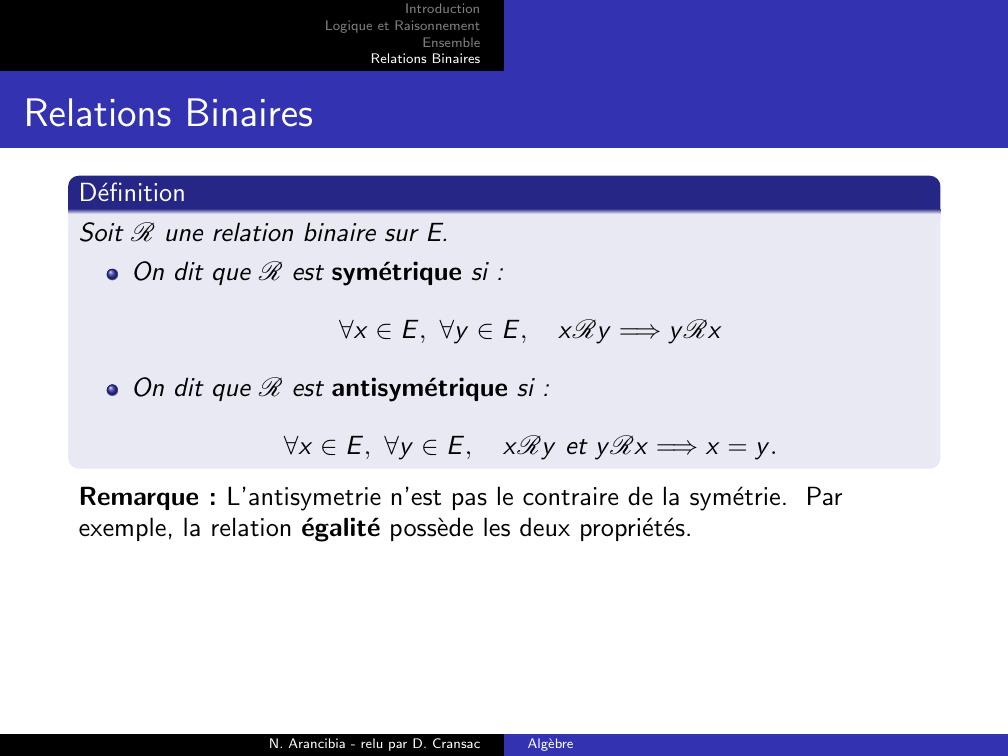
Page 8 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesDefinitionSoit R une relation binaire sur E.On dit que R est symetrique si :x E, y E,xRy =⇒yRxOn dit que R est antisymetrique si :x E, y E,xRy et yRx =⇒x = y.Remarque : L’antisymetrie n’est pas le contraire de la symetrie. Parexemple, la relation egalite possede les deux proprietes.N. Arancibia - relu par D. CransacAlgebre
Page 9 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesExemple :La relation d’egalite ” = ” sur E est reflexive, transitive, symetrique etantisymetrique.La relation d’inclusion sur PE est reflexive, transitive etantisymetrique.La relation sur R est reflexive, transitive et antisymetrique. Elle n’estpas symetrique car par exemple : 2 5 mais : 5 2.La relation sur R est transitive et antisymetrique, mais elle n’est nireflexive, ni symetrique.La relation de divisibilite sur Z est reflexive et transitive, mais elle n’estni symetrique, ni antisymetrique car par exemple : 5 5 et 55 mais5 ̸= 5.Nous allons etudier deux importants types des relations binaires : Lesrelations d’equivalence et les relations d’ordre.Commen¸cons par etudier les relations d’equivalence.N. Arancibia - relu par D. CransacAlgebre
Page 10 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’equivalenceDefinitionOn dit qu’une relation binaire R sur E est une relation d’equivalence siR est a la fois reflexive, transitive et symetrique.Pour a E, l’ensemble des elements x E en relation avec a est appelela classe d’equivalence de a, noteeclaouaoua.C’est-a-direcla = x E : aRx.Exemple : Soit n un entier naturel. La relation sur Z definie paraRb⇐⇒n divise a best une relation d’equivalence.Si aRb on dit que a et b sont congrus modulo n.N. Arancibia - relu par D. CransacAlgebre
Page 11 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’equivalenceProposition Partition d’un ensemble en classes d’equivalenceSoit R une relation d’equivalence sur un ensemble E. Alors les classesd’equivalences forment une partition de E, c’est-a-dire quetoute classe d’equivalence est non vide :x E,clx ̸= ,deux classes d’equivalence sont soit disjointes soit egales :x, y Etel queclx ̸= clyon aclx cly = ,la reunion des classes d’equivalence est egale a E :E =xEclx.N. Arancibia - relu par D. CransacAlgebre
Page 12 : IntroductionLogique et RaisonnementEnsembleRelations BinairesE =xEclx ?L’inclusion SxE clx E est evidente ;Soit x E alors x clx donc x SxE clxx E, clx ̸= ?On a x clx donc clx ̸= x, y E 2, clx ̸= cly =⇒clx cly = ?On montre la contraposee :Supposons clx cly ̸= .On choisit z clx cly il existe !.Alors zRx et zRy et par transitivite, xRy.Par transitivite encore, tous les elements de clx, en relation avec xsont donc en relation avec y donc appartiennent a cly. On endeduit clx cly.On raisonne de mˆeme pour montrer que cly clxOn conclut : clx = cly.N. Arancibia - relu par D. CransacAlgebre
Page 13 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordrePassons a etudier les relations d’ordre.DefinitionOn dit qu’une relation binaire R sur E est une relation d’ordre si R est a lafois reflexive, transitive et antisymetrique.Les relations d’ordre sont generalement notees ou ou .Soit une relation d’ordre sur E, on dit alors que E, est unensemble ordonne.Definition Ordre total ou ordre partielSoit une relation d’ordre sur E.Deux elements x et y de E sont dits comparables pour six youy x.Si deux elements quelconques sont toujours comparables, on dit que est une relation d’ordre total. E est dit totalement ordonne par .Sinon, on dit que est une relation d’ordre partiel. E est ditpartiellement ordonne par .N. Arancibia - relu par D. CransacAlgebre
Page 14 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreExemple :Sur N, Z, Q et R on a une relation d’ordre total, notee .Sur PE, la relationA B ⇐⇒A Bc’est une relation d’ordre partiel sauf si E = ou E = a. Eneffet, si a E, b E, a et b non comparables.Sur R2x, y x′, y ′ ⇐⇒x x′ety y ′est un ordre partiel. Par exemple 1, 2 et 4, 0 non comparables.N. Arancibia - relu par D. CransacAlgebre
Page 15 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreDefinition Relation stricte associee a une relation d’ordreSoit une relation d’ordre sur E. On definit alors une nouvelle relationsur E parx, y E,x y ⇐⇒x yetx ̸= y.La relation on l’appelle la relation stricte associee a .Exemple : Naturellement, la relation usuelle sur R est la relationstricte de la relation .Attention ! La relation stricte n’est pas une relation d’ordre car elle n’estpas reflexive :On ne peut avoir x y, y x et x = yN. Arancibia - relu par D. CransacAlgebre
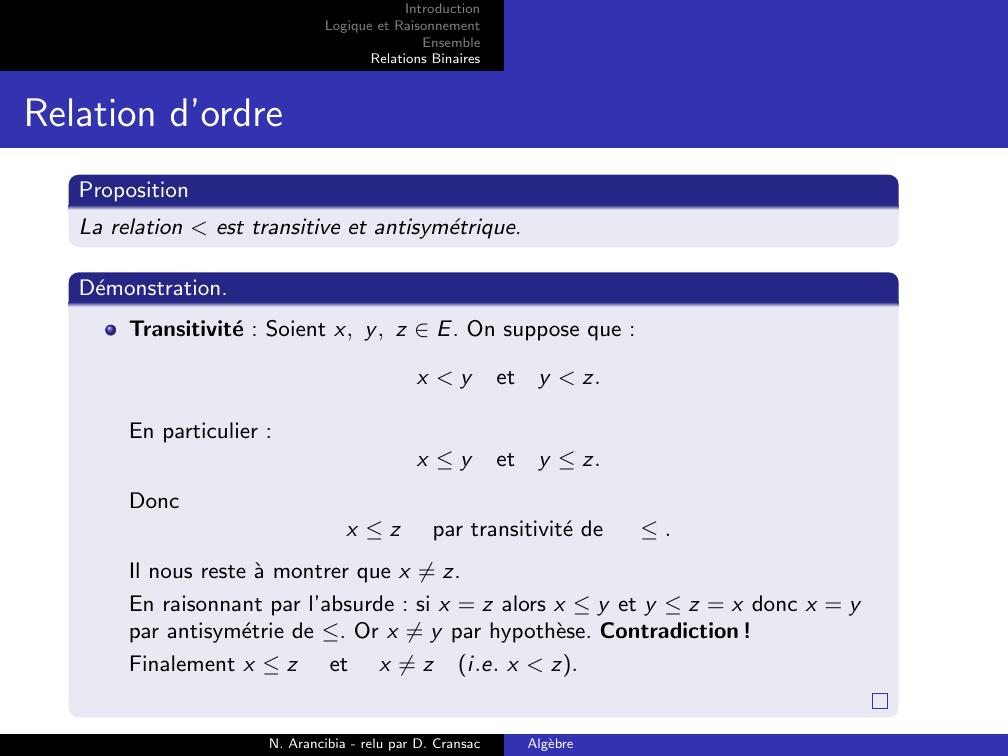
Page 16 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordrePropositionLa relation est transitive et antisymetrique.Demonstration.Transitivite : Soient x, y, z E. On suppose que :x yety z.En particulier :x yety z.Doncx zpar transitivite de.Il nous reste a montrer que x ̸= z.En raisonnant par l’absurde : si x = z alors x y et y z = x donc x = ypar antisymetrie de . Or x ̸= y par hypothese. Contradiction !Finalement x zetx ̸= zi.e. x z.N. Arancibia - relu par D. CransacAlgebre
Page 17 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelations BinairesDemonstration.Antisymetrie : Soient x, y E. On suppose que :x yety x.En particulier :x yety x.Donc x = y par antisymetrie de . Par consequent estantisymetrique.Remarque : L’antisymetrie de est peu utile car on a obtenu unecontradiction donc l’hypothese de depart est toujours fausse ! Car six y, x ̸= y et on conclut que x = y donc la condition de depart ne serealise jamais.N. Arancibia - relu par D. CransacAlgebre
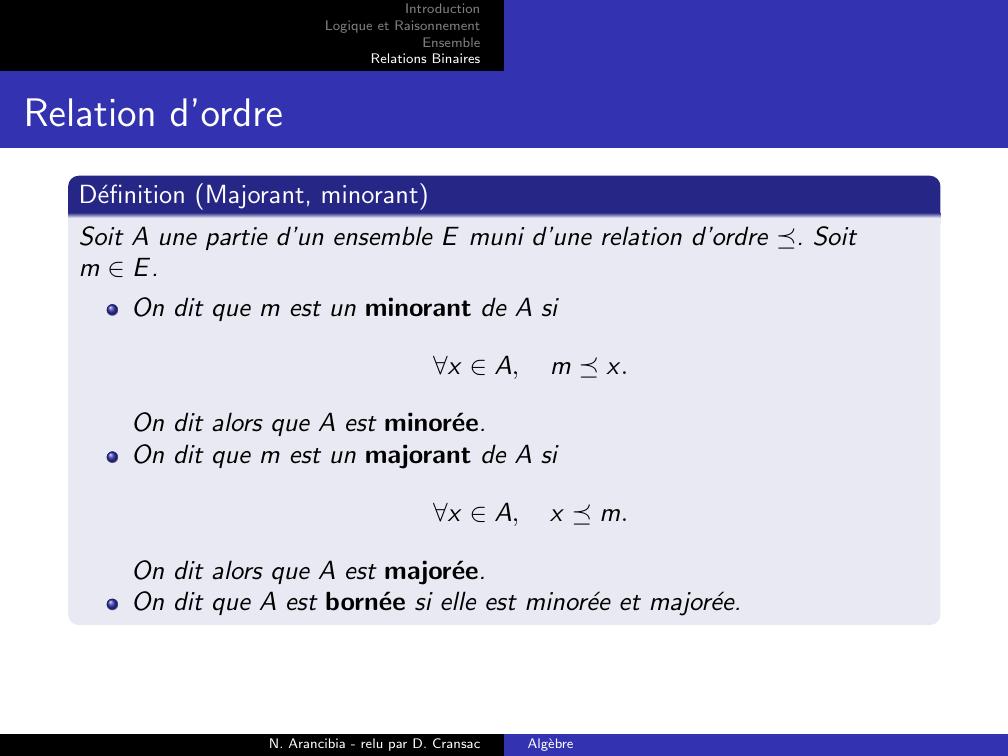
Page 18 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreDefinition Majorant, minorantSoit A une partie d’un ensemble E muni d’une relation d’ordre ⪯. Soitm E.On dit que m est un minorant de A six A,m ⪯x.On dit alors que A est minoree.On dit que m est un majorant de A six A,x ⪯m.On dit alors que A est majoree.On dit que A est bornee si elle est minoree et majoree.N. Arancibia - relu par D. CransacAlgebre
Page 19 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreExemple :L’ensemble 8, 10, 12 est minore par 2 et majore par 120 pour larelation de divisibilite sur N.PE est minore par et majore par E pour la relation d’inclusion .Tout reel inferieur ou egal a 0 est un minorant de l’intervalle 0, 1. Toutreel superieur ou egal a 1 est un majorant de l’intervalle 0, 1.N. Arancibia - relu par D. CransacAlgebre
Page 20 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreDefinition Plus petit element, plus grand elementSoit A une partie d’un ensemble E muni d’une relation d’ordre.On appelle plus petit element ou un minimum de A tout elementde A qui minore A. S’il en existe un, un tel plus petit element estunique et donc appele le plus petit element de A, note MinA.On appelle plus grands element ou un maximum de A toutelement de A qui majore A. S’il en existe un, un tel plus grandelement est unique et donc appele le plus grand element de A, noteMaxA.Exemple : On travaille dans cette serie d’exemples avec l’ordre usuel surR.0 est le plus petit element de R+ et le plus grand element de R.0, 1 ne possede ni plus petit element ni plus grand element.0 est le plus petit element de 0, 1, et 1 est le plus grand element de0, 1.N. Arancibia - relu par D. CransacAlgebre
Page 21 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreExemple : On travaille dans cette serie d’exemples avec la relation dedivisibilite sur N.L’ensemble 2, 3, 6 possede un plus grand element, c’est 6, maispas de plus petit element.0 est le plus grand element de N et 1 est son plus petit element.L’ensemble N \ 0, 1 ne possede ni plus petit element ni plus grandelement.N. Arancibia - relu par D. CransacAlgebre
Page 22 : IntroductionLogique et RaisonnementEnsembleRelations BinairesDefinitionSoit A une partie de un ensemble E muni d’une relation d’ordre.Si l’ensemble des minorants de A admet un plus grand element, onl’appelle borne inferieure de A et on le note InfA.Si l’ensemble des majorants de A admet un plus petit element, onl’appelle borne superieure de A et on le note SupA.Remarque : La difference essentielle entre les plus grands elements et lesbornes superieures d’une partie A, c’est que les bornes superieuresn’appartiennent pas forcement a A.Exemple :Avec l’ordre usuel sur R, 0 est le Inf de 0, 1, et 1 est le Supde 0, 1.N. Arancibia - relu par D. CransacAlgebre
Page 23 : IntroductionLogique et RaisonnementEnsembleRelations BinairesRelation d’ordreTheoreme Lien entre les plus grands/petits elements et les bornessuperieures/inferieuresSoient une relation d’ordre et A une partie de E. Si A possede un plusgrand resp. petit element pour , alors A possede une borne superieureresp. inferieure pour etMaxA = SupAresp. InfA = MinAExemple :Avec l’ordre usuel sur R on a :Inf0, 1 = Min0, 1 = 0et Sup0, 1 = Max0, 1 = 1.N. Arancibia - relu par D. CransacAlgebre
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23