CM2 Representation des nombres part1
Télécharger le CM2 Representation des nombres part1 en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Page 1 : INFORMATIQUE 1I I . R E P R E S E N TAT I O N D E S N O M B R E SEva Ansermin & Romuald Grignon v1.1
Page 2 : Représentation des donnéesUn ordinateur peut traiter/produire plusieurs types de données :textes, chiffresimagessons...Toutes ces informations sont stockées et traitées sous forme binaire : avec des 0 et des 1.Cette unité d’information 0 0u 1 est le binary digit le bit.Ce type de données est plus facile à gérer au niveau électronique : 0 correspond à un circuitouvert, 1 à un circuit fermé.0 : le courant ne passe pas1 : le courant passeEva ANSERMIN & Romuald GRIGNON2
Page 3 : Représentation des donnéesUn ordinateur peut traiter/produire plusieurs types de données :textes, chiffresimagessons...Toutes ces informations sont stockées et traitées sous forme binaire : avec des 0 et des 1.Cette unité d’information 0 ou 1 est le binary digit le bit.Comment sont représentés les nombres en binaire ?Eva ANSERMIN & Romuald GRIGNON3
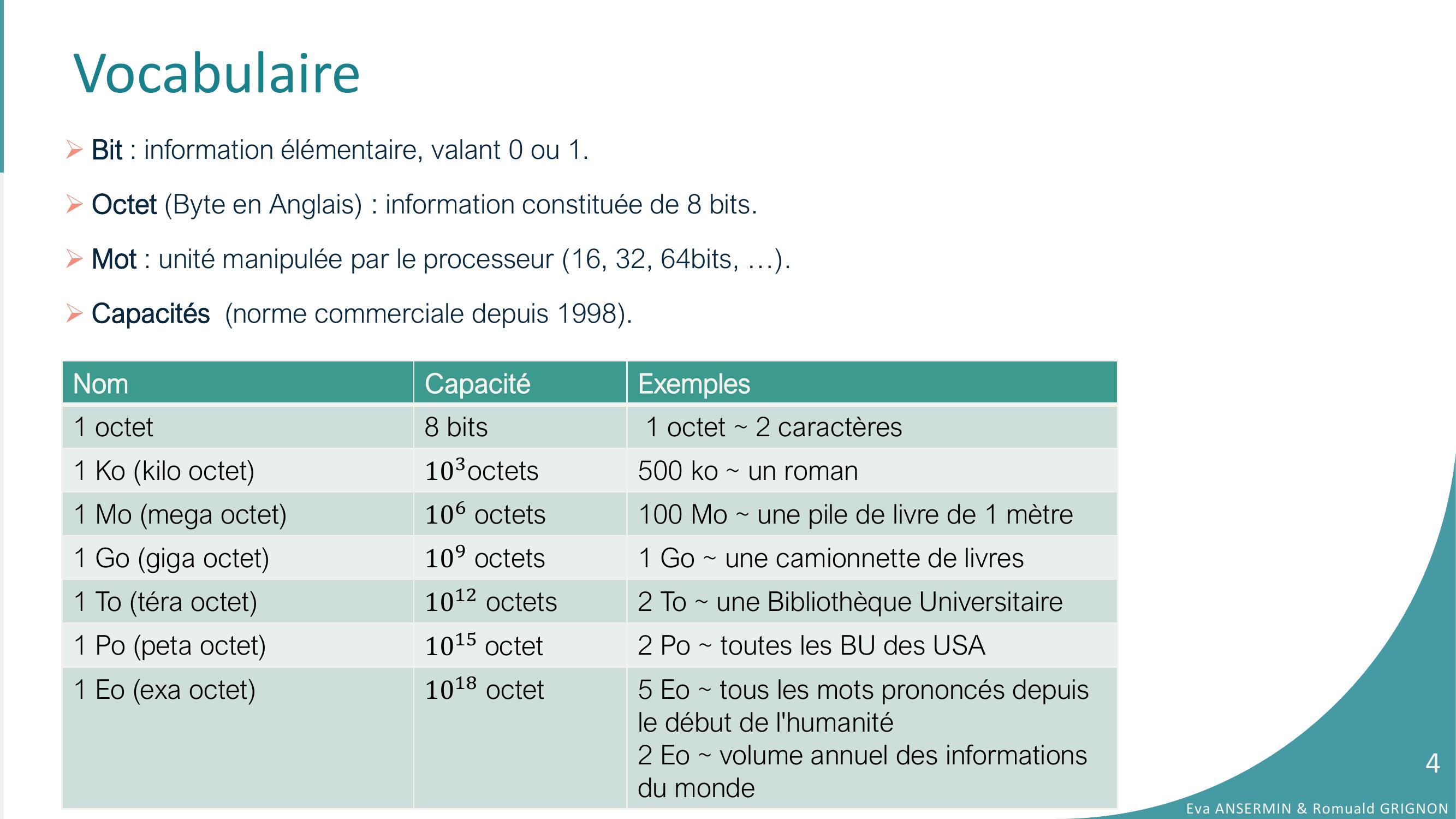
Page 4 : VocabulaireBit : information élémentaire, valant 0 ou 1.Octet Byte en Anglais : information constituée de 8 bits.Mot : unité manipulée par le processeur 16, 32, 64bits, ….Capacités norme commerciale depuis 1998.NomCapacitéExemples1 octet8 bits1 octet 2 caractères1 Ko kilo octet103octets500 ko un roman 1 Mo mega octet106 octets100 Mo une pile de livre de 1 mètre1 Go giga octet109 octets1 Go une camionnette de livres1 To téra octet1012 octets2 To une Bibliothèque Universitaire 1 Po peta octet1015 octet 2 Po toutes les BU des USA1 Eo exa octet1018 octet5 Eo tous les mots prononcés depuis le début de l'humanité 2 Eo volume annuel des informations du monde Eva ANSERMIN & Romuald GRIGNON4
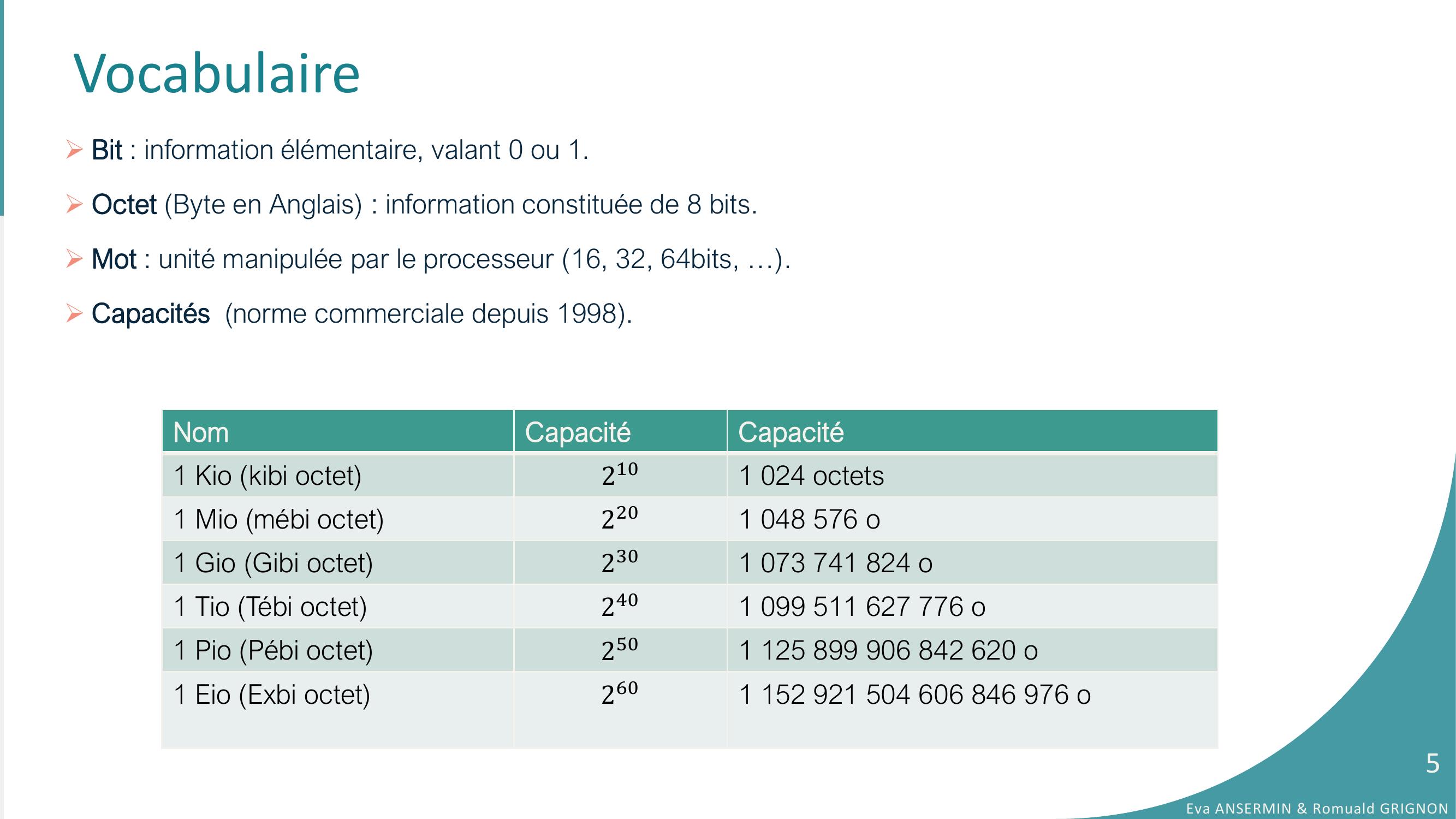
Page 5 : VocabulaireNomCapacitéCapacité1 Kio kibi octet2101 024 octets1 Mio mébi octet2201 048 576 o1 Gio Gibi octet2301 073 741 824 o1 Tio Tébi octet2401 099 511 627 776 o1 Pio Pébi octet2501 125 899 906 842 620 o1 Eio Exbi octet2601 152 921 504 606 846 976 oEva ANSERMIN & Romuald GRIGNON5Bit : information élémentaire, valant 0 ou 1.Octet Byte en Anglais : information constituée de 8 bits.Mot : unité manipulée par le processeur 16, 32, 64bits, ….Capacités norme commerciale depuis 1998.
Page 6 : Les basesNous comptons en base 10 base décimale : Les chiffres vont de 0 à 9.Exemple de décomposition d’un nombre : 542 = 5 100 + 4 10 + 2 1 = 5 10 2 + 4 101 + 2 1Soit N un entier dont les chiffres sont 𝑎𝑛, 𝑎𝑛1, 𝑎𝑛2, … , 𝑎0 en base décimale:𝑁= 𝑎𝑛10𝑛+ 𝑎𝑛1 10𝑛1 + … + 𝑎0 100𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖Eva ANSERMIN & Romuald GRIGNON6
Page 7 : Les basesNous comptons en base 10 base décimale : Les chiffres vont de 0 à 9.Exemple de décomposition d’un nombre : 542 = 5 100 + 4 10 + 2 1 = 5 10 2 + 4 101 + 2 1Soit N un entier dont les chiffres sont 𝑎𝑛, 𝑎𝑛1, 𝑎𝑛2, … , 𝑎0 en base décimale:𝑁= 𝑎𝑛10𝑛+ 𝑎𝑛1 10𝑛1 + … + 𝑎0 100𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖On parle de poids fort pour le chiffre le plus à gauche plus haute puissance et de poids faible pour celui le plus à droite puissance la plus faiblei est le poids du chiffre.Eva ANSERMIN & Romuald GRIGNON7
Page 8 : Les basesNous utilisons plusieurs bases dans notre vie quotidienne:Eva ANSERMIN & Romuald GRIGNON8
Page 9 : Les basesEn base décimale : chiffre allant de 0 à 9 et 𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖En base binaire ou base 2 :Les chiffres sont :Eva ANSERMIN & Romuald GRIGNON9
Page 10 : Les basesEn base décimale : chiffre allant de 0 à 9 et 𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖En base binaire ou base 2 :Les chiffres sont : 0,1Eva ANSERMIN & Romuald GRIGNON10
Page 11 : Les basesEn base décimale : chiffre allant de 0 à 9 et 𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖En base binaire ou base 2 :Les chiffres sont : 0,1On multiplie les chiffres par des puissances de 2 :Soit N un entier dont les chiffres sont 𝑝𝑛, 𝑝𝑛1, 𝑝𝑛2, … , 𝑝0 en base binaire :𝑁= 𝑖=0𝑛𝑝𝑖2𝑖𝑁= 𝑝𝑛2𝑛+ 𝑝𝑛1 2𝑛1 + … +𝑝0 20Eva ANSERMIN & Romuald GRIGNON11
Page 12 : Les basesEn base décimale : chiffre allant de 0 à 9 et 𝑁= σ𝑖=0𝑛𝑎𝑖10𝑖En base binaire ou base 2 :Les chiffres sont : 0,1On multiplie les chiffres par des puissances de 2 :Soit N un entier dont les chiffres sont 𝑝𝑛, 𝑝𝑛1, 𝑝𝑛2, … , 𝑝0 en base binaire :Exemple : 0112 = 0 22 + 1 21 + 1 20 = 0 + 2 + 1 = 3𝑁= 𝑖=0𝑛𝑝𝑖2𝑖𝑁= 𝑝𝑛2𝑛+ 𝑝𝑛1 2𝑛1 + … +𝑝0 20Eva ANSERMIN & Romuald GRIGNON12
Page 13 : Binaire - décimalIl suffit d’ajouter les puissances de deux des chiffres dont le bit est à 1.Il faut donc connaître les puissances de deux !Exemple : 1001002 →25 + 22 = 32 + 4 = 36000011Eva ANSERMIN & Romuald GRIGNON13
Page 14 : Décimal - binaire1ère méthode : la division Euclidienne. On utilise les restes successifs de la division entière par 2.173 / 2 = 86 reste 186 / 2 = 43 reste 043 / 2 = 21 reste 121 / 2 = 10 reste 110 / 2 = 5 reste 05 / 2 = 2 reste 12 / 2 = 1 reste 01 / 2 = 0 reste 1 Arrêt lorsque le quotient est nulEva ANSERMIN & Romuald GRIGNON14
Page 15 : Décimal - binaire1ère méthode : la division Euclidienne. On utilise les restes successifs de la division entière par 2.173 / 2 = 86 reste 186 / 2 = 43 reste 043 / 2 = 21 reste 121 / 2 = 10 reste 110 / 2 = 5 reste 05 / 2 = 2 reste 12 / 2 = 1 reste 01 / 2 = 0 reste 1 Arrêt lorsque le quotient est nulEva ANSERMIN & Romuald GRIGNON1517310 = 101011012
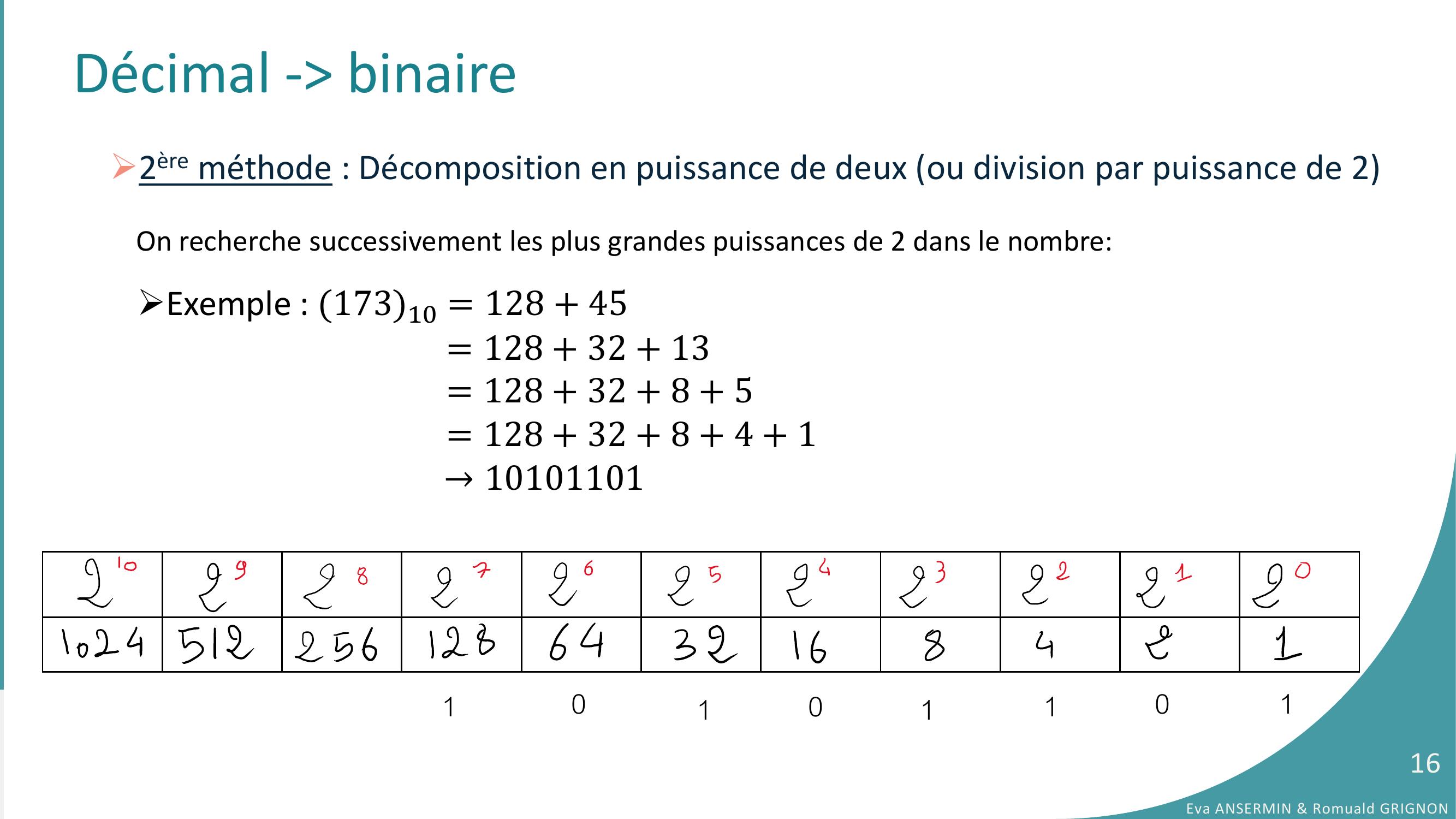
Page 16 : On recherche successivement les plus grandes puissances de 2 dans le nombre:Décimal - binaire2ère méthode : Décomposition en puissance de deux ou division par puissance de 2Exemple : 17310 = 128 + 45= 128 + 32 + 13= 128 + 32 + 8 + 5= 128 + 32 + 8 + 4 + 1→1010110111111000Eva ANSERMIN & Romuald GRIGNON16
Page 17 : Opération en binaireLes règles de posage des opérations classiques restent les mêmes en binaire : opérations chiffre par chiffre avec les règles de retenue.Exemple : l’addition 1110 0011+0110 01101 0100 10011111Eva ANSERMIN & Romuald GRIGNON17
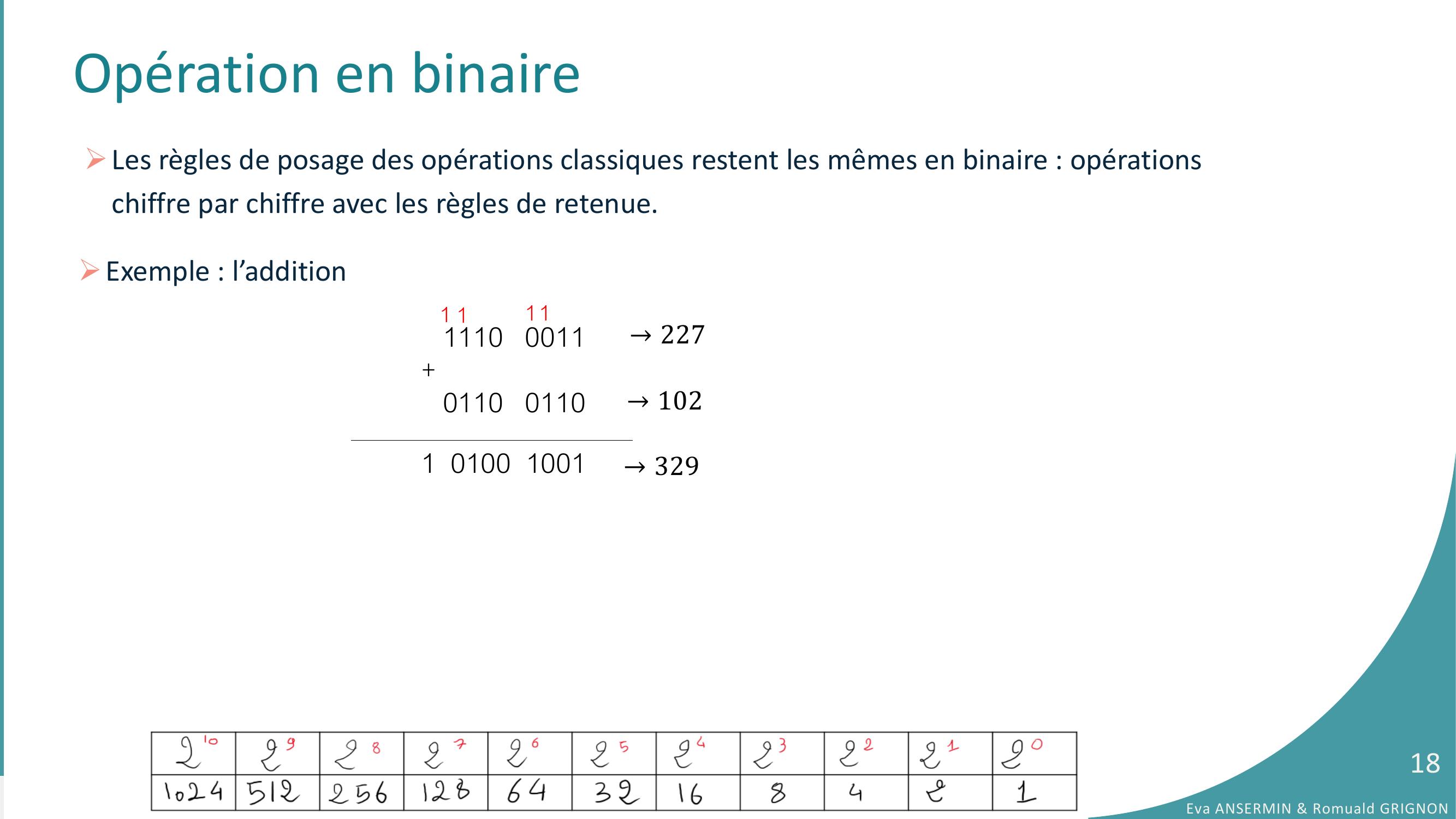
Page 18 : Opération en binaireLes règles de posage des opérations classiques restent les mêmes en binaire : opérations chiffre par chiffre avec les règles de retenue.Exemple : l’addition 1110 0011+0110 01101 0100 10011111→227→102→329Eva ANSERMIN & Romuald GRIGNON18
Page 19 : Conclusion • Toutes les données d’un ordinateur sont stockées et gérées sous forme binaire qui représente la présence ou l’absence de courant. • En binaire, les chiffres d’un nombre sont multipliés par des puissances de 2 puissances de 10 en base décimale• Nous avons vu comment représenter un entier en nombre binaire mais est-ce suffisant?• Dans le prochain cours nous verront comment représenter d’autres nombres ainsi que d’autres types de données. Eva ANSERMIN & Romuald GRIGNON19