CM3 Arbres
Télécharger le CM3 Arbres en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152
Page 1 : INFORMATIQUE 3I I I . A R B R E SEva ANSERMIN & Renaud VERIN & Romuald GRIGNONv1.1
Page 2 : Rappel: les listes chaînées• Les chaînons de la liste pointent sur le chaînon suivant. • Contrairement aux tableaux statiques, la taille des listes chaînées n’est pas limitée.Structure Chainon :elmt : Elementsuivant : pointeur sur structure ChainonE.ANSERMIN R.VERIN R.GRIGNON2
Page 3 : Et si on rajoutais une dimension ? typedef struct chainonint elmt;struct chainonsuivant1;struct chainonsuivant2;struct chainonsuivant3; Chainon;elmtsuivant1suivant2suivant3• Le principe des listes chaînées est utilisé pour de nombreux autres concepts!• Exemple : une Chainon avec plusieurs « suivant »…E.ANSERMIN R.VERIN R.GRIGNON3
Page 4 : Et si on rajoutais une dimension ? • Le principe des listes chaînées est utilisé pour de nombreux autres concepts!• Exemple : une Chainon avec plusieurs « suivant »… permet de construire un arbre !……E.ANSERMIN R.VERIN R.GRIGNON4
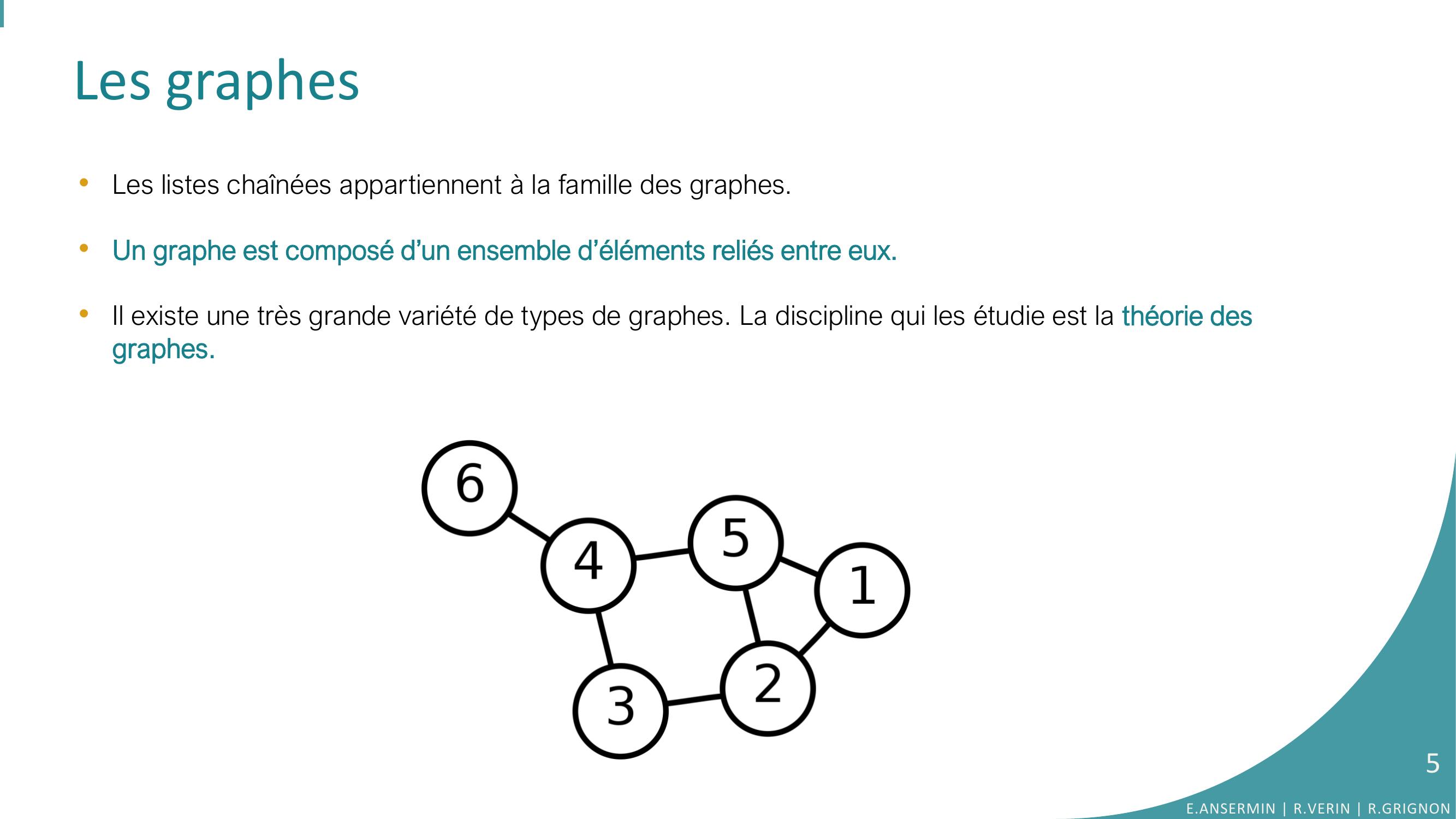
Page 5 : Les graphes •Les listes chaînées appartiennent à la famille des graphes. •Un graphe est composé d’un ensemble d’éléments reliés entre eux.•Il existe une très grande variété de types de graphes. La discipline qui les étudie est la théorie des graphes. E.ANSERMIN R.VERIN R.GRIGNON5
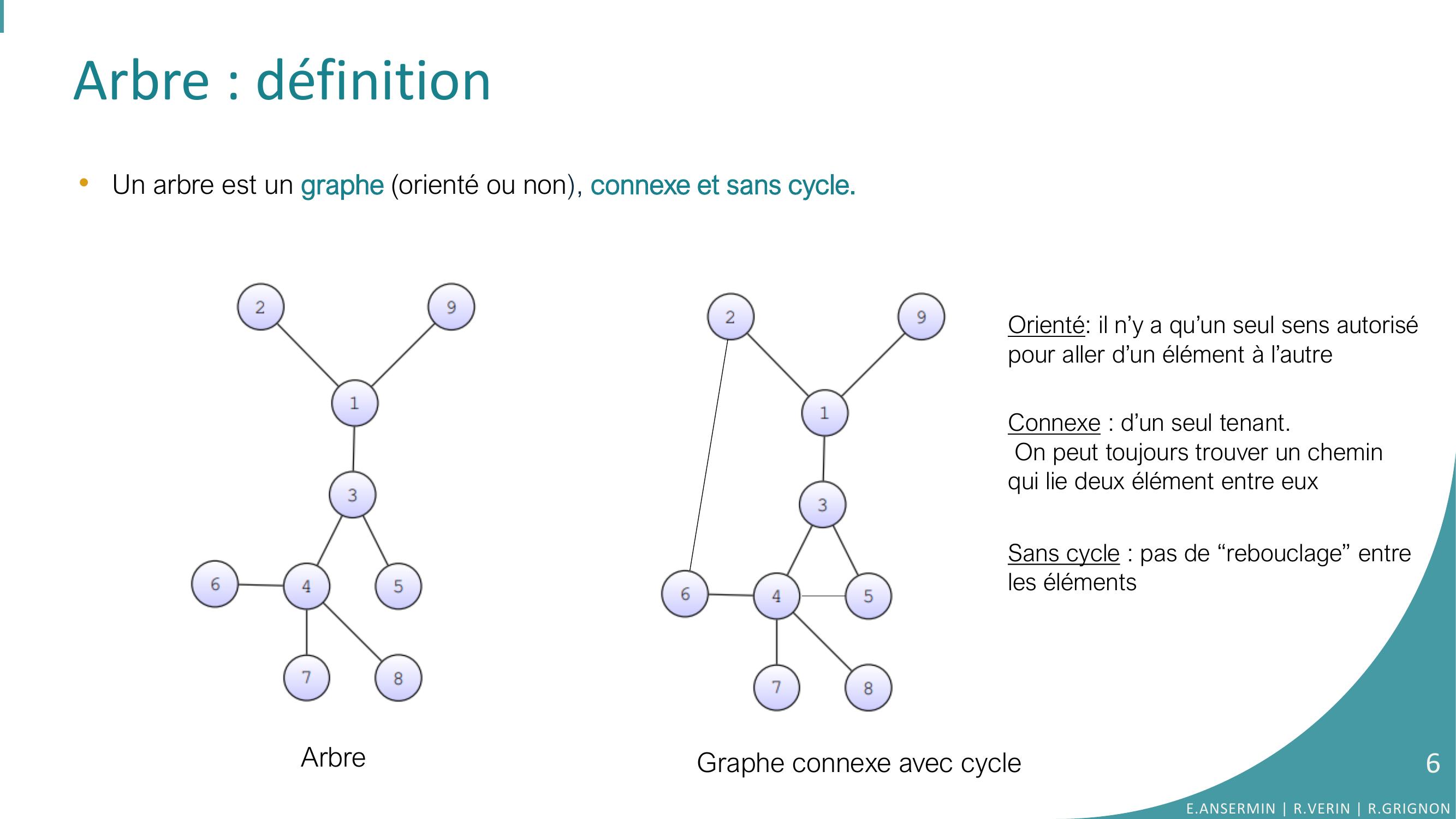
Page 6 : Arbre : définition •Un arbre est un graphe orienté ou non, connexe et sans cycle. ArbreConnexe : d’un seul tenant.On peut toujours trouver un cheminqui lie deux élément entre euxSans cycle : pas de “rebouclage” entre les élémentsGraphe connexe avec cycle Orienté: il n’y a qu’un seul sens autorisépour aller d’un élément à l’autreE.ANSERMIN R.VERIN R.GRIGNON6
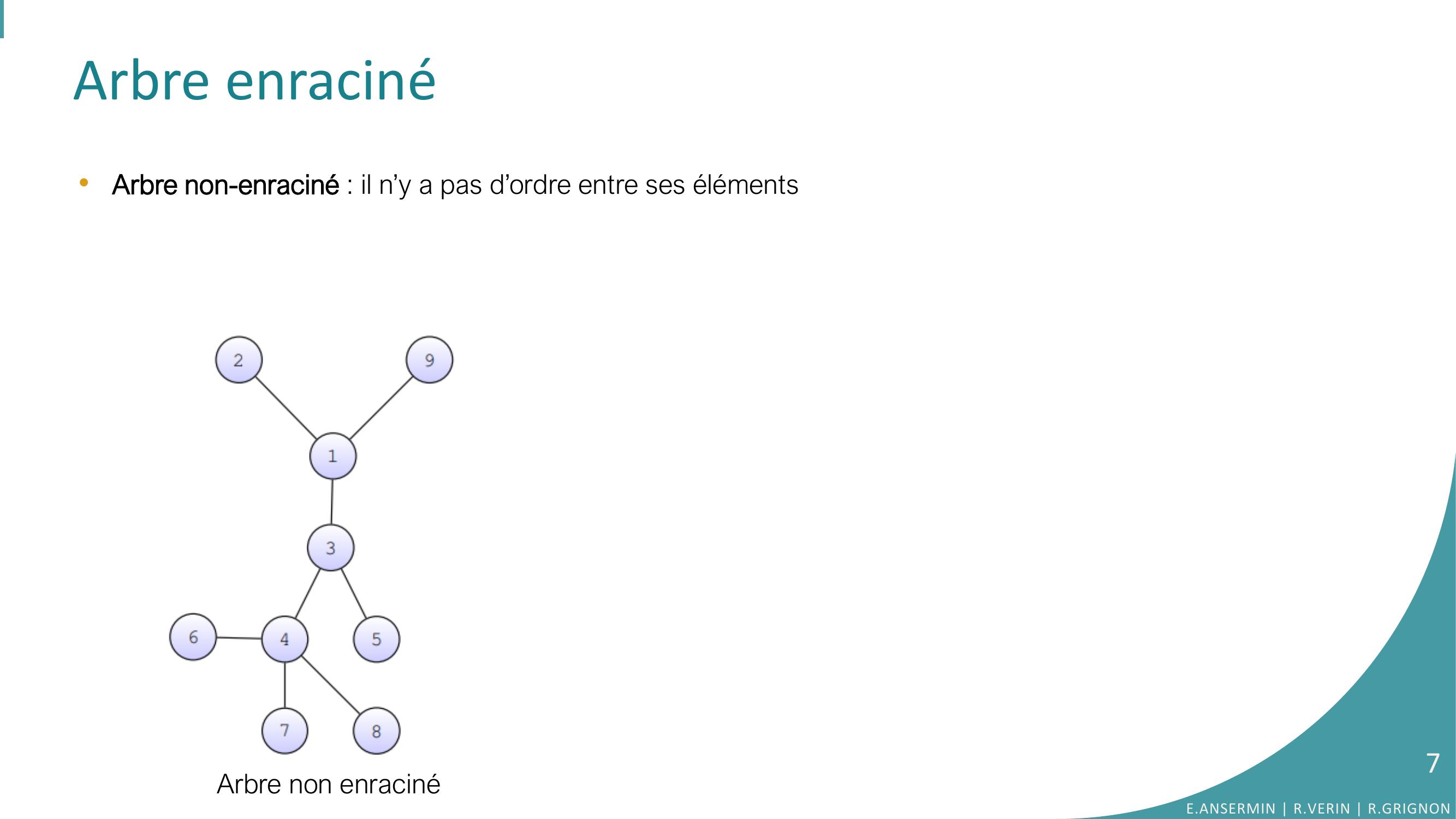
Page 7 : Arbre enraciné•Arbre non-enraciné : il n’y a pas d’ordre entre ses élémentsArbre non enracinéE.ANSERMIN R.VERIN R.GRIGNON7
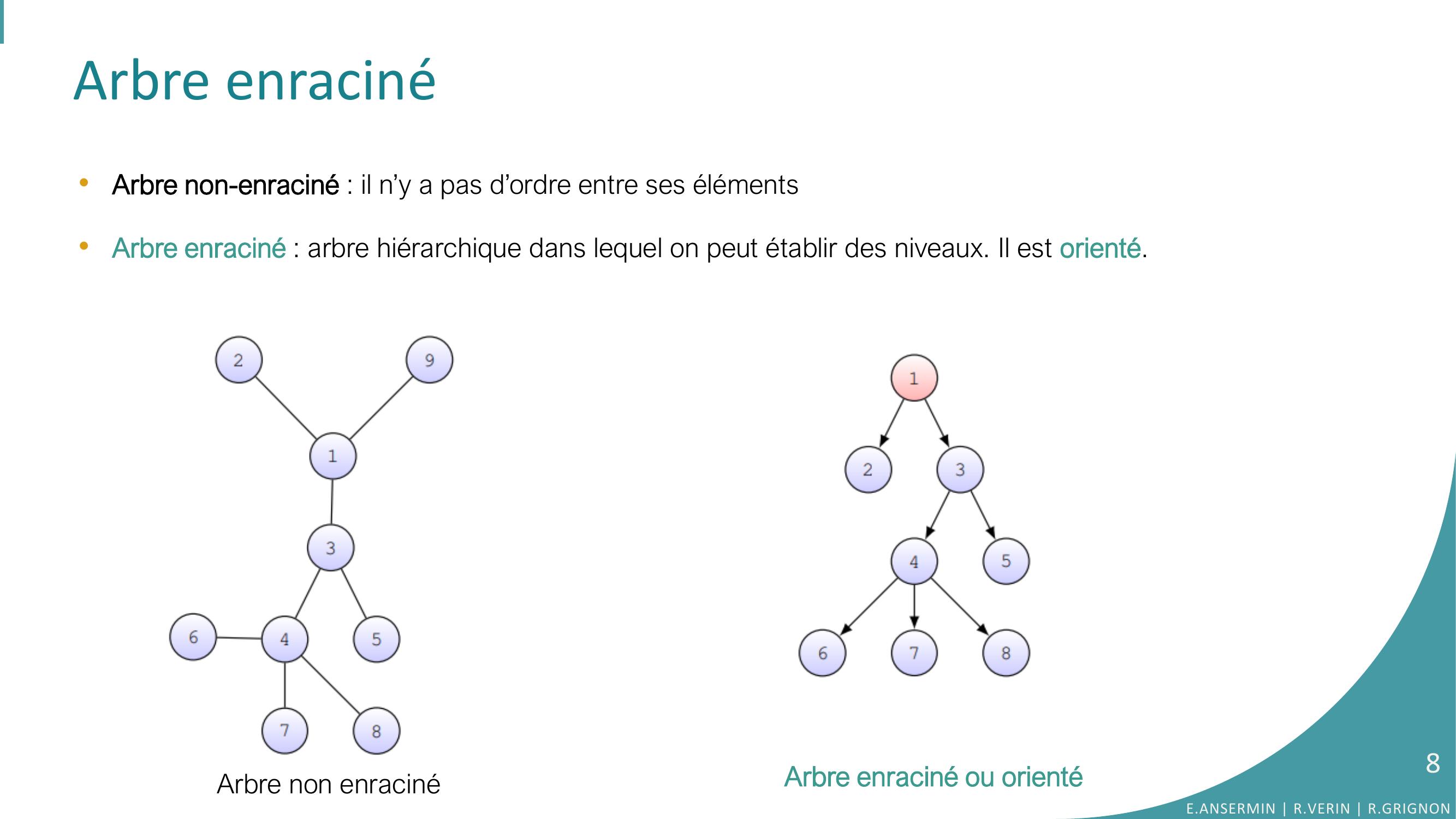
Page 8 : Arbre enraciné•Arbre non-enraciné : il n’y a pas d’ordre entre ses élémentsArbre non enraciné•Arbre enraciné : arbre hiérarchique dans lequel on peut établir des niveaux. Il est orienté.Arbre enraciné ou orientéE.ANSERMIN R.VERIN R.GRIGNON8
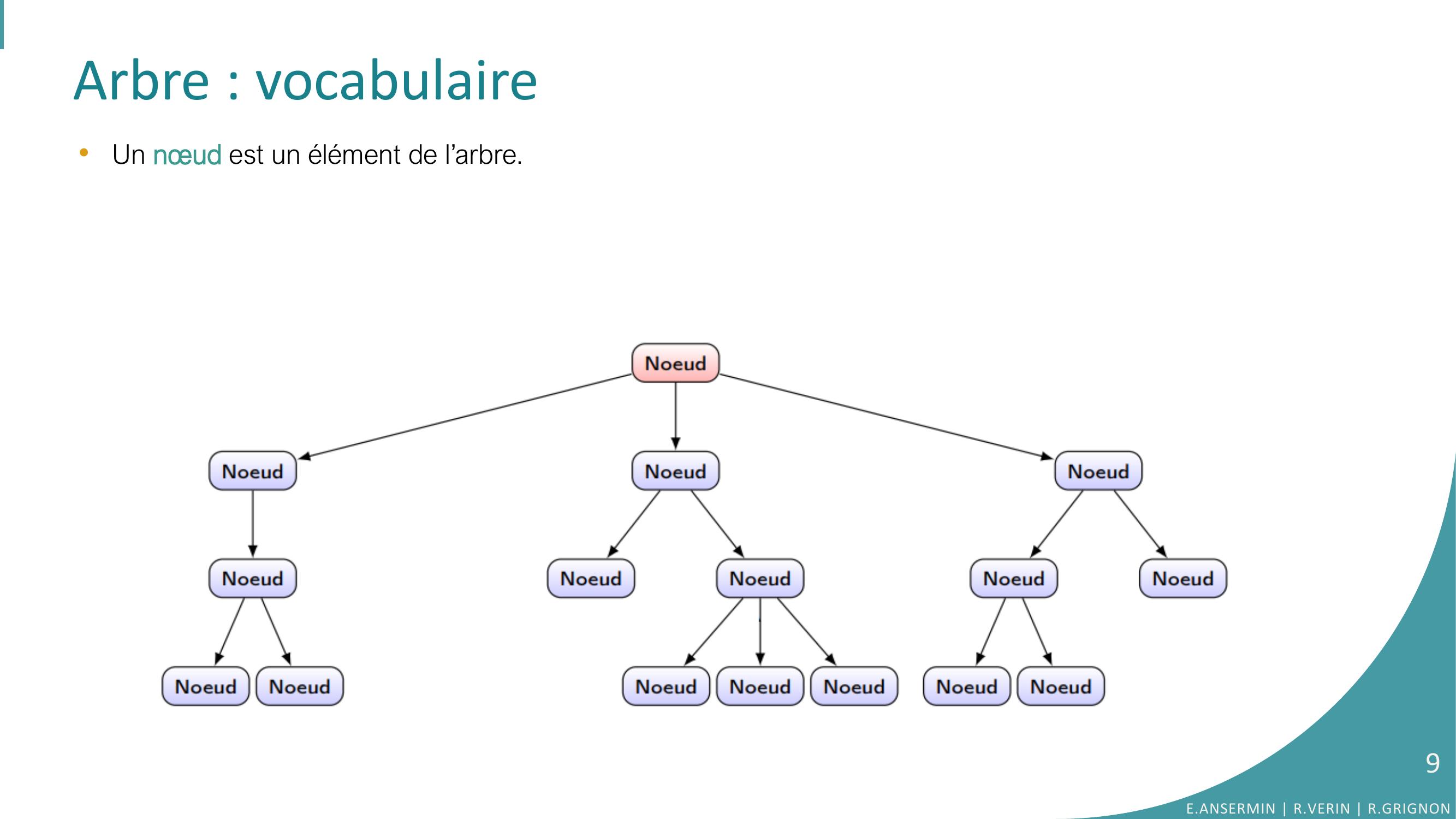
Page 9 : Arbre : vocabulaire•Un nœud est un élément de l’arbre. E.ANSERMIN R.VERIN R.GRIGNON9
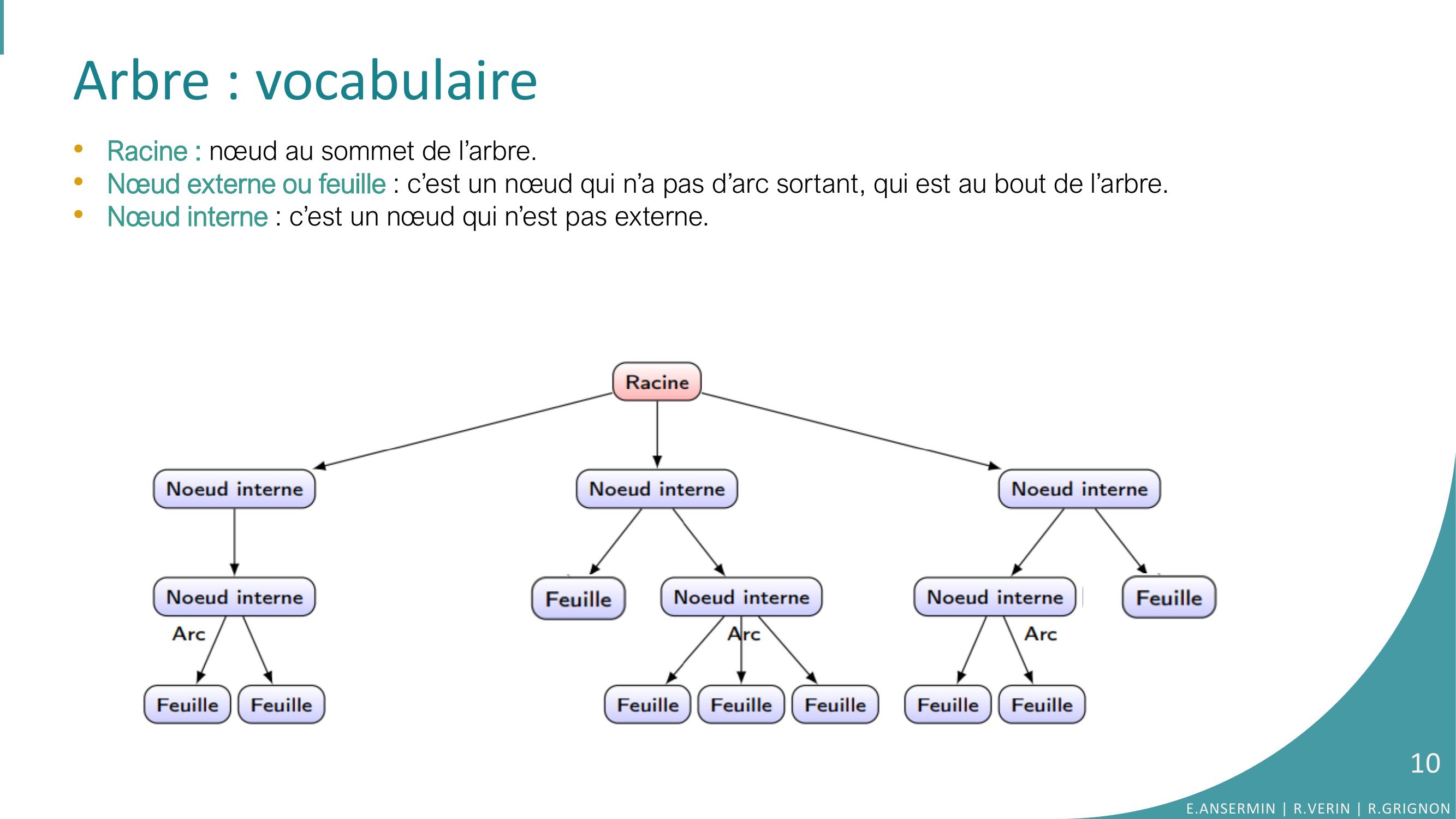
Page 10 : Arbre : vocabulaire•Racine : nœud au sommet de l’arbre.•Nœud externe ou feuille : c’est un nœud qui n’a pas d’arc sortant, qui est au bout de l’arbre.•Nœud interne : c’est un nœud qui n’est pas externe.E.ANSERMIN R.VERIN R.GRIGNON10
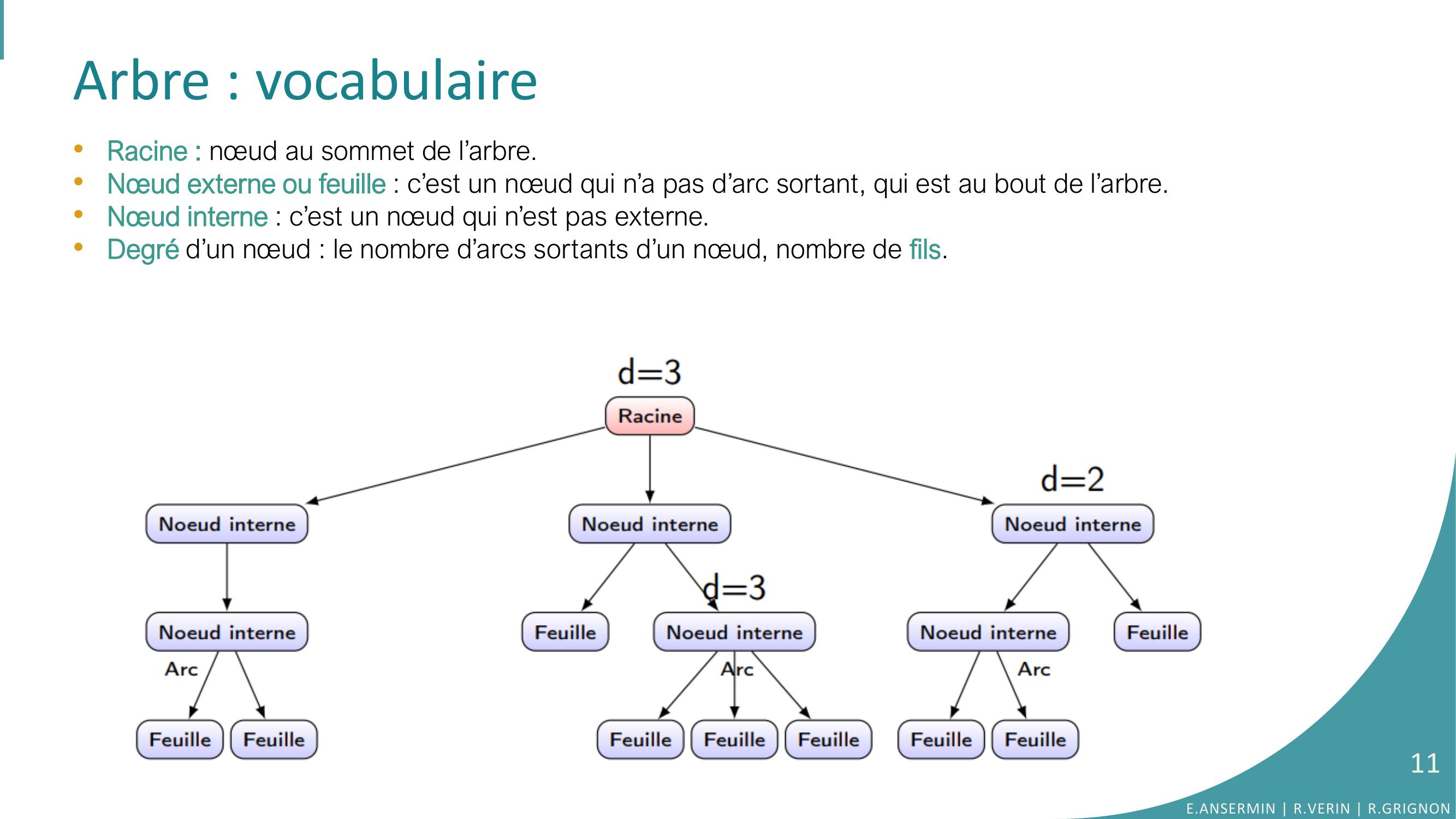
Page 11 : Arbre : vocabulaire•Racine : nœud au sommet de l’arbre.•Nœud externe ou feuille : c’est un nœud qui n’a pas d’arc sortant, qui est au bout de l’arbre.•Nœud interne : c’est un nœud qui n’est pas externe.•Degré d’un nœud : le nombre d’arcs sortants d’un nœud, nombre de fils. E.ANSERMIN R.VERIN R.GRIGNON11
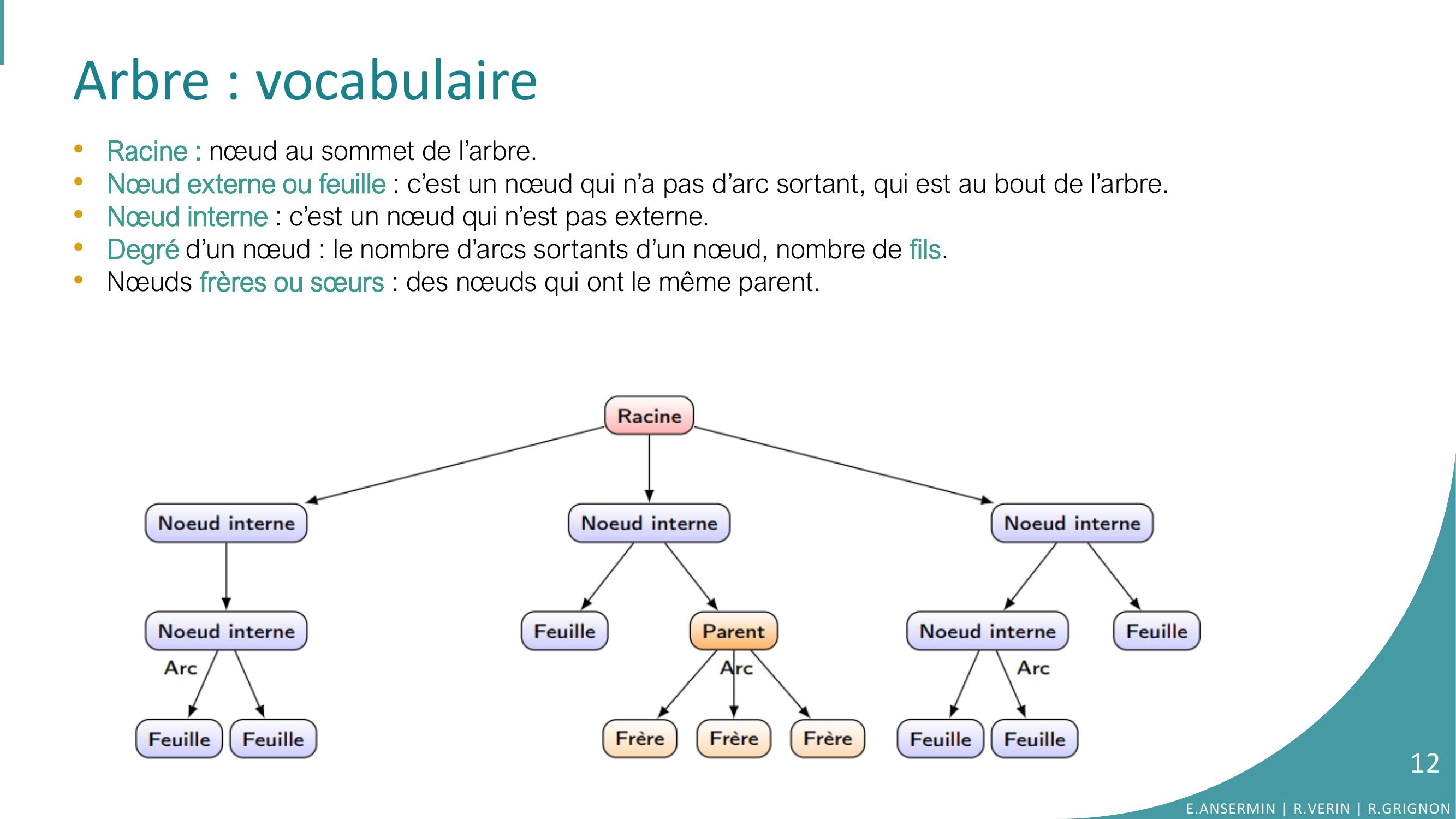
Page 12 : Arbre : vocabulaire•Racine : nœud au sommet de l’arbre.•Nœud externe ou feuille : c’est un nœud qui n’a pas d’arc sortant, qui est au bout de l’arbre.•Nœud interne : c’est un nœud qui n’est pas externe.•Degré d’un nœud : le nombre d’arcs sortants d’un nœud, nombre de fils. •Nœuds frères ou sœurs : des nœuds qui ont le même parent. E.ANSERMIN R.VERIN R.GRIGNON12
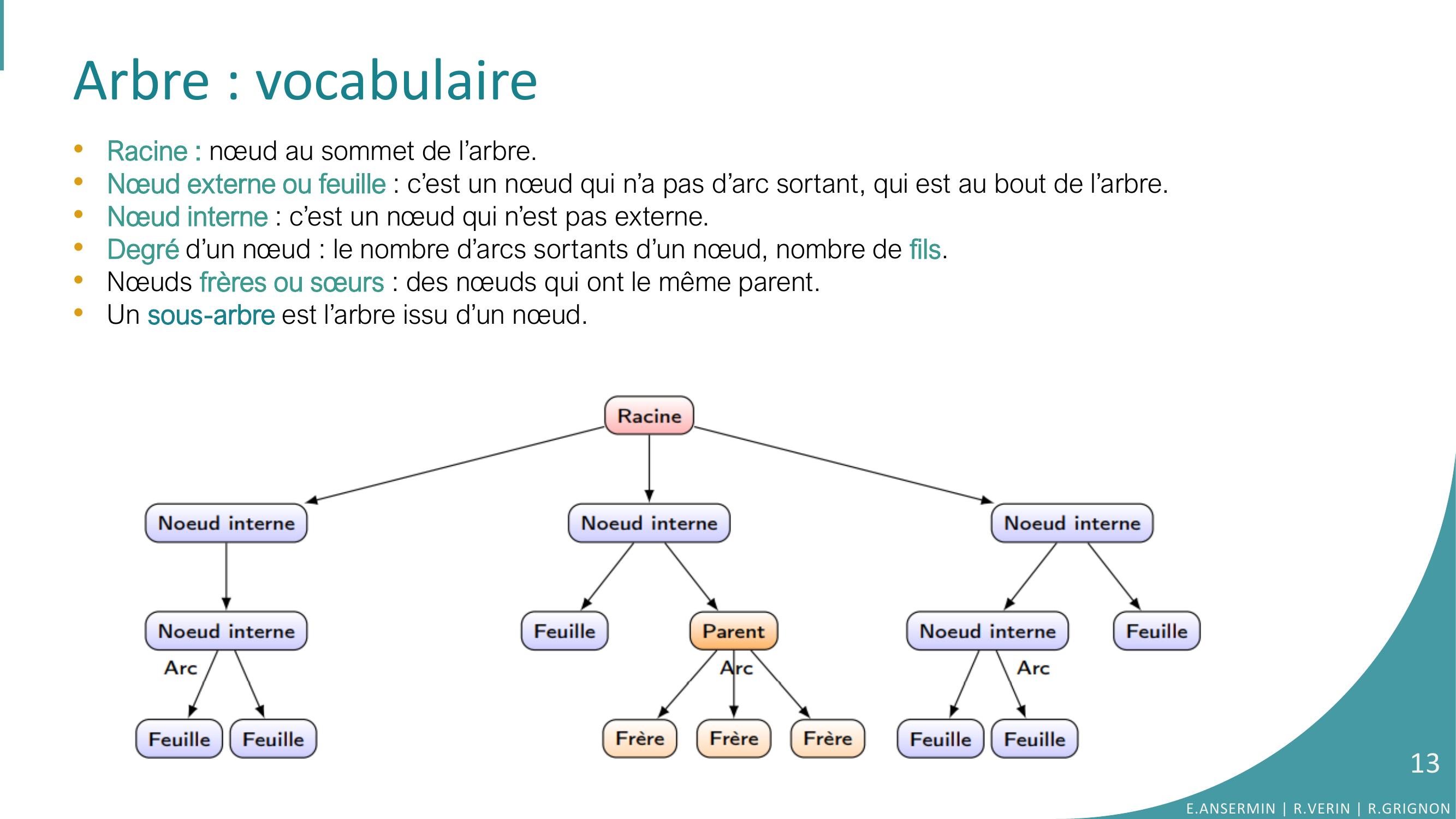
Page 13 : Arbre : vocabulaire•Racine : nœud au sommet de l’arbre.•Nœud externe ou feuille : c’est un nœud qui n’a pas d’arc sortant, qui est au bout de l’arbre.•Nœud interne : c’est un nœud qui n’est pas externe.•Degré d’un nœud : le nombre d’arcs sortants d’un nœud, nombre de fils. •Nœuds frères ou sœurs : des nœuds qui ont le même parent. •Un sous-arbre est l’arbre issu d’un nœud. E.ANSERMIN R.VERIN R.GRIGNON13
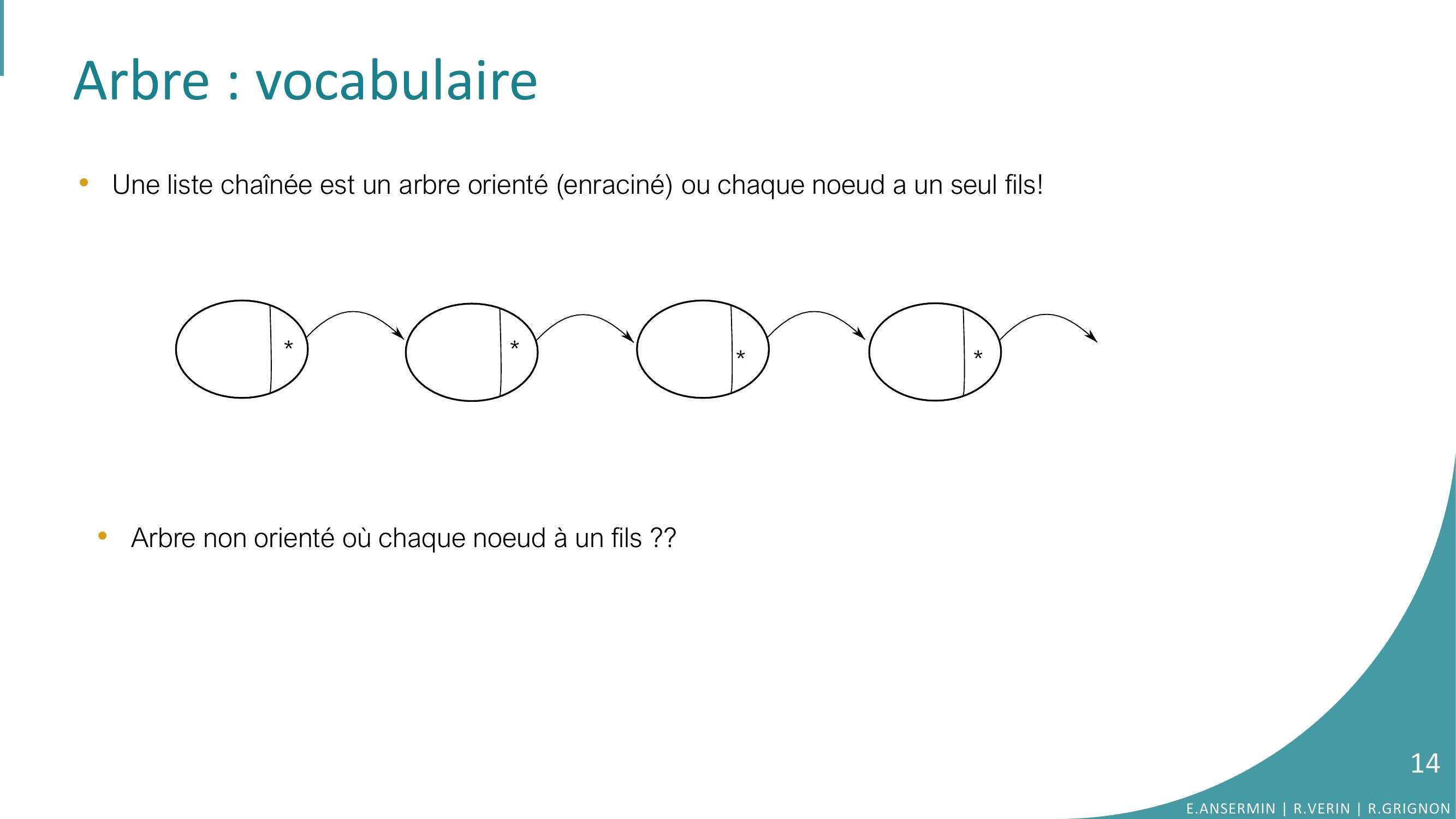
Page 14 : Arbre : vocabulaire•Une liste chaînée est un arbre orienté enraciné ou chaque noeud a un seul fils! •Arbre non orienté où chaque noeud à un fils ?? E.ANSERMIN R.VERIN R.GRIGNON14
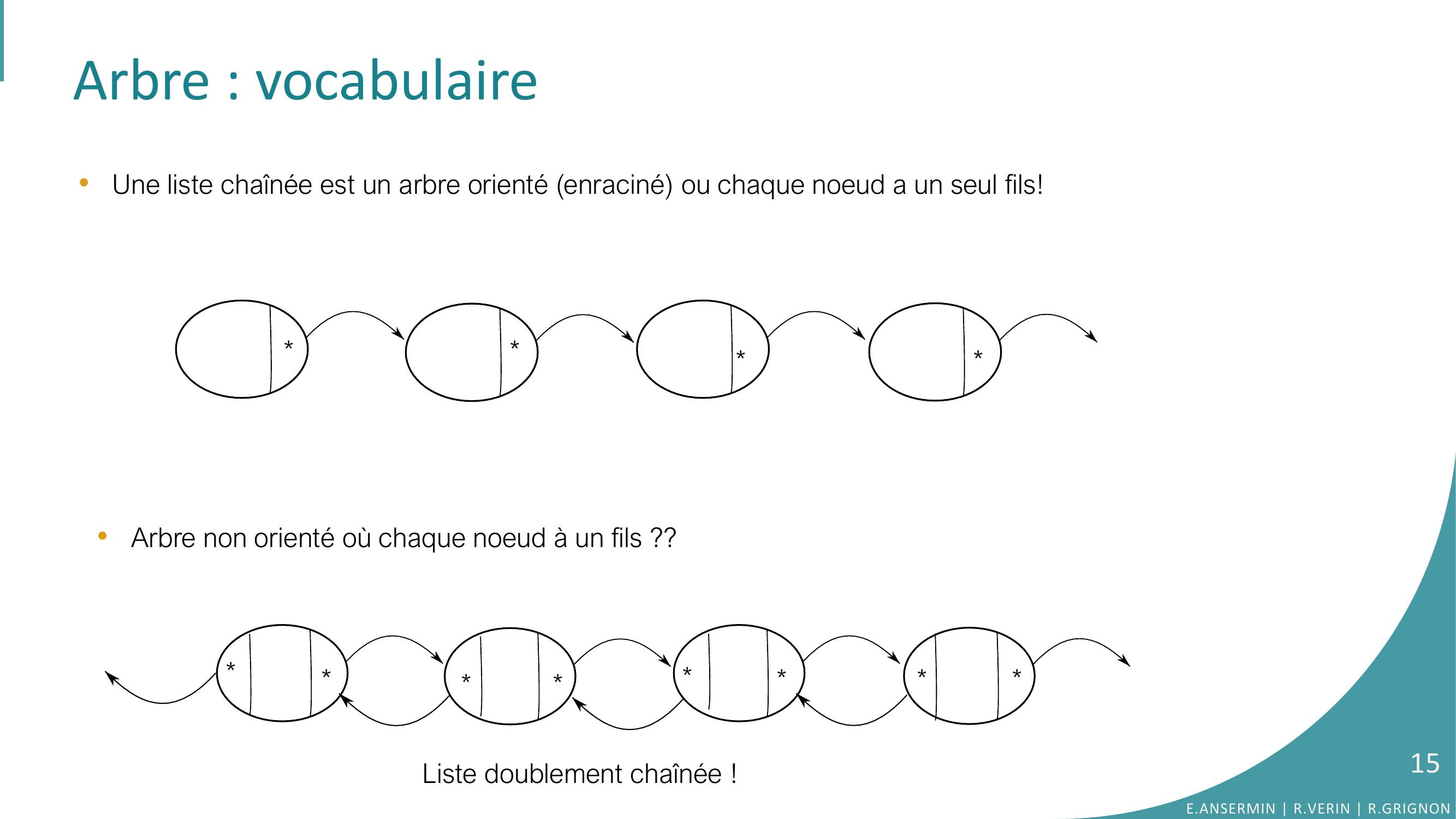
Page 15 : Arbre : vocabulaire•Une liste chaînée est un arbre orienté enraciné ou chaque noeud a un seul fils! Liste doublement chaînée !•Arbre non orienté où chaque noeud à un fils ?? E.ANSERMIN R.VERIN R.GRIGNON15
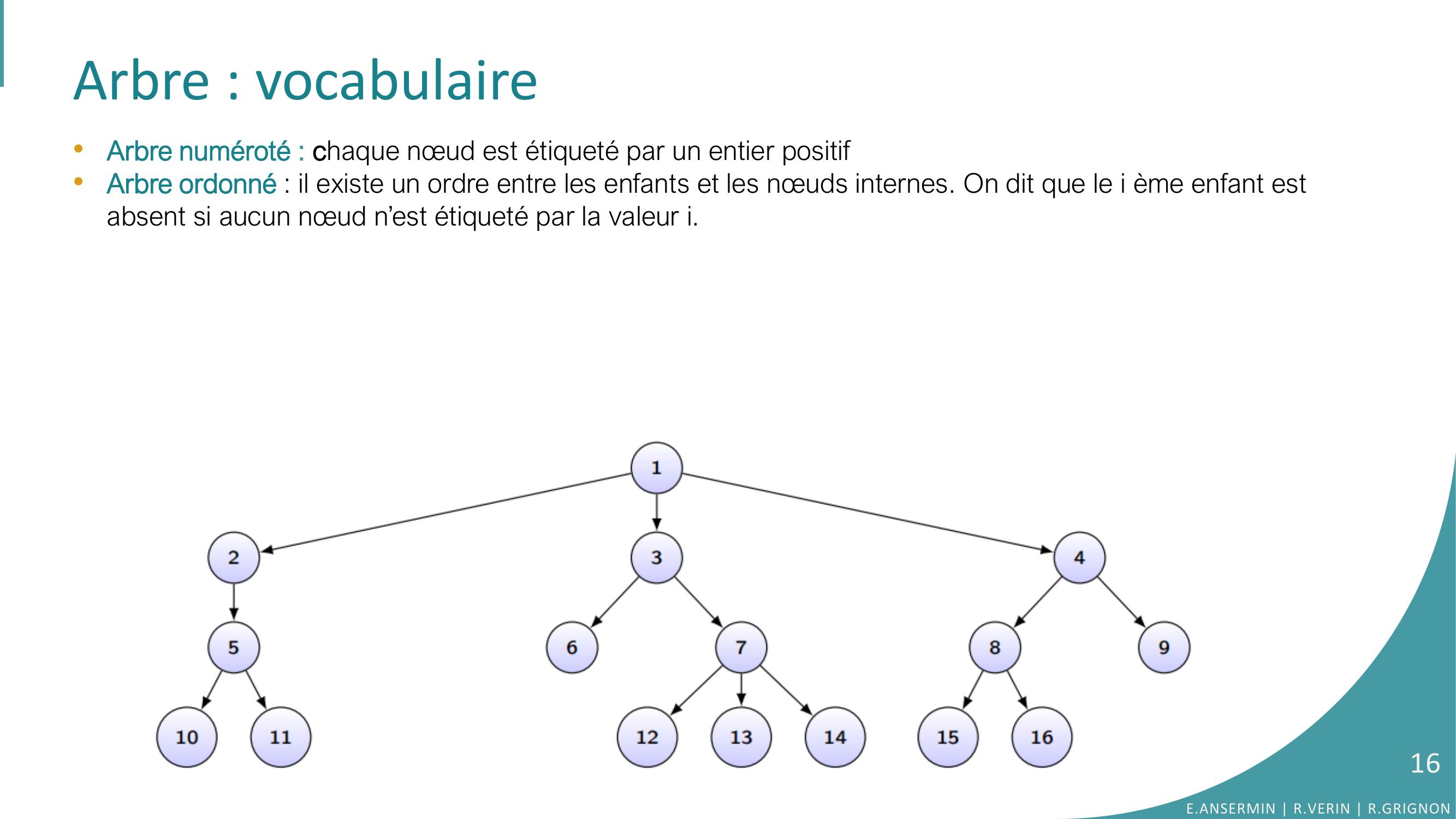
Page 16 : Arbre : vocabulaire•Arbre numéroté : chaque nœud est étiqueté par un entier positif•Arbre ordonné : il existe un ordre entre les enfants et les nœuds internes. On dit que le i ème enfant est absent si aucun nœud n’est étiqueté par la valeur i. E.ANSERMIN R.VERIN R.GRIGNON16
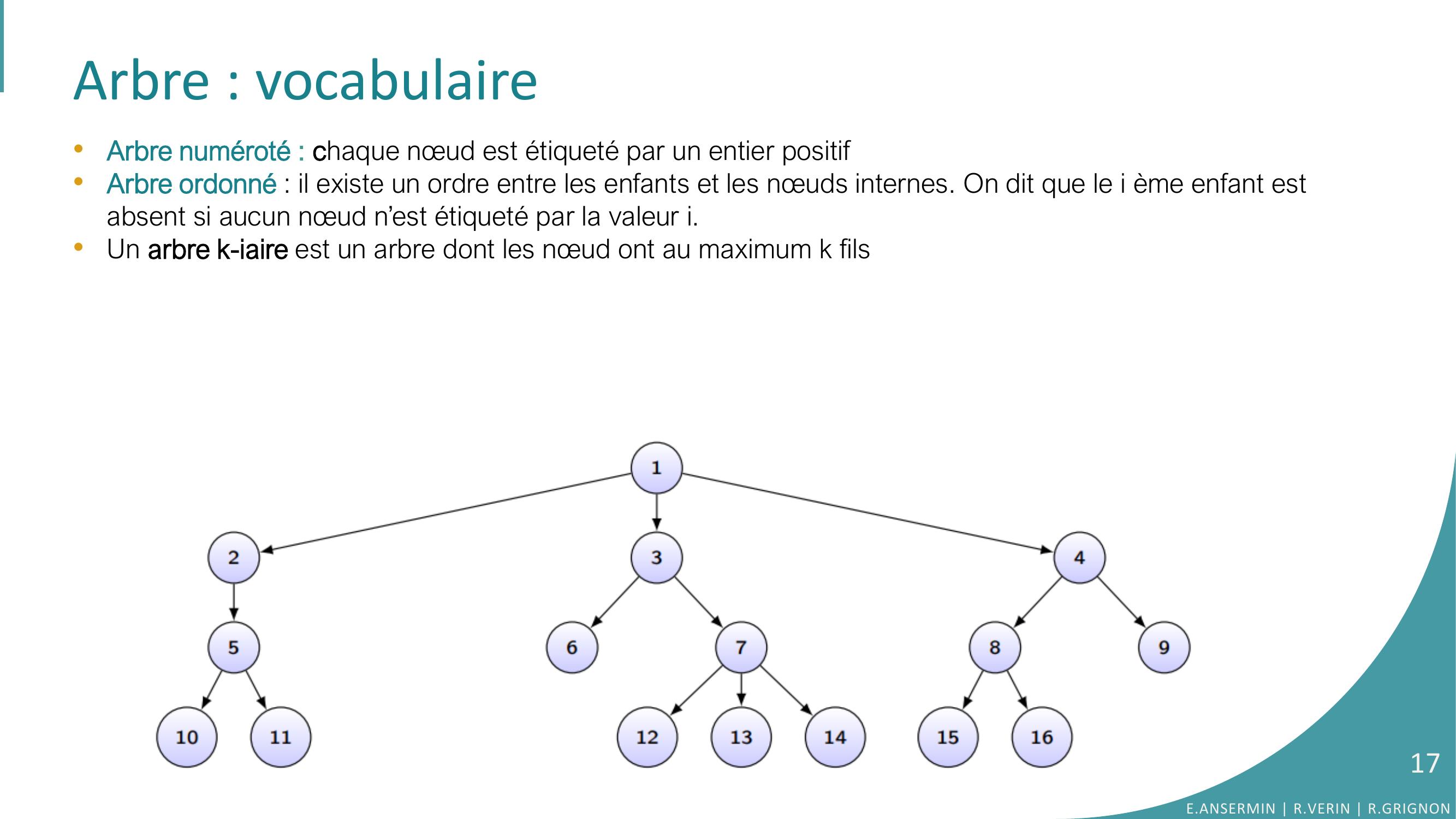
Page 17 : Arbre : vocabulaire•Arbre numéroté : chaque nœud est étiqueté par un entier positif•Arbre ordonné : il existe un ordre entre les enfants et les nœuds internes. On dit que le i ème enfant est absent si aucun nœud n’est étiqueté par la valeur i. •Un arbre k-iaire est un arbre dont les nœud ont au maximum k fils E.ANSERMIN R.VERIN R.GRIGNON17
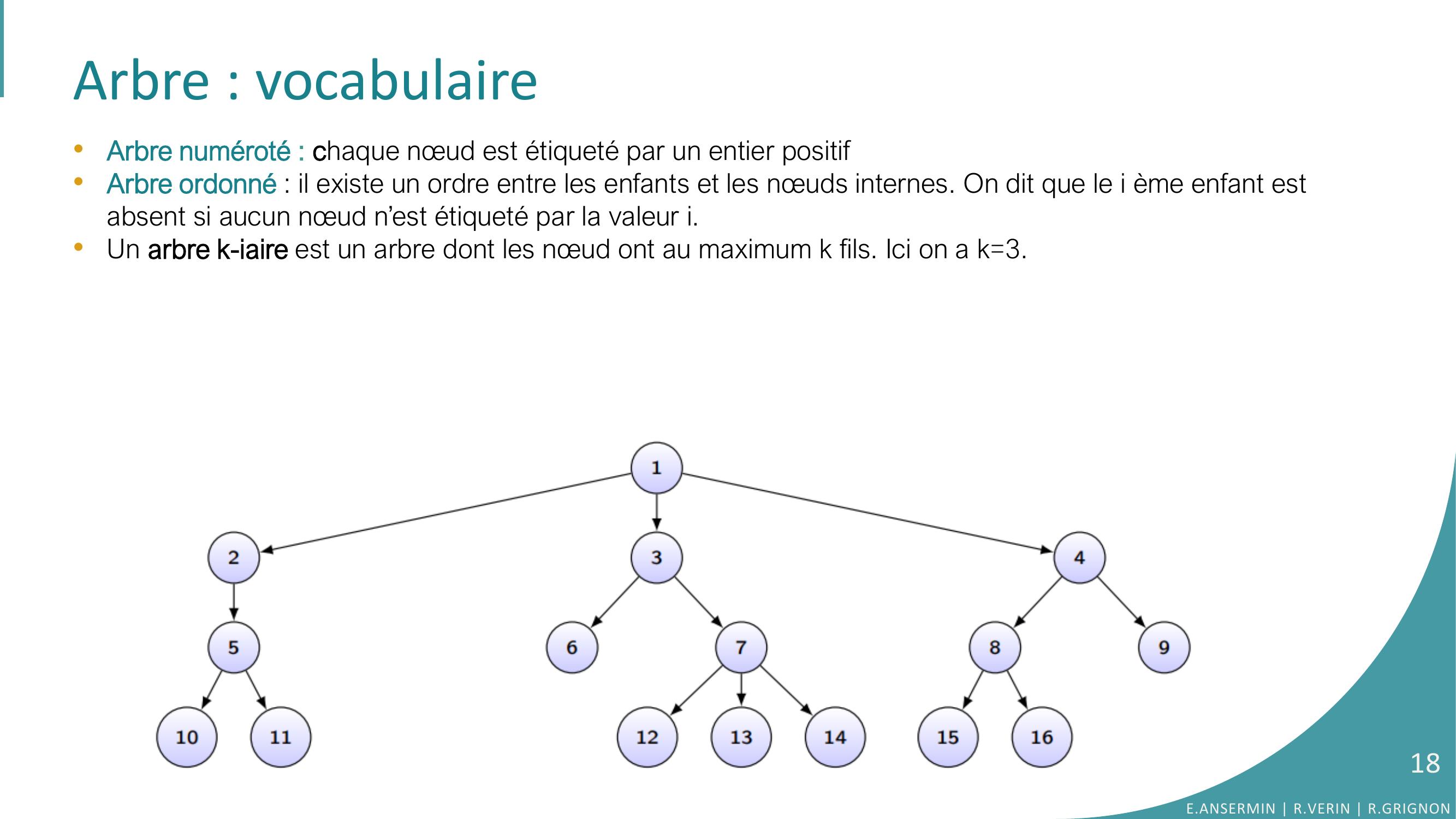
Page 18 : Arbre : vocabulaire•Arbre numéroté : chaque nœud est étiqueté par un entier positif•Arbre ordonné : il existe un ordre entre les enfants et les nœuds internes. On dit que le i ème enfant est absent si aucun nœud n’est étiqueté par la valeur i. •Un arbre k-iaire est un arbre dont les nœud ont au maximum k fils. Ici on a k=3.E.ANSERMIN R.VERIN R.GRIGNON18
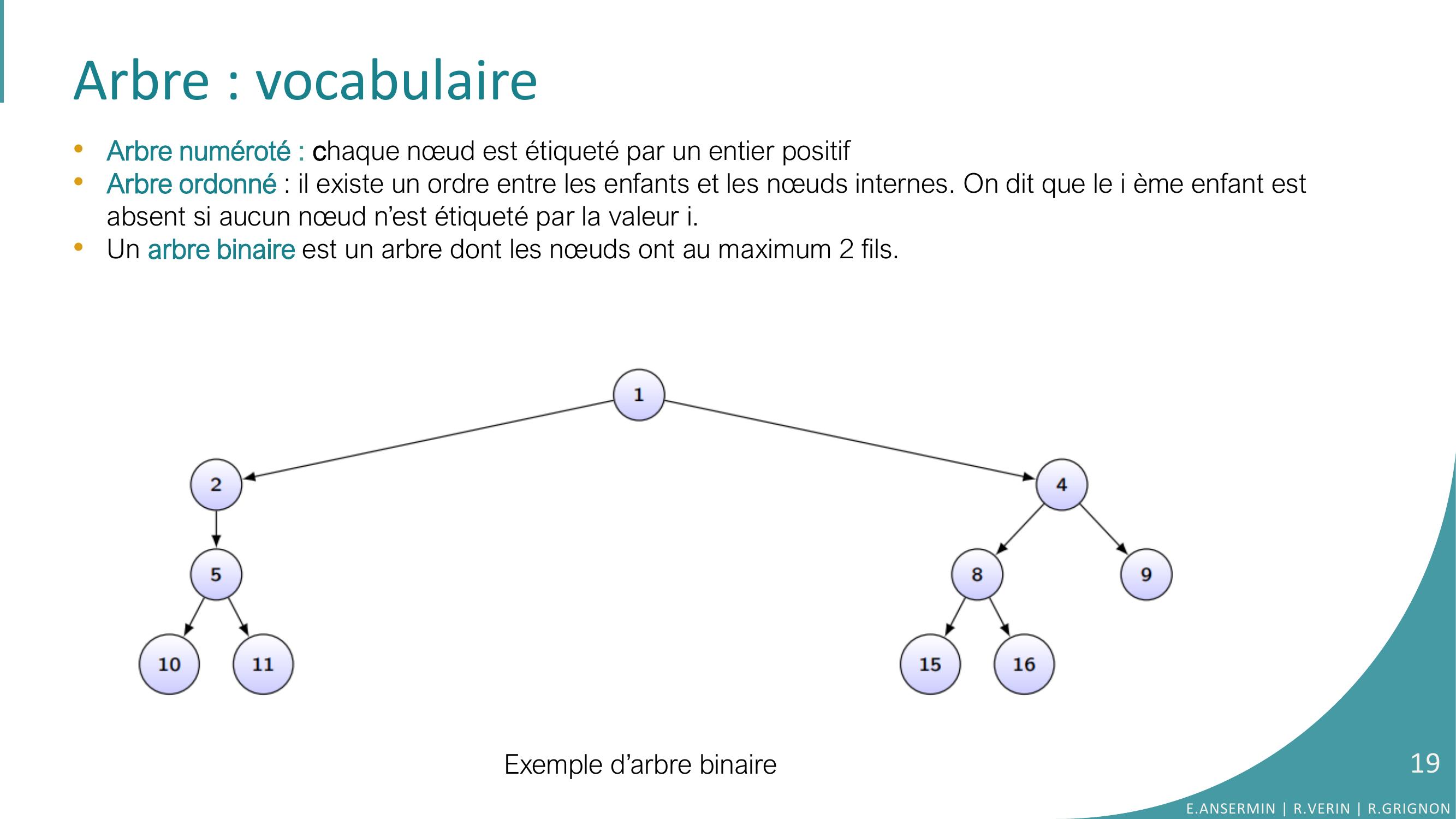
Page 19 : Arbre : vocabulaire•Arbre numéroté : chaque nœud est étiqueté par un entier positif•Arbre ordonné : il existe un ordre entre les enfants et les nœuds internes. On dit que le i ème enfant est absent si aucun nœud n’est étiqueté par la valeur i. •Un arbre binaire est un arbre dont les nœuds ont au maximum 2 fils. Exemple d’arbre binaireE.ANSERMIN R.VERIN R.GRIGNON19
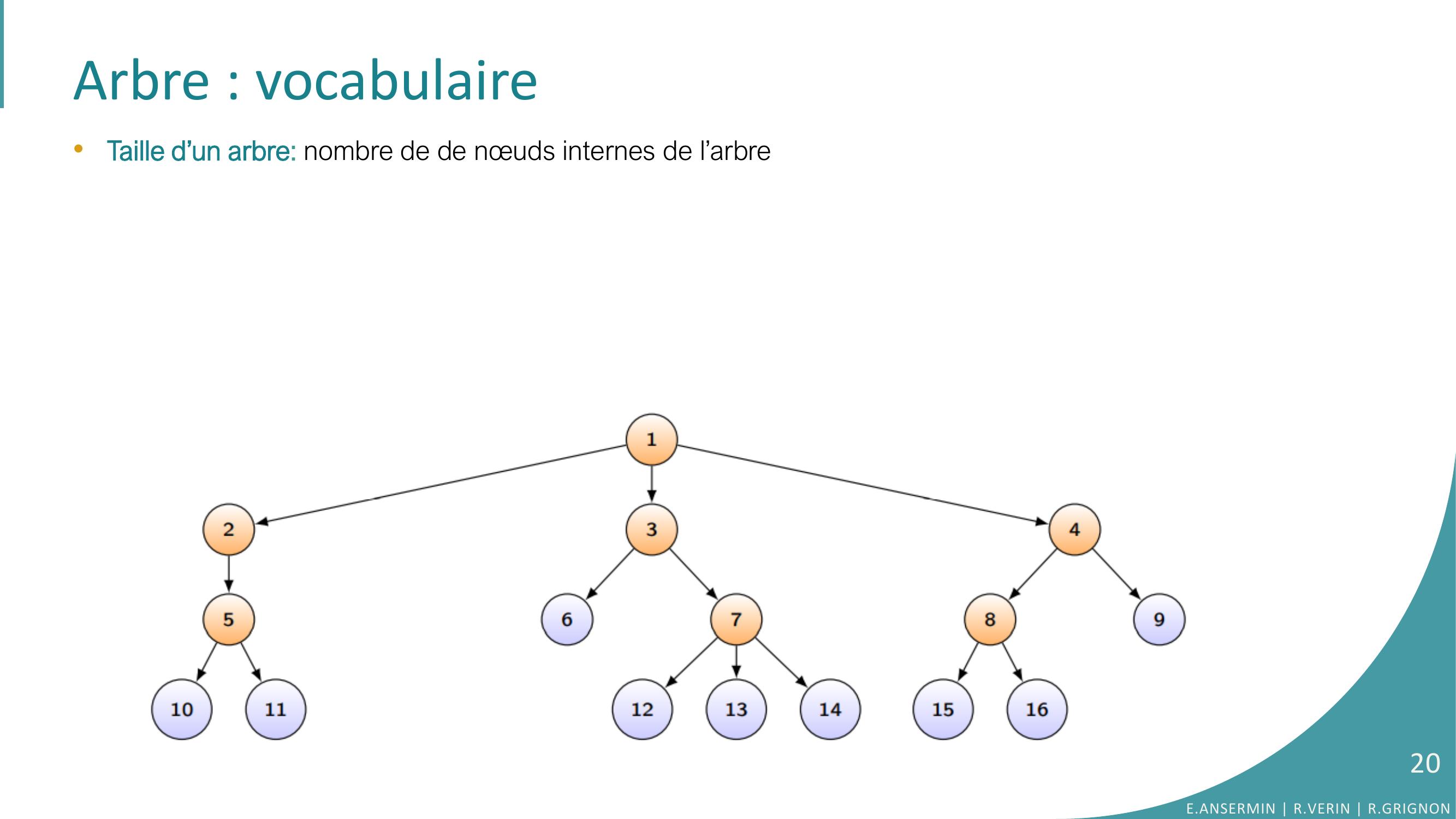
Page 20 : Arbre : vocabulaire•Taille d’un arbre: nombre de de nœuds internes de l’arbreE.ANSERMIN R.VERIN R.GRIGNON20
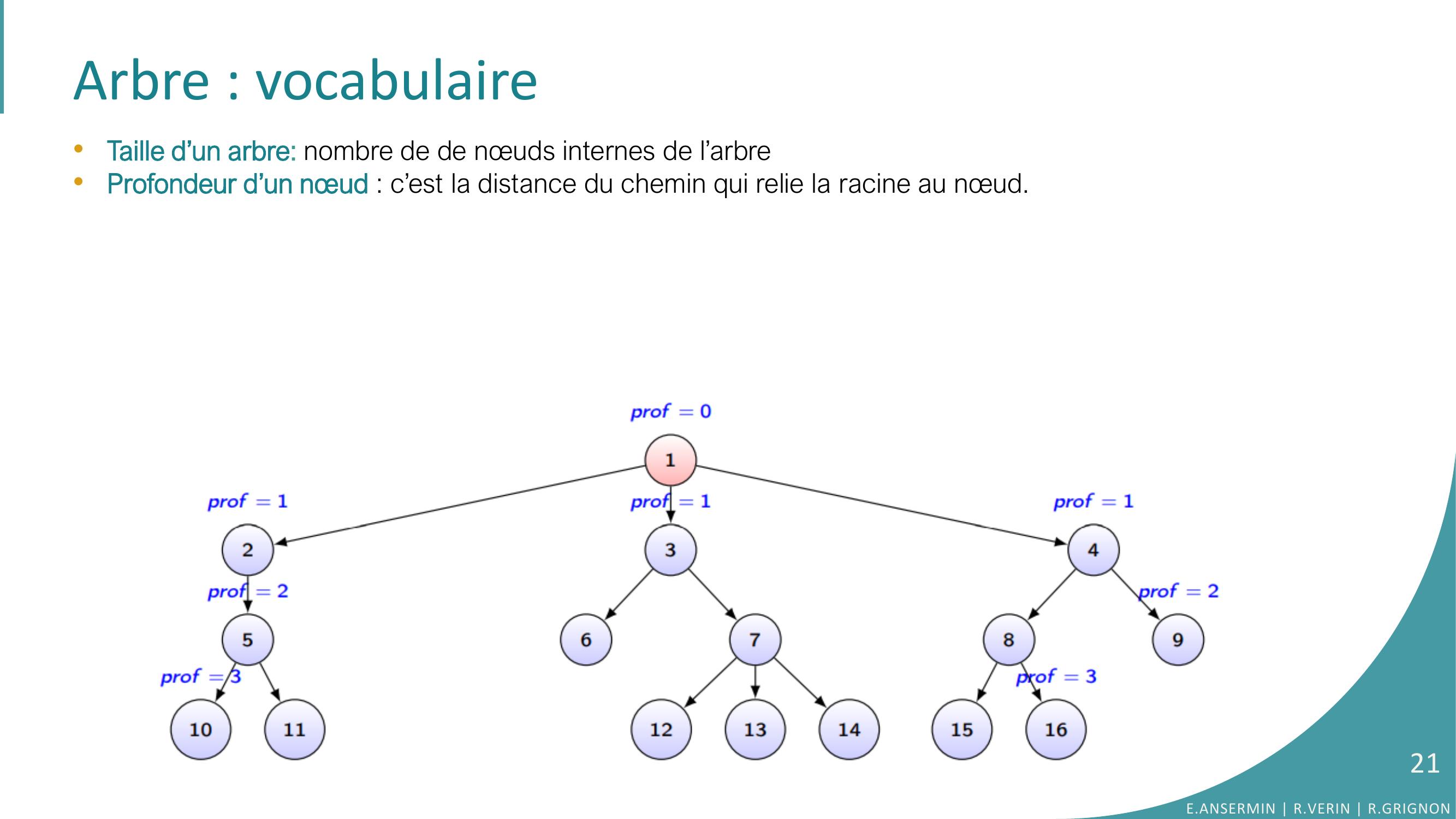
Page 21 : Arbre : vocabulaire•Taille d’un arbre: nombre de de nœuds internes de l’arbre•Profondeur d’un nœud : c’est la distance du chemin qui relie la racine au nœud.E.ANSERMIN R.VERIN R.GRIGNON21
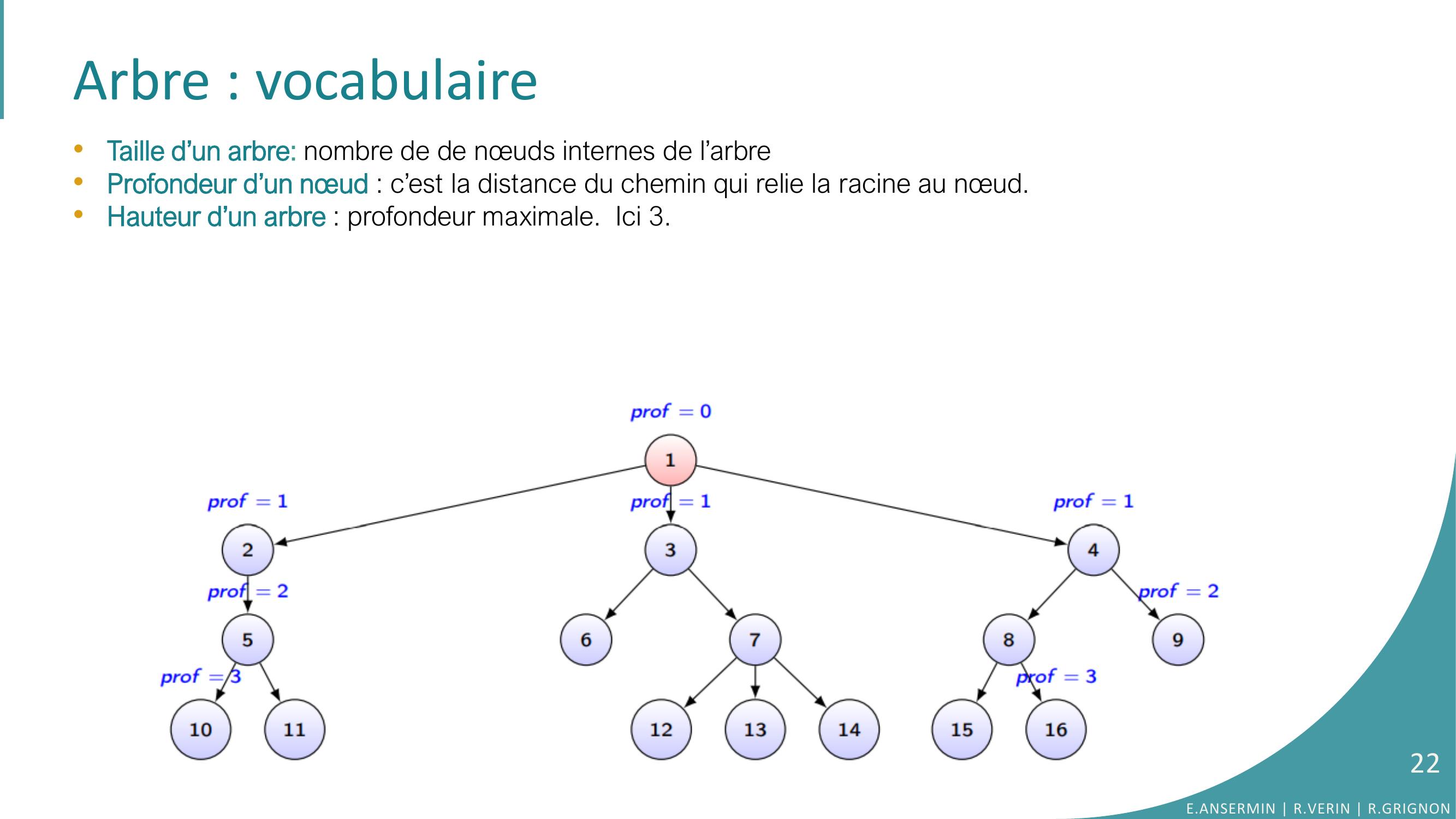
Page 22 : Arbre : vocabulaire•Taille d’un arbre: nombre de de nœuds internes de l’arbre•Profondeur d’un nœud : c’est la distance du chemin qui relie la racine au nœud.•Hauteur d’un arbre : profondeur maximale. Ici 3.E.ANSERMIN R.VERIN R.GRIGNON22
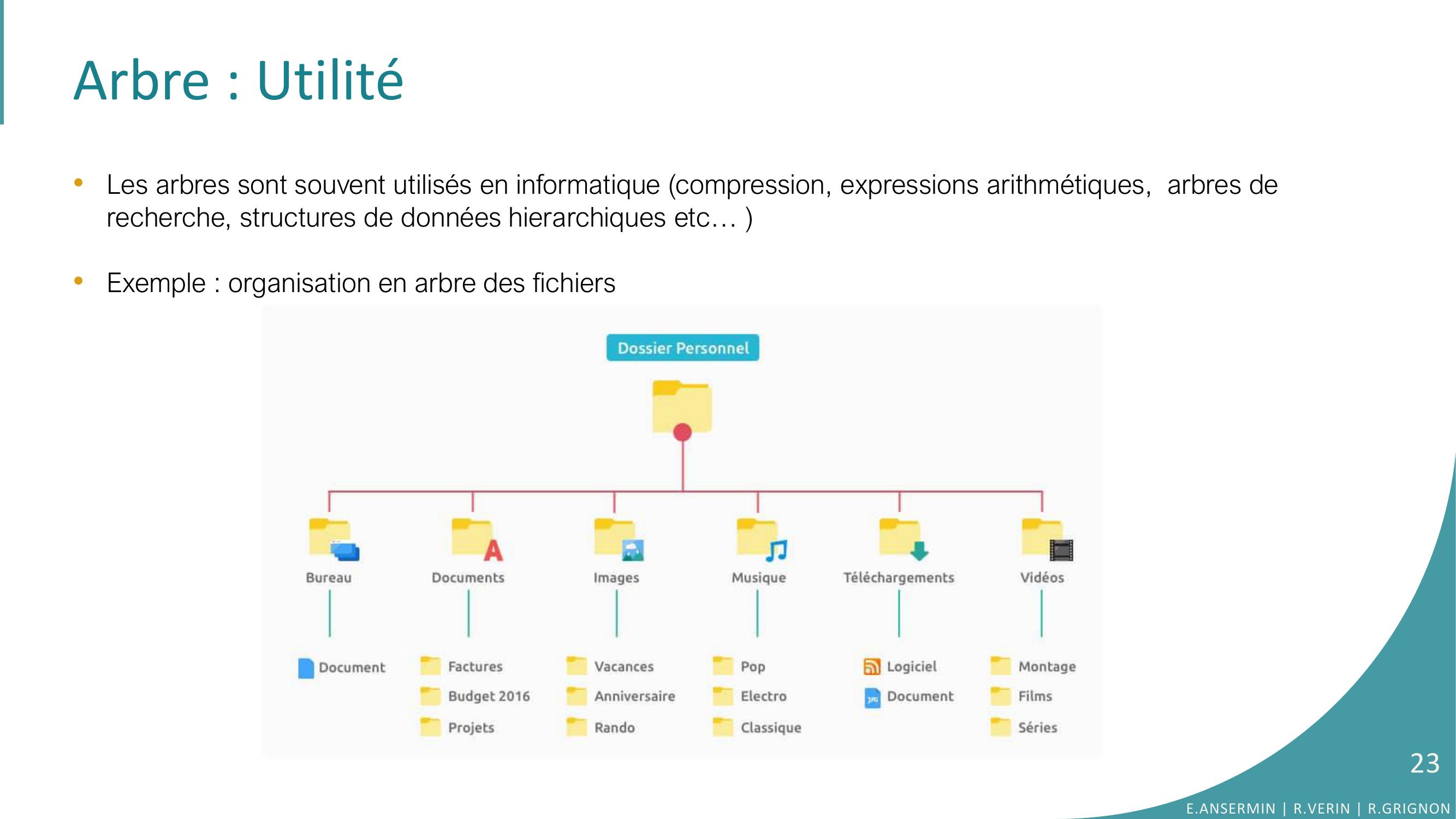
Page 23 : Arbre : Utilité•Les arbres sont souvent utilisés en informatique compression, expressions arithmétiques, arbres de recherche, structures de données hierarchiques etc… •Exemple : organisation en arbre des fichiersE.ANSERMIN R.VERIN R.GRIGNON23
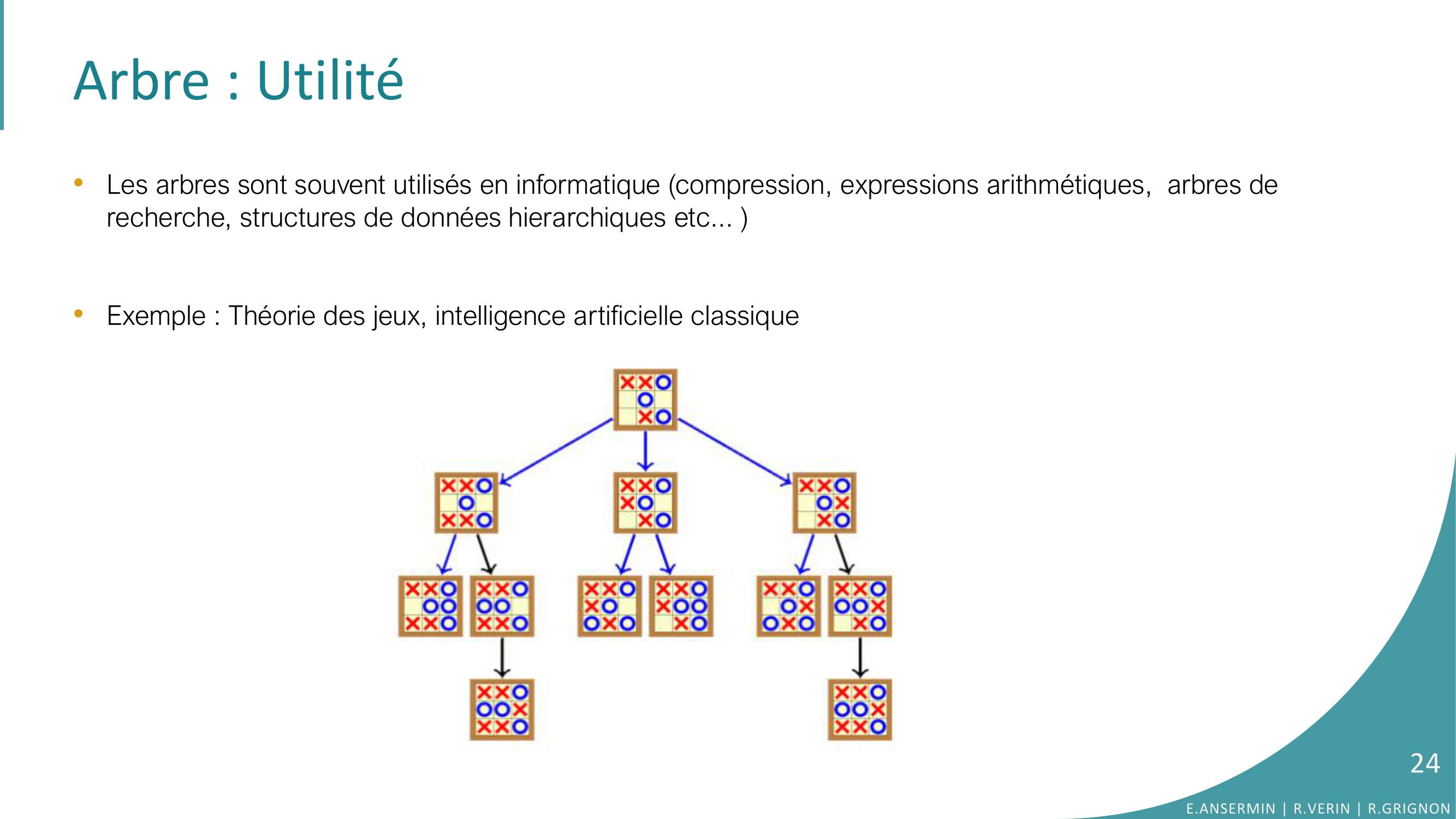
Page 24 : Arbre : Utilité•Les arbres sont souvent utilisés en informatique compression, expressions arithmétiques, arbres de recherche, structures de données hierarchiques etc... •Exemple : Théorie des jeux, intelligence artificielle classiqueE.ANSERMIN R.VERIN R.GRIGNON24
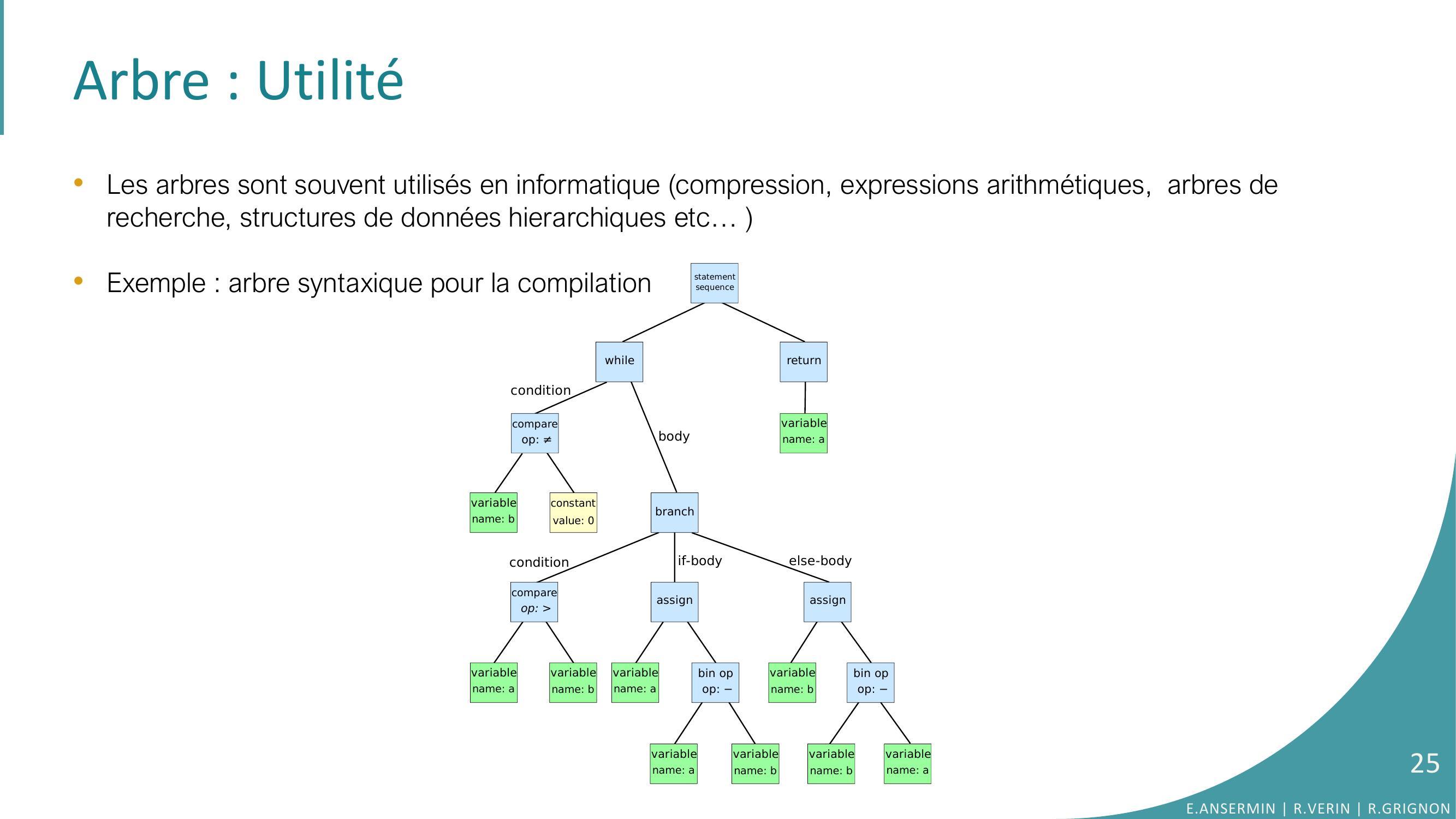
Page 25 : Arbre : Utilité•Les arbres sont souvent utilisés en informatique compression, expressions arithmétiques, arbres de recherche, structures de données hierarchiques etc… •Exemple : arbre syntaxique pour la compilation E.ANSERMIN R.VERIN R.GRIGNON25
Page 26 : Implémentation d’un arbre•Le cas des arbres binaires est le plus facile à étudier et à implémenter car l’on connait par avance le nombre maximal de fils de chaque nœud. •Nous nous concentrons sur ce cas particulier d’arbres pour la suite du cours. •L’extension à des arbres k-aire se fait en augmentant le nombre de fils. E.ANSERMIN R.VERIN R.GRIGNON26
Page 27 : Implémentation d’un arbre binaire•Les nœuds d’un arbre binaire ont maximum deux fils.•La structure d’un nœud de l’arbre peut donc être : Structure Arbre :elmt : Elementfg, fd : pointeurs sur structure Arbre; // fils gauche et droitE.ANSERMIN R.VERIN R.GRIGNON27
Page 28 : Implémentation d’un arbre binaire•Création d’un nœud de l’arbre : FONCTION creerArbrer: Element : pointeur sur ArbreVARIABLEnoeud : pointeur sur ArbreDEBUTnoeud ←reserverMemoireArbreelmtnoeud ←rfgnoeud ←NULL // Le noeud n’a pas de fils à sa créationfdnoeud ←NULLRETOURNER noeudFINE.ANSERMIN R.VERIN R.GRIGNON28
Page 29 : Implémentation d’un arbre binaire•Création d’un nœud de l’arbre : Remarque : comme pour les listes chaînées, on va utiliser des pointeurs sur Arbre plutôt que des structures Arbre afin de pouvoir libérer l’espace mémoire à postériori.FONCTION creerArbrer: Element : pointeur sur ArbreVARIABLEnoeud : pointeur sur ArbreDEBUTnoeud ←reserverMemoireArbreelmtnoeud ←rfgnoeud ←NULL // Le noeud n’a pas de fils à sa créationfdnoeud ←NULLRETOURNER noeudFINE.ANSERMIN R.VERIN R.GRIGNON29
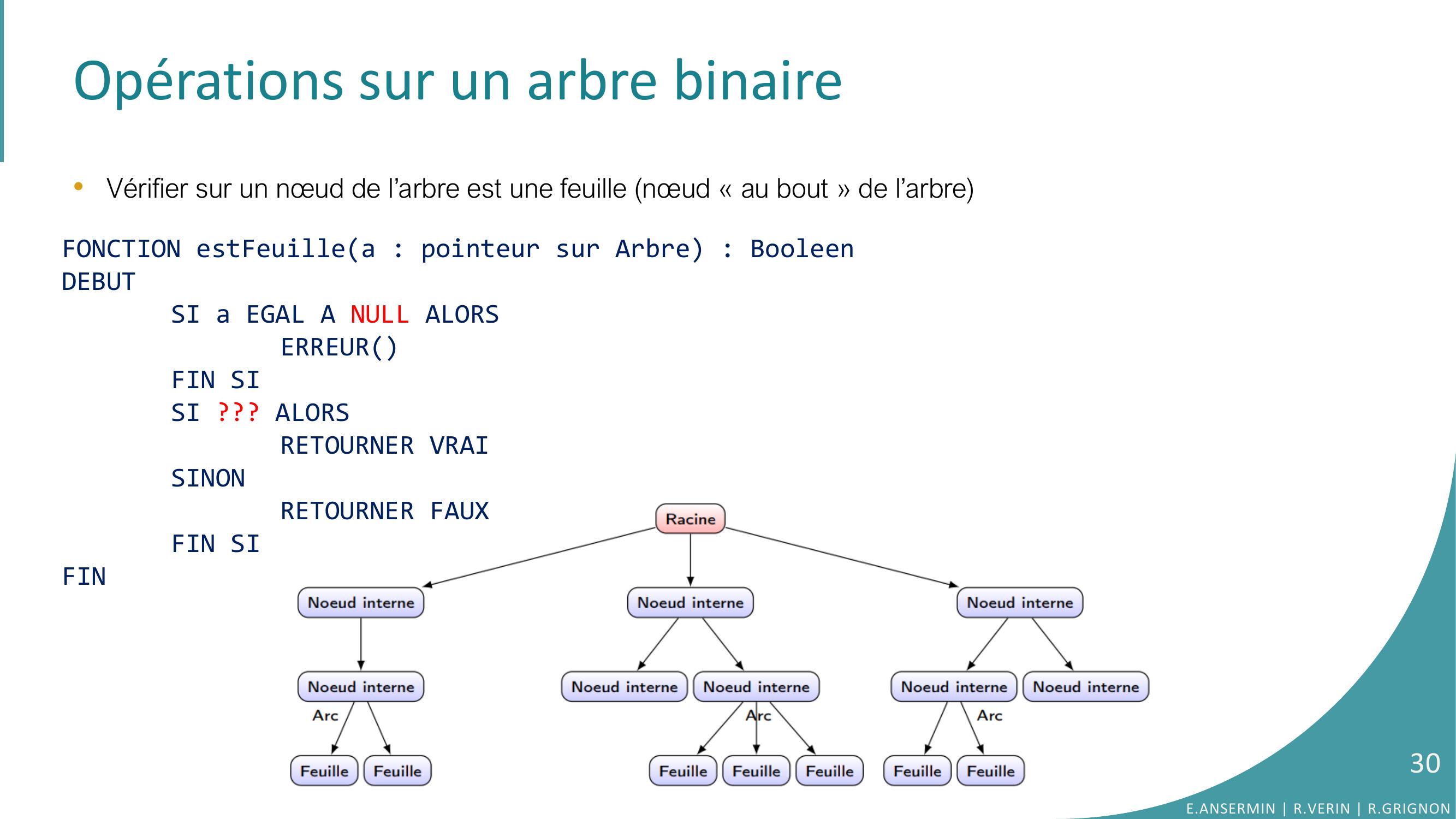
Page 30 : Opérations sur un arbre binaire•Vérifier sur un nœud de l’arbre est une feuille nœud « au bout » de l’arbreFONCTION estFeuillea : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURFIN SISI ??? ALORSRETOURNER VRAISINONRETOURNER FAUXFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON30
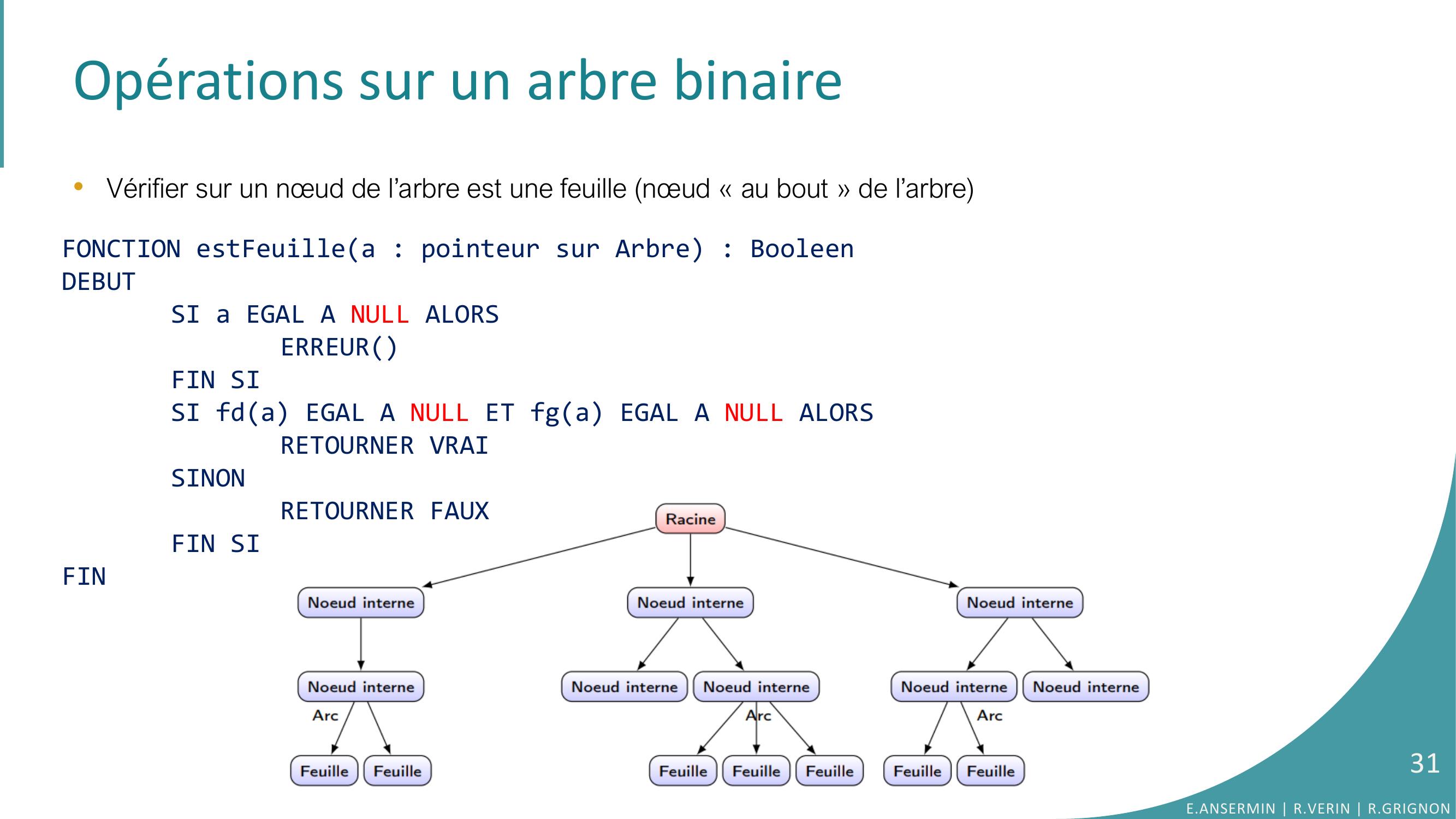
Page 31 : Opérations sur un arbre binaire•Vérifier sur un nœud de l’arbre est une feuille nœud « au bout » de l’arbreFONCTION estFeuillea : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURFIN SISI fda EGAL A NULL ET fga EGAL A NULL ALORSRETOURNER VRAISINONRETOURNER FAUXFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON31
Page 32 : Opérations sur un arbre binaire•Vérifier si le fils droit ou gauche d’un nœud existe : FONCTION existeFilsDroita : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURSINON SI ??? ALORSRETOURNER FAUXSINONRETOURNER VRAIFIN SIFINFONCTION existeFilsGauchea : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURSINON SI ??? ALORSRETOURNER FAUXSINONRETOURNER VRAIFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON32
Page 33 : Opérations sur un arbre binaire•Vérifier si le fils droit ou gauche d’un nœud existe : FONCTION existeFilsDroita : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURSINON SI fda EGAL A NULL ALORSRETOURNER FAUXSINONRETOURNER VRAIFIN SIFINFONCTION existeFilsGauchea : pointeur sur Arbre : BooleenDEBUTSI a EGAL A NULL ALORSERREURSINON SI fga EGAL A NULL ALORSRETOURNER FAUXSINONRETOURNER VRAIFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON33
Page 34 : Opérations sur un arbre binaire•Retourner l’adresse du fils droit ou gauche d’un arbre: FONCTION filsDroita: pointeur sur Arbre : pointeur sur ArbreDEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsDroita ALORSRETOURNER fdaSINONRETOURNER NULLFIN SIFINFONCTION filsGauchea: pointeur sur Arbre : pointeur sur ArbreDEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSRETOURNER fgaSINONRETOURNER NULLFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON34
Page 35 : Opérations sur un arbre binaire•Modifier l’ élément d’un nœud PROCEDURE modifierElementa: pointeur sur Arbre; r: Element : pointeur sur ArbreDEBUTSI a EGAL A NULL ALORSERREURSINONelmta ←rFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON35
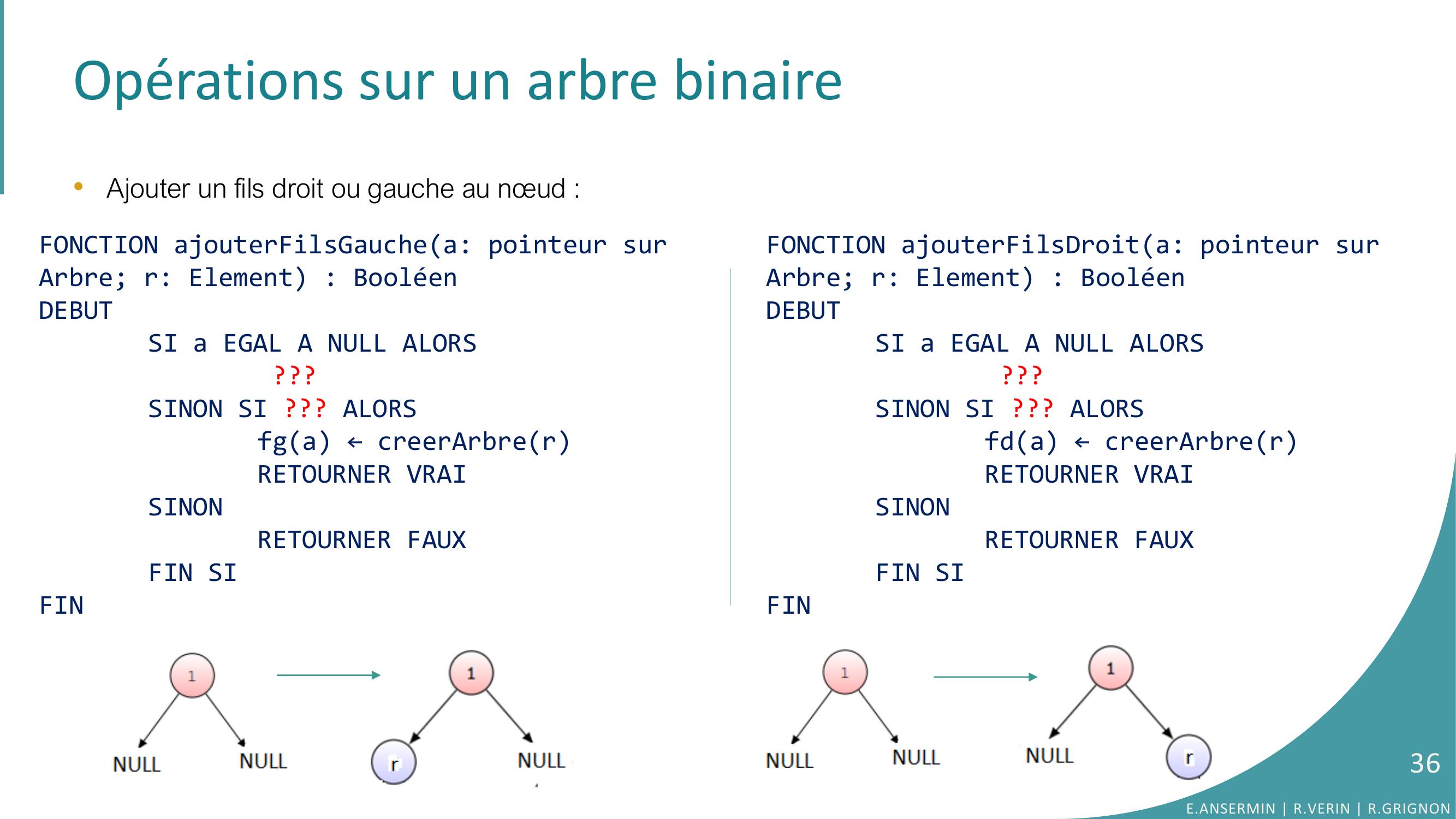
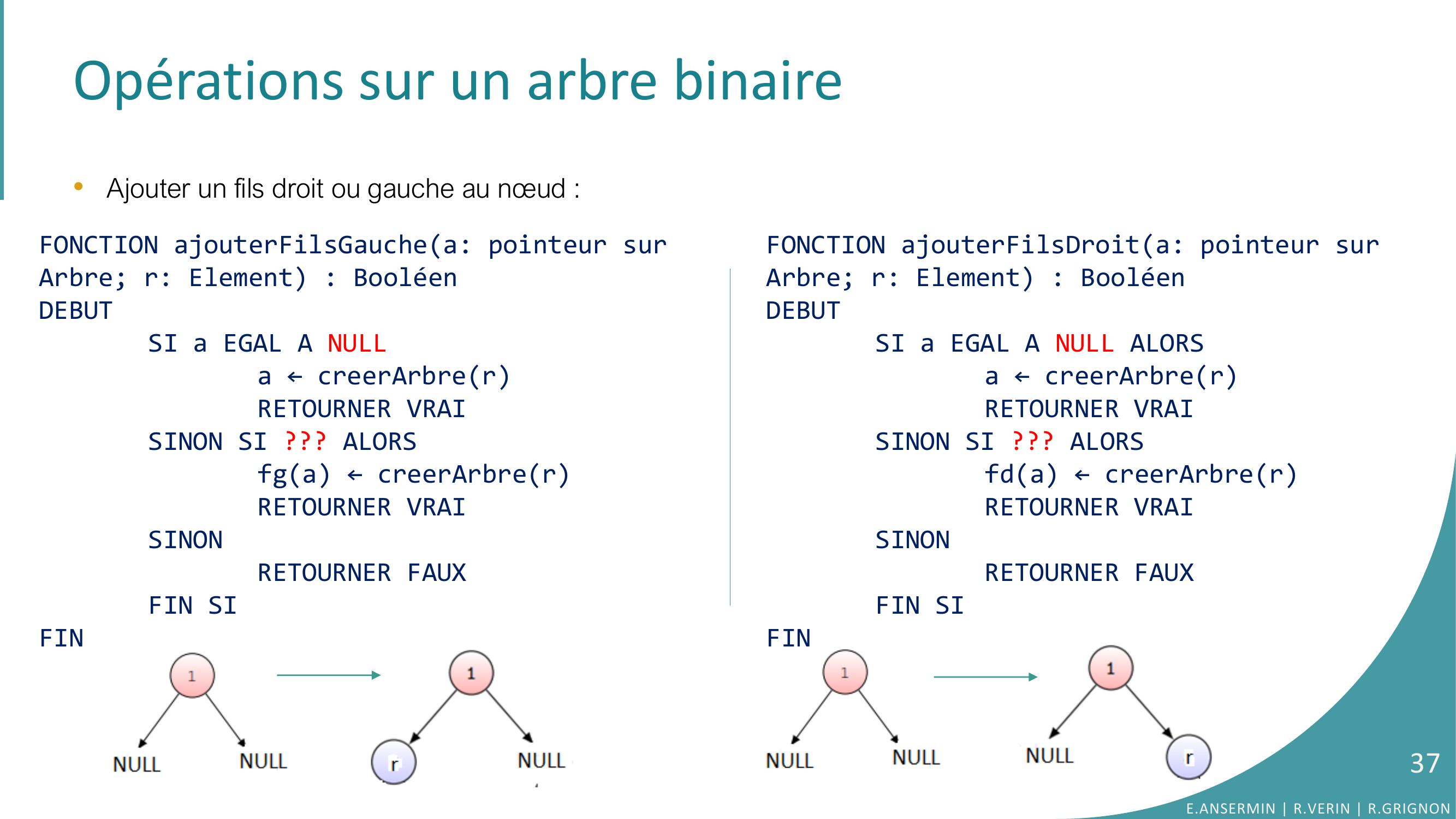
Page 36 : Opérations sur un arbre binaire•Ajouter un fils droit ou gauche au nœud : FONCTION ajouterFilsGauchea: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULL ALORS???SINON SI ??? ALORSfga ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINFONCTION ajouterFilsDroita: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULL ALORS???SINON SI ??? ALORSfda ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON36
Page 37 : Opérations sur un arbre binaire•Ajouter un fils droit ou gauche au nœud : FONCTION ajouterFilsGauchea: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULLa ←creerArbrerRETOURNER VRAISINON SI ??? ALORSfga ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINFONCTION ajouterFilsDroita: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULL ALORSa ←creerArbrerRETOURNER VRAISINON SI ??? ALORSfda ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON37
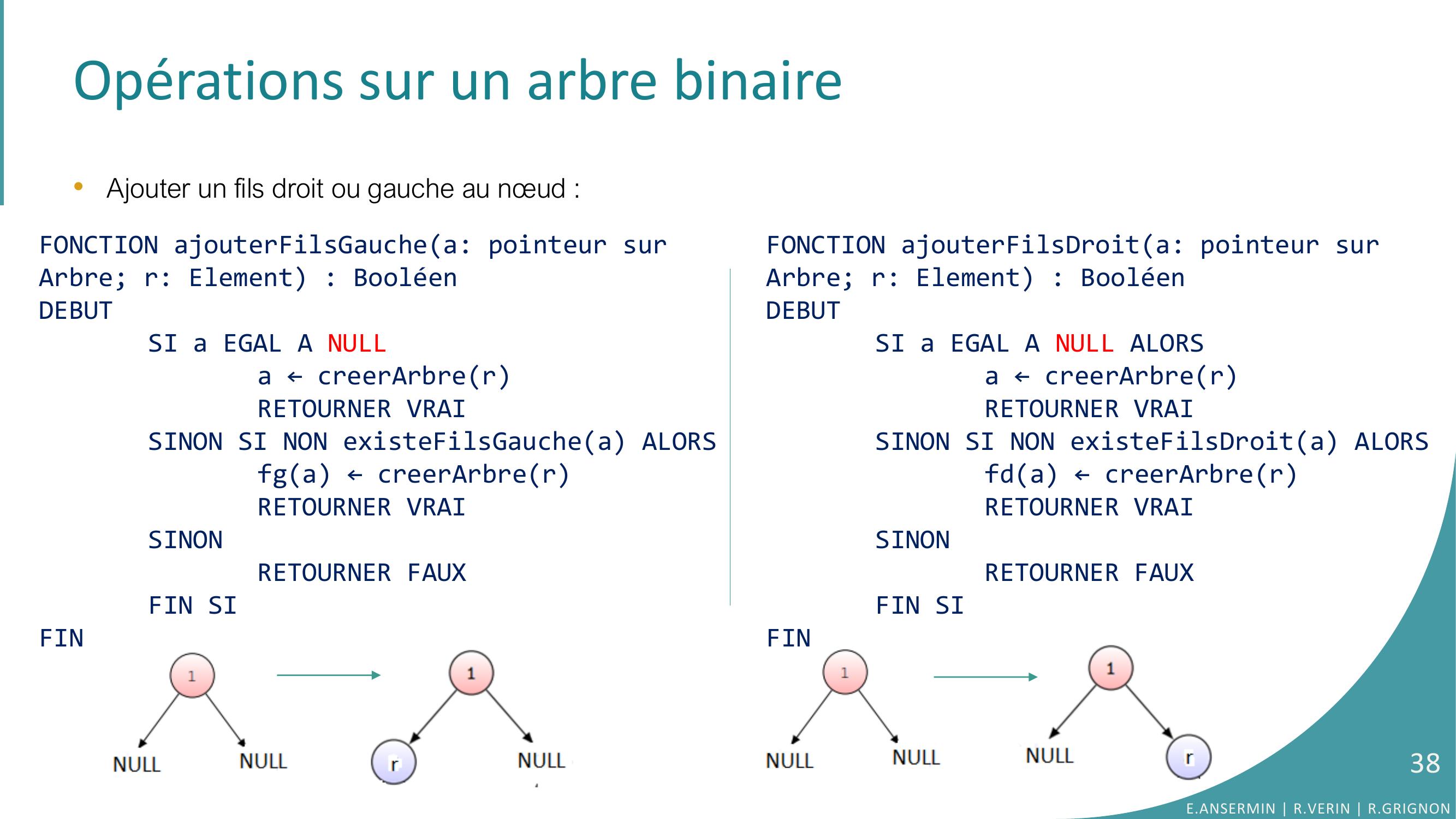
Page 38 : Opérations sur un arbre binaire•Ajouter un fils droit ou gauche au nœud : FONCTION ajouterFilsGauchea: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULLa ←creerArbrerRETOURNER VRAISINON SI NON existeFilsGauchea ALORSfga ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINFONCTION ajouterFilsDroita: pointeur sur Arbre; r: Element : BooléenDEBUTSI a EGAL A NULL ALORSa ←creerArbrerRETOURNER VRAISINON SI NON existeFilsDroita ALORSfda ←creerArbrerRETOURNER VRAISINONRETOURNER FAUXFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON38
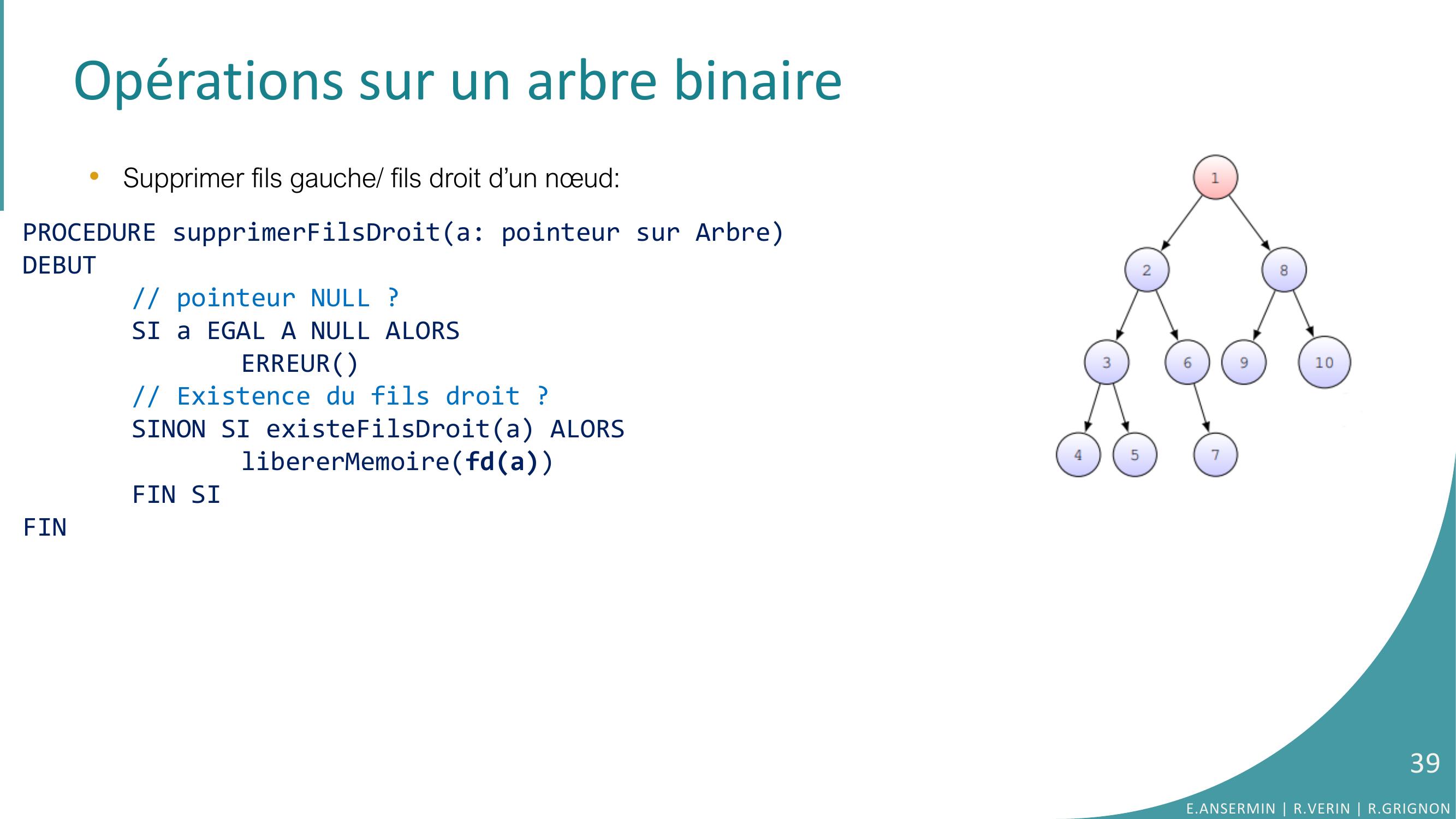
Page 39 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: PROCEDURE supprimerFilsDroita: pointeur sur ArbreDEBUT// pointeur NULL ?SI a EGAL A NULL ALORSERREUR// Existence du fils droit ?SINON SI existeFilsDroita ALORSlibererMemoirefdaFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON39
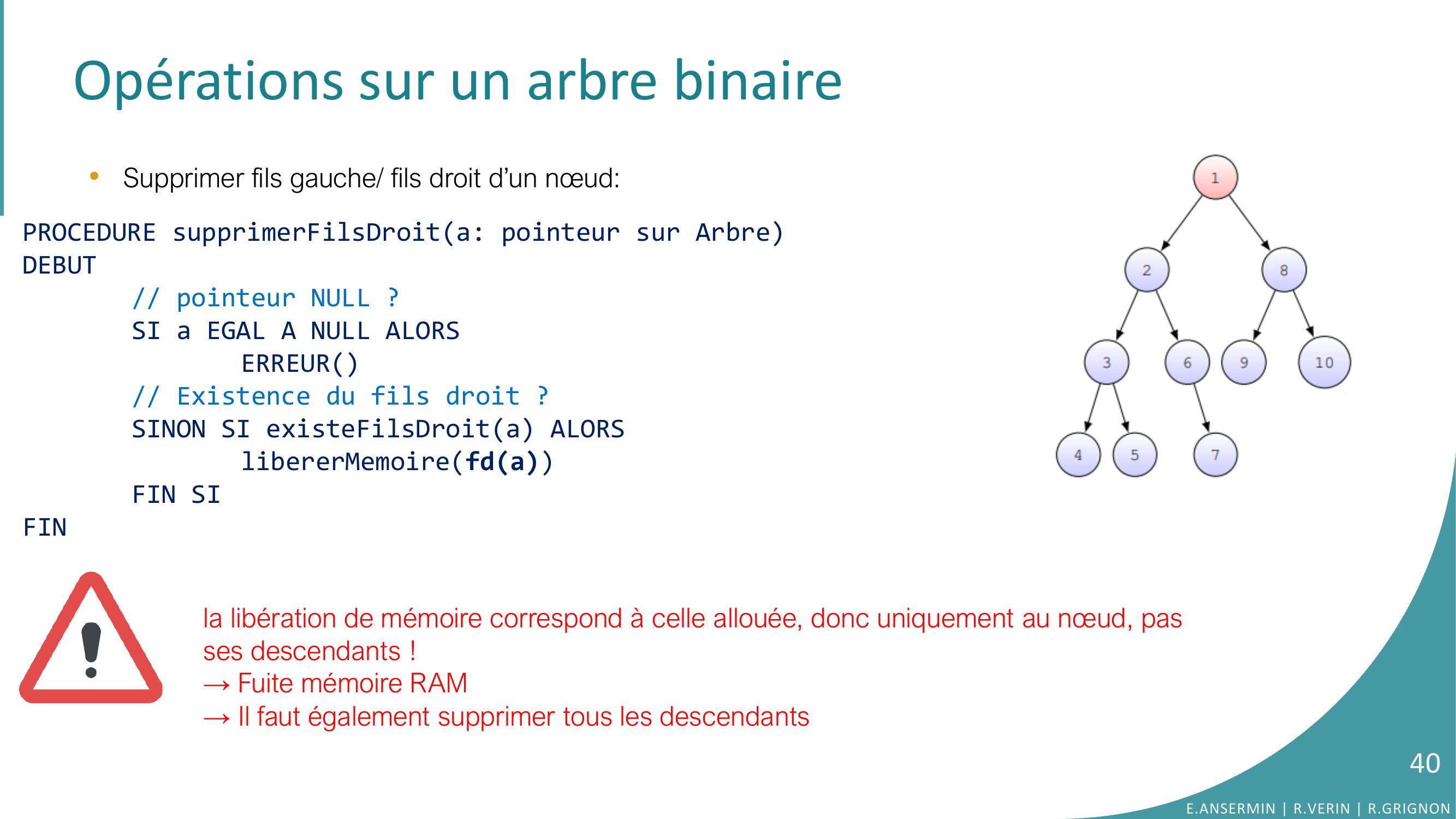
Page 40 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: la libération de mémoire correspond à celle allouée, donc uniquement au nœud, pas ses descendants !→ Fuite mémoire RAM→Il faut également supprimer tous les descendantsPROCEDURE supprimerFilsDroita: pointeur sur ArbreDEBUT// pointeur NULL ?SI a EGAL A NULL ALORSERREUR// Existence du fils droit ?SINON SI existeFilsDroita ALORSlibererMemoirefdaFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON40
Page 41 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: PROCEDURE supprimerFilsDroita: pointeur sur ArbreDEBUT// pointeur NULL ?SI a EGAL A NULL ALORSERREUR// Existence du fils droit ?SINON SI existeFilsDroita ALORS// noeud à supprimer possède un fils droit ?SI existeFilsGauchefda ALORS???FIN SI // noeud à supprimer possède un fils gauche ?SI existeFilsDroitfda ALORS???FIN SIlibererMemoirefdaFIN SIFIN E.ANSERMIN R.VERIN R.GRIGNON41
Page 42 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: PROCEDURE supprimerFilsDroita: pointeur sur ArbreDEBUT// pointeur NULL ?SI a EGAL A NULL ALORSERREUR// Existence du fils droit ?SINON SI existeFilsDroita ALORS// noeud à supprimer possède un fils droit ?SI existeFilsGauchefda ALORSsupprimerFilsGauchefda // appel récursif procédure «miroir»FIN SI // noeud à supprimer possède un fils gauche ?SI existeFilsDroitfda ALORSsupprimerFilsDroitfda// appel récursifFIN SIlibererMemoirefdaFIN SIFIN E.ANSERMIN R.VERIN R.GRIGNON42
Page 43 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: PROCEDURE supprimerFilsDroita: pointeur sur ArbreDEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsDroita ALORSSI existeFilsGauchefda ALORSsupprimerFilsGauchefda FIN SI SI existeFilsDroitfda ALORSsupprimerFilsDroitfdaFIN SIlibererMemoirefdaFIN SIFINPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON43
Page 44 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON44
Page 45 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON45
Page 46 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON46
Page 47 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON47
Page 48 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaaE.ANSERMIN R.VERIN R.GRIGNON48
Page 49 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaaE.ANSERMIN R.VERIN R.GRIGNON49
Page 50 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaaE.ANSERMIN R.VERIN R.GRIGNON50
Page 51 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaaE.ANSERMIN R.VERIN R.GRIGNON51
Page 52 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON52
Page 53 : Opérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON53
Page 54 : PROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINOpérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationE.ANSERMIN R.VERIN R.GRIGNON54
Page 55 : Opérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON55
Page 56 : Opérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON56
Page 57 : Opérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON57
Page 58 : Opérations sur un arbre binaireaaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON58
Page 59 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON59
Page 60 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON60
Page 61 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON61
Page 62 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON62
Page 63 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON63
Page 64 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON64
Page 65 : Opérations sur un arbre binaireaa•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINE.ANSERMIN R.VERIN R.GRIGNON65
Page 66 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON66
Page 67 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON67
Page 68 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON68
Page 69 : Opérations sur un arbre binairea•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON69
Page 70 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON70
Page 71 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON71
Page 72 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON72
Page 73 : Opérations sur un arbre binaire•Supprimer fils gauche/ fils droit d’un nœud: illustrationPROCEDURE supprimerFilsGauchea: pointeur sur Arbre DEBUTSI a EGAL A NULL ALORSERREURSINON SI existeFilsGauchea ALORSSI existeFilsGauchefga ALORS supprimerFilsGauchefgaFIN SISI existeFilsDroitfga ALORSsupprimerFilsDroitfga FIN SI libererMemoirefgaFIN SI FINaE.ANSERMIN R.VERIN R.GRIGNON73
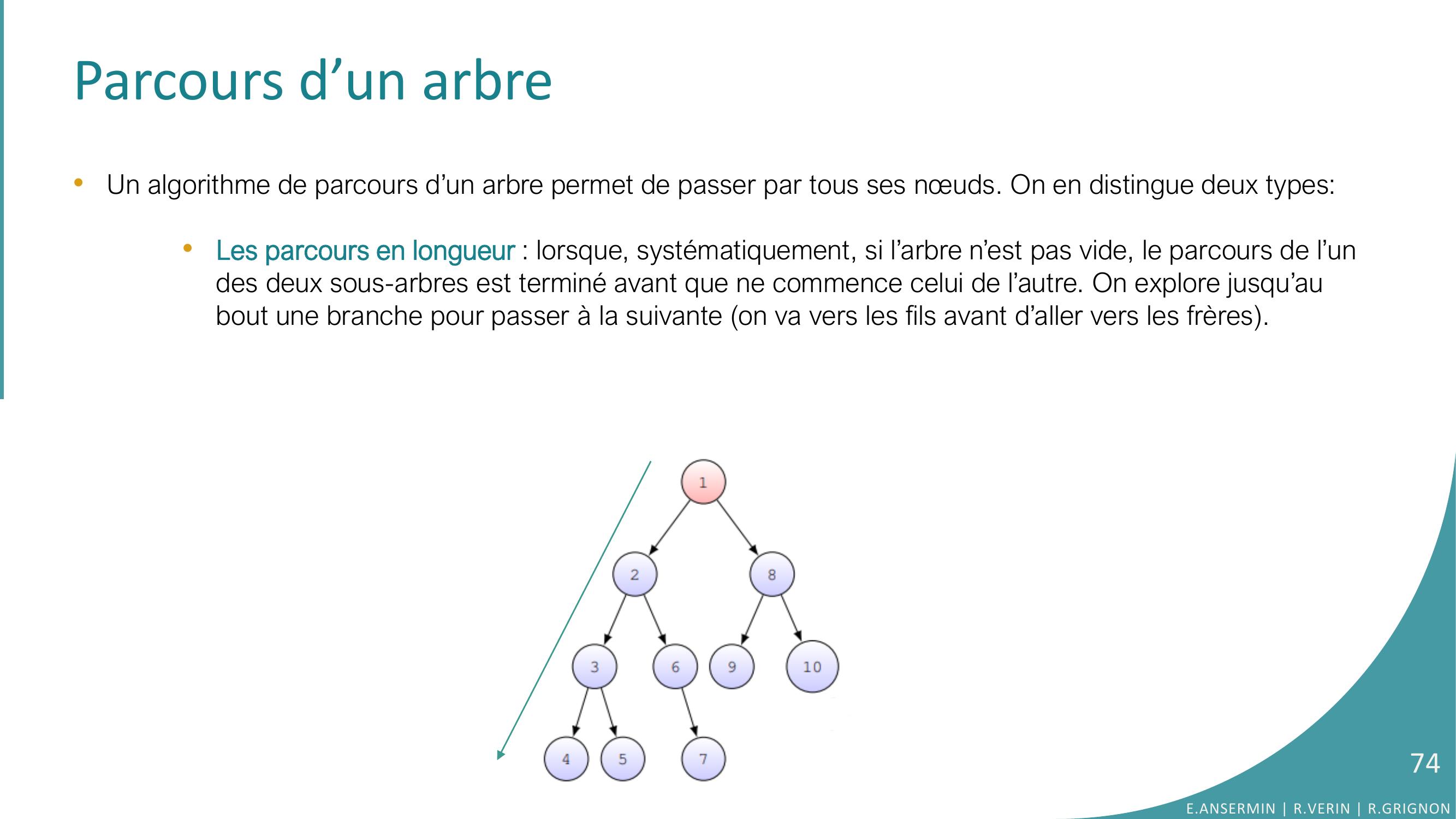
Page 74 : Parcours d’un arbre•Un algorithme de parcours d’un arbre permet de passer par tous ses nœuds. On en distingue deux types:•Les parcours en longueur : lorsque, systématiquement, si l’arbre n’est pas vide, le parcours de l’un des deux sous-arbres est terminé avant que ne commence celui de l’autre. On explore jusqu’au bout une branche pour passer à la suivante on va vers les fils avant d’aller vers les frères. E.ANSERMIN R.VERIN R.GRIGNON74
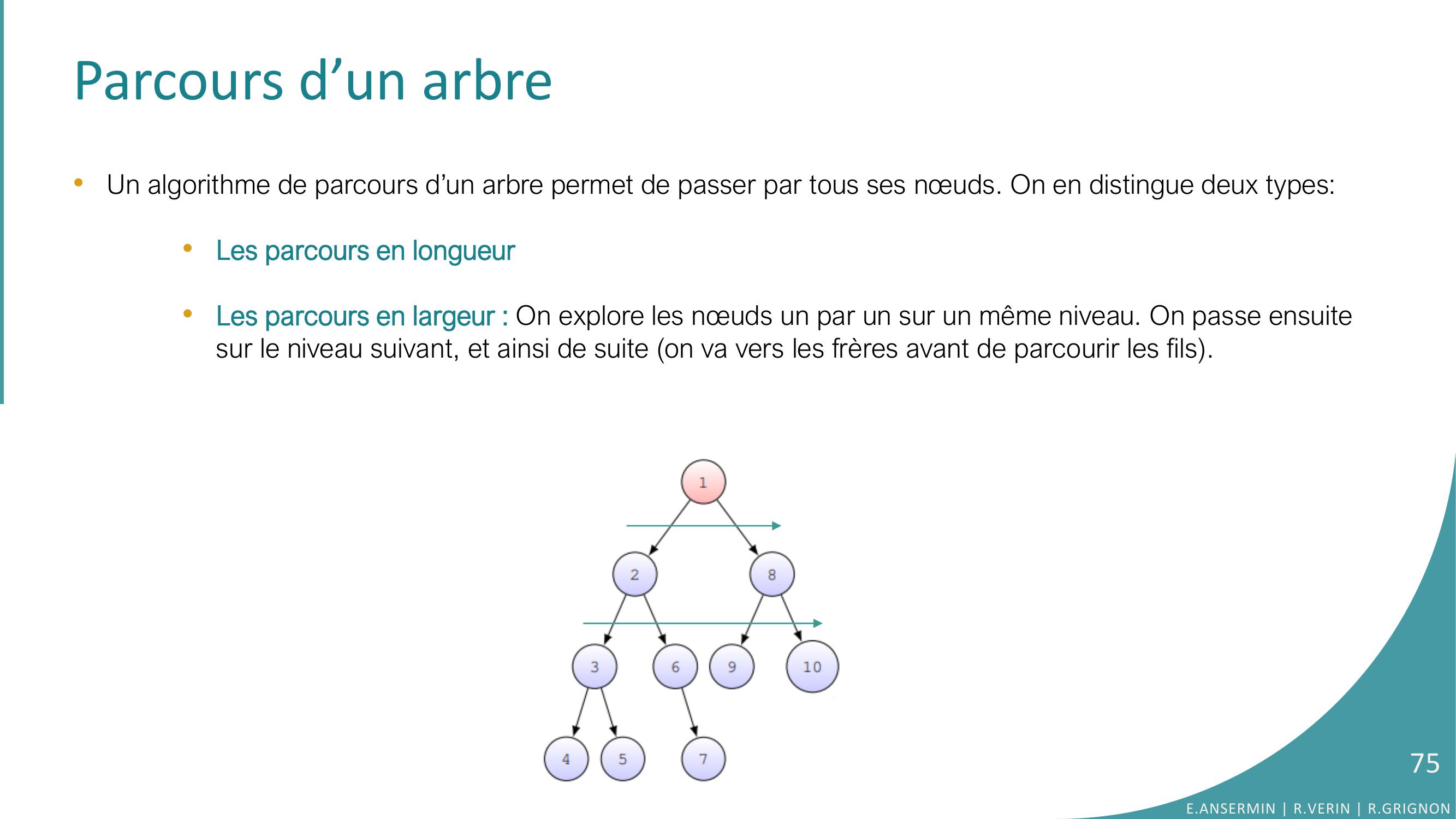
Page 75 : Parcours d’un arbre•Un algorithme de parcours d’un arbre permet de passer par tous ses nœuds. On en distingue deux types:•Les parcours en longueur•Les parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. E.ANSERMIN R.VERIN R.GRIGNON75
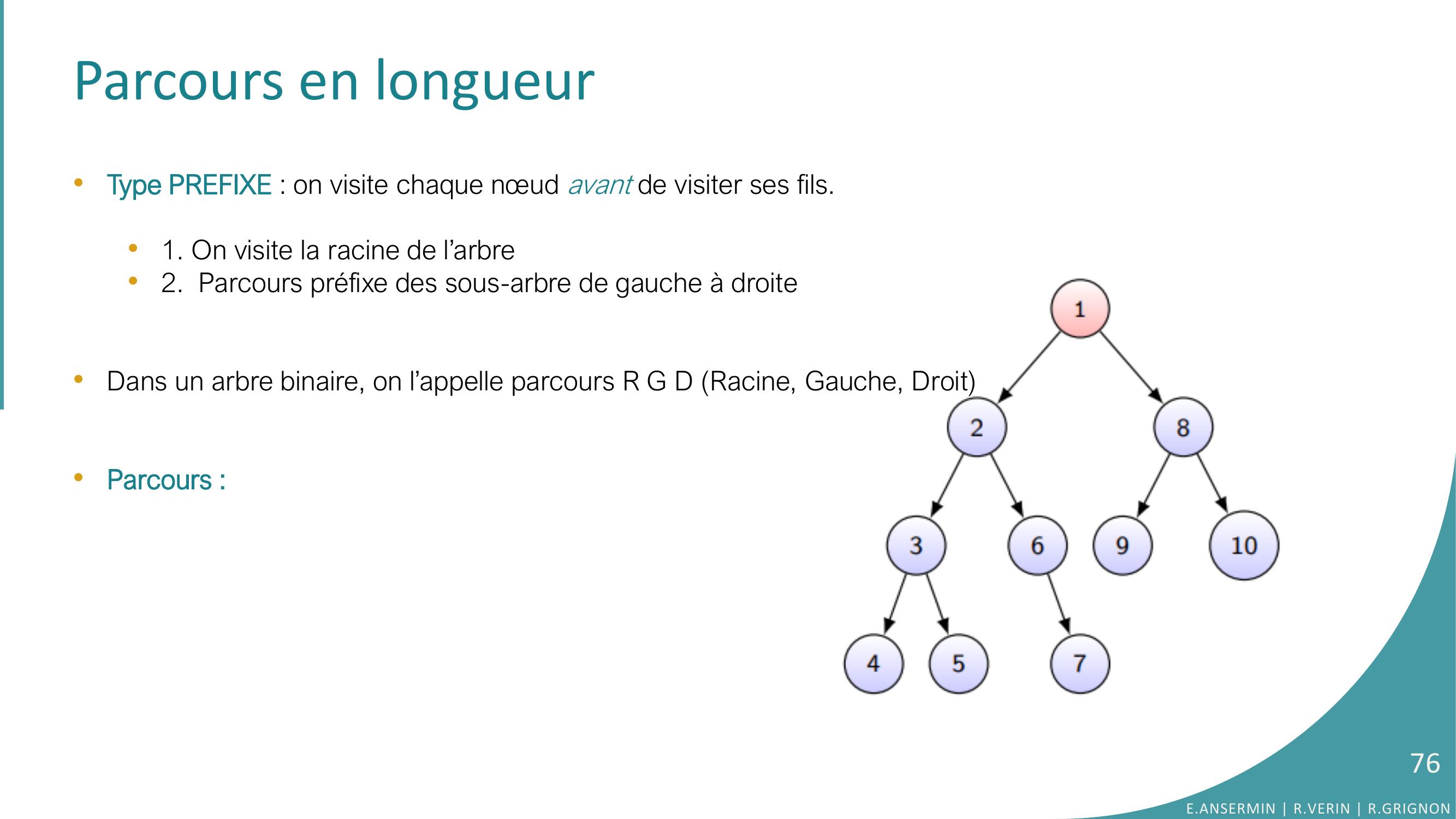
Page 76 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours :E.ANSERMIN R.VERIN R.GRIGNON76
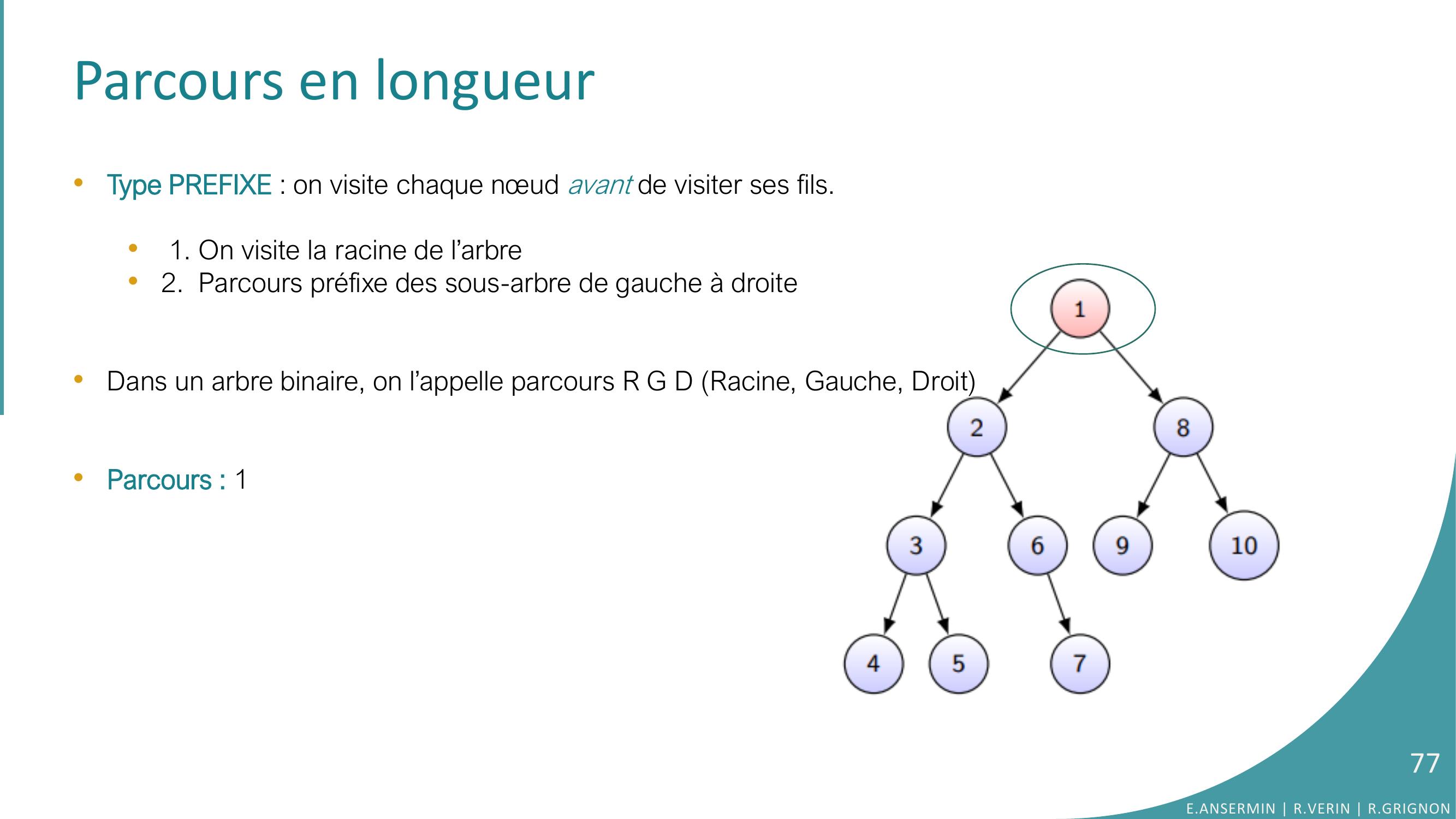
Page 77 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1E.ANSERMIN R.VERIN R.GRIGNON77
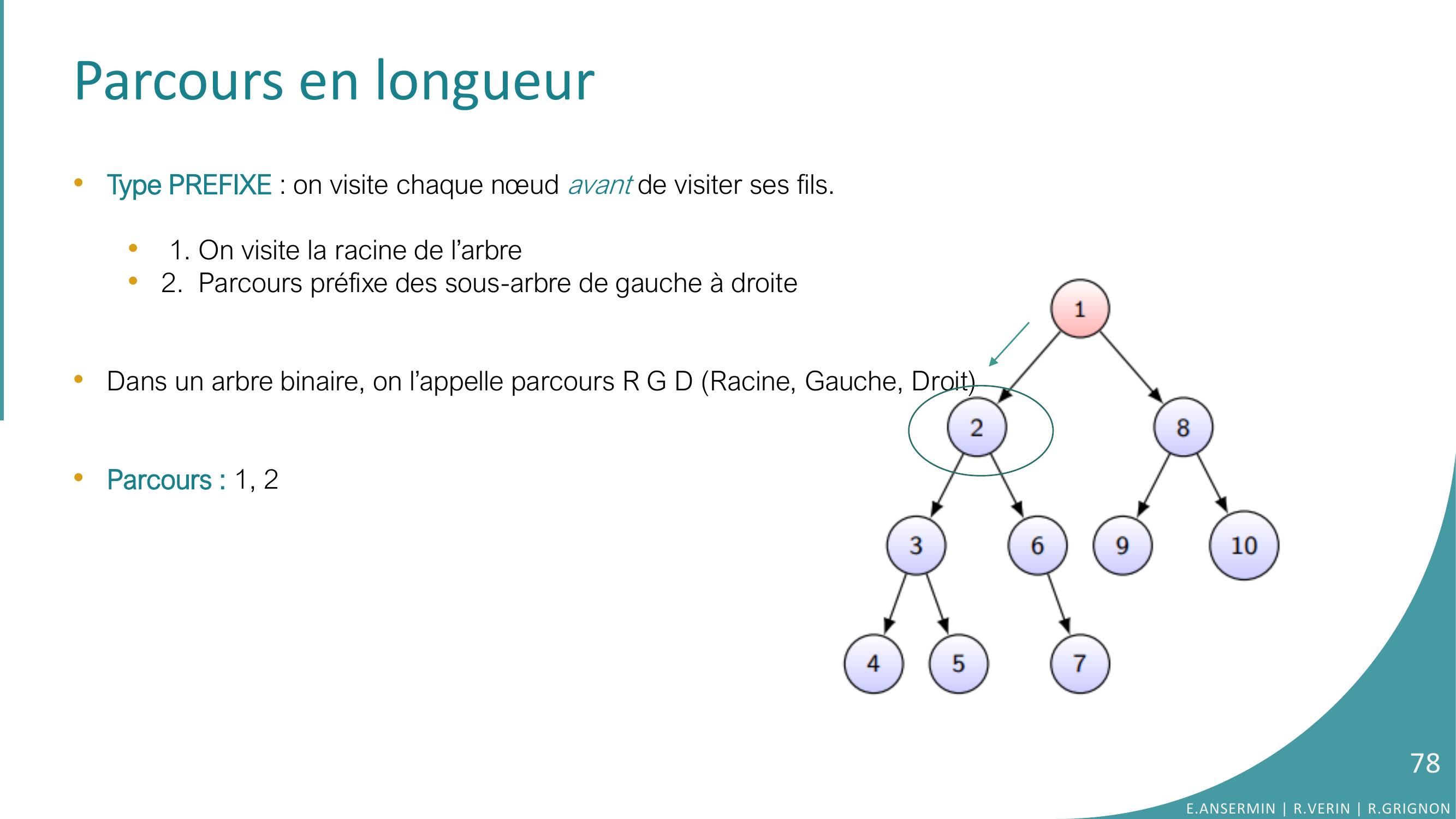
Page 78 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2E.ANSERMIN R.VERIN R.GRIGNON78
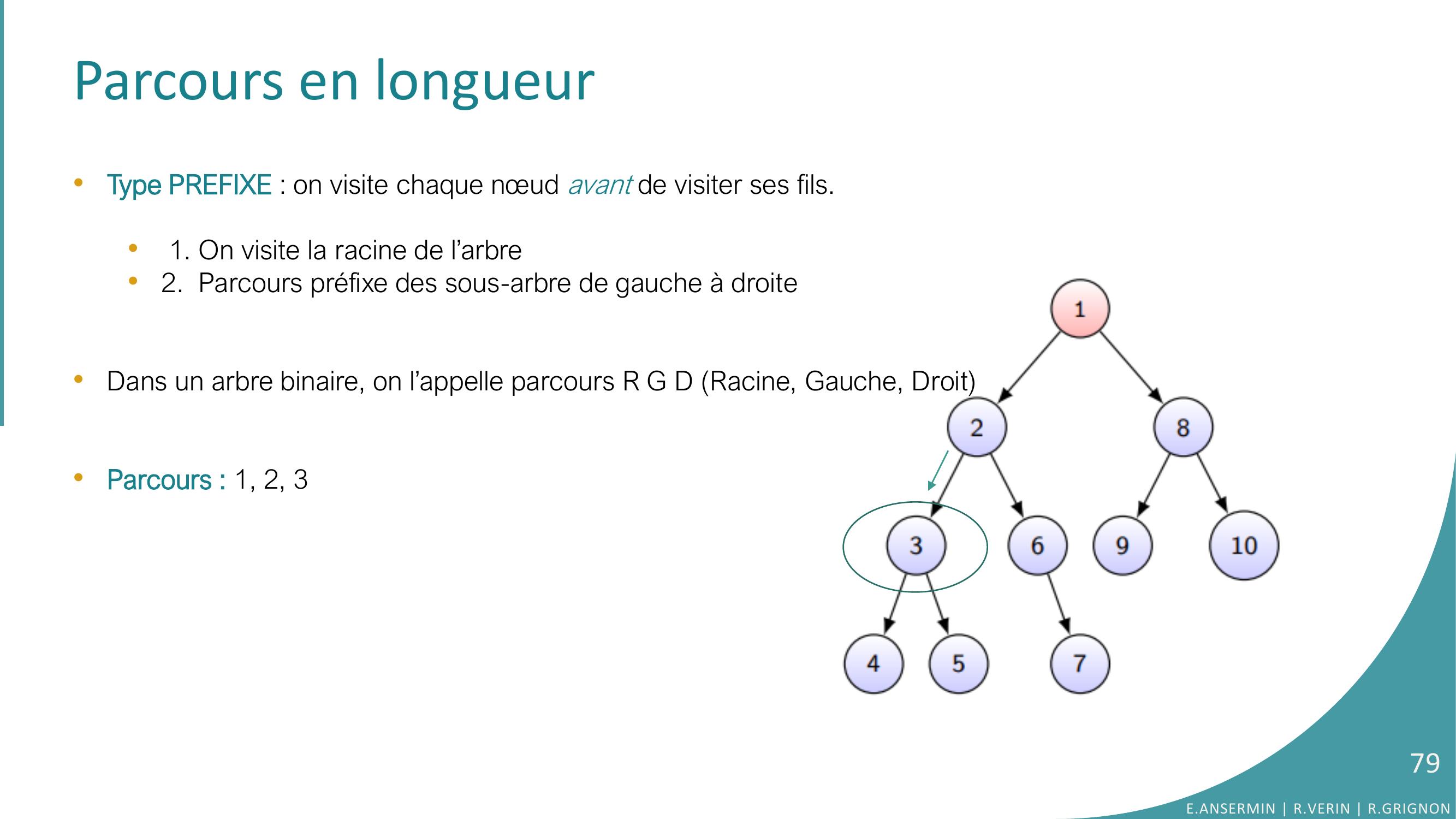
Page 79 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2, 3E.ANSERMIN R.VERIN R.GRIGNON79
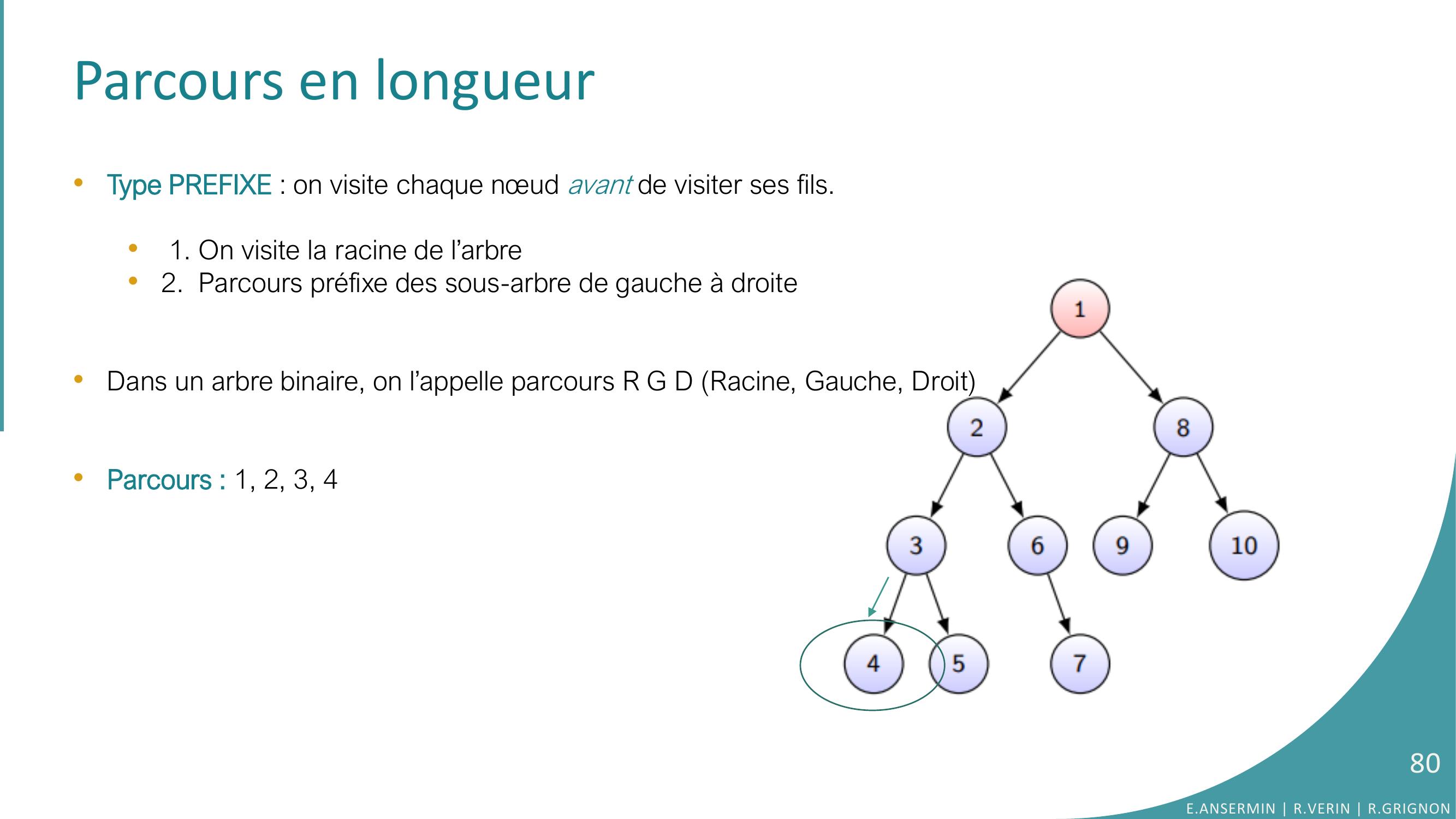
Page 80 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2, 3, 4E.ANSERMIN R.VERIN R.GRIGNON80
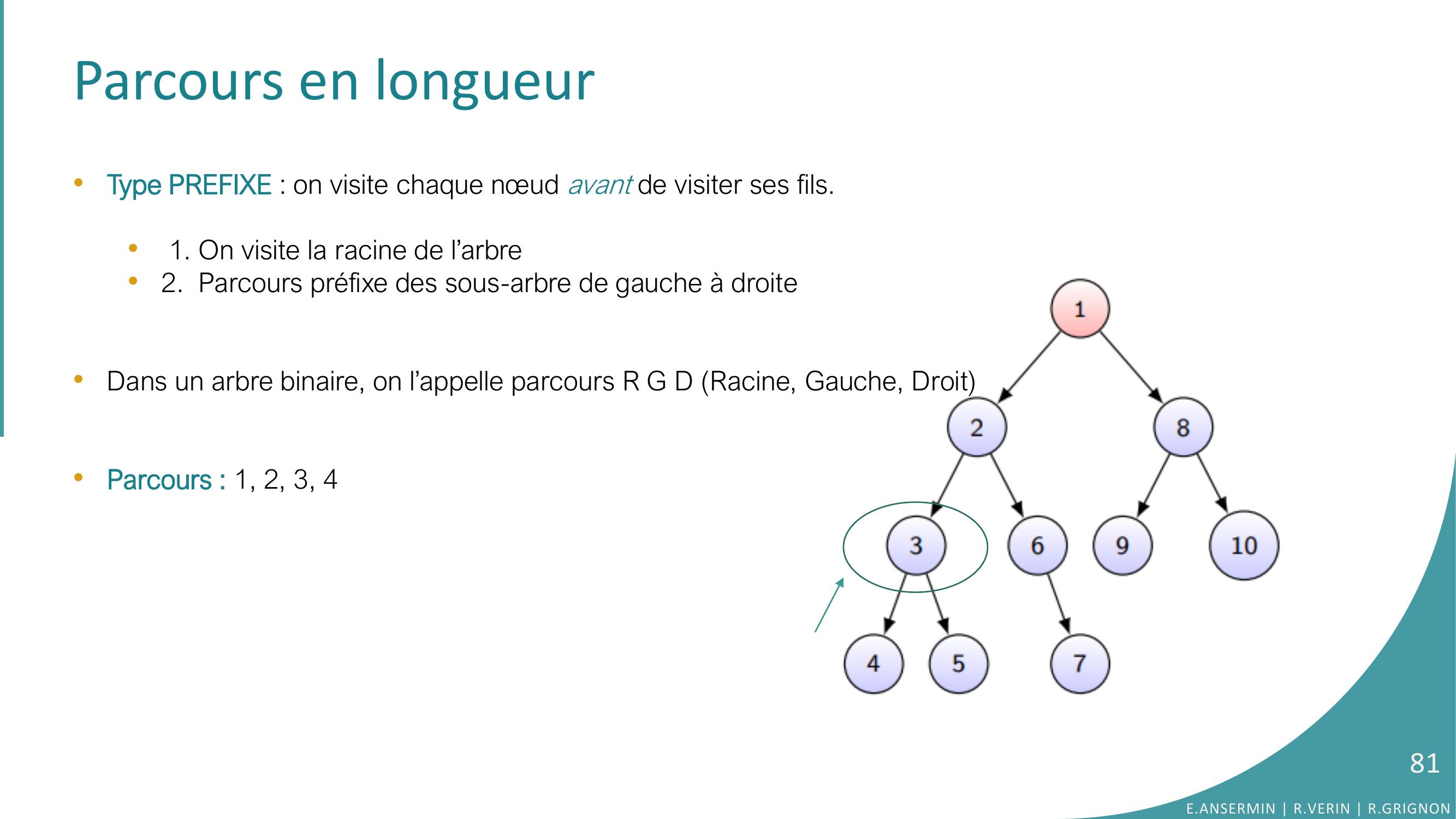
Page 81 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2, 3, 4E.ANSERMIN R.VERIN R.GRIGNON81
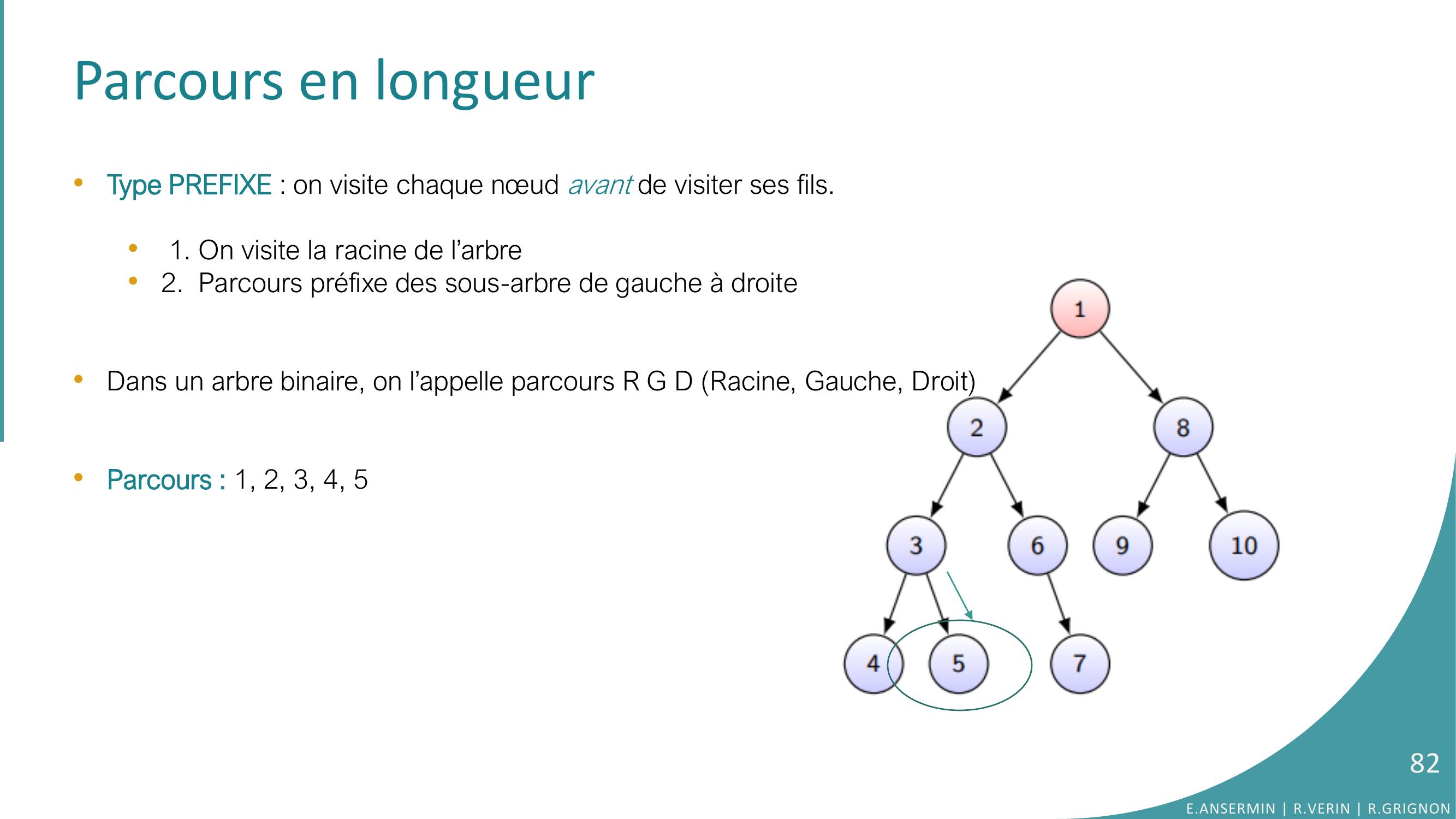
Page 82 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2, 3, 4, 5E.ANSERMIN R.VERIN R.GRIGNON82
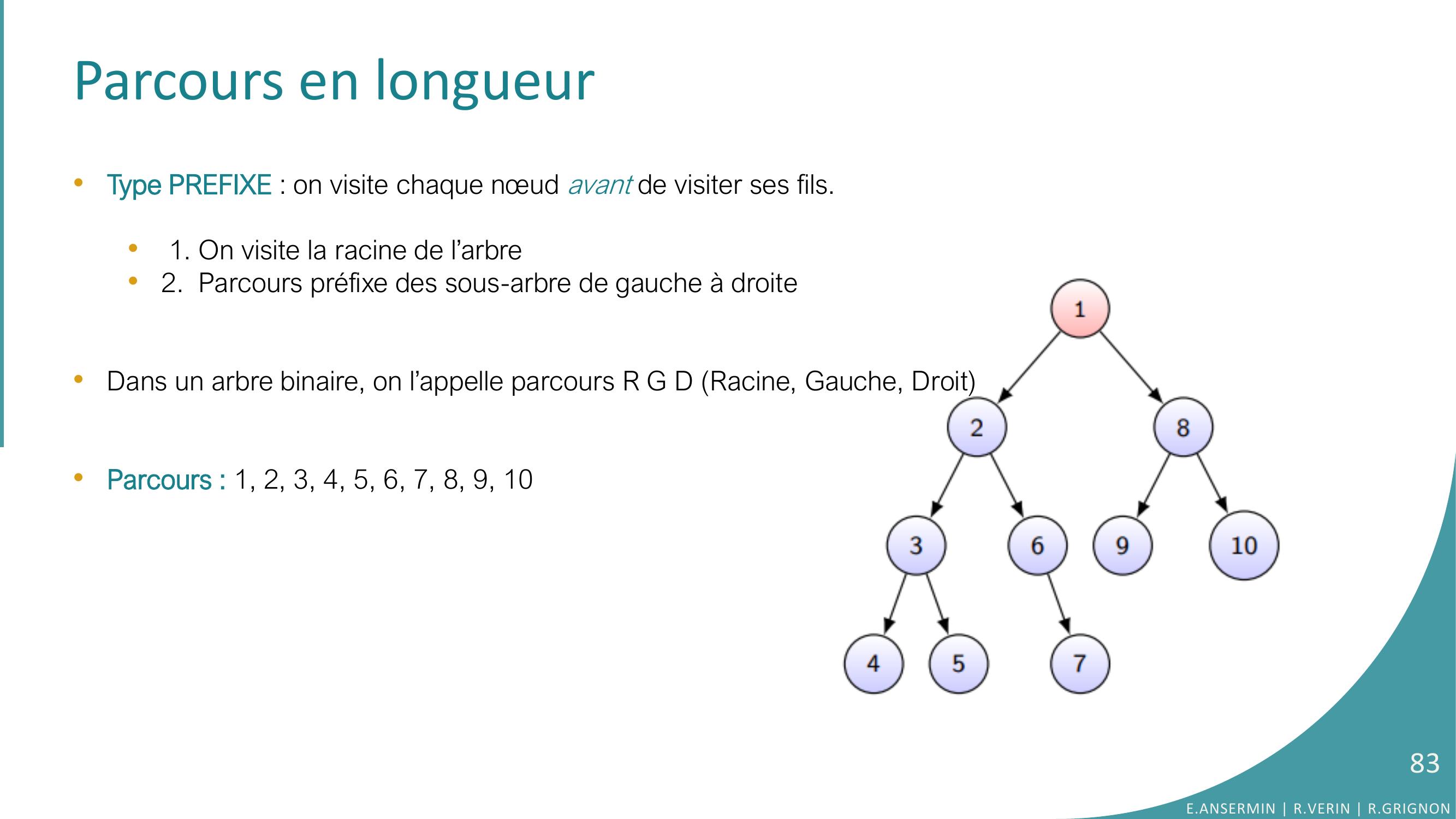
Page 83 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Dans un arbre binaire, on l’appelle parcours R G D Racine, Gauche, Droit•Parcours : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 E.ANSERMIN R.VERIN R.GRIGNON83
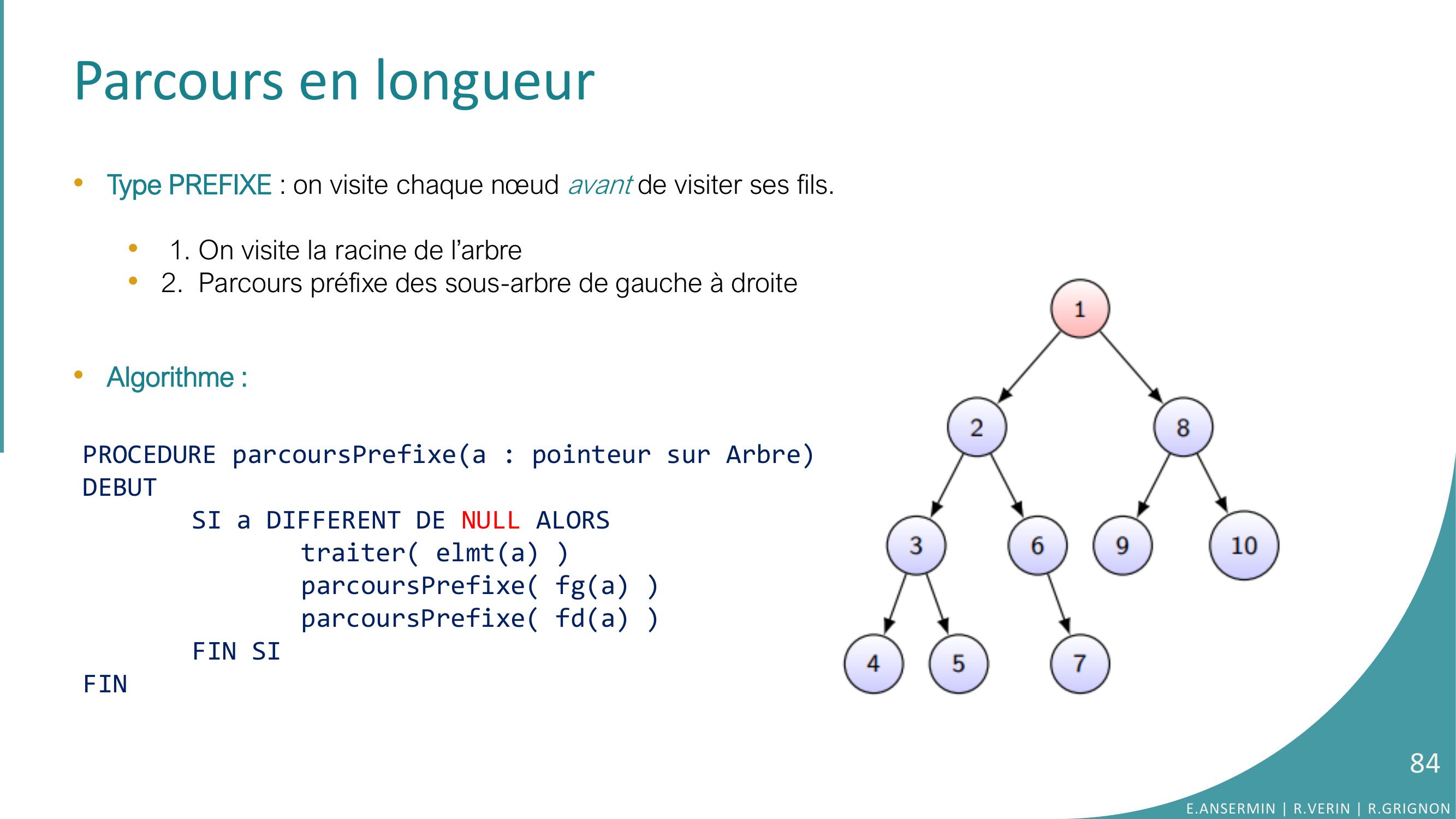
Page 84 : Parcours en longueur•Type PREFIXE : on visite chaque nœud avant de visiter ses fils.•1. On visite la racine de l’arbre•2. Parcours préfixe des sous-arbre de gauche à droite •Algorithme :PROCEDURE parcoursPrefixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORStraiter elmta parcoursPrefixe fga parcoursPrefixe fda FIN SIFINE.ANSERMIN R.VERIN R.GRIGNON84
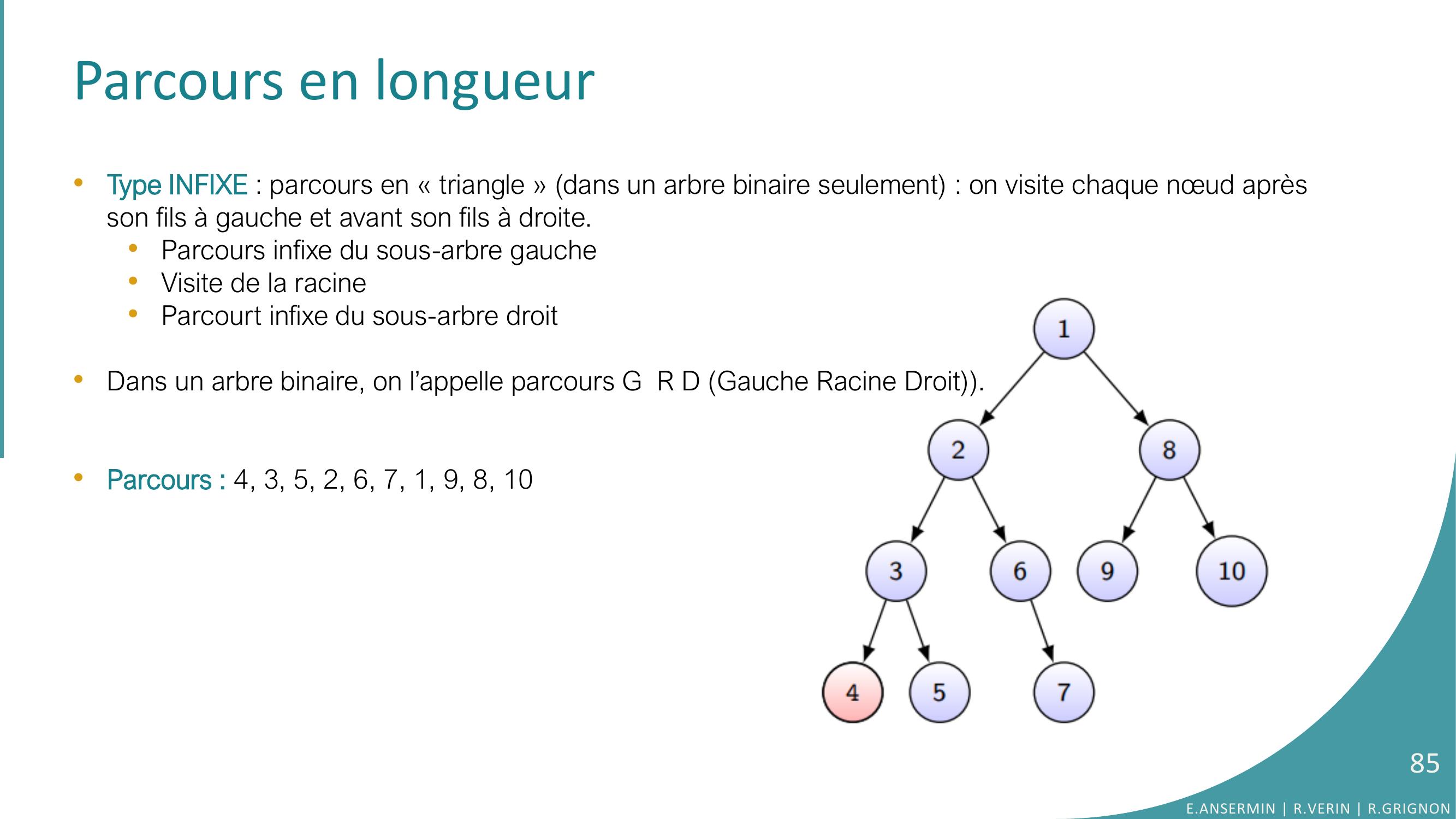
Page 85 : Parcours en longueur•Type INFIXE : parcours en « triangle » dans un arbre binaire seulement : on visite chaque nœud après son fils à gauche et avant son fils à droite.•Parcours infixe du sous-arbre gauche •Visite de la racine•Parcourt infixe du sous-arbre droit•Dans un arbre binaire, on l’appelle parcours G R D Gauche Racine Droit.•Parcours : 4, 3, 5, 2, 6, 7, 1, 9, 8, 10E.ANSERMIN R.VERIN R.GRIGNON85
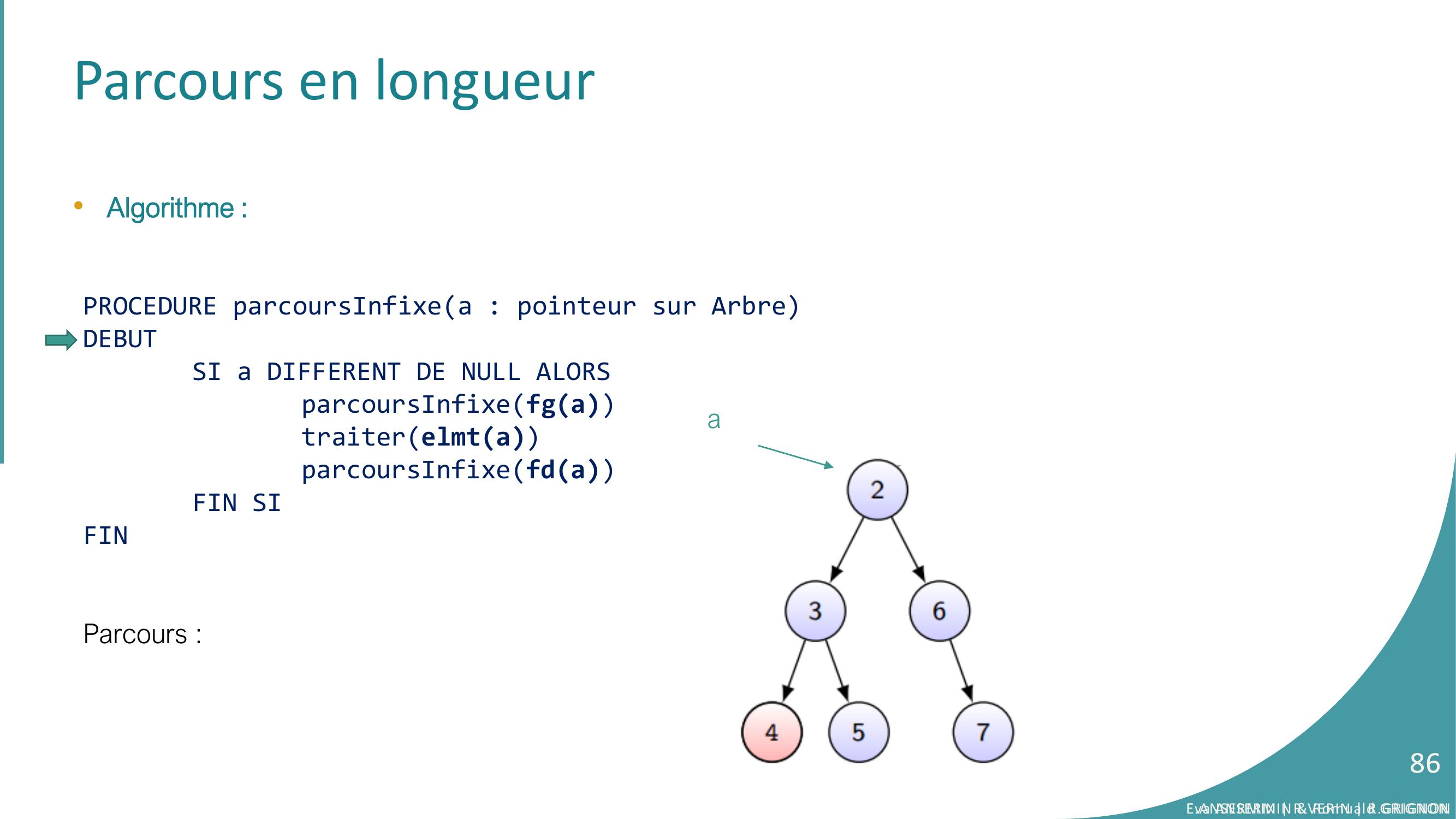
Page 86 : aParcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :Eva ANSERMIN & Romuald GRIGNON86E.ANSERMIN R.VERIN R.GRIGNON86
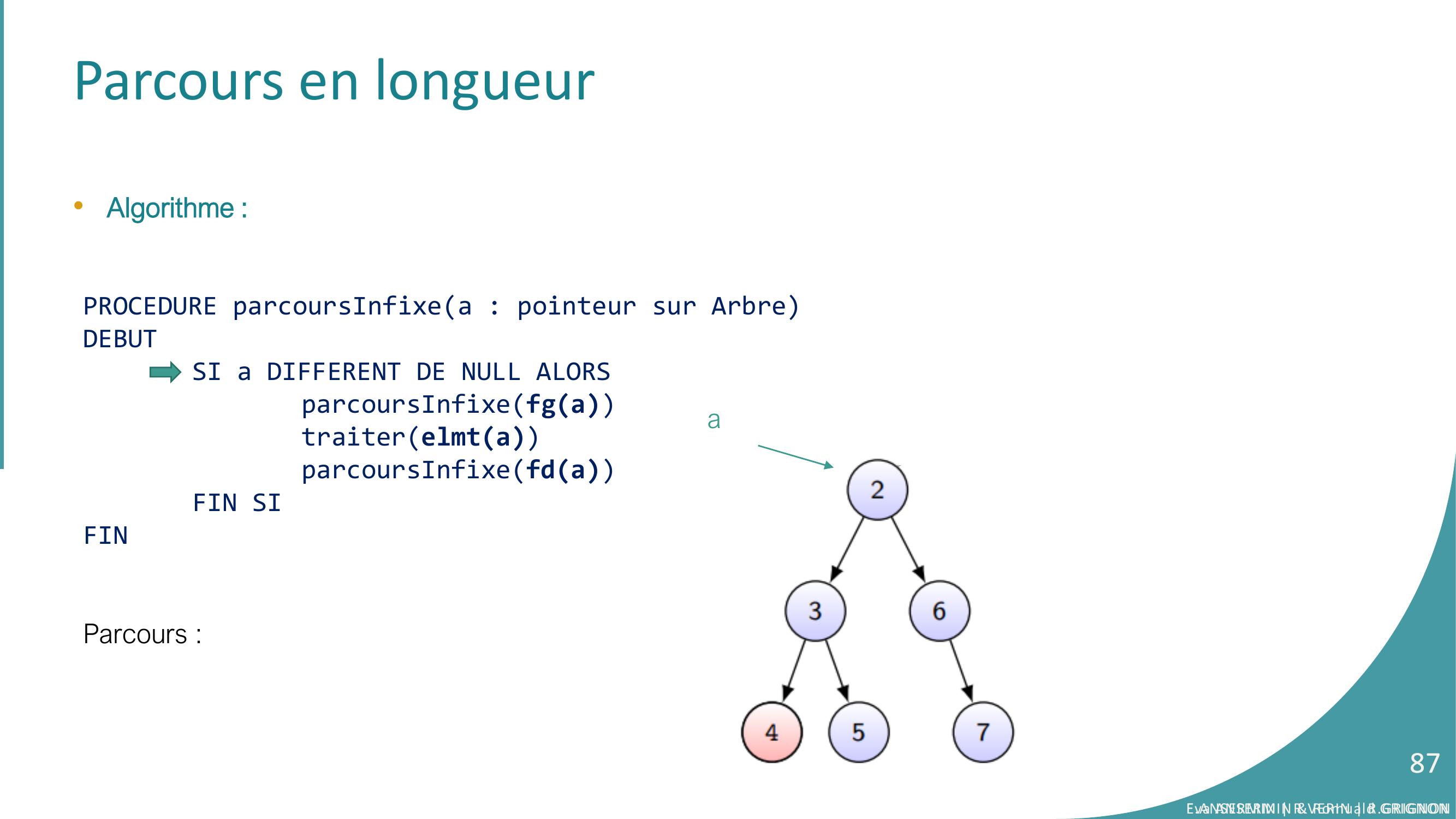
Page 87 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :aEva ANSERMIN & Romuald GRIGNON87E.ANSERMIN R.VERIN R.GRIGNON87
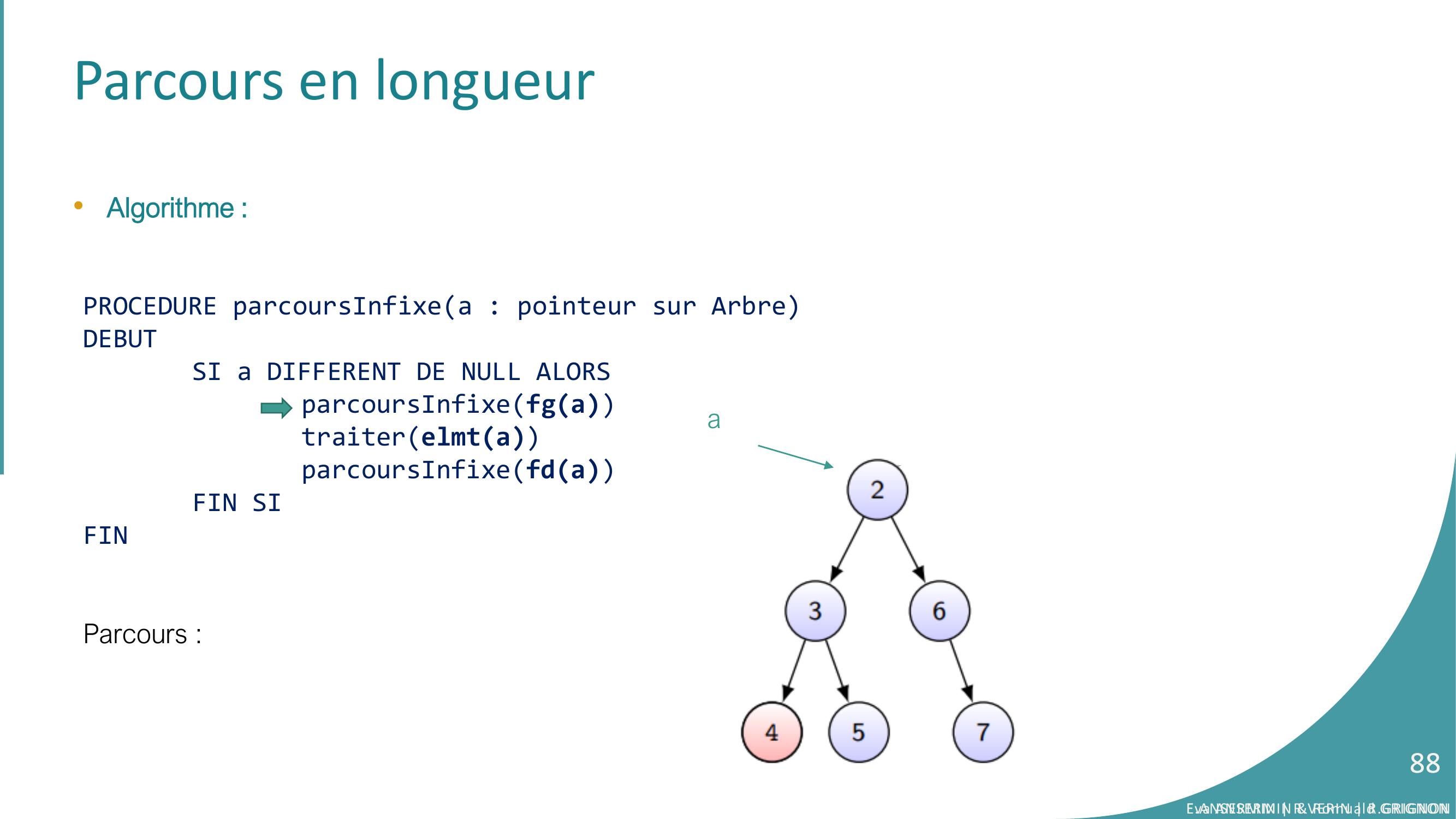
Page 88 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :aEva ANSERMIN & Romuald GRIGNON88E.ANSERMIN R.VERIN R.GRIGNON88
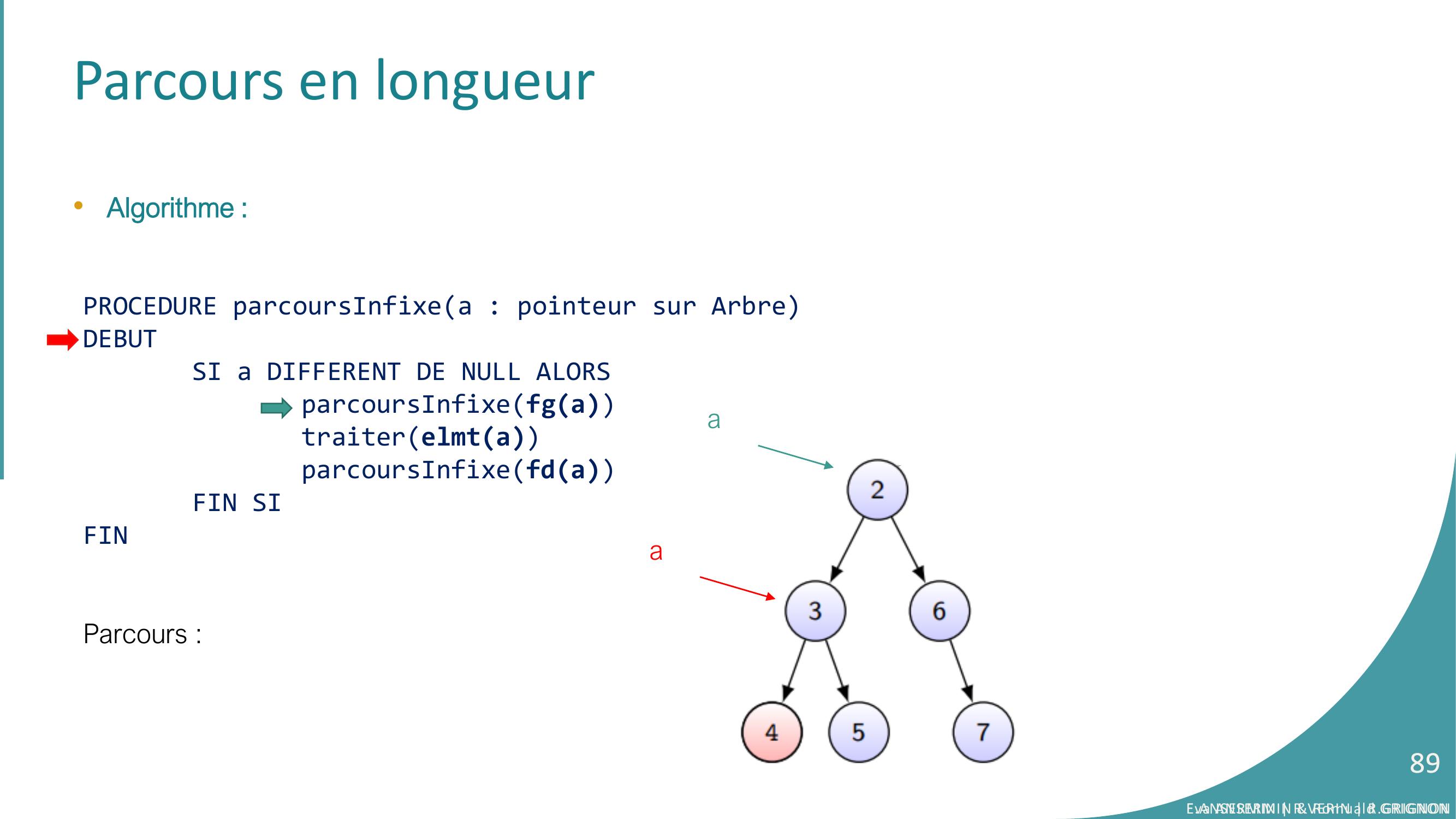
Page 89 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :aaEva ANSERMIN & Romuald GRIGNON89E.ANSERMIN R.VERIN R.GRIGNON89
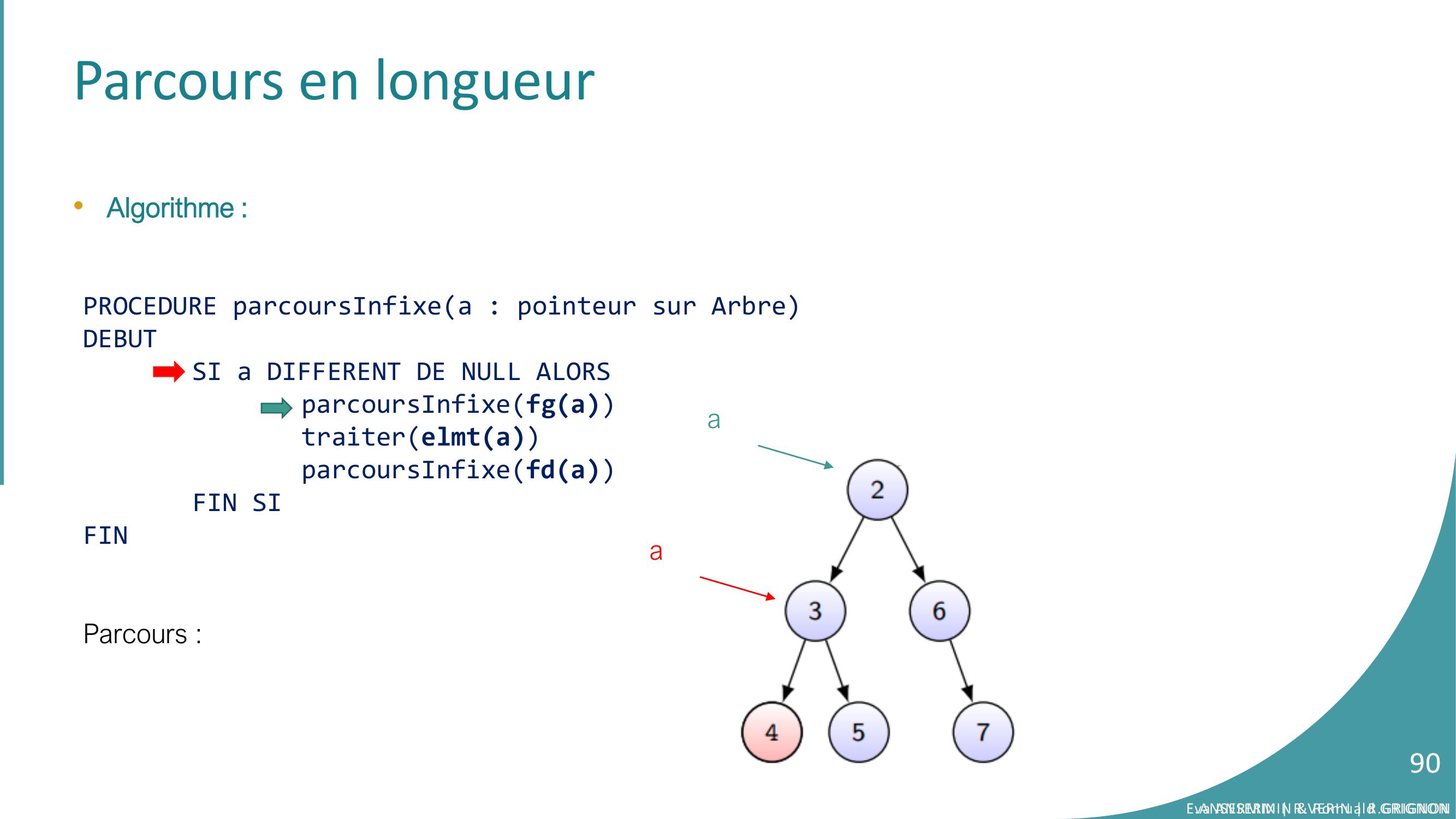
Page 90 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :aaEva ANSERMIN & Romuald GRIGNON90E.ANSERMIN R.VERIN R.GRIGNON90
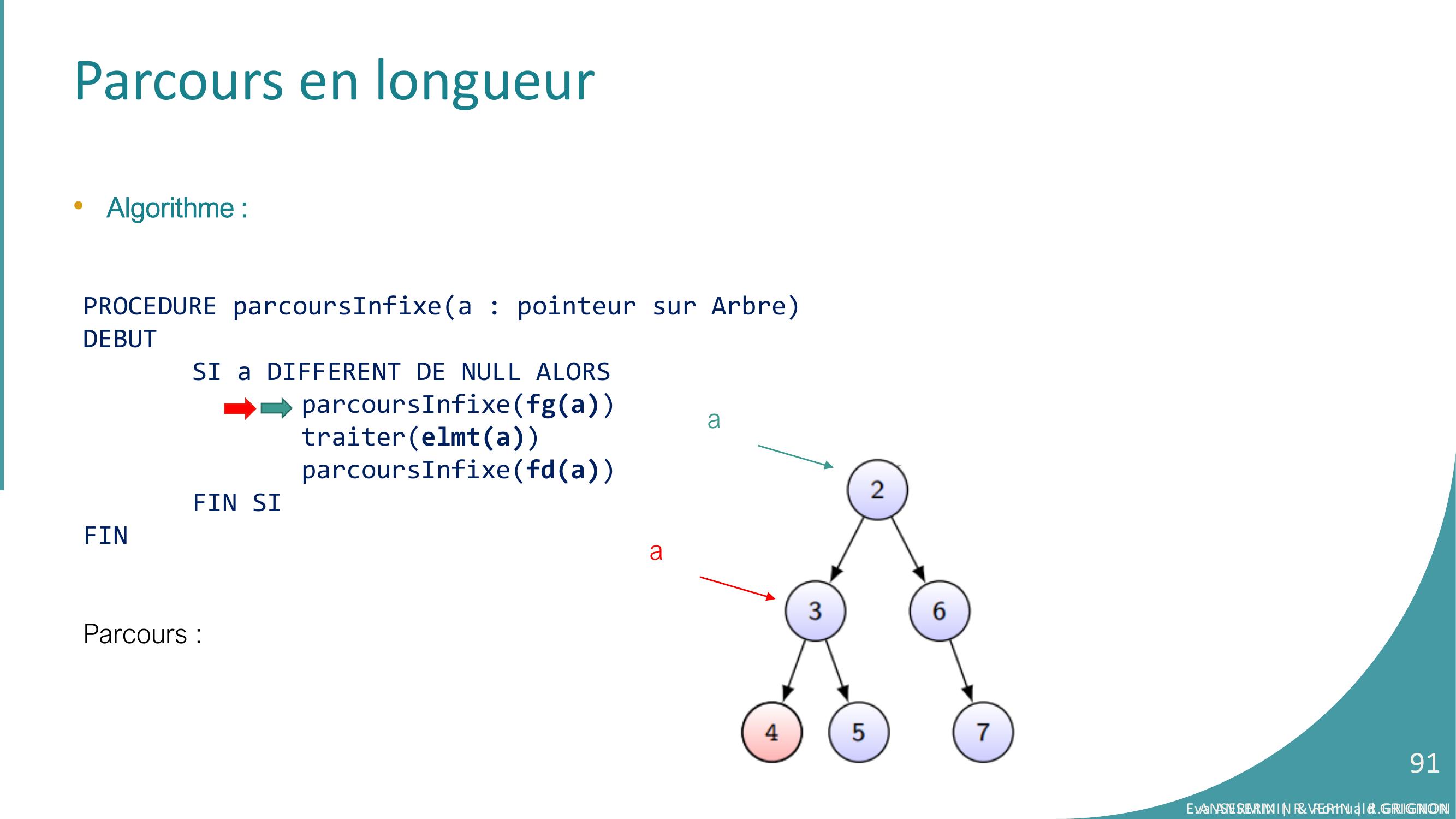
Page 91 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :aaEva ANSERMIN & Romuald GRIGNON91E.ANSERMIN R.VERIN R.GRIGNON91
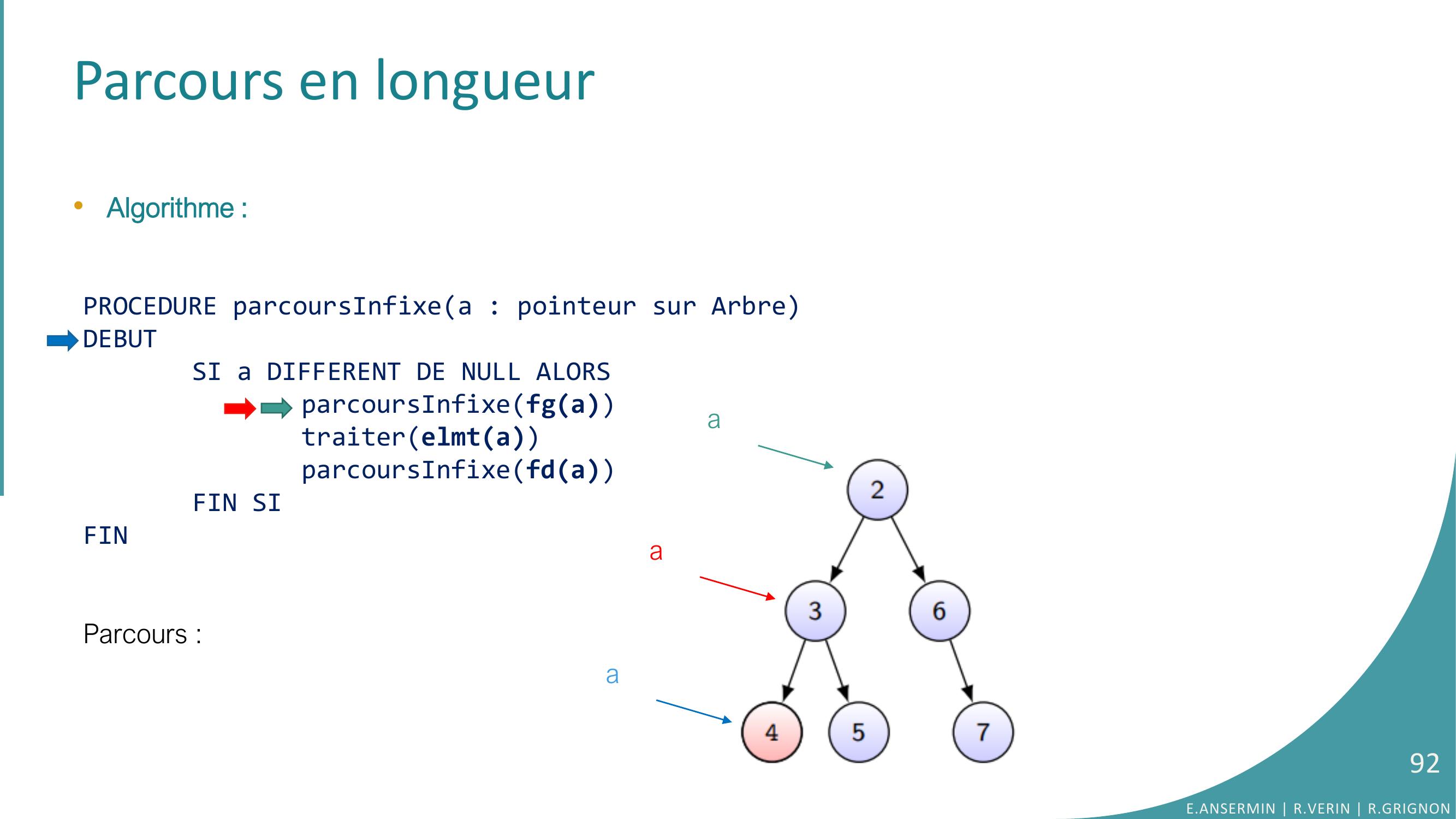
Page 92 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :E.ANSERMIN R.VERIN R.GRIGNON92aaa
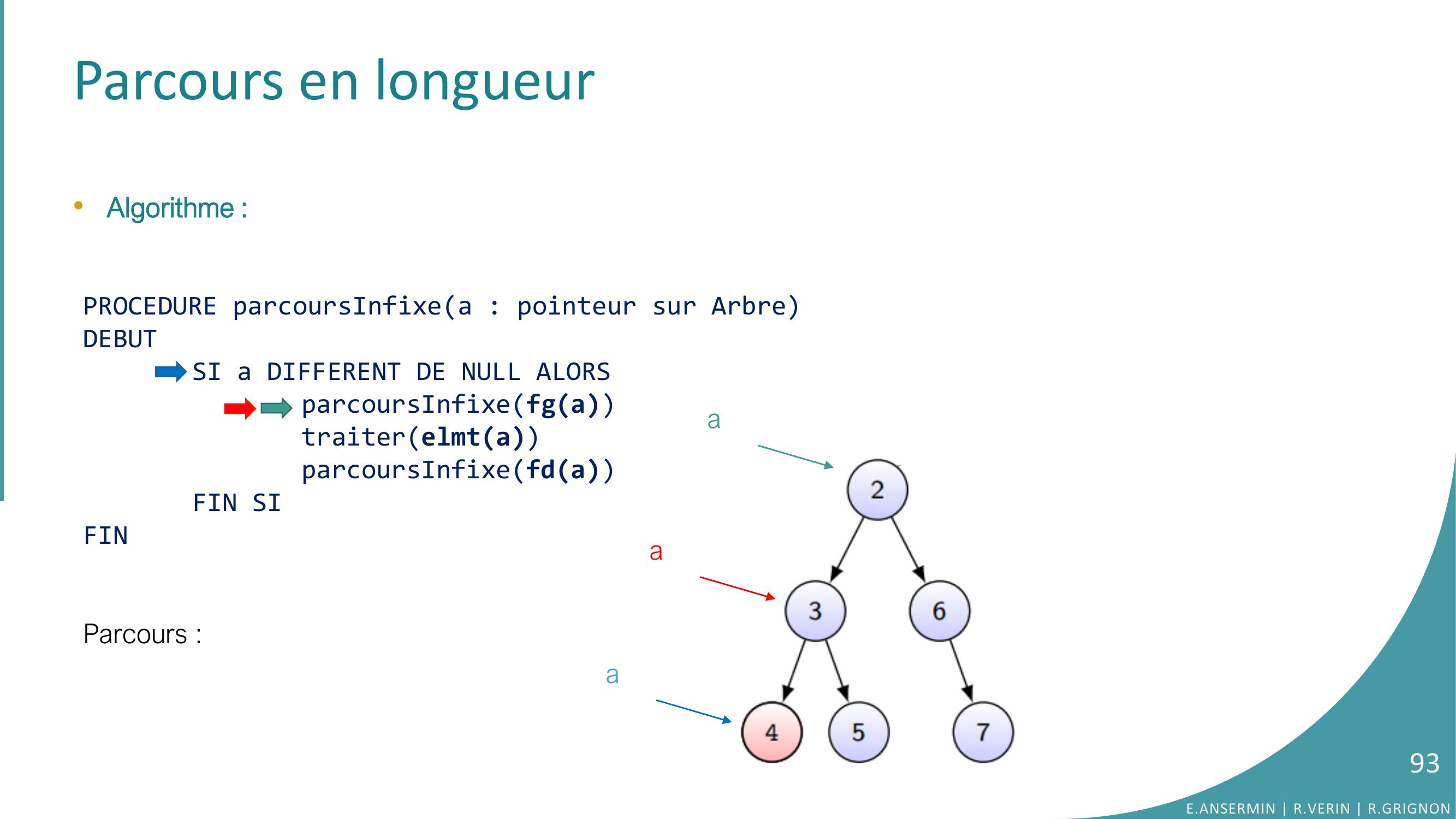
Page 93 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :E.ANSERMIN R.VERIN R.GRIGNON93aaa
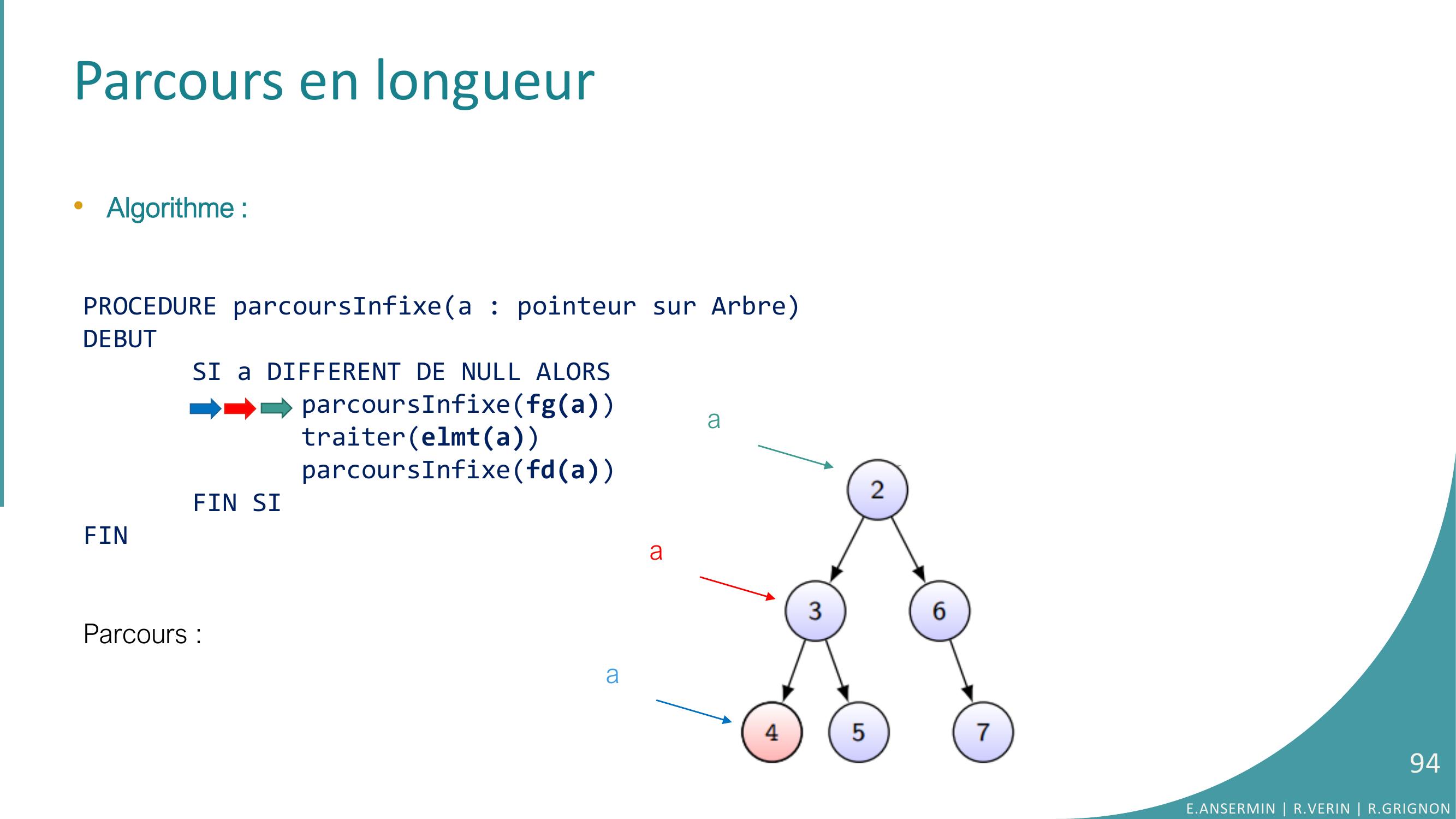
Page 94 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :E.ANSERMIN R.VERIN R.GRIGNON94aaa
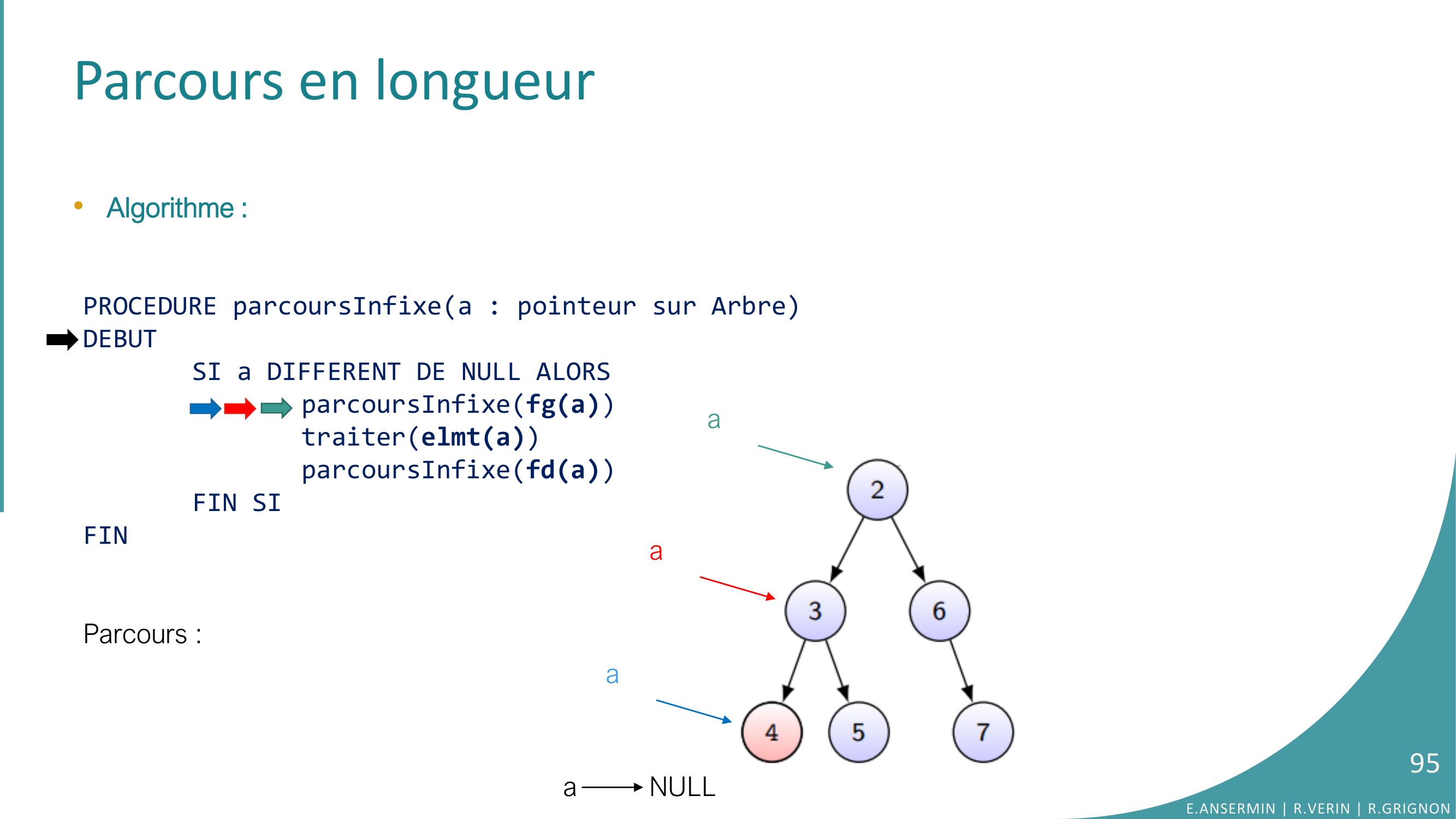
Page 95 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :a NULLE.ANSERMIN R.VERIN R.GRIGNON95aaa
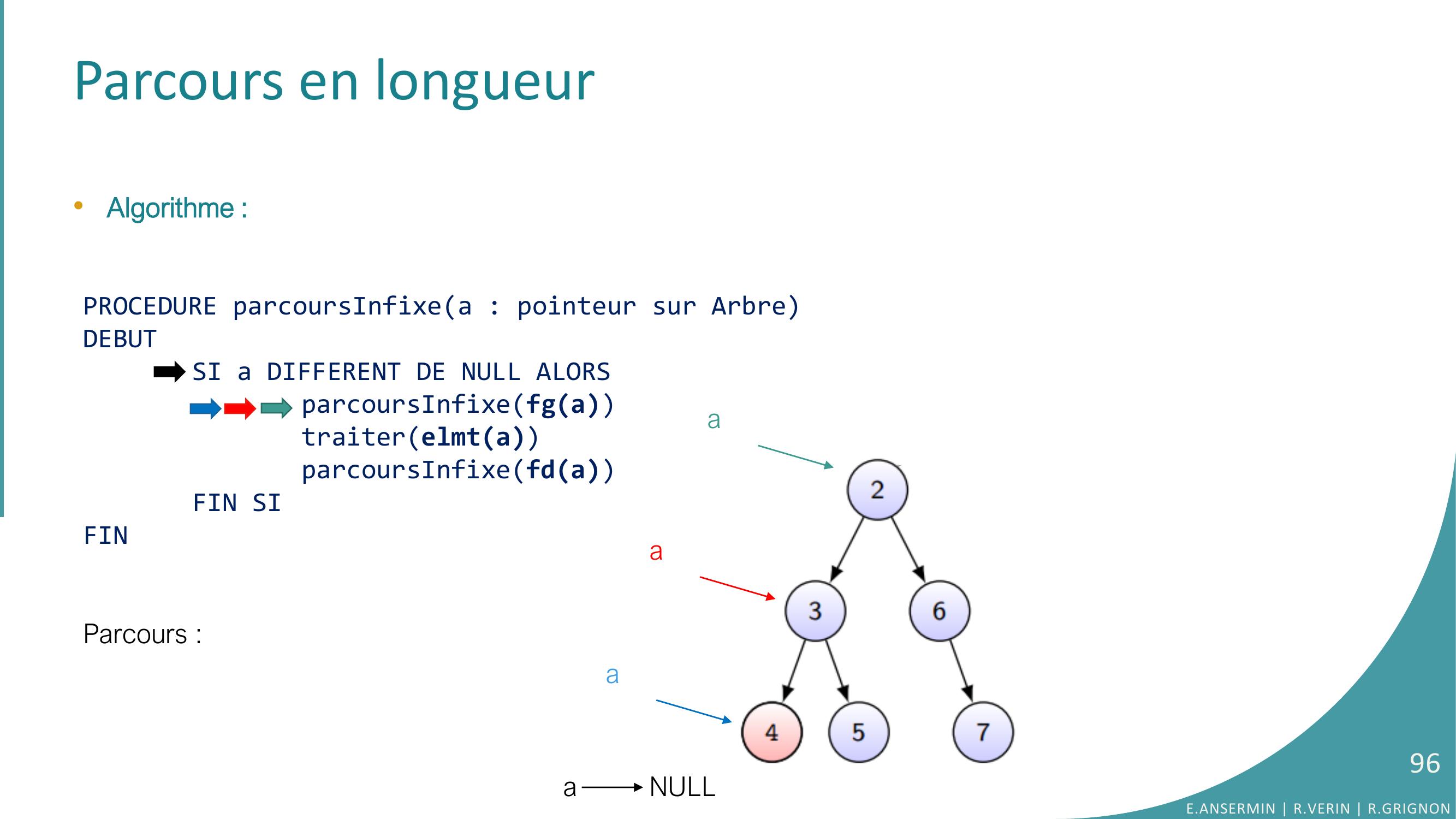
Page 96 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :a NULLE.ANSERMIN R.VERIN R.GRIGNON96aaa
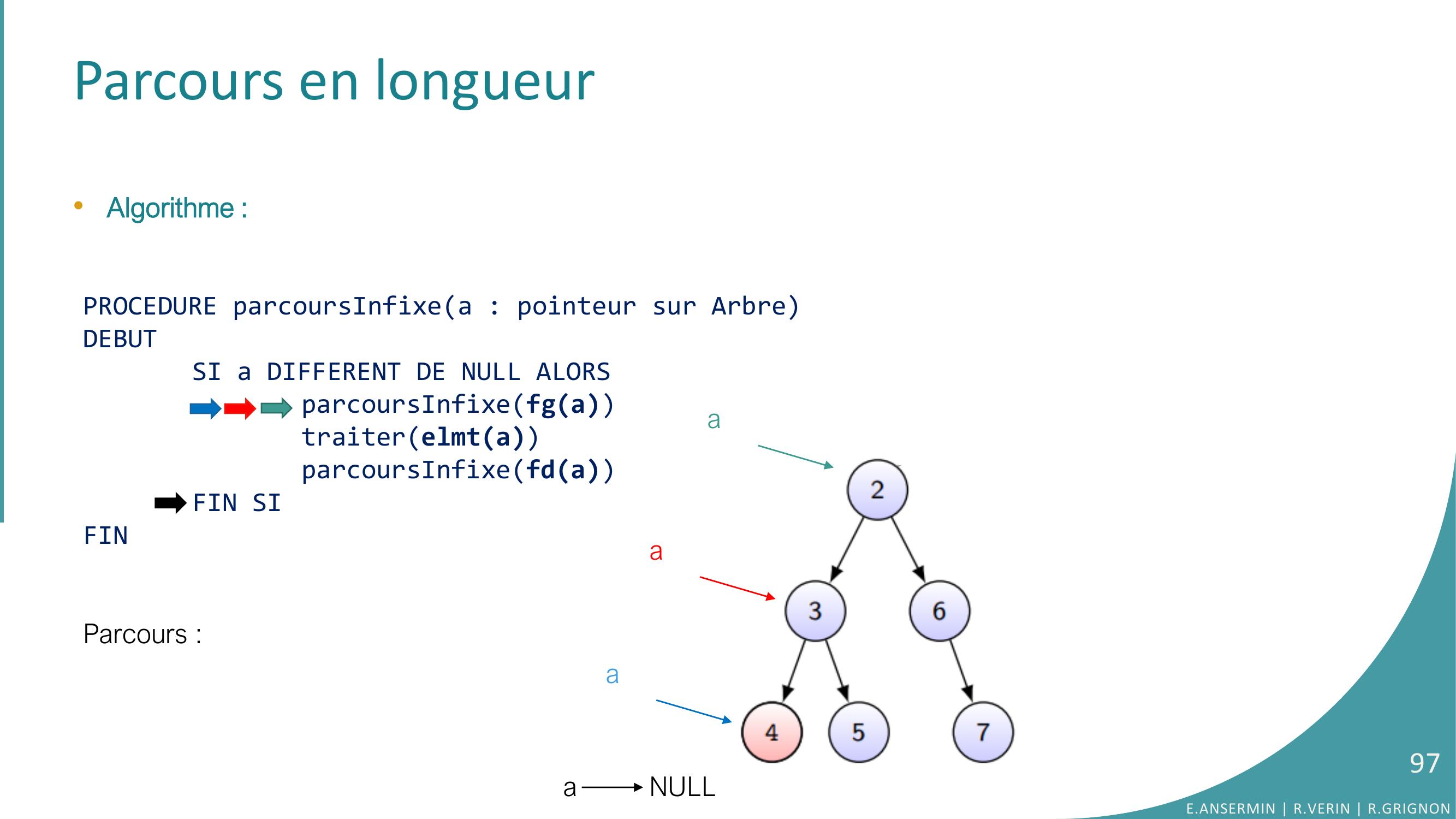
Page 97 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :a NULLE.ANSERMIN R.VERIN R.GRIGNON97aaa
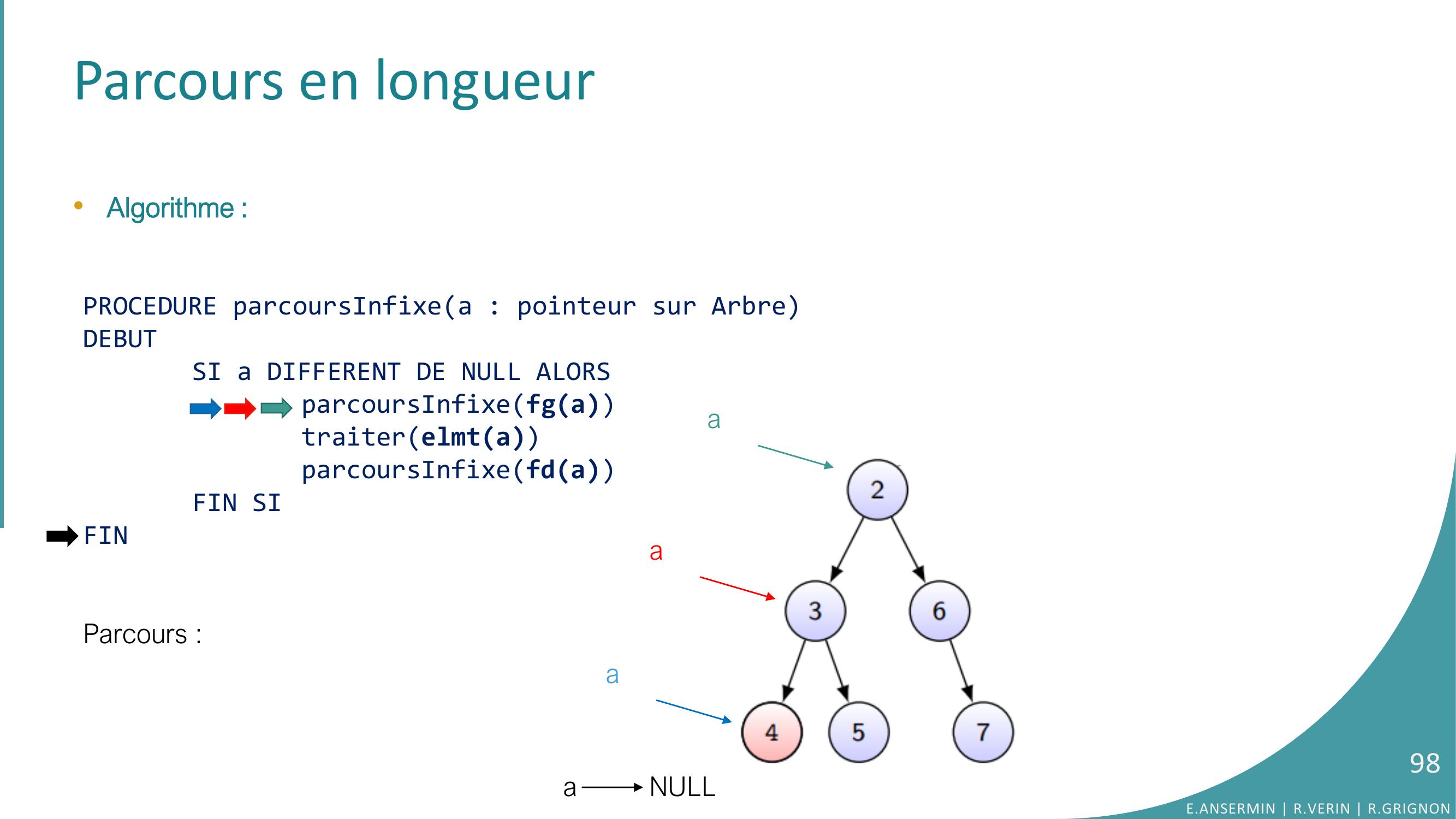
Page 98 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :a NULLE.ANSERMIN R.VERIN R.GRIGNON98aaa
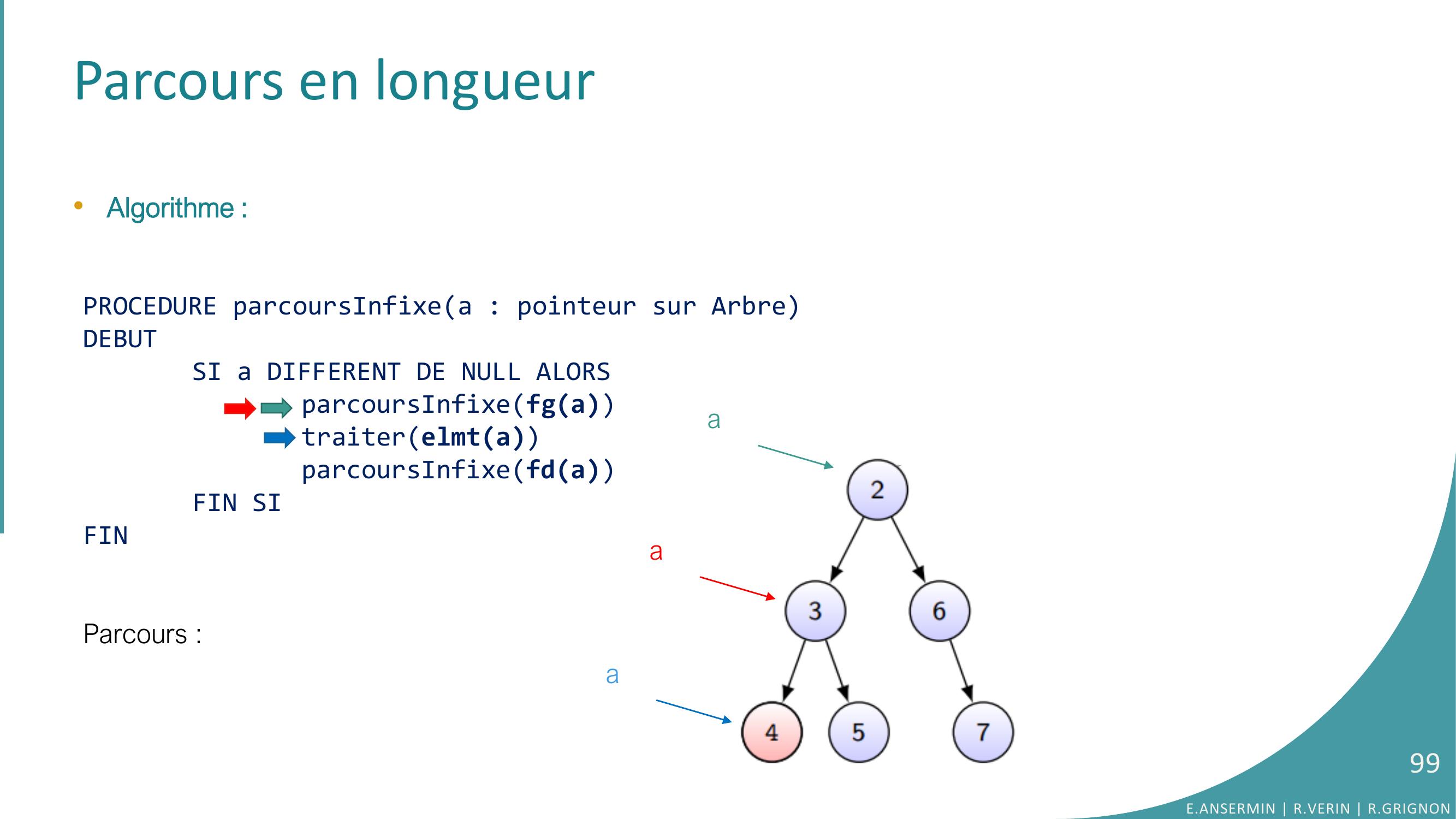
Page 99 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours :E.ANSERMIN R.VERIN R.GRIGNON99aaa
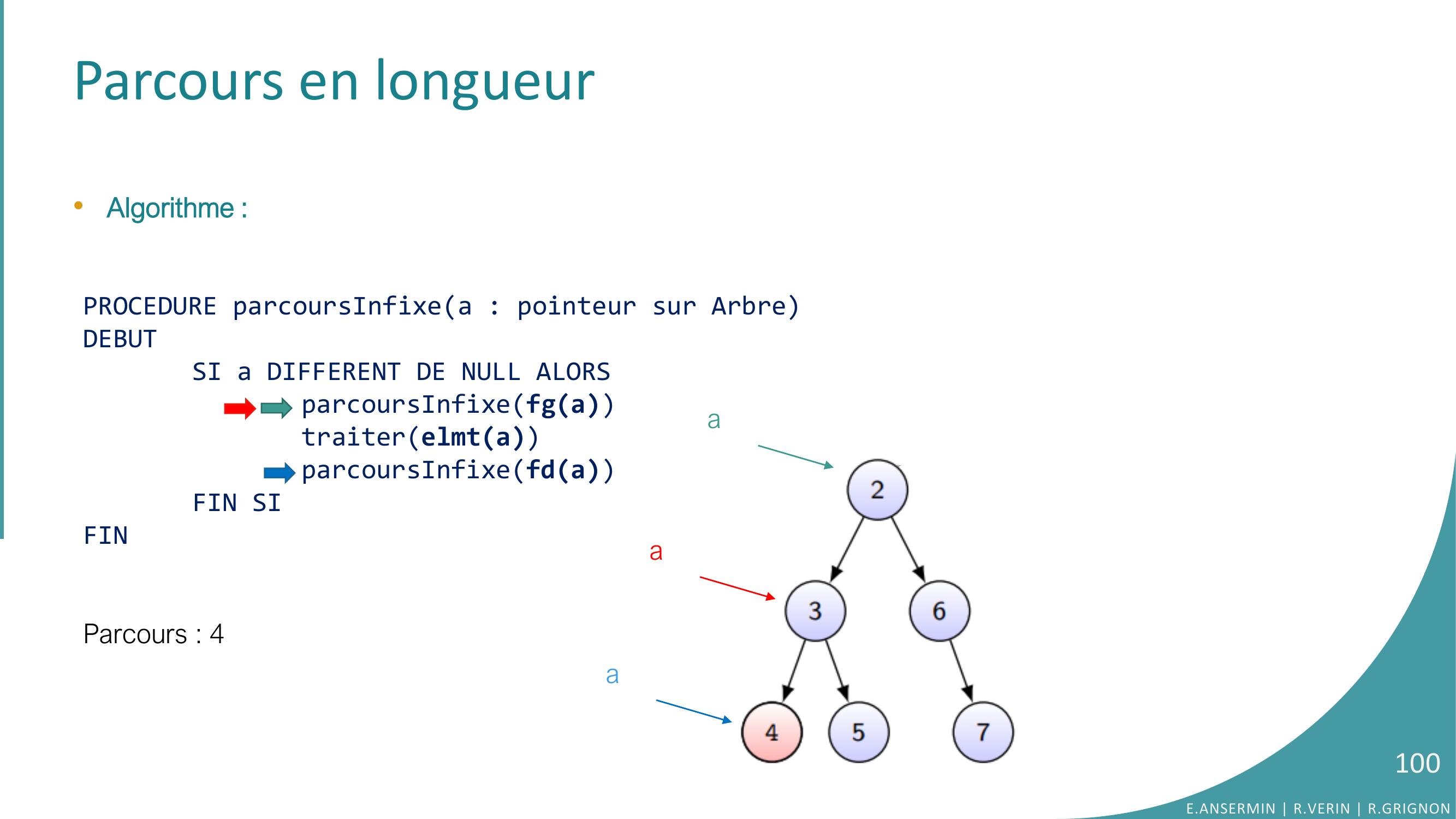
Page 100 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 E.ANSERMIN R.VERIN R.GRIGNON100aaa
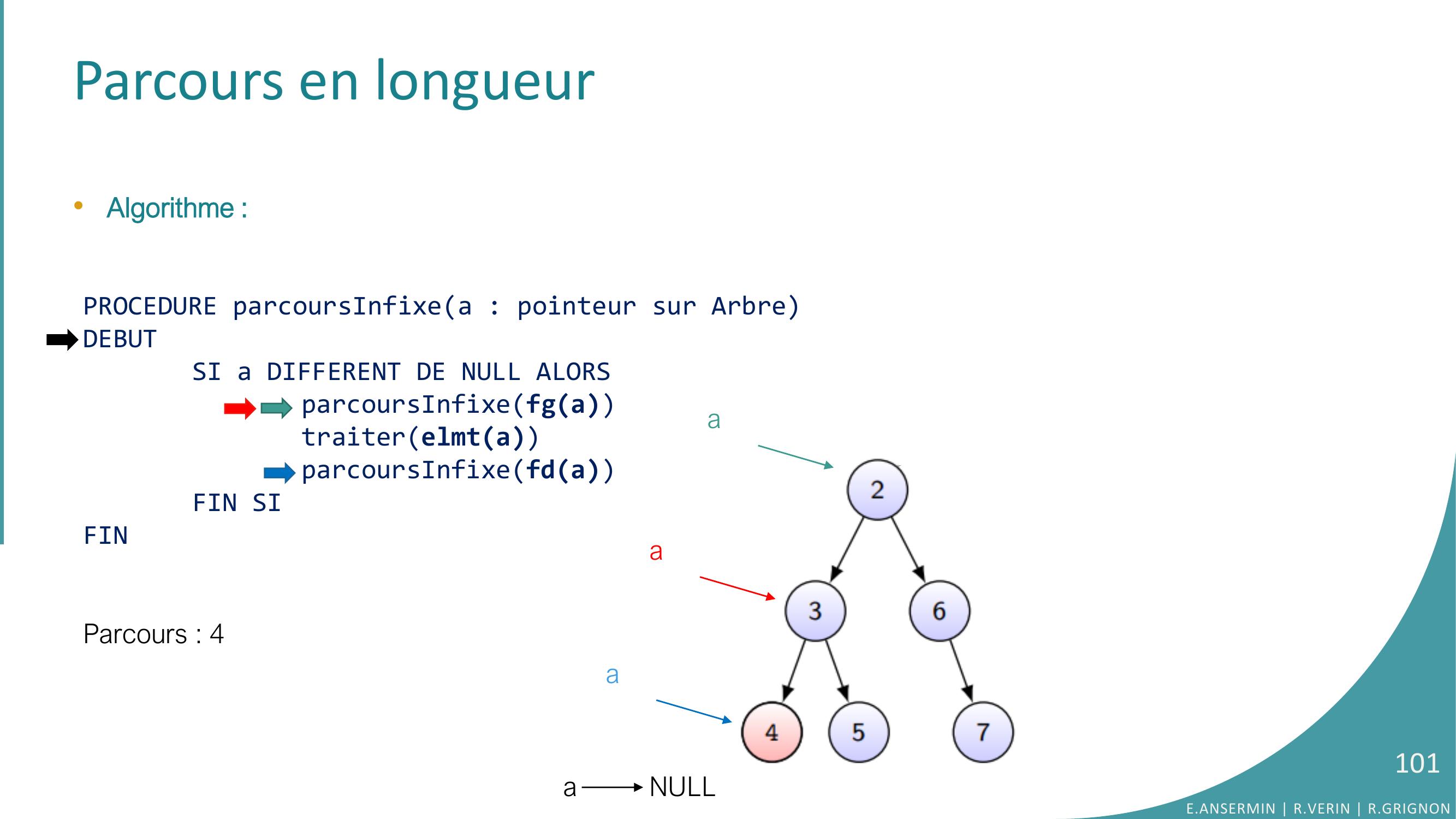
Page 101 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 a NULLE.ANSERMIN R.VERIN R.GRIGNON101aaa
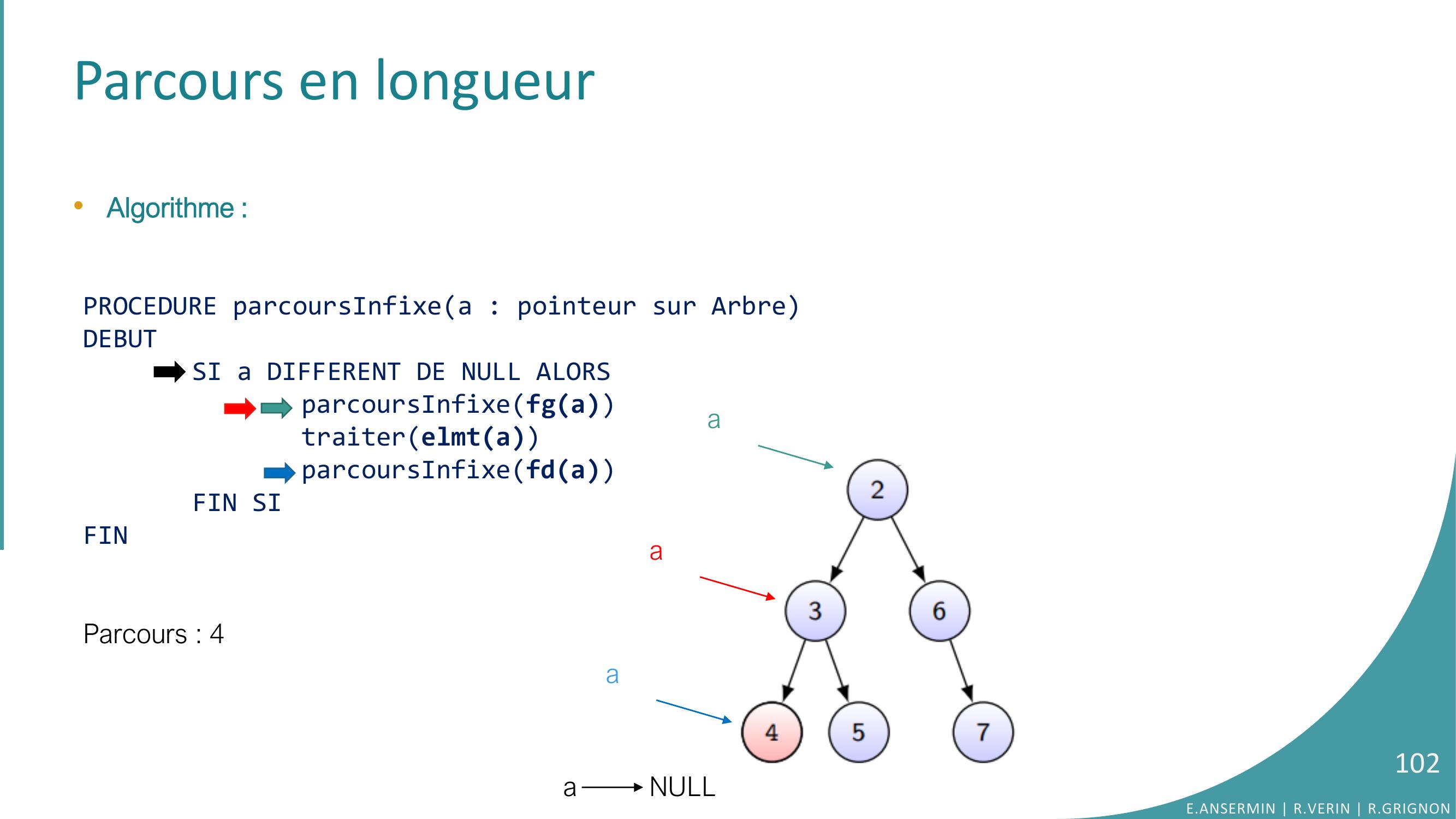
Page 102 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 a NULLE.ANSERMIN R.VERIN R.GRIGNON102aaa
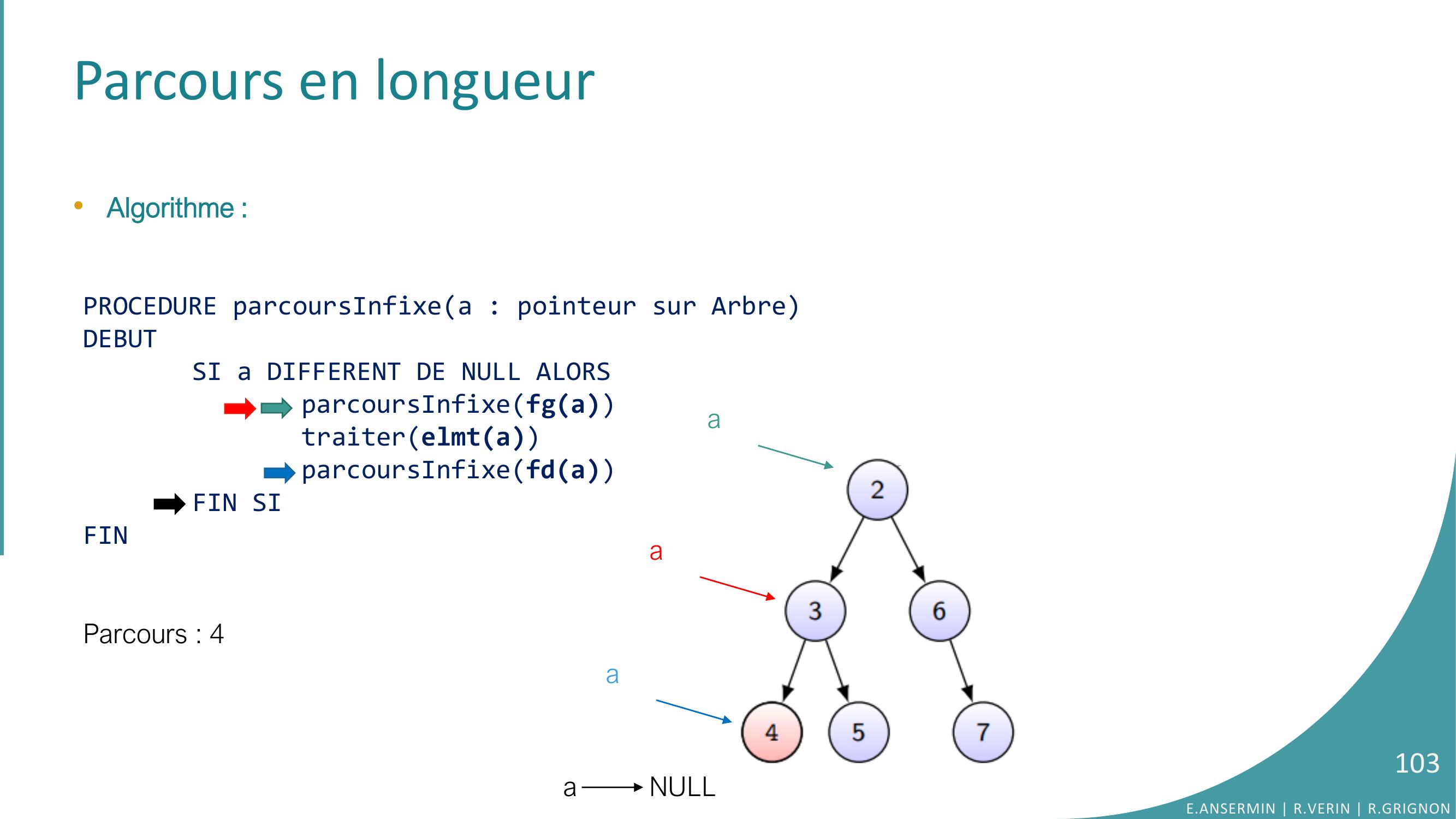
Page 103 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 a NULLE.ANSERMIN R.VERIN R.GRIGNON103aaa
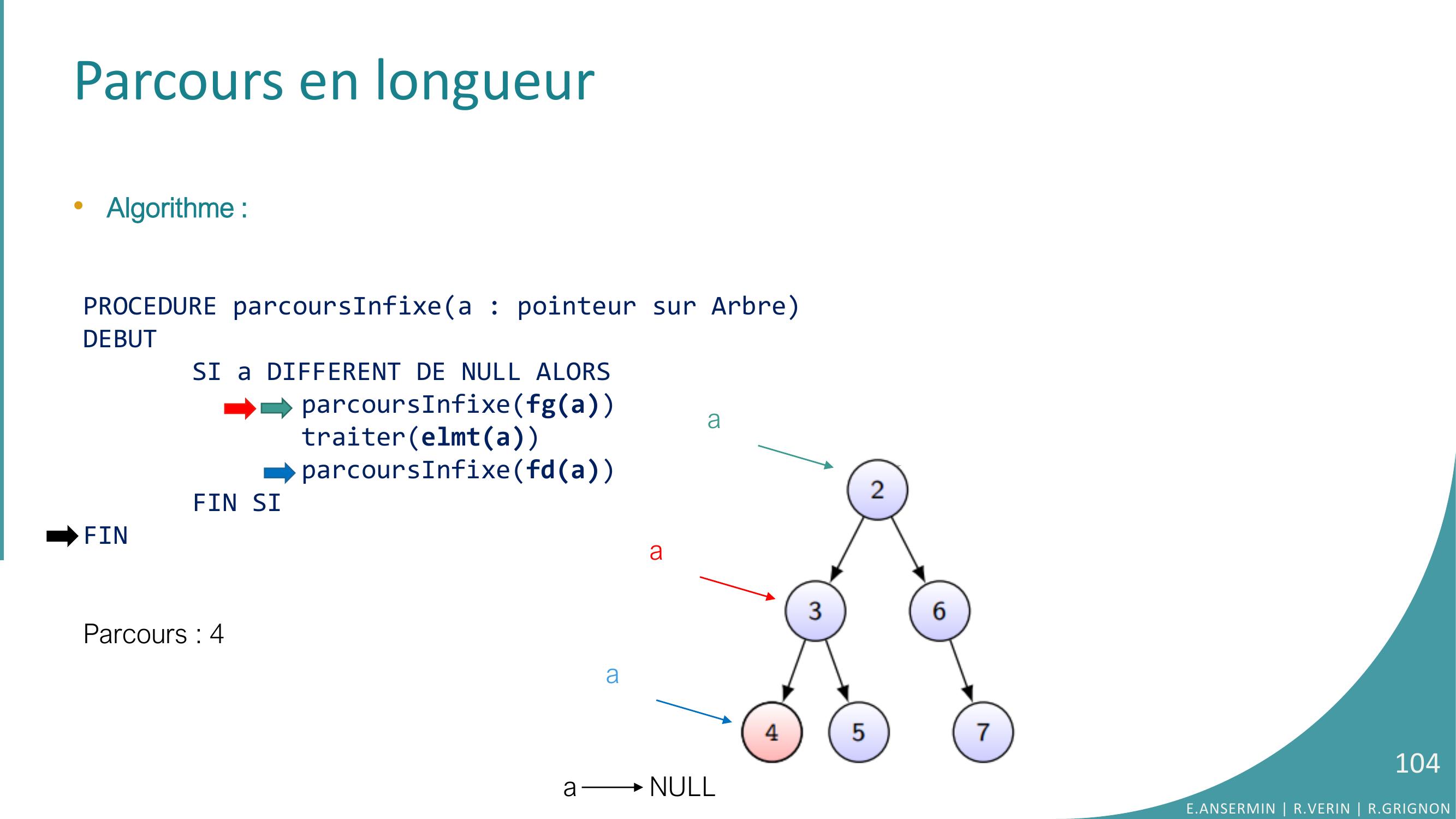
Page 104 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 a NULLE.ANSERMIN R.VERIN R.GRIGNON104aaa
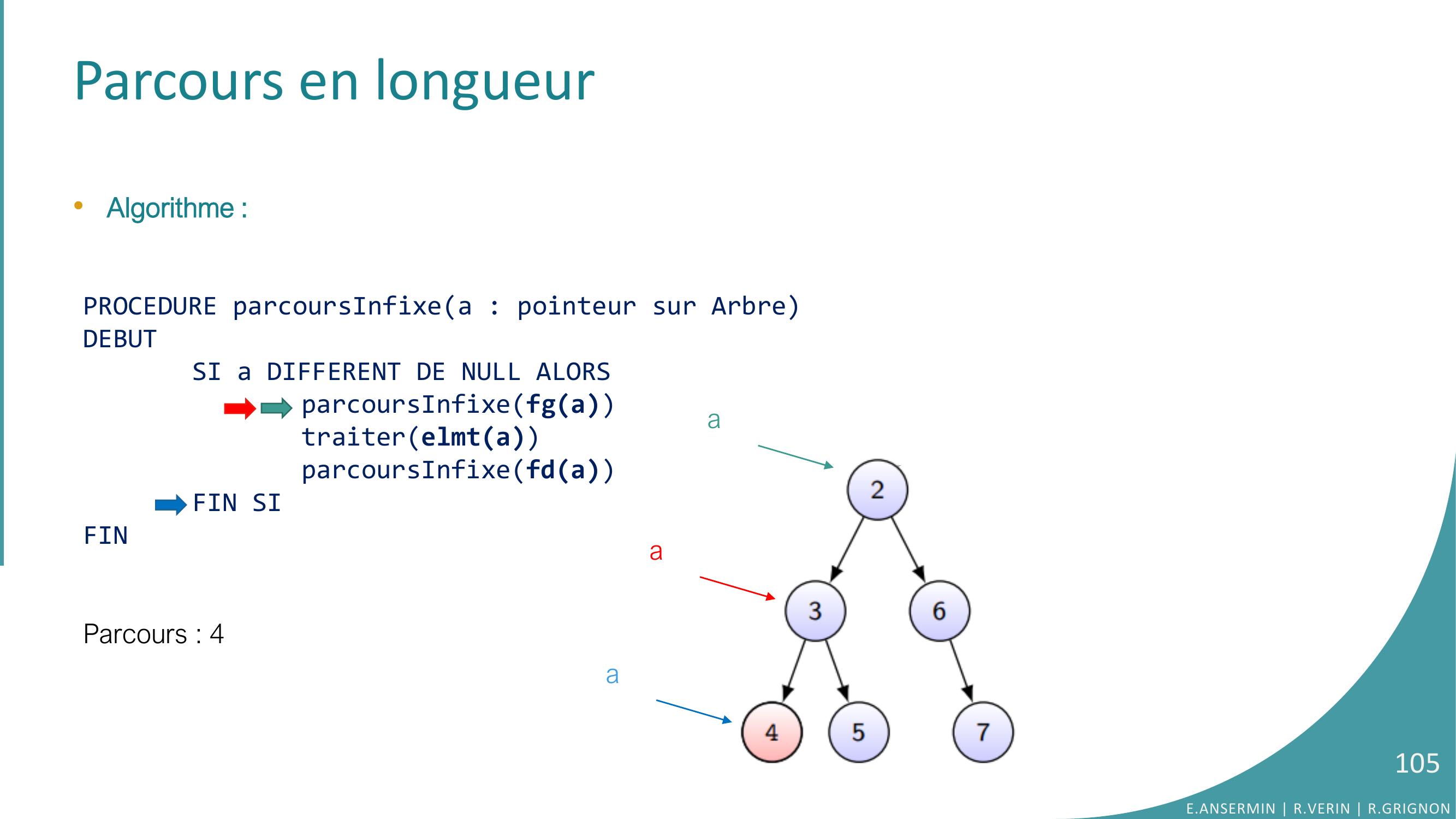
Page 105 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 E.ANSERMIN R.VERIN R.GRIGNON105aaa
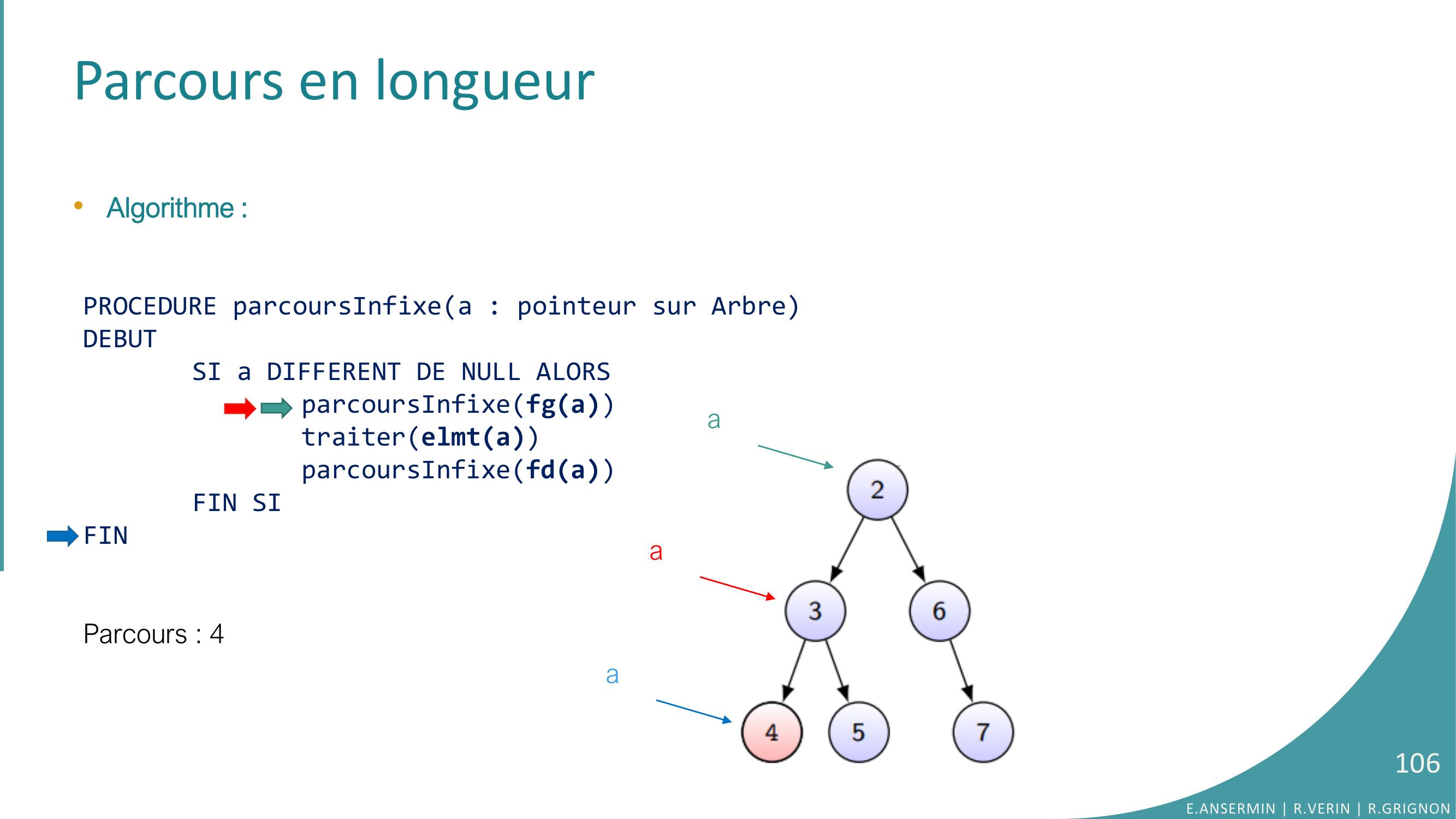
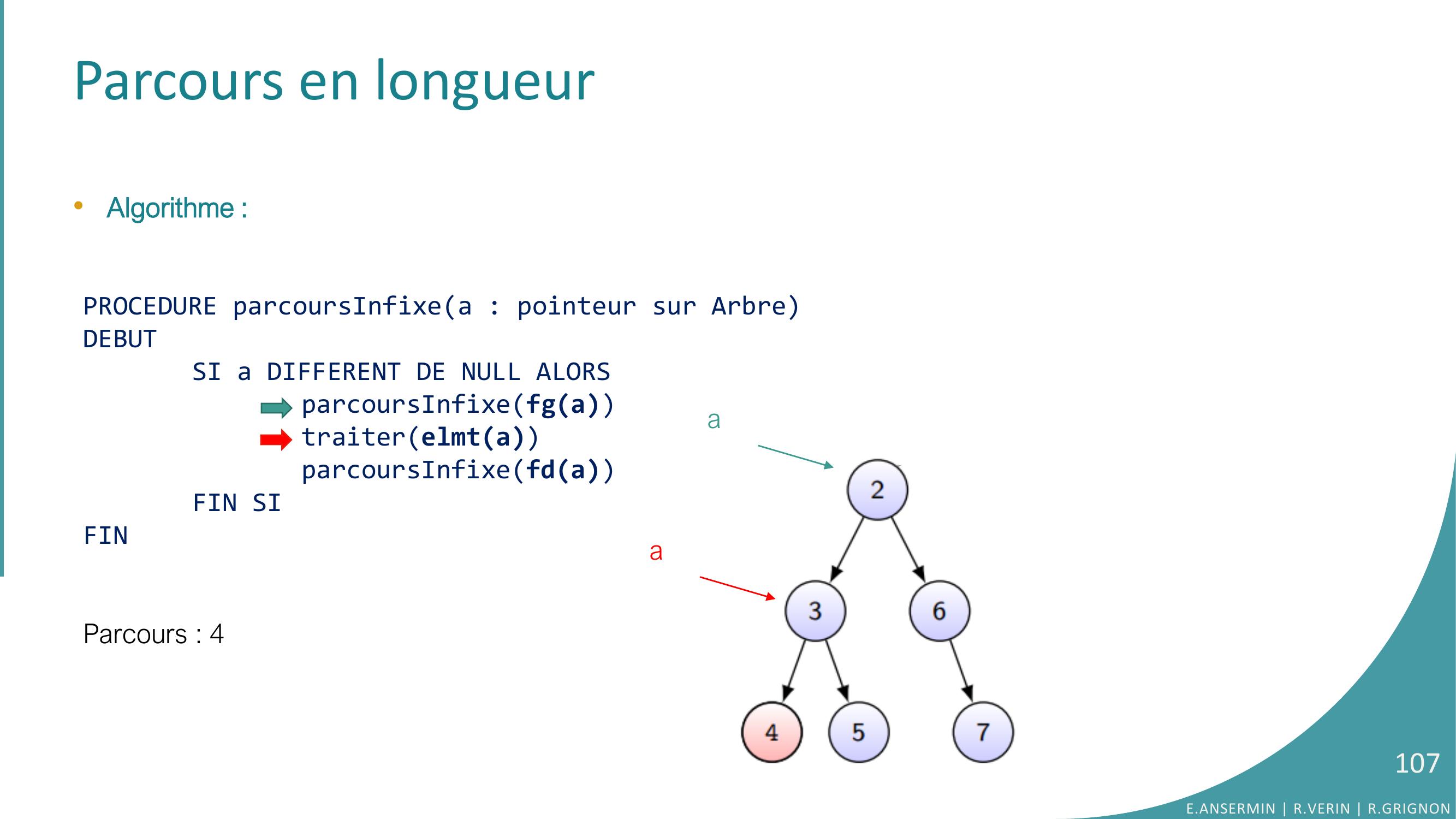
Page 106 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 E.ANSERMIN R.VERIN R.GRIGNON106aaa
Page 107 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4 E.ANSERMIN R.VERIN R.GRIGNON107aa
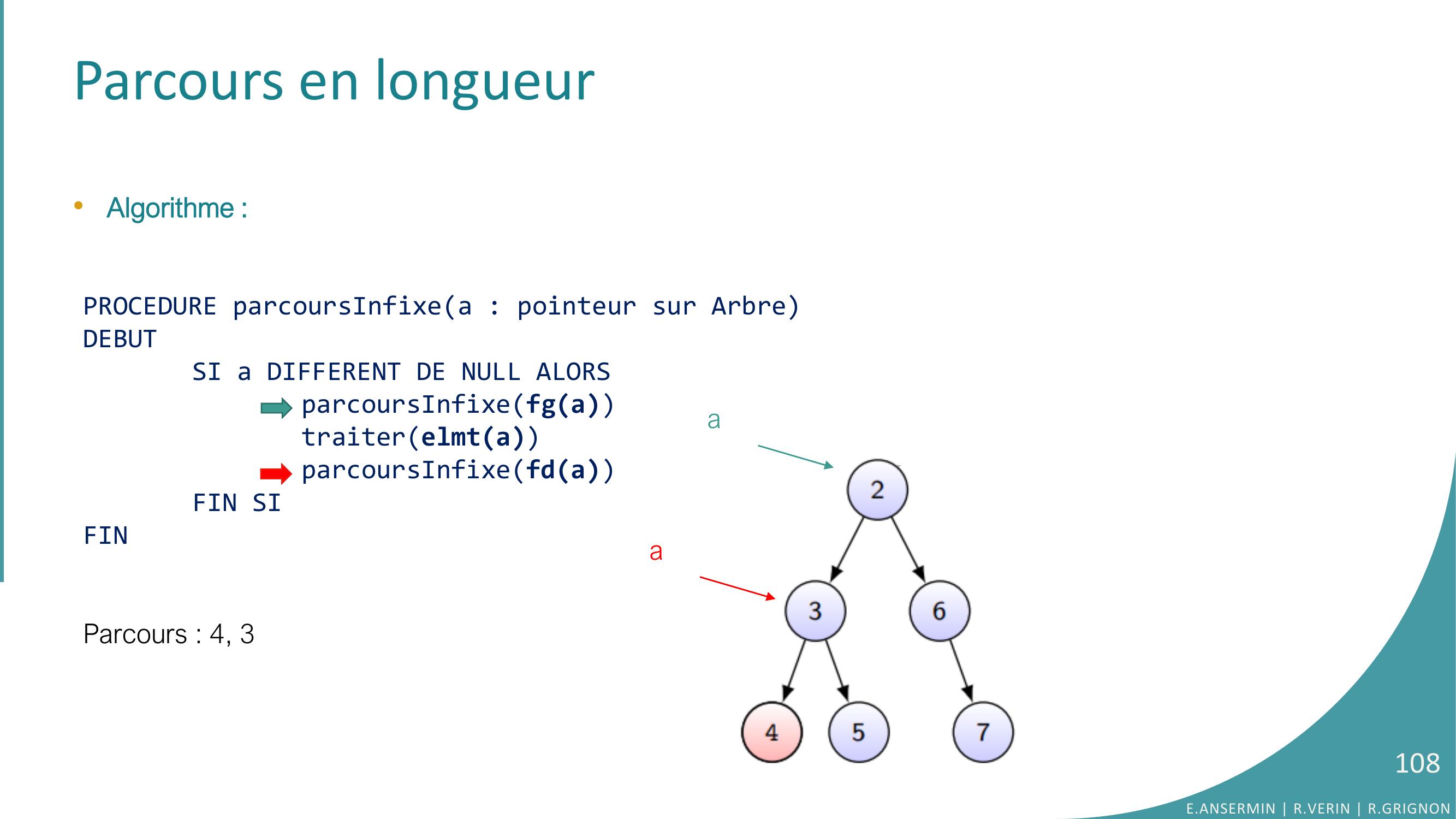
Page 108 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3E.ANSERMIN R.VERIN R.GRIGNON108aa
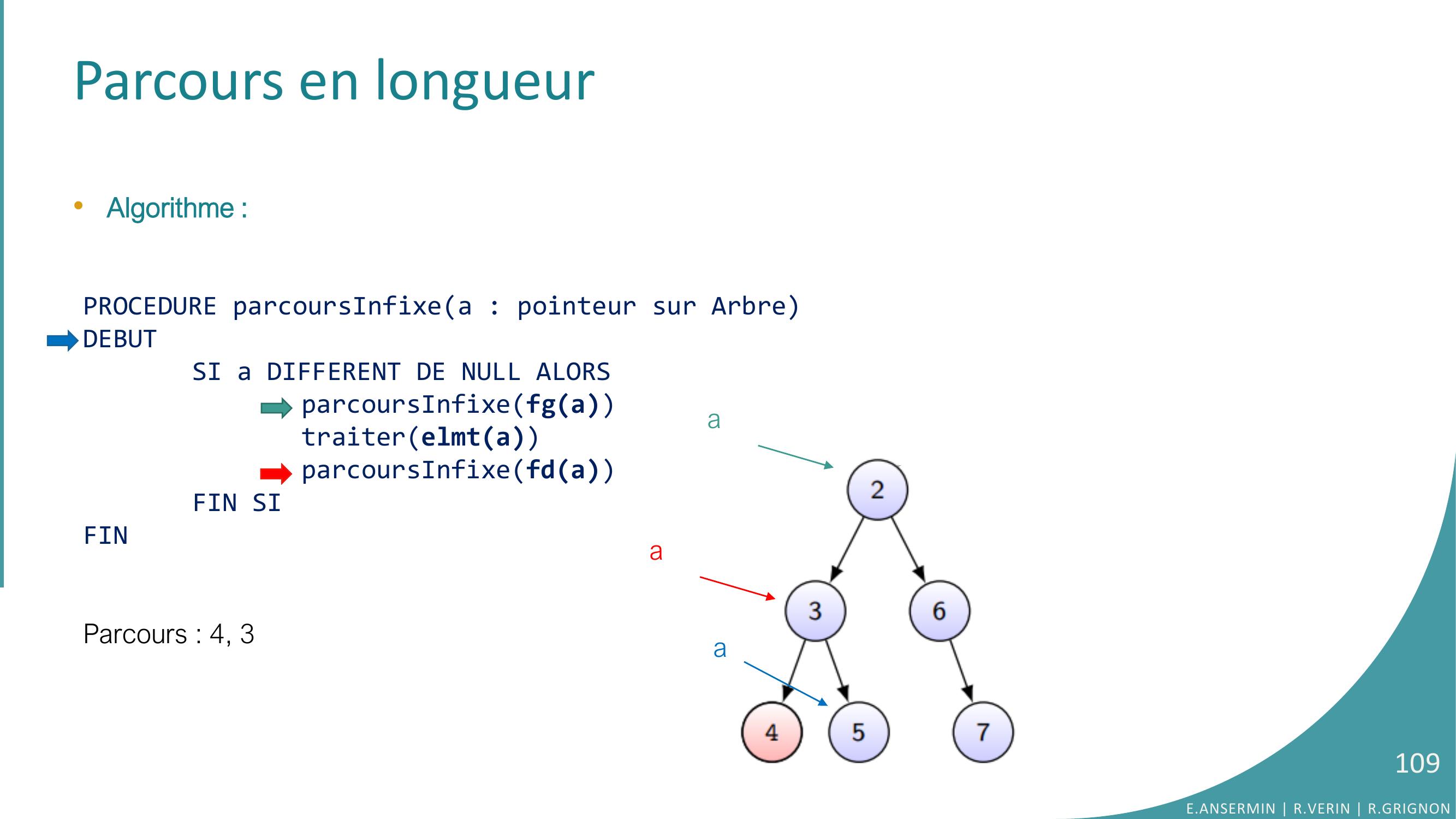
Page 109 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3E.ANSERMIN R.VERIN R.GRIGNON109aaa
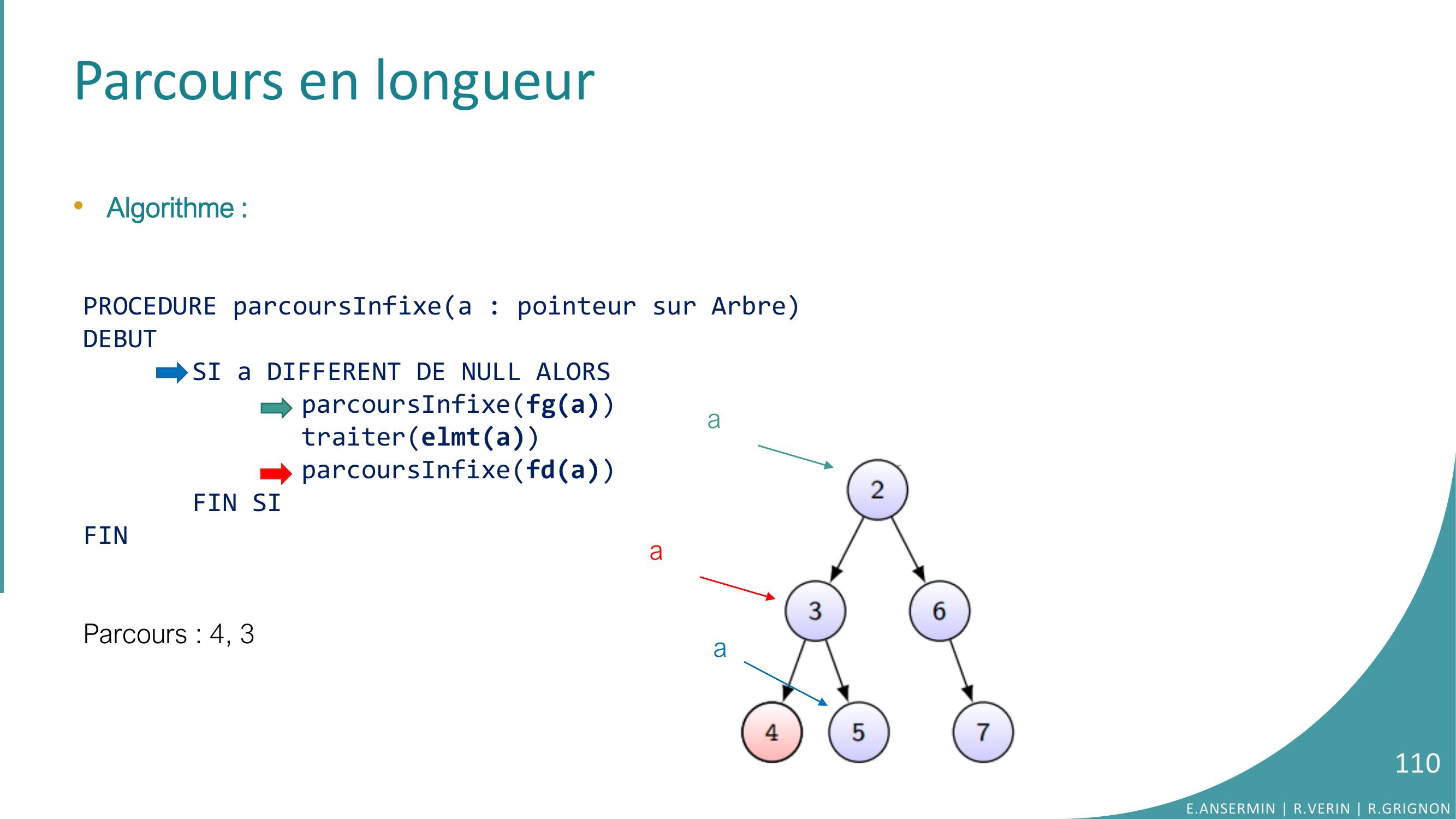
Page 110 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3E.ANSERMIN R.VERIN R.GRIGNON110aaa
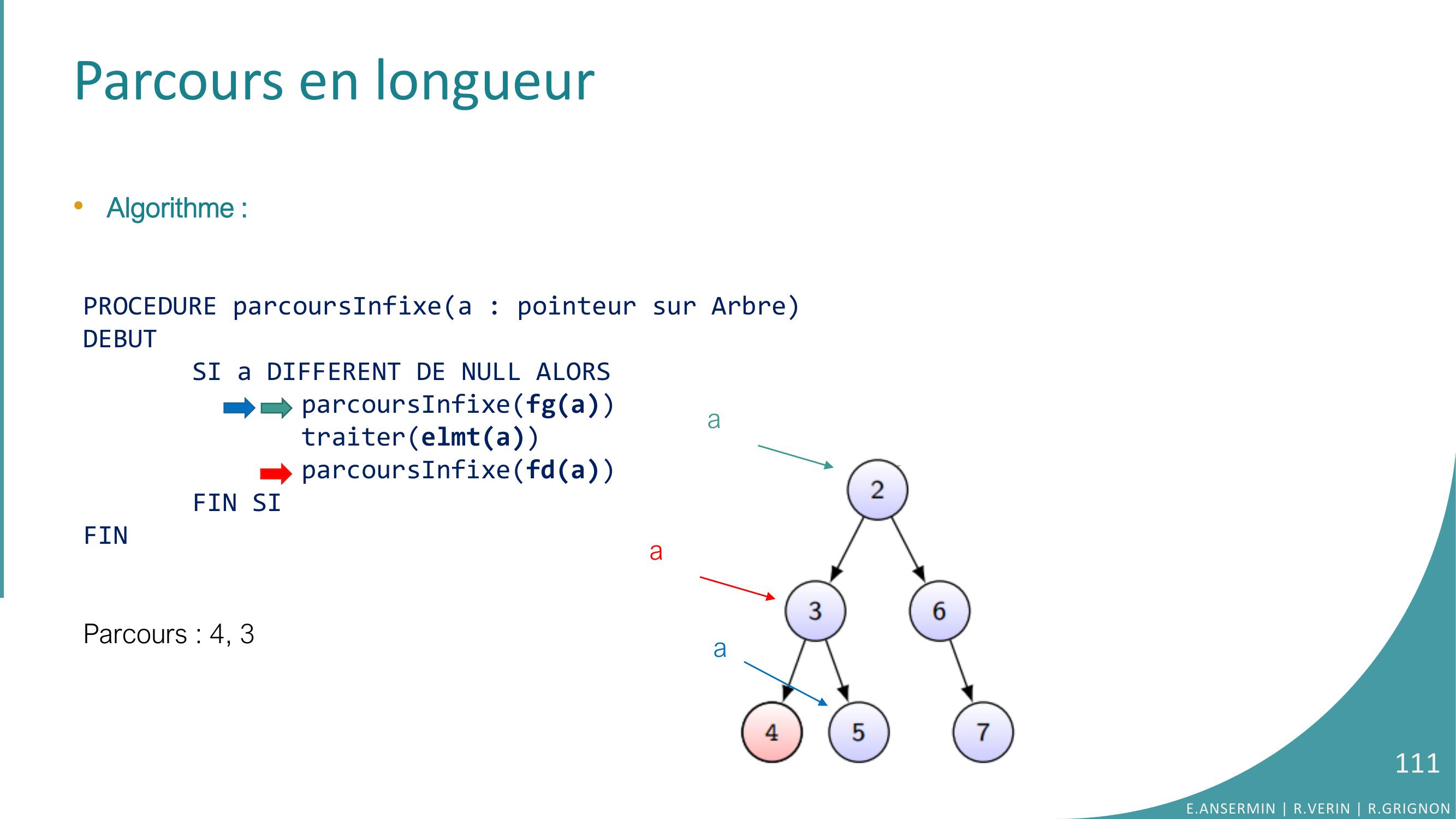
Page 111 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3E.ANSERMIN R.VERIN R.GRIGNON111aaa
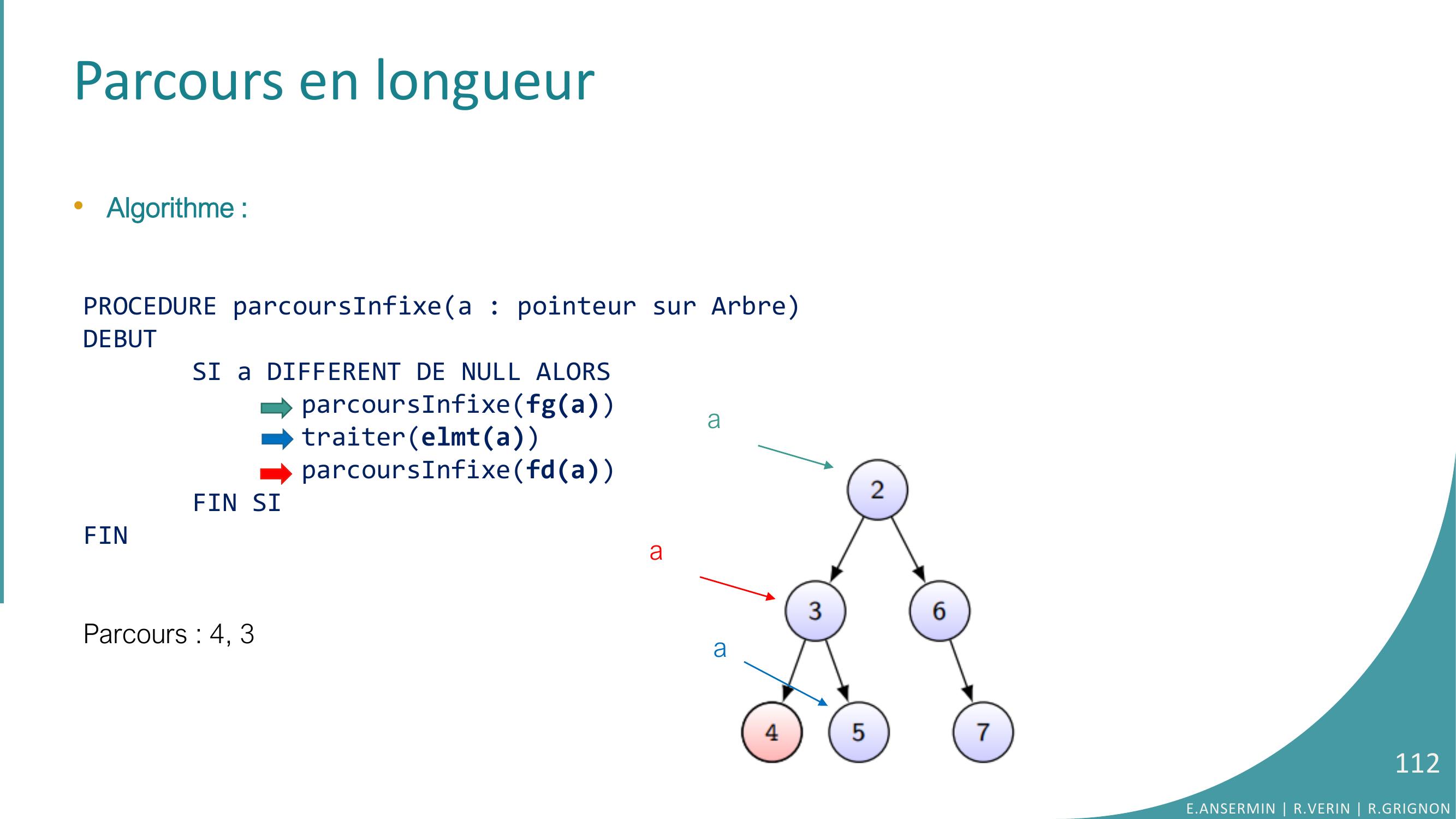
Page 112 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3E.ANSERMIN R.VERIN R.GRIGNON112aaa
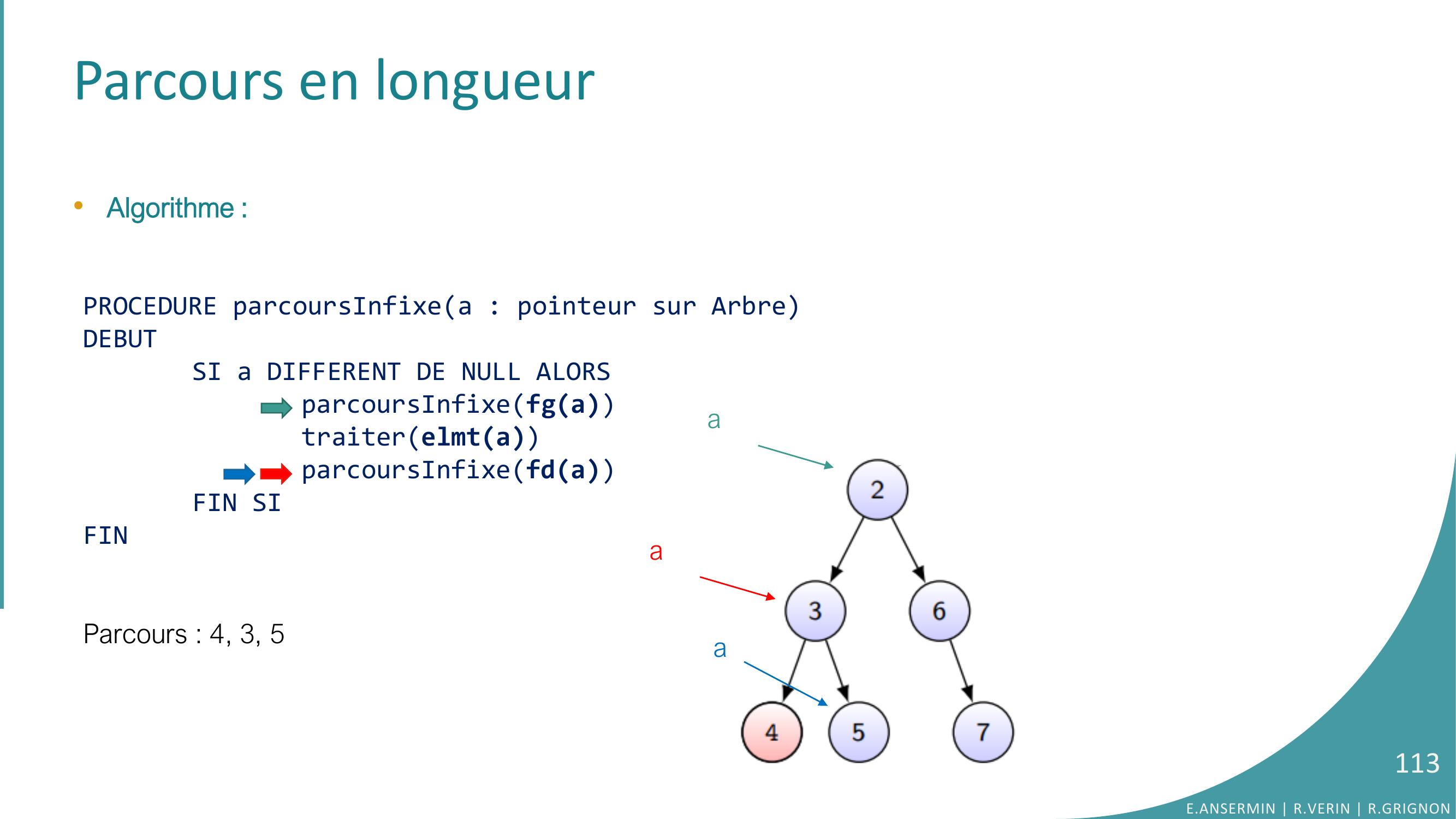
Page 113 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON113aaa
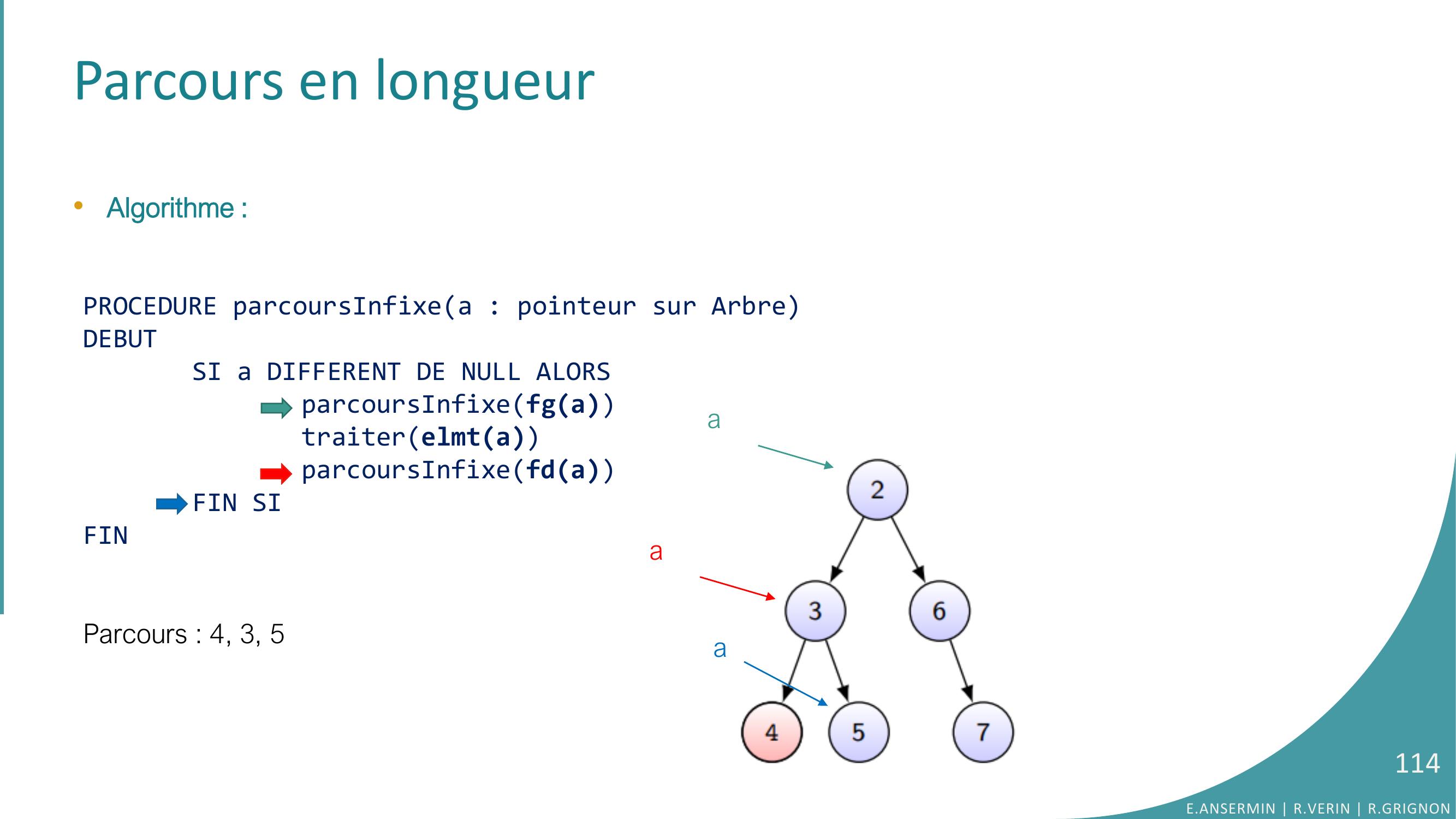
Page 114 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON114aaa
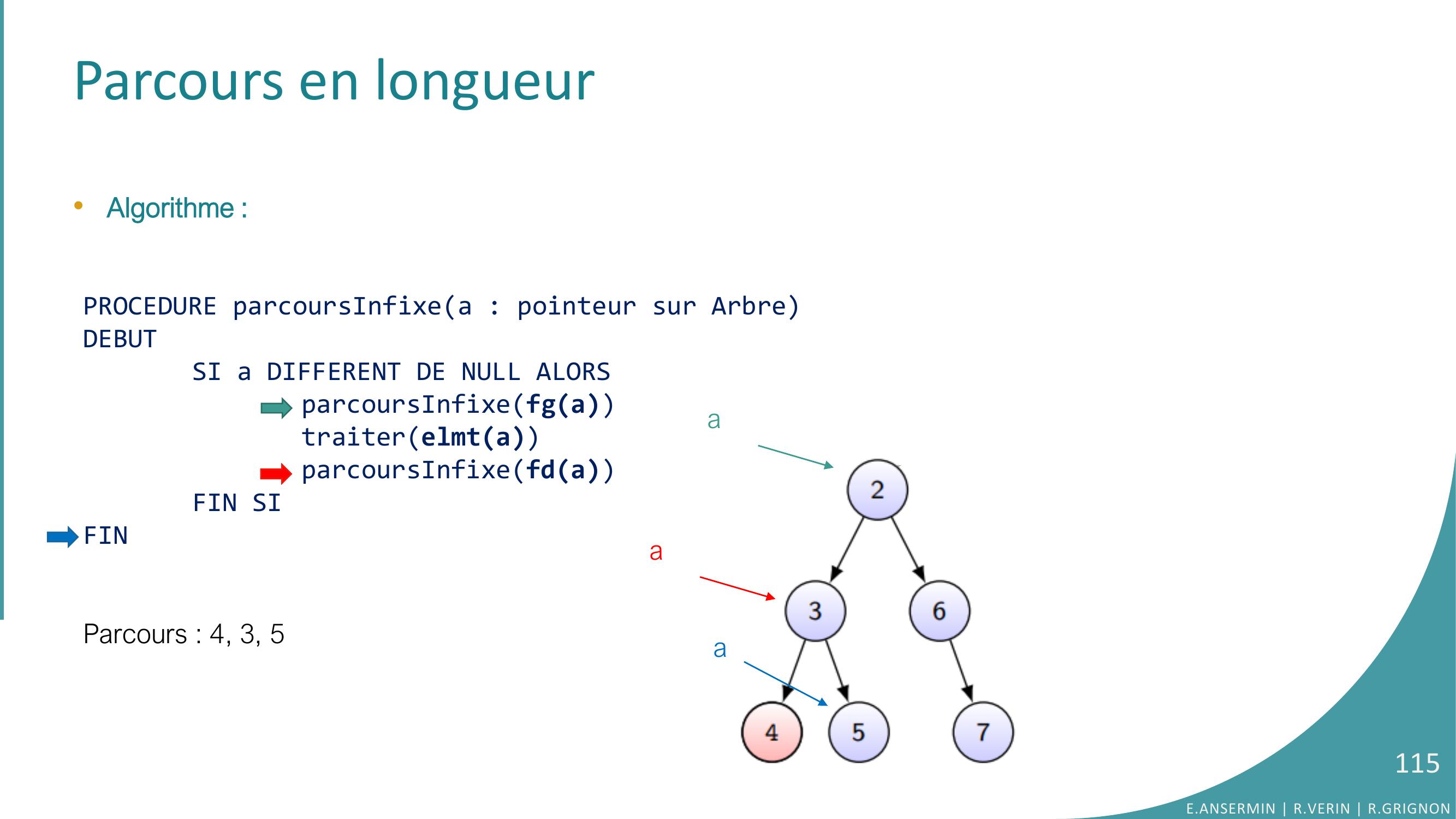
Page 115 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON115aaa
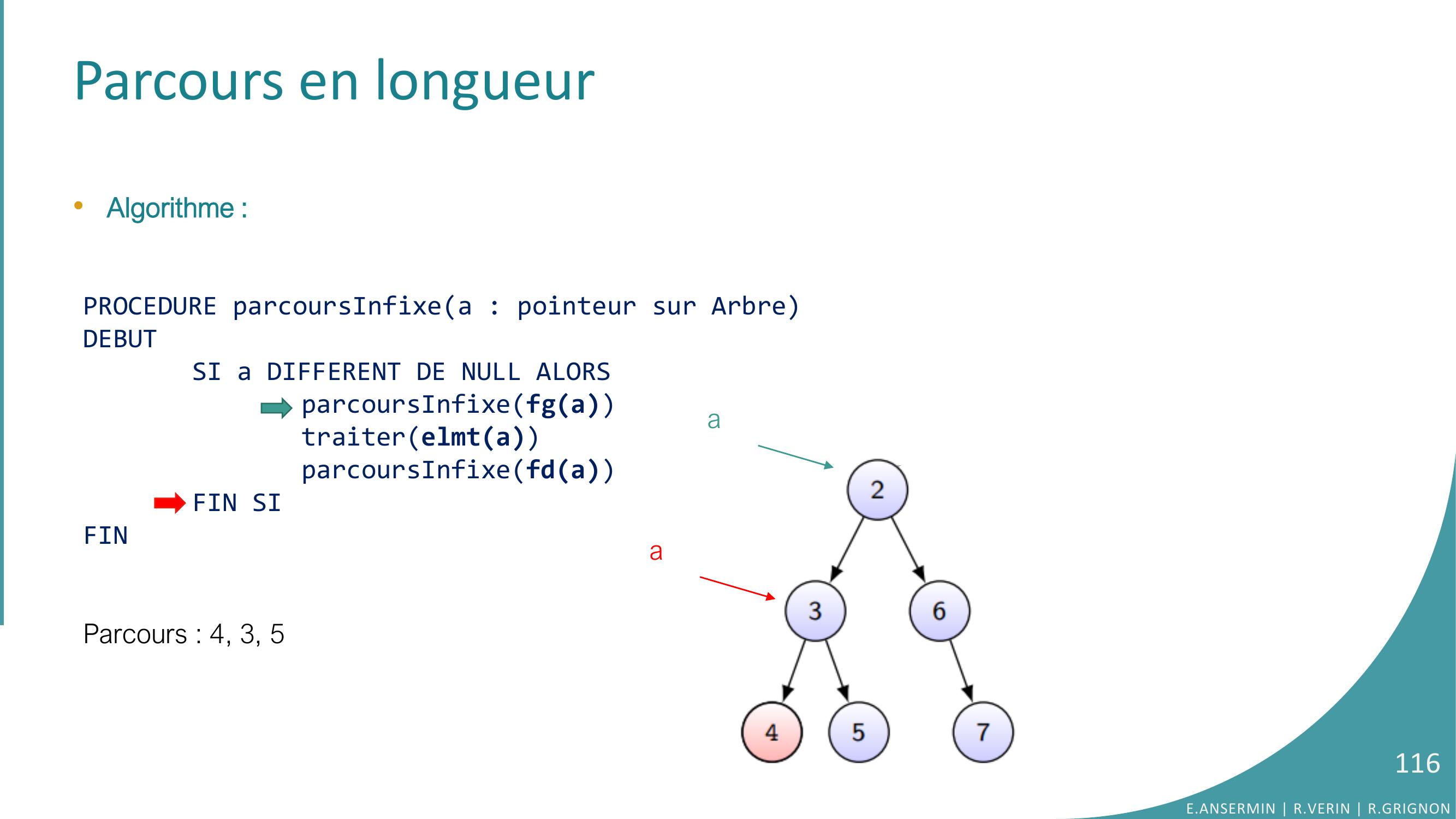
Page 116 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON116aa
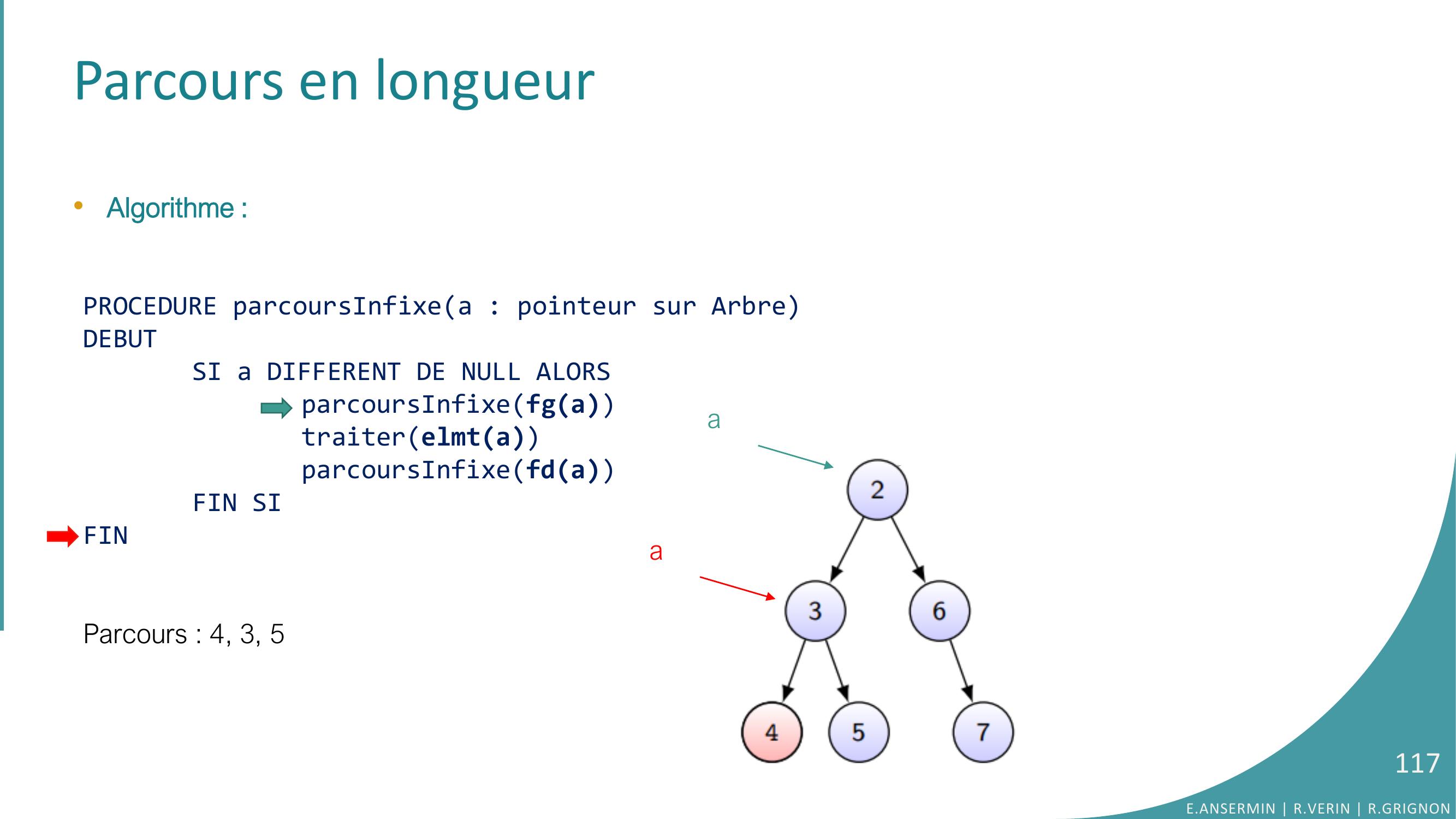
Page 117 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON117aa
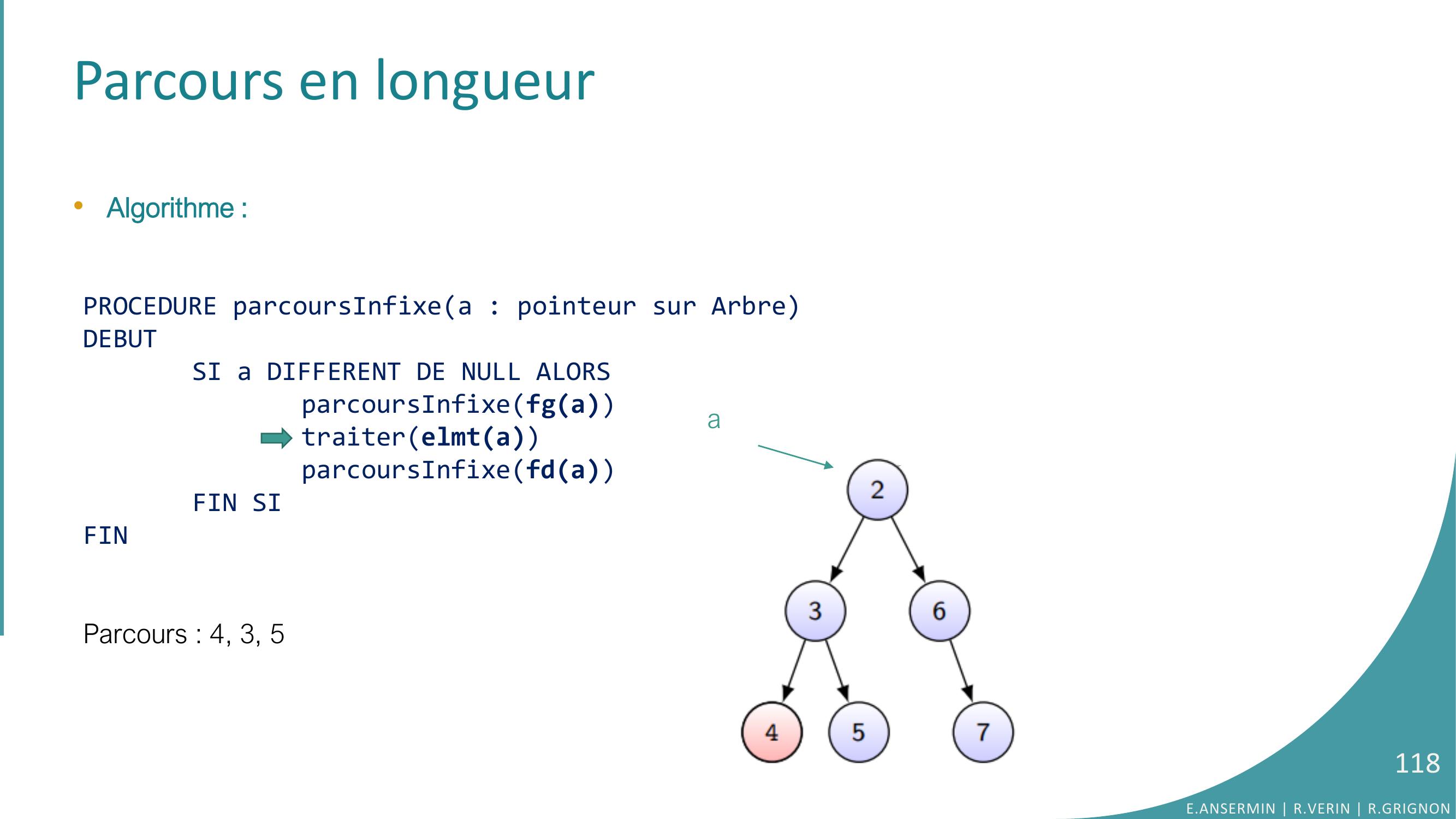
Page 118 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5E.ANSERMIN R.VERIN R.GRIGNON118a
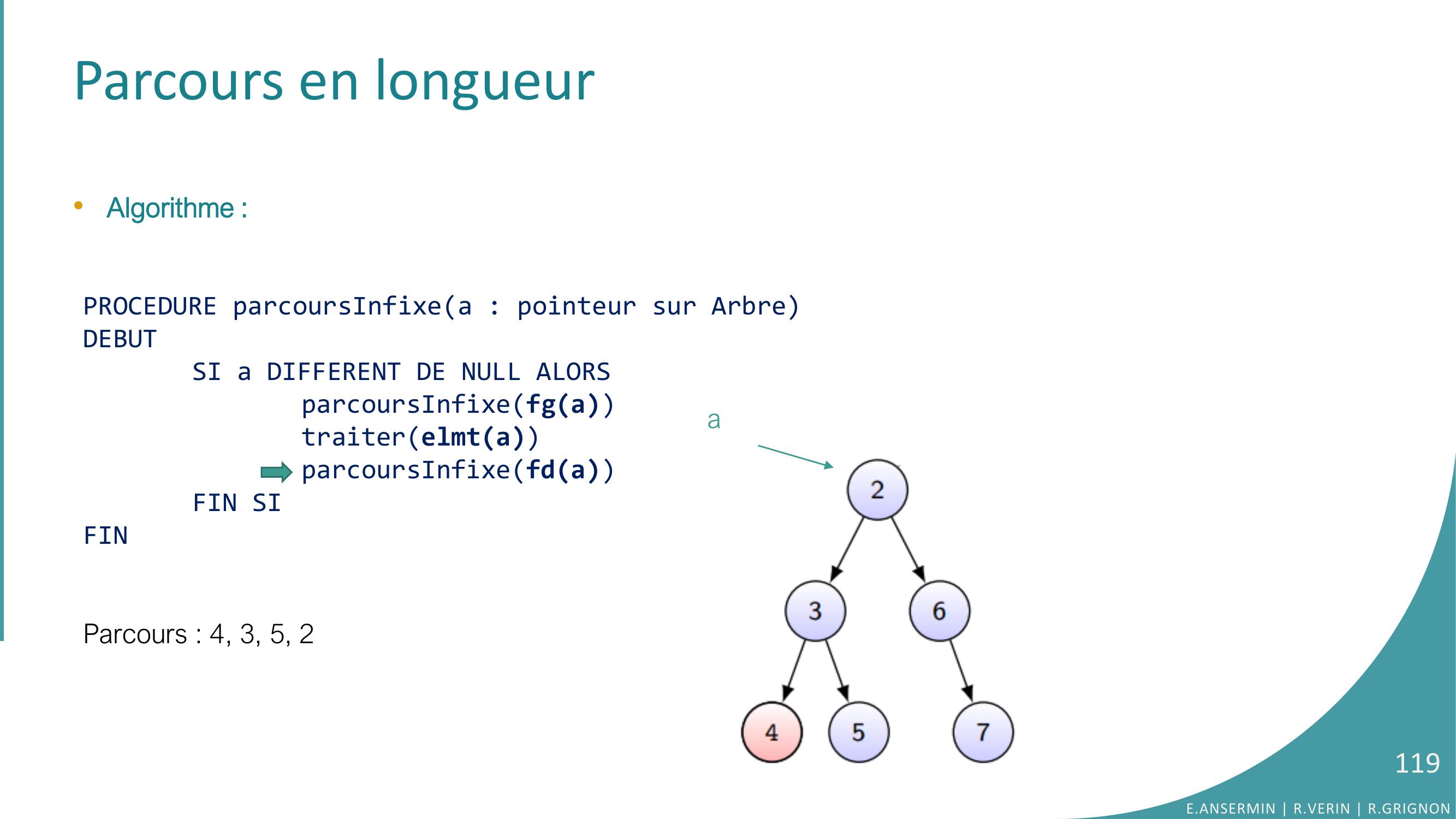
Page 119 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON119a
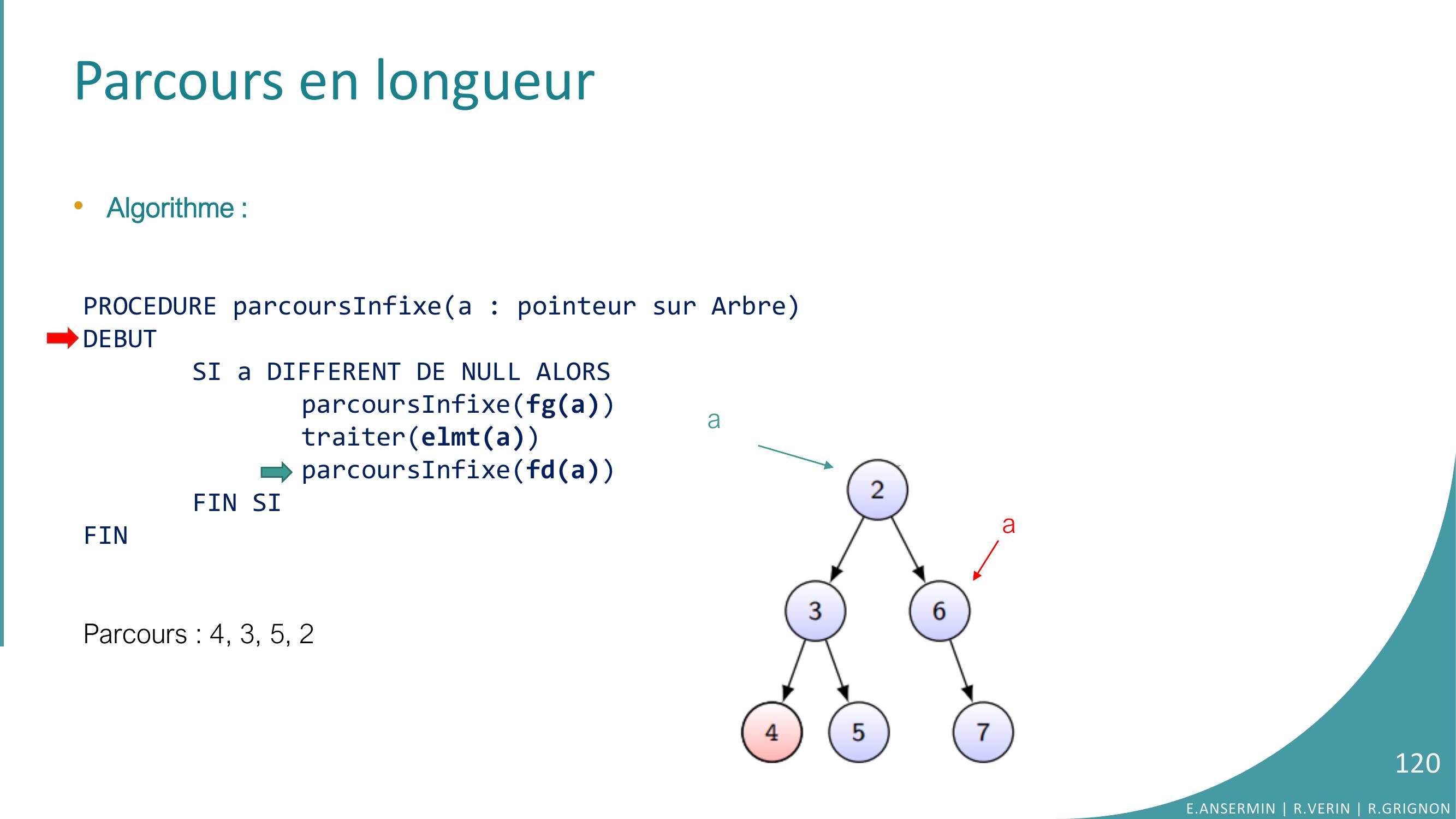
Page 120 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON120aa
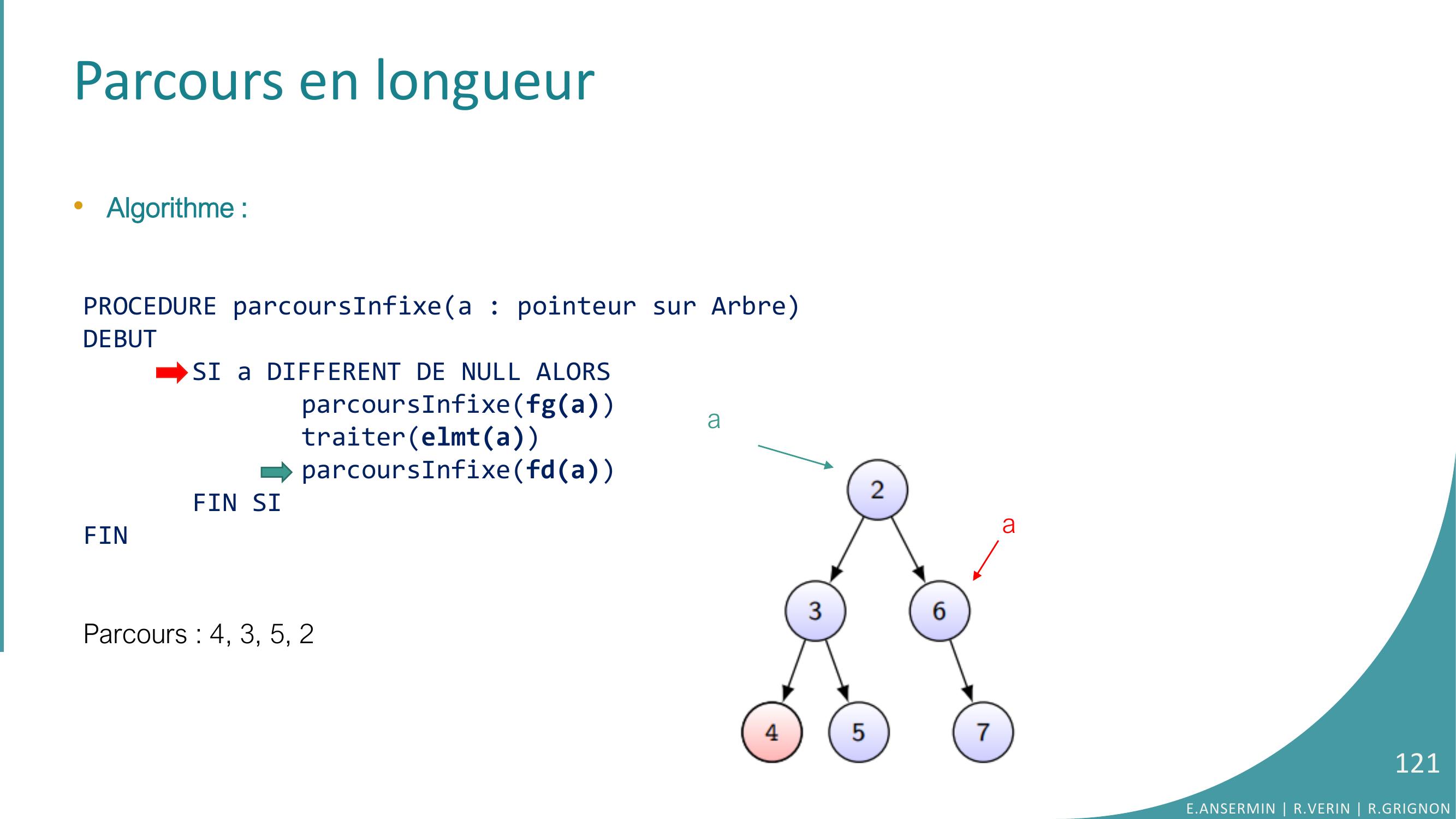
Page 121 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON121aa
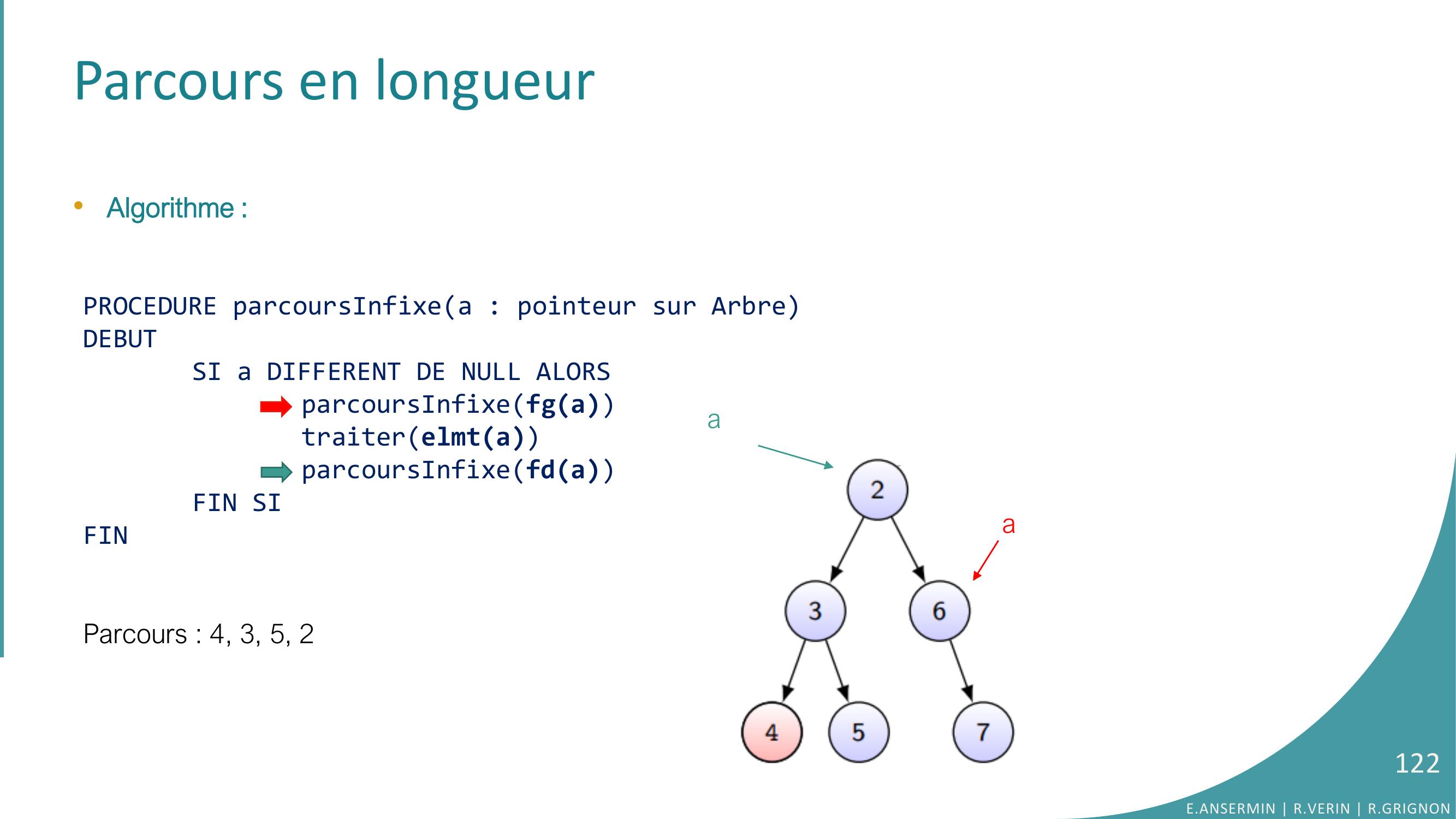
Page 122 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON122aa
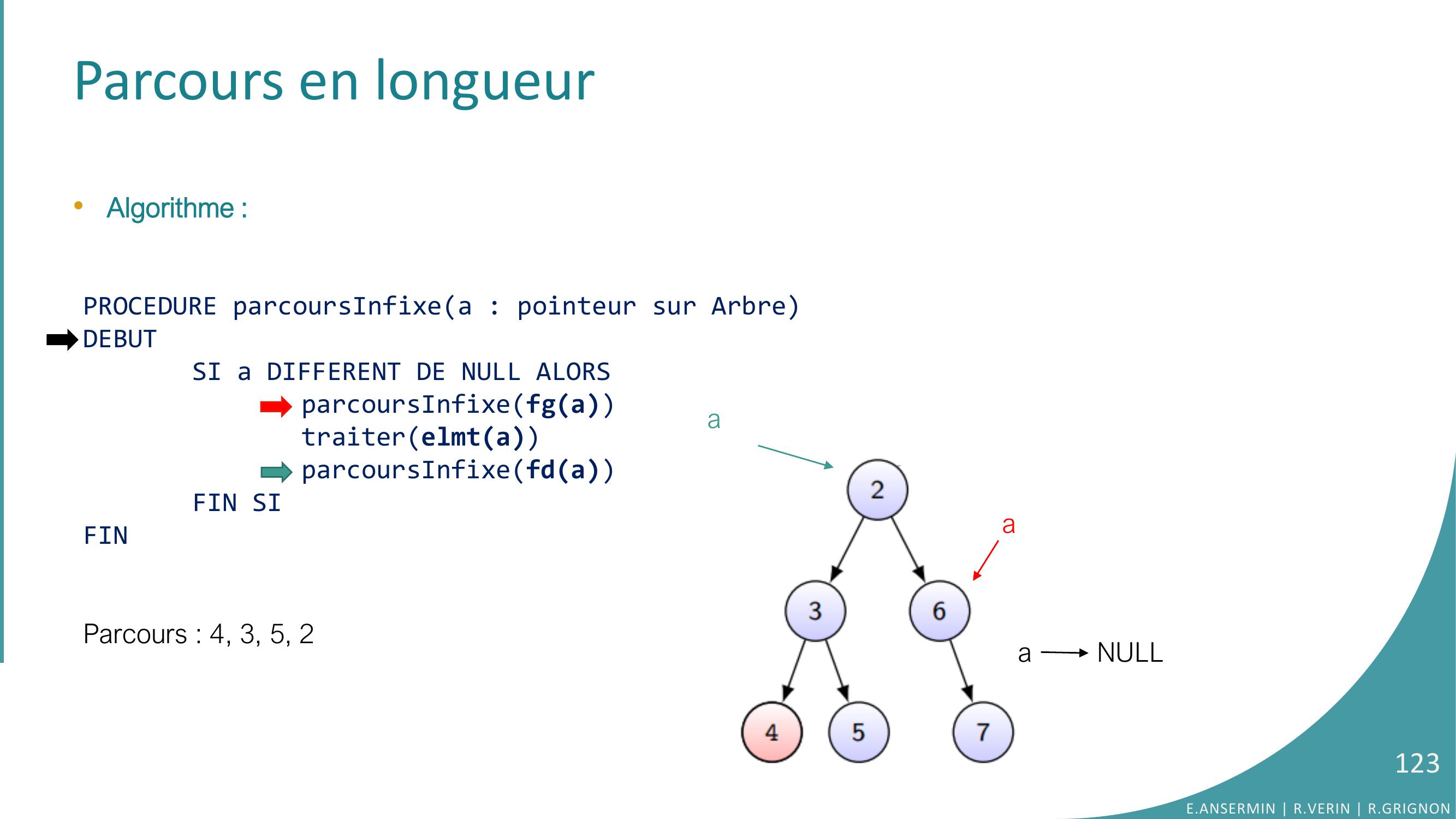
Page 123 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON123aaa NULL
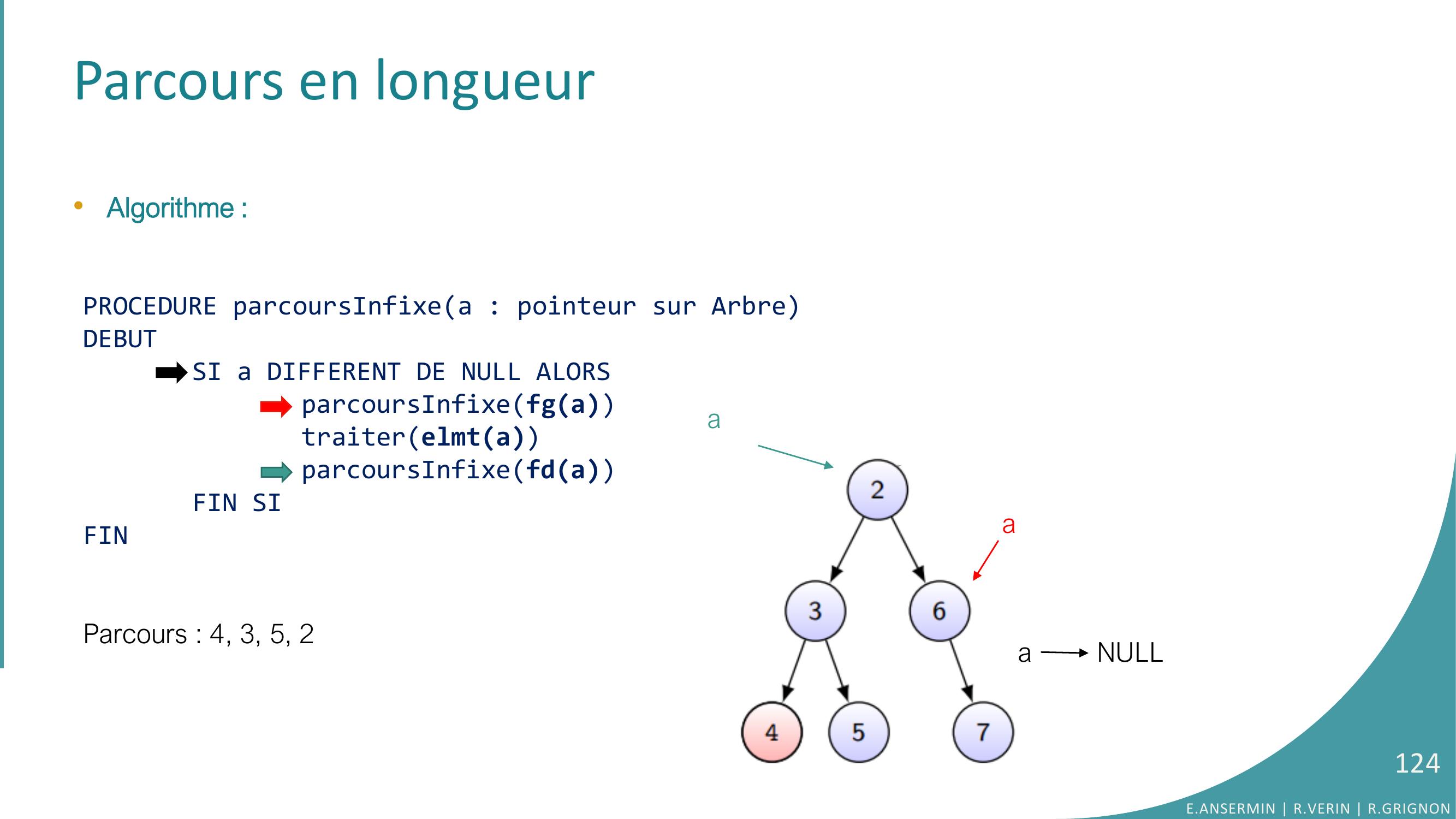
Page 124 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON124aaa NULL
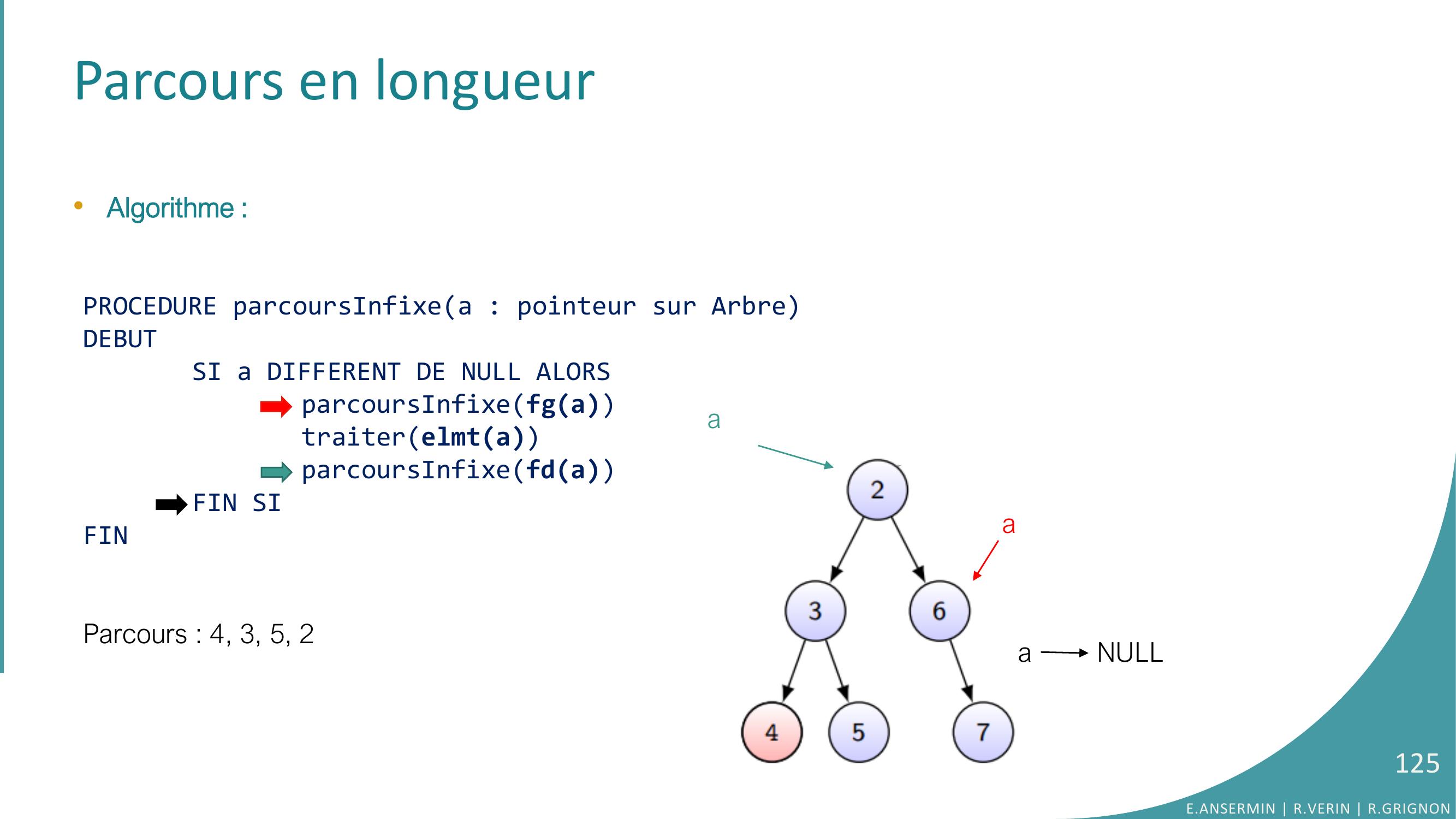
Page 125 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON125aaa NULL
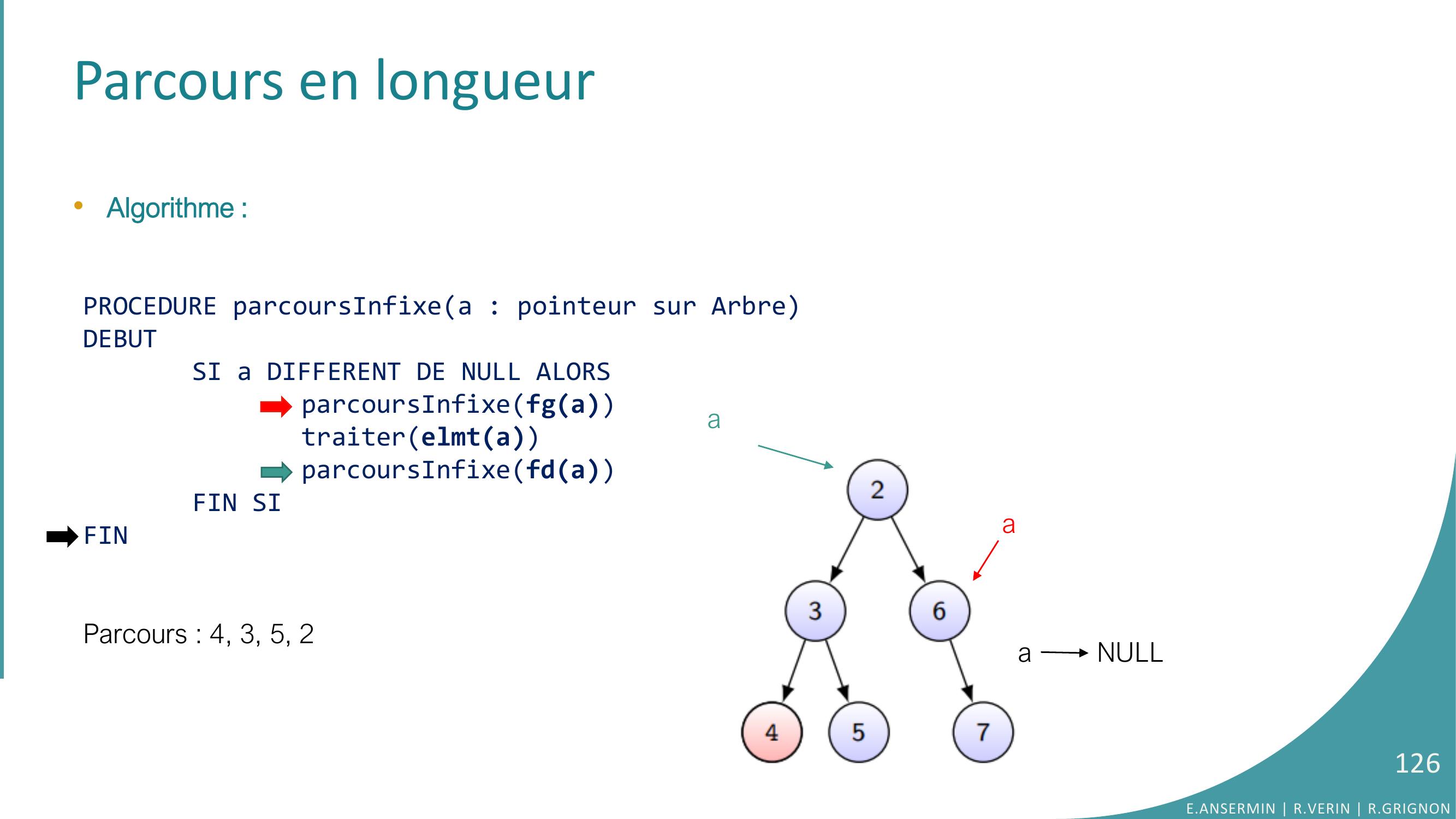
Page 126 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON126aaa NULL
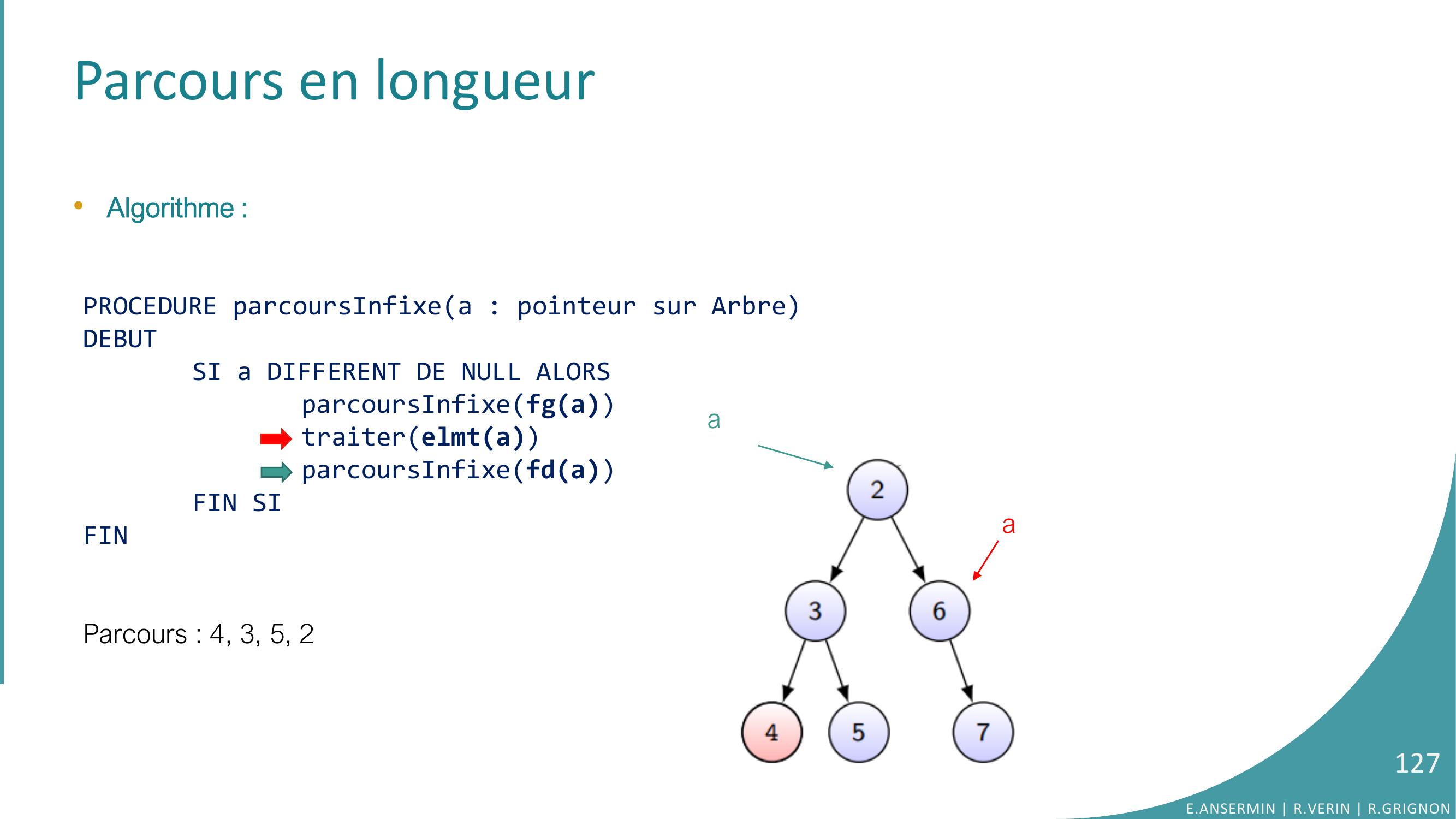
Page 127 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2E.ANSERMIN R.VERIN R.GRIGNON127aa
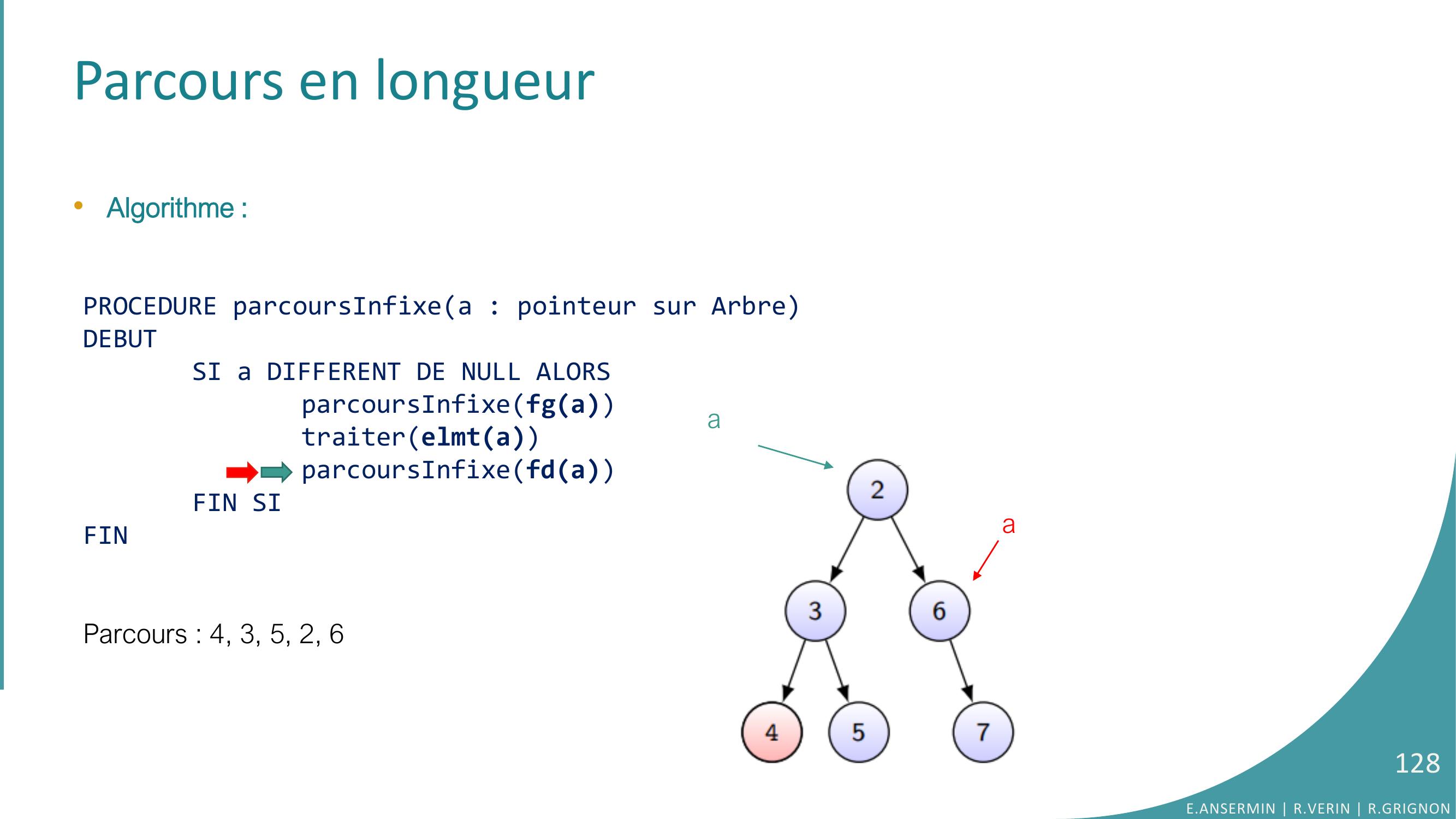
Page 128 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6E.ANSERMIN R.VERIN R.GRIGNON128aa
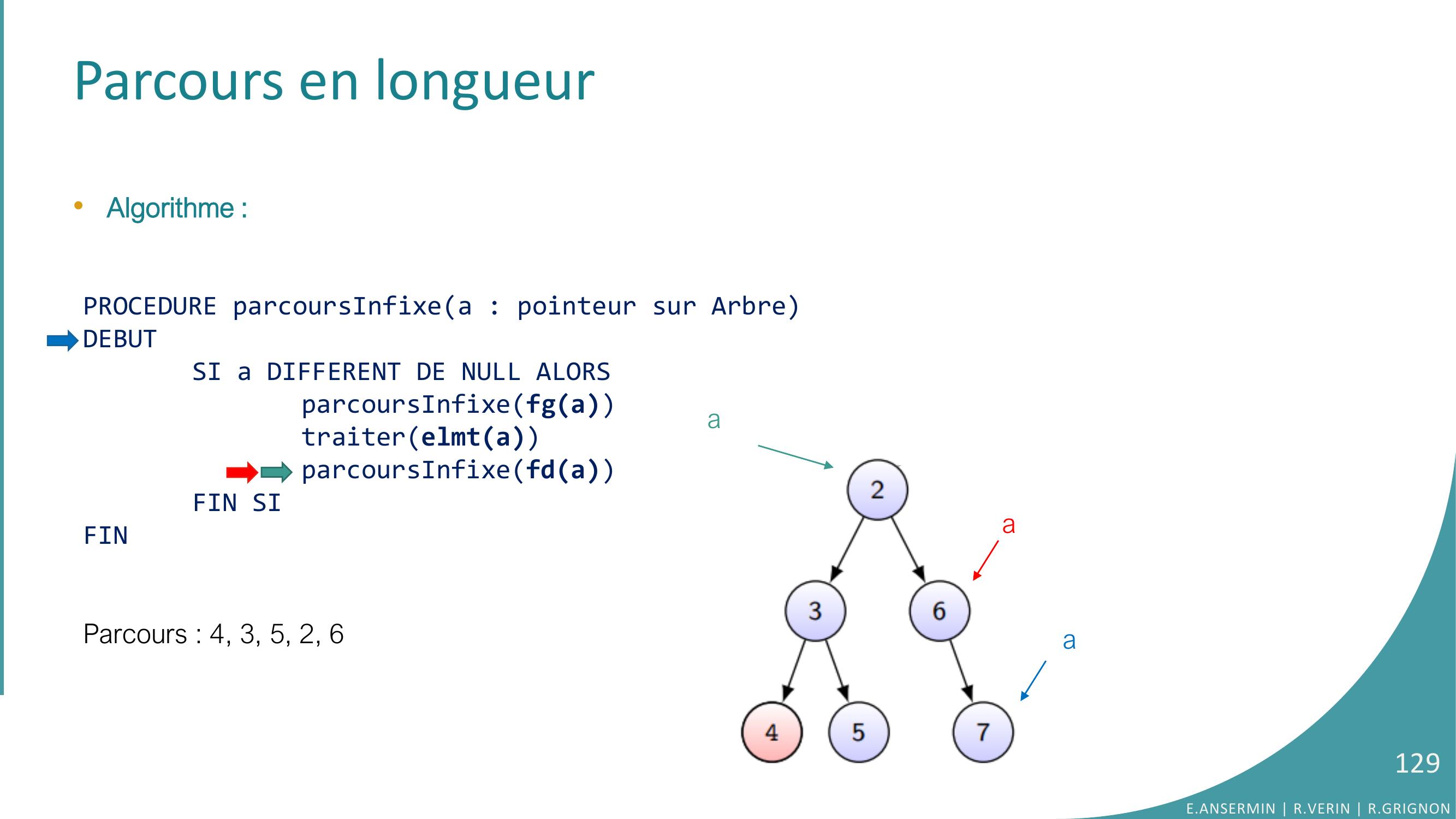
Page 129 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6E.ANSERMIN R.VERIN R.GRIGNON129aaa
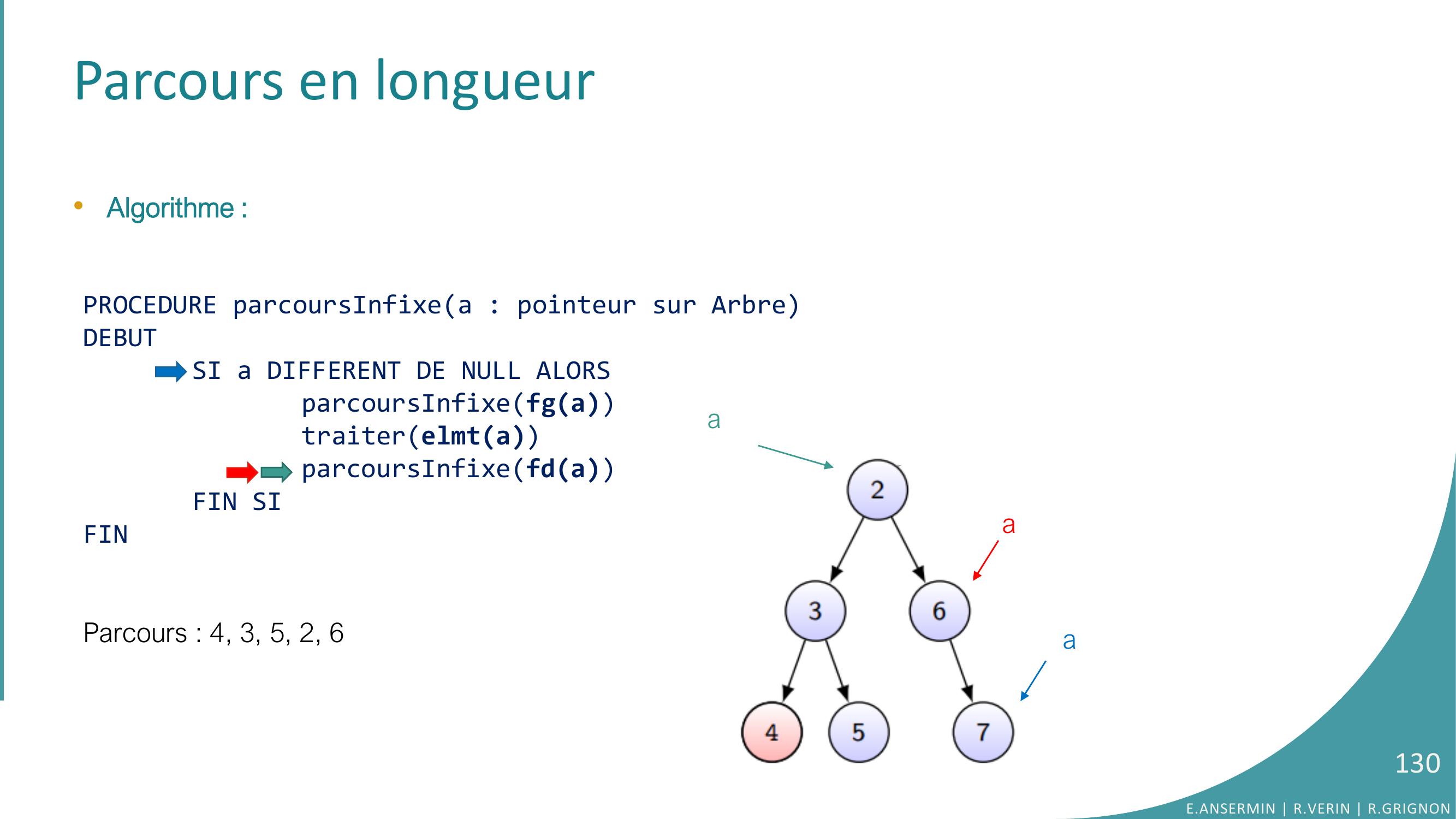
Page 130 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6E.ANSERMIN R.VERIN R.GRIGNON130aaa
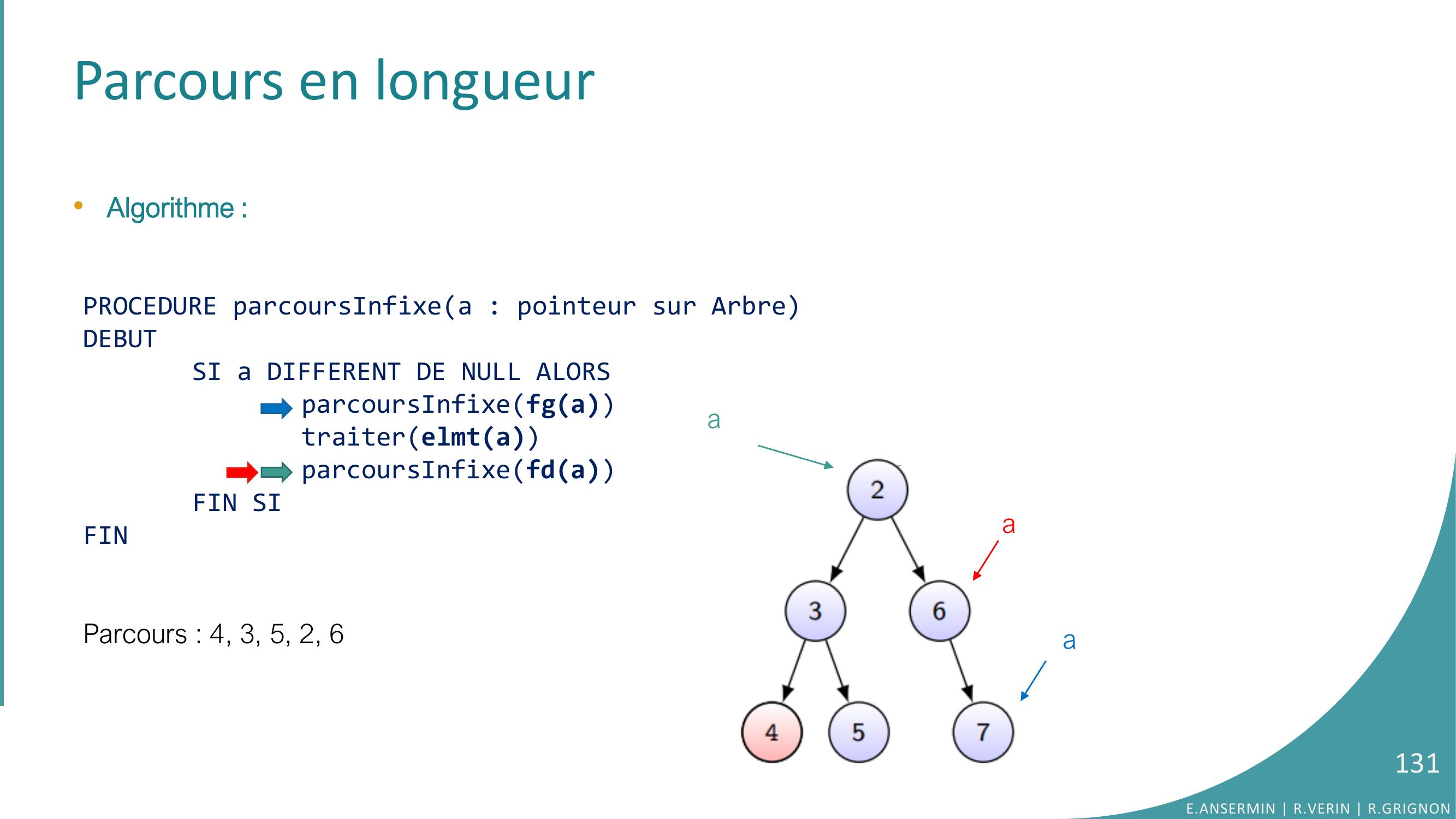
Page 131 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6E.ANSERMIN R.VERIN R.GRIGNON131aaa
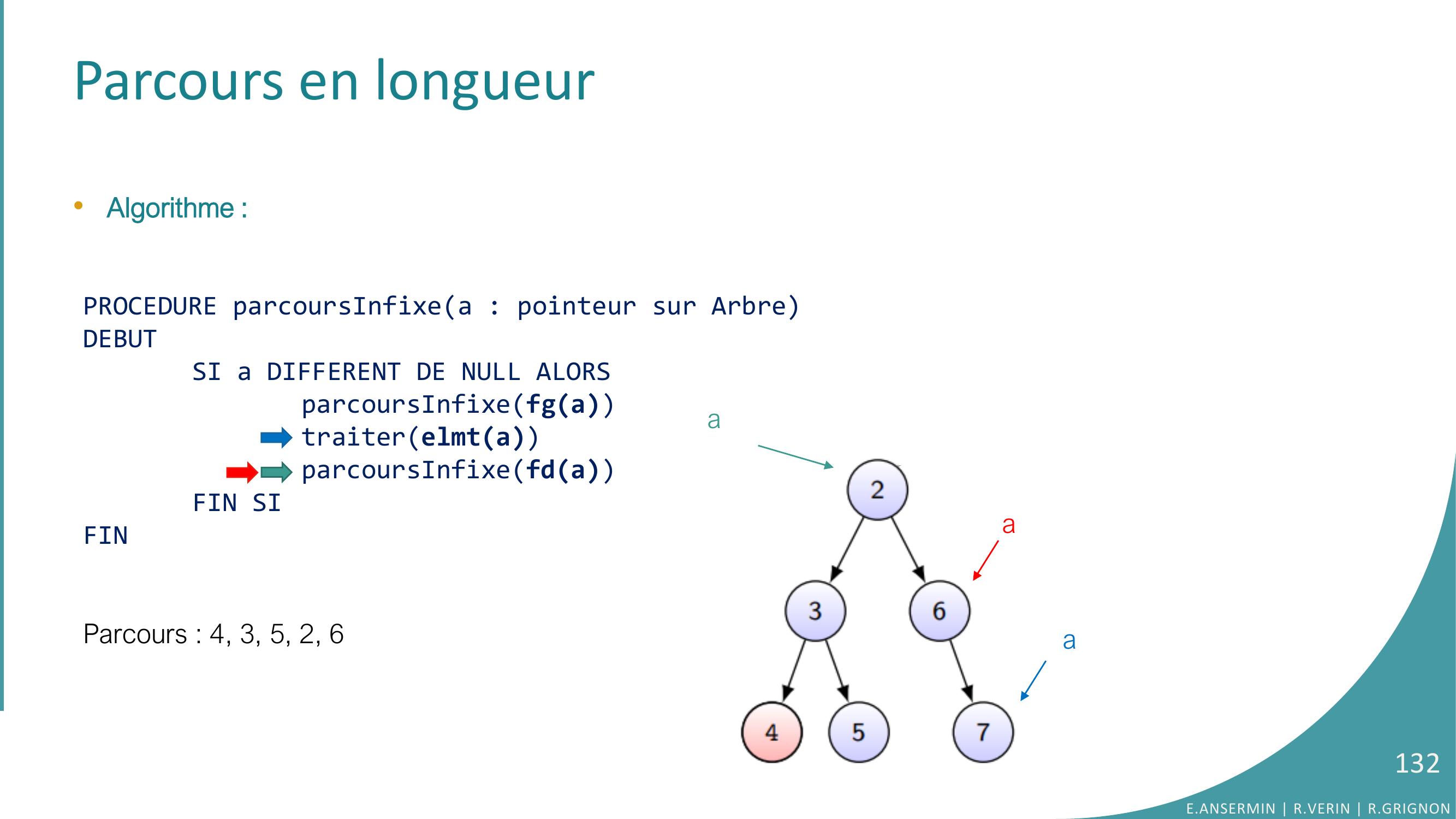
Page 132 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6E.ANSERMIN R.VERIN R.GRIGNON132aaa
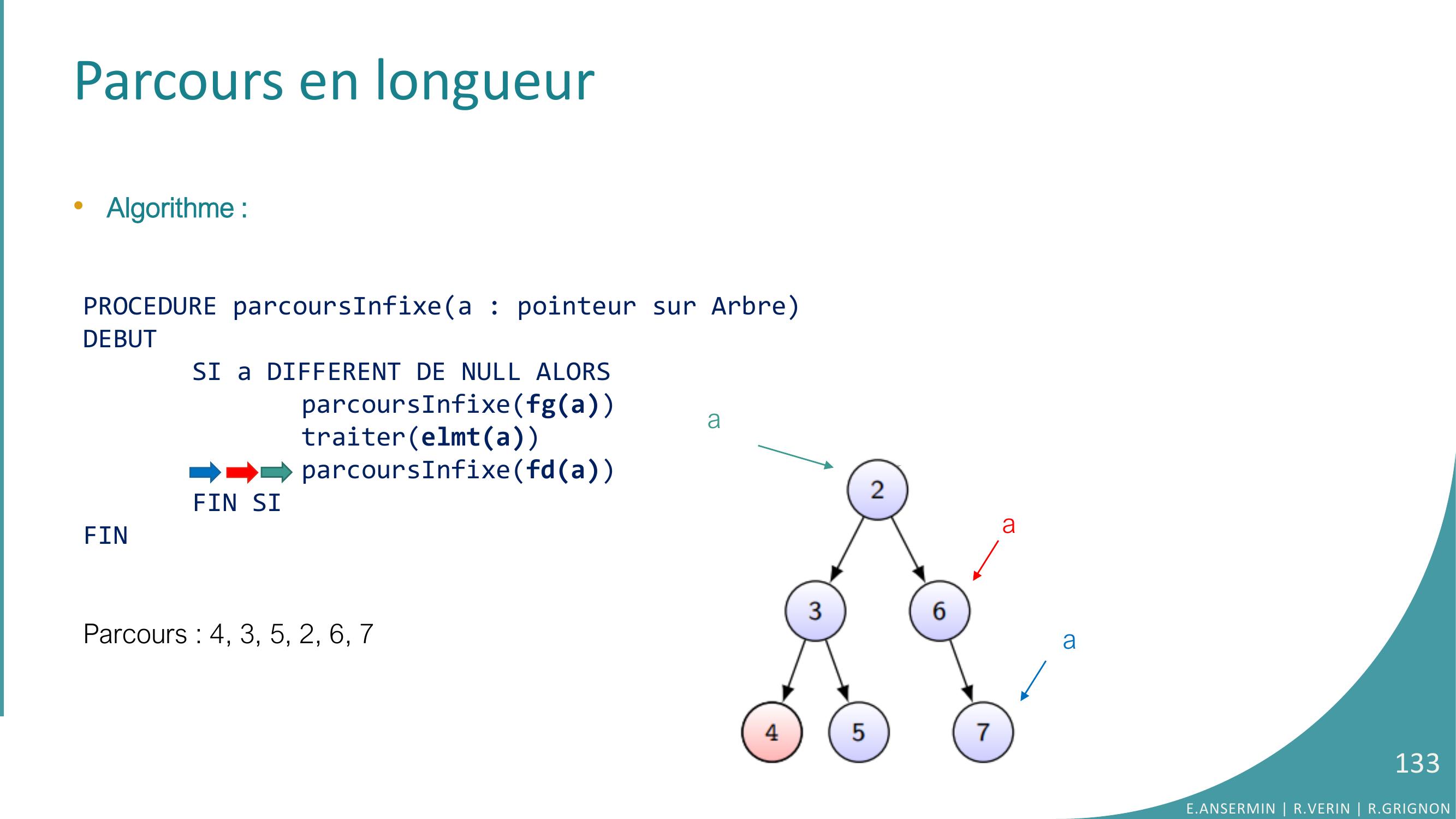
Page 133 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON133aaa
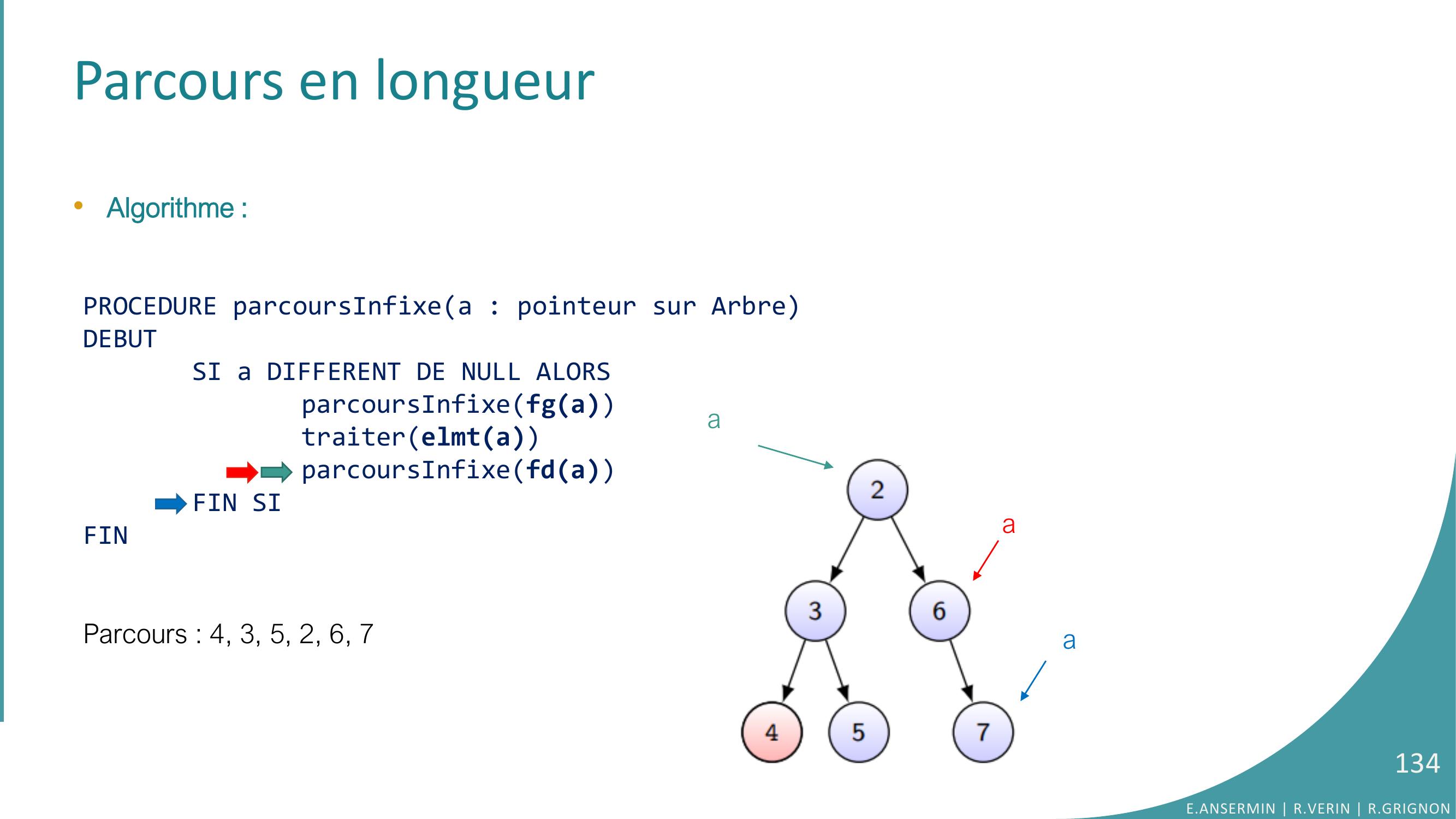
Page 134 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON134aaa
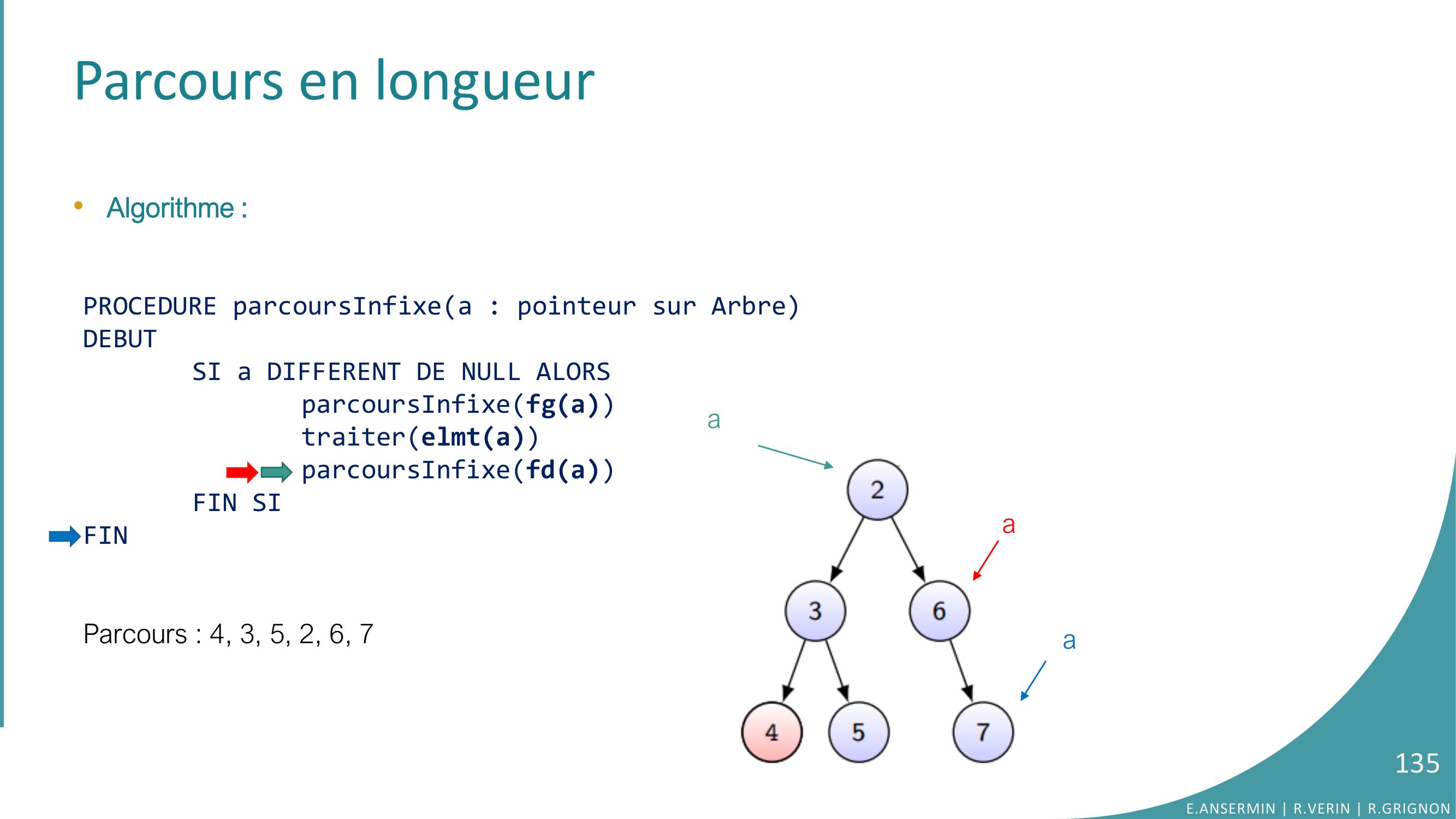
Page 135 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON135aaa
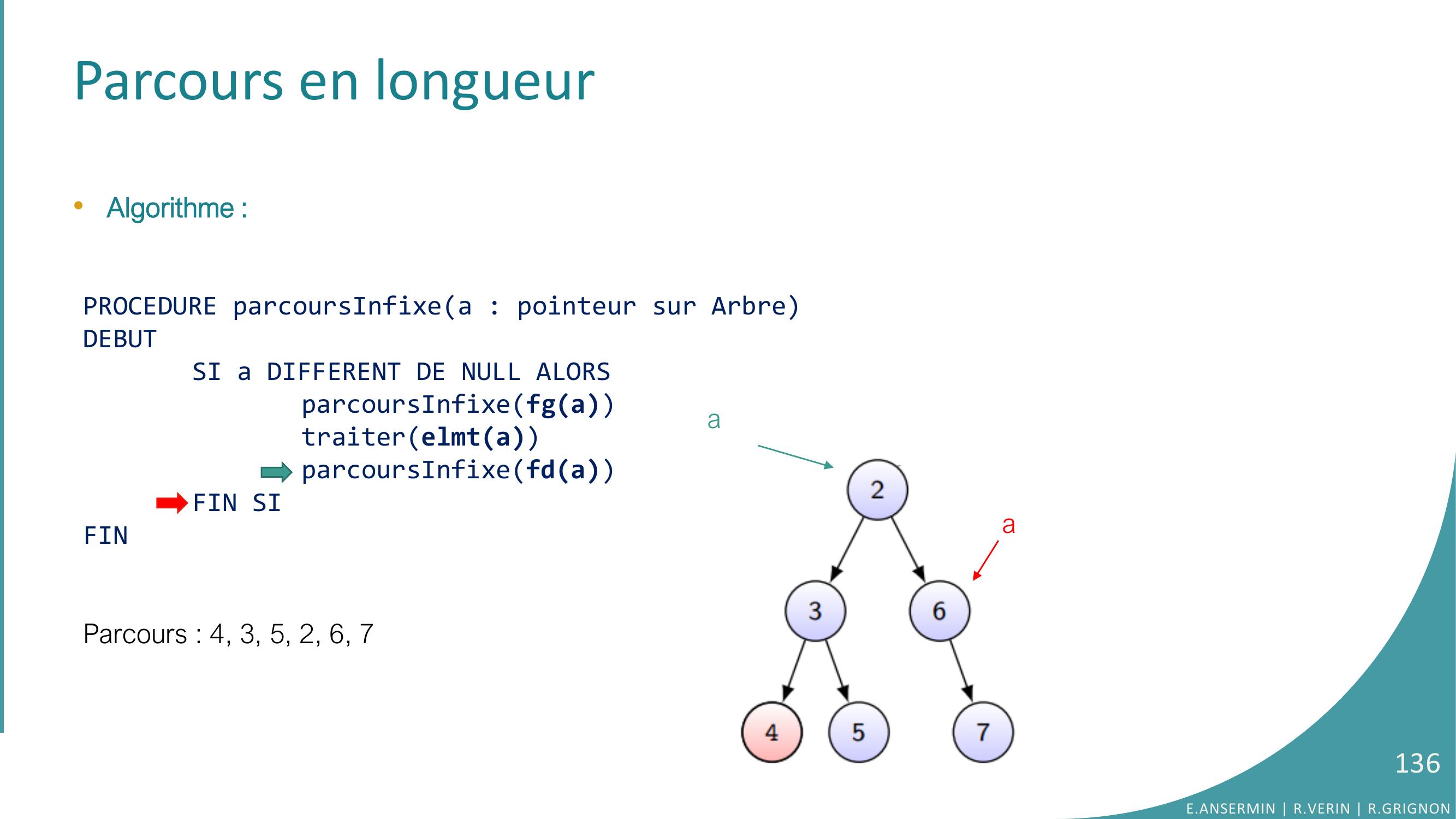
Page 136 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON136aa
Page 137 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON137aa
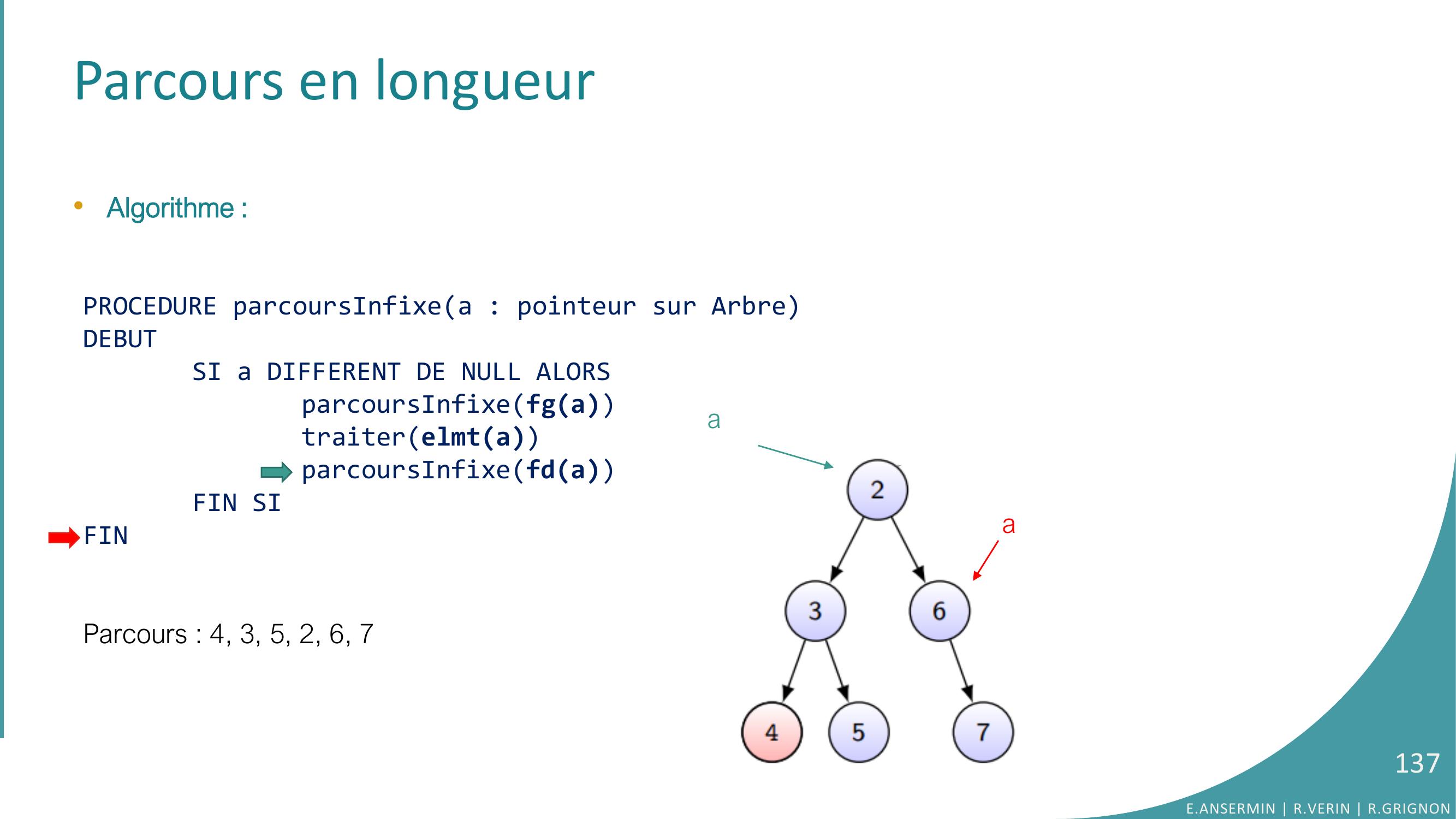
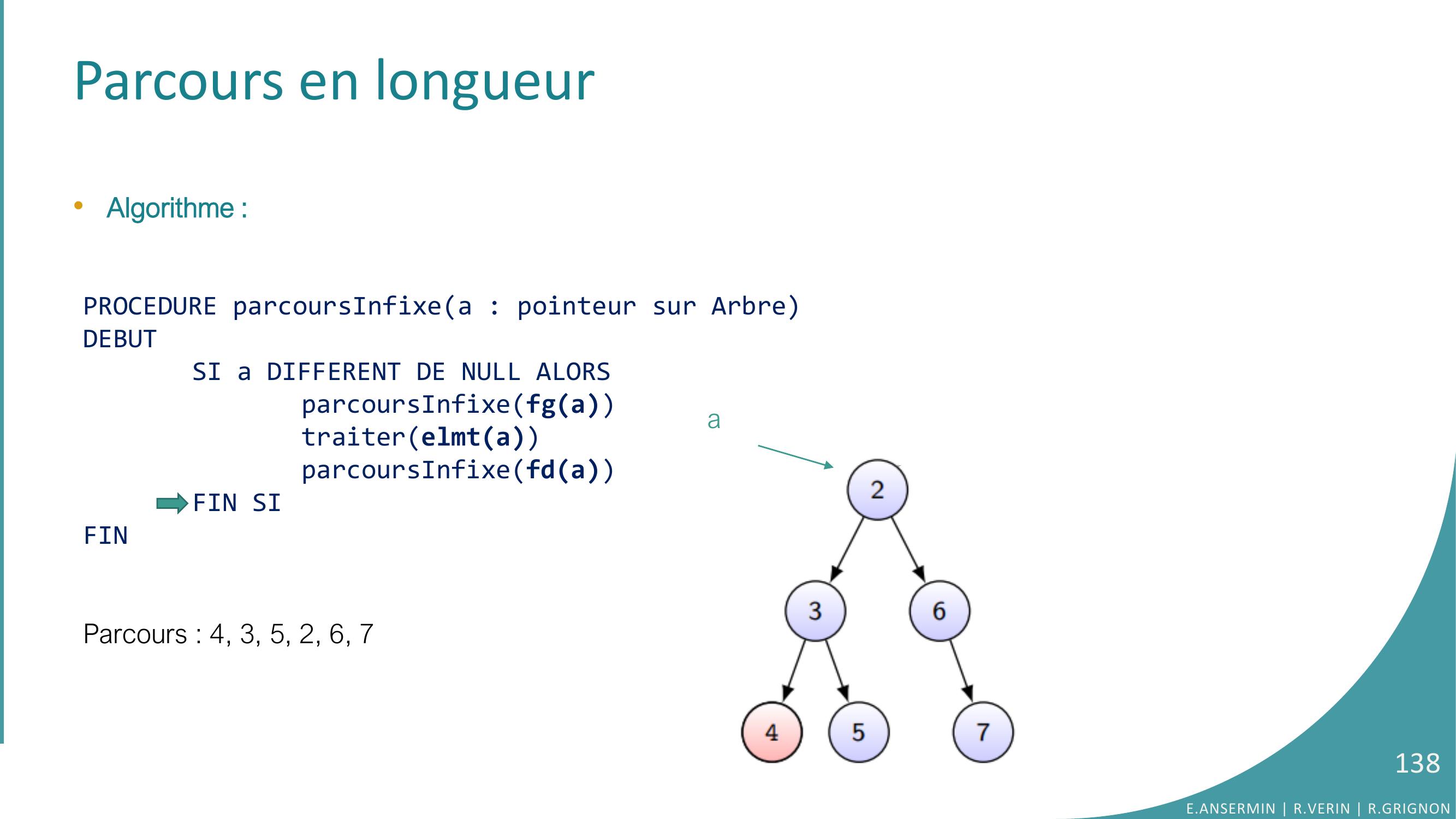
Page 138 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON138a
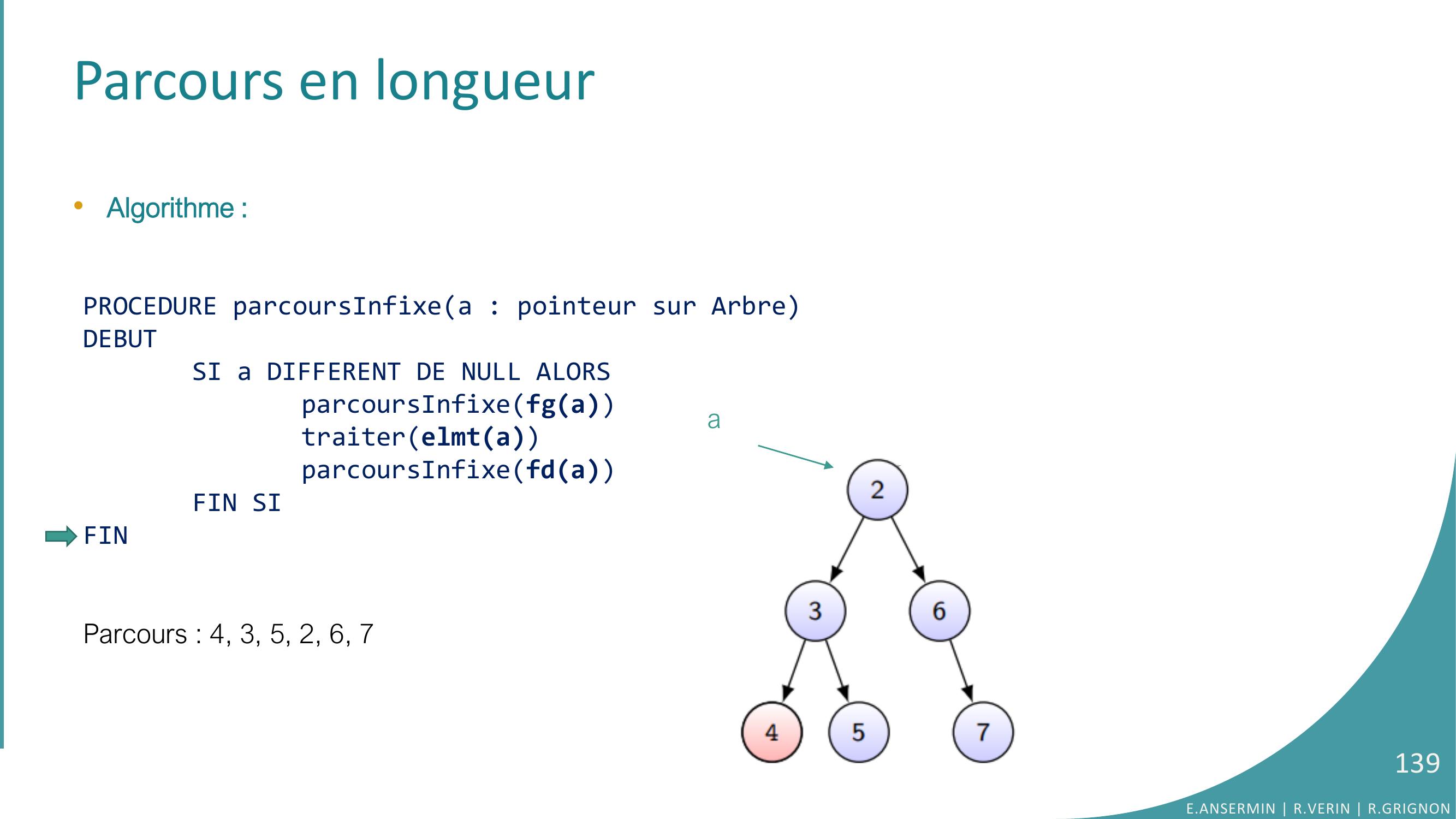
Page 139 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON139a
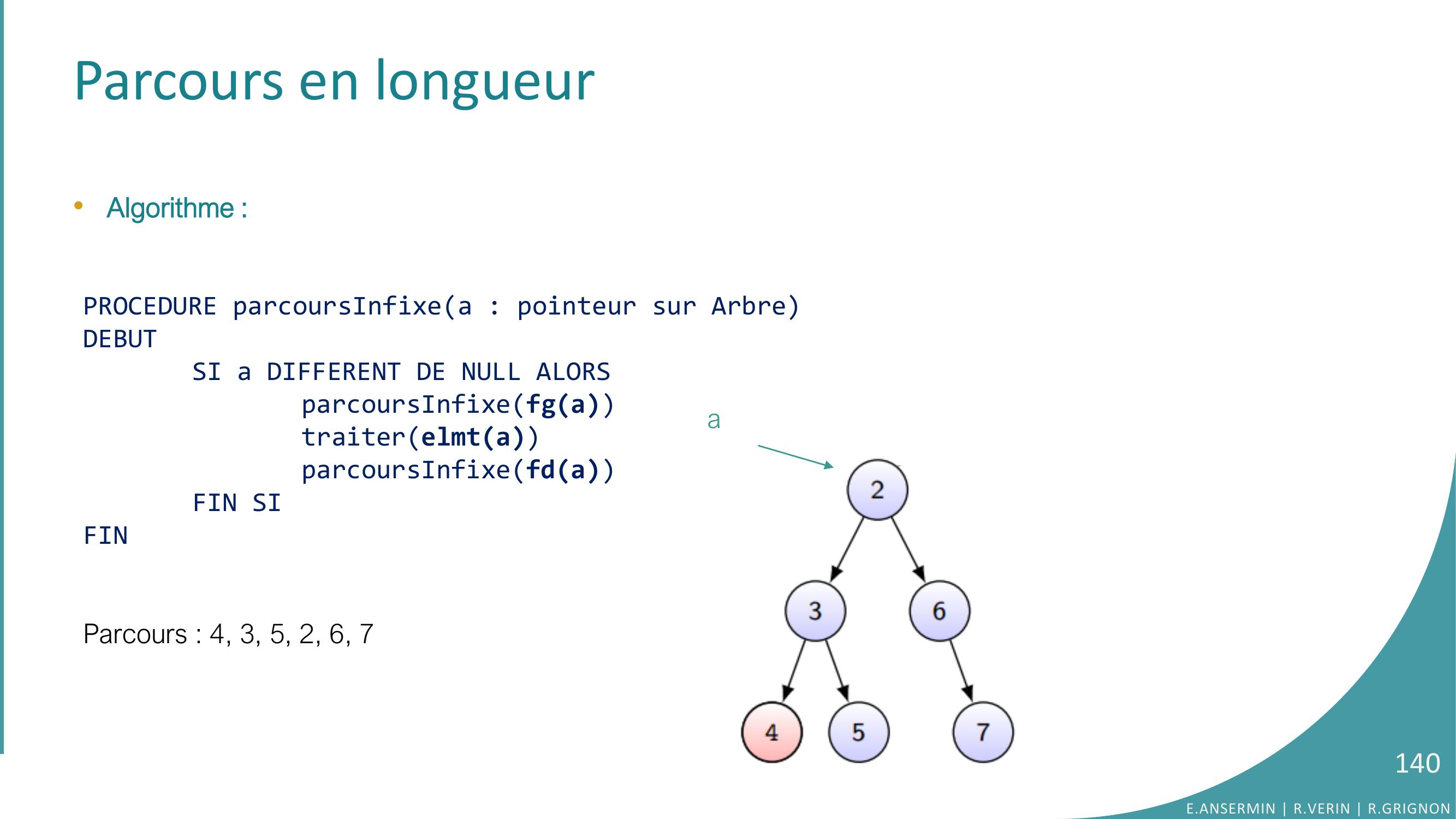
Page 140 : Parcours en longueur•Algorithme :PROCEDURE parcoursInfixea : pointeur sur ArbreDEBUTSI a DIFFERENT DE NULL ALORSparcoursInfixefgatraiterelmtaparcoursInfixefdaFIN SIFINParcours : 4, 3, 5, 2, 6, 7E.ANSERMIN R.VERIN R.GRIGNON140a
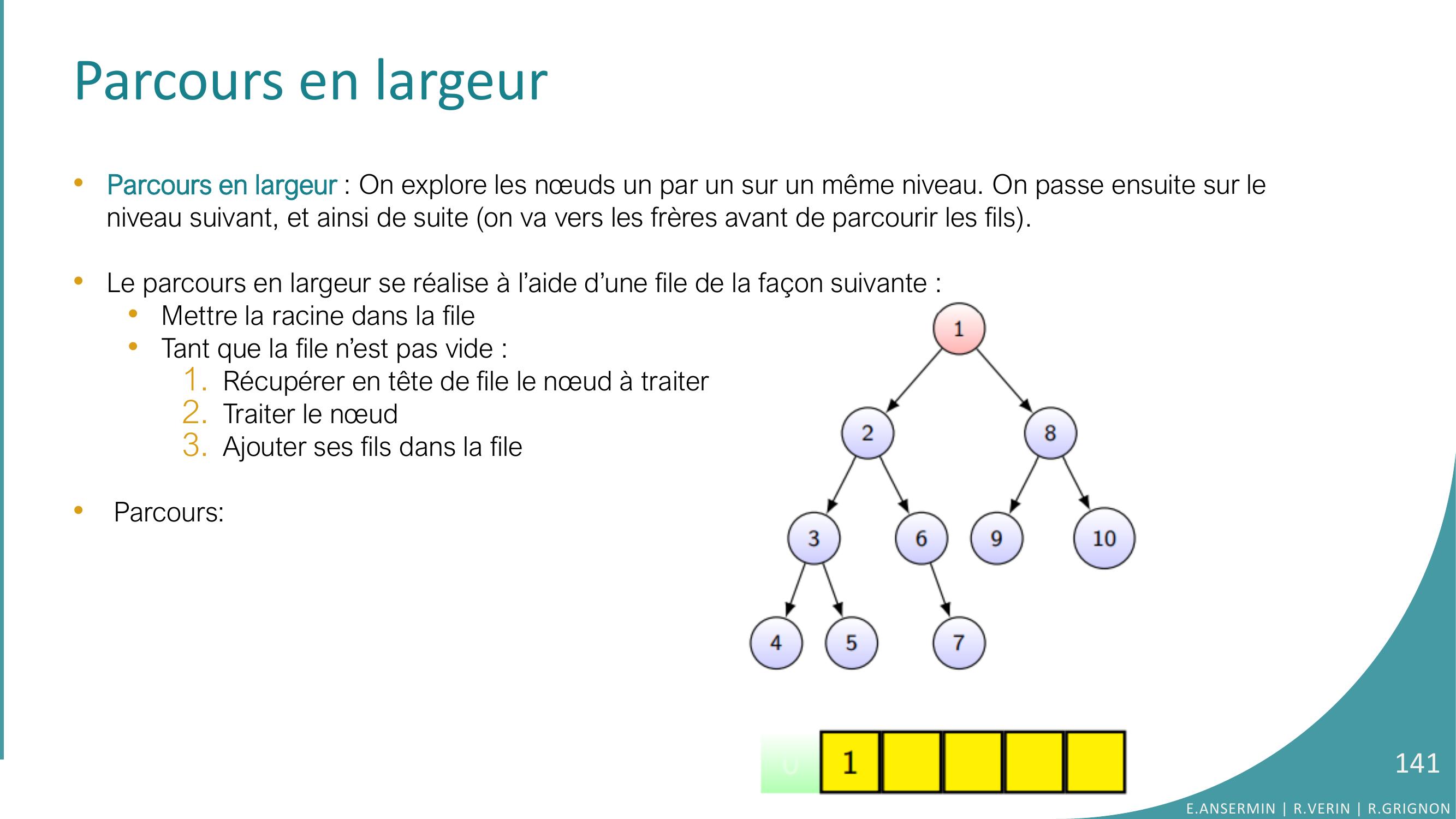
Page 141 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: E.ANSERMIN R.VERIN R.GRIGNON141
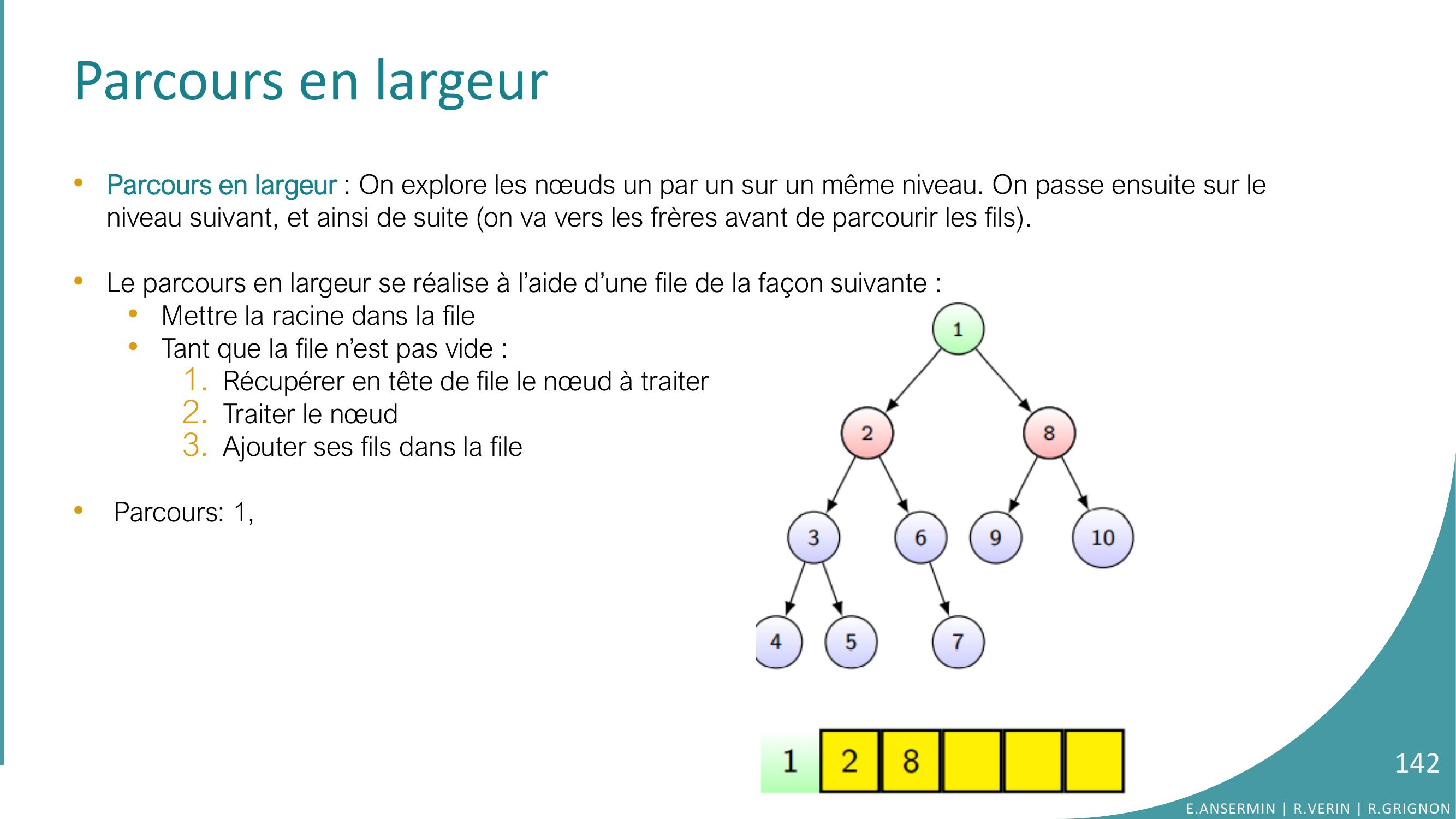
Page 142 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1,E.ANSERMIN R.VERIN R.GRIGNON142
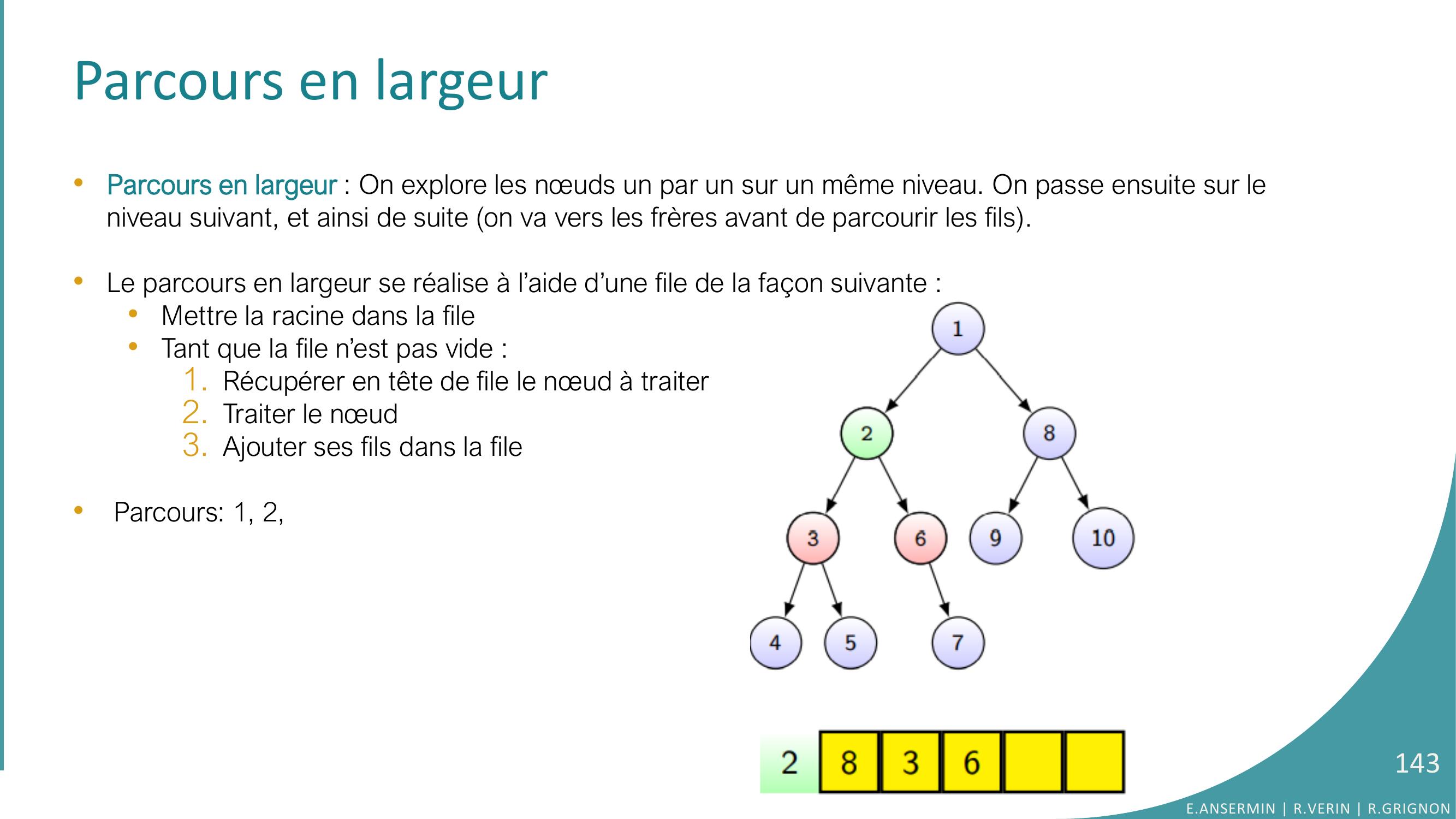
Page 143 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, E.ANSERMIN R.VERIN R.GRIGNON143
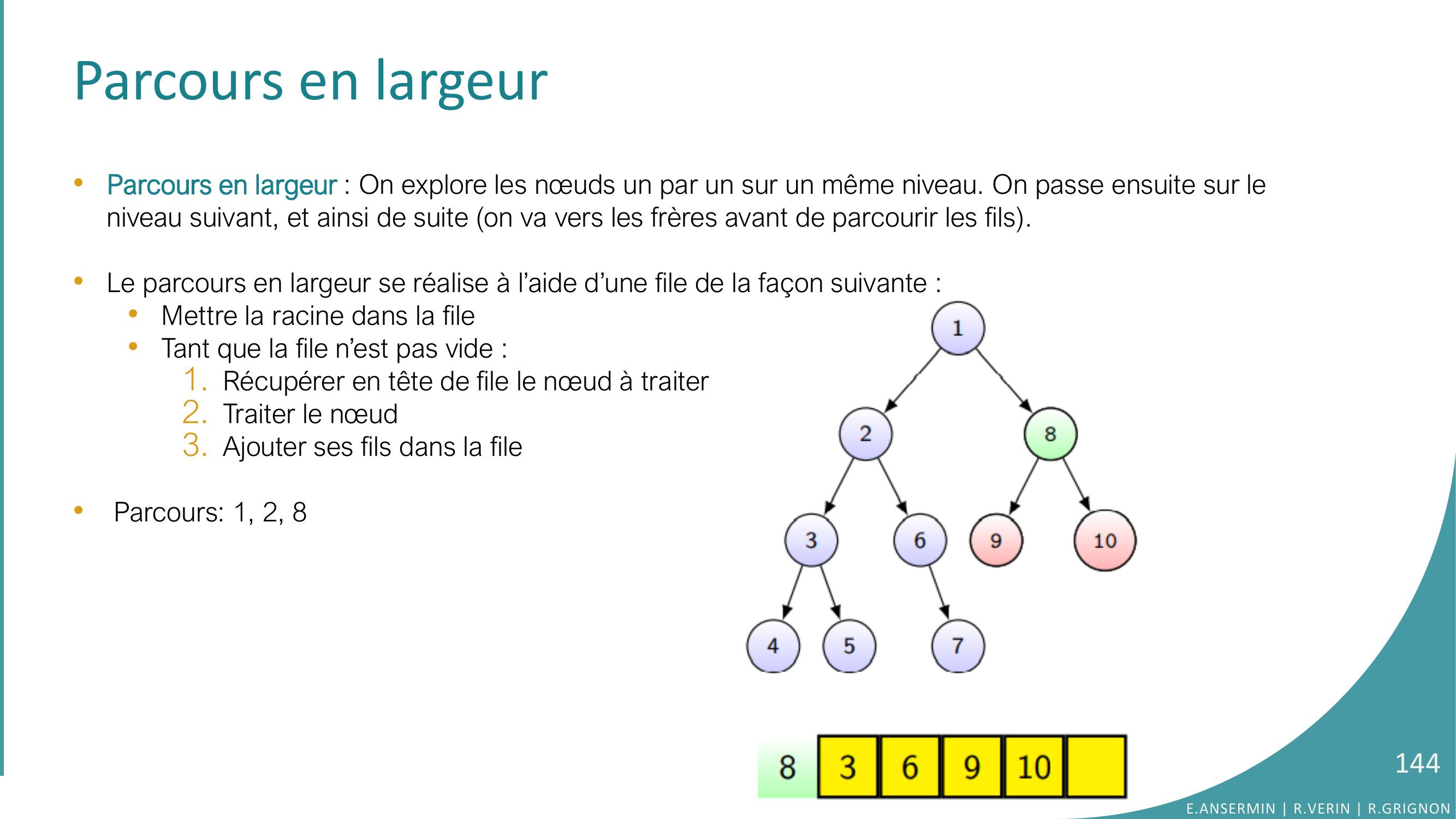
Page 144 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8E.ANSERMIN R.VERIN R.GRIGNON144
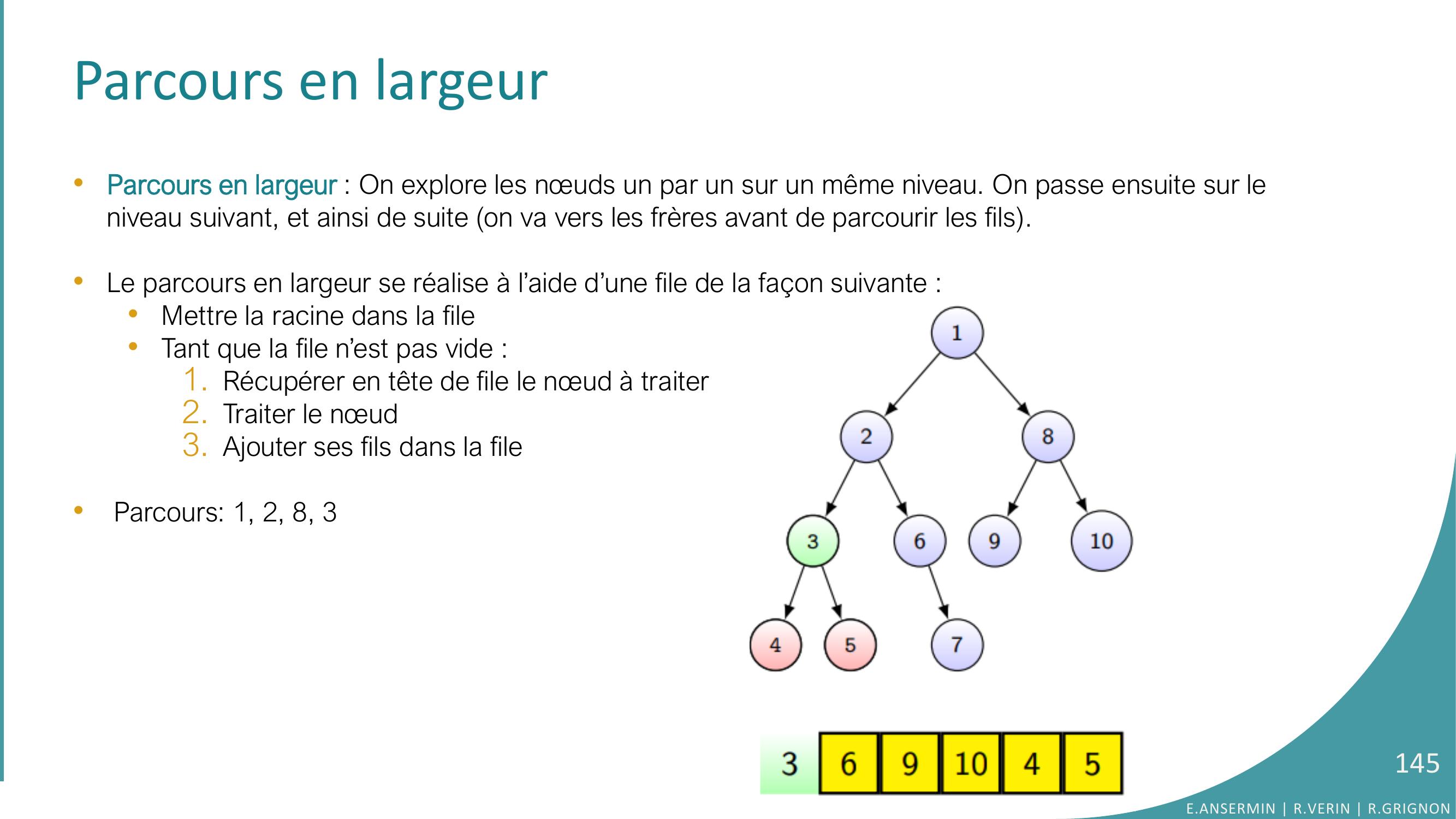
Page 145 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3E.ANSERMIN R.VERIN R.GRIGNON145
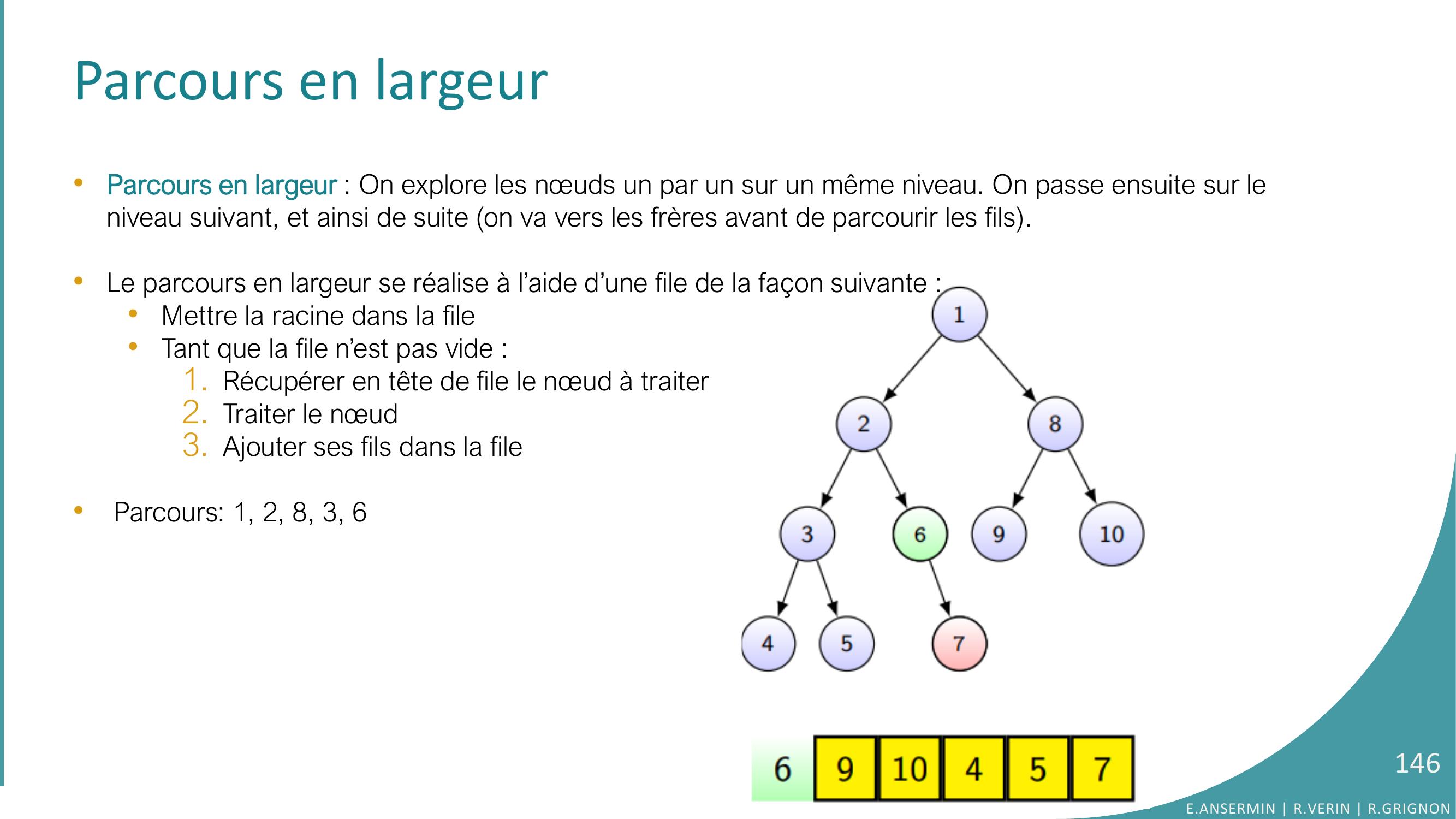
Page 146 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6E.ANSERMIN R.VERIN R.GRIGNON146
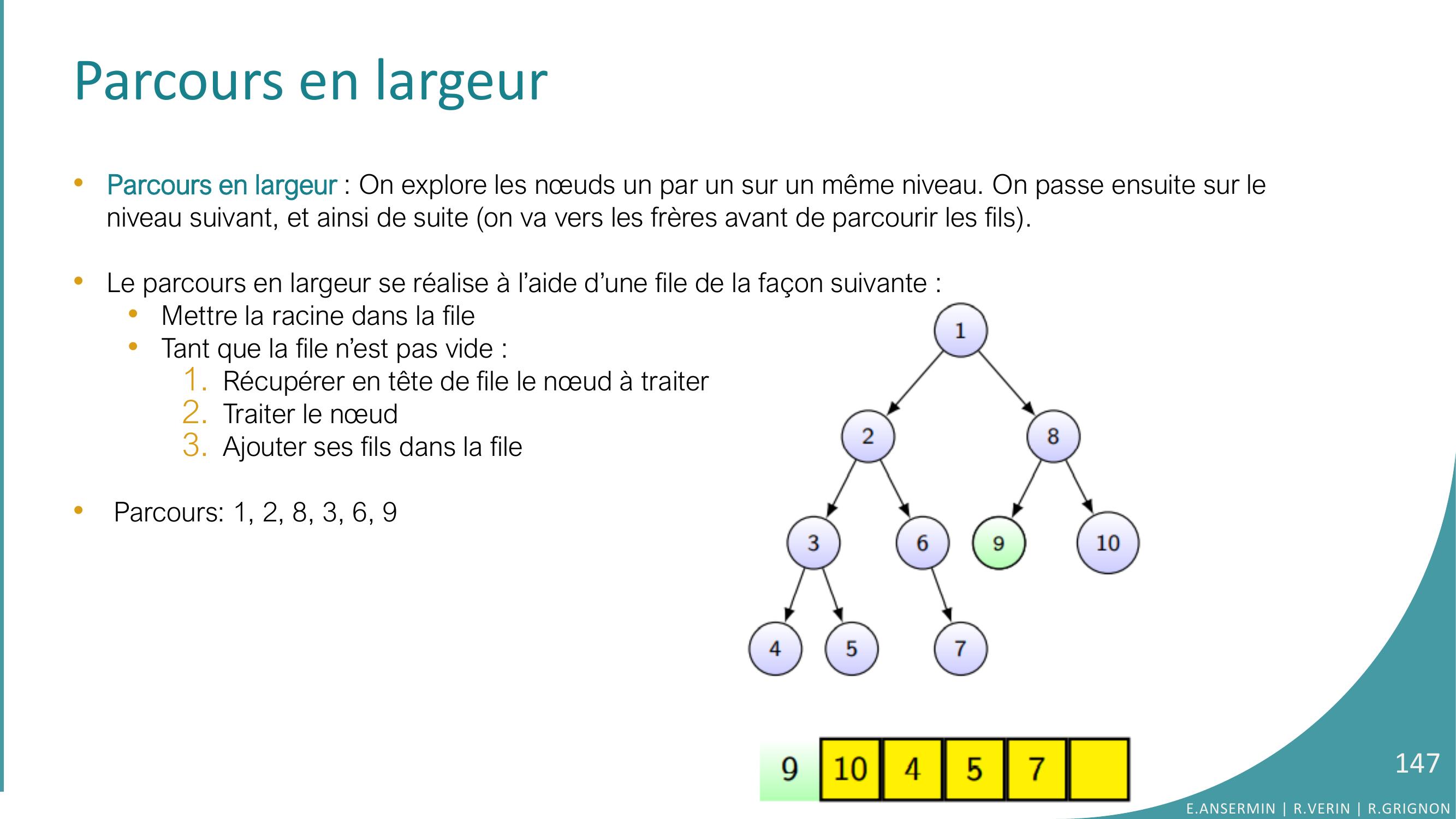
Page 147 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6, 9E.ANSERMIN R.VERIN R.GRIGNON147
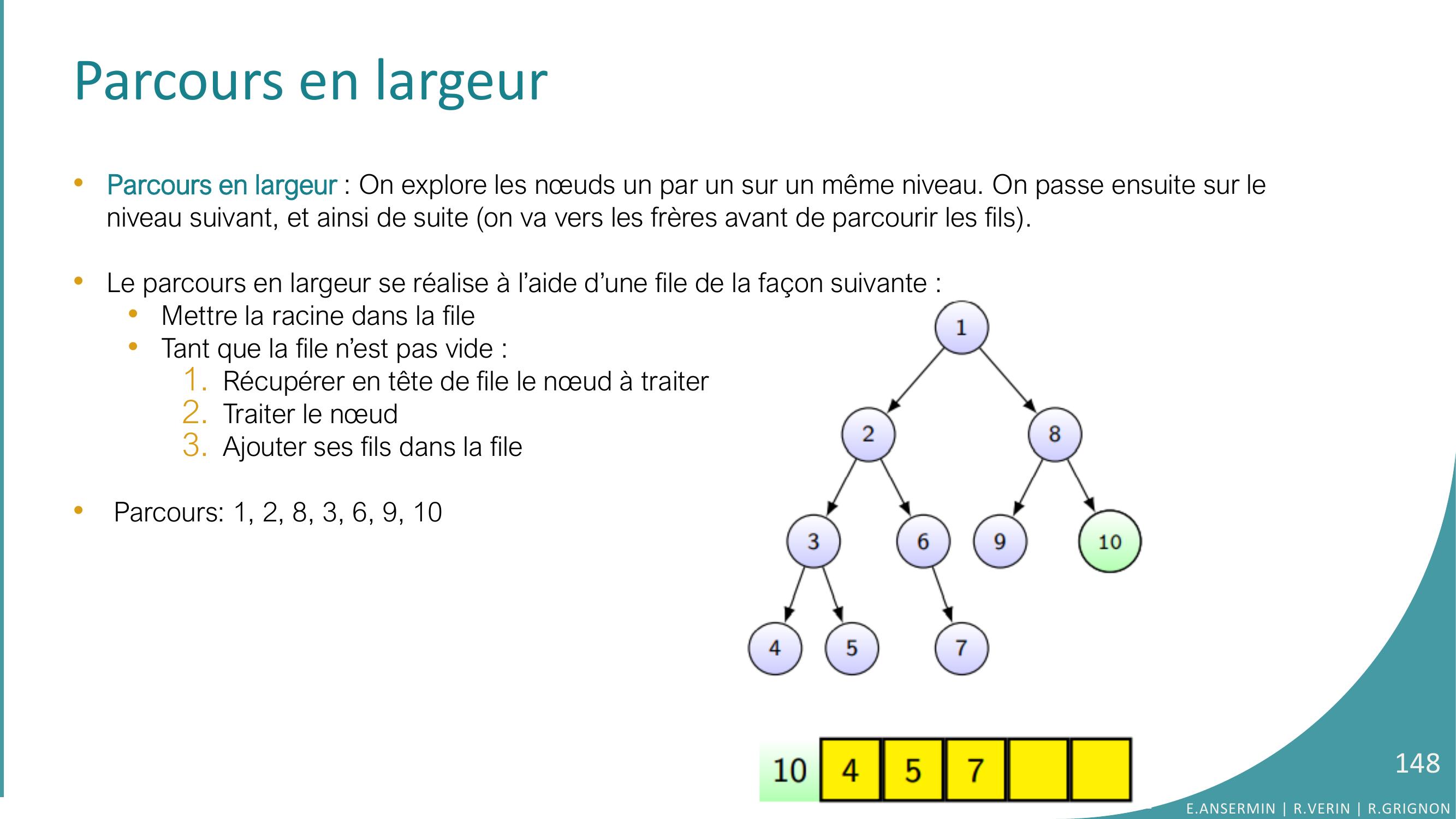
Page 148 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6, 9, 10E.ANSERMIN R.VERIN R.GRIGNON148
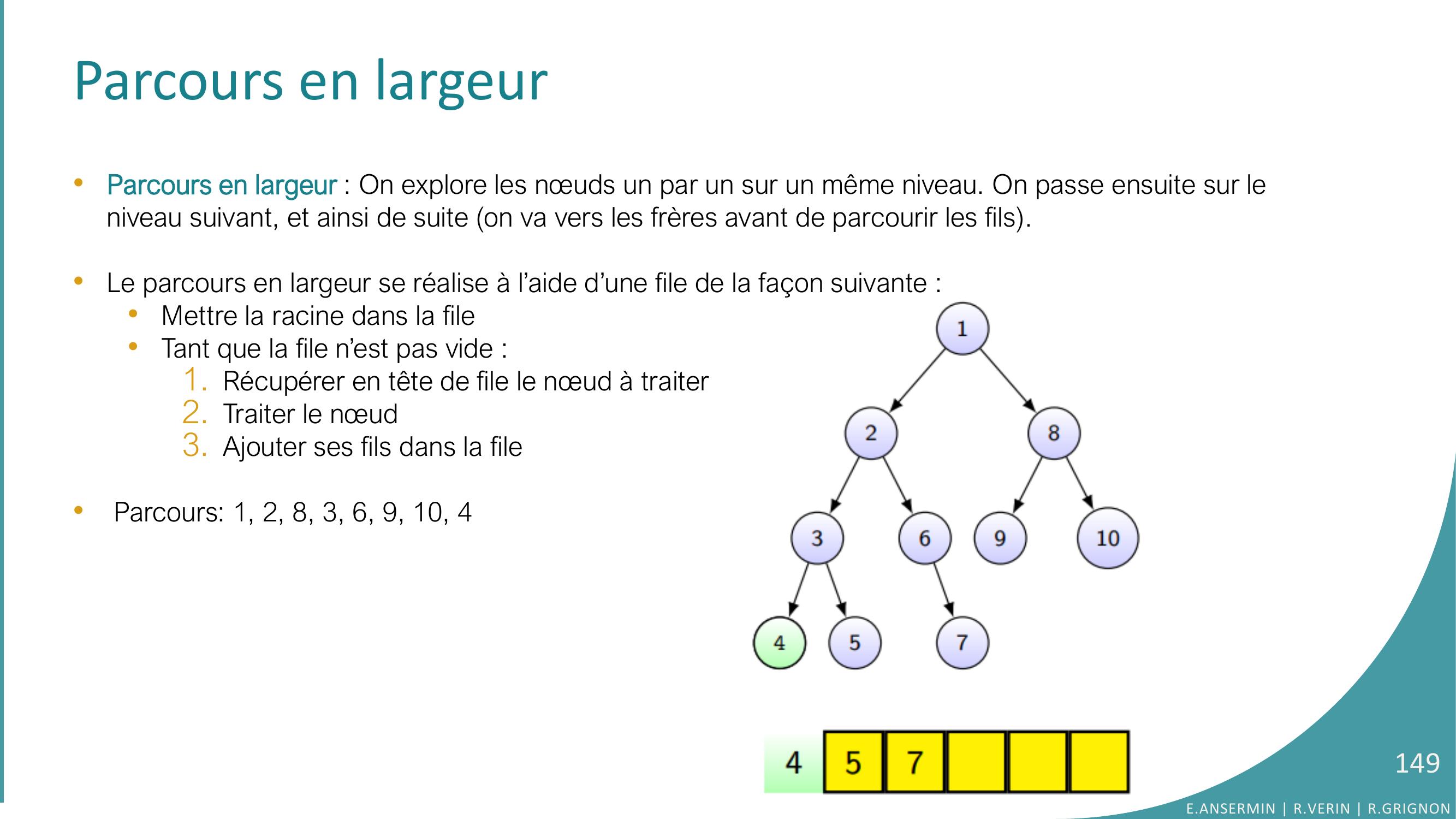
Page 149 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6, 9, 10, 4E.ANSERMIN R.VERIN R.GRIGNON149
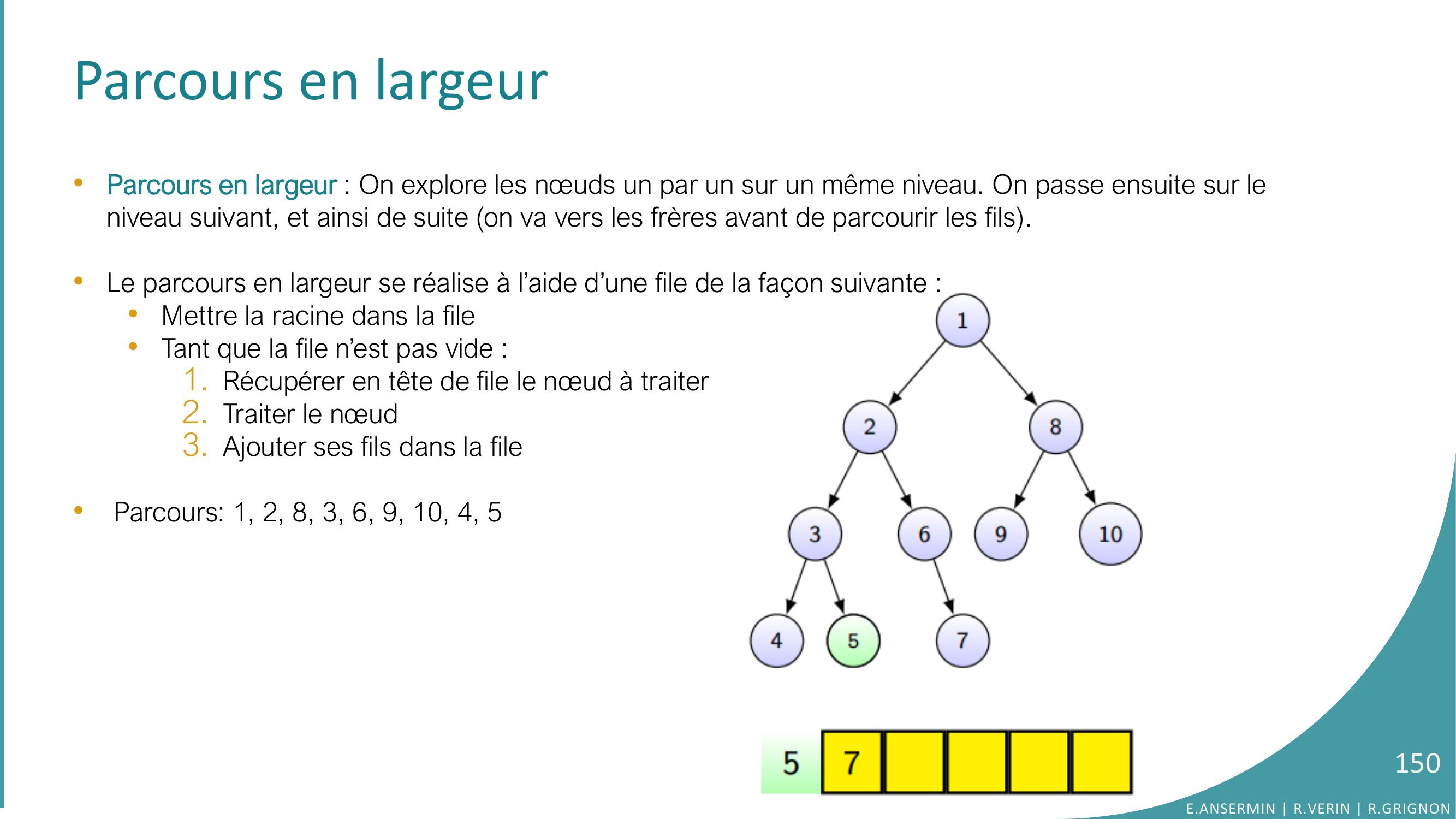
Page 150 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6, 9, 10, 4, 5E.ANSERMIN R.VERIN R.GRIGNON150
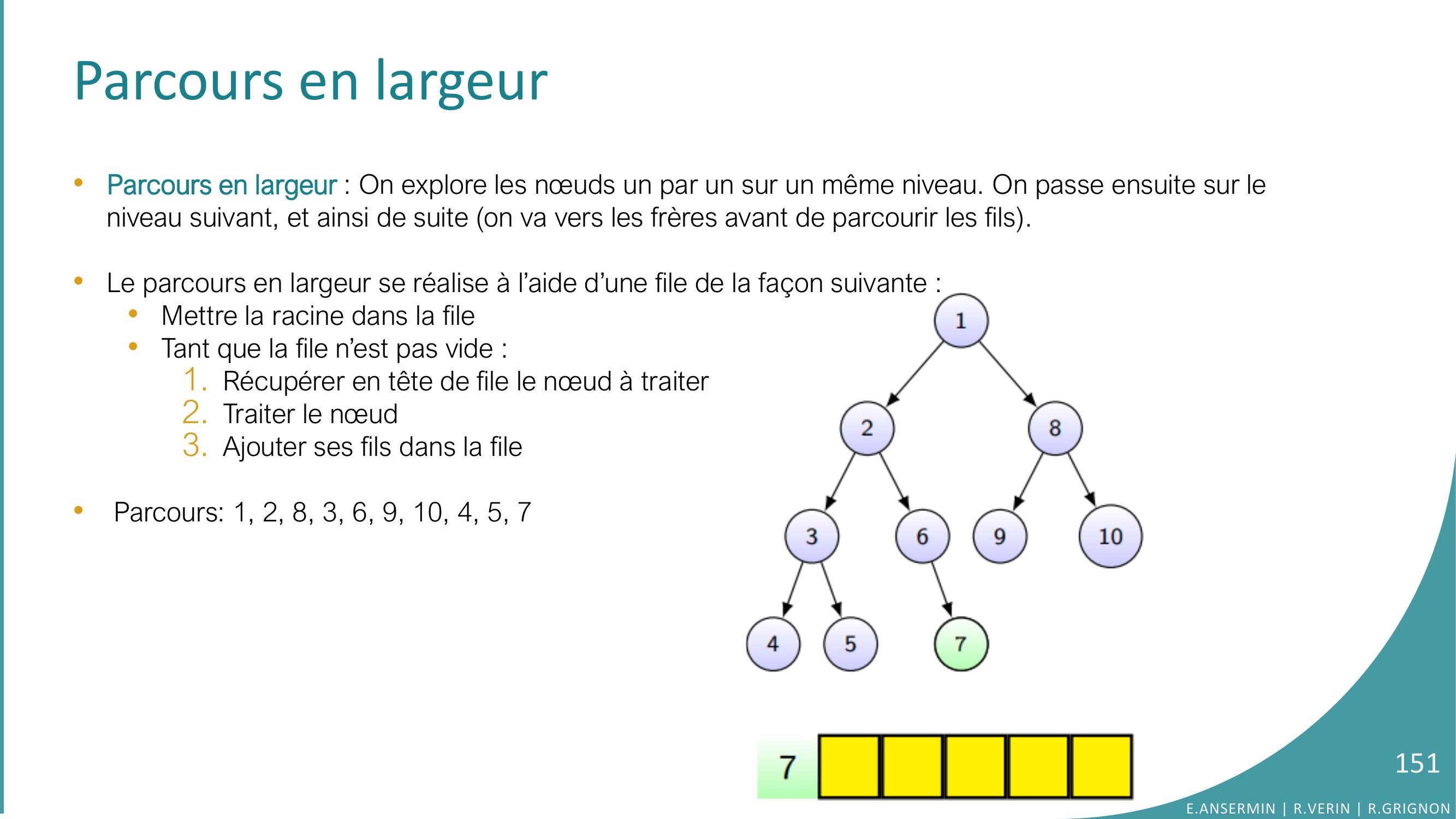
Page 151 : Parcours en largeur•Parcours en largeur : On explore les nœuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite on va vers les frères avant de parcourir les fils. •Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la file•Parcours: 1, 2, 8, 3, 6, 9, 10, 4, 5, 7E.ANSERMIN R.VERIN R.GRIGNON151
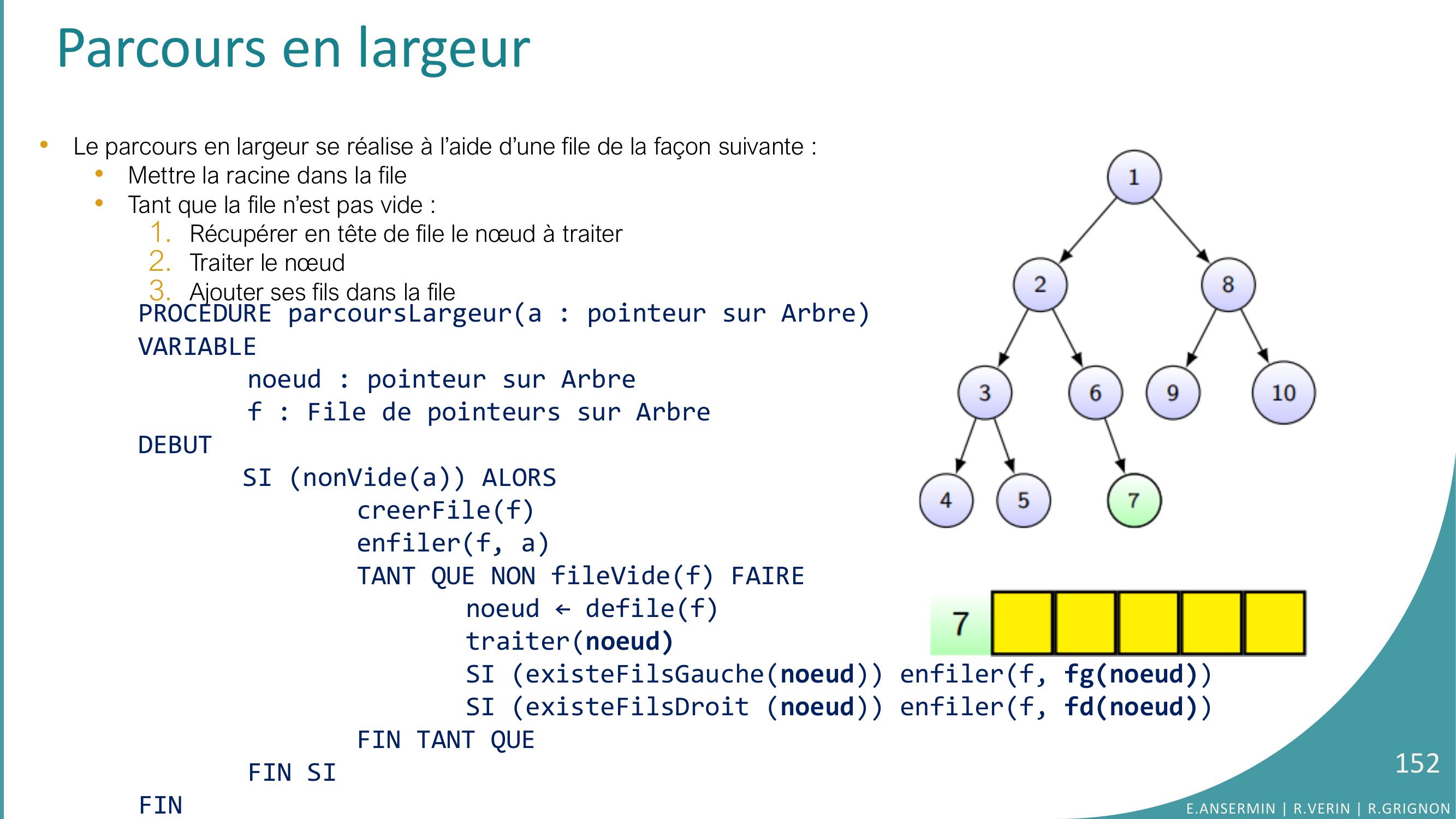
Page 152 : Parcours en largeur•Le parcours en largeur se réalise à l’aide d’une file de la façon suivante : •Mettre la racine dans la file•Tant que la file n’est pas vide :1. Récupérer en tête de file le nœud à traiter2. Traiter le nœud 3. Ajouter ses fils dans la filePROCEDURE parcoursLargeura : pointeur sur ArbreVARIABLEnoeud : pointeur sur Arbref : File de pointeurs sur ArbreDEBUTSI nonVidea ALORScreerFilefenfilerf, aTANT QUE NON fileVidef FAIREnoeud ← defileftraiternoeudSI existeFilsGauchenoeud enfilerf, fgnoeudSI existeFilsDroit noeud enfilerf, fdnoeudFIN TANT QUEFIN SIFINE.ANSERMIN R.VERIN R.GRIGNON152
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152