CM3 Ensemble
Télécharger le CM3 Ensemble en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Page 1 : IntroductionLogique et RaisonnementEnsembleAlgebre-Premier semestre 20211Introduction2Logique et Raisonnement3EnsembleN. Arancibia - relu par D. CransacAlgebre
Page 2 : IntroductionLogique et RaisonnementEnsembleAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre
Page 3 : IntroductionLogique et RaisonnementEnsembleEnsemblesIntroduction a la theorie des ensembles :Definition et exemples.Inclusion, Egalite.Ensemble des partiesOperation sur les ensembles :Intersection, Union.Difference, Complementaire.Partition d’un ensemble.Produit Cartesien.N. Arancibia - relu par D. CransacAlgebre
Page 4 : IntroductionLogique et RaisonnementEnsembleEnsemblesDefinition EnsembleUn ensemble E est une collection ou un groupement d’objets distincts.Les objets x de E s’appellent les elements de E.Si E est un ensemble et si x est un element de E, on dit que xappartient a E ou que x est dans E et on ecritx E.Dans le cas contraire, si x n’est pas un element de E, on dit que xn’appartient pas a E ou que x n’est pas dans E et on ecritx /E.Remarque :Il existe un unique ensemble ne contenant aucun element. C’estl’ensemble vide note .Un ensemble qui ne contient qu’un seul element est appelesingleton.N. Arancibia - relu par D. CransacAlgebre
Page 5 : IntroductionLogique et RaisonnementEnsembleEnsemblesPour definir un ensemble, on peut le decrire :Par extension : en donnant la liste complete explicite de tous seselements. On note cette liste entre accolades, l’ordre des elementslistes n’ayant aucune importance.Exemple :1, 1, 4, 1, 4, 9 et1, 4, 9, 11 = 9, 4, 11, 1.2N = 0, 2, 4, · · · : L’ensemble des entiers naturels pairs.2N + 1 = 1, 3, 5, · · · : L’ensemble des entiers naturels impairs.N. Arancibia - relu par D. CransacAlgebre
Page 6 : IntroductionLogique et RaisonnementEnsembleEnsemblesPar comprehension : en donnant une propriete P que ses elementsverifient et sont seuls a verifier. On notex E : Pxoux E Pxl’ensemble des elements de E qui verifient P.Exemple :2N = n N : k N, n = 2k : L’ensemble des entiers naturelspairs.2N + 1 = n N : k N, n = 2k + 1 : L’ensemble des entiersnaturels impairs.Q =x R : p Z, q N, x = pq: L’ensemble des rationnels.a, b = x R : a x b : l’intervalle semi-ouvert a droite.N. Arancibia - relu par D. CransacAlgebre
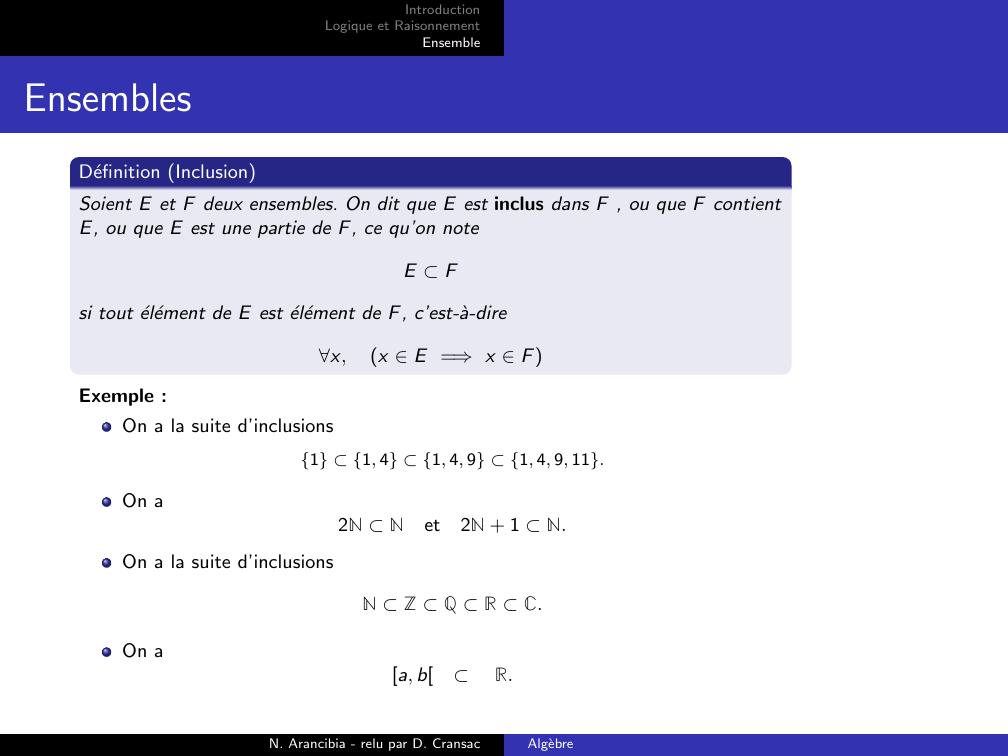
Page 7 : IntroductionLogique et RaisonnementEnsembleEnsemblesDefinition InclusionSoient E et F deux ensembles. On dit que E est inclus dans F , ou que F contientE, ou que E est une partie de F, ce qu’on noteE Fsi tout element de E est element de F, c’est-a-direx,x E =⇒x FExemple :On a la suite d’inclusions1 1, 4 1, 4, 9 1, 4, 9, 11.On a2N Net2N + 1 N.On a la suite d’inclusionsN Z Q R C.On aa, bR.N. Arancibia - relu par D. CransacAlgebre
Page 8 : IntroductionLogique et RaisonnementEnsembleEnsemblesAttention ! : Ne pas confondre appartenance et inclusion.On a bien0 Nmais0 ̸N.Neanmoins0 N.Un element appartient a un ensemble.Par rapport a N, 0 est donc une bille dans un sac et non un sac dans unsac.On a bienN ZmaisN /Z.Un ensemble est contenu dans un ensemble.Par rapport a Z, N est donc un sac dans un sac et non une bille dans unsac.N. Arancibia - relu par D. CransacAlgebre
Page 9 : IntroductionLogique et RaisonnementEnsembleEnsemblesQuand on veut montrer une inclusion :E F,on ecrit sans reflechir :Soit x E. Montrons que x F est vraie....Preuve que x F.Exemple : Montrer quex R : y R+, x y R+.Preuve : Soit x R. On suppose qu’il existe y R+ tel que x y. Montronsque x R+. Or y 0 par hypothese et x y, doncx 0.Ainsi, x R : y R+, x y R+.N. Arancibia - relu par D. CransacAlgebre
Page 10 : IntroductionLogique et RaisonnementEnsembleEnsemblesExemple :Montrer queE = kk + 1 : k N 2N.Preuve : Soit n E, alorsn = kk + 1pour un certain k N.Montrons que n 2N. On peut affirmer que k est pair ou impair, et si k estimpair alors k + 1 est pair.Dans tous les caskouk + 1est pair.Par produit, n = kk + 1 l’est aussi, donc n 2N.A faire chez soi :Soit E l’ensemble des entiers naturels multiples de 6 et F l’ensemble desentiers naturels pairs. Montrer que E F.Soit E = 2, 3 et F = x R : x2 3x 10 0. Montrer que E F.N. Arancibia - relu par D. CransacAlgebre
Page 11 : IntroductionLogique et RaisonnementEnsembleEnsemblesDefinition EgaliteSoient E et F deux ensembles. Les ensembles E et F sont egaux s’ils ontexactement les mˆemes elements, i.e. si :x,x E ⇐⇒x F.Exemples :Nous avonsx R : x2 3x 10 0 = 2, 5.Nous avons0, 1 = n N : n2 = n.TheoremeSoient E et F deux ensembles. Alors :E = Fsi et seulement siE Fet F E.N. Arancibia - relu par D. CransacAlgebre
Page 12 : IntroductionLogique et RaisonnementEnsembleEnsemblesPour montrer une egalite d’ensembles :E = F,on a deux possibilites :Soit on raisonne par double inclusion :En montrant d’abord E F :Soit x E. Montrons que x F est vraie....Preuve que x F.Puis, en montrant F E :Soit x F. Montrons que x E est vraie....Preuve que x E.Soit on raisonne directement par equivalence :x :x E ⇐⇒· · · ⇐⇒· · · ⇐⇒x F.N. Arancibia - relu par D. CransacAlgebre
Page 13 : IntroductionLogique et RaisonnementEnsembleEnsemblesExemple : Montrer queR= x R : y R+x y.Preuve : On raisonne par double inclusionMontronsRx R : y R+x y.Soit x R. Nous devons montrer que y R+, x ysoit y R+ on a y 0 mais par hypothese x 0. Doncx 0 y et x yMontronsx R : y R+x y R.Soit x R tel que y R+, x y. Alors en particulier, pour y = 0on a x 0. C’est-a-dire x R.N. Arancibia - relu par D. CransacAlgebre
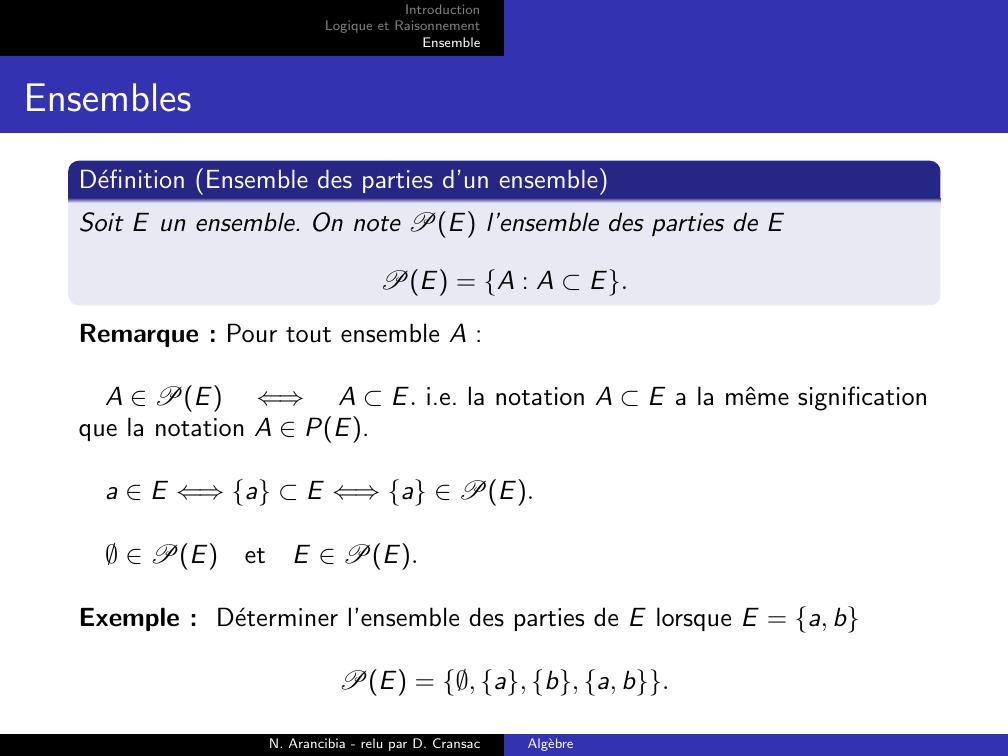
Page 14 : IntroductionLogique et RaisonnementEnsembleEnsemblesDefinition Ensemble des parties d’un ensembleSoit E un ensemble. On note PE l’ensemble des parties de EPE = A : A E.Remarque : Pour tout ensemble A :A PE⇐⇒A E. i.e. la notation A E a la mˆeme significationque la notation A PE.a E ⇐⇒a E ⇐⇒a PE.PEetE PE.Exemple : Determiner l’ensemble des parties de E lorsque E = a, bPE = , a, b, a, b.N. Arancibia - relu par D. CransacAlgebre
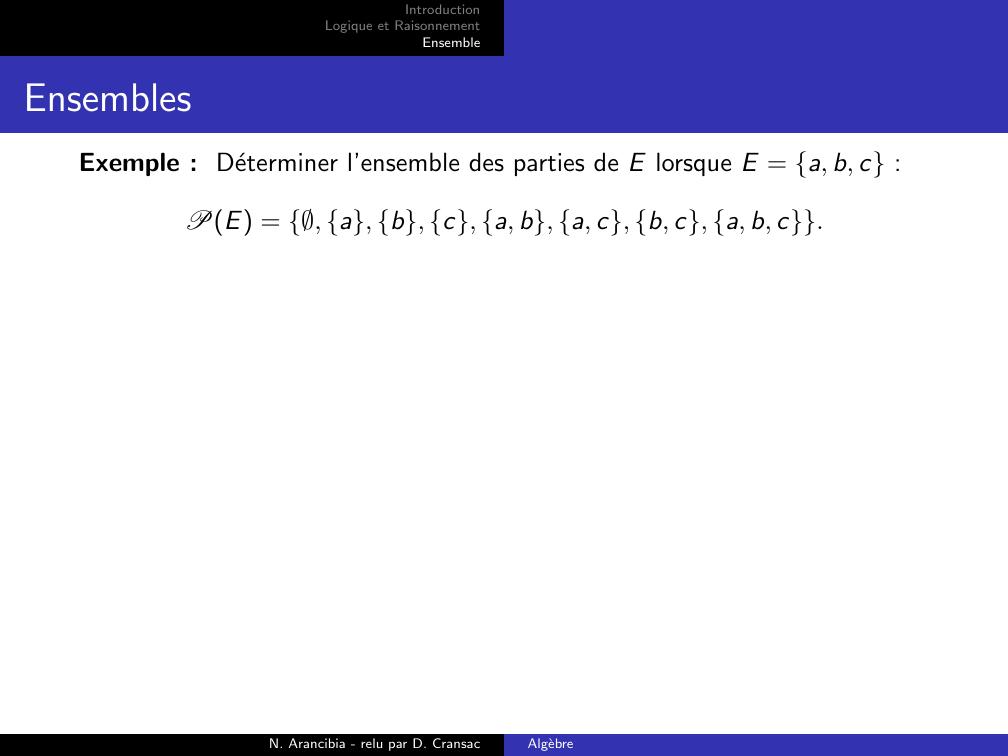
Page 15 : IntroductionLogique et RaisonnementEnsembleEnsemblesExemple : Determiner l’ensemble des parties de E lorsque E = a, b, c :PE = , a, b, c, a, b, a, c, b, c, a, b, c.N. Arancibia - relu par D. CransacAlgebre
Page 16 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesEtudions certaines operations sur les ensembles.Definition IntersectionSoit E un ensemble, et soient A et B deux sous-ensembles de E.L’intersection de A et B est l’ensemble, note A B, defini par :A B = x E : x Aetx B.En d’autres termes, l’intersection de A et de B est l’ensemble deselements qui sont a la fois dans A et dans B.Diagramme de Venn :N. Arancibia - relu par D. CransacAlgebre
Page 17 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesExemple :1, 4, 7 3, 5, 7, 11 = 7.Z Q = Z.1, 5 0, 7 4, 9 = 0, 5 4, 9 = 4, 5.-150749On ax, y R2 : x2 + y 2 = 1 x, y R2 : x = y=22 , 22,22 ,22.R+ R= 0.2N 2N + 1 = .N. Arancibia - relu par D. CransacAlgebre
Page 18 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDefinition Ensembles disjointsSoient A et B deux ensembles. On dit que A et B sont disjoints siA B = .Autrement dit si A et B n’ont aucun element commun.N. Arancibia - relu par D. CransacAlgebre
Page 19 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDefinition UnionSoit E un ensemble, et soient A et B deux sous-ensembles de E.L’union de A et B est l’ensemble, note A B, defini par :A B = x E : x Aoux B.En d’autres termes, l’union de A et de B est l’ensemble des elements quiappartiennent a A ou a B. Le ”ou” utilise ici est inclusif : x est unelement de A ou un element de B ou un element de A et de B.Diagramme de Venn :N. Arancibia - relu par D. CransacAlgebre
Page 20 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesExemple :3, 4, 7, 9 2, 7, 9, 10, 21, 84 = 2, 3, 4, 7, 9, 10, 21, 84.R+ R= R.Q I = R.1, 1 1, 1 = 1, 1.Remarque :Si A B. AlorsA B = AetA B = B.Soient A et B deux ensembles. Alors on a toujours les inclusionssuivantes :A B A A BetA B B A B.N. Arancibia - relu par D. CransacAlgebre
Page 21 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesRemarque : L’union et l’intersection se generalisent facilement au cas deplus de deux ensembles : Soit E un ensemble, et consideronsAi : i Iune famille de sous-ensembles de E, cela veut dire que I est un ensembleon l’appelle ensemble d’indices, et quei I,Ai est un sous-ensemble de E.Union :iIAi = x E : i I, x Ai.i.e. l’ensemble des objets qui appartiennent a l’un des Ai.Intersection :\iIAi = x E : i I, x Ai.i.e. l’ensemble des objets qui appartiennent a tous les Ai.N. Arancibia - relu par D. CransacAlgebre
Page 22 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesL’union et l’intersection satisfont les proprietes suivantes.TheoremeSoit E un ensemble, et considerons trois sous-ensembles A, B, C de E.L’intersection et l’union sont commutatives :A B = B AetA B = B A.L’intersection et l’union sont associatives :A B C = A B C = A B C,A B C = A B C = A B C.Pour tout sous-ensemble A de E on aA E = A.Pour tout sous-ensemble A de E on aA = A.N. Arancibia - relu par D. CransacAlgebre
Page 23 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesTheoremeSoit E un ensemble, et considerons trois sous-ensembles A, B, C de E.L’intersection et la reunion sont distributives l’une par rapport al’autre :A B C=A B A C,A B C=A B A C.Demonstration.Montrons que A B C = A B A C. On a :x A B C ⇐⇒x A et x B C⇐⇒x A et x B ou x C⇐⇒x A et B ou x A et C⇐⇒x A B ou x A C⇐⇒x A B A C.On montre de mˆeme l’egalite A B C = A B A C.N. Arancibia - relu par D. CransacAlgebre
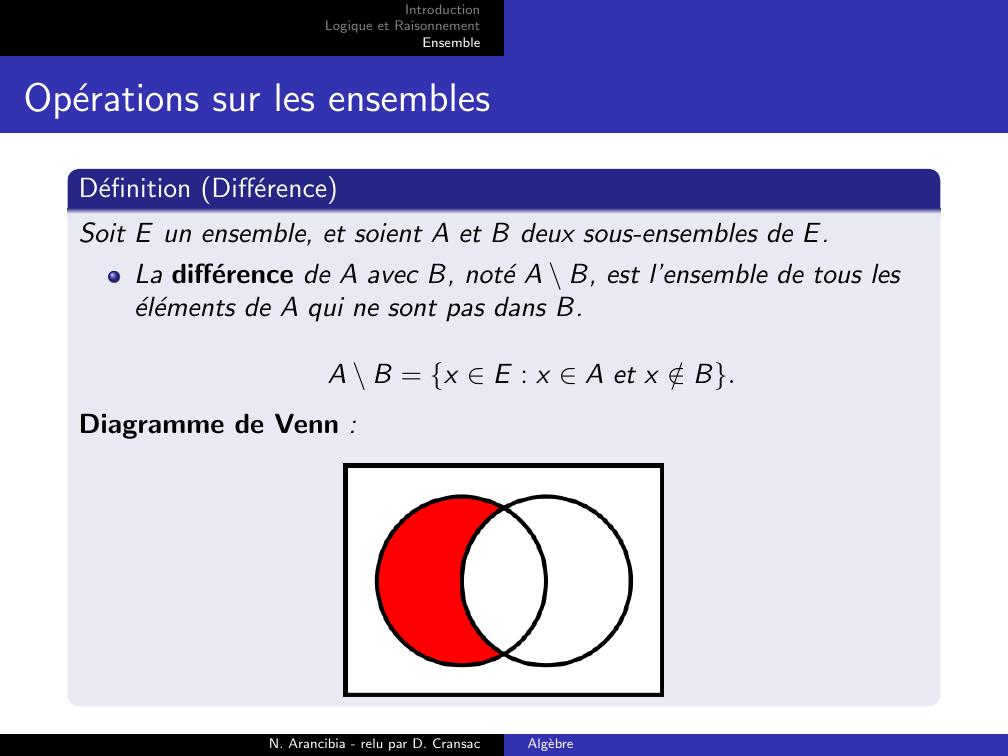
Page 24 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDefinition DifferenceSoit E un ensemble, et soient A et B deux sous-ensembles de E.La difference de A avec B, note A \ B, est l’ensemble de tous leselements de A qui ne sont pas dans B.A \ B = x E : x A et x /B.Diagramme de Venn :N. Arancibia - relu par D. CransacAlgebre
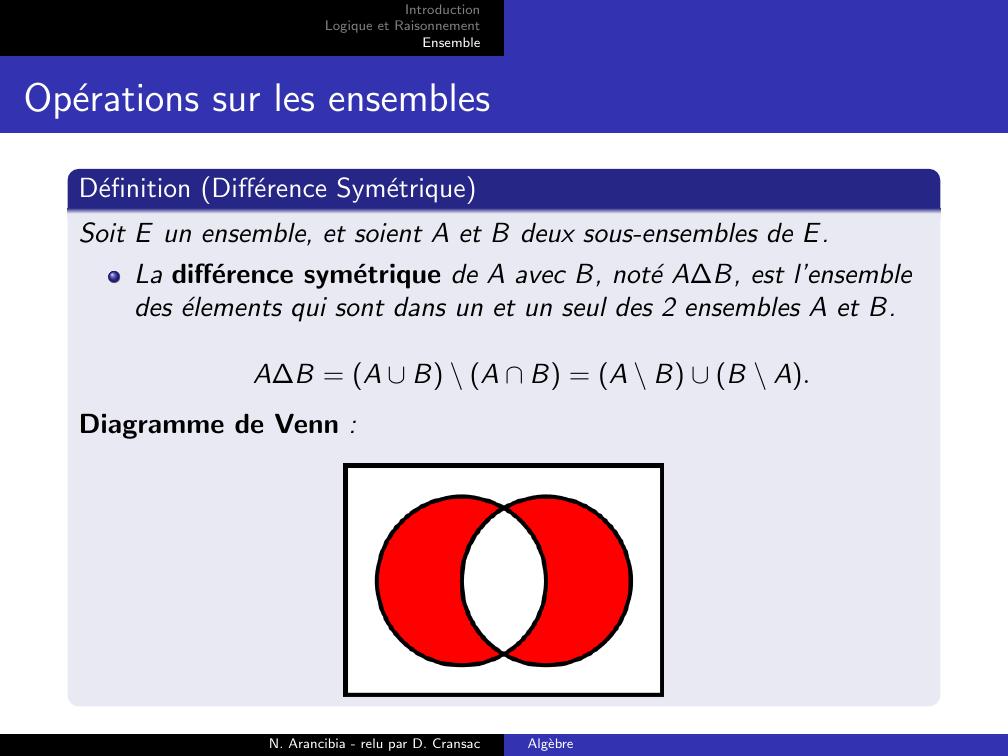
Page 25 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDefinition Difference SymetriqueSoit E un ensemble, et soient A et B deux sous-ensembles de E.La difference symetrique de A avec B, note AB, est l’ensembledes elements qui sont dans un et un seul des 2 ensembles A et B.AB = A B \ A B = A \ B B \ A.Diagramme de Venn :N. Arancibia - relu par D. CransacAlgebre
Page 26 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDefinition ComplementSoient E un ensemble et A une partie de E.Le complementaire de A dans E est l’ensemble, note C EA , de tous leselements de E qui ne sont pas dans A.C EA = x : x E et x /A = E \ A.Diagramme de Venn :Remarque : S’il n’y a pas d’ambig¨uite sur l’ensemble E, on privilegiera lanotation Ac pour C EA .N. Arancibia - relu par D. CransacAlgebre
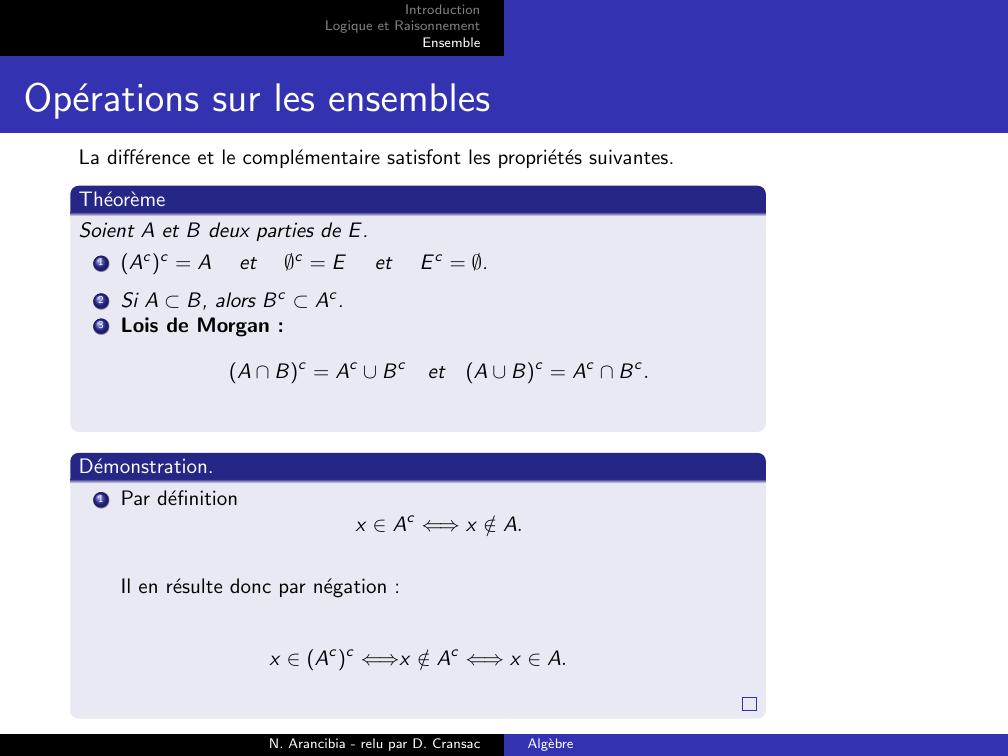
Page 27 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesLa difference et le complementaire satisfont les proprietes suivantes.TheoremeSoient A et B deux parties de E.1Acc = Aetc = EetE c = .2Si A B, alors Bc Ac.3Lois de Morgan :A Bc = Ac BcetA Bc = Ac Bc.Demonstration.1Par definitionx Ac ⇐⇒x /A.Il en resulte donc par negation :x Acc ⇐⇒x /Ac ⇐⇒x A.N. Arancibia - relu par D. CransacAlgebre
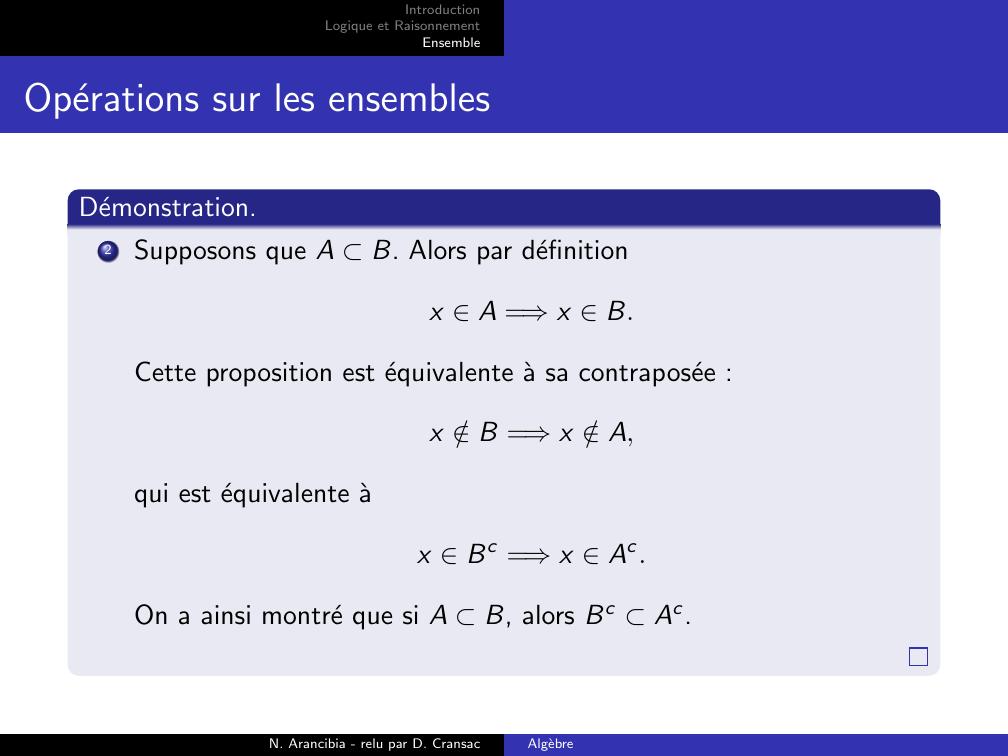
Page 28 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDemonstration.2Supposons que A B. Alors par definitionx A =⇒x B.Cette proposition est equivalente a sa contraposee :x /B =⇒x /A,qui est equivalente ax Bc =⇒x Ac.On a ainsi montre que si A B, alors Bc Ac.N. Arancibia - relu par D. CransacAlgebre
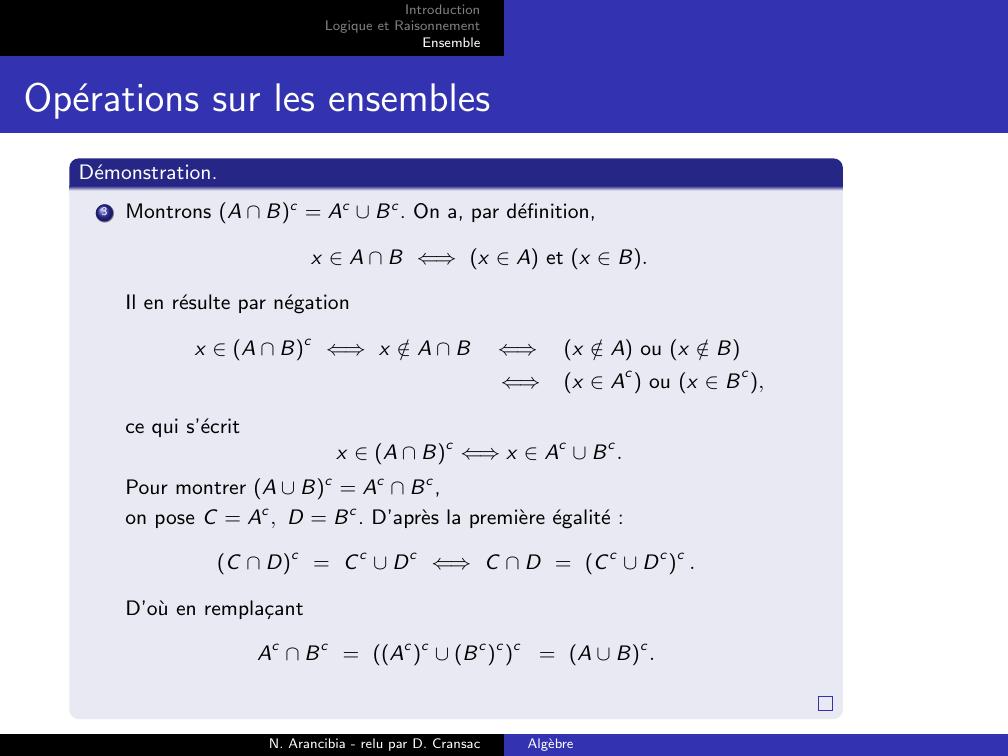
Page 29 : IntroductionLogique et RaisonnementEnsembleOperations sur les ensemblesDemonstration.3Montrons A Bc = Ac Bc. On a, par definition,x A B ⇐⇒x A et x B.Il en resulte par negationx A Bc ⇐⇒x /A B⇐⇒x /A ou x /B⇐⇒x Ac ou x Bc,ce qui s’ecritx A Bc ⇐⇒x Ac Bc.Pour montrer A Bc = Ac Bc,on pose C = Ac, D = Bc. D’apres la premiere egalite :C Dc = C c Dc ⇐⇒C D = C c Dcc .D’ou en rempla¸cantAc Bc = Acc Bccc= A Bc.N. Arancibia - relu par D. CransacAlgebre
Page 30 : IntroductionLogique et RaisonnementEnsemblePartition d’un ensembleDefinition PartitionUne partition d’un ensemble E est un ensembleA1, A2, · · · , Anconstitue de parties de E verifiant :Pour tout k 1, · · · , n, Ak ̸= , i.e. aucun Ak ne doit ˆetre videSnk=1 Ak = E, i.e. la reunion des Ak est egale a E.Pour tout couple Ai, Aj avec Ai ̸= Aj on a Ai Aj = , i.e. les Ai sontdeux a deux disjoints.Diagramme de Venn :N. Arancibia - relu par D. CransacAlgebre
Page 31 : IntroductionLogique et RaisonnementEnsemblePartition d’un ensembleExemples :L’ensemble 2N, 2N + 1 definit une partition de N.L’ensemble Q, I definit une partition de R.L’ensemble 0, 12, 12, 32, 32, 2 definit une partition de 0, 2.L’ensemble 2N, 3N n’est pas une partition de N.Exercice : Donner toutes les partitions de l’ensembleE = a, b, c.Solution :P1 = a, b, cP2a = a, b, c et P2b = b, a, c et P2c = a, b, c.P3 = a, b, c = EN. Arancibia - relu par D. CransacAlgebre
Page 32 : IntroductionLogique et RaisonnementEnsembleProduit CartesienDefinitionSoient A et B deux parties de E. Le produit cartesien de A et B estl’ensemble, noteA × B,constitue de tous les couples x, y oux Aety B.On a donc :A × B = x, y : x A et y B.Exemple : Soit A = a, b et B = 1, 2, alorsA × B = a, 1, a, 2, b, 1, b, 2N. Arancibia - relu par D. CransacAlgebre
Page 33 : IntroductionLogique et RaisonnementEnsembleProduit CartesienExemple :AvecC = 1, 2etD = 1, 2, 3on aC × D =1, 1, 1, 2, 1, 3, 2, 1, 2, 2, 2, 3Remarque : On ne confond pas les couples a, b et b, a qui designentdeux objets differents, alors que a, b et b, a designent le mˆemeensemble.L’exemple montre que le premier et le deuxieme terme du couplen’appartiennent pas au mˆeme ensemble.N. Arancibia - relu par D. CransacAlgebre
Page 34 : IntroductionLogique et RaisonnementEnsembleProduit CartesienRemarque :La definition precedente se generalise. Soient n un entier superieur ouegale a 2 etA1, A2, · · · , Anune famille de n sous-ensembles de E.Alors le produit cartesien de A1, A2, · · · , An est l’ensemble defini parA1 × A2 × · · · × An =nx1, x2, · · · , xn : i 1, · · · , n, xi Aio.L’element x1, x2, · · · , xn est appele un n-tuple de composants x1, x2,· · · , xn.Lorsque A = B, on noteA × A = A2.et on generalise cette notation pour l’ensembleAn = A × A × · · · × A.produit cartesien de n facteurs egaux a A.N. Arancibia - relu par D. CransacAlgebre
Page 35 : IntroductionLogique et RaisonnementEnsembleProduit CartesienLe produit cartesien satisfait les proprietes suivantes.PropositionSoient A, B, C, D des parties d’un ensemble E.A × C A × D = A × C D.A × C B × D = A B × C D.Demonstration.On montre le premier pointx, y A × C A × D ⇐⇒x, y A × C ou x, y A × D⇐⇒x A et y C ou x A et y D⇐⇒x A et y C ou y D⇐⇒x, y A × C D.Le deuxieme point se montre de la mˆeme fa¸con remplacer ”et” par ”ou”N. Arancibia - relu par D. CransacAlgebre
Page 36 : IntroductionLogique et RaisonnementEnsembleCardinal d’un ensemble finiDefinitionOn dit qu’un ensemble fini E est de cardinal ou taille n N s’il a nelements.PropositionLe cardinal d’un ensemble fini est unique.DefinitionPour ensemble tout ensemble fini E de cardinal n, on noteCardE = E = EN. Arancibia - relu par D. CransacAlgebre
Page 37 : IntroductionLogique et RaisonnementEnsembleCardinal d’un ensemblePropositionPour deux ensembles A et B finis.A B ⇒cardA cardB̸⇐A B et cardA = cardB ⇔A = BcardA B + cardA B = cardA + cardBRemarque : Cela revient aux formulescardA B = cardA + cardB cardA BoucardA B = cardA + cardB cardA BN. Arancibia - relu par D. CransacAlgebre
Page 38 : IntroductionLogique et RaisonnementEnsembleCardinal d’un ensemble finiPropositionSoit E un ensemble fini de cardinal n N.cardPE = 2nExempleA = a, b, c, PA = , a, b, c, a, b, a, c, b, c, a, b, cOn a biencardPA = 23N. Arancibia - relu par D. CransacAlgebre
Page 39 : IntroductionLogique et RaisonnementEnsembleCardinal d’un ensemblePropositionSoient E et F deux ensembles finis,cardE × F = cardE × cardFN. Arancibia - relu par D. CransacAlgebre
Page 40 : IntroductionLogique et RaisonnementEnsembleFonction caracteristique d’un ensembleDefinitionSoit E un ensemble et A un sous-ensemble de E.La fonction caracterstique de A, notee 1A est la fonction definie sur Edans 0, 1 par :1A :E →0; 1x →1si x A0si x /APropositionSoit E un ensemble et A et B deux sous-ensembles de E.A = x E, 1Ax = 11AB = 1A · 1B1A = 1 1A1AB = 1A + 1B 1A1BN. Arancibia - relu par D. CransacAlgebre
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40