CM3 Espace Vectoriel

Télécharger le CM3 Espace Vectoriel en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449

Page 1 : Espace vectorielL’ensemble K désigne toujours R ou C.1/73D. CransacAnalyse

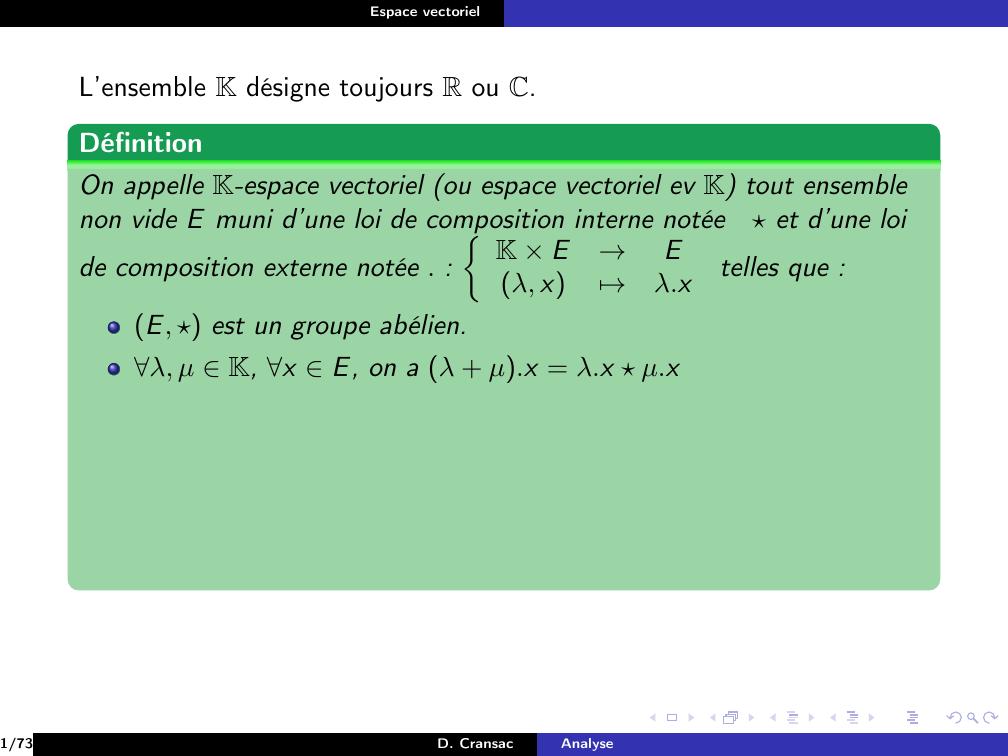
Page 2 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :1/73D. CransacAnalyse

Page 3 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.1/73D. CransacAnalyse

Page 4 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.x1/73D. CransacAnalyse

Page 5 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.y1/73D. CransacAnalyse

Page 6 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.yλ, µ K, x E, on a λ.µ.x = λ × µ.x.1/73D. CransacAnalyse

Page 7 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.yλ, µ K, x E, on a λ.µ.x = λ × µ.x.x E, on a 1.x = x1/73D. CransacAnalyse

Page 8 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.yλ, µ K, x E, on a λ.µ.x = λ × µ.x.x E, on a 1.x = x1/73D. CransacAnalyse

Page 9 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.yλ, µ K, x E, on a λ.µ.x = λ × µ.x.x E, on a 1.x = xLes éléments d’un espace vectoriel sont appelés vecteurs et les élémentsde K sont appelés scalaires.1/73D. CransacAnalyse

Page 10 : Espace vectorielL’ensemble K désigne toujours R ou C.DéfinitionOn appelle K-espace vectoriel ou espace vectoriel ev K tout ensemblenon vide E muni d’une loi de composition interne notéeet d’une loide composition externe notée . : K × E→Eλ, x7→λ.xtelles que :E, est un groupe abélien.λ, µ K, x E, on a λ + µ.x = λ.x µ.xλ K, x, y E, on a λ.x y = λ.x λ.yλ, µ K, x E, on a λ.µ.x = λ × µ.x.x E, on a 1.x = xLes éléments d’un espace vectoriel sont appelés vecteurs et les élémentsde K sont appelés scalaires.Lorsqu’il n’y a pas de confusion, on dira espace vectoriel au lieu deK-espace vectoriel.1/73D. CransacAnalyse

Page 11 : Espace vectorielExempleL’ensemble des vecteurs du plan est un espace vectoriel.2/73D. CransacAnalyse

Page 12 : Espace vectorielExempleL’ensemble des vecteurs du plan est un espace vectoriel.K, +, × est un K-espace vectoriel.2/73D. CransacAnalyse

Page 13 : Espace vectorielExempleL’ensemble des vecteurs du plan est un espace vectoriel.K, +, × est un K-espace vectoriel.Sur R2, on définit les deux lois suivantes : pour x, y, x′, y ′ R2et λ R,x, y x′, y ′ = x + x′, y + y ′ et λ x, y = λ × x, λ × yalors R2, , est un R-espace vectoriel.2/73D. CransacAnalyse

Page 14 : Espace vectorielExempleL’ensemble des vecteurs du plan est un espace vectoriel.K, +, × est un K-espace vectoriel.Sur R2, on définit les deux lois suivantes : pour x, y, x′, y ′ R2et λ R,x, y x′, y ′ = x + x′, y + y ′ et λ x, y = λ × x, λ × yalors R2, , est un R-espace vectoriel.Plus généralement :Si E1, E2, . . . , En sont n espaces vectoriels, alors l’espace produitE = E1 × E2 × · · · × En est un espace vectoriel pour les loissuivantes :Pour tous x1, x2, . . . , xn, y1, y2, . . . , yn E et λ K, on définitx1, x2, . . . , xn y1, y2, . . . , yn = x1 + y1, x2 + y2, . . . , xn + ynλ x1, x2, . . . , xn = λ × x1, λ × x2, . . . , λ × xn.2/73D. CransacAnalyse

Page 15 : Espace vectorielExempleL’ensemble des vecteurs du plan est un espace vectoriel.K, +, × est un K-espace vectoriel.Sur R2, on définit les deux lois suivantes : pour x, y, x′, y ′ R2et λ R,x, y x′, y ′ = x + x′, y + y ′ et λ x, y = λ × x, λ × yalors R2, , est un R-espace vectoriel.Plus généralement :Si E1, E2, . . . , En sont n espaces vectoriels, alors l’espace produitE = E1 × E2 × · · · × En est un espace vectoriel pour les loissuivantes :Pour tous x1, x2, . . . , xn, y1, y2, . . . , yn E et λ K, on définitx1, x2, . . . , xn y1, y2, . . . , yn = x1 + y1, x2 + y2, . . . , xn + ynλ x1, x2, . . . , xn = λ × x1, λ × x2, . . . , λ × xn.L’ensemble KnX, +, × des polynômes de degré inférieur ou égalà n additionné du polynôme nul est un espace vectoriel.2/73D. CransacAnalyse

Page 16 : Espace vectorielPropositionPour tout λ K et pour tout x E, on a :λx = 0E ⇐⇒λ = 0 ou x = 0E3/73D. CransacAnalyse

Page 17 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.4/73D. CransacAnalyse

Page 18 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :4/73D. CransacAnalyse

Page 19 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :0E F.4/73D. CransacAnalyse

Page 20 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :0E F.x, y F, x y F.Autrement dit F est stable pour l’addition.4/73D. CransacAnalyse

Page 21 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :0E F.x, y F, x y F.Autrement dit F est stable pour l’addition.x F et λ K, λ.x F.Autrement dit, F est stable pour la multiplication par un scalaire.4/73D. CransacAnalyse

Page 22 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :0E F.x, y F, x y F.Autrement dit F est stable pour l’addition.x F et λ K, λ.x F.Autrement dit, F est stable pour la multiplication par un scalaire.4/73D. CransacAnalyse

Page 23 : Espace vectorielDans toute la suite l’ensemble E, , . désignera un espace vectoriel surK.DéfinitionSoit F un sous-ensemble de E.On dit que F est un sous-espace vectoriel de E si F possède lespropriétés suivantes :0E F.x, y F, x y F.Autrement dit F est stable pour l’addition.x F et λ K, λ.x F.Autrement dit, F est stable pour la multiplication par un scalaire.RemarqueTout sous-espace vectoriel de E est un espace vectoriel pour les loisinduites par E.4/73D. CransacAnalyse

Page 24 : Espace vectorielExempleSi E est un espace vectoriel, alors 0E et E sont des sous-espacesvectoriel de E.5/73D. CransacAnalyse

Page 25 : Espace vectorielExempleSi E est un espace vectoriel, alors 0E et E sont des sous-espacesvectoriel de E.Si E = R25/73D. CransacAnalyse

Page 26 : Espace vectorielExempleSi E est un espace vectoriel, alors 0E et E sont des sous-espacesvectoriel de E.Si E = R2F = x, 0, x R est un sous-espace vectoriel de E.5/73D. CransacAnalyse

Page 27 : Espace vectorielExempleSi E est un espace vectoriel, alors 0E et E sont des sous-espacesvectoriel de E.Si E = R2F = x, 0, x R est un sous-espace vectoriel de E.Si x0, y0 R2, alors Fλx0, λy0, λ R est un sous-espacevectoriel de E.5/73D. CransacAnalyse

Page 28 : Espace vectorielExempleSi E est un espace vectoriel, alors 0E et E sont des sous-espacesvectoriel de E.Si E = R2F = x, 0, x R est un sous-espace vectoriel de E.Si x0, y0 R2, alors Fλx0, λy0, λ R est un sous-espacevectoriel de E.L’ensemble F = x, y, z R3 z = 0 est un sous-espace vectorielde R3.5/73D. CransacAnalyse

Page 29 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :6/73D. CransacAnalyse

Page 30 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.6/73D. CransacAnalyse

Page 31 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn6/73D. CransacAnalyse

Page 32 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn0 = 0, . . . , 0 H car 0 + · · · + 0 = 0.6/73D. CransacAnalyse

Page 33 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn0 = 0, . . . , 0 H car 0 + · · · + 0 = 0.Soient λ, µ R et x = x1, . . . , xn, y = y1, . . . , yn H.On a λx + µy = λx1 + µy1, . . . , λxn + µyn.6/73D. CransacAnalyse

Page 34 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn0 = 0, . . . , 0 H car 0 + · · · + 0 = 0.Soient λ, µ R et x = x1, . . . , xn, y = y1, . . . , yn H.On a λx + µy = λx1 + µy1, . . . , λxn + µyn.6/73D. CransacAnalyse

Page 35 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn0 = 0, . . . , 0 H car 0 + · · · + 0 = 0.Soient λ, µ R et x = x1, . . . , xn, y = y1, . . . , yn H.On a λx + µy = λx1 + µy1, . . . , λxn + µyn. Orλx1+µy1+· · ·+λxn+µyn = λx1+· · ·+xn+µy1+· · ·+yn = 0car x1 + · · · + xn = y1 + · · · + yn = 0 puisque x, y H6/73D. CransacAnalyse

Page 36 : Espace vectorielExempleSoitH = x1, . . . , xn Rn x1 + · · · + xn = 0H est un sous-espace vectoriel de Rn.En effet :Rn est un R-espace vectoriel de vecteur nul 0 = 0, . . . , 0.H Rn0 = 0, . . . , 0 H car 0 + · · · + 0 = 0.Soient λ, µ R et x = x1, . . . , xn, y = y1, . . . , yn H.On a λx + µy = λx1 + µy1, . . . , λxn + µyn. Orλx1+µy1+· · ·+λxn+µyn = λx1+· · ·+xn+µy1+· · ·+yn = 0car x1 + · · · + xn = y1 + · · · + yn = 0 puisque x, y H doncλx + µy H.6/73D. CransacAnalyse

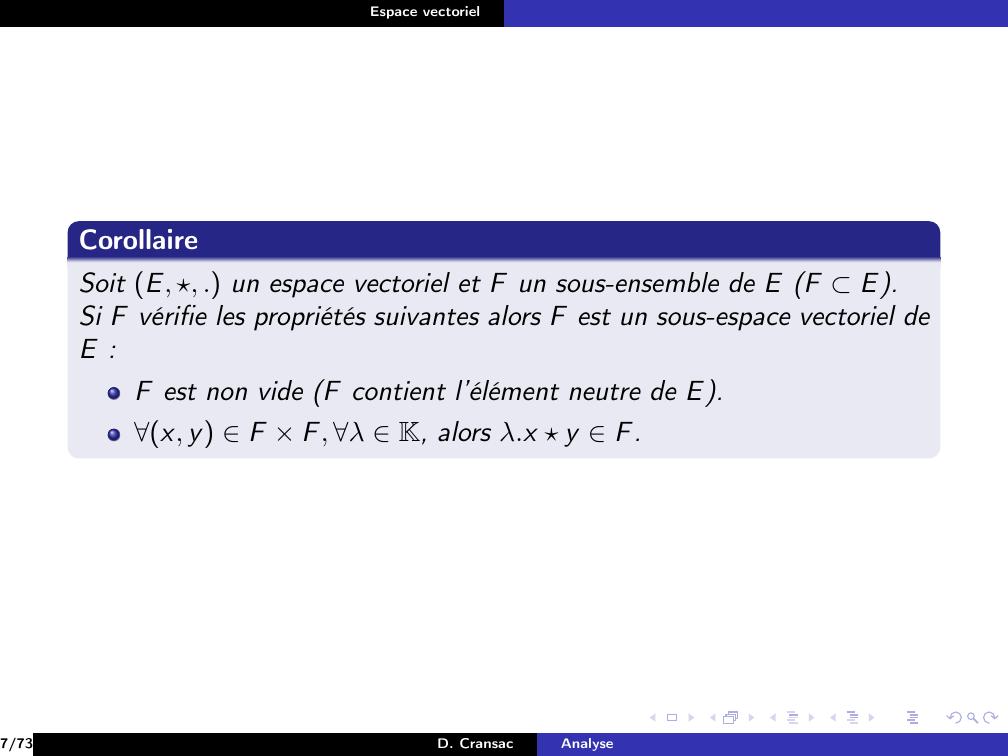
Page 37 : Espace vectorielCorollaireSoit E, , . un espace vectoriel et F un sous-ensemble de E F E.7/73D. CransacAnalyse

Page 38 : Espace vectorielCorollaireSoit E, , . un espace vectoriel et F un sous-ensemble de E F E.Si F vérifie les propriétés suivantes alors F est un sous-espace vectoriel deE :7/73D. CransacAnalyse

Page 39 : Espace vectorielCorollaireSoit E, , . un espace vectoriel et F un sous-ensemble de E F E.Si F vérifie les propriétés suivantes alors F est un sous-espace vectoriel deE :F est non vide F contient l’élément neutre de E.7/73D. CransacAnalyse

Page 40 : Espace vectorielCorollaireSoit E, , . un espace vectoriel et F un sous-ensemble de E F E.Si F vérifie les propriétés suivantes alors F est un sous-espace vectoriel deE :F est non vide F contient l’élément neutre de E.x, y F × F, λ K, alors λ.x y F.7/73D. CransacAnalyse

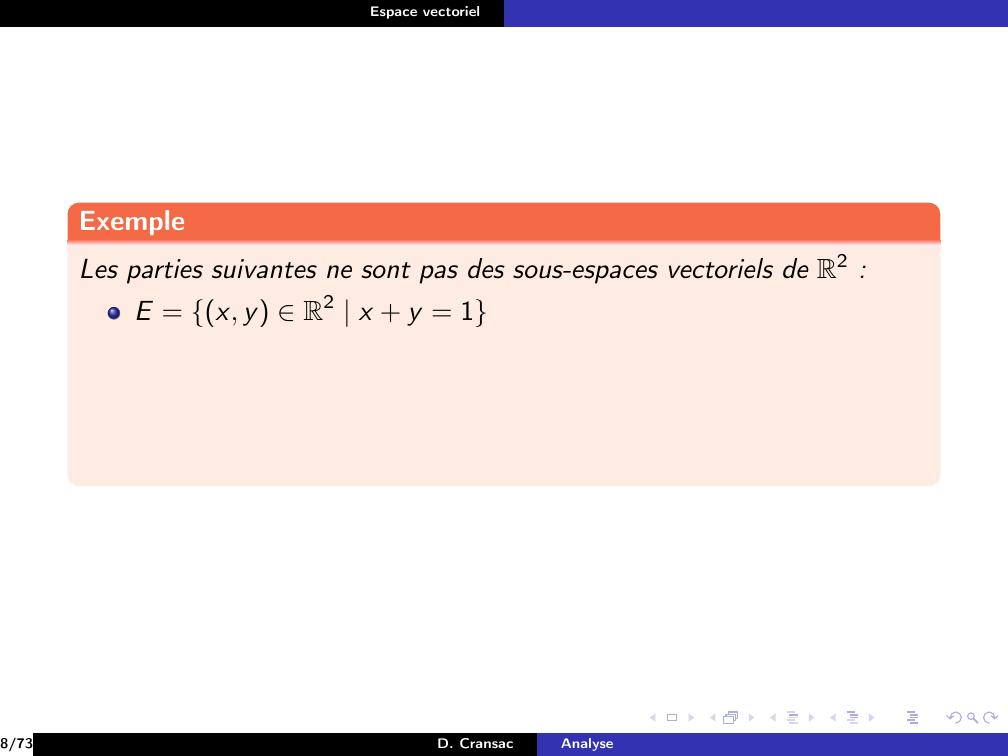
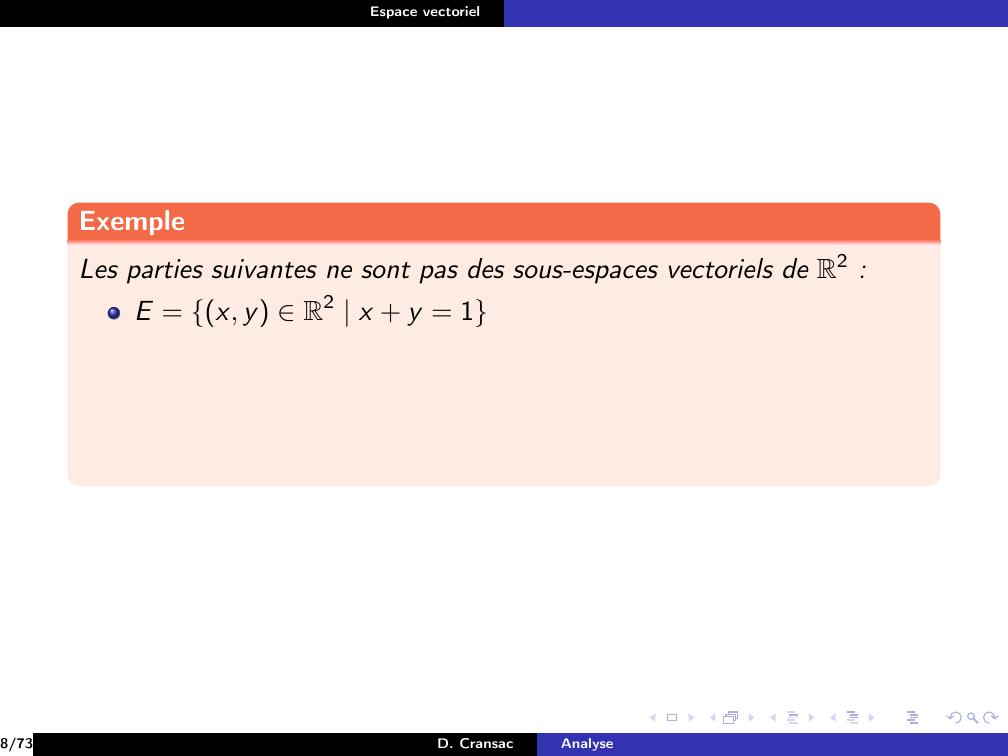
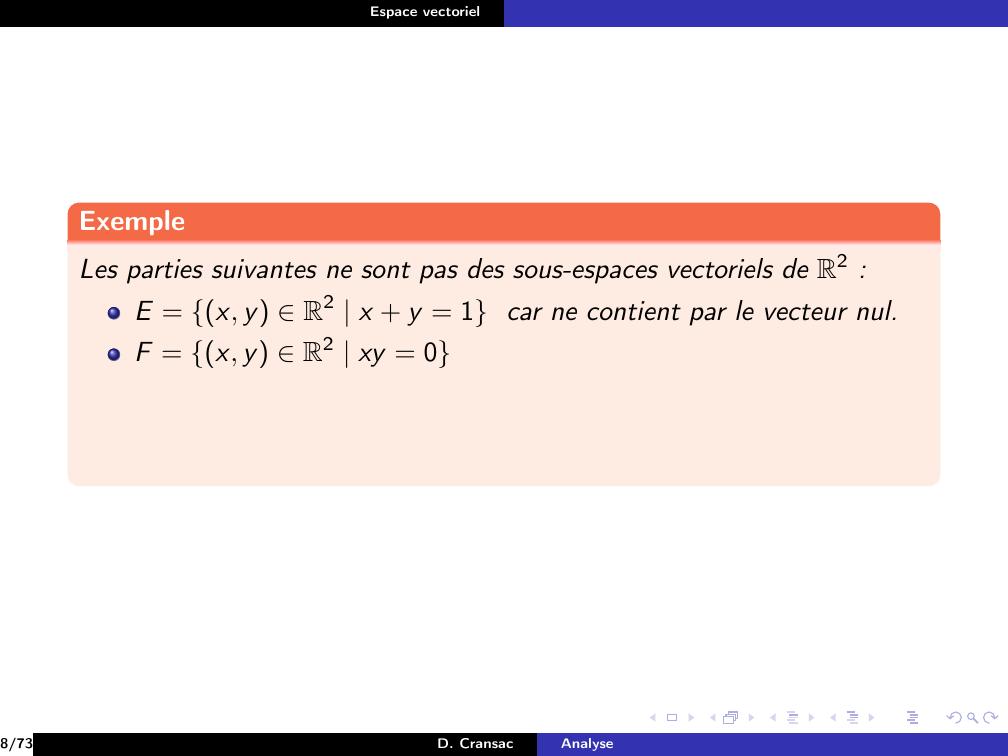
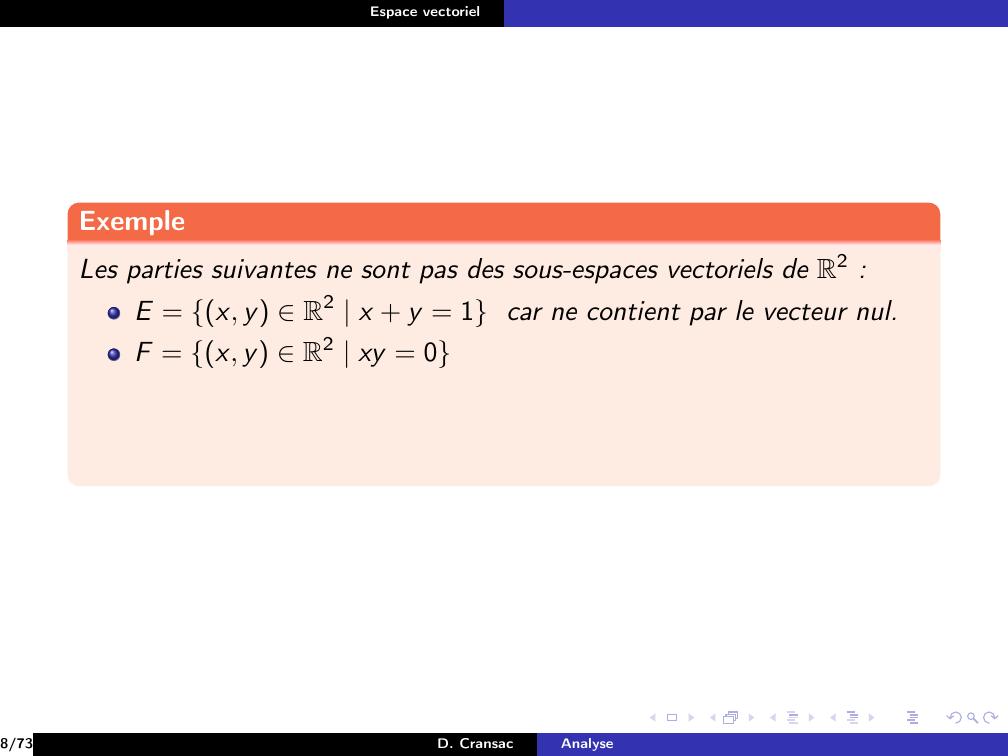
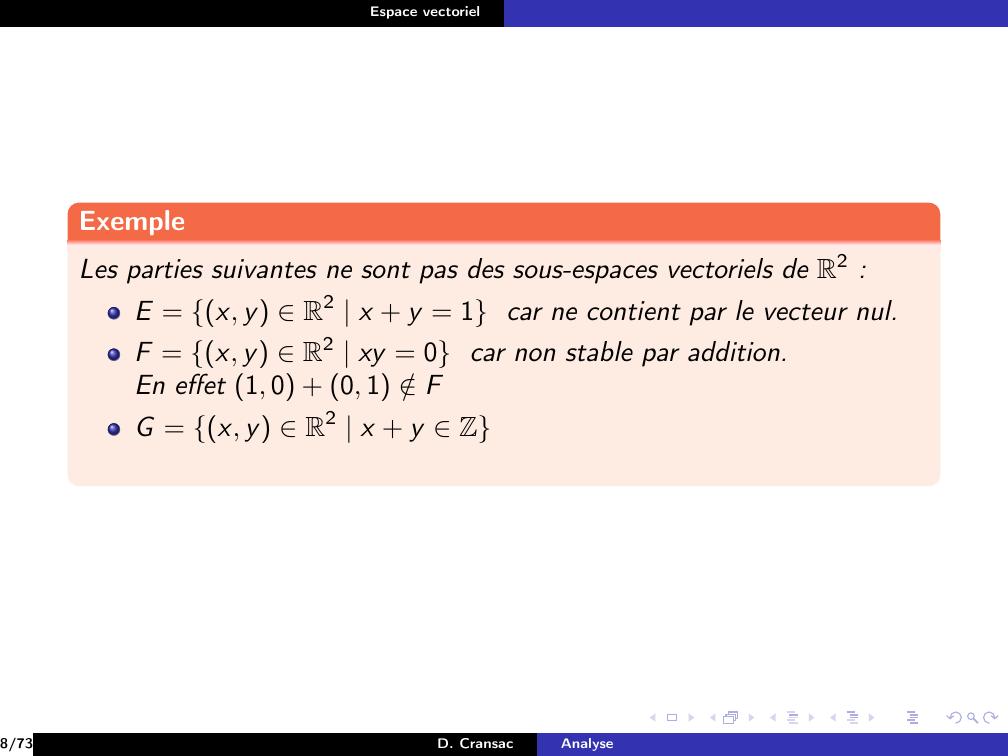
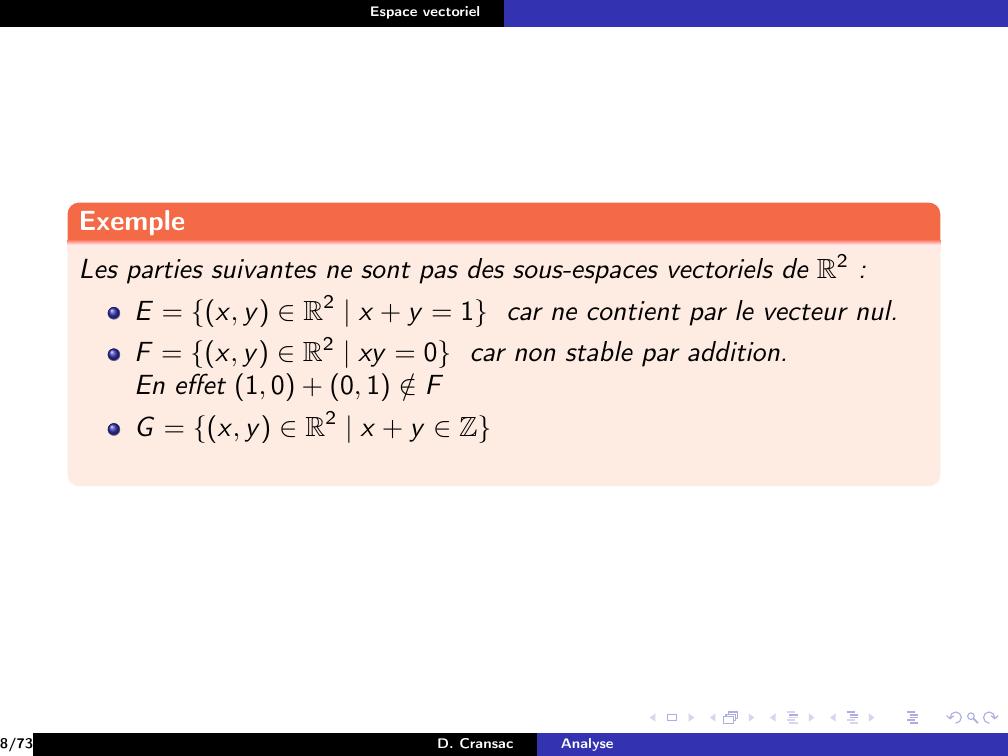
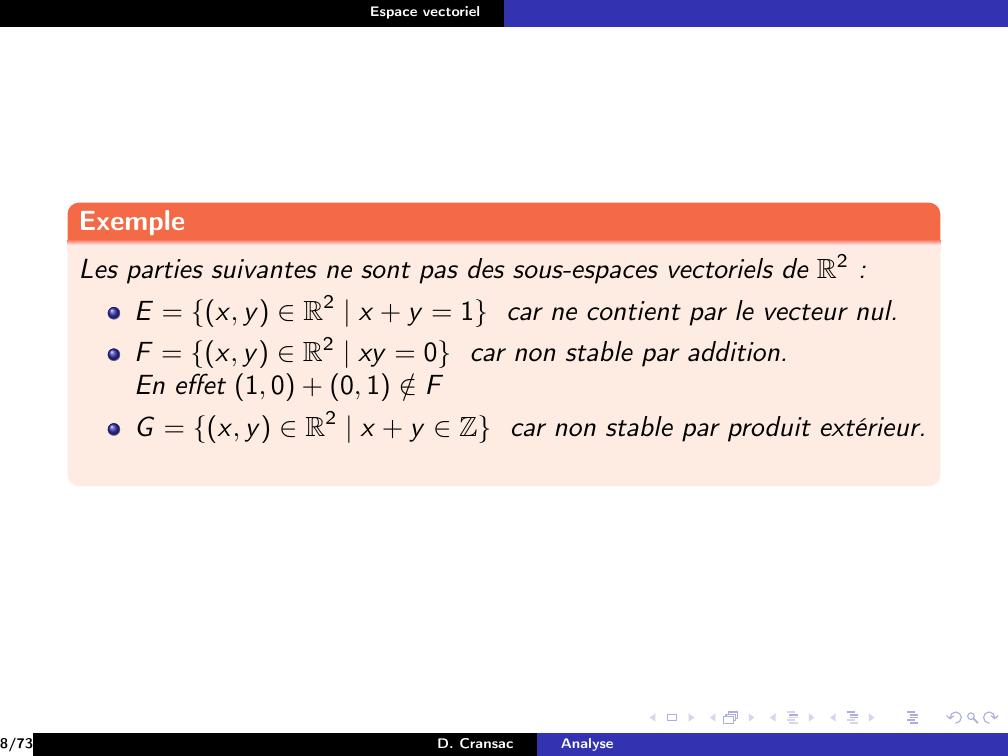
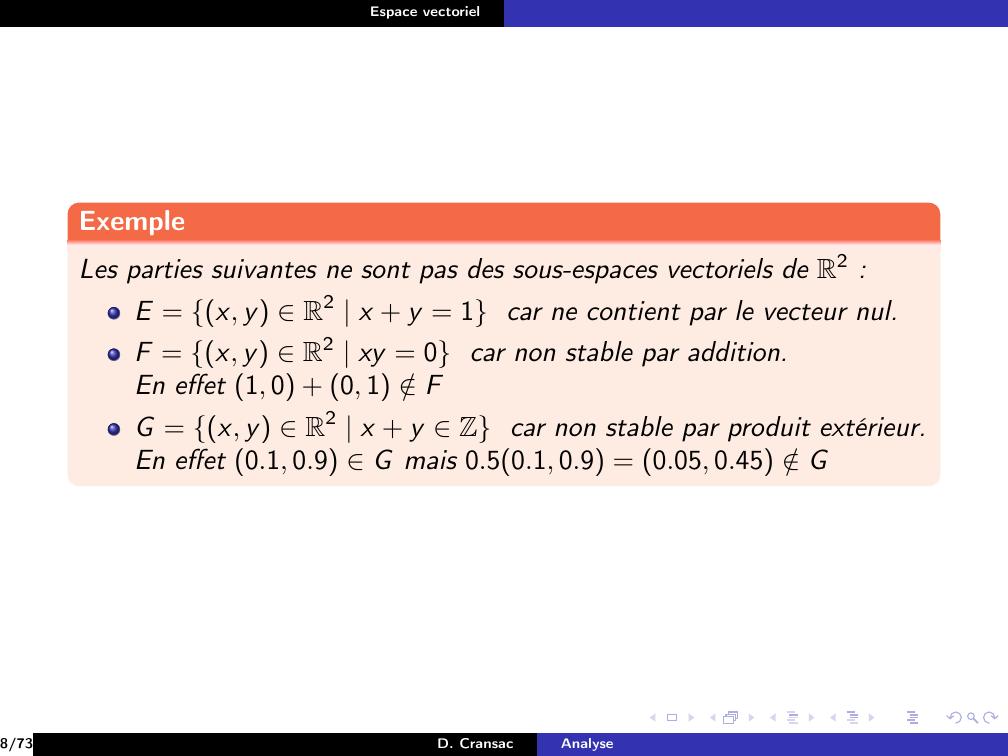
Page 41 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :8/73D. CransacAnalyse

Page 42 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 18/73D. CransacAnalyse

Page 43 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 18/73D. CransacAnalyse

Page 44 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 08/73D. CransacAnalyse

Page 45 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 08/73D. CransacAnalyse

Page 46 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 0 car non stable par addition.En effet 1, 0 + 0, 1 /FG = x, y R2 x + y Z8/73D. CransacAnalyse

Page 47 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 0 car non stable par addition.En effet 1, 0 + 0, 1 /FG = x, y R2 x + y Z8/73D. CransacAnalyse

Page 48 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 0 car non stable par addition.En effet 1, 0 + 0, 1 /FG = x, y R2 x + y Z car non stable par produit extérieur.8/73D. CransacAnalyse

Page 49 : Espace vectorielExempleLes parties suivantes ne sont pas des sous-espaces vectoriels de R2 :E = x, y R2 x + y = 1 car ne contient par le vecteur nul.F = x, y R2 xy = 0 car non stable par addition.En effet 1, 0 + 0, 1 /FG = x, y R2 x + y Z car non stable par produit extérieur.En effet 0.1, 0.9 G mais 0.50.1, 0.9 = 0.05, 0.45 /G8/73D. CransacAnalyse

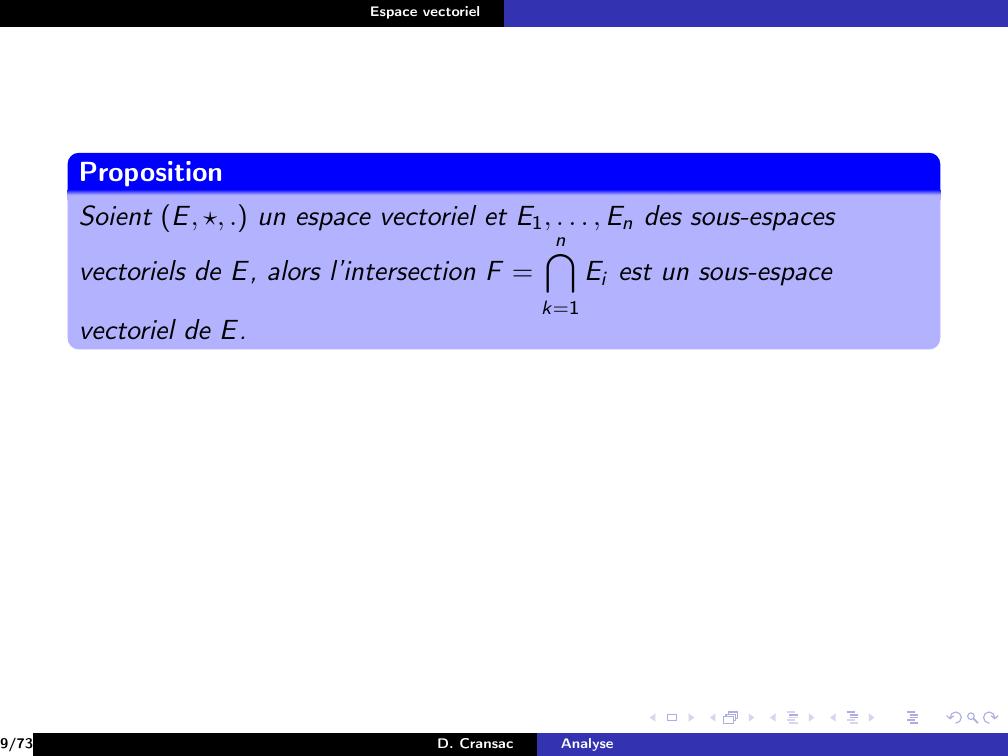
Page 50 : Espace vectorielPropositionSoient E, , . un espace vectoriel et E1, . . . , En des sous-espacesvectoriels de E, alors l’intersection F =n\k=1Ei est un sous-espacevectoriel de E.9/73D. CransacAnalyse

Page 51 : Espace vectorielPropositionSoient E, , . un espace vectoriel et E1, . . . , En des sous-espacesvectoriels de E, alors l’intersection F =n\k=1Ei est un sous-espacevectoriel de E.Démonstration.Pour tout i, on a 0 Ei, donc 0 F.9/73D. CransacAnalyse

Page 52 : Espace vectorielPropositionSoient E, , . un espace vectoriel et E1, . . . , En des sous-espacesvectoriels de E, alors l’intersection F =n\k=1Ei est un sous-espacevectoriel de E.Démonstration.Pour tout i, on a 0 Ei, donc 0 F.Soient x, y F et λ K9/73D. CransacAnalyse

Page 53 : Espace vectorielPropositionSoient E, , . un espace vectoriel et E1, . . . , En des sous-espacesvectoriels de E, alors l’intersection F =n\k=1Ei est un sous-espacevectoriel de E.Démonstration.Pour tout i, on a 0 Ei, donc 0 F.Soient x, y F et λ Kalors i J1, nK, λ.x µ.y Ei9/73D. CransacAnalyse

Page 54 : Espace vectorielPropositionSoient E, , . un espace vectoriel et E1, . . . , En des sous-espacesvectoriels de E, alors l’intersection F =n\k=1Ei est un sous-espacevectoriel de E.Démonstration.Pour tout i, on a 0 Ei, donc 0 F.Soient x, y F et λ Kalors i J1, nK, λ.x µ.y Ei donc λ.x µ.y est dans l’intersection detout les Ei.9/73D. CransacAnalyse

Page 55 : Espace vectorielRemarque10/73D. CransacAnalyse

Page 56 : Espace vectorielRemarqueLa réunion de deux sous-espace vectoriels n’est pas en général unsous-espace vectoriel.10/73D. CransacAnalyse

Page 57 : Espace vectorielRemarqueLa réunion de deux sous-espace vectoriels n’est pas en général unsous-espace vectoriel.En effet, si E, , . = R2, , , les sous-ensembles :E1 = x, y R2 x + y = 0etE2 = x, y R2 x y = 0sont deux sous-espaces vectoriels de R210/73D. CransacAnalyse

Page 58 : Espace vectorielRemarqueLa réunion de deux sous-espace vectoriels n’est pas en général unsous-espace vectoriel.En effet, si E, , . = R2, , , les sous-ensembles :E1 = x, y R2 x + y = 0etE2 = x, y R2 x y = 0sont deux sous-espaces vectoriels de R2mais E1 E2 n’est pas un sous-espace vectoriel.10/73D. CransacAnalyse

Page 59 : Espace vectorielRemarqueLa réunion de deux sous-espace vectoriels n’est pas en général unsous-espace vectoriel.En effet, si E, , . = R2, , , les sous-ensembles :E1 = x, y R2 x + y = 0etE2 = x, y R2 x y = 0sont deux sous-espaces vectoriels de R2mais E1 E2 n’est pas un sous-espace vectoriel.En effet 1, 1 E1 et 1, 1 E2 mais 1, 1 1, 1 = 2, 0n’appartient ni à E1 ni à E2.10/73D. CransacAnalyse

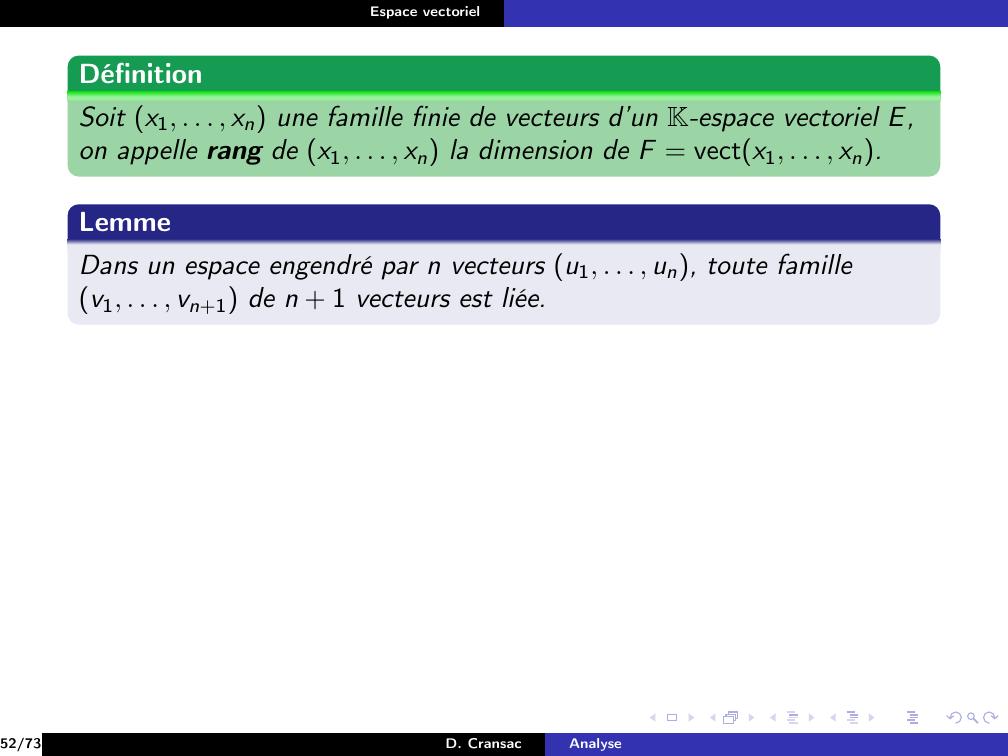
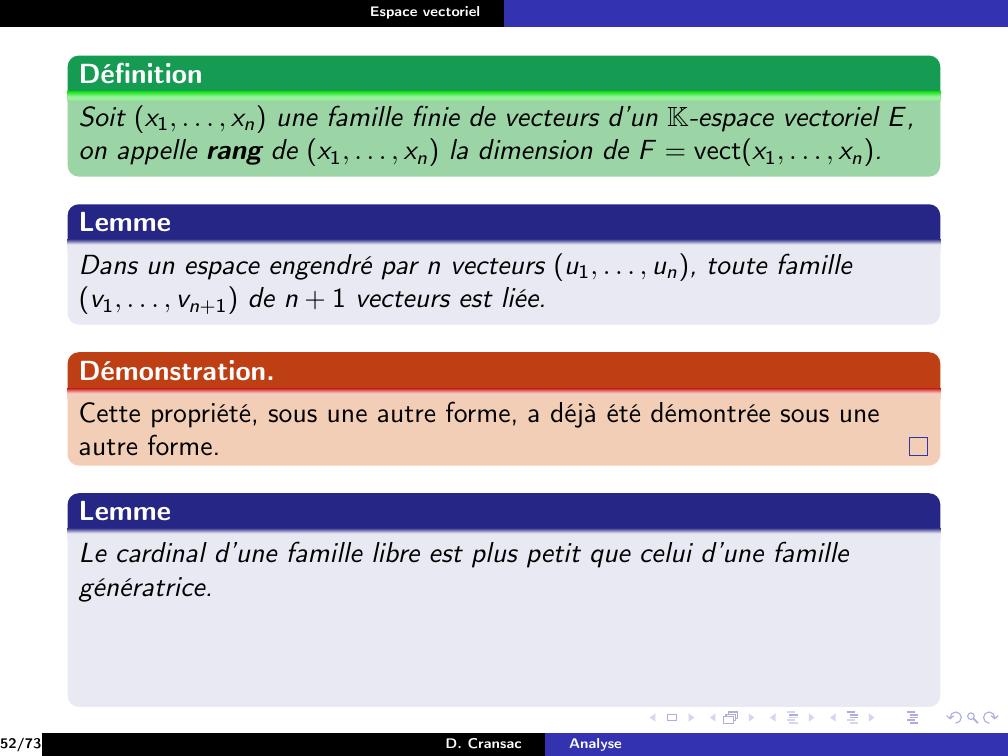
Page 60 : Espace vectorielDéfinitionSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .11/73D. CransacAnalyse

Page 61 : Espace vectorielDéfinitionSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrirex = λ1a1 + λ2a2 + . . . + λnan =nXi=1λiai avec λ1, . . . , λn Kn11/73D. CransacAnalyse

Page 62 : Espace vectorielDéfinitionSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrirex = λ1a1 + λ2a2 + . . . + λnan =nXi=1λiai avec λ1, . . . , λn KnRemarque11/73D. CransacAnalyse

Page 63 : Espace vectorielDéfinitionSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrirex = λ1a1 + λ2a2 + . . . + λnan =nXi=1λiai avec λ1, . . . , λn KnRemarqueOn peut généraliser cette notion à une famille infinie de vecteurs, maisdans ce cas il faut que la suite des scalaires soit à support fini il y a unnombre fini de scalaires non nul.11/73D. CransacAnalyse

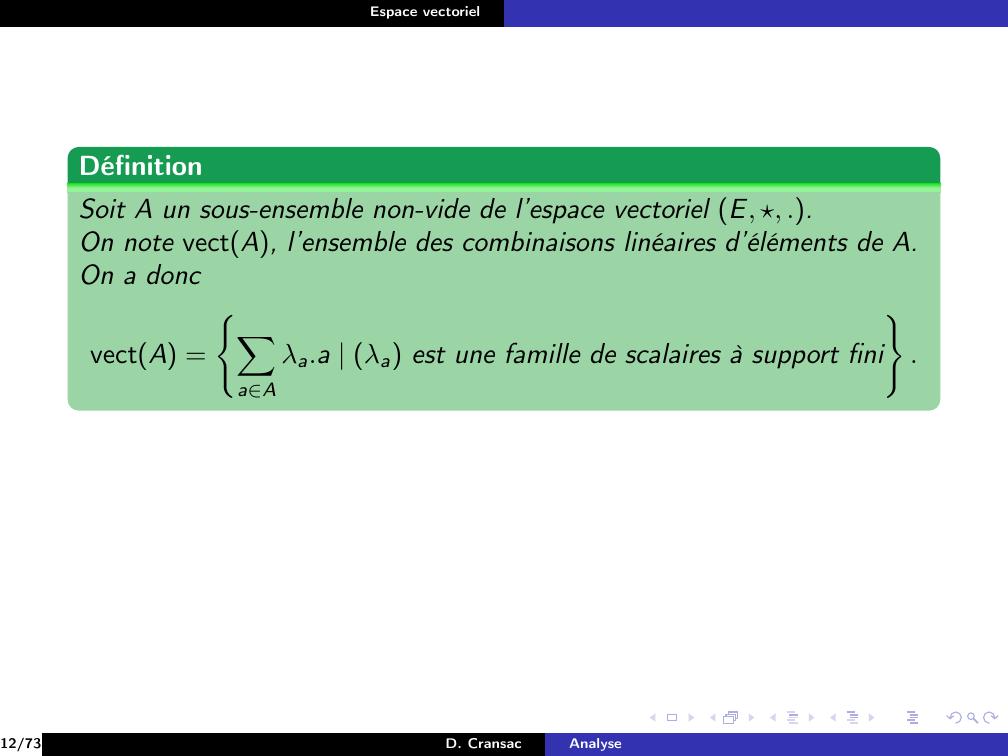
Page 64 : Espace vectorielDéfinitionSoit A un sous-ensemble non-vide de l’espace vectoriel E, , ..12/73D. CransacAnalyse

Page 65 : Espace vectorielDéfinitionSoit A un sous-ensemble non-vide de l’espace vectoriel E, , ..On note vectA, l’ensemble des combinaisons linéaires d’éléments de A.12/73D. CransacAnalyse

Page 66 : Espace vectorielDéfinitionSoit A un sous-ensemble non-vide de l’espace vectoriel E, , ..On note vectA, l’ensemble des combinaisons linéaires d’éléments de A.On a doncvectA =XaAλa.a λa est une famille de scalaires à support fini.12/73D. CransacAnalyse

Page 67 : Espace vectorielDéfinitionSoit A un sous-ensemble non-vide de l’espace vectoriel E, , ..On note vectA, l’ensemble des combinaisons linéaires d’éléments de A.On a doncvectA =XaAλa.a λa est une famille de scalaires à support fini.Donc un élément x de E appartient à vectA, si et seulement si, ilexiste x1, . . . , xn An et des scalaires λ1, . . . , λn, tels que :x = λ1.x1 · · · λn.xn12/73D. CransacAnalyse

Page 68 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.13/73D. CransacAnalyse

Page 69 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.13/73D. CransacAnalyse

Page 70 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.13/73D. CransacAnalyse

Page 71 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu Ku13/73D. CransacAnalyse

Page 72 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu Ku13/73D. CransacAnalyse

Page 73 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectu13/73D. CransacAnalyse

Page 74 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.13/73D. CransacAnalyse

Page 75 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.13/73D. CransacAnalyse

Page 76 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.13/73D. CransacAnalyse

Page 77 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.Ainsi Ku + Kv vectu, v.Soit x vectu, v alors x est combinaison linéaire d’éléments deu, v13/73D. CransacAnalyse

Page 78 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.Ainsi Ku + Kv vectu, v.Soit x vectu, v alors x est combinaison linéaire d’éléments deu, v13/73D. CransacAnalyse

Page 79 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.Ainsi Ku + Kv vectu, v.Soit x vectu, v alors x est combinaison linéaire d’éléments deu, v donc λ, µ K2, x = λu + µv13/73D. CransacAnalyse

Page 80 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.Ainsi Ku + Kv vectu, v.Soit x vectu, v alors x est combinaison linéaire d’éléments deu, v donc λ, µ K2, x = λu + µv donc vectu, v Ku + Kv13/73D. CransacAnalyse

Page 81 : Espace vectorielExempleSoit A = u. Montrons que vectu = λu λ K = Ku.Comme vectA est un sous-espace vectoriel et u A vectA, ona λ K, λu vectA.Ainsi Ku vectu.Soit x vectu alors x est combinaison linéaire d’éléments de udonc x = λu donc vectuu KuDonc Ku = vectuSoit A = u, v.Montrons que vectu, v = λu + µv λ, µ K2 = Ku + Kv.Comme vectA est un sous-espace vectoriel et u A vectA etv vectA, on a λ, µ K2, λu + µv vectA.Ainsi Ku + Kv vectu, v.Soit x vectu, v alors x est combinaison linéaire d’éléments deu, v donc λ, µ K2, x = λu + µv donc vectu, v Ku + KvDoncvectu, v = Ku + Kv = λu + µv λ, µ K13/73D. CransacAnalyse

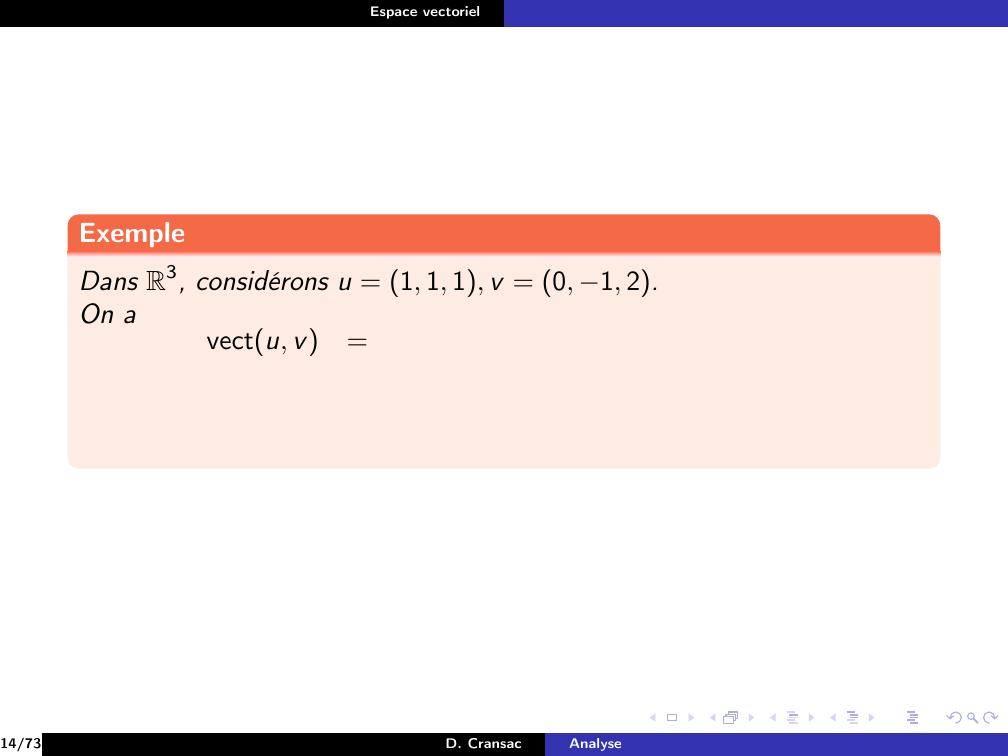
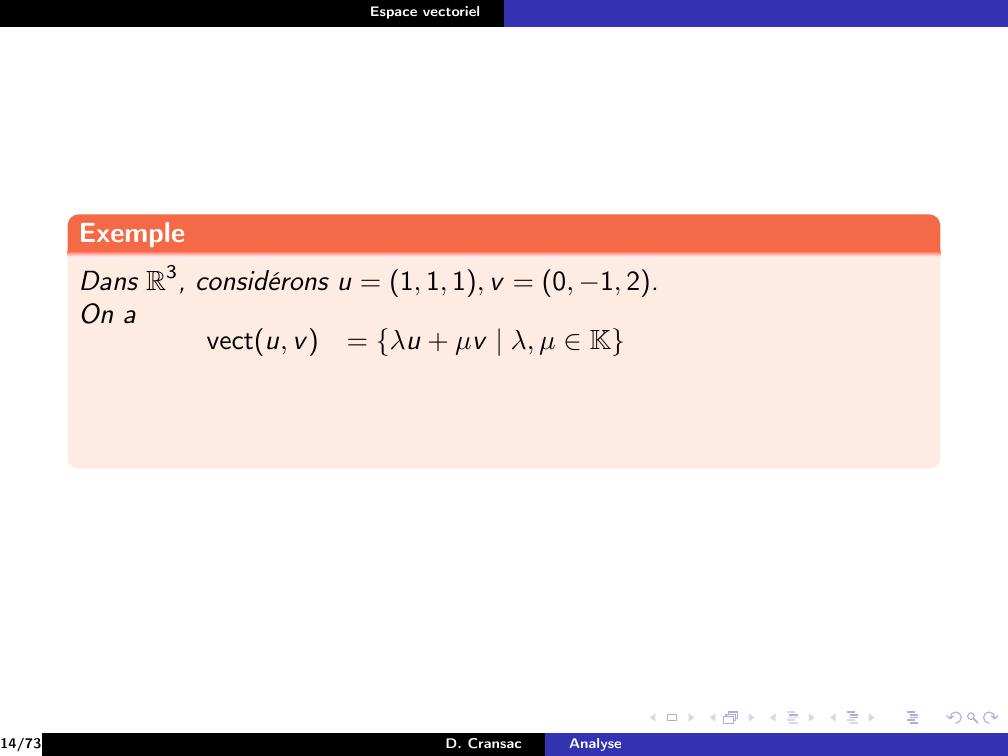
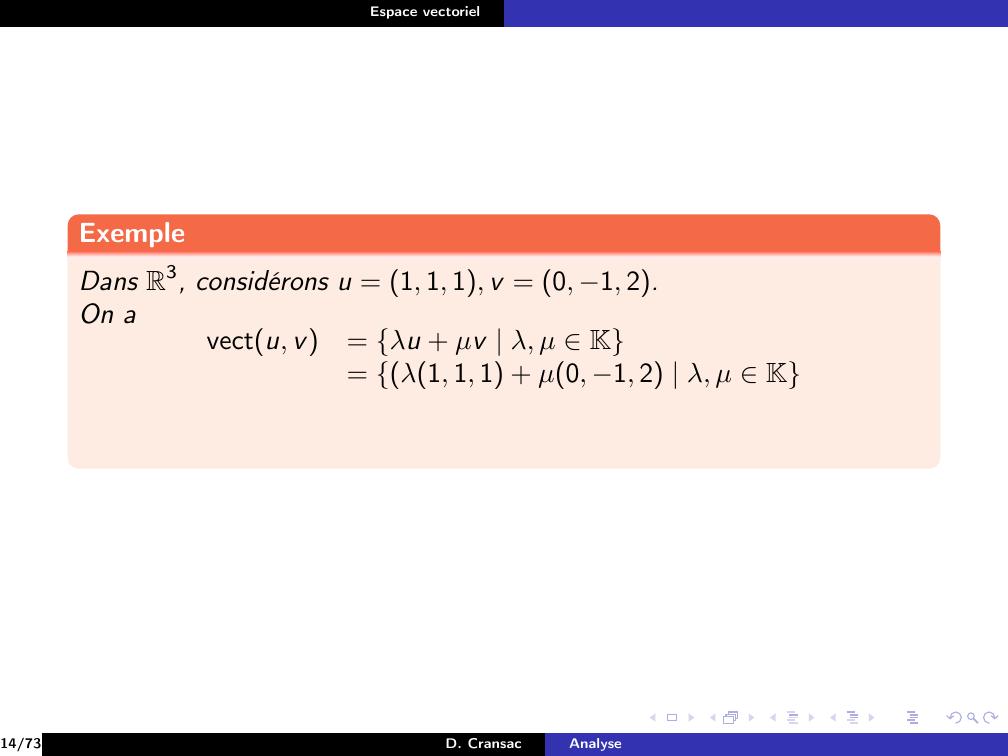
Page 82 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.14/73D. CransacAnalyse

Page 83 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.On avectu, v=14/73D. CransacAnalyse

Page 84 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.On avectu, v= λu + µv λ, µ K14/73D. CransacAnalyse

Page 85 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.On avectu, v= λu + µv λ, µ K= λ1, 1, 1 + µ0, 1, 2 λ, µ K14/73D. CransacAnalyse

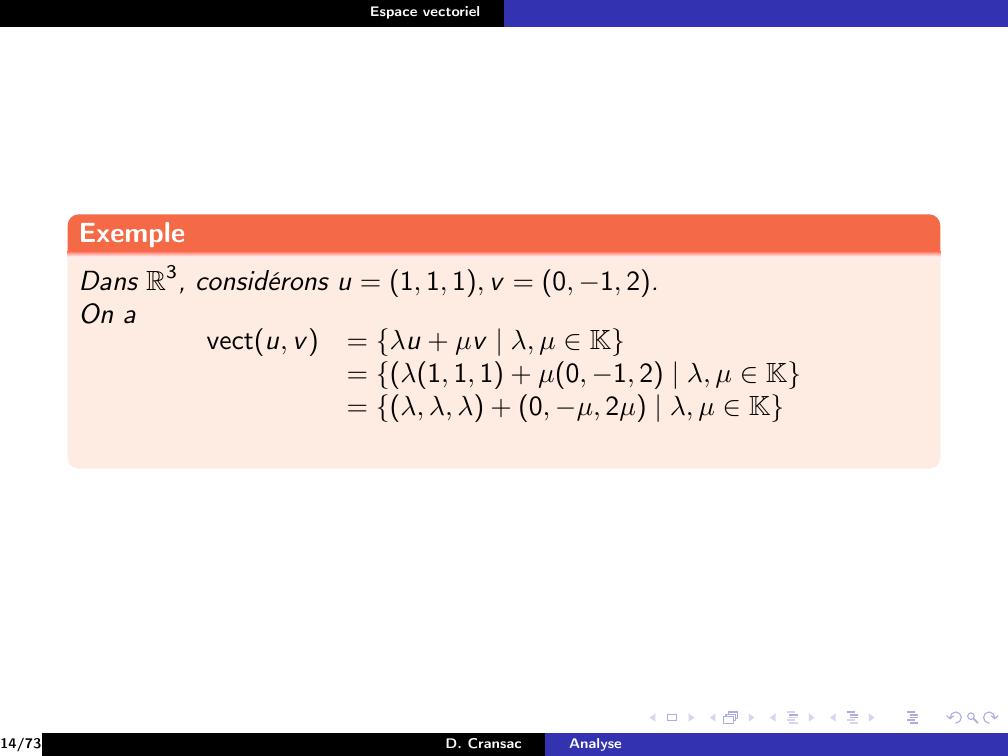
Page 86 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.On avectu, v= λu + µv λ, µ K= λ1, 1, 1 + µ0, 1, 2 λ, µ K= λ, λ, λ + 0, µ, 2µ λ, µ K14/73D. CransacAnalyse

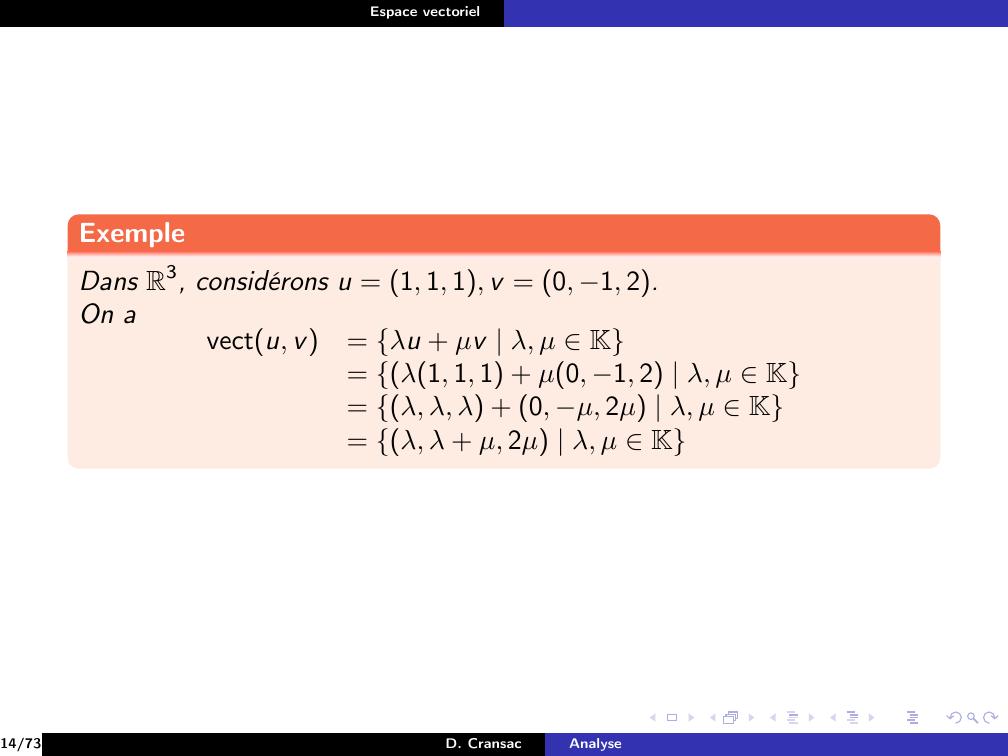
Page 87 : Espace vectorielExempleDans R3, considérons u = 1, 1, 1, v = 0, 1, 2.On avectu, v= λu + µv λ, µ K= λ1, 1, 1 + µ0, 1, 2 λ, µ K= λ, λ, λ + 0, µ, 2µ λ, µ K= λ, λ + µ, 2µ λ, µ K14/73D. CransacAnalyse

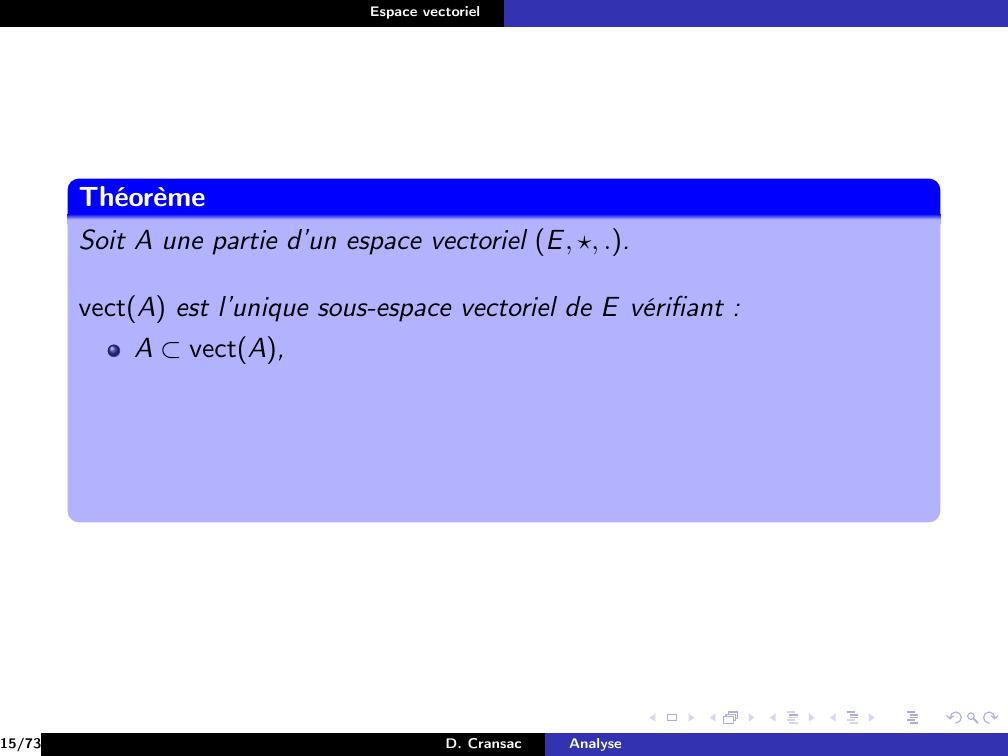
Page 88 : Espace vectorielThéorèmeSoit A une partie d’un espace vectoriel E, , ..vectA est l’unique sous-espace vectoriel de E vérifiant :A vectA,15/73D. CransacAnalyse

Page 89 : Espace vectorielThéorèmeSoit A une partie d’un espace vectoriel E, , ..vectA est l’unique sous-espace vectoriel de E vérifiant :A vectA,vectA est inclus dans tout sous-espace vectoriel contenant A.15/73D. CransacAnalyse

Page 90 : Espace vectorielThéorèmeSoit A une partie d’un espace vectoriel E, , ..vectA est l’unique sous-espace vectoriel de E vérifiant :A vectA,vectA est inclus dans tout sous-espace vectoriel contenant A.15/73D. CransacAnalyse

Page 91 : Espace vectorielThéorèmeSoit A une partie d’un espace vectoriel E, , ..vectA est l’unique sous-espace vectoriel de E vérifiant :A vectA,vectA est inclus dans tout sous-espace vectoriel contenant A.Le sous-espace vectoriel vectA se comprend donc comme étant le pluspetit sous-espace vectoriel contenant A,15/73D. CransacAnalyse

Page 92 : Espace vectorielThéorèmeSoit A une partie d’un espace vectoriel E, , ..vectA est l’unique sous-espace vectoriel de E vérifiant :A vectA,vectA est inclus dans tout sous-espace vectoriel contenant A.Le sous-espace vectoriel vectA se comprend donc comme étant le pluspetit sous-espace vectoriel contenant A, on l’appelle espace vectorielengendré par A.15/73D. CransacAnalyse

Page 93 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.16/73D. CransacAnalyse

Page 94 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.16/73D. CransacAnalyse

Page 95 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐16/73D. CransacAnalyse

Page 96 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA16/73D. CransacAnalyse

Page 97 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.16/73D. CransacAnalyse

Page 98 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel.16/73D. CransacAnalyse

Page 99 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car16/73D. CransacAnalyse

Page 100 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.16/73D. CransacAnalyse

Page 101 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA16/73D. CransacAnalyse

Page 102 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA alors x =nXi=1λixi avec i J1, nK, xi A16/73D. CransacAnalyse

Page 103 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA alors x =nXi=1λixi avec i J1, nK, xi A or comme A estun espace vectoriel,16/73D. CransacAnalyse

Page 104 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA alors x =nXi=1λixi avec i J1, nK, xi A or comme A estun espace vectoriel, x A16/73D. CransacAnalyse

Page 105 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA alors x =nXi=1λixi avec i J1, nK, xi A or comme A estun espace vectoriel, x A donc vectA A16/73D. CransacAnalyse

Page 106 : Espace vectorielCorollairevectA est l’intersection de tous les sous-espaces vectoriels de Econtenant A.CorollaireA est un sous-espace vectoriel, si et seulement si, vect A = A.Démonstration.⇐La réciproque est assez claire : si A = vectA alors A est un espace vectoriel.⇒Supposons que A est un espace vectoriel. Alors tout élément x de A estcombinaison linéaire d’un élément de A car x = 1.x donc A vectA.Soit x vectA alors x =nXi=1λixi avec i J1, nK, xi A or comme A estun espace vectoriel, x A donc vectA AdoncA = vectA16/73D. CransacAnalyse

Page 107 : Espace vectorielExemplevectensemble vide = 0E car l’espace nul est le plus petitsous-espace vectoriel de E.vectE = E car vect E est le plus petit sous-espace vectorielcontenant E.17/73D. CransacAnalyse

Page 108 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.18/73D. CransacAnalyse

Page 109 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.Démonstration.Supposons que A B.18/73D. CransacAnalyse

Page 110 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.Démonstration.Supposons que A B.Alors A vectB18/73D. CransacAnalyse

Page 111 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.Démonstration.Supposons que A B.Alors A vectB or vectB est un sous-espace vectoriel18/73D. CransacAnalyse

Page 112 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.Démonstration.Supposons que A B.Alors A vectB or vectB est un sous-espace vectorielet vect A est le plus petit espace vectoriel contenant A18/73D. CransacAnalyse

Page 113 : Espace vectorielPropositionSi A et B deux parties de E alors A B =⇒vectA vectB.Démonstration.Supposons que A B.Alors A vectB or vectB est un sous-espace vectorielet vect A est le plus petit espace vectoriel contenant Adonc vectA vectB.18/73D. CransacAnalyse

Page 114 : Espace vectorielPropositionSi A et B sont deux parties de E alors vectA B = vectA + vectB.19/73D. CransacAnalyse

Page 115 : Espace vectorielPropositionSi A et B sont deux parties de E alors vectA B = vectA + vectB.Démonstration.z vectA B19/73D. CransacAnalyse

Page 116 : Espace vectorielPropositionSi A et B sont deux parties de E alors vectA B = vectA + vectB.Démonstration.z vectA B⇔λ1, λ2, . . . , λn Kn, x1, x2, . . . , xn An, µ1, µ2, . . . , µn Km, y1, y2, . . . , ym Bm tels que19/73D. CransacAnalyse

Page 117 : Espace vectorielPropositionSi A et B sont deux parties de E alors vectA B = vectA + vectB.Démonstration.z vectA B⇔λ1, λ2, . . . , λn Kn, x1, x2, . . . , xn An, µ1, µ2, . . . , µn Km, y1, y2, . . . , ym Bm tels quez =mXiλixi + µiyi =mXiλixi +mXiµiyi19/73D. CransacAnalyse

Page 118 : Espace vectorielPropositionSi A et B sont deux parties de E alors vectA B = vectA + vectB.Démonstration.z vectA B⇔λ1, λ2, . . . , λn Kn, x1, x2, . . . , xn An, µ1, µ2, . . . , µn Km, y1, y2, . . . , ym Bm tels quez =mXiλixi + µiyi =mXiλixi +mXiµiyi⇔z vectA + vectB.19/73D. CransacAnalyse

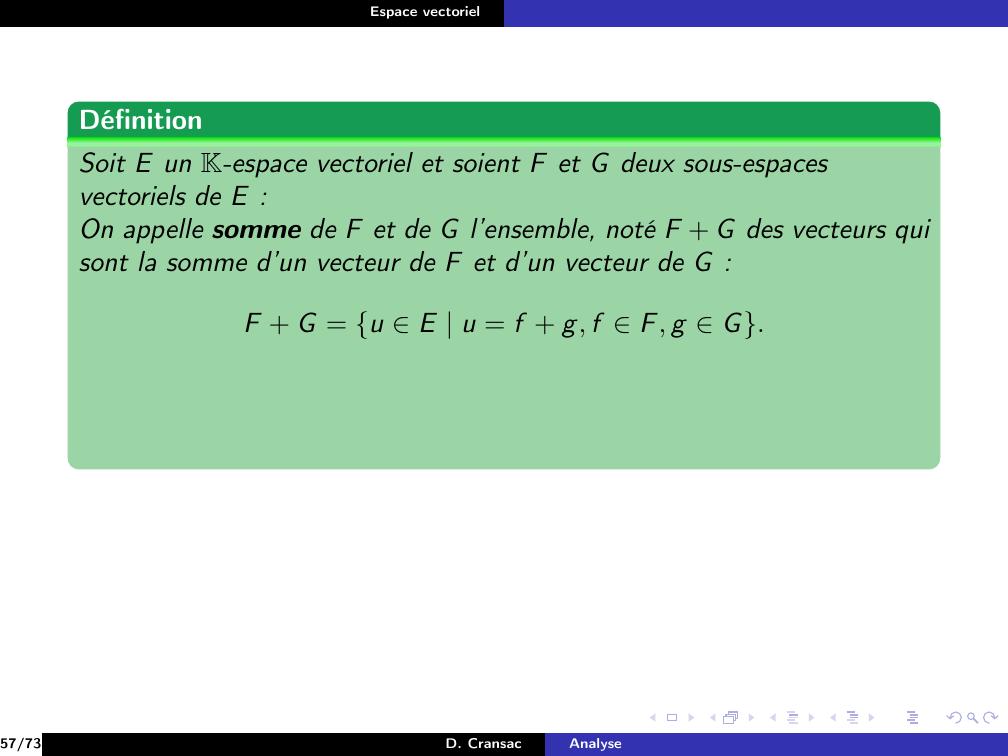
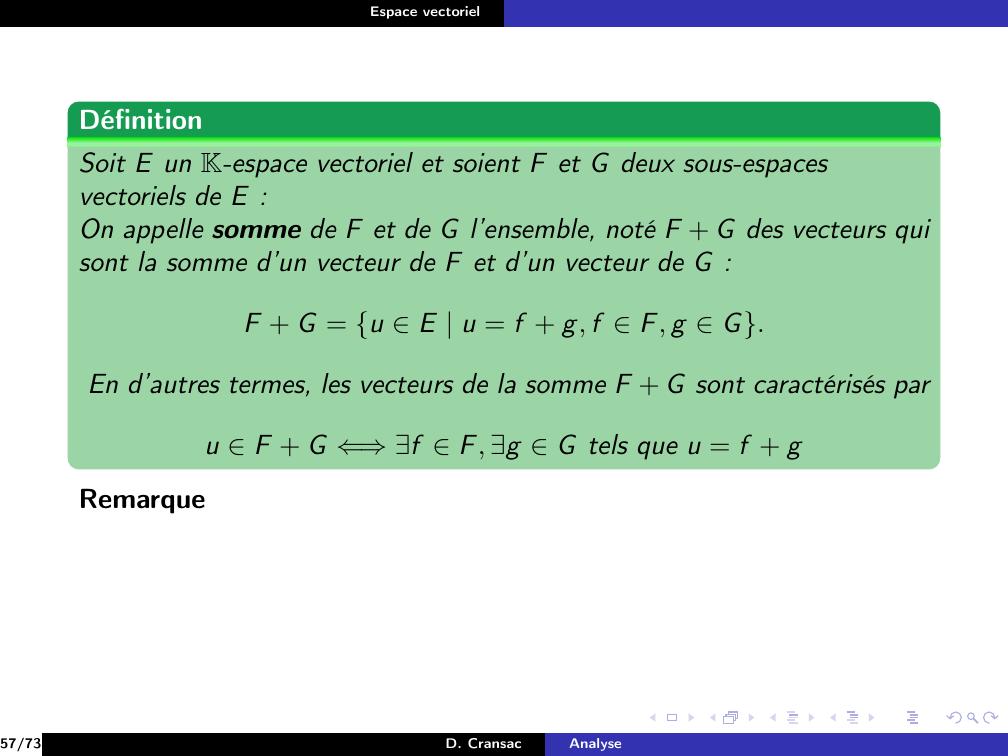
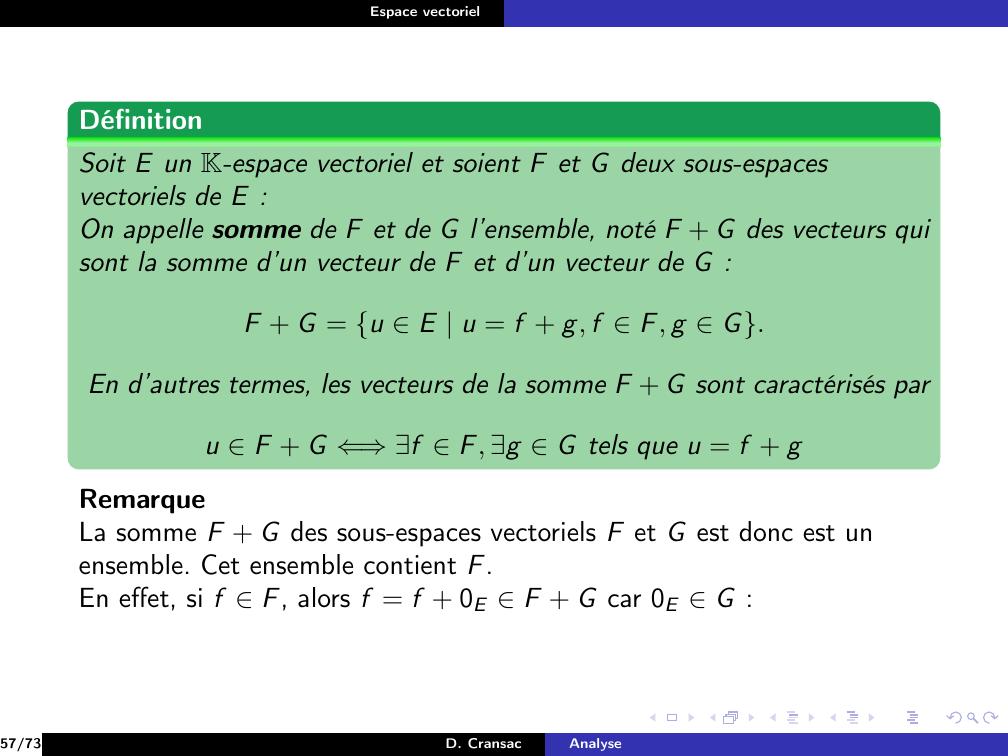
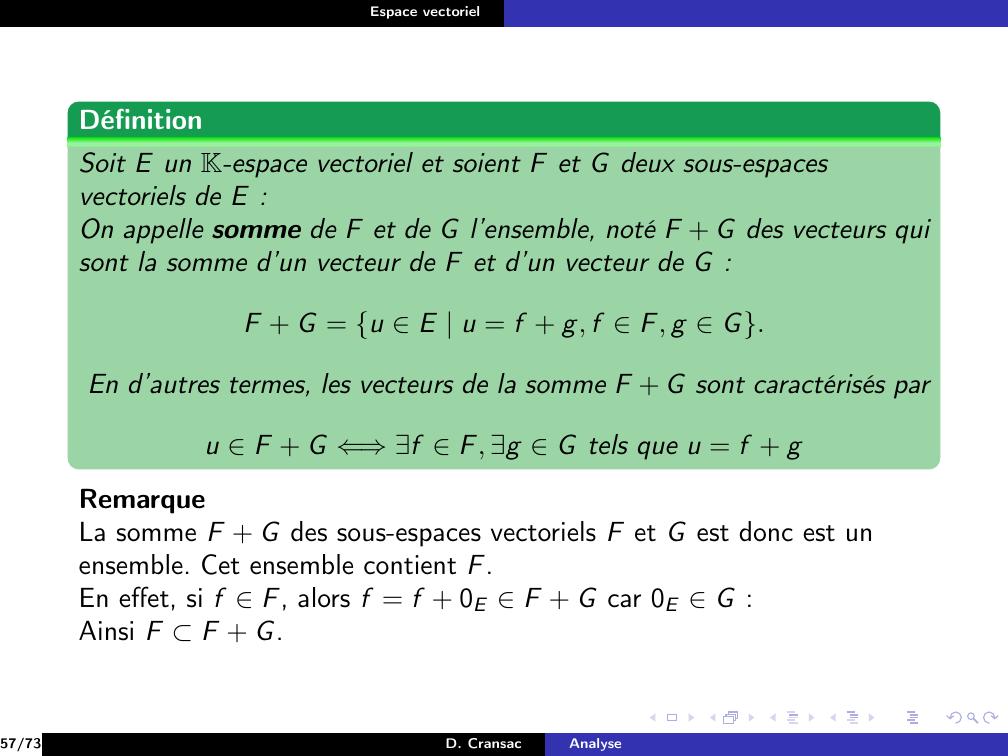
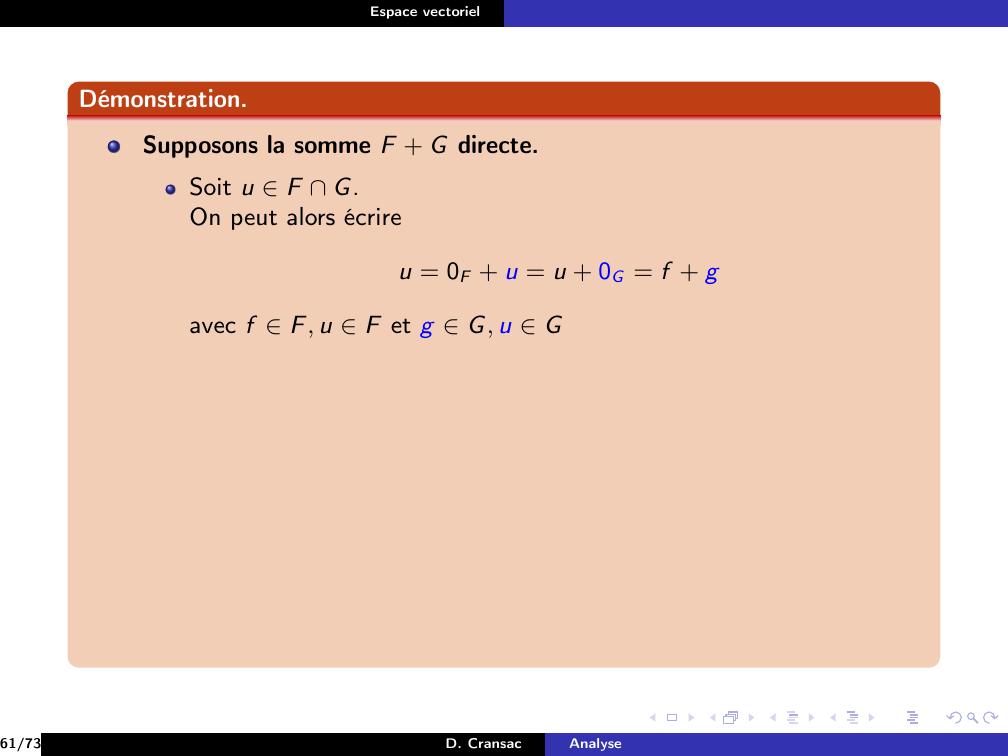
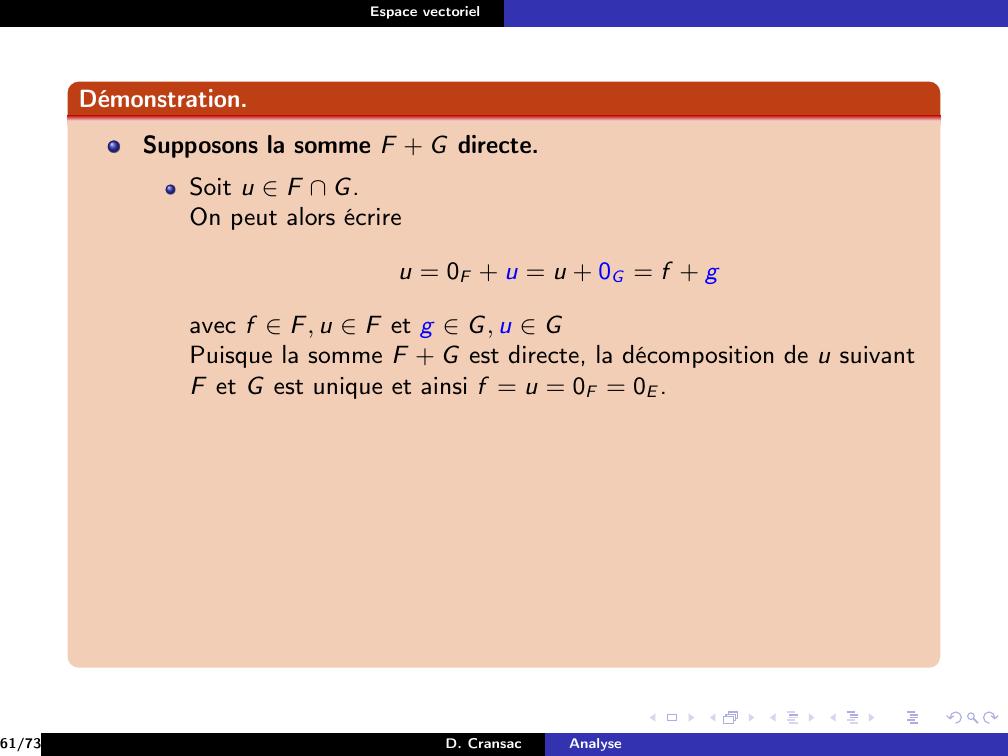
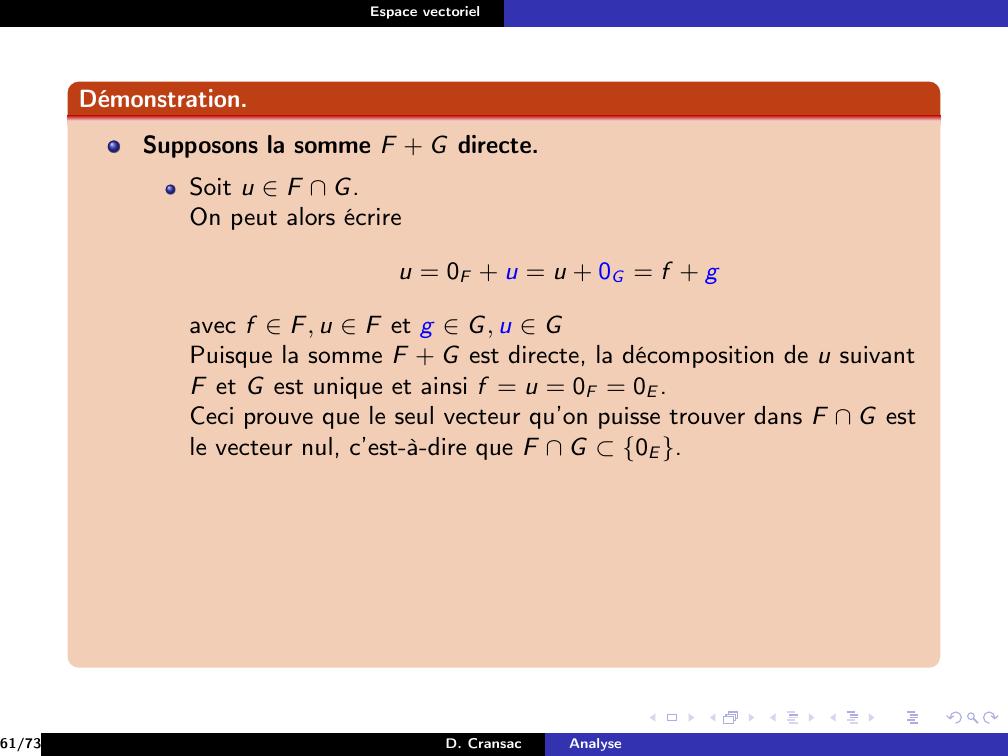
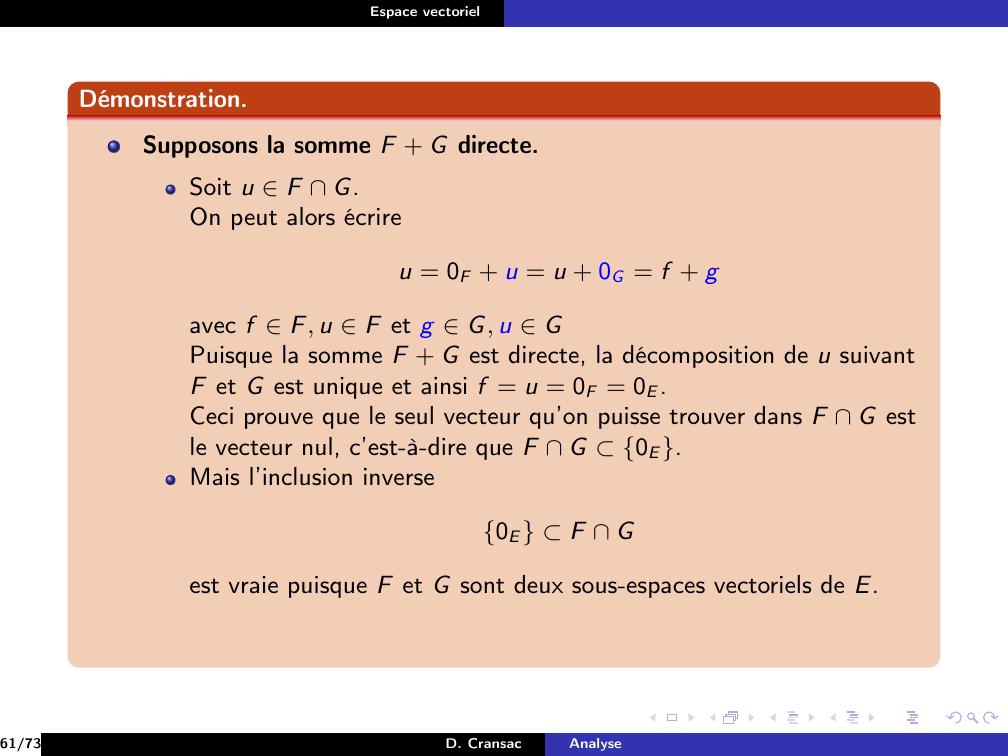
Page 119 : Espace vectorielExemplePour F et G deux sous-espaces vectoriels de E.20/73D. CransacAnalyse

Page 120 : Espace vectorielExemplePour F et G deux sous-espaces vectoriels de E.vectF G = F + G20/73D. CransacAnalyse

Page 121 : Espace vectorielExemplePour F et G deux sous-espaces vectoriels de E.vectF G = F + GAinsi F + G apparaît comme étant le plus petit sous-espace vectorielcontenant F et G.20/73D. CransacAnalyse

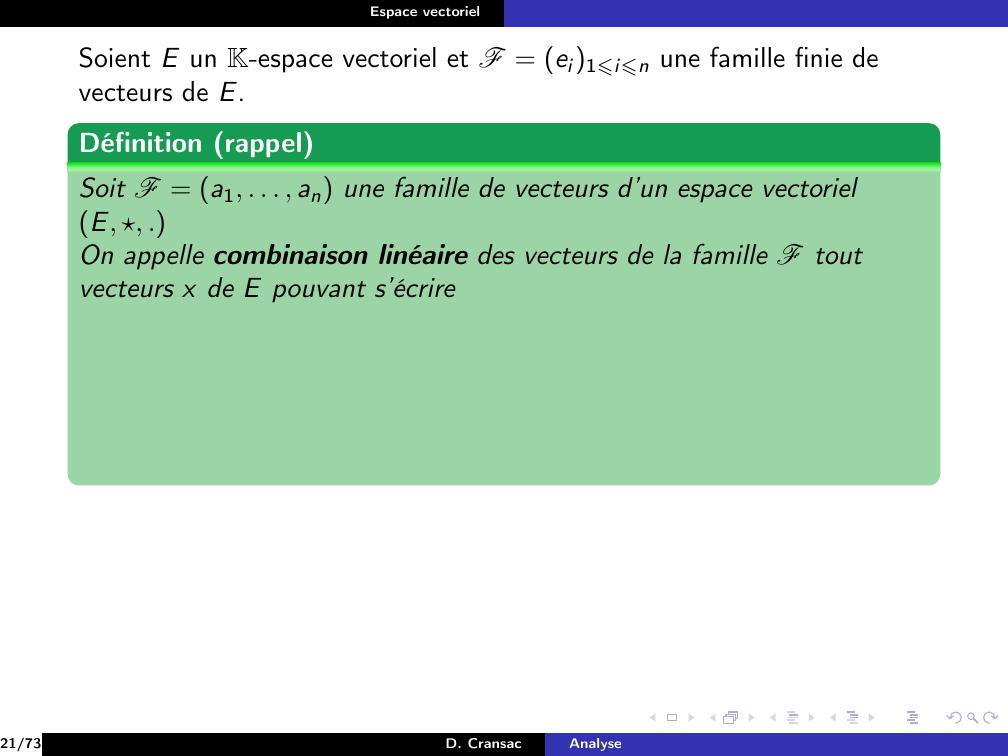
Page 122 : Espace vectorielSoient E un K-espace vectoriel et F = ei1⩽i⩽n une famille finie devecteurs de E.21/73D. CransacAnalyse

Page 123 : Espace vectorielSoient E un K-espace vectoriel et F = ei1⩽i⩽n une famille finie devecteurs de E.Définition rappelSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .21/73D. CransacAnalyse

Page 124 : Espace vectorielSoient E un K-espace vectoriel et F = ei1⩽i⩽n une famille finie devecteurs de E.Définition rappelSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrire21/73D. CransacAnalyse

Page 125 : Espace vectorielSoient E un K-espace vectoriel et F = ei1⩽i⩽n une famille finie devecteurs de E.Définition rappelSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrirex = λ1a1 + λ2a2 + . . . + λnan =nXi=1λiai avec λ1, . . . , λn Kn.21/73D. CransacAnalyse

Page 126 : Espace vectorielSoient E un K-espace vectoriel et F = ei1⩽i⩽n une famille finie devecteurs de E.Définition rappelSoit F = a1, . . . , an une famille de vecteurs d’un espace vectorielE, , .On appelle combinaison linéaire des vecteurs de la famille F toutvecteurs x de E pouvant s’écrirex = λ1a1 + λ2a2 + . . . + λnan =nXi=1λiai avec λ1, . . . , λn Kn.Définition rappelOn appelle espace vectoriel engendré par la famille F = ei1⩽i⩽n, lesous-espace vectoriel des combinaisons linéaires des éléments dee1, . . . , en.On le note vect F, vectei1⩽i⩽n ou vecte1, . . . , en.21/73D. CransacAnalyse

Page 127 : Espace vectorielRemarqueIl est efficace d’établir qu’une partie est un sous-espace vectoriel enobservant que celle-ci est engendré par une famille de vecteurs.22/73D. CransacAnalyse

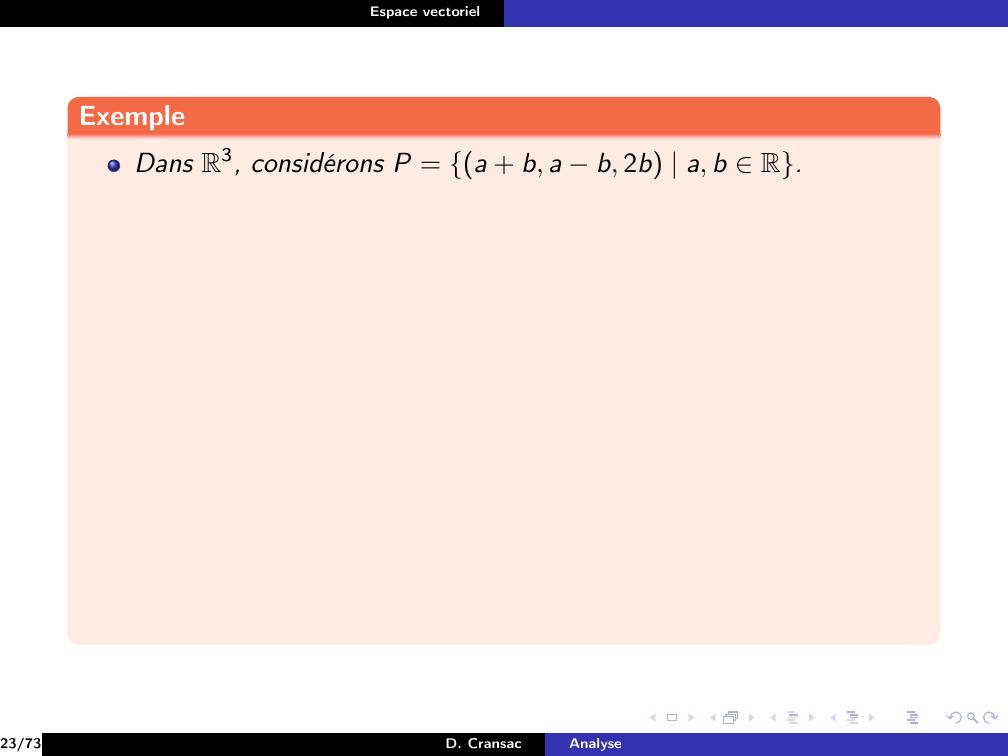
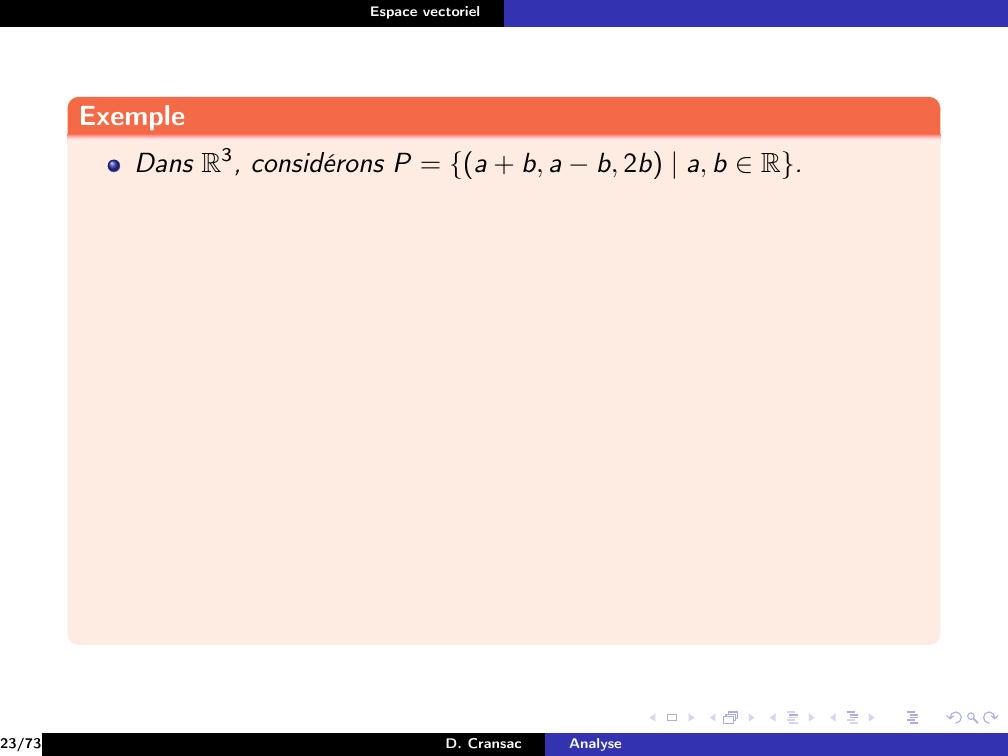
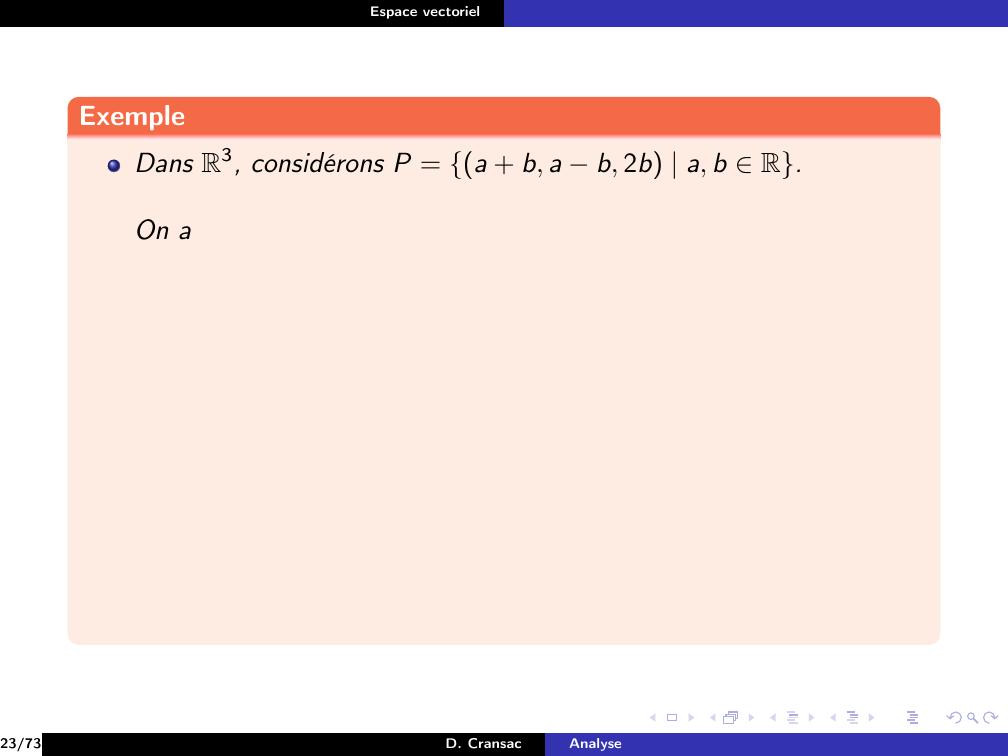
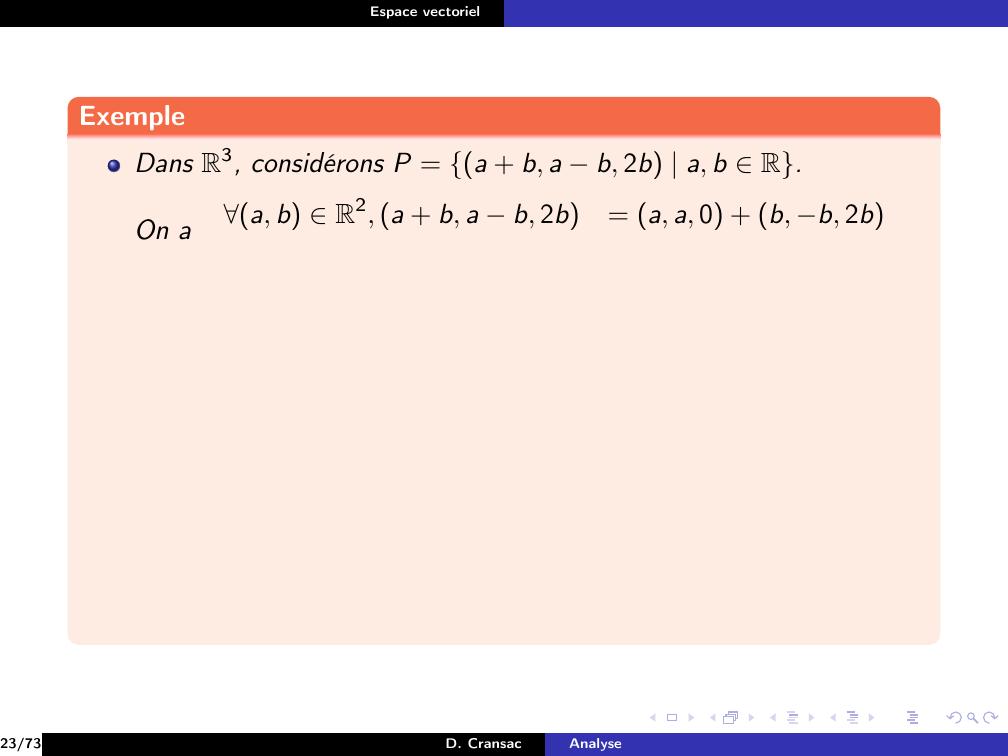
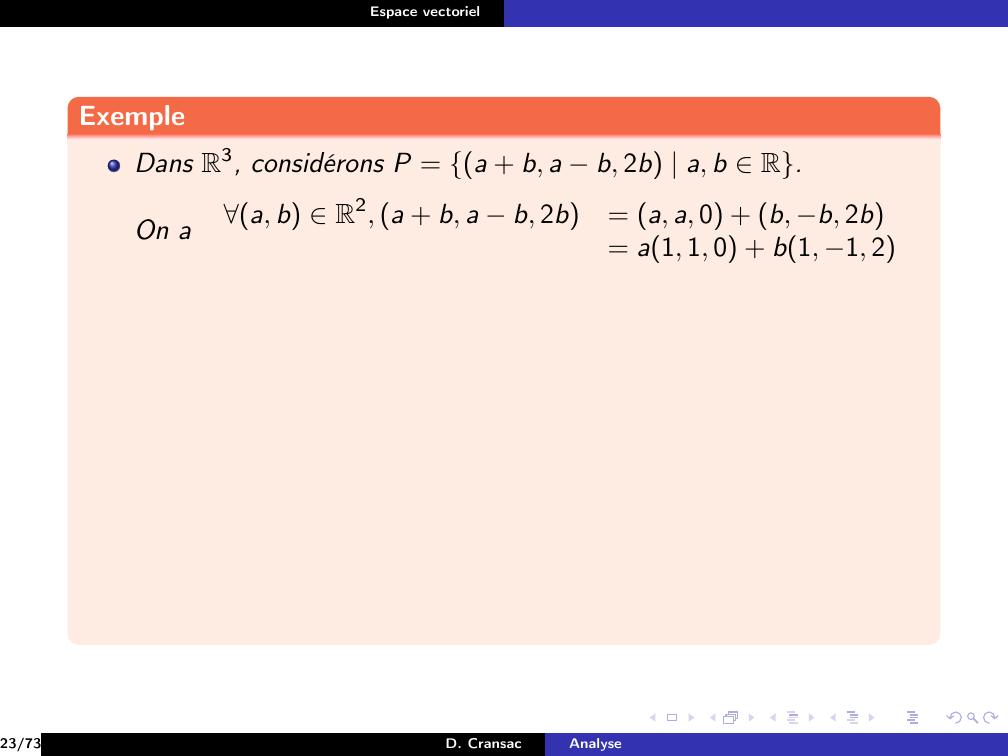
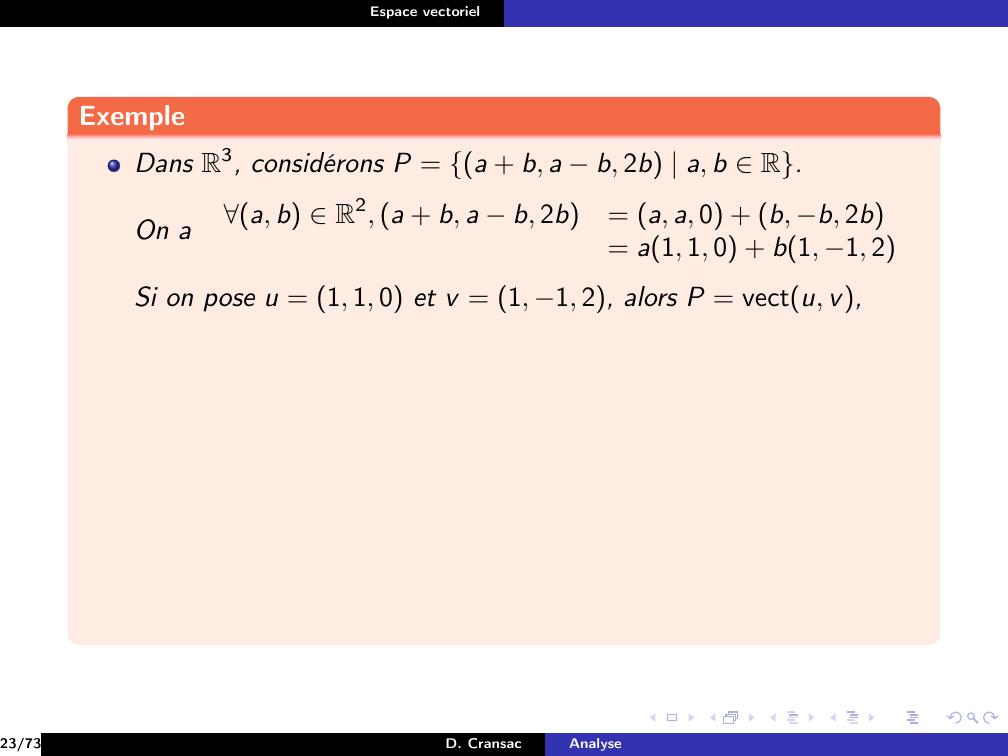
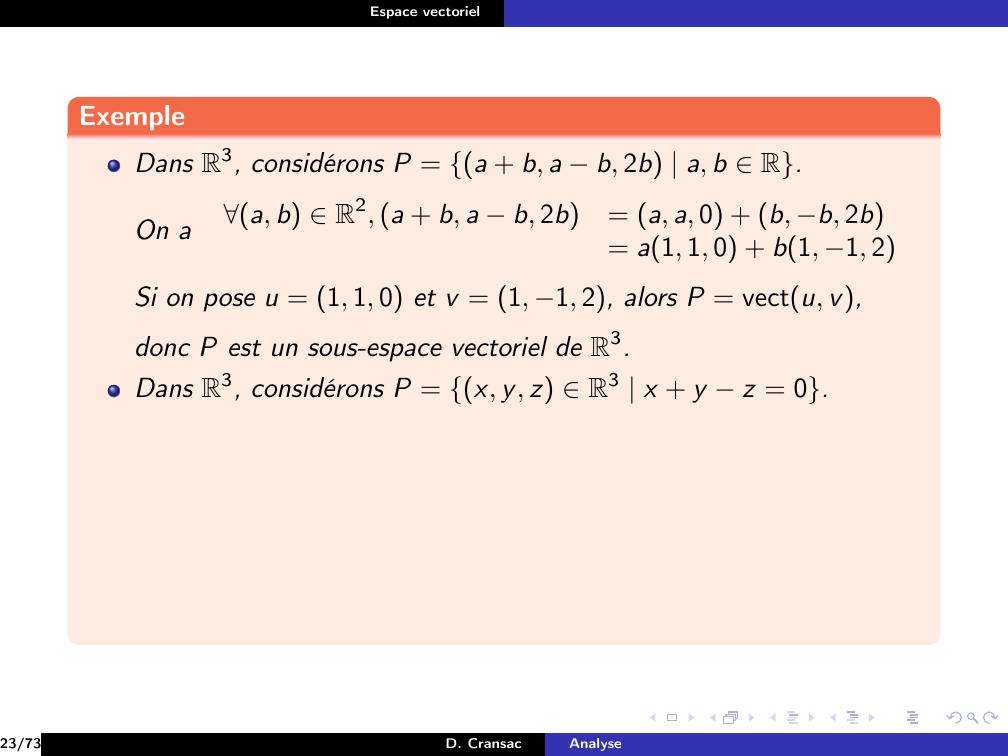
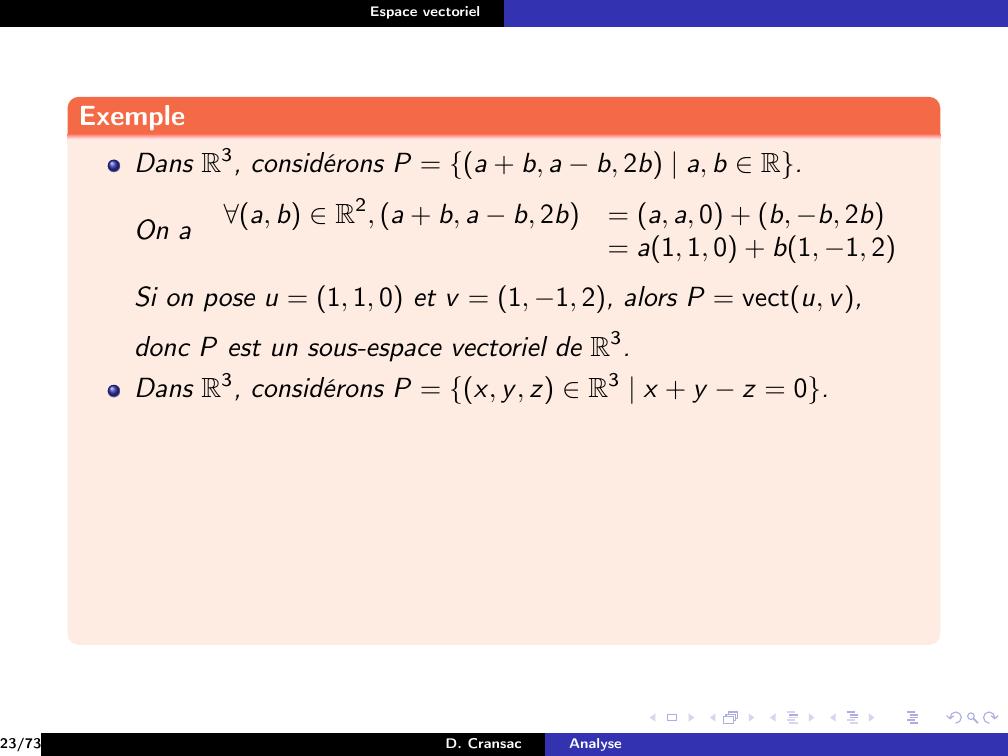
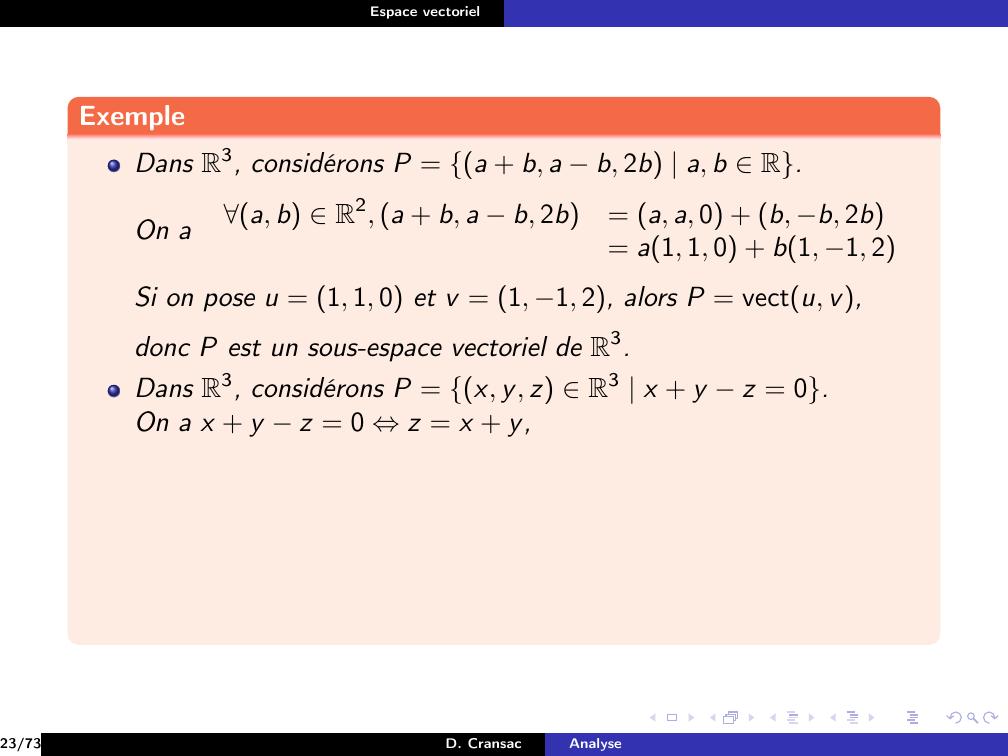
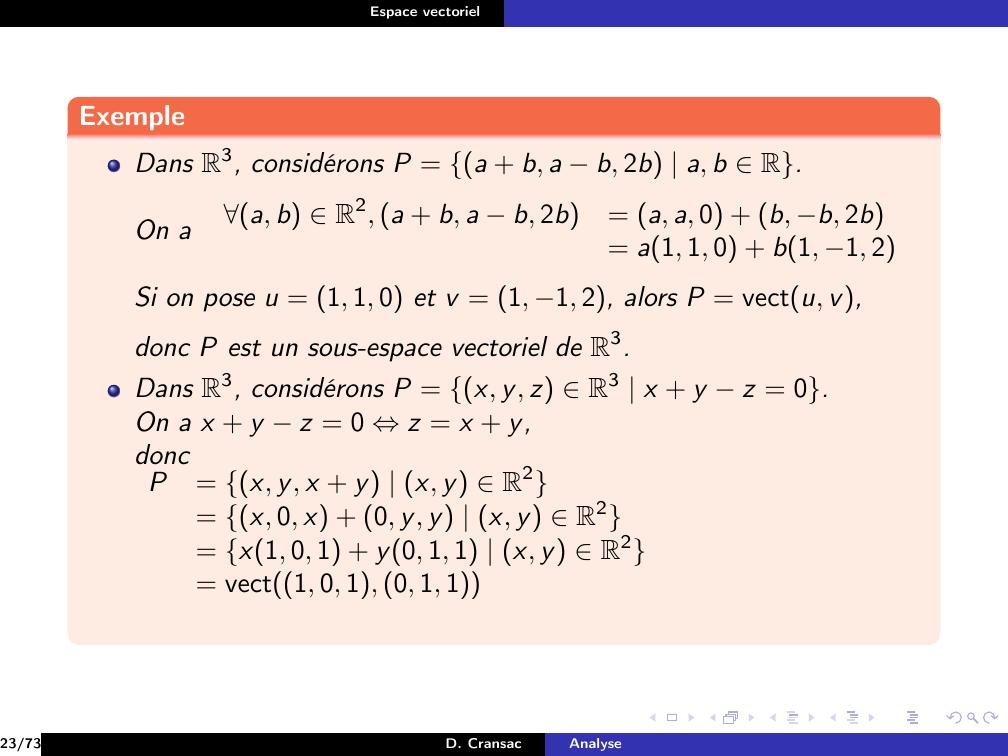
Page 128 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.23/73D. CransacAnalyse

Page 129 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.23/73D. CransacAnalyse

Page 130 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On a23/73D. CransacAnalyse

Page 131 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b23/73D. CransacAnalyse

Page 132 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 223/73D. CransacAnalyse

Page 133 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,23/73D. CransacAnalyse

Page 134 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.23/73D. CransacAnalyse

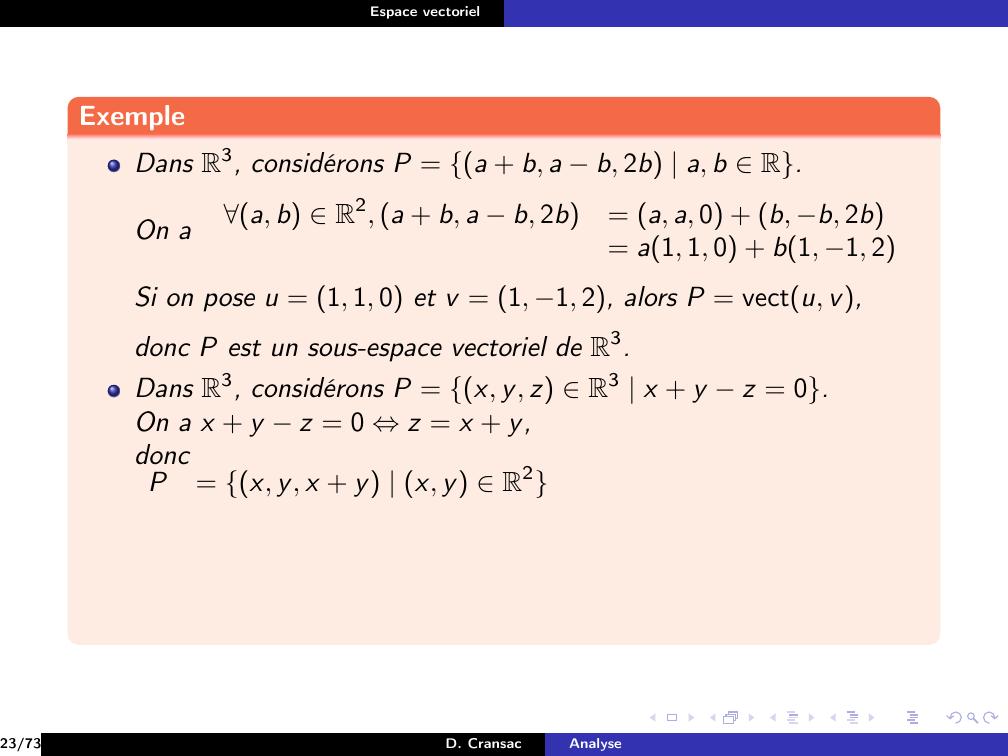
Page 135 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.23/73D. CransacAnalyse

Page 136 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.23/73D. CransacAnalyse

Page 137 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,23/73D. CransacAnalyse

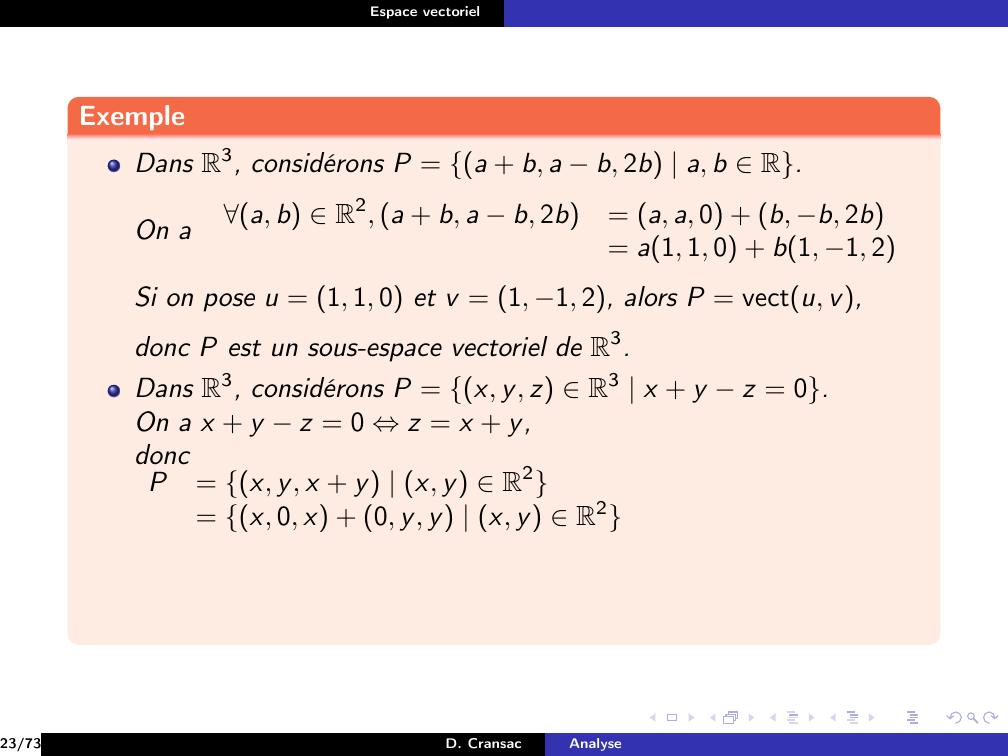
Page 138 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,doncP= x, y, x + y x, y R223/73D. CransacAnalyse

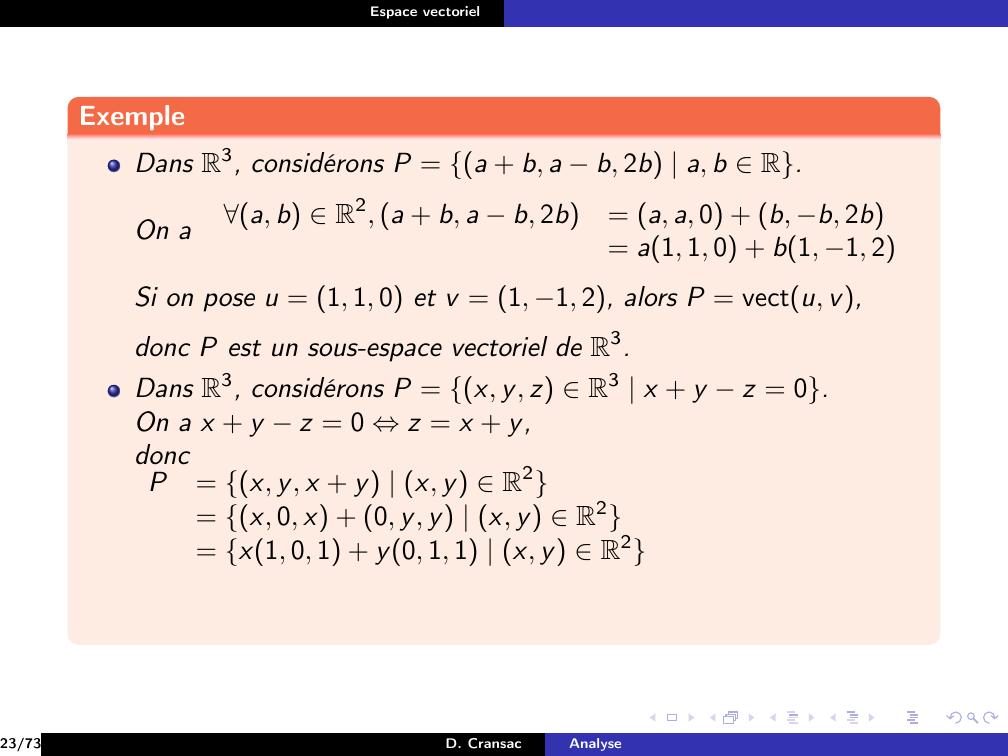
Page 139 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,doncP= x, y, x + y x, y R2= x, 0, x + 0, y, y x, y R223/73D. CransacAnalyse

Page 140 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,doncP= x, y, x + y x, y R2= x, 0, x + 0, y, y x, y R2= x1, 0, 1 + y0, 1, 1 x, y R223/73D. CransacAnalyse

Page 141 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,doncP= x, y, x + y x, y R2= x, 0, x + 0, y, y x, y R2= x1, 0, 1 + y0, 1, 1 x, y R2= vect1, 0, 1, 0, 1, 123/73D. CransacAnalyse

Page 142 : Espace vectorielExempleDans R3, considérons P = a + b, a b, 2b a, b R.On aa, b R2, a + b, a b, 2b= a, a, 0 + b, b, 2b= a1, 1, 0 + b1, 1, 2Si on pose u = 1, 1, 0 et v = 1, 1, 2, alors P = vectu, v,donc P est un sous-espace vectoriel de R3.Dans R3, considérons P = x, y, z R3 x + y z = 0.On a x + y z = 0 ⇔z = x + y,doncP= x, y, x + y x, y R2= x, 0, x + 0, y, y x, y R2= x1, 0, 1 + y0, 1, 1 x, y R2= vect1, 0, 1, 0, 1, 1Ainsi P est un sous-espace vectoriel de R3.23/73D. CransacAnalyse

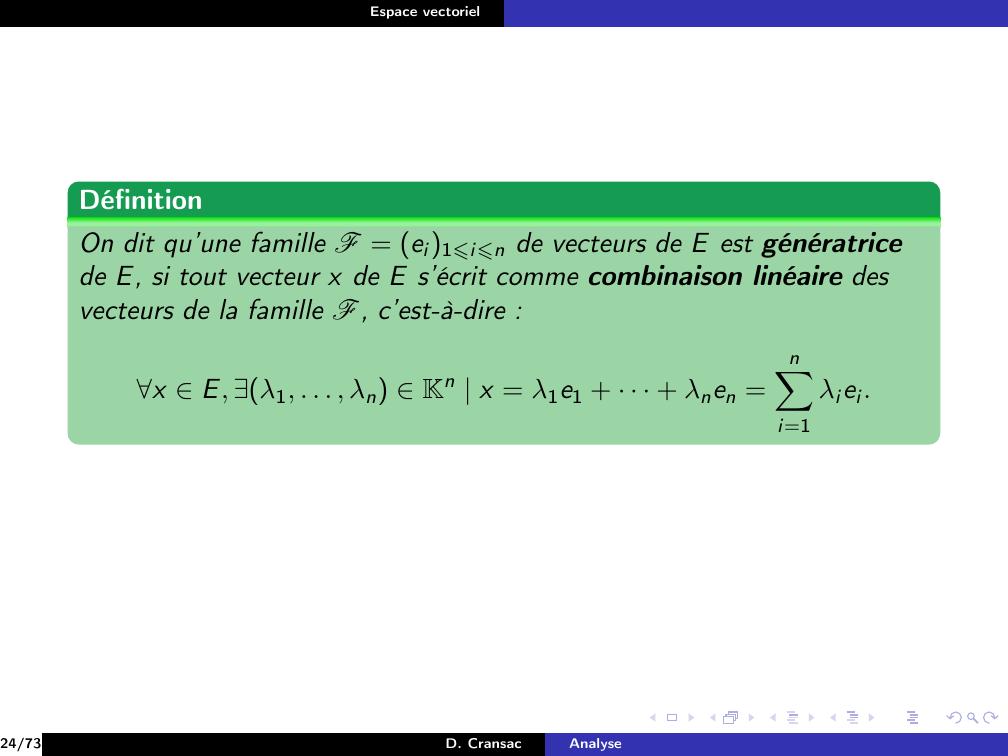
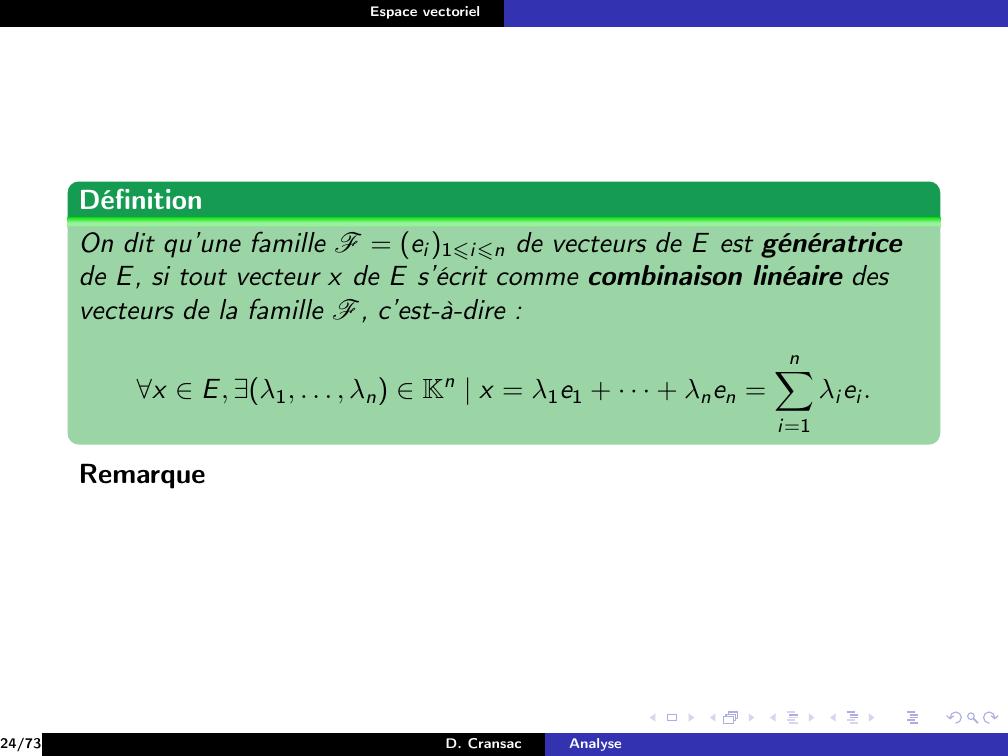
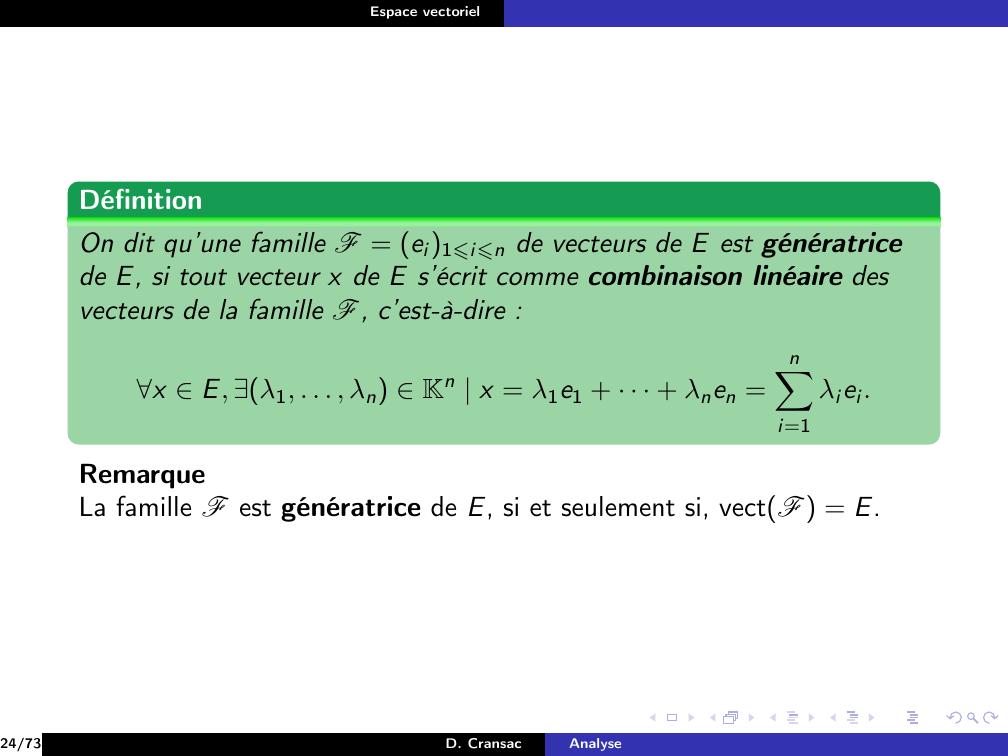
Page 143 : Espace vectorielDéfinitionOn dit qu’une famille F = ei1⩽i⩽n de vecteurs de E est génératricede E, si tout vecteur x de E s’écrit comme combinaison linéaire desvecteurs de la famille F, c’est-à-dire :x E, λ1, . . . , λn Kn x = λ1e1 + · · · + λnen =nXi=1λiei.24/73D. CransacAnalyse

Page 144 : Espace vectorielDéfinitionOn dit qu’une famille F = ei1⩽i⩽n de vecteurs de E est génératricede E, si tout vecteur x de E s’écrit comme combinaison linéaire desvecteurs de la famille F, c’est-à-dire :x E, λ1, . . . , λn Kn x = λ1e1 + · · · + λnen =nXi=1λiei.Remarque24/73D. CransacAnalyse

Page 145 : Espace vectorielDéfinitionOn dit qu’une famille F = ei1⩽i⩽n de vecteurs de E est génératricede E, si tout vecteur x de E s’écrit comme combinaison linéaire desvecteurs de la famille F, c’est-à-dire :x E, λ1, . . . , λn Kn x = λ1e1 + · · · + λnen =nXi=1λiei.RemarqueLa famille F est génératrice de E, si et seulement si, vectF = E.24/73D. CransacAnalyse

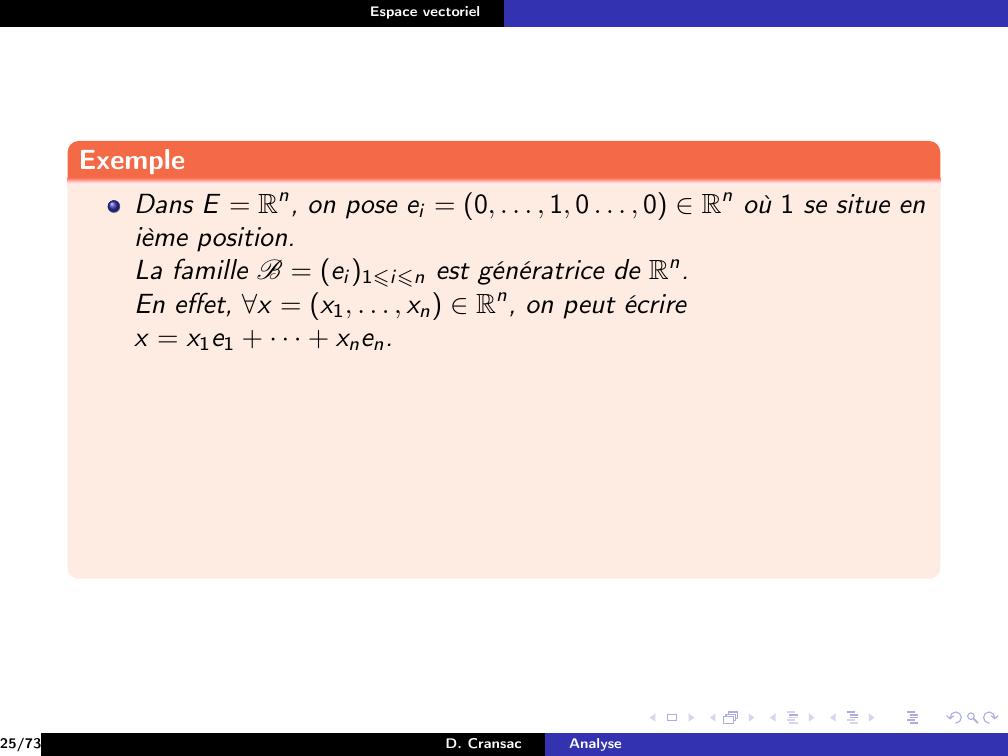
Page 146 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.25/73D. CransacAnalyse

Page 147 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.25/73D. CransacAnalyse

Page 148 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.25/73D. CransacAnalyse

Page 149 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn,25/73D. CransacAnalyse

Page 150 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.25/73D. CransacAnalyse

Page 151 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.25/73D. CransacAnalyse

Page 152 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.25/73D. CransacAnalyse

Page 153 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.En effet, x R, x = x.1.25/73D. CransacAnalyse

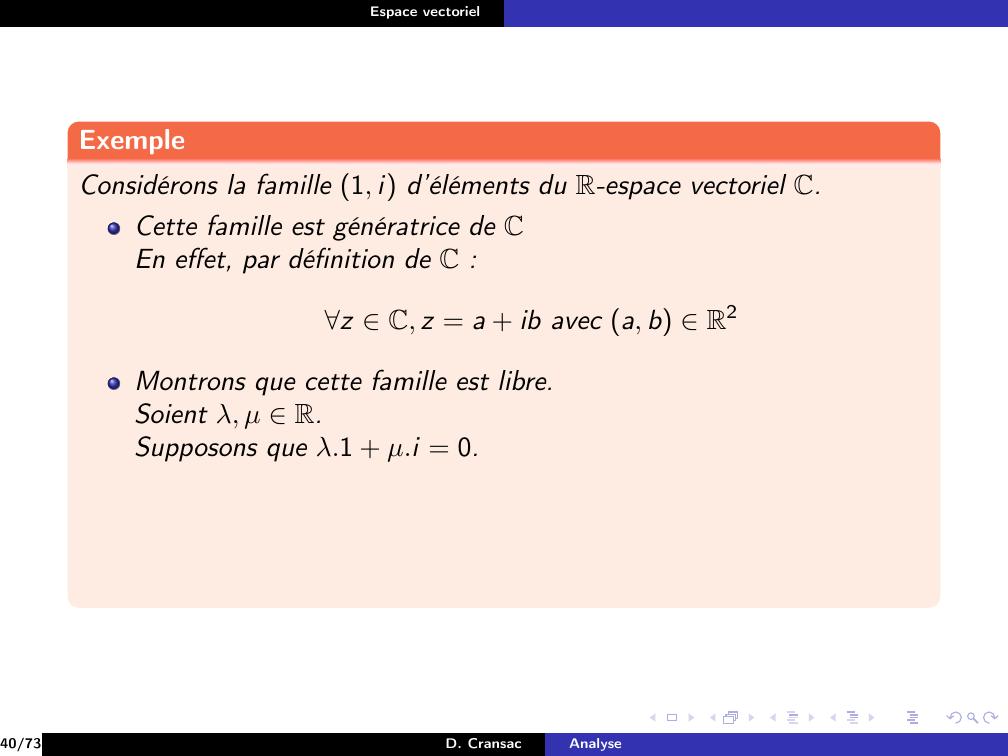
Page 154 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.En effet, x R, x = x.1.Dans E = C vu comme R-espace vectoriel, la famille F = 1, i estgénératrice.25/73D. CransacAnalyse

Page 155 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.En effet, x R, x = x.1.Dans E = C vu comme R-espace vectoriel, la famille F = 1, i estgénératrice.25/73D. CransacAnalyse

Page 156 : Espace vectorielExempleDans E = Rn, on pose ei = 0, . . . , 1, 0 . . . , 0 Rn où 1 se situe enième position.La famille B = ei1⩽i⩽n est génératrice de Rn.En effet, x = x1, . . . , xn Rn, on peut écrirex = x1e1 + · · · + xnen.Dans E = R, la famille 1 est génératrice.En effet, x R, x = x.1.Dans E = C vu comme R-espace vectoriel, la famille F = 1, i estgénératrice.En effet, pour tout z C, on peut écrire z = a.1 + b.i, aveca = Rez et b = Imz.25/73D. CransacAnalyse

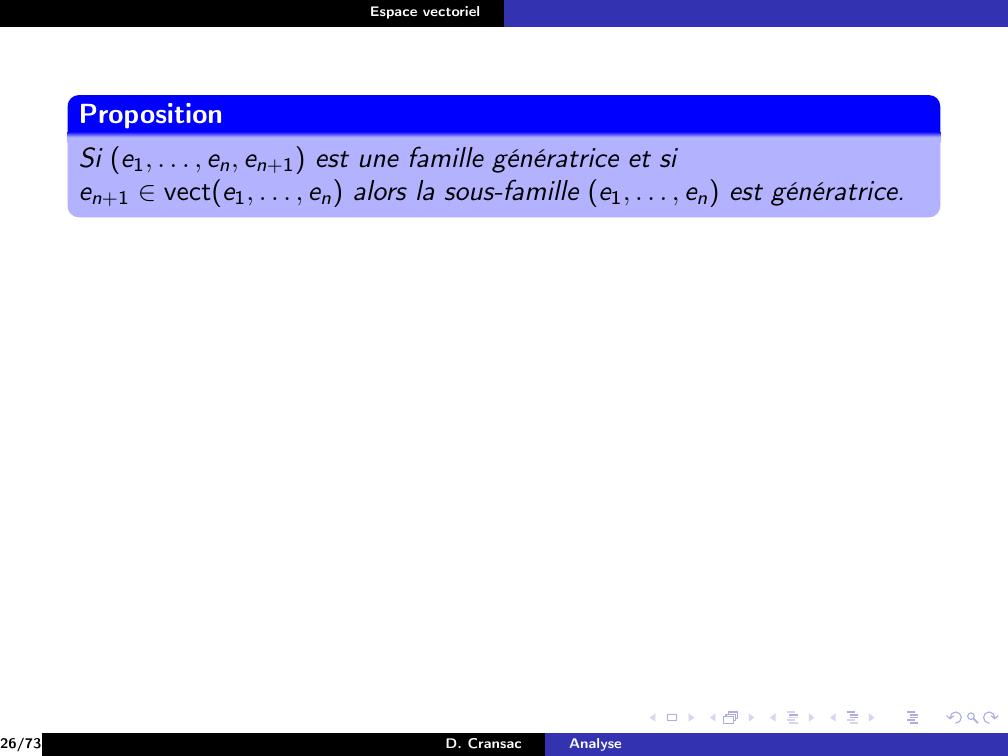
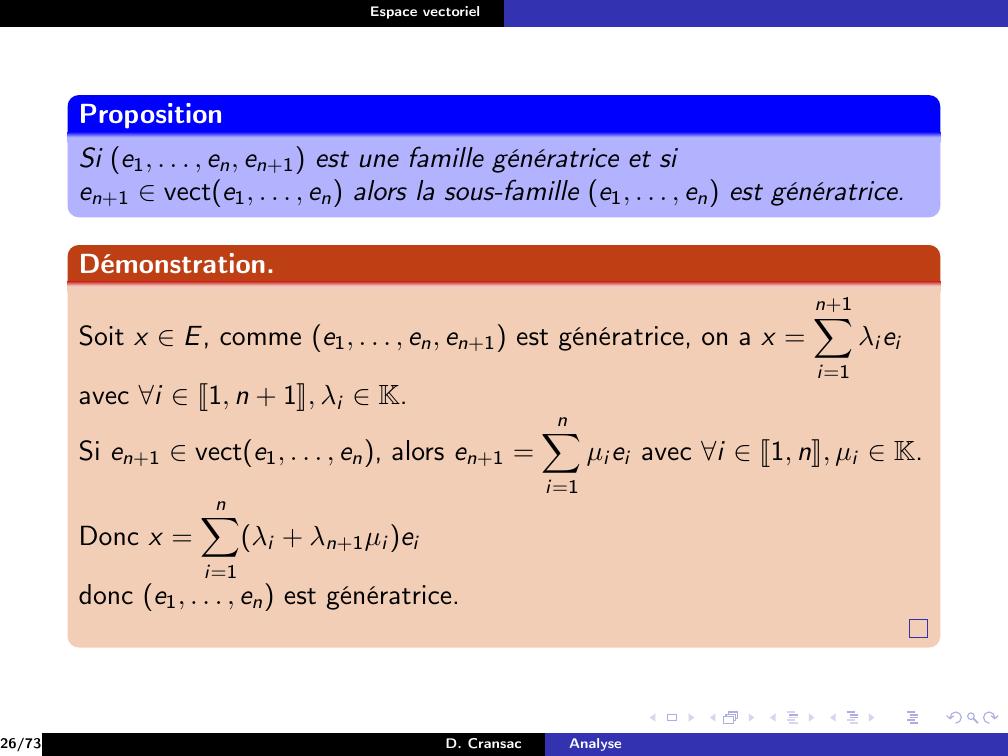
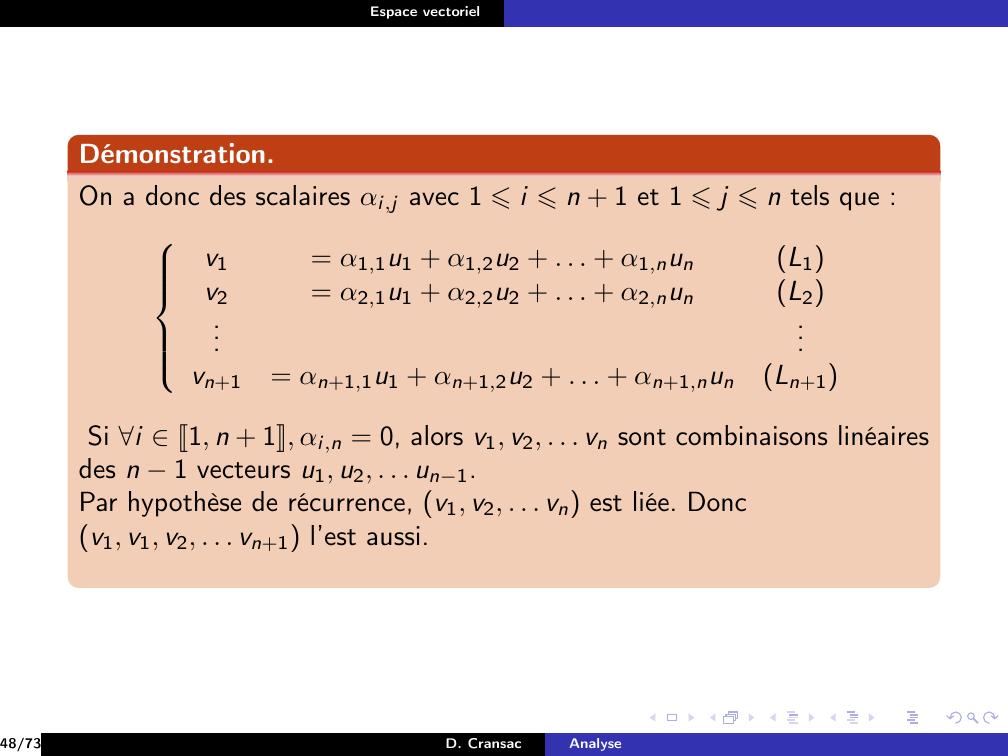
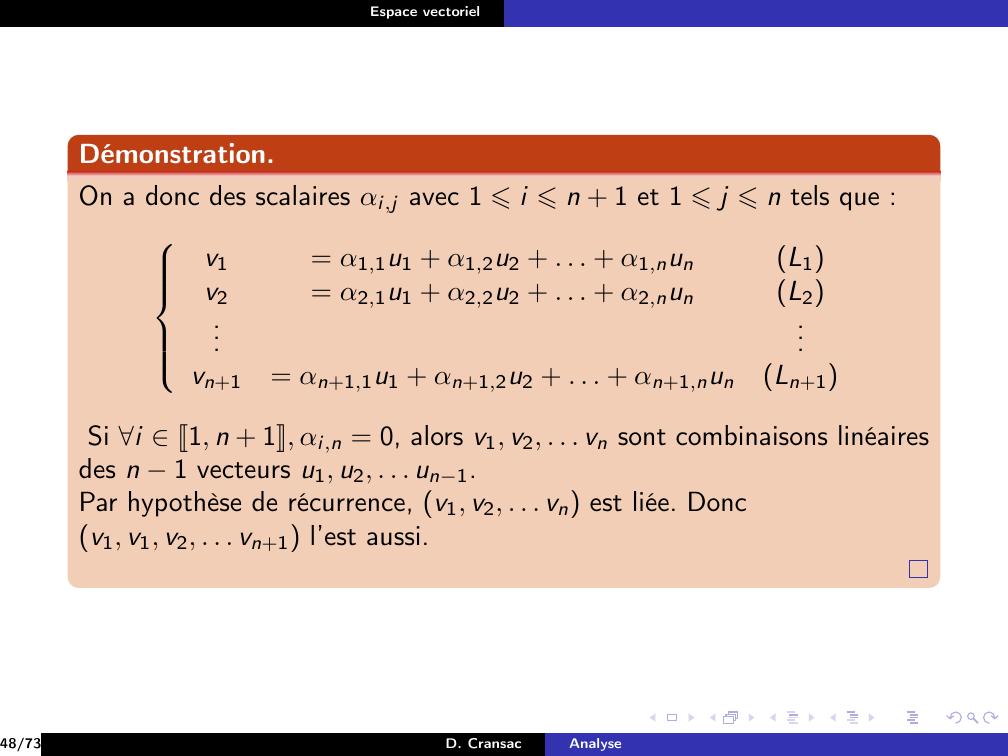
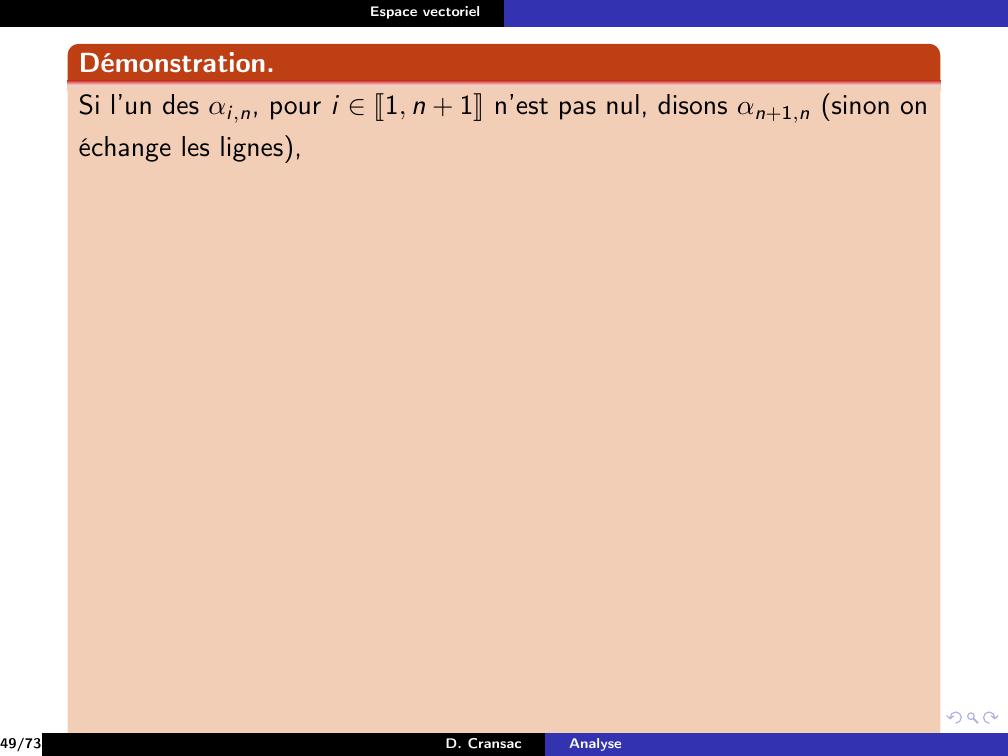
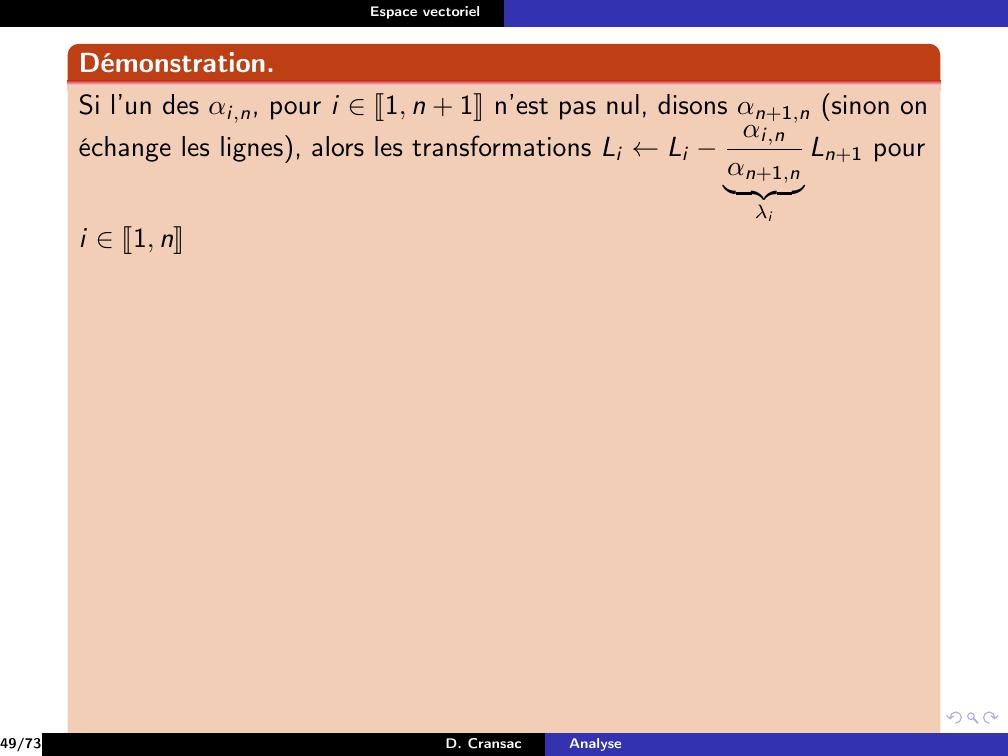
Page 157 : Espace vectorielPropositionSi e1, . . . , en, en+1 est une famille génératrice et sien+1 vecte1, . . . , en alors la sous-famille e1, . . . , en est génératrice.26/73D. CransacAnalyse

Page 158 : Espace vectorielPropositionSi e1, . . . , en, en+1 est une famille génératrice et sien+1 vecte1, . . . , en alors la sous-famille e1, . . . , en est génératrice.Démonstration.Soit x E, comme e1, . . . , en, en+1 est génératrice, on a x =n+1Xi=1λieiavec i J1, n + 1K, λi K.Si en+1 vecte1, . . . , en, alors en+1 =nXi=1µiei avec i J1, nK, µi K.Donc x =nXi=1λi + λn+1µieidonc e1, . . . , en est génératrice.26/73D. CransacAnalyse

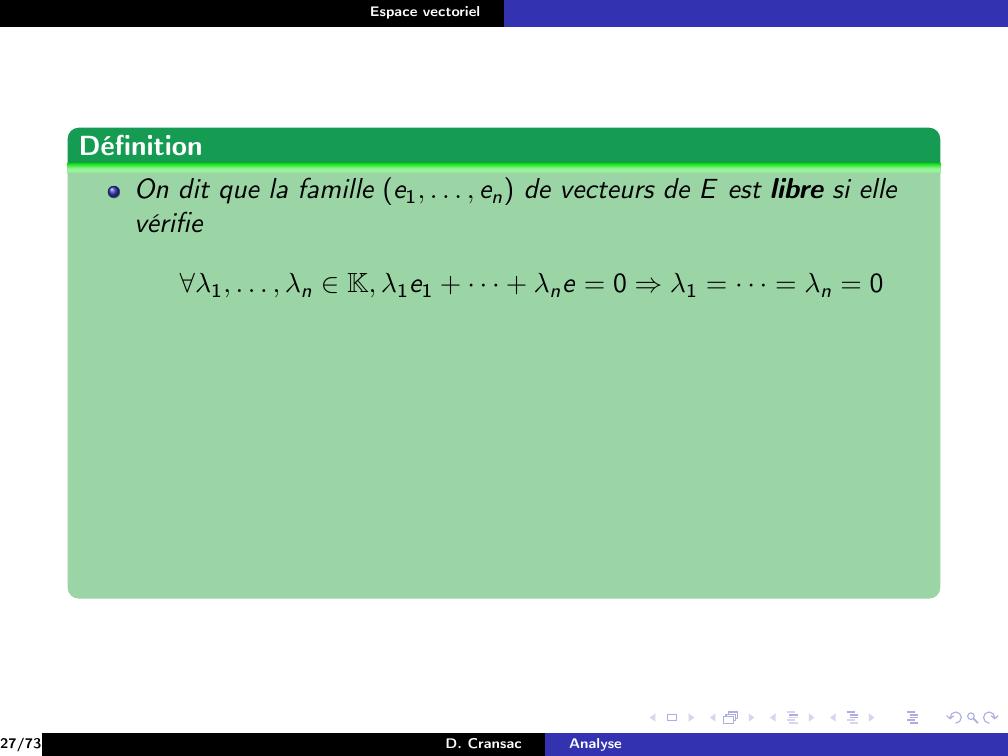
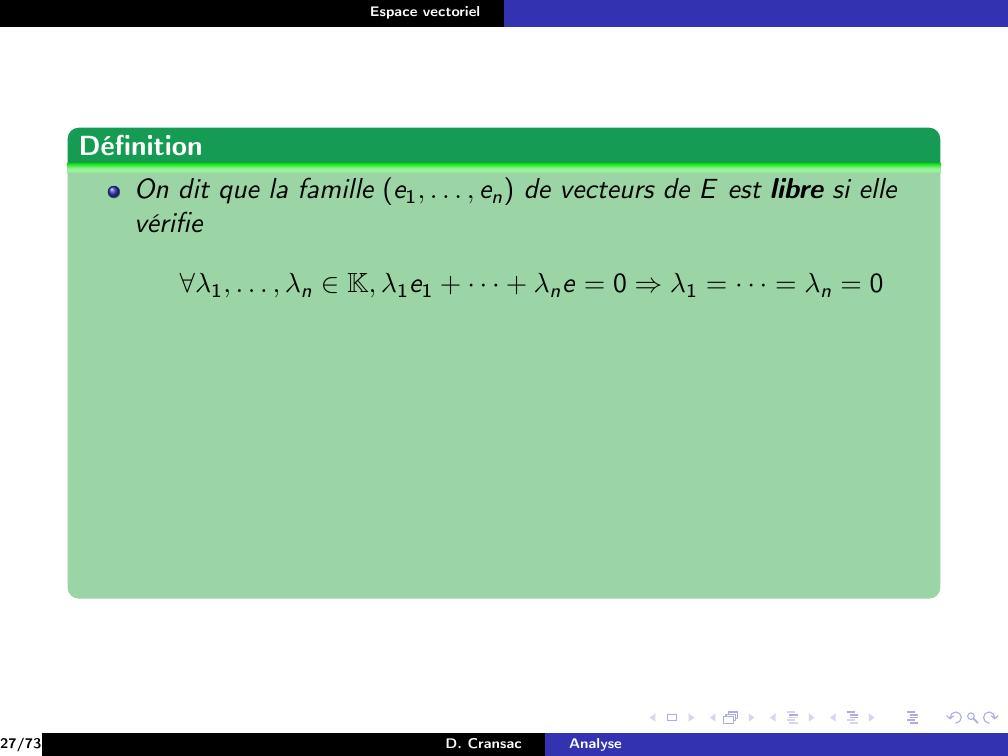
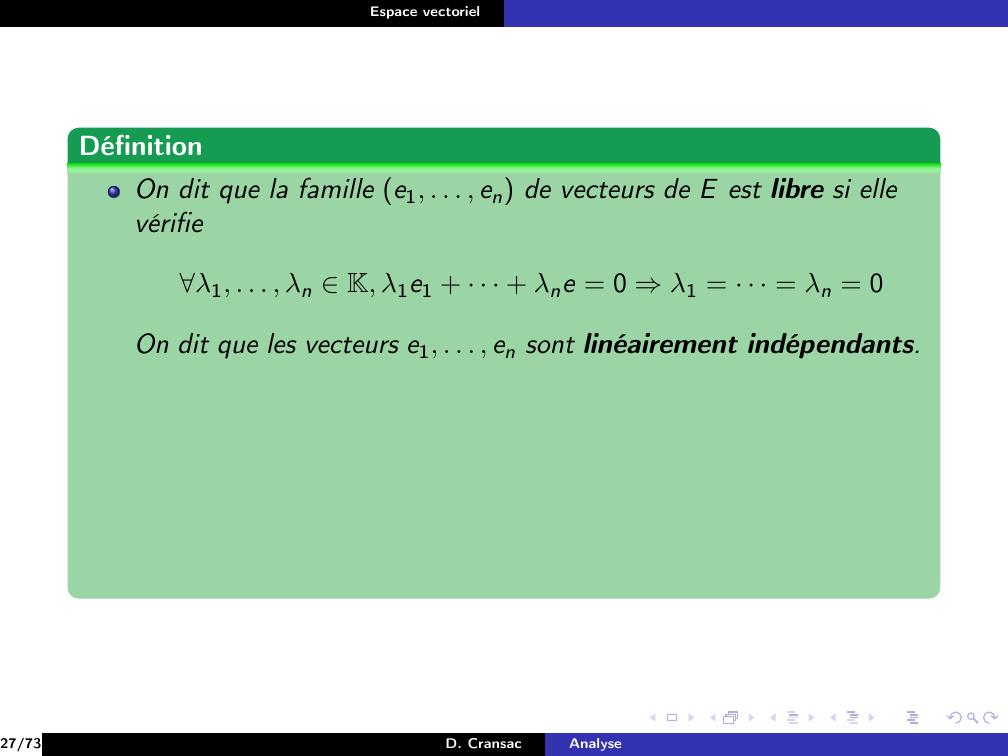
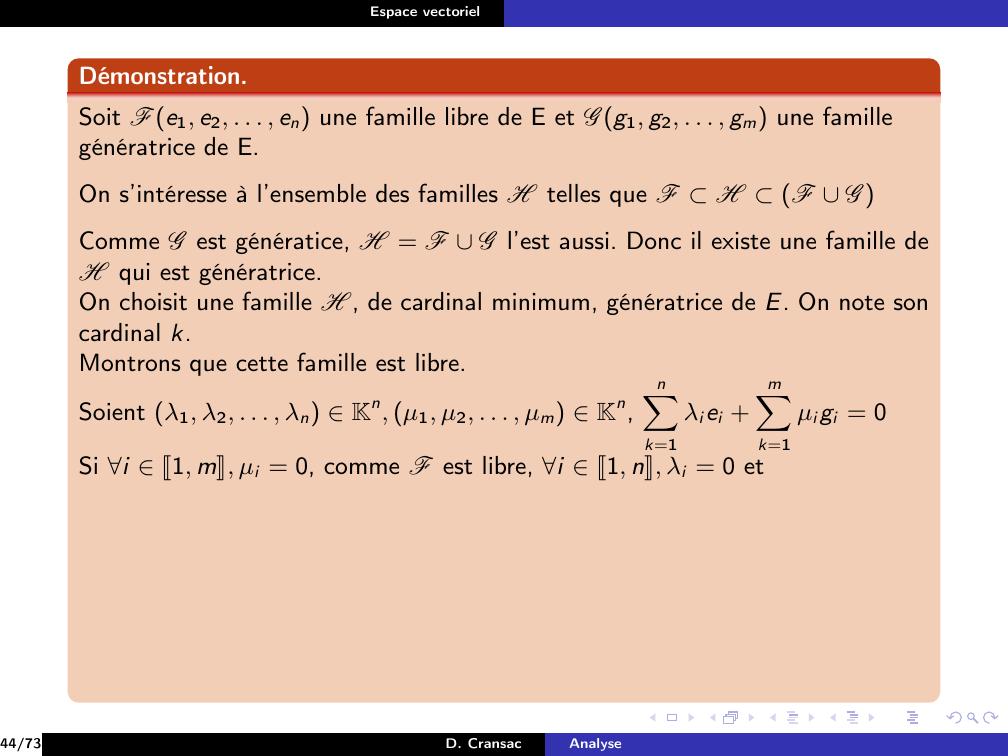
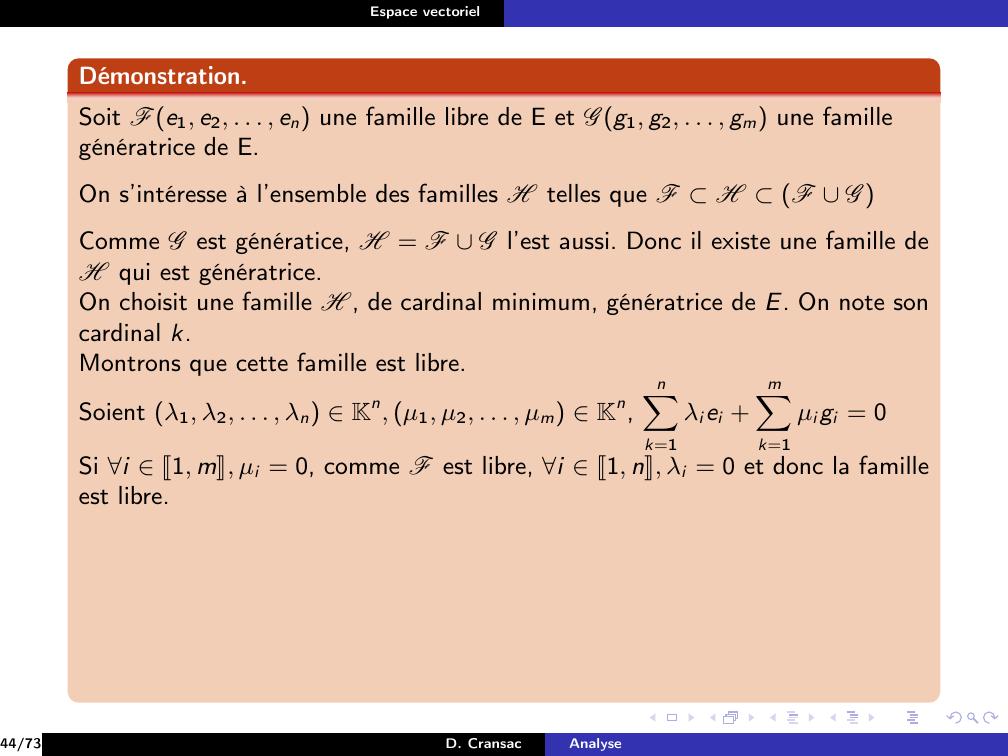
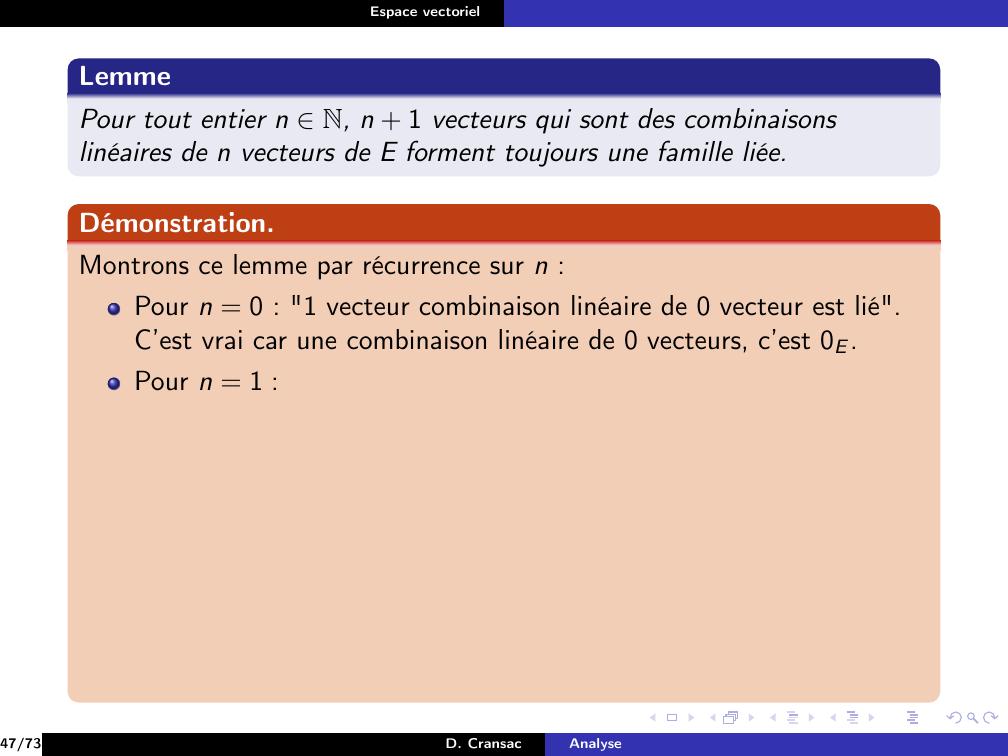
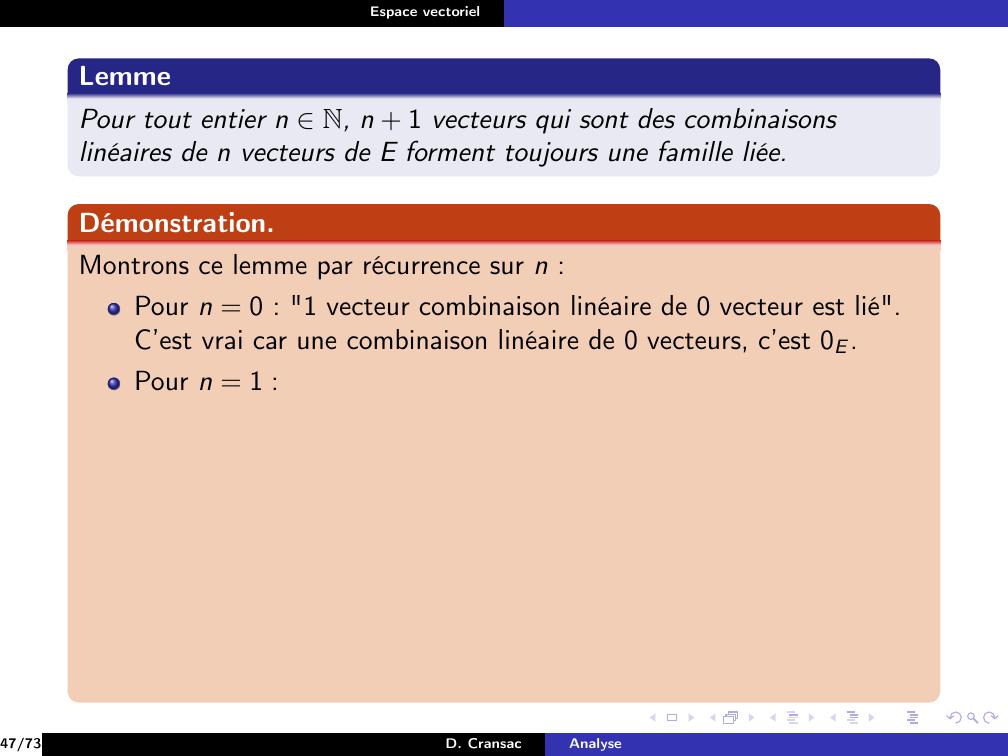
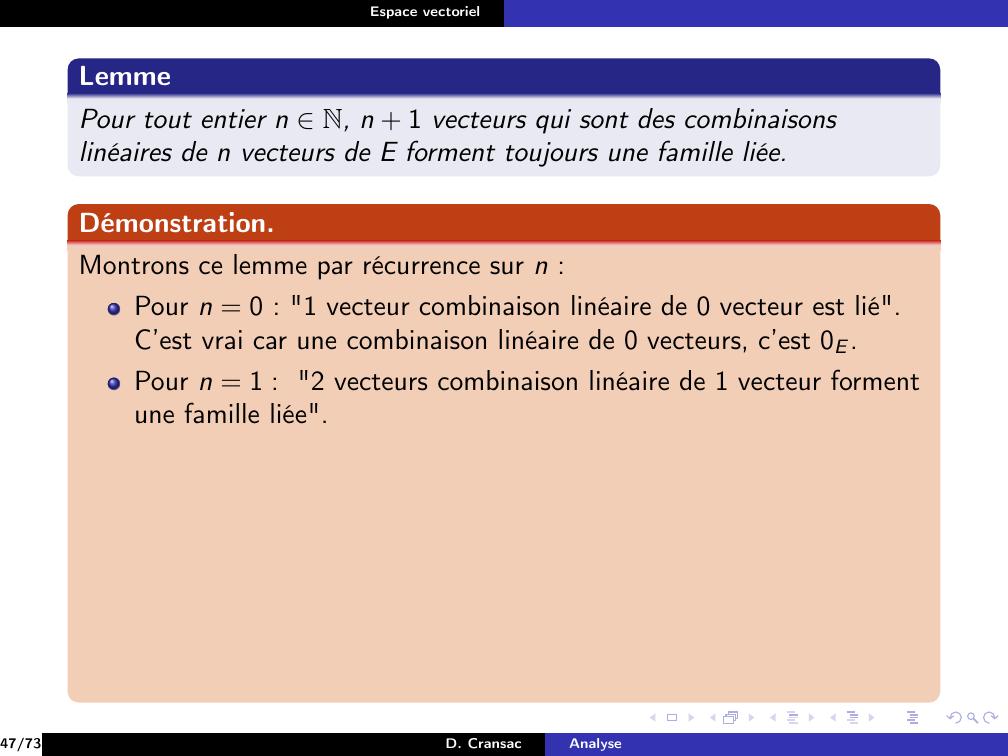
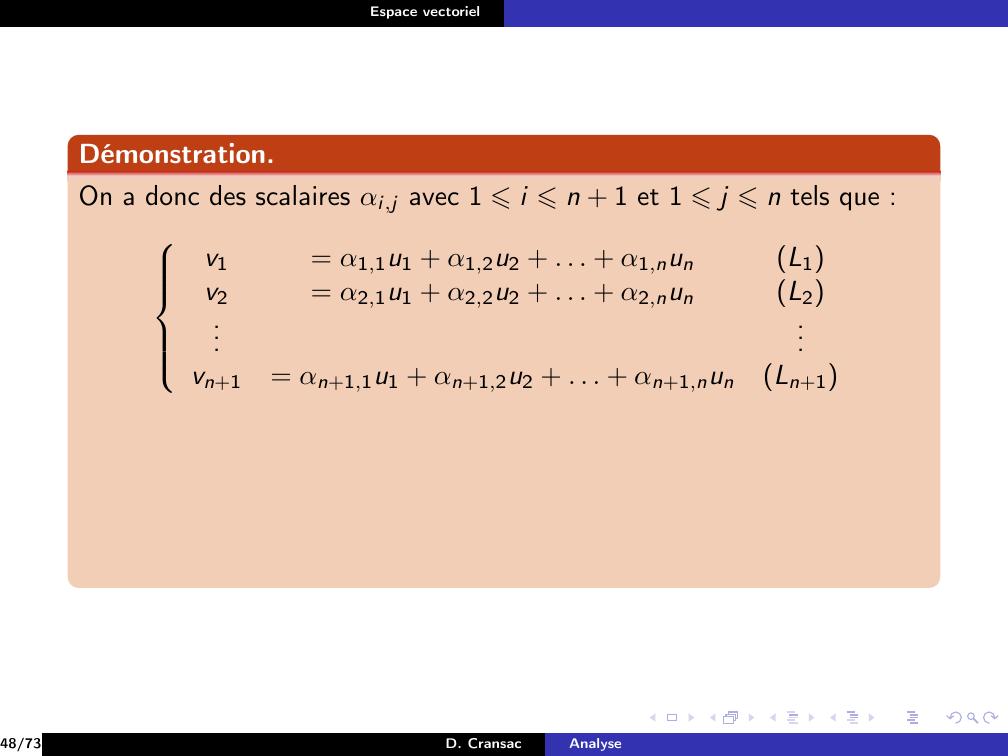
Page 159 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 027/73D. CransacAnalyse

Page 160 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 027/73D. CransacAnalyse

Page 161 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 0On dit que les vecteurs e1, . . . , en sont linéairement indépendants.27/73D. CransacAnalyse

Page 162 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 0On dit que les vecteurs e1, . . . , en sont linéairement indépendants.On dit que la famille e1, . . . , en est liée si elle n’est pas libre ce quisignifieλ1, . . . , λn K, λ1e1 + . . . λnen = 0 et λ1, . . . , λn ̸= 0, . . . , 027/73D. CransacAnalyse

Page 163 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 0On dit que les vecteurs e1, . . . , en sont linéairement indépendants.On dit que la famille e1, . . . , en est liée si elle n’est pas libre ce quisignifieλ1, . . . , λn K, λ1e1 + . . . λnen = 0 et λ1, . . . , λn ̸= 0, . . . , 027/73D. CransacAnalyse

Page 164 : Espace vectorielDéfinitionOn dit que la famille e1, . . . , en de vecteurs de E est libre si ellevérifieλ1, . . . , λn K, λ1e1 + · · · + λne = 0 ⇒λ1 = · · · = λn = 0On dit que les vecteurs e1, . . . , en sont linéairement indépendants.On dit que la famille e1, . . . , en est liée si elle n’est pas libre ce quisignifieλ1, . . . , λn K, λ1e1 + . . . λnen = 0 et λ1, . . . , λn ̸= 0, . . . , 0Une égalité λ1e1 + · · · + λnen = 0 avec λ1, . . . , λn non tous nuls estappelée relation linéaire sur les vecteurs e1, . . . , en.27/73D. CransacAnalyse

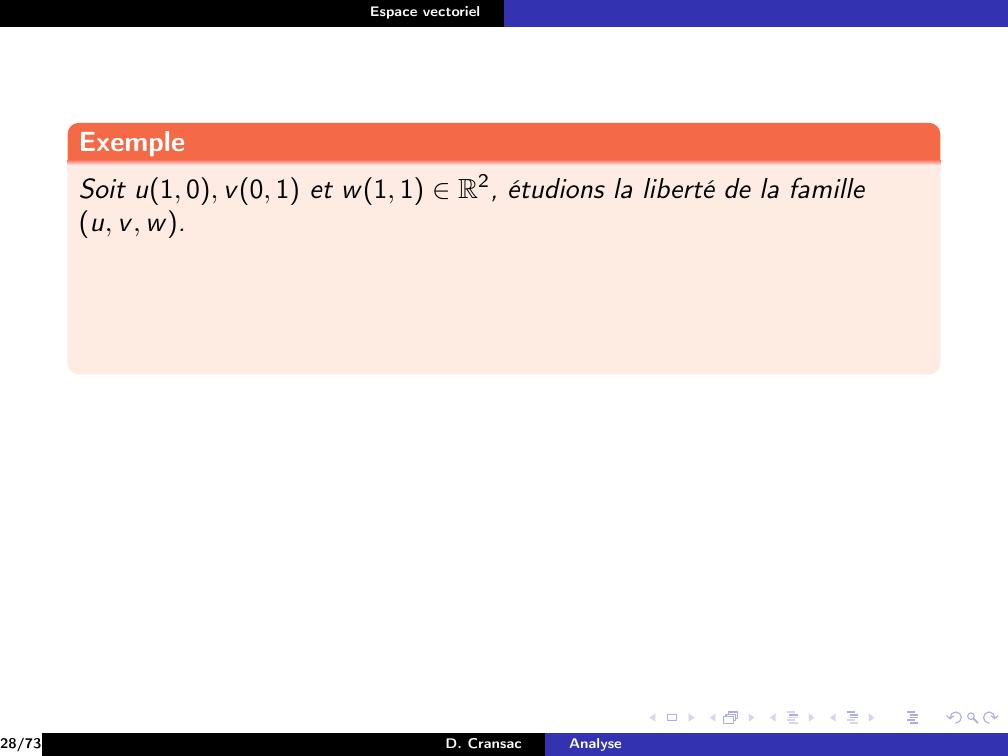
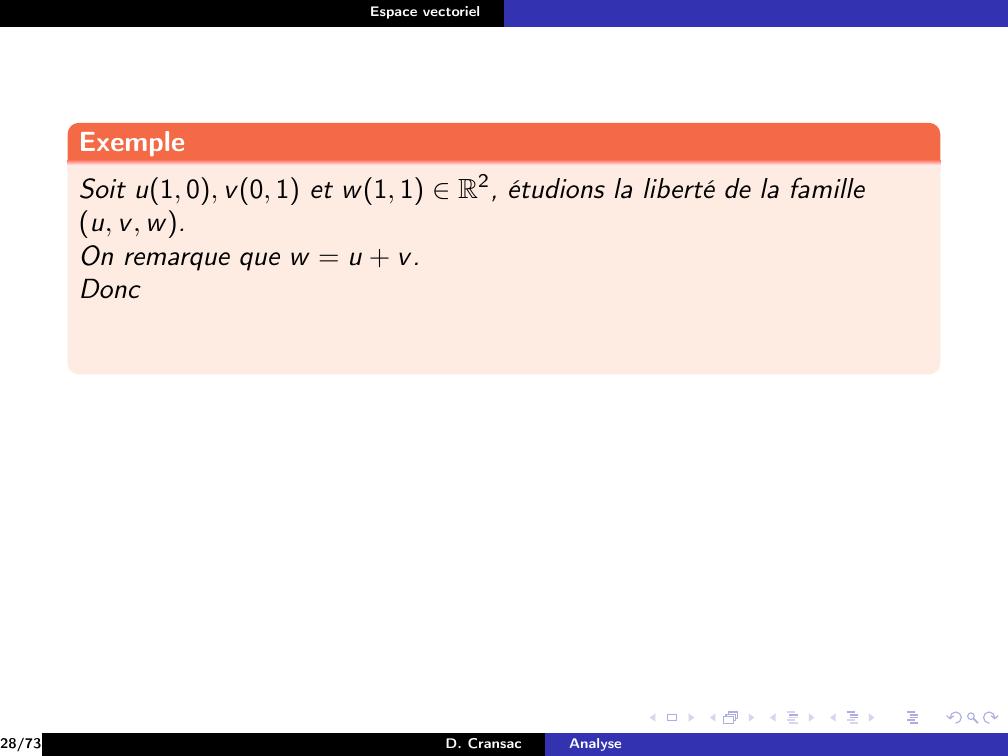
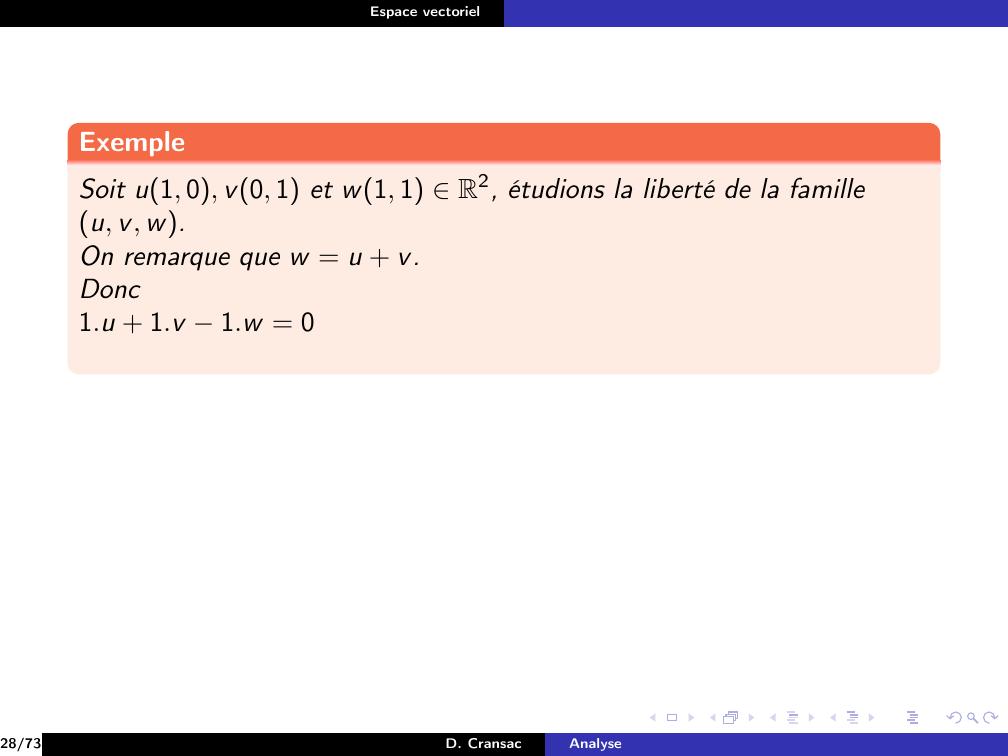
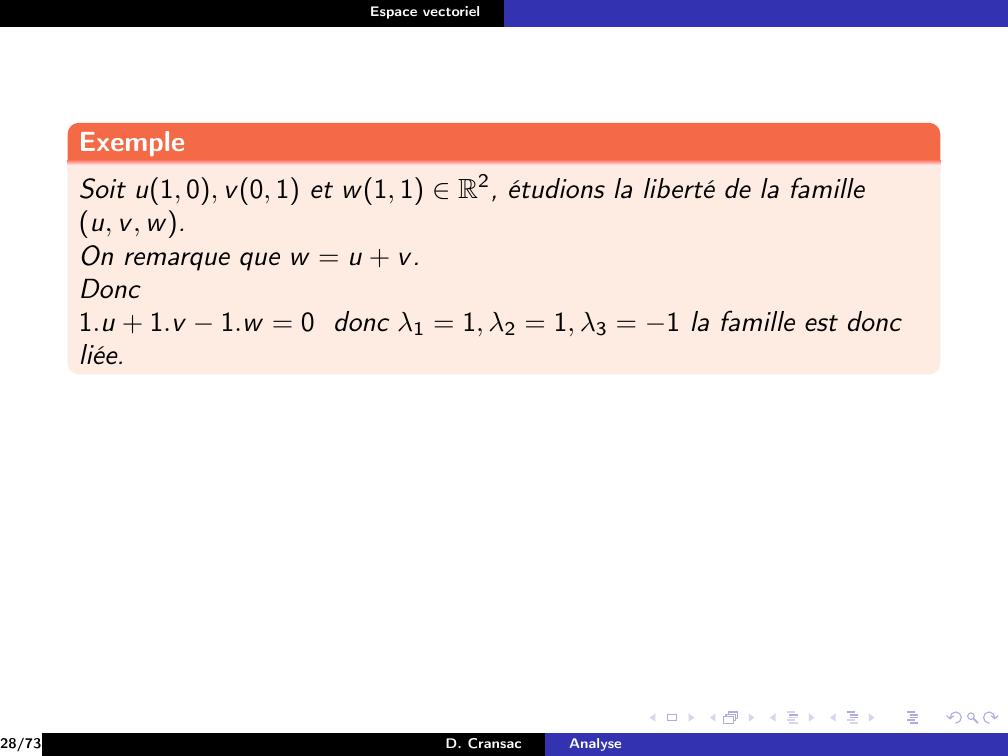
Page 165 : Espace vectorielExempleSoit u1, 0, v0, 1 et w1, 1 R2, étudions la liberté de la familleu, v, w.28/73D. CransacAnalyse

Page 166 : Espace vectorielExempleSoit u1, 0, v0, 1 et w1, 1 R2, étudions la liberté de la familleu, v, w.On remarque que w = u + v.Donc28/73D. CransacAnalyse

Page 167 : Espace vectorielExempleSoit u1, 0, v0, 1 et w1, 1 R2, étudions la liberté de la familleu, v, w.On remarque que w = u + v.Donc1.u + 1.v 1.w = 028/73D. CransacAnalyse

Page 168 : Espace vectorielExempleSoit u1, 0, v0, 1 et w1, 1 R2, étudions la liberté de la familleu, v, w.On remarque que w = u + v.Donc1.u + 1.v 1.w = 0 donc λ1 = 1, λ2 = 1, λ3 = 1 la famille est doncliée.28/73D. CransacAnalyse

Page 169 : Espace vectorielExempleSoit u1, 0, v0, 1 et w1, 1 R2, étudions la liberté de la familleu, v, w.On remarque que w = u + v.Donc1.u + 1.v 1.w = 0 donc λ1 = 1, λ2 = 1, λ3 = 1 la famille est doncliée.PropositionSoient n ⩾2 et e1, . . . , en une famille de vecteurs de E.On a une équivalence entre :e1, . . . , en est liée.L’un des vecteurs e1, . . . , en est combinaison linéaire des autres.28/73D. CransacAnalyse

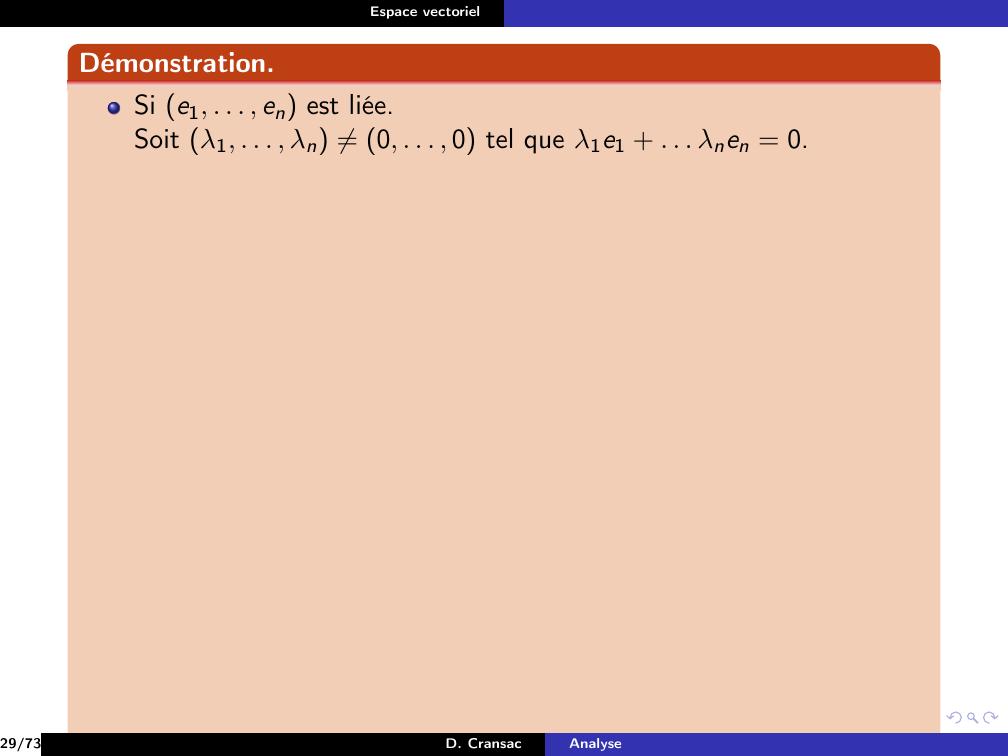
Page 170 : Espace vectorielDémonstration.Si e1, . . . , en est liée.29/73D. CransacAnalyse

Page 171 : Espace vectorielDémonstration.Si e1, . . . , en est liée.29/73D. CransacAnalyse

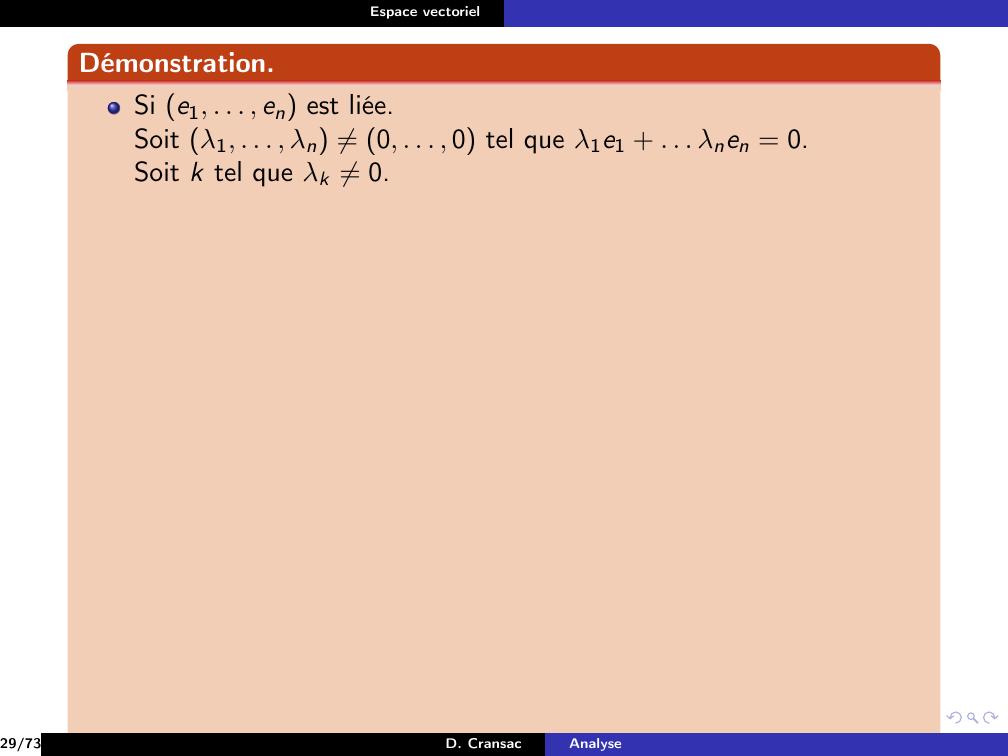
Page 172 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.29/73D. CransacAnalyse

Page 173 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.29/73D. CransacAnalyse

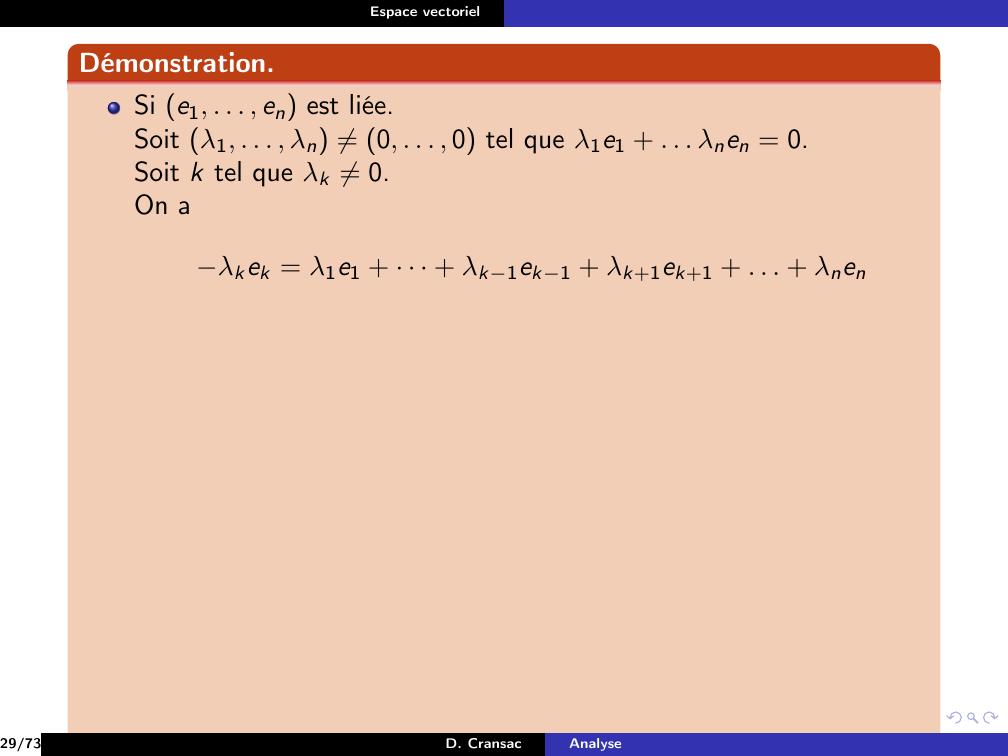
Page 174 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnen29/73D. CransacAnalyse

Page 175 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλken29/73D. CransacAnalyse

Page 176 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.29/73D. CransacAnalyse

Page 177 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.Supposons qu’un vecteur soit une combinaison linéaires des autresvecteurs.29/73D. CransacAnalyse

Page 178 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.Supposons qu’un vecteur soit une combinaison linéaires des autresvecteurs.29/73D. CransacAnalyse

Page 179 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.Supposons qu’un vecteur soit une combinaison linéaires des autresvecteurs. Alors il existe k J1, nK, tel queek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnen29/73D. CransacAnalyse

Page 180 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.Supposons qu’un vecteur soit une combinaison linéaires des autresvecteurs. Alors il existe k J1, nK, tel queek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenIl vient λ1e1 + · · · + λk1ek1 + 1ek + λk+1ek+1 + . . . + λnen = 029/73D. CransacAnalyse

Page 181 : Espace vectorielDémonstration.Si e1, . . . , en est liée.Soit λ1, . . . , λn ̸= 0, . . . , 0 tel que λ1e1 + . . . λnen = 0.Soit k tel que λk ̸= 0.On aλkek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenalors ek = λ1λke1 + · · · + λk1λkek1 + λk+1λkek+1 + . . . + λnλkendonc ek est une combinaison linéaire des autres vecteurs.Supposons qu’un vecteur soit une combinaison linéaires des autresvecteurs. Alors il existe k J1, nK, tel queek = λ1e1 + · · · + λk1ek1 + λk+1ek+1 + . . . + λnenIl vient λ1e1 + · · · + λk1ek1 + 1ek + λk+1ek+1 + . . . + λnen = 0En remarquant que λ1, . . . , λk1, 1, λk+1, . . . , λn ̸= 0, . . . , 0,on peut conclure que la famille e1, . . . , en est liée.29/73D. CransacAnalyse

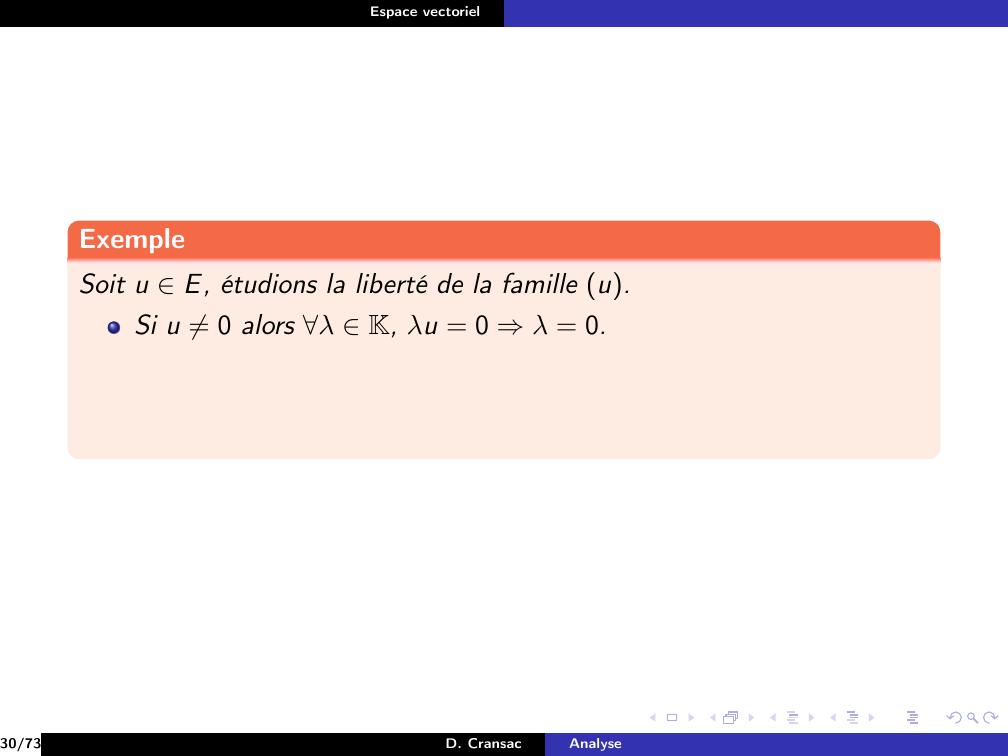
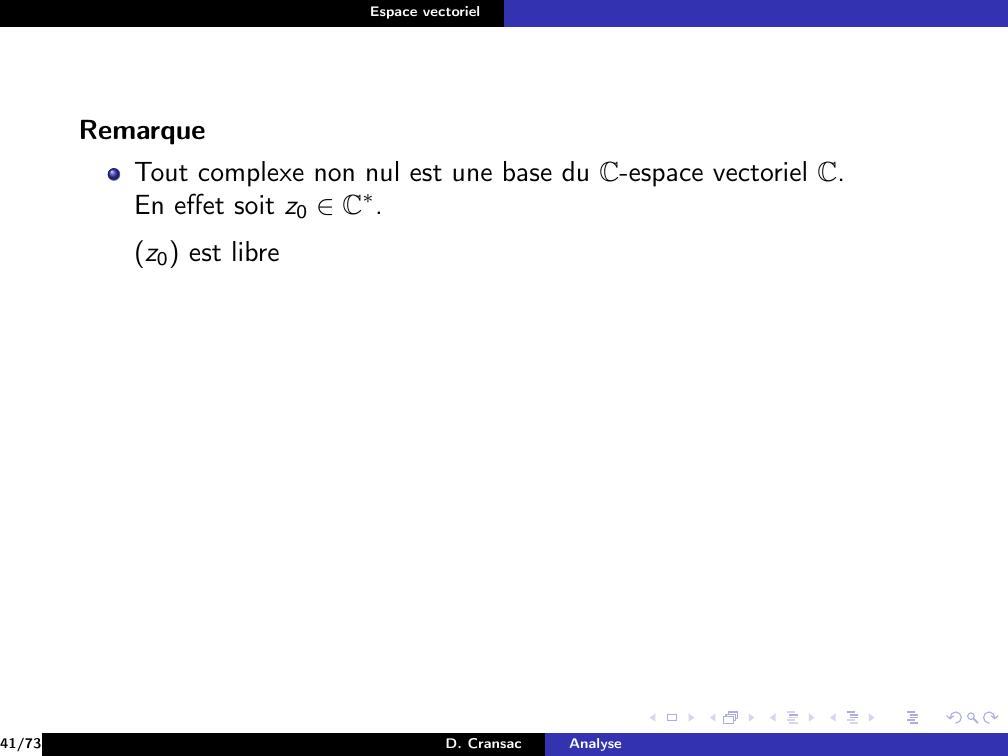
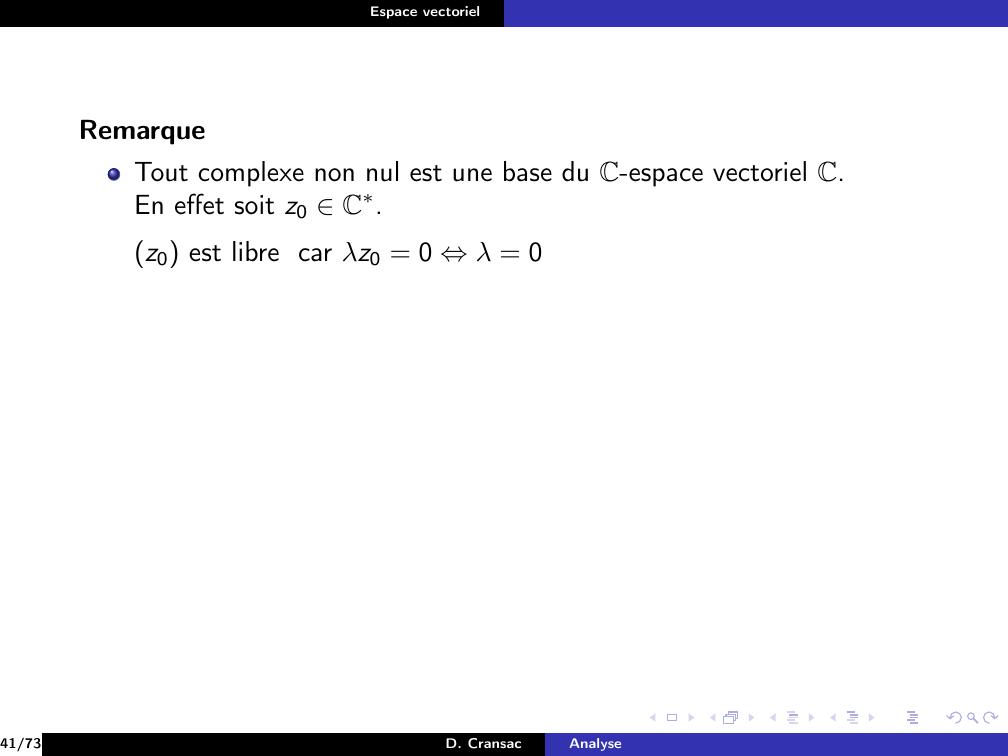
Page 182 : Espace vectorielExempleSoit u E, étudions la liberté de la famille u.Si u ̸= 0 alors λ K, λu = 0 ⇒λ = 0.30/73D. CransacAnalyse

Page 183 : Espace vectorielExempleSoit u E, étudions la liberté de la famille u.Si u ̸= 0 alors λ K, λu = 0 ⇒λ = 0.30/73D. CransacAnalyse

Page 184 : Espace vectorielExempleSoit u E, étudions la liberté de la famille u.Si u ̸= 0 alors λ K, λu = 0 ⇒λ = 0.Par suite, la famille u est libre.Si u = 0E alors on peut écrire λu = 0 avec λ = 1 ̸= 0.Par suite, la famillle 0E est liée.30/73D. CransacAnalyse

Page 185 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.31/73D. CransacAnalyse

Page 186 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.Deux vecteurs u et v sont dits colinéaires si l’un des deux estcolinéaire à l’autre.31/73D. CransacAnalyse

Page 187 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.Deux vecteurs u et v sont dits colinéaires si l’un des deux estcolinéaire à l’autre.31/73D. CransacAnalyse

Page 188 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.Deux vecteurs u et v sont dits colinéaires si l’un des deux estcolinéaire à l’autre.Attention31/73D. CransacAnalyse

Page 189 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.Deux vecteurs u et v sont dits colinéaires si l’un des deux estcolinéaire à l’autre.Attentionu est colinéaire à v n’équivaut pas à v est colinéaire à u.31/73D. CransacAnalyse

Page 190 : Espace vectorielDéfinition Cas particulier de deux vecteurs liésUn vecteur u est dit colinéaire à un autre vecteur v de E s’il existeα K tel que u = αv.Deux vecteurs u et v sont dits colinéaires si l’un des deux estcolinéaire à l’autre.Attentionu est colinéaire à v n’équivaut pas à v est colinéaire à u.En effet, le vecteur nul est colinéaire à tout vecteur mais tout vecteurn’est pas colinéaire au vecteur nul.En effet u E, 0 = 0u donc 0 est colinéaire à u.Mais u E, u ̸= 0 on a u ̸= α0 donc u n’est pas colinéaire à 0.31/73D. CransacAnalyse

Page 191 : Espace vectorielExempleSoient u, v E 2.u, v est liée,si et seulement si,α K, u = αv ou β K, v = βu.32/73D. CransacAnalyse

Page 192 : Espace vectorielExempleSoient u, v E 2.u, v est liée,si et seulement si,α K, u = αv ou β K, v = βu.Ainsi, la famille u, v est liée, si et seulement si, u et v sont colinéaires.32/73D. CransacAnalyse

Page 193 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.33/73D. CransacAnalyse

Page 194 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0R3 ⇔α + β + γ = 012α β + γ = 02α + β = 0333/73D. CransacAnalyse

Page 195 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0R3 ⇔α + β + γ = 012α β + γ = 02α + β = 03L’équation 1 3 implique γ = 0.33/73D. CransacAnalyse

Page 196 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0R3 ⇔α + β + γ = 012α β + γ = 02α + β = 03L’équation 1 3 implique γ = 0.L’équation 2 + 3 permet de conclure que α = 0 donc β = 033/73D. CransacAnalyse

Page 197 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0R3 ⇔α + β + γ = 012α β + γ = 02α + β = 03L’équation 1 3 implique γ = 0.L’équation 2 + 3 permet de conclure que α = 0 donc β = 0On obtient donc αu + βv + γw = 0 ⇔α = β = γ = 0,33/73D. CransacAnalyse

Page 198 : Espace vectorielExemple famille libreDans E = R3, considérons les vecteursu = 1, 2, 1, v = 1, 1, 1, w = 1, 1, 0et la familleF = u, v, wEtudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0R3 ⇔α + β + γ = 012α β + γ = 02α + β = 03L’équation 1 3 implique γ = 0.L’équation 2 + 3 permet de conclure que α = 0 donc β = 0On obtient donc αu + βv + γw = 0 ⇔α = β = γ = 0, la famille F estdonc libre.33/73D. CransacAnalyse

Page 199 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.Solution34/73D. CransacAnalyse

Page 200 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=0334/73D. CransacAnalyse

Page 201 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β34/73D. CransacAnalyse

Page 202 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β L’équation 3 permetde déduire que γ = β34/73D. CransacAnalyse

Page 203 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β L’équation 3 permetde déduire que γ = β L’équation 2 revient 2β β β = 0 qui esttoujours vraie.34/73D. CransacAnalyse

Page 204 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β L’équation 3 permetde déduire que γ = β L’équation 2 revient 2β β β = 0 qui esttoujours vraie. Le système est donc compatible.34/73D. CransacAnalyse

Page 205 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β L’équation 3 permetde déduire que γ = β L’équation 2 revient 2β β β = 0 qui esttoujours vraie. Le système est donc compatible.On a donc β R, 2βu + βv βw = 0 donc, pour β = 1,2u + v w = 034/73D. CransacAnalyse

Page 206 : Espace vectorielExemple famille liéeDans E = R3, considérons les vecteursu = 1, 1, 0, v = 2, 1, 1, w = 0, 1, 1et la famille F = u, v, w.Etudions la liberté de la famille F.SolutionSoient α, β, γ R.αu + βv + γw = 0 ⇔α+2β=01αβ+γ=02β+γ=03L’équation 1 permet de déduire que α = 2β L’équation 3 permetde déduire que γ = β L’équation 2 revient 2β β β = 0 qui esttoujours vraie. Le système est donc compatible.On a donc β R, 2βu + βv βw = 0 donc, pour β = 1,2u + v w = 0On en déduit que la famille F est liée.34/73D. CransacAnalyse

Page 207 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.Solution35/73D. CransacAnalyse

Page 208 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ R35/73D. CransacAnalyse

Page 209 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.35/73D. CransacAnalyse

Page 210 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.35/73D. CransacAnalyse

Page 211 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.Pour x = π2 , on obtient l’équation α + γ = 02.35/73D. CransacAnalyse

Page 212 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.Pour x = π2 , on obtient l’équation α + γ = 02.Pour x = π, on obtient l’équation α β = 03.35/73D. CransacAnalyse

Page 213 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.Pour x = π2 , on obtient l’équation α + γ = 02.Pour x = π, on obtient l’équation α β = 03.35/73D. CransacAnalyse

Page 214 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.Pour x = π2 , on obtient l’équation α + γ = 02.Pour x = π, on obtient l’équation α β = 03.1 et 3 somme et différence donnent α = β = 0 et par 2 onobtient γ = 0.35/73D. CransacAnalyse

Page 215 : Espace vectorielExempleDans E = FR, R, considérons les fonctionsf : x 7→1,g : x 7→cosx,h : x 7→sinxet montrons que la famille f , g, h est libre.SolutionSoient α, β, γ RSupposons αf + βg + γh = 0.Pour tout x R, on a : α + βcosx + γsinx = 0.Pour x = 0, on obtient l’équation α + β = 01.Pour x = π2 , on obtient l’équation α + γ = 02.Pour x = π, on obtient l’équation α β = 03.1 et 3 somme et différence donnent α = β = 0 et par 2 onobtient γ = 0.Finalement la famille f , g, h est libre.35/73D. CransacAnalyse

Page 216 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.36/73D. CransacAnalyse

Page 217 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.36/73D. CransacAnalyse

Page 218 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.36/73D. CransacAnalyse

Page 219 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.36/73D. CransacAnalyse

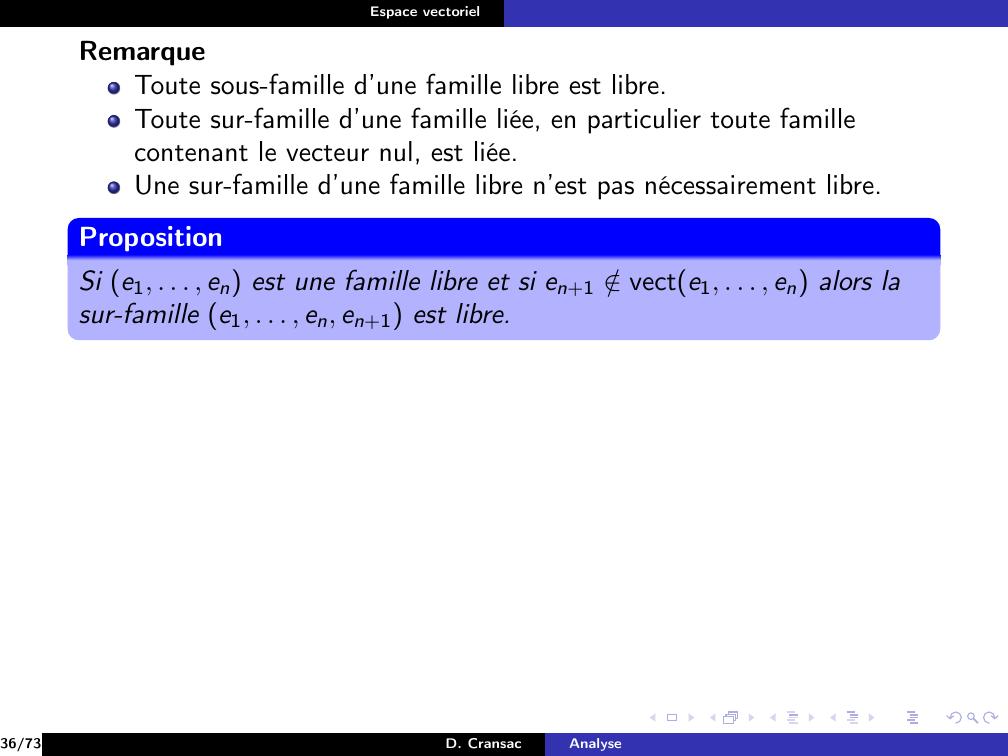
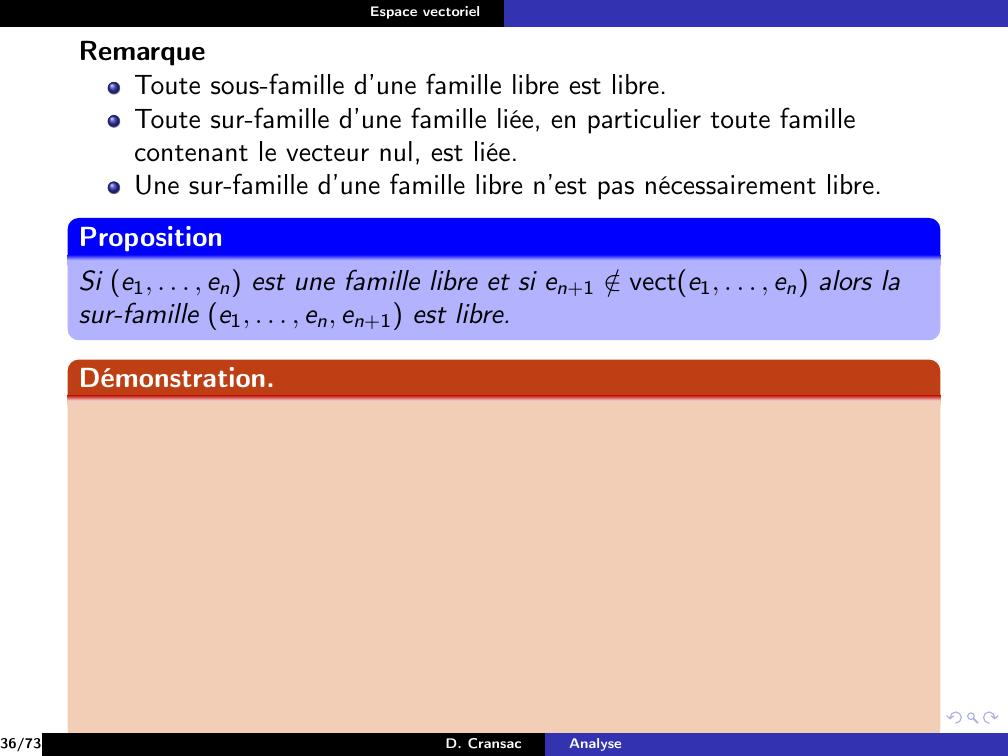
Page 220 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.36/73D. CransacAnalyse

Page 221 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.Démonstration.36/73D. CransacAnalyse

Page 222 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.Démonstration.Soient λ1, λ2, . . . , λn, λn+1 tels quen+1Xk=1λiei = 0.36/73D. CransacAnalyse

Page 223 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.Démonstration.Soient λ1, λ2, . . . , λn, λn+1 tels quen+1Xk=1λiei = 0.Si λn+1 ̸= 0, on peut écrire en+1 = n+1Xk=1λiλn+1ei ce qui signifierait queen+1 vecte1, . . . , en ce qui est faux donc λn+1 = 036/73D. CransacAnalyse

Page 224 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.Démonstration.Soient λ1, λ2, . . . , λn, λn+1 tels quen+1Xk=1λiei = 0.Si λn+1 ̸= 0, on peut écrire en+1 = n+1Xk=1λiλn+1ei ce qui signifierait queen+1 vecte1, . . . , en ce qui est faux donc λn+1 = 0doncnXk=1λiei = 0 et comme la famille est libre J1, nK, λi = 0.36/73D. CransacAnalyse

Page 225 : Espace vectorielRemarqueToute sous-famille d’une famille libre est libre.Toute sur-famille d’une famille liée, en particulier toute famillecontenant le vecteur nul, est liée.Une sur-famille d’une famille libre n’est pas nécessairement libre.PropositionSi e1, . . . , en est une famille libre et si en+1 /vecte1, . . . , en alors lasur-famille e1, . . . , en, en+1 est libre.Démonstration.Soient λ1, λ2, . . . , λn, λn+1 tels quen+1Xk=1λiei = 0.Si λn+1 ̸= 0, on peut écrire en+1 = n+1Xk=1λiλn+1ei ce qui signifierait queen+1 vecte1, . . . , en ce qui est faux donc λn+1 = 0doncnXk=1λiei = 0 et comme la famille est libre J1, nK, λi = 0.Donc la famille e1, . . . , en, en+1 est libre.36/73D. CransacAnalyse

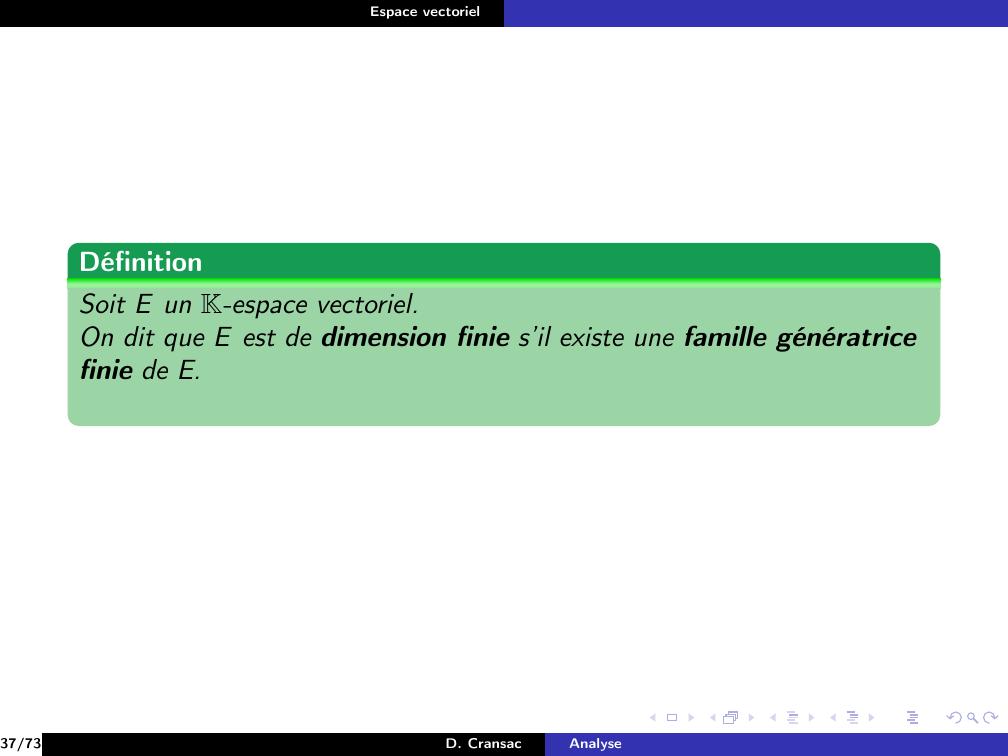
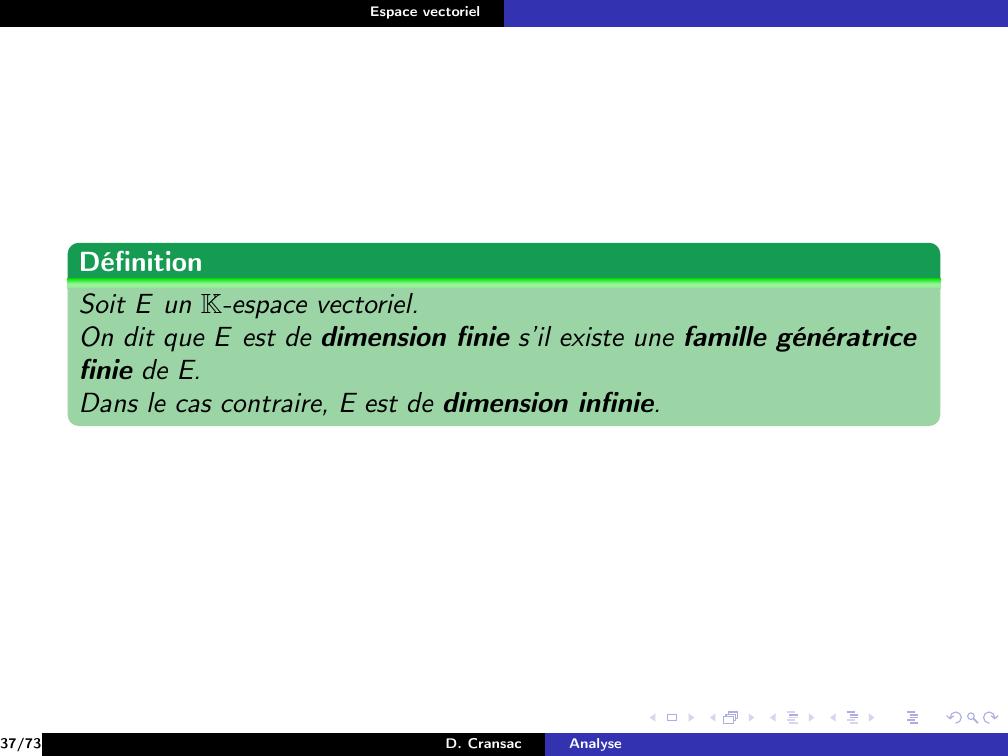
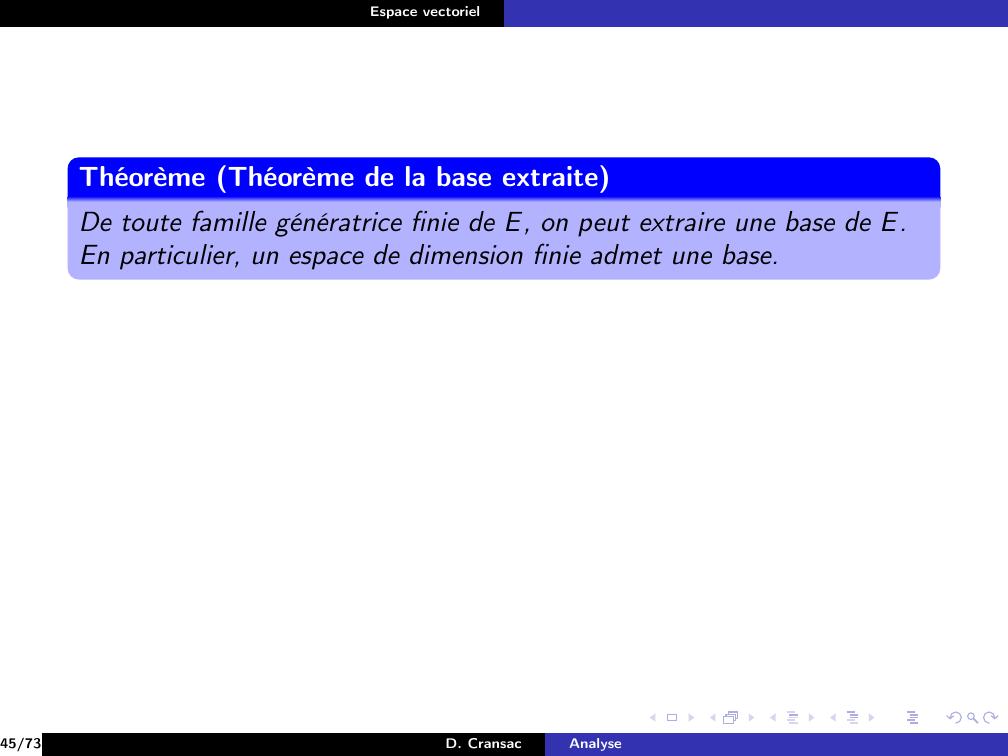
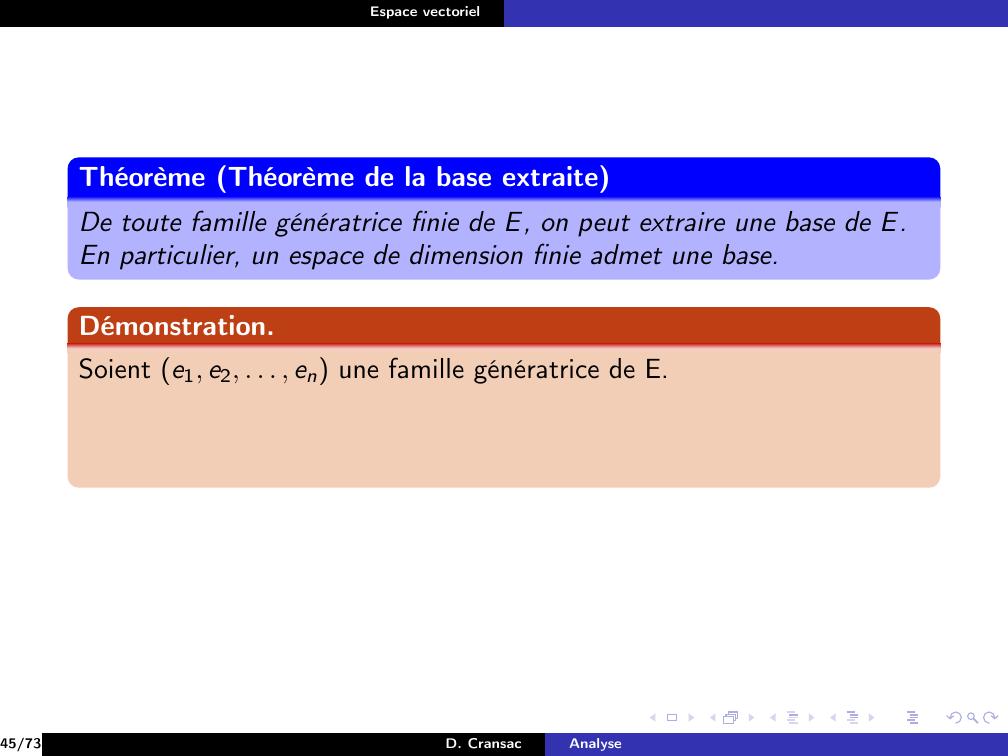
Page 226 : Espace vectorielDéfinitionSoit E un K-espace vectoriel.On dit que E est de dimension finie s’il existe une famille génératricefinie de E.37/73D. CransacAnalyse

Page 227 : Espace vectorielDéfinitionSoit E un K-espace vectoriel.On dit que E est de dimension finie s’il existe une famille génératricefinie de E.Dans le cas contraire, E est de dimension infinie.37/73D. CransacAnalyse

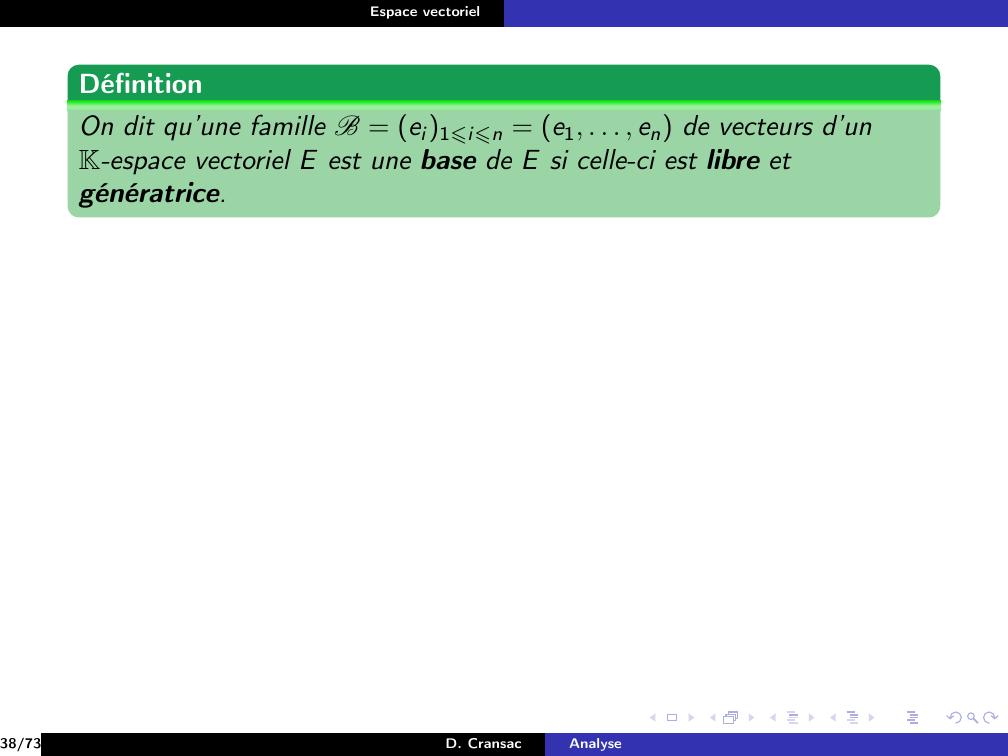
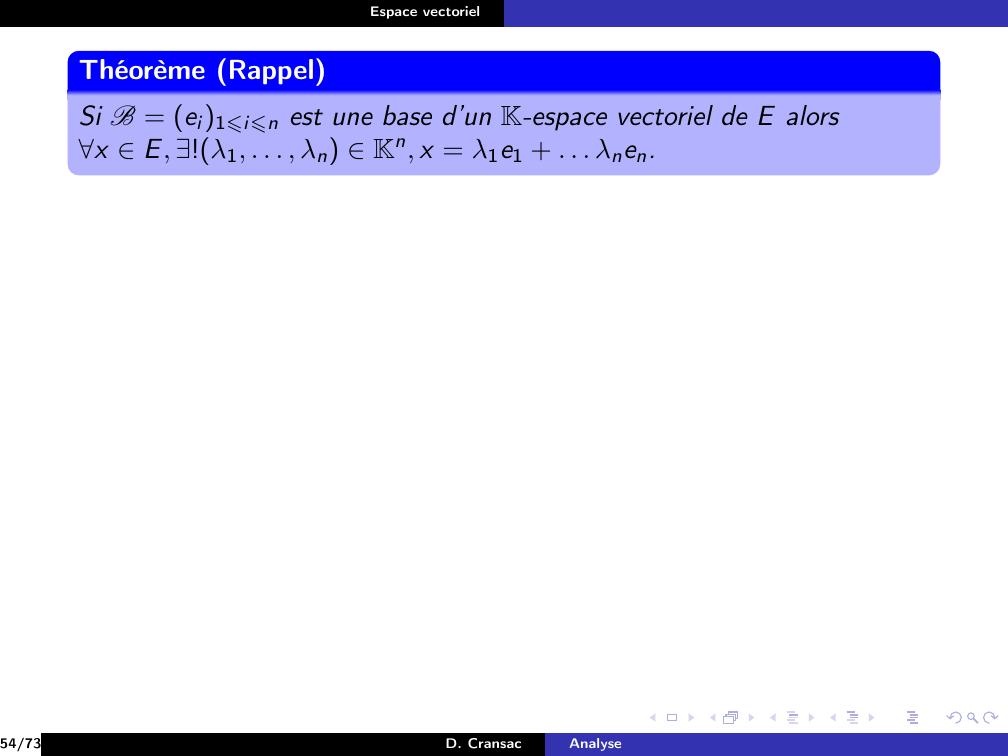
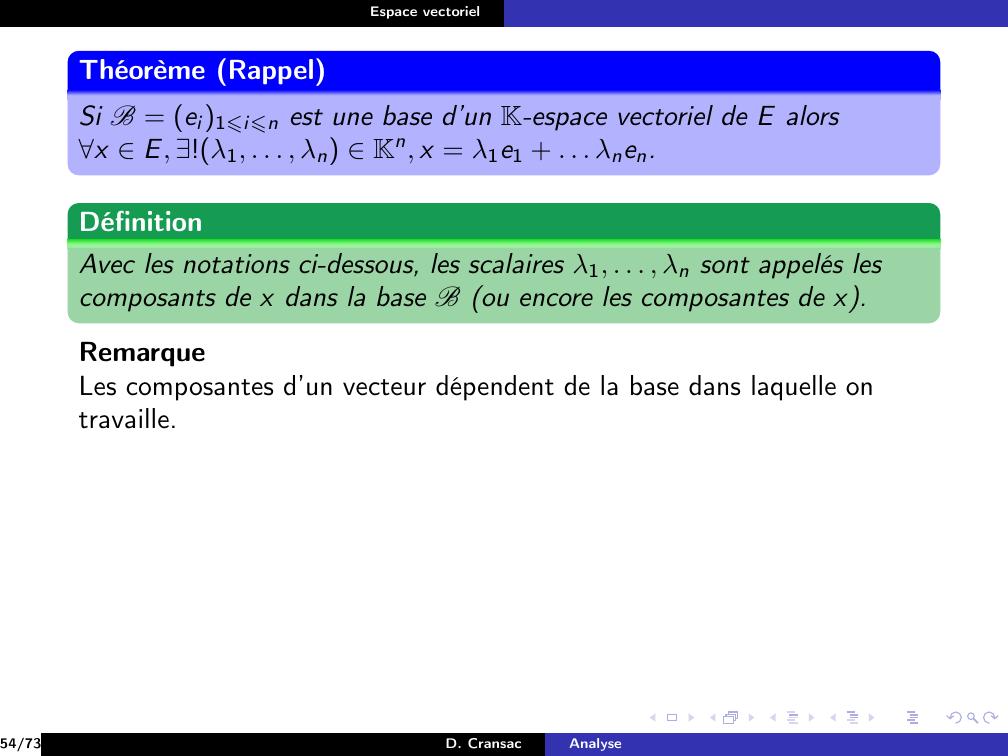
Page 228 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.38/73D. CransacAnalyse

Page 229 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 138/73D. CransacAnalyse

Page 230 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze338/73D. CransacAnalyse

Page 231 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze338/73D. CransacAnalyse

Page 232 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.38/73D. CransacAnalyse

Page 233 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 038/73D. CransacAnalyse

Page 234 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 038/73D. CransacAnalyse

Page 235 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 0 alors λ1, λ2, λ3 = 0, 0, 038/73D. CransacAnalyse

Page 236 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 0 alors λ1, λ2, λ3 = 0, 0, 0Donc λ1 = 0, λ2 = 0 et λ3 = 038/73D. CransacAnalyse

Page 237 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 0 alors λ1, λ2, λ3 = 0, 0, 0Donc λ1 = 0, λ2 = 0 et λ3 = 0Donc la famille e1, e2, e3 est libre.Comme la famille est libre et génératrice, c’est une base.38/73D. CransacAnalyse

Page 238 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 0 alors λ1, λ2, λ3 = 0, 0, 0Donc λ1 = 0, λ2 = 0 et λ3 = 0Donc la famille e1, e2, e3 est libre.Comme la famille est libre et génératrice, c’est une base.38/73D. CransacAnalyse

Page 239 : Espace vectorielDéfinitionOn dit qu’une famille B = ei1⩽i⩽n = e1, . . . , en de vecteurs d’unK-espace vectoriel E est une base de E si celle-ci est libre etgénératrice.ExempleDans E = R3.On pose e1 = 1, 0, 0, e2 = 0, 1, 0 et e3 = 0, 0, 1Soit u = x, y, z R3, alorsu = x, 0, 0 + 0, y, 0 + 0, 0, z = xe1 + ye2 + ze3 donc e1, e2, e3est génératrice.Supposons λ1e1 + λ2e2 + λ3e3 = 0 alors λ1, λ2, λ3 = 0, 0, 0Donc λ1 = 0, λ2 = 0 et λ3 = 0Donc la famille e1, e2, e3 est libre.Comme la famille est libre et génératrice, c’est une base.On appelle cette base la base canonique de R3 : c’est la base laplus simple qui vient à l’esprit.38/73D. CransacAnalyse

Page 240 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de Kn39/73D. CransacAnalyse

Page 241 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.39/73D. CransacAnalyse

Page 242 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.39/73D. CransacAnalyse

Page 243 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.39/73D. CransacAnalyse

Page 244 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.Supposons que λ1e1 + · · · + λnen = 0E.39/73D. CransacAnalyse

Page 245 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.Supposons que λ1e1 + · · · + λnen = 0E.C’est équivalent à λ1, . . . , λn = 0, . . . , 0 et doncλ1 = · · · = λn = 0.39/73D. CransacAnalyse

Page 246 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.Supposons que λ1e1 + · · · + λnen = 0E.C’est équivalent à λ1, . . . , λn = 0, . . . , 0 et doncλ1 = · · · = λn = 0.Finalement , la famille B est libre et génératrice de Kn,39/73D. CransacAnalyse

Page 247 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.Supposons que λ1e1 + · · · + λnen = 0E.C’est équivalent à λ1, . . . , λn = 0, . . . , 0 et doncλ1 = · · · = λn = 0.Finalement , la famille B est libre et génératrice de Kn, c’est unebase de Kn.39/73D. CransacAnalyse

Page 248 : Espace vectorielExemple Généralisation de l’exemple précédentDans E = Kn, on pose ei = 0, . . . , 0, 1, 0, . . . , 0 Kn où 1 se situe enième position.On a déja vu que B = e1, . . . , en est génératrice de KnMontrons que B est libre.Soient λ1, . . . , λn K.Supposons que λ1e1 + · · · + λnen = 0E.C’est équivalent à λ1, . . . , λn = 0, . . . , 0 et doncλ1 = · · · = λn = 0.Finalement , la famille B est libre et génératrice de Kn, c’est unebase de Kn.On appelle cette base la base canonique de Kn39/73D. CransacAnalyse

Page 249 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.40/73D. CransacAnalyse

Page 250 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R240/73D. CransacAnalyse

Page 251 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.40/73D. CransacAnalyse

Page 252 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.40/73D. CransacAnalyse

Page 253 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.40/73D. CransacAnalyse

Page 254 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.40/73D. CransacAnalyse

Page 255 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.En identifiant parties réelles et imaginaires, on obtient λ = µ = 0.40/73D. CransacAnalyse

Page 256 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.En identifiant parties réelles et imaginaires, on obtient λ = µ = 0.Donc la famille B est libre.40/73D. CransacAnalyse

Page 257 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.En identifiant parties réelles et imaginaires, on obtient λ = µ = 0.Donc la famille B est libre.Comme la famille B est libre et génératrice du R-espace vectoriel C,40/73D. CransacAnalyse

Page 258 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.En identifiant parties réelles et imaginaires, on obtient λ = µ = 0.Donc la famille B est libre.Comme la famille B est libre et génératrice du R-espace vectoriel C,40/73D. CransacAnalyse

Page 259 : Espace vectorielExempleConsidérons la famille 1, i d’éléments du R-espace vectoriel C.Cette famille est génératrice de CEn effet, par définition de C :z C, z = a + ib avec a, b R2Montrons que cette famille est libre.Soient λ, µ R.Supposons que λ.1 + µ.i = 0.En identifiant parties réelles et imaginaires, on obtient λ = µ = 0.Donc la famille B est libre.Comme la famille B est libre et génératrice du R-espace vectoriel C,c’est une base de C.40/73D. CransacAnalyse

Page 260 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.41/73D. CransacAnalyse

Page 261 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.41/73D. CransacAnalyse

Page 262 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.41/73D. CransacAnalyse

Page 263 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre41/73D. CransacAnalyse

Page 264 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 041/73D. CransacAnalyse

Page 265 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz041/73D. CransacAnalyse

Page 266 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C41/73D. CransacAnalyse

Page 267 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératrice41/73D. CransacAnalyse

Page 268 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.41/73D. CransacAnalyse

Page 269 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.41/73D. CransacAnalyse

Page 270 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.En effet 11 + ii = 041/73D. CransacAnalyse

Page 271 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.En effet 11 + ii = 0Elle n’est pas donc une base du C-espace vectoriel C.41/73D. CransacAnalyse

Page 272 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.En effet 11 + ii = 0Elle n’est pas donc une base du C-espace vectoriel C.une base de C est 1 par exemple.41/73D. CransacAnalyse

Page 273 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.En effet 11 + ii = 0Elle n’est pas donc une base du C-espace vectoriel C.une base de C est 1 par exemple.41/73D. CransacAnalyse

Page 274 : Espace vectorielRemarqueTout complexe non nul est une base du C-espace vectoriel C.En effet soit z0 C.z0 est libre car λz0 = 0 ⇔λ = 0 et z C, z = zz0z0 = λz0donc λ = zz0C donc z0 est génératriceLa famille 1, i est liée dans le C-espace vectoriel C.En effet 11 + ii = 0Elle n’est pas donc une base du C-espace vectoriel C.une base de C est 1 par exemple.La nature du corps K peut donc avoir une importance fondamentale surla structure du K espace vectoriel.41/73D. CransacAnalyse

Page 275 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.42/73D. CransacAnalyse

Page 276 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,42/73D. CransacAnalyse

Page 277 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn Kn42/73D. CransacAnalyse

Page 278 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn KnSupposons que x =nXi=1µiei avec µ1, µ2, . . . , µn Kn42/73D. CransacAnalyse

Page 279 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn KnSupposons que x =nXi=1µiei avec µ1, µ2, . . . , µn KnEn effectuant la différence,nXi=1λi µiei = 042/73D. CransacAnalyse

Page 280 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn KnSupposons que x =nXi=1µiei avec µ1, µ2, . . . , µn KnEn effectuant la différence,nXi=1λi µiei = 0Comme la famille est libre, J1, nKλi µi = 0 donc42/73D. CransacAnalyse

Page 281 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn KnSupposons que x =nXi=1µiei avec µ1, µ2, . . . , µn KnEn effectuant la différence,nXi=1λi µiei = 0Comme la famille est libre, J1, nKλi µi = 0 donc J1, nKλi = µi42/73D. CransacAnalyse

Page 282 : Espace vectorielThéorèmeSoit E, un K espace vectoriel, et B = e1, e2, . . . en une base de E.Alors tout vecteur s’écrit de manière unique comme combinaison linéairedes vecteurs e1, e2, . . . en.Démonstration.Soit x E, comme B est génératrice,x =nXi=1λiei avec λ1, λ2, . . . , λn KnSupposons que x =nXi=1µiei avec µ1, µ2, . . . , µn KnEn effectuant la différence,nXi=1λi µiei = 0Comme la famille est libre, J1, nKλi µi = 0 donc J1, nKλi = µiLa décomposition est bien unique.42/73D. CransacAnalyse

Page 283 : Espace vectorielThéorème Théorème de la base incomplèteSi E est de dimension finie, alors toute famille libre de E peut-êtrecomplétée en une base de E.Pour la compléter, il suffit de considérer certains vecteurs d’une famillegénératrice de E.43/73D. CransacAnalyse

Page 284 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.44/73D. CransacAnalyse

Page 285 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G 44/73D. CransacAnalyse

Page 286 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.44/73D. CransacAnalyse

Page 287 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.44/73D. CransacAnalyse

Page 288 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.44/73D. CransacAnalyse

Page 289 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 044/73D. CransacAnalyse

Page 290 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et44/73D. CransacAnalyse

Page 291 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et donc la familleest libre.44/73D. CransacAnalyse

Page 292 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et donc la familleest libre.Sinon, il existe k J1, mK, µk ̸= 0.44/73D. CransacAnalyse

Page 293 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et donc la familleest libre.Sinon, il existe k J1, mK, µk ̸= 0. Donc gk = nXk=1λiµk ei mXk=1µiµk gi44/73D. CransacAnalyse

Page 294 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et donc la familleest libre.Sinon, il existe k J1, mK, µk ̸= 0. Donc gk = nXk=1λiµk ei mXk=1µiµk gion pourrait exprimer gk comme combinaison linéaire des autres vecteurs doncen enlevant ce vecteur à cette famille, on obtiendrait une nouvelle famillecontenant k 1 vecteurs qui serait génératrice, ce qui contredit la définition dek.44/73D. CransacAnalyse

Page 295 : Espace vectorielDémonstration.Soit Fe1, e2, . . . , en une famille libre de E et G g1, g2, . . . , gm une famillegénératrice de E.On s’intéresse à l’ensemble des familles H telles que F H F G Comme G est génératice, H = F G l’est aussi. Donc il existe une famille deH qui est génératrice.On choisit une famille H , de cardinal minimum, génératrice de E. On note soncardinal k.Montrons que cette famille est libre.Soient λ1, λ2, . . . , λn Kn, µ1, µ2, . . . , µm Kn,nXk=1λiei +mXk=1µigi = 0Si i J1, mK, µi = 0, comme F est libre, i J1, nK, λi = 0 et donc la familleest libre.Sinon, il existe k J1, mK, µk ̸= 0. Donc gk = nXk=1λiµk ei mXk=1µiµk gion pourrait exprimer gk comme combinaison linéaire des autres vecteurs doncen enlevant ce vecteur à cette famille, on obtiendrait une nouvelle famillecontenant k 1 vecteurs qui serait génératrice, ce qui contredit la définition dek. Donc H est libre.44/73D. CransacAnalyse

Page 296 : Espace vectorielThéorème Théorème de la base extraiteDe toute famille génératrice finie de E, on peut extraire une base de E.En particulier, un espace de dimension finie admet une base.45/73D. CransacAnalyse

Page 297 : Espace vectorielThéorème Théorème de la base extraiteDe toute famille génératrice finie de E, on peut extraire une base de E.En particulier, un espace de dimension finie admet une base.Démonstration.Soient e1, e2, . . . , en une famille génératrice de E.45/73D. CransacAnalyse

Page 298 : Espace vectorielThéorème Théorème de la base extraiteDe toute famille génératrice finie de E, on peut extraire une base de E.En particulier, un espace de dimension finie admet une base.Démonstration.Soient e1, e2, . . . , en une famille génératrice de E.D’après le théorème précédent, on peut compléter la famille e1 qui estévidemment libre par des éléments de e1, e2, . . . , en pour produire unebase.45/73D. CransacAnalyse

Page 299 : Espace vectorielThéorème Théorème de la base extraiteDe toute famille génératrice finie de E, on peut extraire une base de E.En particulier, un espace de dimension finie admet une base.Démonstration.Soient e1, e2, . . . , en une famille génératrice de E.D’après le théorème précédent, on peut compléter la famille e1 qui estévidemment libre par des éléments de e1, e2, . . . , en pour produire unebase.En particulier, on déduit des résultats précédents que tout espacevectoriel de dimension finie admet une base finie.45/73D. CransacAnalyse

Page 300 : Espace vectorielThéorème Théorème et définitionSi E est de dimension finie, alors toutes les bases de E ont le mêmenombre d’éléments.Ce nombre s’appelle la dimension de E et est noté dimE.46/73D. CransacAnalyse

Page 301 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :47/73D. CransacAnalyse

Page 302 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".47/73D. CransacAnalyse

Page 303 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".47/73D. CransacAnalyse

Page 304 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 :47/73D. CransacAnalyse

Page 305 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 :47/73D. CransacAnalyse

Page 306 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".47/73D. CransacAnalyse

Page 307 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0,47/73D. CransacAnalyse

Page 308 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0,47/73D. CransacAnalyse

Page 309 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.47/73D. CransacAnalyse

Page 310 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.Sinon v0 = 0E.47/73D. CransacAnalyse

Page 311 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.Sinon v0 = 0E.47/73D. CransacAnalyse

Page 312 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.Sinon v0 = 0E. Donc v0 et v1 sont colinéaires.Soit n ⩾2, supposons le résultat vrai pour n 1.47/73D. CransacAnalyse

Page 313 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.Sinon v0 = 0E. Donc v0 et v1 sont colinéaires.Soit n ⩾2, supposons le résultat vrai pour n 1.47/73D. CransacAnalyse

Page 314 : Espace vectorielLemmePour tout entier n N, n + 1 vecteurs qui sont des combinaisonslinéaires de n vecteurs de E forment toujours une famille liée.Démonstration.Montrons ce lemme par récurrence sur n :Pour n = 0 : "1 vecteur combinaison linéaire de 0 vecteur est lié".C’est vrai car une combinaison linéaire de 0 vecteurs, c’est 0E.Pour n = 1 : "2 vecteurs combinaison linéaire de 1 vecteur formentune famille liée".Si v0 = λ0u1 et v1 = λ1u1, alors v0, v1 est liée :Si λ0 ̸= 0, alors v1 = λ1λ0 v0.Sinon v0 = 0E. Donc v0 et v1 sont colinéaires.Soit n ⩾2, supposons le résultat vrai pour n 1.Considérons n + 1 vecteurs v1, v2, . . . vn+1, combinaisons linéaires den vecteurs u1, u2, . . . un.47/73D. CransacAnalyse

Page 315 : Espace vectorielDémonstration.On a donc des scalaires αi,j avec 1 ⩽i ⩽n + 1 et 1 ⩽j ⩽n tels que :v1= α1,1u1 + α1,2u2 + . . . + α1,nunL1v2= α2,1u1 + α2,2u2 + . . . + α2,nunL2......vn+1= αn+1,1u1 + αn+1,2u2 + . . . + αn+1,nunLn+148/73D. CransacAnalyse

Page 316 : Espace vectorielDémonstration.On a donc des scalaires αi,j avec 1 ⩽i ⩽n + 1 et 1 ⩽j ⩽n tels que :v1= α1,1u1 + α1,2u2 + . . . + α1,nunL1v2= α2,1u1 + α2,2u2 + . . . + α2,nunL2......vn+1= αn+1,1u1 + αn+1,2u2 + . . . + αn+1,nunLn+1Si i J1, n + 1K, αi,n = 0, alors v1, v2, . . . vn sont combinaisons linéairesdes n 1 vecteurs u1, u2, . . . un1.48/73D. CransacAnalyse

Page 317 : Espace vectorielDémonstration.On a donc des scalaires αi,j avec 1 ⩽i ⩽n + 1 et 1 ⩽j ⩽n tels que :v1= α1,1u1 + α1,2u2 + . . . + α1,nunL1v2= α2,1u1 + α2,2u2 + . . . + α2,nunL2......vn+1= αn+1,1u1 + αn+1,2u2 + . . . + αn+1,nunLn+1Si i J1, n + 1K, αi,n = 0, alors v1, v2, . . . vn sont combinaisons linéairesdes n 1 vecteurs u1, u2, . . . un1.Par hypothèse de récurrence, v1, v2, . . . vn est liée.48/73D. CransacAnalyse

Page 318 : Espace vectorielDémonstration.On a donc des scalaires αi,j avec 1 ⩽i ⩽n + 1 et 1 ⩽j ⩽n tels que :v1= α1,1u1 + α1,2u2 + . . . + α1,nunL1v2= α2,1u1 + α2,2u2 + . . . + α2,nunL2......vn+1= αn+1,1u1 + αn+1,2u2 + . . . + αn+1,nunLn+1Si i J1, n + 1K, αi,n = 0, alors v1, v2, . . . vn sont combinaisons linéairesdes n 1 vecteurs u1, u2, . . . un1.Par hypothèse de récurrence, v1, v2, . . . vn est liée. Doncv1, v1, v2, . . . vn+1 l’est aussi.48/73D. CransacAnalyse

Page 319 : Espace vectorielDémonstration.On a donc des scalaires αi,j avec 1 ⩽i ⩽n + 1 et 1 ⩽j ⩽n tels que :v1= α1,1u1 + α1,2u2 + . . . + α1,nunL1v2= α2,1u1 + α2,2u2 + . . . + α2,nunL2......vn+1= αn+1,1u1 + αn+1,2u2 + . . . + αn+1,nunLn+1Si i J1, n + 1K, αi,n = 0, alors v1, v2, . . . vn sont combinaisons linéairesdes n 1 vecteurs u1, u2, . . . un1.Par hypothèse de récurrence, v1, v2, . . . vn est liée. Doncv1, v1, v2, . . . vn+1 l’est aussi.48/73D. CransacAnalyse

Page 320 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes,49/73D. CransacAnalyse

Page 321 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK49/73D. CransacAnalyse

Page 322 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK c’est un pivot de Gauss ! donnent :49/73D. CransacAnalyse

Page 323 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK c’est un pivot de Gauss ! donnent :v1 λ1vn+1 = Combinaison linéaire de u1, u2, . . . un1v2 λ2vn+1 = Combinaison linéaire de u1, u2, . . . un1...vn λnvn+1 = Combinaison linéaire de u1, u2, . . . un149/73D. CransacAnalyse

Page 324 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK c’est un pivot de Gauss ! donnent :v1 λ1vn+1 = Combinaison linéaire de u1, u2, . . . un1v2 λ2vn+1 = Combinaison linéaire de u1, u2, . . . un1...vn λnvn+1 = Combinaison linéaire de u1, u2, . . . un1Les vecteurs vi λivn+1, i J1, nK forment donc une famille liée puisquece sont n vecteurs combinaisons linéaires de n 1 hypothèse derécurrence.49/73D. CransacAnalyse

Page 325 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK c’est un pivot de Gauss ! donnent :v1 λ1vn+1 = Combinaison linéaire de u1, u2, . . . un1v2 λ2vn+1 = Combinaison linéaire de u1, u2, . . . un1...vn λnvn+1 = Combinaison linéaire de u1, u2, . . . un1Les vecteurs vi λivn+1, i J1, nK forment donc une famille liée puisquece sont n vecteurs combinaisons linéaires de n 1 hypothèse derécurrence.Il existe donc des scalaires β1, β2, . . . βn non tous nuls tels quenXi=1βivi λivn+1 = 0 doncnXi=1βivi nXi=1βiλi!vn+1 = 049/73D. CransacAnalyse

Page 326 : Espace vectorielDémonstration.Si l’un des αi,n, pour i J1, n + 1K n’est pas nul, disons αn+1,n sinon onéchange les lignes, alors les transformations Li ←Li αi,nαn+1,n z λiLn+1 pouri J1, nK c’est un pivot de Gauss ! donnent :v1 λ1vn+1 = Combinaison linéaire de u1, u2, . . . un1v2 λ2vn+1 = Combinaison linéaire de u1, u2, . . . un1...vn λnvn+1 = Combinaison linéaire de u1, u2, . . . un1Les vecteurs vi λivn+1, i J1, nK forment donc une famille liée puisquece sont n vecteurs combinaisons linéaires de n 1 hypothèse derécurrence.Il existe donc des scalaires β1, β2, . . . βn non tous nuls tels quenXi=1βivi λivn+1 = 0 doncnXi=1βivi nXi=1βiλi!vn+1 = 0Donc la famille v1, v2, . . . , vn+1 est liée.49/73D. CransacAnalyse

Page 327 : Espace vectorielCorollaireSi E est de dimension n et si x1 . . . , xn est une famille de n vecteurs deE, alors les conditions suivantes sont équivalentes :x1, . . . , xn est une famille libre de E.50/73D. CransacAnalyse

Page 328 : Espace vectorielCorollaireSi E est de dimension n et si x1 . . . , xn est une famille de n vecteurs deE, alors les conditions suivantes sont équivalentes :x1, . . . , xn est une famille libre de E.x1, . . . , xn est une famille génératrice de E.50/73D. CransacAnalyse

Page 329 : Espace vectorielCorollaireSi E est de dimension n et si x1 . . . , xn est une famille de n vecteurs deE, alors les conditions suivantes sont équivalentes :x1, . . . , xn est une famille libre de E.x1, . . . , xn est une famille génératrice de E.x1, . . . , xn est une base de E.50/73D. CransacAnalyse

Page 330 : Espace vectorielRemarqueEn particulier, dans un espace de dimension n, une famille libre atoujours au plus n éléments, et une famille génératrice a toujours aumoins n éléments.51/73D. CransacAnalyse

Page 331 : Espace vectorielRemarqueEn particulier, dans un espace de dimension n, une famille libre atoujours au plus n éléments, et une famille génératrice a toujours aumoins n éléments.Si E et F sont de dimension finie, alorsdimE × F = dimE + dimFEn particulier, dimKn = n.51/73D. CransacAnalyse

Page 332 : Espace vectorielRemarqueEn particulier, dans un espace de dimension n, une famille libre atoujours au plus n éléments, et une famille génératrice a toujours aumoins n éléments.Si E et F sont de dimension finie, alorsdimE × F = dimE + dimFEn particulier, dimKn = n.Si E et F sont de dimension finie, alorsdimL E, F = dimE × dimF51/73D. CransacAnalyse

Page 333 : Espace vectorielRemarqueEn particulier, dans un espace de dimension n, une famille libre atoujours au plus n éléments, et une famille génératrice a toujours aumoins n éléments.Si E et F sont de dimension finie, alorsdimE × F = dimE + dimFEn particulier, dimKn = n.Si E et F sont de dimension finie, alorsdimL E, F = dimE × dimFdimKnX = n + 1.51/73D. CransacAnalyse

Page 334 : Espace vectorielDéfinitionSoit x1, . . . , xn une famille finie de vecteurs d’un K-espace vectoriel E,on appelle rang de x1, . . . , xn la dimension de F = vectx1, . . . , xn.52/73D. CransacAnalyse

Page 335 : Espace vectorielDéfinitionSoit x1, . . . , xn une famille finie de vecteurs d’un K-espace vectoriel E,on appelle rang de x1, . . . , xn la dimension de F = vectx1, . . . , xn.LemmeDans un espace engendré par n vecteurs u1, . . . , un, toute famillev1, . . . , vn+1 de n + 1 vecteurs est liée.52/73D. CransacAnalyse

Page 336 : Espace vectorielDéfinitionSoit x1, . . . , xn une famille finie de vecteurs d’un K-espace vectoriel E,on appelle rang de x1, . . . , xn la dimension de F = vectx1, . . . , xn.LemmeDans un espace engendré par n vecteurs u1, . . . , un, toute famillev1, . . . , vn+1 de n + 1 vecteurs est liée.Démonstration.Cette propriété, sous une autre forme, a déjà été démontrée sous uneautre forme.LemmeLe cardinal d’une famille libre est plus petit que celui d’une famillegénératrice.52/73D. CransacAnalyse

Page 337 : Espace vectorielDéfinitionSoit x1, . . . , xn une famille finie de vecteurs d’un K-espace vectoriel E,on appelle rang de x1, . . . , xn la dimension de F = vectx1, . . . , xn.LemmeDans un espace engendré par n vecteurs u1, . . . , un, toute famillev1, . . . , vn+1 de n + 1 vecteurs est liée.Démonstration.Cette propriété, sous une autre forme, a déjà été démontrée sous uneautre forme.LemmeLe cardinal d’une famille libre est plus petit que celui d’une famillegénératrice.Si F1 est une famille libre et F2 une famille génératrice de E, on aCardF1 ⩽CardF252/73D. CransacAnalyse

Page 338 : Espace vectorielRemarqueSoit E est K-espace vectoriel.Si E = 0E, on a dim E = 0.53/73D. CransacAnalyse

Page 339 : Espace vectorielRemarqueSoit E est K-espace vectoriel.Si E = 0E, on a dim E = 0.Si F est une famille libre de E, on a : Card F ⩽dim E53/73D. CransacAnalyse

Page 340 : Espace vectorielRemarqueSoit E est K-espace vectoriel.Si E = 0E, on a dim E = 0.Si F est une famille libre de E, on a : Card F ⩽dim ESi F est une famille génératrice de E, on a : Card F ⩾dim E53/73D. CransacAnalyse

Page 341 : Espace vectorielRemarqueSoit E est K-espace vectoriel.Si E = 0E, on a dim E = 0.Si F est une famille libre de E, on a : Card F ⩽dim ESi F est une famille génératrice de E, on a : Card F ⩾dim E53/73D. CransacAnalyse

Page 342 : Espace vectorielRemarqueSoit E est K-espace vectoriel.Si E = 0E, on a dim E = 0.Si F est une famille libre de E, on a : Card F ⩽dim ESi F est une famille génératrice de E, on a : Card F ⩾dim EPropositionSi E est un espace vectoriel de dimension finie et si F est un sous-espacevectoriel de E, alors F est de dimension finie et on a dimF ⩽dimE.De plus, on a dimF = dimE ⇔F = E.53/73D. CransacAnalyse

Page 343 : Espace vectorielThéorème RappelSi B = ei1⩽i⩽n est une base d’un K-espace vectoriel de E alorsx E, !λ1, . . . , λn Kn, x = λ1e1 + . . . λnen.54/73D. CransacAnalyse

Page 344 : Espace vectorielThéorème RappelSi B = ei1⩽i⩽n est une base d’un K-espace vectoriel de E alorsx E, !λ1, . . . , λn Kn, x = λ1e1 + . . . λnen.DéfinitionAvec les notations ci-dessous, les scalaires λ1, . . . , λn sont appelés lescomposants de x dans la base B ou encore les composantes de x.54/73D. CransacAnalyse

Page 345 : Espace vectorielThéorème RappelSi B = ei1⩽i⩽n est une base d’un K-espace vectoriel de E alorsx E, !λ1, . . . , λn Kn, x = λ1e1 + . . . λnen.DéfinitionAvec les notations ci-dessous, les scalaires λ1, . . . , λn sont appelés lescomposants de x dans la base B ou encore les composantes de x.RemarqueLes composantes d’un vecteur dépendent de la base dans laquelle ontravaille.54/73D. CransacAnalyse

Page 346 : Espace vectorielThéorème RappelSi B = ei1⩽i⩽n est une base d’un K-espace vectoriel de E alorsx E, !λ1, . . . , λn Kn, x = λ1e1 + . . . λnen.DéfinitionAvec les notations ci-dessous, les scalaires λ1, . . . , λn sont appelés lescomposants de x dans la base B ou encore les composantes de x.RemarqueLes composantes d’un vecteur dépendent de la base dans laquelle ontravaille.ExempleDans E = Kn, considérons la base canonique B = e1, . . . , en et levecteur x = x1, . . . , xn. Puisque x = x1e1 + · · · + xnen, lescomposantes du vecteurs x dans la base B sont les scalairesx1, . . . , xn.54/73D. CransacAnalyse

Page 347 : Espace vectorielThéorème RappelSi B = ei1⩽i⩽n est une base d’un K-espace vectoriel de E alorsx E, !λ1, . . . , λn Kn, x = λ1e1 + . . . λnen.DéfinitionAvec les notations ci-dessous, les scalaires λ1, . . . , λn sont appelés lescomposants de x dans la base B ou encore les composantes de x.RemarqueLes composantes d’un vecteur dépendent de la base dans laquelle ontravaille.ExempleDans E = Kn, considérons la base canonique B = e1, . . . , en et levecteur x = x1, . . . , xn. Puisque x = x1e1 + · · · + xnen, lescomposantes du vecteurs x dans la base B sont les scalairesx1, . . . , xn.Dans le R-espace vectoriel C, les composantes de z C dans labase canonique 1, i sont Rez et Imz54/73D. CransacAnalyse

Page 348 : Espace vectorielThéorèmeSi B = ei1⩽i⩽n est une base de E alors pour tout vecteur x et y decomposantes x1, . . . , xn et y1, . . . , yn dans B, les composantes de x + ysont x1 + y1, . . . , xn + yn et celle de λx sont λx1, . . . , λxn.55/73D. CransacAnalyse

Page 349 : Espace vectorielLa réunion de deux sous-espaces n’est pas en général un sous-espace,sauf cas très particulier.56/73D. CransacAnalyse

Page 350 : Espace vectorielLa réunion de deux sous-espaces n’est pas en général un sous-espace,sauf cas très particulier.L’opération d’addition permet de définir la somme de deux sous-espaces,cette somme s’avère être en fait le plus petit sous-espace contenant leurréunion.56/73D. CransacAnalyse

Page 351 : Espace vectorielLa réunion de deux sous-espaces n’est pas en général un sous-espace,sauf cas très particulier.L’opération d’addition permet de définir la somme de deux sous-espaces,cette somme s’avère être en fait le plus petit sous-espace contenant leurréunion.La propriété d’unicité de l’écriture d’un vecteur comme somme devecteurs appartenant à deux sous-espaces donnés conduit à la notion desomme directe et de sous-espaces supplémentaires.56/73D. CransacAnalyse

Page 352 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :57/73D. CransacAnalyse

Page 353 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :On appelle somme de F et de G l’ensemble, noté F + G des vecteurs quisont la somme d’un vecteur de F et d’un vecteur de G :F + G = u E u = f + g, f F, g G.57/73D. CransacAnalyse

Page 354 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :On appelle somme de F et de G l’ensemble, noté F + G des vecteurs quisont la somme d’un vecteur de F et d’un vecteur de G :F + G = u E u = f + g, f F, g G.En d’autres termes, les vecteurs de la somme F + G sont caractérisés paru F + G ⇐⇒f F, g G tels que u = f + gRemarque57/73D. CransacAnalyse

Page 355 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :On appelle somme de F et de G l’ensemble, noté F + G des vecteurs quisont la somme d’un vecteur de F et d’un vecteur de G :F + G = u E u = f + g, f F, g G.En d’autres termes, les vecteurs de la somme F + G sont caractérisés paru F + G ⇐⇒f F, g G tels que u = f + gRemarqueLa somme F + G des sous-espaces vectoriels F et G est donc est unensemble. Cet ensemble contient F.57/73D. CransacAnalyse

Page 356 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :On appelle somme de F et de G l’ensemble, noté F + G des vecteurs quisont la somme d’un vecteur de F et d’un vecteur de G :F + G = u E u = f + g, f F, g G.En d’autres termes, les vecteurs de la somme F + G sont caractérisés paru F + G ⇐⇒f F, g G tels que u = f + gRemarqueLa somme F + G des sous-espaces vectoriels F et G est donc est unensemble. Cet ensemble contient F.En effet, si f F, alors f = f + 0E F + G car 0E G :57/73D. CransacAnalyse

Page 357 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E :On appelle somme de F et de G l’ensemble, noté F + G des vecteurs quisont la somme d’un vecteur de F et d’un vecteur de G :F + G = u E u = f + g, f F, g G.En d’autres termes, les vecteurs de la somme F + G sont caractérisés paru F + G ⇐⇒f F, g G tels que u = f + gRemarqueLa somme F + G des sous-espaces vectoriels F et G est donc est unensemble. Cet ensemble contient F.En effet, si f F, alors f = f + 0E F + G car 0E G :Ainsi F F + G.57/73D. CransacAnalyse

Page 358 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.58/73D. CransacAnalyse

Page 359 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.58/73D. CransacAnalyse

Page 360 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + G58/73D. CransacAnalyse

Page 361 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + G58/73D. CransacAnalyse

Page 362 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E G58/73D. CransacAnalyse

Page 363 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.58/73D. CransacAnalyse

Page 364 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.58/73D. CransacAnalyse

Page 365 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.58/73D. CransacAnalyse

Page 366 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.58/73D. CransacAnalyse

Page 367 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.Or F est un sous-espace vectoriel de E58/73D. CransacAnalyse

Page 368 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.Or F est un sous-espace vectoriel de E donc λf1 + µf2 F.58/73D. CransacAnalyse

Page 369 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.Or F est un sous-espace vectoriel de E donc λf1 + µf2 F.De même, λg1 + µg2 G.58/73D. CransacAnalyse

Page 370 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.Or F est un sous-espace vectoriel de E donc λf1 + µf2 F.De même, λg1 + µg2 G. Ainsi λu + µv F + G.58/73D. CransacAnalyse

Page 371 : Espace vectorielThéorèmeLa somme F + G de deux sous-espaces vectoriels F et G d’un espacevectoriel E est un sous-espace vectoriel de E.Démonstration.F + G E puisque tout élément h de F + G s’écrit h = f + g avecf dans F donc dans E et g dans G donc dans E, et que lasomme de deux éléments de E est un élément de E.Le vecteur nul 0E est dans F + GEn effet 0E = 0E + 0E avec 0E F et 0E GF et G sont des sous-espaces vectoriels de E.Si u et v sont dans E + F et si λ et µ sont des scalaires, on peutécrire u = f1 + g1 et v = f2 + g2 avec f1 et f2 dans F et g1 et g2dans G.Alors λu + µv = λf1 + µf2 + λg1 + µg2.Or F est un sous-espace vectoriel de E donc λf1 + µf2 F.De même, λg1 + µg2 G. Ainsi λu + µv F + G.Donc F + G est un sous-espace vectoriel de E.58/73D. CransacAnalyse

Page 372 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?Solution59/73D. CransacAnalyse

Page 373 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu359/73D. CransacAnalyse

Page 374 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + g59/73D. CransacAnalyse

Page 375 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait que59/73D. CransacAnalyse

Page 376 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u259/73D. CransacAnalyse

Page 377 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u259/73D. CransacAnalyse

Page 378 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu359/73D. CransacAnalyse

Page 379 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu3 ⇐⇒a3 K tel que g = a3u3.59/73D. CransacAnalyse

Page 380 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu3 ⇐⇒a3 K tel que g = a3u3.On en déduit donc finalement queu vectu1, u2 + vectu359/73D. CransacAnalyse

Page 381 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu3 ⇐⇒a3 K tel que g = a3u3.On en déduit donc finalement queu vectu1, u2 + vectu3⇐⇒a1, a2, a3 K3tel que u = a1u1 + a2u2 + a3u359/73D. CransacAnalyse

Page 382 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu3 ⇐⇒a3 K tel que g = a3u3.On en déduit donc finalement queu vectu1, u2 + vectu3⇐⇒a1, a2, a3 K3tel que u = a1u1 + a2u2 + a3u3⇐⇒u vectu1, u2, u359/73D. CransacAnalyse

Page 383 : Espace vectorielExempleSoient u1, u2, u3 trois vecteurs de l’espace vectoriel E.Que peut-on dire de la somme vectu1, u2 + vectu3?SolutionOn au vectu1, u2 + vectu3⇐⇒f vectu1, u2, g vectu3 tels que u = f + gOr, on sait quef vectu1, u2 ⇐⇒a1, a2 K2 tel que f = a1u1 + a2u2et g vectu3 ⇐⇒a3 K tel que g = a3u3.On en déduit donc finalement queu vectu1, u2 + vectu3⇐⇒a1, a2, a3 K3tel que u = a1u1 + a2u2 + a3u3⇐⇒u vectu1, u2, u3Ceci prouve que vectu1, u2 + vectu3 = vectu1, u2, u3.59/73D. CransacAnalyse

Page 384 : Espace vectorielDéfinitionSoient F et G deux sous-espaces vectoriels de E :60/73D. CransacAnalyse

Page 385 : Espace vectorielDéfinitionSoient F et G deux sous-espaces vectoriels de E :On dit que la somme F + G est directe si tout vecteur de F + G sedécompose de manière unique comme la somme d’un élément de F etd’un élément de G.60/73D. CransacAnalyse

Page 386 : Espace vectorielDéfinitionSoient F et G deux sous-espaces vectoriels de E :On dit que la somme F + G est directe si tout vecteur de F + G sedécompose de manière unique comme la somme d’un élément de F etd’un élément de G.Lorsque F et G sont en somme directe, on note F + G = F G.Pratiquement, les sous-espaces vectoriels en somme directe sontcaractérisés par le théorème suivant :60/73D. CransacAnalyse

Page 387 : Espace vectorielDéfinitionSoient F et G deux sous-espaces vectoriels de E :On dit que la somme F + G est directe si tout vecteur de F + G sedécompose de manière unique comme la somme d’un élément de F etd’un élément de G.Lorsque F et G sont en somme directe, on note F + G = F G.Pratiquement, les sous-espaces vectoriels en somme directe sontcaractérisés par le théorème suivant :ThéorèmeSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E. Alors :F + G est directe ⇔F G = 0E60/73D. CransacAnalyse

Page 388 : Espace vectorielDémonstration.Supposons la somme F + G directe.61/73D. CransacAnalyse

Page 389 : Espace vectorielDémonstration.Supposons la somme F + G directe.61/73D. CransacAnalyse

Page 390 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.61/73D. CransacAnalyse

Page 391 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.61/73D. CransacAnalyse

Page 392 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u G61/73D. CransacAnalyse

Page 393 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.61/73D. CransacAnalyse

Page 394 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.Ceci prouve que le seul vecteur qu’on puisse trouver dans F G estle vecteur nul, c’est-à-dire que F G 0E.61/73D. CransacAnalyse

Page 395 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.Ceci prouve que le seul vecteur qu’on puisse trouver dans F G estle vecteur nul, c’est-à-dire que F G 0E.Mais l’inclusion inverse0E F Gest vraie puisque F et G sont deux sous-espaces vectoriels de E.61/73D. CransacAnalyse

Page 396 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.Ceci prouve que le seul vecteur qu’on puisse trouver dans F G estle vecteur nul, c’est-à-dire que F G 0E.Mais l’inclusion inverse0E F Gest vraie puisque F et G sont deux sous-espaces vectoriels de E.61/73D. CransacAnalyse

Page 397 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.Ceci prouve que le seul vecteur qu’on puisse trouver dans F G estle vecteur nul, c’est-à-dire que F G 0E.Mais l’inclusion inverse0E F Gest vraie puisque F et G sont deux sous-espaces vectoriels de E.61/73D. CransacAnalyse

Page 398 : Espace vectorielDémonstration.Supposons la somme F + G directe.Soit u F G.On peut alors écrireu = 0F + u = u + 0G = f + gavec f F, u F et g G, u GPuisque la somme F + G est directe, la décomposition de u suivantF et G est unique et ainsi f = u = 0F = 0E.Ceci prouve que le seul vecteur qu’on puisse trouver dans F G estle vecteur nul, c’est-à-dire que F G 0E.Mais l’inclusion inverse0E F Gest vraie puisque F et G sont deux sous-espaces vectoriels de E.Donc F G = 0E.61/73D. CransacAnalyse

Page 399 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.62/73D. CransacAnalyse

Page 400 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.62/73D. CransacAnalyse

Page 401 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.62/73D. CransacAnalyse

Page 402 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.Alors f1 f2 = g2 g1.62/73D. CransacAnalyse

Page 403 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.Alors f1 f2 = g2 g1.Puisque f1 f2 F et g2 g1 G, le vecteur v = f1 f2 = g2 g1appartient à F G.62/73D. CransacAnalyse

Page 404 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.Alors f1 f2 = g2 g1.Puisque f1 f2 F et g2 g1 G, le vecteur v = f1 f2 = g2 g1appartient à F G.Puisque F G = 0E, on a donc f1 f2 = g2 g1 = 0E,62/73D. CransacAnalyse

Page 405 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.Alors f1 f2 = g2 g1.Puisque f1 f2 F et g2 g1 G, le vecteur v = f1 f2 = g2 g1appartient à F G.Puisque F G = 0E, on a donc f1 f2 = g2 g1 = 0E, ce quiassure que f1 = f2 et g1 = g2.62/73D. CransacAnalyse

Page 406 : Espace vectorielDémonstration.Réciproquement, supposons que F G = 0E et montrons quela somme F + G est directe.Supposons que l’on ait u = f1 + g1 = f2 + g2 avec f1 et f2 dans F etg1 et g2 dans G.Alors f1 f2 = g2 g1.Puisque f1 f2 F et g2 g1 G, le vecteur v = f1 f2 = g2 g1appartient à F G.Puisque F G = 0E, on a donc f1 f2 = g2 g1 = 0E, ce quiassure que f1 = f2 et g1 = g2.Ainsi, l’écriture de u comme somme d’un élément de F et d’unélément de G est unique, ce qui signife que la somme F + G estdirecte.62/73D. CransacAnalyse

Page 407 : Espace vectorielExempleDeux droites sécantes du plan R2 ou de l’espace R3 sont en sommedirecte puisque leur intersection est réduite au vecteur nul.63/73D. CransacAnalyse

Page 408 : Espace vectorielExempleDeux droites sécantes du plan R2 ou de l’espace R3 sont en sommedirecte puisque leur intersection est réduite au vecteur nul.Deux plans sécants de l’espace R3 ne peuvent être en somme directepuisque leur intersection est une droite et ne contient donc pas quele vecteur nul.63/73D. CransacAnalyse

Page 409 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E.64/73D. CransacAnalyse

Page 410 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E.On dit que F et G sont supplémentaires dans E si la somme F + G estdirecte et si celle-ci vaut E.On a donc :F et G supplémentaires dans E ⇔E = F G.64/73D. CransacAnalyse

Page 411 : Espace vectorielDéfinitionSoit E un K-espace vectoriel et soient F et G deux sous-espacesvectoriels de E.On dit que F et G sont supplémentaires dans E si la somme F + G estdirecte et si celle-ci vaut E.On a donc :F et G supplémentaires dans E ⇔E = F G.On dit aussi que G est un supplémentaire de F dans E.64/73D. CransacAnalyse

Page 412 : Espace vectorielLa caractérisation des sous-espaces espaces vectoriels supplémentaires setraduit par le théorème suivant :65/73D. CransacAnalyse

Page 413 : Espace vectorielLa caractérisation des sous-espaces espaces vectoriels supplémentaires setraduit par le théorème suivant :ThéorèmeSoient F et G sont deux sous-espaces vectoriels de E.Les propriétés suivantes sont équivalentes :F et G sont supplémentaires dans E.65/73D. CransacAnalyse

Page 414 : Espace vectorielLa caractérisation des sous-espaces espaces vectoriels supplémentaires setraduit par le théorème suivant :ThéorèmeSoient F et G sont deux sous-espaces vectoriels de E.Les propriétés suivantes sont équivalentes :F et G sont supplémentaires dans E.Pour tout u E il existe un couple unique de vecteurs f F etg G et tels que u = f + g.65/73D. CransacAnalyse

Page 415 : Espace vectorielLa caractérisation des sous-espaces espaces vectoriels supplémentaires setraduit par le théorème suivant :ThéorèmeSoient F et G sont deux sous-espaces vectoriels de E.Les propriétés suivantes sont équivalentes :F et G sont supplémentaires dans E.Pour tout u E il existe un couple unique de vecteurs f F etg G et tels que u = f + g.dim F + dim G = dim E et F G = 0E.65/73D. CransacAnalyse

Page 416 : Espace vectorielLa caractérisation des sous-espaces espaces vectoriels supplémentaires setraduit par le théorème suivant :ThéorèmeSoient F et G sont deux sous-espaces vectoriels de E.Les propriétés suivantes sont équivalentes :F et G sont supplémentaires dans E.Pour tout u E il existe un couple unique de vecteurs f F etg G et tels que u = f + g.dim F + dim G = dim E et F G = 0E.Si BF est une base de F et si BG est une base de G alorsB = BF BG est une base de E.65/73D. CransacAnalyse

Page 417 : Espace vectorielRemarque66/73D. CransacAnalyse

Page 418 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.66/73D. CransacAnalyse

Page 419 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.Par exemple, deux droites sécantes de R3 sont supplémentaires dans leplan qui les contient, mais pas dans l’espace R3 : en effet, leur somme estdirecte et vaut exactement le plan P = D1 D2, et non l’espace toutentier.Remarque66/73D. CransacAnalyse

Page 420 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.Par exemple, deux droites sécantes de R3 sont supplémentaires dans leplan qui les contient, mais pas dans l’espace R3 : en effet, leur somme estdirecte et vaut exactement le plan P = D1 D2, et non l’espace toutentier.RemarqueUn sous-espace possède plusieurs supplémentaires.66/73D. CransacAnalyse

Page 421 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.Par exemple, deux droites sécantes de R3 sont supplémentaires dans leplan qui les contient, mais pas dans l’espace R3 : en effet, leur somme estdirecte et vaut exactement le plan P = D1 D2, et non l’espace toutentier.RemarqueUn sous-espace possède plusieurs supplémentaires.Par exemple, si D1, D2 et D3 sont trois droites deux à deux sécantes en0, 0 de E = R2, alors D2 et D3 sont chacune des supplémentaires deD1 dans R266/73D. CransacAnalyse

Page 422 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.Par exemple, deux droites sécantes de R3 sont supplémentaires dans leplan qui les contient, mais pas dans l’espace R3 : en effet, leur somme estdirecte et vaut exactement le plan P = D1 D2, et non l’espace toutentier.RemarqueUn sous-espace possède plusieurs supplémentaires.Par exemple, si D1, D2 et D3 sont trois droites deux à deux sécantes en0, 0 de E = R2, alors D2 et D3 sont chacune des supplémentaires deD1 dans R2 puisque dim D1 + dim D2 = dim R2 = 2 etdim D1 + dim D3 = dim R2 et D1 D2 = D1 D3 = 0, 0.66/73D. CransacAnalyse

Page 423 : Espace vectorielRemarqueAttention de ne pas confondre la notion d’espaces en somme directe avecla notion d’espaces supplémentaires dans un autre.Par exemple, deux droites sécantes de R3 sont supplémentaires dans leplan qui les contient, mais pas dans l’espace R3 : en effet, leur somme estdirecte et vaut exactement le plan P = D1 D2, et non l’espace toutentier.RemarqueUn sous-espace possède plusieurs supplémentaires.Par exemple, si D1, D2 et D3 sont trois droites deux à deux sécantes en0, 0 de E = R2, alors D2 et D3 sont chacune des supplémentaires deD1 dans R2 puisque dim D1 + dim D2 = dim R2 = 2 etdim D1 + dim D3 = dim R2 et D1 D2 = D1 D3 = 0, 0.Donc D1 admet deux supplémentaire distincts.66/73D. CransacAnalyse

Page 424 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.67/73D. CransacAnalyse

Page 425 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.Solution67/73D. CransacAnalyse

Page 426 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.SolutionOn montre d’abord que F = vect1, 1, 0, 0, 1, 1.67/73D. CransacAnalyse

Page 427 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.SolutionOn montre d’abord que F = vect1, 1, 0, 0, 1, 1. F est donc un planvectoriel de R3 et aussi un sous-espace vectoriel de R3.67/73D. CransacAnalyse

Page 428 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.SolutionOn montre d’abord que F = vect1, 1, 0, 0, 1, 1. F est donc un planvectoriel de R3 et aussi un sous-espace vectoriel de R3.De même G = vect1, 1, 1 est une droite vectorielle de R3 est donc unsous-espace vectoriel de R3.67/73D. CransacAnalyse

Page 429 : Espace vectorielExempleSoit E = R3.On demande de vérifier que F = x, y, z R3 x y + z = 0 etG = x, x, x R3 sont supplémentaires dans E.SolutionOn montre d’abord que F = vect1, 1, 0, 0, 1, 1. F est donc un planvectoriel de R3 et aussi un sous-espace vectoriel de R3.De même G = vect1, 1, 1 est une droite vectorielle de R3 est donc unsous-espace vectoriel de R3.Une méthode pour montrer que F et G sont supplémentaires dans R3 estde vérifier que tout vecteur u = x1, x2, x3 de R3 se décompose demanière unique comme somme d’un vecteur f = f1, f2, f3 de F et d’unvecteur g = g1, g2, g3 de G.67/73D. CransacAnalyse

Page 430 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.68/73D. CransacAnalyse

Page 431 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.Or, f F ⇐⇒f2 = f1 + f3 ⇐⇒f = f1, f1 + f3, f3.68/73D. CransacAnalyse

Page 432 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.Or, f F ⇐⇒f2 = f1 + f3 ⇐⇒f = f1, f1 + f3, f3.De même g G ⇐⇒g = g1, g1, g1.On a donc :x = f +g ⇐⇒68/73D. CransacAnalyse

Page 433 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.Or, f F ⇐⇒f2 = f1 + f3 ⇐⇒f = f1, f1 + f3, f3.De même g G ⇐⇒g = g1, g1, g1.On a donc :x = f +g ⇐⇒f1 + g1 = x1f1 + g1 + f3 = x2f3 + g1 = x3⇐⇒68/73D. CransacAnalyse

Page 434 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.Or, f F ⇐⇒f2 = f1 + f3 ⇐⇒f = f1, f1 + f3, f3.De même g G ⇐⇒g = g1, g1, g1.On a donc :x = f +g ⇐⇒f1 + g1 = x1f1 + g1 + f3 = x2f3 + g1 = x3⇐⇒f1 + g1 = x1f3 = x2 x1g1 = x3 f3 = x1 x2 + x368/73D. CransacAnalyse

Page 435 : Espace vectorielExempleNous résolvons l’équation u = f + g, d’inconnues f et g et montronsqu’elle admet une solution unique.Or, f F ⇐⇒f2 = f1 + f3 ⇐⇒f = f1, f1 + f3, f3.De même g G ⇐⇒g = g1, g1, g1.On a donc :x = f +g ⇐⇒f1 + g1 = x1f1 + g1 + f3 = x2f3 + g1 = x3⇐⇒f1 + g1 = x1f3 = x2 x1g1 = x3 f3 = x1 x2 + x3On voit donc que ce système admet une unique solution donnée par :f1 = x1 g1 = x2 x3f3 = x2 x1g1 = x1 x2 + x3Ceci signifie donc que les vecteurs f et g recherchés existent et qu’ilssont uniques. On a bien prouvé que R3 = F G.68/73D. CransacAnalyse

Page 436 : Espace vectorielExempleOn aurait également pu montrer que les trois vecteursu1 = 1, 1, 0, u2 = 0, 1, 1 et u3 = 1, 1, 1 sont libres.69/73D. CransacAnalyse

Page 437 : Espace vectorielExempleOn aurait également pu montrer que les trois vecteursu1 = 1, 1, 0, u2 = 0, 1, 1 et u3 = 1, 1, 1 sont libres.On remarque en effet que u3 u2 = 1, 0, 0, u3 u1 = 0, 0, 1 etu1 + y2 u3 = 0, 1, 069/73D. CransacAnalyse

Page 438 : Espace vectorielExempleSoit E = FR, RVérifier que F = f : R →R f est paire et G = f : R →R f est impaire sont supplémentaires dans E.Solution70/73D. CransacAnalyse

Page 439 : Espace vectorielExempleSoit E = FR, RVérifier que F = f : R →R f est paire et G = f : R →R f est impaire sont supplémentaires dans E.SolutionOn a déjà vu que F est un sous-espace vectoriel de E70/73D. CransacAnalyse

Page 440 : Espace vectorielExempleSoit E = FR, RVérifier que F = f : R →R f est paire et G = f : R →R f est impaire sont supplémentaires dans E.SolutionOn a déjà vu que F est un sous-espace vectoriel de E On prouve de même queG est un sous-espace vectoriel de E.70/73D. CransacAnalyse

Page 441 : Espace vectorielExempleSoit E = FR, RVérifier que F = f : R →R f est paire et G = f : R →R f est impaire sont supplémentaires dans E.SolutionOn a déjà vu que F est un sous-espace vectoriel de E On prouve de même queG est un sous-espace vectoriel de E. Il nous reste à vérifier que tout élément deE se décompose de manière unique comme la somme d’un élément de F etd’un élément de G, ce qui revient à prouver que toute fonction f de R dans Rpeut s’écrire d’une seule façon comme la somme d’une fonction paire et d’unefonction impaire.70/73D. CransacAnalyse

Page 442 : Espace vectorielExempleNous allons ici procéder à l’aide d’un raisonnement par analyse etsynthèse.71/73D. CransacAnalyse

Page 443 : Espace vectorielExempleNous allons ici procéder à l’aide d’un raisonnement par analyse etsynthèse.Analyse du problème : Supposons que l’on puisse écrire f = p + i avecp paire et i impaire, et essayons d’exprimer p et i en fonction de f . Pourtout x R, on a d’abord f x = px + ix.71/73D. CransacAnalyse

Page 444 : Espace vectorielExempleNous allons ici procéder à l’aide d’un raisonnement par analyse etsynthèse.Analyse du problème : Supposons que l’on puisse écrire f = p + i avecp paire et i impaire, et essayons d’exprimer p et i en fonction de f . Pourtout x R, on a d’abord f x = px + ix. Puisque px = px etix = ix on a aussi, pour tout réel x, on af x = px + ix = px ix.71/73D. CransacAnalyse

Page 445 : Espace vectorielExempleNous allons ici procéder à l’aide d’un raisonnement par analyse etsynthèse.Analyse du problème : Supposons que l’on puisse écrire f = p + i avecp paire et i impaire, et essayons d’exprimer p et i en fonction de f . Pourtout x R, on a d’abord f x = px + ix. Puisque px = px etix = ix on a aussi, pour tout réel x, on af x = px + ix = px ix.En ajoutant et soustrayant membre à membre f x et f x, il vientpx = 12f x + f xix = 12f x f x71/73D. CransacAnalyse

Page 446 : Espace vectorielExempleNous allons ici procéder à l’aide d’un raisonnement par analyse etsynthèse.Analyse du problème : Supposons que l’on puisse écrire f = p + i avecp paire et i impaire, et essayons d’exprimer p et i en fonction de f . Pourtout x R, on a d’abord f x = px + ix. Puisque px = px etix = ix on a aussi, pour tout réel x, on af x = px + ix = px ix.En ajoutant et soustrayant membre à membre f x et f x, il vientpx = 12f x + f xix = 12f x f xCette analyse du problème nous permet donc de conclure que, si ladécomposition de f en somme d’une fonction paire et d’une fonctionimpaire est possible, alors celle-ci est unique puisqu’on a trouvé une seulevaleur posible de px et de ix : Il nous reste simplement à vérifier queles fonctions données répondent bien aux exigences du problème posé,c’est-à-dire que p est paire, que i est impaire et que p + i = f :71/73D. CransacAnalyse

Page 447 : Espace vectorielExempleSynthèse du problème :Partant de f fonction quelconque de R dans R. Soient p et i définies par :px = 12f x + f xix = 12f x f xOn a bien px + ix = f x, c’est-à-dire f = p + i. De plus, on apx = 12f x + f x = px, donc p est paire. On vérifie de mêmeque i est impaire. Ainsi, F et G sont supplémentaires dans E.72/73D. CransacAnalyse

Page 448 : Espace vectorielPropositionTout sous-espace d’un espace de dimension finie admet unsupplémentaire.73/73D. CransacAnalyse

Page 449 : Espace vectorielPropositionTout sous-espace d’un espace de dimension finie admet unsupplémentaire.Théorème Formule de GrassmannSoit E un espace vectoriel de dimension finie et soient F,G deuxsous-espaces vectoriels de E. AlorsdimF + G = dimF + dimG dimF G.En particulier, F et G sont en somme directe si et seulement sidimF + G = dimF + dimG.73/73D. CransacAnalyse

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449