CM3 Integration de fonctions mesurables et positives
Télécharger le CM3 Integration de fonctions mesurables et positives en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Page 1 : Ingénieurs 1ère année : Mathématiques appliquéesMesure et intégrationCM3 – Intégration de fonctions mesurables positivesNisrine FORTIN CAMDAVANT
Page 2 : 1Fonctions étagées2Intégrale d’une fonction étagée positive3Intégration de fonctions mesurables positives
Page 3 : Fonctions étagéesLes fonctions étagées jouent, dans la construction de l’intégrale de Lebesgue, lerôle réservé aux fonctions en escalier dans la théorie de l’intégrale de Riemann.
Page 4 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesFonctions étagéesDans la suite de ce cours, on considère l’espace mesuré Ω, T , µ.DéfinitionSoit f une fonction de Ωdans R. La fonction f est dite T -étagée si :f est T , BR-mesurable.f Ω est un sous-ensemble fini de R.::::::::::::::::::::::::::Exemple d’une fonction étagée : Soit n N. φ =nPi=1ai1Ai , ai R, Ai T .φ est mesurable car combinaison linéaire de fonctions mesurables.φ prend un nombre fini de valeurs aii=1,...,nDonc φ est une fonction T -étagée.NotationsEΩ, T =nf : Ω→R T - étagéesoE+Ω, T =nf : Ω→0, + T - étagéeso4/24
Page 5 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesReprésentation canonique d’une fonction étagéeSoit f une fonction étagée. Désignons par a1, . . . , am les éléments de f Ω, lasuite ai1im étant strictement croissante, et posons pour tout i 1, . . . , mAi = f 1ai.Les sous-ensembles A1, A2, . . . , Am de Ωsont non vides, mesurables, deux àdeux disjoints et de réunion Ω. Ainsi f s’écrit sous la formef =mXi=1ai1Ai1f mesurable, ai un borélien donc f 1aiest mesurable.Pour i ̸= j, x Ai Aj ⇒f x = ai et f x = aj, impossible car ai ̸= aj doncAi Aj = .Inversement, étant données une suite strictement croissante ai1imd’éléments de R et une suite Ai1im de sous-ensembles de Ω, mesurables,non vides, deux à deux disjoints et dont la réunion est Ω, il existe une fonctionétagée f de Ωdans R et une seule telle quef =mXi=1ai1Ai .a1, . . . , am, A1, . . . , Amle couple canonique de f et 1 est laéiid f5/24
Page 6 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positives1Soit A T \ . La fonction u = 1A est étagée et a pourreprésentation canoniqueu = 0 × 1AC + 1 × 1A.2Ω= R, T = BR. Soit φ = 10,+, son écriture canonique est :φ = 0 × 1,0 + 1 × 10,+.D’autres écritures non canoniques de φ :φ=0za1×1,0 +1za2×10,1 +1za3×11,+a2 = a3 =⇒pas canoniqueφ= 0 × 1 , 0zA1+ 13 × 10, + z A2+ 23 × 10, + z A3A2 A3 ̸= =⇒pas canoniqueExemples6/24
Page 7 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesSoient f et g deux fonctions étagées sur Ω, α et β deux réels alors lesfonctions suivantesαf + βg,fg,supf , g etinff , gsont des fonctions étagées sur Ω.Opérations sur les fonctions étagées7/24
Page 8 : Intégrale d’une fonction étagée positive
Page 9 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesDéfinitionSoit φ E+Ω, T etmXi=1ai1Ai sa représentation canonique. On appelleintégrale de φ sur Ωpar rapport à la mesure µ et on noteZΩφdµ ouZΩφxdµx, la sommemXi=1aiµAi.En vertu de la convention 0 × µA = 0 si µA = +, la sommemXi=1aiµAia toujours un sens dans 0, + puisque chaque terme aiµAi appartient à0, +.On dit qu’une fonction étagée et positive φ est µ-intégrable siZΩφdµ +.9/24
Page 10 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesOn prend Ω, T =R, BRet φ = 1R. Il est clair que φ E+Ω, T .Pour µ = λ, on aZRφdλ = λR = +.Pour µ = δ0, on aZRφdδ0 = δ0R = 1ExemplesDéfinitionSoit φ E+Ω, T etmXi=1ai1Ai sa représentation canonique. Soit A une partiemesurable. On définit l’intégrale de φ sur A :ZAφdµ =ZΩφ1Adµ =mXi=1aiµAi A.10/24
Page 11 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesLe calcul de l’intégrale d’une fonction étagée à partir de la définition nécessitela décomposition canonique. Le lemme suivant permet d’alléger le recourssystématique à cette décomposition.LemmeSoit φ une fonction étagée positive telle que φ =pXi=1ti1Ci où Ci sont desensembles mesurables et disjoints deux à deux et ti sont des constantes pasforcément distinctes alorsZΩφdµ =pXi=1tiµCi.11/24
Page 12 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positives1Si φ E+Ω, T et si r 0, +, alorsZrφdµ = rZφdµ.2Si φ E+Ω, T et si ψ E+Ω, T alorsZφ + ψdµ =Zφdµ +Zψdµ.3Si φ E+Ω, T et si ψ E+Ω, T alorsφ ψ ⇒Zφdµ Zψdµ.4Si φnnN est une suite croissante de fonctions étagées positivesqui tend µ-p.p vers une fonction étagée φ, alors la suiteZφndµnNtend versZφdµ :limn→+Zφndµ=Zlimn→+φndµ =Zφdµ.Propriétés.::::::::::::Démonstration. Voir Notes de cours.12/24
Page 13 : Intégration de fonctions mesurables positivesOn note L+Ω, T l’ensemble des fonctions mesurables et positivesL+Ω, T =nf : Ω→0, +,T , BR+-mesurables.oLe théorème suivant nous permettra de faire le lien entre les fonctionsétagées positives et les fonctions mesurables positives. Il sera d’une grandeutilité dans la démonstration de beaucoup de propriétés dans les exercices.Si f L+Ω, T , il existe une suite croissante φnn dans E+Ω, T telle queφnn converge simplement vers f sur Ω.Si de plus, f est bornée, alors φnn converge uniformément vers f sur Ω.Dans ce cours, Ωdésigne un ensemble quelconque non vide, T une tribu de parties de Ωet µune mesure positive sur T . On considère l’espace mesuré Ω, T , µ.
Page 14 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesSoit f L+Ω, T . On appelle intégrale de Lebesgue de f sur Ωpar rapport àla mesure µ, et on noteZΩfdµ ouZΩf xdµx, l’élément de 0, + suivantf = supZφdµ,φ E+Ω, T , φ f.Autrement dit,RΩfdµ = supZφdµ,φ E+Ω, T , φ f.Plus généralement, si A T , on poseZAfdµ =ZΩf 1Adµ.14/24
Page 15 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesUne fonction mesurable intégrableBien distinguer le fait queZΩfdµ a toujours un sens dans 0, + et lefait queZΩfdµ est finie, c’est à direZΩfdµ 0, +. D’où la définitionsuivante :Mise en gardeDéfinitionSoit f L+Ω, T . On dit que f est µ-intégrable sur X ou simplementintégrable quand il n’y a pas de risque de confusion si l’intégraleZΩfdµ estfinie :ZΩfdµ +.15/24
Page 16 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesSoient f et g deux fonctions mesurables et positives sur Ω. Soient A et B deuxensembles mesurables. α 0, +.1ZΩαf dµ = αZΩfdµ Homogénéité positive.La démonstration découle aisément de la définition de l’intégrale d’une fonctionmesurable positive et en distinguant les cas α = 0 et α 0.2ZΩf + g dµ =ZΩfdµ +ZΩgdµ Additivité.La démonstration découle du théorème 1 et du théorème de la convergencemonotone.3 f g =⇒ZΩfdµ ZΩgdµ Croissance de l’intégrale.4A B =⇒ZAfdµ ZBfdµ.Règles opératoires des intégrales de fonctions mesurables et positives16/24
Page 17 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positives5Soit Aii une famille d’ensembles mesurables et disjoints deux àdeux, alorsZSi1Aif dµ =Xi1ZAifdµ.6Si N est µ-négligeable alorsZNfdµ = 0 etZΩ\Nfdµ =ZΩfdµ.7f = 0 µ-p.p si et seulement siZΩfdµ = 0.8Si f L+Ω, T et siZΩfdµ +, alors x Ω,f x = +est µ-négligeable.Règles opératoires des intégrales de fonctions mesurables et positives::::::::::::Démonstration. Voir Notes de cours.17/24
Page 18 : Principaux théorèmes d’intégration defonctions mesurables positivesLe développement de la théorie de l’intégration sur L+Ω, T repose surun important théorème de convergence des intégrales, propre aux suitescroissantes de fonctions mesurables et positives, qui permet sous unminimum d’hypothèses de commuter "intégration" et "passage à lalimite".En l’absence de l’hypothèse de croissance sur la suite de fonctions deL+Ω, T , on a tout de même un résultat partiel.
Page 19 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesThéorème de la convergence monotone ou de Beppo-LeviThéorème ♣♣Soit fnnN une suite croissante de fonctions de L+Ω, T qui tend µ-p.p versune fonction f , alors1f L+Ω, T .2La suiteZfn dµnNconverge en croissant versZf dµ :limn→+ZΩfndµ =ZΩlimn→+fndµ.19/24
Page 20 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesUne application du théorème de la convergence monotone::::::::::Conséquence:: Soit AnnN une suite d’ensembles de T , telle que An An+1pour n N alorslimn→+µ An = µ SnNAn.La fonction indicatrice 1An est mesurable car An est mesurable.La fonction indicatrice 1An est positive.La fonction indicatrice 1An est croissante car An An+1.limn→+1An = 1SnAn .D’après le théorème de Beppo-Lévilimn→+ZΩ1An dµ =ZΩ1SnAn dµ. Et commeZΩ1An dµ = µAnalorslimn→+µAn = µ nAnN!.20/24
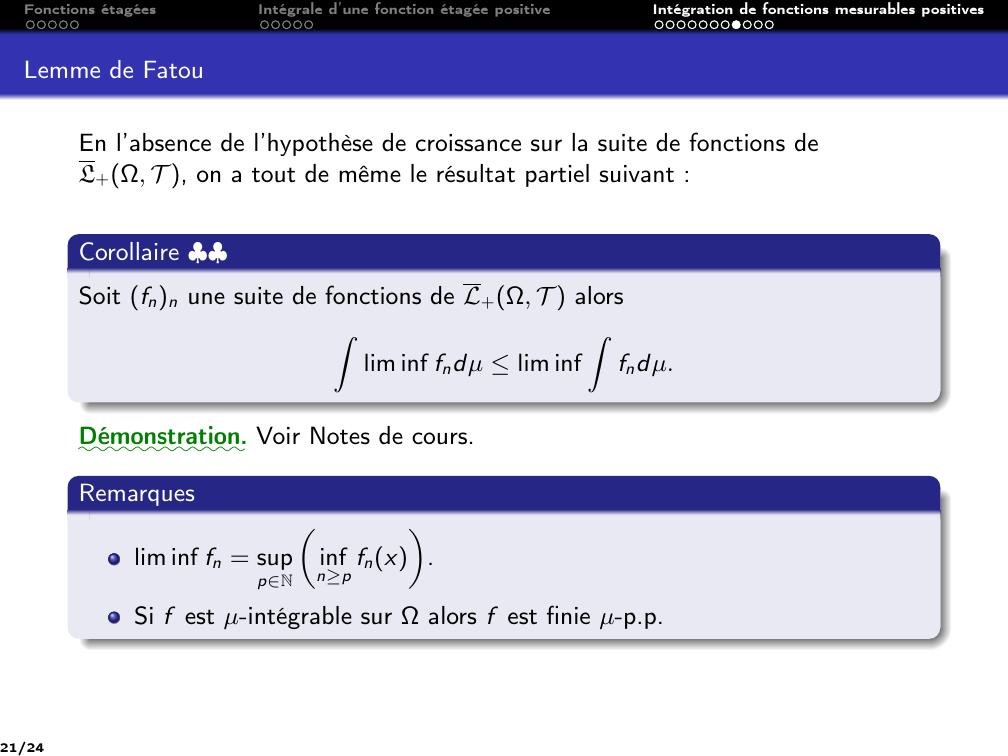
Page 21 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesLemme de FatouEn l’absence de l’hypothèse de croissance sur la suite de fonctions deL+Ω, T , on a tout de même le résultat partiel suivant :Corollaire ♣♣Soit fnn une suite de fonctions de L+Ω, T alorsZlim inf fndµ lim infZfndµ.::::::::::::Démonstration. Voir Notes de cours.Remarqueslim inf fn = suppNinfnp fnx.Si f est µ-intégrable sur Ωalors f est finie µ-p.p.21/24
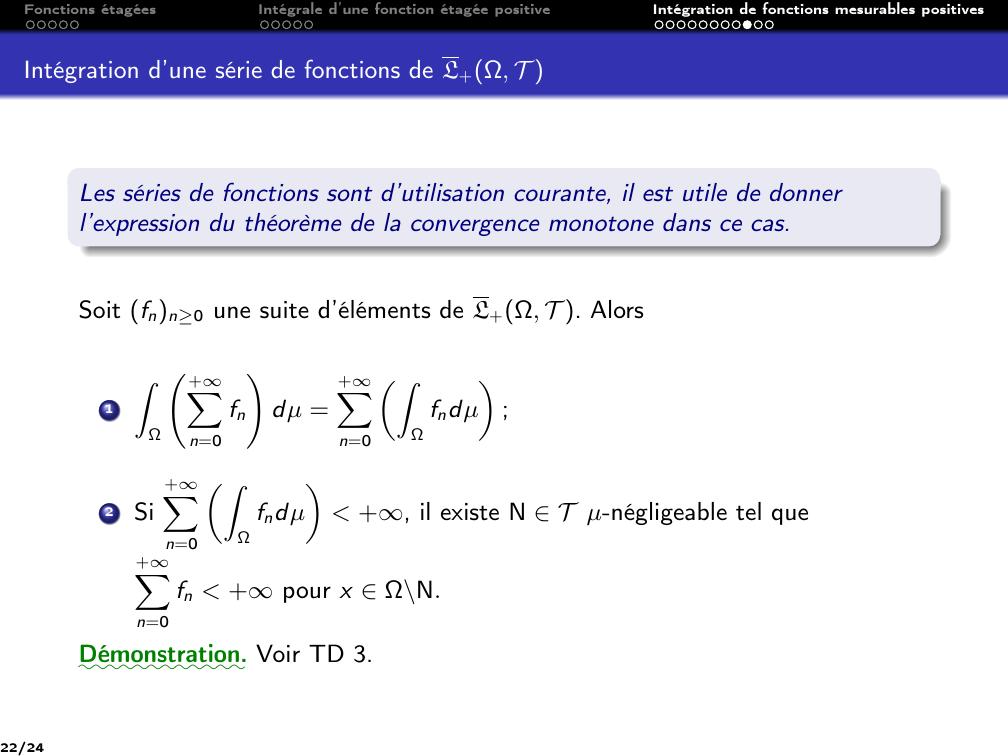
Page 22 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesIntégration d’une série de fonctions de L+Ω, T Les séries de fonctions sont d’utilisation courante, il est utile de donnerl’expression du théorème de la convergence monotone dans ce cas.Soit fnn0 une suite d’éléments de L+Ω, T . Alors1ZΩ +Xn=0fn!dµ =+Xn=0ZΩfndµ;2Si+Xn=0ZΩfndµ +, il existe N T µ-négligeable tel que+Xn=0fn +pour x Ω\N.::::::::::::Démonstration. Voir TD 3.22/24
Page 23 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesIntégration au sens de Riemann et au sens de LebesgueEn pratique, on utilisera souvent des intégrales par rapport à la mesure deLebesgue, les théorèmes suivants expriment des cas où on peut se ramener à uncalcul d’intégrale au sens de Riemann. Les propriétés suivantes seront valablespour des fonctions mesurables positives ou de signe quelconque.Soit f : a, b →R une fonction mesurable.1Si f est Riemann intégrable, alors f est Lebesgue intégrable et lesintégrales sont égales, autrement ditZa,bf dλ =Z baf x dx2Si f est bornée alors f est Riemann intégrable ssiλ x a, b tel que f n’est pas continue en x = 0,autrement dit, si et seulement si l’ensemble des points de discontinuitésde f dans a, b est de mesure de Lebesgue nulle.23/24
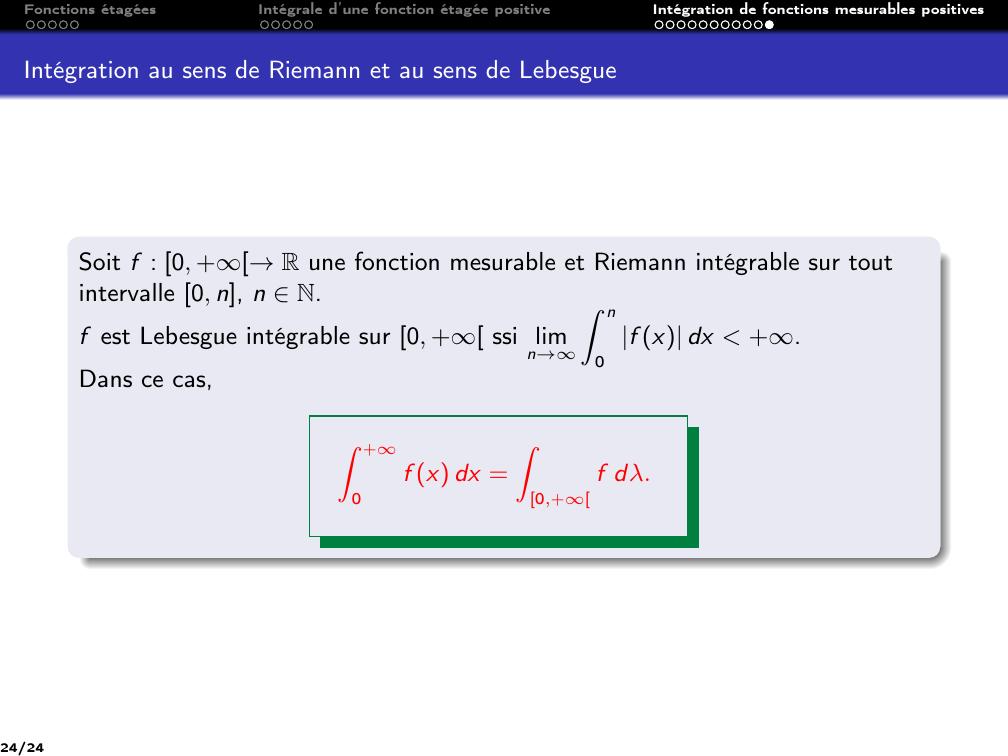
Page 24 : Fonctions étagéesIntégrale d’une fonction étagée positiveIntégration de fonctions mesurables positivesIntégration au sens de Riemann et au sens de LebesgueSoit f : 0, +→R une fonction mesurable et Riemann intégrable sur toutintervalle 0, n, n N.f est Lebesgue intégrable sur 0, + ssi limn→Z n0f x dx +.Dans ce cas,Z +0f x dx =Z0,+f dλ.24/24
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24