CM3 Integration

Télécharger le CM3 Integration en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

Page 1 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration1Intégrale d'une fonction en escalier2Intégrale d'une fonction continue par morceaux3Calcul IntégralPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variables4Recherche de primitivesIntégration des éléments simplesIntégration des fonctions trigonométriques5Approximations d'intégrales, sommes de RiemannD. CransacAnalyse

Page 2 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégrale d'une fonction en escalierD. CransacAnalyse

Page 3 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannSubdivisionDénitionOn appelle subdivision d'un segment a, b toute suite nies = x0, x1, . . . , xn de nombres réels tels que :a = x0 x1 · · · xn = b.ax0x1 x2x3x4x5 . . .bxnD. CransacAnalyse

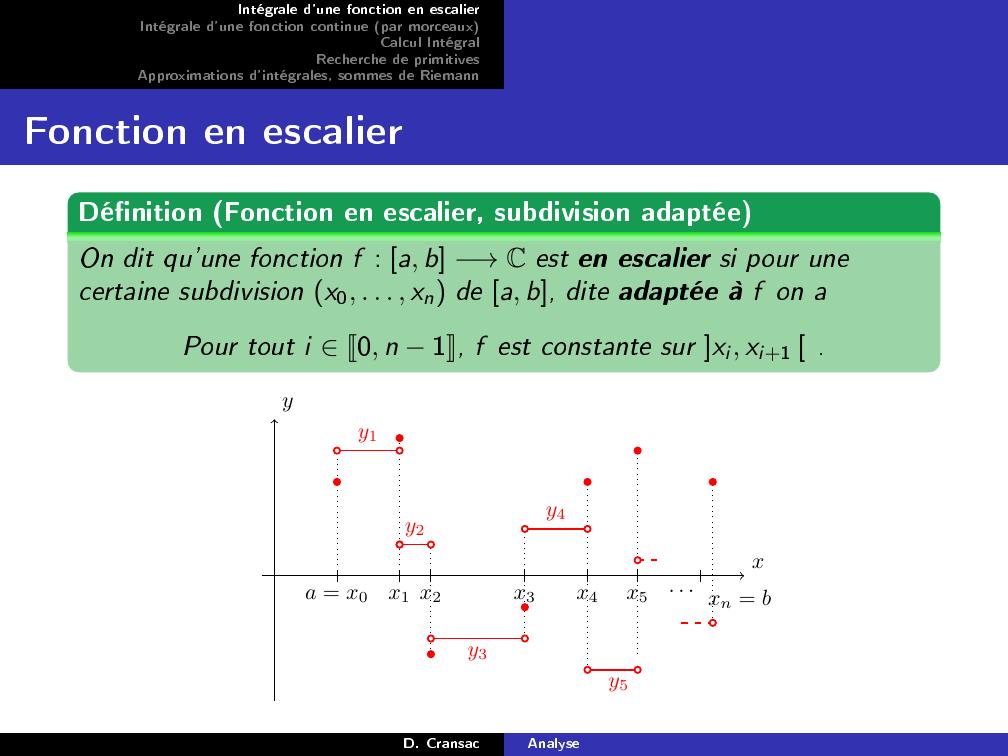
Page 4 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannFonction en escalierDénition Fonction en escalier, subdivision adaptéeOn dit qu'une fonction f : a, b →C est en escalier si pour unecertaine subdivision x0, . . . , xn de a, b, dite adaptée à f on aPour tout i J0, n 1K, f est constante sur xi, xi+1 .y1y2y3y4y5yxa = x0x1 x2x3x4x5. . . xn = bD. CransacAnalyse

Page 5 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannNotation Au besoin on utilisera la notationEa;b = φ : a; b →R en escalier sur a; b Théorème Propriétés élémentaires des fonctions en escalierSoient f : a, b →C et g : a, b →C en escalier.Lorsqu'on ajoute un nombre ni de points à une subdivision de a, badaptée à f , le résultat est encore une subdivision de a, b adaptée àf .A fortiori, la réunion d'une subdivision de a, b adaptée à f et d'unesubdivision de a, b adaptée à g est une subdivision de a, badaptée à f ET à g.Pour tous λ, µ C, λf + µg est une fonction en escalier sur a, b,de même que f , Ref , Imf et fg.D. CransacAnalyse

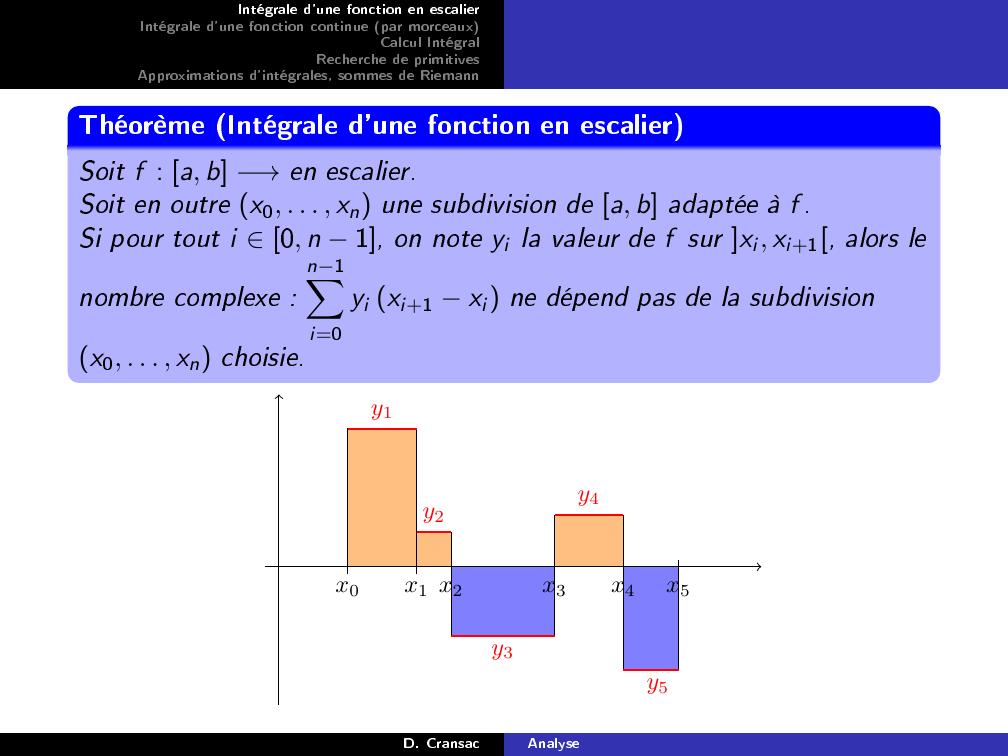
Page 6 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannThéorème Intégrale d'une fonction en escalierSoit f : a, b →en escalier.Soit en outre x0, . . . , xn une subdivision de a, b adaptée à f .Si pour tout i 0, n 1, on note yi la valeur de f sur xi, xi+1, alors lenombre complexe :n1Xi=0yi xi+1 xi ne dépend pas de la subdivisionx0, . . . , xn choisie.y1y2y3y4y5x0x1 x2x3x4x5D. CransacAnalyse

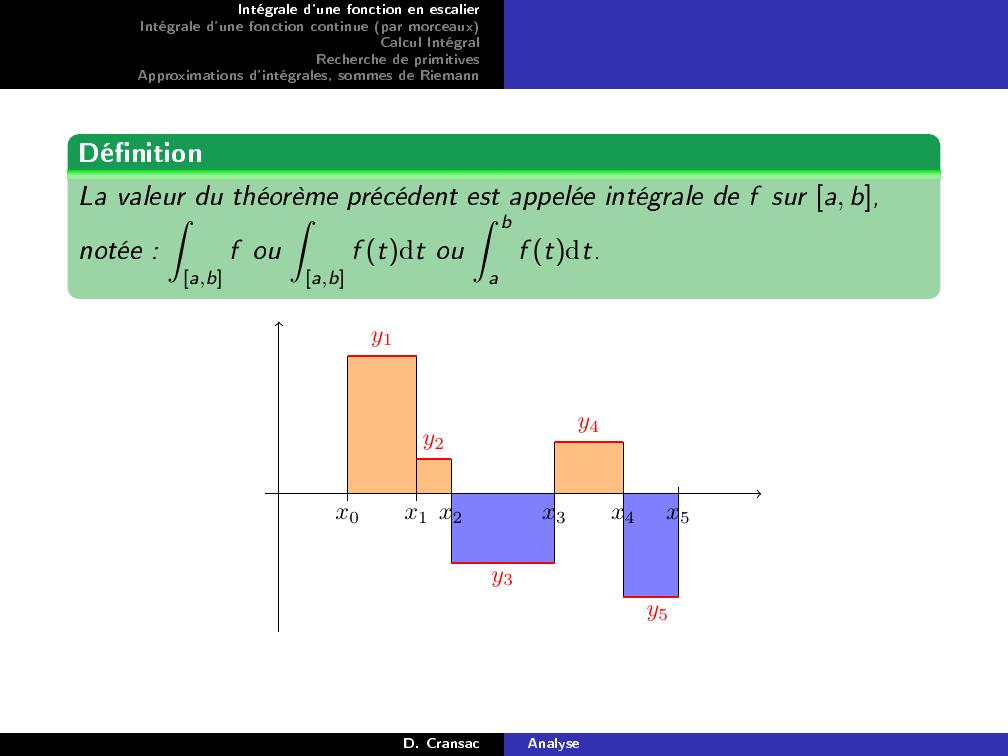
Page 7 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDénitionLa valeur du théorème précédent est appelée intégrale de f sur a, b,notée :Za,bf ouZa,bf tdt ouZ baf tdt.y1y2y3y4y5x0x1 x2x3x4x5D. CransacAnalyse

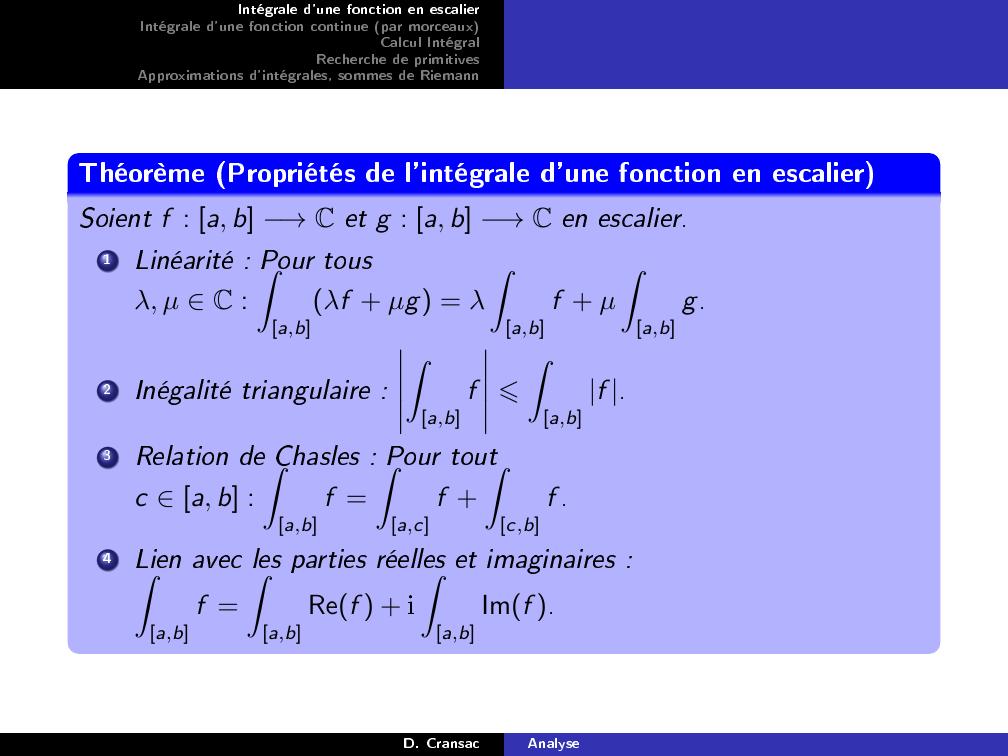
Page 8 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannThéorème Propriétés de l'intégrale d'une fonction en escalierSoient f : a, b →C et g : a, b →C en escalier.1Linéarité : Pour tousλ, µ C :Za,bλf + µg = λZa,bf + µZa,bg.2Inégalité triangulaire :Za,bf ⩽Za,bf .3Relation de Chasles : Pour toutc a, b :Za,bf =Za,cf +Zc,bf .4Lien avec les parties réelles et imaginaires :Za,bf =Za,bRef + iZa,bImf .D. CransacAnalyse

Page 9 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.Donnons-nous λ, µ C, c a, b et une subdivision x0, . . . , xn de a, badaptée à f ET à g - mais donc aussi à λf + µg, f , Ref et Imf .1Za,bλf + µg =n1Xi=0Valeur de λf +µgzλf + µgxi + xi+12xi+1 xi= λn1Xi=0fxi + xi+12xi+1 xi + µn1Xi=0gxi + xi+12xi+1 xi= λZa,bf + µZa,bgD. CransacAnalyse

Page 10 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.2D'après l'inégalité triangulaire sur C :Za,bf =n1Xi=0fxi + xi+12xi+1 xi⩽n1Xi=0fxi + xi+12 xi+1 xi =Za,bf .D. CransacAnalyse

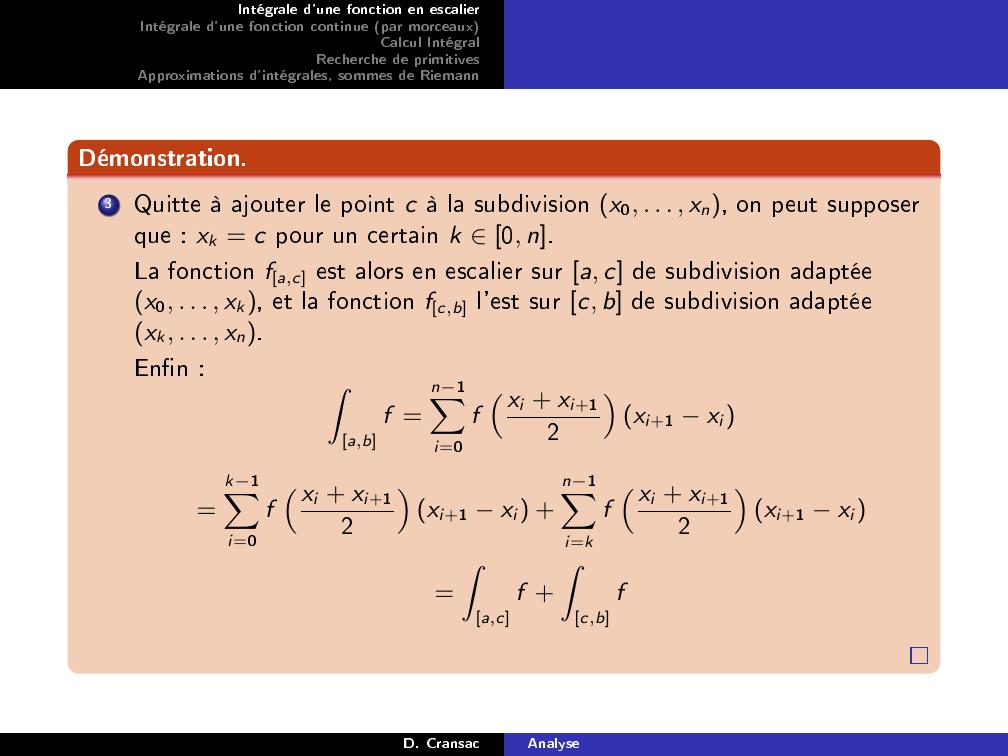
Page 11 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.3Quitte à ajouter le point c à la subdivision x0, . . . , xn, on peut supposerque : xk = c pour un certain k 0, n.La fonction fa,c est alors en escalier sur a, c de subdivision adaptéex0, . . . , xk, et la fonction fc,b l'est sur c, b de subdivision adaptéexk, . . . , xn.Enn :Za,bf =n1Xi=0fxi + xi+12xi+1 xi=k1Xi=0fxi + xi+12xi+1 xi +n1Xi=kfxi + xi+12xi+1 xi=Za,cf +Zc,bfD. CransacAnalyse

Page 12 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.4Cela découle de la linéarité de l'intégrale pour λ = 1 et µ = i.On peut aussi le démontrer directement :Za,bf =n1Xi=0fxi + xi+12xi+1 xi=n1Xi=0Ref xi + xi+12xi+1 xi + in1Xi=0Imf xi + xi+12xi+1 xi=Za,bRef + iZa,bImf D. CransacAnalyse

Page 13 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégrale d'une fonction continuepar morceauxD. CransacAnalyse

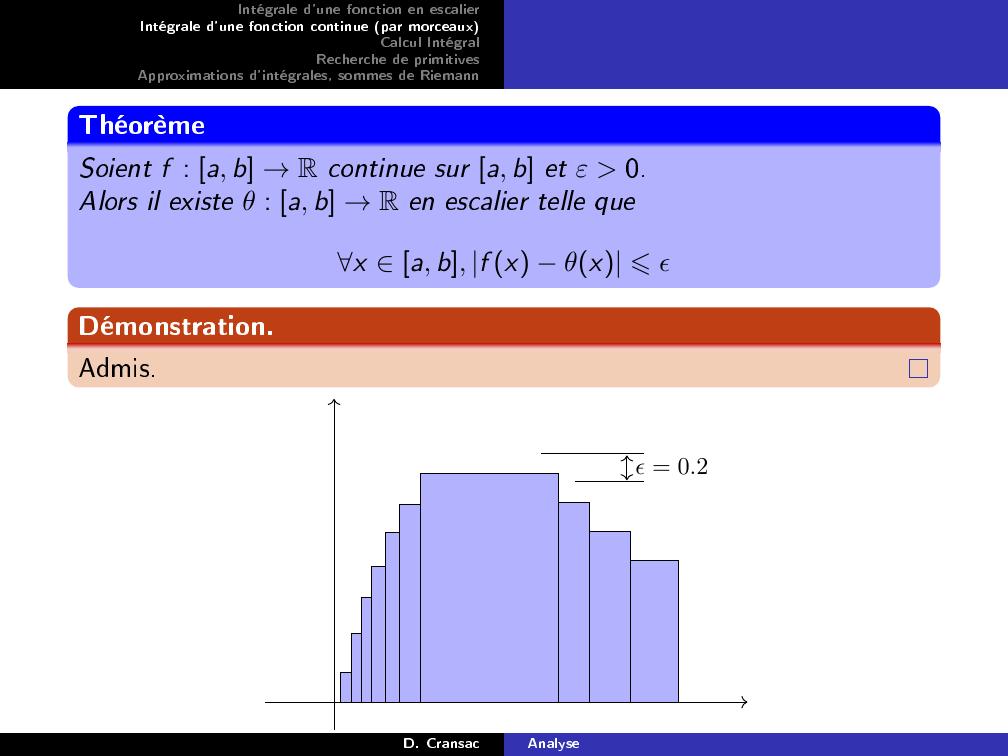
Page 14 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannThéorèmeSoient f : a, b →R continue sur a, b et ε 0.Alors il existe θ : a, b →R en escalier telle quex a, b, f x θx ⩽ϵDémonstration.Admis.ϵ = 0.2D. CransacAnalyse

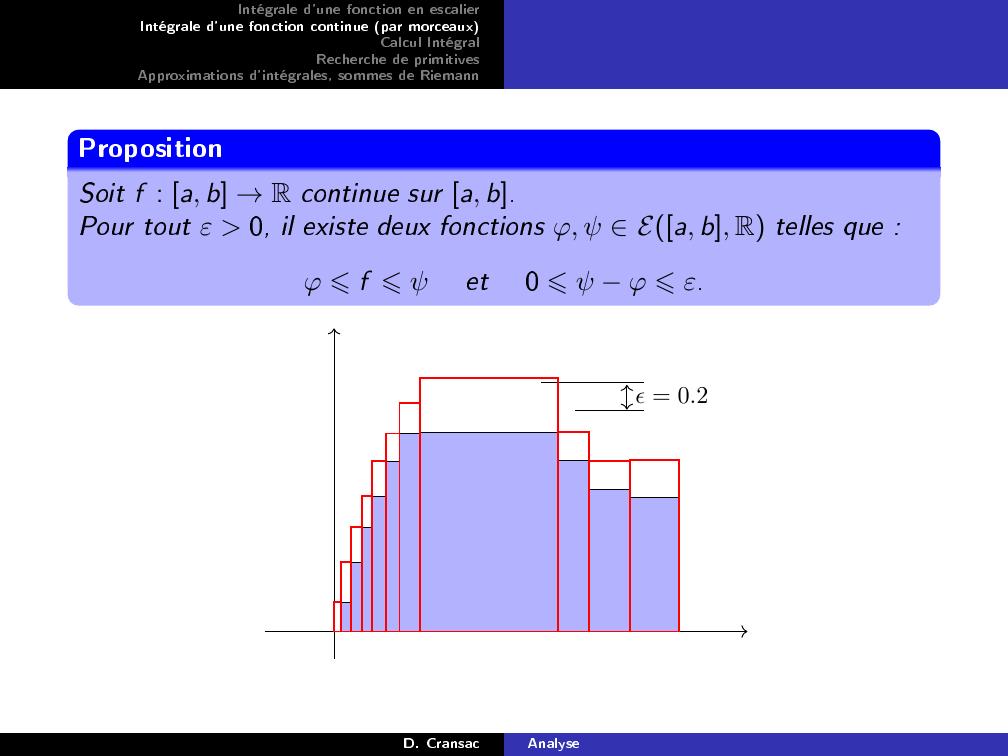
Page 15 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPropositionSoit f : a, b →R continue sur a, b.Pour tout ε 0, il existe deux fonctions ϕ, ψ Ea, b, R telles que :ϕ ⩽f ⩽ψet0 ⩽ψ ϕ ⩽ε.ϵ = 0.2D. CransacAnalyse

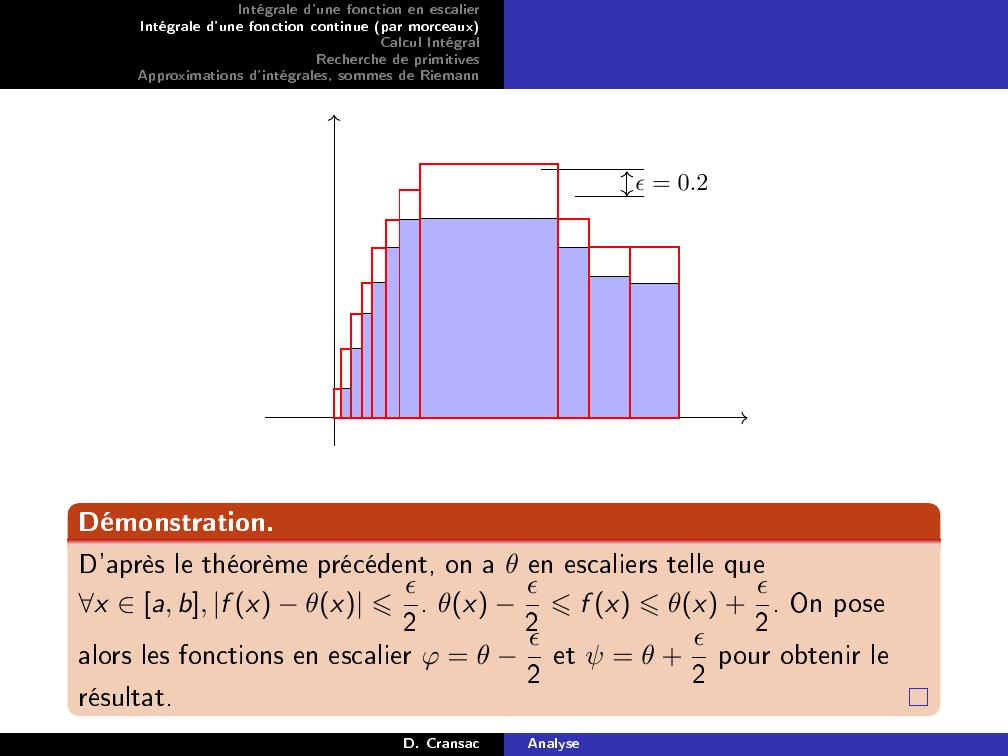
Page 16 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de Riemannϵ = 0.2Démonstration.D'après le théorème précédent, on a θ en escaliers telle quex a, b, f x θx ⩽ϵ2. θx ϵ2 ⩽f x ⩽θx + ϵ2. On posealors les fonctions en escalier ϕ = θ ϵ2 et ψ = θ + ϵ2 pour obtenir lerésultat.D. CransacAnalyse

Page 17 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannOn suppose à présent que f : a, b →R est une fonction bornéequelconque.ThéorèmeSi f : a, b →R est continue, alors :1Aa,bf =Z baφxdx φ en escalier et φ ⩽fadmet une bornesupérieure,2A+a,bf =Z baψxdx ψ en escalier et f ⩽ψadmet uneborne inférieure, et ces deux bornes sont égales.Notation Au besoin on utilisera les notationsEa;bf = φ en escalier sur a; b telle que φ ⩽f E+a;bf = ψ en escalier sur a; b telle que f ⩽ψD. CransacAnalyse

Page 18 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.La fonction f étant continue sur le segment a, b, elle est bornée sura, b.Posons m =infxa,b f x et M = supxa,bf x.Aa,bf est non vide puisqu'il contient la fonction constante m.Ainsi Aa,bf est une partie non vide de R.De plus pour tout ϕ Aa,bf , on a ϕ ⩽f ⩽M.Donc :Za,bϕ ⩽Za,bM = Mb a.L'ensemble Aa,bf est donc une partie non vide de R et majoréepar Mb a . Il possède donc une borne supérieure que l'on noteα.De même, A+a,bf est une partie non vide de R et minorée parmb a. Il possède donc une borne inférieure que l'on note β.D. CransacAnalyse

Page 19 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.Supposons β α.Alors, comme α est la borne sup de A, il existe φ en escalier telque φ ⩽f et β Za,bϕ α.Alors pour toute fonction ψ en escalier tel que f ⩽ψ, on aϕ ⩽f ⩽ψdoncZa,bϕ ⩽Za,bψDoncZa,bϕ ⩽β Ce qui est contradictoire avec β Za,bϕ. Doncα ⩽βD. CransacAnalyse

Page 20 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannAutre démonstrationDémonstration.Puisque pour tout ϕ en escalier telle que ϕ ⩽f et ψ en escalier telleque f ⩽ψ, on a ϕ ⩽ψ, on aZa,bϕ ⩽Za,bψ.AinsiZa,bψ est un majorant de Af , la borne supérieure α deAf est donc plus petite queZa,bψ.On obtient :Pour toute fonction en escalier ψ telle que f ⩽ψ,α ⩽Za,bψDe même, α est un minorant de A+a,bf , et β est le plus grand desminorants de cette partie. Donc α ⩽β.D. CransacAnalyse

Page 21 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.Soit ϵ 0.On sait qu'il existe ϕ Ea;bf et ψ Ea;bf telles queφ ⩽f ⩽ψ telles que pour tout x a, b, ψx ϕx ⩽ϵ.On a alors :Za,bψ Za,bϕ ⩽ϵb aOr par dénition de α et β, on a :Za,bϕ ⩽α ⩽β ⩽Za,bψD'où pour tout ε 0,on a0 ⩽β α ⩽Za,bψ Za,bϕ ⩽ϵb aFinalement, on a bien α = β.D. CransacAnalyse

Page 22 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDénitionSoit f : a, b →R une fonction continue.On appelle intégrale de f sur a, b le nombre réel notéZa,bf déni par :Za,bf = supZa,bϕ ϕ Ea,bf = infZa,bψ ψ E+a,bf Proposition LinéaritéSoient f , g : a, b →R continues et λ, µ R2.Za,bλf + µg = λZa,bf + µZa,bgD. CransacAnalyse

Page 23 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannProposition LemmeSoit ε 0.Si f : a, b →R continue et θ Ea,b telles que f θ ⩽ε, alorsZa,bf Za,bθ ⩽b aεDémonstration.On a θ ε ⩽f ⩽θ + ε, d'où par dénition de l'intégrale :Za,bθ ε ⩽Za,bf ⩽Za,bθ + εPar linéarité de l'intégrale des fonctions en escalier :Za,bf Za,bθ ⩽Za,bε ⩽b aε.D. CransacAnalyse

Page 24 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.On dénitθ1 tel que f θ1 ϵθ2 tel que g θ2 ϵh = λf + µgθ = λθ1 + µθ2I =Za,bθ = λZa,bθ1 + µZa,bθ2 par linéarité pour les fonctionsen escalier.On a :h θ ⩽λf θ1 + µg θ2 ⩽λ + µεPar le lemme :Za,bh I ⩽Za,bh Za,bθ ⩽b aλ + µεD. CransacAnalyse

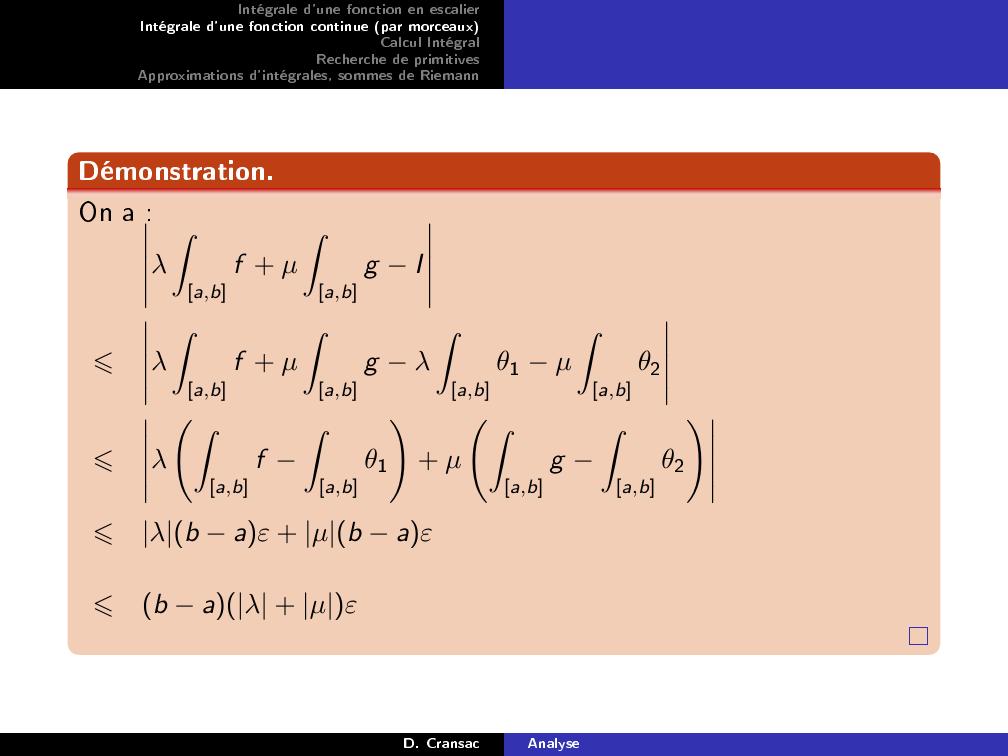
Page 25 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.On a :λZa,bf + µZa,bg I⩽λZa,bf + µZa,bg λZa,bθ1 µZa,bθ2⩽λ Za,bf Za,bθ1!+ µ Za,bg Za,bθ2!⩽λb aε + µb aε⩽b aλ + µεD. CransacAnalyse

Page 26 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.Finalement on obtient :=Za,bλf + µg λZa,bf + µZa,bg!=Za,bλf + µg I + I λZa,bf µZa,bg!=Za,bλf + µg I +I λZa,bf µZa,bg!⩽2b aλ + µε.Comme c'est vrai quelque soit ε 0, on en déduit = 0, et donc lalinéarité de l'intégrale.D. CransacAnalyse

Page 27 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannProposition Relation de ChaslesSoient f : a, b →R continues et c a, b.Za,bf =Za,cf +Zc,bf .Démonstration.Soit ϕ Ea,bf .On a alors :ϕa,c Ea,cf et ϕc,b Ec,bf .Par dénition de l'intégrale, on obtient :Za,bϕ =Za,cϕ +Zc,bϕ ⩽Za,cf +Zc,bfD. CransacAnalyse

Page 28 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.AinsiZa,cf +Zc,bf est un majorant de Aa,bf .Par dénition de la borne supérieure :Za,bf ⩽Za,qf +Zc,bfEn appliquant linéarité ce résultat à f , on en déduit l'inégalitéinverse, et donc :Za,bf =Za,cf +Zc,bfD. CransacAnalyse

Page 29 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannNotation.Soient a et b deux réels quelconques en particulier on ne suppose plusnécessairement a b.Soit f une fonction continue entre a et b.On dénit le réelZ baf xdx par :si a b,Z baf xdx =Za,bf xdx ;si a = b,Z baf xdx = 0 ;si b a,Z baf xdx = Zb,af xdx.La relation de Chasles et la linéarité sont alors vraies pour a, b, cquelconques.D. CransacAnalyse

Page 30 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPropositionSoient f , g : I →R continues sur un intervalle I et a, b I.1f ⩾0 et a ⩽b ⇒Z baf xdx ⩾0positivité de l'intégrale2f ⩽g et a ⩽b ⇒Z baf xdx ⩽Z bagxdx passage aux inégalités3a ⩽b ⇒Z baf xdx ⩽Z baf xdx inégalité de la norme4Si a ⩽b et m ⩽f ⩽M entre a et b, alorsmb a ⩽Z baf xdx ⩽Mb a.Attention Bien vérier a b.D. CransacAnalyse

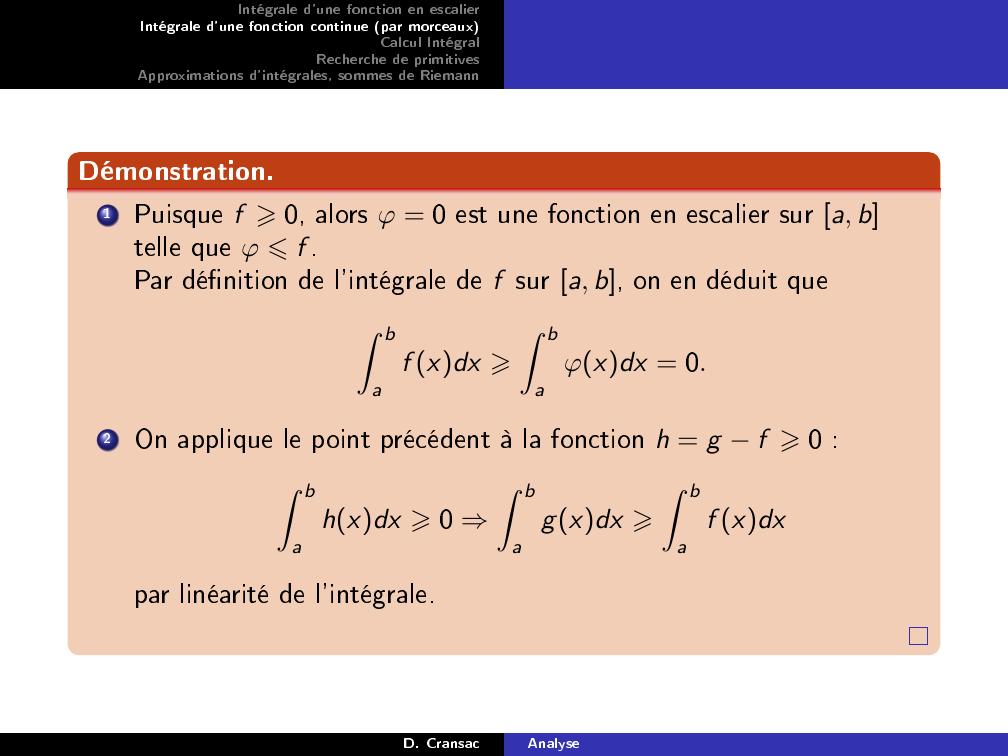
Page 31 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.1Puisque f ⩾0, alors ϕ = 0 est une fonction en escalier sur a, btelle que ϕ ⩽f .Par dénition de l'intégrale de f sur a, b, on en déduit queZ baf xdx ⩾Z baϕxdx = 0.2On applique le point précédent à la fonction h = g f ⩾0 :Z bahxdx ⩾0 ⇒Z bagxdx ⩾Z baf xdxpar linéarité de l'intégrale.D. CransacAnalyse

Page 32 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.3On a pour tout x a, b, f x ⩽f x ⩽f x. D'où parcroissance de l'intégrale :Z baf xdx ⩽Z baf xdx ⩽Z baf xdxAinsi, on obtientZ baf xdx ⩽Z baf xdx.4Il sut de prendre l'intégrale dans les inégalités m ⩽f ⩽M.Remarque. La majoration suivante, vraie également si b a, peut êtreutile :Z baf xdx Z baf x dxD. CransacAnalyse

Page 33 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDénitionLa valeur moyenne d'une fonction f : a, b →R continue est :µ =1b aZa,bfRemarque. La valeur moyenne est la constante µ qui vérieZa,bf =Za,bµD. CransacAnalyse

Page 34 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPropositionSoit f : a, b →R une fonction continue sur a, b et positive alorsZa,bf = 0 si et seulement si f est nulle sur a, b.Démonstration.⇐Si f est nulle, son intégrale est nulle.⇒Par contraposition, supposons que f n'est pas nulle sur a, b : c a, b tel quef c 0.D'après la dénition de la continuité de f en c avec ε = f c2:a ⩽α β ⩽b, x a, b, x α, β ⇒f x f c ⩽εAinsi pour tout x α, β, on a f x ⩽ℓc2 .En prenant l'intégrale, on en déduit donc que :Z baf xdx ⩾Z βαf xdx ⩾Z βαεdx = β αε 0.D. CransacAnalyse

Page 35 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannRemarque. Si f n'est pas supposée continue, le résultat est faux : parexemple f x = 0 sur 0, 1 et f 0 = f 1 = 1 est positive, non nullemaisZ 10f = 0.D. CransacAnalyse

Page 36 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesCalcul intégralD. CransacAnalyse

Page 37 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesDénitionSoient I un intervalle et f : I 7→K une fonction continue.On appelle primitive de f sur I toute fonction F de classe C1 sur I dontla dérivée est f .Proposition Lien entre deux primitives d'une même fonctionDeux primitives d'une même fonction sur un intervalle dièrent d'uneconstante c'est à dire :Si F1 et F2 sont des primitives de f alorsC K, F1 F2 = CDémonstration.Si F1 et F2 sont deux primitives de la fonction F sur I, alorsF1 F2′ = F ′1 F ′2 = f f = 0 donc la fonction F1 F2 est constantesur I.D. CransacAnalyse

Page 38 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesProposition Théorème fondamental de l'analyseSoient I un intervalle de R, f : I →K une fonction continue, et a I.1La fonction F :I→Kx7→Z xaf tdtest l'unique primitive de fs'annulant en a.2Pour toute primitive F : I →K de f , on aZ xaf tdt = Fx FaD. CransacAnalyse

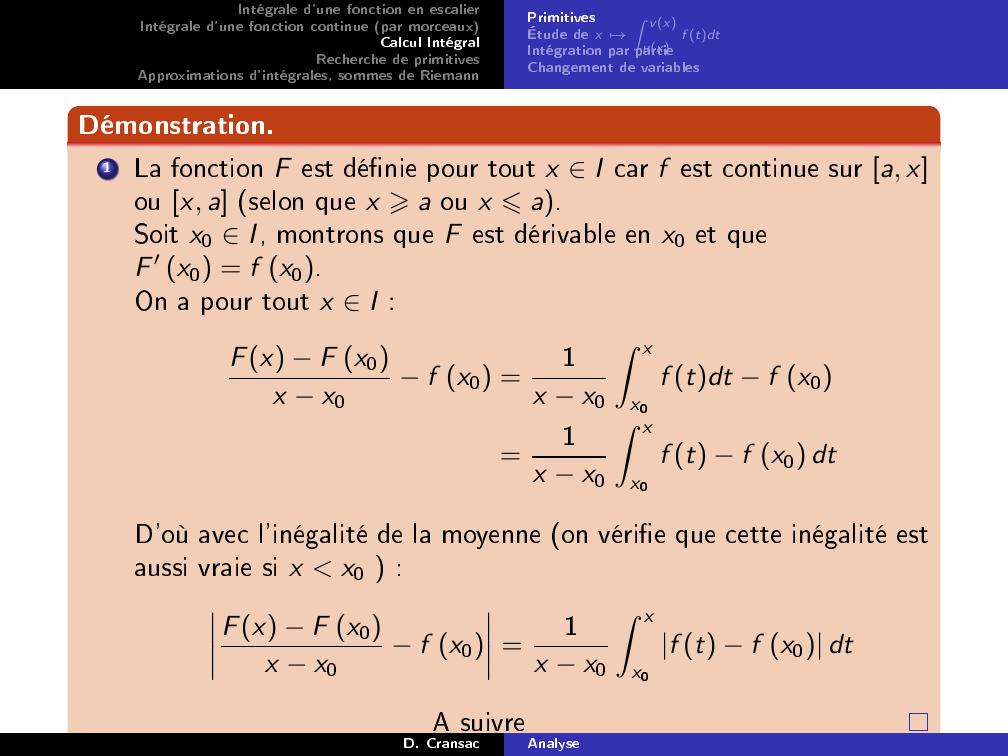
Page 39 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesDémonstration.1La fonction F est dénie pour tout x I car f est continue sur a, xou x, a selon que x ⩾a ou x ⩽a.Soit x0 I, montrons que F est dérivable en x0 et queF ′ x0 = f x0.On a pour tout x I :Fx F x0x x0f x0 =1x x0Z xx0f tdt f x0=1x x0Z xx0f t f x0 dtD'où avec l'inégalité de la moyenne on vérie que cette inégalité estaussi vraie si x x0 :Fx F x0x x0f x0 =1x x0Z xx0f t f x0 dtA suivreD. CransacAnalyse

Page 40 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesDémonstration.1suite Or f est continue en x0, donc :ε 0, α 0, t I, t x0 ⩽α ⇒f t f x0 ⩽ε.Alors pour tout x I, x x0 ⩽α, on a pour toutt x0, x , f t f x0 ⩽ε et en reportant :Fx F x0x x0f x0 =1x x0Z xx0εdt ⩽ε.Ainsi on a montré que limx→x0Fx F x0x x0= f x0. Donc F estdérivable en x0 et F ′ x0 = f x0. Puisque c'est vrai pour toutx0 I et que f est continue, on en déduit nalement que F est declasse C1 et que F ′ = f .A suivreD. CransacAnalyse

Page 41 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesDémonstration.1suiteReste à montrer que F est l'unique primitive de f qui s'annule en a.Si G satisfait aussi ces propriétés, alors on a vu qu'il existe C Ktel que F = G + C.En évaluant en x = a, on obtient C = 0, et donc F = G.2Soit h : x 7→Fx Fa. Alors h est dérivable sur I commecombinaison linéaire de fonctions qui le sont, et pourx I, h′x = F ′x = f x. De plus ha = 0, donc h est uneprimitive de f s'annulant en a. D'après l'unicité du point précédent,on a pour tout x I, hx =Z xaf tdt. D'où le résultat.D. CransacAnalyse

Page 42 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesNotations.Le symboleZf xdx introduit par Leibniz désigne une primitivequelconque de f . Elle est donc dénie à une constante additive près.La fonction x 7→Z xaf t dt est la primitive de f s'annulant en a.D. CransacAnalyse

Page 43 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesPropositionSoient I, J deux intervalles de R, u, v : I →R de classe C1 telles queuI, vI J et f : J →K continue. Alors la fonctiong : x 7→Z vxuxf tdt est dénie sur I, de classe C1 etx I, g ′x = f vxv ′x f uxu′x.Démonstration.Pour tout x I, on a ux, vx J et J est un intervalle. Donc ux, vx J etgx existe pour tout x I.La fonction f : J →K étant continue sur J, elle admet une primitive F de classe C1sur J. On a alors pour tout x I,gx = Fvx FuxLa fonction g est donc de classe C1 en tant que diérence et composées de fonctionsde classe C1, et pour tout x I, on a :g′x = v′xf vx u′xf uxD. CransacAnalyse

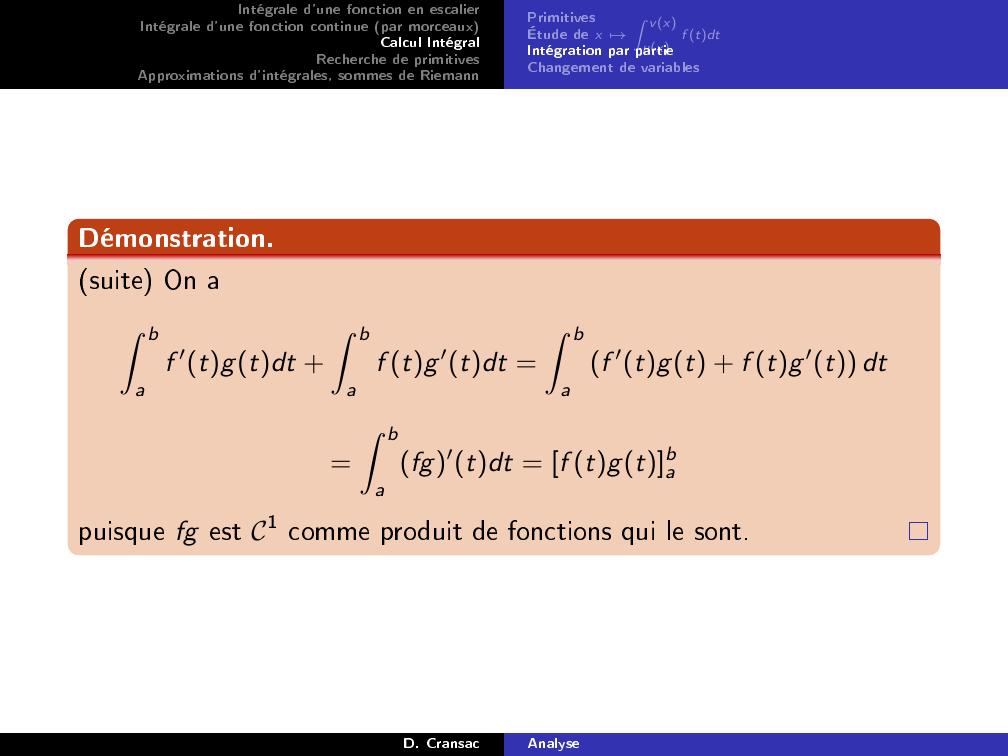
Page 44 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesProposition Intégration par partiesSoient f et g sont deux fonctions de classe C1 sur a, b à valeur dans K.Z baf ′tgtdt = f tgtba Z baf tg ′tdtDémonstration.On aZ baf ′tgtdt +Z baf tg ′tdt =Z baf ′tgt + f tg ′t dt=Z bafg′tdt = f tgtbapuisque fg est C1 comme produit de fonctions qui le sont.D. CransacAnalyse

Page 45 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesDémonstration.suite On aZ baf ′tgtdt +Z baf tg ′tdt =Z baf ′tgt + f tg ′t dt=Z bafg′tdt = f tgtbapuisque fg est C1 comme produit de fonctions qui le sont.D. CransacAnalyse

Page 46 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesProposition Changement de variableSoient I un intervalle de R et f : I →K une fonction continue sur I.Soient ϕ : a, b →I une fonction de classe C1 sur a, b. AlorsZ ϕbϕaf xdx =Z baf ϕtϕ′tdt.On dit qu'on a eectué le changement de variables x = ϕt.Démonstration.Si F est une primitive de f , alors F ◦ϕ est une primitive de f ◦ϕ × ϕ′ et on a :Z ϕbϕaf xdx = Fxϕbϕa = Fϕb Fϕa.Z baf ◦ϕtϕ′tdt = F ◦ϕtba = Fϕb Fϕa.D. CransacAnalyse

Page 47 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannPrimitivesÉtude de x 7→Z vxuxf tdtIntégration par partieChangement de variablesEn pratique, il faut modier trois élémentsla variable x = φt,l'élément diérentiel dx = φ′tdt,les bornes de l'intégrale : si t varie entre a et b, x = φt doit varierentre φa et φb.PropositionSoit f : R →K une fonction continue.1si f est périodique de période T, alors pour tous a, b R :Z baf tdt =Z b+Ta+Tf tdt,Z a+Taf tdt =Z b+Tbf tdt2si f est une fonction paire, alors pour tout a R :Z aaf tdt = 2Z a0f tdt.3si f est une fonction impaire, alors pour tout a R :Z aaf tdt = 0.D. CransacAnalyse

Page 48 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesRecherche de primitivesD. CransacAnalyse

Page 49 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesRappelons au cas où que nous savons primitiver aisément un certainnombre de fonctions classiques :les fonctions de la forme x 7→eax cosbx ou x 7→eax sinbx aveca, b Rgrâce à l'exponentielle complexe,les fonctions de la forme x 7→sinm x cosn x avec m, n N parlinéarisation,les fonctions rationnelles par décomposition en éléments simples.Les tableaux ci-dessous donnent enn la liste des quelques primitives qu'ilfaut connaitre à tout prix.FonctionPrimitiveexexln xx ln x x1xln xxαα ̸= 1xα+1α + 1D. CransacAnalyse

Page 50 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des éléments simplesSoit PxQx une fraction rationnelle, où Px, Qx sont des polynômes àcoecients réels.Alors la fraction PxQx s'écrit comme somme d'un polynôme Ex Rxla partie entière et d'éléments simples d'une des formes suivantes :γx x0kouαx + βax2 + bx + ck avec b2 4ac 0où α, β, γ, a, b, c R et k N\0.1Intégration du polynôme Ex. On sait faire.2Intégration de l'élément simpleγx x0x3Intégration de l'élément simpleax + βax2 + bx + cx .D. CransacAnalyse

Page 51 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des éléments simples2Intégration de l'élément simpleγx x0x .1Si k = 1 alorsZγdxx x0 = γ ln x x0 + c0 sur , x0 oux0, + .2Si k ⩾2 alorsZγdxx x0k = γZx x0k dx =γk + 1 x x0k+1 + c0 sur , x0 ou x0, +.D. CransacAnalyse

Page 52 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des éléments simples3Intégration de l'élément simpleax + βax2 + bx + cx . On écrit cette fractionsous la formeαx + βax2 + bx + ck = γ2ax + bax2 + bx + ck + δ1ax2 + bx + ckaPour le terme2ax + bax2 + bx + ck1Si k = 1, calcul deZ2ax + bax2 + bx + c dx =Z u′xux dx =ln ux + c0 = lnax2 + bx + c + c0.2Si k ⩾2, calcul deZ2ax + bax2 + bx + c2 dx =Zu′xuxk dx =1k + 1 uxk+1 + c0 =1k + 1ax2 + bx + ck+1 + c0.D. CransacAnalyse

Page 53 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des éléments simplesbPour le terme1ax2 + bx + ck1Si k = 1, calcul deZ1ax2 + bx + c dx. Par un changement devariable u = px + q on se ramène à calculer une primitive du typeZduu2 + 1 = arctan u + c0.2Si k ⩾2, calcul deZax2+bx+ck dx. On eectue le changement devariable u = px + q pour se ramener au calcul de Ik =Zduu2 + 12 .Une intégration par parties permet de passer de Ik à Ik1.D. CransacAnalyse

Page 54 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesExemple Calculons I2. Partant de I1 =Zduu2 + 1 on pose f =1u2 + 1 etg ′ = 1. La formule d'intégration par partiesZfg ′ = fg Z ′f ′g donneavec f ′ = 2uu2 + 12 et g = u I1 =Zduu2 + 1 =uu2 + 1+Z2u2duu2 + 12 =uu2 + 1+ 2Z u2 + 1 1u2 + 12 du=uu2 + 1+ 2Zduu2 + 1 2Zduu2 + 12 =uu2 + 1+ 2I1 2I2On en déduit I2 = 12I1 + 12uu2 + 1 + c0. Mais comme I1 = arctan u alorsI2 =Zduu2 + 12 = 12 arctan u + 12uu2 + 1 + c0D. CransacAnalyse

Page 55 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des fonctions trigonométriquesOn peut aussi calculer les primitives de la formeZPcos x, sin xdx oude la formeZ Pcos x, sin xQcos x, sin xdx quand P et Q sont des polynômes, en seramenant à intégrer une fraction rationnelle. Il existe deux méthodes :les règles de Bioche sont assez ecaces mais ne fonctionnent pastoujours ;le changement de variable t = tan x2 fonctionne tout le temps maisconduit à davantage de calculs.D. CransacAnalyse

Page 56 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesIntégration des fonctions trigonométriquesLes règles de Bioche.On note ωx = f xdx. On a alors ωx = f xdx = f xdxet ωπ x = f π xdπ x = f π xdx.Si ωx = ωx alors on eectue le changement de variableu = cos x.Si ωπ x = ωx alors on eectue le changement de variableu = sin x.Si ωπ + x = ωx alors on eectue le changement de variableu = tan x.D. CransacAnalyse

Page 57 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesExempleCalcul de la primitiveZcos xdx2 cos2 x On note ωx =cos xdx2 cos2 x .Comme ωπ x = cosn xdπ x2 cos2π x= cos xdx2 cos2 x= ωx alors lechangement de variable qui convient est u = sin x pour lequel du = cos xdx.Ainsi :Zcos xdx2 cos2 x =Zcos xdx2 1 sin2 x =Zdu1 + u2 = arctan u = arctansin x+c.Le changement de variable t = tan x2 . Les formules de la tangente de l'arcmoitié " permettent d'exprimer sinus, cosinus et tangente en fonction de tanx2 .Avect = tan x2on acos x = 1 t21 + t2sin x =2t1 + t2tan x =2t1 t2etdx =2dt1 + t2 .D. CransacAnalyse

Page 58 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannIntégration des éléments simplesIntégration des fonctions trigonométriquesExempleCalcul de l'intégraleZ 0π/2dx1 sin x .Le changement de variable t = tan x2 dénit une bijection dehπ2 , 0ivers 1, 0 pour x = π2 , t = 1 et pour x = 0, t = 0 . De plus on asin x =2t1 + t2 et dx =2dt1 + t2 .Z 0π2dx1 sin x =Z 012dt1+t21 2t1+t2= 2Z 01dt1 + t2 2t= 2Z 01dt1 t2 = 211 t01= 21 12= 1D. CransacAnalyse

Page 59 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannRecherche de primitivesD. CransacAnalyse

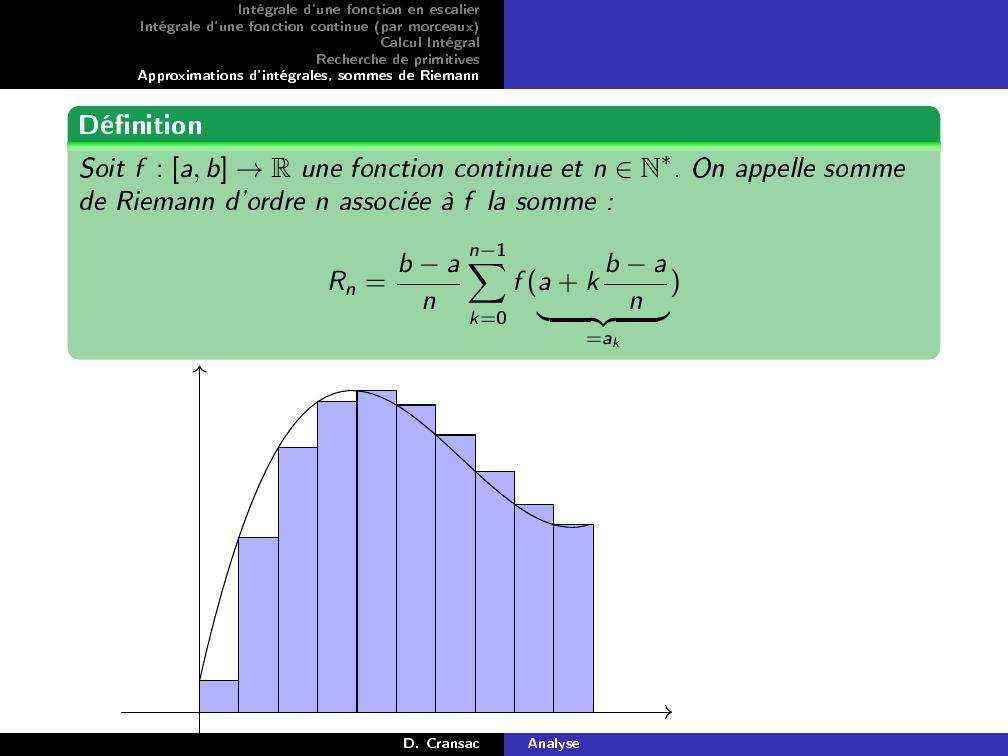
Page 60 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDénitionSoit f : a, b →R une fonction continue et n N. On appelle sommede Riemann d'ordre n associée à f la somme :Rn = b ann1Xk=0f a + k b anz=akD. CransacAnalyse

Page 61 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannDémonstration.On fait la preuve dans le cas où f est lipschitzienne ce qui est en particulier lecas si f est de classe C1 sura, b. Notons K la constante de lipschitz associéeà f sur a, b.Z baf xdx Rn =n1Xk=0Z ak+1akf xdx b ann1Xk=0f ak=n1Xk=0Z ak+1akf x f ak dx ⩽n1Xk=0Z ak+1akf x f ak dx par inégalitétriangulaire ⩽n1Xk=0Z ak+1akf x f ak dx ⩽n1Xk=0Z ak+1akK x ak dx car f estlipschitzienne ⩽n1Xk=0Z ak+1akK ak+1 ak dx car f est lipschitzienne⩽Kn1Xk=0ak+1 ak2 = Kn1Xk=0b a2n2= K b a2nComme enn limK b a2n= 0, on obtient par théorème d'encadrement limRn =Z baf xdx.D. CransacAnalyse

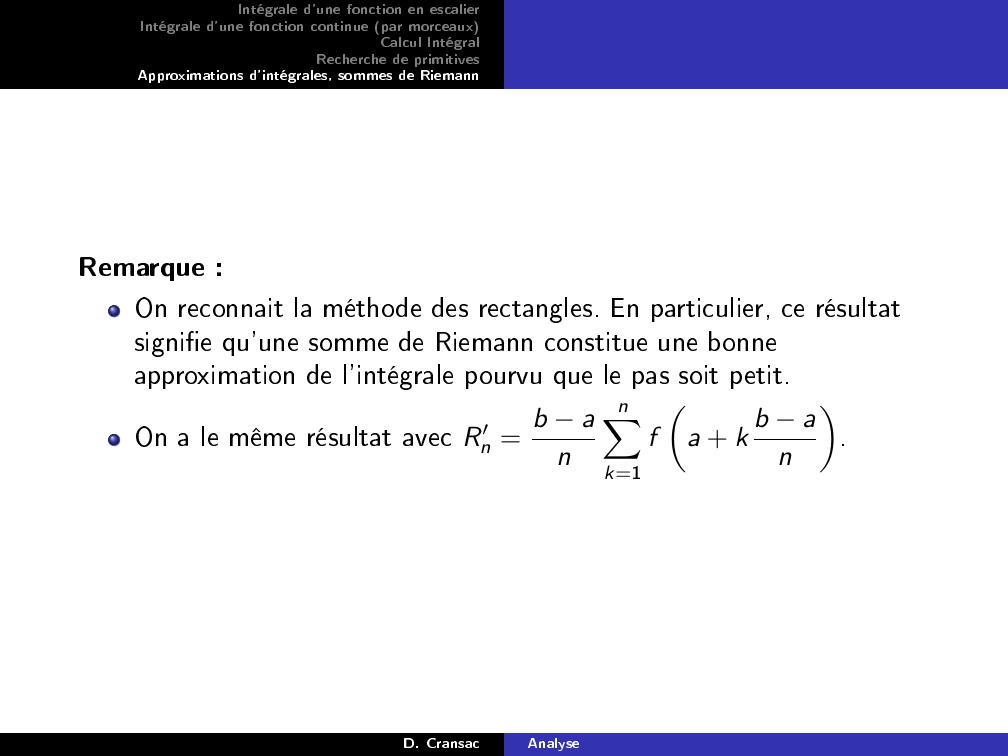
Page 62 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannRemarque :On reconnait la méthode des rectangles. En particulier, ce résultatsignie qu'une somme de Riemann constitue une bonneapproximation de l'intégrale pourvu que le pas soit petit.On a le même résultat avec R′n = b annXk=1fa + k b an.D. CransacAnalyse

Page 63 : Intégrale d'une fonction en escalierIntégrale d'une fonction continue par morceauxCalcul IntégralRecherche de primitivesApproximations d'intégrales, sommes de RiemannRemarque. Méthode des trapèzes. La vitesse de convergence de lasomme de Riemann vers l'intégrale est en 1n. On peut améliorer laprécision en utilisant la méthode des trapèzes.On approche alorsZa,bf parTnf = b ann1Xk=0f ak + f ak+12On obtient alors une approximation en 1n2 : Si f est de classe C2 sura, b, on peut montrer queZ baf xdx Tnf ⩽M2b a312n2où M2 = supxa,bf ′′x.D. CransacAnalyse

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63