CM3 Quanti Quali
Télécharger le CM3 Quanti Quali en pdf
Page 1 : Analyse bivariée quantitatif-qualitatifData explorationStatistiques descriptives bivariéesObserver simultanément des individus d'une population sur deux caractèresMesurer un lien éventuel entre deux caractères en utilisant un résumé chiffré qui traduit l'importance de ce lienQualifier ce lien : –en cherchant une relation numérique approchée entre deux caractères quantitatifs–en cherchant des correspondances entre les modalités de deux caractères qualitatifs• qualitatif ×qualitatif2 types de variables 3 types de croisements : • qualitatif ×quantitatif• quantitatif ×quantitatif
Page 2 : Analyse bivariée quantitatif-qualitatifCroisement Quantitatif - QualitatifSous-populationsPour étudier le lien entre une variable qualitative à p modalités et un caractère quantitatif,on partitionne la population p en sous-populations : une sous-population pour chaquemodalité de la variable qualitative.Prenons l’exemple de l’étude comparative de la taille entre les hommes et les femmes.La variable qualitative est le genre. On divise donc la population en deux sous-populations, celui des hommes et celui des femmes.Sur chaque sous-population, il est possible de calculer les résumés numériques usuels.Une comparaison des boites de Tukey permet d’avoir une première idée du lien antre les variablesGENREEffectifsMoyenne Écart-typeHommes23162,3014,21Femmes35149,2910,52Total58154,4513,61130140150160170180190200HOMMES130140150160170180190200FEMMESL’idée est de décomposer la moyenne et la variance sur les différents sous-populations.
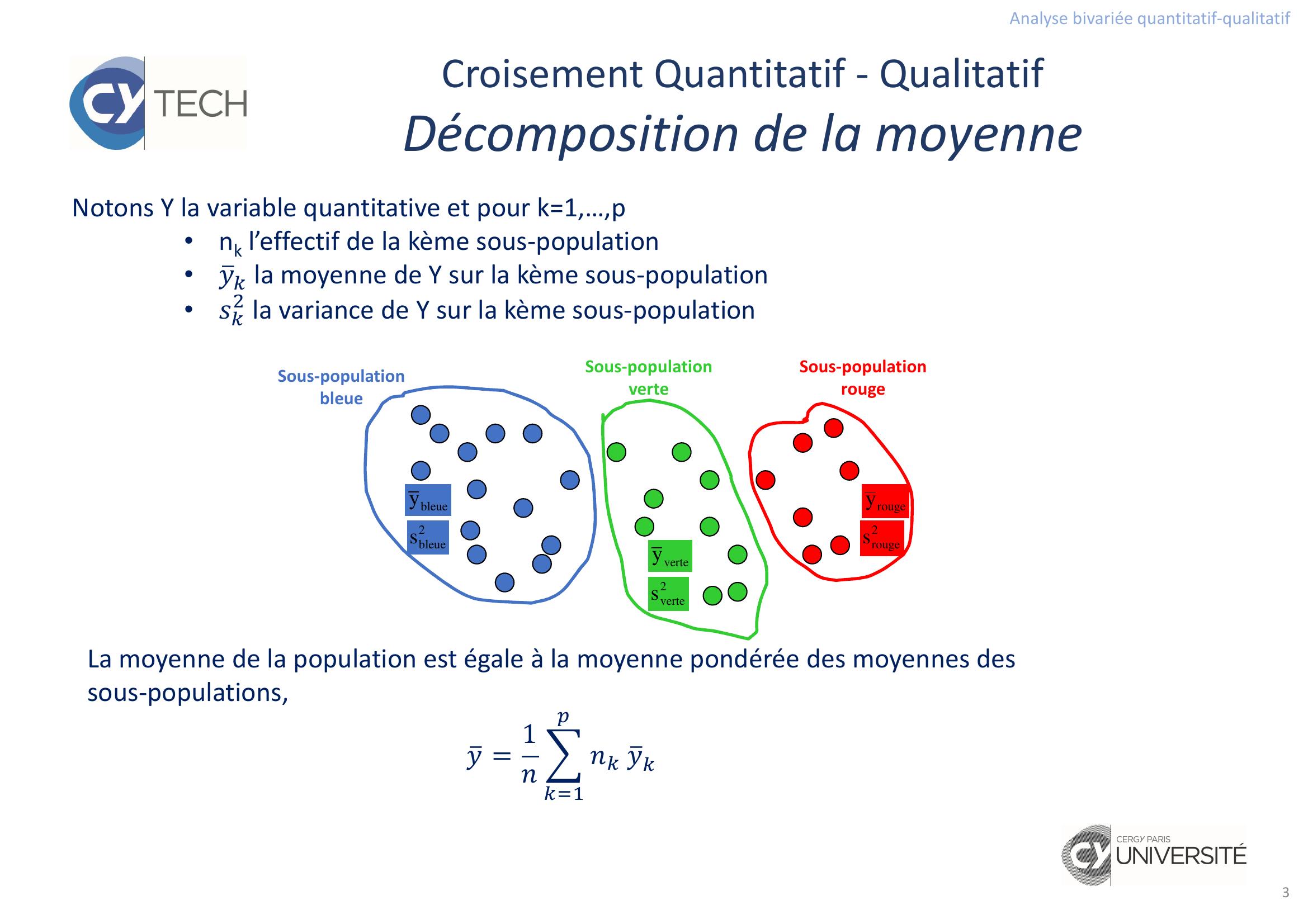
Page 3 : Analyse bivariée quantitatif-qualitatif3Croisement Quantitatif - QualitatifDécomposition de la moyenneSous-population bleueSous-population verteSous-population rougebleuey2vertesvertey2bleuesrougey2rougesNotons Y la variable quantitative et pour k=1,…,p•nk l’effectif de la kème sous-population• la moyenne de Y sur la kème sous-population• la variance de Y sur la kème sous-populationLa moyenne de la population est égale à la moyenne pondérée des moyennes des sous-populations, = 1
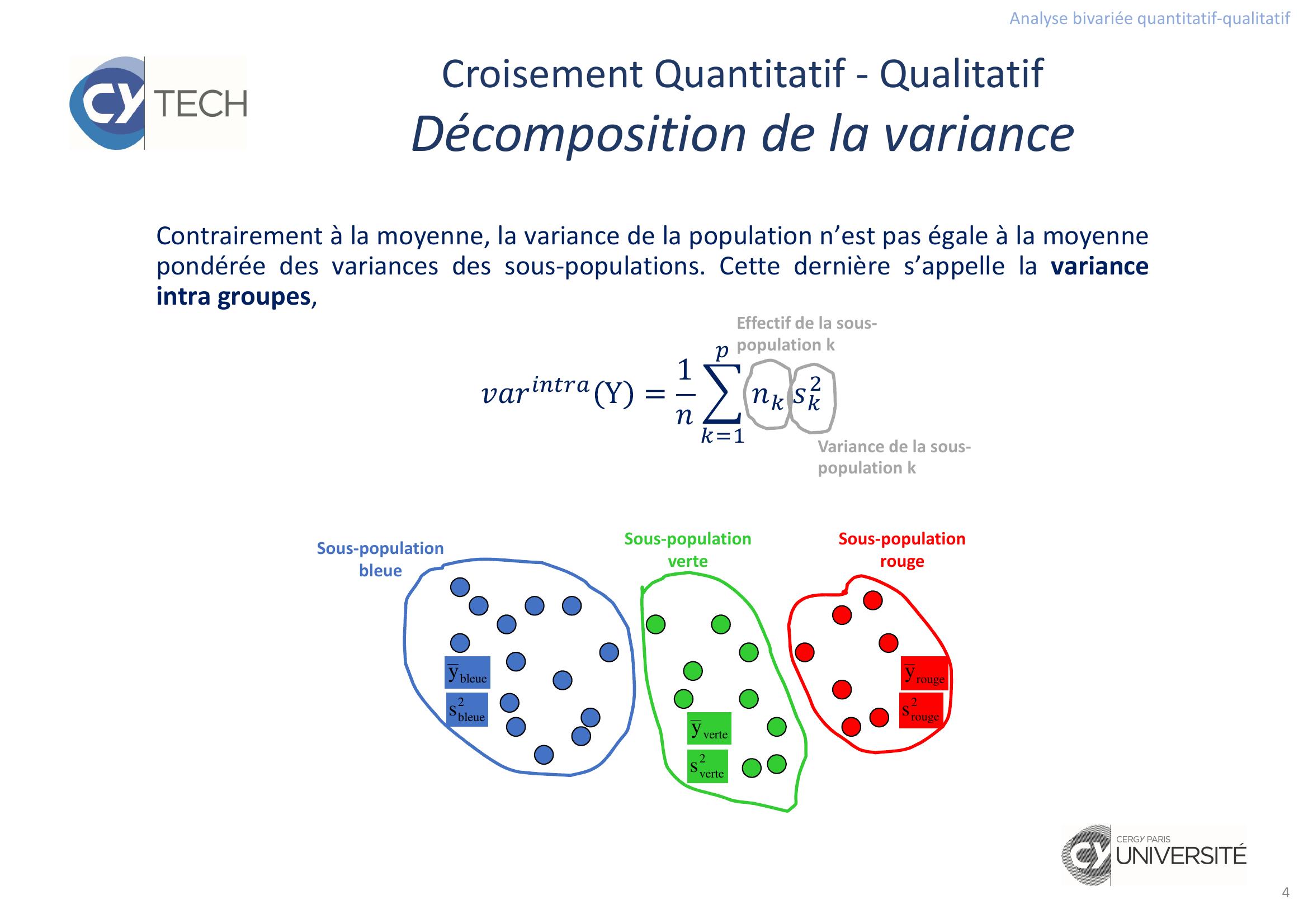
Page 4 : Analyse bivariée quantitatif-qualitatif4Croisement Quantitatif - QualitatifDécomposition de la varianceSous-population bleueSous-population verteSous-population rougeContrairement à la moyenne, la variance de la population n’est pas égale à la moyennepondérée des variances des sous-populations. Cette dernière s’appelle la varianceintra groupes, Y = 1 bleuey2vertesvertey2bleuesrougey2rougesVariance de la sous-population kEffectif de la sous-population k
Page 5 : Analyse bivariée quantitatif-qualitatif5Croisement Quantitatif - QualitatifDécomposition de la varianceA la variance intra groupes, on ajoute la variance inter groupes, Y = 1 ²Sous-population bleueSous-population rougeIndividu virtuel représentant la population bleueIndividu virtuel représentant la population verteIndividu virtuel représentant la population rougeSous-population vertebleueyverteyrougey•Pour chaque sous-population, on crée un individu virtuel dont la valeur sur Yestégale à la moyenne des valeurs de Y des individus de la sous-population.•On crée donc une nouvelle population formée de ces individus virtuels. Chaqueindividu aura un poids de nk , l'effectif de chaque sous-population.
Page 6 : Analyse bivariée quantitatif-qualitatif6Croisement Quantitatif - QualitatifDécomposition de la varianceOn peut donc définir trois variances sur variable Y.•une première qui explique les variations de Ydans toute la population : totale•une deuxième qui explique les variations de Ydans les sous-populations: intra•une troisième qui explique les variations de Y entre les sous-populations : interNous avons la décomposition de la variance suivante : = + On en déduit une mesure du lien entre X et Y avec le rapport de corrélation Le rapport de corrélation représente le pourcentage de variabilité de Y expliquée par X. Il varie entre 0et 1. Si• S’il est nul alors la variance expliquée est nulle, il n’y a donc aucun lien entre Y et X• S’il vaut 1 alors la variance expliquée est égale à la variance de Y donc Y est entièrementexpliquée par X.Variance expliquée Variance résiduelle
Page 7 : Analyse bivariée quantitatif-qualitatif7Croisement Quantitatif - QualitatifExempleGENREEffectifsMoyenne VarianceVar intraHommes23162,0193,323×193,3=4444,9Femmes35149,3107,635×107,6 =3765,1Total58154,4182,14444,9+3765,1/58 =141,5Etude comparative de la taille entre les hommes et les femmes.GENREEffectifsMoyenne VarianceVar interHommes23162,3193,323×162,3-154,4² =1419,5Femmes35149,3107,635×149,3-154,4² =932,8Total58154,4182,11419,5+932,8/58 = 40,6Rapport de corrélation : 2201182640,,,=22 de la variabilité de la taille est expliquée par le genreOn vérifie la formule de la décomposition de la variance : 141,5+40,6=182,1