CM3 Representation des nombres part2

Télécharger le CM3 Representation des nombres part2 en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

Page 1 : INFORMATIQUE 1I I . R E P R E S E N TAT I O N D E S N O M B R E S P A R T I E 2 Eva Ansermin & Romuald Grignon v1.4

Page 2 : Rappel Tableau des puissances de 21000 10102 →2 + 8 + 128 = 138Exemple :Eva ANSERMIN & Romuald GRIGNON2

Page 3 : L’hexadécimalEn base hexadécimale ou base 16:Les chiffres sont : 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,FOn multiplie les chiffres par des puissances de 16 :Soit N un entier dont les chiffres sont𝑝𝑛, 𝑝𝑛1, 𝑝𝑛2, … , 𝑝0en basedécimale :Exemple : 2𝐶16 →2 161 + C 160 = 32 + 12 = 44𝑁= ෍𝑖=0𝑛𝑝𝑖16𝑖Eva ANSERMIN & Romuald GRIGNON3

Page 4 : L’hexadécimalConnaître les puissances de 16 n’est pas simple ! Mais on peut remarquer que :24 = 16 𝑒𝑡1111 = 15-Un chiffre en hexadécimal correspond donc à 4 bits en binaire.Il est souvent plus aisé de passer par le binaire quand on souhaite faire uneconversion décimal/hexadécimal.Exemple: 173 →1010 1101 →𝐴𝐷Exemple: 240 →1111 0000 →𝐹0Eva ANSERMIN & Romuald GRIGNON4

Page 5 : Soit N, un nombre entier naturel codé sur n bitsLa plus petite valeur possible est 0La plus grande valeur possible est 1111…11Valeurs représentables : Eva ANSERMIN & Romuald GRIGNON5

Page 6 : Soit N, un nombre entier naturel codé sur n bitsLa plus petite valeur possible est 0La plus grande valeur possible est 1111…1111111 … 111 + 1 = 1 0000 … 00Valeurs représentables : = 2𝑛Donc 𝟏𝟏𝟏𝟏… 𝟏𝟏𝟏= 𝟐𝒏𝟏Eva ANSERMIN & Romuald GRIGNON6On remarque que : nn

Page 7 : Soit N, un nombre entier naturel codé sur n bits, la gamme de valeursreprésentables en base 2 est : 𝟎𝟐𝒏𝟏Soit sur :8 bits:0 25516 bits:0 6553532 bits:0 4 294 967 295Valeurs représentables : Eva ANSERMIN & Romuald GRIGNON7

Page 8 : Soit un ordinateur dont les nombres sont encodés sur un octet.Que se passe-t-il lorsqu’on effectue l’opération suivante ?Valeurs représentables : overflow1110 0011+0110 01101 0100 1001Le résultat est sur 9 bits : le premier chiffre ne peut pas être stocké !Lorsque le résultat d’une opération ne peut pas être représenté avec le nombre de chiffres disponible on parle d’overflow dépassement en français.Eva ANSERMIN & Romuald GRIGNON8

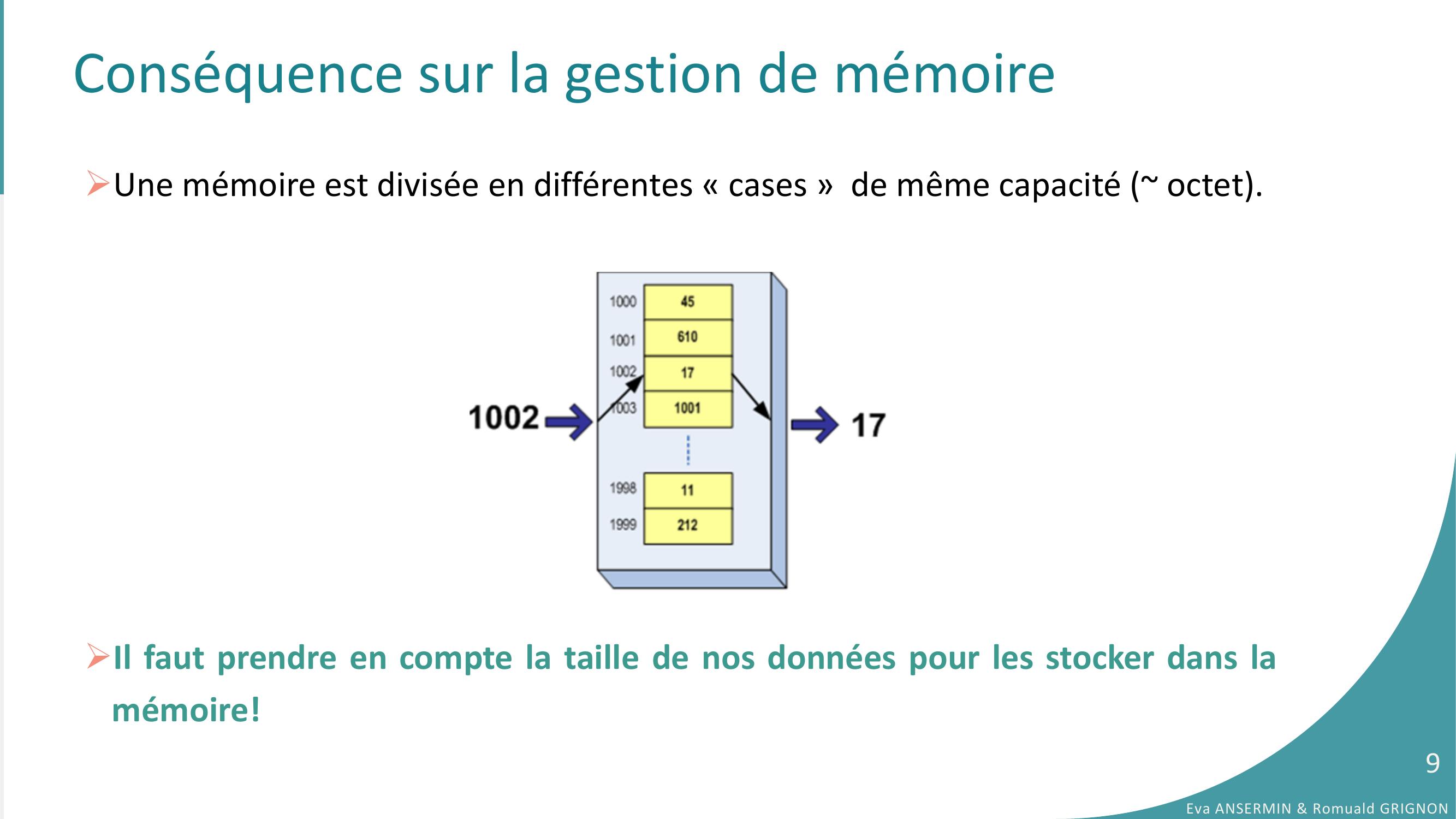
Page 9 : Conséquence sur la gestion de mémoireUne mémoire est divisée en différentes « cases » de même capacité octet.Il faut prendre en compte la taille de nos données pour les stocker dans lamémoire!Eva ANSERMIN & Romuald GRIGNON9

Page 10 : Autre types de donnéesLa gestion des textes données alphanumériques : Des standards code ASCII, unicode… permettent d’associer des caractères à des nombres :Extrait de la table ASCIIEva ANSERMIN & Romuald GRIGNON10

Page 11 : Représentation du signe 1/2I. Signe grandeur: Le bit de signe est le bit de plus fort poids celui situé le plus à gauche du nombre binaire- Il vaut 0 lorsque le nombre est positif et 1 lorsqu’il est négatif.Exemple :Inconvénients : la soustraction ne marche pas avec cette méthode A - A 0Il y a deux manières de représenter le zéro01001001 représente + 731011001001 représente - 7310Eva ANSERMIN & Romuald GRIGNON11

Page 12 : II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Le bit de poids fort indique le signe :si 0, nombre positifsi 1 nombre négatifReprésentation du signe 2/2Eva ANSERMIN & Romuald GRIGNON12𝑁= 𝑁+ 1

Page 13 : Représentation du signe 2/2II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Méthode décimal - binaire : 1. On transforme la valeur absolue du nombre 7310 = 0100 10012. On passe au complément :73 = 0100 1001 = 1011 01103. On ajoute +1 :73 = 1011 0110 + 1 = 1011 0111𝑁= 𝑁+ 1Eva ANSERMIN & Romuald GRIGNON13

Page 14 : Représentation du signe 2/2II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Méthode binaire - décimal : 1 . On regarde le bit de poids fort : s’il vaut 0 alors le nombre est positif, traduire directement.2. Si le bit de poids fort vaut 1, le nombre est négatif, il faut faire l’opération inversea. Retirer 1 1011 0111 1 = 1011 0110b. Faire le complément 1011 0110 = 0100 1001c. Traduire le nombre obtenu et le mettre en négatif0100 1001 ⇒7310 ⟺1011 0111 = 7310𝑁= 𝑁+ 1Eva ANSERMIN & Romuald GRIGNON14

Page 15 : Représentation du signe 2/2Eva ANSERMIN & Romuald GRIGNON15II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Valeurs représentables sur n bits: Le plus grand nombre : 𝑁= 𝑁+ 1

Page 16 : Représentation du signe 2/2n-1 bits2𝑛1 1Eva ANSERMIN & Romuald GRIGNON16II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Valeurs représentables sur n bits: Le plus grand nombre : 0111…111 = 𝑁= 𝑁+ 1

Page 17 : II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Valeurs représentables sur n bits: Le plus grand nombre : 0111…111 = Le plus petit nombre : Représentation du signe 2/2n-1 bits2𝑛1 1Eva ANSERMIN & Romuald GRIGNON17𝑁= 𝑁+ 1

Page 18 : II. Le complément à 2:On appelle complément à 1 d’un nombre binaire N le nombre N dont les 1 et les 0 sont inversés.On représente –N de la manière suivante en complément à 2 :Valeurs représentables sur n bits: Le plus grand nombre : 0111…111 = Le plus petit nombre : 1000…000 ⇔-0111…111 +1 = Représentation du signe 2/2n-1 bits2𝑛1 1Eva ANSERMIN & Romuald GRIGNON18𝑁= 𝑁+ 12𝑛1

Page 19 : Représentation du signe 2/2II. Le complément à 2:Intérêts : Une seule manière de représenter le 0 : on couvre un valeur de plus sur le même nombre de bits: sur n bits є 𝟐𝒏𝟏: 𝟐𝒏𝟏𝟏Les soustractions / additions fonctionnent ! Soit sur 8 bits : -128 : 127 16 bits : -32768 : 32767 32 bits : - 2 147 483 648 : 2 147 483 647 C’est cette convention qui est utilisée pour représenter les entiers négatifs dans les ordinateurs. Eva ANSERMIN & Romuald GRIGNON19

Page 20 : Représentation nombres réels 1/3PrincipeComme pour le symbole “-” il n’y a pas de moyen de représenterexplicitement la virgule en binaire.En decimal, les chiffres derrière la virgule sont multipliés par des puissance de 10 negatives :Ex : 26,75 = 2 10 + 6 100 + 7 101 + 5 102Plus généralement :En binaire, on utilise des puissances de 2 négatives.𝑁= 𝑎𝑛𝑎𝑛1 … 𝑎0 . 𝑎1𝑎2 … 𝑎𝑝= ෍𝑖=𝑝𝑛𝑎𝑖10𝑖Eva ANSERMIN & Romuald GRIGNON20

Page 21 : Représentation nombres réels 2/3I. La virgule fixeOn défini explicitement le nombre de bits avant puissance de 2 positive et après puissance de 2 negatives la virgule. 𝑁= 𝑏𝑚𝑏𝑚1 … 𝑏0 𝑏1𝑏2 … 𝑎𝑛= ෍𝑖=𝑛𝑚𝑎𝑖2𝑖Eva ANSERMIN & Romuald GRIGNON21

Page 22 : Représentation nombres réels 2/3I. La virgule fixeExemple : Sur 8 bits, on définit 5 bits avant et 3 bits après la virgule.11000,1102 →24 + 23 + 21 + 22 = 16 + 8 + 0,5 + 0,25 = 24,7510,62510 →8 + 2 + 0,5 + 0,125 = 23 + 21 + 21 + 23 = 01010101221 = 222 = 423 = 824 = 1622 = 0,2523 = 0,12520 = 121 = 0,5Eva ANSERMIN & Romuald GRIGNON22

Page 23 : Représentation nombres réels 2/3I. La virgule fixe :Exemple : Sur 8 bits, on définit 5 bits avant et 3 bits après la virgule.32,5 ? Il faudrait plus de bits avant la virgule et moins après.32,5 →100000,10Mais ici on ne peut plus representer 10,625!21 = 222 = 423 = 824 = 1622 = 0,2523 = 0,12520 = 121 = 0,521 = 222 = 423 = 824 = 1622 = 0,2520 = 121 = 0,525 = 32Eva ANSERMIN & Romuald GRIGNON23

Page 24 : Représentation nombres réels 2/3I. La virgule fixe :Exemple : Sur 8 bits, on définit 5 bits avant et 3 bits après la virgule.3,5625 ? Il faudrait plus de bits après la virgule et moins avant.3,5625 →0011,1001Mais dans ce cas 16 n’est plus représentable !21 = 222 = 423 = 824 = 1622 = 0,2523 = 0,12520 = 121 = 0,5Eva ANSERMIN & Romuald GRIGNON2421 = 222 = 423 = 822 = 0,25 23 = 0,12520 = 1 21 = 0,524 = 0,0625

Page 25 : Représentation nombres réels 2/3I. La virgule fixe :Avantages:- facile à calculer- Opération faciles à effectuerInconvénients : nécessite de trouver un compromis entre précision et grand nombre !Ce n’est pas ce qui est utilisé dans les ordinateurs du fait du manque de souplesse de cette représentation. Eva ANSERMIN & Romuald GRIGNON25

Page 26 : Représentation nombres réels 3/3II. La virgule flottante :La virgule flottante est la convention utilisée dans les ordinateurs.La norme d’utilisation des virgules flottantes est la norme IEEE754 avec :Simple precision pour les nombres sur 32 bitsDouble précision pour les nombres sur 64 bitsPlus complexe que la virgule fixe, elle permet de représenter des nombresà la fois précis et grands sans changer de règle de représentation. Eva ANSERMIN & Romuald GRIGNON26

Page 27 : Représentation nombres réels 3/3II. La virgule flottante : principeEn decimal, on peut mettre les nombres sous forme “scientifique”:Exemple : 548,96 = 5,4896 102𝑁= ±𝑎𝑛, 𝑎𝑛1𝑎𝑛2 … 𝑎0 10𝑝Un seul chiffre avant la virguleUne puissance 0 ou 0 Eva ANSERMIN & Romuald GRIGNON27

Page 28 : Représentation nombres réels 3/3II. La virgule flottante : principeEn decimal, on peut mettre les nombres sous forme “scientifique”:De la même façon en binaire :Exemple : 7,125 →111,001 = 1,11001 22𝑁= ±𝑎𝑛, 𝑎𝑛1𝑎𝑛2 … 𝑎0 10𝑝Un seul chiffre avant la virguleUne puissance 0 ou 0 Eva ANSERMIN & Romuald GRIGNON28𝑁= ±𝑏𝑛, 𝑏𝑛1𝑏𝑛2 … 𝑏0 2𝑝

Page 29 : Représentation nombres réels 3/3II. La virgule flottante : principeL’écriture en virgule flottante consiste à traduire séparément les différentesparties d’un nombre binaire écrit sous cette forme : Avec• s : le signe qui vaut 0 ou 1• m : la mantisse• e : l’exposant𝑁= ±𝑏𝑛, 𝑏𝑛1𝑏𝑛2 … 𝑏0 2𝑝= 1 𝑠1, 𝑚2𝑒Eva ANSERMIN & Romuald GRIGNON29

Page 30 : Représentation nombres réels 3/3II. La virgule flottante : principeL’écriture en virgule flottante consiste à traduire séparément les différentesparties d’un nombre binaire écrit sous cette forme : Avec• s : le signe qui vaut 0 ou 1• m : la mantisse• e : l’exposant𝑁= ±𝑏𝑛, 𝑏𝑛1𝑏𝑛2 … 𝑏0 2𝑝= 1 𝑠1, 𝑚2𝑒Eva ANSERMIN & Romuald GRIGNON30

Page 31 : Représentation nombres réels 3/3II. La virgule flottante : simple precision En norme simple precision 32 bits un nombre binaire sera représenté: Eva ANSERMIN & Romuald GRIGNON311 𝑠1, 𝑚2𝑒

Page 32 : Représentation nombres réels 3/3II. La virgule flottante : simple precision En norme simple precision 32 bits un nombre binaire sera représenté: Méthode de calcul de decimal à simple precision :1. Traduire de decimal en binaire et mettre sous la forme2. En déduire les différentes parties a. le signe ‘s’ sera à 0 si le nombre est positif, à 1 sinon1 𝑠1, 𝑚2𝑒Eva ANSERMIN & Romuald GRIGNON32

Page 33 : Représentation nombres réels 3/3II. La virgule flottante : simple precision En norme simple precision 32 bits un nombre binaire sera représenté: Méthode de calcul de decimal à simple precision :1. Traduire de decimal en binaire et mettre sous la forme2. En déduire les différentes parties a. le signe ‘s’ sera à 0 si le nombre est positif, à 1 sinonb. la mantisse ‘m’ sur 23 bits1 𝑠1, 𝑚2𝑒Eva ANSERMIN & Romuald GRIGNON33

Page 34 : Représentation nombres réels 3/3II. La virgule flottante : simple precision En norme simple precision 32 bits un nombre binaire sera représenté: Méthode de calcul de decimal à simple precision :1. Traduire de decimal en binaire et mettre sous la forme2. En déduire les différentes parties a. le signe ‘s’ sera à 0 si le nombre est positif, à 1 sinonb. la mantisse ‘m’ sur 23 bitsc. 𝐸𝑥𝑝= 𝑒+ 𝑏𝑖𝑎𝑖𝑠= 𝑒+ 127 . Le biais sert à s’assurer que l’exposant est positif1 𝑠1, 𝑚2𝑒Eva ANSERMIN & Romuald GRIGNON34

Page 35 : Représentation nombres réels 3/3II. La virgule flottante : simple precision Exemple : 45,251. Traduire de décimal en binaire-45,25 = 32 + 8 + 4 + 1 + 0,25 = 101101.01= 1.0110101 252. En déduire les différentes parties :a. le signe : 1 car nombre négatifb. la mantisse = 𝟎𝟏𝟏𝟎𝟏𝟎𝟏c. 𝐸𝑥𝑝= 5 + 127 = 132= 128 + 4 = 𝟏𝟎𝟎𝟎𝟎𝟏𝟎𝟎Donc on a 45,25 →11000 010001101010000000000000000Exposant 8 bitsMantisse 23 bitssigneEva ANSERMIN & Romuald GRIGNON35

Page 36 : Représentation nombres réels 3/3II. La virgule flottante : remarquesValeurs particulièresIl est impossible d’obtenir un nombre à la fois très grand et très précis comme en décimal sur un nombre de chiffres fixe!.Certains nombres comme les irrationnels ne sont pas représentables : on utilise des arrondis. Eva ANSERMIN & Romuald GRIGNON36

Page 37 : Représentation des nombresLorsque l’on va stocker/utiliser un nombre binaire on doit faire plusieurs choix :1. Quelle convention de representation? Pour savoir comment interpréter un nombre binaire il faut connaître la convention avec laquelle il est encodé !2. Quelle taille nombre de bits?Pas assez de chiffres : nombre non représentableTrop : mémoire gâchéeLorsque l’on programme, on indique à l’ordinateur ces différentes propriétés. C’est le type .ℚ𝑛𝑜𝑚𝑏𝑟𝑒𝑟𝑎𝑡𝑖𝑜𝑛𝑒𝑙Binaire classiqueComplément à 2Virgule flottanteℕ𝑒𝑛𝑡𝑖𝑒𝑟𝑛𝑎𝑡𝑢𝑟𝑒𝑙ℚ𝑒𝑛𝑡𝑖𝑒𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑓Eva ANSERMIN & Romuald GRIGNON37

Page 38 : ConclusionL’ordinateur ne pouvant stocker que des 1 et des 0, il est impossible d’utiliser les symboles habituels mathématiques pour représenter des nombres.On utilise diverses conventions virgule flottante, complement à 2 pour gérer la représentation des nombres. Il est important de savoir la taille d’une donnée pour gérer son stockage ainsi que sa convention de représentation pour que l’ordinateur sachel’interpreter.Nous connaissons la forme de stockage des données d’un ordinateur. Comment se déroule des opérations sur ces données? Eva ANSERMIN & Romuald GRIGNON38

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38