CM4 ABR
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155
Page 1 : INFORMATIQUE 3I V . A R B R E S B I N A I R E S D E R E C H E R C H EEva ANSERMIN & Renaud VERIN & Romuald GRIGNONv1.00
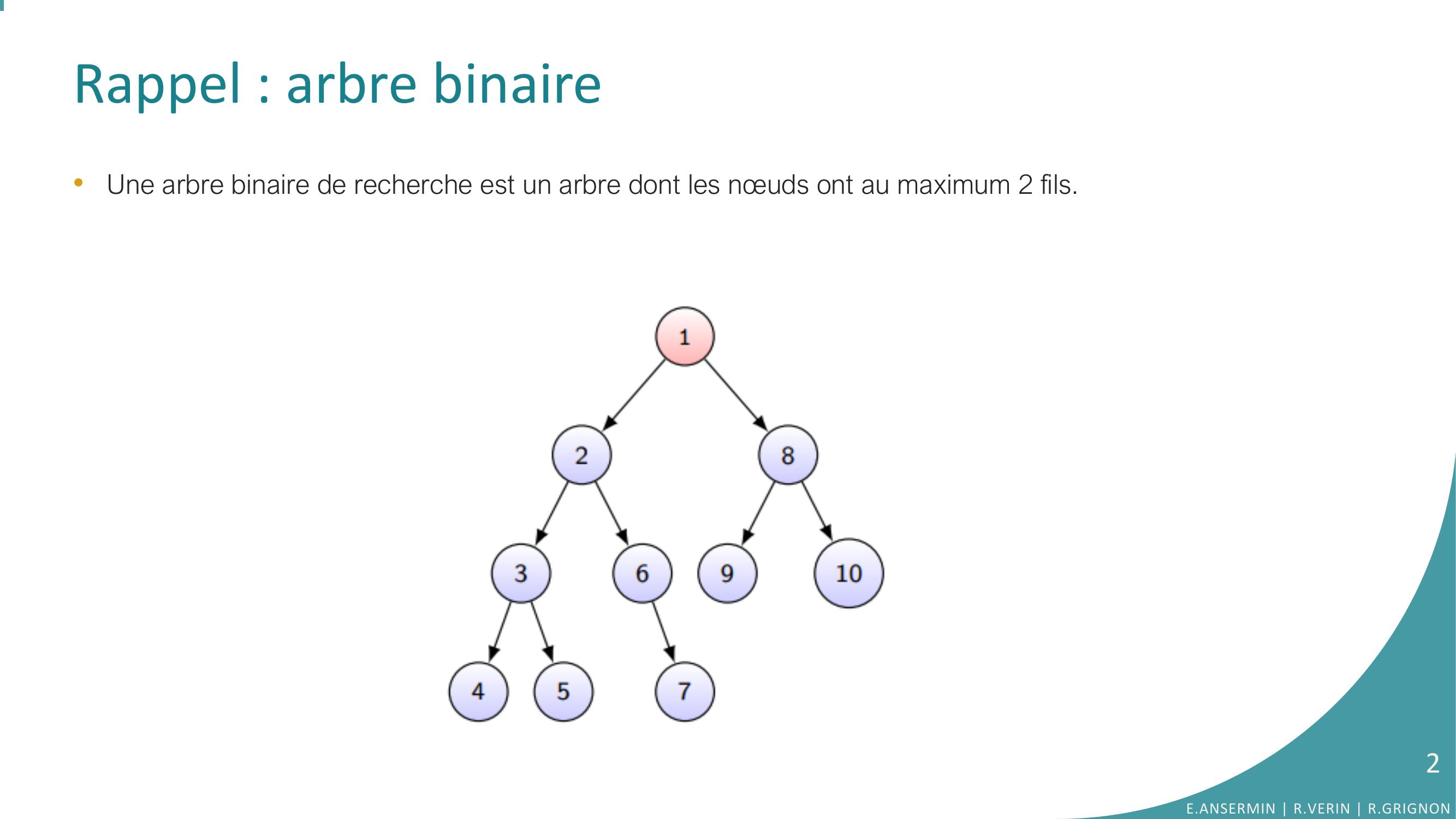
Page 2 : Rappel : arbre binaire•Une arbre binaire de recherche est un arbre dont les nœuds ont au maximum 2 fils.E.ANSERMIN R.VERIN R.GRIGNON2
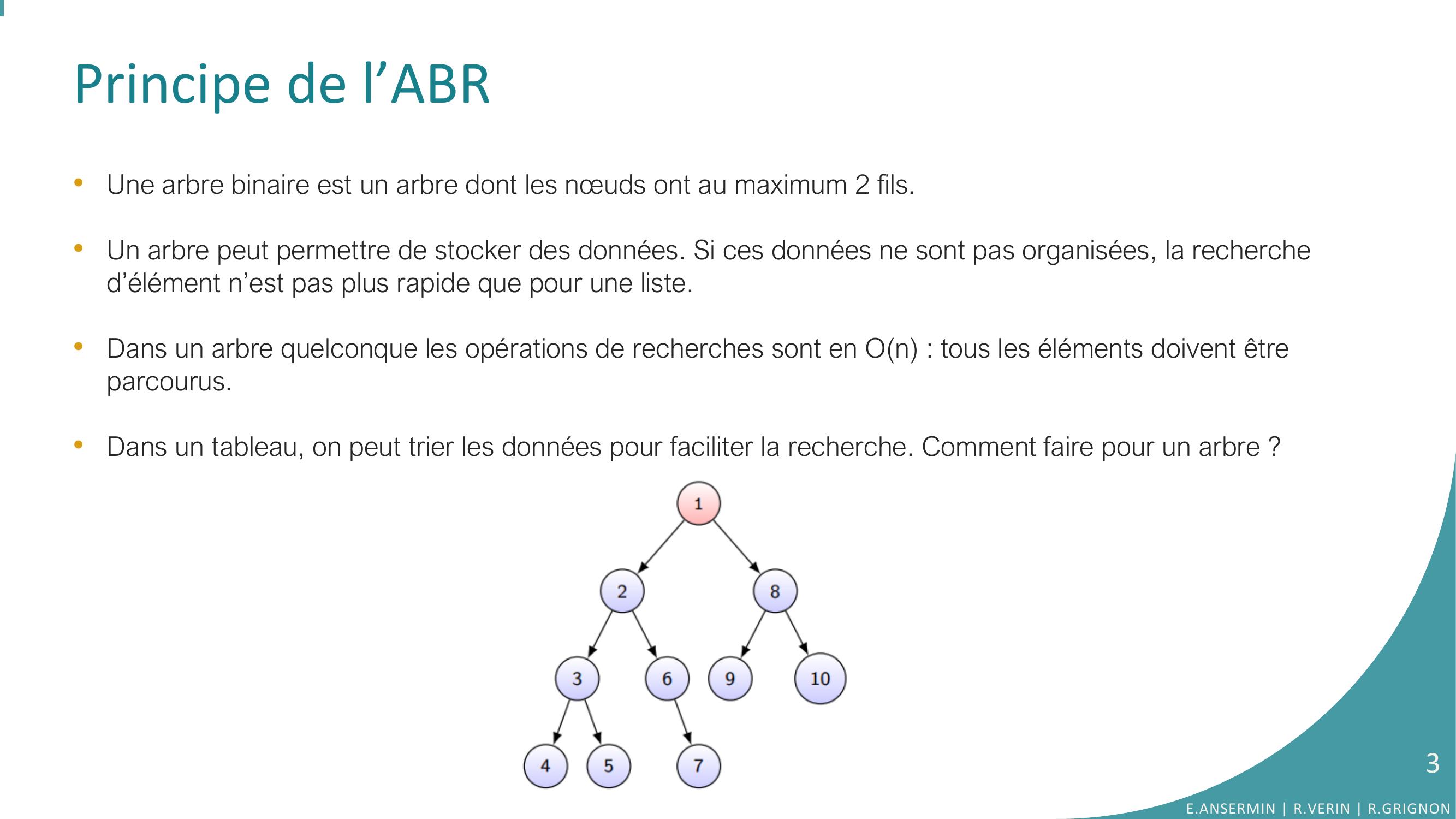
Page 3 : Principe de l’ABR•Une arbre binaire est un arbre dont les nœuds ont au maximum 2 fils.•Un arbre peut permettre de stocker des données. Si ces données ne sont pas organisées, la recherche d’élément n’est pas plus rapide que pour une liste.•Dans un arbre quelconque les opérations de recherches sont en On : tous les éléments doivent être parcourus.•Dans un tableau, on peut trier les données pour faciliter la recherche. Comment faire pour un arbre ? E.ANSERMIN R.VERIN R.GRIGNON3
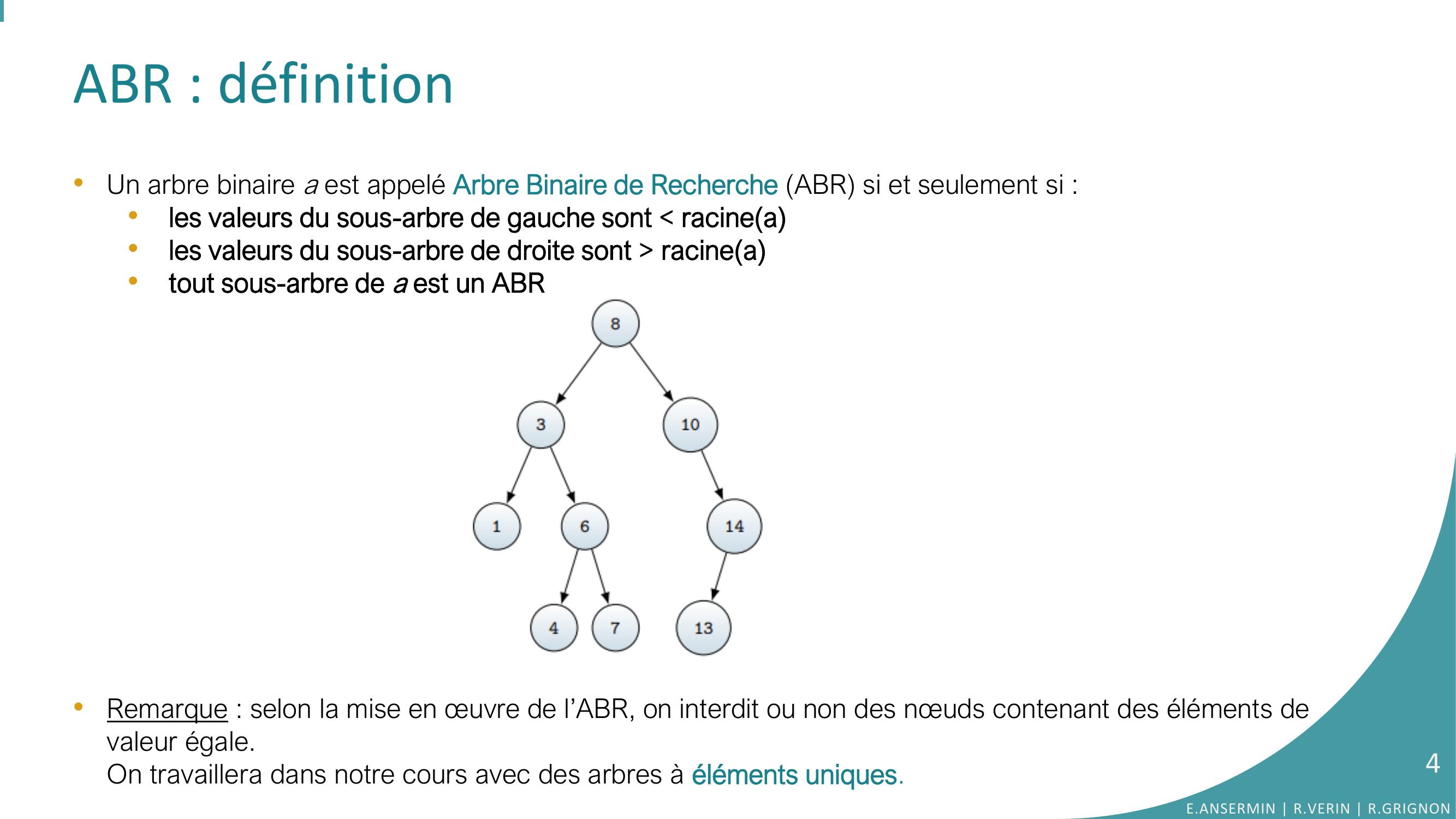
Page 4 : ABR : définition •Un arbre binaire a est appelé Arbre Binaire de Recherche ABR si et seulement si :•les valeurs du sous-arbre de gauche sont racinea•les valeurs du sous-arbre de droite sont racinea •tout sous-arbre de a est un ABR•Remarque : selon la mise en œuvre de l’ABR, on interdit ou non des nœuds contenant des éléments de valeur égale.On travaillera dans notre cours avec des arbres à éléments uniques.E.ANSERMIN R.VERIN R.GRIGNON4
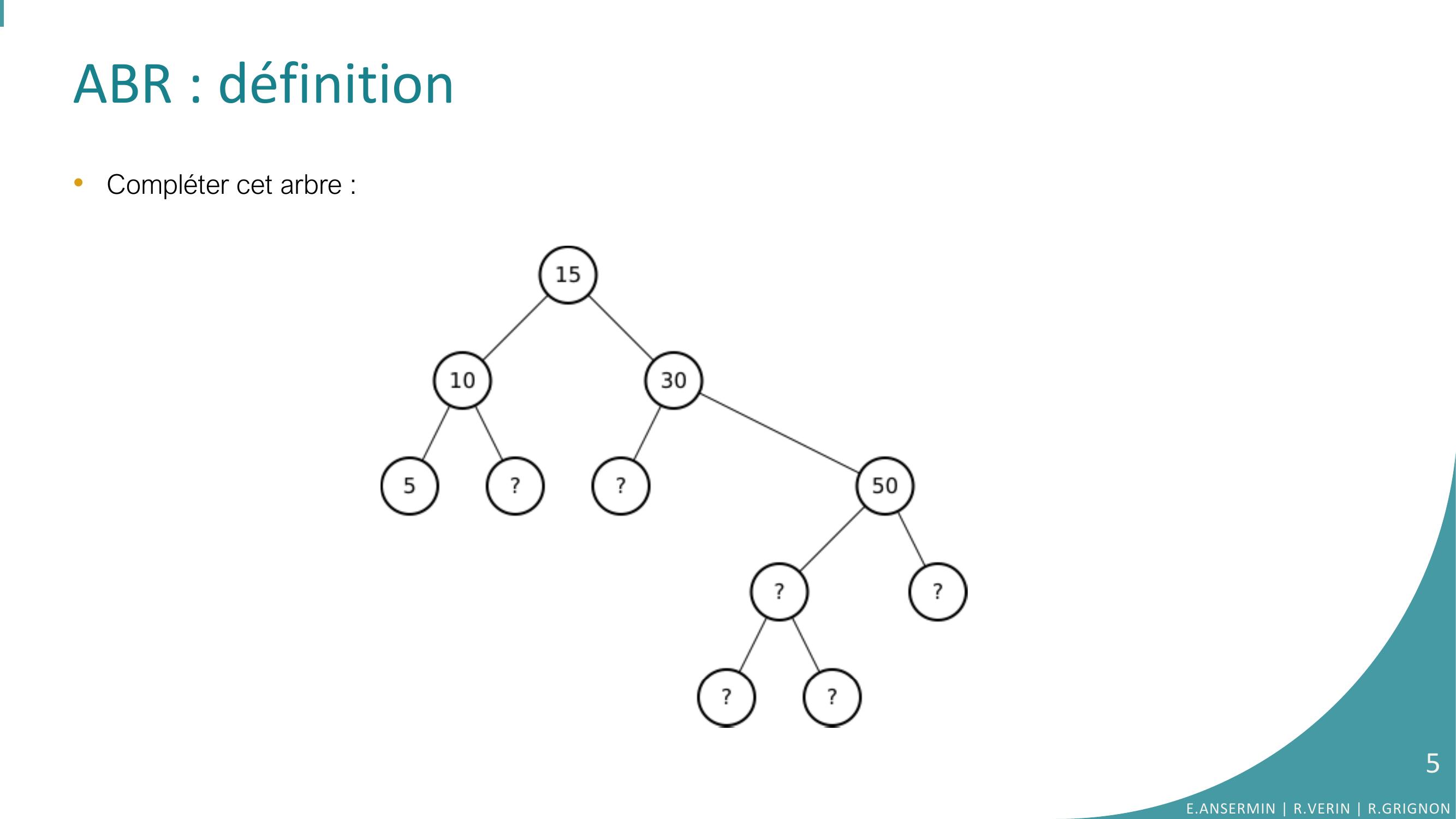
Page 5 : ABR : définition •Compléter cet arbre :E.ANSERMIN R.VERIN R.GRIGNON5
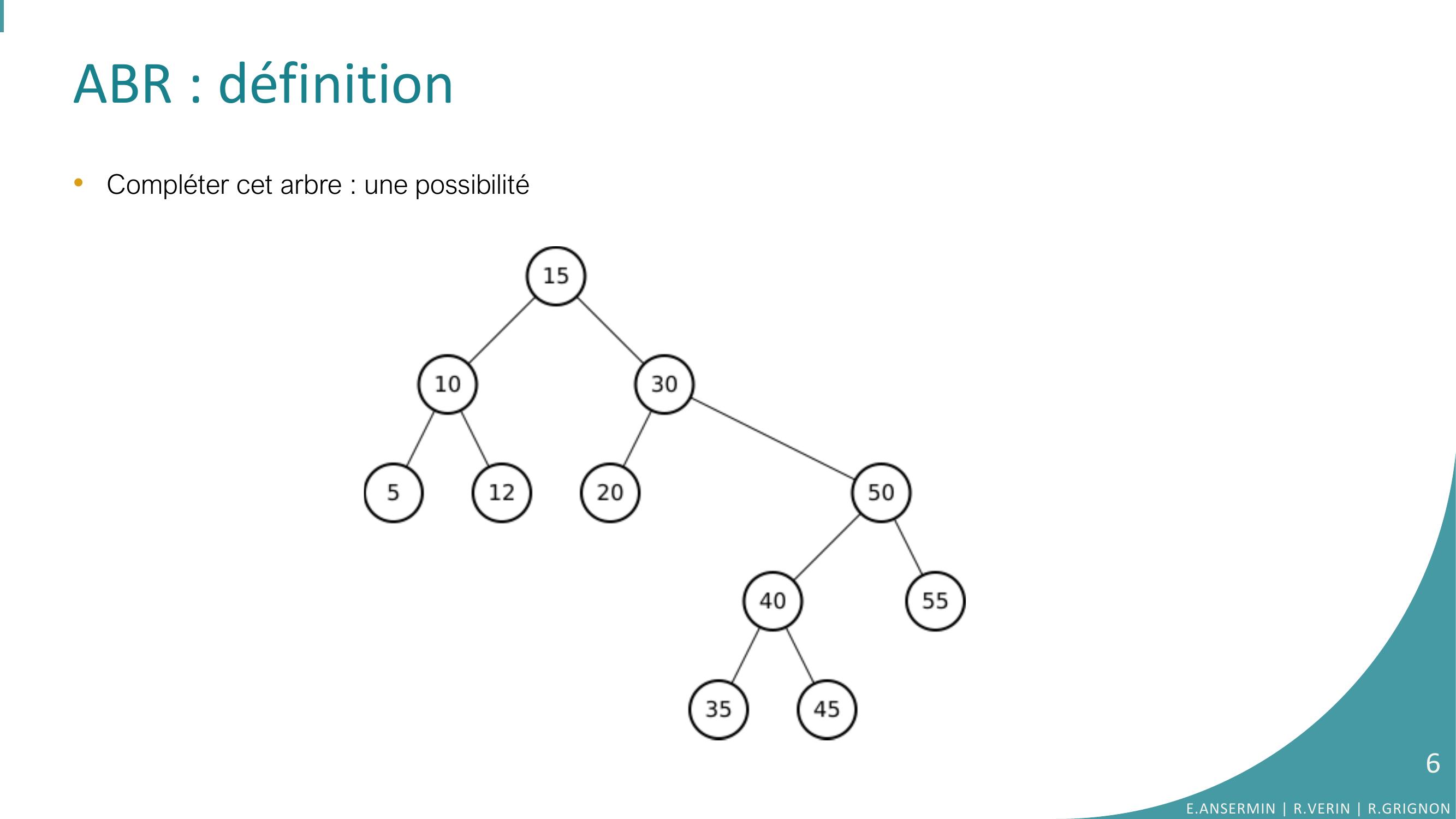
Page 6 : ABR : définition •Compléter cet arbre : une possibilitéE.ANSERMIN R.VERIN R.GRIGNON6
Page 7 : ABR : opération de recherche•Les ABR facilitent grandement les opérations de recherche : on sait quel sous-arbre explorer en fonction de la valeur du nœud sur lequel on se trouve.•Principe:•Comparaison avec la racine du nœud :•s’il est inférieur, recherche dans le sous-arbre gauche •s’il est supérieur, recherche dans le sous-arbre droit •Fin lorsque :•racine égale à la valeur cherchée •le sous-arbre gauche ou droit n’existe pas : la valeur n’est pas dans l’arbreE.ANSERMIN R.VERIN R.GRIGNON7
Page 8 : ABR : opération de recherche•AlgorithmeFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL Alors???SINON SI elementa EST EGAL A e Alors???SINON SI e EST INF. STRICT. A elementa ALORS???SINON???FIN SIFinE.ANSERMIN R.VERIN R.GRIGNON8
Page 9 : ABR : opération de recherche•AlgorithmeFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON9
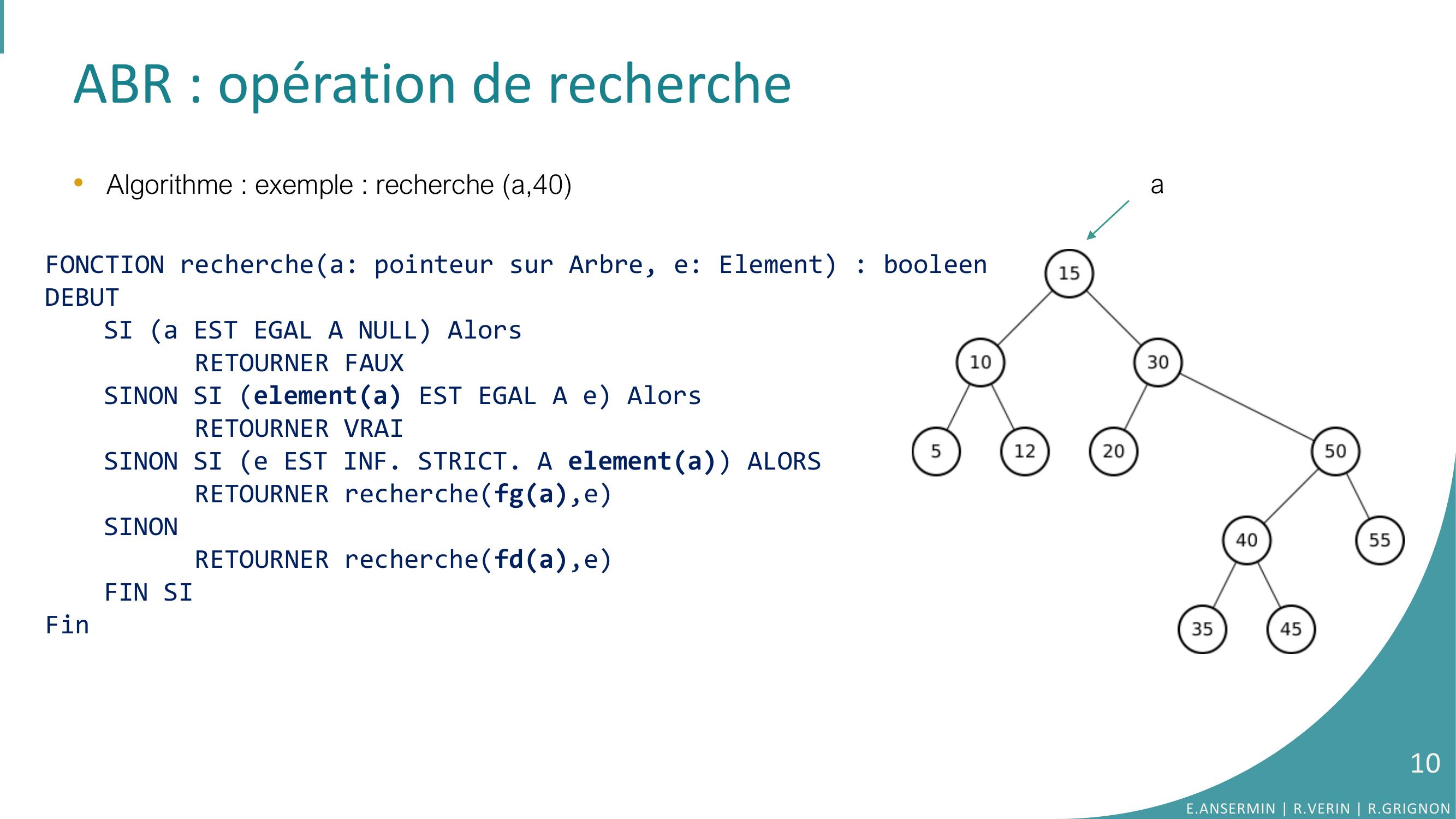
Page 10 : ABR : opération de recherche•Algorithme : exemple : recherche a,40aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON10
Page 11 : ABR : opération de recherche•Algorithme : exemple : recherche a,40aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON11
Page 12 : ABR : opération de recherche•Algorithme : exemple : recherche a,40aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON12
Page 13 : ABR : opération de recherche•Algorithme : exemple : recherche a,40aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON13
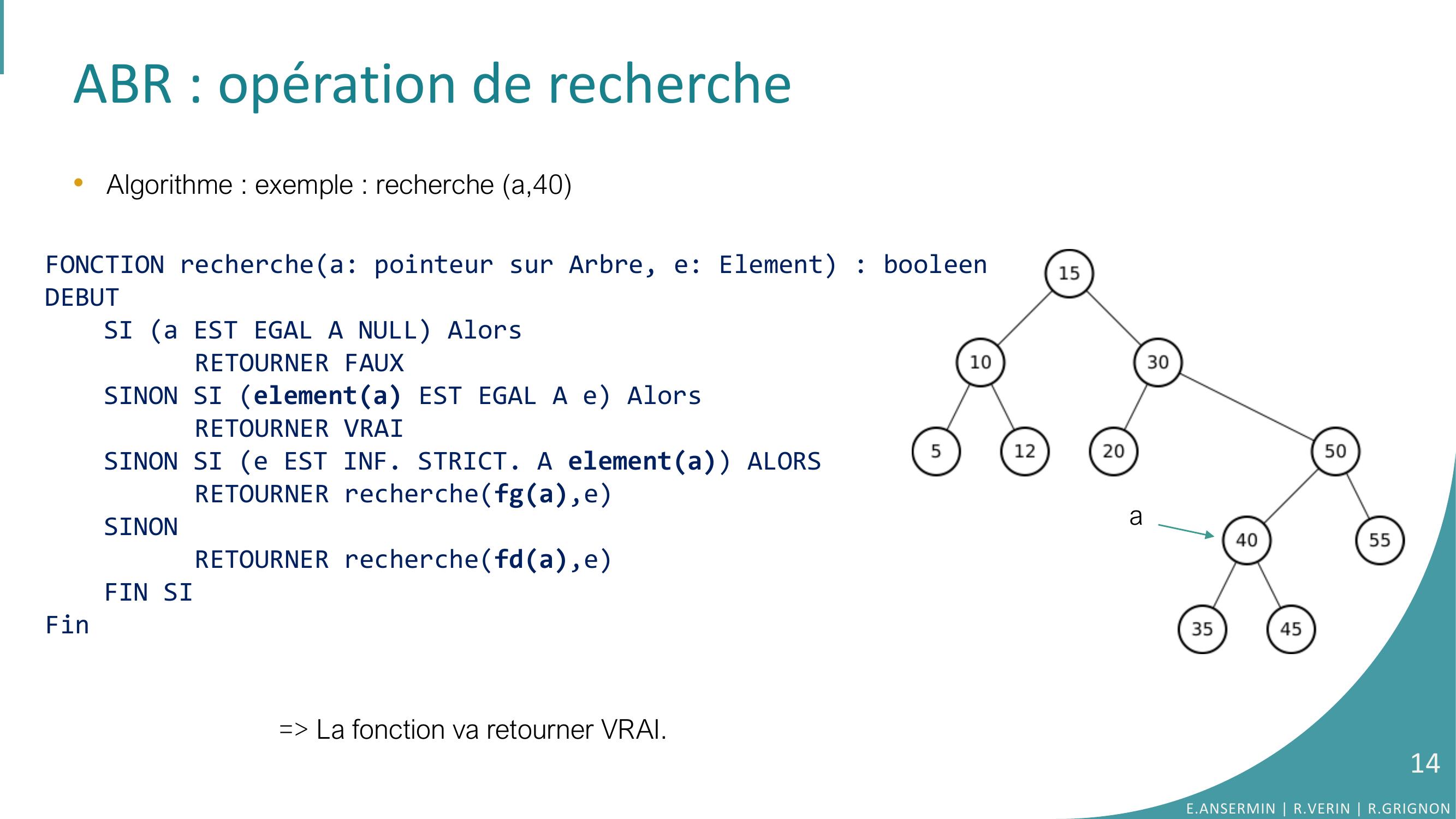
Page 14 : ABR : opération de recherche•Algorithme : exemple : recherche a,40a= La fonction va retourner VRAI.FONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON14
Page 15 : ABR : opération de recherche•Algorithme : exemple : recherche a,14aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON15
Page 16 : FONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinABR : opération de recherche•Algorithme : exemple : recherche a,14aE.ANSERMIN R.VERIN R.GRIGNON16
Page 17 : ABR : opération de recherche•Algorithme : exemple : recherche a,14aFONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON17
Page 18 : ABR : opération de recherche•Algorithme : exemple : recherche a,14a NULL= La fonction va retourner FAUX FONCTION recherchea: pointeur sur Arbre, e: Element : booleenDEBUTSI a EST EGAL A NULL AlorsRETOURNER FAUXSINON SI elementa EST EGAL A e AlorsRETOURNER VRAISINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON18
Page 19 : ABR : opération de recherche•Compléxité :•Meilleur des cas :•Pire cas : •Cas moyen :E.ANSERMIN R.VERIN R.GRIGNON19
Page 20 : ABR : opération de recherche•Compléxité :•Meilleur des cas : élément trouvé de suite : O1•Pire cas : Tous les éléments à parcourir : Onquestion : a quoi ressemble l’arbre dans ce cas?•Cas moyen : O𝒍𝒐𝒈𝟐𝒏E.ANSERMIN R.VERIN R.GRIGNON20
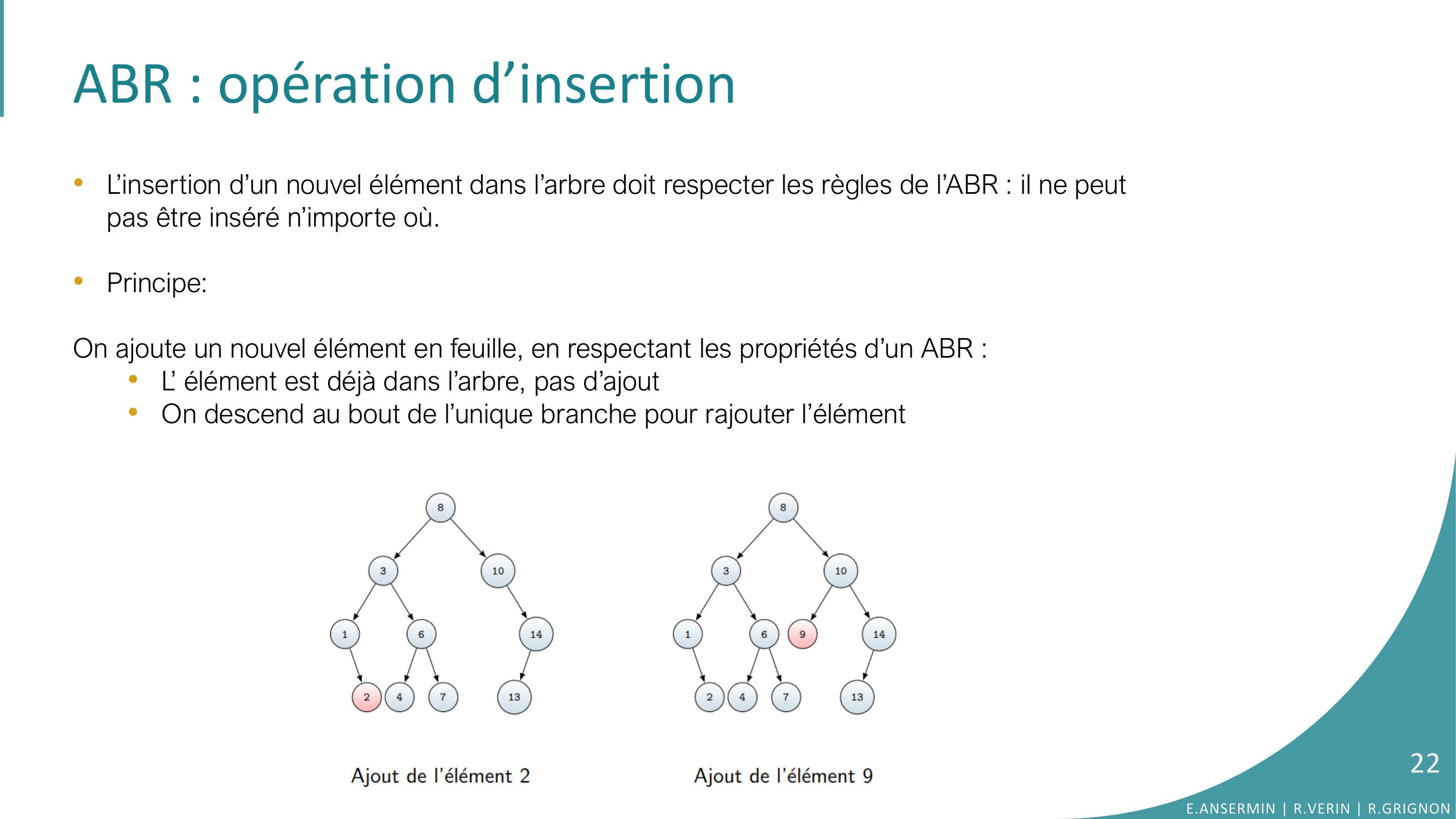
Page 21 : ABR : opération d’insertion•L’insertion d’un nouvel élément dans l’arbre doit respecter les règles de l’ABR : il ne peut pas être inséré n’importe où. •Principe:On ajoute un nouvel élément en feuille, en respectant les propriétés d’un ABR :•L’ élément est déjà dans l’arbre, pas d’ajout •On descend au bout de l’unique branche pour rajouter l’élémentE.ANSERMIN R.VERIN R.GRIGNON21
Page 22 : ABR : opération d’insertion•L’insertion d’un nouvel élément dans l’arbre doit respecter les règles de l’ABR : il ne peut pas être inséré n’importe où. •Principe:On ajoute un nouvel élément en feuille, en respectant les propriétés d’un ABR :•L’ élément est déjà dans l’arbre, pas d’ajout •On descend au bout de l’unique branche pour rajouter l’élémentE.ANSERMIN R.VERIN R.GRIGNON22
Page 23 : ABR : opération d’insertion•Algorithme : FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON23
Page 24 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON24
Page 25 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON25
Page 26 : ABR : opération d’insertiona•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON26
Page 27 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON27
Page 28 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON28
Page 29 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON29
Page 30 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON30
Page 31 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON31
Page 32 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON32
Page 33 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON33
Page 34 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON34
Page 35 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON35
Page 36 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON36
Page 37 : ABR : opération d’insertiona NULL•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON37
Page 38 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaa NULLE.ANSERMIN R.VERIN R.GRIGNON38
Page 39 : ABR : opération d’insertion•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaa NULLE.ANSERMIN R.VERIN R.GRIGNON39
Page 40 : •Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINABR : opération d’insertiona 11aaaE.ANSERMIN R.VERIN R.GRIGNON40
Page 41 : •Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINABR : opération d’insertiona 11aaaE.ANSERMIN R.VERIN R.GRIGNON41
Page 42 : ABR : opération d’insertion11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON42
Page 43 : •Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINABR : opération d’insertion11aaaE.ANSERMIN R.VERIN R.GRIGNON43
Page 44 : ABR : opération d’insertion11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON44
Page 45 : ABR : opération d’insertion11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON45
Page 46 : ABR : opération d’insertiona11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON46
Page 47 : ABR : opération d’insertiona11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON47
Page 48 : ABR : opération d’insertion11•Algorithme : Exemple : insertionABRa, 11FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON48
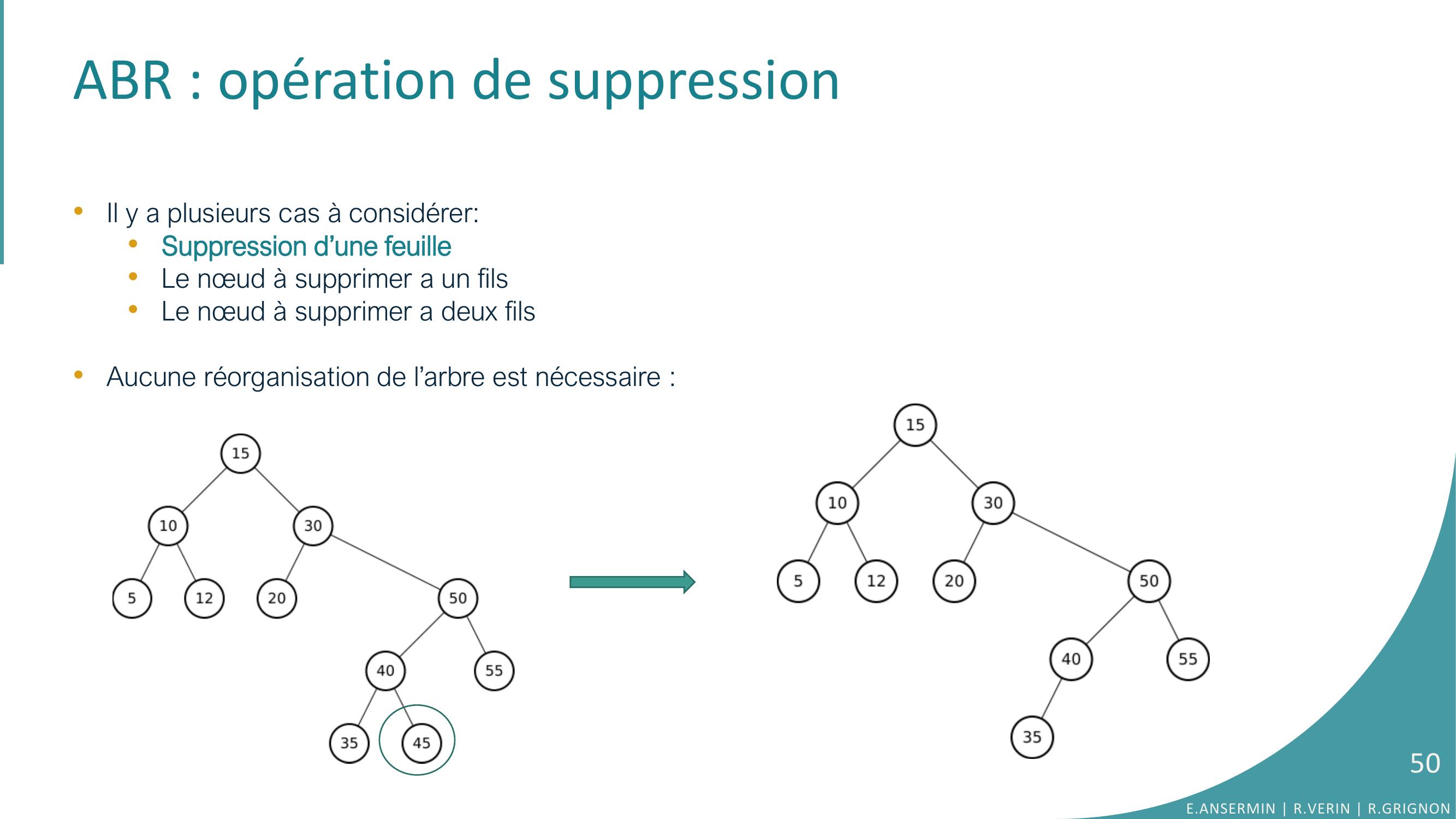
Page 49 : ABR : opération de suppression•La suppression d’un nœud dans un arbre binaire consiste à supprimer uniquement le nœud ciblé : ses fils doivent rester dans l’arbre.•Il faut maintenir la relation d’ordre imposée par l’ABR !•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux filsE.ANSERMIN R.VERIN R.GRIGNON49
Page 50 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•Aucune réorganisation de l’arbre est nécessaire : E.ANSERMIN R.VERIN R.GRIGNON50
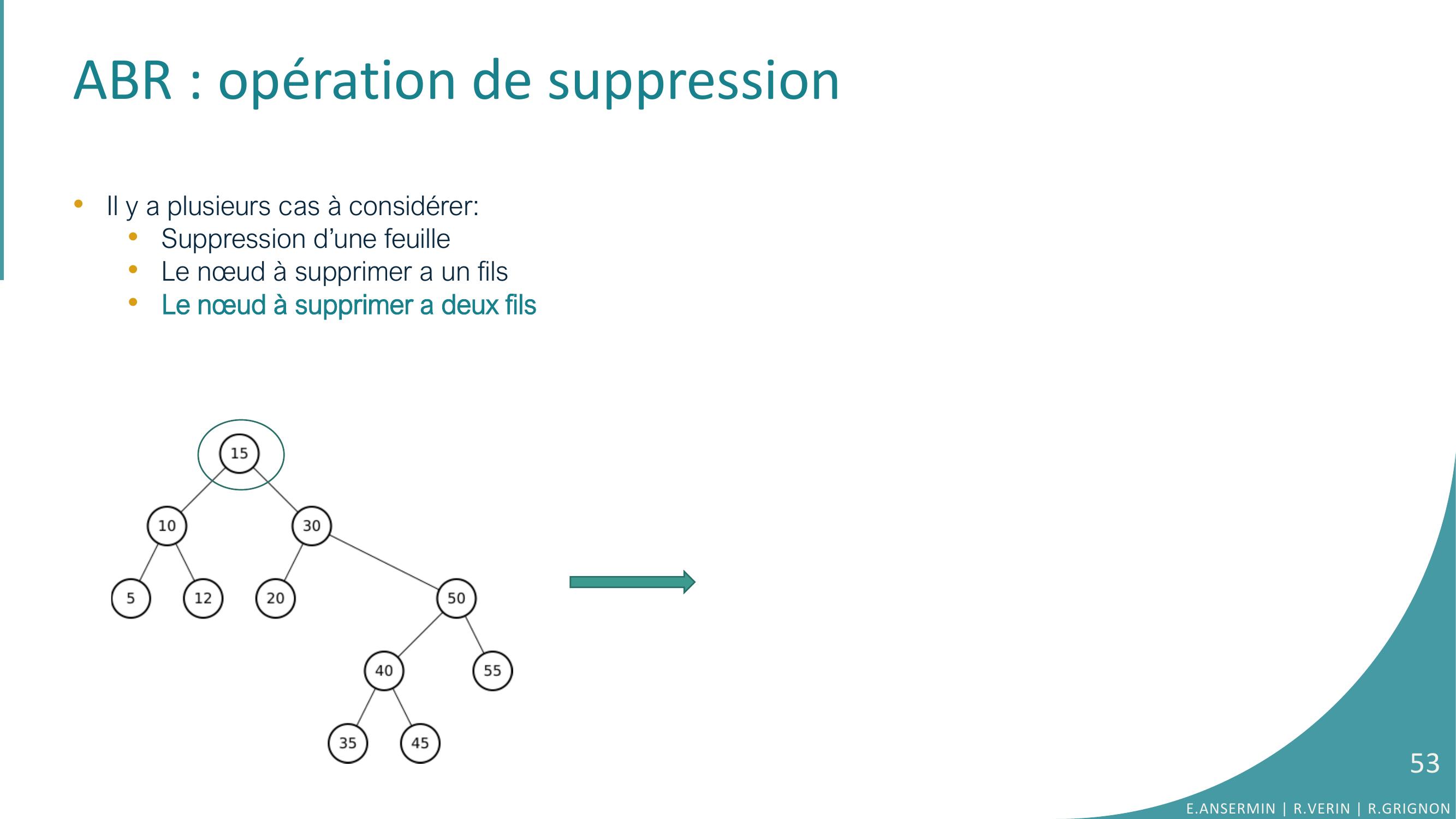
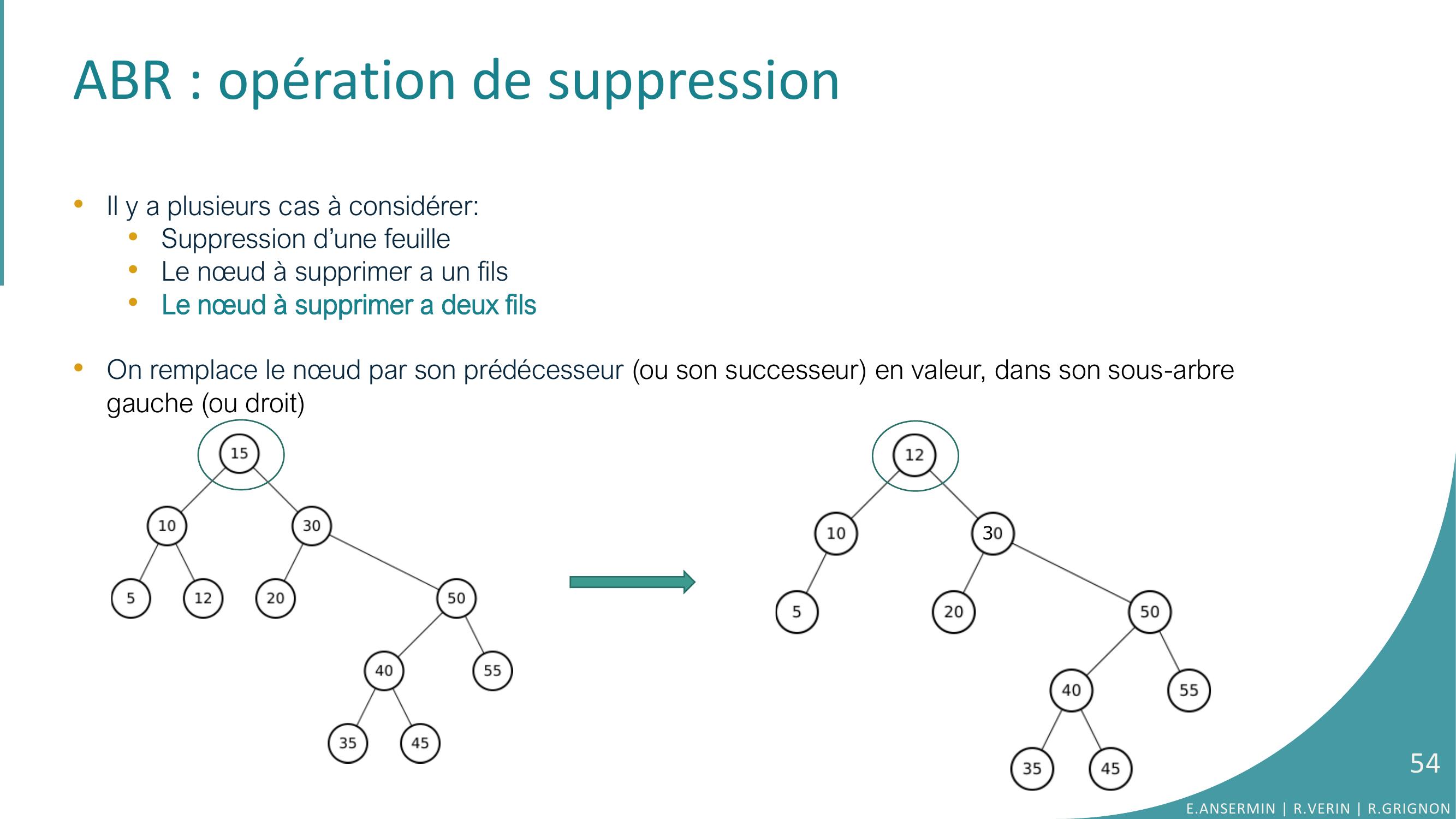
Page 51 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux filsE.ANSERMIN R.VERIN R.GRIGNON51
Page 52 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•On remplace le nœud par son fils unique :E.ANSERMIN R.VERIN R.GRIGNON52
Page 53 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux filsE.ANSERMIN R.VERIN R.GRIGNON53
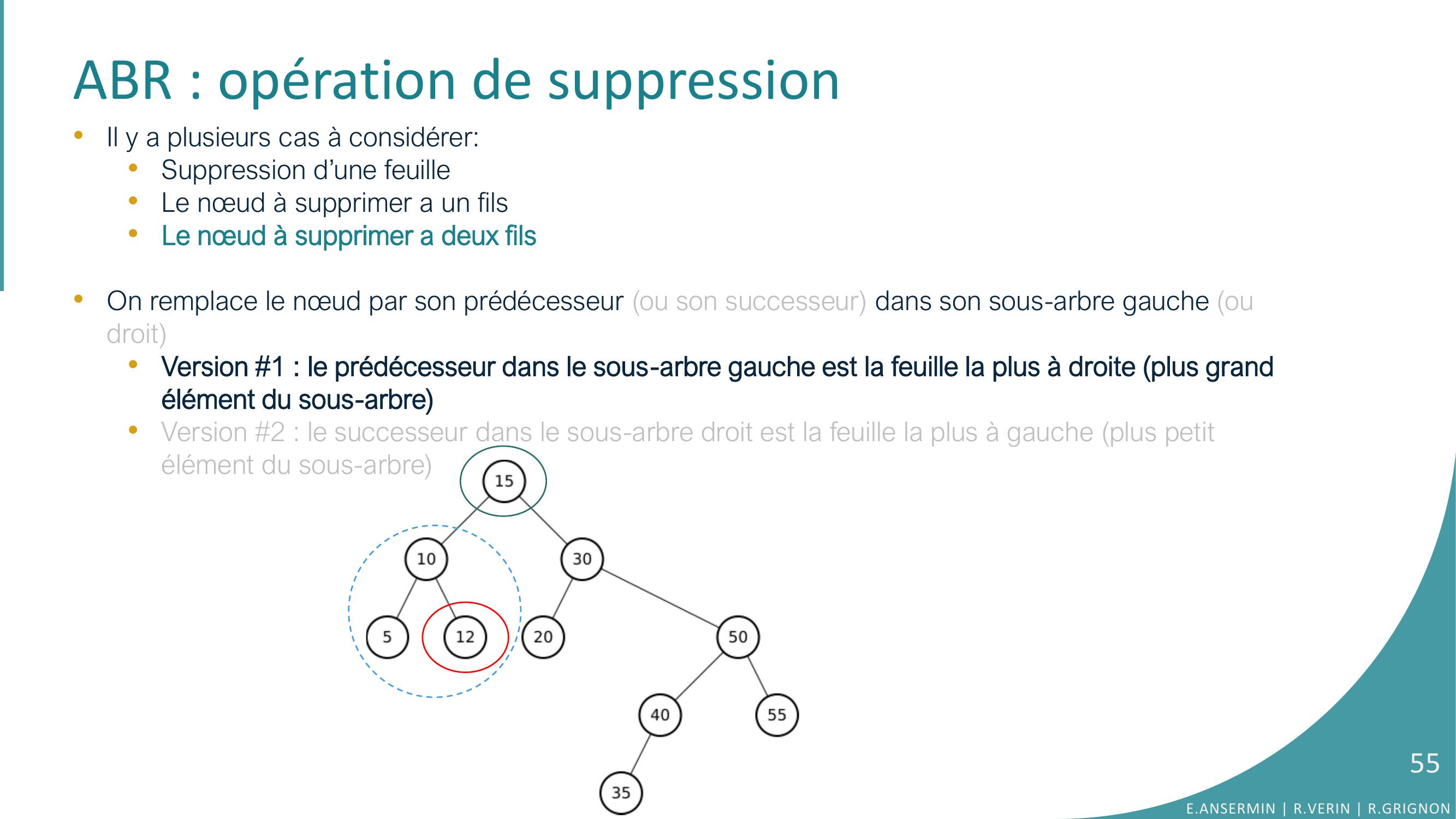
Page 54 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•On remplace le nœud par son prédécesseur ou son successeur en valeur, dans son sous-arbre gauche ou droit3E.ANSERMIN R.VERIN R.GRIGNON54
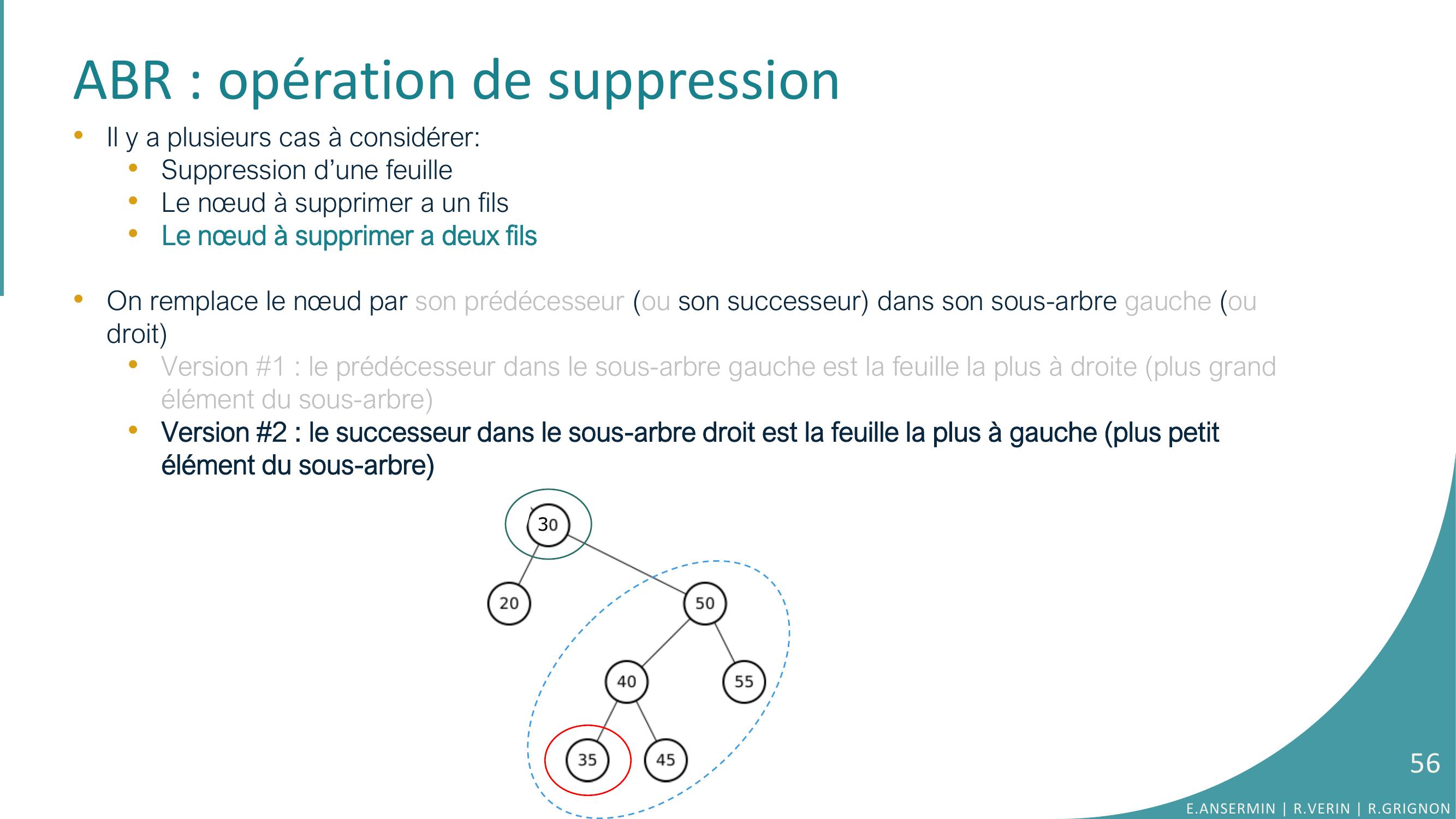
Page 55 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•On remplace le nœud par son prédécesseur ou son successeur dans son sous-arbre gauche ou droit•Version 1 : le prédécesseur dans le sous-arbre gauche est la feuille la plus à droite plus grand élément du sous-arbre•Version 2 : le successeur dans le sous-arbre droit est la feuille la plus à gauche plus petit élément du sous-arbreE.ANSERMIN R.VERIN R.GRIGNON55
Page 56 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•On remplace le nœud par son prédécesseur ou son successeur dans son sous-arbre gauche oudroit•Version 1 : le prédécesseur dans le sous-arbre gauche est la feuille la plus à droite plus grand élément du sous-arbre•Version 2 : le successeur dans le sous-arbre droit est la feuille la plus à gauche plus petit élément du sous-arbre3E.ANSERMIN R.VERIN R.GRIGNON56
Page 57 : ABR : opération de suppression•Il y a plusieurs cas à considérer:•Suppression d’une feuille •Le nœud à supprimer a un fils•Le nœud à supprimer a deux fils•On remplace le nœud par son prédécesseur ou son successeur dans son sous-arbre gauche ou droit•Version 1 : le prédécesseur dans le sous-arbre gauche est la feuille la plus à droite plus grand élément du sous-arbre•Version 2 : le successeur dans le sous-arbre droit est la feuille la plus à gauche plus petit élément du sous-arbre•Principe : •On recherche le nœud à supprimer•S’il n’a pas de fils gauche, on le remplace par son fils droit fils unique•Sinon on cherche la plus grande valeur du sous-arbre gauche valeur la plus à droite et on échange sa valeur avec la valeur du nœud à supprimer. E.ANSERMIN R.VERIN R.GRIGNON57
Page 58 : ABR : opération de suppression•Algorithme :FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbre SINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e…FIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON58
Page 59 : ABR : opération de suppression•Algorithme :FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp…FIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON59
Page 60 : ABR : opération de suppression•Algorithme :FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON60
Page 61 : ABR : opération de suppression•Algorithme :FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON61
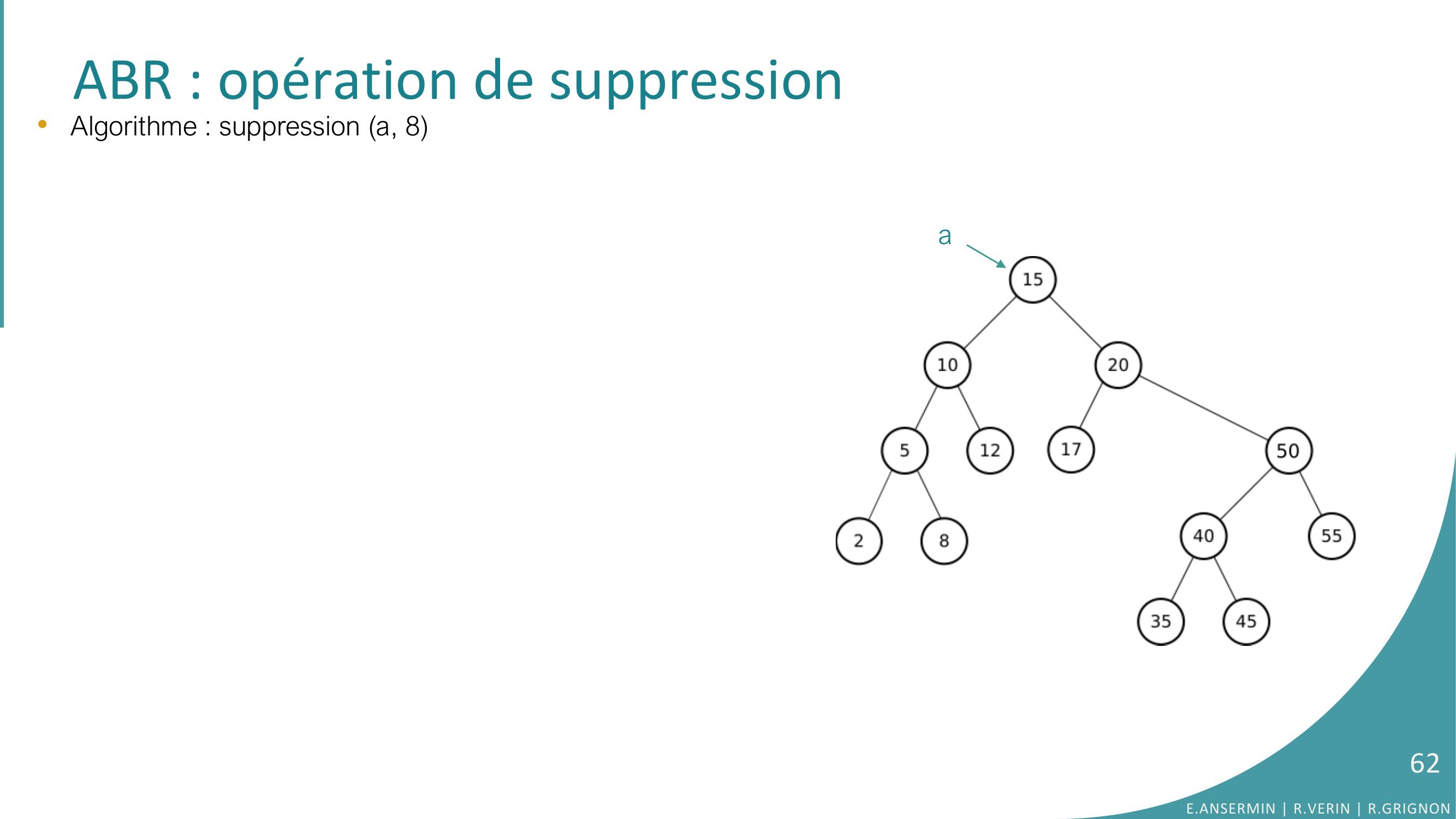
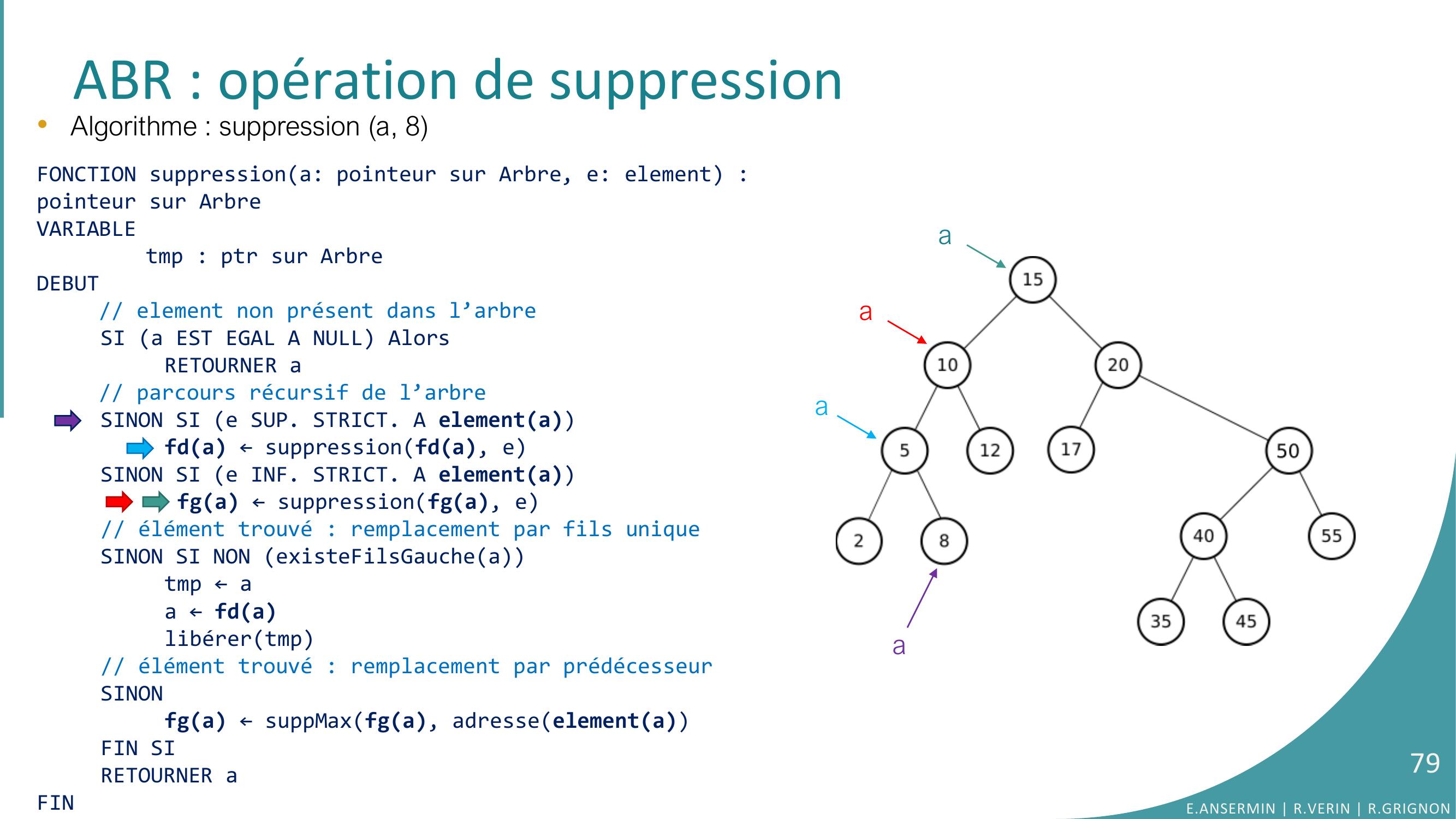
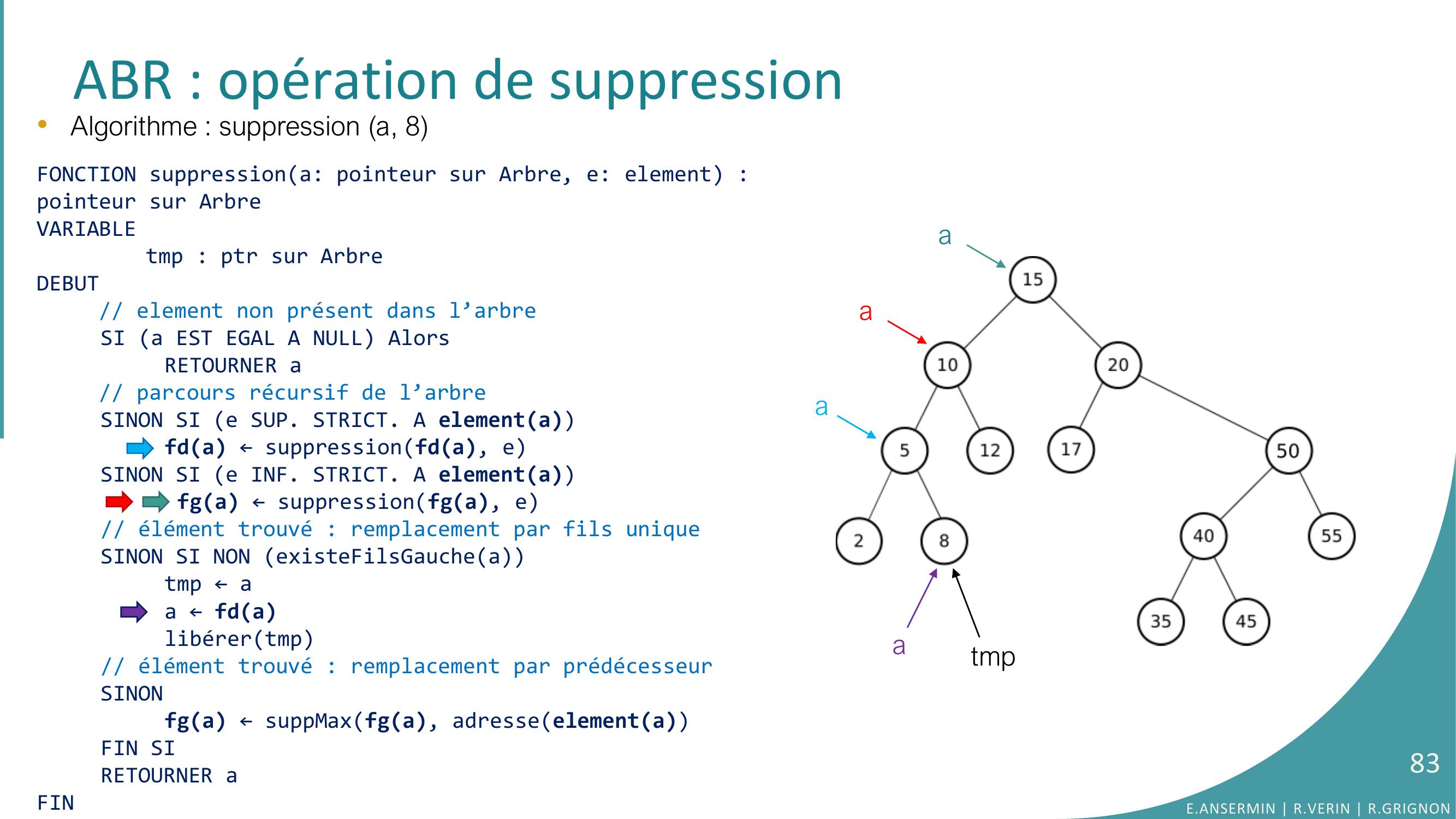
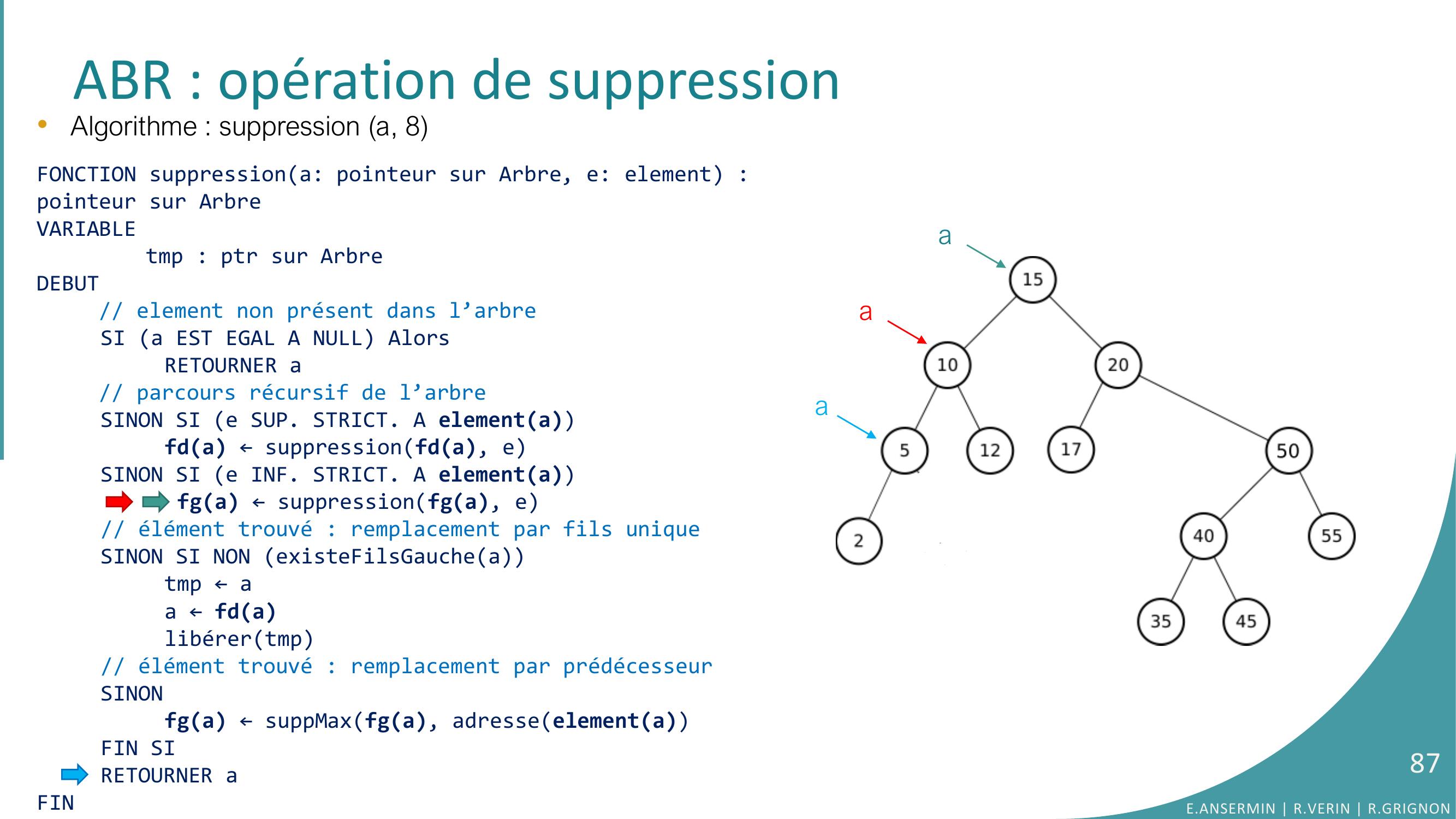
Page 62 : ABR : opération de suppressiona•Algorithme : suppression a, 8E.ANSERMIN R.VERIN R.GRIGNON62
Page 63 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON63
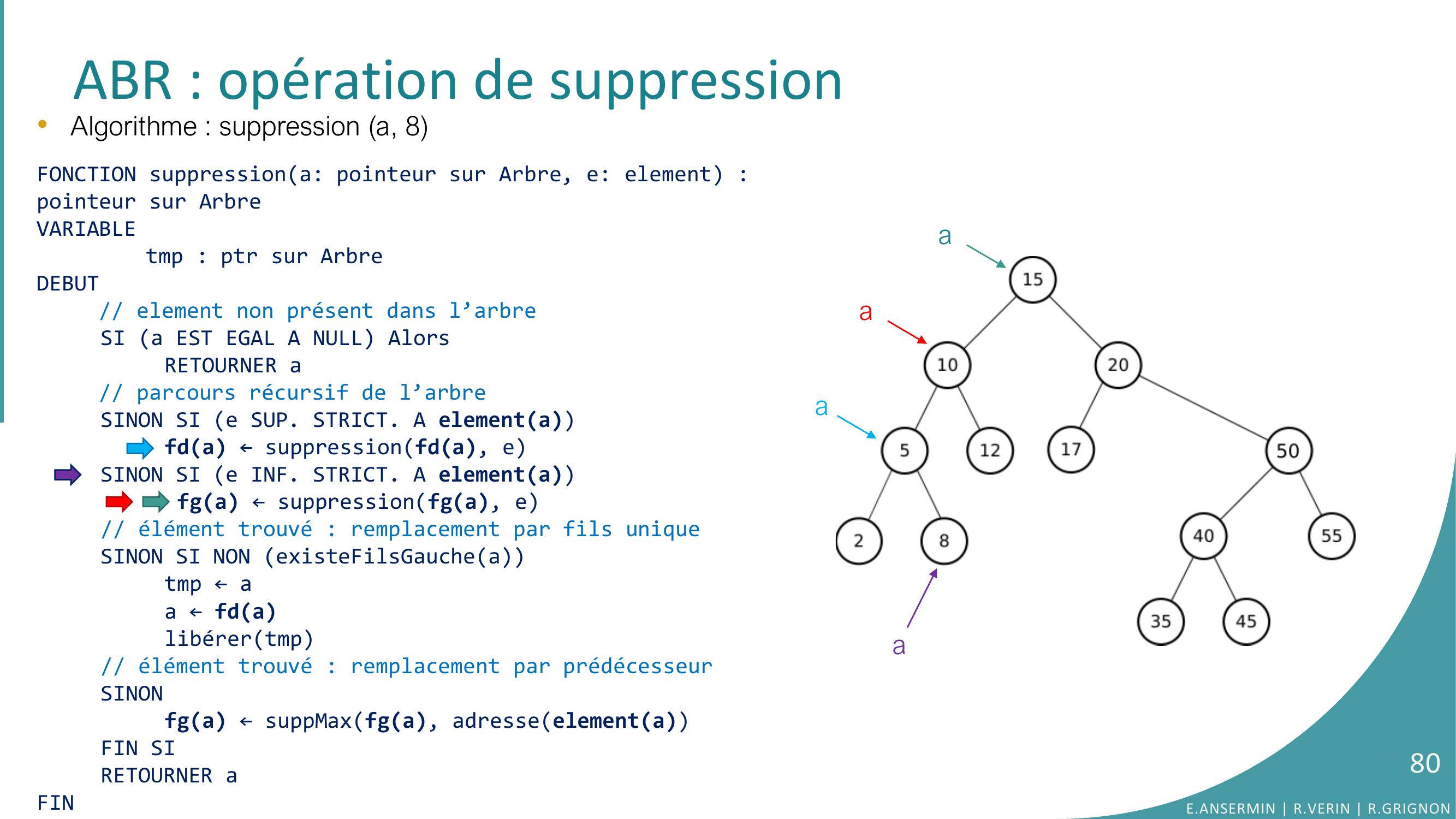
Page 64 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON64
Page 65 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON65
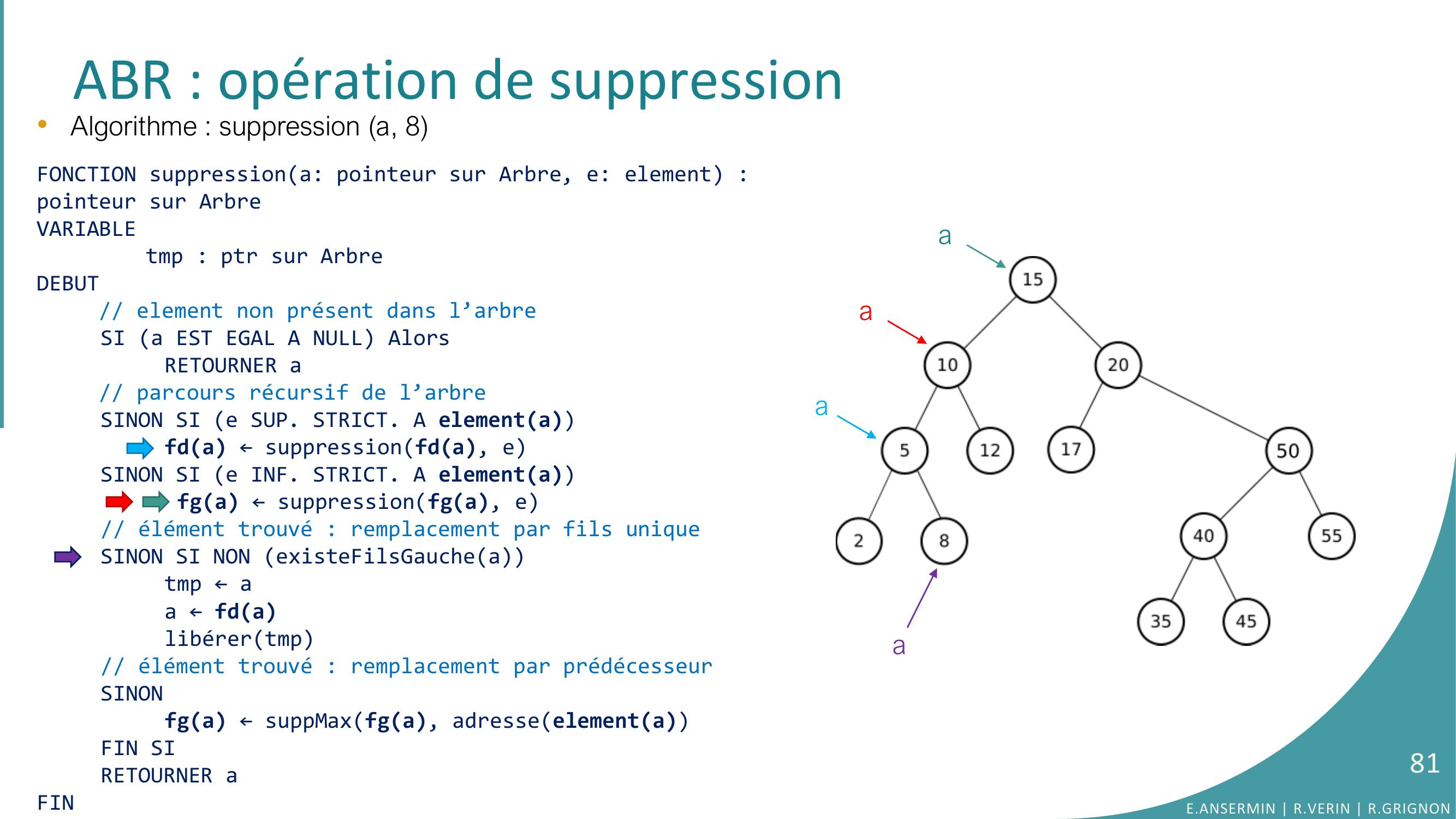
Page 66 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON66
Page 67 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON67
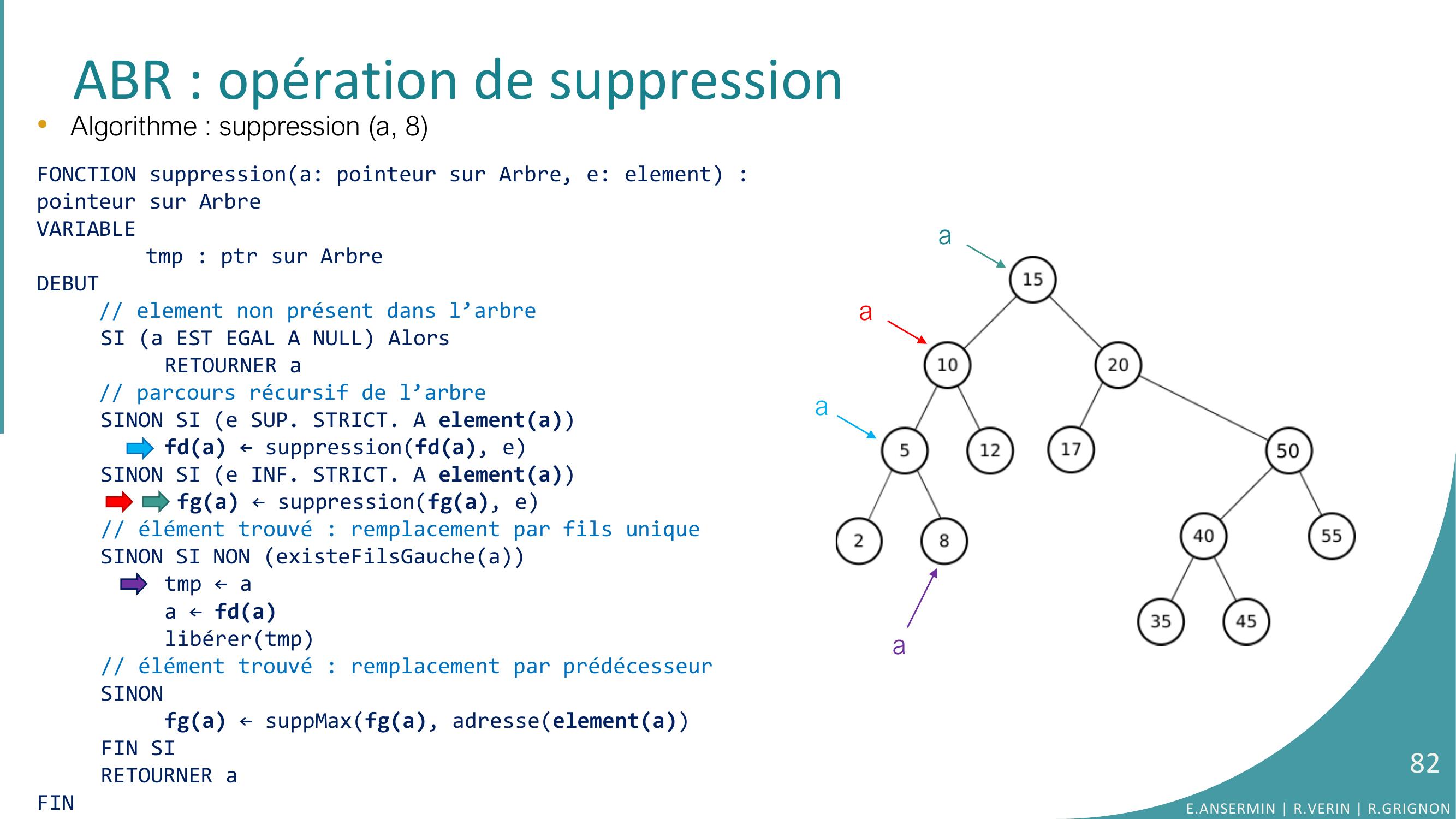
Page 68 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON68
Page 69 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON69
Page 70 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON70
Page 71 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON71
Page 72 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON72
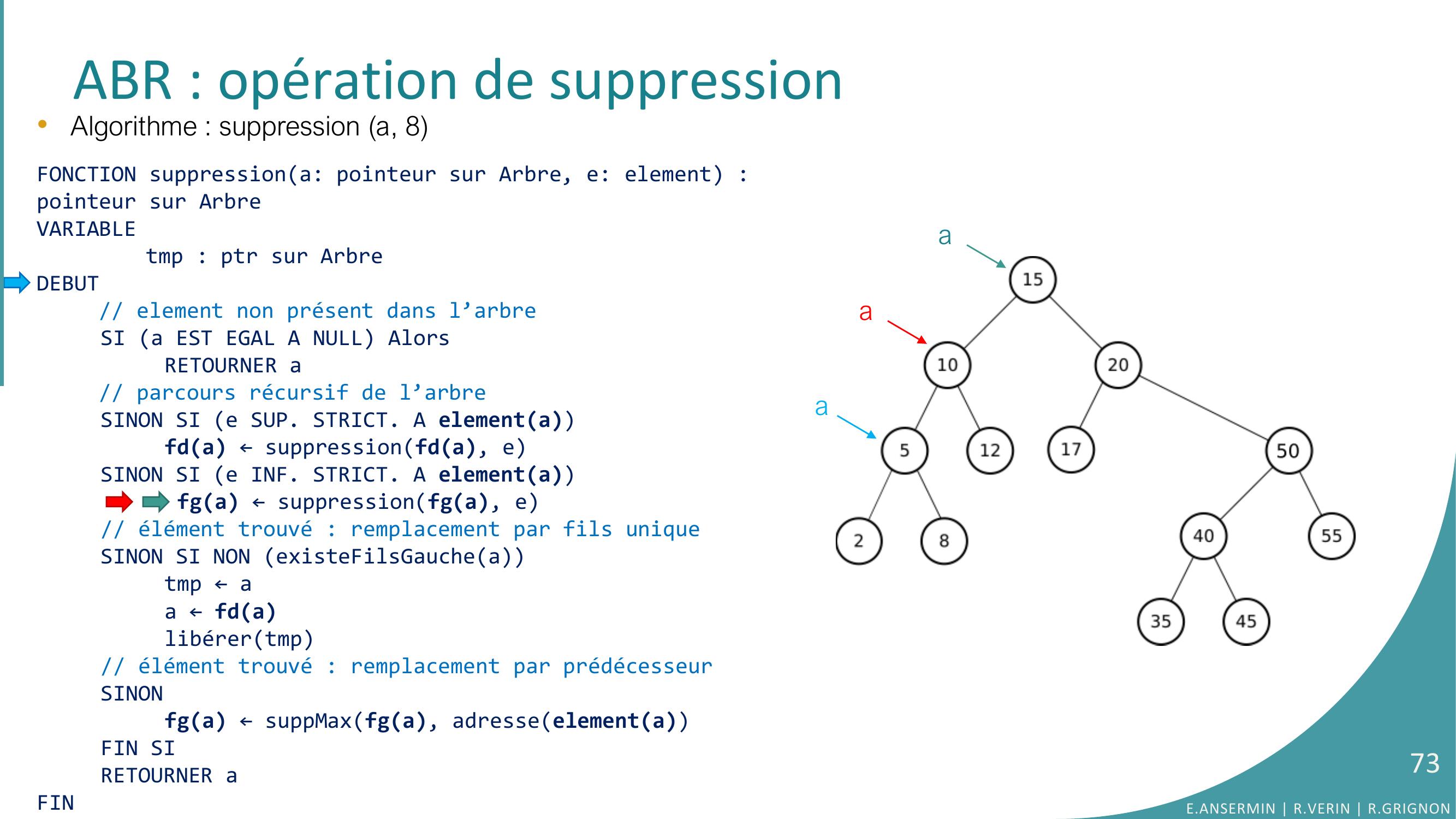
Page 73 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON73
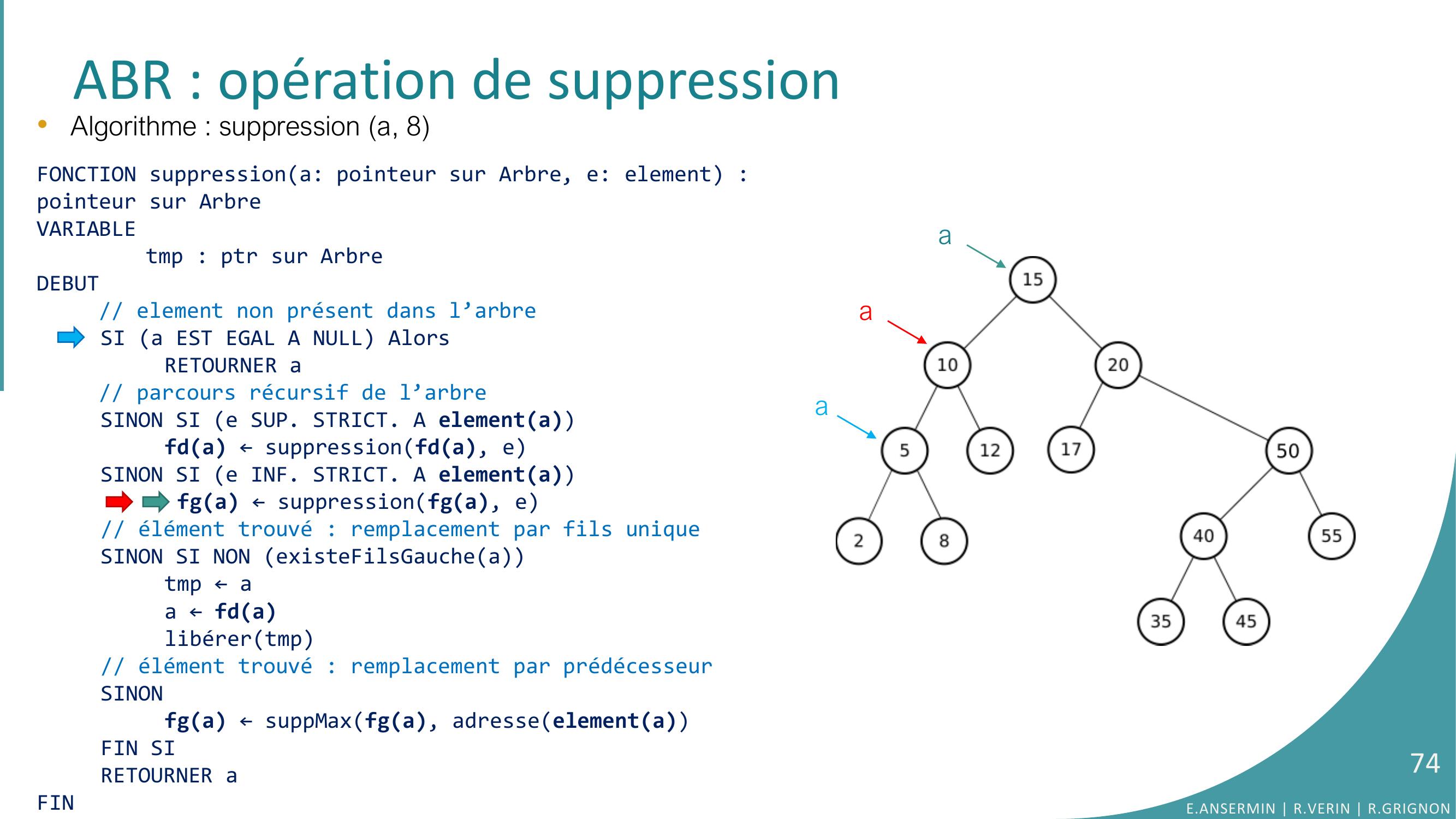
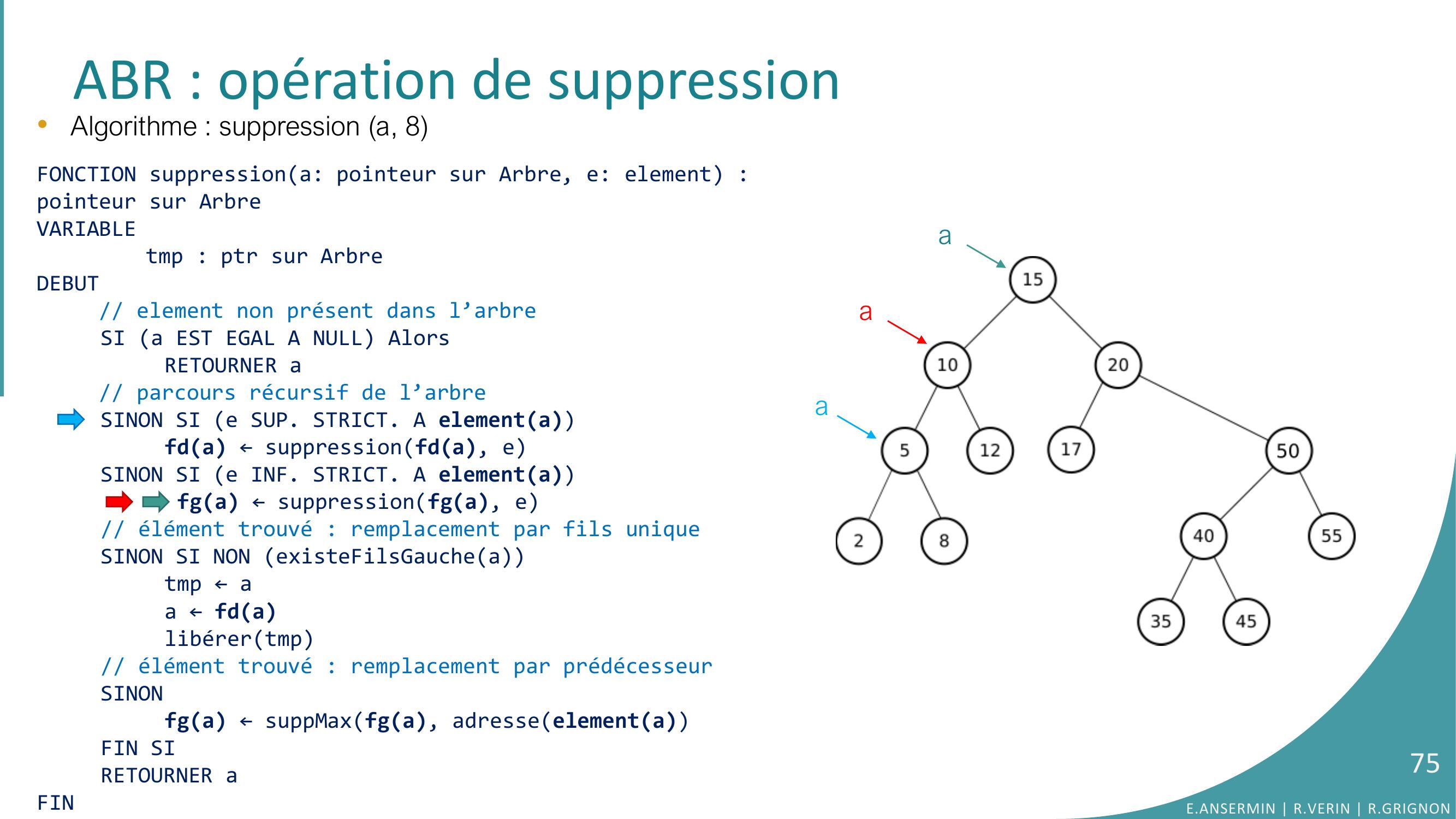
Page 74 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON74
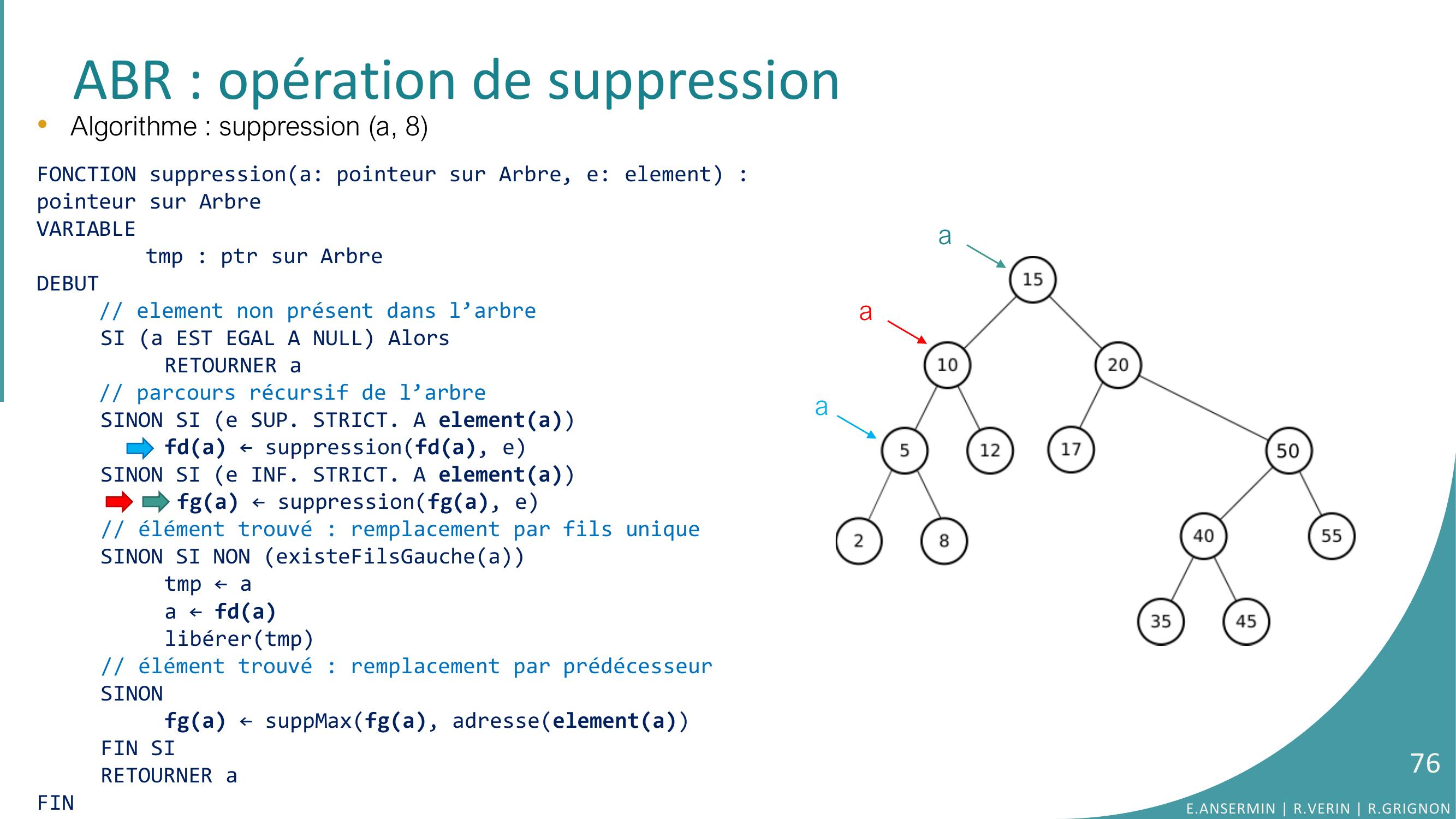
Page 75 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON75
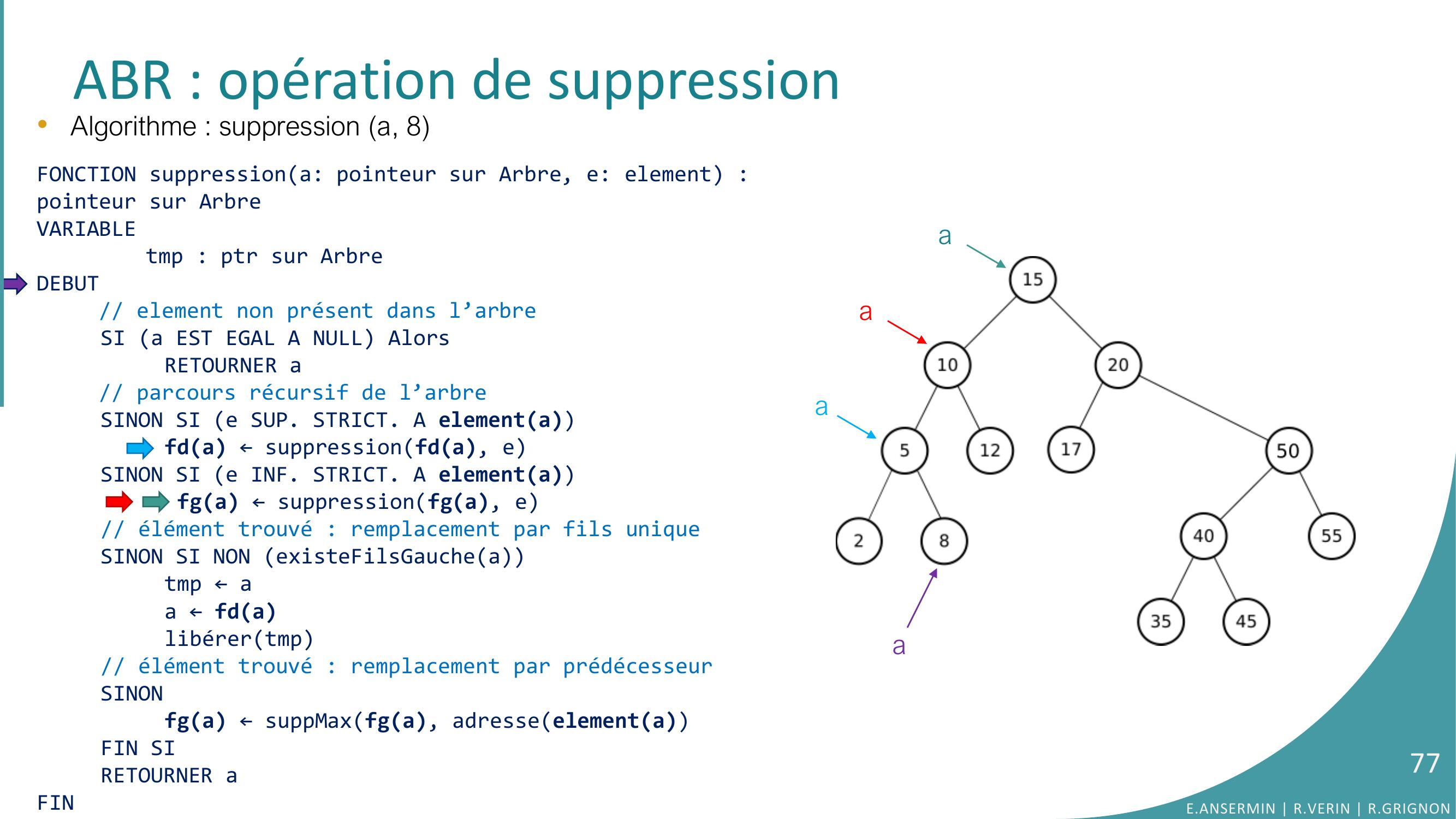
Page 76 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON76
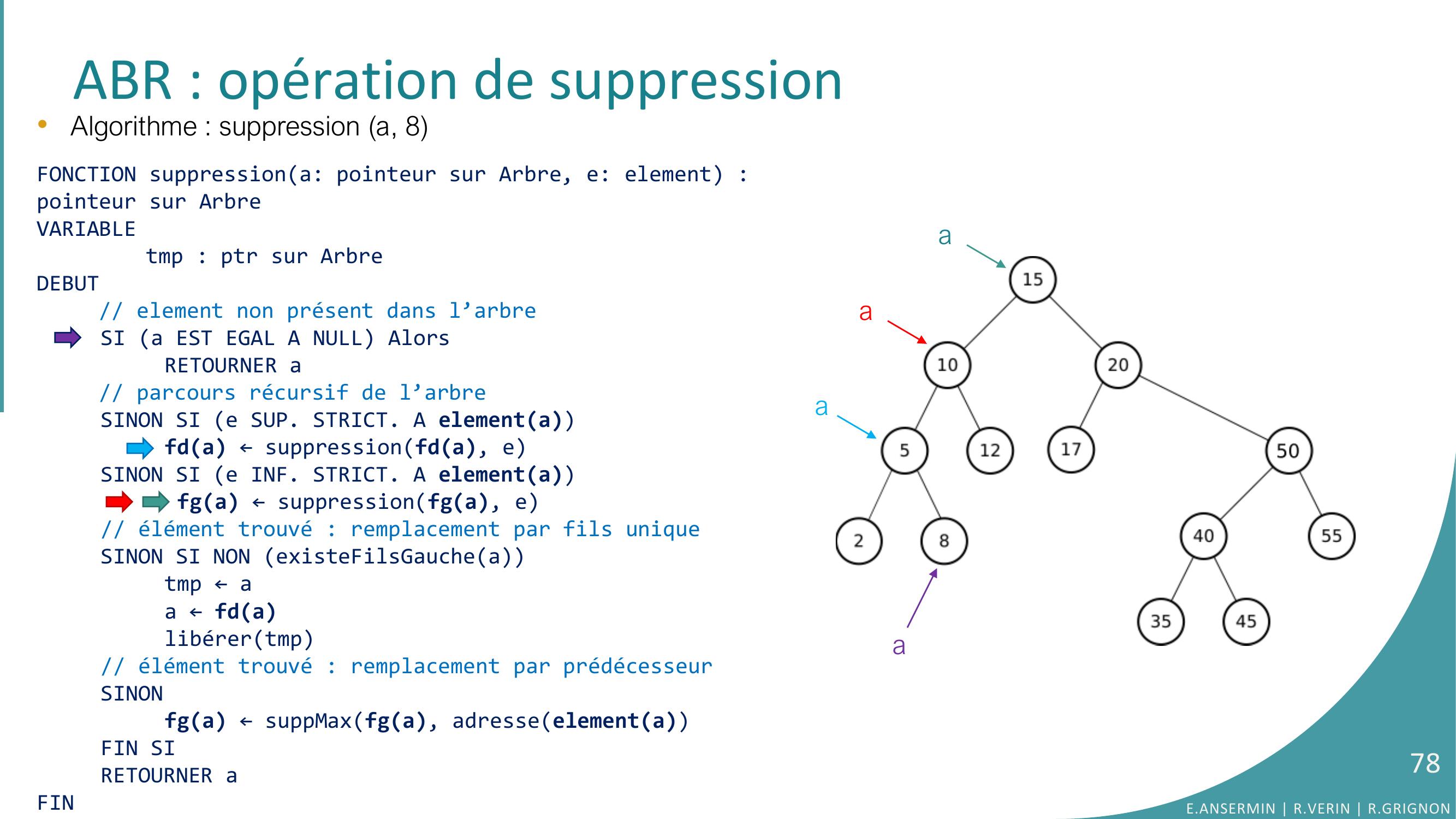
Page 77 : •Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaaE.ANSERMIN R.VERIN R.GRIGNON77
Page 78 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON78
Page 79 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON79
Page 80 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON80
Page 81 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON81
Page 82 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON82
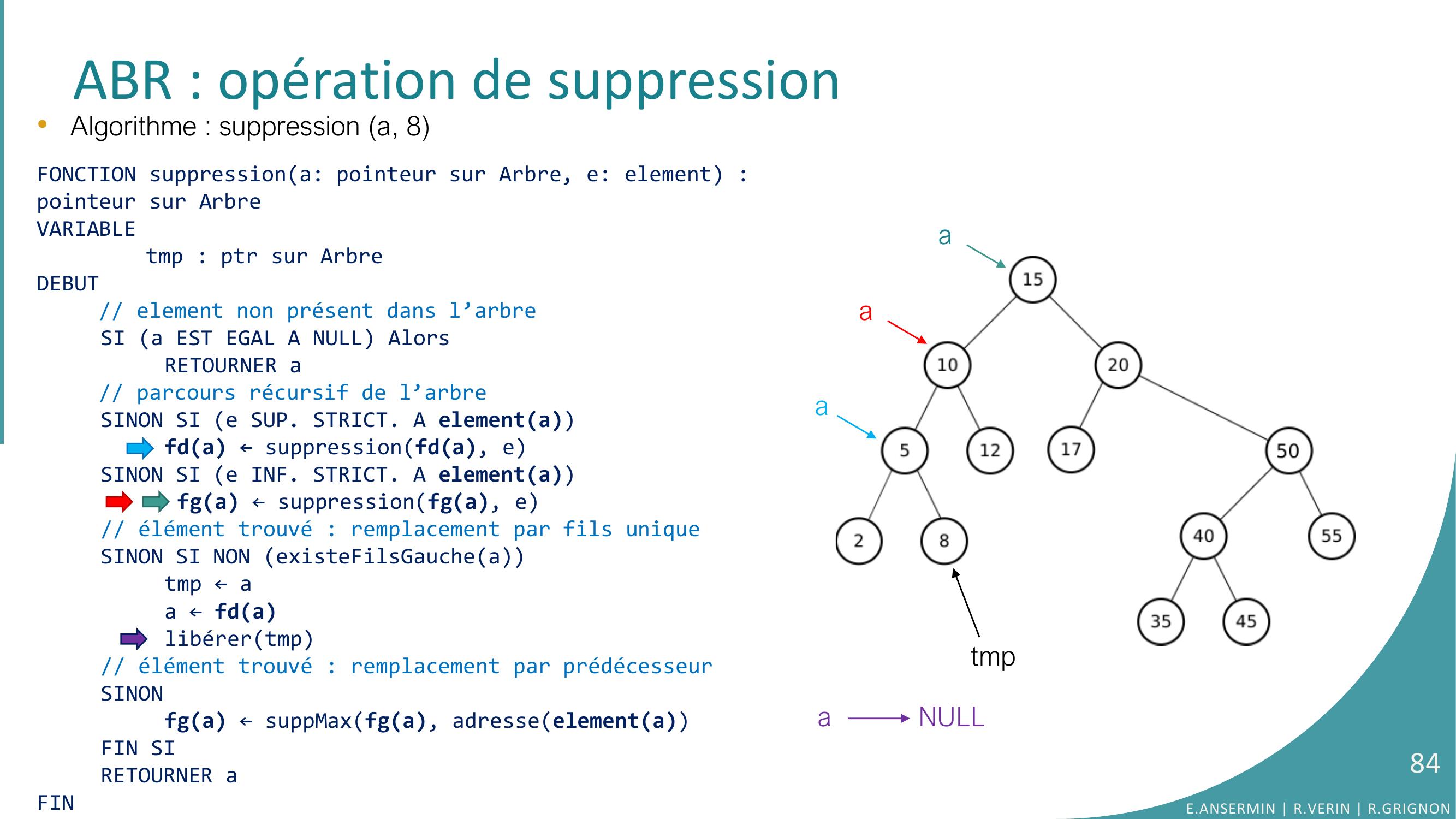
Page 83 : ABR : opération de suppressiontmp•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaaE.ANSERMIN R.VERIN R.GRIGNON83
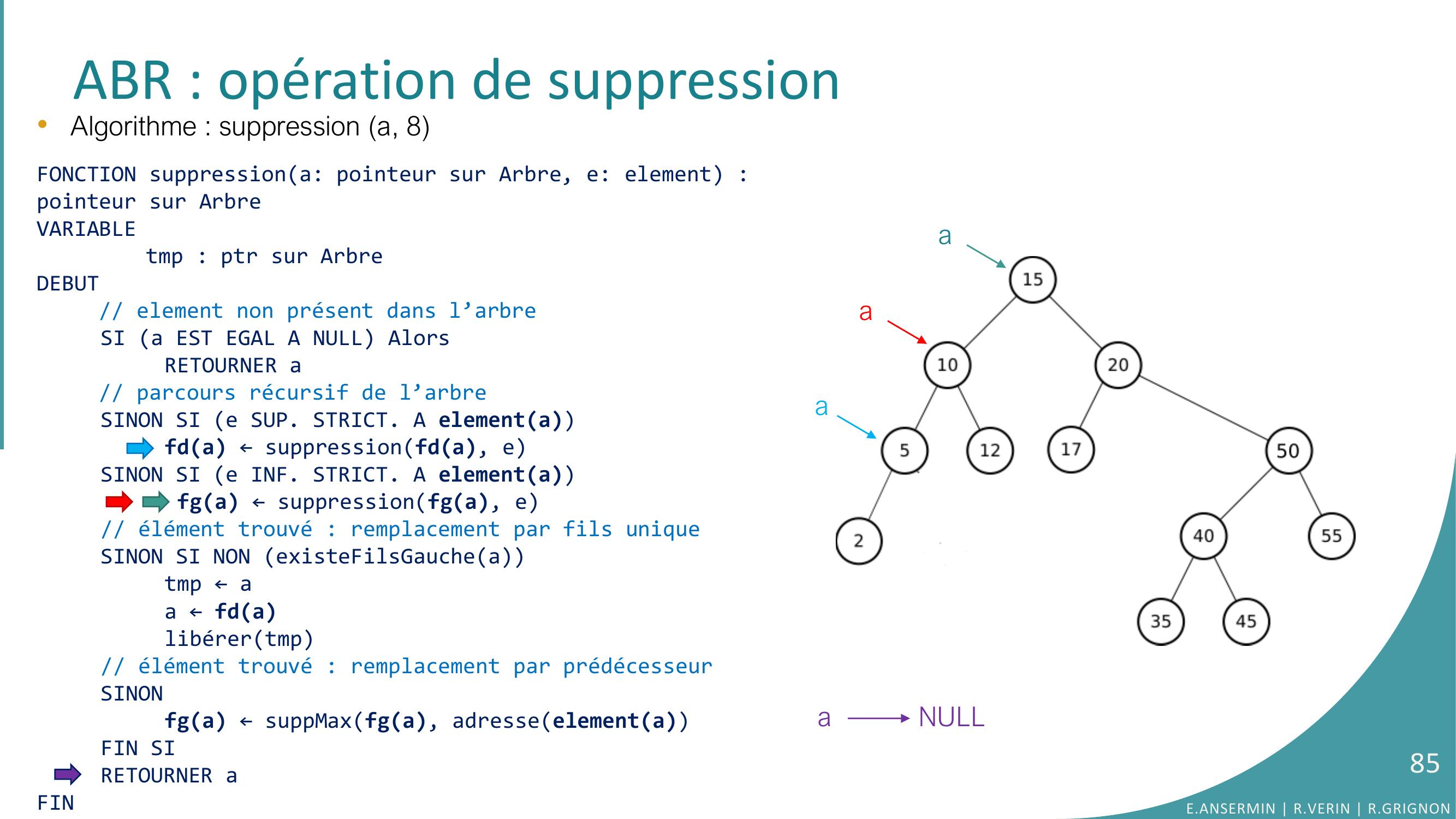
Page 84 : ABR : opération de suppressiona NULLtmp•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON84
Page 85 : ABR : opération de suppressiona NULL•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON85
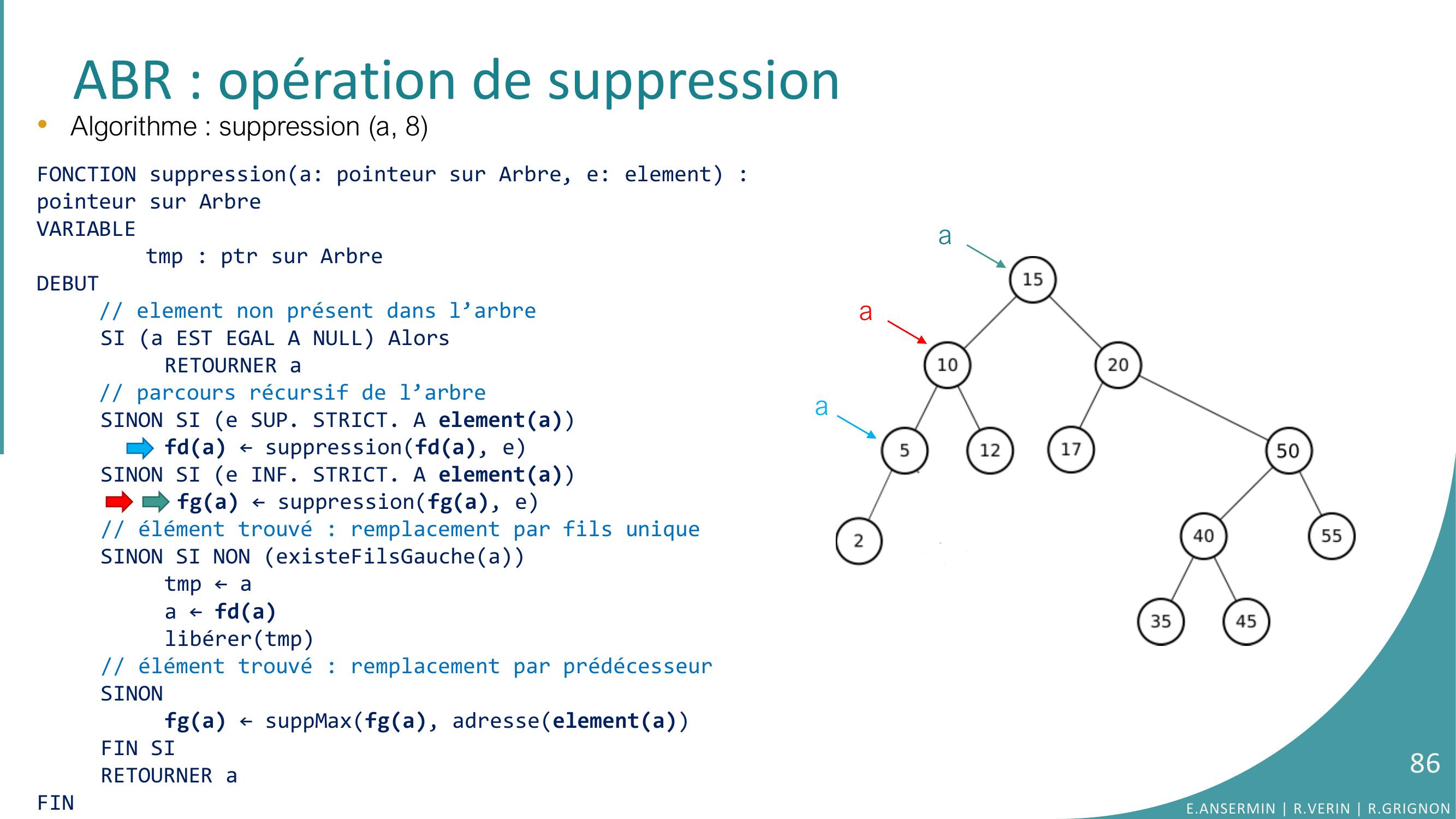
Page 86 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON86
Page 87 : ABR : opération de suppression•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON87
Page 88 : ABR : opération de suppressionaa•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON88
Page 89 : ABR : opération de suppressionaa•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON89
Page 90 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON90
Page 91 : ABR : opération de suppressiona•Algorithme : suppression a, 8FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON91
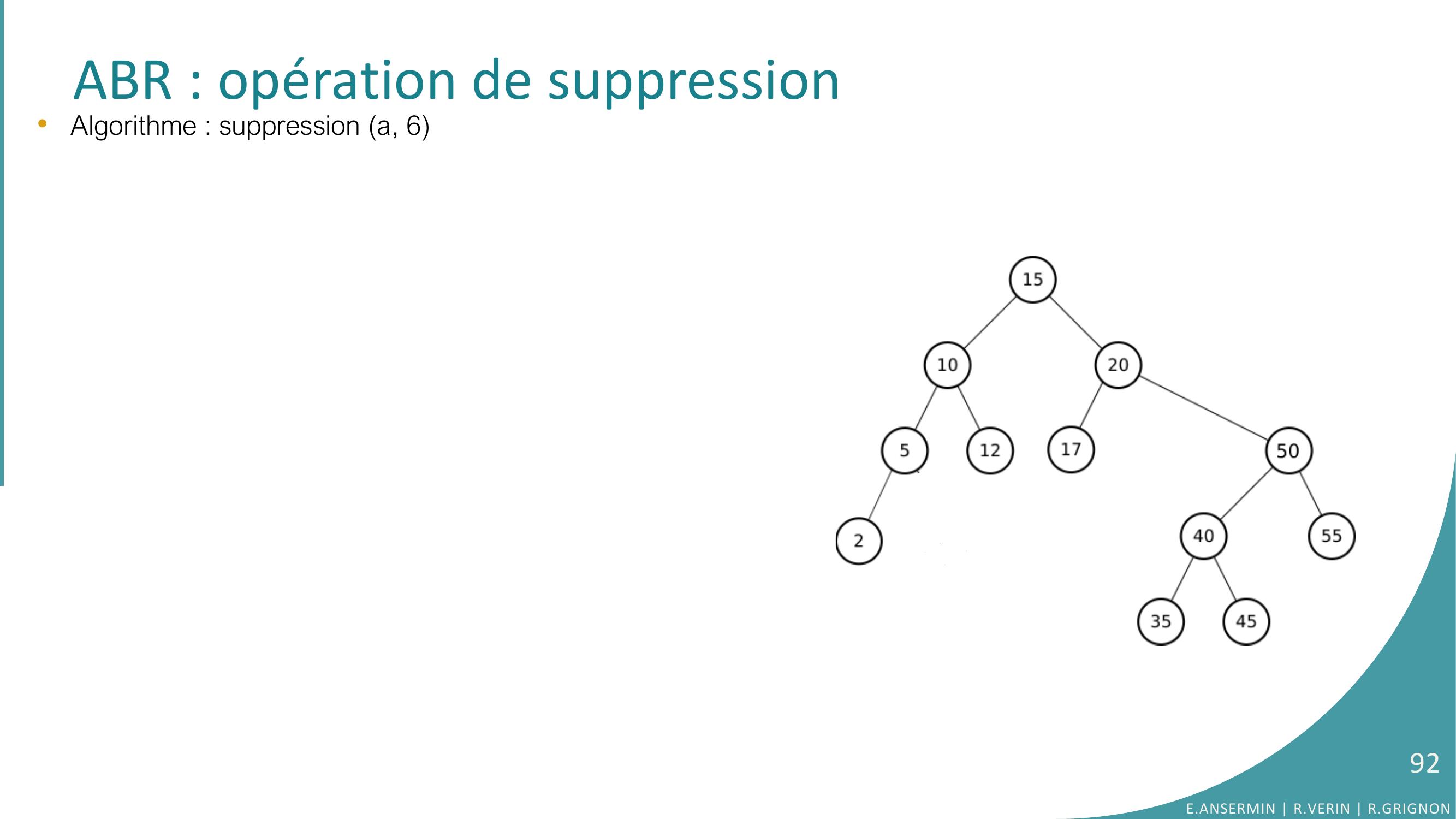
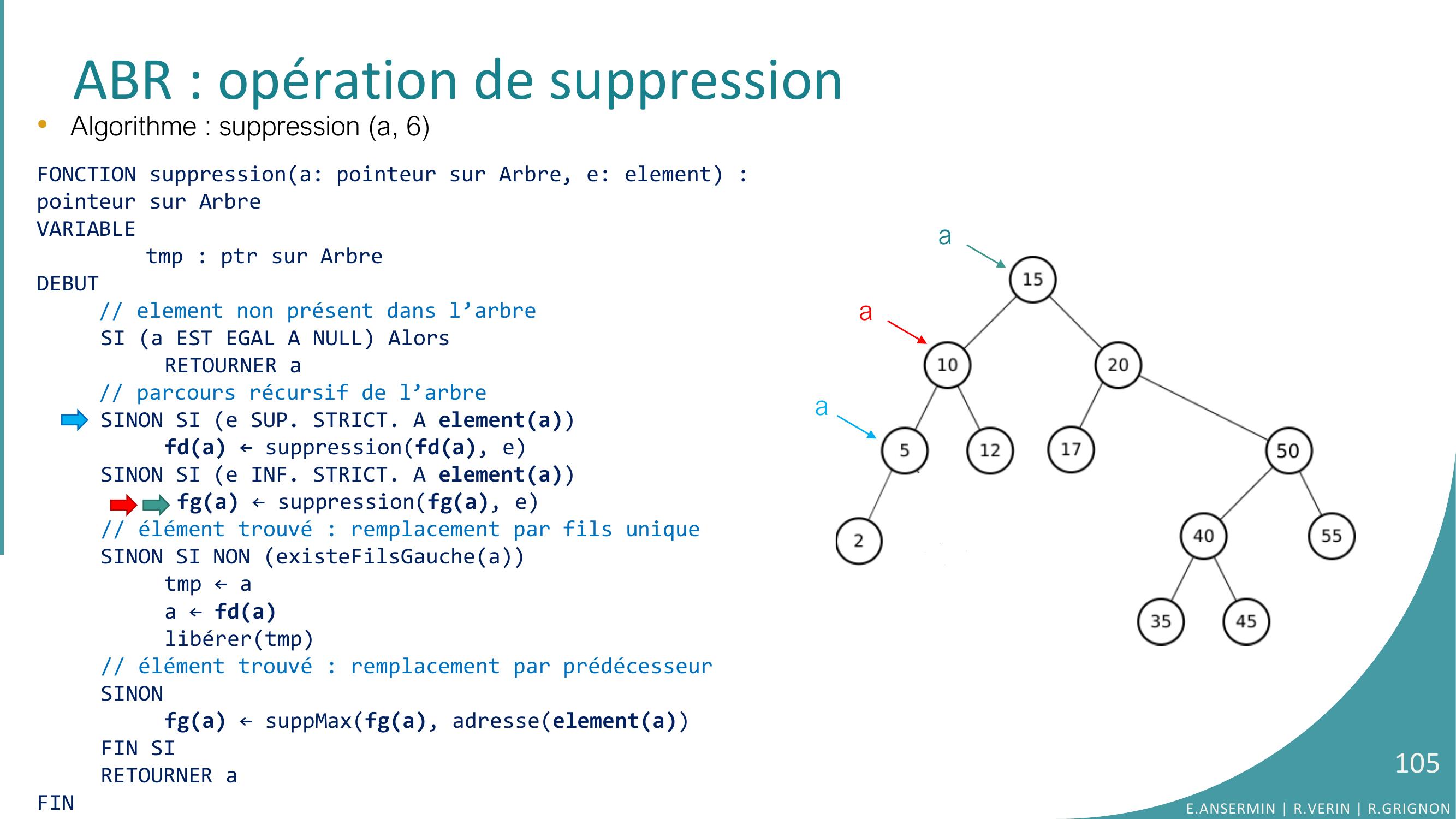
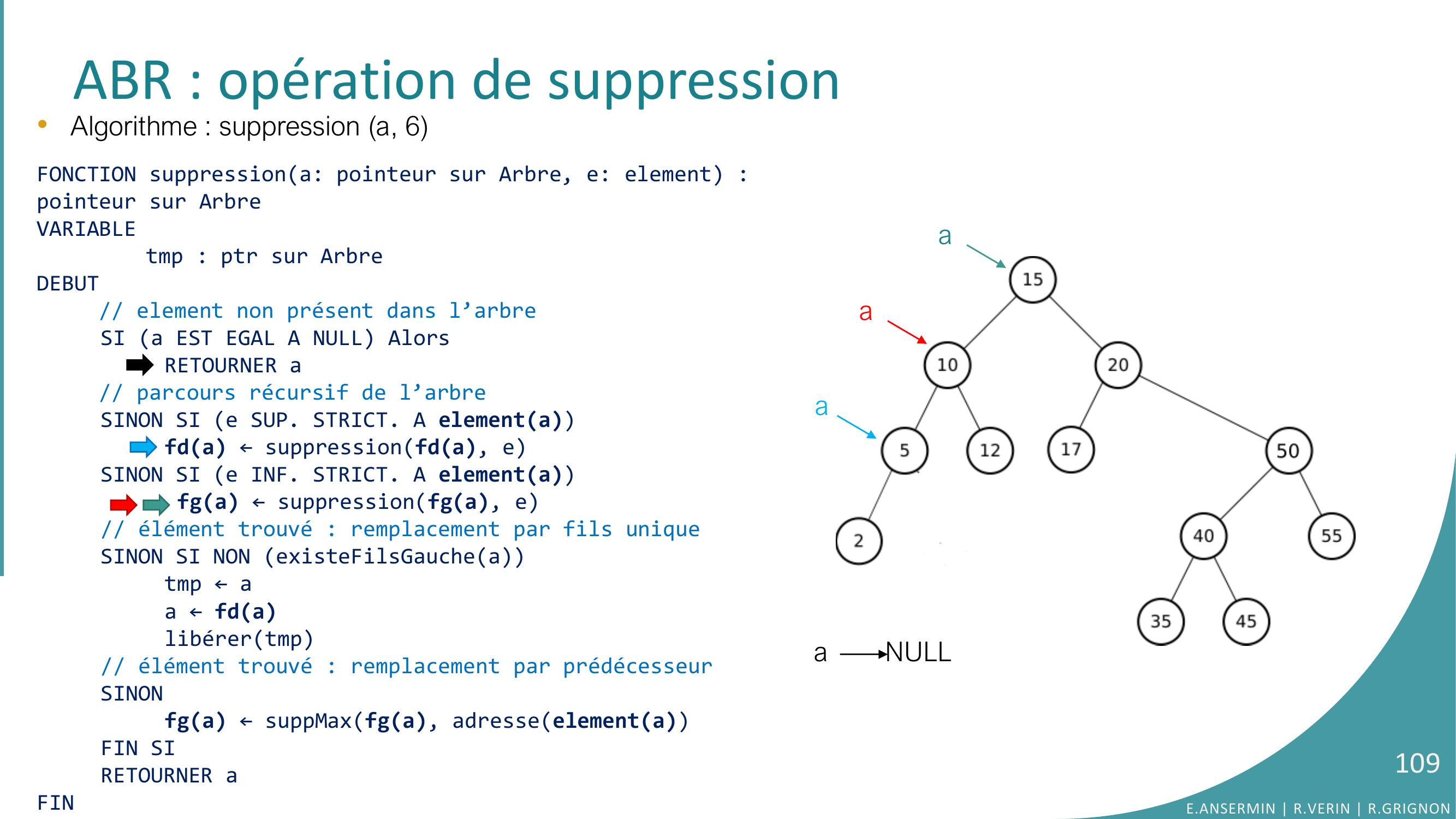
Page 92 : ABR : opération de suppression•Algorithme : suppression a, 6E.ANSERMIN R.VERIN R.GRIGNON92
Page 93 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON93
Page 94 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON94
Page 95 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON95
Page 96 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON96
Page 97 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON97
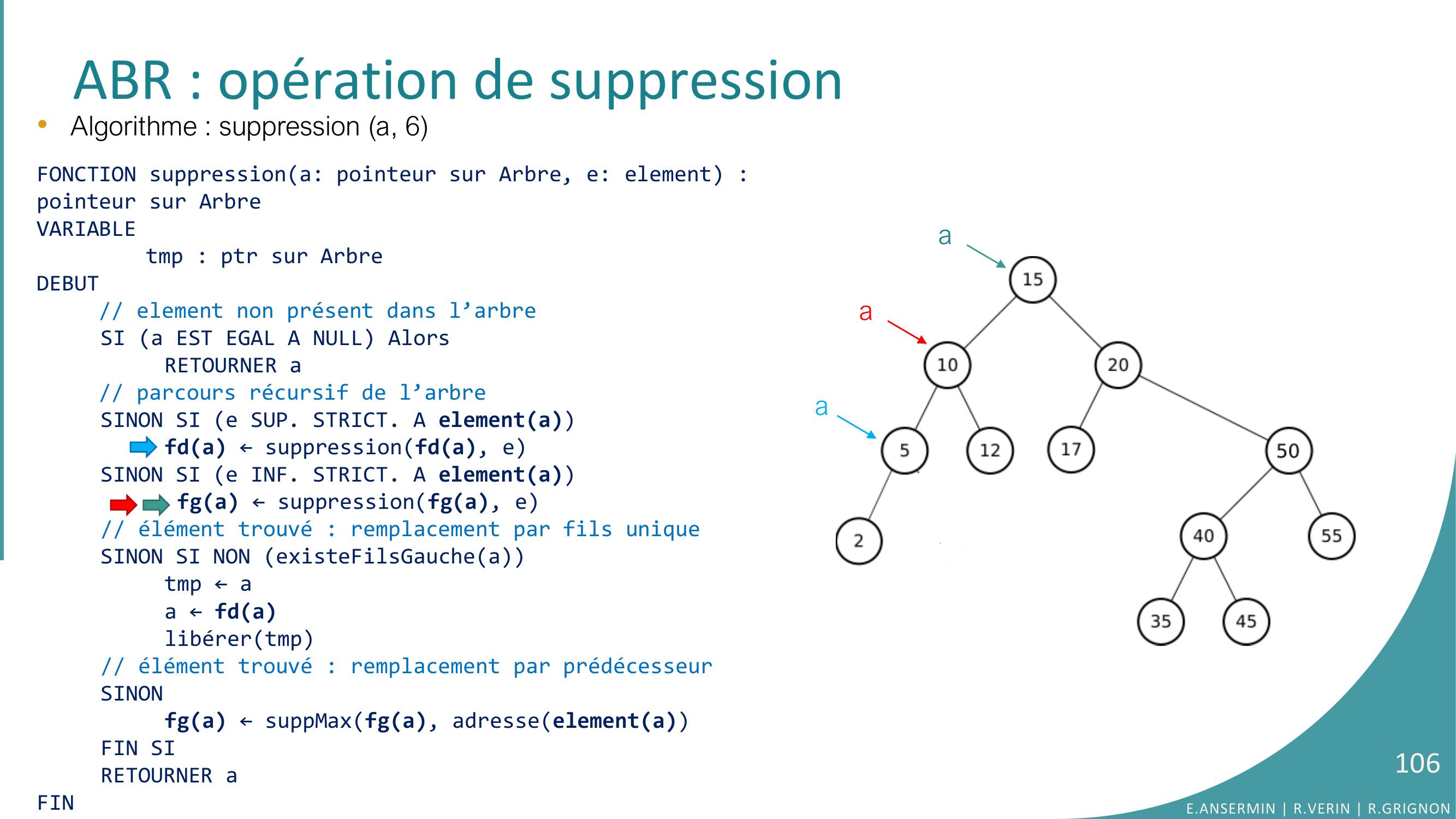
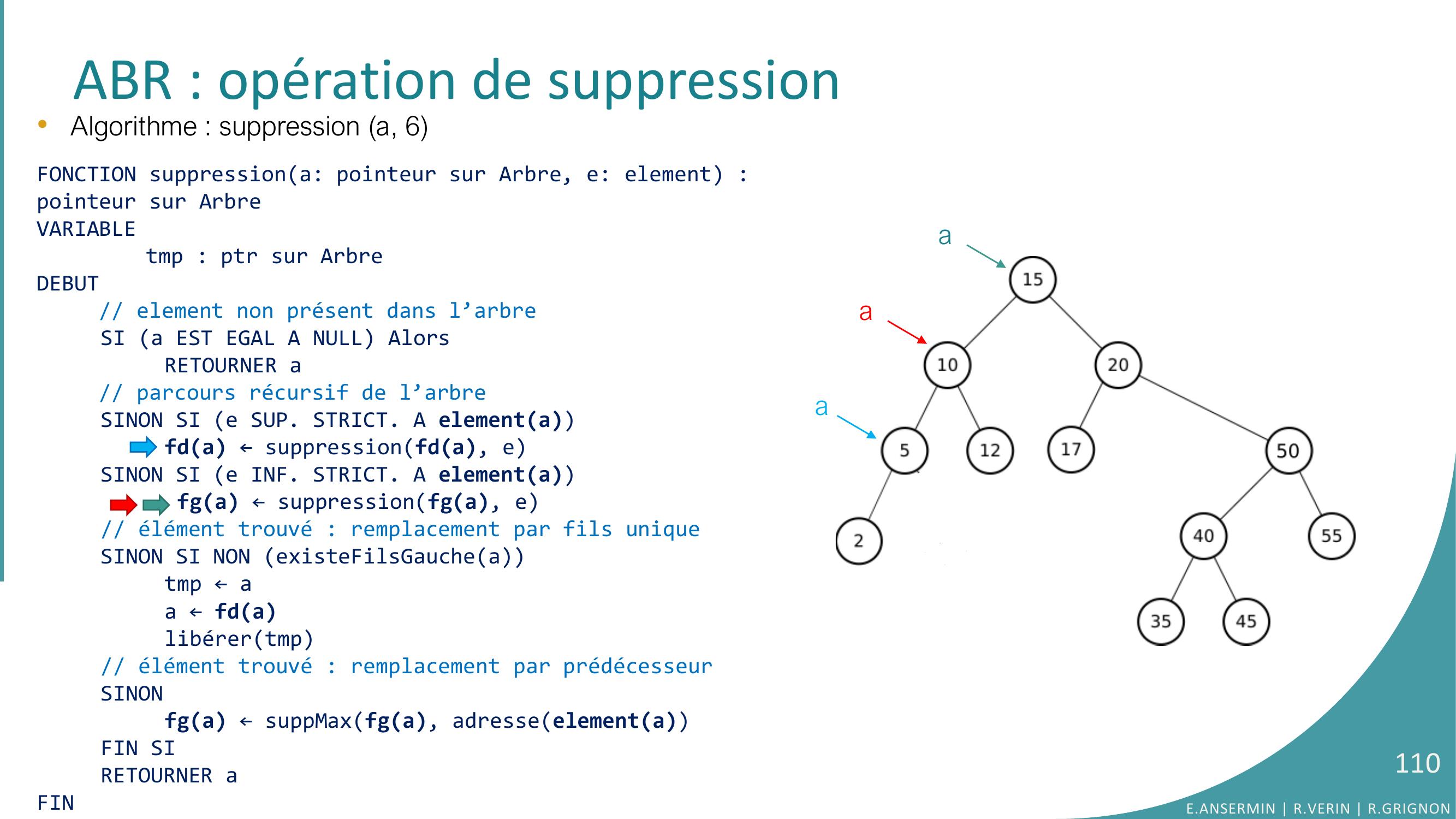
Page 98 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON98
Page 99 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON99
Page 100 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON100
Page 101 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON101
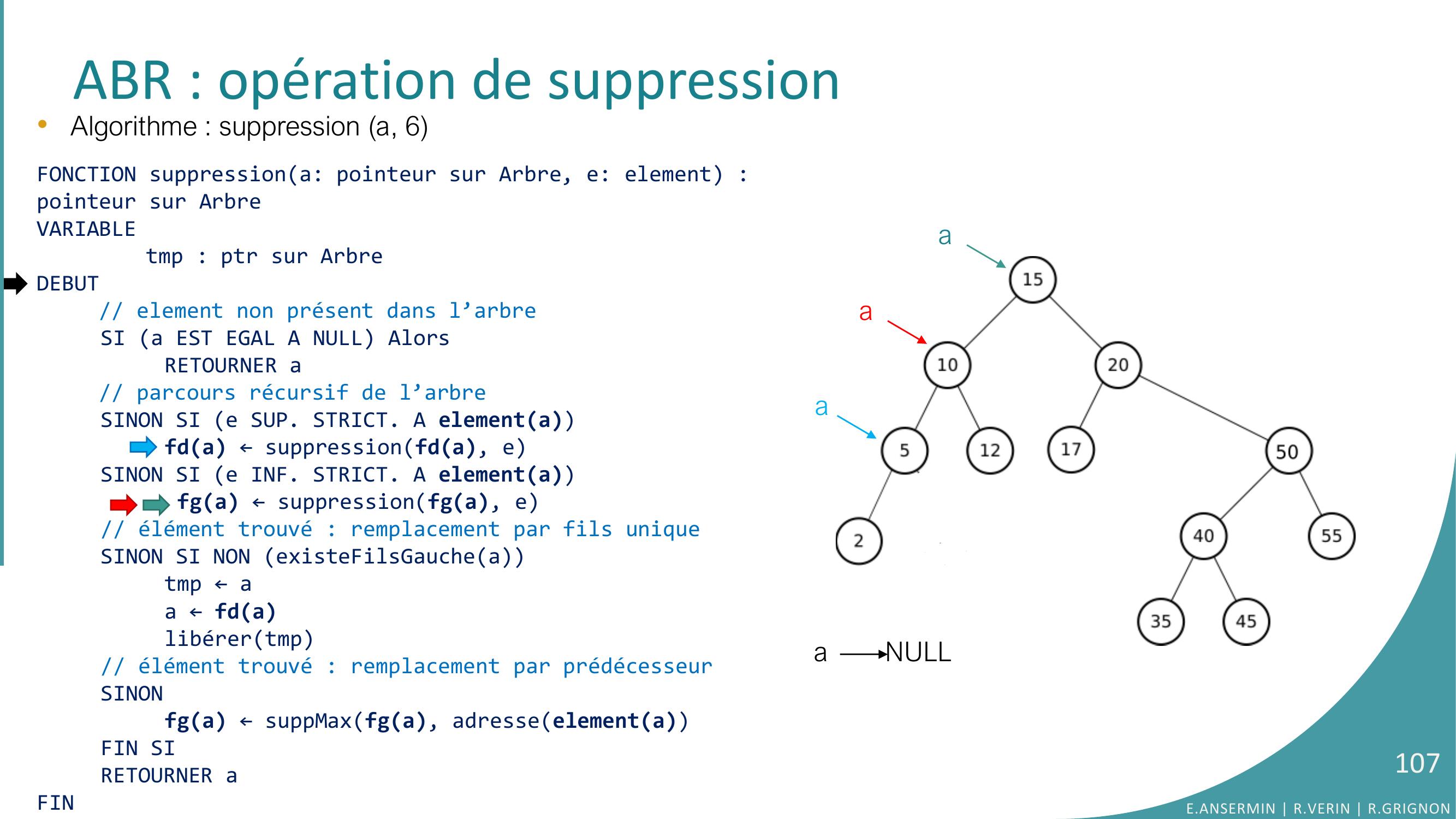
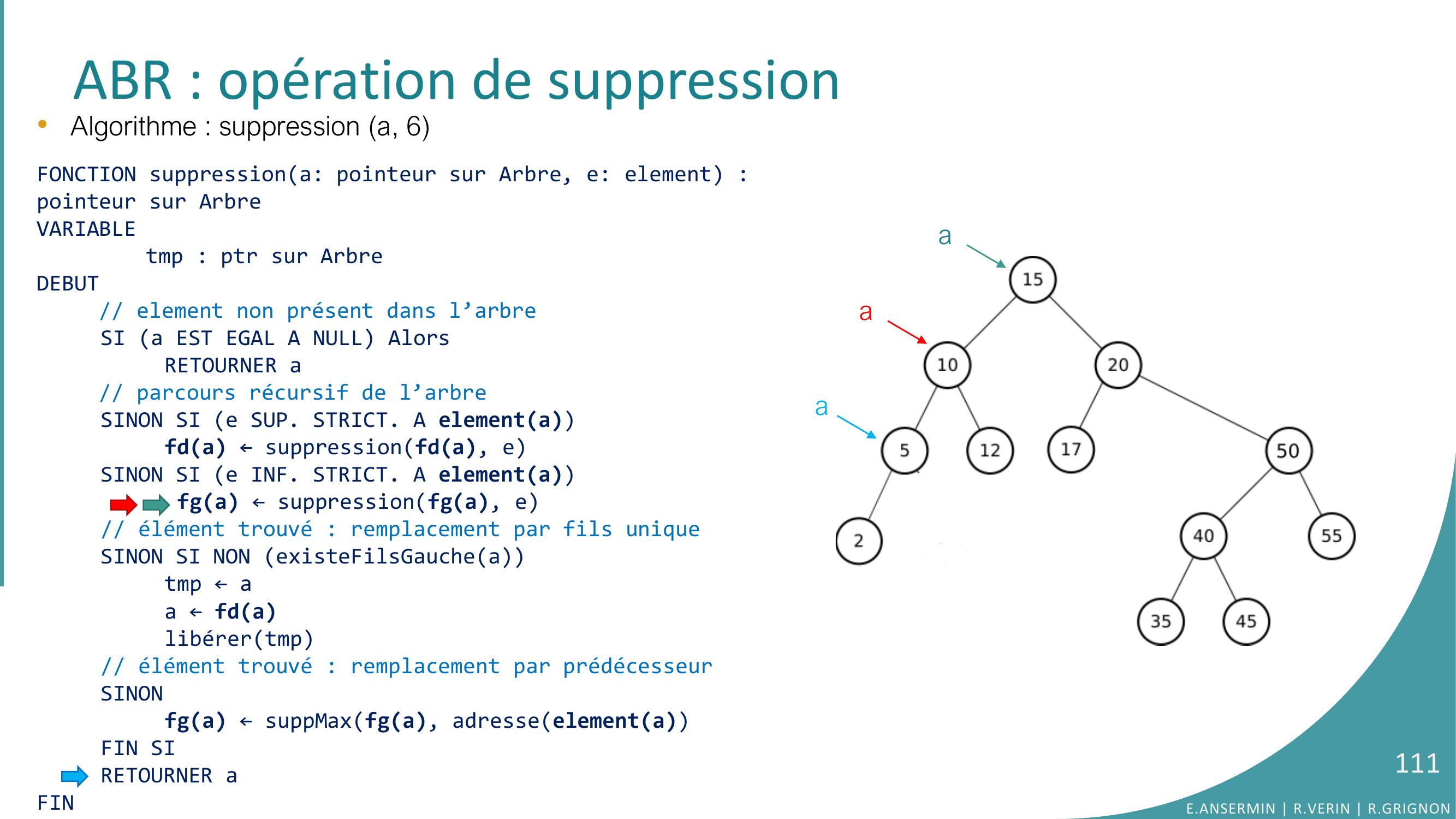
Page 102 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON102
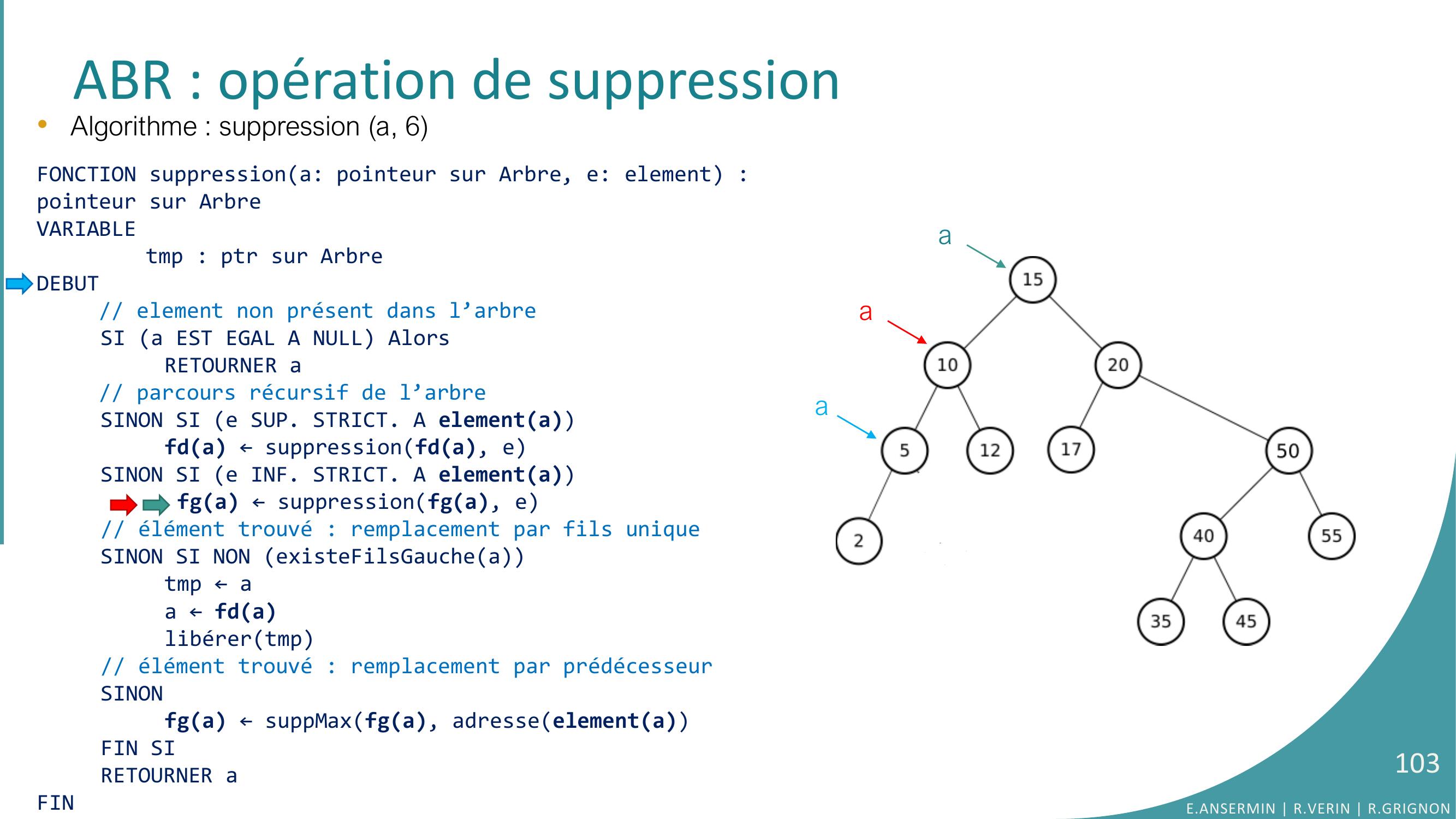
Page 103 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON103
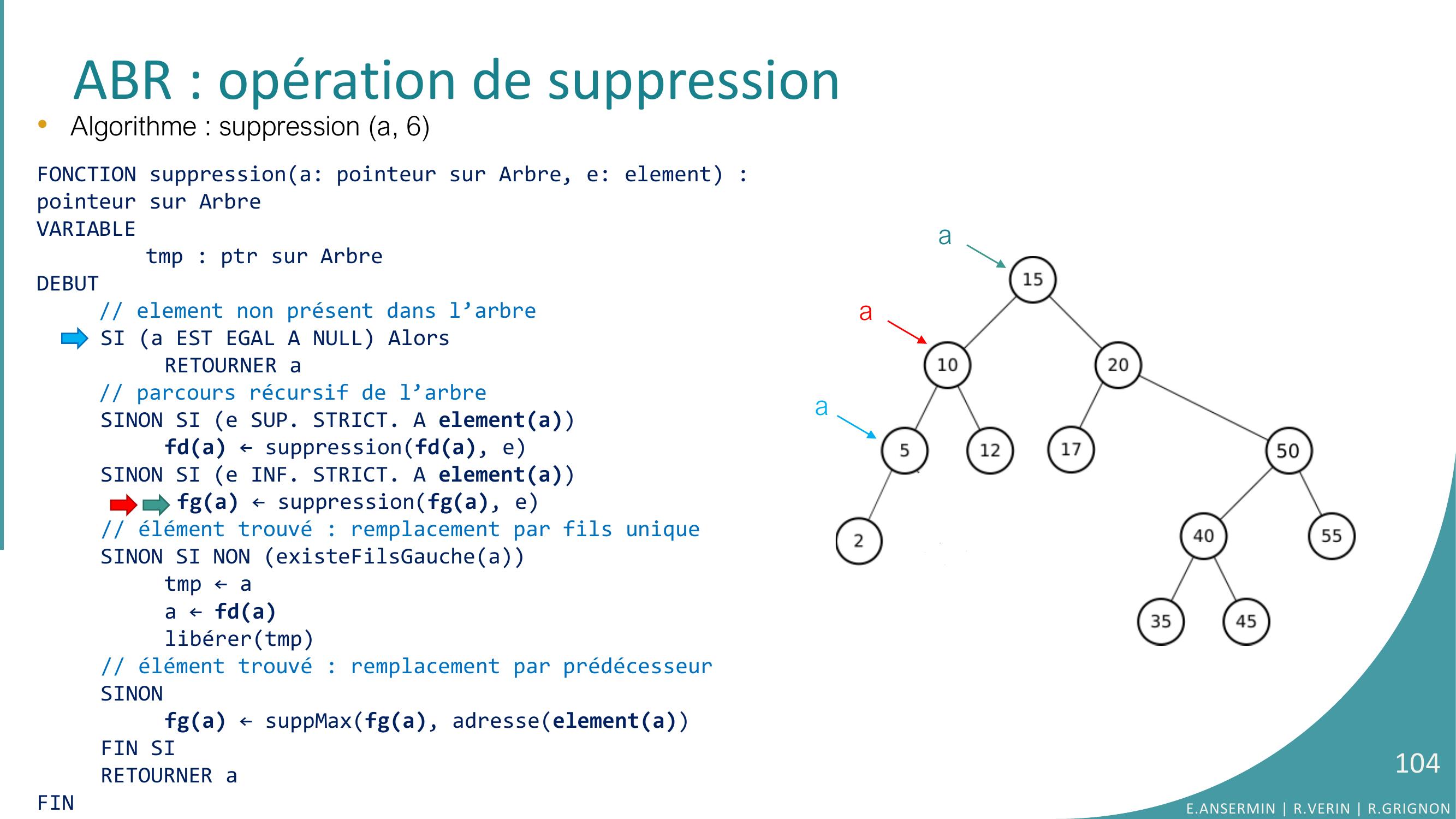
Page 104 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON104
Page 105 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON105
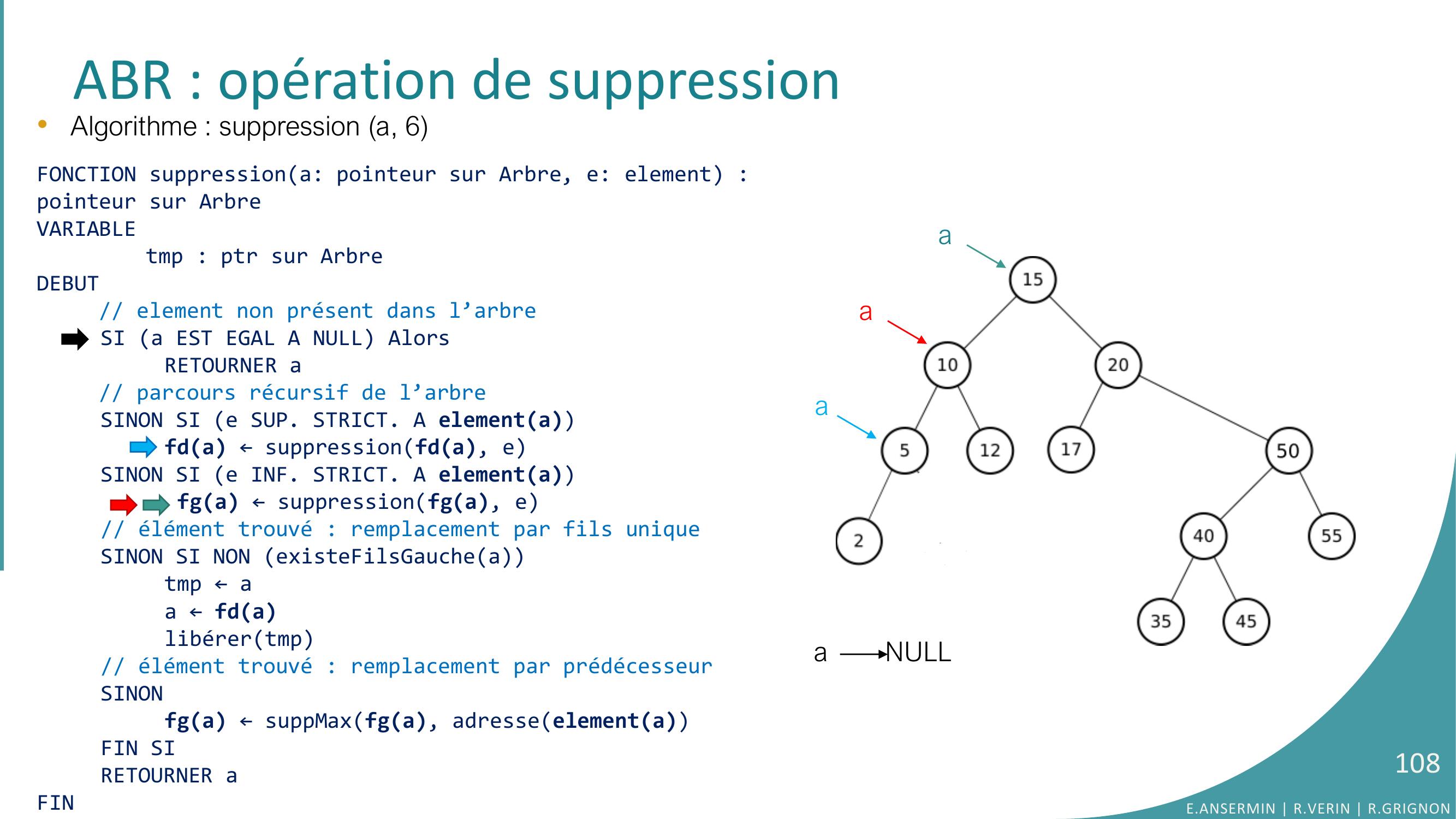
Page 106 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON106
Page 107 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaa NULLaaE.ANSERMIN R.VERIN R.GRIGNON107
Page 108 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaa NULLaaE.ANSERMIN R.VERIN R.GRIGNON108
Page 109 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaa NULLaaE.ANSERMIN R.VERIN R.GRIGNON109
Page 110 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON110
Page 111 : •Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINABR : opération de suppressionaaaE.ANSERMIN R.VERIN R.GRIGNON111
Page 112 : ABR : opération de suppression•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON112
Page 113 : ABR : opération de suppressionaa•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON113
Page 114 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON114
Page 115 : ABR : opération de suppressiona•Algorithme : suppression a, 6FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON115
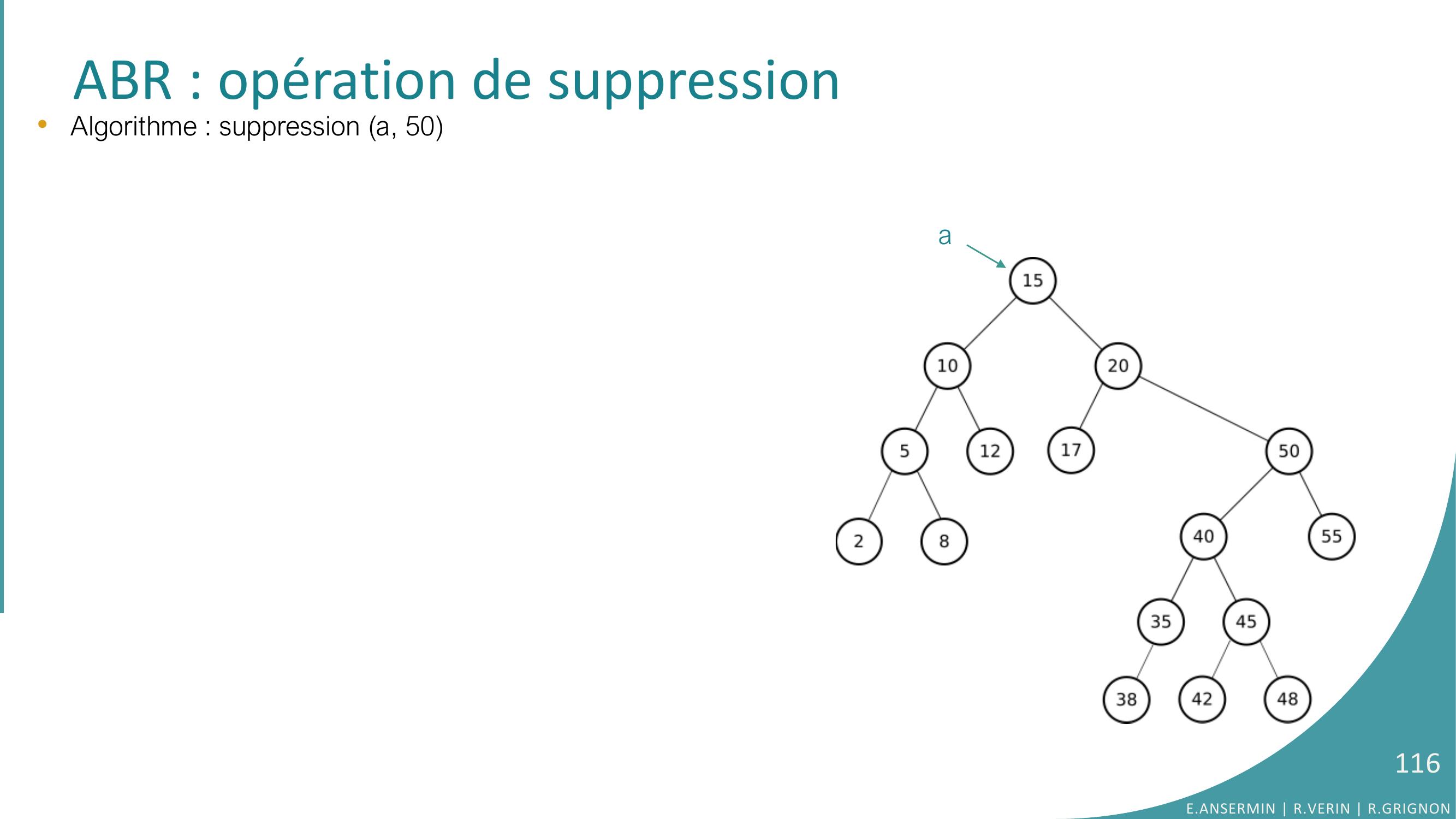
Page 116 : ABR : opération de suppressiona•Algorithme : suppression a, 50 E.ANSERMIN R.VERIN R.GRIGNON116
Page 117 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON117
Page 118 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON118
Page 119 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON119
Page 120 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON120
Page 121 : ABR : opération de suppressionaa•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON121
Page 122 : ABR : opération de suppressionaa•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON122
Page 123 : ABR : opération de suppressionaa•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON123
Page 124 : ABR : opération de suppressionaa•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON124
Page 125 : ABR : opération de suppressionaaa•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON125
Page 126 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON126
Page 127 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON127
Page 128 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON128
Page 129 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON129
Page 130 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON130
Page 131 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON131
Page 132 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON132
Page 133 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON133
Page 134 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON134
Page 135 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON135
Page 136 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON136
Page 137 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON137
Page 138 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON138
Page 139 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON139
Page 140 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON140
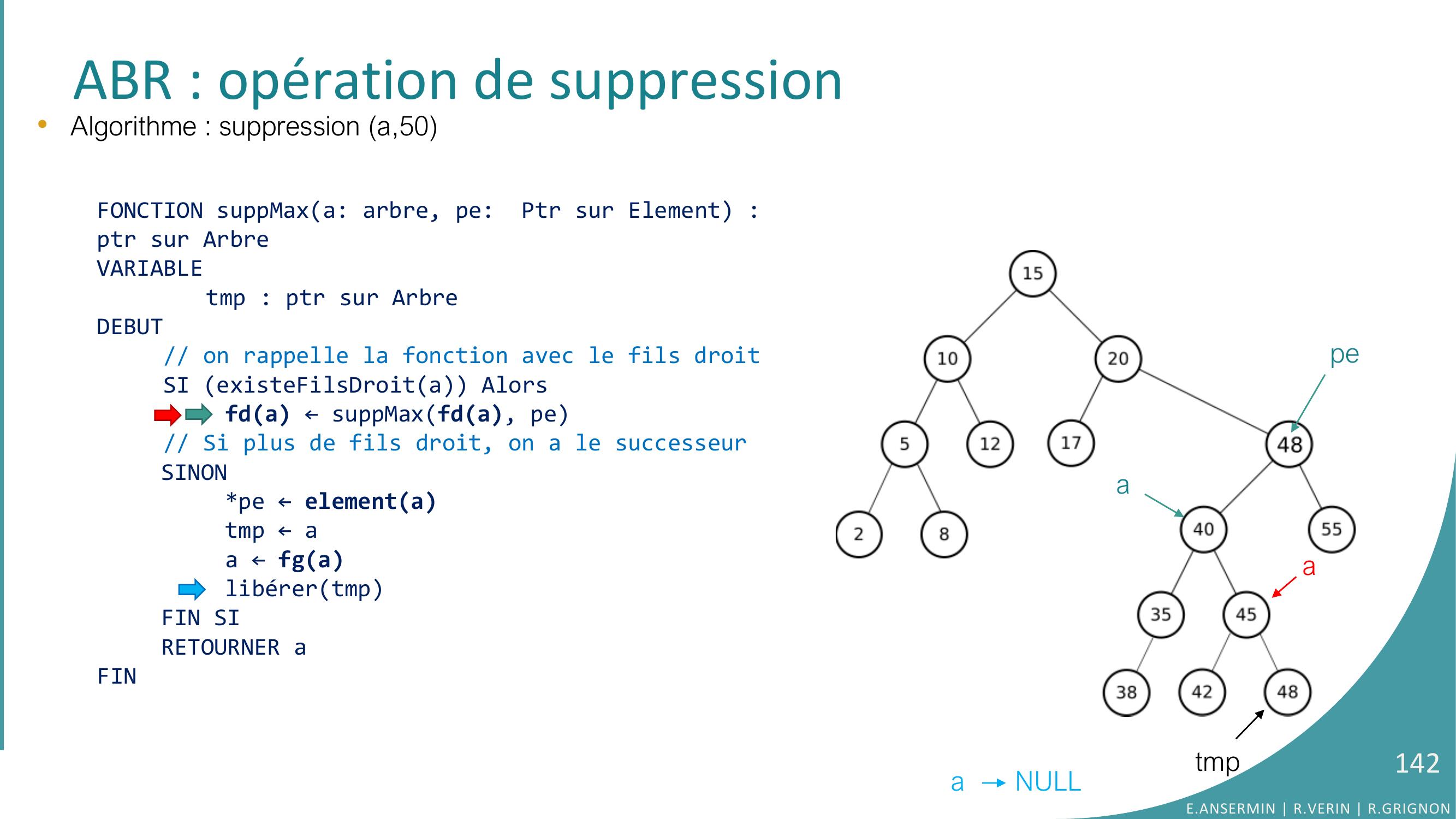
Page 141 : ABR : opération de suppression•Algorithme : suppression a,50 apeaatmpFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON141
Page 142 : ABR : opération de suppression•Algorithme : suppression a,50 pea NULLtmpFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON142
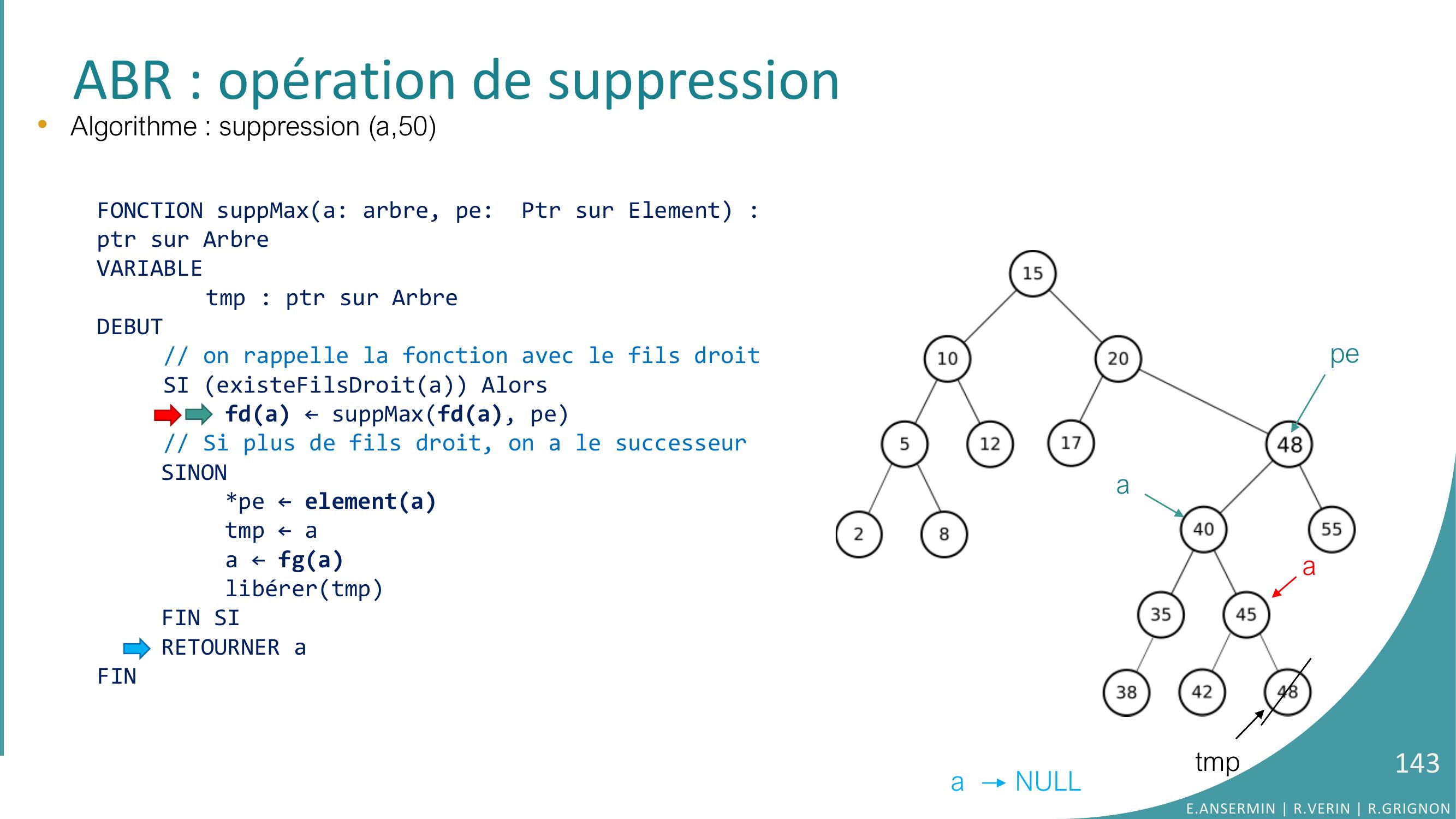
Page 143 : ABR : opération de suppression•Algorithme : suppression a,50 pea NULLFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINtmpaaE.ANSERMIN R.VERIN R.GRIGNON143
Page 144 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON144
Page 145 : ABR : opération de suppression•Algorithme : suppression a,50 peFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON145
Page 146 : ABR : opération de suppression•Algorithme : suppression a,50 apeFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON146
Page 147 : ABR : opération de suppression•Algorithme : suppression a,50 apeFONCTION suppMaxa: arbre, pe: Ptr sur Element : ptr sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// on rappelle la fonction avec le fils droitSI existeFilsDroita Alorsfda ← suppMaxfda, pe// Si plus de fils droit, on a le successeur SINONpe ← elementatmp ← aa ← fgalibérertmpFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON147
Page 148 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON148
Page 149 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaaE.ANSERMIN R.VERIN R.GRIGNON149
Page 150 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON150
Page 151 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON151
Page 152 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON152
Page 153 : ABR : opération de suppressiona•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON153
Page 154 : ABR : opération de suppression•Algorithme : suppression a, 50FONCTION suppressiona: pointeur sur Arbre, e: element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUT// element non présent dans l’arbreSI a EST EGAL A NULL AlorsRETOURNER a// parcours récursif de l’arbreSINON SI e SUP. STRICT. A elementafda ← suppressionfda, eSINON SI e INF. STRICT. A elementa fga ← suppressionfga, e// élément trouvé : remplacement par fils uniqueSINON SI NON existeFilsGaucheatmp ← aa ← fdalibérertmp// élément trouvé : remplacement par prédécesseurSINONfga ← suppMaxfga, adresseelementaFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON154
Page 155 : Résumé•Les arbres binaires de recherche sont des arbres binaires dont les éléments respectent une relation d’ordre :•tout élément d’un sous-arbre gauche doit être inférieur strictement à la racine•tout élément d’un sous-arbre droit doit être supérieur strictement à la racine•Dans notre cours, nous imposons un cas particulier : l’arbre ne contient que des valeurs distinctes d’éléments •Cette structure permet d’accélérer les opérations de recherche O𝑙𝑜𝑔2 plutôt que On pour les arbres binaires classiques.•Les opérations d’insertions et de suppressions doivent maintenir la relation d’ordre. •Il existe encore d’autres moyens d’optimiser la recherche dans un ABR : c’est le sujet du prochain cours !E.ANSERMIN R.VERIN R.GRIGNON155
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155