CM4 Algebre de Boole
Télécharger le CM4 Algebre de Boole en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
Page 1 : INFORMATIQUE 1I I I . A L G E B R E D E B O O L EEva Ansermin & Romuald Grignon v1.2
Page 2 : Algèbre de Boole : introductionNous avons vu que les ordinateurs ne peuvent manipuler que des 0 et des 1. Comment parviennent-ils à effectuer des opérations ? Les opérations effectuées « électroniquement » dans un ordinateur sont basées sur l’algèbre de Boole.L’algèbre de Boole est une approche algébrique de la logique.George BOOLE 1815-1864Eva ANSERMIN & Romuald GRIGNON2
Page 3 : Algèbre de Boole : VariablesL’algèbre de Boole permet de modéliser des raisonnements logiques.Elle manipule des données qui ne peuvent prendre que 2 valeurs:VRAI FAUXCe sont des variables logiques ou booléennesL’algèbre de Boole est donc exploité pour faire des opérations par l’ordinateur. On aura :VRAI 1FAUX 0On peut construire des fonctions dépendant d’une ou plusieurs variables logiques : ce sont des fonctions logiques George BOOLE 1815-1864Eva ANSERMIN & Romuald GRIGNON3
Page 4 : Algèbre de Boole : Fonctions logiques Les fonctions logiques permettent d’exprimer une sortie logique en fonction d’entrées logiques.Les fonctions logiques peuvent se représenter sous plusieurs formes : 𝑒1𝑒2…𝑒𝑛𝑠00…000…1…………11….011….1Eva ANSERMIN & Romuald GRIGNON4
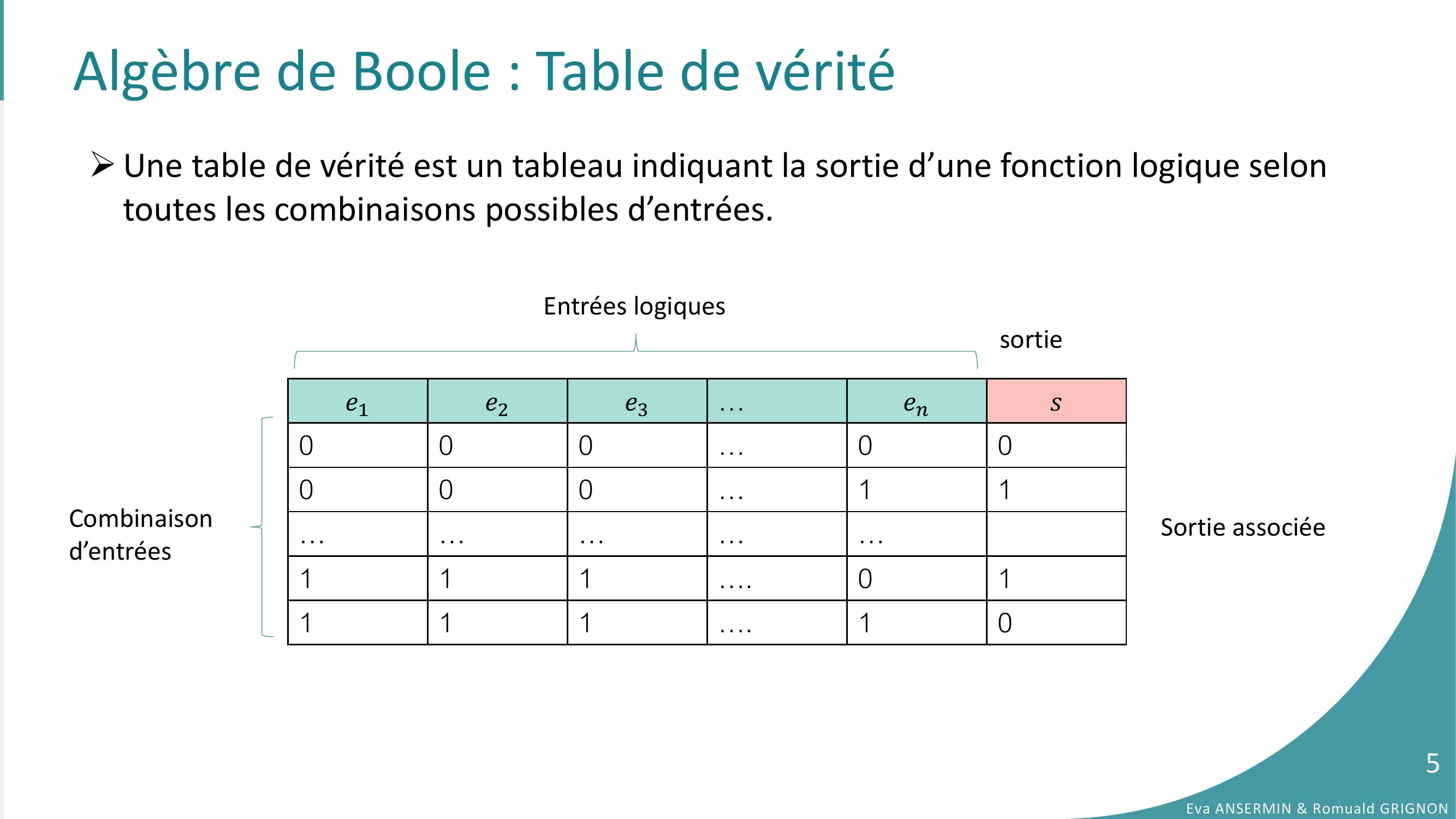
Page 5 : Algèbre de Boole : Table de véritéUne table de vérité est un tableau indiquant la sortie d’une fonction logique selon toutes les combinaisons possibles d’entrées. sortieEntrées logiquesCombinaison d’entréesSortie associée𝑒1𝑒2𝑒3…𝑒𝑛𝑠000…00000…11……………111….01111….10Eva ANSERMIN & Romuald GRIGNON5
Page 6 : Algèbre de Boole : Table de véritéExemple avec 2 entréesPour ne pas oublier de lignes, on peut compter en binaire.Pour n entrées, il y a 2𝑛combinaisons différentes d’entrées, soit 2𝑛lignes dans la table de vérité.𝑒1𝑒2𝑠00011011Eva ANSERMIN & Romuald GRIGNON6
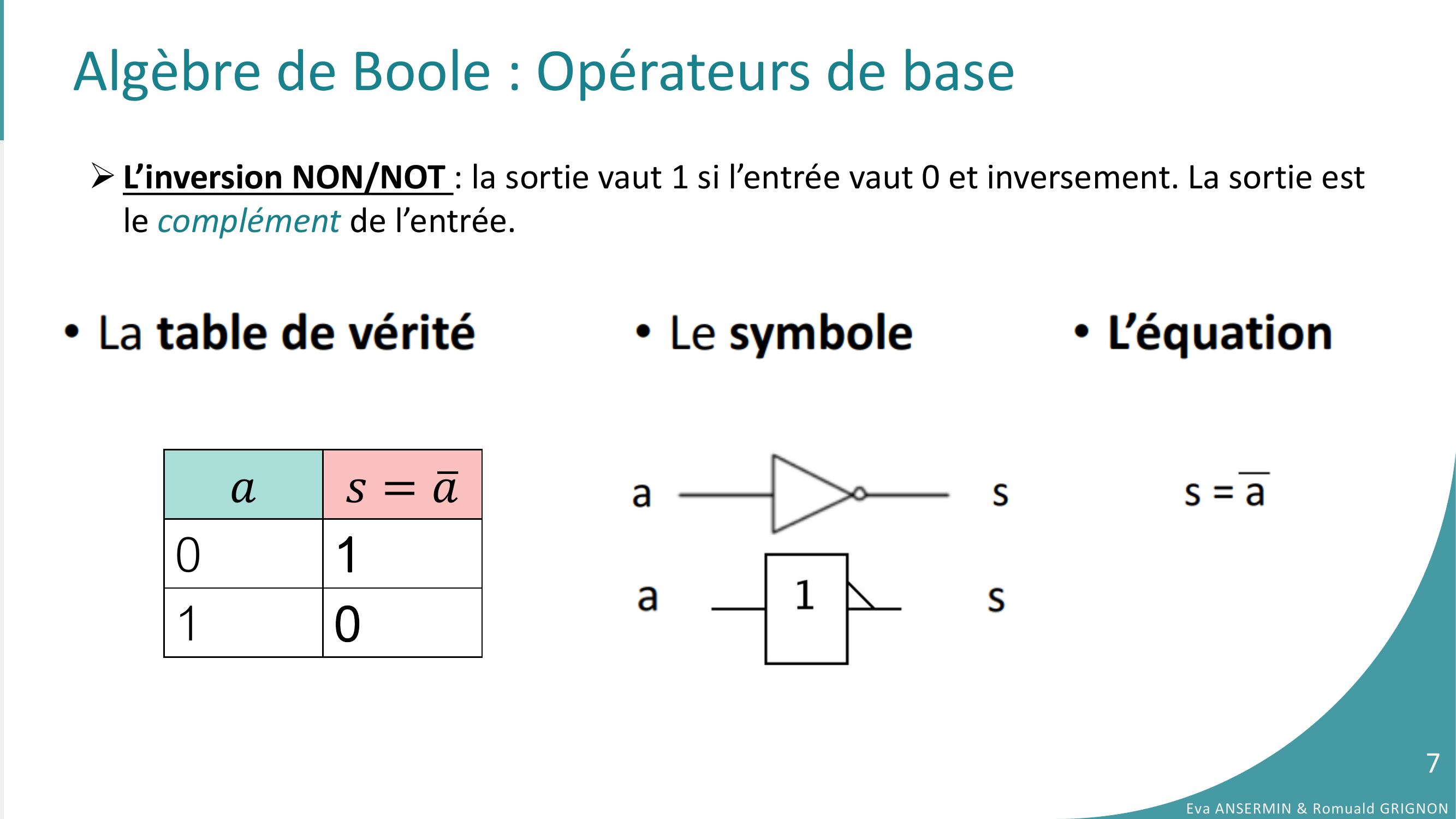
Page 7 : Algèbre de Boole : Opérateurs de baseL’inversion NON/NOT : la sortie vaut 1 si l’entrée vaut 0 et inversement. La sortie est le complément de l’entrée. 𝑎𝑠= ത𝑎0110Eva ANSERMIN & Romuald GRIGNON7
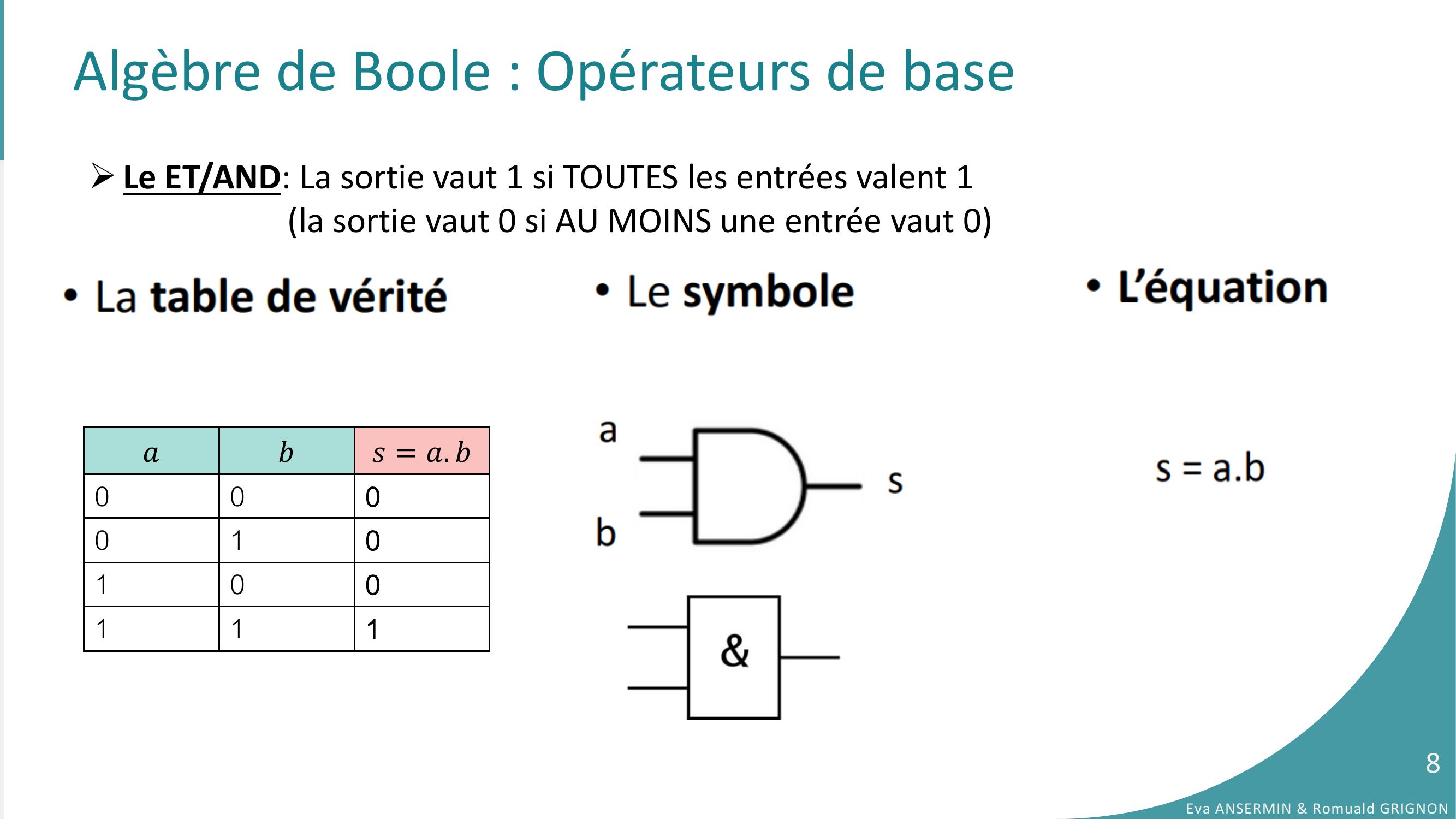
Page 8 : Algèbre de Boole : Opérateurs de baseLe ET/AND: La sortie vaut 1 si TOUTES les entrées valent 1la sortie vaut 0 si AU MOINS une entrée vaut 0𝑎𝑏𝑠= 𝑎. 𝑏000010100111Eva ANSERMIN & Romuald GRIGNON8
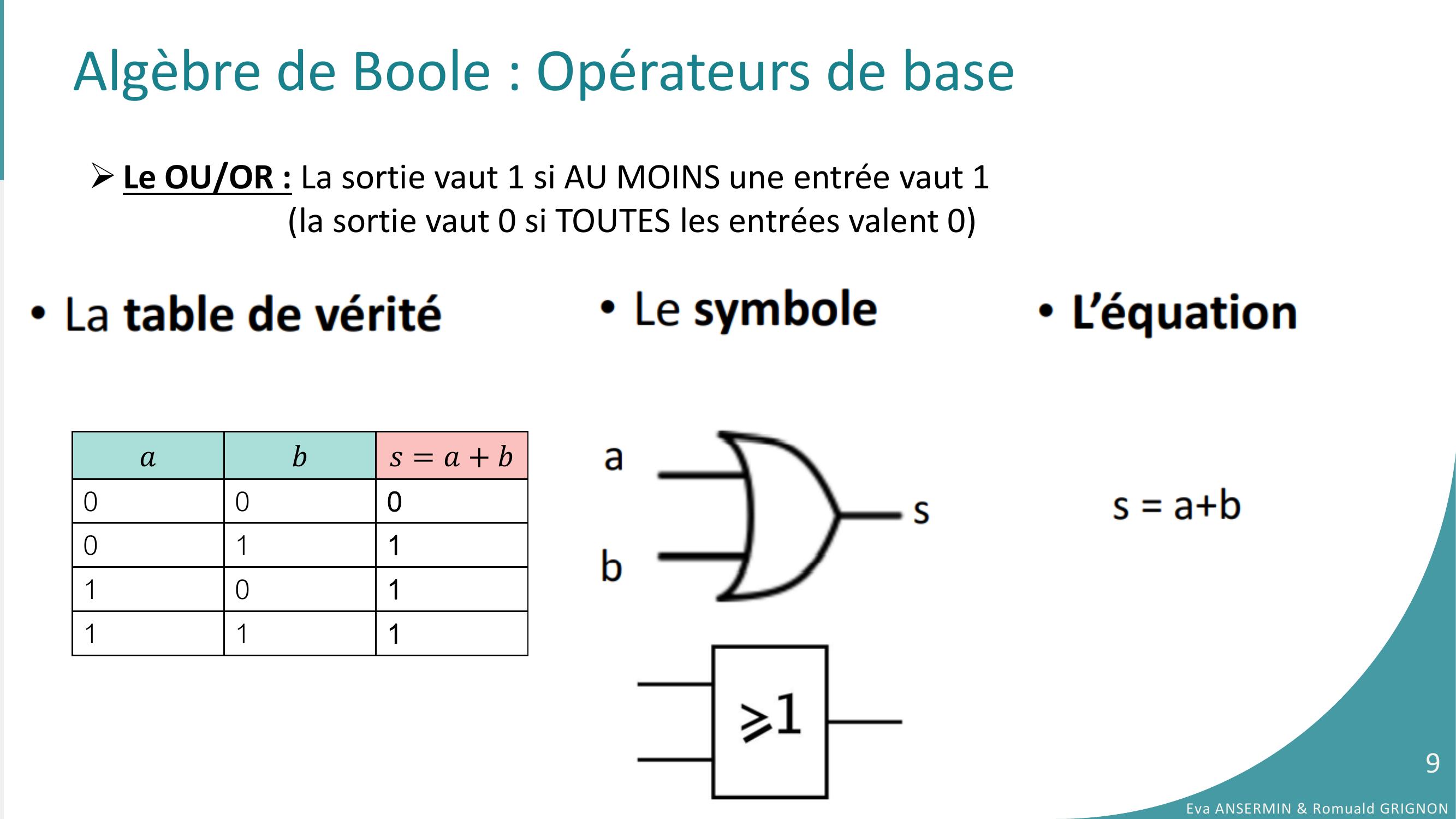
Page 9 : Algèbre de Boole : Opérateurs de base𝑎𝑏𝑠= 𝑎+ 𝑏000011101111Eva ANSERMIN & Romuald GRIGNON9Le OU/OR : La sortie vaut 1 si AU MOINS une entrée vaut 1la sortie vaut 0 si TOUTES les entrées valent 0
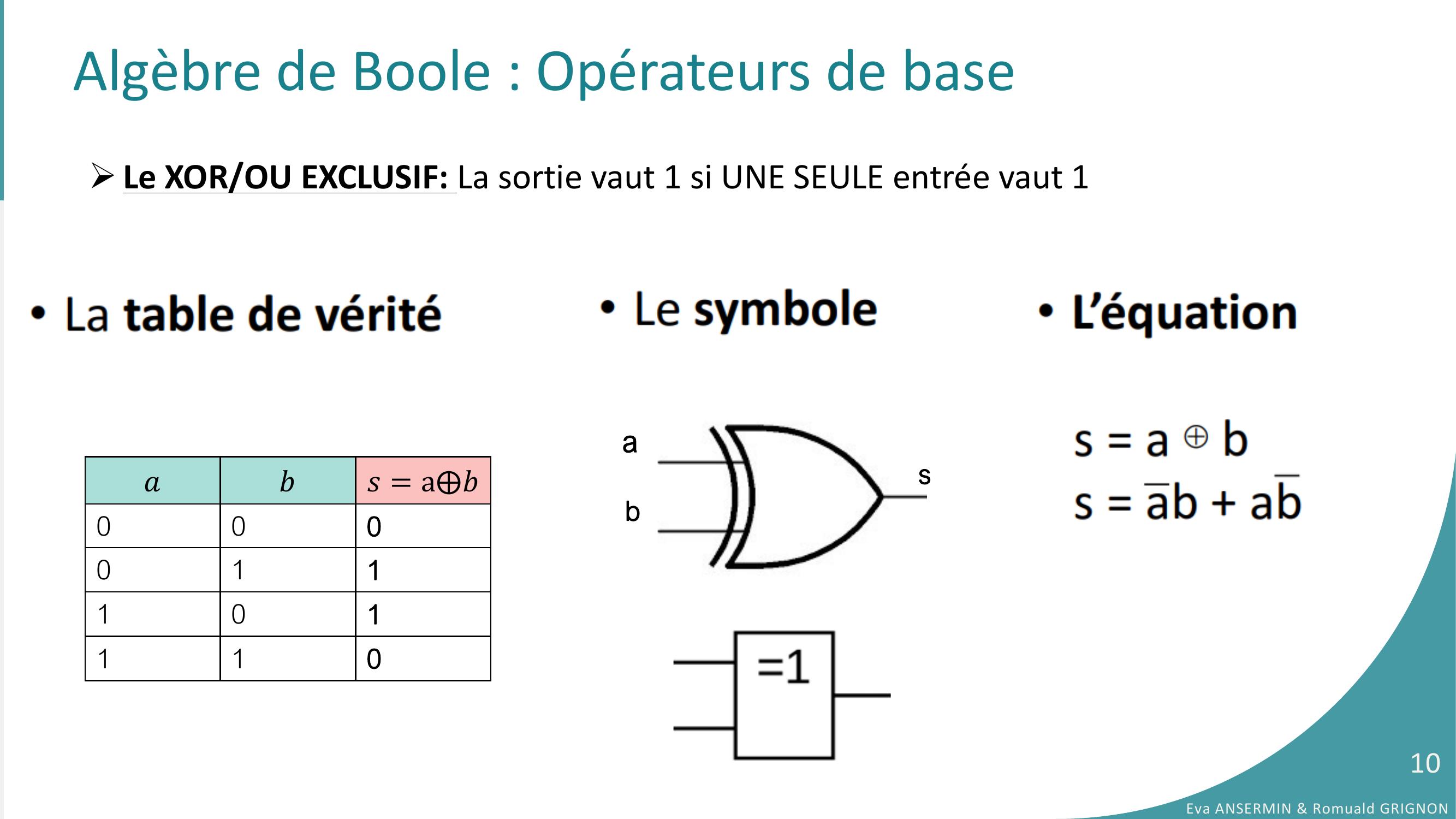
Page 10 : Algèbre de Boole : Opérateurs de baseLe XOR/OU EXCLUSIF: La sortie vaut 1 si UNE SEULE entrée vaut 1𝑎𝑏𝑠= a⨁𝑏000011101110asbEva ANSERMIN & Romuald GRIGNON10
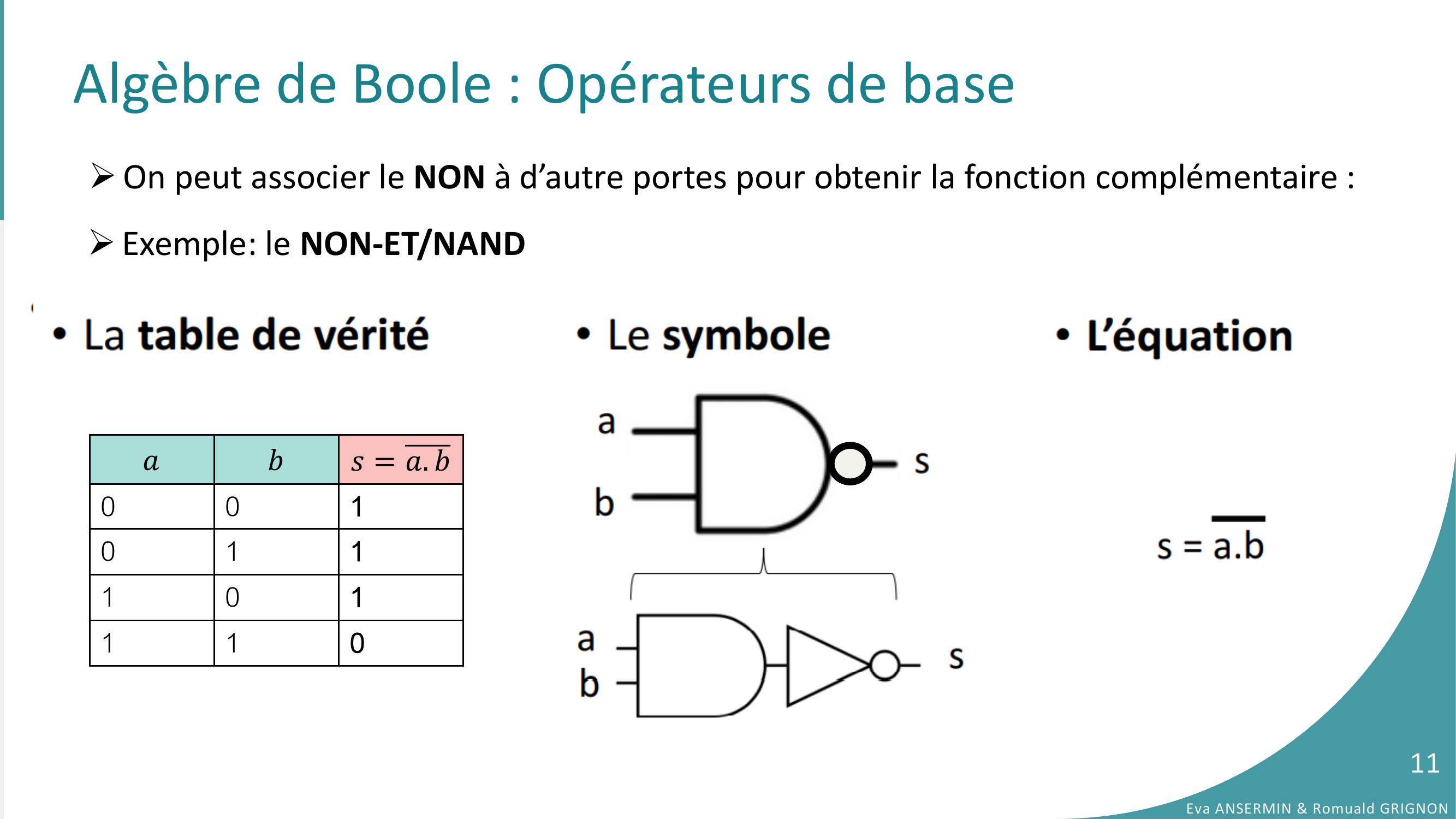
Page 11 : Algèbre de Boole : Opérateurs de baseExemple: le NON-ET/NAND𝑎𝑏𝑠= 𝑎. 𝑏001011101110Eva ANSERMIN & Romuald GRIGNON11On peut associer le NON à d’autre portes pour obtenir la fonction complémentaire :
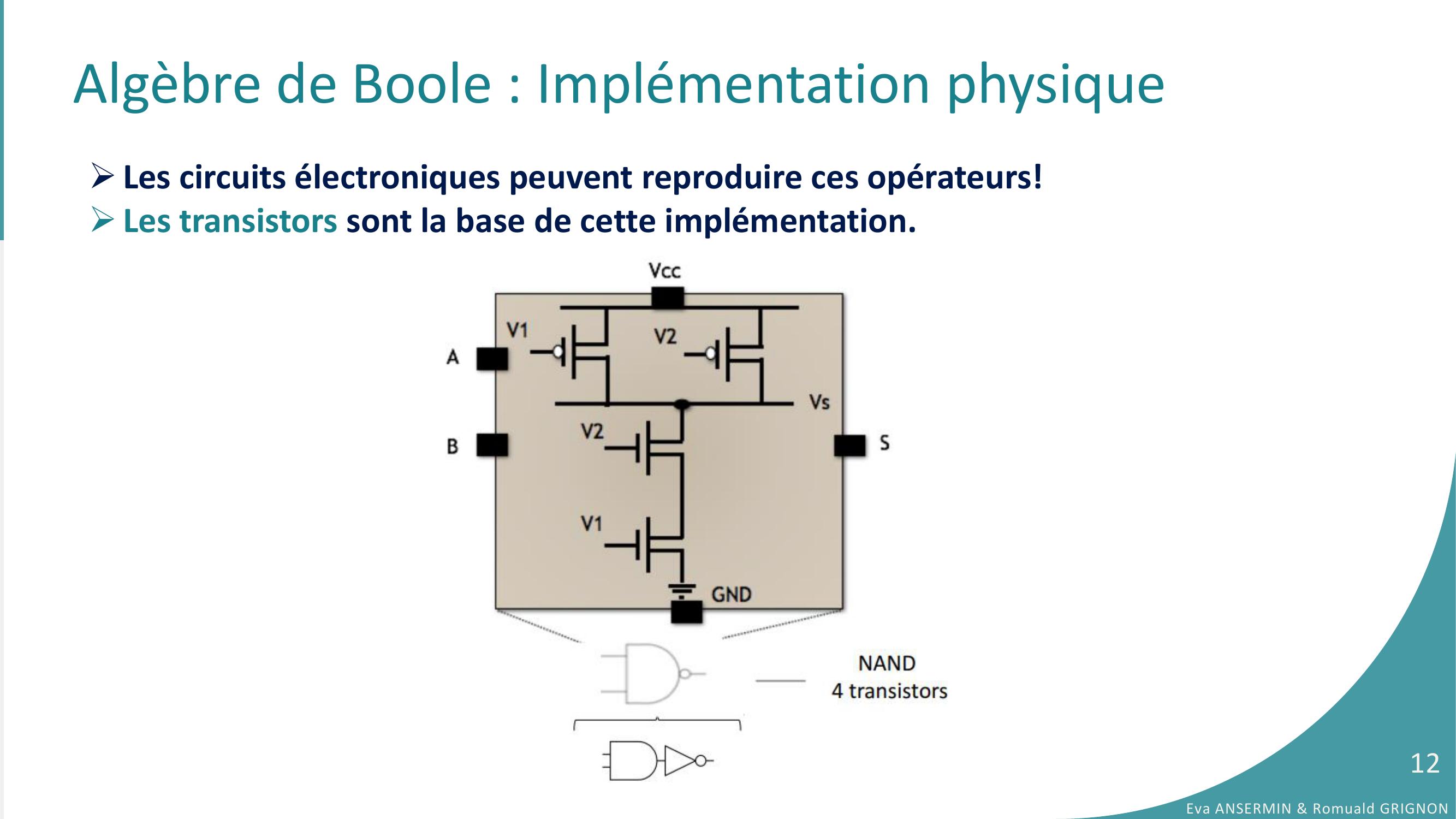
Page 12 : Algèbre de Boole : Implémentation physiqueLes circuits électroniques peuvent reproduire ces opérateurs!Les transistors sont la base de cette implémentation.Eva ANSERMIN & Romuald GRIGNON12
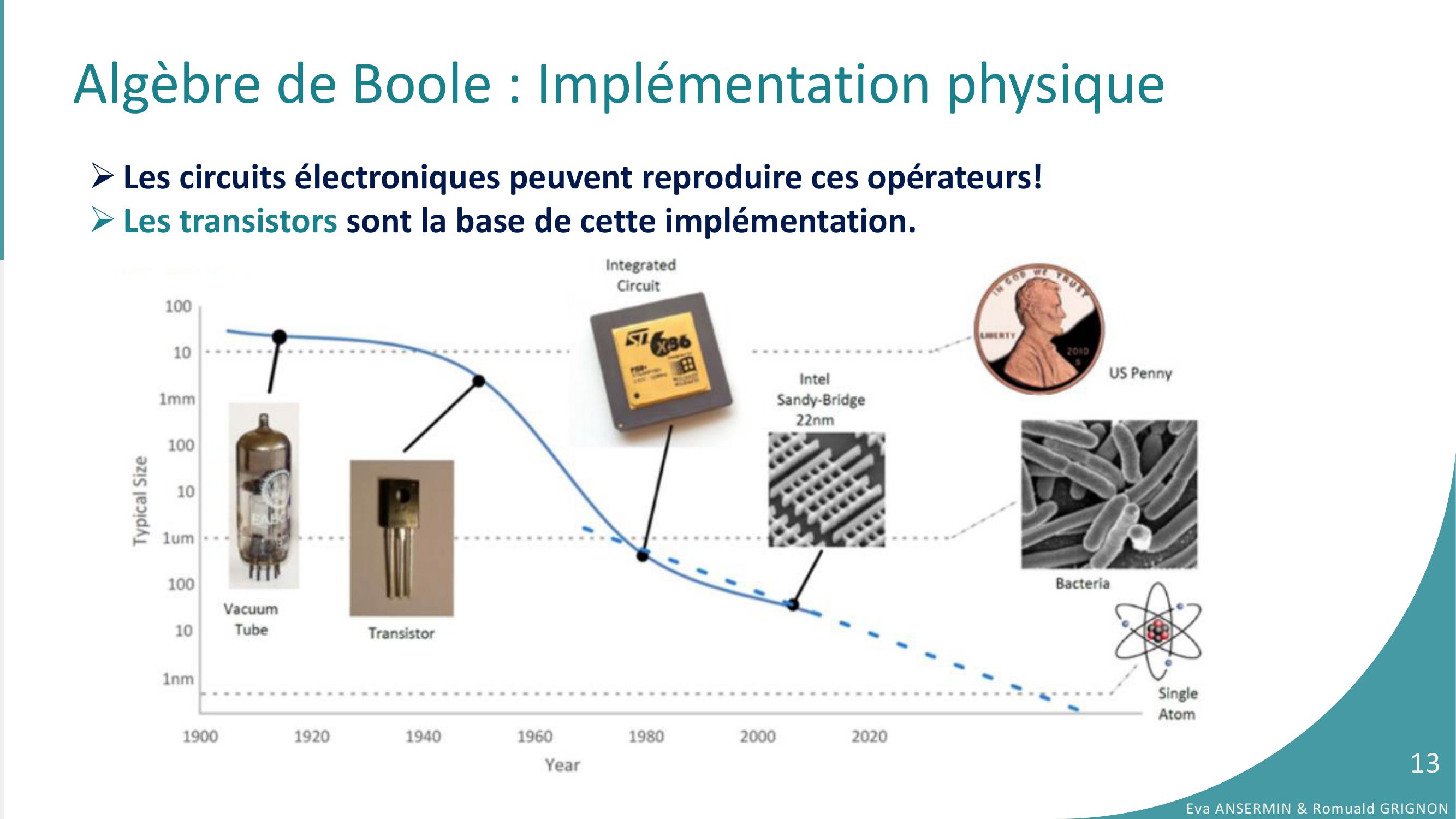
Page 13 : Algèbre de Boole : Implémentation physiqueLes circuits électroniques peuvent reproduire ces opérateurs!Les transistors sont la base de cette implémentation.Eva ANSERMIN & Romuald GRIGNON13
Page 14 : Algèbre de Boole : Implémentation physiqueLes circuits électroniques peuvent reproduire ces opérateurs!Les transistors sont la base de cette implémentation.Les portes logiques pouvant être reproduites par des circuits électroniques, on peut donc implanter physiquement des fonctions logiques dans un ordinateur pour effectuer des opérations.Pour économiser des ressources, il faut utiliser le moins de portes logiques possibles pour une même fonction logique.A l’aide des propriétés de l’algèbre de Boole, on va chercher à réduire et simplifier les fonctions logiques. Eva ANSERMIN & Romuald GRIGNON14
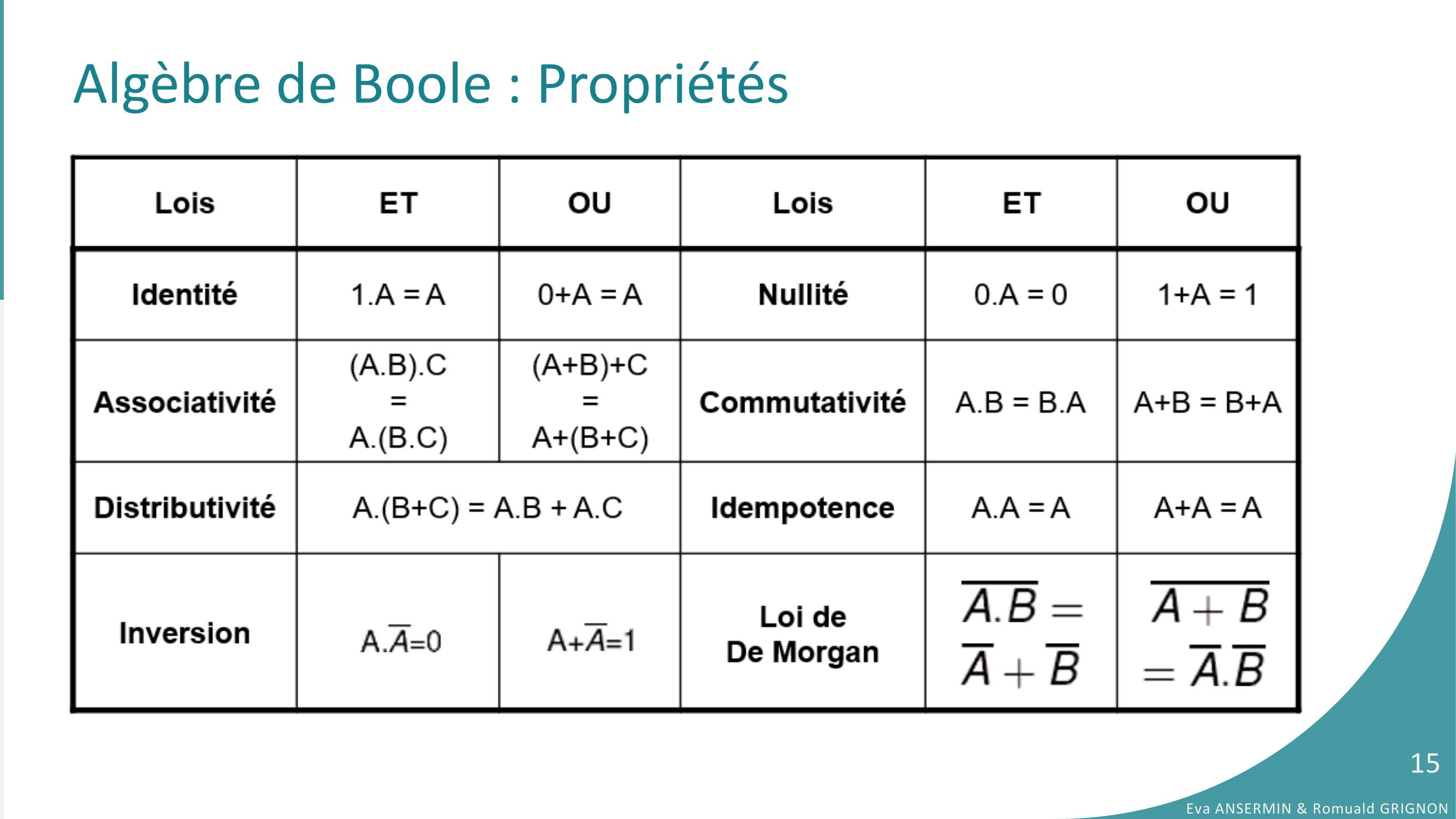
Page 15 : Algèbre de Boole : PropriétésEva ANSERMIN & Romuald GRIGNON15
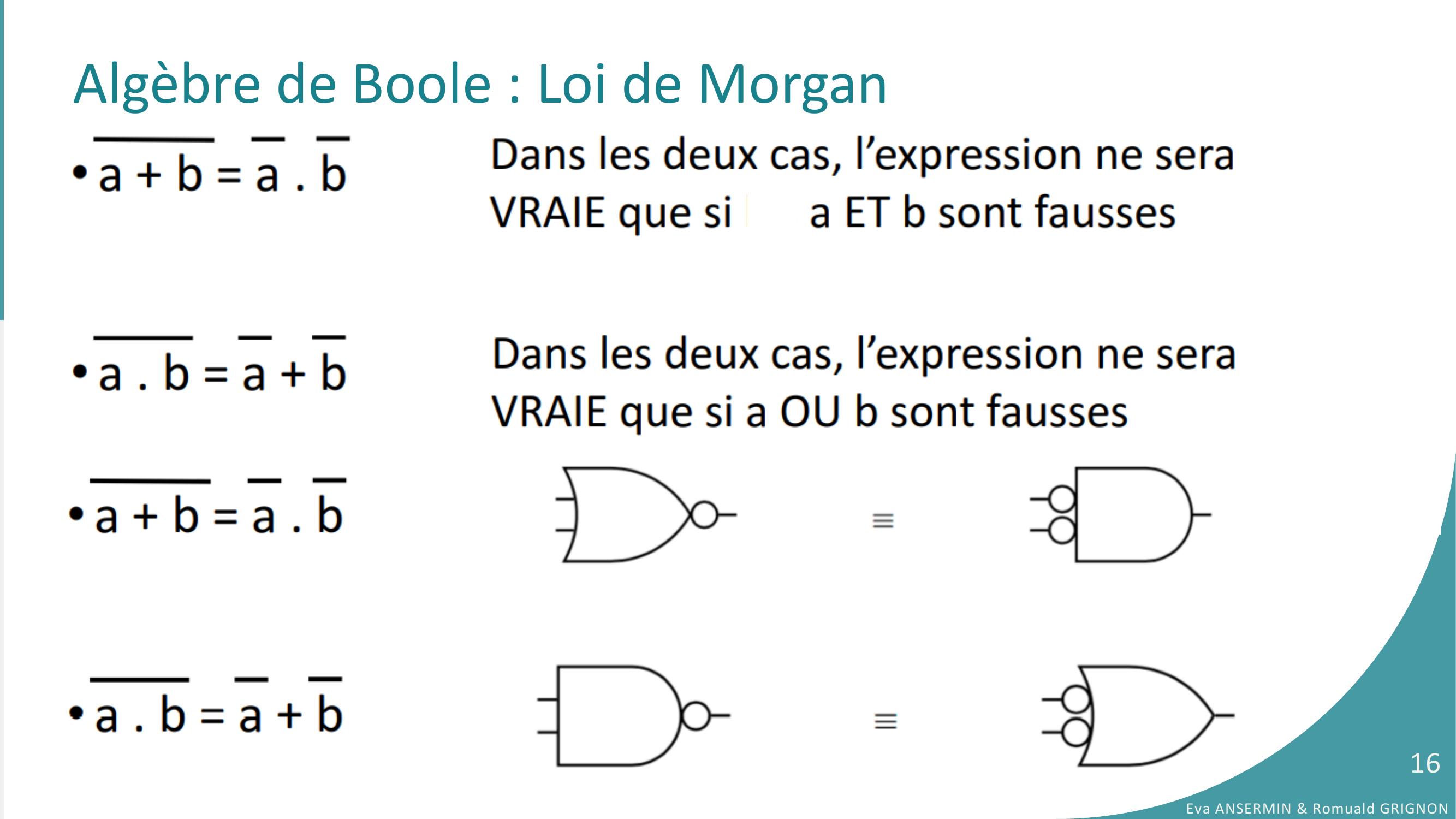
Page 16 : Algèbre de Boole : Loi de MorganEva ANSERMIN & Romuald GRIGNON16
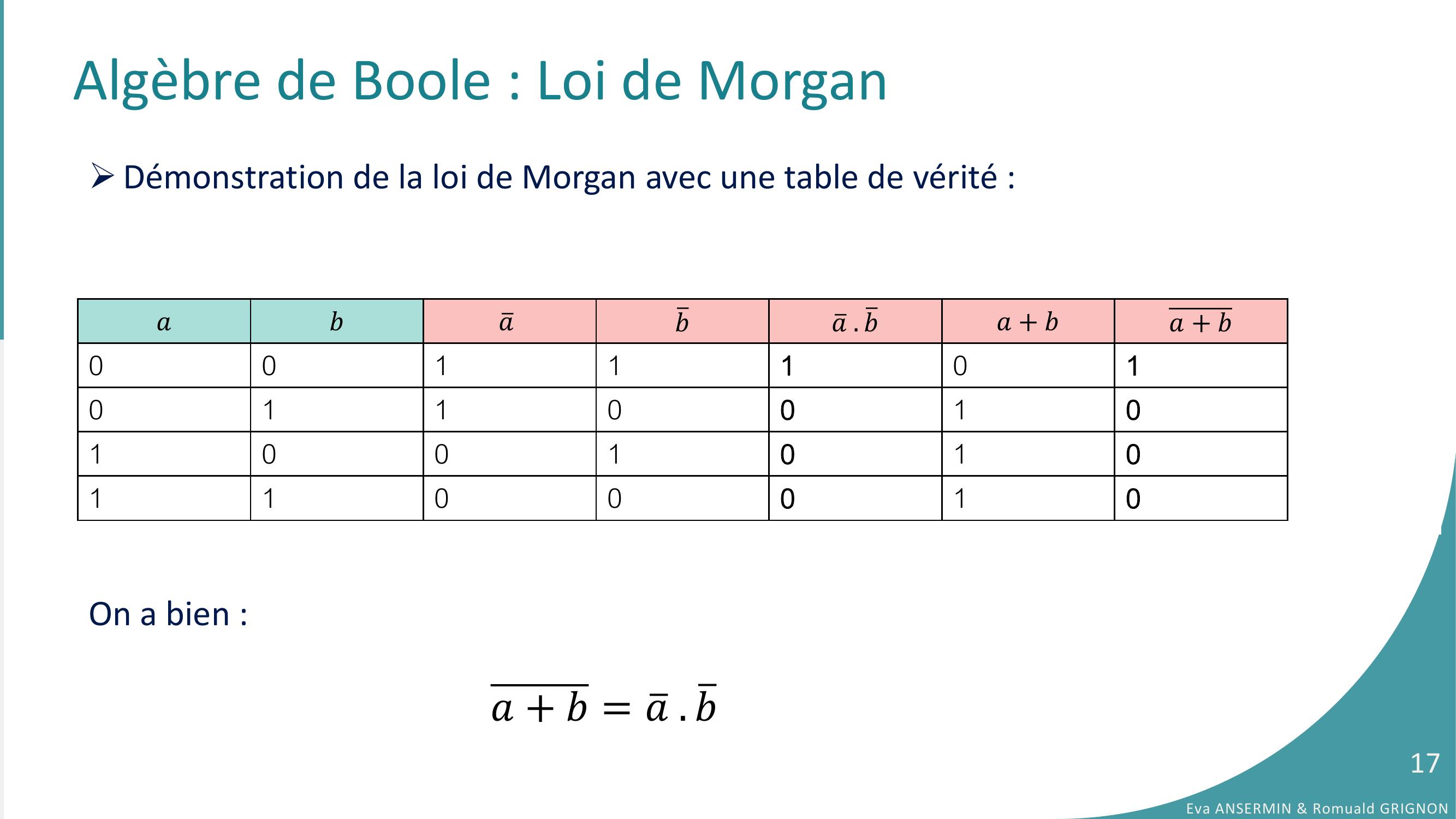
Page 17 : Algèbre de Boole : Loi de MorganDémonstration de la loi de Morgan avec une table de vérité :On a bien :𝑎𝑏ത𝑎ത𝑏ത𝑎. ത𝑏𝑎+ 𝑏𝑎+ 𝑏0011101011001010010101100010𝑎+ 𝑏= ത𝑎. ത𝑏Eva ANSERMIN & Romuald GRIGNON17
Page 18 : Algèbre de Boole : Loi de MorganDémonstration de la loi de Morgan par énoncé logique:Soit l’énoncé suivant :« Je sors s’il ne pleut pas et s’il fait chaud. »Quelle est la contraposée de cet énoncé?« Je ne sors pas s’il pleut ou s’il fait froid »Eva ANSERMIN & Romuald GRIGNON18
Page 19 : Algèbre de Boole : Simplification d’expressionA l’aide de propriétés Booléennes démontrer les règles suivantes:1. Règle d’absorption : Démonstration : 𝑎. 𝑎+ 𝑏= 𝑎𝑎. 𝑎+ 𝑏= 𝑎. 𝑎+ 𝑎. 𝑏distributivité du ET= 𝑎+ 𝑎. 𝑏𝑎. 𝑎= 𝑎= 𝑎1 + 𝑏factorisation par a et a. 1 = a= 𝑎1 + b = 1 bEva ANSERMIN & Romuald GRIGNON19
Page 20 : Algèbre de Boole : Simplification d’expressionA l’aide de propriétés Booléennes démontrer les règles suivantes:1. Règle de simplification : Démonstration : 𝑎+ ത𝑎. 𝑏= 𝑎+ 𝑏𝑎+ ത𝑎. 𝑏= 𝑎. 𝑎+ 𝑏+ ത𝑎. 𝑏voir slide précédente= 𝑎. 𝑎+ 𝑎. 𝑏+ ത𝑎. 𝑏= 𝑎+ 𝑎. 𝑏+ ത𝑎. 𝑏𝑎. 𝑎= 𝑎= 𝑎+ 𝑏 𝑎+ ത𝑎factorisation= 𝑎+ 𝑏𝑎+ ത𝑎= 1Eva ANSERMIN & Romuald GRIGNON20
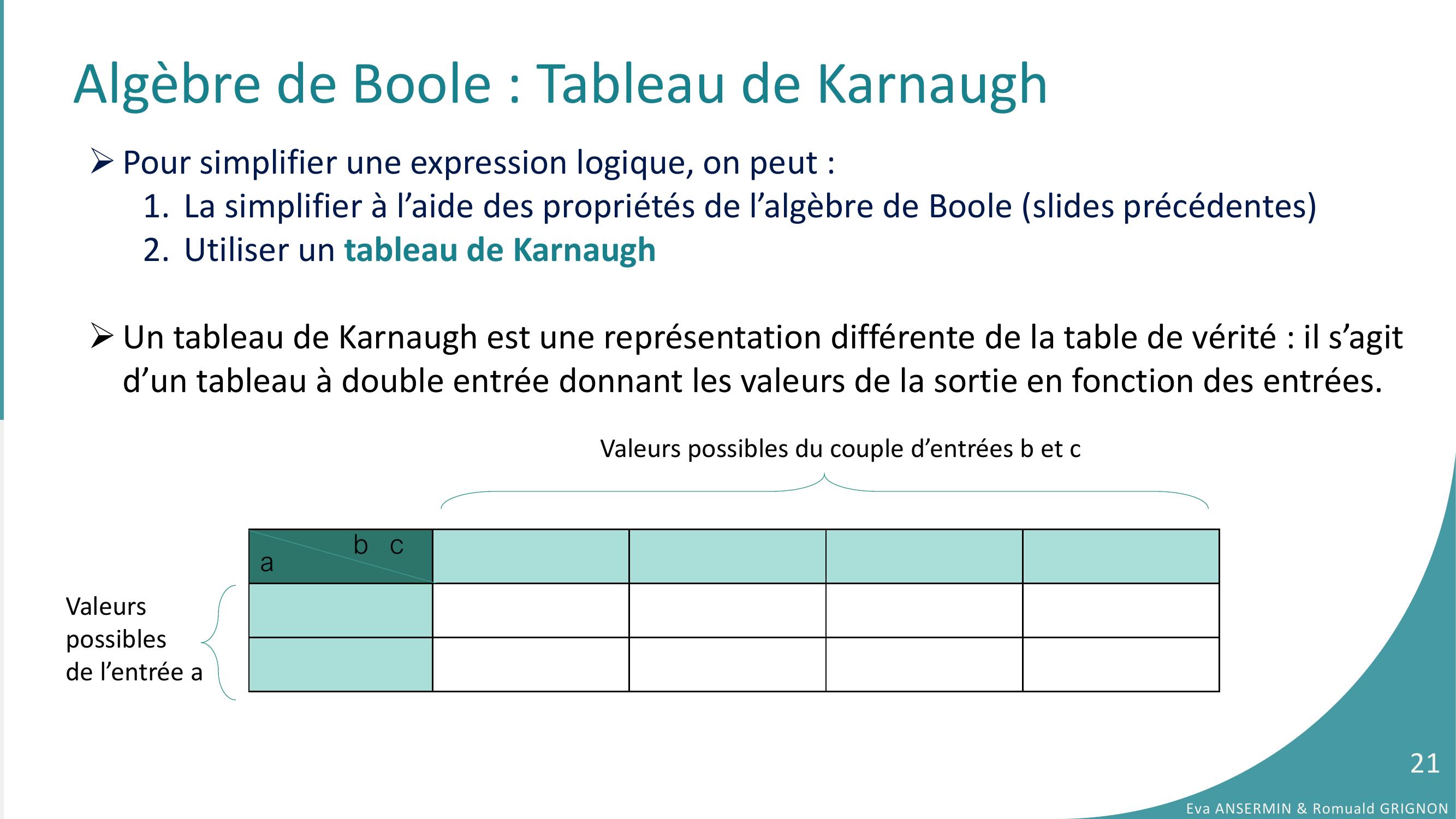
Page 21 : Algèbre de Boole : Tableau de Karnaugh Pour simplifier une expression logique, on peut :1. La simplifier à l’aide des propriétés de l’algèbre de Boole slides précédentes2. Utiliser un tableau de KarnaughUn tableau de Karnaugh est une représentation différente de la table de vérité : il s’agit d’un tableau à double entrée donnant les valeurs de la sortie en fonction des entrées.ab cValeurspossiblesde l’entrée aValeurs possibles du couple d’entrées b et cEva ANSERMIN & Romuald GRIGNON21
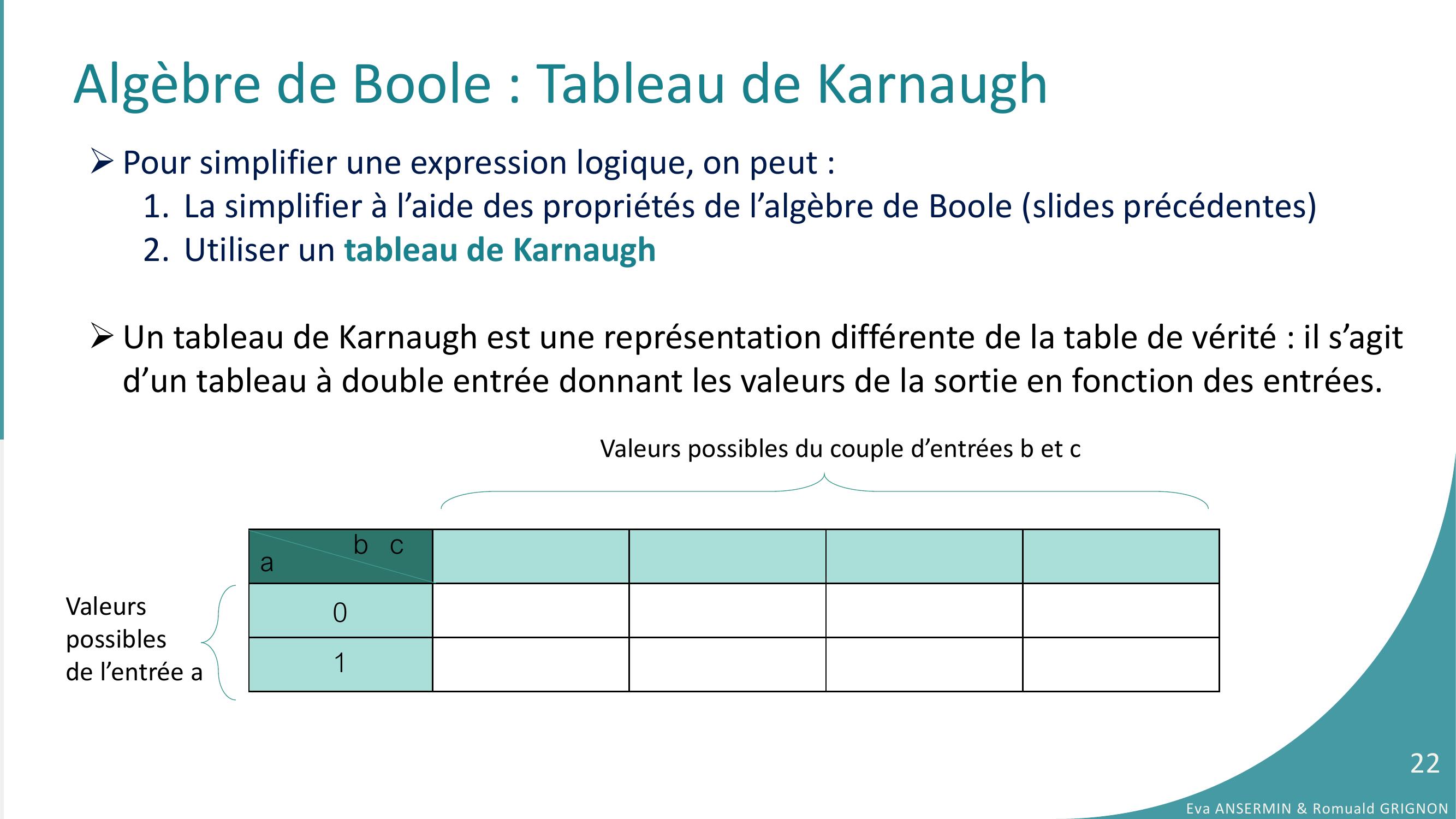
Page 22 : Pour simplifier une expression logique, on peut :1. La simplifier à l’aide des propriétés de l’algèbre de Boole slides précédentes2. Utiliser un tableau de KarnaughUn tableau de Karnaugh est une représentation différente de la table de vérité : il s’agit d’un tableau à double entrée donnant les valeurs de la sortie en fonction des entrées.ab cValeurspossiblesde l’entrée aValeurs possibles du couple d’entrées b et cAlgèbre de Boole : Tableau de Karnaugh Eva ANSERMIN & Romuald GRIGNON2201
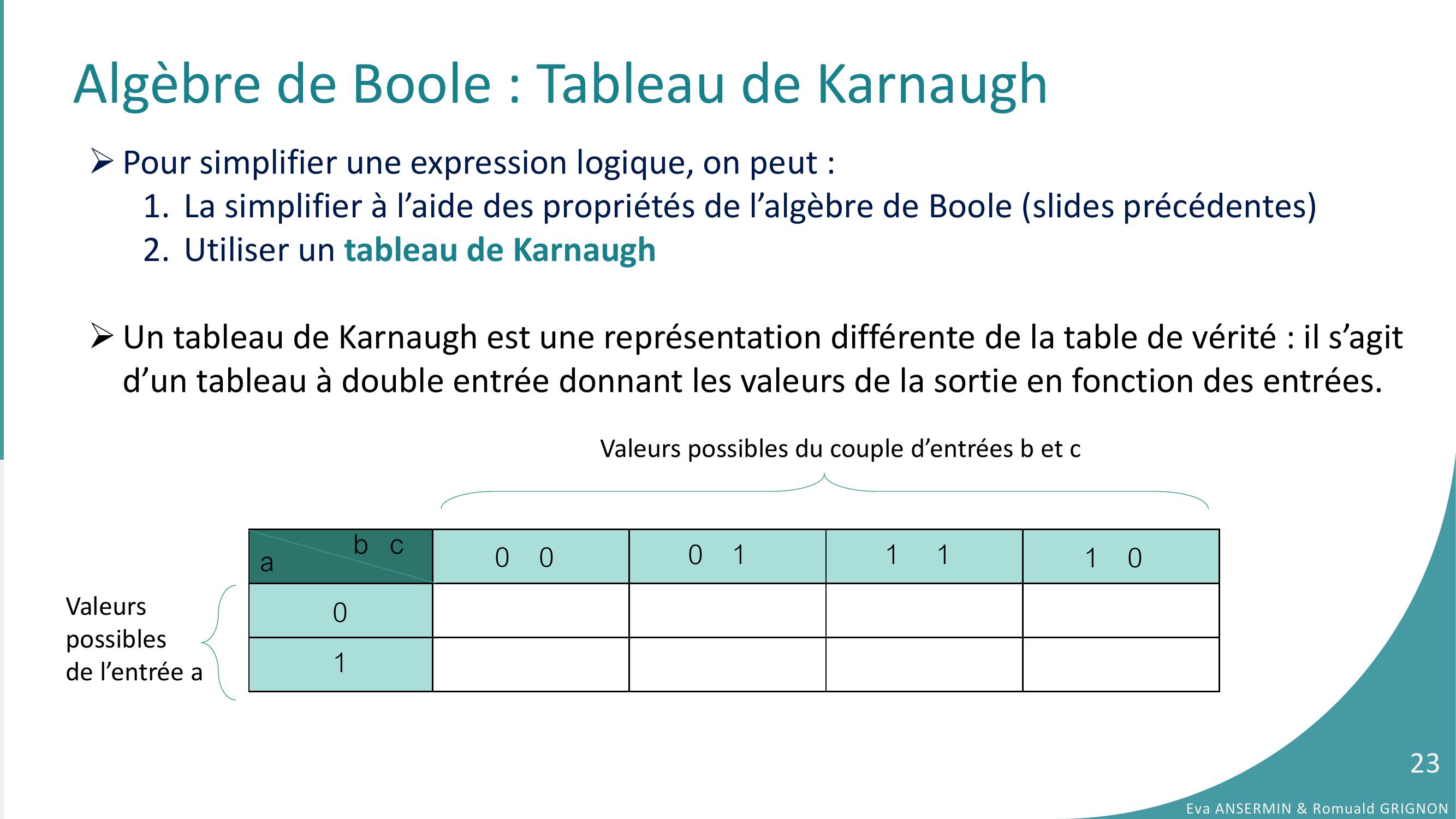
Page 23 : Pour simplifier une expression logique, on peut :1. La simplifier à l’aide des propriétés de l’algèbre de Boole slides précédentes2. Utiliser un tableau de KarnaughUn tableau de Karnaugh est une représentation différente de la table de vérité : il s’agit d’un tableau à double entrée donnant les valeurs de la sortie en fonction des entrées.ab cValeurspossiblesde l’entrée aValeurs possibles du couple d’entrées b et c01Algèbre de Boole : Tableau de Karnaugh 0 00 11 11 0Eva ANSERMIN & Romuald GRIGNON23
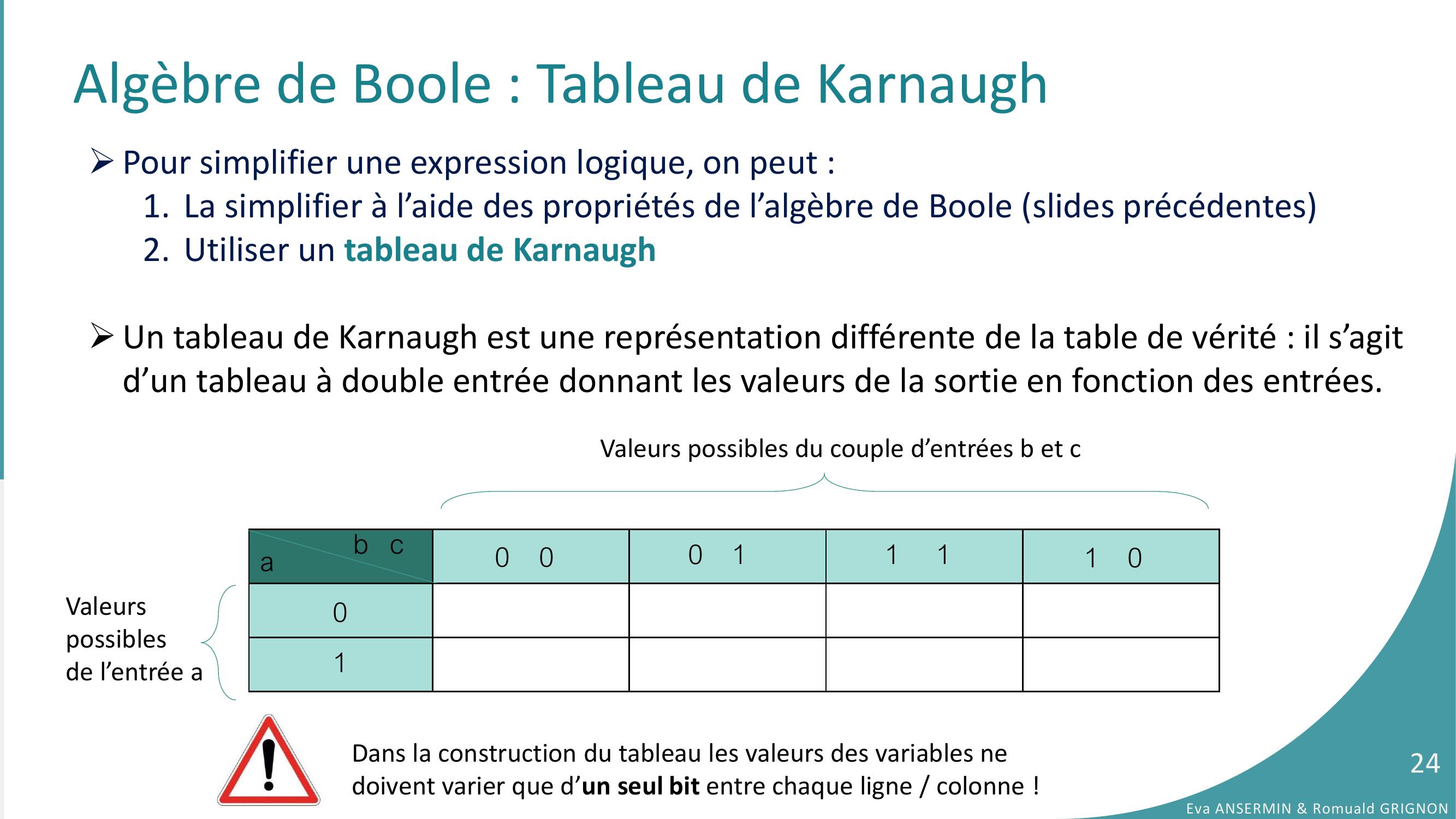
Page 24 : Algèbre de Boole : Tableau de Karnaugh Dans la construction du tableau les valeurs des variables ne doivent varier que d’un seul bit entre chaque ligne / colonne !Eva ANSERMIN & Romuald GRIGNON24Pour simplifier une expression logique, on peut :1. La simplifier à l’aide des propriétés de l’algèbre de Boole slides précédentes2. Utiliser un tableau de KarnaughUn tableau de Karnaugh est une représentation différente de la table de vérité : il s’agit d’un tableau à double entrée donnant les valeurs de la sortie en fonction des entrées.ab cValeurspossiblesde l’entrée aValeurs possibles du couple d’entrées b et c00 00 11 11 01
Page 25 : Algèbre de Boole : Tableau de Karnaugh Pour simplifier une expression logique, on peut :1. La simplifier à l’aide des propriétés de l’algèbre de Boole slides précédentes2. Utiliser un tableau de KarnaughUn tableau de Karnaugh est une représentation différente de la table de vérité : il s’agit d’un tableau à double entrée donnant les valeurs de la sortie en fonction des entrées.Une fois le tableau rempli, on regroupe TOUTES les cases contenant ‘1’ par des groupes de tailles en puissances de 2 1, 2, 4, …. Il faut prendre les groupes les plus grands possibles.En analysant ces groupes, on peut trouver une équation directement simplifiée.Eva ANSERMIN & Romuald GRIGNON25
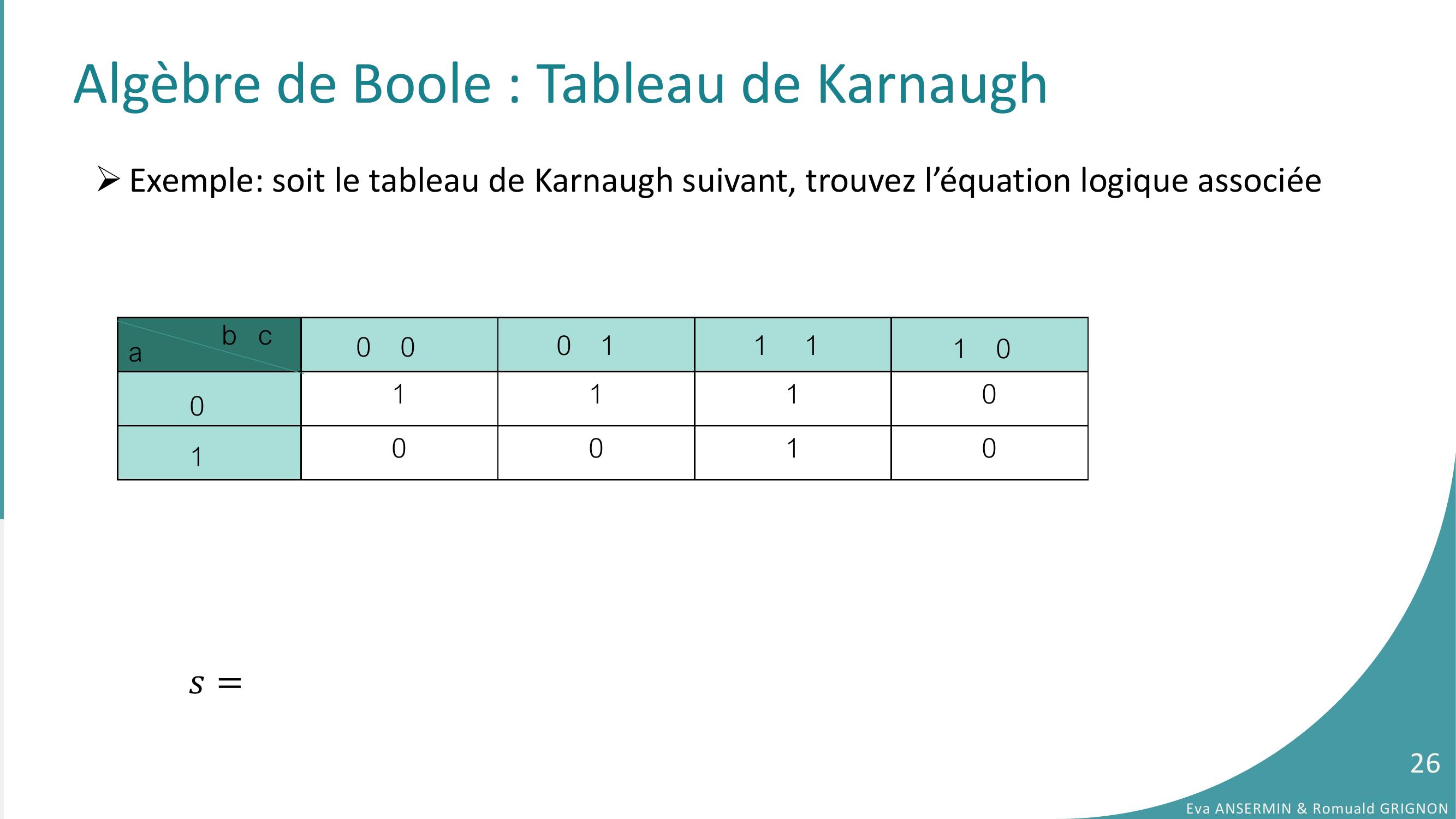
Page 26 : Algèbre de Boole : Tableau de Karnaugh Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée𝑠=11100010ab c010 00 11 11 0Eva ANSERMIN & Romuald GRIGNON26
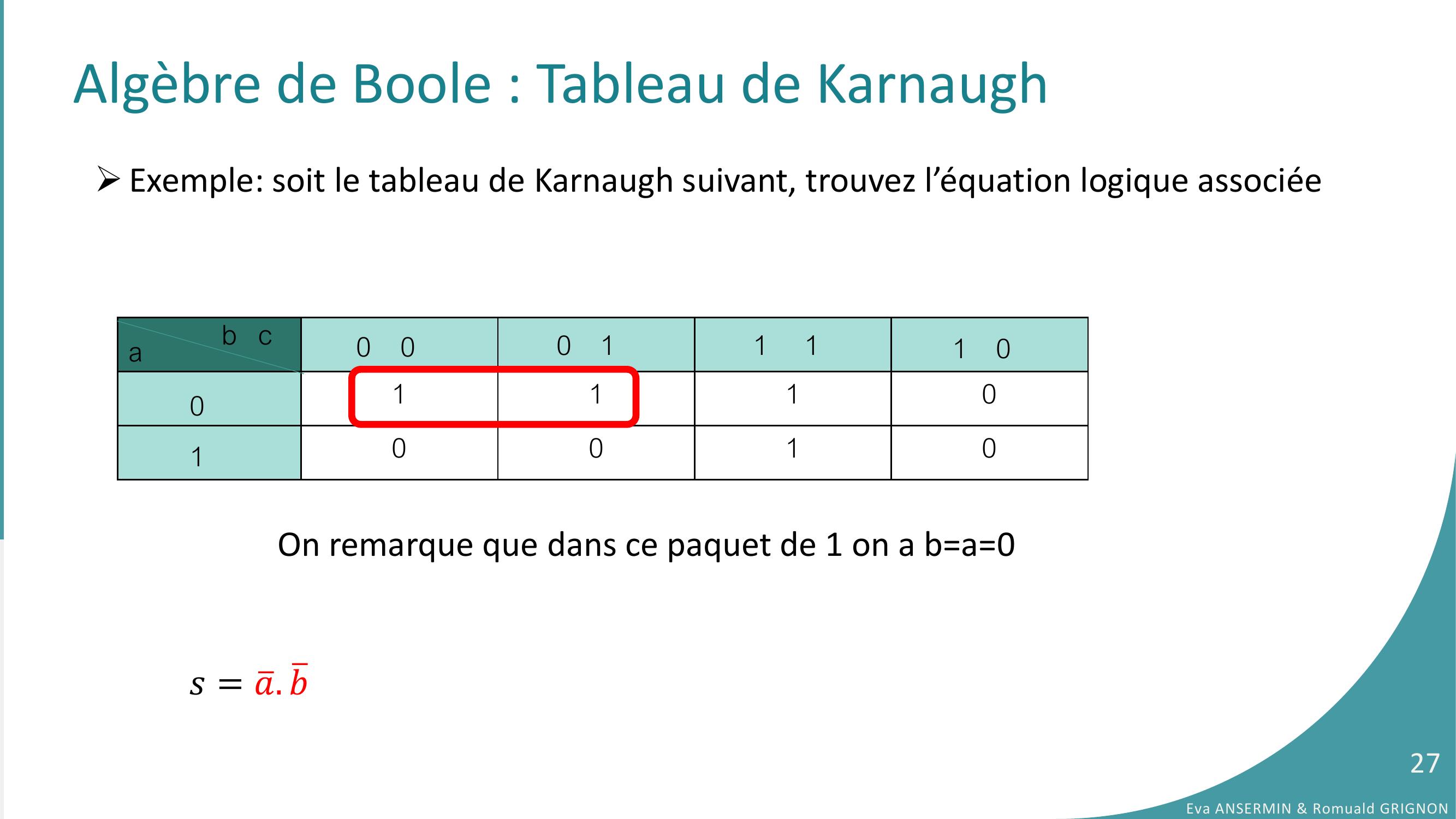
Page 27 : Algèbre de Boole : Tableau de Karnaugh Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée𝑠= ത𝑎. ത𝑏11100010ab c010 00 11 11 0On remarque que dans ce paquet de 1 on a b=a=0Eva ANSERMIN & Romuald GRIGNON27
Page 28 : Algèbre de Boole : Tableau de Karnaugh Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée𝑠= ത𝑎. ത𝑏+ 𝑏. 𝑐11100010ab c010 00 11 11 0On remarque que dans ce paquet de 1 on a b=c=1Eva ANSERMIN & Romuald GRIGNON28
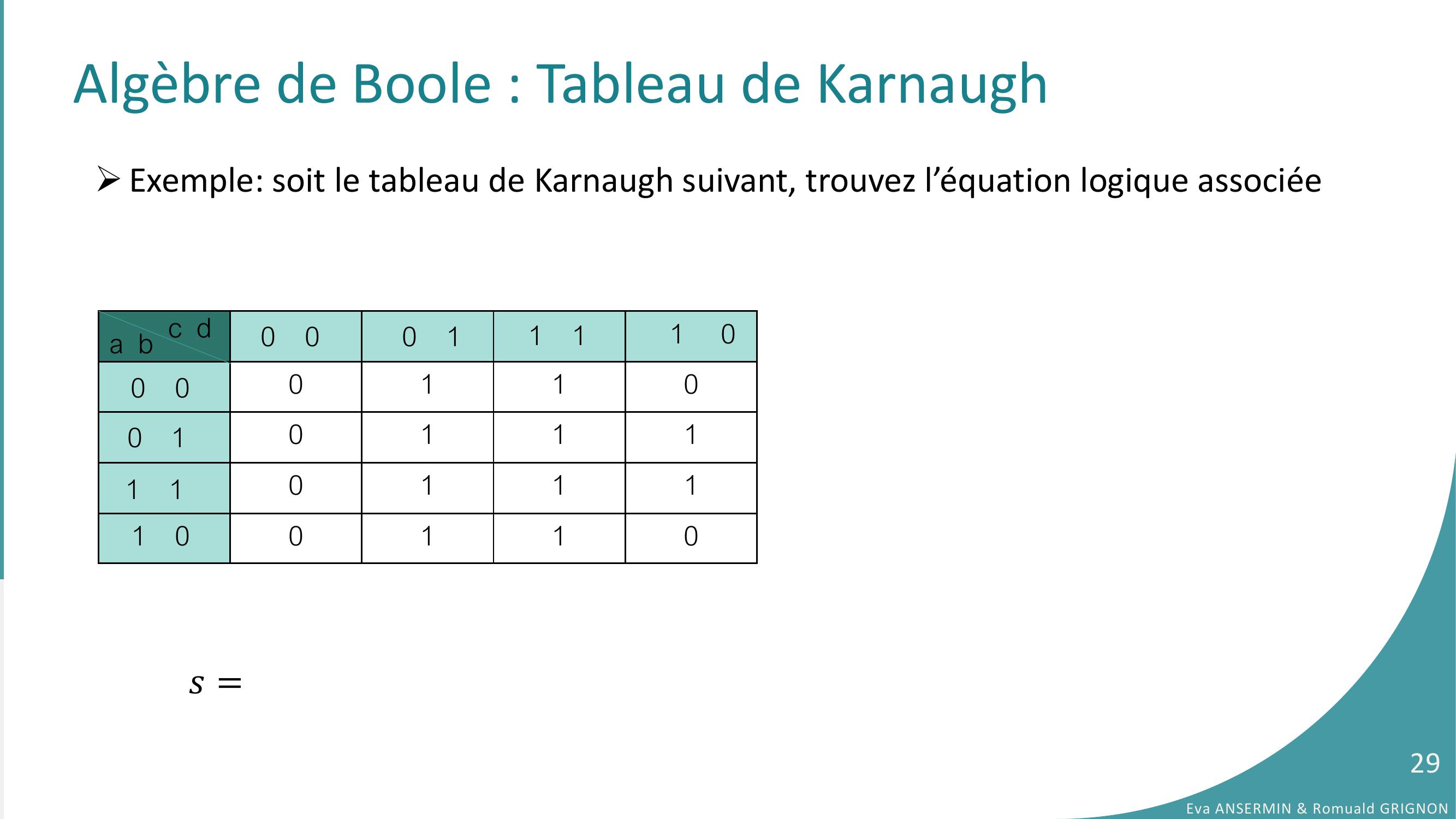
Page 29 : Algèbre de Boole : Tableau de Karnaugh 0110011101111 00110a b c d 0 00 11 01 10 00 11 1𝑠=Eva ANSERMIN & Romuald GRIGNON29Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée
Page 30 : Algèbre de Boole : Tableau de Karnaugh 0110011101111 00110a b c d 0 00 11 01 10 00 11 1𝑠= 𝑑+On remarque que dans ce paquet, on a : d=1Eva ANSERMIN & Romuald GRIGNON30Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée
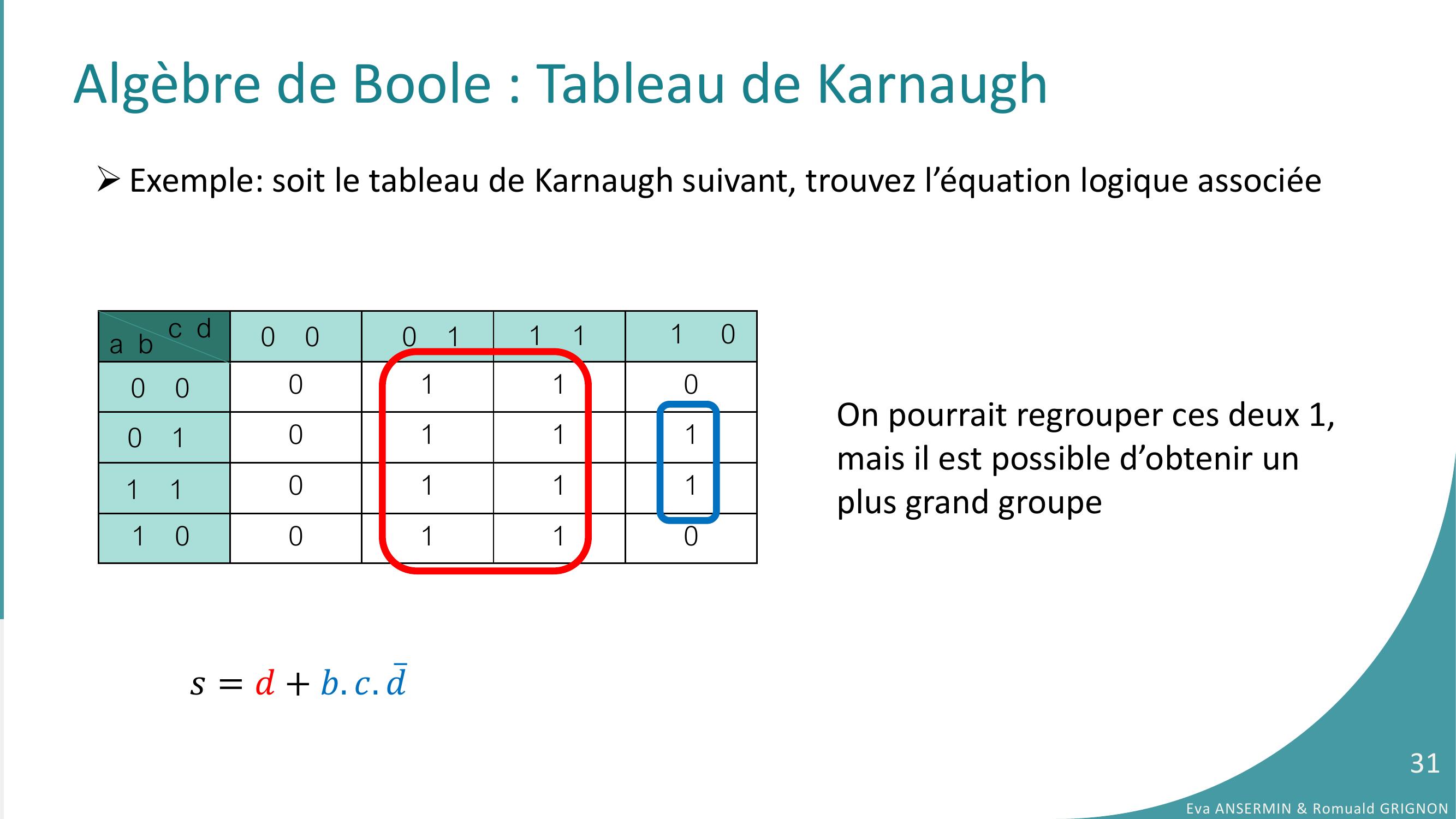
Page 31 : Algèbre de Boole : Tableau de Karnaugh 0110011101111 00110a b c d 0 00 11 01 10 00 11 1𝑠= 𝑑+ 𝑏. 𝑐. ҧ𝑑On pourrait regrouper ces deux 1,mais il est possible d’obtenir unplus grand groupeEva ANSERMIN & Romuald GRIGNON31Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée
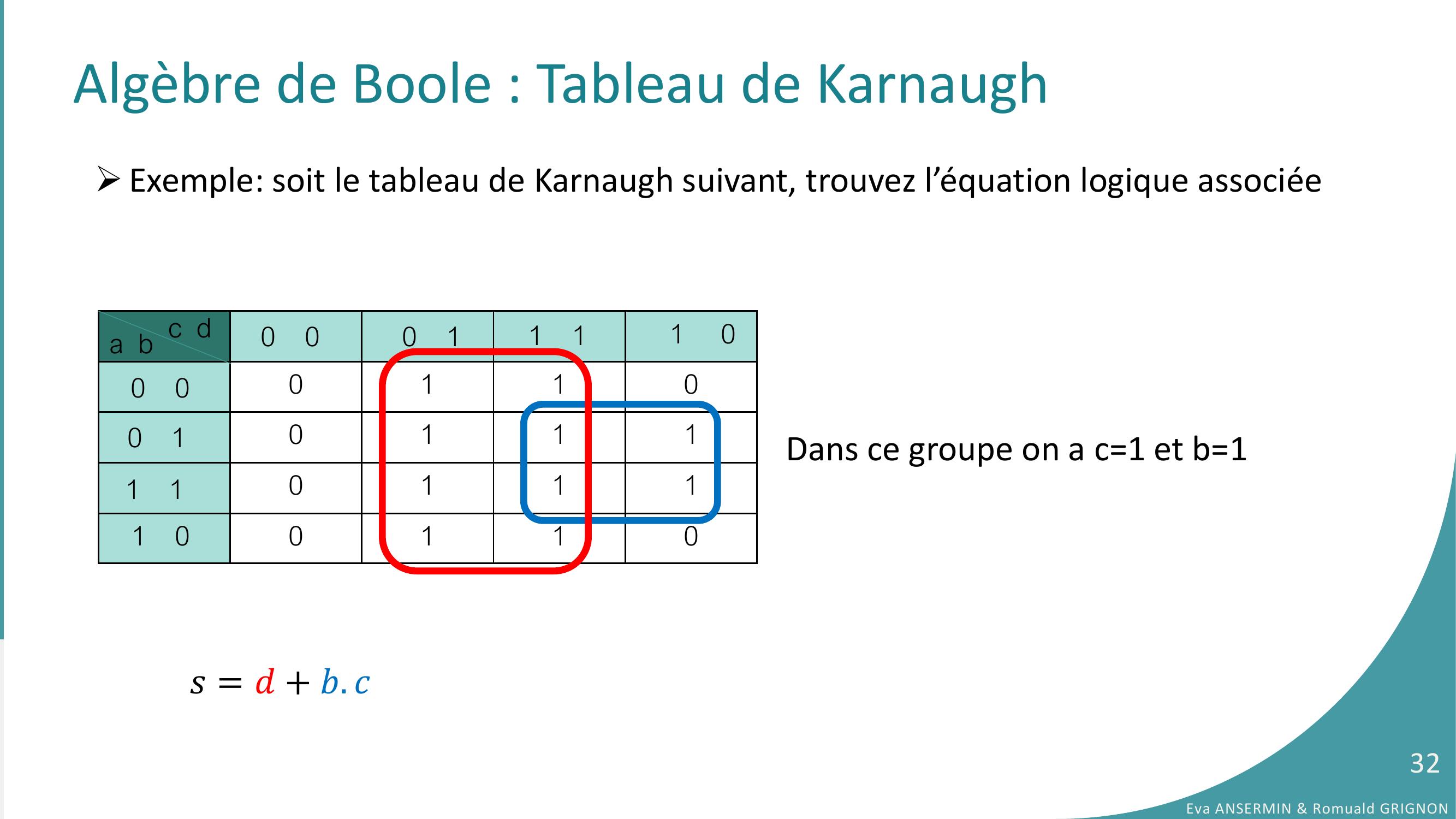
Page 32 : Algèbre de Boole : Tableau de Karnaugh 0110011101111 00110a b c d 0 00 11 01 10 00 11 1𝑠= 𝑑+ 𝑏. 𝑐Dans ce groupe on a c=1 et b=1Eva ANSERMIN & Romuald GRIGNON32Exemple: soit le tableau de Karnaugh suivant, trouvez l’équation logique associée
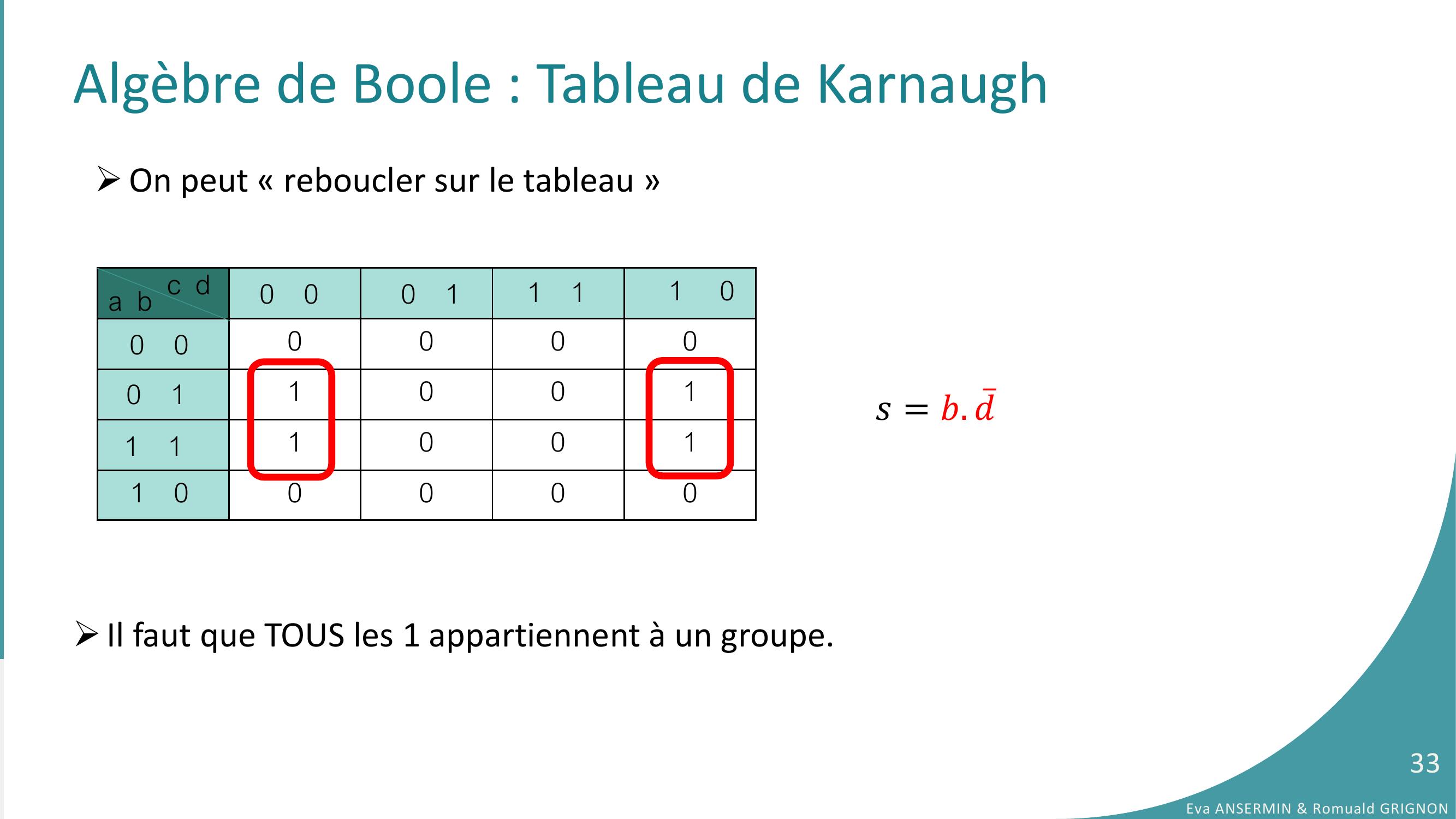
Page 33 : Algèbre de Boole : Tableau de Karnaugh On peut « reboucler sur le tableau »0000100110011 00000a b c d 0 00 11 01 10 00 11 1𝑠= 𝑏. ҧ𝑑Il faut que TOUS les 1 appartiennent à un groupe.Eva ANSERMIN & Romuald GRIGNON33
Page 34 : Algèbre de Boole : Construction de circuit logiquePour construire un circuit logique à partir d’un énoncé:1. Construire la table de vérité2. Déterminer l’équation logique grâce :à la simplification de l’équation logique OUau tableau de Karnaugh3. Dessiner le circuit à l’aide de portes logiques.Eva ANSERMIN & Romuald GRIGNON34
Page 35 : Algèbre de Boole : Représentation logiqueABCS00000010010001111000101111011111Exemple : « SA,B,C = 1 si et seulement si la majorité des trois variables A, B, C valent 1. »1. Table de vérité : Eva ANSERMIN & Romuald GRIGNON35
Page 36 : Algèbre de Boole : Représentation logique« SA,B,C = 1 ssi la majorité destrois variables A, B, C valent 1. »2 Equation :1. On regroupe les cas ou S=12. On simplifie l’équation𝑠= ത𝑎𝑏𝑐+ 𝑎ത𝑏c + ab ҧ𝑐+ 𝑎𝑏𝑐𝑠= ത𝑎𝑏𝑐+ 𝑎ത𝑏c + ab ҧ𝑐+ 𝑎+ 𝑎+ 𝑎𝑏𝑐𝑎+ 𝑎= 𝑎𝑠= ത𝑎𝑏𝑐+ 𝑎ത𝑏c + ab ҧ𝑐+ 𝑎𝑏𝑐+ 𝑎𝑏𝑐+ 𝑎𝑏𝑐𝑠= 𝑏𝑐ത𝑎+ 𝑎+ 𝑎𝑏ҧ𝑐+ 𝑐+ 𝑎𝑐ത𝑏+ 𝑏𝒔= 𝒃𝒄+ 𝒂𝒃+ 𝒂𝒄𝑎+ ത𝑎= 1Eva ANSERMIN & Romuald GRIGNON36
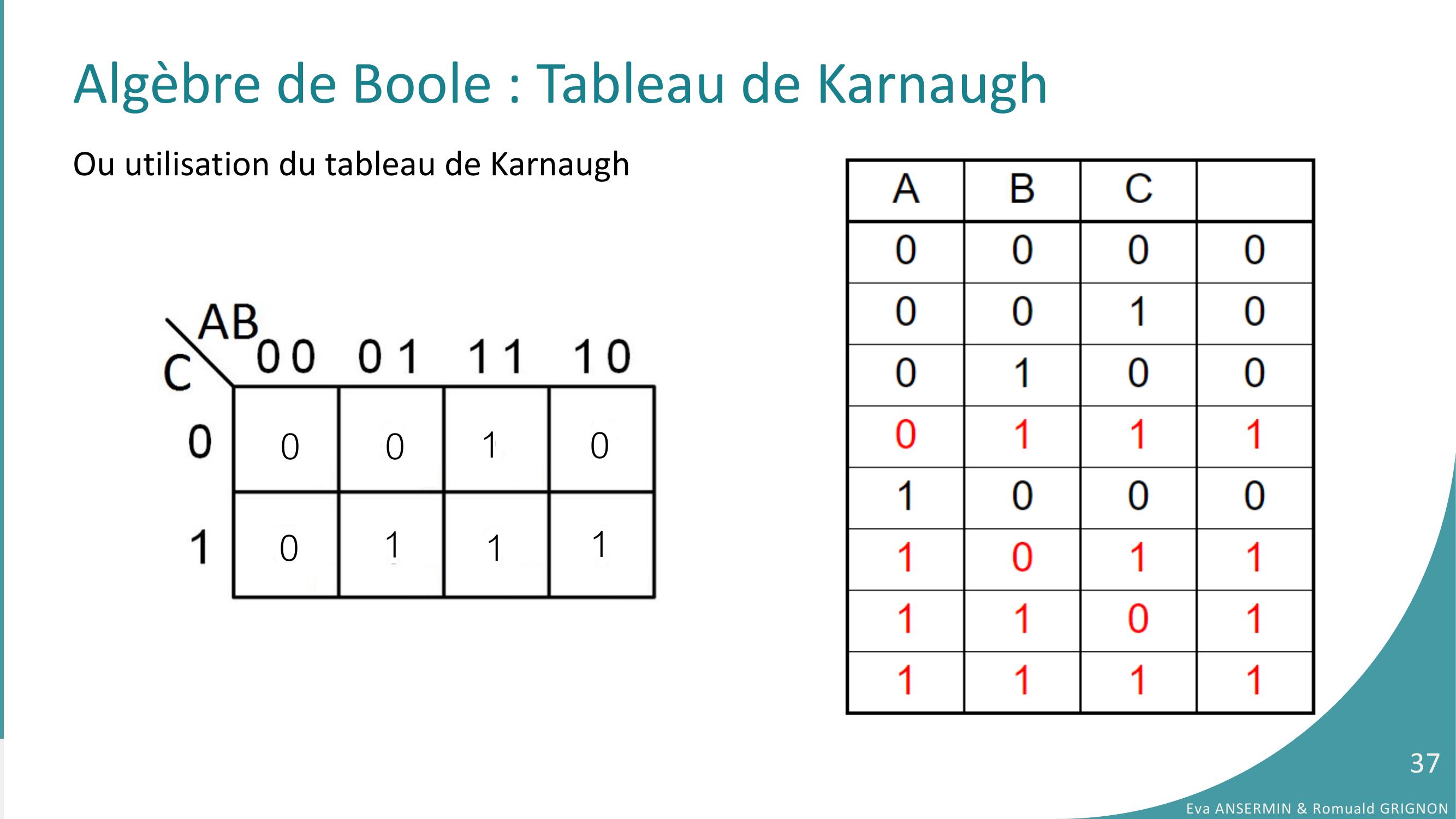
Page 37 : Algèbre de Boole : Tableau de KarnaughOu utilisation du tableau de Karnaugh00011110Eva ANSERMIN & Romuald GRIGNON37
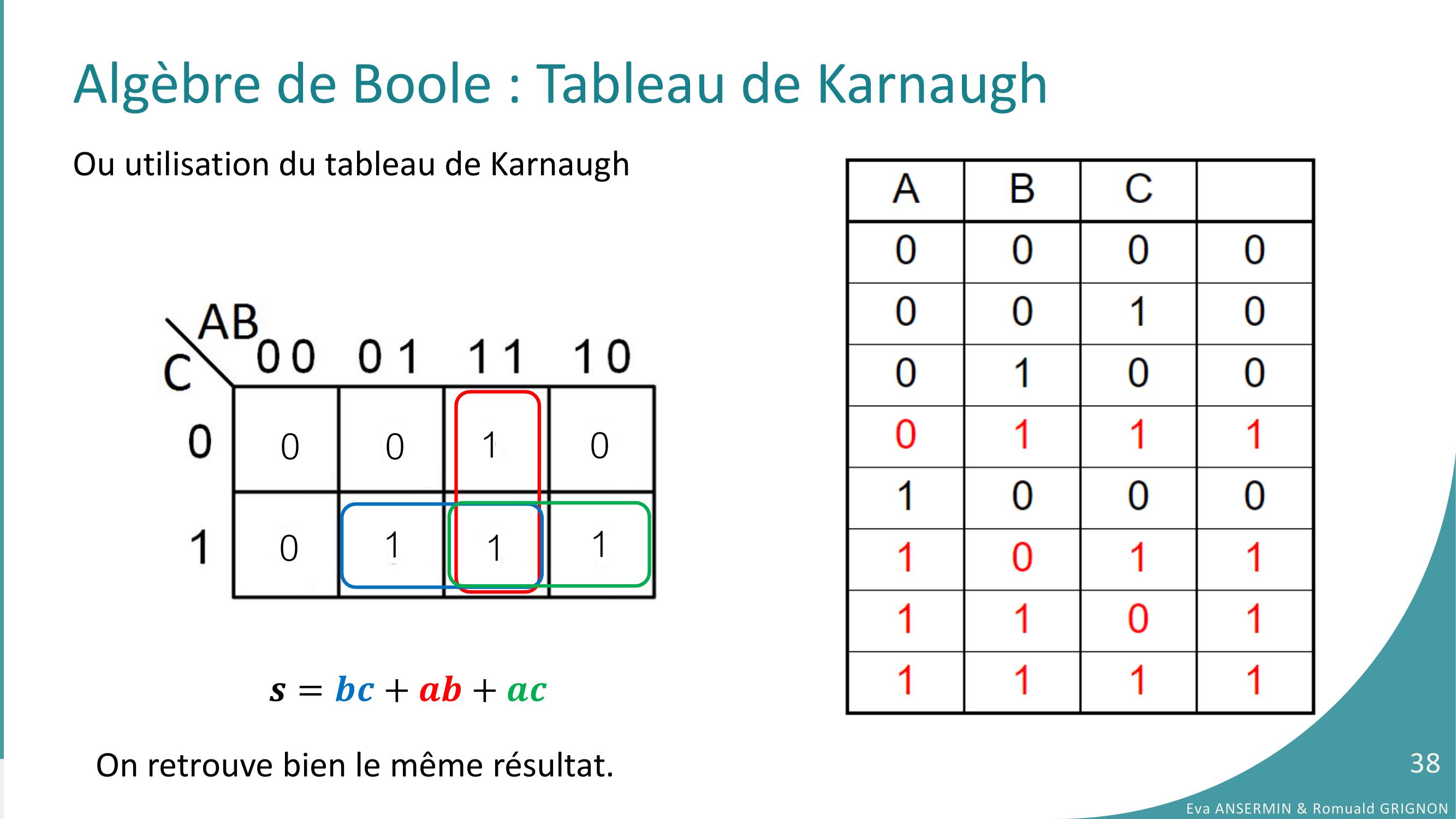
Page 38 : Algèbre de Boole : Tableau de Karnaugh𝒔= 𝒃𝒄+ 𝒂𝒃+ 𝒂𝒄On retrouve bien le même résultat.Eva ANSERMIN & Romuald GRIGNON3800011110Ou utilisation du tableau de Karnaugh
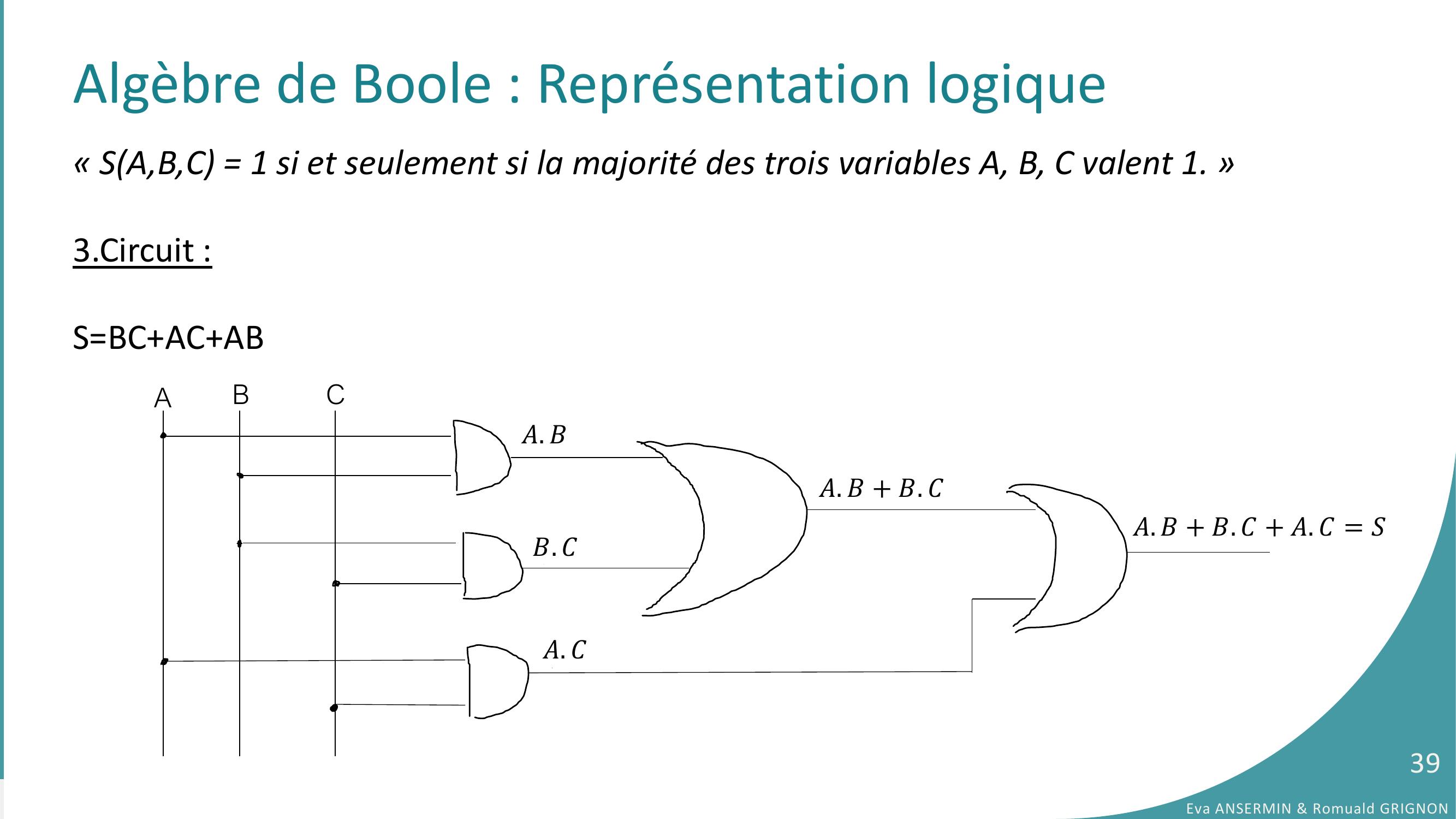
Page 39 : Algèbre de Boole : Représentation logique« SA,B,C = 1 si et seulement si la majorité des trois variables A, B, C valent 1. »3.Circuit :S=BC+AC+ABABC𝐴. 𝐵𝐵. 𝐶𝐴. 𝐶𝐴. 𝐵+ 𝐵. 𝐶𝐴. 𝐵+ 𝐵. 𝐶+ 𝐴. 𝐶= 𝑆Eva ANSERMIN & Romuald GRIGNON39
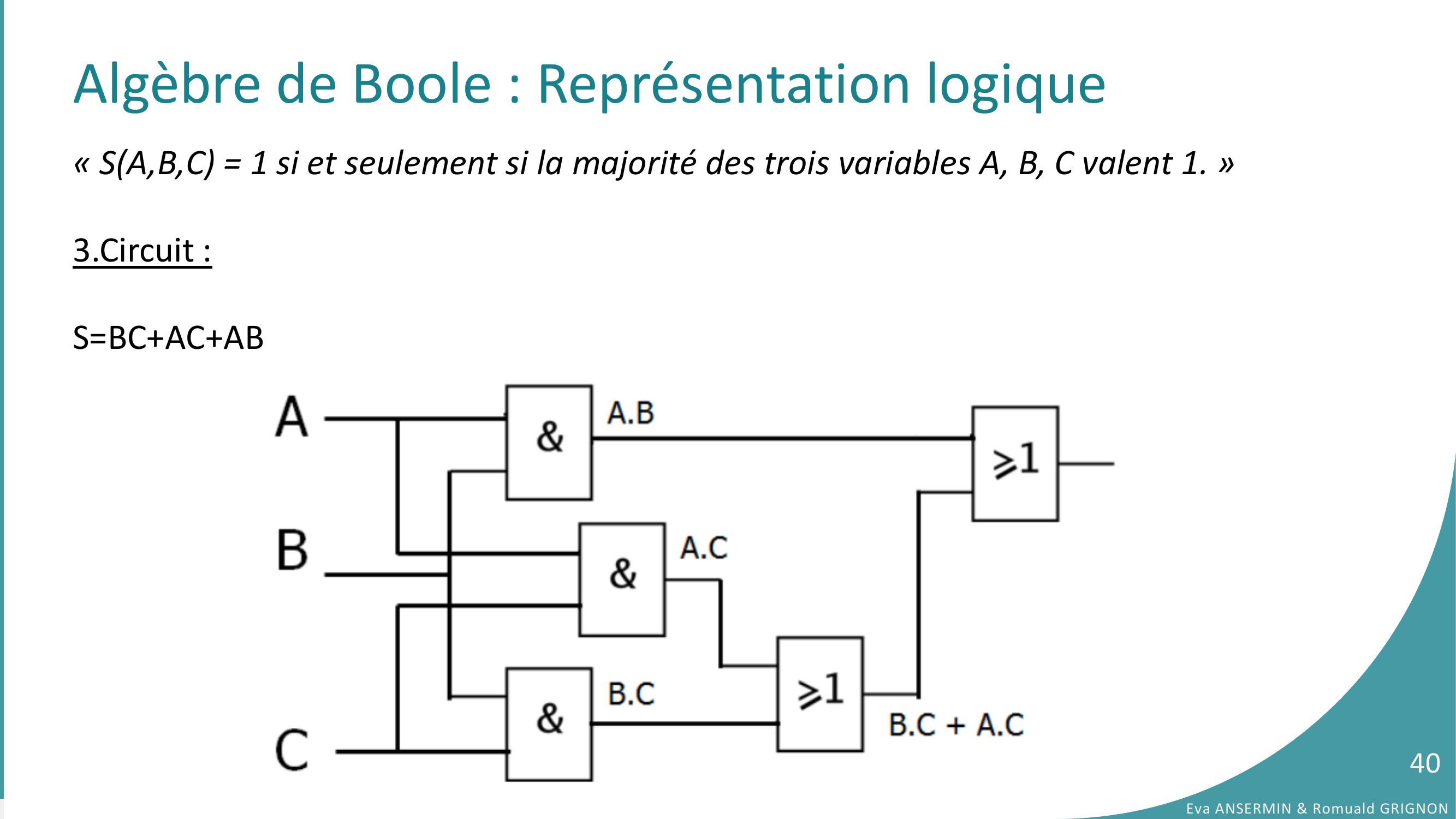
Page 40 : Algèbre de Boole : Représentation logiqueEva ANSERMIN & Romuald GRIGNON40« SA,B,C = 1 si et seulement si la majorité des trois variables A, B, C valent 1. »3.Circuit :S=BC+AC+AB
Page 41 : ConclusionL’algèbre de Boole permet de modéliser des énoncés logiques et utilise des variables dont les valeurs possibles sont VRAI 1 ou FAUX 0.A partir d’un énoncé, on peut déterminer une équation et un circuit logique répondant au problème.Les différents opérateurs de l’algèbre de Boole sont implémentables sur des circuits électroniques grâce aux transistors. Le fonctionnement d’un ordinateur se base sur l’algèbre de Boole : les différents calculs et traitements de données effectués par un ordinateur comparaison, addition etc. sont modélisés par des circuits logiques implémentés sur carte électronique.Eva ANSERMIN & Romuald GRIGNON41
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41