CM4 Application
Télécharger le CM4 Application en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
Page 1 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsAlgebre-Premier semestre 20211Introduction2Logique et Raisonnement3Ensemble4Relations Binaires5ApplicationsN. Arancibia - relu par D. CransacAlgebre
Page 2 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre
Page 3 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsApplicationsDefinition ApplicationSoient E et F deux ensembles.Une application f de E vers F est une relation qui associe, a chaqueelement de E un unique element de F.Plus formellement, on appelle application ou fonction de E dans F touterelation f dont le graphe Γ E × F est tel que :x E, !y F,x, y ΓE est l’ensemble de depart de f et F est l’ensemble d’arrivee de f .Definition image, antecedentSoit f une application de E dans F, x E, y F.Si x, y f , on note y = f x, et on dit quey = f x est l’image de x par fet x est l’antecedent de y par f .On note f : E→Fx7→y = f x.N. Arancibia - relu par D. CransacAlgebre
Page 4 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsApplicationsDefinition Graphe d’une fonctionOn appelle graphe de l’application f le sous-ensemble Γ de E × F definipar :Γ = x, f x : x E.Remarque Une fonction est definie par des couples.Si l’ensemble des couples est modifie, on n’a pas le mˆeme graphe, on nedefinit plus la mˆeme fonction :f : R→Rx7→x2etg : 0; 2→Rx7→x2ne sont pas les mˆemes fonctionsDefinition Ensemble d’applicationsL’ensemble des applications de E dans F est note FE, F ou F E.PropositionSoit E et F deux ensembles finis cardF E = cardFcardE.N. Arancibia - relu par D. CransacAlgebre
Page 5 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsApplicationsExemples d’applications :Application identite : On appelle application identite d’un ensemble E,et on note IdE, l’application de E dans E definie parIdE : E →Ex 7→x.Application constante : Une application f : E →F est dite constantes’il existe α F tel que x E, f x = α. C’est-a-diref : E →Fx 7→α.N. Arancibia - relu par D. CransacAlgebre
Page 6 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsApplicationsExemples d’applications suite :Definition Fonction indicatrice d’une partie d’un ensembleSoit E un ensemble et A une partie de E.On appelle fonction indicatrice de A et on note 1A la fonction de E dans0, 1 definie par :f : E →0, 1x 7→1Ax = 1si x A,0si x /A.N. Arancibia - relu par D. CransacAlgebre
Page 7 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsApplicationsExemples :Definition Famille d’elementsSoit E un ensemble et I un ensemble.On appelle famille d’elements de E indexee par I toute application de Idans Ef : I →Ei 7→f iOn notef i = xiE.On represente un telle famille par xiiI.Remarque : Une suite numerique est une famille d’elements de E = R avecI = Jn0; +J et n0 NN. Arancibia - relu par D. CransacAlgebre
Page 8 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueDefinitionDeux applications f et g sont egales sielles ont le mˆeme ensemble de depart E et le mˆeme ensemble d’arrivee,etsi pour tout x E, on af x = gx.Definition Image directe d’une partie, image d’une applicationSoit f : E →F une application.Pour toute partie A de E, on appelle image directe de A par f , noteef A, l’ensemble :f A = y F : a A, y = f a = f a : a A.L’image de E tout entier est simplement appelee l’image de f et estnotee generalement Imf plutˆot que f E.N. Arancibia - relu par D. CransacAlgebre
Page 9 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueExemple :L’image de R par la fonctionx 7→x2est R+.L’image de 0, 3 par cette mˆeme fonction est 0, 9.L’image deπZ = · · · , 2π , π , 0 , π , 2π , · · · par la fonctionx 7→sin xest le singleton 0.L’image de 0, π est 0, 1.et l’image de π/2, π/2 est 1, 1.N. Arancibia - relu par D. CransacAlgebre
Page 10 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueDefinition Expression a valeurs dans · · ·Soient f : E →F une application et B une partie de F.On dit que f est a valeurs dans B si toute valeur de f est element de B, i.e.six E, f x B,ou encore siImf B.Remarque : En general, Imf est plus petit que F Imf F.N. Arancibia - relu par D. CransacAlgebre
Page 11 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueEtudions comme l’image directe reagit par rapport a certaines operations surles ensembles.PropositionSoit f : E →F. Soit A et B deux parties quelconques de E. On aA B =⇒f A f B.f A B = f A f B.f = et f a = f a.f A B f A f B.Remarque : L’inclusion est stricte :AB = mais f Af B ̸= ×××××××BAN. Arancibia - relu par D. CransacAlgebre
Page 12 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueDefinition Image reciproque d’une partieSoient f : E →F une application et B une partie de F.L’image reciproque de B par f , notee f 1B est l’ensemble des elementsde E dont l’image est dans B :f 1B = x E, f x B.C’est la partie de E formee par les antecedents des elements de B.Remarque :On peut ecrire x f 1B ⇐⇒f x B.On af 1 = etf 1F = E.Pour tout b Ff 1b = x E : f x = b.Par consequent, si b /ImF on a f 1b = .N. Arancibia - relu par D. CransacAlgebre
Page 13 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueExemple :L’image reciproque de R+ par la fonction exponentielle est R tout entier.L’image reciproque de 9, 25 par la fonction carree est5, 3 3, 5.L’image reciproque de 0 par la fonction sinus estπZ = kπ : k ZL’image reciproque de 4, 6 est l’ensemble vide.N. Arancibia - relu par D. CransacAlgebre
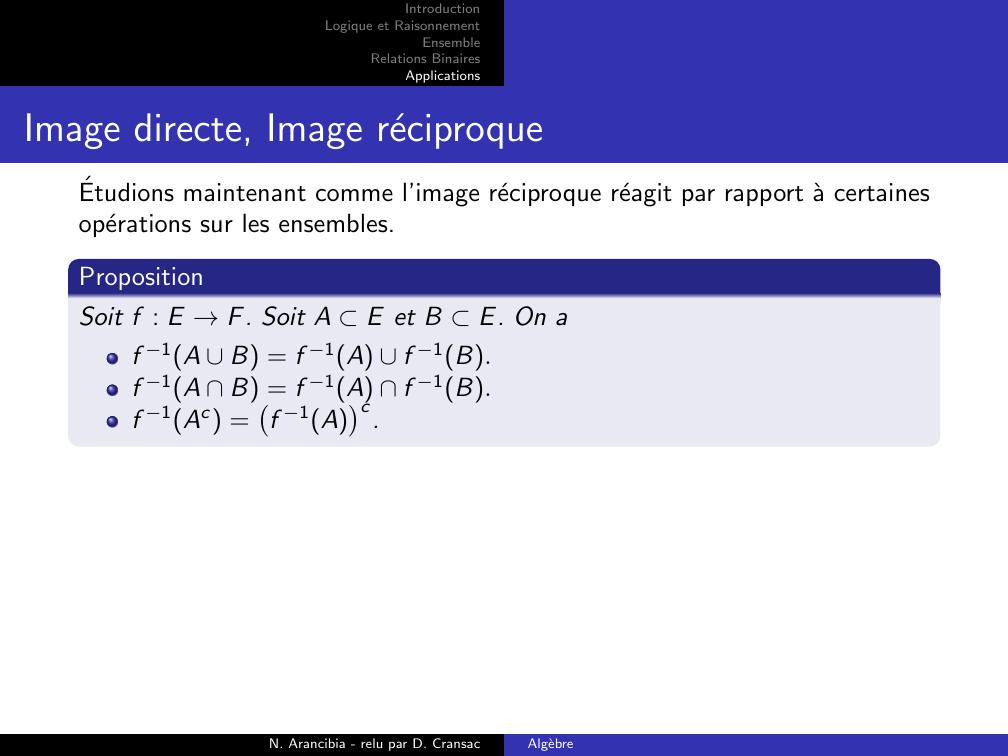
Page 14 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsImage directe, Image reciproqueEtudions maintenant comme l’image reciproque reagit par rapport a certainesoperations sur les ensembles.PropositionSoit f : E →F. Soit A E et B E. On af 1A B = f 1A f 1B.f 1A B = f 1A f 1B.f 1Ac =f 1Ac.N. Arancibia - relu par D. CransacAlgebre
Page 15 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsIntroduisons certaines operations qui vont nous permettre de creer denouvelles applications.Definition CompositionSoient E, F et G trois ensembles, f une application de E dans F et g uneapplication de F dans G. La composee de f par g est l’application de Edans G, notee g ◦f et definie pour tout x E parg ◦f x = gf x.c’est-a-direg ◦f : Ef→Fg→Gx 7→f x 7→gf x.Remarque : La composition, en general, n’est possible que dans un seulsens, et quand elle est possible dans les deux, on n’a aucune raison d’avoir :f ◦g = g ◦f .N. Arancibia - relu par D. CransacAlgebre
Page 16 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsRemarque :La composition, en general, n’est possible que dans un seul sens, et quandelle est possible dans les deux, on n’a aucune raison d’avoir :f ◦g = g ◦f .ExempleSoit f : x 7→x2 definie sur E = R a valeurs dans F = R+ etg : x 7→x + 1 definie sur F = R+ a valeurs dans G = R.Alors g ◦f peut ˆetre definie de R a valeurs dans R etg ◦f x = gf x = gx2 =x2 + 1.Mais f ◦g ne peut pas ˆetre definie de R dans R.Si l’on se restreint a F, on af ◦gx = f gx = f x + 1 = x + 1N. Arancibia - relu par D. CransacAlgebre
Page 17 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsLa composition satisfait les proprietes suivantes.PropositionSoient E, F, G, H des ensembles.Pour tout f FE, F, on a : f ◦IdE = f . Neutralite de l’identitef ◦IdE : EIdE→Ef→Fx 7→x 7→f x.Pour tout f FE, F, on a : IdF ◦f = f . Neutralite de l’identiteIdF ◦f : Ef→FIdF→Fx 7→f x 7→f x.La composition est associative : f FE, F, g FF, G,h FG, H, on a :h ◦g ◦f = h ◦g ◦f .N. Arancibia - relu par D. CransacAlgebre
Page 18 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsDemonstration.Montrons l’egaliteh ◦g ◦f = h ◦g ◦f .Pour tout x E on ah ◦g ◦f x = hg ◦f x= hgf x= h ◦gf x=h ◦g ◦fx.N. Arancibia - relu par D. CransacAlgebre
Page 19 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsSoit f FE, F. On peut aussi creer de nouvelles applications en nemodifiant que l’ensemble de depart ou l’ensemble d’arrivee de f .DefinitionSoit A une partie de E.Soit f : E →F une application. On appelle restriction de f a Al’application noteef A : A →Fdefinie parx A,f Ax = f x.Soit f : A →F une application. On appelle prolongement de f a Etoute application g de E dans F telle que :x A,f x = gx.C’est-a-dire f est la restriction de g a E gA = f .N. Arancibia - relu par D. CransacAlgebre
Page 20 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsOperations sur les applicationsRemarque :Restreindre/prolonger une application, c’est diminuer/augmenter la taillede son ensemble de definition.Parce que il existe en general beaucoup de prolongements d’uneapplication donnee, on parle d’un prolongement et non duprolongement. Par exemple, si f est l’identite de R+, elle possede uneinfinite de prolongements a R tout entier, parmi lesquelsL’application identite de R.L’application valeur absolue de R.L’applicationh : R →Rx 7→12x + x.Notons que h est identiquement nulle sur Ri.e. hx = 0 pour toutx 0.N. Arancibia - relu par D. CransacAlgebre
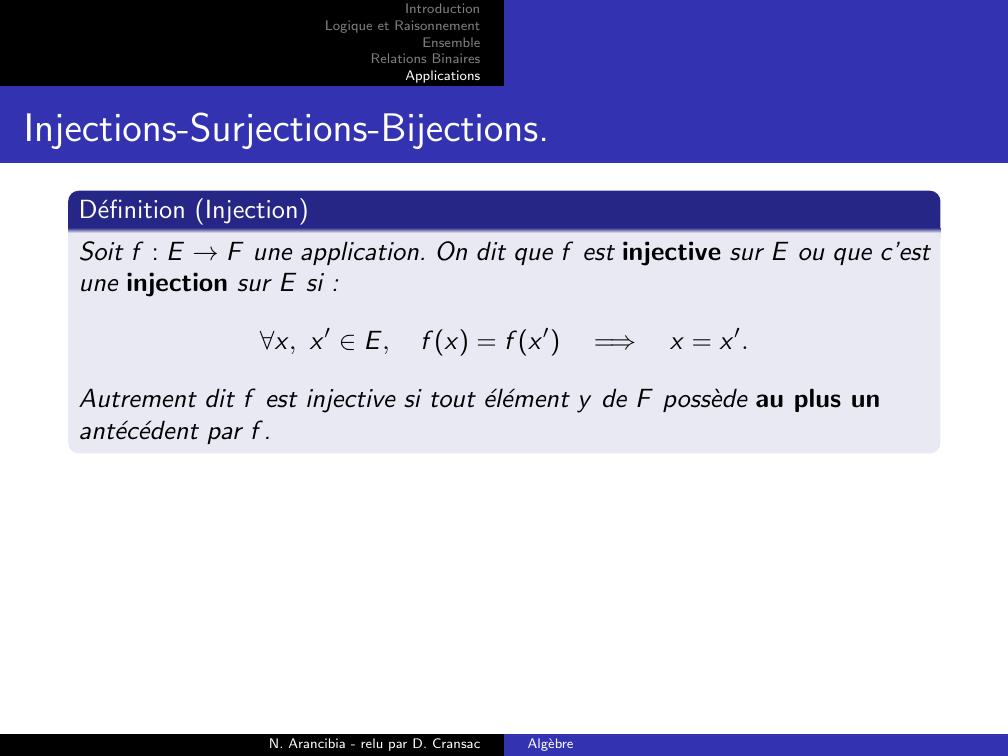
Page 21 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Definition InjectionSoit f : E →F une application. On dit que f est injective sur E ou que c’estune injection sur E si :x, x′ E,f x = f x′=⇒x = x′.Autrement dit f est injective si tout element y de F possede au plus unantecedent par f .N. Arancibia - relu par D. CransacAlgebre
Page 22 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Exemples :La application identite sur un ensemble E, est injective.Soit a R. Alors toute application affine sur R de la forme :f x = ax + best injective.L’application f : R →R definie parf x = x3est injective.L’application exponentielle f x = ex, x R, est injective.N. Arancibia - relu par D. CransacAlgebre
Page 23 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Remarques :Une definition equivalente de l’injectivite estx, x′ E,x ̸= x′=⇒f x ̸= f x′.Notons que la proposition precedente est la contraposition dex, x′ E,f x = f x′=⇒x = x′.Le changement de l’ensemble de depart d’une application peut modifierla propriete d’ˆetre injective.Par exemple :• La fonction carre n’est pas injective sur R, mais elle l’est sur R+.• La restriction de cos : R →R a l’intervalle 0, π est injective.N. Arancibia - relu par D. CransacAlgebre
Page 24 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Etudions certaines proprietes des fonctions injectives.PropositionOn considere deux applications f : E →F et g : F →G.Si f et g sont injectives, alors g ◦f est injective.Si g ◦f est injective, alors f est injective.Demonstration.Soient x, y E. Supposons g ◦f x = g ◦f y. Nous voulons montrerque : x = y. Orgf x = gf y=⇒zg injectivef x = f y=⇒zf injectivex = y.Soient x, y E. Supposons f x = f y. Nous voulons montrer que :x = y. Orf x = f y=⇒g ◦f x = g ◦f y=⇒zg◦f injectivex = y.N. Arancibia - relu par D. CransacAlgebre
Page 25 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Definition SurjectionSoit f : E →F une application. On dit que f est une application surjectivede E sur F ou que c’est une surjection de E sur F si :y F,x E,y = f x.Cela revient a dire que :Imf = F.Autrement dit, f est surjective de E sur F si et seulement si tout element deF possede au moins un antecedent dans E par f .Exemple :L’application · : Z →N definie par n 7→n. est surjective.L’application f : R3 →R2 definie par x, y, z 7→x, y.est surjective.N. Arancibia - relu par D. CransacAlgebre
Page 26 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Remarques :Pour montrer qu’une application f : E →F est surjective, on se donneun element quelconque y de F et on montre qu’il a au moins unantecedent dans E, c’est-a-dire on montre qu’il existe x E avecf x = y.Toute application est surjective de son ensemble de definition sur sonimage.Le changement de l’ensembles d’arrivee d’une application peut modifierla propriete d’ˆetre surjective.Par exemple :• L’application f de R dans R+ definie par f x = x2 est surjective.• L’application f de R dans R definie par f x = x2 n’est passurjective.N. Arancibia - relu par D. CransacAlgebre
Page 27 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Etudions certaines proprietes des fonctions surjectives.PropositionOn considere deux applications f : E →F et g : F →G.Si f et g sont surjectives, alors g ◦f est surjective.Si g ◦f est surjective, alors g est surjective.Demonstration.Montrons que g ◦f est surjective. Soit y G. Nous voulons montrerqu’il existe x E tel que y = g ◦f x. Or g est surjective, donc il existt F tel que y = gt. Mais f est aussi surjective, donc : t = f xpour un certain x E. Finalement, comme voulu :y = gt = gf x = g ◦f x.Montrons que g est surjective. Soit y G. Nous voulons montrer qu’ilexiste x F tel que y = gx. Or g ◦f est surjective, donc :y = g ◦f t pour un certain t E. Il suffit des lors de poser :x = f t pour avoir y = gx.N. Arancibia - relu par D. CransacAlgebre
Page 28 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Definition BijectionSoit f : E →F une application. On dit que f est une application bijectiveou encore une bijection siy F,!x E,y = f x.Autrement dit, f est bijective de E sur F si et seulement si tout element deF possede un et un seul antecedent dans E par f .PropositionSoit f une application d’un ensemble E dans un ensemble F. Alorsf est bijective⇐⇒f est injective et surjectiveRemarque : Pour montrer qu’une application f : E →F est bijective, onpourra raisonner en deux etapes en montrant l’injectivite et la surjectivite def .N. Arancibia - relu par D. CransacAlgebre
Page 29 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Exemples :Soit m R.Alors toute application affine de la forme x 7→mx + nest bijective.L’application x 7→x3est bijective.On sait que l’applicationf : R →Rx 7→x2.n’est ni injective, ni surjective. Or si on restreint l’ensemble de depart def a R+, et on modifie l’ensemble d’arrivee de R a R+, on obtient que lafonctiong : R+ →R+x 7→x2.est bijective. Le changement de l’ensembles de depart et d’arriveed’une application peut modifier la propriete d’ˆetre bijective.N. Arancibia - relu par D. CransacAlgebre
Page 30 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Definition Bijection ReciproqueSoit f : E →F une application. On appelle reciproque de f touteapplication g : F →E pour laquelleg ◦f = IdEetf ◦g = IdF.Remarque : Les identites : x E, g ◦f x = x et y F, f ◦gy = yexpriment l’idee que g defait le travail que f opere et vice versa.TheoremeSoit f : E →F une application. Alorsf est bijective de E sur F si et seulement si f possede une reciproque.Une telle reciproque est alors unique, appelee la reciproque de f et noteef 1. Pour tous x E et y F on af 1y = x⇐⇒y = f x.N. Arancibia - relu par D. CransacAlgebre
Page 31 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Remarque : Si f : E →F est une application bijective. Alors son applicationreciproque f 1 est l’unique application de F dans E, qui a tout element de Fassocie son unique antecedent par f . C’est-a-diref 1 : F →Ey 7→f 1y = l’unique antecedent de y par f .Exemples :L’application IdE est bijective de E sur E de reciproque elle-mˆeme. EneffetIdE ◦IdE = IdE.Soient a Ret b R. La fonction x 7→ax + best bijective.Pour trouver sa reciproque, notons quey = ax + b⇐⇒y ba= x.Par consequent, la reciproque de ax + b est x 7→xba .N. Arancibia - relu par D. CransacAlgebre
Page 32 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.Etudions certaines proprietes des fonctions bijectives.PropositionOn considere deux applications f : E →F et g : F →G.Si g ◦f est bijective, alors f est injective et g est surjective.Si f et g sont bijectives, alors g ◦f est bijective et on ag ◦f 1 = f 1 ◦g 1.Si f est une bijection de E dans F, alors sa bijection reciproque f 1 estaussi bijective et :f 11 = f .N. Arancibia - relu par D. CransacAlgebre
Page 33 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.En pratique, comment montrer concretement qu’une application f : E →F est bijective ?Le tableau suivant, resume la marche a suivre.PrioriteCe qu’on faitCe qu’on obtient1Si on connaˆıt spontanement une expression expli-cite de f 1, on appelle g la fonction en questionet on verifie simplement que :g ◦f = IdEetf ◦g = IdF .Bijectivite + Reciproque2Si on ne connaˆıt pas spontanement f 1, on peutessayer d’en trouver une expression explicite vial’equivalence :y = f x⇐⇒x = f 1y.Bijectivite + Reciproque3Si on ne se sent pas capable de trouver une ex-pression explicite de f 1, on montre en deuxtemps que f est a la fois injective et surjective.BijectiveN. Arancibia - relu par D. CransacAlgebre
Page 34 : IntroductionLogique et RaisonnementEnsembleRelations BinairesApplicationsInjections-Surjections-Bijections.C’est important de ne pas confondre l’application reciproque avec l’imagereciproquef 1 : PE →PEqui existe mˆeme lorsque f n’est pas bijective. Quand l’application estbijective, nous avons la suivant relation entre l’image reciproque de f etl’image directe de f 1.PropositionSoit f une bijection de E sur F et B une partie de F. Alorsf 1B = f 1Bouf 1B a gauche correspond a l’image reciproque de B par f .f 1B a droite correspond a l’image directe de B par f 1.N. Arancibia - relu par D. CransacAlgebre
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34