CM4 Equations Diff

Télécharger le CM4 Equations Diff en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191

Page 1 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsEquations Différentielles1Généralités2Equations différentielles du premier ordreDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes3Équation différentielle linéaire du second ordre à coefficientsconstantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesD. CransacAnalyse

Page 2 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralités sur les équationsdifférentiellesD. CransacAnalyse

Page 3 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsIntroductionDéfinitionSoit une fonctionf : Rn+1 →ROn note y les fonctions définies de R dans R, n fois dérivables.On définit l’équation différentiellef y, y ′, . . . , y n, t = 0ED. CransacAnalyse

Page 4 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsIntroductionDéfinitionSoit une fonctionf : Rn+1 →ROn note y les fonctions définies de R dans R, n fois dérivables.On définit l’équation différentiellef y, y ′, . . . , y n, t = 0EDéfinitionUn équation différentielle E est d’ordre n N lorsque n est le plus petitentier naturel telle qu’il existe une fonction f : Rn+1 →Rtelle que E peut s’écriref y, y ′, . . . , y n, t = 0D. CransacAnalyse

Page 5 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionRésoudre une équation différentielle c’est déterminer l’ensemble desfonctions y dérivables n fois sur I qui vérifient cette équation.On les nomme solutions de l’équation.D. CransacAnalyse

Page 6 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionRésoudre une équation différentielle c’est déterminer l’ensemble desfonctions y dérivables n fois sur I qui vérifient cette équation.On les nomme solutions de l’équation.D. CransacAnalyse

Page 7 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionRésoudre une équation différentielle c’est déterminer l’ensemble desfonctions y dérivables n fois sur I qui vérifient cette équation.On les nomme solutions de l’équation.Exemples :E1y ′′ 2x2 + 1y ′ + y 2 = xexUne fonction f est solution de E1 différentielle si et seulement si :x R,f ′′x 2x2 + 1f ′x + f x2 = xexD. CransacAnalyse

Page 8 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :D. CransacAnalyse

Page 9 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.D. CransacAnalyse

Page 10 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex2D. CransacAnalyse

Page 11 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xD. CransacAnalyse

Page 12 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = xD. CransacAnalyse

Page 13 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = x2f x = 2ex cosx3 pour l’équation différentielle :y ′′ + 2y ′ + 4y = 0D. CransacAnalyse

Page 14 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = x2f x = 2ex cosx3 pour l’équation différentielle :y ′′ + 2y ′ + 4y = 0f ′x = 2excosx3 3 sinx3D. CransacAnalyse

Page 15 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = x2f x = 2ex cosx3 pour l’équation différentielle :y ′′ + 2y ′ + 4y = 0f ′x = 2excosx3 3 sinx3f ′′x = 2excosx3 +3 sinx3 +3 sinx3 3 cosx3=D. CransacAnalyse

Page 16 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = x2f x = 2ex cosx3 pour l’équation différentielle :y ′′ + 2y ′ + 4y = 0f ′x = 2excosx3 3 sinx3f ′′x = 2excosx3 +3 sinx3 +3 sinx3 3 cosx3= 2ex2 cosx3 + 23 sinx3D. CransacAnalyse

Page 17 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsVérifions que les fonctions suivantes sont solutions des équationsdifférentielles indiquées :1f x = 3ex2 + 12 pour l’équation différentielle : y ′ + 2xy = x.f ′x = 32xex2 = 6xex22xf x = 6xex2 + xOn vérifie bien que : f ′x + 2xf x = x2f x = 2ex cosx3 pour l’équation différentielle :y ′′ + 2y ′ + 4y = 0f ′x = 2excosx3 3 sinx3f ′′x = 2excosx3 +3 sinx3 +3 sinx3 3 cosx3= 2ex2 cosx3 + 23 sinx3On vérifie que l’on a bien :f ′′x + 2f ′x + 4f x = 0D. CransacAnalyse

Page 18 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentiellesdu premier ordreD. CransacAnalyse

Page 19 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionsD. CransacAnalyse

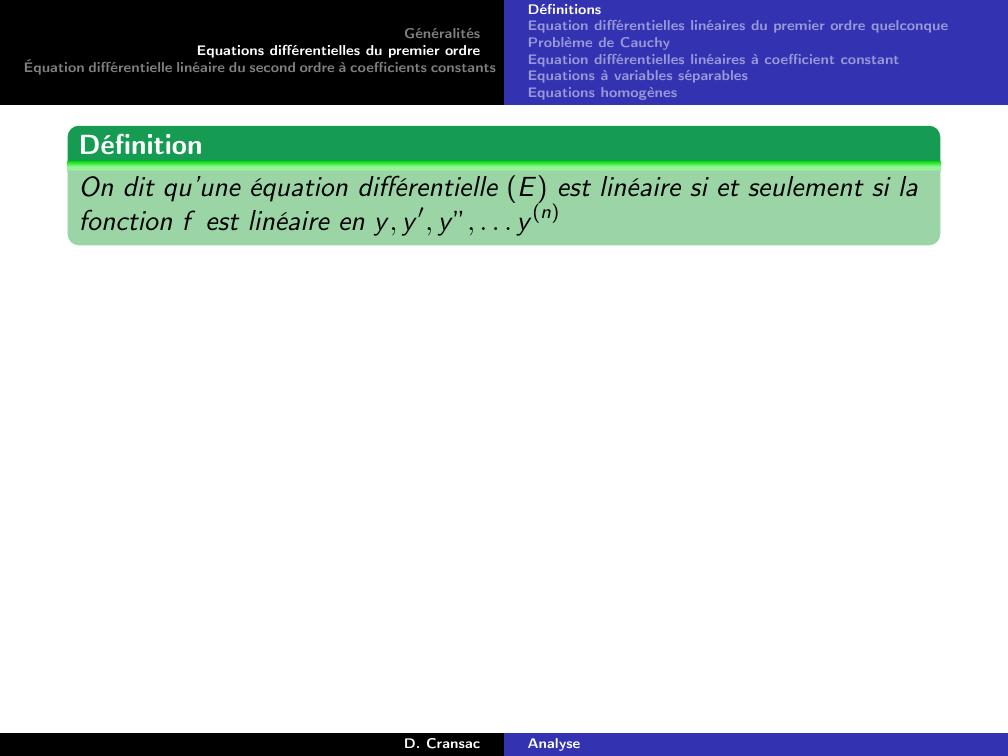
Page 20 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionOn dit qu’une équation différentielle E est linéaire si et seulement si lafonction f est linéaire en y, y ′, y”, . . . y nD. CransacAnalyse

Page 21 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionOn dit qu’une équation différentielle E est linéaire si et seulement si lafonction f est linéaire en y, y ′, y”, . . . y nDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.On appelle équation différentielle linéaire du premier ordre ou d’ordre 1l’équation :y ′ + atyt = btD. CransacAnalyse

Page 22 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionOn dit qu’une équation différentielle E est linéaire si et seulement si lafonction f est linéaire en y, y ′, y”, . . . y nDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.On appelle équation différentielle linéaire du premier ordre ou d’ordre 1l’équation :y ′ + atyt = btRemarqueD. CransacAnalyse

Page 23 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionOn dit qu’une équation différentielle E est linéaire si et seulement si lafonction f est linéaire en y, y ′, y”, . . . y nDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.On appelle équation différentielle linéaire du premier ordre ou d’ordre 1l’équation :y ′ + atyt = btRemarqueSoit f une solution de E sur I, f est C 1 sur I.En effet f ′t = atf t + btD. CransacAnalyse

Page 24 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionOn dit qu’une équation différentielle E est linéaire si et seulement si lafonction f est linéaire en y, y ′, y”, . . . y nDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.On appelle équation différentielle linéaire du premier ordre ou d’ordre 1l’équation :y ′ + atyt = btRemarqueSoit f une solution de E sur I, f est C 1 sur I.En effet f ′t = atf t + btSi on a une équation de type αty ′t + βtyt = γt, on peutla ramener à une équation linéaire du premier ordre en travaillantdans une intervalle où α ne s’annule pas et en divisant par αt.D. CransacAnalyse

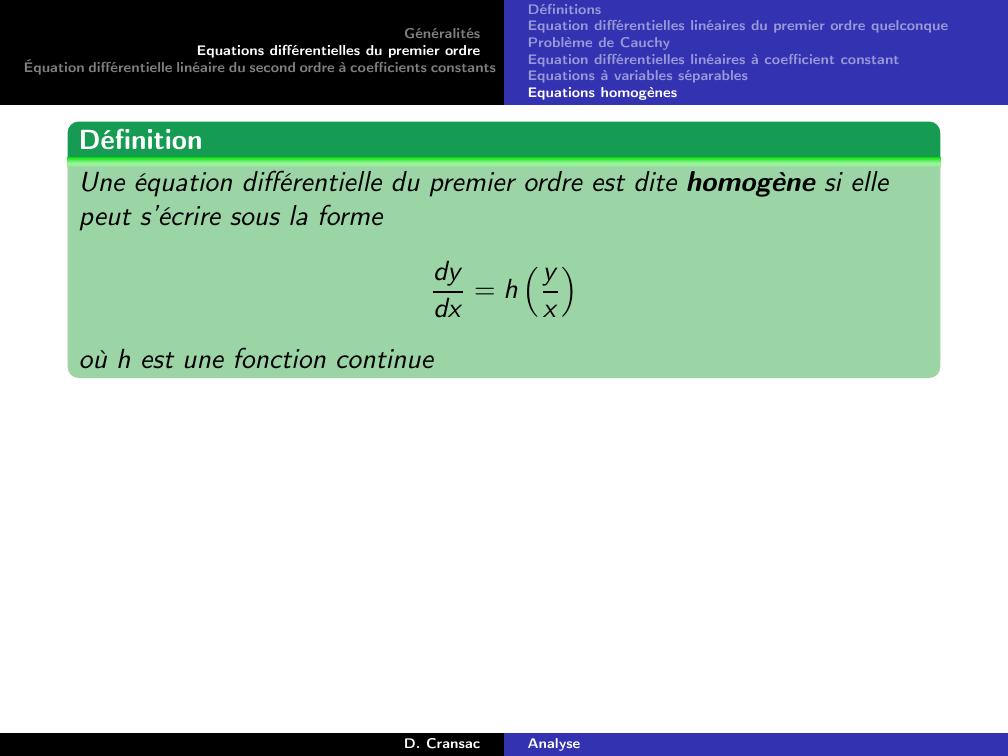
Page 25 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.Soit l’équation différentielleEy ′ + aty = btOn appelle équation différentielle homogène associée à E l’équationobtenue en remplaçant le second membre par 0 dans l’équation E :Ey ′ + aty = 0D. CransacAnalyse

Page 26 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionSoient I un intervalle de R, a et b : I →K des fonctions continues.Soit l’équation différentielleEy ′ + aty = btOn appelle équation différentielle homogène associée à E l’équationobtenue en remplaçant le second membre par 0 dans l’équation E :Ey ′ + aty = 0Attention Ne pas confondre équation différentielle homogène sansprécision : yx et équation différentielle homogène associée à ED. CransacAnalyse

Page 27 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentiellesdu premier ordreà coefficients constantsD. CransacAnalyse

Page 28 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionPour toute équation différentielle linéaire homogène, la combinaisonlinéaire de deux solutions de l’équation est également solution del’équation.C’est à diref et g solution de E, λ, µ R2λf + µg est solution de ED. CransacAnalyse

Page 29 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRésolution des équations homogènesPropositionSoit une équation linéaire homogène :Ey ′ + axy = 0avec a fonction continue sur un intervalle IL’ensemble des solutions de cette équation estnf /x I, f x = λeR xx0 atdt, λ RoD. CransacAnalyse

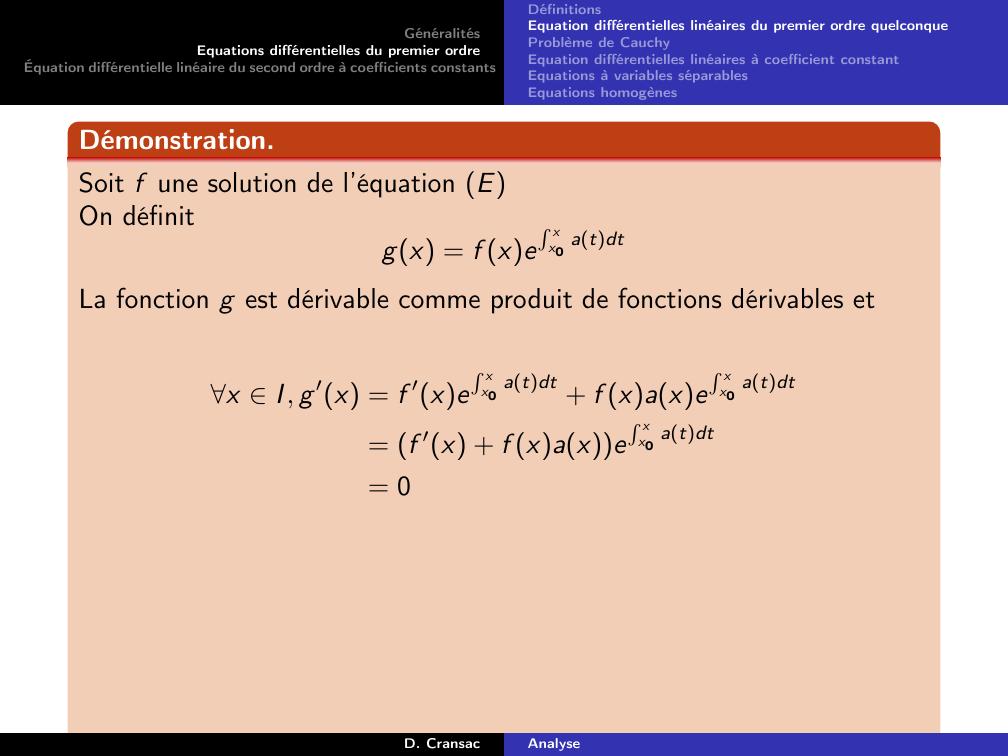
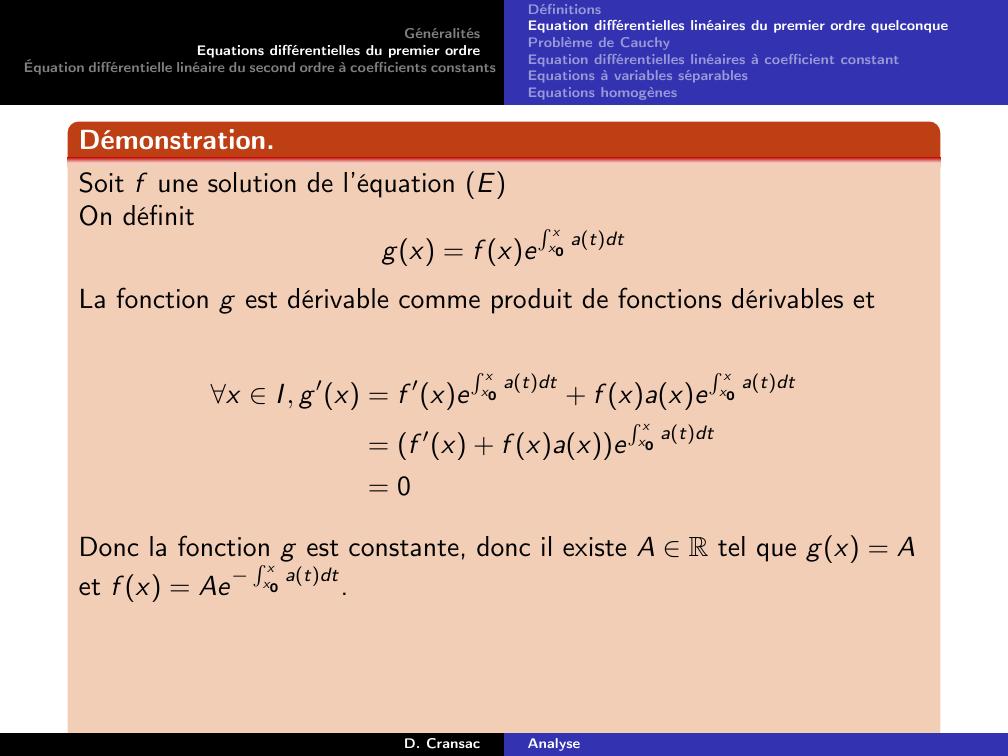
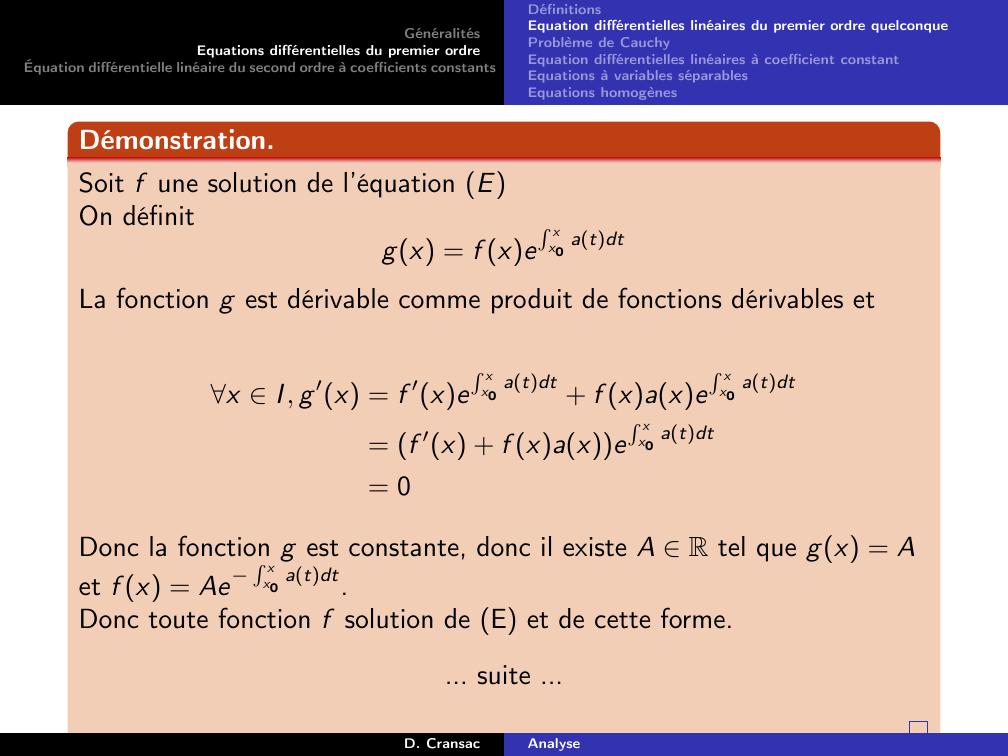
Page 30 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit f une solution de l’équation EOn définitgx = f xeR xx0 atdtD. CransacAnalyse

Page 31 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit f une solution de l’équation EOn définitgx = f xeR xx0 atdtLa fonction g est dérivable comme produit de fonctions dérivables etD. CransacAnalyse

Page 32 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit f une solution de l’équation EOn définitgx = f xeR xx0 atdtLa fonction g est dérivable comme produit de fonctions dérivables etx I, g ′x = f ′xeR xx0 atdt + f xaxeR xx0 atdt= f ′x + f xaxeR xx0 atdt= 0D. CransacAnalyse

Page 33 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit f une solution de l’équation EOn définitgx = f xeR xx0 atdtLa fonction g est dérivable comme produit de fonctions dérivables etx I, g ′x = f ′xeR xx0 atdt + f xaxeR xx0 atdt= f ′x + f xaxeR xx0 atdt= 0Donc la fonction g est constante, donc il existe A R tel que gx = Aet f x = AeR xx0 atdt.D. CransacAnalyse

Page 34 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit f une solution de l’équation EOn définitgx = f xeR xx0 atdtLa fonction g est dérivable comme produit de fonctions dérivables etx I, g ′x = f ′xeR xx0 atdt + f xaxeR xx0 atdt= f ′x + f xaxeR xx0 atdt= 0Donc la fonction g est constante, donc il existe A R tel que gx = Aet f x = AeR xx0 atdt.Donc toute fonction f solution de E et de cette forme.... suite ...D. CransacAnalyse

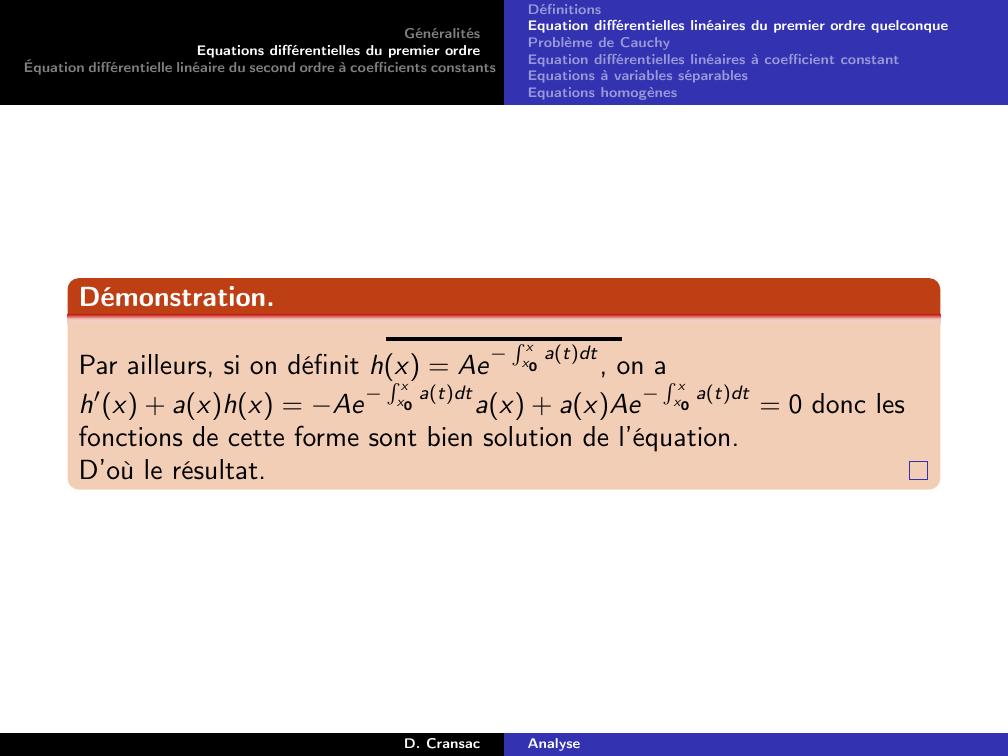
Page 35 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Par ailleurs, si on définit hx = AeR xx0 atdt, on ah′x + axhx = AeR xx0 atdtax + axAeR xx0 atdt = 0 donc lesfonctions de cette forme sont bien solution de l’équation.D’où le résultat.D. CransacAnalyse

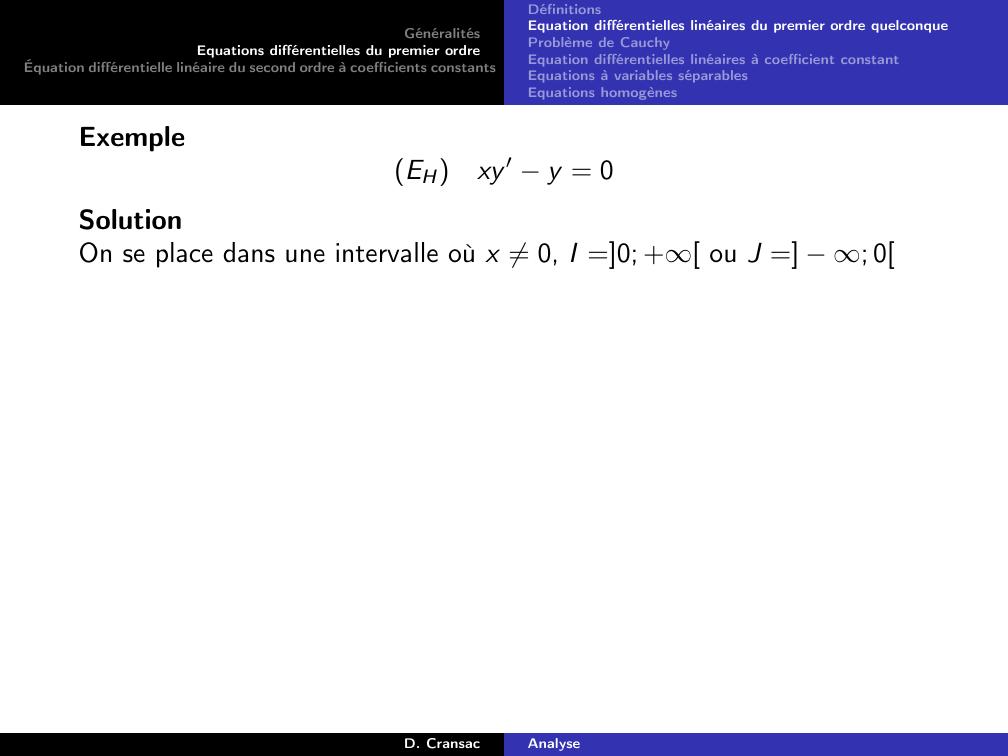
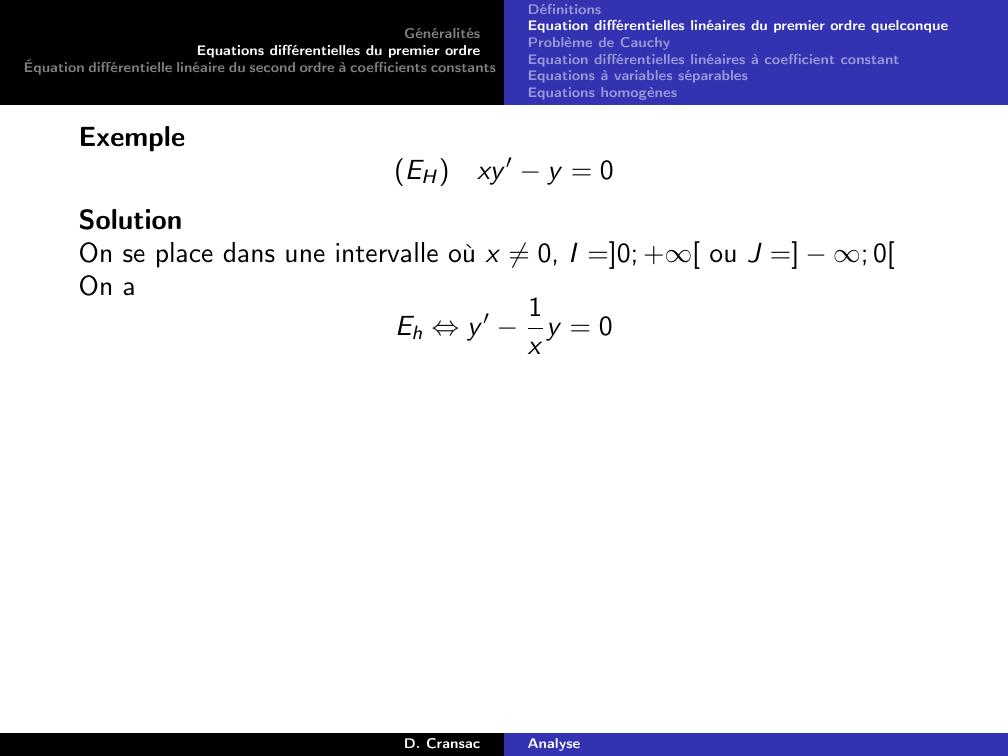
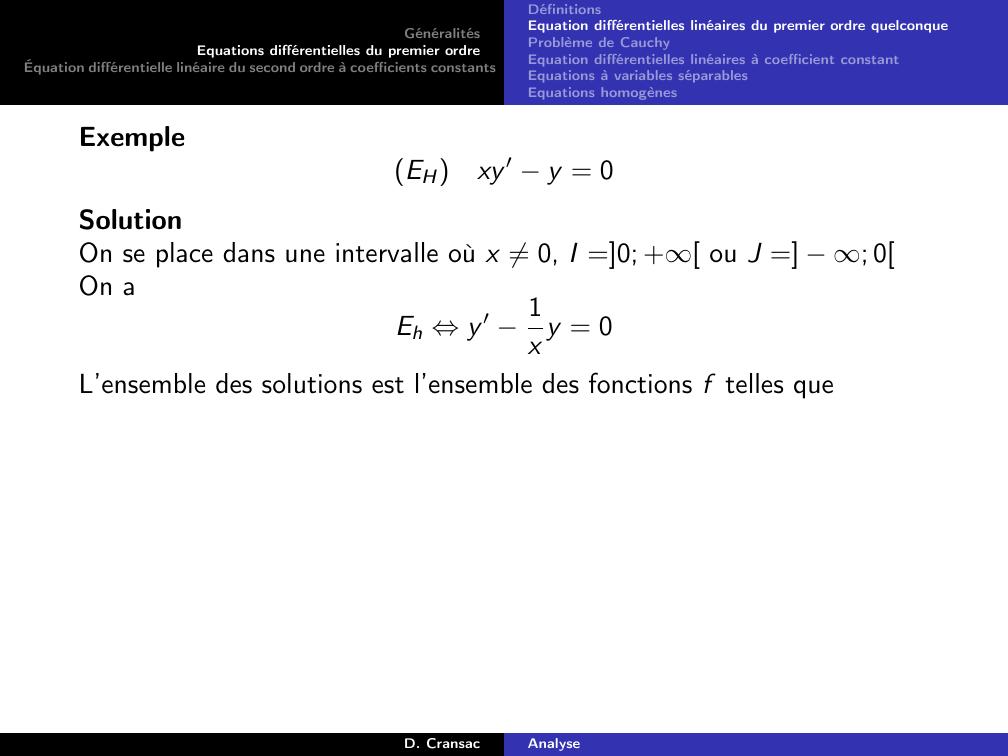
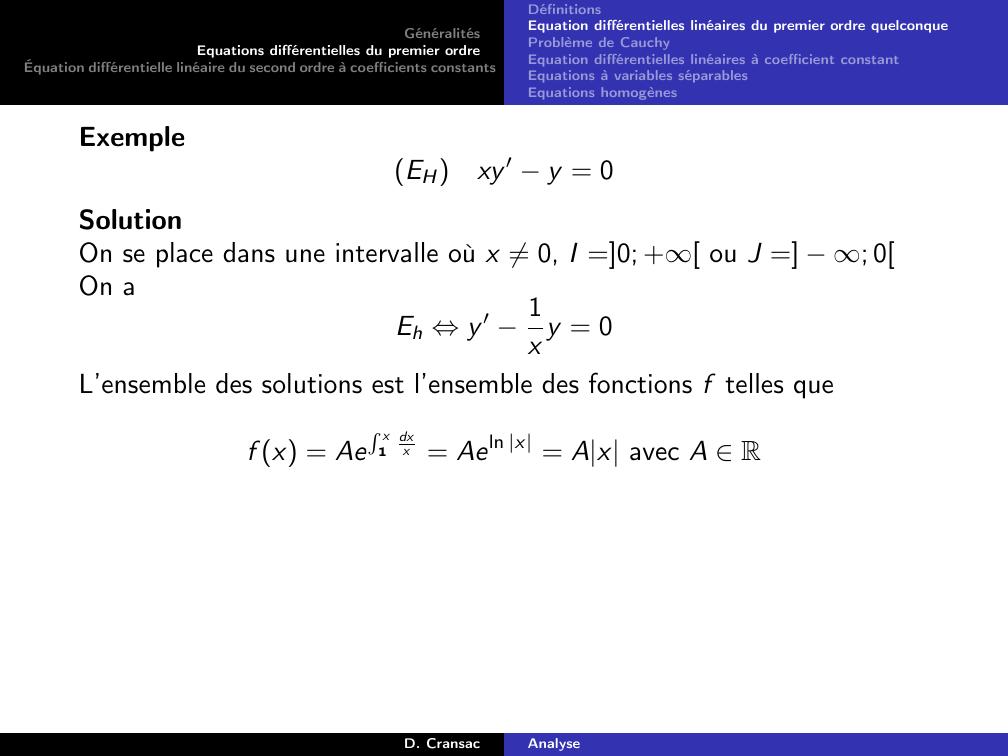
Page 36 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0D. CransacAnalyse

Page 37 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0D. CransacAnalyse

Page 38 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0D. CransacAnalyse

Page 39 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles queD. CransacAnalyse

Page 40 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RD. CransacAnalyse

Page 41 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RConstruction des solutions sur RD. CransacAnalyse

Page 42 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.D. CransacAnalyse

Page 43 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur ; 0, f x = Bx et sur 0; +, f x = Ax.D. CransacAnalyse

Page 44 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur ; 0, f x = Bx et sur 0; +, f x = Ax.Pour que la fonction soit de classe C 1 il faut et il suffit que A = B.D. CransacAnalyse

Page 45 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEHxy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 1x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dxx = Aeln x = Ax avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur ; 0, f x = Bx et sur 0; +, f x = Ax.Pour que la fonction soit de classe C 1 il faut et il suffit que A = B.Donc l’ensemble des solutions de l’équation E est l’ensemble desfonctions linéaires.D. CransacAnalyse

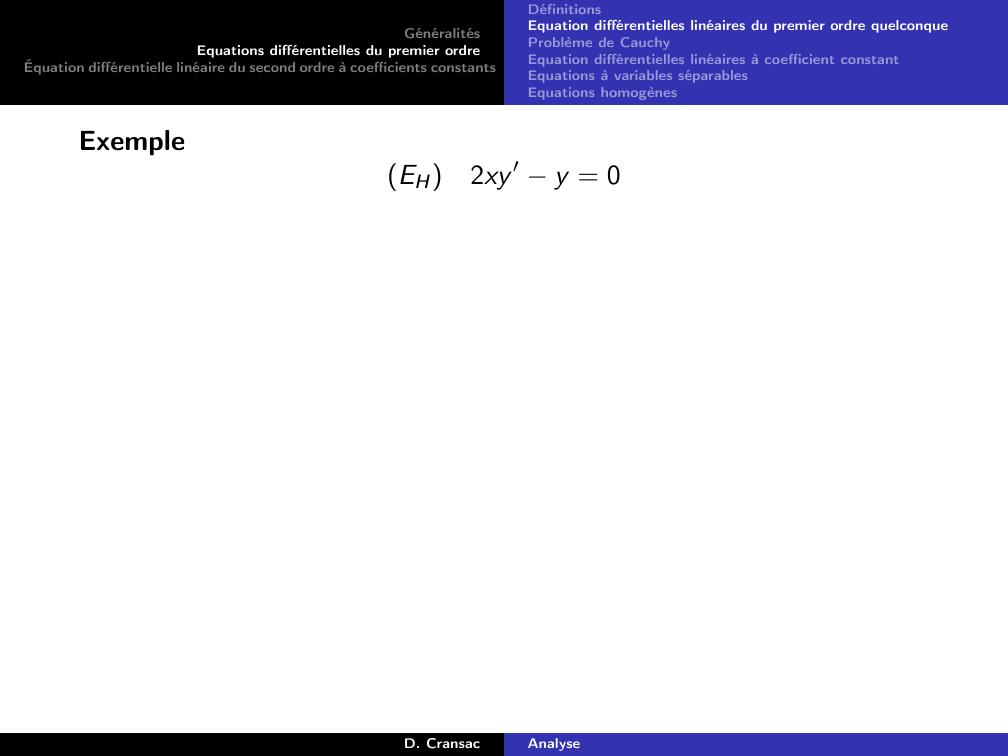
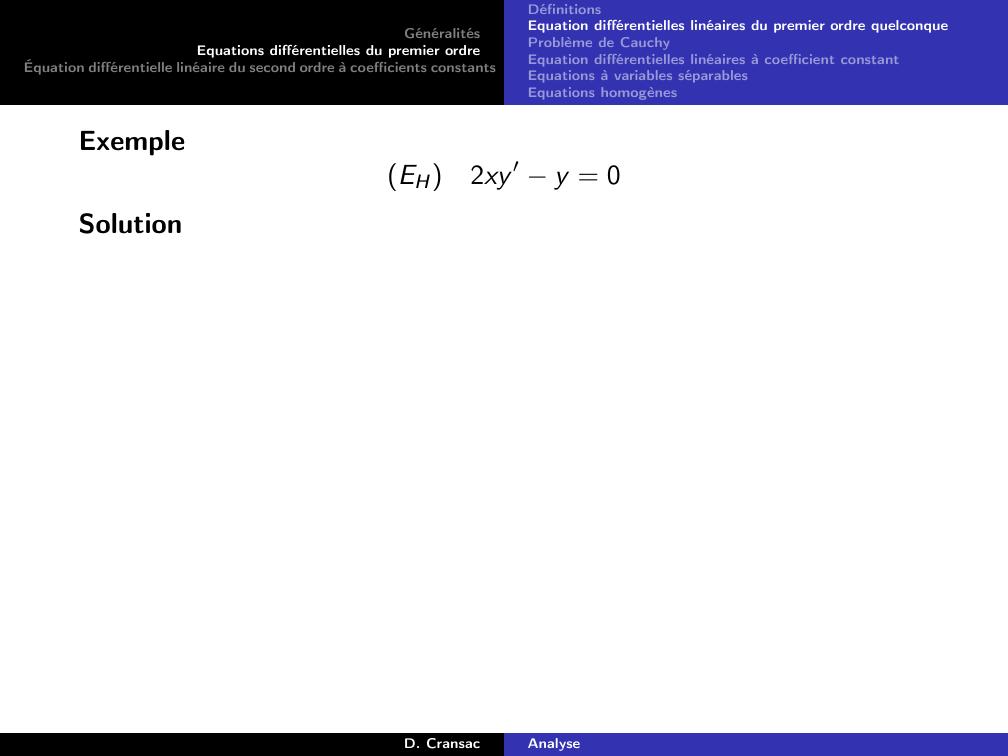
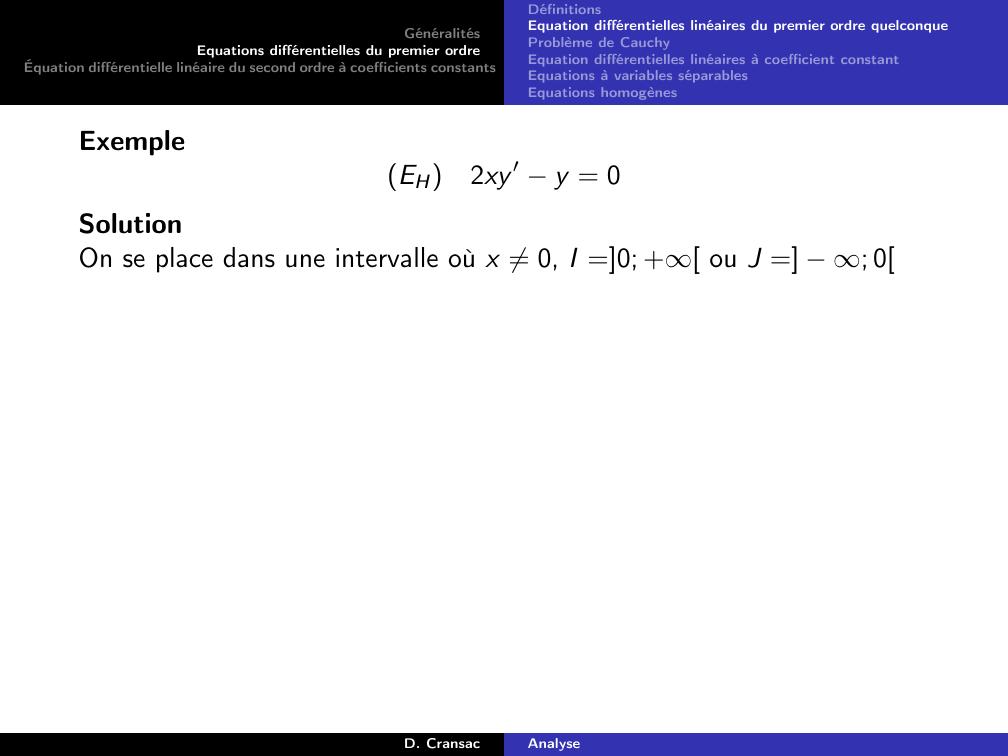
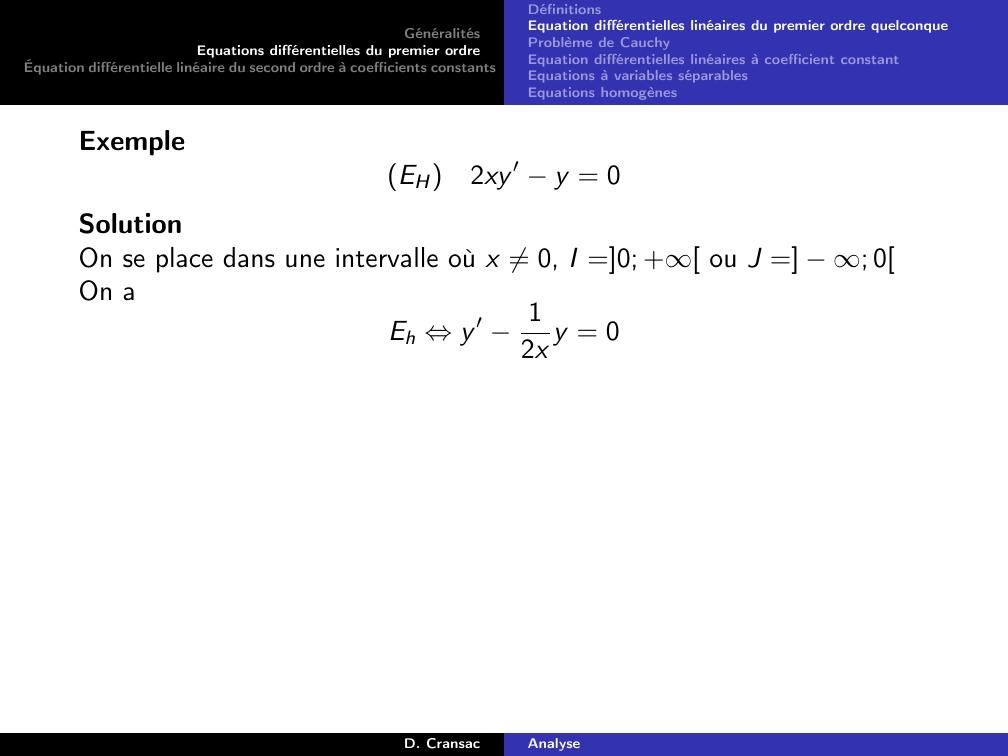
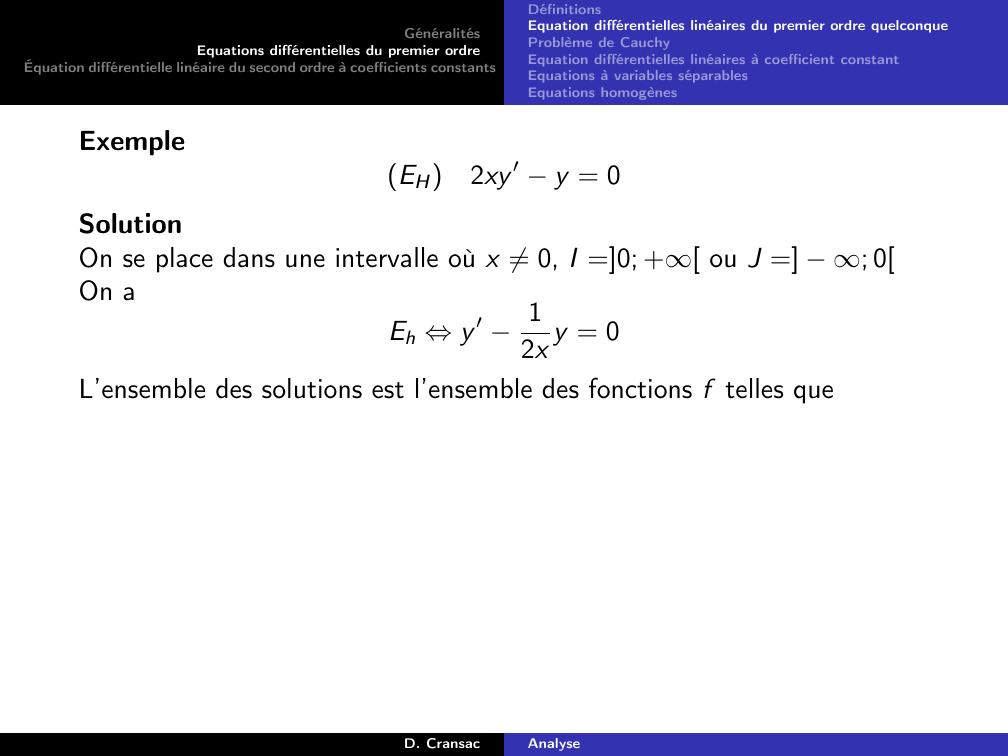
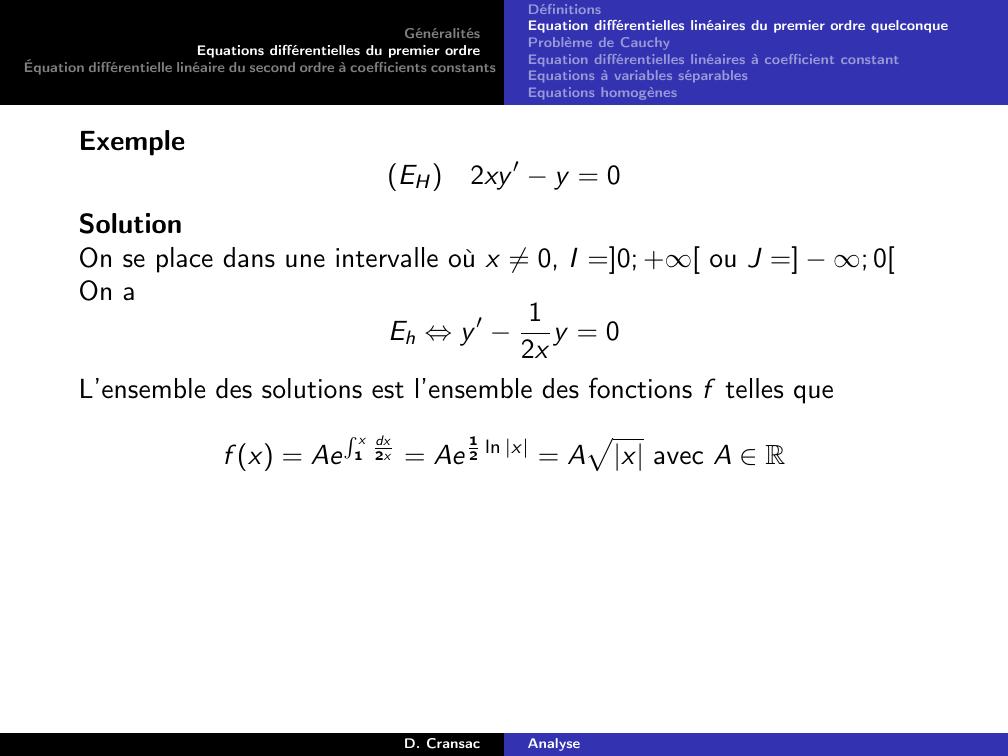
Page 46 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0D. CransacAnalyse

Page 47 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionD. CransacAnalyse

Page 48 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0D. CransacAnalyse

Page 49 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0D. CransacAnalyse

Page 50 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles queD. CransacAnalyse

Page 51 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RD. CransacAnalyse

Page 52 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RConstruction des solutions sur RD. CransacAnalyse

Page 53 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.D. CransacAnalyse

Page 54 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur 0; +, f x = Ax.Si A ̸= 0, cette fonction est prolongeable par continuité en 0 mais lafonction obtenue n’est pas dérivable.D. CransacAnalyse

Page 55 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur 0; +, f x = Ax.Si A ̸= 0, cette fonction est prolongeable par continuité en 0 mais lafonction obtenue n’est pas dérivable. Donc il n’y a pas de solution sur R.D. CransacAnalyse

Page 56 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleEH2xy ′ y = 0SolutionOn se place dans une intervalle où x ̸= 0, I =0; + ou J = ; 0On aEh ⇔y ′ 12x y = 0L’ensemble des solutions est l’ensemble des fonctions f telles quef x = AeR x1dx2x = Ae12 ln x = Apx avec A RConstruction des solutions sur ROn veut définir une fonction f sur R qui est de classe C 1.On a donc sur 0; +, f x = Ax.Si A ̸= 0, cette fonction est prolongeable par continuité en 0 mais lafonction obtenue n’est pas dérivable. Donc il n’y a pas de solution sur R.L’unique solution est donc la fonction nulle.D. CransacAnalyse

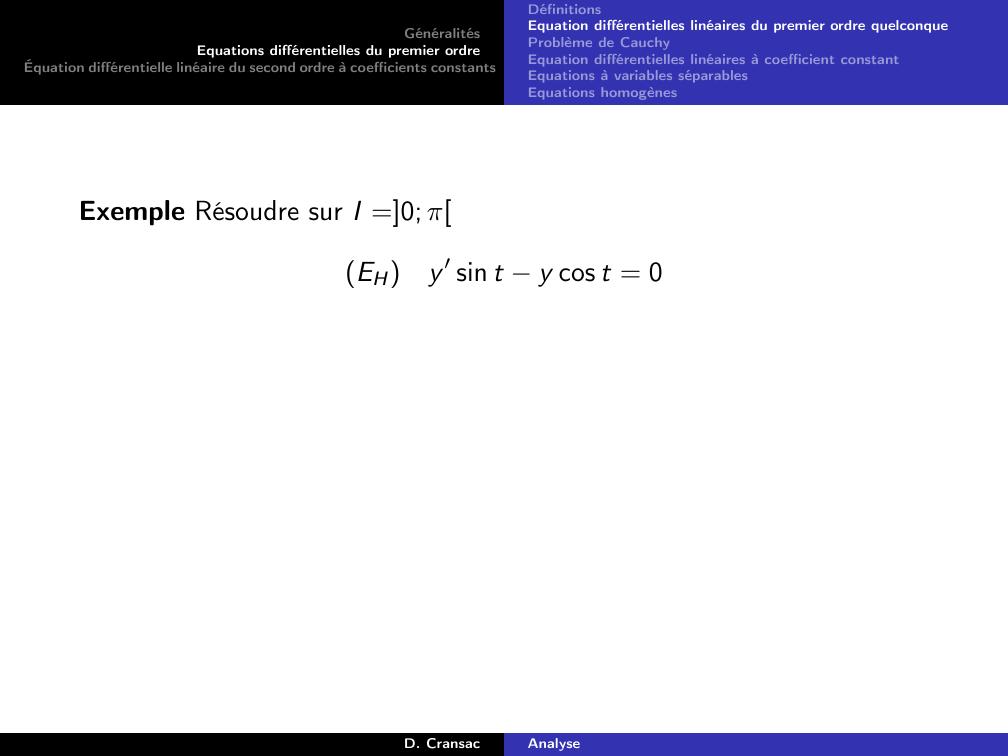
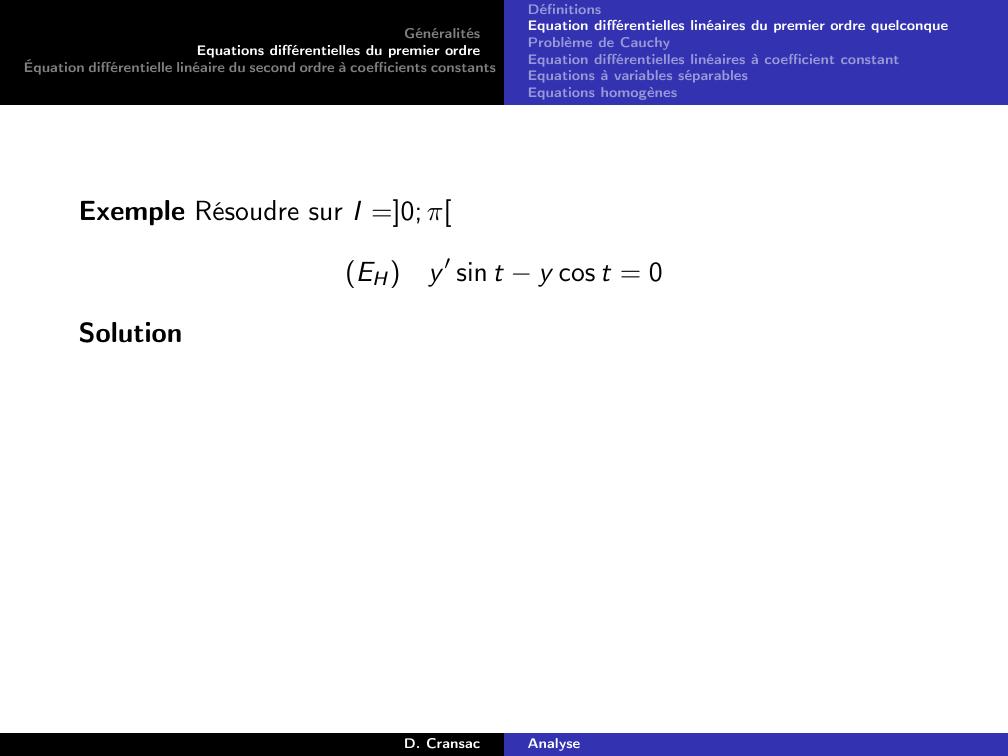
Page 57 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre sur I =0; πEHy ′ sin t y cos t = 0D. CransacAnalyse

Page 58 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre sur I =0; πEHy ′ sin t y cos t = 0SolutionD. CransacAnalyse

Page 59 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre sur I =0; πEHy ′ sin t y cos t = 0SolutionLa fonction sin ne s’annule par sur I donc l’équation revient àD. CransacAnalyse

Page 60 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre sur I =0; πEHy ′ sin t y cos t = 0SolutionLa fonction sin ne s’annule par sur I donc l’équation revient ày ′ cos xsin x y = 0D. CransacAnalyse

Page 61 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre sur I =0; πEHy ′ sin t y cos t = 0SolutionLa fonction sin ne s’annule par sur I donc l’équation revient ày ′ cos xsin x y = 0Donc les solutions sontf t = AeR xπ2cos tsin t dt = Aeln sin t = A sin t avec A RD. CransacAnalyse

Page 62 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoit une équation différentielle linéaireEy ′ + axy = bxavec a et b fonctions continues sur un intervalle ISoit yP une solution de l’équation E, alorsyH est une solution de l’équation homogène E0 associée à Esi et seulement si yH + yP est une solution de l’équation ED. CransacAnalyse

Page 63 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoit une équation différentielle linéaireEy ′ + axy = bxavec a et b fonctions continues sur un intervalle ISoit yP une solution de l’équation E, alorsyH est une solution de l’équation homogène E0 associée à Esi et seulement si yH + yP est une solution de l’équation EDémonstration.yH solution de E0 ⇔y ′H + ayH = 0⇔y ′H + axyH + y ′P + axyP = bx⇔y ′H + y ′P + axyH + axyP = bx⇔yH + yP′ + axyH + yP = bx⇔yH + yP solution de ED. CransacAnalyse

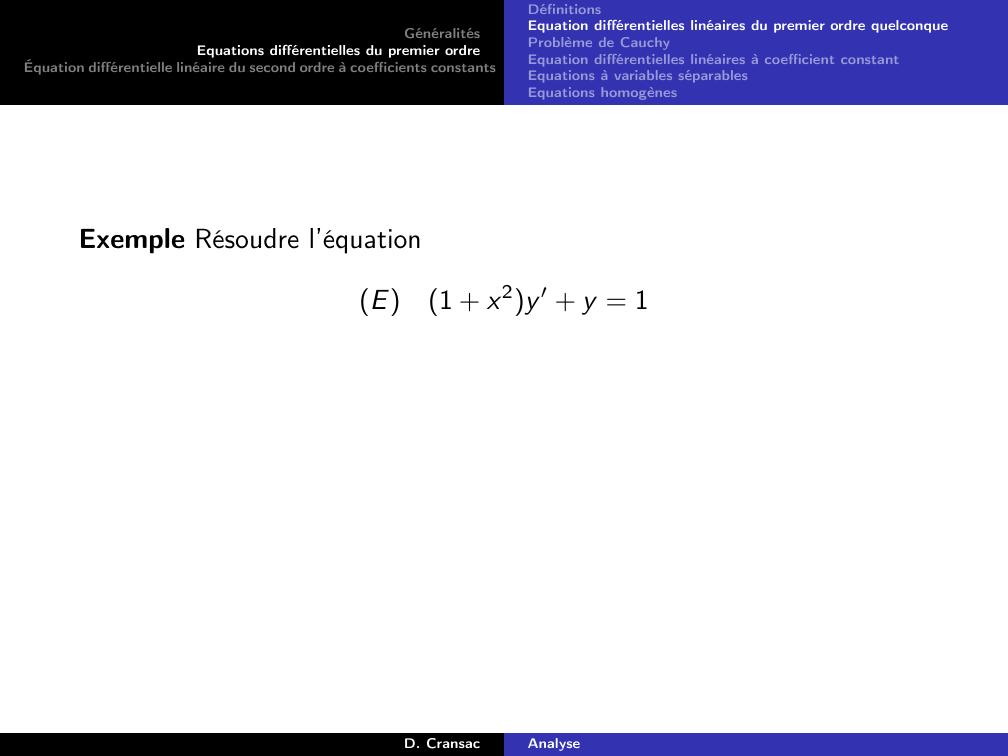
Page 64 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1D. CransacAnalyse

Page 65 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1SolutionD. CransacAnalyse

Page 66 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1SolutionLa solution de l’equation homogène est x 7→λearctan x, λ RD. CransacAnalyse

Page 67 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1SolutionLa solution de l’equation homogène est x 7→λearctan x, λ RLa solution constante x 7→1 est une solution particulière évidente doncD. CransacAnalyse

Page 68 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1SolutionLa solution de l’equation homogène est x 7→λearctan x, λ RLa solution constante x 7→1 est une solution particulière évidente doncL’ensemble des solutions de l’équation est l’ensemble des fonctions :D. CransacAnalyse

Page 69 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple Résoudre l’équationE1 + x2y ′ + y = 1SolutionLa solution de l’equation homogène est x 7→λearctan x, λ RLa solution constante x 7→1 est une solution particulière évidente doncL’ensemble des solutions de l’équation est l’ensemble des fonctions :x 7→1 + λearctan xλ RD. CransacAnalyse

Page 70 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoient a, b1, b2 : I →K des fonctions continues.Si f1 est solution sur I de y ′ + aty = b1t et f2 est solution sur I dey ′ + aty = b2t alors pour tout λ, µ K, λf1 + µf2 est solution sur I dey ′ + aty = λb1 + µb2D. CransacAnalyse

Page 71 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoient a, b1, b2 : I →K des fonctions continues.Si f1 est solution sur I de y ′ + aty = b1t et f2 est solution sur I dey ′ + aty = b2t alors pour tout λ, µ K, λf1 + µf2 est solution sur I dey ′ + aty = λb1 + µb2RemarqueCette proposition peut être utile dans la pratique : pour résoudre uneéquation différentielle linéaire, on peut éventuellement scinder le secondmembre afin de se ramener à plusieurs équations différentielles dont lesseconds membres seront plus simples à traiter.D. CransacAnalyse

Page 72 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesProblème de CauchyDéfinitionÉtant données deux fonctions a et b continues sur un intervalle I et àvaleurs dans K, on considère l’équation différentielleE :y ′ + aty = bt.Le problème de Cauchy associé au couple t0, y0 où t0 I, y0 K estla recherche des solutions y de E vérifiant la condition initiale oucondition de Cauchy y t0 = y0.PropositionOn considère deux fonctions a et b continues sur un intervalle I et à valeursdans K, on considère l’équation différentielley ′ + aty = bt.Pour t0, y0 I × K, le problème de Cauchy associé à la condition initialey t0 = y0 admet une unique solution sur I.D. CransacAnalyse

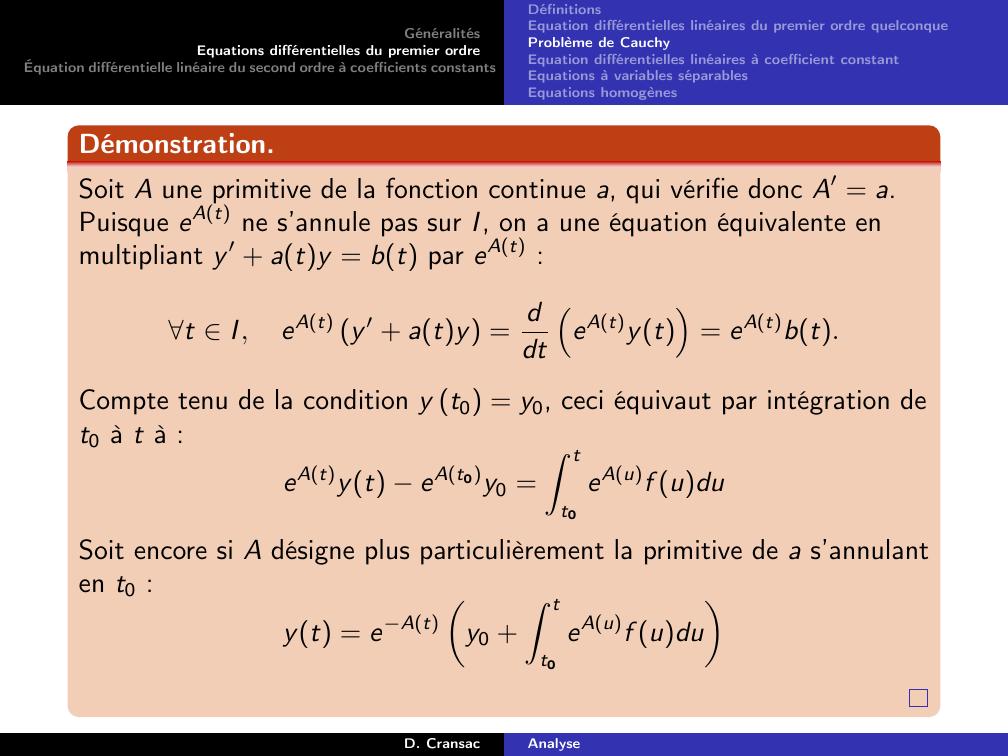
Page 73 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Soit A une primitive de la fonction continue a, qui vérifie donc A′ = a.Puisque eAt ne s’annule pas sur I, on a une équation équivalente enmultipliant y ′ + aty = bt par eAt :t I,eAt y ′ + aty = ddteAtyt= eAtbt.Compte tenu de la condition y t0 = y0, ceci équivaut par intégration det0 à t à :eAtyt eAt0y0 =Z tt0eAuf uduSoit encore si A désigne plus particulièrement la primitive de a s’annulanten t0 :yt = eAty0 +Z tt0eAuf uduD. CransacAnalyse

Page 74 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRemarque On a montré en particulier dans la preuve de ce résultat quetoute solution de E est bien de la forme t 7→λteAt, ce qui justifiela méthode de variation de la constante.Exemple. Résoudre y ′ 12x y = x sur I = R+, avec pour conditioninitiale y1 = 1.Solution Il s’agit d’une équation linéaire du première ordre à coefficientcontinus sur I.La solution générale de son équation homogène associée est doncx 7→λ exp12 ln x= λx, λ R.Par la méthode de la variation de la constante, on cherche une solutionparticulière de E sous la forme x 7→λxx, avec λ dérivable sur I.En reportant dans l’équation, il vient λ′xx = x donc λ′x = 1 puis onpeut prendre λ : x 7→x et une solution particulière de E est x 7→xx.La solution générale de E est donc x 7→λ + xx, λ R.Pour trouver l’unique solution du problème considéré, il faut résoudrel’équation λ + 1 = 1 i.e. λ = 0.Ainsi la solution du problème de Cauchy considéré est x 7→xx.D. CransacAnalyse

Page 75 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionOn considère deux fonctions a et b continues sur un intervalle I et àvaleurs dans R, on considère l’équation différentielley ′ + aty = bt.Une seule courbe intégrale définie sur I passe par tout pointt0, y0 I × R.D. CransacAnalyse

Page 76 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionOn considère deux fonctions a et b continues sur un intervalle I et àvaleurs dans R, on considère l’équation différentielley ′ + aty = bt.Une seule courbe intégrale définie sur I passe par tout pointt0, y0 I × R.Deux telles courbes intégrales distinctes ne peuvent se couper dansI × R.D. CransacAnalyse

Page 77 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.Le premier point est une reformulation du résultat précédent.Montrons le deuxième point : supposons que deux courbes intégrales secoupent en M0 t0, y0.Notons y1 et y2 les solutions de E sur I correspondantes. Elles sontdonc toutes deux solutions du même problème de Cauchy : Ey t0 = y0Par unicité, on a donc y1 = y2.Remarque. La seule solution de E0 : y ′ + aty = 0 telle quey t0 = 0 est la fonction nulle.En effet, la fonction nulle est solution de E0.Et par la proposition précédente, c’est l’unique solution telle quey t0 = 0.En particulier, la seule solution de E0 qui s’annule est la fonction nulle.D. CransacAnalyse

Page 78 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesOn revient sur le cas des équations différentielles linéaires du premierordre non normalisées :aty ′ + bty = ctoù a, b, c sont continues sur un intervalle I, mais où a est susceptible des’annuler sur I. Nous allons voir sur des exemples que les résultatsprécédents, comme le théorème de Cauchy, peuvent alors tomber endéfaut. Supposons par exemple que a s’annule en un unique point t0 deI. On procèdera alors comme suit.D. CransacAnalyse

Page 79 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesMéthode pour étudier les raccordementsPour résoudre E sur I :On commence par résoudre l’équation sur les intervallesIg = , t0 I et Id = t0, +I où a ne s’annule pas.On cherche ensuite une solution f de E sur I. On remarque que fest solution de E sur Ig.On en connait donc la forme explicite f = fg.De même sur l’intervalle Id, on connait la forme fd de f .La fonction f étant solution de E sur I, la fonctiont I\ t0 7→ fgt si t Igfdt si t Iddoit être :prolongeable par continuité en t0,de classe C1 sur I c’est à dire en t0 solution de l’équation différentielle sur I c’est à dire en t0 .On va voir sur des exemples que ces conditions sont satisfaites danscertains cas, pas dans d’autres.D. CransacAnalyse

Page 80 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de E : ty ′ 2y = t3 sur R.SolutionC’est une équation différentielle linéaire d’ordre un à coefficients variableset continus, non normalisée.On commence par la résoudre sur des intervalles sur lesquels t ̸= 0, soitsur R+ et sur R.On montre alors alors que :SR+ =t →λt2 + t3, λ Ret SR=t →µt2 + t3, µ R.On cherche à présent les solutions de E sur R. Soit f une solution del’équation sur R. Elle est donc solution sur R+ et sur R, et on a :λ R, f t = λt2 + t3 pour tout t 0,µ R, f t = µt2 + t3 pour tout t 0.D. CransacAnalyse

Page 81 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPrenons t = 0 dans l’équation, on obtient : 0 × f ′0 2f 0 = 0, soitf 0 = 0.La fonction f doit être continue et dérivable en 0 . D’où :limx→0+ f t = f 0 = limx→0f tIci on a :limx→0+ λt2 + t3 = 0 etlimx→0µt2 + t3 = 0.Donc cette condition est bien satisfaite pour tout λ, µ R.D. CransacAnalyse

Page 82 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesOn étudie la dérivabilité :limt→0+f t f 0t= limt→0+λt2 + t3t= 0limt→0f t f 0t= limt→0µt2 + t3t= 0Là encore, cette condition est bien satisfaite pour tout λ, µ R.Finalement, on obtient que les solutions de E sur R sont les fonctionsde la forme :t 7→ λt2 + t3 si t 0µt2 + t3 si t 0pour tout λ, µ R.On représente plusieurs de ces solutions :D. CransacAnalyse

Page 83 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRemarque Le problème de CauchyEy0 = 0a donc une infinité desolutions.À l’opposé, le problème de Cauchy Ey0 = 1n’a aucune solution.On voit ici que le théorème de Cauchy tombe en défaut en t = 0, là où lecoefficient t de y ′ s’annule.D. CransacAnalyse

Page 84 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple. Résoudre 1 ty ′ y = t sur R.SolutionC’est une équation différentielle linéaire d’ordre un à coefficients variableset continus, non normalisée.On commence par la résoudre sur des intervalles sur lesquels 1 t ̸= 0,soit sur 1, + et sur , 1.On montre alors alors que :S1,+ =t →λ1 t +t221 t, λ RetS,1 =t →µ1 t +t221 t, λ RD. CransacAnalyse

Page 85 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesOn cherche à présent les solutions de E sur R.Soit f l’une d’elles.On a alors :λ R, f t =λ1 t +t221 t pour tout t 1µ R, f t =µ1 t +t221 t pour tout t 1Prenons t = 1 dans l’équation, on obtient : 0 × f ′1 f 1 = 1, soitf 1 = 1.La fonction f doit être continue et dérivable en 1 :limx→1+λ1 t +t221 t =+si λ 1/2si λ 1/21 si λ = 1/2.Ainsi on a nécessairement λ = 1/2.De même, µ = 1/2. On obtient alors f t = 12 t2 sur R. Enparticulier f est bien dérivable sur R.D. CransacAnalyse

Page 86 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesFinalement, on obtient qu’il y a une unique solutions de E sur R, quiest :t 7→12 t2Le problème de Cauchy Ey1 = 0n’a pas de solution dans ce cas.Le problème de Cauchy Ey1 = 1a pour sa part une uniquesolution.D. CransacAnalyse

Page 87 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentiellesdu premier ordreà coefficient constantD. CransacAnalyse

Page 88 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentielles linéaires à coefficientconstantPropositionSoit une équation différentielle linéaireEy ′ + ay = b avec a R et b RL’ensemble des solutions estf : R →R, λ Rx R, f x = ba + λeaxPour tout x0, y0 R2, il existe une unique solution telle que f x0 = y0D. CransacAnalyse

Page 89 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentielles linéaires à coefficientconstantPropositionSoit une équation différentielle linéaireEy ′ + ay = b avec a R et b RL’ensemble des solutions estf : R →R, λ Rx R, f x = ba + λeaxPour tout x0, y0 R2, il existe une unique solution telle que f x0 = y0Remarque Si b = 0f : R →R, λ Rx R, f x = λeaxD. CransacAnalyse

Page 90 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDémonstration.On cherche une solution particulière constante :0 + af0x = b ⇔f0x = baOn connaît les solutions de l’équation homogène :fHx = λeR xx0 atdt = λeaxOn peut donc conclure que les solutions de l’équation sont f = f0 + fHDonc l’ensemble des solutions est bienf : R →R, λ Rx R, f x = ba + λeaxOn résout f x0 = y0 pour obtenirf x = ba +y0 baeaxx0D. CransacAnalyse

Page 91 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesMéthode de résolution RappelPour résoudreEy ′ + axy = bxavec a et b fonctions continues sur un intervalle Ion procède en général en deux étapes :Etape 1 : on résout l’équation homogène, obtenue en remplaçant lesecond membre par zéro,EHy ′ + axy = 0la solution générale est alors notée yH.Etape 2 : on cherche une solution particulière yP de l’équationinitiale E.La solution générale de E est alors la somme des deux : y = yH + yP.Elle comporte toujours une constante, qui ne peut être déterminée quepar une condition initiale.D. CransacAnalyse

Page 92 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRecherche de solutions particulièresRechercher des solutions particulièresMéthodeIl faut toujours commencer par rechercher d’éventuelles solutionsévidentes par exemple solution constante aisé car dans ce cas :y ′ = 0.D. CransacAnalyse

Page 93 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRecherche de solutions particulièresRechercher des solutions particulièresMéthodeIl faut toujours commencer par rechercher d’éventuelles solutionsévidentes par exemple solution constante aisé car dans ce cas :y ′ = 0.Si l’on n’en trouve pas, on peut toujours utiliser la méthode devariation de la constante :On part de la solution générale de l’équation homogène et onremplace la constante λ par une fonction λx.D. CransacAnalyse

Page 94 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleD. CransacAnalyse

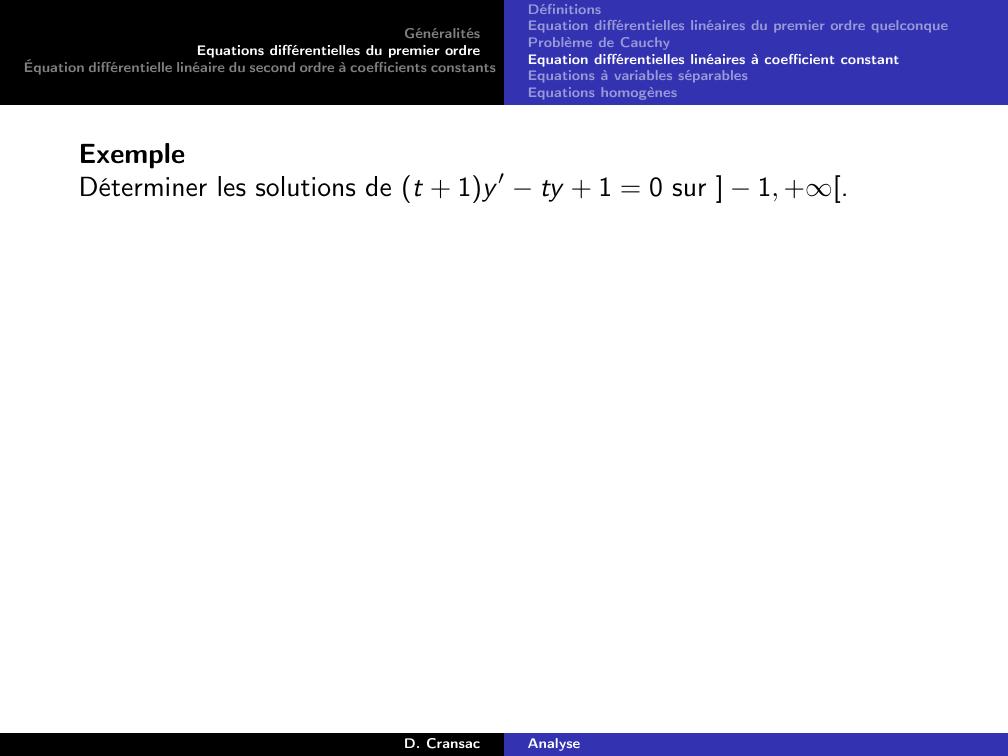
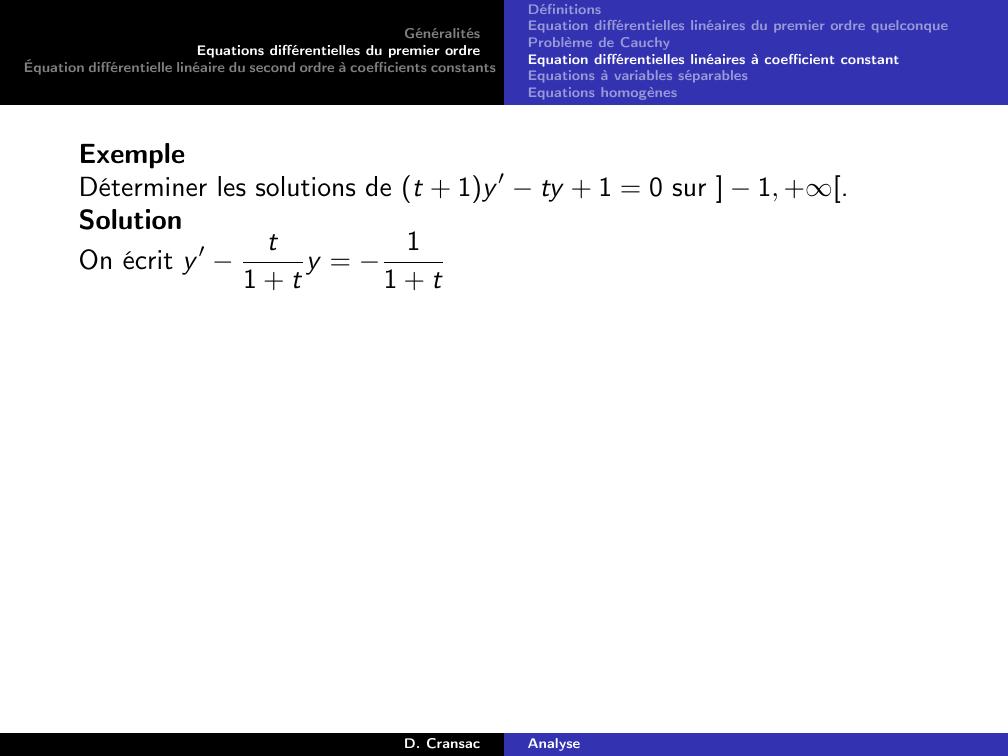
Page 95 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.D. CransacAnalyse

Page 96 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionD. CransacAnalyse

Page 97 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tD. CransacAnalyse

Page 98 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tEquation différentielle homogèneLes solutions de l’équation homogène sont de la forme :D. CransacAnalyse

Page 99 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tEquation différentielle homogèneLes solutions de l’équation homogène sont de la forme :f t = AeR t1 u1+u dt = Aetln1+t = Aet1 + tD. CransacAnalyse

Page 100 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tEquation différentielle homogèneLes solutions de l’équation homogène sont de la forme :f t = AeR t1 u1+u dt = Aetln1+t = Aet1 + tSolution particulièreD. CransacAnalyse

Page 101 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tEquation différentielle homogèneLes solutions de l’équation homogène sont de la forme :f t = AeR t1 u1+u dt = Aetln1+t = Aet1 + tSolution particulièreOn cherche une solution g de la forme gt = Atet1 + tg ′t = A′tett + 1 + Atett + 1 Atett + 12D. CransacAnalyse

Page 102 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleDéterminer les solutions de t + 1y ′ ty + 1 = 0 sur 1, +.SolutionOn écrit y ′ t1 + t y = 11 + tEquation différentielle homogèneLes solutions de l’équation homogène sont de la forme :f t = AeR t1 u1+u dt = Aetln1+t = Aet1 + tSolution particulièreOn cherche une solution g de la forme gt = Atet1 + tg ′t = A′tett + 1 + Atett + 1 Atett + 12donc t + 1g ′t = A′tet + Atet Atett + 1D. CransacAnalyse

Page 103 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesOn a obtenut + 1g ′t = A′tet + Atet Atett + 1On a donc t + 1g ′t tgt + 1= A′tet + Atet Atett + 1 tAtett + 1+ 1= A′tet + 1Donc A′t = e1 et At = et donc une solution particulière estgt = 11 + tL’ensemble des solutions est l’ensemble des fonctions de la formef t = Aet 1t + 1 , A RD. CransacAnalyse

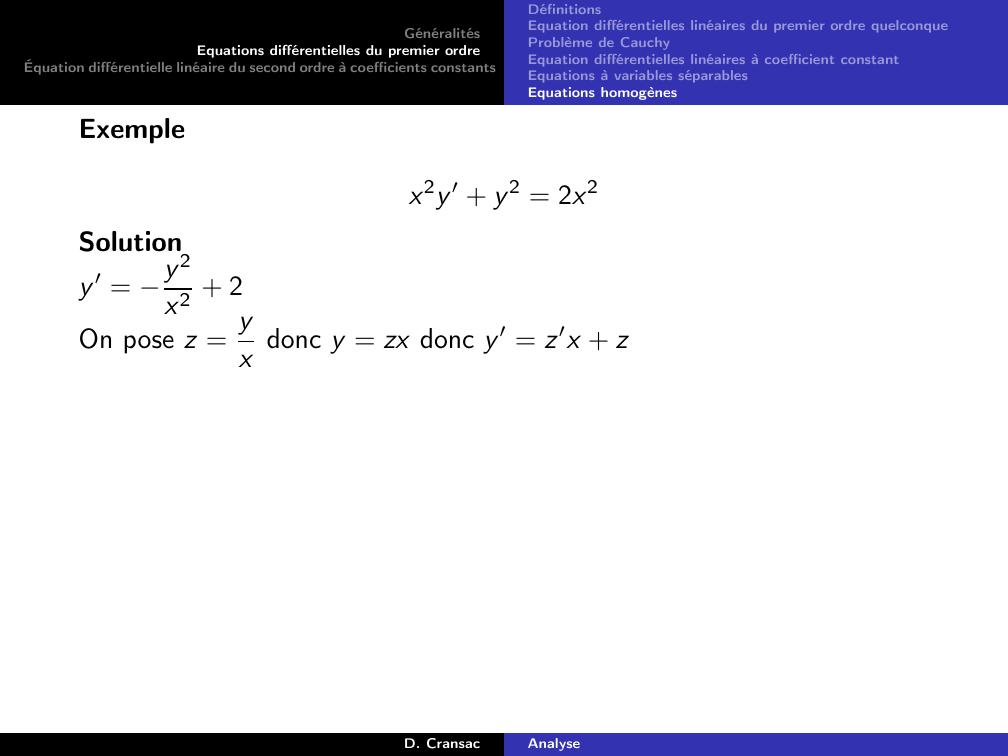
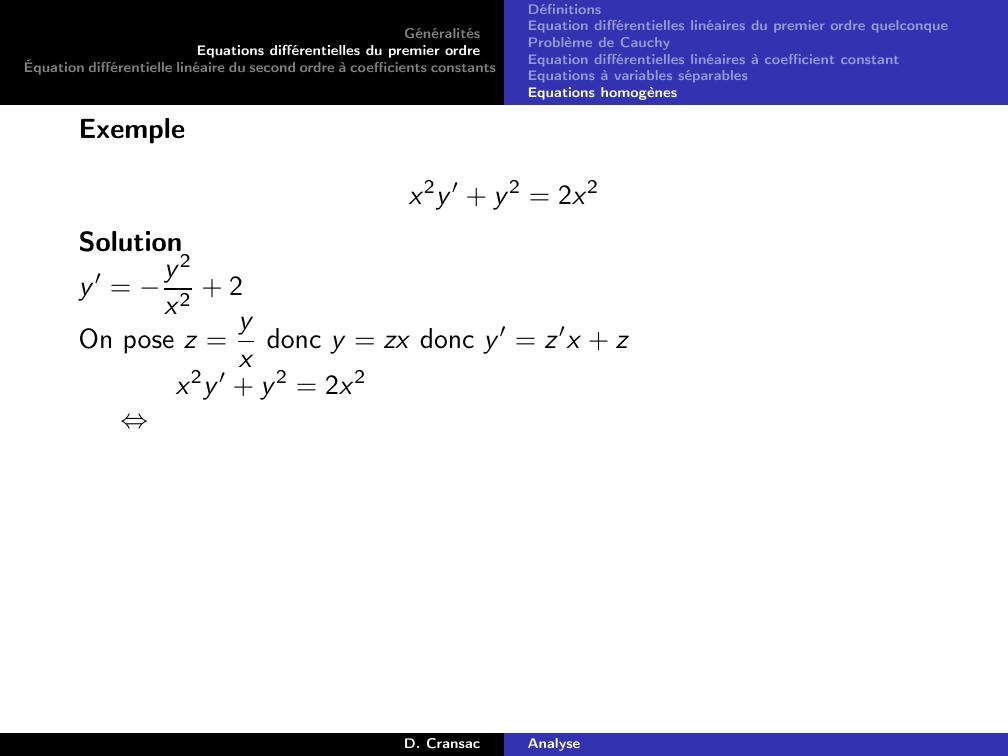
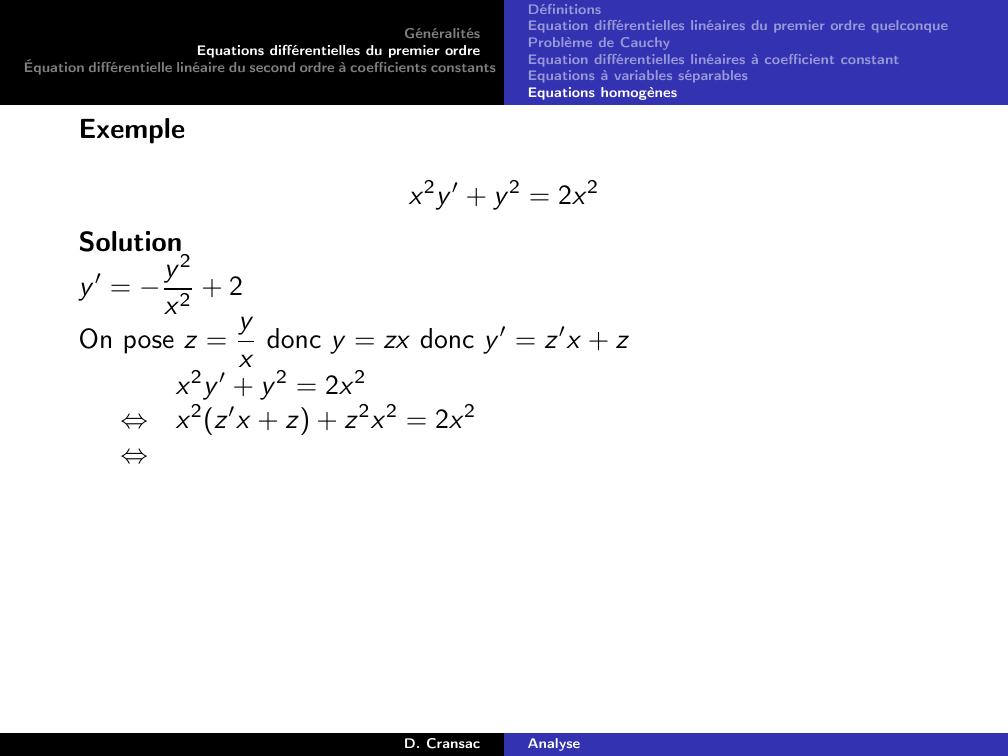
Page 104 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleExy ′ y = x2 + 1D. CransacAnalyse

Page 105 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleExy ′ y = x2 + 1SolutionOn a vu que la solution de l’équation homogène EH était :yHx = λxD. CransacAnalyse

Page 106 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleExy ′ y = x2 + 1SolutionOn a vu que la solution de l’équation homogène EH était :yHx = λxOn va donc chercher une solution particulière sous la forme :yx = λxxD. CransacAnalyse

Page 107 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleExy ′ y = x2 + 1SolutionOn a vu que la solution de l’équation homogène EH était :yHx = λxOn va donc chercher une solution particulière sous la forme :yx = λxxOn l’injecte dans l’équation différentielle E, ce qui donne :xy ′ y = x2 + 1 ⇐⇒x λ′xx + λx λxx = x2 + 1⇔λ′xx2 = x2 + 1 ⇐⇒λ′x = 1 + 1x2D. CransacAnalyse

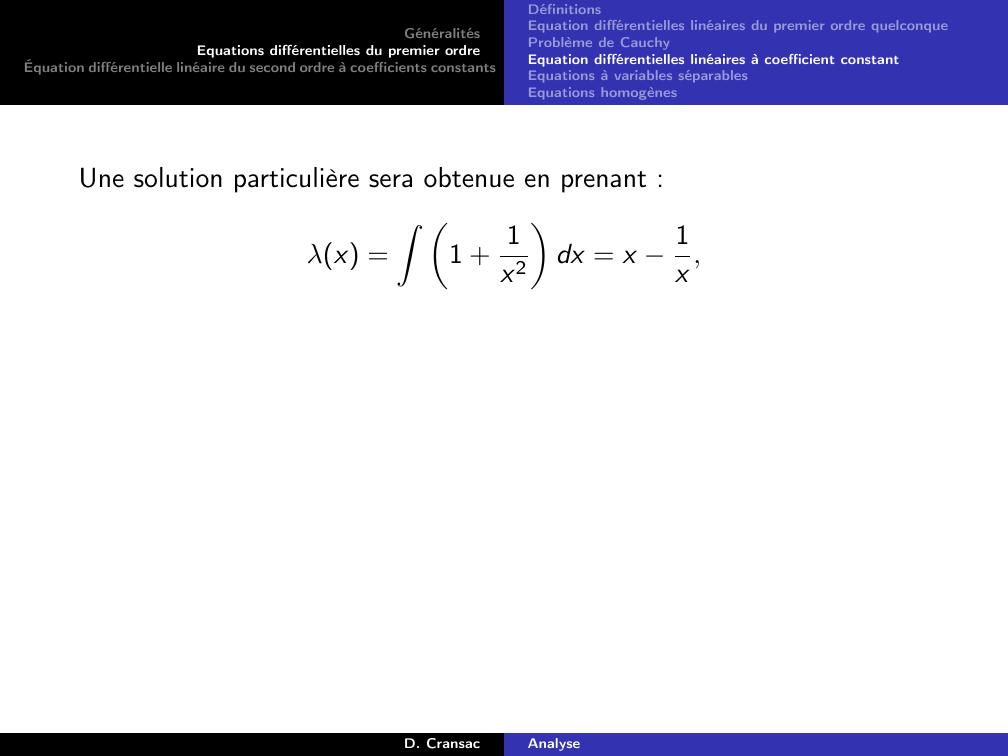
Page 108 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleExy ′ y = x2 + 1SolutionOn a vu que la solution de l’équation homogène EH était :yHx = λxOn va donc chercher une solution particulière sous la forme :yx = λxxOn l’injecte dans l’équation différentielle E, ce qui donne :xy ′ y = x2 + 1 ⇐⇒x λ′xx + λx λxx = x2 + 1⇔λ′xx2 = x2 + 1 ⇐⇒λ′x = 1 + 1x2Une solution particulière sera obtenue en prenant :λx =Z 1 + 1x2dx = x 1x ,D. CransacAnalyse

Page 109 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesUne solution particulière sera obtenue en prenant :λx =Z 1 + 1x2dx = x 1x ,D. CransacAnalyse

Page 110 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesUne solution particulière sera obtenue en prenant :λx =Z 1 + 1x2dx = x 1x ,ce qui donne comme solution particulière de l’équation différentielle :yPx = λxx =x 1xx = x2 1D. CransacAnalyse

Page 111 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesUne solution particulière sera obtenue en prenant :λx =Z 1 + 1x2dx = x 1x ,ce qui donne comme solution particulière de l’équation différentielle :yPx = λxx =x 1xx = x2 1La solution générale de l’équation différentielle avec second membre estalors donnée par en prolongeant en 0 :D. CransacAnalyse

Page 112 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesUne solution particulière sera obtenue en prenant :λx =Z 1 + 1x2dx = x 1x ,ce qui donne comme solution particulière de l’équation différentielle :yPx = λxx =x 1xx = x2 1La solution générale de l’équation différentielle avec second membre estalors donnée par en prolongeant en 0 :yx = yPx + yHx = x2 1 + λx,avec λ réel quelconque.D. CransacAnalyse

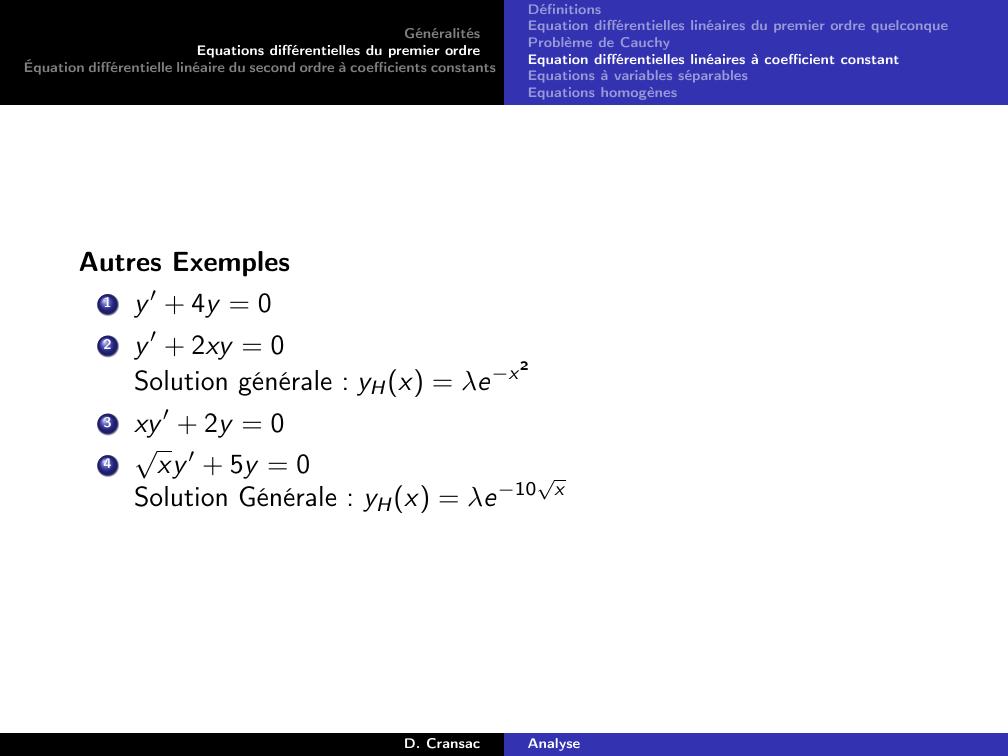
Page 113 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesAutres Exemples1y ′ + 4y = 02y ′ + 2xy = 0Solution générale : yHx = λex23xy ′ + 2y = 04xy ′ + 5y = 0Solution Générale : yHx = λe10xD. CransacAnalyse

Page 114 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplesy ′ + 2xy = 6x2ex2SolutionOn sait que la solution générale de l’équation homogène est :yHx = λex2On va chercher une solution particulière sous la forme :yx = λxex2On a alors :y ′x = λ′xex2 + λx2xex2y solution de E2 ⇐⇒y ′ + 2xy = 6x2ex2⇐⇒λ′xex2 + λx2xex2 + 2xλxex2 = 6x2ex2⇐⇒λ′xex2 = 6x2ex2⇐⇒λ′x = 6x2D. CransacAnalyse

Page 115 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesOn peut donc prendre λx = 2x3 ⇒ypx = λxex2 = 2x3ex2La solution générale de E2 est donc :yx = yPx + yHx = yx = 2x3ex2 + λex2 =2x3 + λex2yx =2x3 + λex2avec λ réel déterminé par une éventuelle condition initiale.D. CransacAnalyse

Page 116 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplesxy ′ + 5y = 10xD. CransacAnalyse

Page 117 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDans certains cas, il y a des méthode plus rapides que celle de lavariation de la constante :Proposition Solution particulière avec second membreexponentielle-polynômeOn considère un nombre a K, une fonction polynomiale P àcoefficients dans K et l’équation différentielle linéaire :y ′ + ay = eλtPtAlors l’équation E a au moins une solution particulière de la formet →eλttmQtoù Q est une fonction polynomiales à coefficients dans K telle quedegQ = degP et :m = 0 si λ + a ̸= 0.m = 1 si λ + a = 0.D. CransacAnalyse

Page 118 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.D. CransacAnalyse

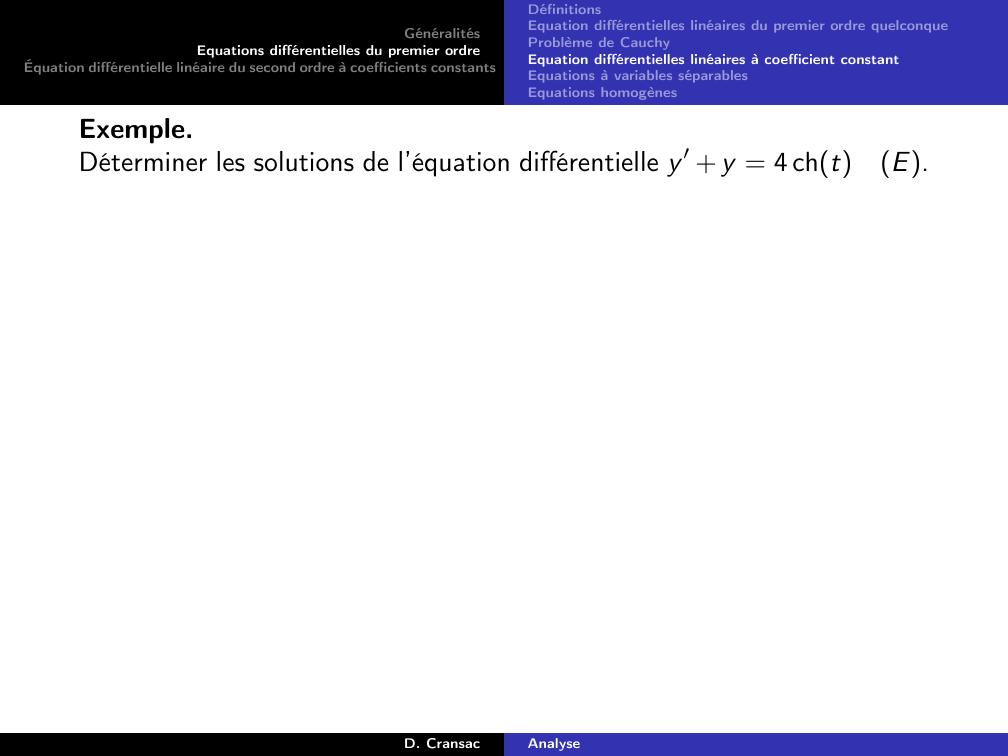
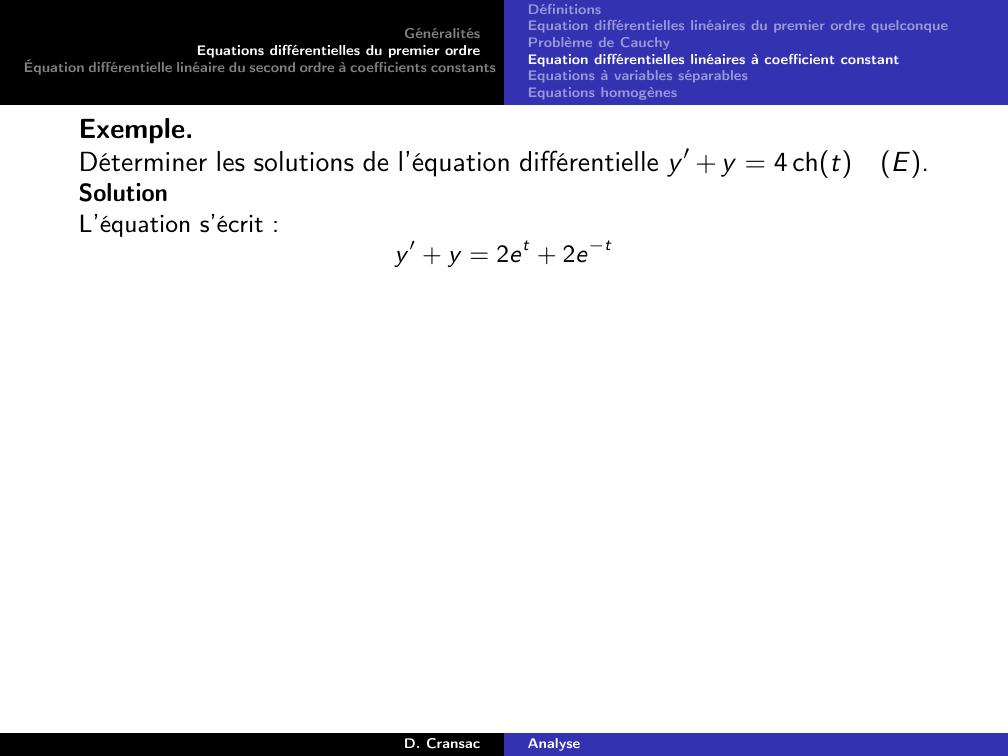
Page 119 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.D. CransacAnalyse

Page 120 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etD. CransacAnalyse

Page 121 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etPar superposition, on résouty ′ + y = 2etE1 et y ′ + y = 2etE2D. CransacAnalyse

Page 122 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etPar superposition, on résouty ′ + y = 2etE1 et y ′ + y = 2etE2Pour E1, on cherche f t = λetOn résout f ′t + f t = 2e2 ⇔2λet = 2et ⇔λ = 1Donc t 7→et est une solution de E1D. CransacAnalyse

Page 123 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etPar superposition, on résouty ′ + y = 2etE1 et y ′ + y = 2etE2Pour E1, on cherche f t = λetOn résout f ′t + f t = 2e2 ⇔2λet = 2et ⇔λ = 1Donc t 7→et est une solution de E1Pour E2, on cherche f t = αtetOn résout f ′t + f t = 2et ⇔α αt + αtet = 2et ⇔α = 2Donc t 7→2tet est une solution de E2D. CransacAnalyse

Page 124 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etPar superposition, on résouty ′ + y = 2etE1 et y ′ + y = 2etE2Pour E1, on cherche f t = λetOn résout f ′t + f t = 2e2 ⇔2λet = 2et ⇔λ = 1Donc t 7→et est une solution de E1Pour E2, on cherche f t = αtetOn résout f ′t + f t = 2et ⇔α αt + αtet = 2et ⇔α = 2Donc t 7→2tet est une solution de E2L’ensemble des solutions de l’équation E est l’ensemble des fonctions f tellesque :D. CransacAnalyse

Page 125 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple.Déterminer les solutions de l’équation différentielle y ′ + y = 4 chtE.SolutionL’équation s’écrit :y ′ + y = 2et + 2etPar superposition, on résouty ′ + y = 2etE1 et y ′ + y = 2etE2Pour E1, on cherche f t = λetOn résout f ′t + f t = 2e2 ⇔2λet = 2et ⇔λ = 1Donc t 7→et est une solution de E1Pour E2, on cherche f t = αtetOn résout f ′t + f t = 2et ⇔α αt + αtet = 2et ⇔α = 2Donc t 7→2tet est une solution de E2L’ensemble des solutions de l’équation E est l’ensemble des fonctions f tellesque :f x = λet + et + 2tetλ RD. CransacAnalyse

Page 126 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesRechercher des solutions particulièresPour une équation du typeaty ′ + bty = ctEn général on imite le second membre :Si ct est un polynôme, rechercher une solution particulière demême degré.Si ct est une fonction trigonométrique, rechercher une solutionparticulière trigonométrique : α cos ωt + β sin ωtSi ct est solution de l’équation homogène associée, rechercher unesolution particulière αtctD. CransacAnalyse

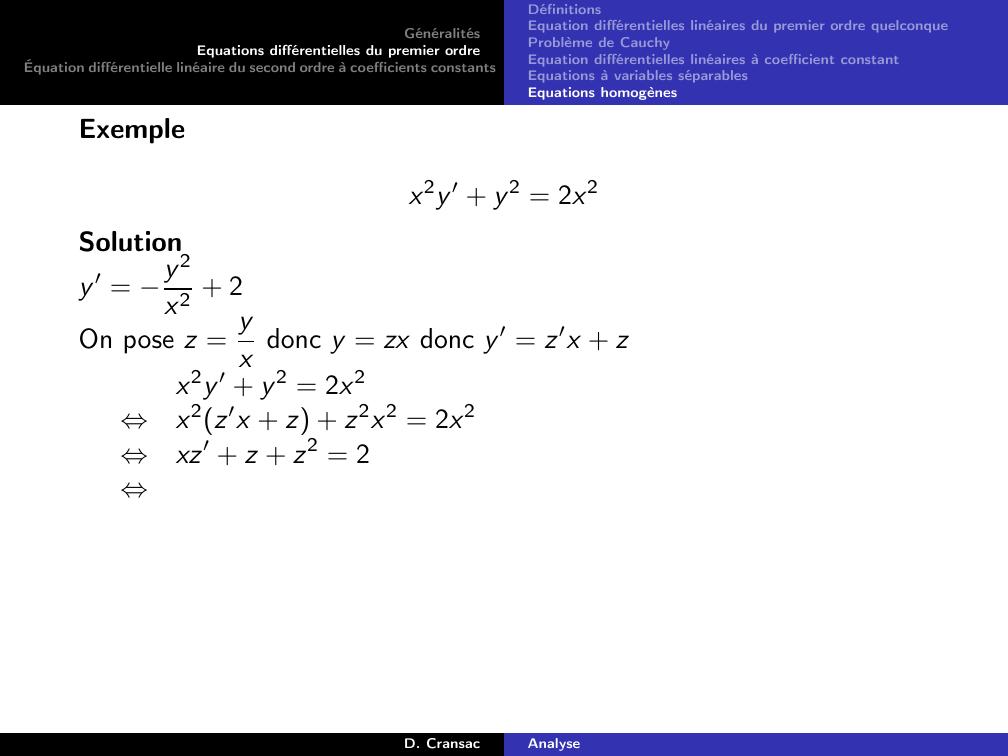
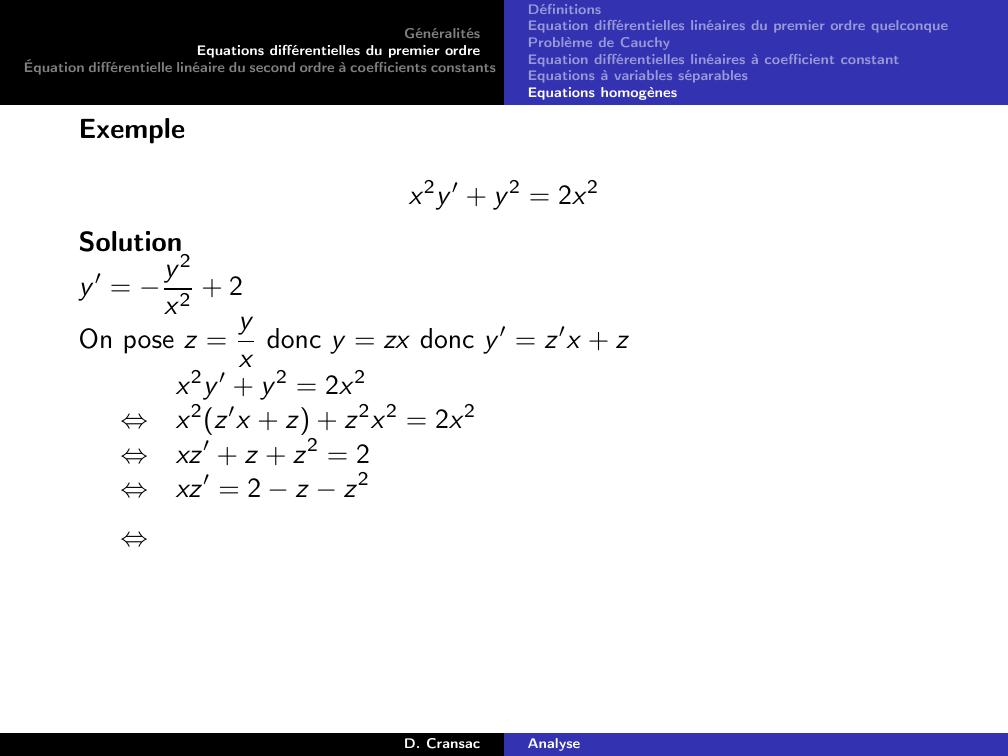
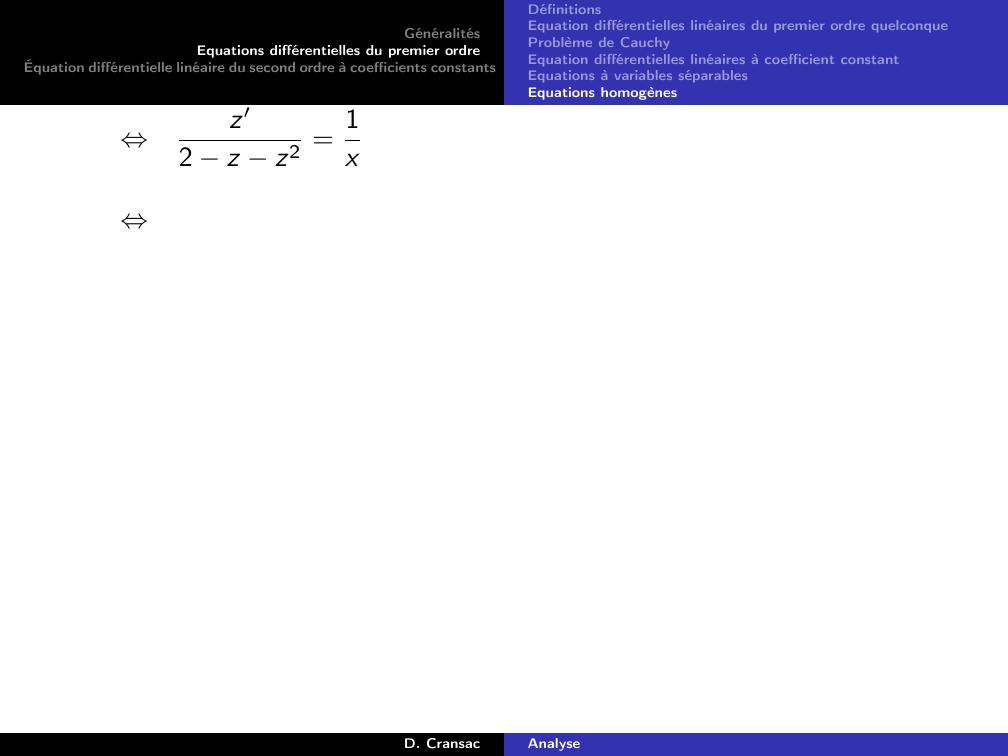
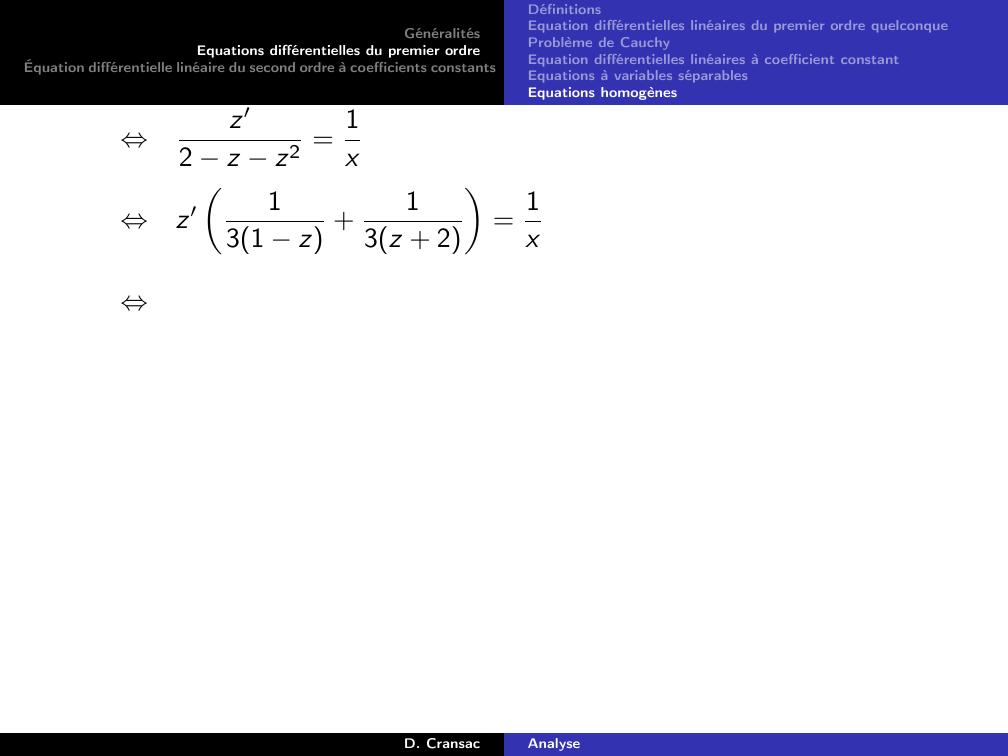
Page 127 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple 15.y ′ 2y = t2 3t + 1On pose yPt = αt2 + βt + γ et on cherche les coefficients α, β et γ.yPt = αt2 + βt + γdoncy ′Pt = 2αt + βComme on veut que yP soit solution de 2, on cherche α, β et γ telsque :y ′P 2yP = t2 3t + 1 ⇔2αt + β 2αt2 + βt + γ= t2 3t + 1⇔2αt2 + 2α βt + β 2γ = t2 3t + 1⇔2α = 12α 2β= 3β 2γ= 1⇔α =12β =1γ =0D. CransacAnalyse

Page 128 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple 16.y ′ 2y = e8tOn pose yPt = αe8t et on cherche le coefficient α.yPt = αe8tdoncy ′Pt = 8αe8tComme on veut que yP soit solution de 3, on cherche α tel que :y ′P 2yP = e8t ⇔8αe8t 2αe8t = e8t⇔6αe8t = e8t⇔6α = 1⇔α = 16Donc yPt = 16e8t est une solution particulière de l’équation 3.D. CransacAnalyse

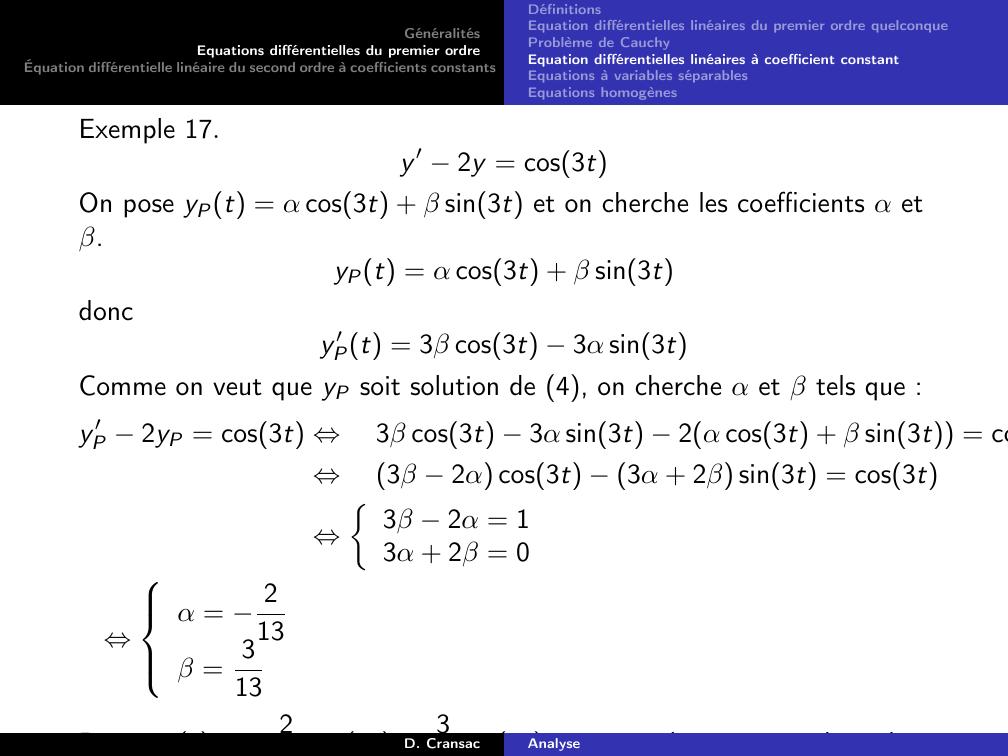
Page 129 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple 17.y ′ 2y = cos3tOn pose yPt = α cos3t + β sin3t et on cherche les coefficients α etβ.yPt = α cos3t + β sin3tdoncy ′Pt = 3β cos3t 3α sin3tComme on veut que yP soit solution de 4, on cherche α et β tels que :y ′P 2yP = cos3t ⇔3β cos3t 3α sin3t 2α cos3t + β sin3t = co⇔3β 2α cos3t 3α + 2β sin3t = cos3t⇔3β 2α = 13α + 2β = 0⇔α = 213β = 313Donc yPt = 213 cos3t + 313 sin3t est une solution particulière deD. CransacAnalyse

Page 130 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemple 18.y ′ 3y = e3tLes solutions de l’équation homogène associée y ′ 3y = 0 sont de laforme yHt = ke3t pour tout k R. On remarque donc que le secondmembree3tde l’équation différentielle y ′ 3y = e3t est solution del’équation homogène associée. On pose yPt = αte3t et on cherche lecoefficient α.yPt = αte3tdoncy ′Pt = αe3t + 3αte3tComme on veut que yP soit solution de 5, on cherche α tel que :y ′P 3yP = e3t ⇔αe3t + 3αte3t 3αte3t = e3t⇔αe3t = e3t⇔α = 1Donc yPt = te3t est une solution particulière de 5.D. CransacAnalyse

Page 131 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentiellesdu premier ordreà variables séparablesD. CransacAnalyse

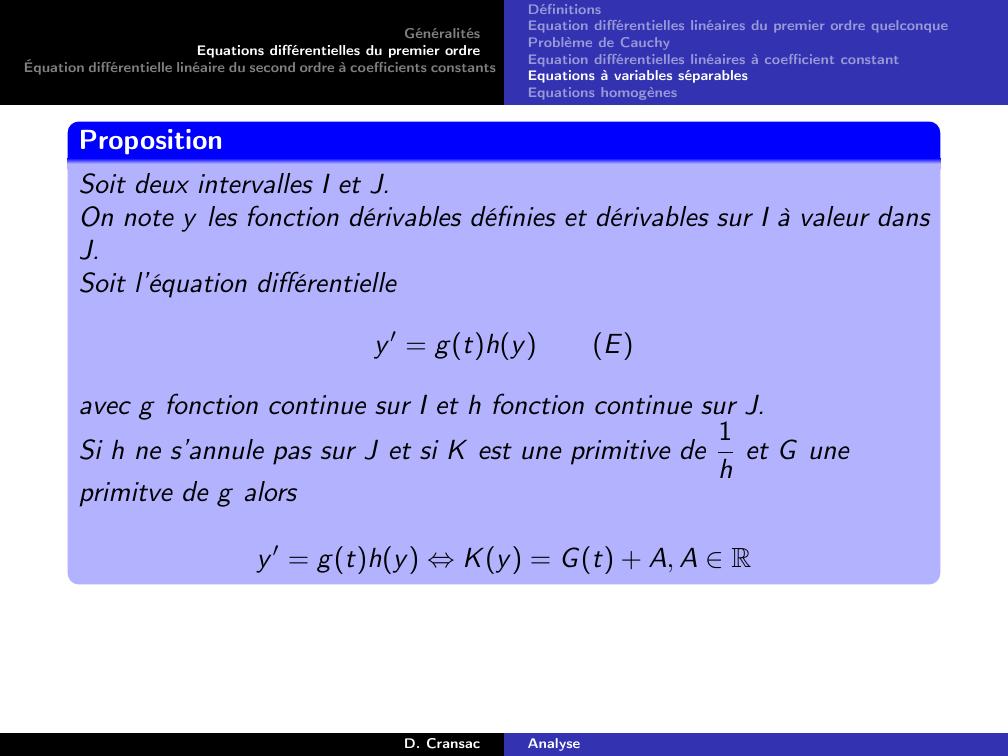
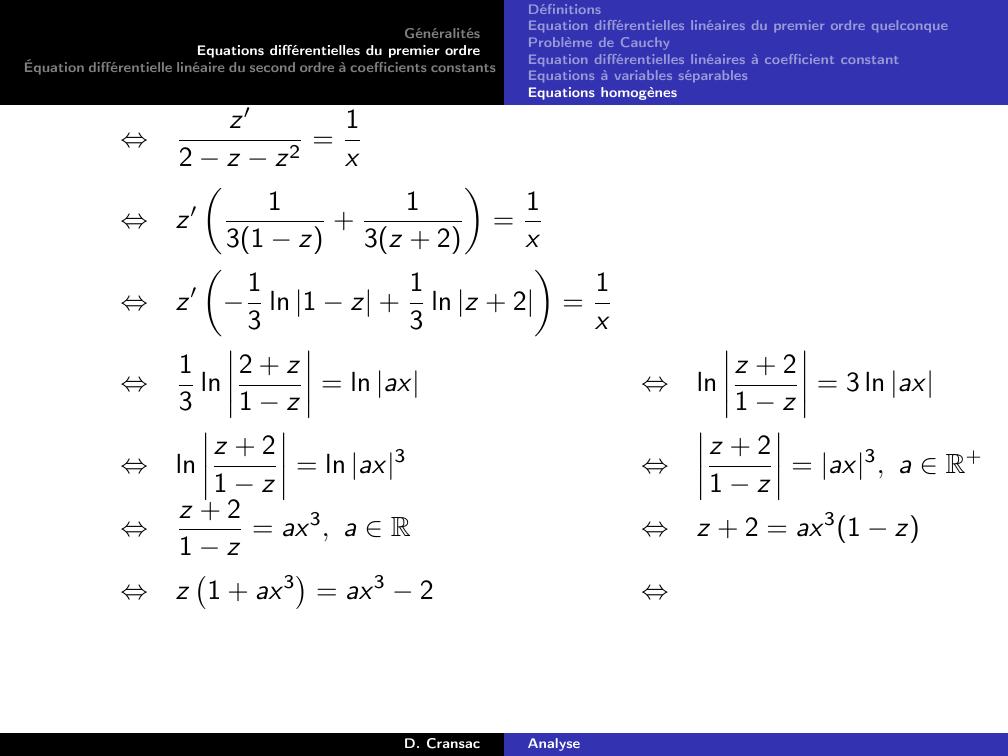
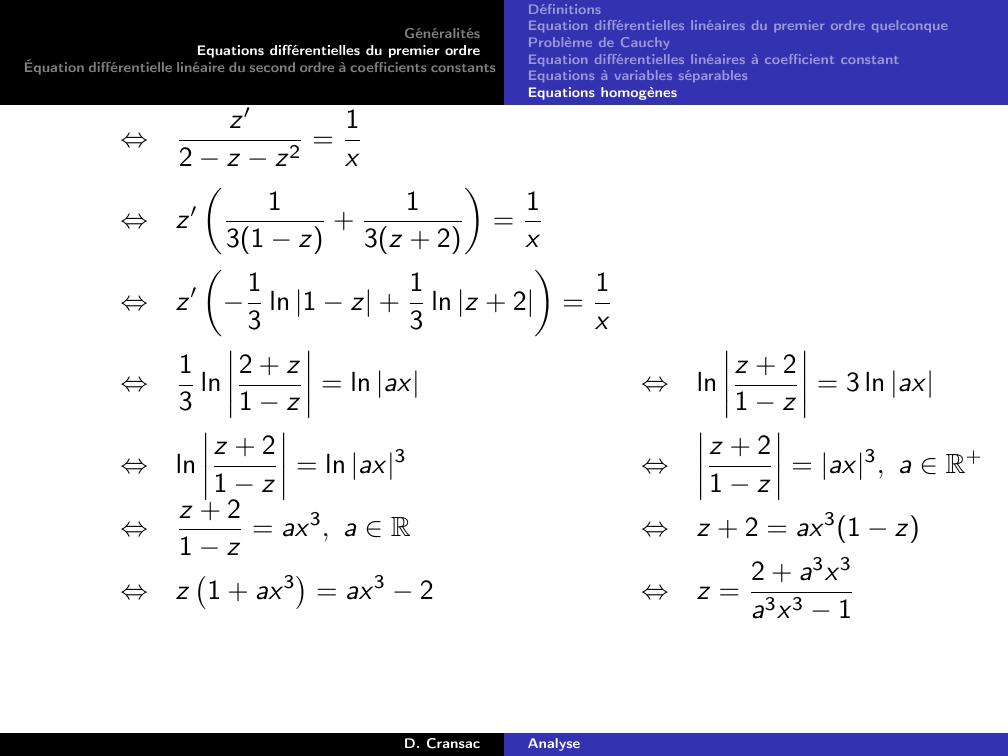
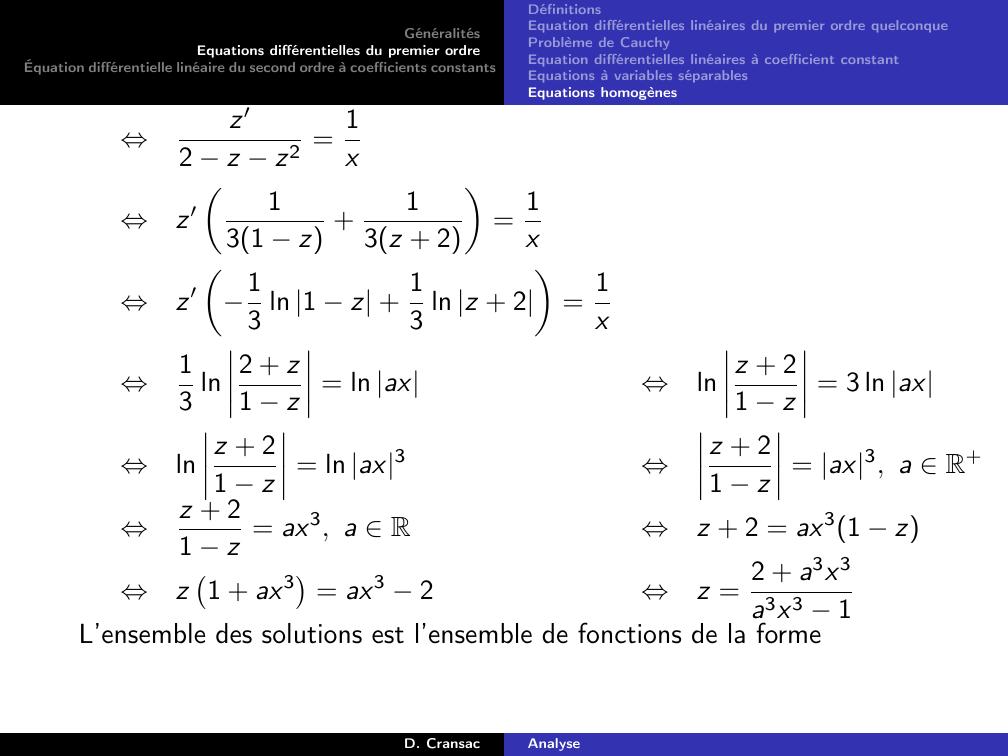
Page 132 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionSoit deux intervalles I et J.On note y les fonction dérivables définies et dérivables sur I à valeur dansJ.On appelle équation différentielle à variables séparables, toute équationqui peut se mettre sous la forme :y ′ = gthyEavec g fonction continue sur I et h fonction continue sur J.D. CransacAnalyse

Page 133 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionSoit deux intervalles I et J.On note y les fonction dérivables définies et dérivables sur I à valeur dansJ.On appelle équation différentielle à variables séparables, toute équationqui peut se mettre sous la forme :y ′ = gthyEavec g fonction continue sur I et h fonction continue sur J.PropositionSi ha = 0 alors yt = a est une solution constante de E.D. CransacAnalyse

Page 134 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionSoit deux intervalles I et J.On note y les fonction dérivables définies et dérivables sur I à valeur dansJ.On appelle équation différentielle à variables séparables, toute équationqui peut se mettre sous la forme :y ′ = gthyEavec g fonction continue sur I et h fonction continue sur J.PropositionSi ha = 0 alors yt = a est une solution constante de E.Exemple Résoudre l’équation y ′ = 2yt , t 0Ici gt = 1t et hy = 2yIci h0 = 0 donc yt = 0 est une solution de l’équation.D. CransacAnalyse

Page 135 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoit deux intervalles I et J.On note y les fonction dérivables définies et dérivables sur I à valeur dansJ.Soit l’équation différentielley ′ = gthyEavec g fonction continue sur I et h fonction continue sur J.Si h ne s’annule pas sur J et si K est une primitive de 1h et G uneprimitve de g alorsy ′ = gthy ⇔Ky = Gt + A, A RD. CransacAnalyse

Page 136 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesPropositionSoit deux intervalles I et J.On note y les fonction dérivables définies et dérivables sur I à valeur dansJ.Soit l’équation différentielley ′ = gthyEavec g fonction continue sur I et h fonction continue sur J.Si h ne s’annule pas sur J et si K est une primitive de 1h et G uneprimitve de g alorsy ′ = gthy ⇔Ky = Gt + A, A RDémonstration.y ′ = gthy ⇔y ′hy = gt ⇔Ky = Gt + A, A RD. CransacAnalyse

Page 137 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0D. CransacAnalyse

Page 138 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionD. CransacAnalyse

Page 139 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tD. CransacAnalyse

Page 140 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tEn intégrant :D. CransacAnalyse

Page 141 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tEn intégrant :12 ln y = ln t + A= ln t + ln a= ln at en posant ln a = AD. CransacAnalyse

Page 142 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tEn intégrant :12 ln y = ln t + A= ln t + ln a= ln at en posant ln a = AOn a donc ln y = 2 ln at = lnat2D. CransacAnalyse

Page 143 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tEn intégrant :12 ln y = ln t + A= ln t + ln a= ln at en posant ln a = AOn a donc ln y = 2 ln at = lnat2donc y = at2 donc y = bt2 b RD. CransacAnalyse

Page 144 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExempleRésoudre l’équation y ′ = 2yt , t 0SolutionSi y ̸= 0,y ′2y = 1tEn intégrant :12 ln y = ln t + A= ln t + ln a= ln at en posant ln a = AOn a donc ln y = 2 ln at = lnat2donc y = at2 donc y = bt2 b RL’ensemble des solutions est l’ensemble des fonctions de la formef t = at2, a RD. CransacAnalyse

Page 145 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesEquations différentielleshomogènesdu premier ordreD. CransacAnalyse

Page 146 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionUne équation différentielle du premier ordre est dite homogène si ellepeut s’écrire sous la formedydx = hyxoù h est une fonction continueD. CransacAnalyse

Page 147 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionUne équation différentielle du premier ordre est dite homogène si ellepeut s’écrire sous la formedydx = hyxoù h est une fonction continueRésolution d’une équation homogèneEn posant le changement de fonction z = yx , on obtient une équation àvariables séparées.D. CransacAnalyse

Page 148 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesDéfinitionUne équation différentielle du premier ordre est dite homogène si ellepeut s’écrire sous la formedydx = hyxoù h est une fonction continueRésolution d’une équation homogèneEn posant le changement de fonction z = yx , on obtient une équation àvariables séparées.Démonstration.On a xz = y donc z + xz′ = y ′ doncy ′ = hyz⇔z + xz′ = hz ⇔z′hz z = 1xD. CransacAnalyse

Page 149 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2D. CransacAnalyse

Page 150 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zD. CransacAnalyse

Page 151 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zx2y ′ + y 2 = 2x2⇔D. CransacAnalyse

Page 152 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zx2y ′ + y 2 = 2x2⇔x2z′x + z + z2x2 = 2x2⇔D. CransacAnalyse

Page 153 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zx2y ′ + y 2 = 2x2⇔x2z′x + z + z2x2 = 2x2⇔xz′ + z + z2 = 2⇔D. CransacAnalyse

Page 154 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zx2y ′ + y 2 = 2x2⇔x2z′x + z + z2x2 = 2x2⇔xz′ + z + z2 = 2⇔xz′ = 2 z z2⇔D. CransacAnalyse

Page 155 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènesExemplex2y ′ + y 2 = 2x2Solutiony ′ = y 2x2 + 2On pose z = yx donc y = zx donc y ′ = z′x + zx2y ′ + y 2 = 2x2⇔x2z′x + z + z2x2 = 2x2⇔xz′ + z + z2 = 2⇔xz′ = 2 z z2⇔z′2 z z2 = 1xOn décompose la fraction en éléments simples :12 z z2 =11 zz + 2 =131 z +13z + 2D. CransacAnalyse

Page 156 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔D. CransacAnalyse

Page 157 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔D. CransacAnalyse

Page 158 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔z′13 ln 1 z + 13 ln z + 2= 1x⇔D. CransacAnalyse

Page 159 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔z′13 ln 1 z + 13 ln z + 2= 1x⇔13 ln2 + z1 z = ln ax⇔lnz + 21 z = 3 ln ax⇔lnz + 21 z = ln ax3⇔z + 21 z = ax3, a R+⇔z + 21 z = ax3, a R⇔z + 2 = ax31 z⇔z1 + ax3= ax3 2⇔D. CransacAnalyse

Page 160 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔z′13 ln 1 z + 13 ln z + 2= 1x⇔13 ln2 + z1 z = ln ax⇔lnz + 21 z = 3 ln ax⇔lnz + 21 z = ln ax3⇔z + 21 z = ax3, a R+⇔z + 21 z = ax3, a R⇔z + 2 = ax31 z⇔z1 + ax3= ax3 2⇔z = 2 + a3x3a3x3 1D. CransacAnalyse

Page 161 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔z′13 ln 1 z + 13 ln z + 2= 1x⇔13 ln2 + z1 z = ln ax⇔lnz + 21 z = 3 ln ax⇔lnz + 21 z = ln ax3⇔z + 21 z = ax3, a R+⇔z + 21 z = ax3, a R⇔z + 2 = ax31 z⇔z1 + ax3= ax3 2⇔z = 2 + a3x3a3x3 1L’ensemble des solutions est l’ensemble de fonctions de la formeD. CransacAnalyse

Page 162 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsDéfinitionsEquation différentielles linéaires du premier ordre quelconqueProblème de CauchyEquation différentielles linéaires à coefficient constantEquations à variables séparablesEquations homogènes⇔z′2 z z2 = 1x⇔z′131 z +13z + 2= 1x⇔z′13 ln 1 z + 13 ln z + 2= 1x⇔13 ln2 + z1 z = ln ax⇔lnz + 21 z = 3 ln ax⇔lnz + 21 z = ln ax3⇔z + 21 z = ax3, a R+⇔z + 21 z = ax3, a R⇔z + 2 = ax31 z⇔z1 + ax3= ax3 2⇔z = 2 + a3x3a3x3 1L’ensemble des solutions est l’ensemble de fonctions de la formef x = x 2 + Ax3Ax3 1, A RD. CransacAnalyse

Page 163 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesÉquation différentielle linéaire du secondordre à coefficients constantsD. CransacAnalyse

Page 164 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesOn désigne toujours par K l’ensemble des réels R ou des complexes C.DéfinitionSoient I un intervalle de R, a, b, c Ka ̸= 0, et f : I →K une fonctioncontinue. On appelle équation différentielle linéaire du second ordre àcoefficients constants :ay ′′ + by ′ + cy = f tLa fonction f s’appelle le second membre. On appelle solution sur I deE toute fonction y : I →K deux fois dérivable sur I telle que :t I, ay ′′t + by ′t + cyt = f tLa courbe représentative d’une solution y sur I est alors appelée courbeintégrale sur I.Remarque Soit y une solution de E sur I, alors f est de classe C2 surI. En effet, elle est supposée deux fois dérivable sur I.De plus f ′′ est continue sur I puisque y ′′t = 1af t ba y ′t cayt.D. CransacAnalyse

Page 165 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesExemples d’équations différentielles linéaires du second ordre.La tension U aux bornes d’un condensateur de capacité C en sérieavec une résistance R, une bobine d’inductance L et un générateurde force électromotrice Et vérifie l’équation différentielle :LCU′′ + RCU′ + U = EtL’intensité I dans un circuit LC constitué d’un condensateur decapacité R et d’une bobine d’inductance L vérifie l’équationdifférentielle :I ′′ + 1LC I = 0D. CransacAnalyse

Page 166 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDéfinitionSoient I un intervalle de R, a, b, c Ka ̸= 0, et f : I →K une fonctioncontinue. On considère l’équation différentielle linéaire suivante :ay ′′ + by ′ + cy = f tOn appelle équation différentielle homogène sans second membreassociée à E l’équation :ay ′′ + by ′ + cy = 0PropositionL’ensemble des solutions S0 de E0 est stable par combinaison linéaire,c’est à dire :λ, µ K, f , g S0, λf + µg S0PropositionPour r K, la fonction t 7→ert est solution de E0 sur R si etseulement si ar 2 + br + c = 0.D. CransacAnalyse

Page 167 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDéfinitionOn appelle équation caractéristique associée à E l’équationar 2 + br + c = 0 d’inconnue r C.D. CransacAnalyse

Page 168 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesProposition Résolution de l’équation homogène dans COn considère trois nombres a, b, c C où a ̸= 0, et l’équationdifférentielle :ay ′′ + by ′ + c = 0Soit = b2 4ac le discriminant de l’équation caractéristique.Si ̸= 0, l’équation caractéristique admet deux racines complexesdistinctes r et r ′. Les solutions complexes de E0 sur R sont lesfonctions de la forme t 7→λer1t + µer2t, λ, µ C2.S0 =nt R 7→λert + µer ′t; λ, µ C2oD. CransacAnalyse

Page 169 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesProposition Résolution de l’équation homogène dans COn considère trois nombres a, b, c C où a ̸= 0, et l’équationdifférentielle :ay ′′ + by ′ + c = 0Soit = b2 4ac le discriminant de l’équation caractéristique.Si ̸= 0, l’équation caractéristique admet deux racines complexesdistinctes r et r ′. Les solutions complexes de E0 sur R sont lesfonctions de la forme t 7→λer1t + µer2t, λ, µ C2.S0 =nt R 7→λert + µer ′t; λ, µ C2oSi = 0 : l’équation caractéristique admet une racine doubler = b2a C.Les solutions complexes de E0 sur R sont les fonctions de la formet 7→λ + µtert, λ, µ C2.S0 =t R 7→λ + µtert; λ, µ C2D. CransacAnalyse

Page 170 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.Soit r une solution de l’équation caractéristique qui existe toujours sur C.La fonction t 7→ert est solution de E0 sur R.Posons maintenant yt = utert avec u une fonction de classe C2 sur R.On montre alors que y est solution de E0 sur R si et seulement si u estsolution de l’équation :au′′t + 2ar + bu′t +ar 2 + br + cut = 0.Puisque ar 2 + br + c = 0 et r + r ′ = ba , soit 2ar + b = a r r ′,celle-ci s’écrit :u′′t + r r ′ u′t = 0.... suite ...D. CransacAnalyse

Page 171 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.On obtient ici une équation différentielle linéaire d’ordre 1 en u′Si = 0, alors r = r ′ et l’équation devient u′′t = 0, d’où :λ, µ C :ut = λ + µtetyt = λ + µtert.Si ̸= 0, alors r et r ′ sont distinctes, et la résolution de l’équationdonne u′t = λerr ′t avec λ C, et donc :λ, µ C :ut = λerr ′t + µetyt = λert + µer ′tD. CransacAnalyse

Page 172 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesProposition Résolution de l’équation homogène dans ROn considère trois nombres a, b, c R où a ̸= 0, et l’équationdifférentielle :ay ′′ + by ′ + c = 0Soit = b2 4ac le discriminant de l’équation caractéristique.Si 0 : l’équation caractéristique admet deux racines réellesdistinctes r et r ′. Les solutions de E0 sont alors les fonctions de laforme : t 7→λert + µer ′t, λ, µ R2.Si = 0 : l’équation caractéristique admet une racine double r R.La solution générale de E0 est x 7→λ + µxerx, λ, µ R2.Si 0 : l’équation caractéristique admet deux solutionscomplexes non réelles α ± iβ, avec α, β R2.La solution générale de E estx 7→eαxλ cosβx + µ sinβx, λ, µ R2.Remarque. On peut aussi écrire x 7→eαxA cosβx + φ, avecA, φ R2D. CransacAnalyse

Page 173 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.Notons d’abord que les solutions à valeurs réelles de cette équation sontdes solutions à valeurs complexes caractérisées par le fait qu’elles sontégales à leur conjugué. On a donc selon le signe du discriminant :si 0, l’équation caractéristique a deux racines distinctes r r ′.Les solutions complexes sont les fonctions de la forme :t 7→λert + µer ′tavecλ, µ C2. Ces solutions sont réelles si pour tout t Rλert + µer ′t = ¯λert + ¯µer ′tsoit si λ = ¯λ et µ = ¯µ quitte à prendre t = 0 ou à faire t →+.suite ...D. CransacAnalyse

Page 174 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.Inversement si λ = ¯λ et µ = ¯µ, l’égalité précédente est bien vérifiée. Lessolutions réelles dans ce cas sont donc les fonctions de la formet 7→λert + µer ′tavecλ, µ R.On traite le cas = 0 de façon similaire.si 0, l’équation caractéristique admet deux racines complexesconjuguées α ± iβ. Les solutions complexes sont les fonctions de laforme :t 7→λeα+iβt + µeαiβtavecλ, µ C2. Ces solutions sont réelles si pour tout t Rλeα+iβt + µeαiβt = ¯λeαiβt + ¯µeα+iβtsoit si λ = ¯µ quitte à prendre t = 0 ou t = π/2β .suiteD. CransacAnalyse

Page 175 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.Inversement si λ = ¯µ, l’égalité précédente est bien vérifiée. Si on noteλ = a + ib, les solutions réelles sont donc les fonctions de la forme aveca, b R t 7→a + ibeα+iβt + a ibeαiβt = eαt2a cosβt 2b sinβtEnfin :En posant φ tel que cos ϕ =aa2 + b2 et sin ϕ =ba2 + b2On aa cosβt b sinβt = a2 + b2cos β cos ϕ sin β sin ϕ= a2 + b2 cosβ + ϕD. CransacAnalyse

Page 176 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesRemarque On dit que l’ensemble des solutions de E0 forme un planvectoriel, puisque celles-ci sont combinaisons linéaires de deux fonctionsnon proportionnelles que ce soit dans le cas réel ou complexe.Exemple. Déterminer les solutions réelles et complexes de l’équationdifférentielle y ′′ + y ′ + y = 0, et montrer qu’elles tendent vers 0 en +.D. CransacAnalyse

Page 177 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesPropositionSoient I un intervalle de R, a, b, c Ka ̸= 0, et f : I →K une fonctioncontinue. On considère l’équation différentielle :ay ′′ + by ′ + cy = f tAlors toute solution de E s’obtient en ajoutant à une solutionparticulière yP de E une solution de l’équation homogène associée E0.Ainsi l’ensemble S des solutions de E satisfait :S = yp + S0RemarquePour obtenir l’ensemble des solutions de E, il faudra doncdéterminer une solution particulière de E, et lui ajouter l’ensembledes solutions de E0 dont on a vu la forme.L’ensemble S est donc la somme d’un point yp et de combinaisonslinéaires de deux fonctions non proportionnelles. On dit alors que Sest un plan affine.D. CransacAnalyse

Page 178 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesProposition Principe de superpositionSoient I un intervalle de R, a, b, c Ka ̸= 0, et f1, f2 : I →K desfonctions continues sur I et les équations différentielles :E1 : ay ′′ + by ′ + cy = f1tetE2 : ay ′′ + by ′ + cy = f2tSi y1 est solution sur I de E1 , y2 est solution sur I de E2, alors pourtout λ, µ K, λy1 + µy2 est solution sur I de :ay ′′ + by ′ + cy = λf1 + µf2.D. CransacAnalyse

Page 179 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesProposition Solution particulière avec second membreexponentiel-polynômeOn considère des nombres a, b, c, λ K où a ̸= 0 , une fonctionpolynomiale P à coefficients dans K et l’équation différentielle linéaire :ay ′′ + by ′ + c = eλtPt.Alors l’équation E a au moins une solution particulière de la formet 7→eλttmQtoù Q est une fonction polynomiales à coefficients dans K telle quedegQ = degP et :m = 0 si λ n’est pas racine du polynôme caractéristiquem = 1 si λ est racine simple du polynôme caractéristiquem = 2 si λ est racine double du polynôme caractéristiqueD. CransacAnalyse

Page 180 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesExemple.Déterminer les solutions réelles de E : y ′′ 3y ′ + 2y = xe2x.Solutions L’équation caractéristique de E est r 2 3r + 2 = 0, dont lessolutions sont 1 et 2 . Ainsi la solution générale de l’équation homogèneassociée à E estx 7→λe2x + µex, λ, µ R2Comme 2 est solution simple de l’équation caractéristique, on chercheune solution particulière sous la forme y : x 7→xQxe2x, avec Qfonction polynomiale de degré 1 , donc il existe a, b R2 telles queQx = ax + b.y est deux fois dérivable comme produit de fonctions qui le sont, ety ′x = 2ax + be2x + 2ax2 + bxe2x=2ax2 + 2bx + 2ax + be2xpuisy ′′x = 4ax + 2b + 2ae2x + 22ax2 + 2bx + 2ax + be2x=4ax2 + 4bx + 8ax + 4b + 2ae2xD. CransacAnalyse

Page 181 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesEn reportant dans E, il vientxex =4ax2 + 4bx + 8ax + 4b + 2ae2x32ax2 + 2bx + 2ax + be2x + 2ax2 + bxe2x= 2axe2x + b + 2ae2xdonc 2a = 1 et b + 2a = 0 par unicité des coefficients d’un polynôme,i.e. a = 12 et b = 1.Une solution particulière est donc x 7→12x2 xe2x et la solutiongénérale de E estx 7→12x2 xe2x + λe2x + µex, λ, µ R2D. CransacAnalyse

Page 182 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDéfinitionÉtant donnés trois nombres a, b, c de Ka ̸= 0 et une fonction continuef : I →K, on considère l’équation différentielle :ay ′′ + by ′ + cy = f t.Le problème de Cauchy associé à un triplet t0, y0, y ′0 I × K2 est larecherche des solutions de E vérifiant les deux conditions initialesy t0 = y0, y ′ t0 = y ′0.D. CransacAnalyse

Page 183 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesPropositionPour t0, y0, y ′0 I × K2, le problème de Cauchy associé aux conditionsinitiales y t0 = y0, y ′ t0 = y ′0 admet une solution unique sur I.D. CransacAnalyse

Page 184 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesPropositionOn considère trois nombres a, b, c de Ra ̸= 0, une fonction continuef : I →R et l’équation différentielle :ay ′′ + by ′ + cy = f t.1Une seule courbe intégrale définie sur I passe par le point M0 t0, y0de I × R avec une tangente de pente donnée y ′0 R en ce point.2Deux telles courbes intégrales distinctes ne peuvent se couper dansI × R avec une tangente commune.D. CransacAnalyse

Page 185 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesDémonstration.Le premier point est une reformulation du résultat précédent.Montrons le deuxième point : supposons que deux courbes intégrales secoupent en M0 t0, y0 avec une tangente commune de pente y ′0 R.Notons y1 et y2 les solutions de E sur I correspondantes. Elles sontdonc toutes deux solutions du même problème de Cauchy :Ey t0 = y0y ′ t0 = y ′0Par unicité, on a donc y1 = y2.D. CransacAnalyse

Page 186 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesRemarque La seule solution de E0 : ay ′′ + by ′ + cy = 0 telle quey t0 = y ′ t0 = 0 est la fonction nulle. En effet, la fonction nulle estsolution de E0. Et par la proposition précédente, c’est l’unique solutiontelle que y t0 = y ′ t0 = 0.D. CransacAnalyse

Page 187 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesApplication à la mécaniqueD. CransacAnalyse

Page 188 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesExerciceConsidérons le mouvement d’une masse m suspendue à un ressort verticalde raideur K et de longueur L, et soumise à une force de frottementfluide par exemple en plaçant l’oscillateur dans un liquide visqueux⃗Ff = α⃗v.1En utilisant le principe fondamental de la dynamique, montrer quel’équation du mouvement est régie par l’équation différentielle :z′′ + 2λz′ + ω20z = 0avec2λ = αm le coefficient d’amortissement de l’oscillateurω0 =rkm qui représente sa pulsation propre2On précise les conditions initiales : z0 = 10 et z′0 = 0 c’est àdire qu’on suppose l’oscillateur lâché sans vitesse initiale après avoirtiré d’une longueur 10 à partir de sa position d’équilibre.aAvec λ = 0, ω0 = 1, déterminer l’expression explicite du mouvement.bAvec λ = ω0 = 1, déterminer l’expression explicite du mouvement.D. CransacAnalyse

Page 189 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairescAvec λ = 1, ω0 =5, déterminer l’expression explicite dumouvement.Solution1Si l’origine est en haut du ressort et l’axe vertical orienté vers le bas,la loi fondamentale de la dynamique donne :mz′′ = αz′ Kz L + mg ou mz′′ + αz′ + Kz = KL + mg.Cette équation équation différentielle a un second membre constant,et on vérifie que z0 = L + mgKest solution constante correspondantà l’équilibre.En portant l’origine en z0, i.e. en posant Z = z z0, on obtient :mZ ′′ + αZ ′ + KZ = 0 ou Z ′′ + 2λZ ′ + ω20Z = 0.2Dans tous les cas l’équation caractéristique est r 2 + 2λr + ω20 = 0aAvec λ = 0, ω0 = 1, r1 = iω0 et r2 = iω0La solution de l’équation est zt = Aeiω0t + Beiω0tAvec les conditions initiales : A + B = 10 et A B = 0 doncA = B = 5 donc zt = 5eiω0t + eiω0t = 10 cosω0tD. CransacAnalyse

Page 190 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesbAvec λ = ω0 = 1, r1 = 1 + i2cAvec λ = 1, ω0 =5, déterminer l’expression explicite dumouvement.Interprétation géométrique. Dans ce dernier cas, on observe uncomportement transitoire qui présente quelques oscillationspériodiques avant de retrouver un état stable.3Supposons toujours λ = 1, ω0 =5. On impose à présent àl’extrémité supérieure du ressort un mouvement verticale sinusoïdalede sorte que son ordonnée à l’instant t est f t = 5 cost.Déterminer une expression explicite du mouvement. Déterminer lecomportement asymptotique des solutions état stable.Vocabulaire. Le second membre d’une équation différentielleay ′′ + by ′ + cy = f t est également appelé signal d’entrée et lessolutions de l’équation définiront la réponse du système étudié. Onparle de régime libre si f est la fonction nulle, et de régime forcésinon. Dans le cas d’un oscillateur harmonique amorti en régimelibre, on parle de :régime apériodique quand λ ω0,régime critique quand λ = ω0,D. CransacAnalyse

Page 191 : GénéralitésEquations différentielles du premier ordreÉquation différentielle linéaire du second ordre à coefficients constantsGénéralitésRésolution de l’équation homogèneRésolution de l’équation avec second membreRésolution avec conditions initialesApplication aux oscillateurs linéairesrégime pseudo-périodique quand λ ω0.D. CransacAnalyse

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191