CM4 Integration de fonctions mesurables
Télécharger le CM4 Integration de fonctions mesurables en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Page 1 : Ingénieurs 1ère année : Mathématiques appliquéesMesure et intégrationCM4 – Intégration de fonctions mesurablesNisrine FORTIN CAMDAVANT
Page 2 : 1Intégration de fonctions mesurables réelles2Espaces Lp et Lp3Normes sur Lp p 1, +4Espaces L
Page 3 : Intégration de fonctions réellesmesurablesOn note LΩ, T l’ensemble des fonctions réelles mesurables C’est un espacevectorielLΩ, T = f : Ω→R, fest T , B R -mesurables.
Page 4 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LIntégrale de Lebesgue d’une fonction réelle mesurableOn note f + = supf , 0 et f = supf , 0.Une fonction µ-intégrableUne fonction f de Ωdans R est dite µ-intégrable si⇝f est T , BR-mesurable et⇝Zf +dµ +etZf dµ +.Intégrale d’une fonction réelle mesurableSi f est µ-intégrable. On appelle intégrale de f , notéeZfdµ ouZΩfdµ ouZΩf xdµx le nombreZΩf +dµ ZΩf dµ.On note L1RΩ, T , µ ou en abrégé L1 l’ensemble des fonctions µ-intégrables.4/21
Page 5 : Propriétés de l’intégrale de fonctions réelles
Page 6 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces L1Si f LΩ, T , on a l’équivalence suivantef L1Ω, T , µ ⇐⇒Zf dµ +.2Si f L1Ω, T , µ, alorsZfdµ Zf dµ.3Soient f LΩ, T et g L1Ω, T , µ. Si f g µ-p.p alorsf L1Ω, T , µ etZ f dµ Z g dµ.4Soit f LΩ, T . Il existe une suite φnnN dans EΩ, T quiconverge simplement vers f sur Ω. Si de plus, f est bornée, alorsφnnN converge uniformément vers f sur Ω.Propriétés.::::::::::::Démonstration. Voir Notes de cours.6/21
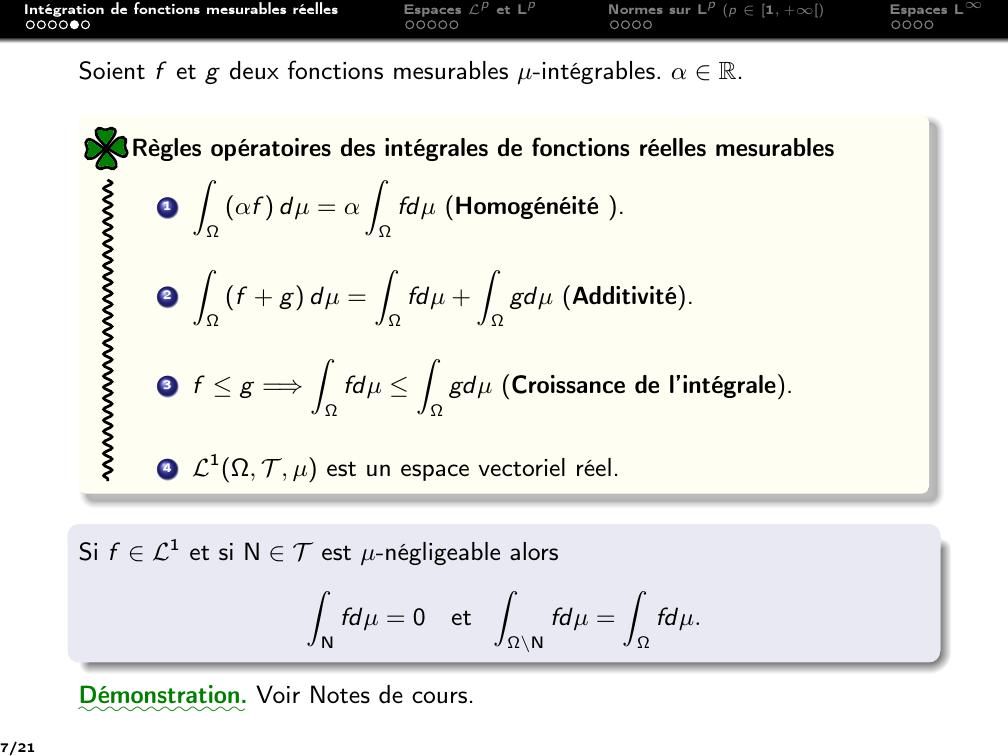
Page 7 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LSoient f et g deux fonctions mesurables µ-intégrables. α R.1ZΩαf dµ = αZΩfdµ Homogénéité .2ZΩf + g dµ =ZΩfdµ +ZΩgdµ Additivité.3f g =⇒ZΩfdµ ZΩgdµ Croissance de l’intégrale.4L1Ω, T , µ est un espace vectoriel réel.Règles opératoires des intégrales de fonctions réelles mesurablesSi f L1 et si N T est µ-négligeable alorsZNfdµ = 0etZΩ\Nfdµ =ZΩfdµ.::::::::::::Démonstration. Voir Notes de cours.7/21
Page 8 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LThéorème de la convergence dominéeThéorème ♣♣Soient fnnN une suite de fonctions de LΩ, T et g L1Ω, T , µ. Onsuppose quefnnN converge vers f µ-p.pPour tout n N, fn g.Alorsf L1Ω, T , µlimn→+Zfndµ =Zfdµ8/21
Page 9 : Espaces Lp
Page 10 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LSoit p 1, +. On dit que f est est de puissance pième-intégrable, et on notef Lp Ω, T , µ, si f est mesurable et f p est µ-intégrable.f Lp Ω, T , µ ⇐⇒f L Ω, T etZΩf p dµ +.1La fonction f p désigne la fonction x 7→f xp ce n’est pas lacomposée.2Pour p = 1, on obtient les fonctions µ-intégrables.Pour p = 2, on obtient les fonctions de carré intégrables.3Si f L Ω, T alors f p L Ω, T .L’espace Lp Ω, T , µ est un espace vectoriel.10/21
Page 11 : Espace Lp⇝On note N = f LΩ, T ,f = 0 µ -p.p .⇝Pour f LΩ, T et g LΩ, T , f g N ⇔f = g µ p.p.N est un espace vectoriel réel et pour tout p 1, +, N Lp.Notation
Page 12 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LL’espace LpΩ, T , µ ou en abrégé Lp est l’espace vectoriel quotient deLpΩ, T , µ par N. C’est l’ensemble des classes d’équivalence d’éléments de Lppar la relation f = g µ p.p.Pour une fonction f Lp, on définit la classe d’équivalence de la fonction f paref Lp Ω, T , µ telle queef Lp Ω, T , µ ⇐⇒ef = g Lp Ω, T , µtel quef g N .Bien que ses éléments soient des classes d’équivalence des fonctions. Ona l’habitude de dire qu’un élément de LpΩ, T , µ est une fonction, bienque strictement il s’agisse d’une classe de fonctions.RemarqueSi N = f0 alors Lp = Lp.S’il existe dans Ω, T , µ un plus gros au sens de l’inclusion ensembleµ-négligeable N, le passage au quotient sera alors inutile.12/21
Page 13 : Normes sur Lp p 1, +
Page 14 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LNotations1Pour f LΩ, T et p 1, +, on noteNpf =Zf xp µ dx 1p.⇝Nppf =Zf xp µ dx .2 Pour ef Lp et p 1, +, on noteef p = Npf .RemarqueSi f LΩ, T alorsf Lp ⇔Npf +.14/21
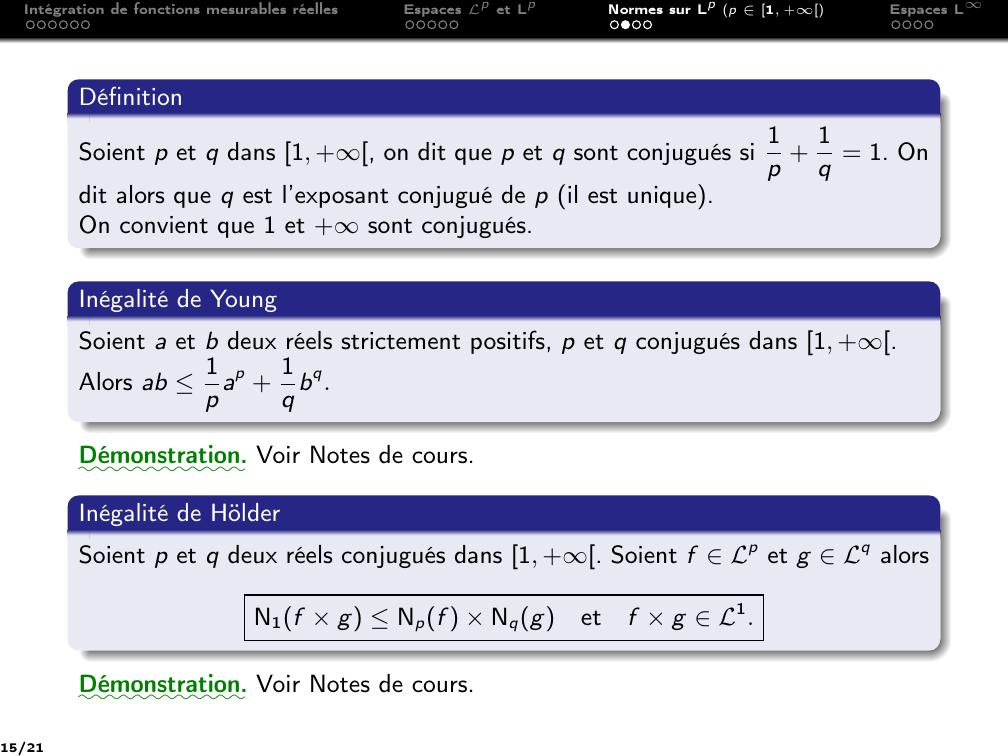
Page 15 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LDéfinitionSoient p et q dans 1, +, on dit que p et q sont conjugués si 1p + 1q = 1. Ondit alors que q est l’exposant conjugué de p il est unique.On convient que 1 et +sont conjugués.Inégalité de YoungSoient a et b deux réels strictement positifs, p et q conjugués dans 1, +.Alors ab 1p ap + 1q bq.::::::::::::Démonstration. Voir Notes de cours.Inégalité de HölderSoient p et q deux réels conjugués dans 1, +. Soient f Lp et g Lq alorsN1f × g Npf × Nqgetf × g L1.::::::::::::Démonstration. Voir Notes de cours.15/21
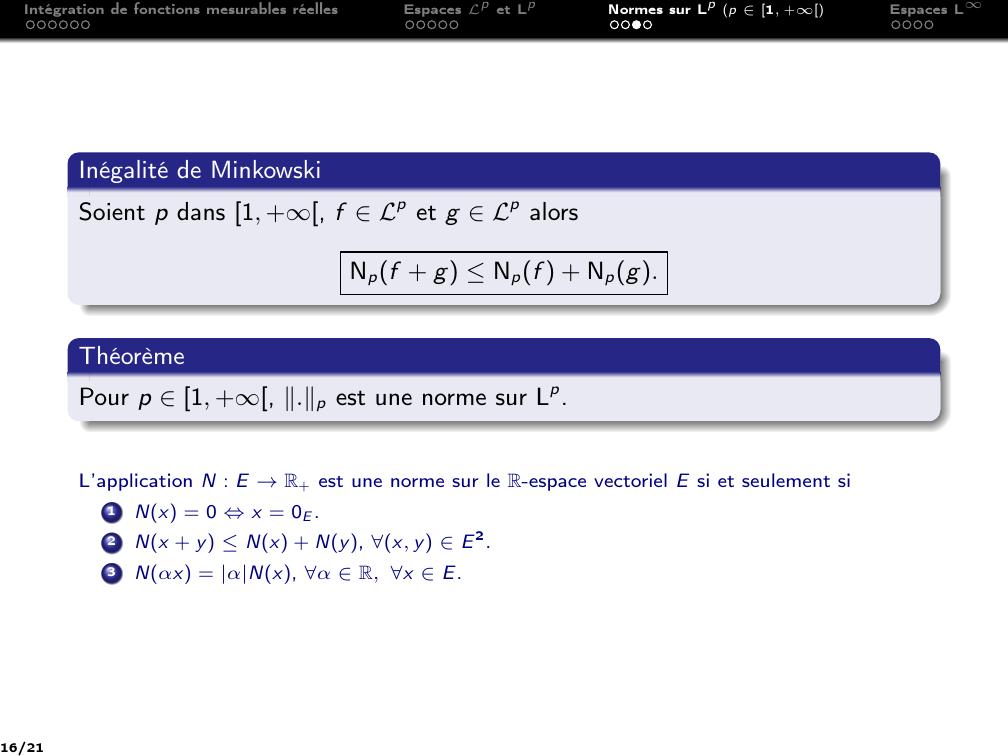
Page 16 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LInégalité de MinkowskiSoient p dans 1, +, f Lp et g Lp alorsNpf + g Npf + Npg.ThéorèmePour p 1, +, .p est une norme sur Lp.L’application N : E →R+ est une norme sur le R-espace vectoriel E si et seulement si1Nx = 0 ⇔x = 0E .2Nx + y Nx + Ny, x, y E 2.3Nαx = αNx, α R, x E.16/21
Page 17 : Espaces L
Page 18 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LFonction essentiellement bornéeDéfinitionUne fonction f de LΩ, T est dite essentiellement bornée s’il existe r 0 telque f r µ-p.p.L’ensemble x Ω,f x r est µ-négligeable.::::::Exemple::: Soit f : R →R la fonction définie pour tout x R parf x =xsix Q1six R \ QLa fonction f n’est pas bornée sur R, en revanche, elle est essentiellementbornée par la mesure de Lebesgue λ sur R car f 1 λ-p.p puisqueλ x R, f x 1 λ Q z =0.Donc λ x R, f x 1 = 0.18/21
Page 19 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LOn note LΩ, T , µ l’ensemble des fonctions essentiellement bornées deLΩ, T .LΩ, T , µ = f LΩ, T ,r 0 tel que f r µ p.p.Lorsqu’il n y a pas d’ambiguité, on notera L.Propriétés1 Lest un espace vectoriel réel.2N L.Définitions1 LΩ, T , µ est l’espace vectoriel quotient de LΩ, T , µ par N.2Si f LΩ, T ,Nf = inf r 0 / f r µ-p.p3Si ef Lalors ef = Nf .19/21
Page 20 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LConséquencesSi f LΩ, T ,f LΩ, T ⇔Nf +.Théorème1Si f est essentiellement bornée sur ΩalorsPour presque tout x Ω,f x Nf 2Si f est continue et essentiellement bornée sur ΩalorsPour tout x Ω,f x Nf Théorème1.est une norme sur L.2Inégalité de Hölder : si f L1 et g Lalors fg est µ-intégrable etN1f × g N1f × Ng.20/21
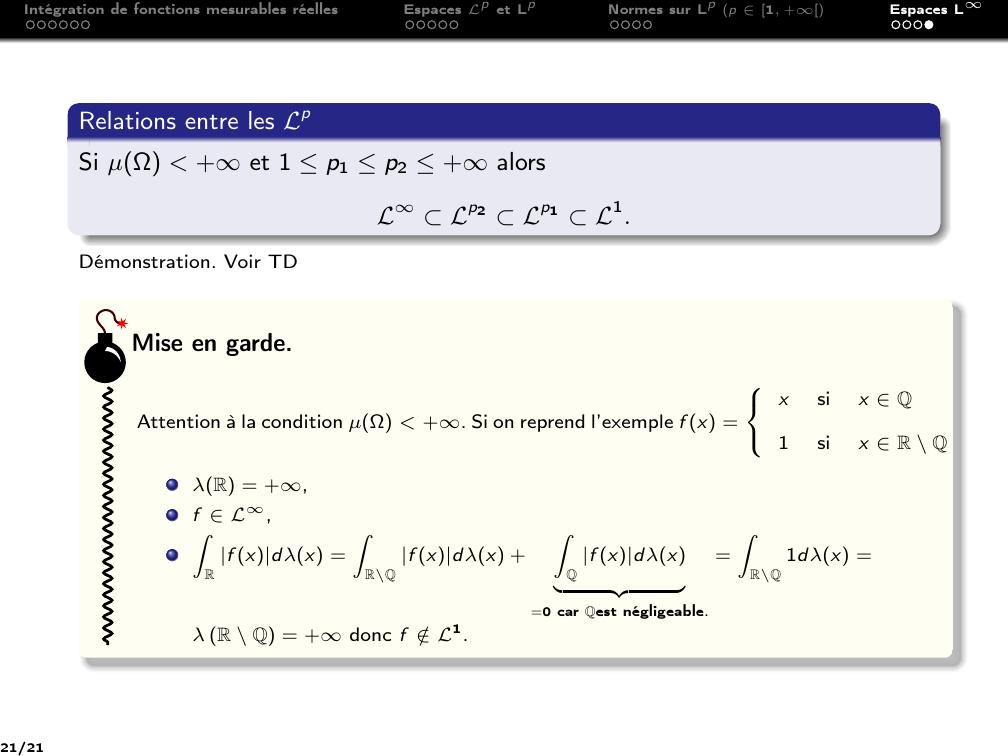
Page 21 : Intégration de fonctions mesurables réellesEspaces Lp et LpNormes sur Lp p 1, +Espaces LRelations entre les LpSi µΩ +et 1 p1 p2 +alorsLLp2 Lp1 L1.Démonstration. Voir TDAttention à la condition µΩ +. Si on reprend l’exemple f x =xsix Q1six R \ QλR = +,f L,ZRf xdλx =ZR\Qf xdλx +ZQf xdλxz=0 car Qest négligeable.=ZR\Q1dλx =λ R \ Q = +donc f /L1.Mise en garde.21/21
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21