CM4 Quali Quali
Télécharger le CM4 Quali Quali en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11
Page 1 : Analyse bivariée qualitatif-qualitatifData explorationStatistiques descriptives bivariéesObserver simultanément des individus d'une population sur deux caractèresMesurer un lien éventuel entre deux caractères en utilisant un résumé chiffré qui traduit l'importance de ce lienQualifier ce lien : –en cherchant une relation numérique approchée entre deux caractères quantitatifs–en cherchant des correspondances entre les modalités de deux caractères qualitatifs• qualitatif ×qualitatif2 types de variables 3 types de croisements : • qualitatif ×quantitatif• quantitatif ×quantitatif
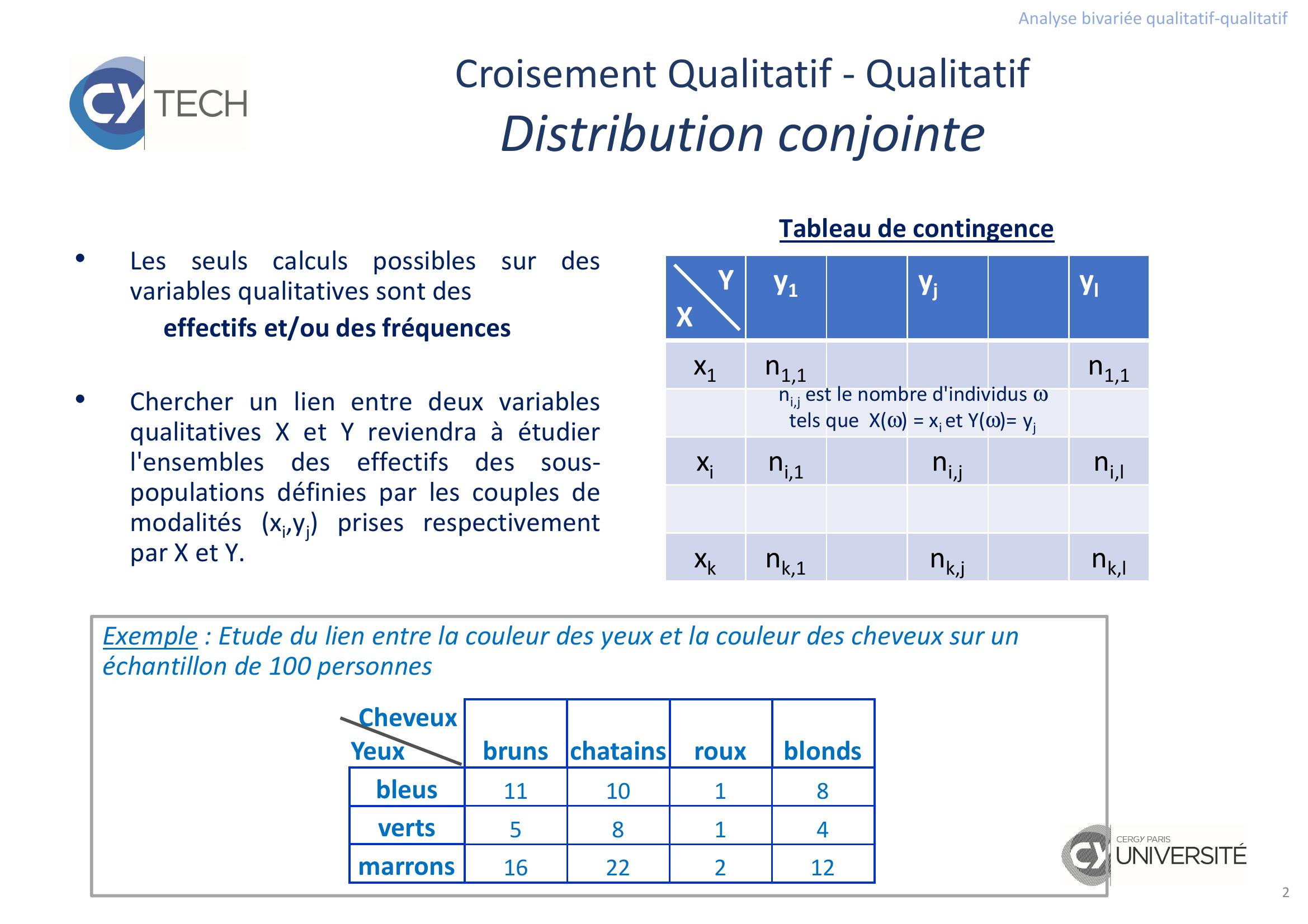
Page 2 : Analyse bivariée qualitatif-qualitatif2Croisement Qualitatif - QualitatifDistribution conjointe•Lesseulscalculspossiblessurdesvariables qualitatives sont deseffectifs et/ou des fréquences•Chercher un lien entre deux variablesqualitatives X et Y reviendra à étudierl'ensemblesdeseffectifsdessous-populations définies par les couples demodalités xi,yj prises respectivementpar X et Y.YXy1yjylx1n1,1n1,1xini,1ni,jni,lxknk,1nk,jnk,lTableau de contingenceni,j est le nombre d'individus ωtels que Xω = xi et Yω= yjExemple : Etude du lien entre la couleur des yeux et la couleur des cheveux sur un échantillon de 100 personnesCheveuxYeuxbruns chatainsrouxblondsbleus111018verts5814marrons1622212
Page 3 : Analyse bivariée qualitatif-qualitatif3Croisement Qualitatif - QualitatifDistribution marginaley1yjylx1n1,1n1,ln1,.xini,1ni,jni,lni,.xknk,1nk,jnk,lnk,.n.,1n.,jn.,lnEffectifs marginaux==l1jj,i,.inn==k1ij,ij.,nn=======k1il1jj,ik1i,.i.l1jj.,nnnnEffectif totalpour X:pour Y:CheveuxYeuxbrunschatainsrouxblondsbleus11101830verts581418marrons1622212523240424100Exemple : Etude du lien entre la couleur des yeux et la couleur des cheveux Comparaison des effectifs non pertinente
Page 4 : Analyse bivariée qualitatif-qualitatif4Croisement Qualitatif - QualitatifDistribution marginaleDes effectifs ne sont pas directement comparables tandis que des fréquences sont toujours comparablesy1yjylx1f1,1f1,lf1,.xifi,1fi,jfi,lfi,.xkfk,1fk,jfk,lfk,.f.,1f.,jf.,l1==l1jj,i,.iff==k1ij,ij.,ff=======k1il1jj,ik1i,.i.l1jj.,fff1fi,j est la proportion d'individus ω tels que Xω = xi et Yω= yjFréquences marginalespour X :pour Y:CheveuxYeuxbrunschatainsrouxblondsbleus0,110,10,010,080,3verts0,050,080,010,040,18marrons0,160,220,020,120,520,320,40,040,241Exemple : Etude du lien entre la couleur des yeux et la couleur des cheveux
Page 5 : Analyse bivariée qualitatif-qualitatif5Croisement Qualitatif - QualitatifProfils ligne et colonneProfil ligne : répartition en fréquence de lavariable Y dans une sous-population définiepar une modalité de la variable XProfil colonne : répartition en fréquence dela variable X dans une sous-populationdéfinie par une modalité de YProfils lignesy1yjylx1f1/1fl/1f1,.xif1/ifj/ifl/ifi,.xkf1/kfj/kfl/kfk,.f.,1f.,jf.,lcomparable avec f.jLa ligne des fréquences marginales de Y est appelée profil moyen.Pour détecter un lien entre les variables X et Y, on compare leurs profils ligne et colonne avec les profils moyens,.ij,ii/jnnf=j.,j,ij/innf=comparable avec fi.Nombres des observations qui ont la modalité i sashant qu'ils ont la modalité j
Page 6 : Analyse bivariée qualitatif-qualitatif6Croisement Qualitatif - QualitatifProfils ligne et colonnebruns chatains roux blondsbleus0,370,330,030,271,00verts0,280,440,060,221,00marrons 0,310,420,040,231,000,320,40,040,24Profils lignesPour les profils lignes, on note que la répartition des couleurs de cheveux est lamême quelle que soit la couleur des yeux et est la même que celle de la populationtotale..Il ne semble pas y avoir de lien entre les modalités de ces deux caractères• 28 des personnes ayant les yeux verts ont les cheveux bruns• 32 des personnes ont les cheveux brunsFreq. marginales372831334442364272223020406080100bleusvertsmarronsblondsrouxchatainsbruns28 ont les cheveux bruns sachant qu'ils ont les yeux verts.
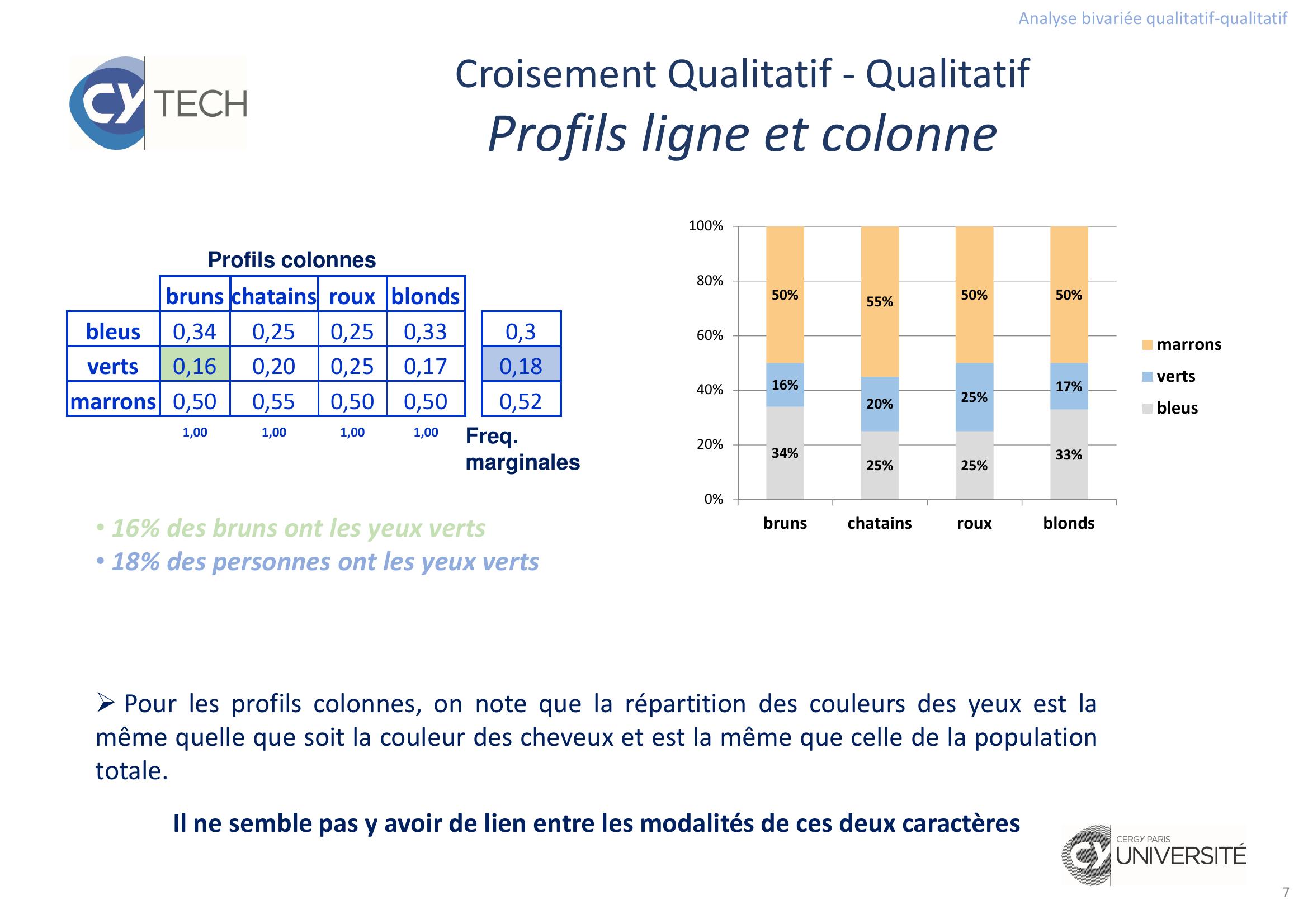
Page 7 : Analyse bivariée qualitatif-qualitatif7Croisement Qualitatif - QualitatifProfils ligne et colonnePour les profils colonnes, on note que la répartition des couleurs des yeux est lamême quelle que soit la couleur des cheveux et est la même que celle de la populationtotale.Il ne semble pas y avoir de lien entre les modalités de ces deux caractères• 16 des bruns ont les yeux verts• 18 des personnes ont les yeux vertsFreq. marginalesbruns chatains roux blondsbleus0,340,250,250,330,3verts0,160,200,250,170,18marrons 0,500,550,500,500,521,001,001,001,00Profils colonnes342525331620251750555050020406080100brunschatainsrouxblondsmarronsvertsbleus
Page 8 : Analyse bivariée qualitatif-qualitatif8Croisement Qualitatif - QualitatifProfils ligne et colonneProfils lignesDans cet exemple, la répartition de la couleur des cheveux suivant la couleur des yeux n’est pas la même que celle de la population totale.Il semble qu’il y ait un lien entre les modalités de ces deux variablesbruns chatainsrouxblondsbleus8101827verts3102419marrons2120112543240424100 Exemple précédent modifié29163932375337404112430202224020406080100bleusvertsmarronsTotalblondsrouxchatainsbruns25252533279255017196650255054020406080100brunschatainsrouxblondsTotalmarronsvertsbleusProfils colonnes
Page 9 : Analyse bivariée qualitatif-qualitatif9Croisement Qualitatif - QualitatifIndépendance des variablesX et Y ne sont pas liés ⇔les profils lignes sont égaux ⇔les profils colonnes sont égaux⇔y1yjylx1f1,.×f.,1f1,.×f.,jf1,.×f.,lf1,.xifi,.×f.,1fi,.×f.,jfi,.×f.,lfi,.xkfk,.×f.,1fk,.×f.,jfk,.×f.,lfk,.f.,1f.,jf.,l1j.,,.ij,ifff×=l,...,1j,k,...,1iy1yjylx1f1,1f1,jf1,lf1,.xifi,1fi,jfi,lfi,.xkfk,1fk,jfk,lfk,.f.,1f.,jf.,l1Tableau de contingence théorique si X et Y sont indépendantsTableau de contingence observéComparaison des tableauxRappel, Si deux événements A et B sont indépendants alors PAB=PA×PB
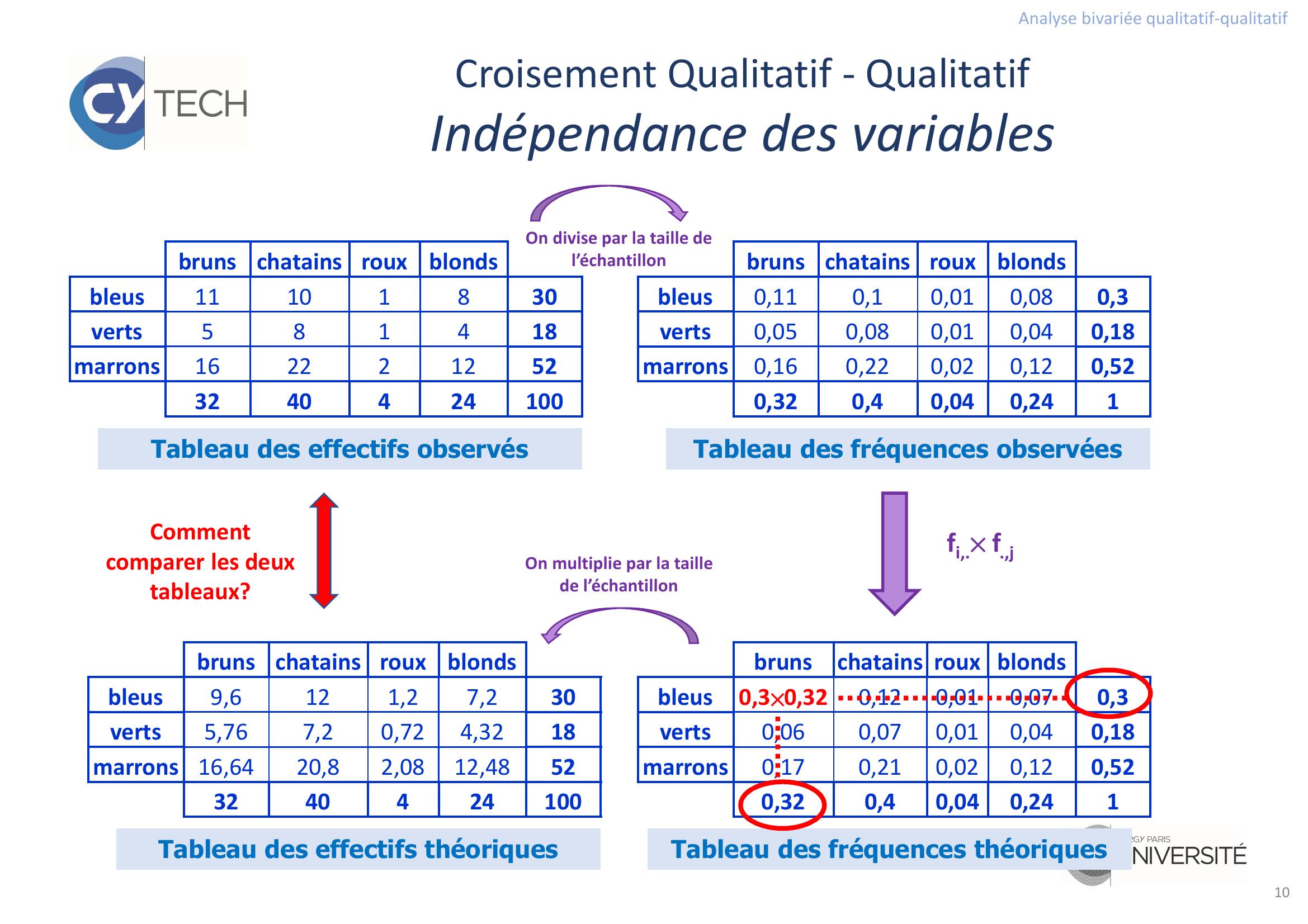
Page 10 : Analyse bivariée qualitatif-qualitatif10Croisement Qualitatif - QualitatifIndépendance des variablesTableau des effectifs observésbrunschatains rouxblondsbleus11101830verts581418marrons1622212523240424100bruns chatains rouxblondsbleus0,110,10,010,080,3verts0,050,080,010,040,18marrons0,160,220,020,120,520,320,40,040,241Tableau des fréquences observéesTableau des fréquences théoriquesTableau des effectifs théoriquesbrunschatains rouxblondsbleus9,6121,27,230verts5,767,20,724,3218marrons 16,6420,82,0812,48523240424100brunschatains roux blondsbleus0,3×0,320,120,010,070,3verts0,060,070,010,040,18marrons0,170,210,020,120,520,320,40,040,241fi,.× f.,jOn divise par la taille de l’échantillonOn multiplie par la taille de l’échantillonComment comparer les deux tableaux?
Page 11 : Analyse bivariée qualitatif-qualitatif11Croisement Qualitatif - QualitatifIndépendance et chi-deuxComment mesurer le lien de dépendance entre les X et Y ? Comment mesurer la« distance » entre les deux tableaux? Mr Pearson a créée la distance du χ² :où ti,j = n×fi,.×f.,j est l'effectifthéorique de la case i,j.===χk1il1jj,i2j,ij,i2ttn1.La distance du χ2 est d'autant plus grande que X et Y sont liées entre eux.2.Malheureusement la distance du χ2dépend aussi :•du nombre de modalités de X et Y•du nombre d'individus.3.Pour savoir si la distance χ2 est suffisamment grande pour décider que les variables sont liées, on la compare à un seuil donné dans le tableau ci-dessous cf. ing2où les degrés de liberté : d.d.l. = s-1k-1 avec s et k les nombres de modalités des deux variables.•distance du χ2 Seuil dépendance•distance du χ2 Seuil indépendance4. La comparaison est efficace si les effectifs théoriques sont 5, sinon on regroupe des modalitésSeuil3,845,997,829,4911,0712,5914,0715,5116,92d.d.l.123456789